摘要: 远离平衡态的开放复杂系统遍及自然、社会和技术领域, 是复杂性科学的主要研究对象. 通过与外界的能量和物质交换, 复杂系统通过自组织形成了多种多样的内在结构、秩序和规律, 对认识和预测复杂系统提出了艰巨的挑战. 随着实验技术的提高和科技的进步, 反映和体现各种复杂系统机理的数据呈指数增长, 为研究复杂系统提供了新的机遇. 通过系统行为表象数据, 揭示复杂系统结构和动力学属于物理领域的反问题, 是认识复杂系统的基础, 是预测系统状态演化的前提, 对于实现系统状态的调控必不可少. 然而, 复杂系统的多样性和复杂性给解决这一反问题造成了极大的困难. 因此, 需要开阔思路, 借助多学科的交叉与融合, 充分挖掘数据中隐藏的知识和深层次机理. 本文综述了近年来复杂系统, 特别是复杂结构重构和推断方面的研究成果, 希望能够启发复杂系统反问题方面的创新. 同时, 也希望呼吁各领域****都能关注复杂系统反问题, 推动自然、社会、经济、生物、科技领域的交叉与融合, 解决大家共同面对的科学问题.
关键词: 统计物理 /
复杂系统 /
反问题 /
网络重构 English Abstract Complex system reconstruction Zhang Hai-Feng 1 ,Wang Wen-Xu 2 1.School of Mathematical Science, Anhui University, Hefei 230601, China Received Date: 02 January 2020Accepted Date: 19 March 2020Published Online: 20 April 2020Abstract: Open complex systems far from equilibrium widely exist in the nature and the fields of society and technology, which are the main research objects of complexity science. Through the exchange of energy and material with the outside world, complex systems can form a variety of internal structures, orders and laws by self-organization behaviors, which poses an arduous challenge to the understanding and predicting complex systems. With the improvement of experimental technology and the progress of science and technology, the data reflecting the mechanism of various complex systems are increasing exponentially, thereby providing new opportunities for studying complex systems. Revealing the structures and dynamics of complex systems from the measured data is an inverse problem in the field of physics, which is the premise of understanding complex systems, predicting the evolution of system state, and regulating system state. However, it is very difficult to solve this inverse problem due to the diversity and complexity of complex system. Therefore, we need to fully mine the hidden knowledge and deep mechanism in the data with the help of interdisciplinary integration. In this paper we briefly review the research results of complex system in recent years, especially the reconstruction of complex network structures, hoping to inspire the innovation to the inverse problem of complex systems. Meanwhile, we hope that researchers in different fields can pay much attention to the inverse problems of complex systems, promote the cross and integration of nature, society, economy, biology and technology, and solve the scientific problems that we are facing.Keywords: statistical physics /complex systems /inverse problem /network reconstruction 全文HTML --> --> --> 1.引 言 小到微生物群落, 大到宇宙星系, 现实世界中的大部分系统属于远离平衡态的开放复杂系统. 这些系统通过与外界进行物质与能量的交换, 对抗内部熵的增加, 从而形成耗散结构和自组织现象, 这是复杂系统自发产生秩序和复杂性的根源[1 ] . 与近平衡态不同, 在远离平衡态的系统中, 由于存在涨落决定的分叉和相变, 系统中的规律由特定的作用机制决定, 因此, 没有统一的定律, 这是统计物理与复杂系统领域所面对的最大挑战[1 ] . BZ化学振荡反应是典型的远离平衡态的物质获得新特性的例子, 表现出了远离平衡态条件下的长程相关性[2 ] . 生物系统也是一大类远离平衡态的稳定系统. 通过从外界吸收能量和物质, 生物系统维持其内部各种各样的非平衡状态和有序结构[3 ] , 并且受到自然选择等竞争的作用, 形成了地球上极大的生物多样性和复杂的生态环境[4 ,5 ] .[6 ] 的发现和元胞自动机[7 ] 的出现, 从根本上改变了人们对复杂性的认识: 确定性的低维非线性系统也可以产生不可预测的复杂性[8 ] . 复杂可以源于简单和复杂性的涌现导致传统还原论的局限性[9 ] , 迫切需要统计物理发展适用于复杂系统的理论与方法. 美国圣塔菲(Santa Fe)研究所在这一历史背景下应运而生, 旨在通过多学科的交叉与融合, 研究各种复杂系统的内在机理和演化规律等跨学科问题. 此后, 由于计算机技术的发展和大量数据的产生, 关于复杂系统的研究成果呈指数律增长[10 ,11 ] .[12 ] . 人的复杂行为源于人脑的复杂性和高级认知功能. 但是, 人并不具有经济学中的完美理性. 人的决策受到各种认知偏见、刻板印象和群体规范的影响. 对人类经济决策行为的深入研究催生了行为经济学[13 ] , 旨在通过实验和数据分析发现人类有限理性经济行为的内在动机和成因. 对于复杂相互作用结构的研究催生了复杂网络这一研究方向[14 ] . 相关研究揭示了复杂系统共有的结构特征, 比如小世界效应、层次结构、社团结构、异质性和多样性等[15 ] . 研究复杂结构如何影响其上的动力学对于理解同步、传播、级联失效、合作、协同、集群等群体行为有重要科学价值[16 ,17 ] ; 同时, 网络社团检测方法、网络控制方法、结构推断和相变等方法对传统方法进行了拓展[18 ,19 ] . 与此同时, 研究人员逐渐认识到网络结构本身作用的局限性. 事实上, 复杂系统的动力学和群体行为由个体、相互作用模式、相互作用结构和环境共同决定. 复杂系统研究需要与相关学科紧密结合, 才能真正打破学科壁垒和促进学科的交叉与融合, 为深入理解社会、经济、金融和生物复杂性提供有效的理论工具和方法.图1(a) 和图1(b) )去推断节点之间的连边关系[20 -23 ] (如图1(c) ). 一个复杂的系统, 其个体的动力学行为不仅仅只取决于个体本身, 还依赖于和其他个体之间的交互, 这些交互就构成了系统的结构, 个体之间的交互形成了网络. 因此, 网络重构问题本质上属于数据驱动的系统辨识范畴[24 ] , 是对哪些个体之间存在交互的辨识. 但鉴于网络结构的复杂性、网络节点动力学的非线性以及结构的稀疏性等性质[25 ] , 一方面需要我们发展系统辨识中的一些经典方法, 如极大似然估计的方法, 另一方面, 需要根据问题的特有属性提出一些新的方法, 如根据网络规模大而稀疏的特点, 我们提出了基于压缩感知的推断方法等. 以下将对近些年在网络重构方面取得的研究进展进行部分总结与展望.图 1 网络重构示意图 (a)通过离散的数据; (b)连续的数据; (c)推断网络结构Figure1. Illustration of network reconstruction: (a) By using the discrete data; (b) the continuous data; (c) reconstruct network.2.基于压缩感知的网络重构方法 22.1.压缩感知理论 2.1.压缩感知理论 压缩感知理论是在信号稀疏的情况下, 通过少量的数据采集可以重构原始信号[26 ] . 给定一个测量矩阵${{A}} \in {\mathbb{R}^{M \times N}}$ , 以及观测值${{Y}} \in {\mathbb{R}^M}$ , 可以通过下面公式来重构信号${{X}} \in {\mathbb{R}^N}$ :X $M \ll N$ )即可重构X [26 -30 ] 准确得到稀疏信号X L 1 范数下的结果是等价于最小L 0 范数结果的, 所以有3 )式是一个凸优化问题, 已有很成熟的算法作为参考[27 -30 ] . 因为网络数据具有天然的稀疏性, 所以可以通过压缩感知的方法对其进行网络重构. 如图2 所示, 就是利用压缩感知方法重构出Karate网络的第4个节点的邻居, 可以看到求出的X 图 2 基于压缩感知方法重构Karate网络中4号节点的邻居(重构方法见2.4 节)Figure2. Reconstructing of node 4 in the Karate network based on compressive sensing framework (the reconstruction method is introduced in Subsec. 2.4 ).2.2.基于耦合振子系统的网络重构 -->2.2.基于耦合振子系统的网络重构 由于描述物理网络中的动力学函数未知, 可以应用幂级数来表示. 又因为级数的高阶项比较多, 因此估计其系数非常困难. 考虑到这些系数非零项很少, 比较稀疏, 而且网络的结构也是稀疏的. 所以可以通过少量的观察数据应用压缩感知的方法重构网络[31 ] .${{{x}}_{{i}}} \in {\mathbb{R}^D}$ 是节点的状态量, ${{{f}}_i}\left( {{{{x}}_i}} \right)$ 为节点自身动力学, 函数形式未知, ${{{C}}_{ij}}$ 是节点i 与j 的耦合矩阵:$C_{ij}^{k, l}$ 表示i 节点状态的第k 个分量与j 节点状态的第l 个分量的耦合. 如果矩阵${{{C}}_{ij}}$ 中有一个非零值, 则i 节点与k 节点有连边, 如果全为零, 则没有连边. 因此可以通过时间序列推断${{{C}}_{ij}}$ 即可重构网络. 令k 个分量可以用n 以下的幂级数的形式表示:${\left( {{{{x}}_{{i}}}} \right)_k}$ 表示第i 个体状态的第k 个分量, 可以通过数据观察得到. ${\left[ {{{\left( {{\alpha _i}} \right)}_k}} \right]_{{l_1}, \cdots {l_D}}}$ 为幂级数的系数, 是未知量. 可以看出(7 )式关于未知量是线性的. 给定一个时刻${t_m}$ , 根据(4 )式与(7 )式有${{\dot {{x}}}_i}\left( {{t_m}} \right)$ 为已知量; ${{{\varGamma }}_i}\left( {{{{x}}_i}\left( {{t_m}} \right)} \right)$ 中只有${\left[ {{{\left( {{\alpha _i}} \right)}_k}} \right]_{{l_1}, \cdots, {l_D}}}$ 为未知量, 且是稀疏的, 线性的; $\displaystyle\sum\nolimits_{j = 1, ~j \ne i}^N {{{{C}}_{ij}} \cdot {{{x}}_j}\left( {{t_m}} \right)} $ 中只有$C_{ij}^{k, l}$ 是未知量, 也是稀疏的, 线性的. 因此(8 )式是关于未知量${\left[ {{{\left( {{\alpha _i}} \right)}_k}} \right]_{{l_1}, \cdots, {l_D}}}$ 与$C_{ij}^{k, l}$ 的D 个线性方程. 可以测量少量的时间序列(M 个), 构造一个类似(1 )式的线性方程组:X ${\left[ {{{\left( {{\alpha _i}} \right)}_k}} \right]_{{l_1}, \cdots, {l_D}}}$ 与$C_{ij}^{k, l}$ , 是稀疏的. 应用压缩感知方法求解, 其中$C_{ij}^{k, l}$ 可以用来揭示网络的结构[31 ,32 ] .2.3.基于演化博弈系统的网络重构 -->2.3.基于演化博弈系统的网络重构 在生物、社会科学和经济学中的许多复杂动力系统都可以用演化博弈建立数学模型[33 ] . 在演化博弈试验中, 每一个人可以处于两种状态: 合作与背叛, 分别可以表示为${{S}}\left( C \right) = {\left[ {1, 0} \right]^{\rm{T}}}$ 与${{S}}\left( D \right) = {\left[ {0, 1} \right]^{\rm{T}}}$ , 博弈中双方收益是由博弈双方的策略, 以及收益矩阵P [34 ] 中${{P}} = \begin{pmatrix} 1& 0 \\ b & 0 \end{pmatrix} $ )决定. 所以第i 节点的收益为M 轮演化博弈实验, 收集每个人状态与收益, 即有M 个线性方程:${a_{ij}}$ 为未知量. 所以上述公式可以写成以下形式:${{{A}}_i} = {\left[ {{a_{i1}}, \cdots, {a_{i, i - 1}}, {a_{i, i + 1}}, \cdots, {a_{iN}}} \right]^{\rm{T}}}$ , ${{{G}}_i}$ 与${{{P}}_i}$ 已知. 应用压缩感知理论即可求解${{{A}}_i}$ , 从而揭示网络的结构[35 -37 ] , 该方法也可以推广到加权网络.2.4.基于二值动力学系统的网络重构 -->2.4.基于二值动力学系统的网络重构 二值动力学是复杂系统中常见的一种动力学形式[38 -41 ] , 如疾病传播动力学中的感染态与易感态、演化博弈中的背叛与合作、Ising动力学中的自旋向上和自旋向下等等. 对于疾病传播动力学, 可以应用SIS(susceptible-infected-susceptible)模型或CP (contact process)模型来模拟其传播过程. 文献[42 ]应用压缩感知的方法给出了详细的重构过程. 这里只简单介绍SIS模型的重构方法.i 节点处于易感态($S_t^i = 0$ ), 且它与一个感染态节点j 相连($S_t^j = 1$ ), 则会以${\lambda _i}$ 的概率被感染, 感染态节点j 会以${\delta _j}$ 的概率恢复成易感态. 因此t 时刻易感状态的节点i 被感染的概率$P_i^{01}\left( t \right)$ 可以表示为[42 ] 在时间序列中统计出$P_i^{01}\left( t \right)$ 以及$S_t^j$ 构造M 个线性方程, 类似${{{X}}_{{i}}}$ 与${{{Y}}_{{i}}}$ 已知. 应用压缩感知理论即可求解${{{A}}_i}$ , 从而揭示网络的结构[42 ] .i 由未激活变为激活态的概率与处于激活态邻居的个数有关, 对其线性化[43 ] :[43 ] , 在时间序列中统计出$P_i^{01}\left( t \right)$ 以及$S_t^j$ 构造M 个线性方程, 可以写成(15 )式的形式, 进而通过压缩感知进行求解, 也可以通过Lasso进行求解[43 ] .[44 ] 利用压缩感知可以重构非线性动力学系统; Su等[45 ] 利用压缩感知重构具有空间地理信息的网络, 不仅可以重构网络结构还可以得到每个节点所在的地理位置; Su等[46 ] 还通过外部事件序列, 利用压缩感知探测隐藏节点; Tang等[47 ] 通过交通流量数据, 利用压缩感知对交通网络进行重构; Chen和Lai[48 ] 通过玻尔兹曼机对动力学进行估计, 然后应用压缩感知方法重构网络; 最近压缩感知方法还被推广到了多层网络[49 -51 ] 、加权网络的重构[52 ] 等.3.重构非线性动力学系统网络 对于连续的非线性动力学系统, 一般情况下, N 个节点的网络动力学可以由以下常微分方程描述:${{{x}}_{{i}}}\left( t \right) = {\left[ {{x_{i1}}\left( t \right), {x_{i2}}\left( t \right), \cdots, {x_{iD}}\left( t \right)} \right]^{\rm{T}}} \in {\mathbb{R}^D}$ 是节点的状态量, ${{{f}}_{{i}}}$ 表示节点自身动力学, ${{{g}}_{ij}}$ 表示节点之间的耦合函数, ${{{I}}_i}\left( t \right)$ 表示外部驱动信号, ${{{\eta }}_i}\left( t \right)$ 表示外部噪音. ${J_{ij}}$ 表示耦合矩阵, 反映网络的拓扑结构, 简单情况下为网络的邻接矩阵${{A}}$ .3.1.直接方法 3.1.直接方法 给定网络动力学:[53 ] . 第i 个体的第d 维动力学公式可以表示为M 个时刻, 将会构造M 个线性方程:${X_{i, m}} = g_{ij, m}^{\left( d \right)}$ , ${Y_{i, m}} = \dot x_{i, m}^{\left( d \right)} - f_{i, m}^{\left( d \right)}$ . 求解${{{J}}_{{i}}} = $ $ {\left[ {{J_{i1}}, {J_{i2}}, \cdots, {J_{iN}}} \right]^{\rm{T}}}$ , 可以得到关于i 个体的连接情况. 对于(21 )式的求解, 文献[53 ]中采用了最小化误差的方法求解. 该方法可以解决各种动力学系统, 当网络比较稀疏时, 可以应用L 1 范数进行约束, 只需观察很少的时间序列即可重构整个网络[54 ] .3.2.自适应同步方法 -->3.2.自适应同步方法 在动力学网络中的局部动力学与耦合函数已知的情况下, 可以根据原系统复制一个辅助系统, 然后通过不停迭代辅助系统中的网络结构使得复制系统与原系统同步. 则得到的辅助系统中的网络结构就是我们要重构的原始系统的结构[55 ] . 考虑一个系统(以一维为例):${f_i}$ 与${g_j}$ 满足利普希茨连续条件. 给原始系统一个副本:${y_i}$ 表示复制系统的状态, ${K_{ij}}$ 表示复制系统的耦合强度, ${I_i}$ 为可控制信号. 根据原系统和复制系统的状态, 可以通过不停迭代${I_i}$ 与${K_{ij}}$ 使得原系统与复制系统同步. 定义同步误差为${I_i} = - \alpha {e_i}$ . 在这里${\gamma _{ij}} > 0$ , $\alpha > 0$ . 文献[55 ]中证明了当$\alpha $ 足够大的情况下, 两个系统的误差随着时间减少, 最终会收敛到同步状态. 此时复制系统的拓扑结构与原系统的拓扑结构相同, 即${K_{ij}} \simeq {J_{ij}}$ , 以此重构网络的局部结构.[56 ] 把该方法推广到了加权网络; Liu等[57 ] 将这一方法推广到了含有耦合延迟的非自治复杂网络的拓扑识别; 更进一步, Wu等[58 ] 利用该方法研究了含时变耦合延迟和受随机扰动影响下的网络重构; Zhao等[59 ] 把这一方法推广到了多层网络, 等等[60 -64 ] .3.3.驱动-响应实验 -->3.3.驱动-响应实验 上述方法都需要在已知节点的局部动力学以及耦合函数情况下重构网络结构, 下面将介绍一些在节点的局部动力学和耦合函数未知情况下的网络重构方法.图3 所示). 因此可以通过多次不同的驱动-响应实验, 以此重构整个网络结构.图 3 驱动-响应实验示意图. 对稳态系统施加(稳态是一个稳定点(a), 或者一个周期轨道(b))一个持续驱动I , 系统达到另外一个稳态. 两个稳态的差异v 包含了网络的拓扑结构Figure3. Driving-response experiments. System is shifted from one stable state (the stable state is a fixed point (a), or a periodical trajectory (b)) to another position by input a driving signal I . The difference of the trajectories contains information about the topology.[65 -67 ] , 其动力学一般可以应用非线性动力系统描述. 当系统趋于稳态时, 这种系统可以近似为一个一阶线性微分方程:${x_i}$ 表示第i 个RNA、蛋白质或代谢物的浓度; 和前面一样, ${\tilde J_{ij}}$ 反映网络的拓扑结构, ${I_i}\left( t \right)$ 表示外部的扰动. 当给定一个持续的微弱的扰动${I_i}\left( t \right) = {I_{i, m}}$ , 系统将趋向一个新的稳态$x_{j, m}^ * $ . 当对每个个体都进行M 次扰动实验, 会得到一个线性方程组:i 都可以构造类似以下方程组:${{\tilde {{J}}}_{{i}}} = {\left[ {{{\tilde J}_{i1}}, {{\tilde J}_{i2}}, \cdots, {{\tilde J}_{iN}}} \right]^{\rm{T}}}$ , 可以得到关于i 个体的连接情况.[68 ] . 网络动力学可以给定:${\phi _i}\left( t \right)$ 表示振荡器i 的相位, ${\omega _i}\left( t \right)$ 表示振荡器i 的频率; 和前面一样, ${J_{ij}}$ 反映网络的拓扑结构, ${I_{i, m}}$ 表示持续的外部扰动. 当外部没有驱动时, $m = 0$ , 此时${I_{i, 0}} = 0$ .${I_{i, m}}$ , 考虑稳态上面的锁相吸引子, 相位差可以表示为${I_{i, 0}}$ )的扰动(${I_{i, m}}$ )是微小的, 则会有$\left| {{\varDelta _{ij, m}} - {\varDelta _{ij, 0}}} \right| \ll 1$ .${I_{i, m}}$ , 集体的频率可以观察:${g_{ij}}$ 在${\varDelta _{ij, 0}}$ 处进行线性展开可以得到包含拓扑结构${J_{ij}}$ 的线性方程[68 ] , 当给定许多次扰动的情况下可以得到类似(28 )式的线性方程组, 求解即可推断网络的拓扑结构.[69 ,70 ] . 考虑一个动力学网络:$\theta $ 足够大, 且${f_i}$ 与${g_{ij}}$ 满足利普希茨连续条件时, 该系统会被驱动到一个稳定点: ${{{x}}_{{s}}} = \left[{x_{1, s}}, {x_{2, s}}, \cdots, \right.$ $\left.{x_{N, s}} \right]^{\rm{T}} $ , 它接近于${\hat{{x}}} = {\left[ {{{\hat x}_1}, {{\hat x}_2}, \cdots, {{\hat x}_N}} \right]^{\rm{T}}}$ . 即有k 与i 的关系, 取${\hat{{x}}} = {\left[ {0, \cdots, {{\hat x}_k}, \cdots, 0} \right]^{\rm{T}}}$ , 则${\hat x_k}$ 进行两次实验, 分别取${\hat x_{k, 1}}$ 与${\hat x_{k, 2}}$ , 然后两式取差有k , 对$\left| {\theta {s_{ik}}} \right|$ 进行排序处理即可得到k 的连接情况[69 ,70 ] .3.4.基于噪音的方法 -->3.4.基于噪音的方法 当一个动力学网络趋向同步时, 在没有外部扰动的情况下, 整个系统的每个个体状态一致, 它们之间有效的相互作用消失, 从而无法提取其中的结构信息. 但是, 噪声会导致去同步化, 可以在时间序列中包含个体之间潜在的交互信息[21 ] .[71 -74 ] . 考虑一个动力学网络:c 为耦合强度, ${{H}}$ 为耦合函数, ${\hat{{L}}} = {L_{ij}}$ 为拉普拉斯矩阵, 其定义为: 如果i 与j 相连, 且$i \ne j$ , 则${L_{ij}} = - 1$ , 否则${L_{ij}} = 0$ , ${L_{ii}}$ 为节点i 的度.${{\bar {{x}}}_{{i}}}$ 表示${{{x}}_{{i}}}$ 无噪音时候的状态, 假设会有一个微小的偏差${{{\xi }}_{{i}}}$ , 因此有${{{x}}_{{i}}} = {{\bar {{x}}}_{{i}}} + {{{\xi }}_{{i}}}$ . 对上述公式在${{\bar {{x}}}_{{i}}}$ 线性化处理, 有${{\xi}} = {\left[ {{\xi _1}, {\xi _2}, \cdots, {\xi _N}} \right]^{\rm{T}}}$ , ${{\eta}} = {\left[ {{\eta _1}, {\eta _2}, \cdots, {\eta _N}} \right]^{\rm{T}}}$ , $D{\hat {{F}}}\left( {{\bar {{x}}}} \right) = {\rm{diag}}[D{{\hat {{F}}}_1}\left( {{{{\bar {{x}}}}_1}} \right), D{{\hat {{F}}}_2}\left( {{{{\bar {{x}}}}_2}} \right), \cdots, D{{\hat {{F}}}_N}\left( {{{{\bar {{x}}}}_N}} \right)]$ , $D{{\hat {{F}}}_1}$ 为${{{f}}_{{i}}}$ 的雅可比矩阵, 同理可以定义$D{\hat{{H}}}\left( {{\bar {{x}}}} \right)$ , $ \otimes $ 表示点乘. 令${\hat {{A}}} = - \left[ {D{\hat {{F}}}\left( {{\bar {{x}}}} \right) - c{\hat{{L}}} \otimes D{\hat{{H}}}\left( {{\bar {{x}}}} \right)} \right]$ , $\hat C = \left\langle {{{\xi}} {{{\xi}} ^{\rm{T}}}} \right\rangle $ , 其中${\hat {{A}}}$ 中包含网络结构. 于是有${\hat {{D}}}$ 是噪音的协方差矩阵, 有$\left\langle {{{\eta}} {{{\xi}} ^{\rm{T}}}} \right\rangle = \left\langle {{{\xi}} {{{\eta}} ^{\rm{T}}}} \right\rangle =$ ${ \hat {{D}}}/2 $ [71 ] . 于是${\hat {{C}}}$ 与${\hat {{D}}}$ 都可以通过时间序列观察得到, 求解${\hat {{A}}}$ 中的${\hat{{L}}}$ 即可重构网络的结构.4.似然估计的方法重构网络 对于二值动力学, 当给定动力学过程以及网络, 会得到一系列时间序列. 但是, 当网络结构未知, 给定时间序列以后, 就变成了什么样的网络结构最有可能产生这种时间序列, 即应用最大似然估计的方法即可以得到[75 -81 ] .$P_i^{01}$ 与$P_i^{10}$ 可以用公式表示出来, 且是关于$\displaystyle\sum\nolimits_{j = 1,\, j \ne i}^N {{a_{ij}}S_t^j} $ 的函数. 因此可以通过大量的时间序列构造似然函数, 但是由于$\displaystyle\sum\nolimits_{j = 1,\, j \ne i}^N {{a_{ij}}S_t^j} $ 这一项在似然函数中往往都是非常复杂的非线性项(如指数函数), 因此需要通过平均场近似(即邻居中被激活个体的比例近似于整个网络中被激活个体的比例)的方法进行处理:$\displaystyle\sum\limits_{j = 1,\, j \ne i}^N {{a_{ij}}S_t^j} $ 在$\dfrac{{{k_i}}}{{N - 1}}\displaystyle\sum\limits_{j = 1, \,j \ne i}^N {S_t^j} $ 处一阶泰勒展开, 得到关于${a_{ij}}$ 的线性方程组, 从而推断出网络结构[75 ] . 该方法还可以推断出符号网络[77 ] 与多层网络[76 ] . 但是该方法有一个缺点, 就是需要知道动力学过程, 因此刘等[78 ] 应用Logistic回归中的Sigmoid函数近似二值动力学过程, 然后再应用平均场近似的方法进行重构, 也得到了很好的效果, 尤为重要的是, 该方法还可以进一步复现原始动力学, 即二值动力学中的转移概率函数.t 时刻)变为激活态(t + 1时刻)只受激活态的邻居的影响, 通过贝叶斯公式, 有$i \to j$ 表示节点i 对节点j 的直接影响. 令${P_{i \to j}} = P\left( {i \to j\left| {S_t^i = 1, S_t^j = 0, S_{t + 1}^j = 1} \right.} \right)$ , 显然${P_{i \to j}} > 0$ , 表示节点i 是节点j 的邻居. 再令$P_i^j = P\left( {S_{t + 1}^j = 1\left| {S_t^i = 1, S_t^j = 0} \right.} \right)$ , 可以通过数据统计出来, 这是一个已知量. 则节点j 在第${t_m}$ 时刻没被激活, ${t_m} + 1$ 时刻被激活的次数的期望可以表示为$\varPsi _i^{{t_m}}$ 表示节点i 在第${t_m}$ 时刻被激活的次数, ${\varepsilon _j}$ 表示重构的噪音项. 然后通过假设激活次数服从泊松分布, 利用时间序列可以写出似然函数, 最后应用expectation-maximization (EM) 算法求解${P_{i \to j}}$ , 从而推断出网络结构[75 ,79 ,80 ] , 图4 为应用此方法推断出的Karate网络的第33个节点的结构. 另外, Ma等[81 ] 应用最大似然估计针对终态数据对网络重构进行了尝试性研究.图 4 EM算法推断Karate网络33号节点的结构 (a)网络结构; (b)二进制数据; (c)EM算法推断出节点33的结构; (d)真实网络33号节点的结构Figure4. Reconstructing the neighbors of node 33 in Karate network: (a) The real structure of the Karate network; (b) the binary state data; (c) inferring the neighbors of node 33 based on EM algorithm; (d) the real neighbors of node 33.5.其他方法 网络重构的方法还有很多, 例如, Wu等[82 ,83 ] 将格兰杰因果关系检验运用到了网络重构当中, 并针对不同的情况, 提出了传统格兰杰因果关系检验、条件格兰杰因果关系检验、分段格兰杰因果关系检验、随机扰动分段格兰杰因果关系检验、偏相关格兰杰因果关系检验等不同的格兰杰因果关系检验识别方法; Li和Li[84 ] 通过时效网络扩散过程的到达时间数据, 提取时效交互过程的统计特征和推断出时效网络的拓扑结构, 并严格证明了推断结构的渐近一致性; Casadiego等[85 ] 通过引入显式依赖矩阵把每个个体的动力学分解成与其他个体两点、三点或更高阶的相互作用, 从而可以通过数据揭示网络(两点)和超网络(三点)的交互作用.6.未来展望 网络重构发展到现在, 虽然已经取得了一些成就, 但是还有很多问题需要解决. 现有的方法主要还是针对简单的动力学网络. 对于多层网络的重构、符号网络的重构、时效网络的重构、多体动力学网络的重构等等, 虽然有一些文献已经对这些问题有所涉及, 但是其重要性还没有受到应有的关注, 也没有很好地解决. 而且现在的网络重构针对的主要还是小规模网络, 如何快速地、精确地重构大规模网络也是以后需要解决的问题.  图 1 网络重构示意图 (a)通过离散的数据; (b)连续的数据; (c)推断网络结构
图 1 网络重构示意图 (a)通过离散的数据; (b)连续的数据; (c)推断网络结构



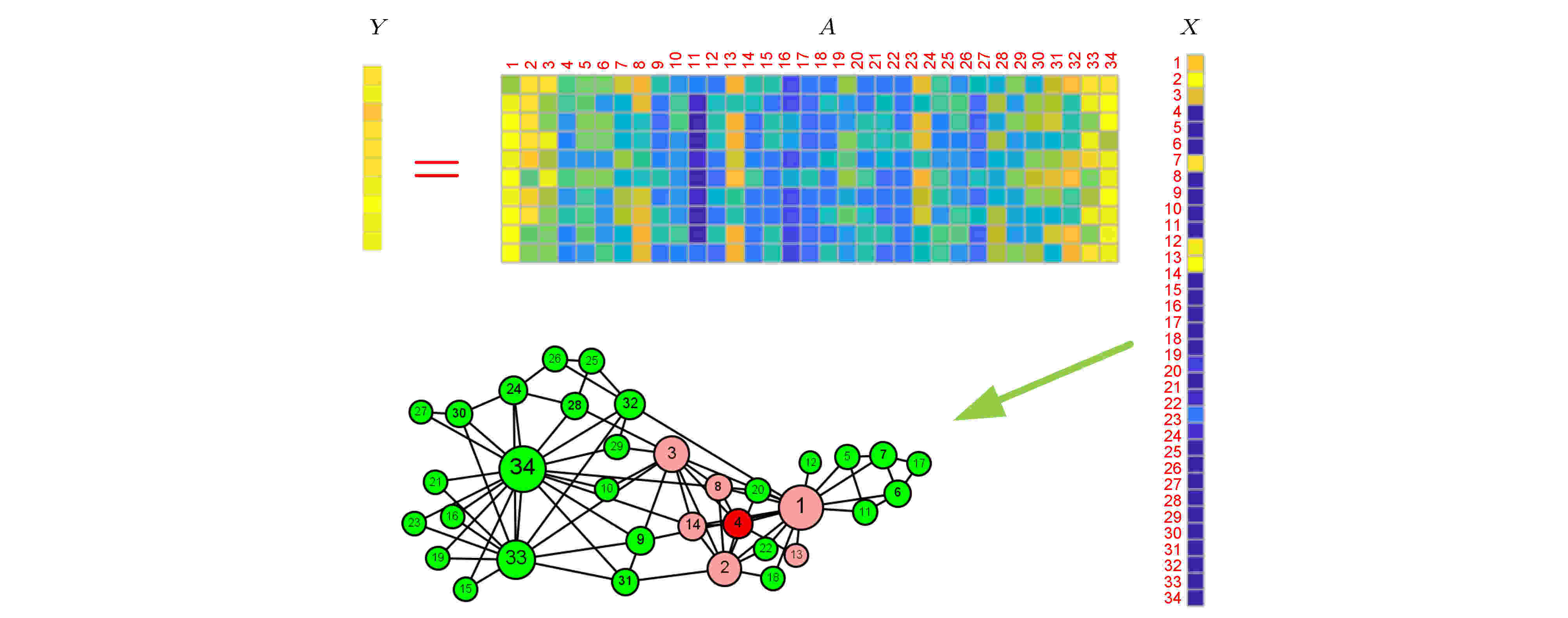 图 2 基于压缩感知方法重构Karate网络中4号节点的邻居(重构方法见2.4节)
图 2 基于压缩感知方法重构Karate网络中4号节点的邻居(重构方法见2.4节)









































































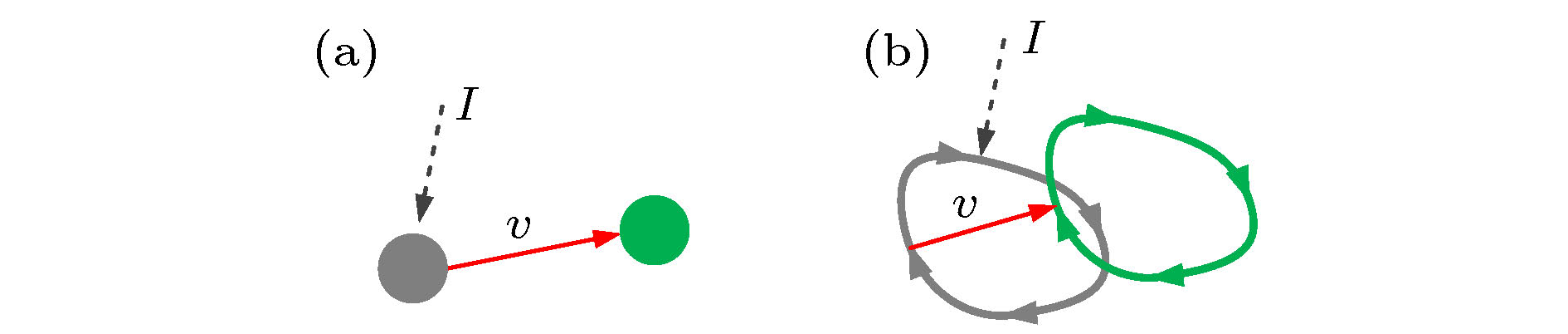 图 3 驱动-响应实验示意图. 对稳态系统施加(稳态是一个稳定点(a), 或者一个周期轨道(b))一个持续驱动I, 系统达到另外一个稳态. 两个稳态的差异v包含了网络的拓扑结构
图 3 驱动-响应实验示意图. 对稳态系统施加(稳态是一个稳定点(a), 或者一个周期轨道(b))一个持续驱动I, 系统达到另外一个稳态. 两个稳态的差异v包含了网络的拓扑结构















































































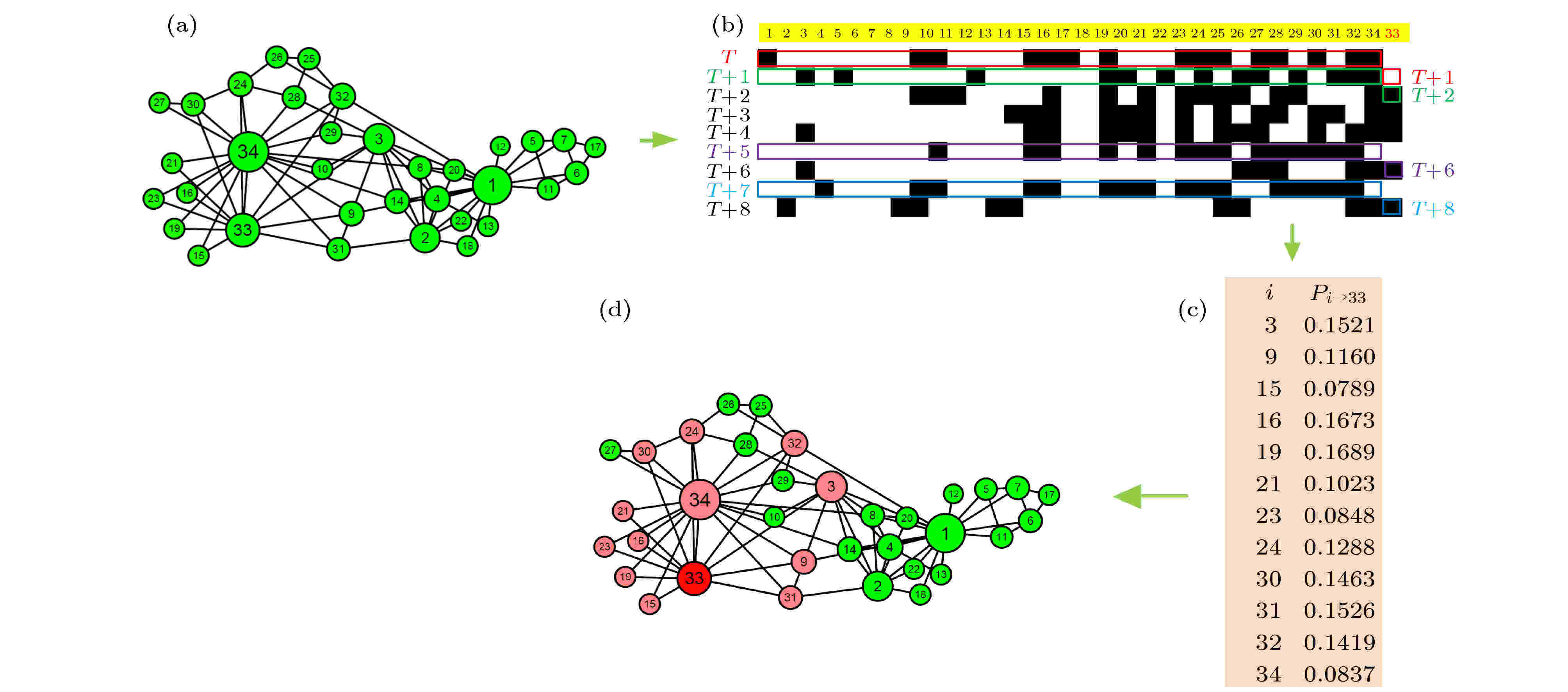 图 4 EM算法推断Karate网络33号节点的结构 (a)网络结构; (b)二进制数据; (c)EM算法推断出节点33的结构; (d)真实网络33号节点的结构
图 4 EM算法推断Karate网络33号节点的结构 (a)网络结构; (b)二进制数据; (c)EM算法推断出节点33的结构; (d)真实网络33号节点的结构