全文HTML
--> --> -->微波无线能量传输系统由发射端与接收端两个部分组成, 其示意图如图1所示. 能量转换效率是评价微波无线能量传输系统的关键技术指标, 研究人员致力于从不同角度提高系统的转换效率, 以获得更高的能量转换能力[7-10]. 主要方法有两种: 第一种是通过构造多频带或宽带的天线收集更多的输入功率使得更多的能量进入整流电路来增大其转换的能量, 但是该方法并未明确提高能量转换效率, 只是增大了负载所能获得的能量; 另一种是优化设计阻抗匹配电路, 输入滤波器以便优化信号、抑制谐波、减小反射, 使得天线接收的能量尽可能的进入整流电路进行整流, 减少接收端的消耗, 这种方法可以提升能量转换效率[11]. 对于整流电路也有部分研究, 主要在于整流器拓扑结构的设计[12]. 但目前尚未发现有研究****从能量转换的关键器件—整流二极管角度上来提高能量转换效率. 整流二极管一般为肖特基二极管, 其为整流电路的核心器件, 决定着能量转换效率的大小, 一旦确定, 整个系统的能量转换效率上限也将确定[13-17].
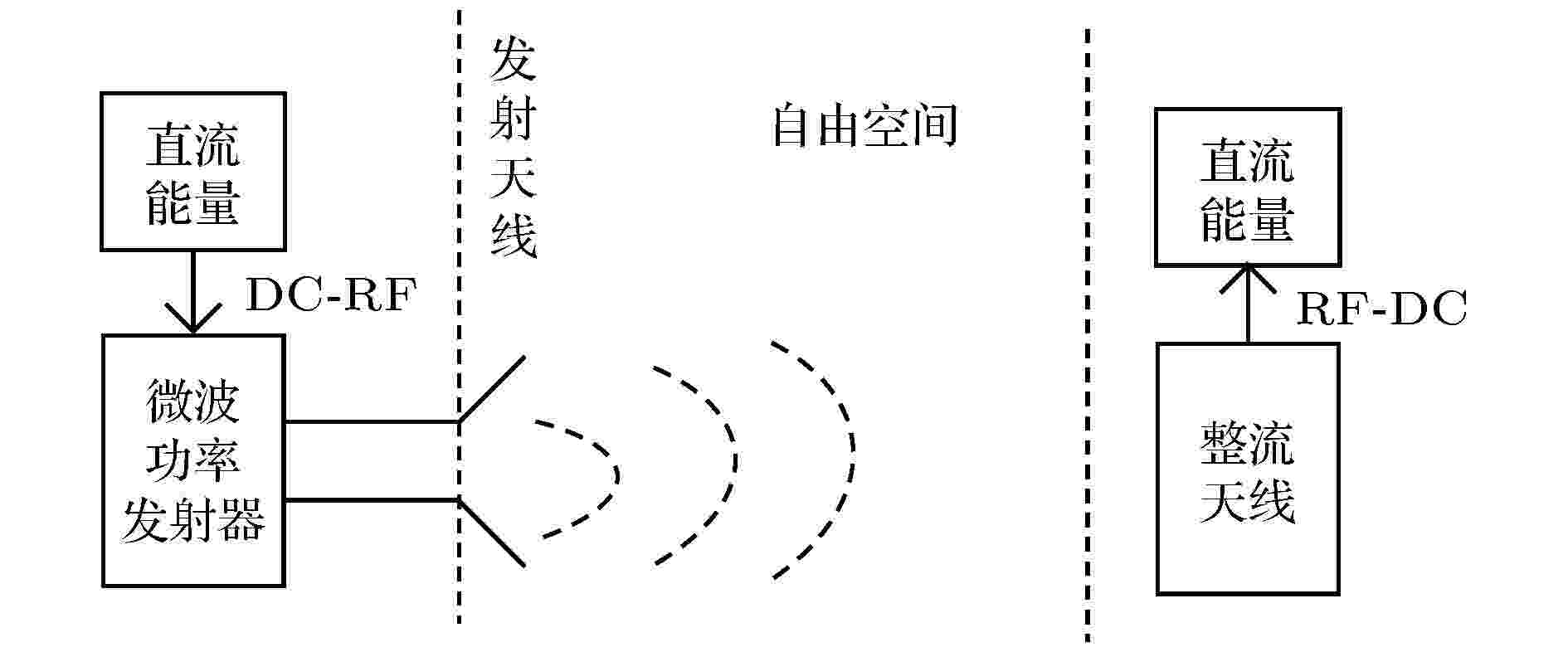图 1 微波无线能量传输系统示意图Figure1. Schematic diagram of microwave wireless energy transmission system.
本文将从关键整流器件肖特基二极管入手, 研究与能量转换效率关系密切的零偏置电容参数, 设计用于微波无线能量传输的具有高能量转换效率的肖特基二极管并完成整流电路仿真, 其研究结论以及相关分析方法可为微波无线能量传输系统的能量转换效率提高提供重要的技术支持.
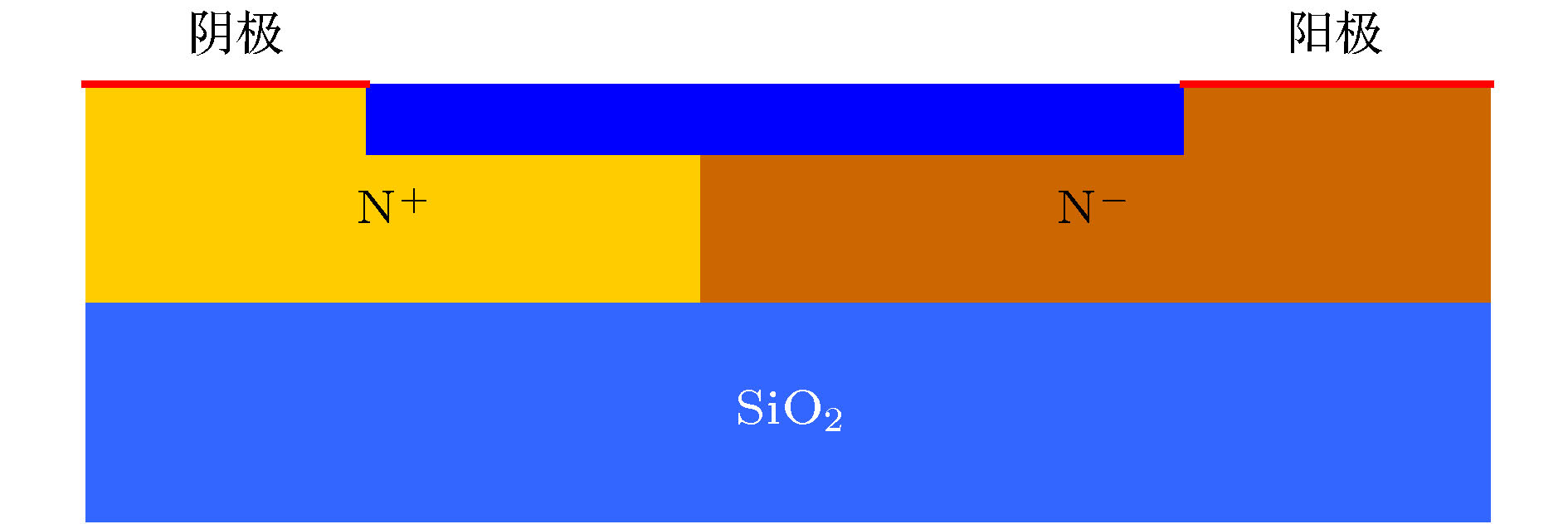图 2 GeOI折叠空间电荷区肖特基二极管结构示意图Figure2. Schematic diagram of GeOI Schottky barrier diode structure withfolded space charge region.
GeOI技术使得肖特基二极管在阳极施加反向电压时, 空间电荷区先纵向耗尽, 当施加的反偏电压足够大时, 纵向完全耗尽之后, 由于半导体材料下面是绝缘层, 因此只能横向耗尽. 即阳极施加反偏电压时, 空间电荷区会经历两个过程, 小电压下先纵向耗尽, 当电压继续增大时, 纵向完全耗尽, 此时纵向耗尽区域宽度不变, 空间电荷区将向横向耗尽. 这类先纵向耗尽, 然后横向耗尽的肖特基二极管称为部分耗尽GeOI SBD. 当肖特基二极管不加偏压时, 金属与半导体接触后形成的空间电荷区宽度已经达到器件结构中半导体材料的纵向厚度时, 即不加偏压时已经纵向耗尽, 施加偏压后只在横向耗尽, 这类肖特基二极管被称为全耗尽GeOI SBD. 与传统肖特基二极管结构不同[18], 本文设计的肖特基二极管在空间电荷区不像传统肖特基二极管只有纵向的空间电荷区, 而是由纵向空间电荷区与横向空间电荷区两个部分组合而成, 类似将原本纵向的空间电荷区折叠成为两个部分, 因此称其为折叠空间电荷区的肖特基二极管. 由于空间电荷区被分为纵向空间电荷区与横向空间电荷区, 所以其电容也被分为两个部分, 分别为纵向电容与横向电容, 在器件的模型中, 这两部分电容属于串联关系, 由于电容串联的特性, 总电容大小将会减小.
2
2.1.GeOI折叠空间电荷区肖特基二极管电容模型分析
为了详细讨论折叠空间电荷区肖特基二极管的内部电容, 分别需要从器件几何结构参数以及材料物理参数两个方面进行研究. 肖特基二极管最大击穿电压
在小电压下, 空间电荷区的宽度为
基于(3)式, 可以得到GeOI肖特基二极管的纵向电容模型为
由于器件最底部绝缘层的存在, 导致外部持续增大反偏电压时, 纵向的空间电荷区完全耗尽, 此时空间电荷区将向横向耗尽. 其工作原理与纵向相同, 基于空间电荷区宽度的计算公式, 横向空间电荷区的宽度x为
2
2.2.肖特基势垒二极管SPICE模型参数使用
拟使用GeOI折叠空间电荷区肖特基二极管的SPICE模型进行对比仿真分析, 以对器件性能进行验证. 为证明在ADS仿真软件中使用SPICE模型代替实际二极管进行验证方法的正确性[20], 首先从二极管在整流电路中的仿真入手, 目前广泛用于微波无线能量传输系统的二极管为安捷伦公司所生产的HSMS-282 X系列肖特基二极管. 选用HSMS-2820, 对其采用ADS仿真软件中的谐波平衡仿真, 仿真原理图如图3所示, 滤波电容设置为100 pF, 负载电阻为1000 Ω. 能量转换效率结果如图4所示, 可以观察到能量转换效率最高值出现在输入功率27.7 dBm处, 效率约为68.5%.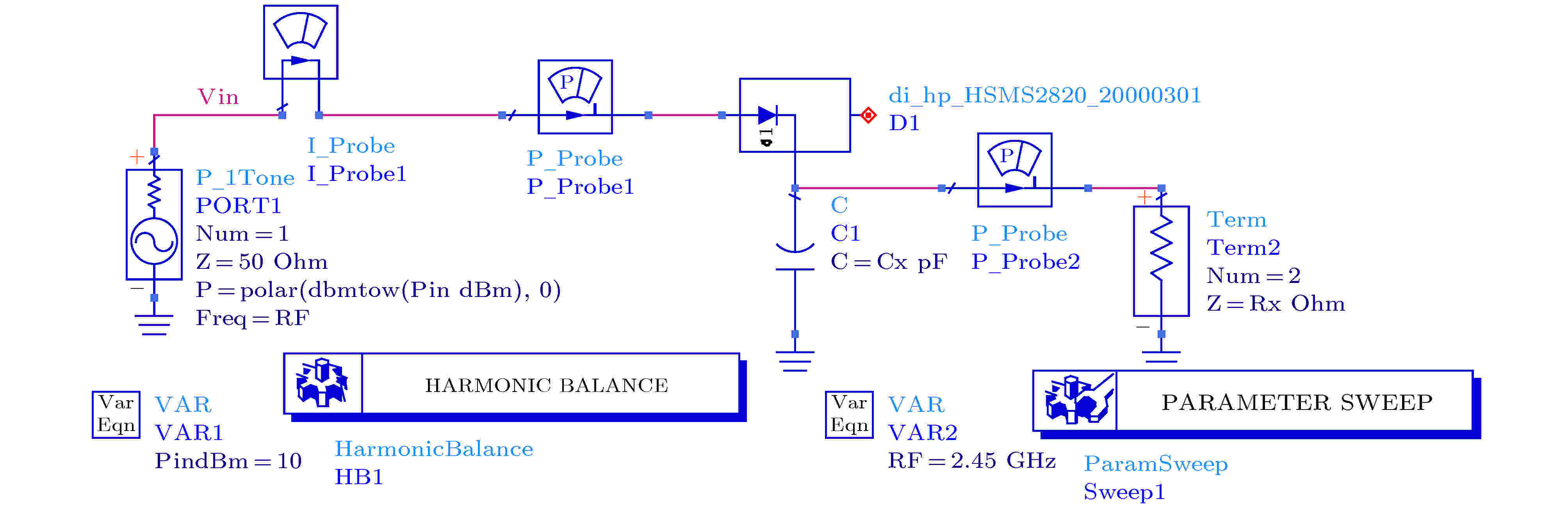
图 3 HSMS-2820肖特基二极管整流电路仿真图Figure3. The rectifier circuit simulation diagram of HSMS-2820.
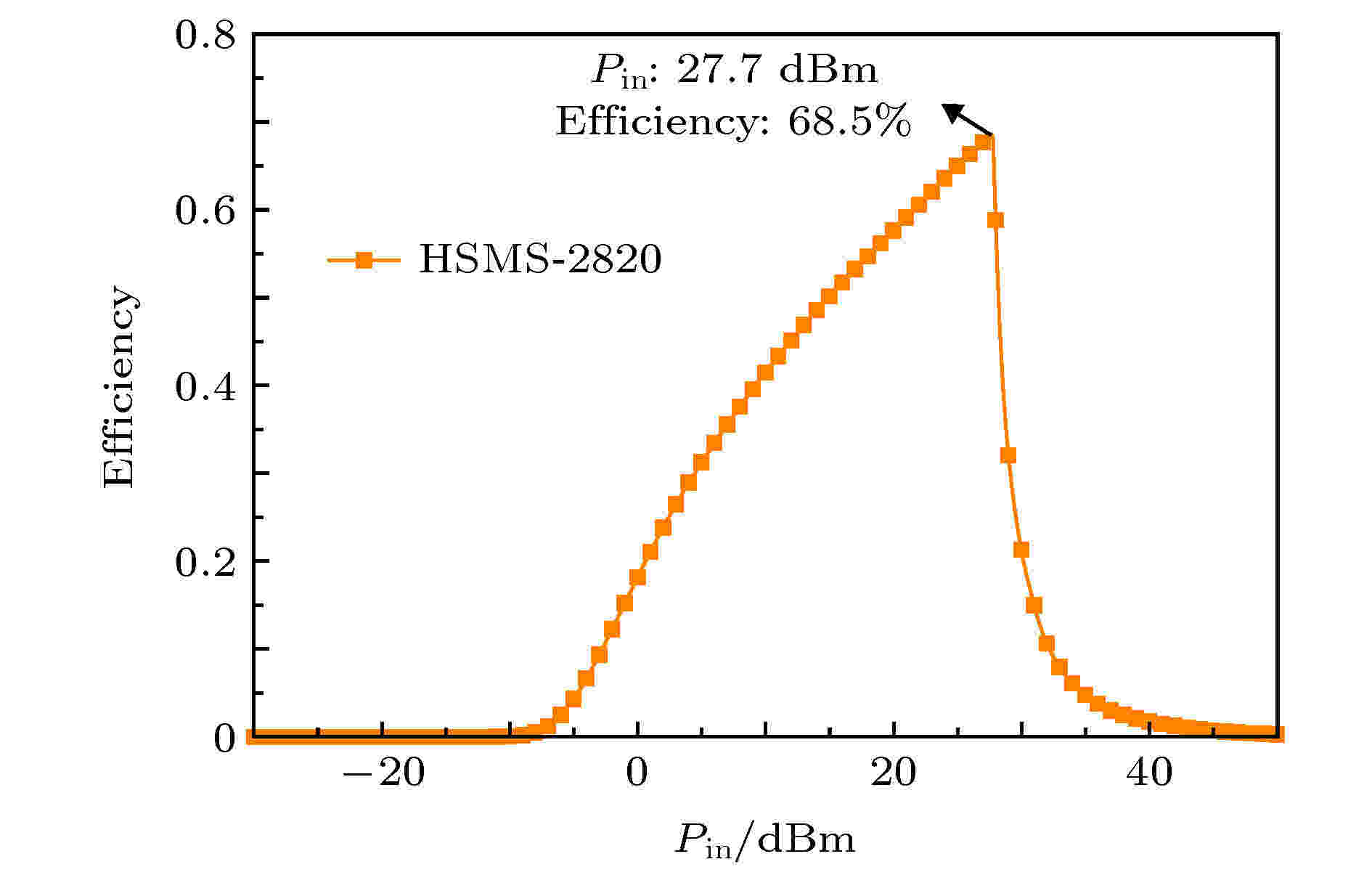图 4 HSMS-2820肖特基二极管整流电路效率图Figure4. The efficiency of rectifier circuit with HSMS-2820.
表1为HSMS-2820肖特基二极管的SPICE模型参数表, 图5为采用SPICE模型的肖特基二极管的整流电路仿真图, 图6为其整流效率曲线图, 能量转换效率最大值出现在23.1 dBm处, 为69.1%. 从图4和图6中可以看出两者的最高能量转换效率差别不大, 能量输入响应有偏差的原因为肖特基二极管在非线性工作区内安捷伦公司所提供的ADS模型与SPICE模型之间有偏差.
| 参数 | 单位 | HSMS2820 | 参数 | 单位 | HSMS2820 |
| $ {B}_{\mathrm{v}} $ | V | 15 | $ {C}_{\mathrm{j}0} $ | pF | 0.7 |
| $ {E}_{\mathrm{G}} $ | eV | 0.69 | $ {I}_{\mathrm{B}\mathrm{V}} $ | A | 1 × 10-4 |
| $ {I}_{\mathrm{S}} $ | A | 2.2 × 10-8 | N | 1.08 | |
| $ {R}_{\mathrm{S}} $ | $\Omega $ | 6.0 | $ {P}_{\mathrm{B}} $ | V | 0.65 |
| $ {P}_{\mathrm{T}} $ | 2 | M | 0.5 |
表1HSMS-2820肖特基二极管SPICE参数表
Table1.The SPICE parameters of HSMS-2820.
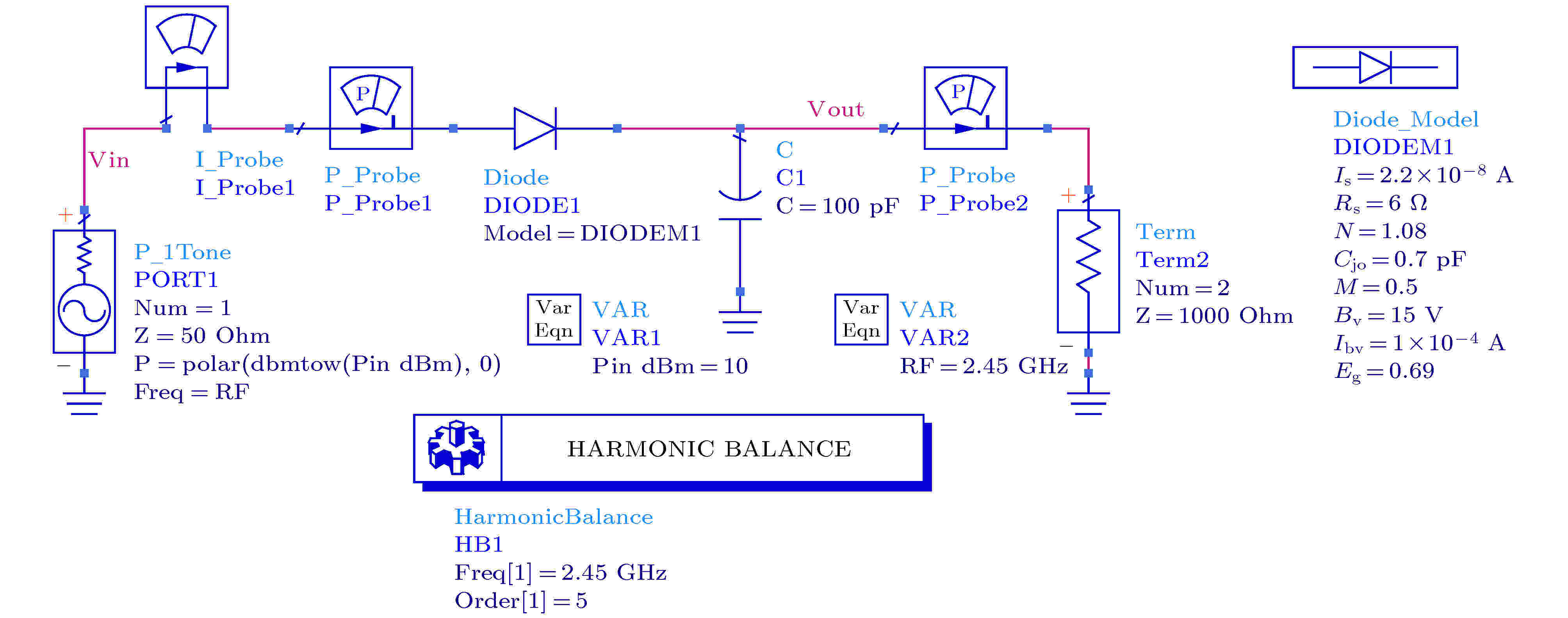图 5 使用SPICE模型的整流电路仿真图Figure5. The rectifier circuit with SPICE model.
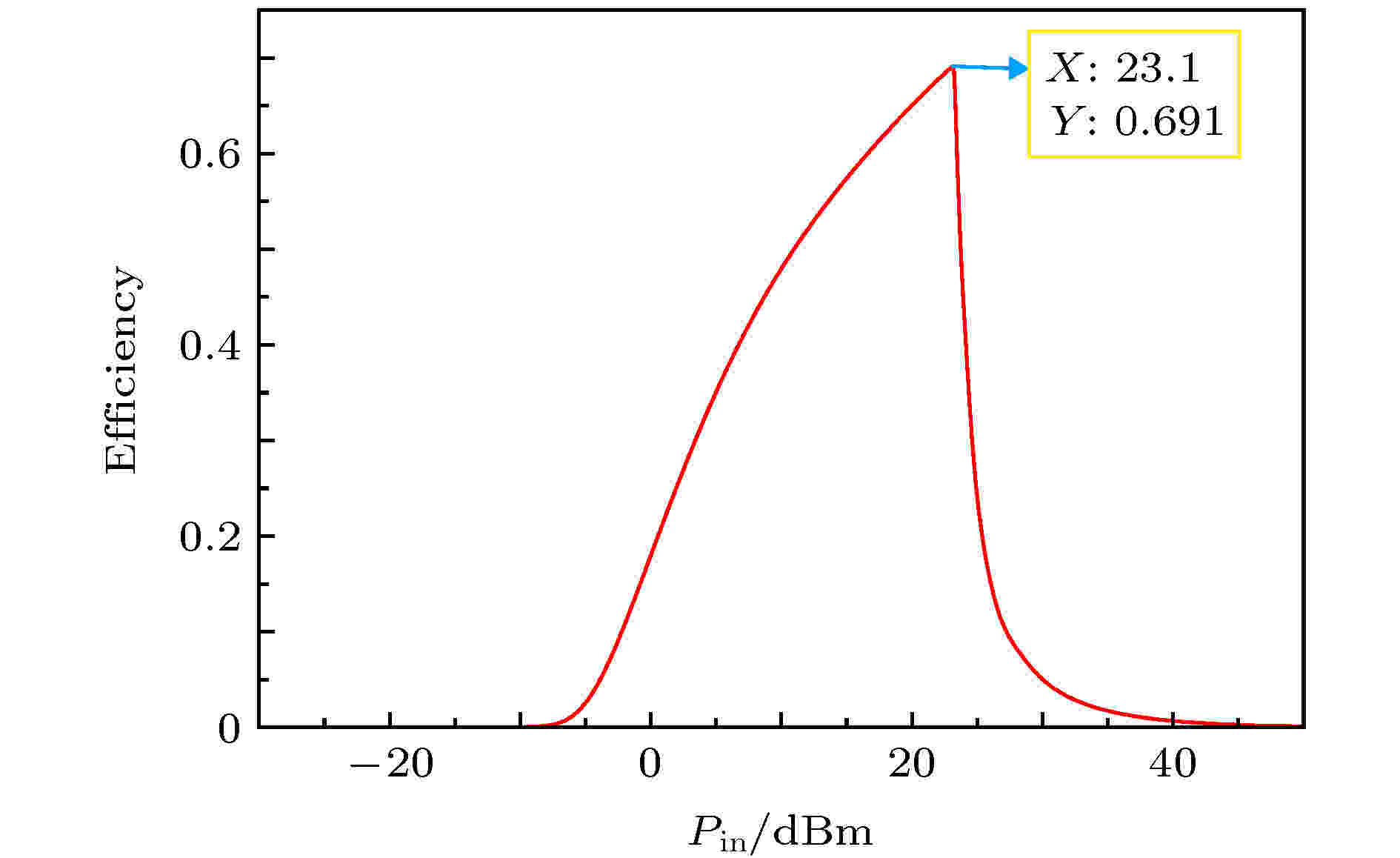图 6 使用SPICE模型构成整流电路的能量转换效率曲线Figure6. The efficiency of rectifier circuit with SPICE model.
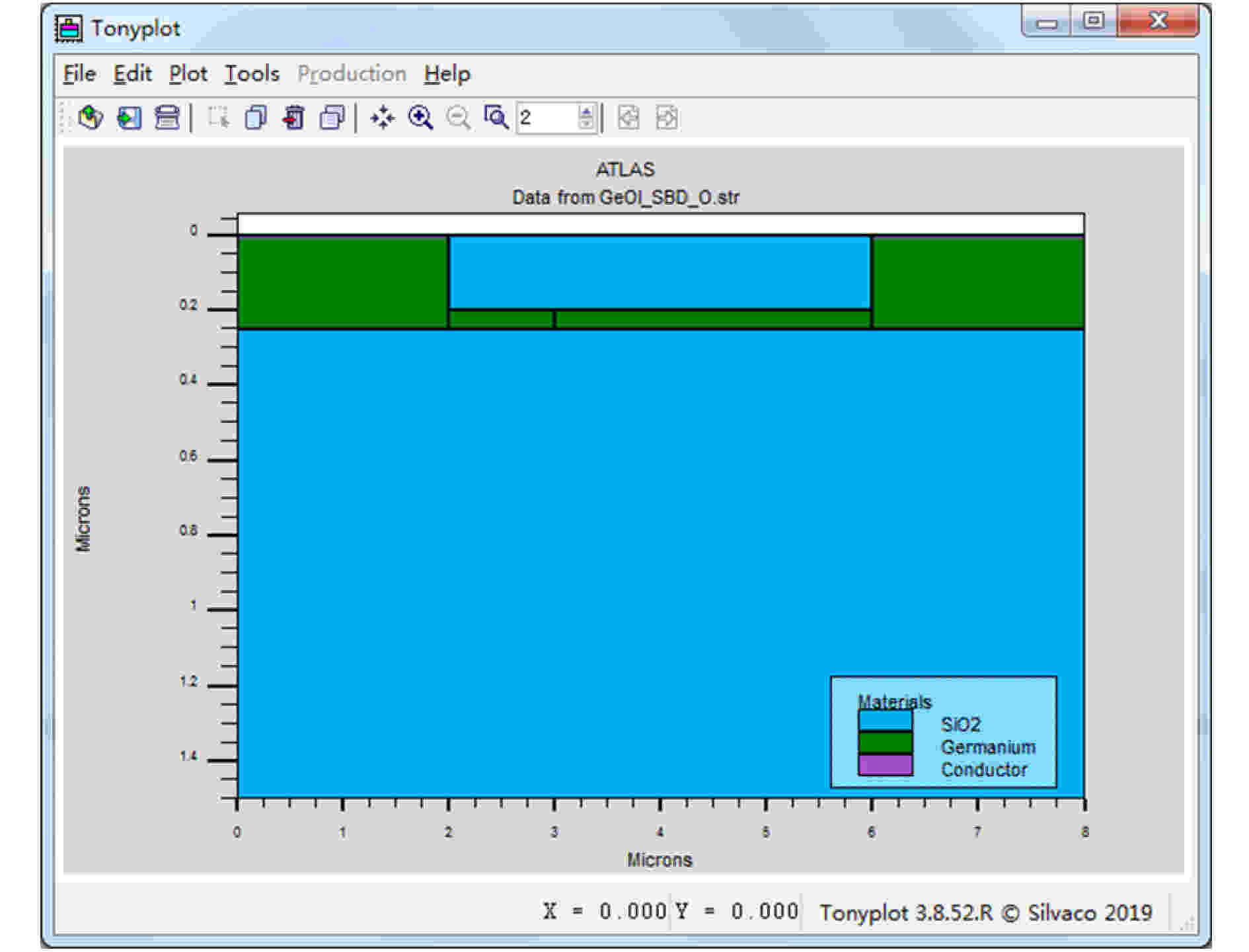图 7 GeOI折叠空间电荷区SBD的仿真结构图Figure7. Structure diagram of GeOI folding space charge region SBD.
如图8是外延层不同掺杂浓度下肖特基二极管的正向I-V曲线, 横轴表示为肖特基二极管的阳极正向电压, 纵轴为肖特基二极管的阳极正向电流, 从图8中可以看出, 随着正向电压的增加, 肖特基二极管开始导通, 针对Ge材料的肖特基二极管, 其阳极金属功函数为4.55 eV, 其开启电压如图8所示约为0.2 V, 随着半导体外延层掺杂浓度的提高, 其正向导通电流也逐渐提高, 这是由于掺杂浓度提高后, 外延层中可自由移动得电子变多而导致的. 随着电压的逐渐增大, 其正向特性也变得平缓, 这是由于二极管在正向导通时, 对外表现的形式为一个电阻所导致的.
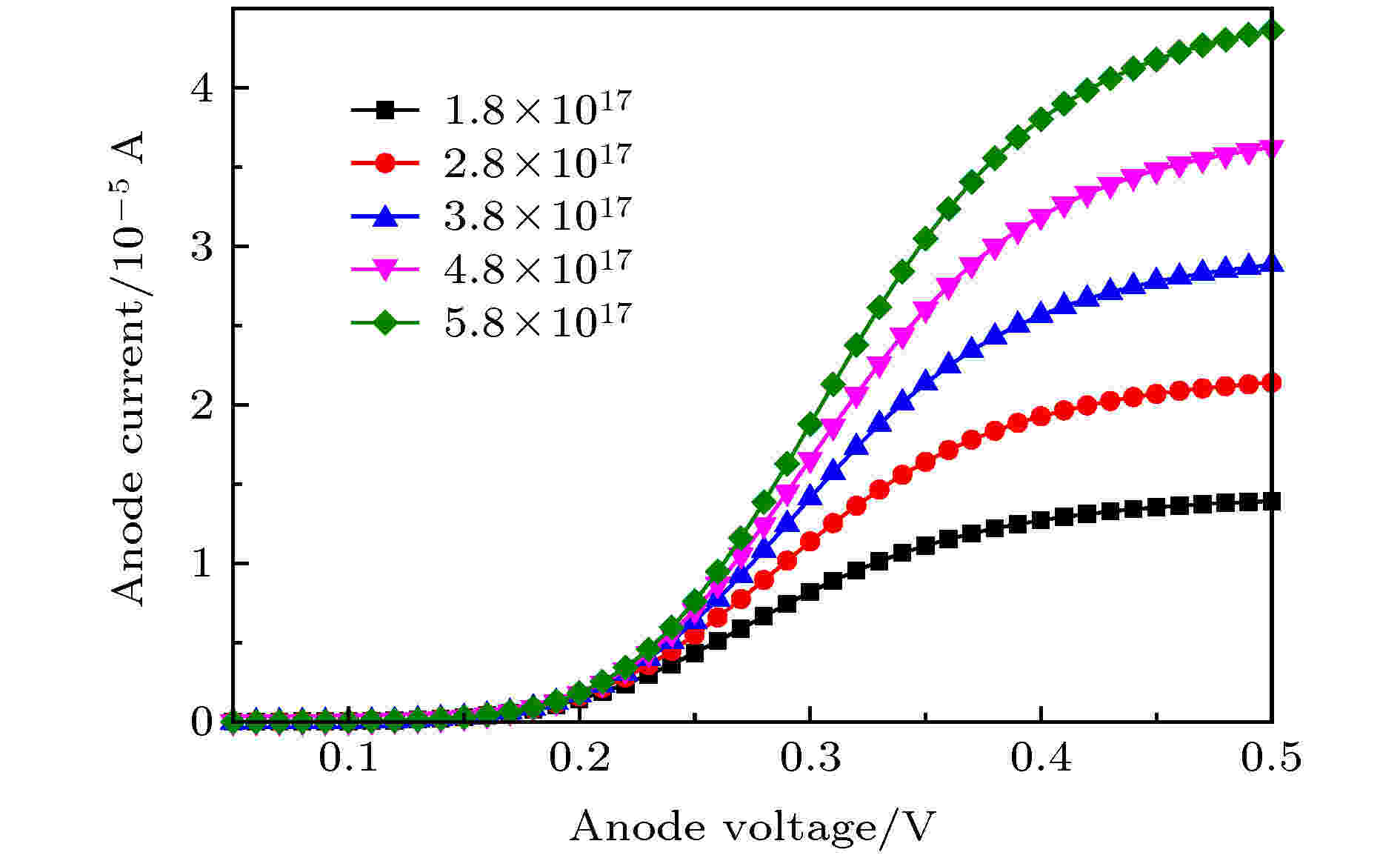图 8 不同掺杂浓度下肖特基二极管正向I-V曲线Figure8. Forward I-V curves of Schottky diode under different doping concentrations.
图9为外延层厚度为0.2 μm时, 不同掺杂浓度下肖特基二极管的反向击穿曲线, 横轴为肖特基二极管的反向电压, 纵轴为肖特基二极管电流. 从图9中可以看出, 随着肖特基二极管反向电压的逐渐增大, 其反向电流会出现急剧增大的趋势, 转折点即为击穿电压值; 外延层掺杂浓度越小, 肖特基二极管的击穿电压越大, 随着外延层掺杂浓度的提高, 二极管的击穿电压值逐渐降低, 当外延层掺杂浓度为3.8 × 1017 cm–3时, 其对应击穿电压约为14 V, 当增加其外延层掺杂浓度为5.8 × 1017 cm–3时, 击穿电压约为11.25 V. 因此当外延层掺杂浓度增大时, 更容易发生击穿.
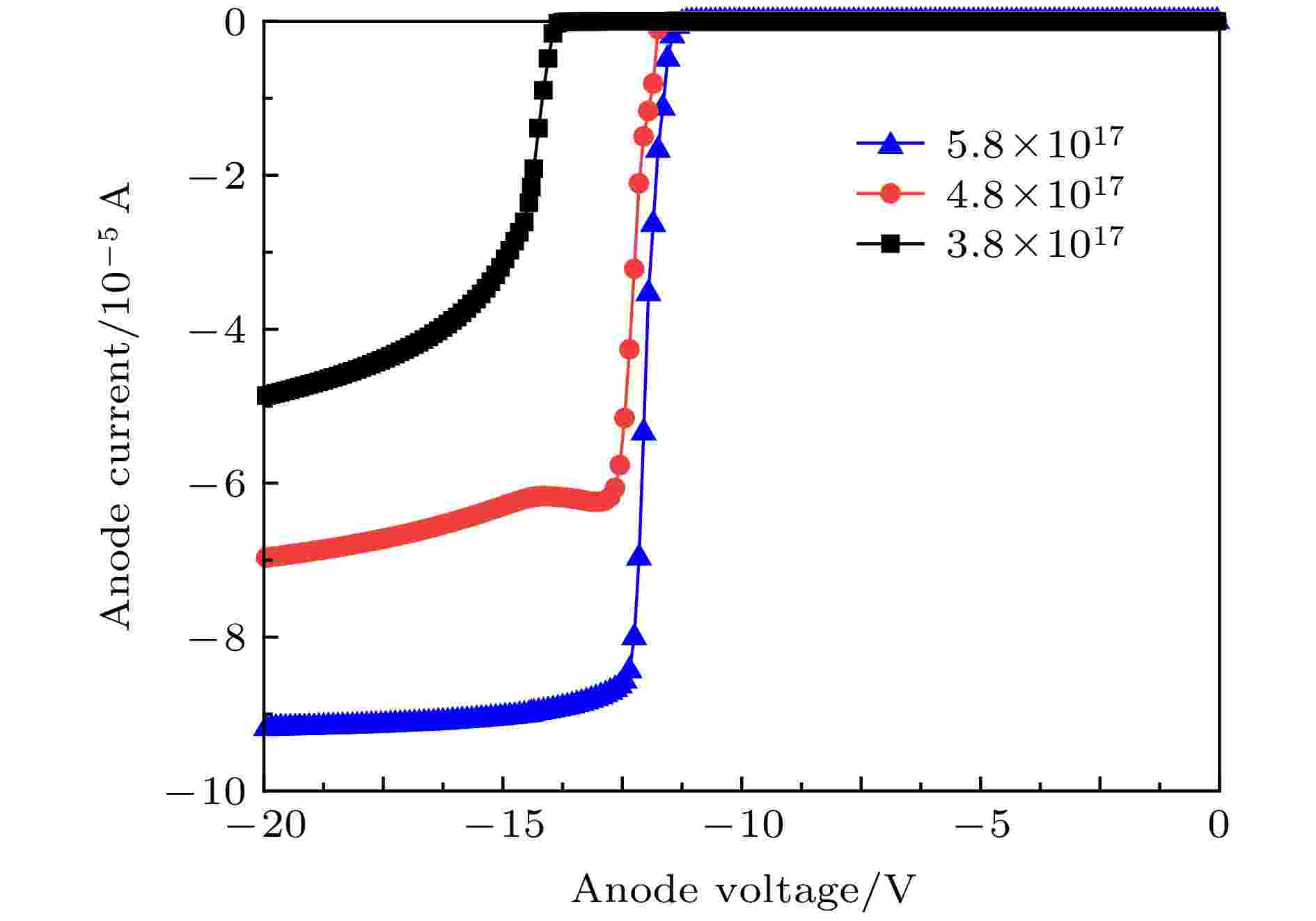图 9 不同掺杂浓度下肖特基二极管反向I-V曲线Figure9. Reverse I-V curves of Schottky diode under different doping concentrations.
折叠空间电荷区类型的肖特基二极管分为两种: 一种是部分区域折叠, 即施加反向电压时, 先纵向耗尽, 直至绝缘衬底时无法再向纵向耗尽, 空间电荷区转而横向扩展, 这种称为部分耗尽; 另一种是在施加反向电压时, 由于外延层厚度较小, 空间电荷区宽度已经大于其外延层厚度, 此时再增大反向电压时, 空间电荷区将只能横向扩散, 这种称为全耗尽. 图10所示为不同掺杂浓度下部分耗尽的肖特基二极管的电容-电压曲线, 电容随着反向电压的增大而减小, 由于肖特基二极管呈反偏状态, 此时空间电荷区增大, 金属半导体势垒变高, 电子不再容易越过势垒流向金属一侧, 随着反向电压的进一步增高, 势垒高度越来越大, 其空间电荷区宽度也随之增大, 而肖特基二极管的结电容类似平行板电容器, 随着空间电荷区宽度的增大, 其电容值逐渐降低. 从图10中可以看出, 针对于不同掺杂浓度其C-V曲线变化规律较为一致, 在较低反向电压时, 即不同浓度下反向电压在0—1 V之间时, 随着反向电压的增大, 部分耗尽类型的肖特基二极管纵向空间电荷区逐渐扩展, 所对应的结电容随着反向电压的增大而降低, 此时肖特基二极管的结电容由纵向空间电荷区电容组成; 当反向电压继续增大时, 不同掺杂浓度下的曲线均产生了转折点, 而这个转折点所对应的电压即为上述所讨论的纵向穿通电压VPT, 这对应着部分耗尽类型的肖特基二极管已经完全纵向耗尽, 空间电荷区开始逐渐横向扩展, 此时其肖特基二极管的结电容表现为纵向空间电荷区电容与横向空间电荷区电容的串联形式. 随着外延层掺杂浓度的增加, 纵向耗尽区域将会产生更大的电场, 其纵向耗尽的电压也会随着掺杂浓度的增加而增大, C-V曲线中对应的掺杂浓度较大的器件其电容变化的转折点也会更大[21].
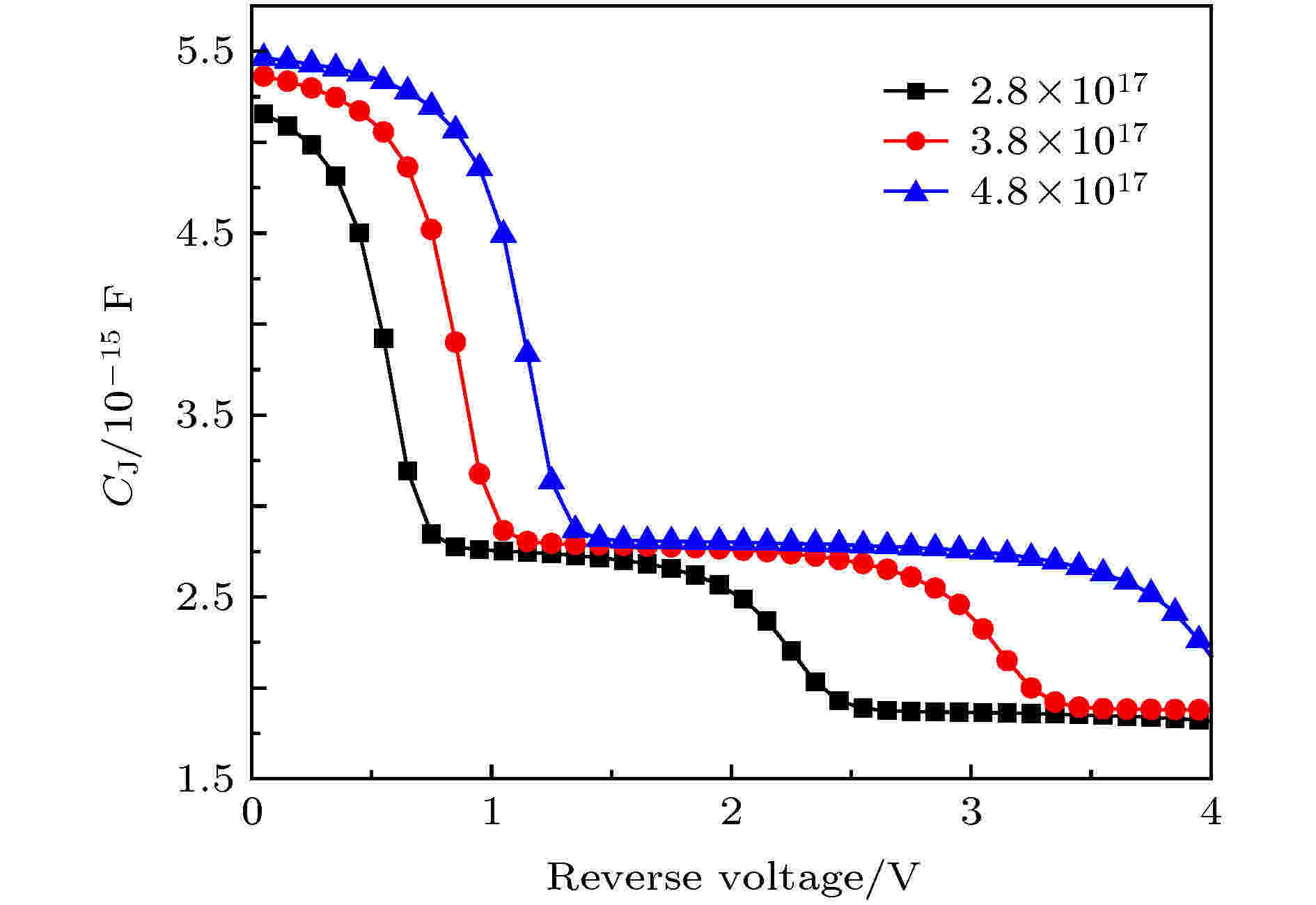图 10 不同掺杂浓度下部分耗尽肖特基二极管C-V曲线Figure10. C-V curves of partially depleted Schottky diode at different doping concentrations.
图11为不同外延层厚度、不同外延层浓度情况下, 部分耗尽的肖特基二极管C-V曲线图. 从图11中可以看出, 当反向电压较低时, 对于同一掺杂浓度不同外延层厚度的部分耗尽肖特基二极管, 其外延层厚度较大时, 所对应的肖特基二极管电容较大, 即对于同一大小的结电容, 外延层厚度较大的肖特基二极管需要更大的反向电压, 在穿通情况下, 外延层厚度大的肖特基二极管的纵向耗尽宽度即为其外延层厚度; 而随着反向电压的逐渐增大, 不同外延层厚度对于肖特基二极管的电容影响不大, 原因在于当肖特基二极管的组成类型均为部分耗尽时, 掺杂浓度固定的情况下, 其所对应的载流子浓度也随之固定, 因此其总电容大小对于其外延层厚度大小变化并不敏感.
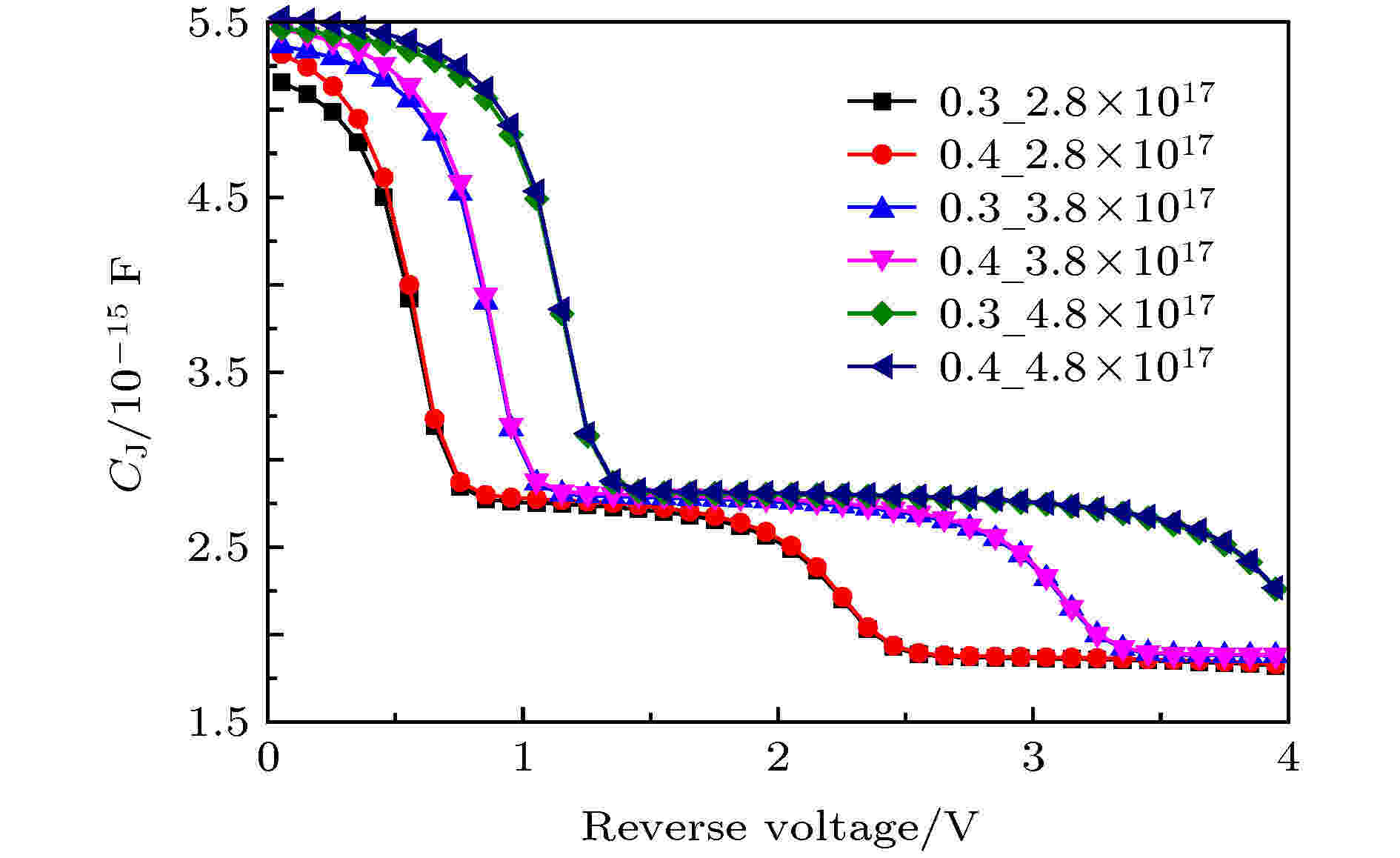图 11 不同外延层厚度、不同外延层浓度下部分耗尽肖特基二极管C-V曲线Figure11. C-V curves of partially depleted Schottky diode with different epitaxial layer thicknesses and different doping concentrations.
图12表示的是全耗尽情况下与传统肖特基二极管电容-电压曲线图, 与传统肖特基二极管相比, 全耗尽的GeOI折叠空间电荷区类型的肖特基二极管在低电压情况下电容值要更低一点, 而在较高电压情况下两者差距没有在低电压情况下明显, 但仍可以看出传统肖特基二极管结电容始终大于新型的全耗尽GeOI折叠空间电荷区肖特基二极管结电容. 在零偏情况下, 肖特基二极管的结电容是由纵向空间电荷区电容与横向空间电荷区串联而成. 因此, 在零偏情况下全耗尽GeOI折叠空间电荷区肖特基二极管的结电容比传统结构的肖特基二极管的结电容明显降低.
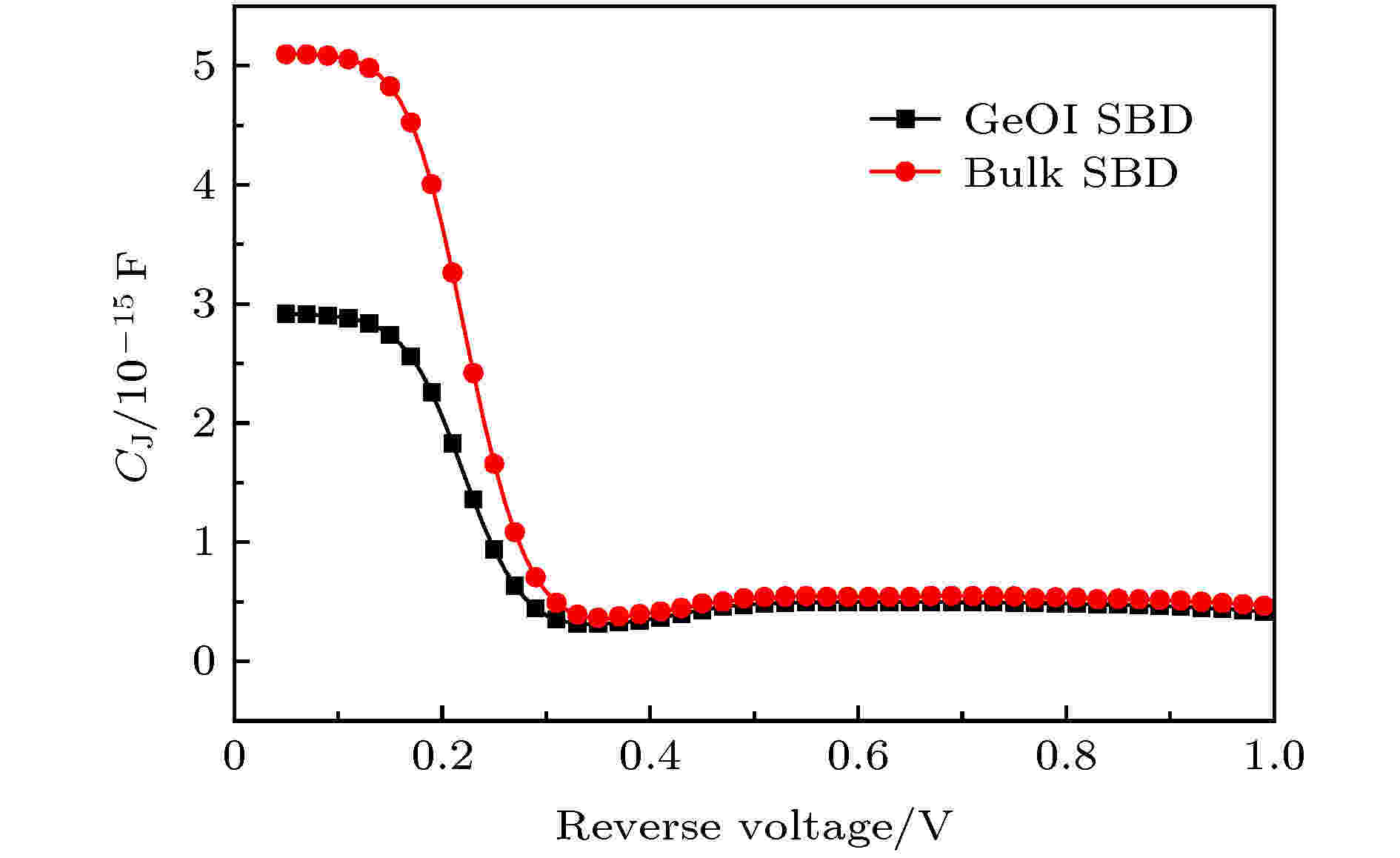图 12 全耗尽GeOI折叠空间电荷区SBD与传统结构SBD的C-V曲线Figure12. C-V curves of fully depleted GeOI folded space charge region SBD and traditional structure SBD.
为了提升微波能量转换效率, 需要设计的肖特基二极管必须满足在零偏情况下结电容降低的目标, 选择全耗尽GeOI折叠空间电荷区肖特基二极管作为研究目标, 所设计器件参数如下: Ge材料左侧重掺杂缓冲层掺杂浓度为2 × 1020 cm–3, 其作用是为了形成欧姆接触, 右侧轻掺杂区域掺杂浓度为3.8 × 1017 cm–3, 折叠区域厚度为0.2 μm, 器件肖特基金属采用金属钨(W)材料, 横向宽度为8 μm, 电极长度为2 μm.
图13所示为所设计全耗尽GeOI折叠空间电荷区肖特基二极管的纵向电场与横向电场图. 从图13中可以看出, 当施加正向电压即肖特基二极管正向偏置下, 纵向区域电场从阳极开始在整个外延层厚度上逐渐降低, 在绝缘层处达到最小值0; 在横向区域, 0—2 μm处于纵向耗尽结束的位置, 在此处电场强度变化不大, 从2 μm处开始, 由于横向电流被限制在较窄区域, 所以横向电场强度比较大, 一直到浓度突变处, 电场强度都比较大, 在浓度突变以外, 电场强度逐渐减小至0.
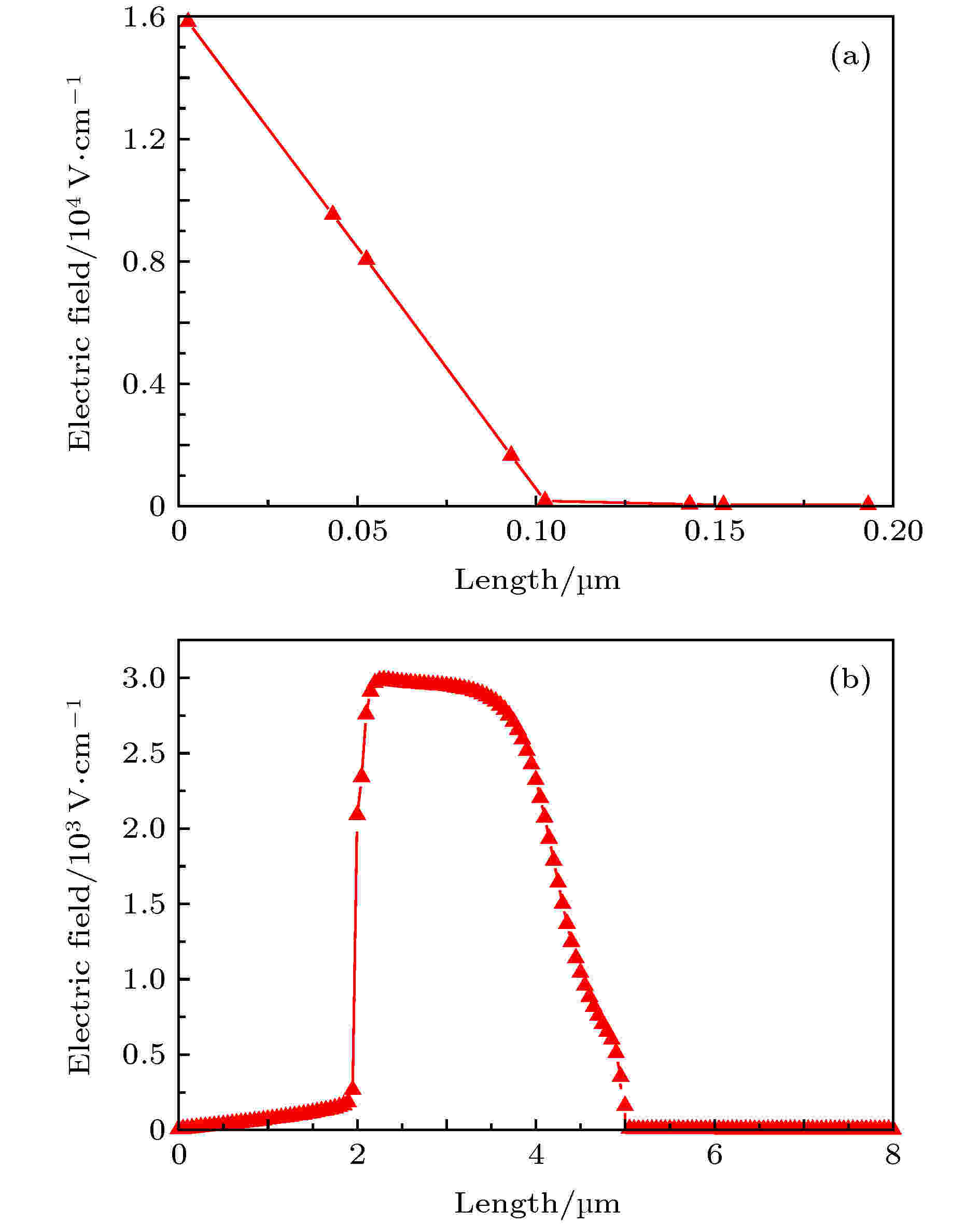图 13 全耗尽GeOI折叠空间电荷区肖特基二极管电场图 (a) 纵向电场分布; (b) 横向电场分布Figure13. The electric field distribution of fully depleted GeOI folded space charge region Schottky diode: (a) Vertical electric field; (b) transverse electric field.
图14为所设计GeOI折叠空间电荷区肖特基二极管正向与反向I-V曲线, 可以看出, 肖特基二极管的开启电压约为0.2 V, 随着阳极电压的增大, 其正向电流逐渐增大, 最后趋于平缓. 观察反向曲线, 可以看出肖特基二极管反向击穿电压约为18 V.
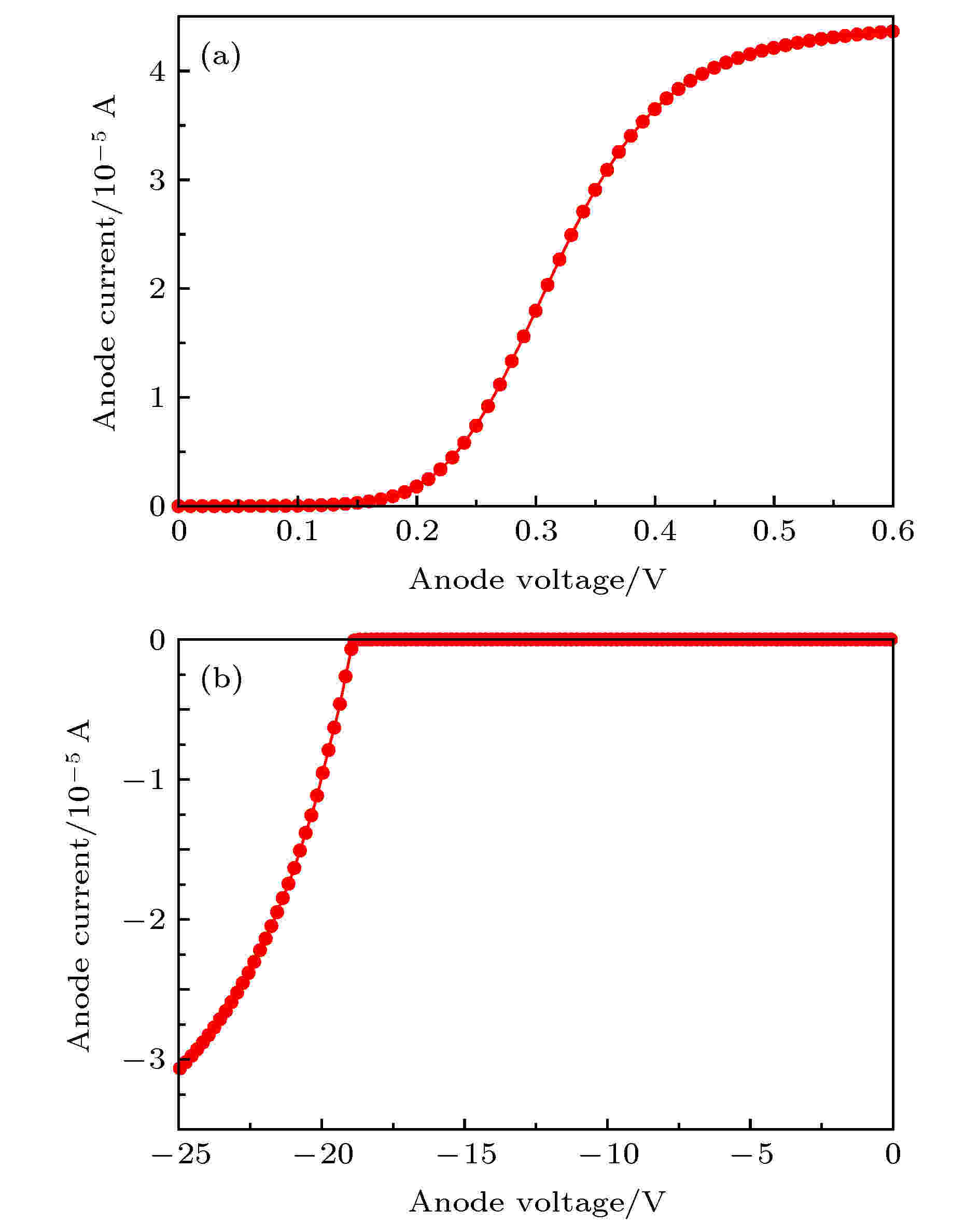图 14 全耗尽GeOI折叠空间电荷区肖特基二极管正向与反向I-V曲线Figure14. The forward and reverse I-V curves of fully depleted GeOI folded space charge region Schottky diode.
图15为所设计全耗尽GeOI折叠空间电荷区肖特基二极管的C-V曲线. 从图15中可以看出, 在零偏电压的情况下, 已经纵向耗尽, 空间电荷区已经扩展至横向, 结电容是由纵向完全耗尽的空间电荷区电容与横向的空间电荷区电容串联而成, 因此其零偏情况下的电容值较小.
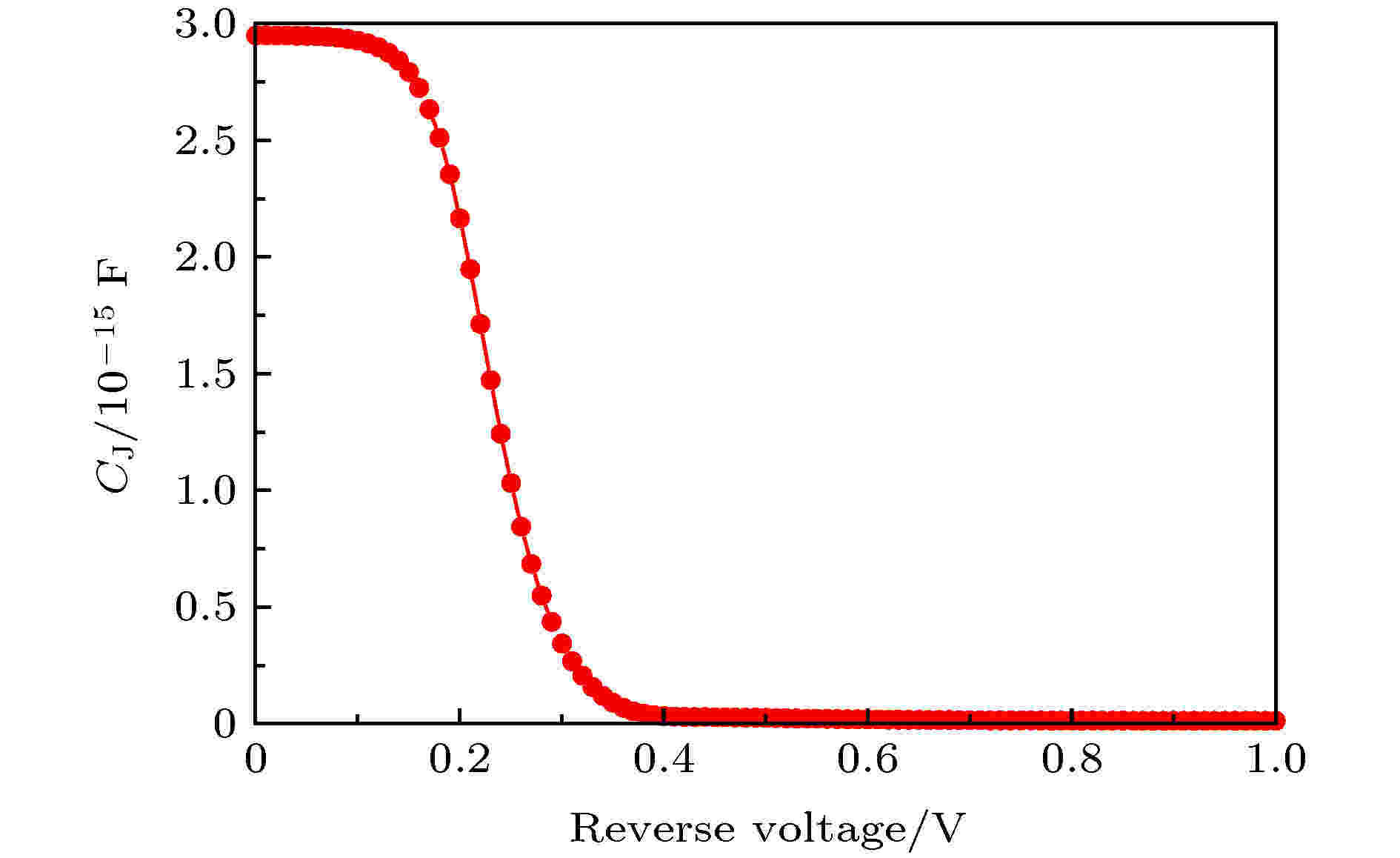图 15 全耗尽GeOI折叠空间电荷区肖特基二极管的C-V曲线Figure15. The C-V curve of fully depleted GeOI folded space charge region SBD.
将所设计的全耗尽GeOI折叠肖特基二极管仿真分析的正向I-V曲线, 反向I-V曲线以及在2.45 GHz频率下的C-V曲线带入Cadance Model Editor软件中提取器件的SPICE参数如表2所列[22].
| 参数 | 单位 | 全耗尽GeOI折叠空间电荷区肖特基二极管 |
| $ {B}_{\mathrm{v}} $ | V | 18 |
| $ {C}_{\mathrm{j}0} $ | pF | 0.3 |
| $ {E}_{\mathrm{G}} $ | eV | 0.69 |
| $ {I}_{\mathrm{B}\mathrm{V}} $ | A | 3 × 10-5 |
| $ {I}_{\mathrm{S}} $ | A | 1.12 × 10-10 |
| N | 1.08 | |
| $ {R}_{\mathrm{S}} $ | $\Omega $ | 6.0 |
| $ {P}_{\mathrm{B}} $ | V | 0.2 |
| $ {P}_{\mathrm{T}} $ | 2 | |
| M | 0.5 |
表2全耗尽GeOI折叠空间电荷区肖特基二极管SPICE参数表
Table2.The SPICE parameters of C-V curve of fully depleted GeOI folded space charge region SBD.
将所设计的全耗尽GeOI折叠肖特基二极管SPICE参数带入ADS仿真软件中, 采用图5所示仿真电路, 使用阻抗自匹配模型, 得到如图16所示的仿真结果, 在输入能量为24.5 dBm时, 能量转换效率达到了75.4%. 通过HSMS-2820肖特基二极管与本文所设计的全耗尽GeOI折叠空间电荷区肖特基二极管相对比, 能量转换效率得到了6.3%的提升.
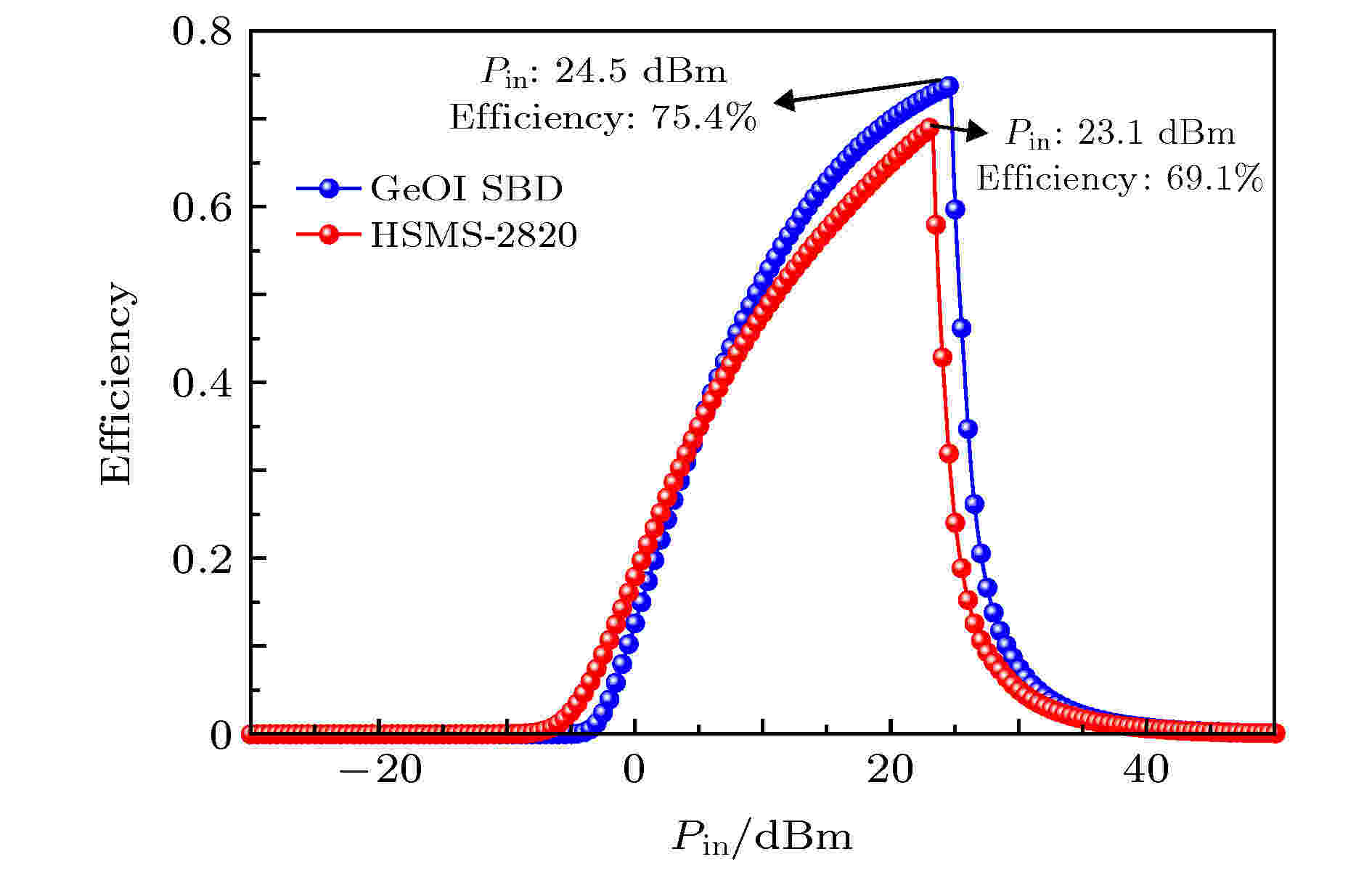图 16 全耗尽GeOI折叠空间电荷区肖特基二极管与HSMS-2820肖特基二极管能量转换效率对比图Figure16. Comparison of energy conversion efficiency between fully depleted GeOI folded space charge region SBD and HSMS-2820 SBD.
