摘要:随着显微镜性能的不断提升, 要求显微目镜具有更大的视场、放大倍率以及更好的成像质量. 显微目镜由于孔径光阑外置, 且焦距较短, 其设计难点在于如何校正大视场带来的畸变与其他轴外像差, 并在此基础上获得符合人眼观察要求的出瞳距离. 本文分析了目镜光学系统存在的主要像差, 特别是带有畸变的光学系统对成像所产生的影响. 将自由曲面应用在显微目镜光学系统畸变校正中, 设计出一款视场角达到60° (即 ± 30°), 放大倍率达到25× 且全视场畸变小于5%的高倍率广角显微目镜. 采用五片三组元式结构, 其中自由曲面镜片采用塑料材料且关于XOZ与YOZ平面对称, 实现了结构简单、易于加工且成本较低的高性能显微目镜设计.
关键词: 显微目镜/
自由曲面/
大视场/
高倍率

English Abstract

全文HTML

--> --> -->

随着各研究领域的深入, 对重要研究工具—显微镜的性能要求也逐渐提升. 目镜广泛应用于显微镜等目视光学系统中, 其功能和设计方法与成像物镜有很大的不同. 目镜需要在人眼可接受的范围内, 将一定距离处的放大图像呈现出来, 因此目镜的出瞳必须外置, 并且具有一定的出瞳距离以满足人眼观察的需求^[1]. 为满足更加复杂的实验要求, 需要目镜的观察视野更大, 放大倍率更高, 以与具有较大线视场的显微物镜相匹配. 普通目镜的视场角在30°左右, 而广角目镜通常是指视场角在50°以上的目镜^[2]. 大视场为目视光学系统引入更大的畸变, 8%—12%的畸变在广角目镜中都是很常见的现象^[1], 所以需要运用更加复杂的光学结构来加以校正. 自由曲面的应用对畸变具有良好的校正效果, 并且能够简化光学系统结构, 减少所需透镜片数^[3,4].
自由曲面拟合通常是利用假想为曲面上的一组离散点, 寻找形式比较简单、性能良好的曲面的解析表达式. 曲面的解析表达式采用参数形式来表示, 这种形式允许多值曲面用统一的形式来表示, 且和坐标系的选取无关. 曲面通常采用数学方程式来定义, 常见自由曲面面型描述方法包含B样条曲面、Bezier曲面、NURBS法等^[5]. 随着塑料材质镜片的出现以及加工技术的进步, 自由曲面的加工变得越来越切实可行^[6-9]. 和传统球面光学相比较, 自由曲面光学具有以下特点:
1)提供更多的设计自由度, 光学面型可由非对称、不规则、复杂的自由曲面随意组合而成^[2];
2)采用先进的数控超精密制造技术, 直接加工出自由曲面光学面, 被加工面可以达到亚微米量级面型精度与纳米量级表面粗糙度^[10];
3)采用光学塑料等新材料技术, 大批量生产光学组件^[11,12].
自由曲面在非成像系统的应用主要包括: 激光整形^[13,14]、汽车照明^[15]、LED均匀照明等^[16,17]. 随着研究的深入, 自由曲面的研究慢慢延伸到了成像领域, 如离轴反射系统^[18,19]、头盔显示器^[20]、自由曲面微透镜阵列^[21]和全景光学系统^[22]中, 用来校正光学系统的各种像差.
本文采用五片三组元式结构, 设计出一款结构简单、且具有高放大倍率与较高成像质量的广角显微目镜. 采用一片塑料自由曲面透镜对小孔径、大视场显微目镜系统中的畸变进行校正, 极大地简化了光学系统结构, 获得了良好的效果.

广角目镜的工作波段设计为486—656 nm, 以便于目视观察. 人眼内虹膜中心的瞳孔为光线进入眼睛的通道, 在目镜光学系统中相当于孔径光阑. 瞳孔括约肌的收缩与扩张可以使瞳孔缩小与扩张从而控制进入瞳孔的光量. 一般人眼瞳孔直径可变动在1.5—8 mm之间, 考虑到显微镜视场的照明强度等因素, 一般将显微目镜出瞳直径设置为1—2 mm.
显微目镜焦距与放大倍率间的关系为

$f_{\rm{e}}' = \frac{{250}}{\varGamma },$

其中$f_{\rm{e}}'$为目镜焦距, Γ为目镜放大倍率.
故目镜焦距越短, 放大倍率越大. 而显微镜的观察方式又要求一定的出瞳距离, 故如何兼顾放大倍率与适当的出瞳距也是本设计的难点. 为便于观察且免除人眼睫毛的影响, 一般要求显微目镜的出瞳距离大于6 mm, 本设计出瞳距离为7.4 mm, 满足目镜设计要求.
目镜系统的调焦距离计算公式为

$x = N\frac{{f_{\rm{e}}'}}{{1000}},$

其中N为视度调节范围, $f_{\rm{e}}'$为焦距, x为调节距离.
一般目镜的视度调节范围$ N = \pm 5 $屈光度, 将$f_{\rm{e}}' = {10}\;{\rm{mm}}$代入(2)式计算可得最后一个面到像面的距离应不小于1 mm, 本系统的工作距离为5 mm, 符合视度调节要求.
目镜光学系统的典型结构如图1所示, 由于目视观察的特殊性, 系统的孔径光阑外置, 对出瞳距离的大小有一定的要求. 这导致轴外光线在各透镜上的入射角与入射高度较大, 为系统引入了较大的轴外光线像差.
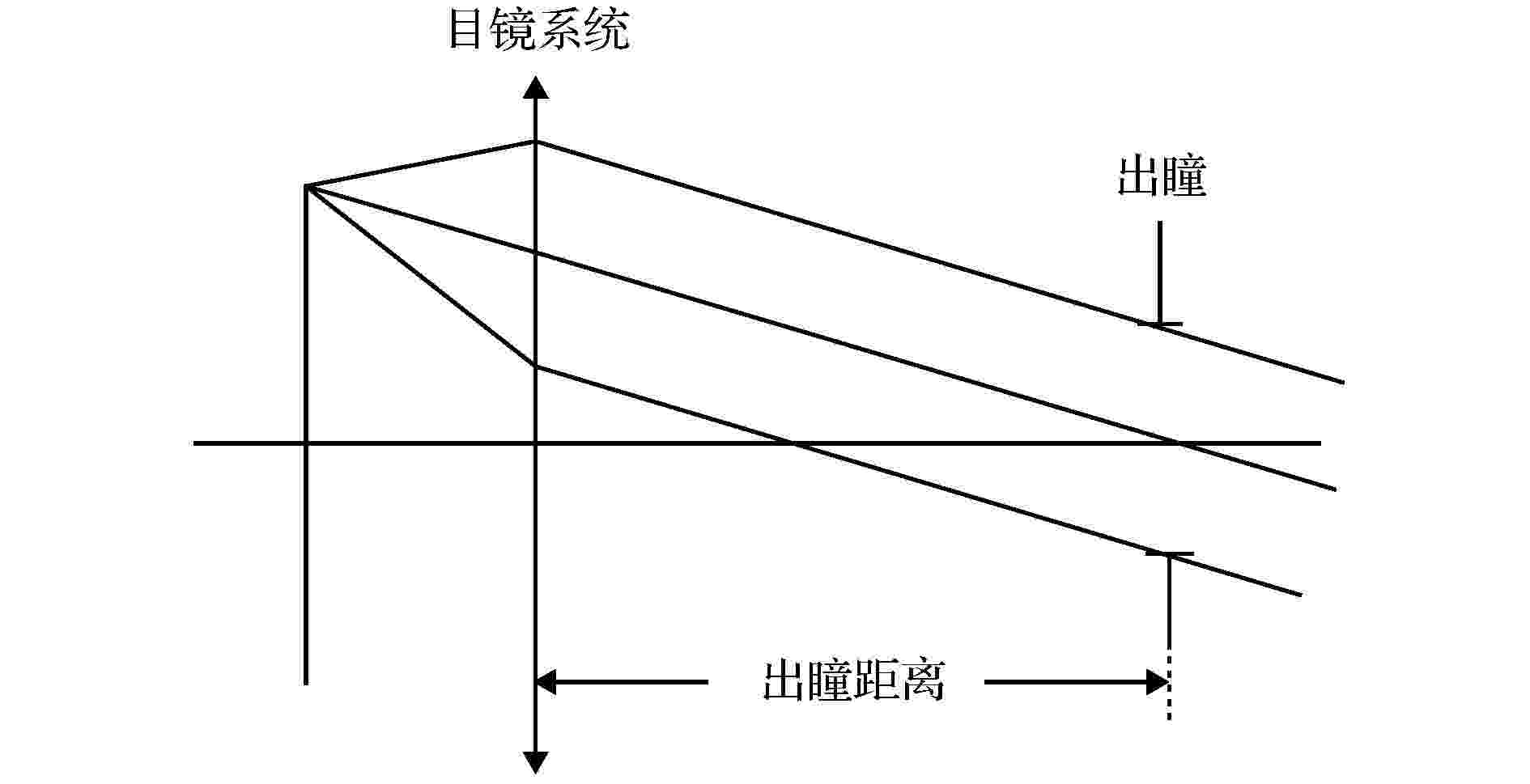图 1 目镜光学系统示意图
Figure1. Schematic diagram of eyepiece.

为便于分析, 把像差展开为孔径和视场的级数^[5]. 那么轴外点的像差空间分量可以表示为

$\Delta A' = {T_1}U_1^my_1^n + {T_2}U_2^my_2^n + {T_3}U_3^my_3^n + \cdots, $

其中$\Delta A'$代表某一种像差; ${T_1}$, ${T_2}$, ${T_3}$为各级像差系数; $y$代表像高, 与视场成正比; $U$代表孔径; $m$, $n$为常数; ${T_1}U_1^my_1^n$为初级像差, ${T_2}U_2^my_2^n$为二级像差, 以此类推.
只保留到二级像差, 大视场小孔径光学系统中彗差、细光束场曲、畸变的级数展开式为

$\left\{ \begin{aligned}& K_{{\rm{ts}}}' = {A_1}y{U^2} + {B_1}{y^3}{U^2},\\& x_{{\rm{ts}}}' = {C_1}{y^2} + {C_2}{y^4},\\& {\rm{d}}Y_z' = {D_1}{y^3} + {D_2}{y^5},\end{aligned} \right.$

其中$K_{{\rm{ts}}}'$, $x_{{\rm{ts}}}'$, ${\rm{d}}Y_z'$代表彗差、细光束场曲和畸变; ${A_1}$和${B_1}$, ${C_1}$和${C_2}$, ${D_1}$和${D_2}$分别代表球差、细光束场曲和畸变系数. 由此可知彗差与视场和孔径都相关. 可知细光束场曲和畸变与光学系统视场成正比. 由(4)式可以得知, 随着视场的增大, 初级彗差、初级像散、初级场曲、初级畸变等与视场有关的像差都会随之增大. 要校正这些像差, 通常都会导致系统的复杂度上升, 透镜片数增多.
基于光学硬件校正畸变的要点在于改变每一个视场的光线的最终出射方向, 使得每个视场的光线最终到达无视觉畸变所对应的新像点. 对具有畸变的光束结构进行分析, 即可得到成像光线与理想像点的偏离量.
设物面坐标为x, y; 入射光瞳面上的坐标为h, z. 由于存在像差, 其通过光学系统后的共轭光线与子午面的交点并不在高斯像面上. ${\rm{d}}Y'$和${\rm{d}}Z'$分别表示子午垂轴像差和弧矢垂轴像差分量. 把${\rm{d}}Y'$和${\rm{d}}Z'$展开成$y$, $x$, $z$和$h$的级数, 推导出空间光线初级像差的表达式为^[5]

$\begin{split}& n_k'u_k'{\rm{d}}Y_k' - {n_1}{u_1}{\rm{d}}{Y_1} \\={}& - {h_1}(h_1^2 + x_1^2){A_h}\sum\limits_{i = 1}^k {{S_{\rm I}}} + {y_1}(3h_1^2 + x_1^2){B_h}\sum\limits_{i = 1}^k {{S_{{\rm I}{\rm I}}}} \\ & - 3{h_1}y_1^2{C_h}\sum\limits_{i = 1}^k {{S_{{\rm I}{\rm I}{\rm I}}}{\rm{ + }}} {h_1}y_1^2{C_h}\sum\limits_{i = 1}^k {{S_{{\rm{{\rm I}V}}}} + y_1^3{D_h}\sum\limits_{i = 1}^k {{S_{\rm{V}}}} }, \\ & n_k'u_k'{\rm{d}}Z' - {n_1}{u_1}{\rm{d}}{Z_1} \\ ={}& - {h_1}(h_1^2 + z_1^2){x_1}{A_h}\sum\limits_{i = 1}^k {{S_{\rm I}}} + 2{y_1}hz{B_h}\sum\limits_{i = 1}^k {{S_{{\rm I}{\rm I}}}}\\ & - {z_1}y_1^2{C_h}\sum\limits_{i = 1}^k {{S_{{\rm I}{\rm I}{\rm I}}}} - {z_1}y_1^2{C_h}\sum\limits_{i = 1}^k {{S_{{\rm I}{\rm{V}}}}},\\[-18pt]\end{split} $

其中${A_h}$, ${B_h}$, ${C_h}$, ${D_h}$为公共因子, 对于每个折射面来说是一个不变量; ${S_{\rm I}}$, ${S_{{\rm I}{\rm I}}}$, ${S_{{\rm I}{\rm I}{\rm I}}}$, ${S_{{\rm I}{\rm{V}}}}$, ${S_{\rm{V}}}$为塞德和系数.
用极坐标来表示入射光瞳面上光线的坐标, 如图2所示, 可得极坐标表达式为

$\left\{ \begin{aligned} &{{{r}}^2} = {{h}}_1^2 + {{z}}_1^2,\\ &{{{h}}_1} = {{r}}\cos q,\\ &{{{z}}_1} = {{r}}\sin q.\end{aligned} \right.$

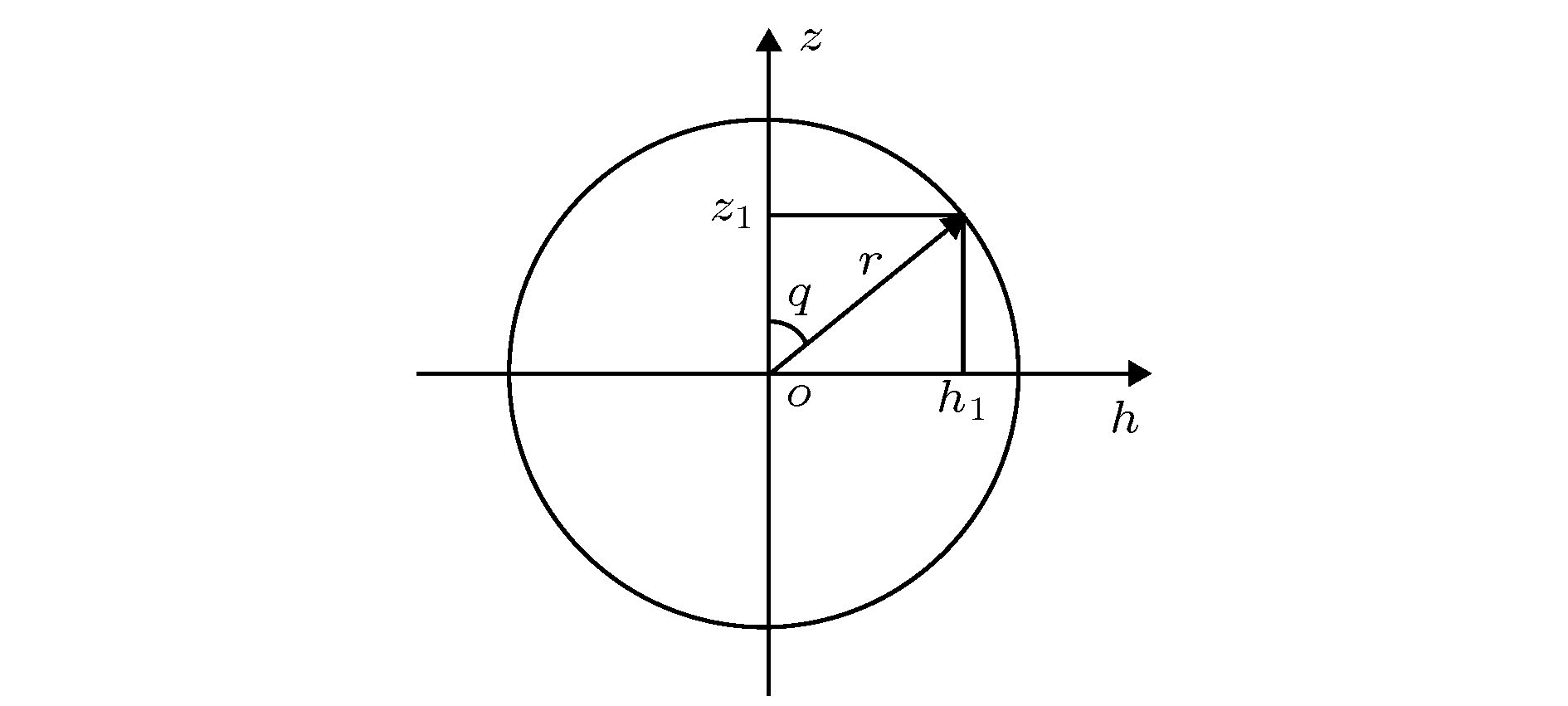图 2 入射光瞳面上光线坐标
Figure2. Coordinates of ray on the entrance pupil surface.

将(6)式代入(5)式可得初级像差的极坐标表达式如下:

$\begin{aligned} & n_k'u_k'{\rm{d}}Y_k' - {n_1}{u_1}{\rm{d}}{Y_1} \\ ={}& {A_h}{{{r}}^3}\cos q\sum\limits_{i = 1}^k {{S_{\rm I}}} + {B_h}{y_1}{{{r}}^2}(1 + 2{\cos ^2}q)\sum\limits_{i = 1}^k {{S_{{\rm I}{\rm I}}}}\\ & - {C_h}y_1^2{{r}}\cos q(3\sum\limits_{i = 1}^k {{S_{{\rm I}{\rm I}}}} + \sum\limits_{i = 1}^k {{S_{\rm III}}) + {D_h}y_1^3\sum\limits_{i = 1}^k {S{D_{{\rm{{\rm I}V}}}}} },\end{aligned} $

$\begin{split}& n_k'u_k'{\rm{d}}Z' - {n_1}{u_1}{\rm{d}}{Z_1} \\={}& {A_h}{{{r}}^3}\sin q\sum\limits_{i = 1}^k {{S_{\rm I}}} + {B_h}{y_1}{{{r}}^2}2\cos q\sin q\sum\limits_{i = 1}^k {{S_{{\rm I}{\rm I}}}} \\ & - {C_h}y_1^2{{r}}\sin q \bigg(\sum\limits_{i = 1}^k {{S_{{\rm I}{\rm I}{\rm I}}}} + \sum\limits_{i = 1}^k {{S_{{\rm{{\rm I}V}}}}} \bigg).\end{split} $

在(7)式中保留含有$\displaystyle\sum {{S_{\rm{V}}}} $的项即可得(8)式:

$\left\{ \begin{aligned}& {\rm{d}}Y' = y_1^3{D_h}\sum {{S_{\rm{V}}},} \\& {\rm{d}}Z' = 0.\end{aligned} \right.$

说明主光线经有畸变像差的光学系统折转后与理想像点偏离量为$y_1^3{D_h}\displaystyle\sum {{S_{\rm{V}}}} $.
在本光学系统中, 自由曲面校正畸变的原理可以概括为: 在传统目镜成像的基础上, 增加自由曲面光学元件, 改变每一个视场的光线的最终出射方向, 使得每个视场的光线都能到达其无视觉畸变所对应的新像点, 从而实现视觉上的畸变校正. 自由曲面光学表面相对于非球面而言具有更大的自由度, 在其表面上的每一点都有不同的曲率半径和法线方向. 由于入射光线、出射光线以及自由曲面上的点满足Snell定律^[23], 可以建立起自由曲面上每一点的入射光线、出射光线和自由曲面上点的位置和法线方向之间的关系为

$\begin{split} & {n_0} \times {\bar{ O}} - {n_1} \times {\bar{ I}} \\ =\; & {\left[ {n_0^2 + n_1^2 - 2 \times {n_0} \times {n_1} \times ({\bar{ O}} \cdot {\bar{ I}})} \right]^{1/2}} \times {\bar{ N}}, \end{split}$

其中${n_{\rm{0}}}$为空气折射率, ${\bar{ O}}$为出射光线单位矢量, ${n_1}$为球面与自由曲面之间的介质折射率, ${\bar{ I}}$为入射光线单位矢量, ${\bar{ N}}$为自由曲面上点的单位法矢量.
根据(9)式的关系以及前文由像差表达式推导得知的主光线偏离量, 可通过光学设计软件对系统成像质量进行模拟并且计算畸变大小, 然后针对自由曲面多项式系数进行优化以改变其面形, 从而对各点光线进行逐一校正. 所以可以利用自由曲面代替图像处理的方法来校正成像系统畸变.
将自由曲面运用到显微目镜这种大视场、小孔径的光学系统中, 可以获得较高的放大倍率以及较小的畸变像差. 本设计应用的XY多项式自由曲面是在二次曲面的基础上增加了最高幂数不大于$p$的多个${x^m}{y^n}$单项式, $(x, y, z)$为自由曲面上点的坐标, 其描述方程为^[24]

$\begin{split} & z = \frac{{c{r^2}}}{{1 + \sqrt {1 - (1 + k){c^2}{r^2}} }} + \sum\limits_{m = 0}^p {\sum\limits_{n = 0}^p {{E_{(m,n)}}{x^m}{y^n}} },\\ & \qquad\quad (1 \leqslant m + n \leqslant p),\\[-12pt]\end{split}$

其中$r = \sqrt {{x^2} + {y^2}} $, c为曲率, $k$为二次曲面系数, ${E_{(m, n)}}$为单项式${x^m}{y^n}$的系数.
由于将自由曲面应用于同轴系统中, 故将自由曲面设计为关于YOZ与XOZ面对称. 又因为$(x, y, z)$为自由曲面上点的坐标, 优化单项式${x^m}{y^n}$的系数${E_{(m, n)}}$即可改变自由曲面面形, 从而校正畸变等像差. 取$p = 8$, 方程为8阶XY多项式曲面, 系统自由曲面的方程为

$\begin{split} z =\; & \frac{{c{r^2}}}{{1 + \sqrt {1 - (1 + k){c^2}{r^2}} }} + {E_3}{x^2} + {E_5}{y^2} \\ &+ {E_{10}}{x^4} + {E_{12}}{y^4} + {E_{14}}{x^2}{y^2} + {E_{21}}{x^6} + {E_{23}}{x^4}{y^2} \\ & + {E_{25}}{x^2}{y^4} + {E_{27}}{y^6} + {E_{36}}{x^8} + {E_{38}}{x^8}{y^2} \\ & + {E_{40}}{x^4}{y^4} + {E_{42}}{x^2}{y^6} + {E_{44}}{y^8}.\\[-10pt]\end{split} $

大倍率广角显微目镜的参数指标如表1所列.

设计指标	数值
焦距/mm	10
放大倍率	25×
出瞳直径/mm	2
出瞳距离/mm	7
视场角/(°)	60
后截距/mm	5
畸变/%	< 5%

表1广角显微目镜参数指标
Table1.Design requirements for the wide-angle microscope eyepiece.

我们的最终设计是只有四个玻璃镜片和一个塑料镜片的组合. 基于自由曲面的大倍率广角显微目镜的光学系统结构示意图如图3所示, 本系统采用反向光路设计, 故以平行光入射. 选择由两个胶合透镜组和一个单正透镜组成的Erfle广角目镜结构作为初始结构, 选择合适的结构后, 使用不同类型玻璃材料的正确组合对镜头进行像差校正, 结合自由曲面进行优化, 即可完成设计过程.
图 3 广角目镜光学系统结构图
Figure3. Structure diagram of wide-angle eyepiece optical system.

广角显微目镜的光学系统数据与XY多项式自由曲面的面型参数如表2和表3所列. 其中第一个元件为光焦度为正的双胶合透镜, 第二元件为光焦度为正的单透镜, 第三元件为光焦度为负的双胶合透镜. 第一、三元件利用正负光焦度结合来校正系统色差, 减小第二元件与第一、三元件的间距以减小场曲. 玻璃材料选自成都光明玻璃库, 第二元件单透镜前后两面都应用了自由曲面, 并选取PMMA这种光学塑料, 因为其便于自由曲面的加工、重量较轻且成本低廉.

表面	半径/mm	厚度/mm	材料
物面	Infinity	Infinity
光阑	Infinity	7.11
2	–16.00	2.26	H-ZLAF78 B
3	–6.00	1.96	ZF4
4	–30.08	0.03
5*	15.27	5.03	PMMA
6*	–8.31	0.02
7	8.92	3.00	H-ZK7
8	33.30	1.98	ZF52
9	6.40	5
像面	Infinity	—
*表面5和6为非球面.

表2广角目镜光学系统参数
Table2.Optical prescription data for wide-angle eyepiece optical system.

	表面5	表面6
Conic	–4.00	–1.71
E3	4.18 × 10–3	0.017
E5	5.64 × 10–3	0.019
E10	2.33 × 10–3	3.00 × 10–3
E12	–8.73 × 10–5	2.58 × 10–4
E14	–4.19 × 10–5	1.10 × 10–4
E21	–4.19 × 10–4	–5.56 × 10–4
E23	4.59 × 10–6	6.61 × 10–6
E25	6.85 × 10–8	4.95 × 10–7
E27	1.38 × 10–7	2.77 × 10–7
E36	–7.25 × 10–6	6.64 × 10–9
E38	6.09 × 10–6	7.13 × 10–6
E40	3.81 × 10–8	3.39 × 10–7
E42	5.18 × 10–10	2.58 × 10–8
E44	–3.43 × 10–10	7.32 × 10–9

表3XY多项式系数
Table3.XY polynomial coefficients.

根据自由曲面描述公式以及各项系数, 用Matlab软件对第5, 6两面的自由曲面面型进行拟合, 得到如图4所示的结果.
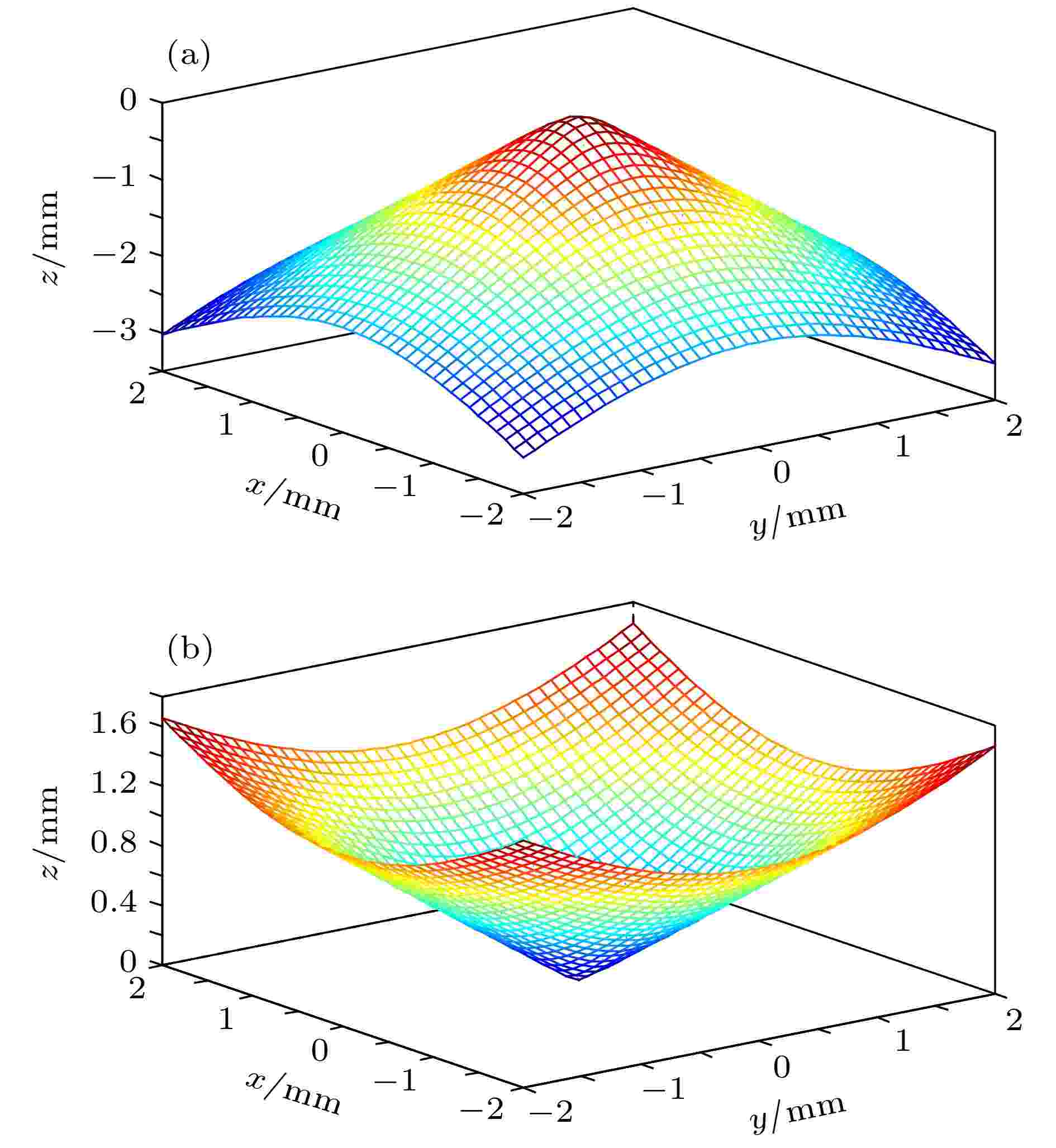图 4 自由曲面面型拟合示意图　(a) 第5面面型; (b) 第6面面型
Figure4. Simulation of freeform surface shape: (a) Shape of surface 5; (b) shape of surface 6.

传统的Erfle目镜通常应用于低倍观测, 在高倍观测表现不佳. 本设计将传统结构与自由曲面相结合, 获得了高放大倍率、大视场且成像质量良好的广角目镜系统.

广角显微目镜的成像评价指标如表4所列.

评价指标	数值
40 lp/mm处MTF	> 0.3
畸变/%	< 5
场曲/mm	< 0.2

表4成像质量评价指标
Table4.Evaluation index of imaging quality

图5显示了本系统7个视场子午和弧矢方向的调制传递函数(MTF)曲线, 在40 lp/mm处所有视场MTF均大于0.3, 平均MTF大于0.5, 满足目视系统分辨率要求, 成像质量良好.
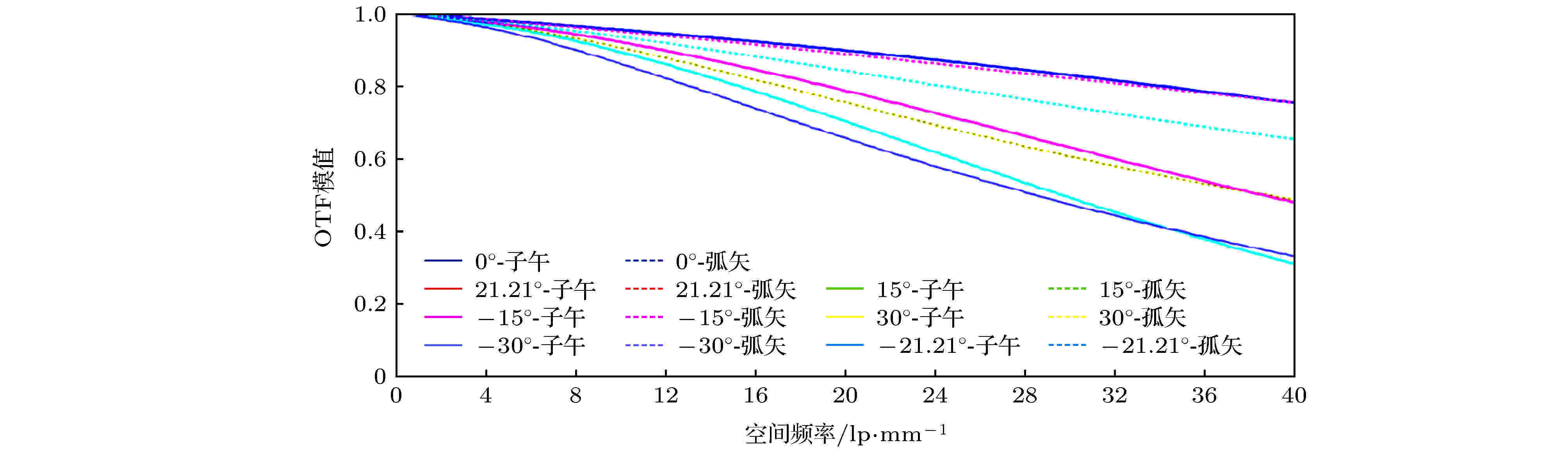图 5 MTF曲线图
Figure5. MTF of microscope eyepiece.

畸变定义为主光线与高斯像面的实际交点和理想像高之间的差异, 相对畸变定义为

$q' = ({{Y_z' - y'}})/{{y'}} \times 100\%, $

其中$q'$代表相对畸变; $Y_z'$为主光线与高斯像面相交的实际像高; $y'$为理想像高. 畸变与视场成正相关, 视场越大, 光学系统畸变越严重. 由于畸变不影响成像清晰度, 故目视系统中允许一定程度的畸变, 如表5所列.

视场角2ω'	相对畸变δyz'
40°	5%
60°—70°	10%
> 70°	> 10%

表5一般目视系统允许的相对畸变^[5]
Table5.Distortion allowed by general visual systems.

图6显示了本目镜系统的场曲与畸变. 本设计的视场角达到60°, 而相对畸变小于5%, 说明自由曲面对大视场小孔径光学系统的畸变校正达到了较好的效果. 图7显示了本光学系统的畸变网格. 由于应用在第5和6面的自由曲面关于YOZ与XOZ面对称, 故产生的畸变也关于这两面对称.
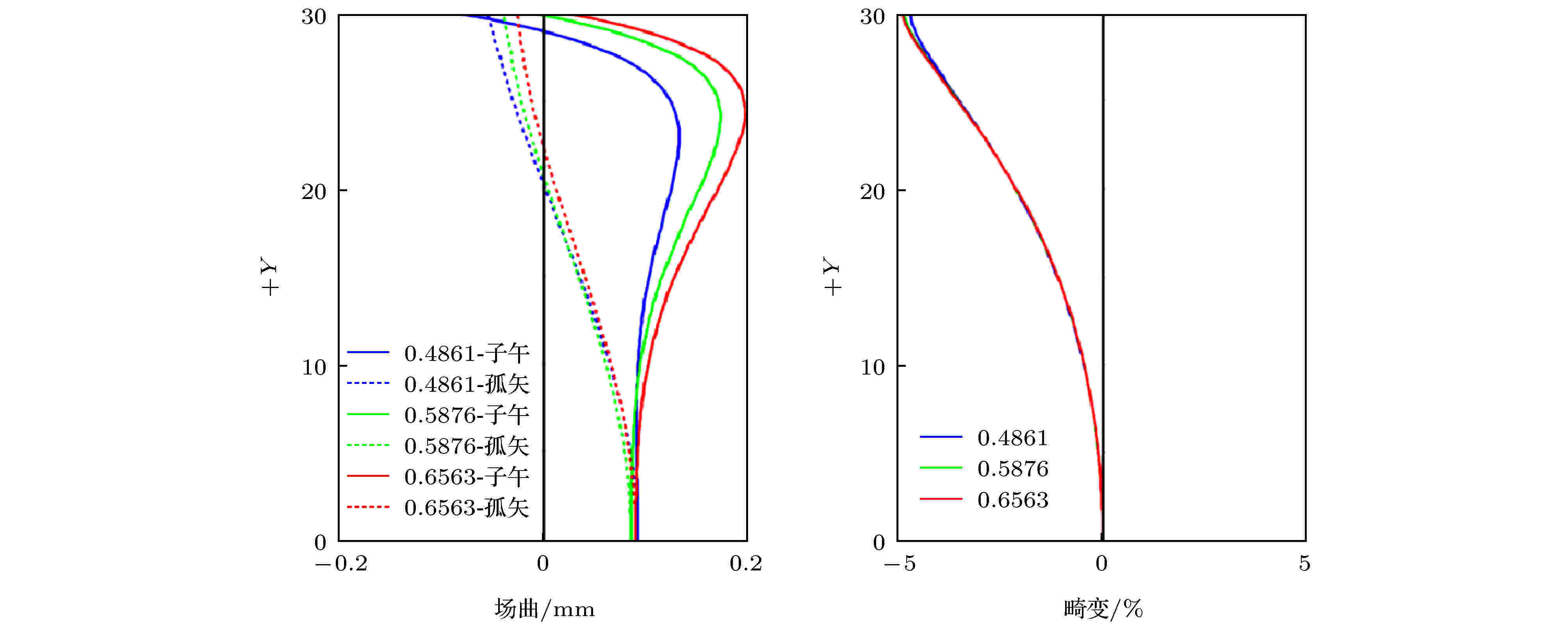图 6 场曲与畸变
Figure6. Field curvature and distortion.

图 7 畸变网格
Figure7. Grid distortion.

对系统进行公差分析以确定该系统是否易于加工, 公差值如表6所列. 公差分析结果证实了制造符合规格的广角目镜的能力. 所有公差均在制造和组装的通常能力范围内. 表7列出了蒙特卡罗分析的结果, 该结果估计了广角目镜在制造和组装后的MTF值. 结果表明, 有50%的蒙特卡罗模拟得出的40 lp/mm处平均MTF ≥ 0.523, 这满足了能接受的标准, 即50%的蒙特卡罗模拟必须大于或等于设计要求的MTF数值. 分析结果表明, 该广角目镜可以被成功地制造和组装.

公差项	公差值
半径/mm	0.02
厚度/mm	0.03
元件倾斜/(°)	0.02
元件偏心/mm	0.02
不规则度/fringes	3
阿贝数/%	2
折射率	0.002

表6公差系数
Table6.Tolerance Parameter.

概率	40 lp/mm处平均MTF
90%	0.508
80%	0.510
50%	0.523
20%	0.540
10%	0.549

表7蒙特卡罗分析结果
Table7.Results of Monte Carlo analysis.

本文根据像差理论, 推导了目镜光学系统的光学特性与像差特点, 对大视场显微目镜的设计方法以及自由曲面对大视场畸变的校正原理进行了分析与说明. 应用自由曲面设计了一款焦距为10 mm、出瞳直径2 mm、视场角$2\omega = {60^ \circ }$、出瞳距离为7 mm的高放大倍率广角显微目镜, 并分析了其成像质量与公差. 设计结果表明, 该显微目镜成像质量良好, 全视场畸变小于5%, 且系统结构简单易于加工与装调, 满足大视场显微镜的使用要求.