删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

HfO<sub>2</sub>基铁电场效应晶体管读写电路的单粒子翻转效应模拟

本站小编 Free考研考试/2021-12-29
摘要:使用器件-电路仿真方法搭建了氧化铪基铁电场效应晶体管读写电路, 研究了单粒子入射铁电场效应晶体管存储单元和外围灵敏放大器敏感节点后读写数据的变化情况, 分析了读写数据波动的内在机制. 结果表明: 高能粒子入射该读写电路中的铁电存储单元漏极时, 处于“0”状态的存储单元产生的电子空穴对在器件内部堆积, 使得栅极的电场强度和铁电极化增大, 而处于“1”状态的存储单元由于源极的电荷注入作用使得输出的瞬态脉冲电压信号有较大波动; 高能粒子入射放大器灵敏节点时, 产生的收集电流使处于读“0”状态的放大器开启, 导致输出数据波动, 但是其波动时间仅为0.4 ns, 数据没有发生单粒子翻转能正常读出. 两束高能粒子时间间隔0.5 ns先后作用铁电存储单元漏极, 比单束高能粒子产生更大的输出数据信号波动, 读写“1”状态的最终输出电压差变小.
关键词: 铁电场效应晶体管/
单粒子瞬态/
单粒子翻转

English Abstract


全文HTML

--> --> -->
1.引　言
航天电子器件长时间工作在太空环境下, 会受到各种辐射粒子的影响而引发各种复杂的辐照问题[1,2]. 铁电存储器是以铁电薄膜的极化特性来存储信息的, 具有非挥发性、高存取速度、低功耗、强抗辐射能力等优点, 在航天电子器件中有独特的优势[3-7]. 铁电存储器根据单元结构的不同可以分为电容型(1T-1C和2T-2C)和晶体管型(1T). 相对电容型铁电存储器来说, 铁电场效应晶体管(ferroelectric field effect transistor, FeFET)可以实现非破坏性读取, 并且具有结构简单、集成度高等优点, 已经引起了研究人员的广泛关注[8-12]. 铁电薄膜是FeFET的核心材料, 其尺寸效应、保持性能和抗辐照能力直接决定FeFET的器件性能[13-15]. 以锆钛酸铅(PZT)为代表的传统钙钛矿材料与互补金属氧化物半导体(complementary metal oxide semiconductor, CMOS)工艺兼容性差, 已经不能满足FeFET高集成度化等的发展需求[16,17], 因此需要寻找与CMOS工艺兼容的新型铁电薄膜材料. 2012年德国科学家发现掺杂HfO2薄膜具有铁电性, 并且厚度可以薄至几纳米, 从此新型氧化铪铁电材料的研究成为一个热点[18,19]. Gong和Ma[20]研究了基于HfO2, PZT和SrBi2Ta2O9铁电薄膜的FeFET的保持性能, 表明HfO2是比较适合FeFET的铁电薄膜材料. Sharma和Roy[21]针对氧化铪基FeFET存储阵列进行了擦写和读取操作, 表明氧化铪基FeFET存储阵列可以在超低功耗下进行读写. HfO2基FeFET应用到航天电子器件时, 需要考虑各种辐射粒子的影响. 刘巧灵[22]发现了氧化铪基FeFET栅结构电容受到5 Mrad(Si)的60Co γ射线辐照后剩余极化值和保持性能基本没有变化, 证明了该器件具有优异的抗总剂量效应性能. HfO2基FeFET比传统FeFET的物理尺寸小, 总剂量辐射效应相对来说较弱, 却更容易产生单粒子效应[23-25]. 目前, HfO2基FeFET存储器仍在试验阶段, 市场上还没有HfO2基FeFET芯片, 因此难以开展其单粒子效应试验研究. 而仿真模拟具有不需要成品器件且能直观系统地分析器件内部变化的优点, 还可以降低研发成本和对铁电存储阵列和铁电电路进行准确的性能评估, 并在性能评估的基础上再对其进行各方面的的参数优化. 因此, 在当前没有HfO2基FeFET成品器件的情况下, 使用器件-混合仿真方法研究HfO2基FeFET单粒子效应是开展HfO2基FeFET单粒子效应研究较为必要且可行的内容.
本文使用半导体仿真软件搭建了45 nm工艺HfO2基FeFET读写电路, 对其不同敏感节点进行了单粒子翻转效应研究, 分析了存储数据发生变化的内在机制, 这对航空电子器件结构的设计和抗单粒子电路的搭建具有重要意义.
2.仿真设置
据报道, Hf0.5Zr0.5O2(HZO)厚度为10 nm时仍有良好铁电性能, 饱和极化强度2Pr可达到40 μC/cm2, 矫顽场强度为1 MV/cm[22], 本文选用HZO铁电薄膜参数和利用Sentaurus TCAD[26]建立45 nm工艺的HfO2基FeFET模型, 如图1所示, 器件的具体工艺参数如表1所列. 随后利用器件-电路混合仿真方法搭建了2 × 2铁电存储阵列的读写电路, 如图2所示, SGS和SGD表示选通控制信号; WL表示字线信号; BL 表示位线信号; Out 1和Out 2表示灵敏放大器输出信号; Sa_in表示铁电存储阵列的输出信号; Sa_ref表示参考输入信号. 其中SPICE (simulation program with integrated circuit emphasis)模型采用亚利桑那州立大学的45 nm工艺BSIM4 SPICE集约模型[27], 进行了读写时序的仿真, 如图3所示.
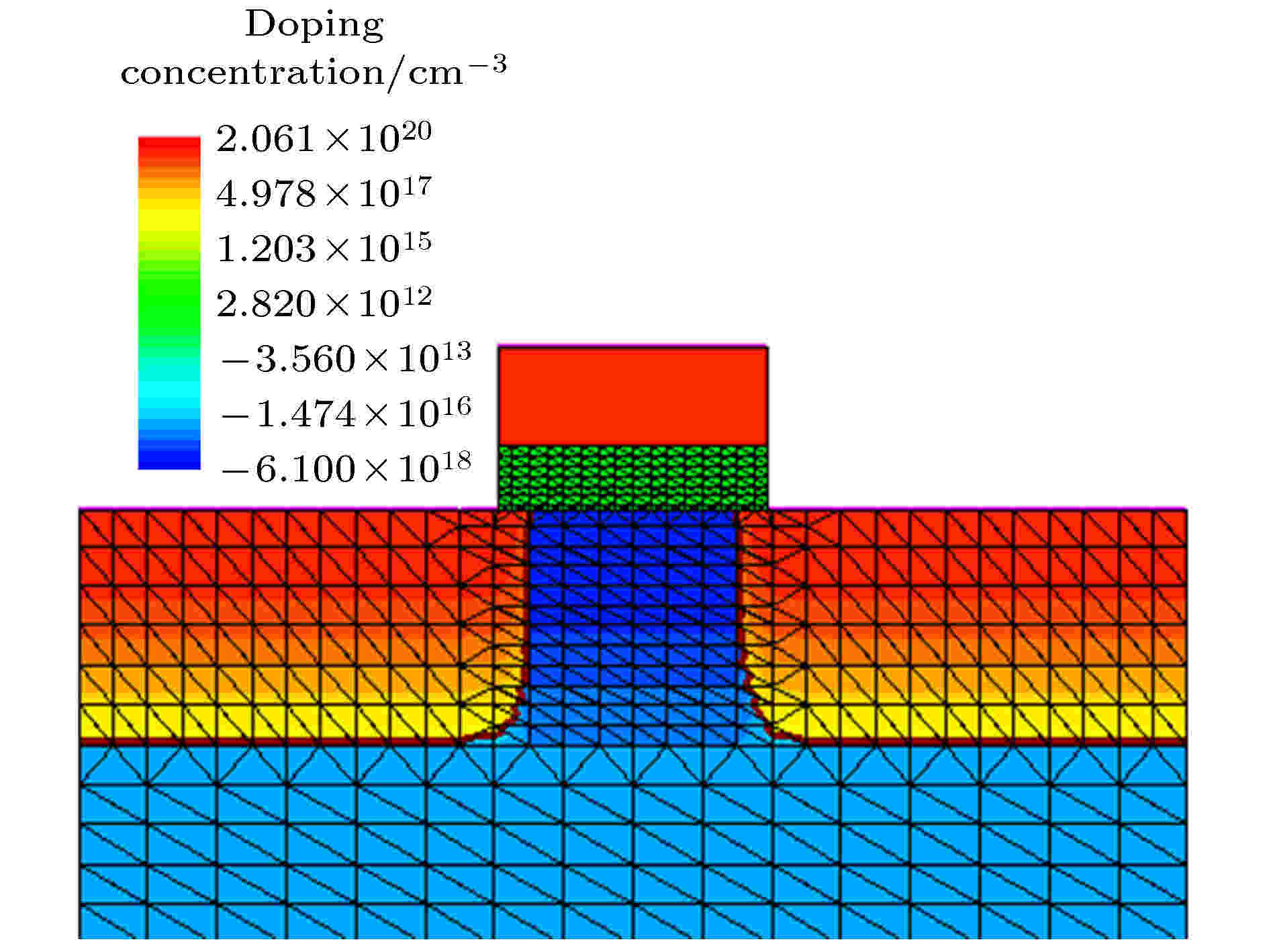图 1 HfO2基FeFET器件物理模型
Figure1. Device physical models of HfO2-based FeFET.

参数 数值
多晶硅厚度/nm20
栅氧层厚度/nm1
铁电层厚度/nm10
沟道长度/nm45
N型衬底浓度/cm–31 × 1016
N阱浓度/cm–35 × 1016
源/漏浓度/cm–32 × 1020
阈值电压掺杂浓度/cm–35 × 1017
饱和极化值Ps/μC·cm–228
剩余极化值Pr/μC·cm–223
矫顽场强度Ec/MV·cm–11
介电常数Eps22


表1HfO2基FeFET工艺参数
Table1.Process parameters of HfO2-FeFET.

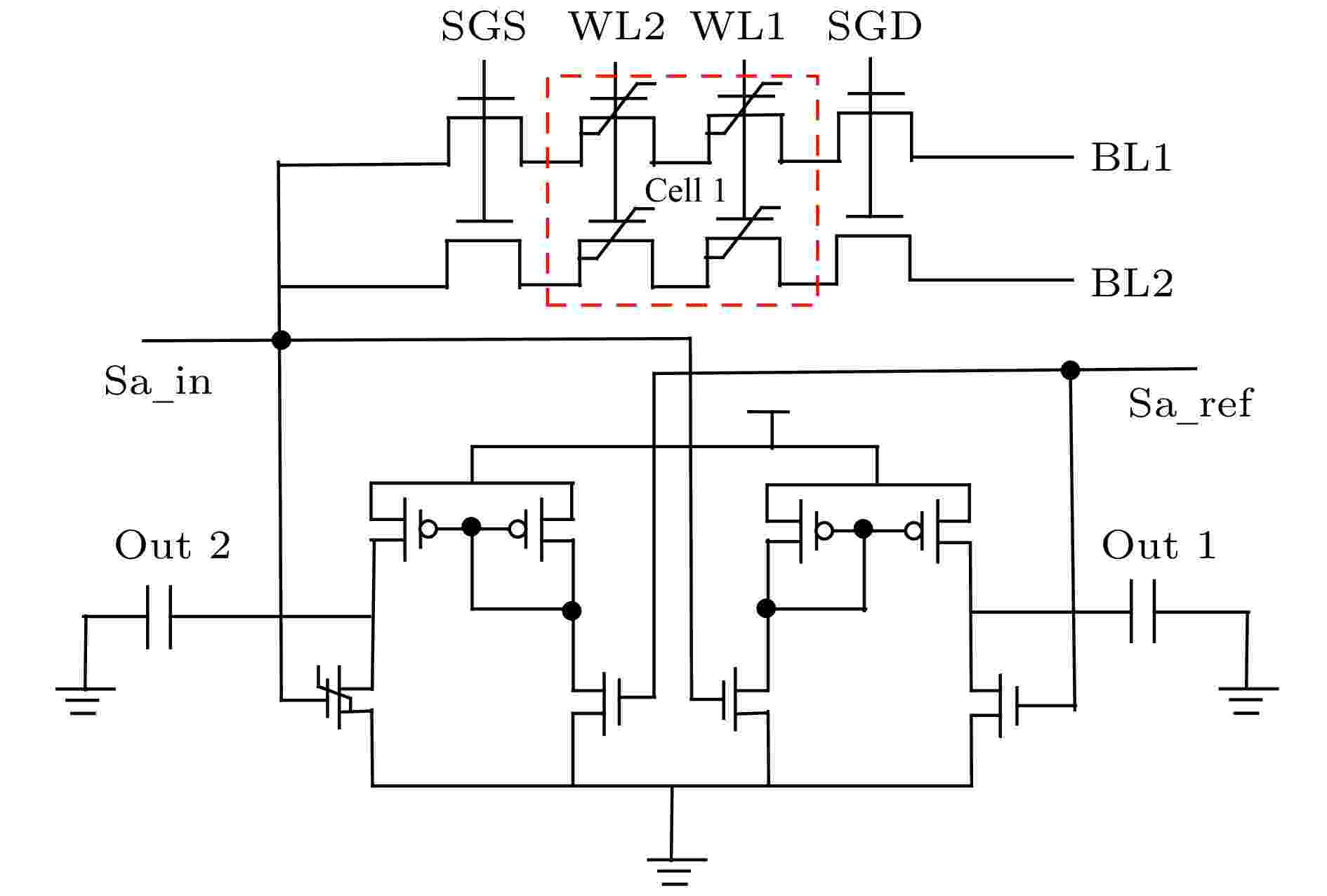图 2 2 × 2铁电存储阵列的读写电路
Figure2. Read and write circuit of 2 × 2 ferroelectric memory array.

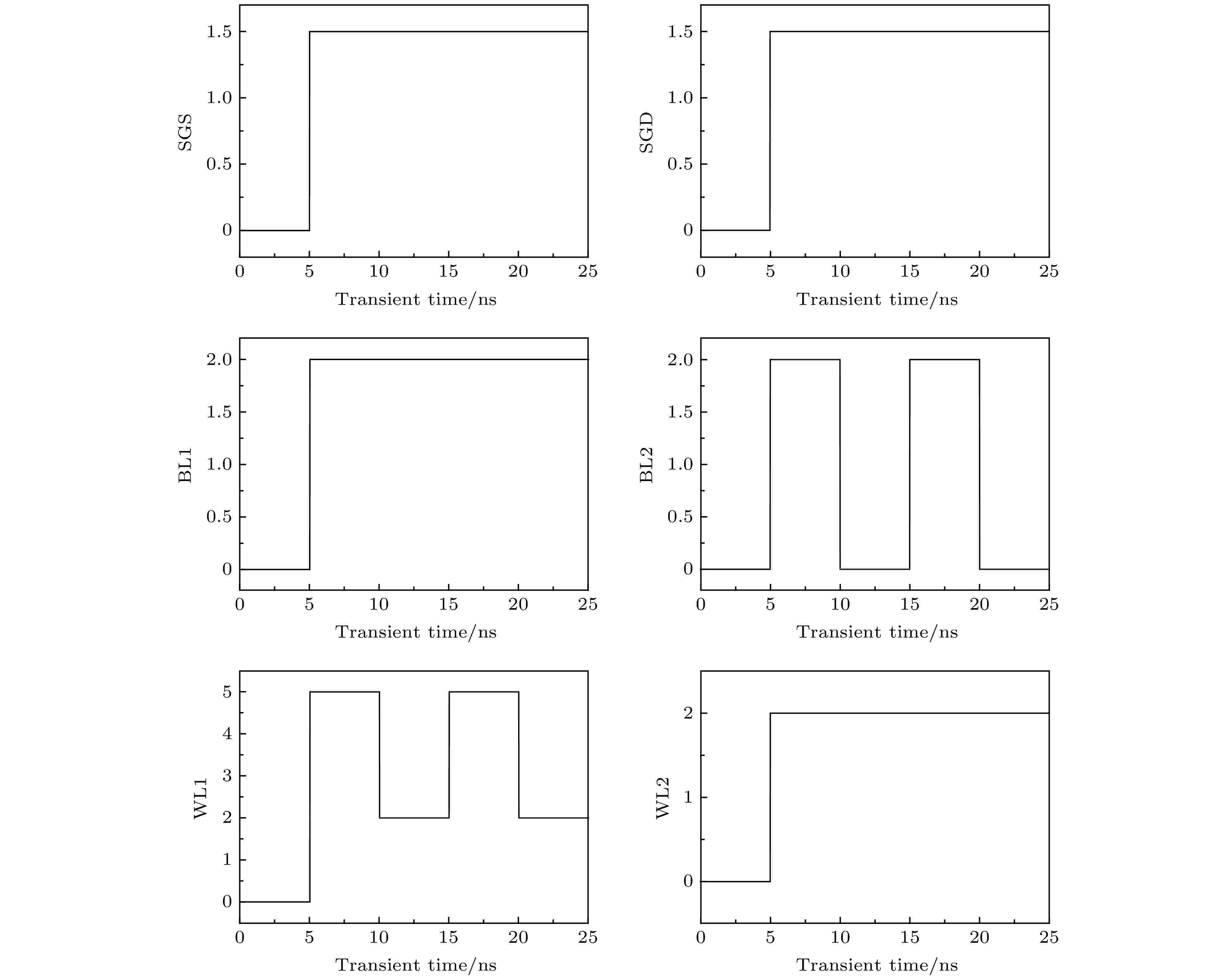图 3 2 × 2铁电存储阵列控制仿真时序
Figure3. Control simulation timing of 2 × 2 ferroelectric memory array.

对于深亚微米级器件, 使用流体动力学模型去描述器件的载流子输运过程, 流体动力学模型有如下几个基本方程:
泊松方程
$\nabla \cdot \varepsilon \nabla \psi = - q\left( {p - n + N_{\rm{D}}^ + - N_{\rm{A}}^ - } \right),$
载流子连续性方程
$\nabla \cdot{{{J}}_{{n}}} = q{R_{{\rm{net}}}} + q\frac{{\partial n}}{{\partial t}},$
$ - \nabla \cdot{{{J}}_{{p}}} = q{R_{{\rm{net}}}} + q\frac{{\partial p}}{{\partial t}},$
电子和空穴流密度方程
${{{J}}_{{n}}} = - qk{\mu _{\rm{n}}}{T_L}\nabla n - qn{\mu _{\rm{n}}}\nabla \psi - n{\mu _{\rm{n}}}\left[ {k{T_{\rm{L}}}\nabla ln{n_{{\rm{ie}}}}} \right],$
${{{J}}_{{p}}} = - qk{\mu _{\rm{p}}}{T_{\rm{L}}}\nabla n - qp{\mu _{\rm{p}}}\nabla \psi - p{\mu _{\rm{p}}}\left[ {k{T_{\rm{L}}}\nabla ln{n_{{\rm{ie}}}}} \right],$
其中ε为介电常数, $\nabla \psi $为静电势的梯度, q为基本电荷量, p和n为空穴和电子密度, $N_{\rm{D}}^ + $和$N_{\rm{A}}^ - $为电离的施主和受主浓度, TL为晶格常数, μn和μp为硅材料中的电子和空穴的迁移率, nie是本征载流子浓度.
FeFET器件中铁电层和沟道是高掺杂区域, 在数值器件模拟中为了更贴合实际器件考虑了掺杂、电场以及载流子之间的散射和碰撞电离模型对迁移率的影响, 主要包括掺杂SRH复合模型、Auger复合模型和高浓度掺杂下的禁带变窄模型. 通过引入量子势(载流子浓度和浓度梯度的函数)来考虑量子效应, 在传输方程中还采用了密度梯度模型、泊松方程和载流子连续方程解算量子势方程. 影响晶体管物理模型电学特性的详见半导体器件仿真工具[26].
铁电性能模型能描述仿真模拟铁电电容的瞬态电学特性和非饱和状态下极化特性, 是根据Miller和Mcwhorter[28]提出的铁电模型进行了优化, 引入了铁电电容率模型, 通过搭建等效电路对铁电极化特征进行了全面准确的描述, 同时包括饱和极化模型和非饱和极化模型. 优化模型的具体表达式如下:
附加电场的瞬态变化,
$\frac{{\rm{d}}}{{{\rm{d}}t}}{F_{{\rm{aux}}}}\left( t \right) = \frac{{F\left( t \right) - {F_{{\rm{aux}}}}\left( t \right)}}{{{\tau _E}}},$
附加极化强度,
${P_{{\rm{aux}}}} = c {P_{\rm{s}}} \tanh \left( {w \left( {{F_{{\rm{aux}}}} \pm {F_{\rm{c}}}} \right)} \right) + {P_{{\rm{off}}}},$
$w = \frac{1}{{2{F_{\rm{c}}}}}\ln \frac{{{P_{\rm{s}}} + {P_{\rm{r}}}}}{{{P_{\rm{s}}} - {P_{\rm{r}}}}},$
实际的极化瞬态行为,
$\frac{{\rm{d}}}{{{\rm{d}}t}}P\left( t \right) = \frac{{{P_{{\rm{aux}}}}\left[ {{F_{{\rm{aux}}}}\left( t \right)} \right] - P\left( t \right)}}{{{\tau _P}}}\left( {1 + {k_{\rm{n}}}\left| {\frac{{\rm{d}}}{{{\rm{d}}t}}{F_{{\rm{aux}}}}\left( t \right)} \right|} \right).$
上述方程式中, τE和τP为材料的附加电场弛豫时间常数和极化强度弛豫时间常数, Ps为饱和极化强度, Pr为剩余极化强度, Fc为矫顽电场, kn为材料的非线性耦合特征常数, c和Poff为铁电材料的极化参数.
采用了Gaussian分布建立单粒子辐射模型, 设置了轰击高能粒子的初始入射半径为0.05 μm, 入射深度为1 μm, 其他参数由TCAD默认设置. 详细求解高能粒子引起的电子空穴对产生率G的基本方程式如下:
$G\left( {l,\;w,\;t} \right) = {G_{{\rm{LET}}}}\left( l \right) \times R\left( {w,\;l} \right) \times T\left( t \right),$
${G_{{\rm{LET}}}}\left( l \right) = \frac{1}{{{\text{π }}w_{\rm{t}}^2}}\left( {1 + LET\_f\left( l \right)} \right),$
$R\left( {w,\;l} \right) = {\rm{exp}}\left[ { - {{\left( {\frac{w}{{{w_{\rm{t}}}\left( l \right)}}} \right)}^2}} \right],$
$T\left( t \right) = \frac{{2 \times {\rm{exp}}\left[ { - \left( {\dfrac{{t - {t_0}}}{{\sqrt 2 \cdot{s_{{\rm{hi}}}}}}} \right)} \right]}}{{\sqrt {2{\text{π}}} \cdot{s_{{\rm{hi}}}}\left[ {1 + {\rm{erf}}\left( {\dfrac{{{t_0}}}{{\sqrt 2 \cdot{s_{{\rm{hi}}}}}}} \right)} \right]}},$
其中$LET\_f\left(l \right)$为辐射产生的线性能量转移值(linear energy transfer, LET), l为入射深度, ${w_{\rm{t}}}\left(l \right)$为高能粒子入射半径, t0为初始入射时间, shi为Gaussian时序分布特征延迟时间.
对器件混合电路进行辐照模拟时, 首先通过(1)—(5)式和(9)式计算器件混合电路的电学特性求得稳态解, 然后结合单粒子辐射模型公式(10)计算出瞬态解.
3.模拟结果
2
3.1.HfO2基FeFET电路的读写
-->

3.1.HfO2基FeFET电路的读写

当栅极电压为负电压, 铁电极化从上指向下为负方向, 在沟道处有大量的累积电荷, 在漏源之间加小电压读出数据“0”; 当栅极电压为正电压, 铁电极化从下指向上为正方向, 沟道处出现了反型层, 在漏源之间加一个小电压读出数据“1”, HfO2基FeFET写入“1”和“0”状态时器件内部的电荷密度分布如图4所示. 输入2 × 2铁电存储阵列读写电路的控制时序如图3所示, 得到了HfO2基FeFET读写电路的灵敏放大器输出信号变化、铁电存储单元cell 1输出信号变化和铁电存储单元cell 1极化强度变化, 如图5所示. 通过输出电压的大小来定义存储状态“1”和“0”, 经过灵敏放大器进行数据读出. 当输入正栅压时, 铁电极化为正, 输出高电压为存储数据“1”; 当输入负栅压时铁电极化为负, 输出低电压为存储数据“0”.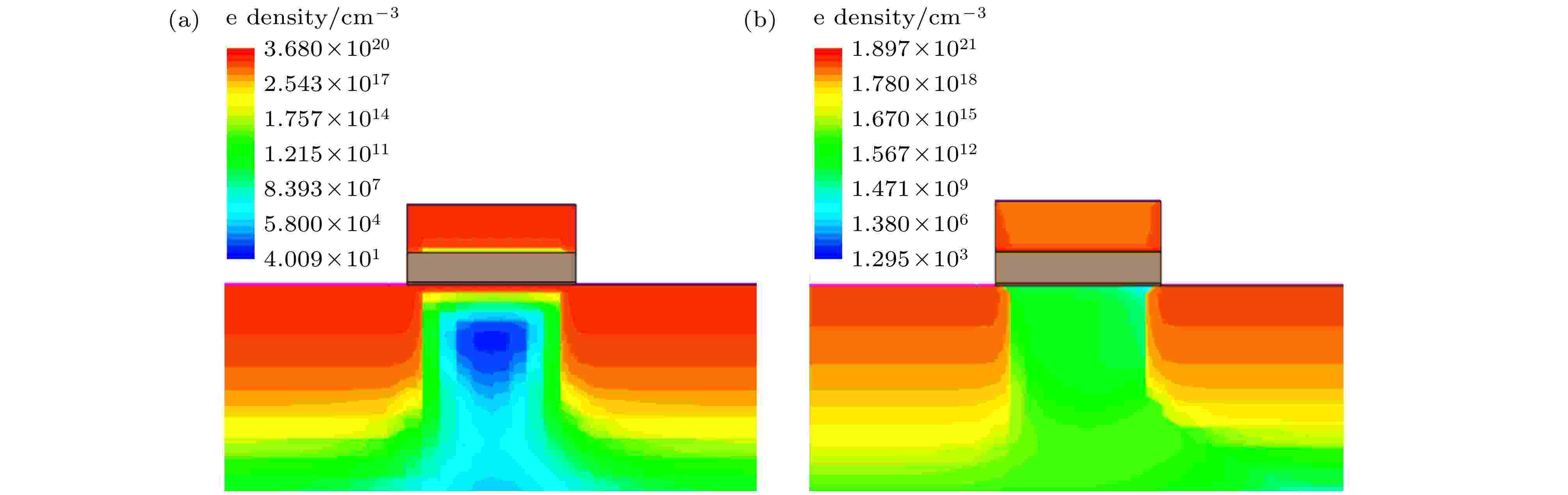
图 4 HfO2基FeFET写入时器件内部的电荷密度分布　(a)写入“1”器件内部电荷分布; (b)写入“0”时器件内部电荷分布
Figure4. Charge density distribution inside the device when HfO2-based FeFET is written: (a) The internal charge distribution of the device is written with “1”; (b) the internal charge distribution of the device is written with “0”.

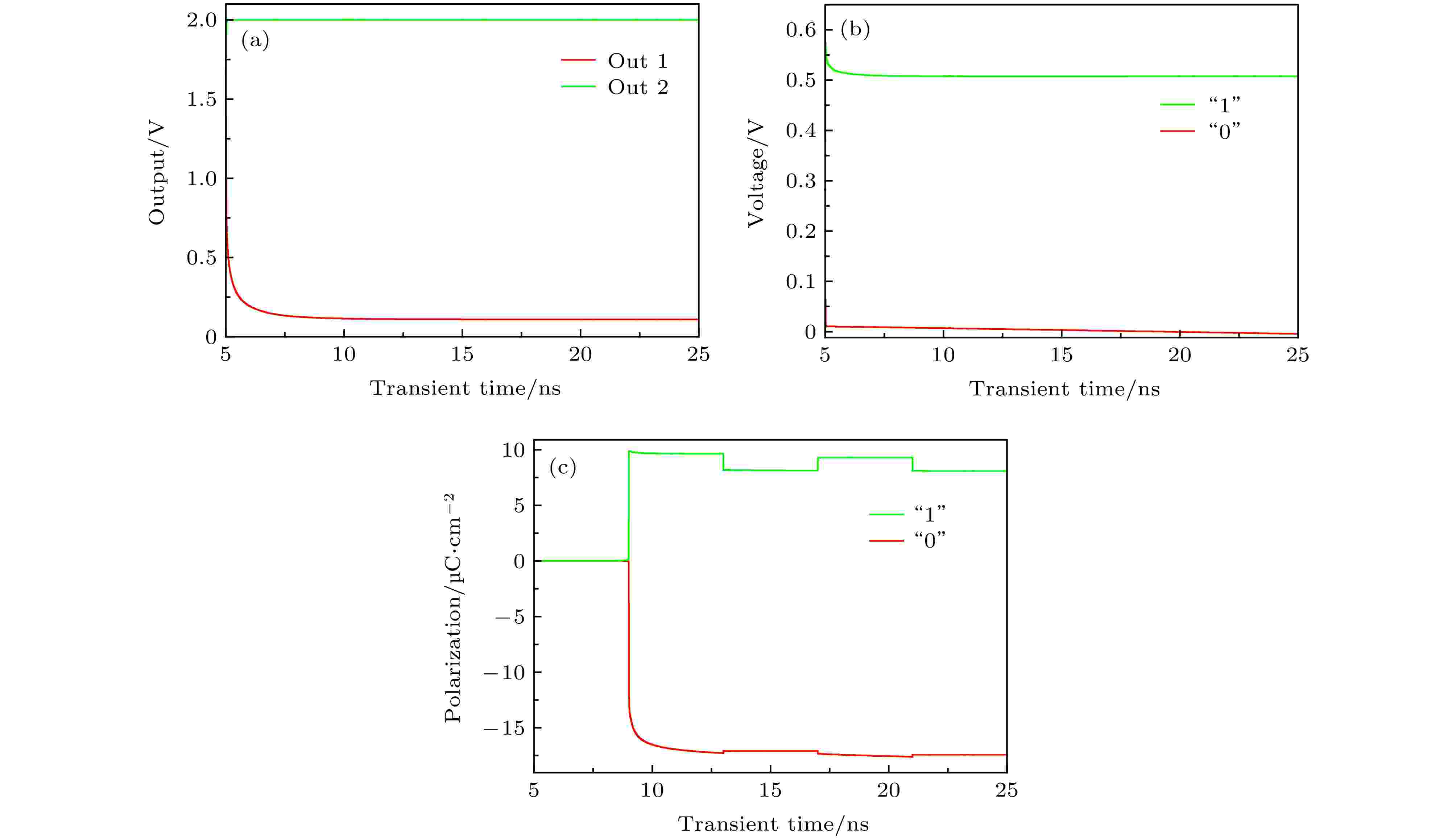图 5 铁电存储阵列的读写信号　(a)灵敏放大器输出信号变化; (b) cell 1输出信号变化; (c) cell 1极化强度变化
Figure5. Reading and writing of ferroelectric memory arrays: (a) Changes in the output signal of the sense amplifier; (b) changes in the output signal of cell 1; (c) changes in the polarization of cell 1.

2
3.2.单粒子入射铁电存储管漏极对存储信息的影响
-->

3.2.单粒子入射铁电存储管漏极对存储信息的影响

铁电存储单元作为FeFET读写电路的主要敏感节点之一, 其对单粒子瞬态效应的敏感度会直接影响数据的擦写, 因此非常有必要研究高能粒子入射其漏极的瞬态效应.
图6为单粒子入射读写“0”的铁电存储单元cell 1时, 漏极的各节点瞬态效应变化. 图6(a)为高能粒子入射铁电存储单元cell 1漏极产生的漏极电流脉冲变化, 漏极电流脉冲随着高能粒子的LET值增加而变大. 如图6(b)所示, 在高能粒子入射存储管漏极后, 在cell 1内部产生了大量电子空穴对, 同时部分电子或空穴被漏极收集导致器件被迫导通, 电流方向变为负, 因此铁电存储单元cell 1输出电压从0 V变为负电压. 如图6(c)所示, 电子空穴对的产生增强了铁电存储单元cell 1栅极和基底的电场强度, 使得极化强度增大. 从图6(d)可以看出, 在读写“0”状态时, 高能粒子进入cell 1内部产生的微小收集电流经灵敏放大器放大后, 仅略微增大了输出电压, 数据能正确读出.
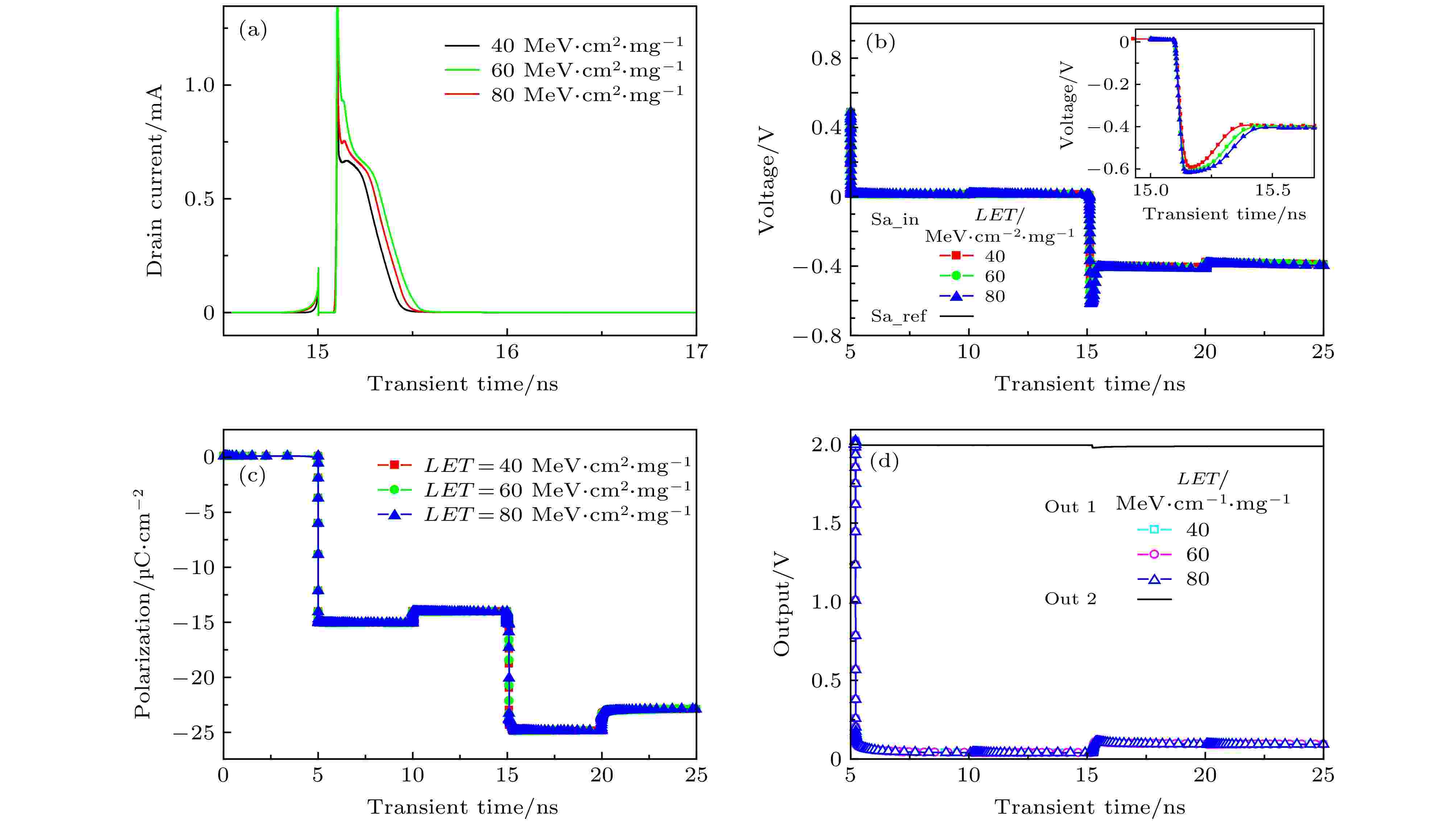图 6 单粒子入射读写“0”铁电存储单元cell 1漏极的瞬态效应　(a) cell 1漏极电流脉冲变化; (b) cell 1输出信号变化; (c) cell 1极化强度变化; (d)灵敏放大器输出信号变化
Figure6. Transient effects of single-particle incident read and write “0” ferroelectric storage tube drain: (a) Change of drain current pulse; (b) change of cell 1 output signal; (c) change of cell 1 polarization intensity; (d) change of sense amplifier output signal.

从图7(a)铁电存储单元cell 1输出信号变化可以看出, 在高能粒子入射铁电存储单元cell 1漏极后, 铁电存储单元cell 1输出电压随着入射粒子的LET值增大而增大. 虽然在器件内部产生了大量电子空穴对, 但是此时cell 1处于开启状态, 电子空穴对能及时导出, 内部电场强度只是稍稍增大, 使得极化强度的变化没有图6(c)明显. 随着高能粒子LET值增大, 图7(b)中铁电存储单元cell 1输出瞬态电压峰值随着增大, 在高能粒子的LET值为30 MeV·cm2/mg时, 铁电存储单元cell 1输出电压的峰值接近于0 V, 在5 ns之后能恢复初始状态, 经过灵敏放大器放大后得到图7(c)灵敏放大器输出信号变化, 但是输出电压出现波动的时间只有0.5 ns, 从而数据能正常读出.
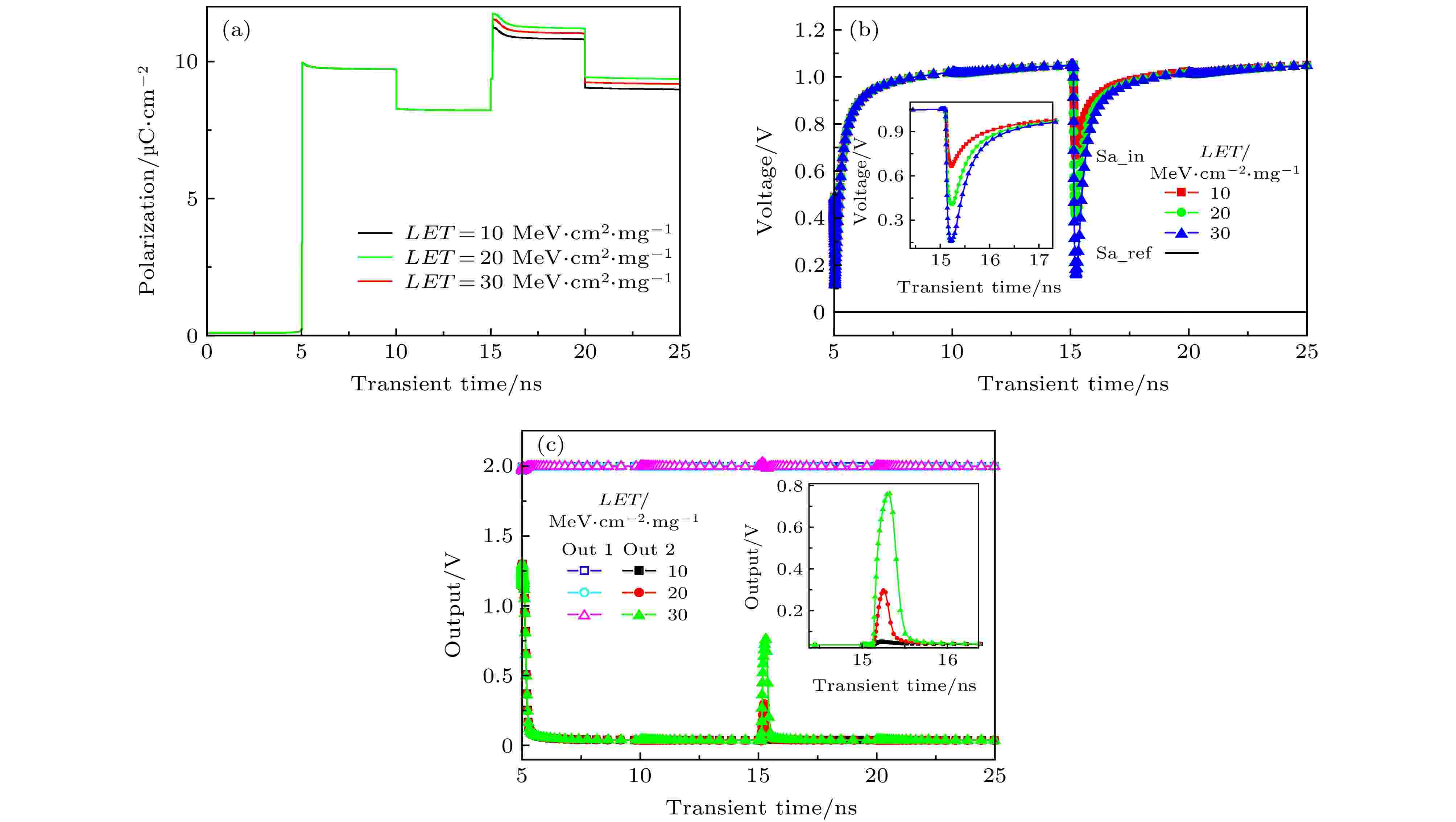图 7 单粒子入射读写“1”铁电存储单元cell 1漏极的瞬态效应　(a) cell 1极化强度变化; (b) cell 1输出信号变化; (c)灵敏放大器输出信号变化
Figure7. Transient effects of single-particle incident read and write “1” ferroelectric storage tube drain: (a) Change of cell 1 polarization intensity; (b) change of cell 1 output signal; (c) change of sense amplifier output signal.

为了更全面地分析单粒子入射铁电存储单元cell 1对存储信息的影响, 表2列出了不同LET值下输出端Out 1和Out 2之间的电位差变化. 尽管Sa_in和Sa_ref之间的电位差随着LET值的增加在不断减小, 但模拟中所采用的是理想型灵敏放大器能正确放大Sa_in和Sa_ref之间微小的电位差, 因此图7(c)中能够正确放大读出数据. 但是实际工作中没有理想型灵敏放大器, 灵敏放大器存在一个能够正确放大的最小输入电压差. 高能粒子入射铁电存储单元cell 1的漏极后, 在某个LET值下Sa_in和Sa_ref之间的电位差可能会小于灵敏放大器的最小分辨电压差, 导致数据信号不能正确放大读出以及回写, 引发单粒子翻转效应.
LET值/MeV·cm2·mg–1
0102030120150180
电压差/V1.91.851.71.210.950.9


表2输出端Out 1和Out 2之间的电位差变化
Table2.Voltage difference change between Out 1 and Out 2.

2
3.3.单粒子入射放大器节点对存储信息的影响
-->

3.3.单粒子入射放大器节点对存储信息的影响

灵敏放大器的作用是正确放大无法正常分辨的微弱信号, 转换为满足数据分辨功能要求的大输出信号, 因此放大器的灵敏节点对单粒子效应的敏感度是直接影响数据能不能正确放大读出的关键.
图8为单粒子入射读写“0”时灵敏放大器输入管后铁电存储单元cell 1极化强度变化和灵敏放大器输出信号变化. 从图8(a)可知高能粒子入射读写“0”的灵敏放大器的输入管时, 对铁电存储单元cell 1极化强度几乎没有影响, 即数据可以正确读写. 图8(b)中高能粒子轰击灵敏放大器输入管产生了一个漏极脉冲电流, 灵敏放大器开始工作而放大输出电压, 灵敏放大器输出电压产生了很大的波动, 但是仅在0.4 ns后就恢复了初始状态, 因此数据能正常读出. 图9为读写“1”时, 单粒子入射灵敏放大器输入管后铁电存储单元cell 1极化强度变化和灵敏放大器输出信号变化. 从图9(a)可知铁电存储单元cell 1极化强度几乎没有影响, 存储单元能正确读写. 高能粒子轰击灵敏放大器输入管产生的漏极脉冲电流极小, 对读“1”时处于开启状态的灵敏放大器工作电流几乎没有影响, 输出信号数据能正常读出, 如图9(b)所示.
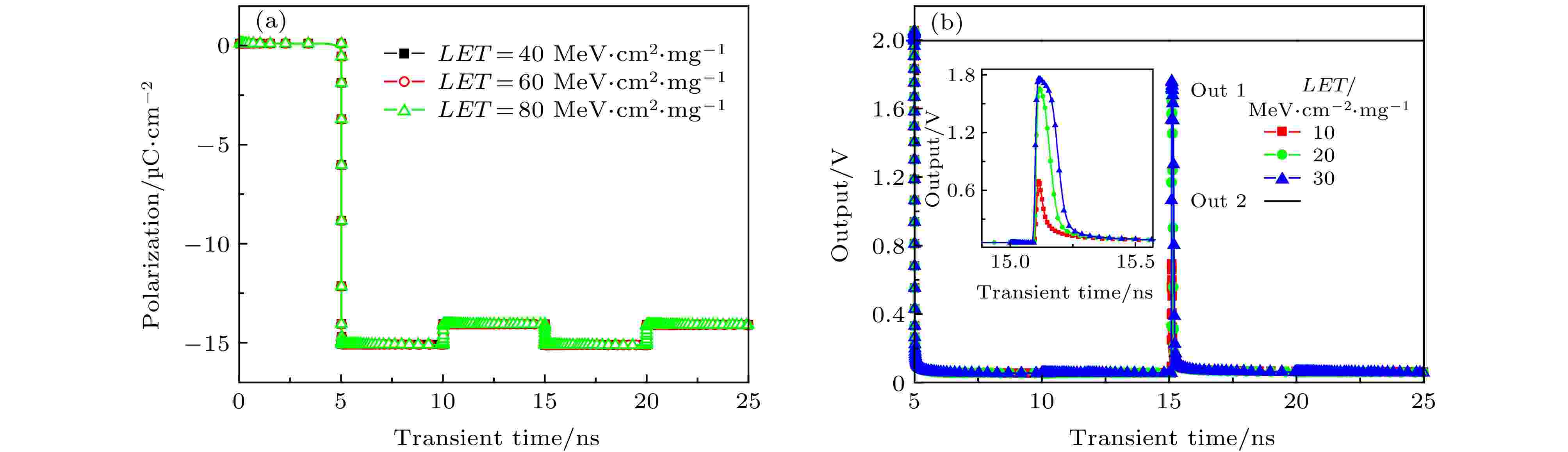图 8 读写“0”时, 单粒子入射灵敏放大器输入管的瞬态效应　(a)铁电存储单元cell 1极化强度变化; (b)灵敏放大器输出信号变化
Figure8. Transient effects of a single-particle incident sensible amplifier input tube when reading and writing “0”: (a) Change of ferroelectric cell 1 polarization intensity; (b) change of sense amplifier output signal.

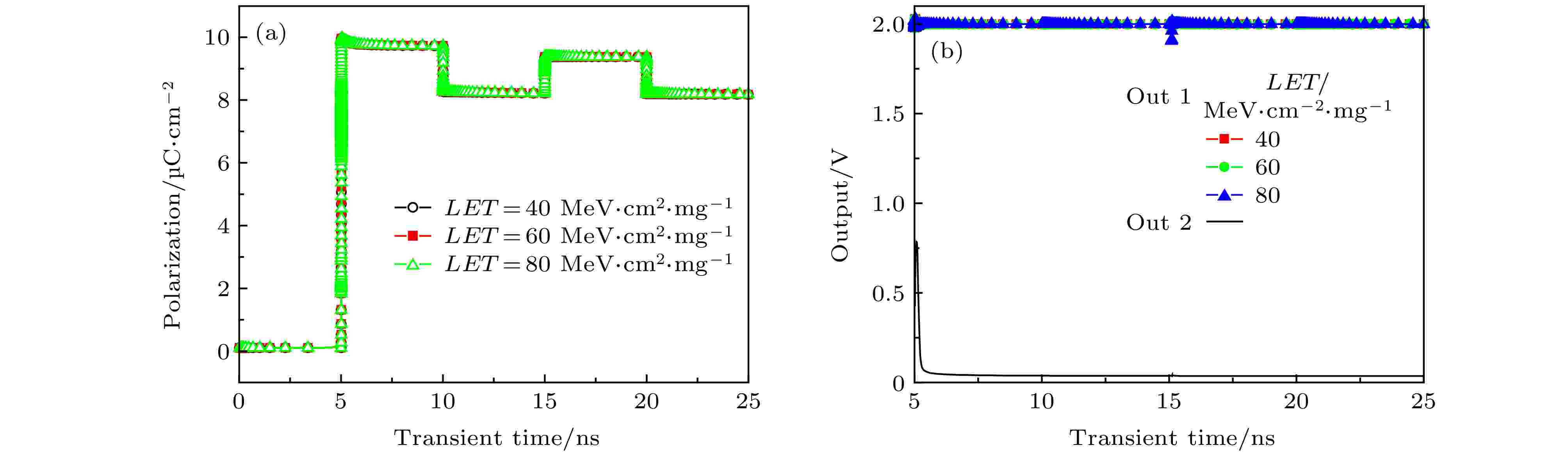图 9 读写“1”时, 单粒子入射灵敏放大器输入管的瞬态效应　(a)铁电存储管极化强度变化; (b)灵敏放大器输出信号变化
Figure9. Transient effects of a single-particle incident sensible amplifier input tube when reading and writing “1”: (a) Change of ferroelectric transistor polarization intensity; (b) change of sense amplifier output signal.

2
3.4.不同剩余极化和矫顽场强度对存储信息的影响
-->

3.4.不同剩余极化和矫顽场强度对存储信息的影响

生长工艺、掺杂水平、厚度等原因致使HZO铁电薄膜具有不同的铁电性能. 因此, 分析HZO铁电薄膜有不同的剩余极化和矫顽场对研究结果的影响, 将使该模拟工作更具有实际应用价值. 铁电薄膜的存储能力决定了存储单元的存储性能. 图10(a)为不同剩余极化和矫顽场强度的HZO铁电薄膜下的铁电存储单元cell 1极化强度. 高能粒子在7 ns时进入cell 1漏极后, 管内电荷增加使得cell 1极化强度增高. 从图10(b)可知, 铁电薄膜的剩余极化强度越大, 铁电存储单元抗单粒子的能力越强, 在辐射环境下工作更加稳定.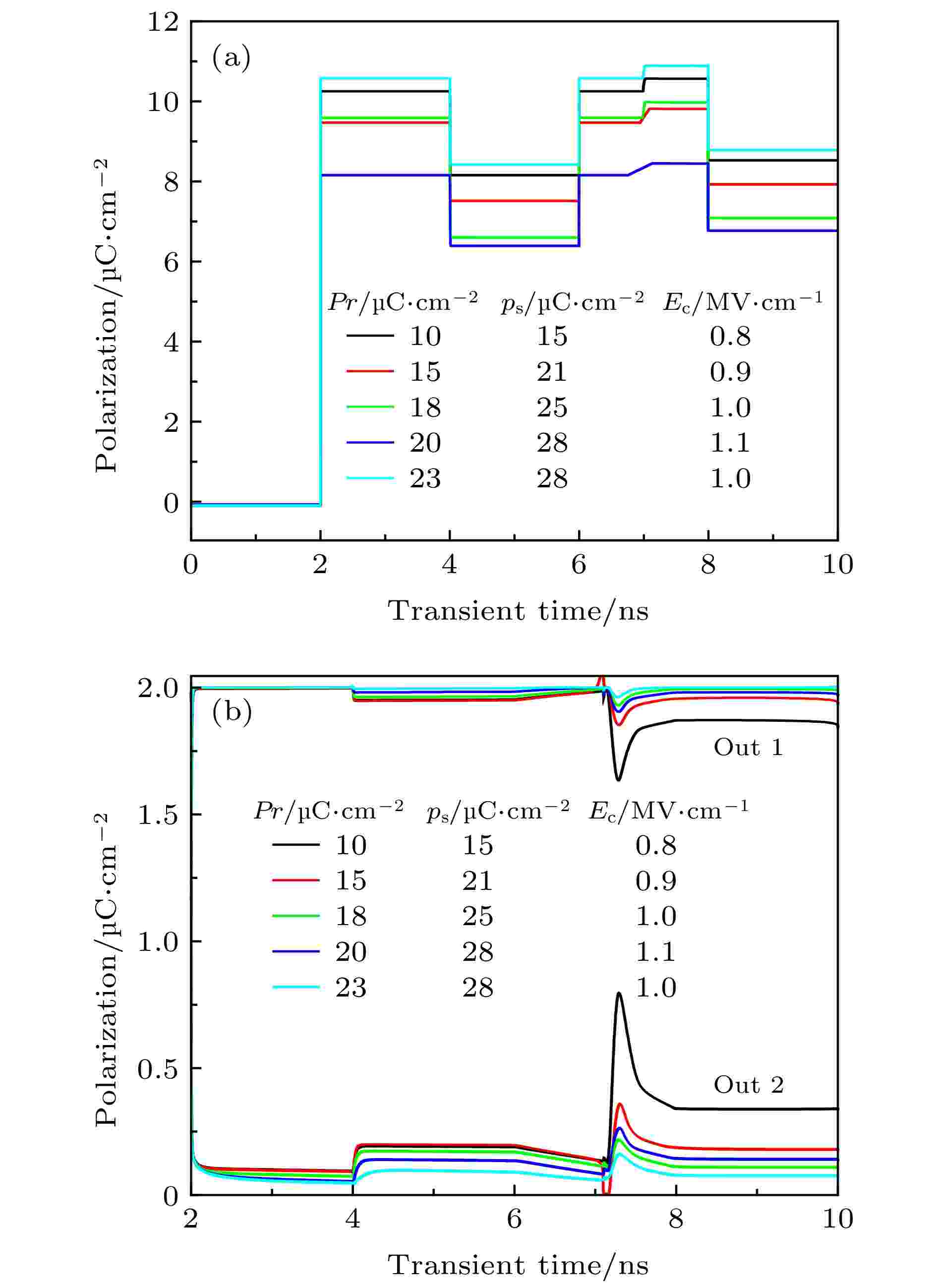
图 10 单粒子作用于不同剩余极化和矫顽场的HZO铁电薄膜下的铁电存储单元cell 1的信号变化　(a) 铁电存储单元的极化强度变化; (b)灵敏放大器输出信号变化
Figure10. Signal change of ferroelectric memory cell cell 1 under single-particle HZO ferroelectric thin film with different remanent polarization and coercive field: (a) Change of ferroelectric transistor polarization intensity; (b) change of sense amplifier output signal.

2
3.5.多束高能粒子对存储信息的影响
-->

3.5.多束高能粒子对存储信息的影响

两束LET值均为60 MeV·cm2/mg的高能粒子先后进入写“1”铁电存储单元cell 1后各节点的信号变化见图11, 时间间隔为0.5 ns. 在图11(a)中的脉冲电流有两个峰值, 时间间隔为0.5 ns. 在图11(b)和图12(a)中, 由于内部大量的电子空穴对使得极化强度增加, 其中图12(a)由于处于关态, 极化强度明显增大. 从图7(c)可知单个单粒子入射cell 1漏极后, 输出数据信号能迅速回复初始位置. 但是, 在图11(c)可以看到输出信号不能回复的初始状态, 且出现了双峰值, 最后两端输出的电压差减小, 影响数据正常的读出. 图12为两束LET值为60 MeV·cm2/mg高能粒子在时间间隔为0.5 ns先后进入写“1”状态的铁电存储单元cell 1后各节点的信号变化. 由图6(d)和图12(b)可以看出, 一束和两束高能粒子作用存储单元漏极都没有致使输出信号发生明显的波动, 说明处于关态的存储单元有很好的抗单粒子的能力.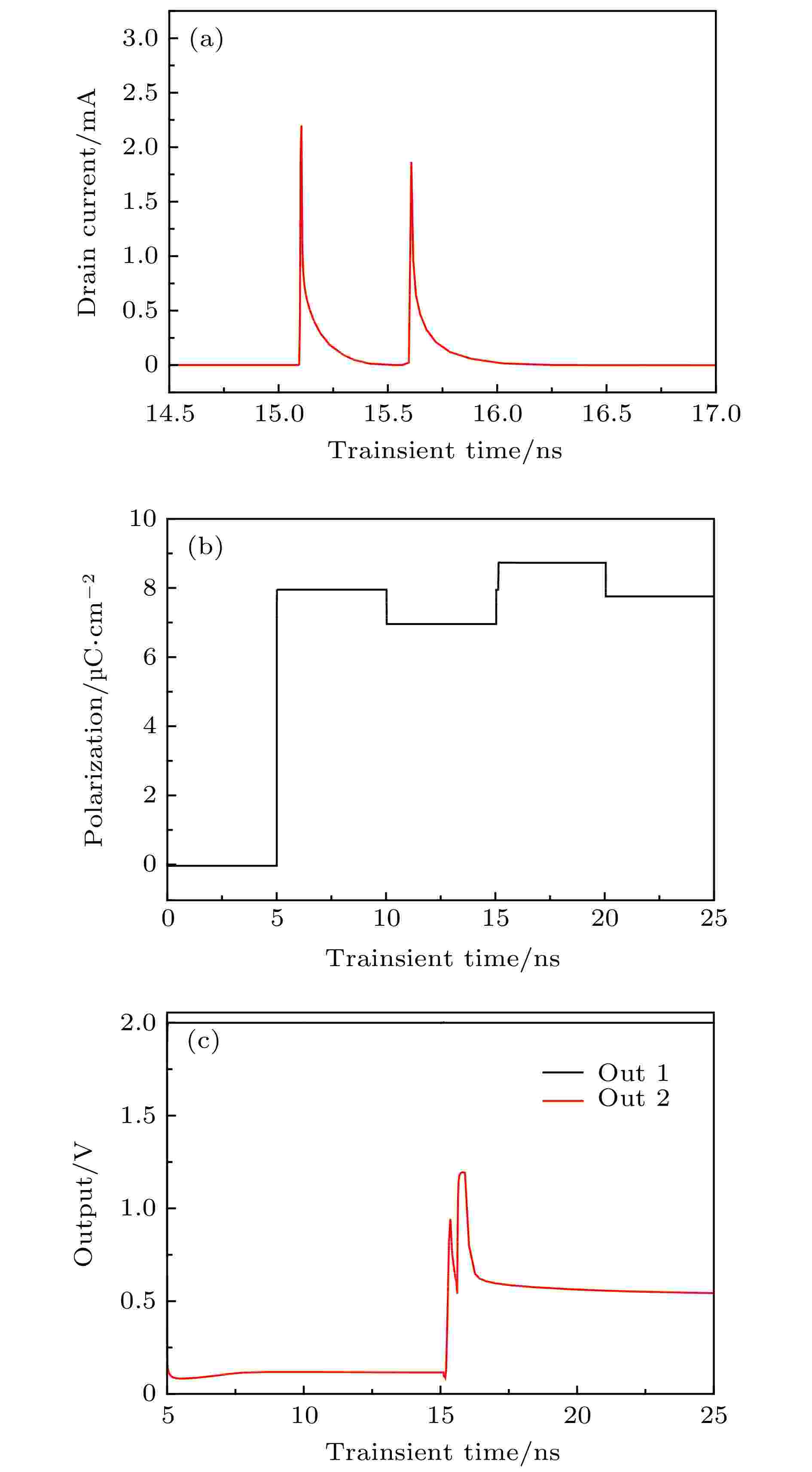
图 11 两束单粒子入射读写“1”铁电存储单元cell 1漏极的瞬态效应　(a) cell 1漏极电流脉冲变化; (b) cell 1极化强度变化; (c)灵敏放大器输出信号变化
Figure11. Transient effects of two single-particle incident read and write “1” ferroelectric storage tube drain: (a) Change of drain current pulse; (b) change of cell 1 polarization intensity; (c) change of sense amplifier output signal.

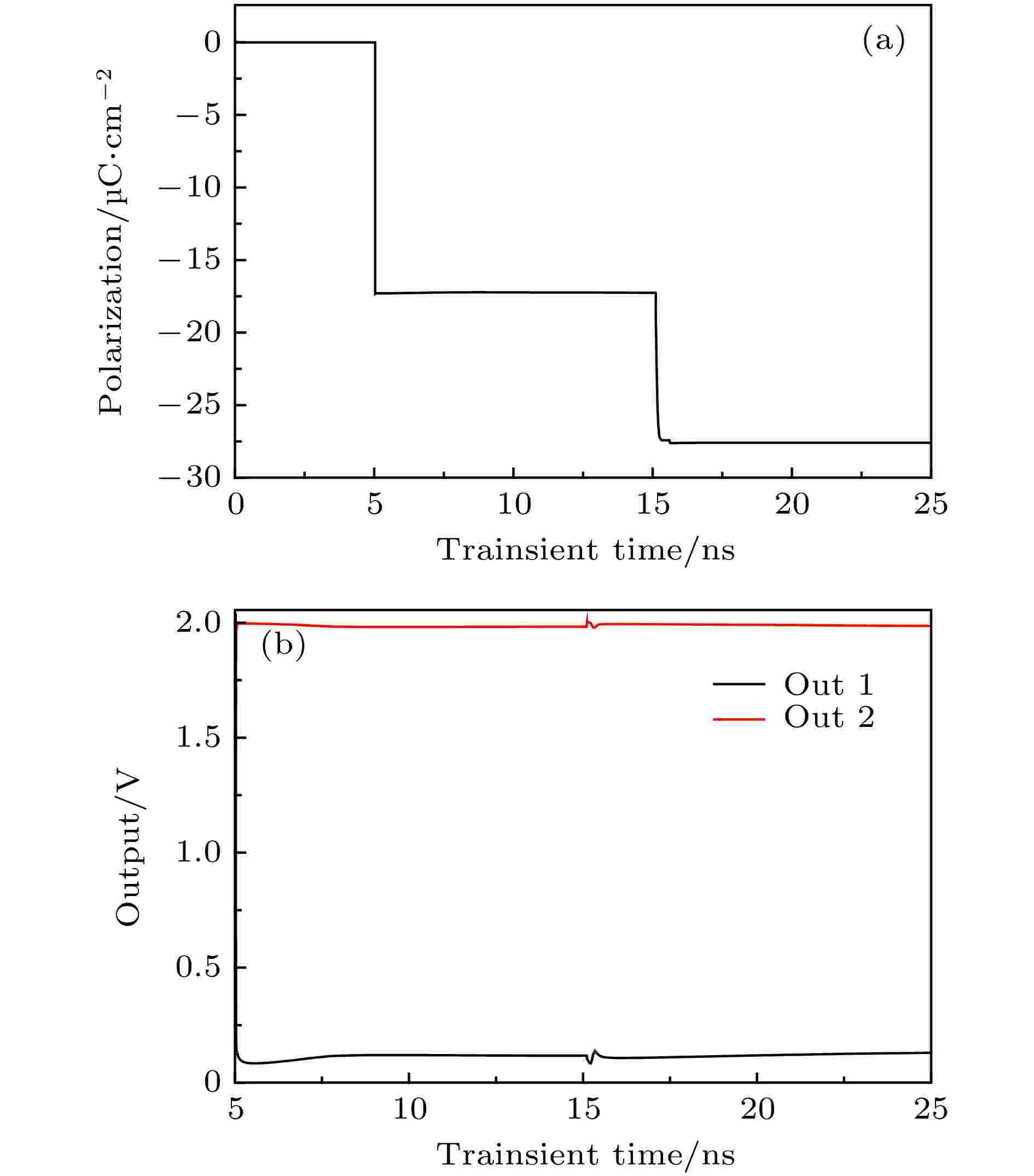图 12 两束单粒子入射读写“0”铁电存储单元cell 1漏极的瞬态效应　(a) cell 1极化强度变化; (b) 灵敏放大器输出信号变化
Figure12. Transient effects of two single-particle incident read and write “0” ferroelectric storage tube drain: (a) Change of cell 1 polarization intensity; (b) change of sense amplifier output signal.

4.结　论
使用半导体仿真软件Sentaurus TCAD对HfO2基FeFET读写电路不同敏感节点进行了单粒子翻转效应研究, 分析了存储数据发生变化的内在机制. 仿真结果表明, 当单粒子入射HfO2基FeFET读写电路的铁电存储单元时, 发生了数据信号的波动, 但是在0.5 ns后可以回复初始状态, 不会引起数据发生单粒子翻转, 说明该铁电存储单元有很好的抗单粒子翻转的性能. 当单粒子入射HfO2基FeFET读写电路的灵敏放大器输入管时, 放大器在读“0”状态的输出信号瞬态脉冲在0.4 ns可以回复初始状态, 因此数据可以正确读出, HfO2基FeFET读写电路具有优异的抗单粒子能力. 两束高能粒子先后间隔0.5 ns进入读写“1”状态的存储单元漏极, 输出数据信号的波动较大, 电压差的减少容易造成数据的读出出错.
相关话题/信号 数据 电压 电路 电子
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 网络直播平台数据挖掘与行为分析综述
    摘要:随着移动通信和互联网技术的不断发展,网络直播逐渐成为了新媒体环境下人们青睐的在线娱乐和信息传播方式.目前广泛应用于课堂教学、真人秀、电竞赛事、品牌营销等方面.数百万主播与数亿计观众的活跃加入和互动,产生了丰富的在线人群行为活动数据,为开展大规模人群行为动力学、平台内容推荐与检测、在线社群演化等 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 电力电子化电力系统稳定的问题及挑战:以暂态稳定比较为例
    摘要:随着电力电子技术的进步和环境保护对清洁能源的要求,以同步发电机为主的传统电力系统正向着多样化电力电子装备为主的电力系统转变,由此电力系统正面临着百年来未有之大变局.近年来,国内外不断报道出以电力电子装备为主的新能源基地和传统高压直流等机理不明的电力事故,严重威胁了电力系统安全稳定运行.针对上述 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 介质材料二次电子发射特性对微波击穿的影响
    摘要:以介质填充的平行板放电结构为例,本文主要研究了介质填充后微波低气压放电和微放电的物理过程.为了探究介质材料特性对微波低气压放电和微放电阈值的影响,本文采用自主研发的二次电子发射特性测量装置,测量了7种常见介质材料的二次电子发射系数和二次电子能谱.依据二次电子发射过程中介质表面正带电的稳定条件, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 微波瑞利散射法测定空气电火花激波等离子体射流的时变电子密度
    摘要:大气压空气电火花激波等离子体射流的电子密度在亚微秒时间尺度上瞬变,其电子密度的测定很难.基于微波瑞利散射原理,本文测量了空气电火花冲击波流注放电等离子体射流的时变电子密度.实验结果表明:测量系统的标定参数A为1.04×105V·Ω·m–2;空气流注放电等离子体射流的电子密度与等离子体射流的半径 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • AlGaN/GaN高电子迁移率器件外部边缘电容的物理模型
    摘要:AlGaN/GaNHEMT外部边缘电容Cofd是由栅极垂直侧壁与二维电子气水平壁之间的电场构成的等效电容.本文基于保角映射法对Cofd进行物理建模,考虑沟道长度调制效应,研究外部偏置、阈值电压漂移和温度变化对Cofd的影响:随着漏源偏压从零开始增加,Cofd先保持不变再开始衰减,其衰减速率随栅 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 量子点-Su-Schrieffer-Heeger原子链系统的电子输运特性
    摘要:Su-Schrieffer-Heeger(SSH)原子链是典型的具有拓扑边缘态的一维系统,并且已在光子和冷原子系统中实验实现.本文在紧束缚近似下,利用传输矩阵方法研究了量子点-SSH原子链系统的电子输运特性,这里,量子点的作用是调节SSH原子链与电极的隧穿耦合强度.当量子点与SSH原子链弱耦合 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • AlGaN/GaN高电子迁移率晶体管器件电离辐照损伤机理及偏置相关性研究
    摘要:本文利用60Coγ射线,针对AlGaN/GaN高电子迁移率晶体管(high-electronmobilitytransistors,HEMT)器件,开展了在不同偏置下器件电离辐照总剂量效应实验研究.采用1/f噪声结合直流电学特性参数对实验结果进行测量分析,分析结果表明,受到辐照诱生氧化物缺陷电 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 电介质/半导体结构样品电子束感生电流瞬态特性
    摘要:电子束照射下电介质/半导体样品的电子束感生电流(electronbeaminducedcurrent,EBIC)是其电子显微检测的重要手段.结合数值模拟和实验测量,研究了高能电子束辐照下SiO2/Si薄膜的瞬态EBIC特性.基于Rutherford模型和快二次电子模型研究电子的散射过程,基于电 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 超紧凑型飞秒电子衍射仪的设计
    摘要:由于空间电荷效应的限制,产生百飞秒的极短电子脉冲是超快电子衍射技术的一大难点.同时,电子的穿透深度随着电子能量的增加而增加,而电子的散射几率却具有相反的规律.因而,除了时间分辨的提升,还需要可宽范围调节的电子能量以优化不同厚度样品对其的需求.基于此,提出并设计了一种新型超紧凑电子枪,结合均匀场 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Ar原子序列双光双电离产生光电子角分布的理论计算
    摘要:基于多组态Dirc-Fock方法和密度矩阵理论,给出了原子序列双光双电离光电子角分布的计算表达式,发展了相应的计算程序.利用该程序对Ar原子3p壳层序列双光双电离过程进行了理论研究,给出了光电离的总截面、磁截面、剩余离子取向以及光电子角分布的各向异性参数与入射光子能量的函数关系.结果显示在光电 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.