摘要:大气压空气电火花激波等离子体射流的电子密度在亚微秒时间尺度上瞬变, 其电子密度的测定很难. 基于微波瑞利散射原理, 本文测量了空气电火花冲击波流注放电等离子体射流的时变电子密度. 实验结果表明: 测量系统的标定参数A为1.04 × 10⁵ V·Ω·m^–2; 空气流注放电等离子体射流的电子密度与等离子体射流的半径和长度有关, 结合高速放电影像展示的等离子体射流的等效半径和等效长度, 测定的电子密度在10²⁰ m^–3的量级, 且随时间先快速增长至峰值再成指数衰减. 此外, 本文还探讨了等离子体射流的不同等效尺度对测定结果的影响; 分析结果表明, 采用时变等效半径和时变等效长度的计算结果最有效, 且第1个快速波峰是由光电离的电离波导致的.
关键词: 微波瑞利散射/
电子密度测量/
流注放电/
空气等离子体射流/
电离波

English Abstract

全文HTML

--> --> -->

大气压空气电火花放电产生的激波等离子体射流, 由于冲击波在狭小的间隙内放电, 气体放电经历了纳秒级的火花放电、微秒级的等离子体射流喷出和毫秒级的吸气补充3个工作流程^[1-4]; 其等离子体射流的温度接近室温, 且富含大量NO、O等活性粒子, 是一种性能优良的大气压等离子体射流装置^[5-8]. 由于其电离过程在亚微秒时间尺度上变化, 其放电的电离机制还未被研究清晰. 大气压等离子体射流的电子密度的时变测定可以很好地帮助理解空气电火花激波等离子体射流的电离过程, 但是测定空气电火花激波等离子体射流时变电子密度是困难的. 原因在于, 一方面电火花放电具有随机性, 不容易触发捕捉特定参数信息; 另一方面, 时变电子密度的测定方法鲜见报道.
常规的大气压等离子体射流电子密度的测定方法, 如光谱分析法, 采用精细光谱测量可以推算出特定时刻的电子密度, 但难以在1次放电过程得出整个时变电子密度的变化过程^[9-13]. 采用微波法测定大气压等离子体电子密度, 直到2009年, 徐金洲等^[14]采用微波共振探针技术, 提出了1种高气压等离子体电子密度的测定方法, 但是该方法空间分辨率较粗略, 且不具有时变测定功能; 瑞利散射是英国物理学家瑞利首先在光学波段发现的1种亚波长尺度的颗粒对光的散射效应. 近十年来, 美国Shneider等^[15-17]提出了微波瑞利散射法测定流注放电的电子密度, 此法具有时间分辨测量功能, 已成功测定激光诱导的等离子团和重频脉冲激励的大气压等离子体射流的电子密度的瞬变过程. 该方法利用微波瑞利散射信号, 结合ICCD高速影像确定等离子体子弹尺寸^[18-21], 推导出电子密度随时间的演化过程, 是一种创造性和先进性的测定方法. 但是, 该方法有两点处理技术影响了测量精度: 1)标定系统参数A时采用了介质子弹法, 介质子弹穿过待测区域的时空偏差直接影响了系数A的精度; 2)对于大气压等离子体射流的测定装置, 由于射流装置大多含有金属电极和介质管, 这些金属电极和介质管也处于散射区, 也有散射信号贡献量, 难以区分散射信号的来源, 从而影响测定结果的准确性.
本文采用微波瑞利散射法测定了大气压电火花激波等离子体射流的时变电子密度. 使用电火花间隙的电压下降沿作为触发信号, 同步分别触发ICCD相机和示波器, 同时捕捉高速影像和瑞利散射信号, 克服了不容易捕捉特定参数信息(电火花流注放电具有随机性)的困难. 在标定系统参数A时, 采用多介质棒作差拟合法标定, 消除了随机误差, 减小了系统误差. 在获取等离子体射流的等效尺度时, 先根据高速影像的亮度(灰度值法)来确定等离子体射流的形貌, 然后再做折合等效, 进而获得等离子体射流的时变等效半径和时变等效长度. 在推算电火花等离子体射流的瑞利散射信号时, 采用作差滤波法处理数据, 区分并提取等离子体射流的瑞利散射信号, 滤去随机噪声, 有效提升了测量精度.

2

-->

2.1.微波瑞利散射法的实验原理

微波瑞利散射法是通过喇叭天线捕获等离子体射流的弹性散射微波信号, 进而得到等离子体射流的电子总数的测定方法. 当等离子体流注电离波头的尺寸L远小于微波波长λ时, 该系统可通过分析等离子体射流通道中的线性极化微波辐射的散射信号, 测定出等离子体射流内的电子总数. 散射体(介质棒或等离子体射流)放置在距离辐射喇叭天线R (R ≥ λ, L)处, 等离子体射流的电离波头可以充当微波激发的偶极子辐射源. 根据文献[15-17], 等离子体偶极子在垂直于偶极子方向的平面上辐射散射信号(由接收喇叭天线探测). 接收天线放置在距离等离子射流R = 15 cm 处, 以确保接收的散射信号与等离子体射流的电子密度线性相关, 从而获得接收喇叭天线内的电场幅值为${E_{\rm{s}}}$; 使用I/Q混频器将微波散射信号转变为时变幅值的直流信号, 得到输出电压${U_{{\rm{out}}}} \propto {E_{\rm{s}}}$; 微波瑞利散射系统中使用的放大器和混频器均工作在线性模式下, 保证了输出信号${U_{{\rm{out}}}}$与散射辐射电场的幅值${E_{\rm{s}}}$成比例. 故散射信号(微波束被等离子体射流散射)与等离子体中的电子数密度成正比例^[15-17]. 根据微波瑞利散射原理, 有如下表达式:

${U_{{\rm{out}}}}{\rm{ = }}\left\{ {\begin{aligned}& {A \cdot \frac{{{e^2}{n_{\rm{e}}}}}{{{m_{\rm{e}}}{\gamma _{{\rm{en}}}}}}{V_{\rm{p}}}\;\;,}\;\;\quad\quad\quad {({\text{对于等离子体}}),}\\& {A \cdot {\varepsilon _0} \cdot ({\varepsilon _{\rm{r}}} - 1)\omega {V_{\rm{d}}}\;,} \quad {({\text{对于介质体}}),}\end{aligned}} \right.$

式中: A为系统参数, 是微波系统的特定性质之一, 可以利用已知物理特性的介质散射体进行标定; e为基元电荷量; ${m_{\rm{e}}}$为电子质量; ${\varepsilon _0}$为真空介电常数; ${\varepsilon _{\rm{r}}}$为介电材料的相对介电常数; $\omega $为微波信号的角频率; ${\gamma _{{\rm{en}}}}$为电子与中性粒子的碰撞频率, 它是气体分子半径${r_0}$、气体压强P (Pa)和电子温度T_e (eV)的函数, 表达式如下^[22-23]:

${\gamma _{{\rm{en}}}} = \frac{{{r_0}^2}}{{4 \times {{10}^{ - 20}}}} \cdot 1.52 \times {10^7}P \cdot \sqrt {{T_{\rm{e}}}} .$

2 -->

2.2.实验装置

图1为便携式电火花放电装置及结构图. 便携式电火花放电装置的结构图如图1(a)所示, 充电模块通过USB充电线与充电接口、充电指示灯及电池连接, 同时电池与升压稳压模块连接, 升压稳压模块通过串联开关与高压模块连接, 高压模块输出端与电容器并联, 电容器的负极与放电装置的金属圆柱阴极连接, 电容器的正极与放电装置内的铁针电极连接. 当通电时, 电火花放电在腔体里产生等离子体, 空气电火花冷等离子体激波射流会从圆柱的前端圆孔快速喷出. 在工作流程上, 如本文引言中所述, 气体放电的工作过程需经历3个阶段: 放电、射流、吸气补充. 便携式大气压空气电火花放电装置如图1(b)所示, 其工作过程为: 由于放电装置里面的铁针电极与空心圆柱形陶瓷之间有直径为4 mm、长为1 mm的间隙和空心圆柱形陶瓷内有直径为2 mm、长为1 mm的空隙, 这些间隙里面充满了空气. 空气间隙处在局域增强电场中, 当电容器的电荷充电增加到一定的程度, 局域增强电场会把间隙内的空气瞬间击穿, 从而产生电弧形成气体放电通道. 在腔体内进行火花放电, 产生等离子体, 放电伴随的高温电火花加热腔内空气, 使其温度和压力瞬时升高, 由放电装置的空心阴极圆柱的前端圆孔快速喷出, 形成空气电火花冷等离子体激波射流, 如图1(c)所示. 阴极腔内电火花通道的温度和气压很高, 致使等离子体射流从阴极孔喷出, 腔外等离子体射流的温度随气压同步陡降. 由于激波效应, 使得从阴极喷口处喷射出的等离子体射流的温度略高于室温(冷等离子体射流), 不会对人体造成热损伤. 该装置不仅体积非常的小、结构简单, 而且喷射出来的空气电火花冷等离子体激波射流内含有大量的活性粒子基团(富含氧活性粒子、含氮活性粒子和自由基等), 作用非常广泛, 具有较强的杀菌灭毒作用等^[24-31].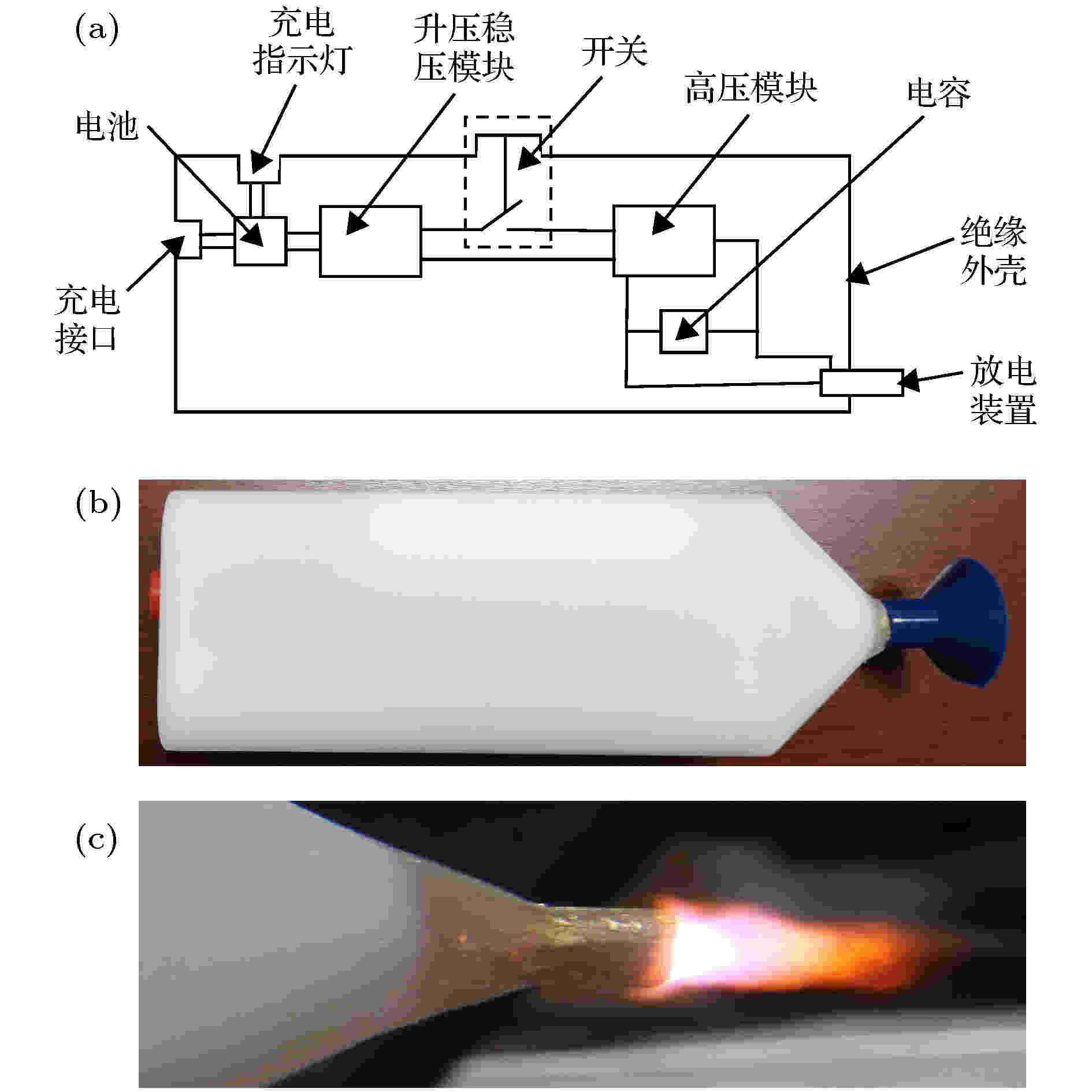
图 1 大气压空气电火花放电产生的等离子体射流　(a)大气压空气电火花放电装置的结构图; (b) 电火花放电装置照片; (c) 空气电火花激波等离子体射流照片
Figure1. Plasma jet generated by atmospheric pressure air spark discharge: (a) Structure diagram of atmospheric pressure air spark discharge device; (b) installation photo of spark discharge device; (c) photo of air spark shock-wave plasma jet.

为了更好地研究空气电火花的放电特性, 实验测量了火花放电时的电压波形, 如图2所示. 火花放电的放电周期间隔大致相等, 这说明放电喷射出来的等离子体激波射流的频度(或时间间隔)具有一致性, 大约每间隔1 s放电1次; 因此, 使用电火花间隙的电压信号的下降沿作为触发信号, 可以同步分别触发ICCD相机和示波器, 从而同时捕捉高速影像和微波瑞利散射信号. 另外, 其电压幅值大约为4.3 × 10³ V; 在这么高的电压下, 其放电电流也比较高, 所以电容器的泄流时间非常短, 而且每次放电之后电压都降到接近于零.
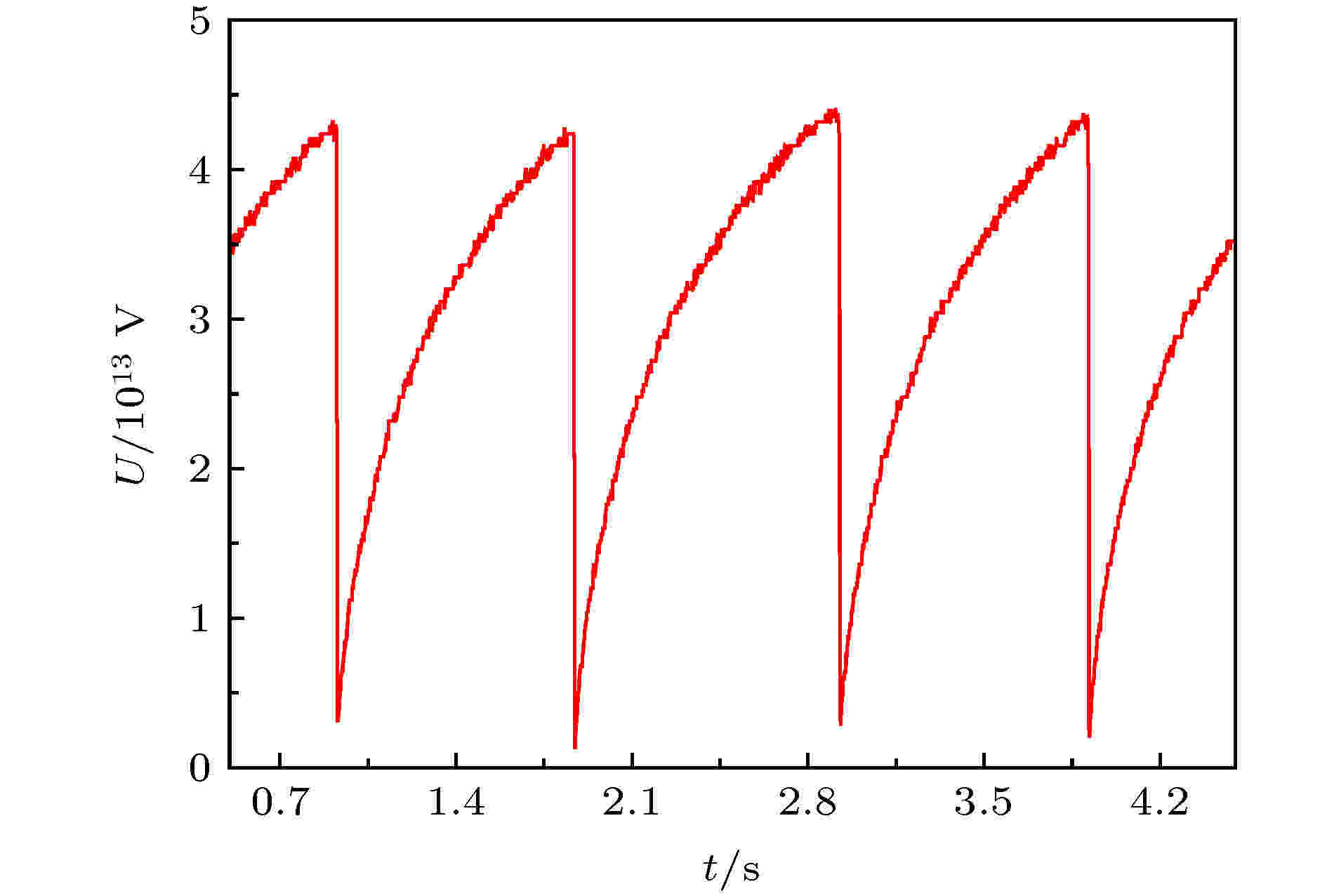图 2 火花放电电压波形
Figure2. Spark discharge voltage waveform.

大气压空气等离子体激波射流的时变电子密度测量方法和装置如图3所示. 微波瑞利散射装置的实验流程图, 如图3(a)所示; 信号源产生12 GHz微波信号分别给前置功放和增益20 dBm的主功放进行信号放大, 然后经过功分器, 分别接到辐射天线和I/Q混频器的LO接口; 等离子体放置在发射喇叭天线与接收喇叭天线之间, 入射波速照射到等离子体射流上发生了瑞利散射; 接收喇叭天线接收的散射信号依次通过低噪声信号放大器和增益15 dBm的功放, 再接到混频器的RF接口; I/Q混频器输出两路时变电压信号, 用示波器采集两路的正交信号${U_{\rm{I}}}$和${U_{\rm{Q}}}$, 则得到总散射电压为${U_{{\rm{out}}}} = $$ \sqrt {U_{\rm{I}}^2 + U_{\rm{Q}}^2} $^[8-10]. 微波瑞利散射系统的装置实物图, 如图3(b)所示. 测量时, 两个喇叭天线垂直放置, 待测的等离子体射流正交置于入射波束的正中央, 且等离子体射流的轴向平行于电场E的方向^[23-30]. 装置的I/Q混频器输出端口直接连示波器, 示波器捕捉电压信号波形; 使用自编的软件程序进行计算处理后, 得到最终数据结果.
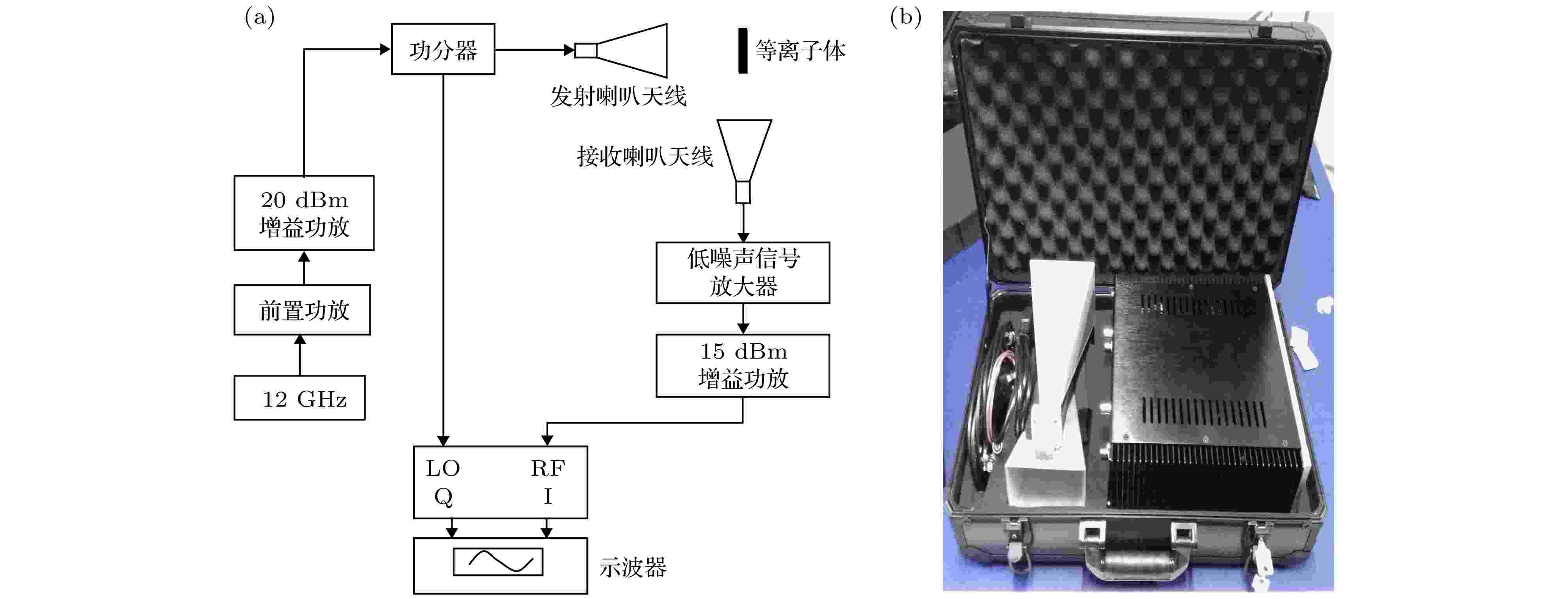图 3 微波瑞利散射装置　(a)实验系统图; (b)实验装置照片
Figure3. Microwave Rayleigh scattering device: (a) Experimental schematic diagram; (b) photo of experimental device.

2 -->

2.3.操作流程

微波瑞利散射法测定大气压电火花激波等离子体射流的时变电子密度的操作流程如下:
第1步　微波瑞利散射装置系统参数的标定. 根据微波瑞利散射原理, 其装置输出电压U与已知物理特性的介质散射体和等离子体的特性有关^[15-17]. 由(1)式可知, 系统参数A可以通过已知物理特性的介质散射体进行标定. 本文采用了相对介电常数为3.8的石英介质棒来标定, 石英棒的直径为3 mm, 长度初始为5 mm, 依次增加5 mm, 最后累加到50 mm(共10根). 真空介电常数${\varepsilon _0}$为$8.854 \times {10^{ - 12}}\;{\rm{F}}/{\rm{m}}$, 微波信号的角频率$\omega $为7.540 × $ {10^{10}}\;{\rm{Hz}}$. 标定时, 需要将石英棒沿着电场E方向放置在微波波束场的正中央, 实际的做法是使用1个介质平台(注意该平台不要使用金属, 相对介电常数避免靠近3.8), 在距离喇叭天线下沿20 mm左右处的平台平面上放置石英棒. 由于介质平台的存在(有散射信号进入接收喇叭天线), 而且I/Q混频器也做不到绝对的零输出电压, 所以即使散射区不放置任何散射体, I和Q的电压也可能不为零. 因此, 我们采用多介质棒作差拟合法标定, 消除随机误差, 减小系统误差. 即分别测定放置石英棒和移去石英棒的I/Q混频器的输出电压${U_{\rm{I}}}$、${U_{\rm{Q}}}$和$U'_{\rm{I}}$、$U'_{\rm{Q}}$, 并依次记录电压值. 石英棒的长度每增加5 mm做1次实验, 每次都需记录4个电压值, 共记录40个电压值. 实验过程中, 采用同样的标定方法, 重复测定5次, 每次结果相比, 最大偏差均小于5%.
第2步　微波瑞利散射装置系统的总散射电压信号的测定. 将已标定的微波瑞利散射装置, 应用于空气电火花放电等离子体激波射流的散射电压的测定. 在已知系统参数A后, 将待测的空气电火花激波等离子体射流置于入射波束的正中央, 且其轴向平行于电场E的方向. 将电火花间隙的电压信号的下降沿作为触发信号, 同步分别触发ICCD相机和示波器, 同时捕捉高速影像和瑞利散射信号; 示波器捕获I/Q混频器的输出${U_{\rm{I}}}(t)$和${U_{\rm{Q}}}(t)$, 即空气电火花等离子体射流的整个电离过程的散射信号${U_{\rm{I}}}(t)$和${U_{\rm{Q}}}(t)$; 在实际操作中, 为了减少随机误差, 提高测量的精度, ${U_{\rm{I}}}$和${U_{\rm{Q}}}$先分别在未放电时随机采集100个数据进行平均值计算, 得到${U_{\rm{I}}}(0)$和${U_{\rm{Q}}}(0)$; 再通过作差法计算出各自的散射电压差值, 得到$\Delta {U_{\rm{I}}}(t) = {U_{\rm{I}}}(t) - {U_{\rm{I}}}(0)$, $\Delta {U_{\rm{Q}}}(t) =$ U_Q(t) – U_Q(0); 最后得到总散射电压为${U_{\rm out}}(t) = $$\sqrt {\Delta {U_{\rm I}}{{(t)}^2} + \Delta {U_{\rm Q}}{{(t)}^2}} $. 在推算瑞利散射信号时, 本文还采用滤波法处理数据, 有效减小了随机噪声, 提升了测量精度.
第3步　空气电火花激波等离子体射流的等效半径和等效长度的测定. 将ICCD高速相机(步长是200 ns, 曝光时间为20 ns)正对着空气电火花激波等离子体射流进行拍摄, 记录不同时刻射流的长度和半径. 由于电火花放电过程是间歇的且具有随机性, 不容易捕捉特定参数信息. 故此, 我们使用电火花间隙的电压信号的下降沿作为触发信号, 拍摄了电火花激波等离子体射流的高速影像. 鉴于不同时刻的激波等离子体射流形状均不规则, 用1个与原形状相近且体积相等的圆柱体进行等效, 得到圆柱体的等效长度和等效半径, 可近似作为等离子体射流的等效长度和等效半径. 需要注意的是, 在对不同时刻的高速影像图进行灰度取值和折合等效时, 引入了测量误差(火花放电具有随机性和等效尺度数据获得). 为了减小误差, 等离子体射流半径和长度都是以影像的外围光圈为基准取得, 然后再折合等效得到等离子体射流的等效长度和等效半径. 即使如此, 但是该部分的误差仍然较大, 我们重复测定了5次放电的影像(相同条件下), 每次测定的结果相比, 最大偏差均接近20%.
第4步 电火花放电等离子体射流的时变电子密度的测定. 在大气压下, 空气分子的碰撞截面半径R约为2 × 10^–10 m、电子温度T_e为0.5 eV的条件下^[25], 结合上述步骤测定的数据, 围绕着电火花激波等离子体射流的等效半径和等效长度是否随时间变化, 分4种情况来进行分析, 并通过自编程序推算出电火花放电等离子体射流羽翼的时变电子密度.

2

-->

3.1.微波瑞利散射装置的标定及输出电压信号

图4所示为微波瑞利散射装置的标定数据. 先根据测得的10组散射信号电压值, 将每组I/Q电压值各自作差, 根据$U \!=\! \sqrt {{{({U_{\rm{I}}} \!-\! U'_{\rm{I}})}^2} \!+\! {{({U_{\rm{Q}}} \!- \!U'_{\rm{Q}})}^2}} $得到输出总电压值, 画出如图4所示的数据点. 再利用最小二乘法将十个数据点拟合成直线, 如直线①(Y轴是电压U, X轴是石英棒的长度). 由于直线①是不过坐标原点的(石英棒没能都在波束的正中对称), 需要平移直线①过坐标原点, 得到直线②. 最后, 取直线②在X = 25 mm处的电压U值(U = 39.55 mV), 带入(1)式中(介质散射体公式), 计算出系统参数A(A = 1.04 × 10⁵ V·Ω·m^–2). 此处理过程, 我们称之为多介质棒作差拟合法, 可以显著提高测量结果的精确度.
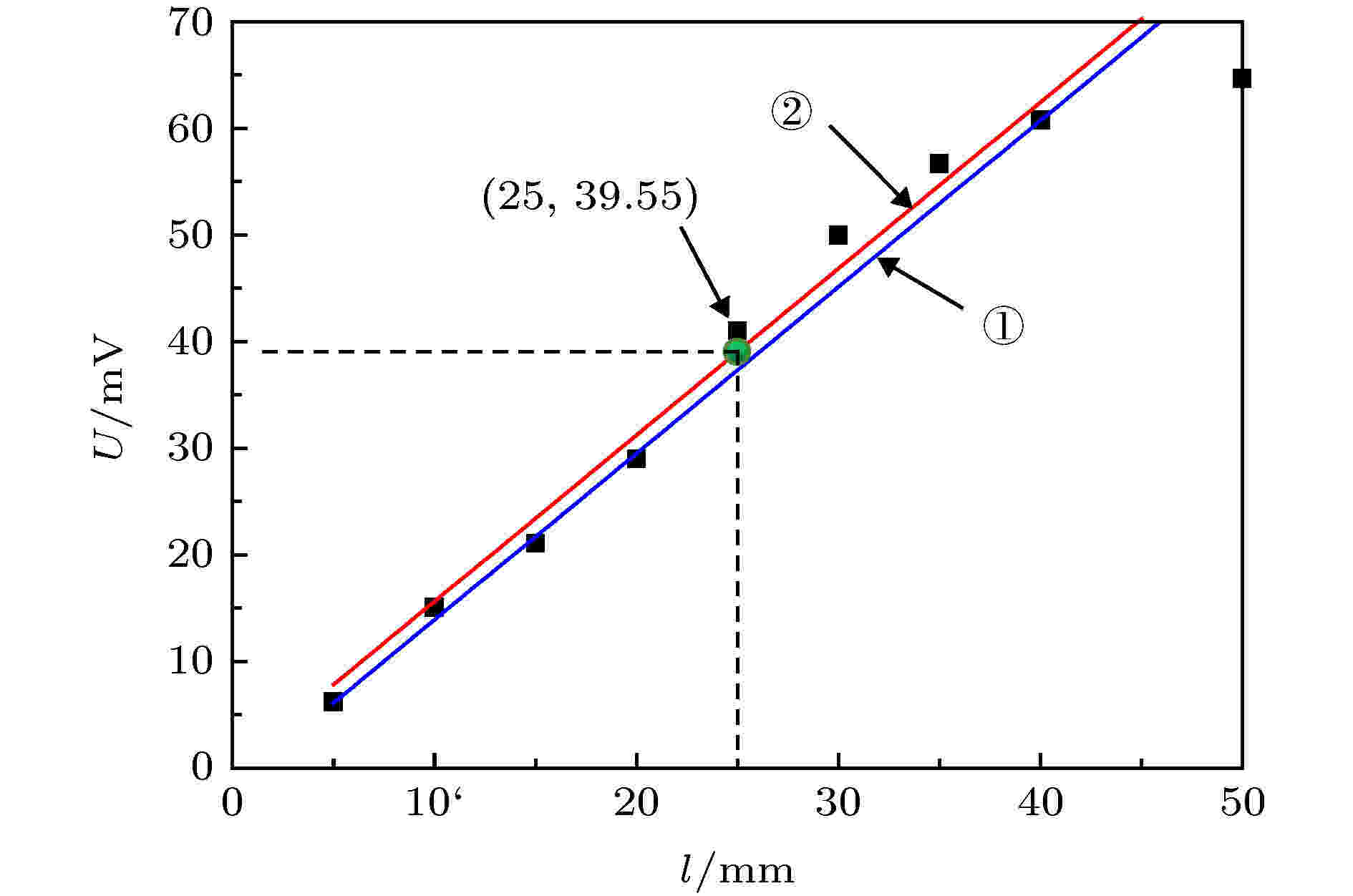图 4 微波瑞利散射装置的系统参数标定
Figure4. Calibration on a constant of microwave Rayleigh scattering device.

图5所示为空气电火花激波等离子体射流的时变瑞利散射信号. 从图中可以看出, 0时刻之前, 放电未发生, ${U_{\rm{I}}}(t)$和${U_{\rm{Q}}}(t)$基本上没有变化, 呈现两条平行线; 在t₁时刻, 等离子体射流开始形成, 此时${U_{\rm{I}}}$和${U_{\rm{Q}}}$均随时间变化. I信道上的电压${U_{\rm{I}}}(t)$先从0时刻的电压约0.047 V增长至峰值约0.09 V, Q信道上的电压${U_{\rm{Q}}}(t)$先从0时刻的电压约0.035 V下降至谷值约0.018 V再快速增长. 随着放电过程的衰弱, 散射的微波信号逐渐减弱, 被接收喇叭接收的微波信号也在变少, 则I信道上的电压开始降低, Q信道上的电压增长到峰值约0.045 V开始下降; t₂时刻后, 散射信号不再变化, 两个信道上的电压再次呈现水平状态, 总电压$U(t)$也呈现0值水平状态. 微波瑞利散射过程如下: 由于两个喇叭天线一开始呈 90°摆放, 入射波束中间没有等离子体射流时, 只有介质管、电极等散射出的微波信号进入接收天线; 当中间有等离子体射流时, 接收天线同时接收等离子体射流、介质管和电极等其他外界的散射信号. 因此, 根据示波器捕捉的I/Q混频器的输出电压${U_{\rm{I}}}(t)$和${U_{\rm{Q}}}(t)$, 从而得到等离子体射流的总散射电压

$U(t) = \sqrt {\Delta U_{\rm{I}}^2(t) + \Delta U_{\rm{Q}}^2(t)} .$

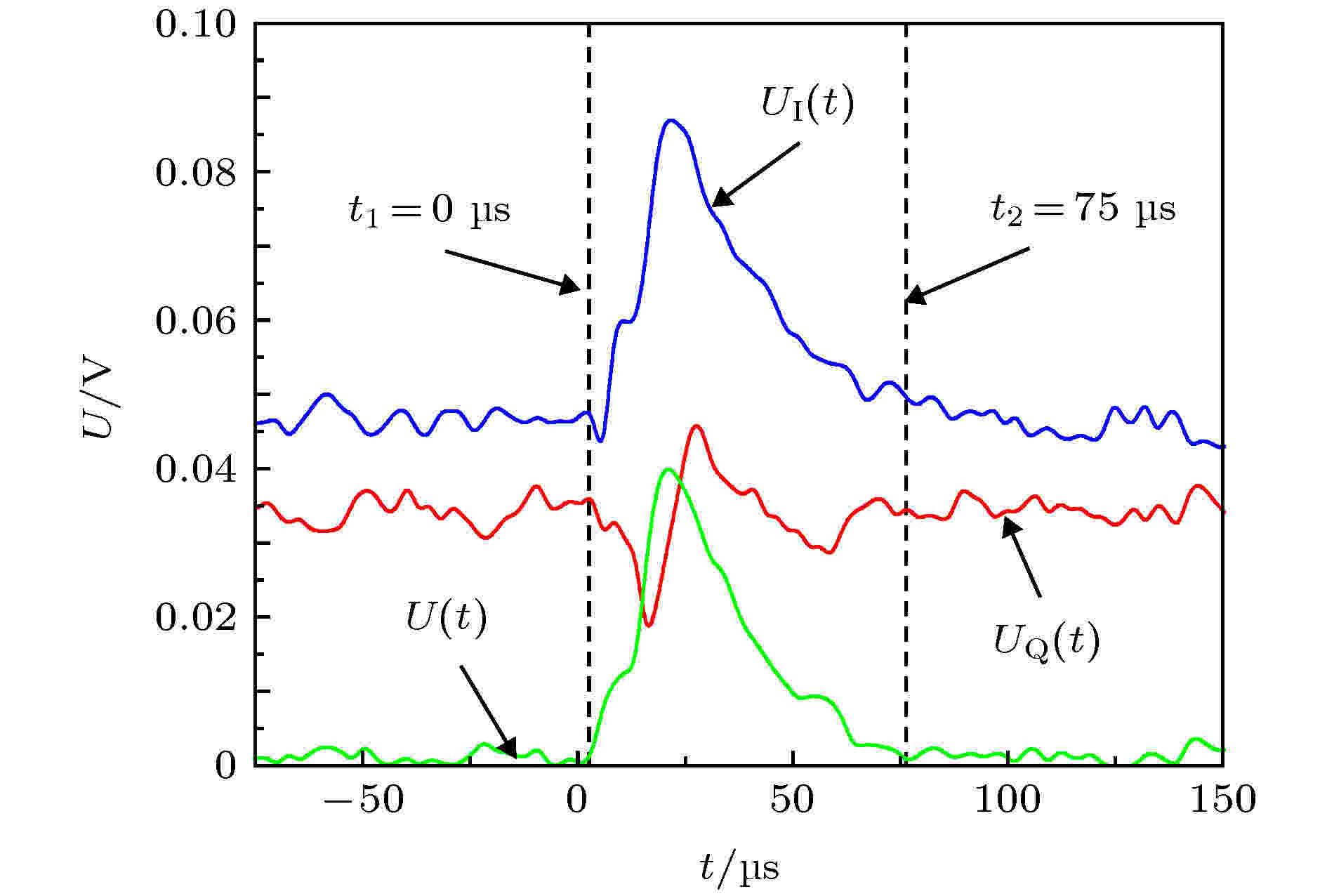图 5 微波瑞利散射装置测定的散射信号
Figure5. Scattering signal measured by microwave Rayleigh scattering device.

2 -->

3.2.空气电火花放电的光学影像

使用高速摄像机拍摄了1组等离子体射流的影像, 不同时刻喷射出的等离子体激波射流在空气中的发展过程如图6所示. 每张照片的曝光时间为20 ns, 图中清晰地显示了等离子体射流在80 μs内的影像发展过程. 从图中看出, 空气电火花放电的等离子体半径基本呈现先增大后减小的变化趋势, 长度也在不断变化, 且长度变化趋势更快. 根据灰度取值和折合等效法, 将获得的高速影像和尺子的照片设置成相同的比例进行比对测量, 获得其等离子体射流的长度; 再根据实际的尺子比例, 对射流的直径进行测量; 从而获得等离子体射流在不同时刻的半径和长度. 因此通过对射流影像的发展过程进行观察和测量, 可以得到等离子体激波射流在不同时刻的半径和长度^[31-33].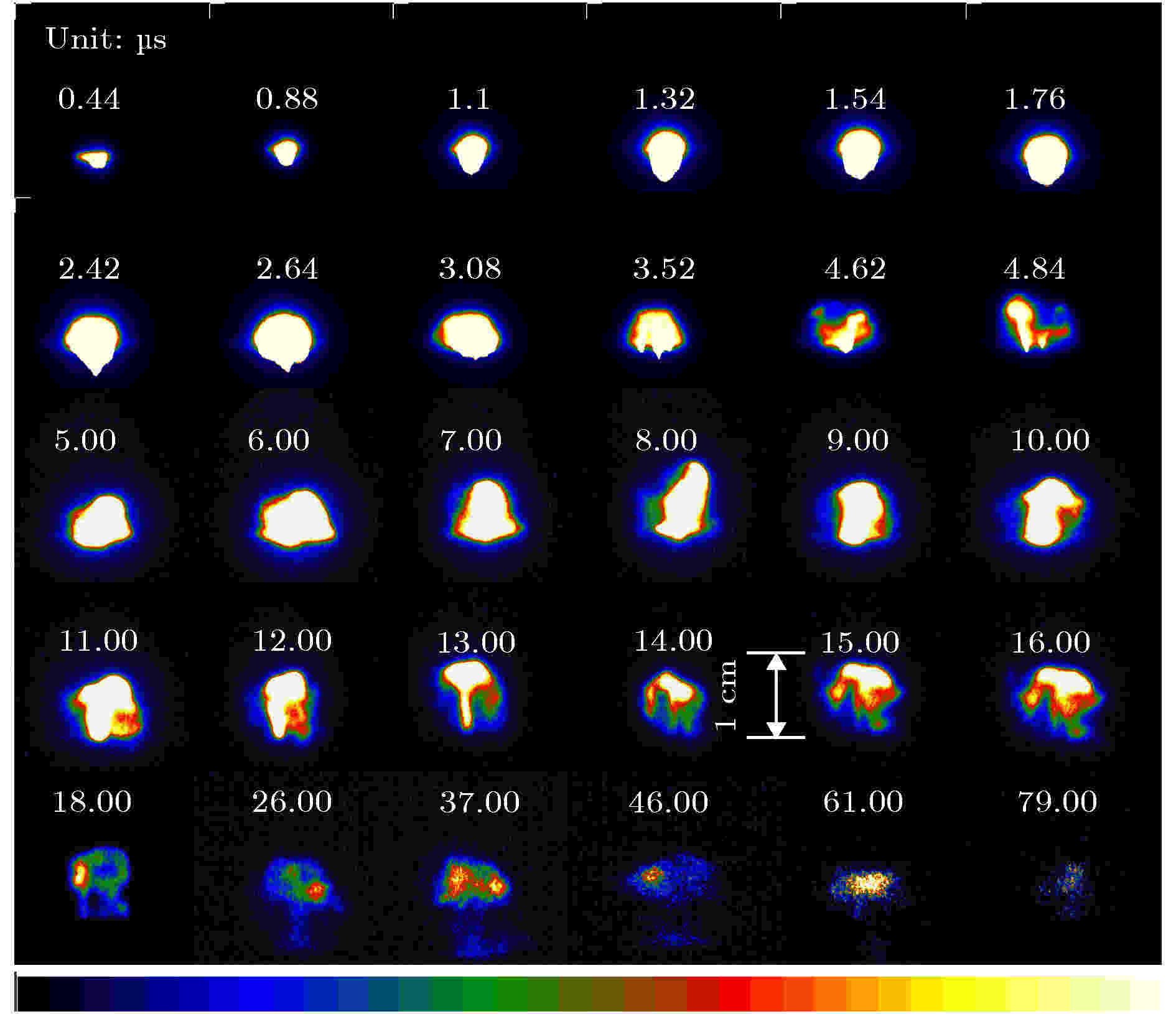
图 6 空气等离子体射流的光学影像
Figure6. Optical images of air plasma jet.

鉴于等离子体射流形状具有不规则性, 为了便于计算, 寻找与原形状相近, 体积相等的圆柱体进行等效, 从而得出等离子体射流的等效半径和等效长度. 特别是在26 μs后, 等离子体射流亮度基本上很弱并集中于头部, 因此, 其等效长度只考虑了头部区域. 图5显示的是等离子体射流的总散射电压, 图6展示的是高速摄像机拍摄的1组等离子体射流影像, 据此得到不同时刻等离子体射流的等效半径和等效长度. 为了能够跟瑞利散射信号数据相匹配, 编写程序对等离子体射流的等效半径和等效长度进行插值拟合, 得到了等效半径和等效长度随时间变化的曲线. 根据拟合后的数据, 画出等效半径和等效长度的时变图, 如图7所示. 从图中可以看出, 等离子体射流的等效长度和等效半径在不断变化, 这是等离子体的激波效应导致的^[5]. 当一段时间后, 放电喷射出的等离子体激波射流越来越弱, 其射流的等效半径和等效长度也在慢慢降低, 最后趋于1个稳定值. 根据微波瑞利散射原理, 等离子体射流的电子密度主要与微波瑞利散射装置的标定参数、等离子体射流的总散射电压以及等离子体射流的不同等效尺度有关, 故结合已知的数据, 即可推算出空气电火花等离子体激波射流的时变电子密度.
图 7 空气等离子体激波射流的半径r(t)和长度l(t)
Figure7. The radius r(t) and length l(t) of air plasma shock-wave jet.

2 -->

3.3.空气电火花等离子体激波射流的时变电子密度

图8所示的是等离子体射流的时变电子密度分布. 由图可见, 随着时间的推进, 等离子体射流的电子密度基本上都呈现先增大后减小的趋势, 但不同等效半径和等效长度对电子密度的影响有区别. 本文采用控制变量法进行分析, 第1种情况考虑的是等离子体射流的等效长度和等效半径都是定值, 其电子密度的时间演化过程, 如图8(a)所示. 从图中可以看出, 在等离子体射流形成之前, 电子密度基本上为零; 当等离子体射流形成后, 其电子密度先增大到约4.64 × 10²⁰ m^–3的峰值, 然后在大约14 μs后衰减. 空气电火花放电等离子体激波射流的时变电子密度波形和微波瑞利散射装置测得的总电压$U(t)$波形相似, 说明了当等离子体射流的等效长度和等效半径不变, 其电子密度和总散射电压成正相关. 第2种情况考虑的是等离子体射流的等效半径r是定值, 等效长度l是时变的, 其电子密度的演化过程. 如图8(b)所示, 在放电过程中, 电子密度基本上从零值逐渐增加到峰值为5.43 × 10²⁰ m^–3, 然后也大致在14 μs后衰减, 不过其衰减速度加快了, 曲线宽度变窄了. 第3种情况考虑的是等离子体射流的等效半径r是时变的, 等效长度l是定值, 其电子密度的演化过程, 如图8(c)所示. 从图中可以看出, 波形整体趋势不变, 但所测得电子密度比第1种情况稍大, 峰值为5.20 × 10²⁰ m^–3; 此外, 我们观察到在波形上升沿上出现了1个小波峰. 第4种情况考虑的是离子体射流的等效半径r和等效长度l都是时变的, 其电子密度的演化过程, 如图8(d)所示. 此种等效处理方式最接近实际情况, 等离子体射流的等效半径和等效长度都是随时空演化的. 与前3种情况相比, 波形变化趋势大体上不变, 其幅值整体上比前3种的结果都大, 峰值为6.10 × 10²⁰ m^–3; 该波形也呈现出图8(c)中的第1个小波峰, 但是该小波峰的峰值明显比第3种情况大. 等离子体射流的电子密度主要与等离子体射流的总散射电压和等离子体射流的不同等效尺度有关, 在此操作步骤中, 基于已知等离子体射流的总散射电压, 主要考虑等离子体射流的不同等效尺度对其电子密度的影响. 对比分析图8所示的4种等效处理方式, 可见其等离子体射流的半径对电子密度的影响最大. 此外, 结合图7的分析, 也可以清楚地看出, 等离子体射流的等效半径和等效长度均在不断变化, 等离子体射流的半径和长度的稍微变化就会致使等离子体激波射流的电子密度波动. 这是因为(1)式中的体积V是与等离子体射流的半径和长度有关.
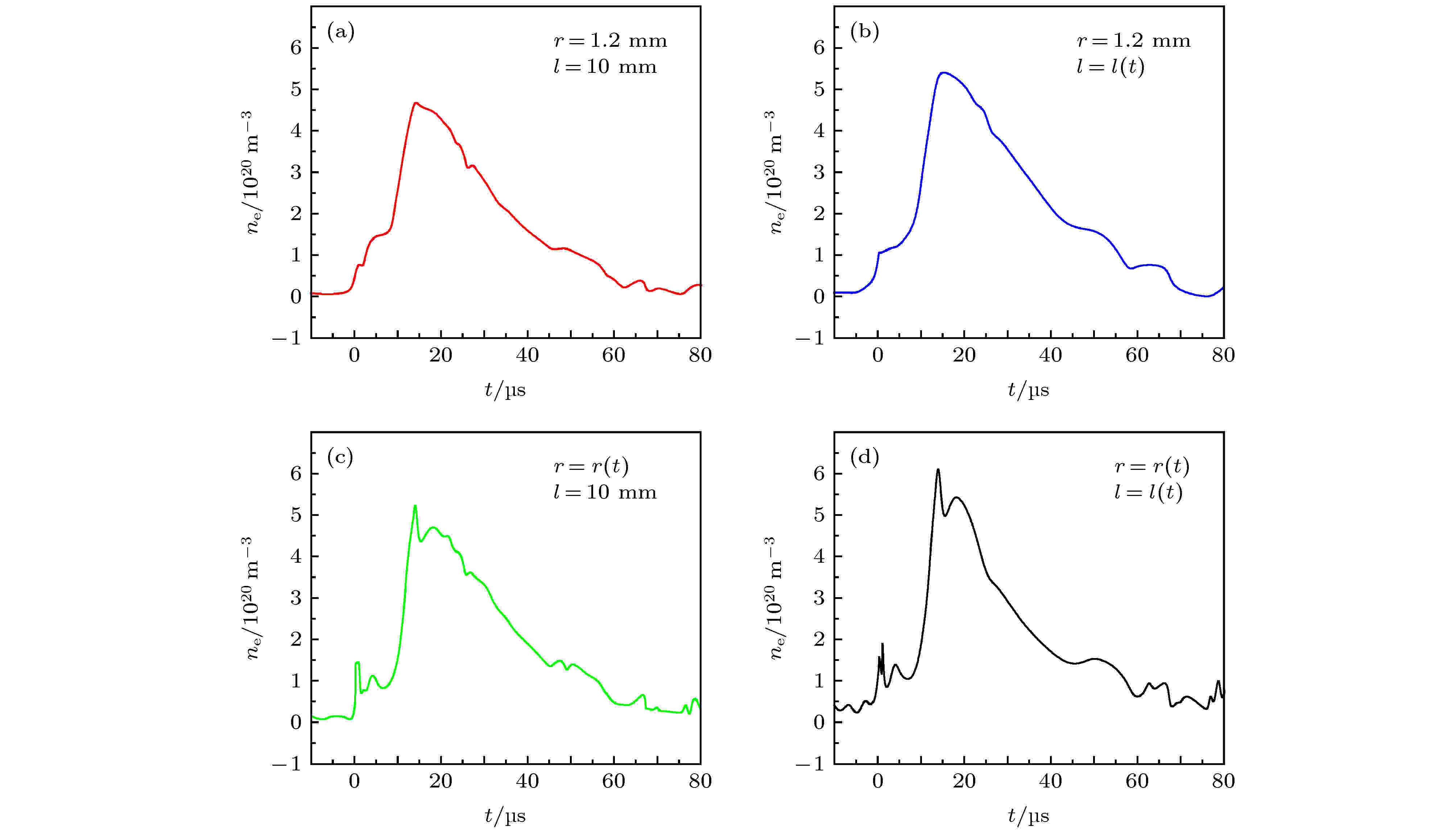图 8 不同等效尺度下的等离子体射流的时变电子密度　(a) r = 1.2 mm, l = 10 mm; (b) r = 1.2 mm, l = l(t); (c) r = r(t), l = 10 mm; (d) r = r(t), l = l(t)
Figure8. Time-varying electron density of plasma jet with the different equivalent scales: (a) r = 1.2 mm, l = 10 mm; (b) r = 1.2 mm, l = l(t); (c) r = r(t), l = 10 mm; (d) r = r(t), l = l(t).

如上所述, 在实验过程中, 我们发现了一个有趣的现象, 在图8(c)、8(d)中均出现了小波峰, 我们认为此时的电子密度峰是由光电离形成的等离子体电离波导致的^[34-36]. 现对该现象进行分析讨论. 如图8(c)和8(d)所示, 在1 μs时出现了电子密度先增大后减小的小波峰. 再结合图6, 在1 μs时, 等离子体射流的照片显示光斑已经存在; 根据Dobrynin等^[37]报道的放电过程流体模拟结果, 在1 μs时, 内部电火花放电的等离子体射流还未喷出; 因此, 等离子体射流在阴极腔体内刚形成不久, 喷出的等离子体射流并没来得及到达阴极喷嘴出口, 此时的电子密度小波峰只能由光电离激发所致. 实际电离过程是, 阴极腔体内的空气电花放电瞬时释放大量的高能光子, 这些光子穿过阴极喷嘴, 投射到喷嘴外的区域; 紧接着, 高能光子光电离空气形成等离子体射流. 根据吴淑群等^[36,38]报道的大气压等离子体射流的光电离实验, 等离子体子弹头部内的N₂分子激发态回迁辐射出的大量高能光子(波长为98—102.5 nm)^[39-42], 该高能光子直接光电离O₂分子, 在等离子体子弹头部前端区域产生种子电子. 也就是说, 喷嘴处发生了光电离, 形成了等离子体射流^[42-50], 这与上述实验现象符合. 之后, 空腔内的等离子体从喷管中喷出, 与光电离形成的等离子体射流会聚在一起, 从而使随后的等离子体射流的强度大大提高. 如图6和图8所示, 在2—14 μs期间, 等离子体射流的亮斑强度相对较强, 电子密度也同步增加至顶峰.

简言之, 本文采用微波瑞利散射装置系统对空气电火花冲击波流注放电等离子体射流的时变电子密度进行了测定. 实验结果表明, 空气电火花放电过程是从纳秒级的火花放电到微秒级的等离子体射流喷出. 在亚微秒时间尺度上, 微波瑞利散射系统可测定出等离子体射流的时变电子密度. 结果显示, 测定的电子密度在10²⁰ m^–3的量级, 且随时间先快速增长至峰值再指数衰减, 其测量的分辨率可达到10¹⁸ m^–3, 验证了微波瑞利散射装置测定大气压等离子体射流时变电子密度的可行性. 本文为了探讨等离子体射流的不同等效尺度对电子密度的影响, 以电火花激波等离子体射流的等效半径和等效长度是否随时间变化为分类依据, 分4种情况进行了探讨. 分析结果表明, 采用时变等效半径和时变等效长度的测定结果最接近于实际情况; 等离子体射流的等效半径对电子密度的影响最大. 另外, 在等离子体射流的等效半径随时间变化时, 在1 μs时电子密度均出现了小波峰, 分析结果显示此刻的电子密度峰是由光电离形成的等离子体电离波导致的.
虽然本文所述的微波瑞利散射装置可以胜任空气电火花等离子体射流的时变电子密度测定, 但是获得的时变电子密度实际上是等离子体射流的平均密度随时间的演化过程. 即所述的微波瑞利散射装置不具有空间分布测定能力, 后续工作, 我们拟采用两种技术手段来克服此缺陷; 一种是微波束电磁聚焦技术, 另一种是结合激光汤姆逊散射的空间分辨测量技术. 本文所述的微波瑞利散射实验装置, 适用于测量气体流注放电(气压为10⁴ Pa以上和等离子体的尺度为40 mm以下)或者液体流注放电等离子体的时变电子密度. 所述的微波瑞利散射装置的测量范围是: 电子密度在10¹⁸ m^–3(12 GHz微波的截至密度为10¹⁸ m^–3)以上, 时间分辨率达到0.1 ns (12 GHz微波的周期为0.085 ns). 本文所述的测量结果, 测量总误差在25%之内, 包括系统参数标定误差(小于5%)和等效尺度误差(接近20%, 由电火花放电的随机性和不规则性致使, 与微波瑞利散射装置无关). 因此, 本文所述的微波瑞利散射装置及其测定方法, 可推广应用于流注放电等离子体的时空电子密度演化测定.