摘要: 采用内收敛多组态相互作用及Davidson修正方法精确地计算了SeH
+ 离子能量最低的3个离解极限对应的12个Λ—S态的势能曲线. 计算中考虑了芯-价电子关联、标量相对论修正和自旋-轨道耦合效应. 结果表明在30000—40000 cm
–1 处Ω态的曲线存在许多避免交叉, 导致a2, b0
+ , A
1 2, A
2 1, A
3 0
– , A
4 0
+ 和c1态变为了双势阱. 通过求解径向薛定谔方程得到了12个Λ—S态和9个Ω态的光谱常数. 基于势能曲线和跃迁偶极矩, 预测出了
$ {{\rm{A}}^3}\Pi \leftrightarrow {{\rm{X}}^3}{\Sigma ^ - }$ 和
$ {{\rm{A}}_2}1 \leftrightarrow {{\rm{X}}_1}{0^ + }$ 跃迁的弗兰克-康登因子、辐射速率和辐射寿命. 首次系统地报道了SeH
+ 离子的光谱与跃迁性质.
关键词: 多组态相互作用 /
自旋-轨道耦合效应 /
光谱常数 /
辐射寿命 English Abstract Theoretical study on electronic structure and transition properties of excited states for SeH+ anion Hua Ya-Wen 1 ,Liu Yi-Liang 1 ,Wan Ming-Jie 2 1.College of Electrical and Information Engineering, Southwest Minzu University, Chengdu 610225, China Received Date: 24 February 2020Accepted Date: 11 May 2020Available Online: 14 May 2020Published Online: 05 August 2020Abstract: Potential energy curves of dipole moments for 12 electronic states correlating with the Se+ (4 Su) + H(2 Sg), Se+ (2 Du) + H(2 Sg) and Se+ (2 Pu) + H(2 Sg) dissociation channels of SeH+ anion are calculated by the ic-MRCI + Q method. The AV5Z-DK basis set for Se atom and H atom are chosen. Scalar relativistic effect, core-valence correction, and spin-orbit coupling effect are also taken into account. In MRCI calculations, Se(1s2s) orbitals are frozen, H(1s) and Se(4s4p) orbitals are selected as active space, and the remaining orbitals are used for the core-valence correlation. Spectroscopic parameters of 12 Λ–S states and 9 low-lying Ω states are obtained. All Λ–S states we selected are bound states. The X3 Σ– , a1 Δ, b1 Σ+ , A3 Π and c1 Π states each possess a large well, but the others each have a shallow well. The a1 Δ, b1 Σ+ , A3 Π, c1 Π and 15 Σ– states cross in 30000–40000 cm–1 regions. The X3 Σ– , a1 Δ and b1 Σ+ come from the 4π2 electronic configuration around the equilibrium region, and three states have similar values of R e . The splitting dissociation channels are obtained at a spin-orbital coupling level. The calculated energy differences among five dissociation channels are in excellent agreement with the experimental data, and the maximal error is smaller than 0.5%. Due to the avoided crossing between the low-lying Ω states, the a2, b0+ , A1 2, A2 1, A3 0– , A4 0+ and c1 states all have two wells. The splitting parameters ASO of the X3 Σ– state and the A3 Π state are predicted at the same time, i. e. ASO (X2 1 – X1 0+ ) = 252.4 cm–1 , ASO (A2 1 – A1 2) = 858.9 cm–1 , ASO (A3 0– – A2 1) = 1213.5 cm–1 and ASO (A4 0+ – A3 0– ) = 199.5 cm–1 . The transition dipole moments of the A3 Π $ \leftrightarrow $ X3 Σ– and A2 1 $ \leftrightarrow $ X1 0+ transitions are obtained. The oscillator strengths, Franck-Condon factors, and radiative lifetimes of these two transitions are also predicted. The radiative lifetime of A3 Π state and A2 1 state are 746.6 and 787.8 ns, respectively. It implies the ability of electron transition for these two transitions. Keywords: multi-reference configuration interaction /spin-orbit coupling effect /spectroscopic constants /spontaneous radiative lifetimes 全文HTML --> --> --> 1.引 言 硒 (Se) 是一种重要的半导体材料. 作为第Ⅵ主簇氢化物, SeH在天体物理中具有潜在意义, 但与OH和SH相比, SeH分子的高分辨率数据有限[1 ] . 它虽然也是一个相对简单的分子, 但其包含了一个重原子Se. SeH是一种具有重要实验和理论意义的自由基. 由于其特殊性, 实验上众多****对SeH和SeD分子的光谱性质和跃迁性质进行了广泛的研究[1 -8 ] . Lindgren[2 ] 在3000—3250 ?区域观察到SeH分子的漫反射光谱, 得到其离解能为3.2 eV ± 0.2 eV. Brown等[4 ] 采用激光磁共振(LMR)技术观测到SeH分子的基态X2 Π的自旋-轨道耦合(SOC) 分裂常数为1780 cm–1 , 结合电子顺磁共振光谱, 得到其分裂常数为1764.02 cm–1 . Cliff等[5 ] 采用远红外LMR技术观测到一系列SeD同位素分子的基态X2 Π3/2 的转动常数. 同年, Bollmark等[6 ] 在1330—1600 ?区域观测SeH和SeD分子的电子跃迁, 得到了SeH分子的F2 Σ– , J2 Δ以及SeD分子的E2 Δ, F2 Σ– 里德伯态到基态的垂直跃迁能T e , 分别为67262.9, 72408.5 cm–1 和66852.6, 67279.2 cm–1 . Ashworth和Brown[8 ] 采用LMR技术测量出SeH分子的偶极矩. Ram和Berbath[1 ] 利用傅里叶变换光谱仪测量了SeH分子基态的光谱, 得到了其光谱常数. 谐振频率ω e 为2421.7 cm–1 , 非谐振频率ω e χ e 为44.60 cm–1 以及平衡核间距R e 为1.4643 ?.+ 离子光谱性质的理论研究几乎没有. Balasubramanian等[9 ] 采用二阶组态相互作用的方法及优化的STO基组计算了SeH+ 离子的${{\rm{X}}^3}\Sigma _{{0^ + }}^ - $ , $^1{\Delta _2}$ , $^1\Sigma _{{0^ + }}^ + $ 和$^3{\Pi _{{0^ + }}}$ 态的势能曲线. 从他们的计算结果推算出在SOC效应下SeH+ 离子最低的两个离解极限的相对能量约为17745 cm–1 , 与实验值[10 ] 的误差为34.8%; 第二和第三离解极限的相对能量约为602 cm–1 , 与实验值[10 ] 较为符合, 误差约为2.3%, 基态${{\rm{X}}^{\rm{3}}}\Sigma _{{0^ + }}^ - $ 的离解能D e 为2.33 eV. 同时他们还计算了4个Ω态的光谱常数. Binning和Curtiss[11 ] 采用Hartree-Fock方法计算得到了SeH+ 基态X3 Σ– 的平衡核间距R e = 1.474 ?. 对于同主簇的氢化物正离子, Guberman[12 ] , Khadri等[13 ] 和Santos等[14 ] 分别采用从头算方法计算了OH+ , SH+ 和TeH+ 离子基态和低激发态的势能曲线和光谱常数. Song等[15 ] 和Zhang等[16 ] 分别研究了H2 S和H2 S+ 分子及其离子的势能面, 并分别拟合得到了SH和SH+ 基态的两体势. 同时, 国内有很多****对氢化物分子和分子离子的电子结构进行了研究[17 ,18 ] .[9 ] 选择的计算方法和基组不够精确, 导致了计算结果和已有实验值误差很大. 本文拟采用高精度的从头算方法计算SeH+ 离子的12个Λ—S态和9个Ω态的势能曲线和偶极矩. 最后计算了部分跃迁的跃迁偶极矩, 并预测其弗兰克-康登因子、爱因斯坦辐射系数和辐射寿命.2.计算方法 使用MOLPRO 2010程序[19 ] 计算了SeH+ 离子12个Λ—S态的电子结构. 由于程序自身的限制, 在计算过程中采用了C 2v 子群代替了C ∞v 群. C 2v 群有4个不可约表示(A 1 , B 1 , B 2 , A 2 ). 在计算中采用Hartree-Fock方法对SeH+ 离子基态的分子轨道进行了初始猜测; 然后以此为基础, 采用完全活性空间自洽场方法 (CASSCF)[20 ,21 ] 进行优化, 得到态平均的多组态波函数; 最后采用内收敛多参考组态相互作用方法(ic-MRCI)[22 ,23 ] 及Davidson修正(+Q )进行优化, 得到各Λ—S态的最终能量.+ 离子进行单点能计算, 扫描步长为0.10 ?, 在平衡核间距附近步长选为0.02 ?以提高拟合精度. 在CASSCF计算中, Se(1s2s)轨道被冻结, Se(2p3s3p3d)为双占据轨道, H(1s)和Se(4s4p)为活性轨道; 在随后MRCI + Q 的计算中考虑了芯-价电子(CV)关联效应, 即Se(2p3s3p3d)轨道参与电子关联的计算. 本文对Se原子和H原子都选择了aug-cc-pV5Z-DK全电子基组[24 ,25 ] . 计算中分别通过引入三阶Douglas-Kroll哈密顿量(DKH3)[26 ,27 ] 以及Breit-Pauli 算符[28 ] 来考虑标量相对论效应和SOC效应.[29 ] 通过求解径向薛定谔方程得到束缚态的光谱常数 (R e , ω e , ω e χ e , D e ) 以及$ {{\rm{A}}^3}\Pi \leftrightarrow {{\rm{X}}^3}{\Sigma ^ - }$ 和$ {{\rm{A}}_2}1 \leftrightarrow {{\rm{X}}_1}{0^ + }$ 跃迁的弗兰克-康登因子$(f_{\nu'\nu''})$ 、辐射速率($A_{\nu' \nu''}$ )和辐射寿命(τ ).3.结果与讨论 23.1.Λ—S态的势能曲线与光谱常数 3.1.Λ—S态的势能曲线与光谱常数 本文采用ic-MRCI方法计算了SeH+ 离子最低的三个离解极限所对应的12个Λ—S态的电子结构. 其Λ—S态的离解关系列于表1 中. 基态X3 Σ– 和15 Σ– 态对应于最低离解极限Se+ (4 Su ) + H(2 Sg ), a1 Δ, A3 Π, c1 Π, B3 Σ– , 11 Σ– 和13 Δ态对应于第二离解极限Se+ (2 Du ) + H(2 Sg ), 而b1 Σ+ , 23 Π, 21 Π和13 Σ+ 态对应于第三离解极限Se+ (2 Pu ) + H(2 Sg ).原子态 Λ–S态 相对能量/cm–1 本文工作a Se+ (4 Su ) + H(2 Sg ) 3, 5 Σ– 0 Se+ (2 Du ) + H(2 Sg ) 1, 3 Σ– , 1, 3 Π, 1, 3 Δ13590.3 Se+ (2 Pu ) + H(2 Sg ) 1, 3 Σ+ , 1, 3 Π22896.5 a 同一离解极限对应的所有电子态的平均能量.
表1 SeH+ 离子Λ—S态的离解关系Table1. Dissociation relationships of Λ-S states of SeH+ .图1 中. 计算结果表明在自旋无关水平下所有电子态都是束缚态且只有一个势阱. 从图1 看到激发态的势能曲线在高能区域有很多交叉. 所有Λ—S态的光谱常数都列在表2 中.图 1 SeH+ 离子的12个Λ—S态的势能曲线Figure1. Potential energy curves of the Λ-S states of SeH+ .电子态 R e /?ω e /cm–1 ω e χ e /cm–1 B e /cm–1 D e /eVT e /cm–1 X3 Σ– 1.4659 2387.48 45.81 7.8816 3.369 0 1.474[11 ] a1 Δ 1.4642 2393.52 40.79 7.8999 3.920 9179.3 b1 Σ+ 1.4622 2406.68 40.39 7.9224 4.006 17761.9 15 Σ– 3.5894 152.17 25.85 1.3340 0.030 26930.2 A3 Π 1.6395 1505.52 57.16 6.2961 1.207 30953.8 c1 Π 1.8168 989.95 59.14 5.1488 0.515 36530.2 B3 Σ– 2.8262 490.08 47.96 2.1460 0.157 39522.1 11 Σ– 3.6892 162.98 19.18 1.2109 0.042 40461.9 13 Δ 3.5593 139.94 20.44 1.2964 0.030 40552.3 23 Π 2.6009 603.15 50.66 2.5253 0.223 48259.6 21 Π 2.7701 400.92 43.54 2.2291 0.116 49124.6 13 Σ+ 3.6000 151.41 25.73 1.3258 0.029 49835.4
表2 SeH+ 离子Λ—S态的光谱常数Table2. Spectroscopic constants of the Λ–S states of SeH+ .+ 离子的基态为X3 Σ– 态, 其在平衡核间距R e 附近的主要电子组态为$(1{{\text{σ}} ^2}2{{\text{σ}} ^2}3{{\text{σ}} ^2}1{{\text{π}} ^4}4{{\text{σ}} ^2} 5{{\text{σ}} ^2} 2{{\text{π}} ^4}6{{\text{σ}} ^2}{\rm{3}}{{\text{π}} ^4}1{\text{δ} ^4})7{{\text{σ}} ^2}8{{\text{σ}} ^2}{\rm{4}}{\text{π}} _x^\alpha {\rm{4}}{\text{π}} _y^\alpha $ , 权重为92.78%. X3 Σ– 态具有很深的势阱, 离解能D e 为3.369 eV. 其平衡核间距为1.4659 ?, 比Binning和Curtiss[11 ] 的计算值1.474 ?略小, 误差仅为0.55%. 谐振频率ω e 为2387.48 cm–1 , 非谐振频率ω e χ e 为45.81 cm–1 . 激发态a1 Δ和b1 Σ+ 在平衡核间距附近的主要电子组态为$7{\text{σ} ^2}8{\text{σ} ^2}{\rm{4}}{\text{π} ^2}$ , 权重分别为93.72%和90.93%. 值得注意的是, 虽然a1 Δ, b1 Σ+ 与X3 Σ– 态来源于三个不同的离解极限, 但在平衡位置附近的电子组态都是${\rm{4}}{{\text{π} }^2}$ , 所以三个电子态的核间距非常接近, 分别是1.4659, 1.4642和1.4622 ?, a1 Δ和b1 Σ+ 态的垂直跃迁能分别为9179.3和17761.9 cm–1 . 同样可以发现这三个电子态的谐振频率ω e 和非谐振频率ω e χ e 也很相似. 谐振频率分别为2387.48, 2393.52和2406.68 cm–1 ; 非谐振频率分别为45.81, 40.79和40.39 cm–1 .3 Π为三重态的第一激发态, 在平衡位置附近的主要电子组态为$7{{\text{σ}} ^2}8{{\text{σ}} ^\alpha }{\rm{4}}{\text{π}} _x^\alpha {\rm{4}}{\text{π}} _y^2$ , 权重为89.02%. X3 Σ– → A3 Π跃迁主要是由$8{{\text{σ}} ^\beta } \to 3{\text{π}} _y^\beta $ 的跃迁. 而c1 Π在平衡位置附近的主要电子组态为$7{{\text{σ}} ^2}8{{\text{σ}} ^\alpha } {\rm{4}}{\text{π}} _x^\beta {\rm{4}}{\text{π}} _y^2$ , 权重为82.77%. 两个态的平衡核间距和离解能分别为1.6395, 1.8168 ?和1.207, 0.515 eV. A3 Π和c1 Π态虽然与a1 Δ和b1 Σ+ 态来源于同一离解极限, 但这两个态与a1 Δ和b1 Σ+ 态在平衡位置处的电子组态不同, 所以两个态的平衡核间距以及谐振频率均与a1 Δ和b1 Σ+ 态有很大的差别. 与SH+ [13 ] 和TeH+ [14 ] 离子类似, 从图1 可以看出, 15 Σ– 激发态在30000—40000 cm–1 区域内与a1 Δ, b1 Σ+ , A3 Π, c1 Π态都相交, 同时其能级比A3 Π态要低约4000 cm–1 . 对于大于40000 cm–1 范围, 曲线相交非常复杂, 而且可以看出其离解能非常小, 故本文没有详细讨论其Λ—S态和Ω态的光谱常数.表2 和表3 中同一主簇氢化物正离子(SH+ , SeH+ 和TeH+ )最低三个电子态X3 Σ– , a1 Δ和b1 Σ+ 的光谱常数, 可以发现三个电子态的平衡核间距随着第Ⅵ主簇原子的核电荷数增加而增加; 谐振频率、非谐振频率、离解能和垂直跃迁能都随着第Ⅵ主簇原子的核电荷数增加而减小[13 ,14 ] . 可以看出本文的计算结果符合同一主簇化合物的变化规律.离子 文献 电子态 R e /?ω e /cm–1 ω e χ e /cm–1 B e /cm–1 D e /eVT e /cm–1 SH+ [13 ] X3 Σ– 1.361 2555.2 49.00 9.279 3.488 0 [13 ] a1 Δ 1.362 2567.2 47.48 9.285 4.102 10186.7 [13 ] b1 Σ+ 1.362 2576.7 47.34 9.298 4.208 18881.3 TeH+ [14 ] X3 Σ– 1.6425 2147.8 36.23 6.2351 2.846 0 [14 ] a1 Δ 1.6404 2171.0 36.57 6.2547 3.287 7590 [14 ] b1 Σ+ 1.6383 2184.2 36.24 6.2711 3.351 15467
表3 第Ⅵ主簇氢化物正离子低电子态的光谱常数Table3. Spectroscopic constants of the low-lying states for the Ⅵ hydride cations.3.2.Ω态的势能曲线与光谱常数 -->3.2.Ω态的势能曲线与光谱常数 由于Se是重元素, 在计算中考虑了SOC效应. Se+ 离子的2 D和2 P原子态分别分裂成2 D3/2 , 2 D5/2 和2 P1/2 , 2 P3/2 . 25个Ω态分别对应了5个离解极限: Se+ (4 S3/2 ) + H(2 S1/2 ), Se+ (2 D3/2 ) + H(2 S1/2 ), Se+ (2 D5/2 ) + H(2 S1/2 ), Se+ (2 P1/2 ) + H(2 S1/2 )和Se+ (2 P3/2 ) + H(2 S1/2 ). 其离解关系列于表4 中. 通过Balasubramanian等[9 ] 报道的离解能和垂直跃迁能的结果可以推出前两个离解极限的相对能量为17745 cm–1 . 与实验值[10 ] 的误差达到了34.8%. Balasubramanian等[9 ] 计算结果的精度有待提高. 本文计算的结果和实验值[10 ] 非常吻合, 最大相对误差不超过0.5%. 所以本文有关SeH+ 离子光谱性质和跃迁性质的计算结果是可靠的.原子态 Ω态 相对能量/cm–1 本文工作 文献[9 ] a 实验值[10 ] Se+ (4 S3/2 ) + H(2 S1/2 ) 2, 1, 1, 0+ , 0– 0 0 0 Se+ (2 D3/2 ) + H(2 S1/2 ) 2, 1, 1, 0+ , 0– 13189.0 17745 13168.2 Se+ (2 D5/2 ) + H(2 S1/2 ) 3, 2, 2, 1, 1, 0+ , 0– 13806.5 18347 13784.4 Se+ (2 P1/2 ) + H(2 S1/2 ) 1, 0+ , 0– 23115.9 23038.3 Se+ (2 P3/2 ) + H(2 S1/2 ) 2, 1, 1, 0+ , 0– 23928.7 23894.8 a 根据文献[9 ]的计算数据推导得到.
表4 SeH+ 离子Ω 态的离解关系Table4. Dissociation relationships of Ω states of SeH+ .图2 所示. 在30000—40000 cm–1 区域内, 本文详细讨论了Ω态的势能曲线存在的交叉和避免交叉现象. 对于J = 2分量, (3)2 (15 Σ– )和A1 2态均在约2.0 ?处出现避免交叉, 而A1 2和a2态均在约2.4 ?处出现避免交叉, 故在2.1—2.4 ?范围A1 2态主要来源于15 Σ– 态, 2.4 ?后A1 2和a2态分别主要来源于a1 Δ和15 Σ– 态; 对于J = 1分量, c1态分别在约2.0, 2.1 ?处与(4)1 (15 Σ– ), A2 1态避免交叉; 对于J = 0+(-) 分量, b1 Σ+ 态对应于Se+ (2 Pu ) + H(2 Sg )离解极限. b0+ 态穿过了A1 2, A2 1, A3 0– 态, 由于其和A4 0+ 态避免交叉, 最后对应到Se+ (2 D3/2 ) + H(2 S1/2 )离解极限. 而A3 0– 态在约2.1 ?处和(2)0– (15 Σ– )态避免相交. 由于Ω态曲线的避免交叉, a2, b0+ , A1 2, A2 1, A3 0– , A4 0+ 和c1态出现了两个势阱.图 2 SeH+ 离子的9个Ω态的势能曲线Figure2. Potential energy curves of nine Ω states of SeH+ .表5 中. 基态X3 Σ– 分裂为X1 0+ 和X2 1, 两个分裂态的能量差为252.4 cm–1 . 两个态的平衡核间距、谐振频率和势阱深度 (离解能) 相比于X3 Σ– 态变化很小. 本文预测了A3 Π态的分裂常数A SO : A SO (A2 1 – A1 2) = 858.9 cm–1 , A SO (A3 0– – A2 1) = 1213.5 cm–1 和A SO (A4 0+ – A3 0– ) = 199.5 cm–1 . A3 0– 态的第二势阱的平衡核间距分别为3.58, 3.59和3.6 ?, 与15 Σ– 态的平衡核间距 (R e = 3.5894 ?) 很接近. 尽管a2, A2 1和A3 0– 态的势阱深度只有0.03 eV, 但三个态均有较大的谐振频率, 分别达到了168.6, 155.22和151.93 cm–1 , 所以三个电子态都是束缚态. 而A1 2, A4 0+ 和c1态第二势阱的最低能量是由电子态之间的避免交叉产生的.电子态 R e /?ω e /cm–1 ω e χ e /cm–1 B e /cm–1 D e /eVT e /cm–1 X1 0+ 1.4661 2385.56 45.66 7.8802 3.380 0 X2 1 1.4662 2386.15 46.02 7.8790 3.348 252.4 a2 第一势阱 1.4645 2392.76 41.29 7.8967 2.525 9408.2 第二势阱 3.5800 168.60 33.67 1.3399 0.030 27016.9 b0+ 1.4631 2406.94 44.20 7.9127 2.758 18213.8 A1 2 第一势阱 1.6418 1396.10 53.29 6.3333 0.340 30201.1 第二势阱 2.4132 2295.44 131.22 2.9938 1.262 30248.9 A2 1 第一势阱 1.6457 1381.37 53.81 6.3229 0.329 31060.0 第二势阱 3.5900 152.22 25.81 1.3353 0.030 27018.9 A3 0– 第一势阱 1.6429 1391.28 55.78 6.3715 0.307 32273.5 第二势阱 3.6000 151.93 25.77 1.3339 0.030 27019.3 A4 0+ 第一势阱 1.6368 1385.24 18.09 6.3123 0.962 32473.0 第二势阱 2.7918 676.20 90.61 2.1897 0.167 39685.4 c1 第一势阱 1.8161 — — — 0.044 36979.9 第二势阱 2.1793 1781.89 149.33 3.5614 0.687 34921.9
表5 SeH+ 离子Ω态的光谱常数Table5. Spectroscopic constants of the Ω states of SeH+ .[30 ] 在先前研究结果的基础上[14 ] 讨论了SOC水平下激光冷却TeH+ 离子的可能性. 作为同一主簇氢化物正离子, 本文计算的Λ—S态和Ω态的势能曲线和光谱常数为进一步研究激光冷却SeH+ 离子的可能性提供了部分理论参数.3.3.偶极矩, 跃迁偶极矩和跃迁性质 -->3.3.偶极矩, 跃迁偶极矩和跃迁性质 偶极矩是分子离子的固有性质, 在自旋无关水平下12个Λ—S态的偶极矩和$ {{\rm{A}}^3}\Pi \leftrightarrow {{\rm{X}}^3}{\Sigma ^ - }$ 跃迁的跃迁偶极矩随核间距的变化曲线描绘于图3(a) 中. SeH+ 是一个离子体系, 基态X3 Σ– 在平衡位置处的偶极矩为0.45 a.u., X3 Σ– , a1 Δ, b1 Σ+ , A3 Π和c1 Π态的偶极矩随着核间距的增加而增大, 分别在2.14, 2.22, 2.24, 1.96和1.78 ?达到最大值, 即: 0.63, 0.66, 0.67, 0.92和0.80 a.u., 然后减小. 核间距增加到9 ?时, 12个Λ—S态的偶极矩都达到了–0.2 a.u., $ {{\rm{A}}^3}\Pi \leftrightarrow {{\rm{X}}^3}{\Sigma ^ - }$ 跃迁的跃迁偶极矩随着核间距的增加而减小, 在平衡核间距处为0.23 a.u.. 图3(b) 描绘了SOC效应下9个Ω态的偶极矩和$ {{\rm{A}}_2}1 \leftrightarrow {{\rm{X}}_1}{0^ + }$ 跃迁的跃迁偶极矩. 相比于自旋无关水平的结果, 不连续的曲线表示电子态之间有避免交叉.图 3 SeH+ 离子的偶极矩和跃迁偶极矩跃迁偶极矩 (a) 自旋无关水平下; (b) SOC水平下Figure3. Dipole moments and transition dipole moments of SeH+ : (a) At spin-free level; (b) at SOC level.[31 ] : $f = 4.70165 \; \times {10^{ - 7}}[{\rm cm}{\kern 1 pt} {D^{ - 2}}]{\tilde \upsilon _{\rm{eg}}}{\left| {{{{\mu}} _{\rm{eg}}}} \right|^2}$ , 其中${\tilde \upsilon _{\rm{eg}}}$ 表示为高态到低态的垂直跃迁能, ${{{\mu}} _{\rm{eg}}}$ 表示跃迁偶极矩. 这样估算出$ {{\rm{A}}^3}\Pi \leftrightarrow {{\rm{X}}^3}{\Sigma ^ - }$ 和$ {{\rm{A}}_2}1 \leftrightarrow {{\rm{X}}_1}{0^ + }$ 跃迁的振子强度分别为5.15 × 10–3 和5.08 × 10–3 , 说明两种跃迁具有较强的跃迁强度. 最后, 基于势能曲线和跃迁偶极矩, 本文预测了$ {{\rm{A}}^3}\Pi \leftrightarrow {{\rm{X}}^3}{\Sigma ^ - }$ 以及$ {{\rm{A}}_2}1 \leftrightarrow {{\rm{X}}_1}{0^ + }$ 跃迁的弗兰克-康登因子、辐射速率和辐射寿命. 所有结果列于表6 中. 由于A3 Π和X3 Σ– 态的平衡核间距之差很大, 故其对角化的弗朗克-康登因子比较小, 说明了两个电子态的波函数重叠较小. 同时预测了A3 Π和A2 1态的辐射寿命分别为746.6和787.8 ns.跃迁 ν' ν'' = 0ν'' = 1ν'' = 2ν'' = 3ν'' = 4ν'' = 5Σ A τ = 1/(Σ A )$ {\rm A^3}\Pi \leftrightarrow {\rm X^3}{\Sigma ^ - }$ 0 0.4079 0.3685 0.1666 0.0470 0.0088 0.0011 1339434 746.6 1 0.3271 0.0013 0.2122 0.2713 0.1398 0.0405 1310290 763.2 $ {\rm A_2}1 \leftrightarrow {\rm X_1}{0^ + }$ 0 0.3841 0.3688 0.1787 0.0549 0.0116 0.0017 1269392 787.8 1 0.3186 0.0001 0.1761 0.2695 0.1629 0.0558 1212188 825.0
表6 $ {{\rm{A}}^3}\Pi \leftrightarrow {{\rm{X}}^3}{\Sigma ^ - }$ 和$ {{\rm{A}}_2}1 \leftrightarrow {{\rm{X}}_1}{0^ + }$ 跃迁的弗兰克-康登因子(单位s-1 )、总辐射速率和辐射寿命(单位: ns)Table6. Franck-Condon Factors, Emission rates (unit of s–1 ) and radiative lifetimes τ (unit of ns) of the $ {{\rm{A}}^3}\Pi \leftrightarrow {{\rm{X}}^3}{\Sigma ^ - }$ and $ {{\rm{A}}_2}1 \leftrightarrow {{\rm{X}}_1}{0^ + }$ transitions.4.结 论 本文采用ic-MRCI+Q 方法计算了SeH+ 离子前三个离解极限所对应的12个Λ—S电子态的势能曲线. 计算中考虑了标量相对论效应, 芯-价电子关联和SOC效应. 文中详细地讨论了在30000—40000 cm–1 区域低激发态的曲线出现避免相交的原因. 其原因是在自旋无关水平下a1 Δ, b1 Σ+ , A3 Π, c1 Π和15 Σ– 态之间有着较复杂的相交. 从而导致了a2, b0+ , A1 2, A2 1, A3 0– , A4 0+ 和c1态出现了两个势阱. 通过求解径向薛定谔方程得到各束缚态的电子态的光谱常数. 最后根据计算的跃迁偶极矩和势能曲线预测出$ {{\rm{A}}^3}\Pi \leftrightarrow {{\rm{X}}^3}{\Sigma ^ - }$ 和$ {{\rm{A}}_2}1 \leftrightarrow {{\rm{X}}_1}{0^ + }$ 跃迁的弗兰克-康登因子、辐射速率和辐射寿命. 本文的计算结果将为进一步研究激光冷却SeH+ 离子的可能性提供了部分理论参数. 








 图 1 SeH+离子的12个Λ—S态的势能曲线
图 1 SeH+离子的12个Λ—S态的势能曲线





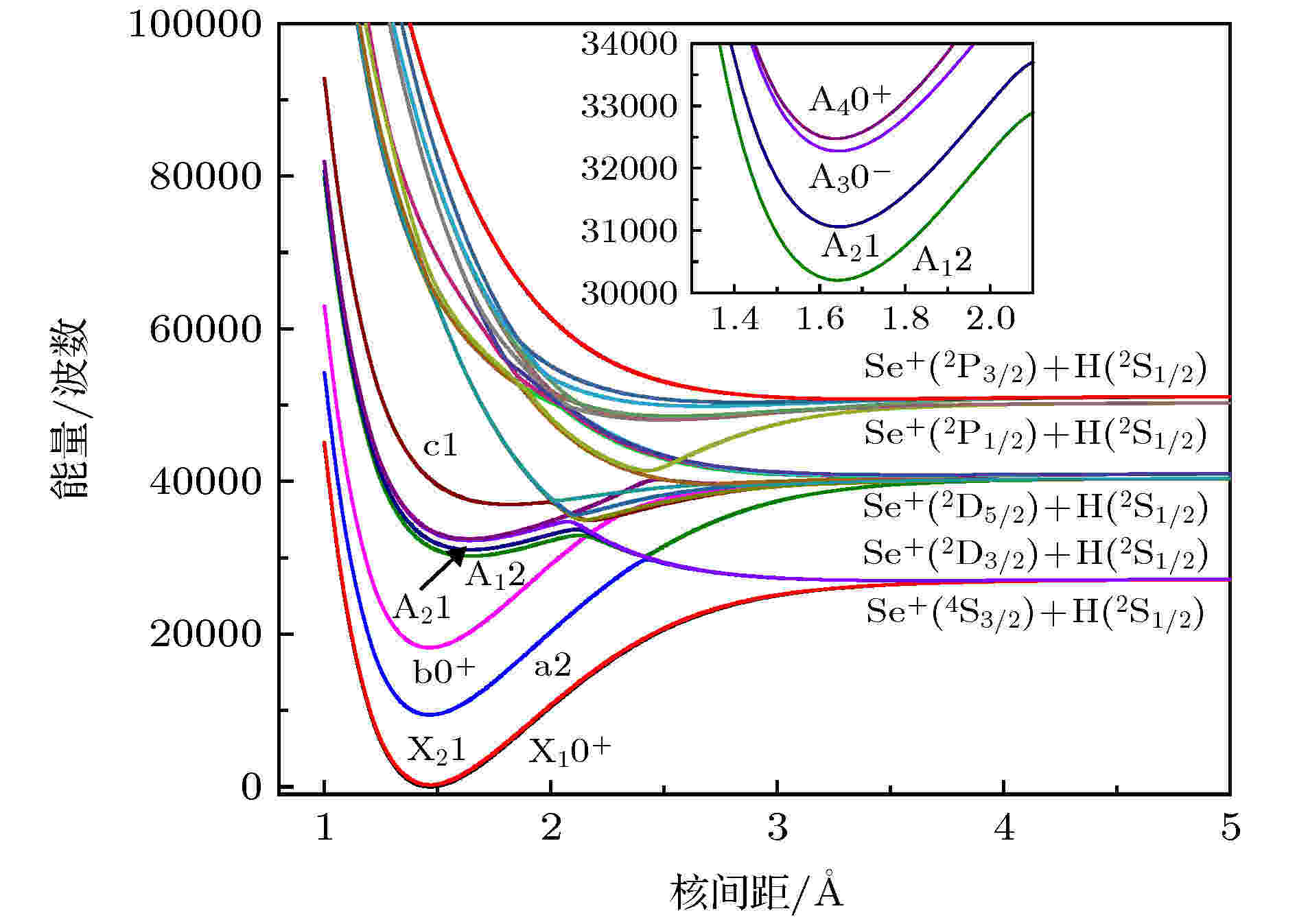 图 2 SeH+离子的9个Ω态的势能曲线
图 2 SeH+离子的9个Ω态的势能曲线




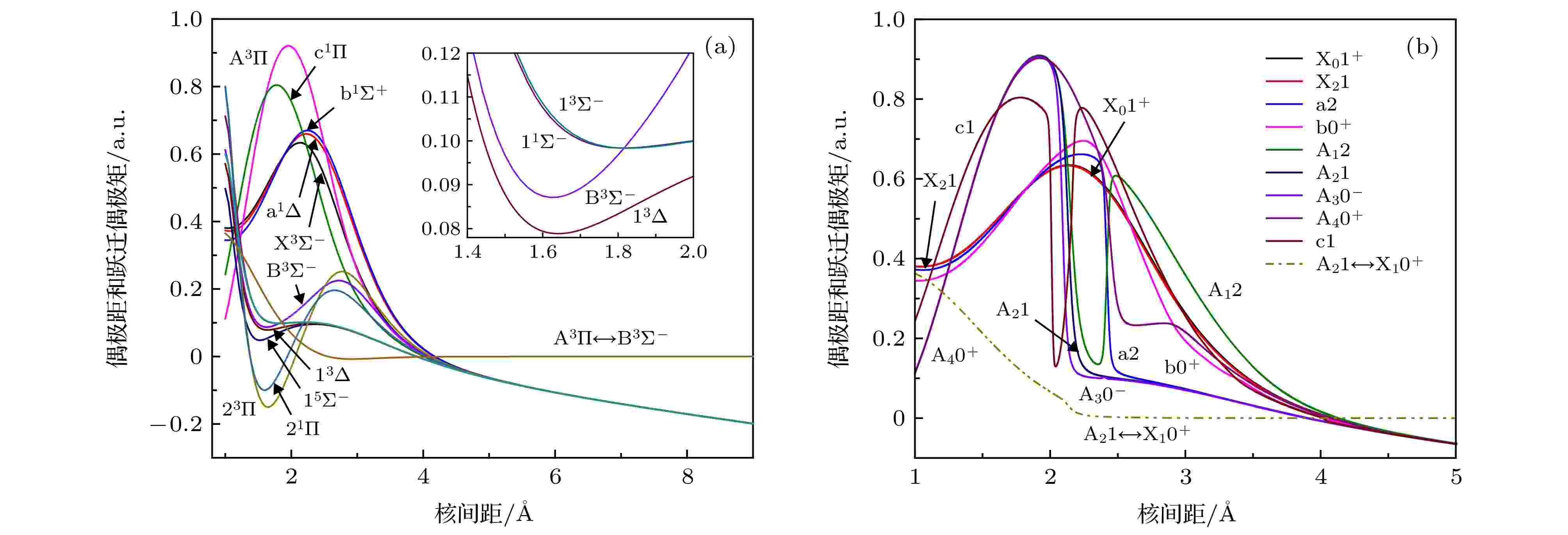 图 3 SeH+离子的偶极矩和跃迁偶极矩跃迁偶极矩 (a) 自旋无关水平下; (b) SOC水平下
图 3 SeH+离子的偶极矩和跃迁偶极矩跃迁偶极矩 (a) 自旋无关水平下; (b) SOC水平下



















