删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于高分辨率激光外差光谱反演大气CO<sub>2</sub>柱浓度及系统测量误差评估方法

本站小编 Free考研考试/2021-12-29
摘要:利用实验室研制的近红外激光外差光谱仪, 开展了基于最优估计算法的温室气体柱浓度反演和系统测量误差的近似评估等相关工作. 首先, 通过光谱数据库、参考正向模型计算结果与傅里叶变换红外光谱技术探测结果筛选出了探测窗口, 并以此为依据选择了相应的激光器和探测器; 其次, 建立了基于参考正向模型最优估计浓度反演算法, 采用Levenberg-Marquardt (LM) 迭代方法, 实现了整层大气CO2柱浓度及垂直分布廓线的反演, 并开展了长期观测对比实验, 验证了反演算法的可行性; 最后, 通过模拟所选探测窗口波段在不同白噪声条件下的正向大气透过率谱, 获得了系统SNR与柱浓度测量误差之间的近似对应关系. 该研究是探测系统不可或缺的理论计算部分, 将有助于完善激光外差技术在大气探测中的应用.
关键词: 激光外差/
测量误差/
参考正向模型/
CO2柱浓度

English Abstract


全文HTML

--> --> -->
1.引　言
气候变化的主要驱动因素之一是地球大气中CO2[1,2]温室气体加速生长的结果, 其生长原因与人类活动和人为排放紧密相关[3], 近几十年来, 约40%的人为CO2[4]排放在大气中, 而其余的则储存在陆地和海洋沉积物中. 尽管目前关于CO2的建模和观测得到了快速的发展, 但大气、陆地和海洋之间的碳交换过程尚未得到充分了解, 导致未来气候变化的预测存在相当大的不确定性, 评估区域温室气体源和汇的准确性取决于地面观测站的密度, 因此需大面积的进行布网, 从而更好地理解CO2及其他温室气体源、汇总量和时空分布. 基于吸收光谱技术的气体探测方法主要包括可调谐半导体激光吸收光谱技术(TDLAS)[5,6]、波长调制光谱技术(WMS)[7-9]、傅里叶变换红外光谱技术 (FTIR)[10,11]、激光外差光谱技术(LHR)[12-16]等.
基于LHR的地基探测仪具有体积小、高分辨率、易集成等优点, 已用于多种气体的遥感探测. Sonnabend等[12]利用10 μm铅盐激光器建立的激光外差系统测量了臭氧的大气太阳透过率谱, 反演了臭氧的浓度廓线. Weidmann等[13]建立的0.0073 cm–1高分辨率激光外差系统, 实现了O3的廓线反演. Tsai等[14]建立了一套可调谐外腔量子级联激光外差辐射计, 测量并反演了大气O3, N2O, CH4, H2O等气体的垂直廓线分布信息. 在国内, 王晶晶等[15]搭建了3.53 μm带间级联激光器为本振光源, 实现了CH4及HDO廓线反演, 其分辨率为0.0033 cm–1. 张尚露等[16]利用逐线积分辐射传输模式, 对实测的激光外差透过率谱进行了非线性最小二乘拟合, 实现了整层大气水汽柱浓度的反演.
本文利用建立的参考正向模型筛选出了适合的大气探测窗口, 提出了精准的激光器波长相关校准方法, 基于最优估算法实现了CO2柱浓度和垂直廓线分布的反演, 并对5个月的探测数据与GOSAT数据进行了对比. 此外, 为了评估系统的测量误差, 提出一种新的系统测量误差评估方法, 通过对参考正向模型模拟的透过率谱加载不同幅度的白噪声, 建立了信噪比与测量误差间的近似对应关系.
2.高分辨率大气CO2垂直廓线的数据反演
图1为高光谱分辨率激光外差技术反演的技术路线图, 主要包括四个模块, 分别为参考正向模型、探测吸收谱系统搭建、高分辨率光谱预处理以及迭代反演算法. 本工作主要为算法研究, 因此关于系统搭建部分在这里就不再赘述.
图 1 激光外差系统整体技术路线
Figure1. Overall technical route of laser heterodyne system.

2
2.1.参考正向模型 (RFM)
-->

2.1.参考正向模型 (RFM)

参考正向模型 (RFM)[17]由英国国家地球观测中心研发, 是一种通用的逐线辐射传输计算模型. 通过对源代码进行编译, 并编辑和调用rfm.drv文件以获得大气透过率谱及雅可比矩阵等结果, 为后期的数据反演提供相应的正向计算数据.
利用RFM对整层大气透过率谱进行模拟可以用于选择合适的探测窗口, 其选择依据需满足以下几点: 1) 避免其他气体分子及太阳谱干扰; 2) 合适的谱线强度; 3) 探测波段有可选的激光器及探测器. 首先, 通过查询HITRAN2016数据库[18], 可知CO2在6230—6245 cm–1 (1.601—1.605 μm) 波段具有较强的吸收; 随后利用参考正向模型 (RFM) 模拟了CO2, NH3, H2O, N2O, NO2, O3, CO等7种小分子的大气透射光谱(如图2所示), 通过对比总的模拟谱、单独的大气CO2和H2O模拟谱以及地基FTIR测量结果, 最终选择了位于6238.2—6239.3 cm–1的探测窗口, 并以此为依据选择了相应的激光器和探测器.
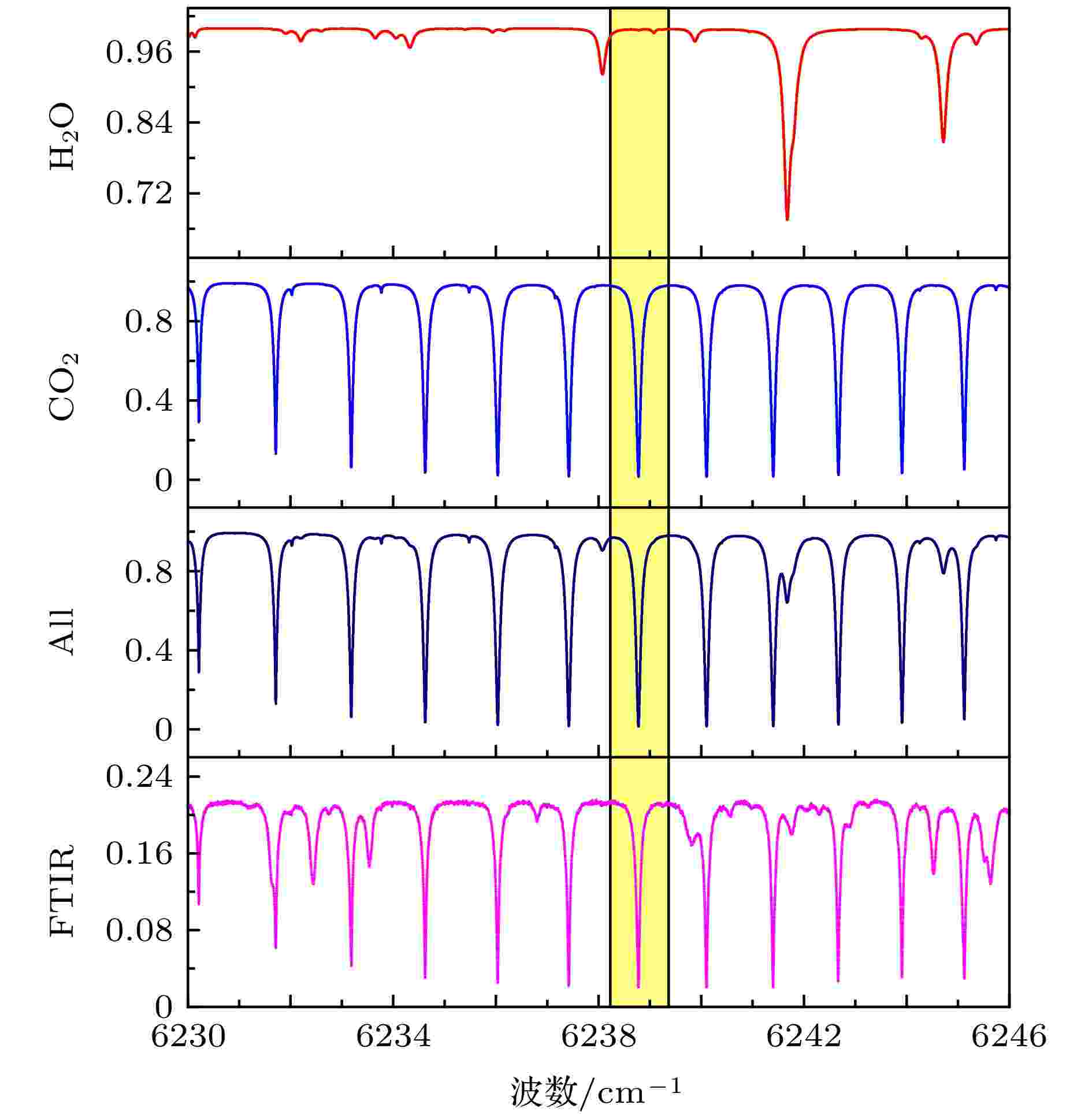图 2 基于RFM模拟的正向透过率谱及所选探测窗口
Figure2. Forward transmittance spectrum based on RFM simulation and selected detection window.

2
2.2.数据预处理
-->

2.2.数据预处理

2019年3月12日在中国科学院合肥物质科学研究院(31.9°N, 117.166°E)采集的0.0073 cm–1高光谱分辨率近红外激光外差数据如图3所示, 采集模式为逐点扫描方式.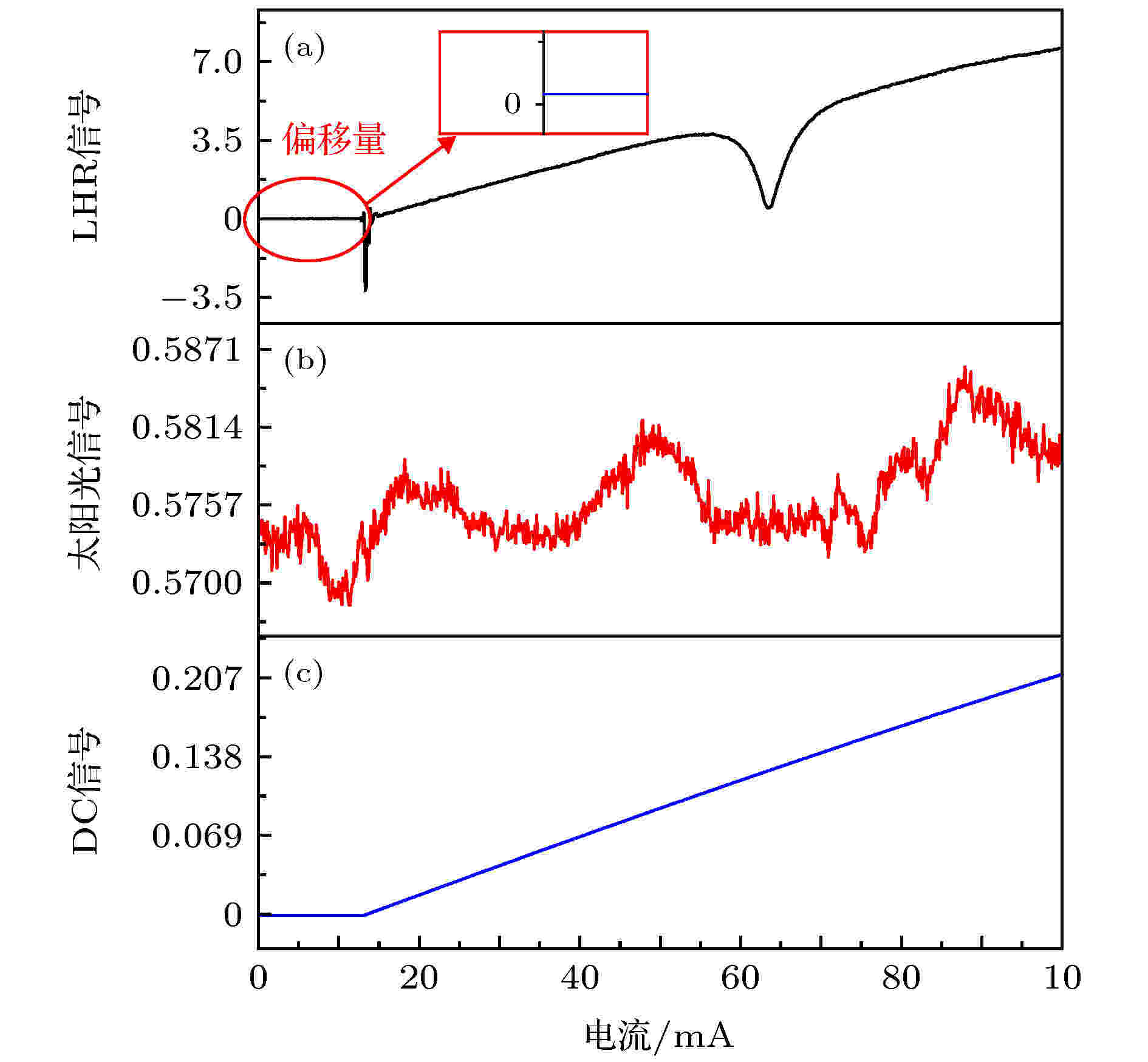
图 3 激光外差实验结果　(a) CO2的高分辨率的外差信号; (b) 实时跟踪的太阳光信号; (c) 激光器的DC信号
Figure3. Experimental results of the laser heterodyne: (a) The high-resolution heterodyne signal of CO2; (b) the sunlight signal tracked in real time; (c) the DC signal of the laser.

首先, 对如图3(a)所示的CO2外差信号进行背景信号扣除处理, 当电流较低时, 激光器仍未出光(红色椭圆标记的部分), 对其取平均得到外差信号的偏移量, 利用外差信号减去该偏移量实现背景扣除.
其次, 利用扣除背景后的外差信号除以图3(c)所示的DC信号对外差信号进行功率校正, 具体过程为
${S_1} = ({{{S_2} - D}})/{B},$
其中, S1为功率校准的激光外差信号, S2为激光外差原始信号, D为偏移量, B为DC信号.
最后, 借助波长计和HITRAN数据库对外差信号进行波长标定, 并与参考正向模型相同的频率间隔进行插值处理. 需特别指出的是, 由于激光电流的工作模式为逐点扫描模式, 利用波长计 (Bristol, 621B) 能够方便地进行实时的波长标定. 但是, 在实际测量过程中, 激光器的工作波长可能会有轻微的变化(如图4(a)所示). 为了准确识别该波长偏移, 如图4(b)所示, 通过移动真实信号, 计算RFM模型计算的参考信号和实际外差信号的相关系数, 其中移动步长可以用插值方法定义为任意小的长度(如0.0001 cm–1). 最后通过相关系数的最大值位置(如图4(b)所示)可以精确地确定波长偏移, 该方法在信噪比较差的情况下依然适用. 最终获得处理后的LHR频谱 (图7(a)中的黑点)以备下一步的数据反演. 特别指出, 对于太阳光功率波动较大的信号(大于平均太阳光功率的10%), 将不再做进一步的处理.
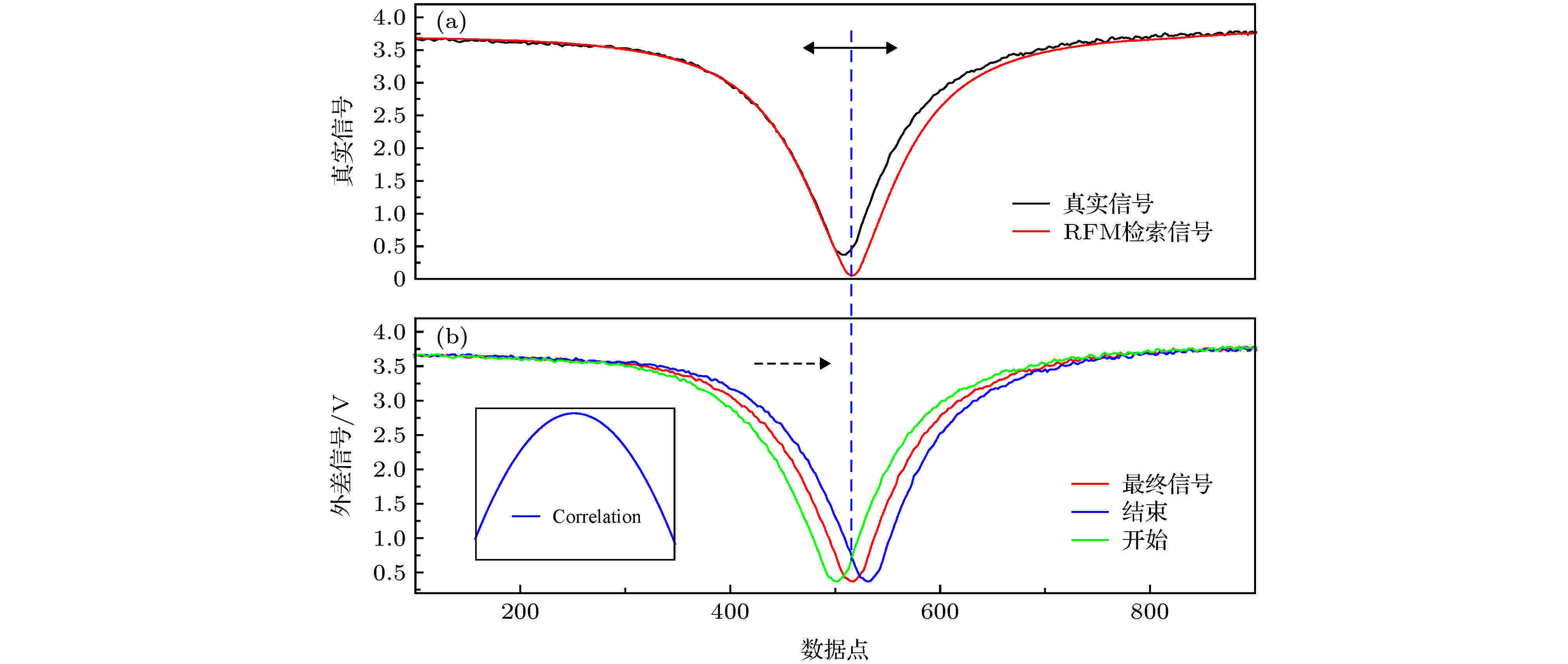图 4 波数偏移校准原理　(a) 参考信号与实验信号之间的波数偏移; (b) 计算波数偏移的过程, 插图为相关系数的结果
Figure4. Principle of the wavenumber shift calibration: (a) Wavenumber shift between the reference signal and real signal; (b) the process of calculating the wavenumber shift. The inset shows the result of correlation coefficients.

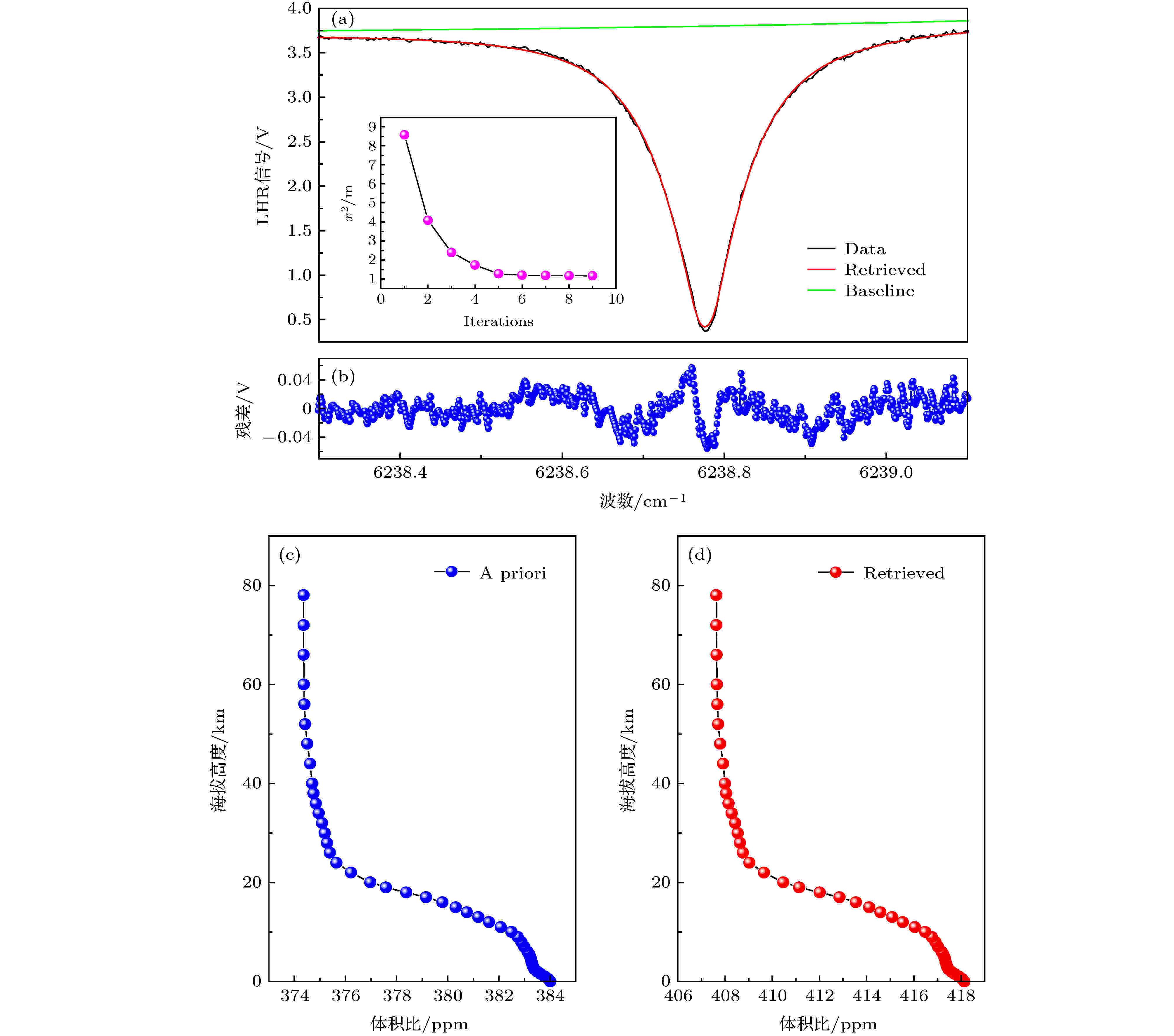图 7 LHR数据反演结果　(a) 实验和拟合LHR谱图以及迭代过程的收敛性 (插图); (b) 残差; (c) 和 (d)分别获取的CO2的先验和反演的垂直浓度分布图
Figure7. Inversion results of LHR data: (a) Experimental and fitted LHR spectrogram and convergence of iterative process (illustration); (b) residue; (c) and (d) obtained prior and inversion vertical concentration profiles of CO2, respectively.

2
2.3.大气参数及状态向量
-->

2.3.大气参数及状态向量

如图5所示, 数据反演所采用的地表温度、压力数据来自于中国气象数据服务中心(CMCC), 而0.2—55.0 km数据源自于美国气象环境预报中心(NCEP)合肥站的数据(蓝点), 对于55 km以上的数据 (红点) 通过对欧洲中期天气预报中心(ECMWF)的月纬向平均廓线数据插值得到. 对于CO2的先验廓线, 使用了典型的中纬度白天廓线数据. 大气分层采用45层, 从地表到78 km高空, 高度网格依次为0.5, 1.0, 2.0, 4.0和6.0 km.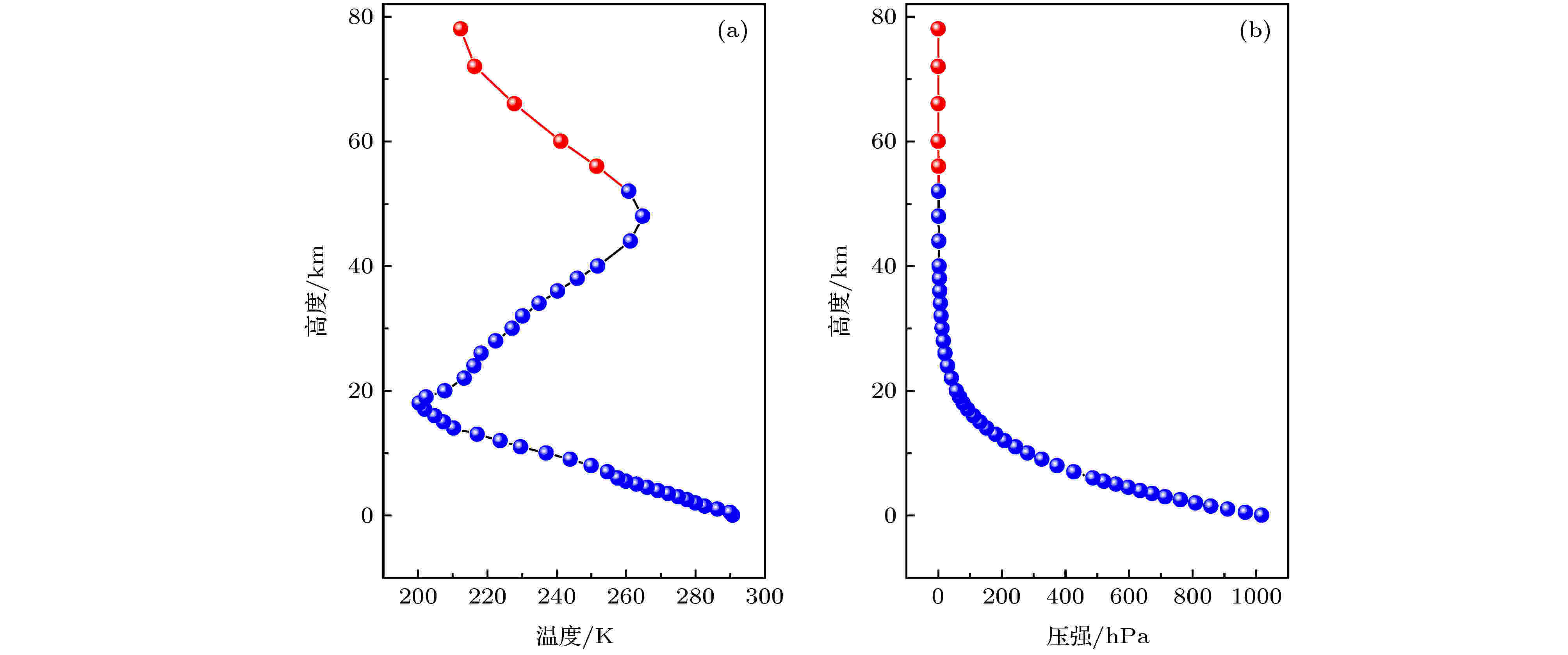
图 5 (a) 温度和 (b) 压力廓线
Figure5. (a) Temperature and (b) pressure profiles.

2
2.4.迭代反演过程
-->

2.4.迭代反演过程

LHR数据反演的流程图如图6所示, 主要由参考正向模型、测量实验数据预处理和迭代反演等过程组成.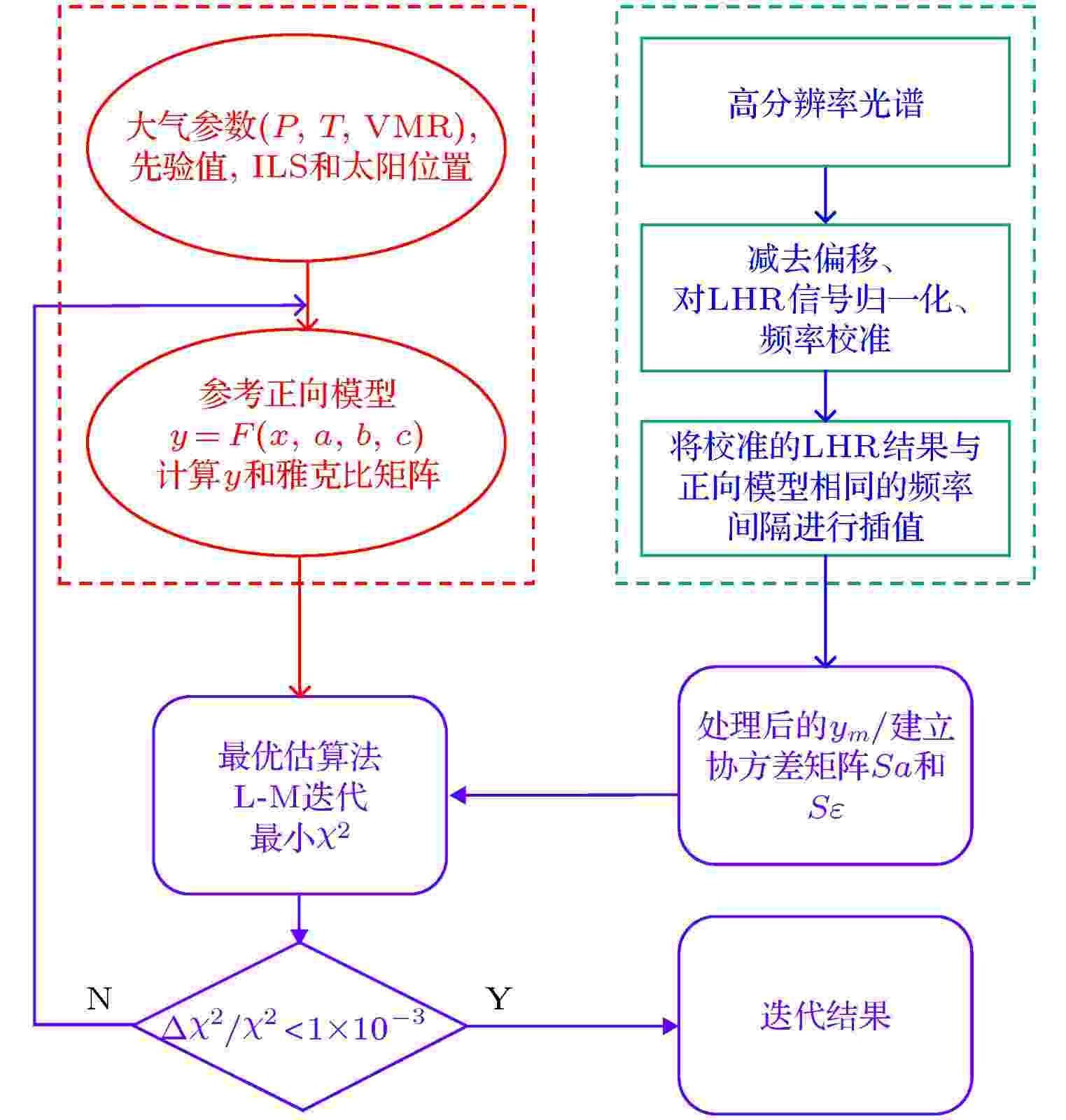
图 6 数据反演流程图　VMR, 体积混合比; ILS, 仪器线形; LM, Levenberg–Marquardt
Figure6. Data inversion flow chart. VMR, volume mixing ratio; ILS, instrument linear; LM, Levenberg–Marquardt.

迭代反演采用Rodgers[19,20]提出的最佳估计方法 (OEM). 对于OEM方法在基于LHR大气探测中的应用, Weidmann等[13]已经做了详细的介绍. 在此仅做简要说明, 测量数据与大气状态向量之间的关系被描述为
${{{y}}_m} = F({{x}},a,b,c) + {{\varepsilon}} , $
其中ym是m维的测量向量, x是n维参考正向模型中状态向量, ε是误差向量, 二阶多项式基线 (系数为a, b和c) 表示目标光谱区域中的非选择性吸收和未校正的功率.
OEM算法为最小化损耗函数χ2的迭代运算过程, 其中损耗函数表示为
${\chi ^2} = {(y - F)^{\rm{T}}}{{S}}_\varepsilon ^{ - 1}(y - F) + {({x_i} - {x_{\rm{a}}})^{\rm{T}}}{{S}}_{\rm{a}}^{ - 1}({x_i} - {x_{\rm{a}}}),$
Sε是测量协方差矩阵, Sa是先验协方差矩阵, xa是先验CO2廓线. 迭代过程采用Levenberg-Marquardt (LM)方法,
$\begin{split}{x_{i + 1}} =\; & {x_i} + {[(1 + \gamma){{S}}_{\rm{a}}^{{\rm{ - 1}}} + K_i^{\rm{T}}{{S}}_\varepsilon ^{ - 1}{K_i}]^{ - 1}} \\ &\times [K_i^{\rm{T}}{{S}}_\varepsilon ^{ - 1}({y_m} - {F_i}) - {{S}}_{\rm{a}}^{{\rm{ - 1}}}({x_i} - {x_{\rm{a}}})],\end{split}$
其中K为雅可比矩阵 (或加权函数), γ为LM (Levenberg–Marquardt) 参数.
在反演过程中, 通过LM算法((4)式)迭代调用参考正向模型以最小化损耗函数((3)式), 最终反演出CO2的廓线. 其中, Sε是基于ym测量向量的标准偏差构建的, 协方差矩阵设为对角矩阵, 而Sa依据先验向量的估计误差构建 (表1). 迭代上限设为20次, 收敛条件设为Δχ2/χ2 < 1 × 10–3. 在条件设置合理的反演中, 最终损耗函数χ2应该接近测量向量的维数大小. 图7(a)显示了经过预处理的LHR数据和在6238.2—6239.3 cm–1的光谱区域内的拟合光谱, 其间隔为0.001 cm–1. 迭代过程如图7(a)的插图所示, 经过8次迭代后获得的χ2/m约为1.17. 预处理数据和拟合结果之间的残差如图7(b)所示, 其随机分布表明拟合良好. 通过将反演得到的比例因子乘以先验廓线, 可以计算出反演后CO2廓线如图7(d)所示.
状态
向量		先验值定义
x (CO2)1先验廓线的比例因子
(ECMWF) 45层.
aa0基线中a0、b0和c0的多项式系数由对预处理的LHR信号与模型结果(去除吸收部分后)的比值进行二阶多项式拟合得到.
bb0
cc0


表1数据反演中使用的状态向量的定义
Table1.Definition of the state vector used in the data retrieval.

利用理想气体状态方程[21] n(h) 以及反演得到的廓线x(h), 则CO2的柱浓度为
${\rm{Column}}\_{\rm{C}}{{\rm{O}}_2} = \int\nolimits_0^{78} {x(h)} n(h){\rm{d}}h,$
其中n(h) 为高度h处的分子数密度, 整个大气层78 km, x(h) 为CO2在高度h处的体积百分比. CO2的柱浓度为8.2184 × 1021 molecule/cm2.
图8(a)显示了2019年3月14日的连续测量结果, $X_{\rm CO_{2}}$ (表示为CO2的柱浓度)的标准偏差约为0.47 ppm. 本研究仅对上午11:00至下午13:00的测量结果进行了分析, 这是因为美国气象环境预报中心NCEP和中国气象数据服务中心CMCC提供的时间点为12:00, 且认为该段时间内大气参数是稳定的.
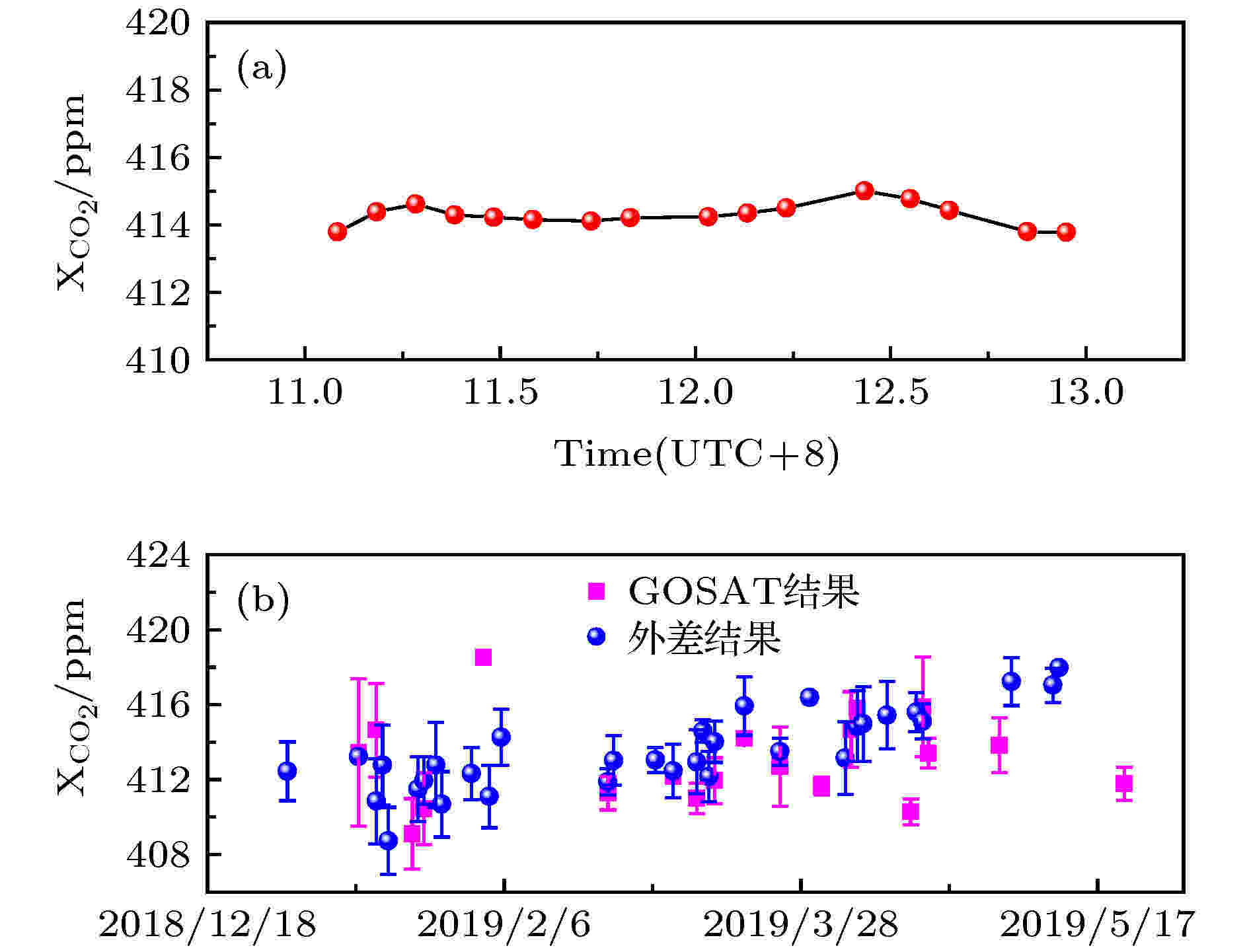图 8 (a) 2019年3月14日从11:00至13:00的$X_{{\rm{CO}}_2} $的反演结果; (b) $X_{{\rm{CO}}_2} $的外差结果和GOSAT结果的时间序列
Figure8. (a) Retrieval results of the $X_{{\rm{CO}}_2} $ versus time from 11:00 to 13:00 on March 14, 2019; (b) time series of the LHR results and GOSAT results of $X_{{\rm{CO}}_2}$.

为了进一步验证系统探测结果, 进行了2019年1月至5月长达5个月的晴天探测, 将实验数据反演结果与温室气体观测卫星GOSAT数据产品进行了比较. 图8(b)显示了该系统$ X_{\rm CO_{2}} $日平均反演结果 (以标准差为误差棒) 和GOSAT结果的时间序列, 其中GOSAT结果选取在以观测点 (合肥, 31.9°N, 117.166°E) 为中心, 3°半径范围内的数据. 在测量过程中, $ X_{{\rm CO}_2} $的标准偏差为0.12— 3.92 ppm, 对应相对误差范围为0.03%—0.95%. 从图8(b)可以看出, 对于$ X_{\rm CO_{2}} $的测量结果与GOSAT结果吻合较好, 其差异与GOSAT数据量较少、经纬度范围较大以及与系统测量误差等相关. 今后将对大气中CO2进行长时间的探测, 进而开展季节和年度变化的研究.
3.系统测量误差近似评估模型
为了近似评估系统测量误差, 通过模拟正向计算谱叠加不同幅度白噪声, 得到SNR, 3σ, Max (平均值加上3σ)、Min (平均值减去3σ) 与白噪声幅度之间的关系; 通过改变CO2的廓线比例, 透过率谱最低点变化引起柱浓度变化; 以此Max, Min进行柱浓度插值, 从而得到了SNR和柱总量的差值(测量误差)间的近似对应关系.
首先, 对正向计算谱叠加不同幅值的白噪声以模拟不同的信噪比, 如图9(a), RFM模型加载0.05幅度的白噪声; 图9(b)为加载5000次幅值为0.05白噪声, 由波段吸收峰波谷位置的变化情况, 获得信噪比计算公式
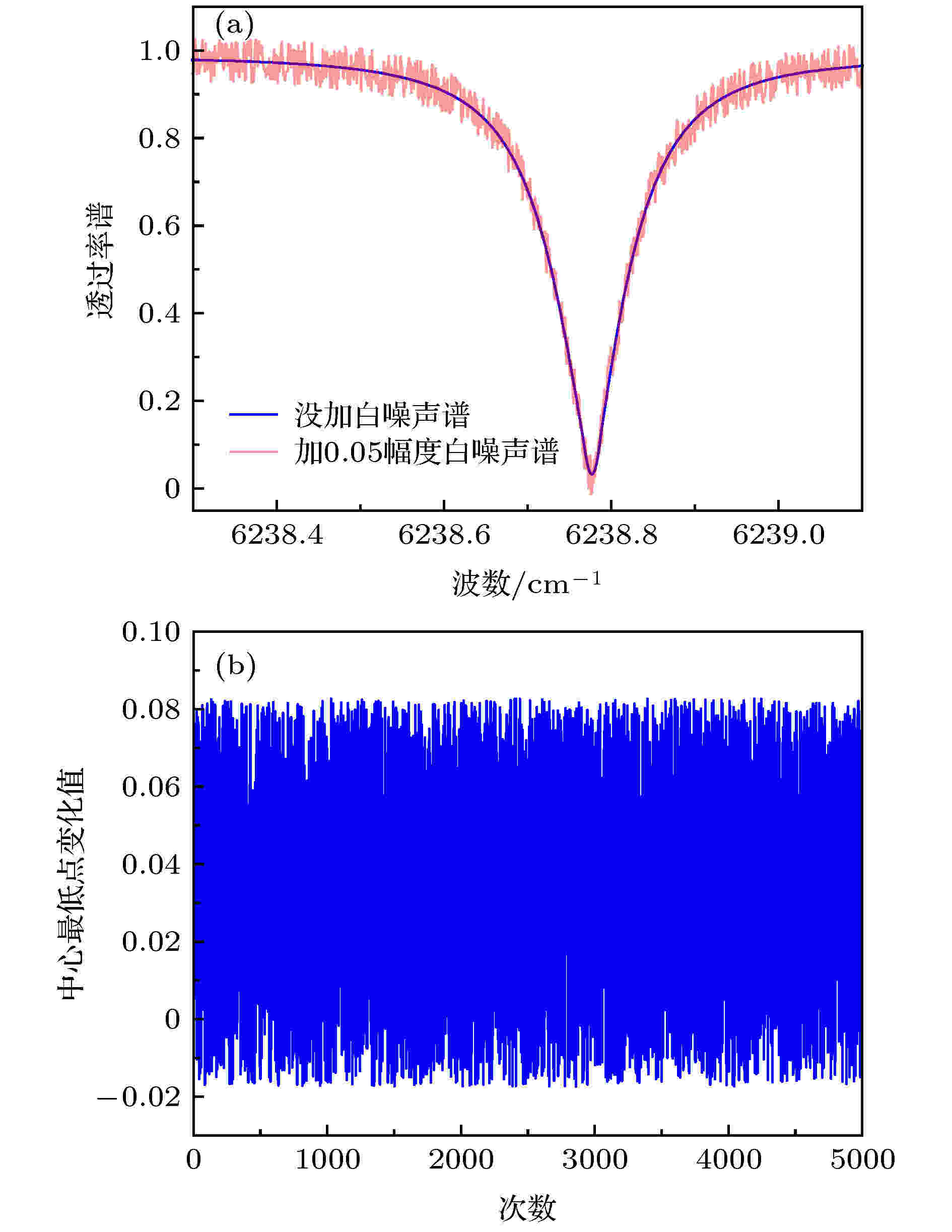图 9 (a) 叠加0.05幅度的白噪声后的透过率谱; (b) 叠加5000次后透过率谱最低点的变化
Figure9. (a) The transmittance spectrum after adding white noise with the amplitude of 0.05; (b) change range of the lowest point of transmittance spectrum after adding 5000 times.

${\rm{SNR}} = ({{T' - T''}})/{\sigma },$
其中$T'$和$T''$分别代表图9(a)透过率谱吸收峰的最大值和最小值, $\sigma $代表图9(b)的5000次数据的标准偏差.
模拟白噪声从幅度0.001到幅度0.050, 步长为0.001, 获得了SNR, $3 \sigma $, Max (平均值加上$ 3\sigma $), Min (平均值减去$3 \sigma $) 的变化, 如图10所示. 从结果分析得到$3 \sigma $ 和Max随着白噪声的幅度增加而增加, 而Min和SNR随着白噪声的幅度减少而减少.
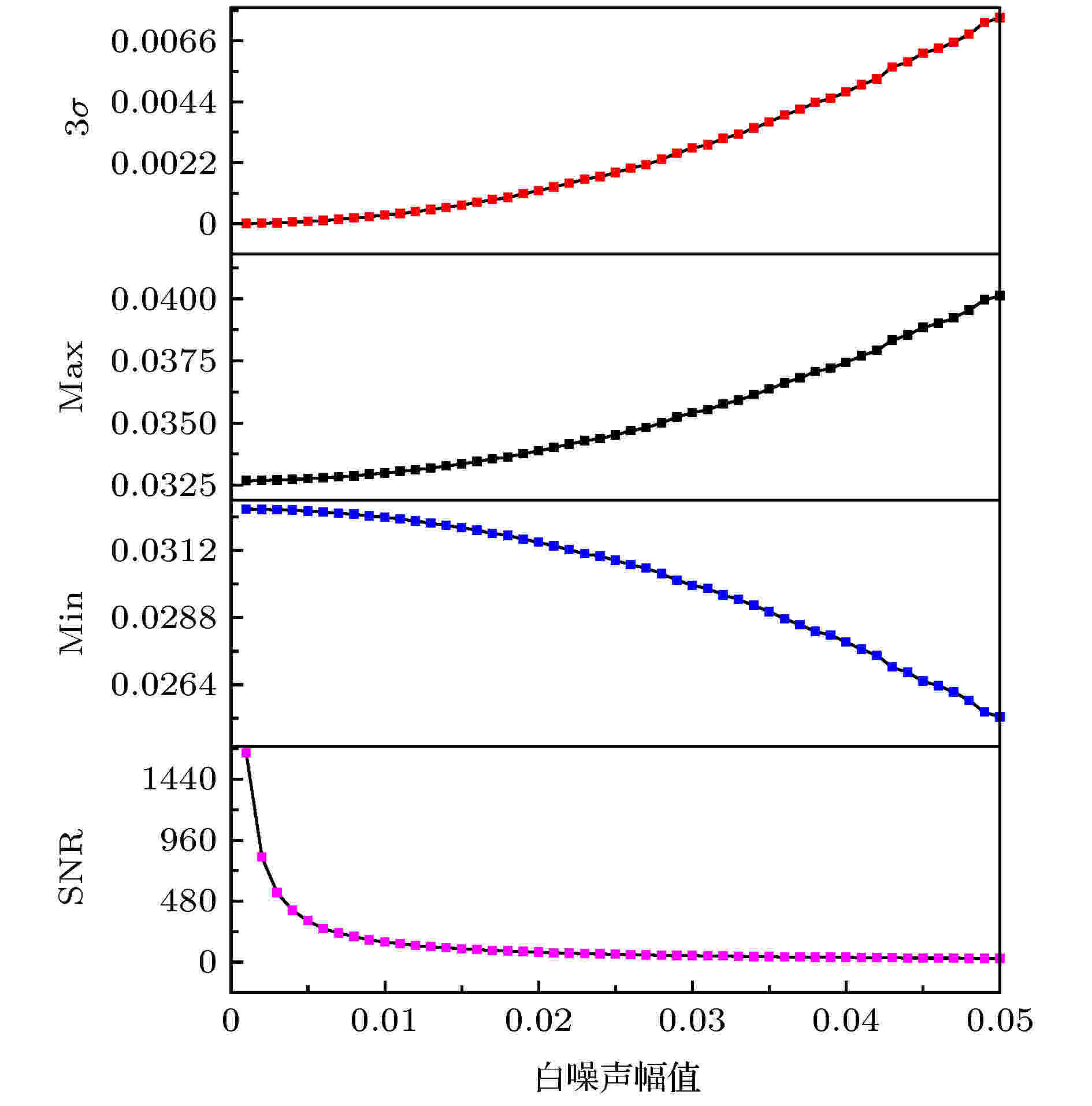图 10 白噪声幅度0.001变化到幅度0.050引起的$3 \sigma $, Max, Min和SNR的变化
Figure10. Changes of $ 3{\rm{\sigma }} $, Max, Min, and SNR caused by the white noise amplitude increasing from 0.001 to 0.050.

其次, 通过改变CO2的廓线比例, 透过率谱最低点也随之变化, 相应的柱浓度变化情况如图11(b). 利用图10中的Max插值获得柱总量1, Min插值获得柱总量2, 柱总量2减去柱总量1为柱浓度差值, 即为测量误差.
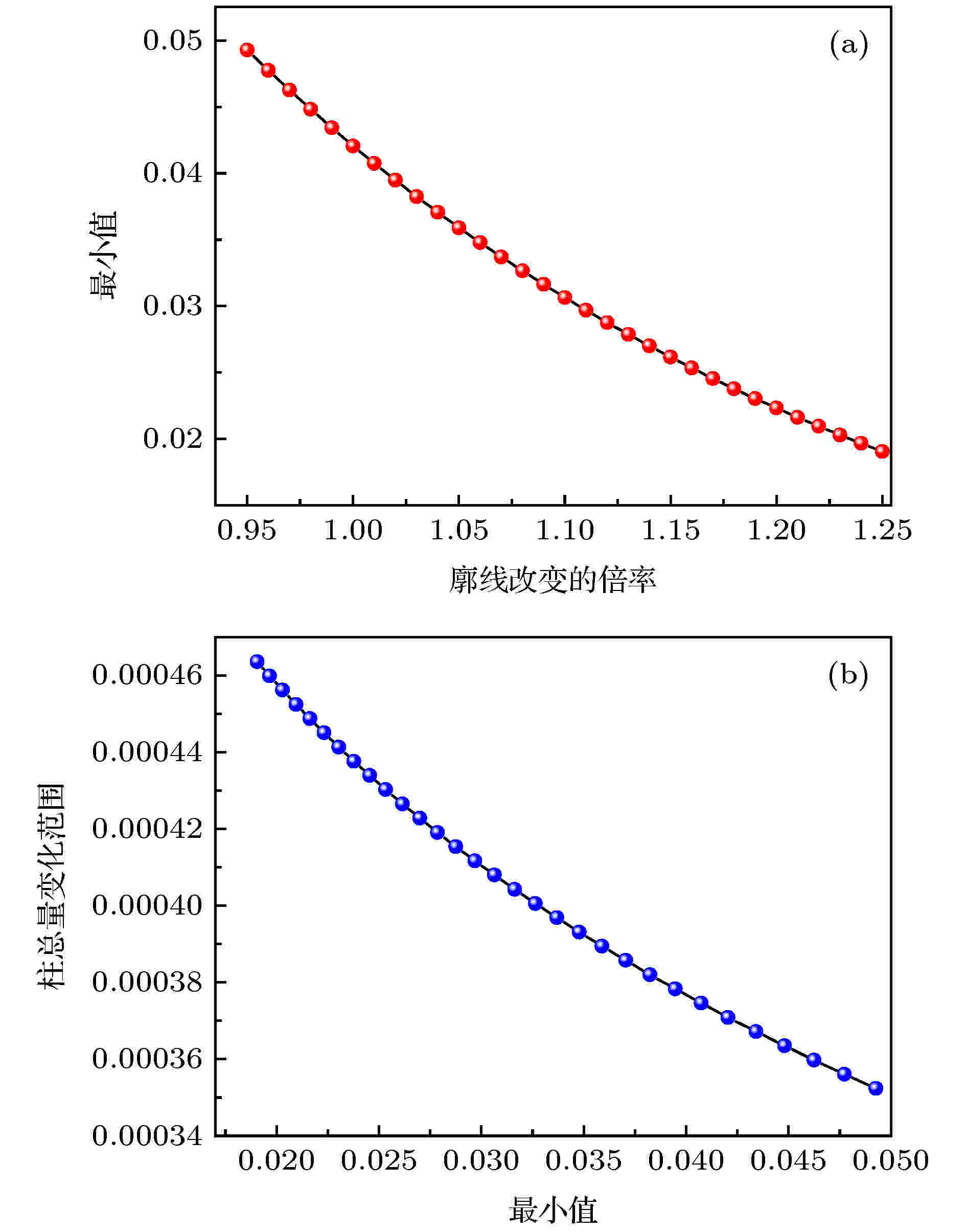图 11 (a) 最小值与廓线变化关系; (b)柱总量变化与最小值关系
Figure11. (a) The relationship between the minimum value and the change of profile; (b) the relationship between the change of column total and the minimum.

最终建立近似SNR和柱总量的差值关系, 如图12所示. SNR越大, 测量误差越低. 2019年3月12日探测结果显示, 信噪比为365.55, 通过此模型获得该系统测量误差为0.44 ppm. 需说明的是, 在此仅考虑了信噪比对测量误差的近似评估, 其他影响如激光频率偏差、路径偏差以及仪器函数等的影响并未考虑, 后期将对该问题做进一步研究.
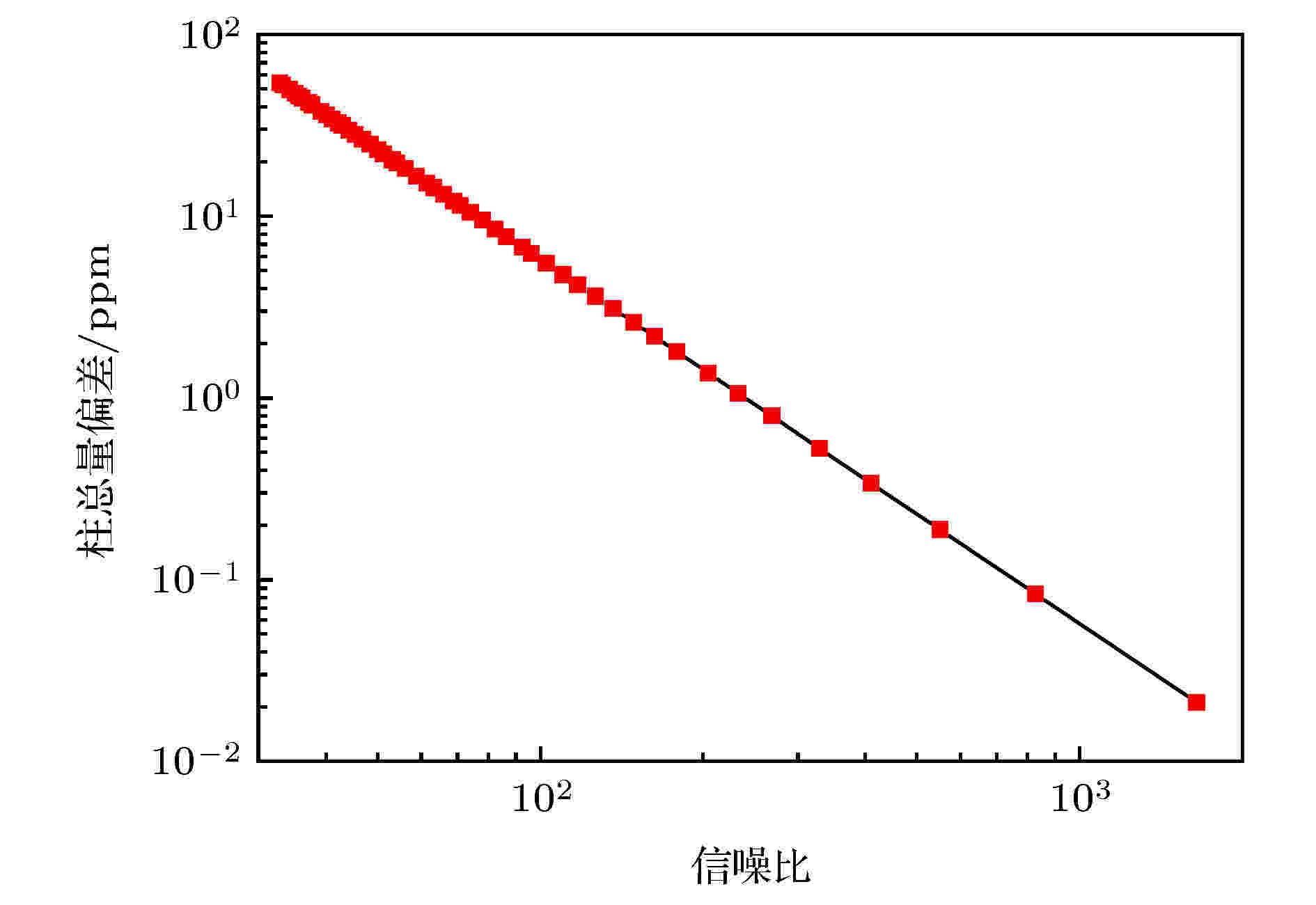图 12 SNR与测量误差间的对应关系
Figure12. The relationship between SNR and measurement error.

4.总　结
本文通过对中国科学院合肥物质科学研究院1号楼探测的6238.2—6239.3 cm–1波段的高分辨率激光外差光谱进行预处理, 提出了精准的波长相关校准方法, 并利用参考正向模型及最优估计算法实现了实际大气整层CO2柱浓度的反演; 随后进行了长期探测对比实验, 在测量过程中, $ X_{{\rm CO}_2} $的标准偏差为0.12—3.92 ppm, 对应其精度范围为0.03%—0.95%, 其数据与同期GOSAT数据吻合较好; 最后, 还提出了将白噪声叠加到正向计算谱上, 建立了系统测量误差的近似评估方法. 后续将对反演算法进行优化完善, 以实现多组分温室气体柱浓度的反演, 并进一步提高系统的测量精度.
相关话题/数据 测量 大气 信号 激光
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 大气湍流信道中聚焦涡旋光束轨道角动量串扰特性
    摘要:携带轨道角动量的涡旋光束作为传输信息的载体能有效提高信息传输效率,然而在传输过程中受大气湍流影响轨道角动量会发生串扰.基于螺旋谱分析理论,推导得到了聚焦拉盖尔高斯光束在各向异性大气湍流中传输时的螺旋谱解析表达式,并对比分析不同湍流和光束参数对聚焦与非聚焦拉盖尔高斯光束接收功率的影响,最后利用多 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 脉冲硬X射线能注量测量技术
    摘要:阐述了全吸收法测量脉冲硬X射线能注量的基本原理,选择了光电管配合硅酸镥(LSO)闪烁体作为探测系统的核心部件,研制了脉冲硬X射线能注量测量系统.利用该系统测量了“闪光二号”加速器产生的脉冲硬X射线强度,结合灵敏度的实验标定结果,计算得到了脉冲硬X射线的能注量.在连续5发次的实验中,能注量平均测 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 大气压氦气介质阻挡放电单-多柱演化动力学
    摘要:介质阻挡放电被众多工业领域用作低温等离子体源,柱状放电是介质阻挡放电的重要形式之一,但其放电理论尚未掌握.进行大气压氦气介质阻挡放电实验,通过降低外施电压低于起始放电电压实现了柱状放电从单柱到多柱的斑图演化,拍摄了电极底面放电图像,测量了外施电压、放电电流、放电转移电荷、放电柱的柱直径和柱间距 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于心音信号的一种血压评估方法
    摘要:心血管疾病尤其是高血压已成为人类生命健康最大杀手之一.本文探究主动脉瓣心音信号与血压之间的关系,提出一种基于心音信号的无创血压估计方法.首先,根据血压与心音信号的关系,提取第一心音和第二心音峰值点的时间间隔以及第二心音的峭度作为特征;接着将第一心音和第二心音峰值点的时间间隔、第二心音的峭度与所 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于网络分析仪的3D Transmon相干测量方法
    摘要:3DTransmon是目前已知退相干时间较长的一种超导量子比特,在超导量子计算、量子光学、腔量子电动力学等方面具有重要的应用.拉比振荡是表征量子系统退相干时间的重要方法,也是体现量子系统能够进行能级演化的基本实验.对3DTransmon进行拉比振荡测试,需要进行严格的时序控制,测试调试的过程较 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 自拉曼混频黄绿波段三波长可切换激光
    摘要:报道了高效的Nd:YVO4晶体自拉曼结合二阶非线性光学混频实现黄绿波段三波长可选输出.从改善热效应和增加拉曼介质长度出发,设计双端键合的YVO4/Nd:YVO4/YVO4晶体用于自拉曼变频.考虑混频转换效率和混频波长切换的便捷性,选用临界相位匹配的BaB2O4(BBO)晶体作为二阶非线性光学混 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 光子增加双模压缩真空态在马赫-曾德尔干涉仪相位测量中的应用
    摘要:量子度量学主要是利用量子效应来提高参数估计的精度,以期突破标准量子极限,甚至达到海森伯极限.本文研究了一般光子增加双模压缩真空态作为马赫-曾德尔干涉仪的探测态时,在何种情况下能够提高待测相位的测量精度.根据量子Fisher信息理论,尽管在探测态具有相同的平均光子数这一约束条件下,对称的和非对称 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 离轴抽运厄米-高斯模固体激光器
    摘要:给出了离轴抽运固体激光器多模速率方程组在阈值附近的小信号求解方法,用这种方法研究了模式随离轴量的变化以及厄米-高斯模的竞争行为.抽运光斑较小时,离轴量增加高阶模式依次出现;抽运光斑较大时,模式变化呈现复杂性.用小信号近似得到的模式光子数比例与较高抽运功率下数值求解速率方程组的结果接近,表明可以 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 不同离子辐照氟化锂材料时原位发光光谱测量分析
    摘要:在BNU400注入机上搭建的离子激发发光(ionbeaminducedluminescence,IBIL)测量装置上,开展了相同能量(100keV)条件下的3种离子(H+、He+以及O+)辐照氟化锂材料时的IBIL光谱的原位测量工作,对比研究离子种类对氟化锂材料辐照缺陷的生成及其演变行为的影响 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于深紫外激光-光发射电子显微技术的高分辨率磁畴成像
    摘要:基于磁二色效应的光发射电子显微镜磁成像技术是研究薄膜磁畴结构的一种重要研究手段,具有空间分辨率高、可实时成像以及对表面信息敏感等优点.以全固态深紫外激光(波长为177.3nm;能量为7.0eV)为激发光源的光发射电子显微技术相比于传统的光发射电子显微镜磁成像技术(以同步辐射光源或汞灯为激发源) ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.