摘要:给出了离轴抽运固体激光器多模速率方程组在阈值附近的小信号求解方法, 用这种方法研究了模式随离轴量的变化以及厄米-高斯模的竞争行为. 抽运光斑较小时, 离轴量增加高阶模式依次出现; 抽运光斑较大时, 模式变化呈现复杂性. 用小信号近似得到的模式光子数比例与较高抽运功率下数值求解速率方程组的结果接近, 表明可以用该方法估算实际较高功率激光器的模式分布, 这可以方便这类激光器的研究. 对离轴抽运下的多厄米-高斯模激光器, 阈值附近的模竞争体现为, 随着抽运功率的增加, 第一个净增益由负变正的模式, 光子数随即开始增加, 增加趋势接近线性. 而第二个净增益由负变正的模式, 光子数并不立即开始增加, 而要等到抽运功率进一步增加后才开始增加, 其开始增加后第一个模式的增长趋势变缓. 从动态过程看, 各个模式经过交叉尖峰和交叉弛豫振荡竞争后, 逐渐达到稳态. 实验获得了HG₀₀-HG₅₀模光束, 实验所得到的模式分布与理论计算结果符合很好.
关键词: 固体激光器/
离轴抽运/
模式竞争/
小信号解

English Abstract

全文HTML

--> --> -->

厄米-高斯(Hermite-Gaussian, HG)光束在光通信^[1]、涡旋光束产生等方面具有重要的应用价值^[2,3], 因此, 这类光束的产生一直备受研究人员的关注. 在低功率情况下, 通常可用空间光调制器将基模高斯光束转换为HG光束^[4-6]. 但受转换元件损伤阈值、实际加工精度等因素的限制, 难以转换出高功率、高纯净度的HG光束. 随着应用研究的深入, 在远距离空间光通信、探测等应用中需要高功率、模式纯净度高的HG光束^[7,8]. 用激光器直接产生HG光束在功率水平、模式纯净度方面具有很大的优势, 可为高功率涡旋光产生、远距离通信、探测等提供理想的光源. 因此, 用激光器直接产生HG光束成为激光技术研究的一个热点^[9-14].
HG模是稳定球面谐振腔的高阶本征模式, 高阶模式的亮斑偏离谐振腔轴线. 在二极管端面抽运固体激光器中, 可使抽运光偏离谐振腔的光轴, 与高阶HG模的亮斑达到模式匹配从而输出特定的HG光束. 众所周知, 谐振腔光电场的HG模组成了完备正交的函数系, 但其模方却不正交, 即谐振腔中各个HG模的光强空间分布存在一定的交叠, 呈现部分交叠部分分离的状态. 这使得离轴抽运时, 抽运光难以作用于单个HG模, 而往往是同时作用于若干个HG模. 受抽运光作用的这些HG模将产生空间增益竞争, 激光器的稳态输出模式与抽运光分布形式、离轴量等因素有关. 对这种激光器振荡模式的计算方面, 文献[15]给出了考虑抽运光空间分布和振荡光模式下各个模式阈值的计算方法, 文献[16]用这种方法研究了各个模式的阈值, 但其成立的条件是只有一个模式振荡, 不能研究多模竞争问题.
目前, 在固体激光器中迫切需要产生单一的HG模并且实现模式的调控^[17-21]. 调控的一个重要方法是使抽运光偏离中心轴线与各个高阶HG模实现匹配, 从而实现模式的调谐输出. 在此调控过程中, 谐振腔结构保持不变, 而抽运光通过横向移动与各个模式发生匹配. 抽运光横向移动过程中, 将作用于若干个HG模. 为了获得可控的模式输出, 需要确定哪些模式最终能够稳定输出. 本文给出了一种离轴抽运下多个HG模激光器模式分布的简便计算方法. 在谐振腔结构保持不变的情况下, 研究了不同的抽运光半径下, 激光器输出模式随离轴量的演变过程, 并研究了模式在阈值附近的竞争行为. 另外, 为了与小信号计算结果比较, 通过直接数值求解速率方程得到了较高抽运功率下的稳态光子数比例, 并研究了模式竞争的动态过程. 论文还实验产生了一些HG模式, 并与理论结果进行了比较分析.

2

-->

2.1.理论模型

为了简化问题, 采用如图1所示的平凹谐振腔进行分析. Nd:YAG晶体的端面镀1064 nm高反射膜和输出耦合镜构成谐振腔. 以晶体抽运端面中心为坐标原点、光传播方向为z轴建立直角坐标系. 谐振腔长度为L, 输出镜的曲率半径为C. 激光晶体的吸收长度一般都比较短, 如常见的1 at.% 掺杂的Nd:YAG晶体, 吸收长度约为1.3 mm. 在这种情况下, 可以近似认为增益集中分布在晶体的抽运端面, 对腔内振荡光, 可以忽略光斑沿z方向的变化, 只考虑二维分布. 用$P\left( {x, y} \right)$表示抽运速率, $N\left( {x, y} \right)$表示反转粒子数体密度, 用${\varPhi _{mn}}\left( {x, y} \right)$表示HG_mn模的光子数体密度, 则多个模式振荡时的速率方程可以写为
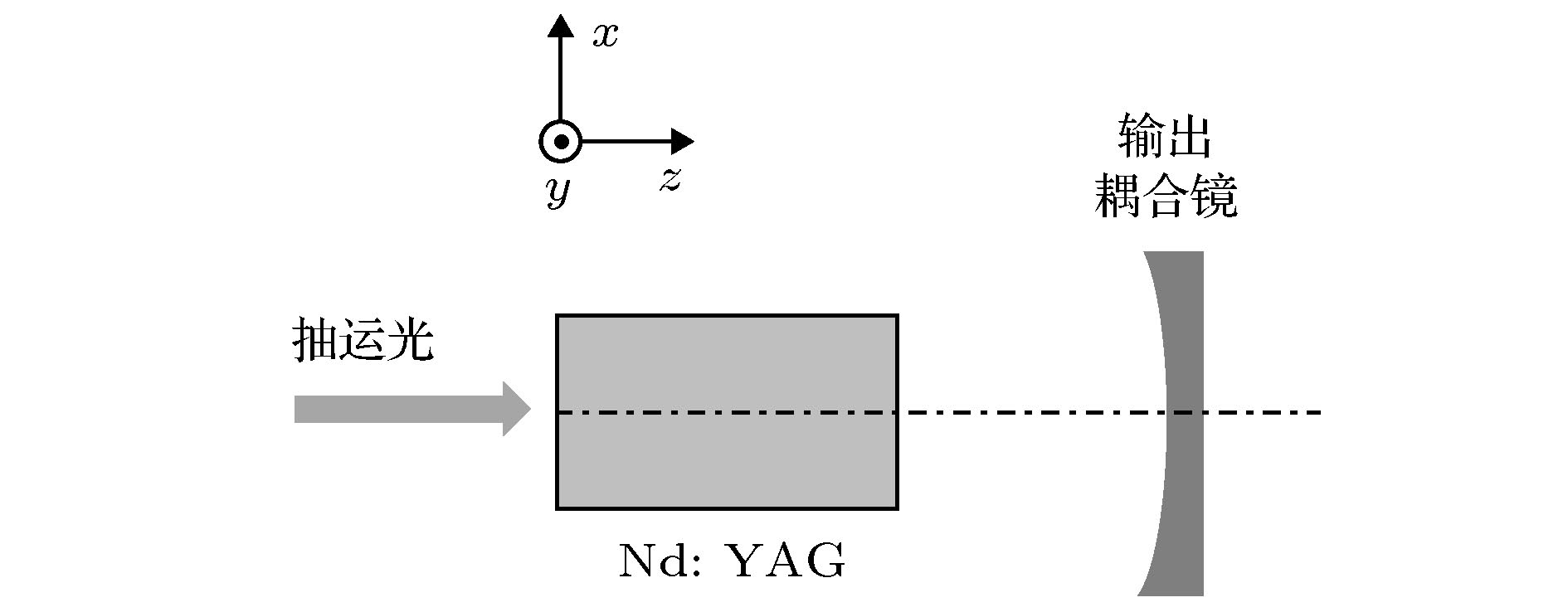图 1 端面离轴抽运固体激光器图示
Figure1. Schematic of an off-axis end-pumped solid-state laser.

$\begin{split}& {{{\rm{d}}N\left( {x,y,t} \right)}}{{{\rm{d}}t}}\\ =\; & P\left( {x,y,{x_0},{y_0}} \right) - c\sigma N\left( {x,y,t} \right) \sum\limits_{m,n} {{\varPhi _{mn}}\left( {x,y,t} \right)} \\& - {{N\left( {x,y,t} \right)}}/{{{\tau _{\rm{f}}}}}, \end{split}\;\;\;\;\;\;\tag{1a}$

$\begin{split}& {{{\rm{d}}{\varPhi _{mn}}\left( {x,y,t} \right)}}/{{\rm d t}} \\ = & \; c\sigma N\left( {x,y,t} \right){\varPhi _{mn}}\left( {x,y,t} \right) - {{{\varPhi _{mn}}\left( {x,y,t} \right)}}/{{{\tau _{mn}}}}, \\& \qquad m,~n = 0,1,2, \cdots , \\[-12pt]\end{split}\tag{1b}$

其中c为介质中的光速, σ为受激发射截面, ${\tau _{\rm{f}}}$为上能级寿命, ${\tau _{mn}}$为HG_mn模的光子寿命, $\left( {{x_0}, {y_0}} \right)$为抽运光的中心坐标.
2 -->

2.2.阈值附近的小信号稳态解

通常情况下, 速率方程(1a)和(1b)不易直接求解. 若激光器工作在阈值附近, 谐振腔中振荡光场很弱, 可求得其小信号稳态解.
令方程(1a)中${{{\rm{d}}N} / {{\rm{d}}t}} = 0$, 可得稳态时的反转粒子数密度为

${N^{\rm{E}}}\left( {x,y} \right) = \dfrac{{{\tau _{\rm{f}}}P\left( {x,y,{x_0},{y_0}} \right)}}{{1 + c\sigma {\tau _{\rm{f}}} \displaystyle\sum\limits_{m,n} {\varPhi _{mn}^{\rm{E}}\left( {x,y} \right)} }},$

其中${N^{\rm{E}}}\left( {x, y} \right)$为稳态反转粒子数体密度, $\varPhi _{mn}^{\rm{E}}\left( {x, y} \right)$为稳态时HG_mn模的光子数体密度. 将方程(1b)两边在谐振腔体积内积分

$\begin{split} & \iint_{A}{{{L}_{\rm{c}}}\dfrac{{\rm{d}}{{\varPhi }_{mn}}\left( x,y,t \right)}{{\rm{d}}t}}{\rm{d}}x{\rm{d}}y \\ =\;&\iint_{A}{{{L}_{\rm{a}}}c\sigma N\left( x,y,t \right){{\varPhi }_{mn}}\left( x,y,t \right){\rm{d}}x{\rm{d}}y}\\ &-\iint_{A}{{{L}_{\rm{c}}}\dfrac{{{\varPhi }_{mn}}\left( x,y,t \right)}{{{\tau }_{mn}}}{\rm{d}}x{\rm{d}}y}, \end{split}$

积分中忽略了z方向反转粒子数和振荡光子数密度的变化, 其中${L_{\rm{c}}}$为谐振腔长度, ${L_{\rm{a}}}$为增益介质的有效长度, 近似等于吸收长度. 振荡过程中, 认为各个模式的分布形式保持不变, 而光子数${S_{mn}}$随时间变化, 可将${\varPhi _{mn}}\left( {x, y, t} \right)$用各模式的光子数${S_{mn}}$和模式的归一化分布函数${\phi _{mn}}\left( {x, y} \right)$表示, 即

${\varPhi _{mn}}\left( {x,y,t} \right) = {S_{mn}}\left( t \right){\phi _{mn}}\left( {x,y} \right),$

归一化分布函数

$\begin{split}&{\phi _{mn}}\left( {x,y} \right) \\=\; &\frac{2}{{{\text{π}}\omega _0^2{L_{\rm{c}}}m!n!}}{2^{ - \left( {m + n} \right)}}\exp \left[ { - \frac{{2\left( {{x^2} + {y^2}} \right)}}{{\omega _0^2}}} \right] \\&\times {\left[ {{H_m}\left( {\frac{{x\sqrt 2 }}{{{\omega _0}}}} \right){H_n}\left( {\frac{{y\sqrt 2 }}{{{\omega _0}}}} \right)} \right]^2},\end{split}$

其中${H_m}\left( x \right)$为m阶厄米多项式, ${\omega _0}$为基模振荡光的半径, 归一化条件为${L_{\rm{c}}}\iint_A {{\phi _{mn}}\left( {x, y} \right){\rm{d}}x{\rm{d}}y} = 1$. 将(4)式代入(3)式, 可得

$\begin{split}& {{{\rm{d}}{S_{mn}}\left( t \right)}}/{{{\rm{d}}t}} \;=\\& {S_{mn}}\left( t \right)\iint_A {{L_{\rm{a}}}c\sigma N\left( {x,y,t} \right){\phi _{mn}}\left( {x,y} \right){\rm{d}}x{\rm{d}}y} \\& - {{{S_{mn}}\left( t \right)}}/{{{\tau _{mn}}}}.\end{split}$

在稳态下, 令${{{\rm{d}}{S_{mn}}\left( t \right)} / {{\rm{d}}t}} = 0$, 可得

$c\sigma {L_{\rm{a}}}\iint_A {{N^{\rm E}}\left( {x,y} \right){\phi _{mn}}\left( {x,y} \right){\rm{d}}x{\rm{d}}y} = \frac{1}{{{\tau _{mn}}}}.$

将(2)式代入(7)式,

$\begin{split}& c\sigma {\tau _{\rm{f}}}{L_{\rm{a}}}{P_0} \iint \frac{{\vartheta \left( {x,y,{x_0},{y_0}} \right)}}{{1 + c\sigma {\tau _{\rm{f}}}\displaystyle\sum\limits_{m,n} {S_{mn}^{\rm{E}}{\phi _{mn}}(x,y)} }} \\ & \times \phi_{mn} (x,y){\rm d}x{\rm d}y = \frac{1}{\tau _{mn}},\\[-16pt]\end{split}$

$P\left( {x, y, {x_0}, {y_0}} \right) = {P_0}\vartheta \left( {x, y, {x_0}, {y_0}} \right)$, $\vartheta \left( x, y, {x_0}, {y_0} \right)$为抽运光归一化分布函数, ${P_0}$为抽运速率, 即单位时间抽运到上能级的粒子数, 近似等于单位时间内增益介质吸收的抽运光子数, $S_{mn}^{\rm{E}}$为稳态时HG_mn模的光子数.
在小信号情况下, 谐振腔中的光子数很小, 所以(8)式可以近似为

$\begin{split}&c\sigma {\tau _{\rm{f}}}{L_a}{P_0}\iint {\vartheta \left( {x,y,{x_0},{y_0}} \right){\phi _{mn}}\left( {x,y} \right)}\\&\times\left[ {1 - c\sigma {\tau _{\rm{f}}}\sum\limits_{m,n} {S_{mn}^{\rm{E}}{\phi _{mn}}\left( {x,y} \right)} } \right]{\rm{d}}x{\rm{d}}y \; = \; \frac{1}{{{\tau _{mn}}}},\end{split}$

即

$\begin{split} &c\sigma {\tau _{\rm{f}}}{L_{\rm{a}}}{P_0}\iint {\vartheta \left( {x,y,{x_0},{y_0}} \right){\phi _{mn}}\left( {x,y} \right){\rm{d}}x{\rm{d}}y} \\ &- {c^2}{\sigma ^2}\tau _{\rm{f}}^2{L_a}{P_0}\sum\limits_{m',n'} S_{m'n'}^{\rm{E}}\iint \vartheta \left( {x,y,{x_0},{y_0}} \right)\\ &\times{\phi _{mn}}\left( {x,y} \right){\phi _{m'n'}}\left( {x,y} \right){\rm{d}}x{\rm{d}}y \; =\; \frac{1}{{{\tau _{mn}}}}. \end{split} $

为了方便, 引入以下参数

$\begin{split}{\alpha _{mn}} =\; & c\sigma {\tau _{\rm{f}}}{L_{\rm{a}}}{P_0}\iint \vartheta \left( {x,y,{x_0},{y_0}} \right)\\&\times{\phi _{mn}}\left( {x,y} \right){\rm{d}}x{\rm{d}}y - {1}/{{{\tau _{mn}}}}, \quad \qquad\end{split}\tag{11a}$

$\begin{split}{\beta _{mnm'n'}} =\;& {c^2}{\sigma ^2}\tau _{\rm{f}}^2{L_{\rm{a}}}{P_0}\iint \vartheta \left( {x,y,{x_0},{y_0}} \right)\\&\times{\phi _{mn}}\left( {x,y} \right){\phi _{m'n'}}\left( {x,y} \right){\rm{d}}x{\rm{d}}y,\end{split}\;\;\;\;\;\;\tag{11b}$

则(10)式可以简写为

$\sum\limits_{mnm'n'} {S_{m'n'}^{\rm{E}}} {\beta _{mnm'n'}} = {\alpha _{mn}},$

其中求和遍历所有可能振荡的模式. ${\alpha _{mn}}$具有s^–1的量纲, 反映了单位时间内光子数的变化, 包含了抽运光与HG_mn模的交叠程度及HG_mn模光子寿命的影响, 这里称之为净增益, 其值为正时表示光子数增大, 为负时表示光子数减小; ${\beta _{mnm'n'}}$反映了抽运光与HG_mn模、${\rm{H}}{{\rm{G}}_{m'n'}}$模三者的交叠程度. 为了简化脚标, 将模式依次编号

$\begin{array}{*{20}{c}}{00}&{10}&{01}&{11}&{21}&{12}&{22}& \cdots, \\1&2&3&4&5&6&7& \cdots, \end{array}\;\;\;\;$

则(12)式可以写为矩阵形式

$\left(\!\! {\begin{array}{*{20}{c}}{{\beta _{11}}}&{{\beta _{12}}}&{{\beta _{13}}}& \ldots &{{\beta _{1N}}}\\{{\beta _{21{\kern 1pt} }}}&{{\beta _{22}}}&{{\beta _{23{\kern 1pt} }}}& \ldots &{{\beta _{2N}}}\\ \vdots & \vdots & \vdots &{}& \vdots \\{{\beta _{N1}}}&{{\beta _{N2}}}&{{\beta _{N3}}}& \ldots &{{\beta _{NN}}}\end{array}} \!\!\right)\left( \!\!{\begin{array}{*{20}{c}}{S_{\rm{1}}^{\rm{E}}}\\{S_{\rm{2}}^{\rm{E}}}\\ \vdots \\{S_N^{\rm{E}}}\end{array}} \!\!\right) = \left( \!\!{\begin{array}{*{20}{c}}{{\alpha _1}}\\{{\alpha _2}}\\ \vdots \\{{\alpha _N}}\end{array}} \!\!\right),$

其中N为参与振荡的模式数目, 利用(13)式可直接求得小信号情况下各个模式的稳态光子数. 需要说明的是, 从(8)式可以看出, 能否满足小信号条件, 不仅与各个模式的光子数有关, 还与模式的归一化分布函数有关. 取${\omega _0} = 0.15{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\rm{mm}}$, ${L_{\rm{c}}} = 15{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\rm{cm}}$, 几个低价模式的光子数密度的最大值为$\phi _{00}^{\max } = 1.89 \times {10^8}$, $\phi _{10}^{\max } = 1.38 \times {10^8}$, $\phi _{20}^{\max } = 1.24 \times {10^8}$, $\phi _{30}^{\max } = 1.15 \times {10^8}$. 对各模式而言, 符合弱信号条件的腔内光子数大约都在${10^8}$量级. 当${\omega _0}$和${L_{\rm{c}}}$增大时, 光子数密度减小, 符合小信号条件的光子数随着增大.

本节根据2.2节中给出的方法, 计算在小功率离轴抽运下激光器的模式分布. 对一定的谐振腔结构, 研究抽运光半径分别为振荡光半径的一半和与振荡光半径相等时, 模式随离轴量的演变过程. 归一化分布函数$\vartheta \left( {x, y, {x_0}, {y_0}} \right)$采用(14)式所给形式,

$\begin{split}&\vartheta \left( {x,y,{x_0},{y_0}} \right) \\=\;& \left\{ {\begin{array}{*{20}{c}}{\dfrac{1}{{{\text{π}}\omega _{\rm{p}}^2{L_{\rm{a}}}}}{\kern 1pt} ,}&{{\kern 1pt} {{\left( {x - {x_0}} \right)}^2} + {{\left( {y - {y_0}} \right)}^2}{\kern 1pt} {\kern 1pt} \leqslant \omega _{\rm{p}}^2,{\kern 1pt} }\\[3mm]{\;\;\;0\;\;\;\;,}&{{{\left( {x - {x_0}} \right)}^2} + {{\left( {y - {y_0}} \right)}^2}{\kern 1pt} {\kern 1pt} > \omega _{\rm{p}}^2,}\end{array}} \right.\\[-26pt]\end{split}\;\;\;\;\;\;\;$

其中${\omega _{\rm{p}}}$为抽运光半径. 抽运速率${P_0} = {{{P_{\rm{a}}}} / {(h{\nu _{\rm{p}}}}})$, ${P_{\rm{a}}}$为抽运光功率, $h{\nu _{\rm{p}}}$为抽运光光子能量. 对于Nd:YAG, $\sigma = 6.5 \times {10^{ - 19}}{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\rm{c}}{{\rm{m}}^2}$, ${\tau _{\rm{f}}} = 230{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt}$ μs, 抽运光波长为808 nm, 吸收长度L_a取为1 mm. 谐振腔长度L_c取为15 cm, 输出镜的曲率半径C取为200 mm, 对应的抽运端面处的HG₀₀模振荡光半径${\omega _0}$约为0.15 mm. 光子寿命${\tau _{mn}}$取决于模式的损耗, 在本文的计算条件下, 谐振腔的菲涅耳数很大, 各模式的衍射损耗近似相等, 可近似认为光子寿命由耦合输出镜的反射率决定, 即${\tau _{mn}} = {{L_{\rm{c}}}} / {\left[ {{c_0}{\rm{ln}}(R)} \right]},$ ${c_0}$为真空中的光速. 计算中, 只考虑沿x轴方向离轴的情形, 即${y_0} = 0$, 这时离轴量${\rm{Δ }}x = \left| {{x_0}} \right|$. 根据Nd:YAG的晶体参数及给定的谐振腔参数, 可以估算出激光器的阈值抽运功率约为0.15 W, 为满足小信号条件, 计算中抽运功率取值略高于阈值功率. 为计算简便又能说明问题, 计算中考虑HG₀₀, HG₁₀, HG₂₀, HG₃₀, HG₄₀, HG₅₀, HG₆₀ 7个模式. 这样, 给定离轴量、抽运功率和抽运光半径, 将(14)式及相关参数代入(11)式, 求解方程组(13)便可得到一定离轴量下各模式的光子数.
2

-->

3.1.抽运光半径${\omega _{\rm{p}}} = 0.5{\omega _0}$时的输出模式

图2是${P_{\rm{a}}}$为0.25 W、抽运光半径${\omega _{\rm{p}}} = 0.5{\omega _0}= 0.075\;{\rm{mm}}$时, 不同离轴量下各模式光子数分布形成的光斑. 图中${\gamma _{00}}:{\gamma _{10}}:{\gamma _{20}}: {\gamma _{30}}: {\gamma _{40}}: {\gamma _{50}}:{\gamma _{60}}$表示模式的光子数比例. 可以看出, 当在中心抽运时, 只有HG₀₀模工作; 随着离轴量的增加, 模式依次出现演变. 当离轴量为0.08 mm时, 为HG₀₀模和HG₁₀模的叠加, 叠加比例为0.58∶0.42, 离轴量为0.11 mm时, HG₀₀模不再出现, 单一HG₁₀模工作. 离轴量再增加时, HG₂₀模出现; 当离轴量为0.13 mm时, HG₁₀模和HG₂₀模的叠加比例为0.9∶0.1; 当增加到0.155 mm时, 这一比例变为0.46∶0.54, 光斑不再有明显的暗线, 呈现出模糊的状态; 当增加到0.16 mm时, 呈现出单一的HG₂₀模. 再往后, 随着离轴量的增加, 各个高阶HG模依次出现, 在离轴量为0.22, 0.26, 0.29和0.33 mm时, 分别出现HG₃₀, HG₄₀, HG₅₀和HG₆₀模. 在每两个模式转换之间, 会出现两个模式的叠加工作状态, 如离轴量为0.27和0.32 mm时. 在模式叠加状态下, 光斑呈现一定程度的模糊. 在此抽运光半径下, 离轴量适当时总会出现单一模式工作的状态, 从而可实现单一模式的选择和调控.
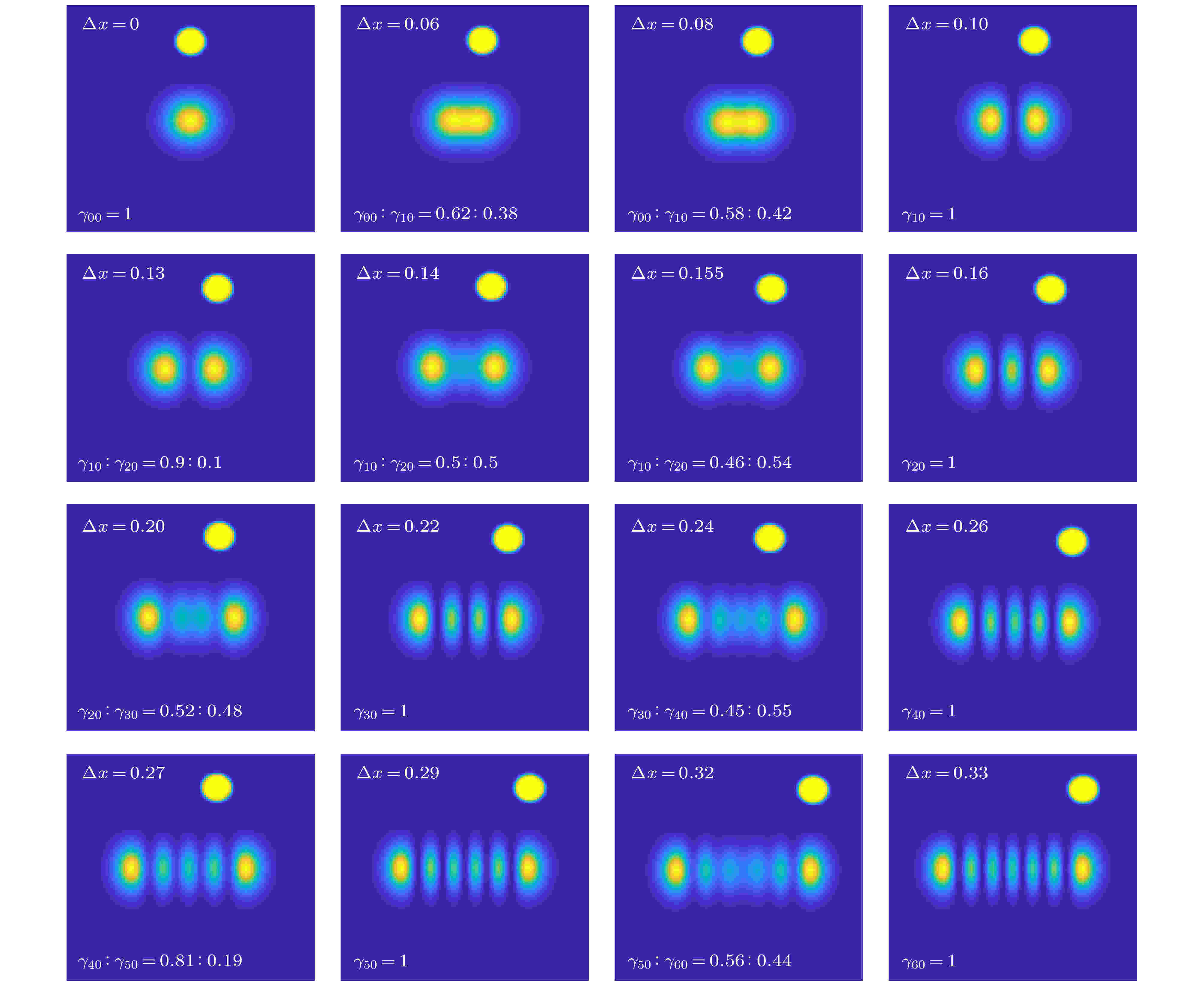图 2 抽运功率0.25 W、抽运光半径0.075 mm时, 16个离轴量下的光斑
Figure2. Laser beam profiles with different mode distributions in the sixteen transverse displacements when the pump power is 0.25 W and the pump beam radius is 0.075 mm.

通常单一模式激光器抽运功率高于阈值后, 振荡光子数随抽运功率的增加线性增加. 这里研究两个模式工作的特点, 图3所示是离轴量为0.08和0.155 mm时, 对应的两个模式的光子数在阈值附近随抽运功率的变化情况. 为了分析, 图4中表示了这两个离轴量对应的两个模式的净增益, 没有表示出的模式, 净增益均小于0. 从图3(a)可以看出, 当抽运功率从0.12 W开始增大时, HG₀₀模的光子数随之增大, 变化趋势接近线性, HG₁₀模的光子数先保持为0; 从图4(a)所示的净增益可以看出, HG₀₀模的净增益由负变正, 这符合单模在阈值附近的工作特点. 当抽运功率增大到0.13 W时, HG₁₀模的净增益也由负变正, 但从图3(a)看出, 这时HG₁₀模的光子数并未立即开始增加, 而是一直到抽运功率增加为0.15 W时, HG₁₀模的光子数才由0开始增加, 这和单模激光器的工作特点明显不同. HG₁₀模的光子数开始增加后, HG₀₀模的光子数变化曲线出现了一个拐点, 增加趋势变缓, HG₁₀模光子数增加斜率要大于HG₀₀模的斜率, 但二者均近似线性增长. 从图3(b)所示的光子数所占比例看出, 随着抽运功率增加, 二者所占比例趋于稳定, HG₀₀模所占比例大于HG₁₀模.
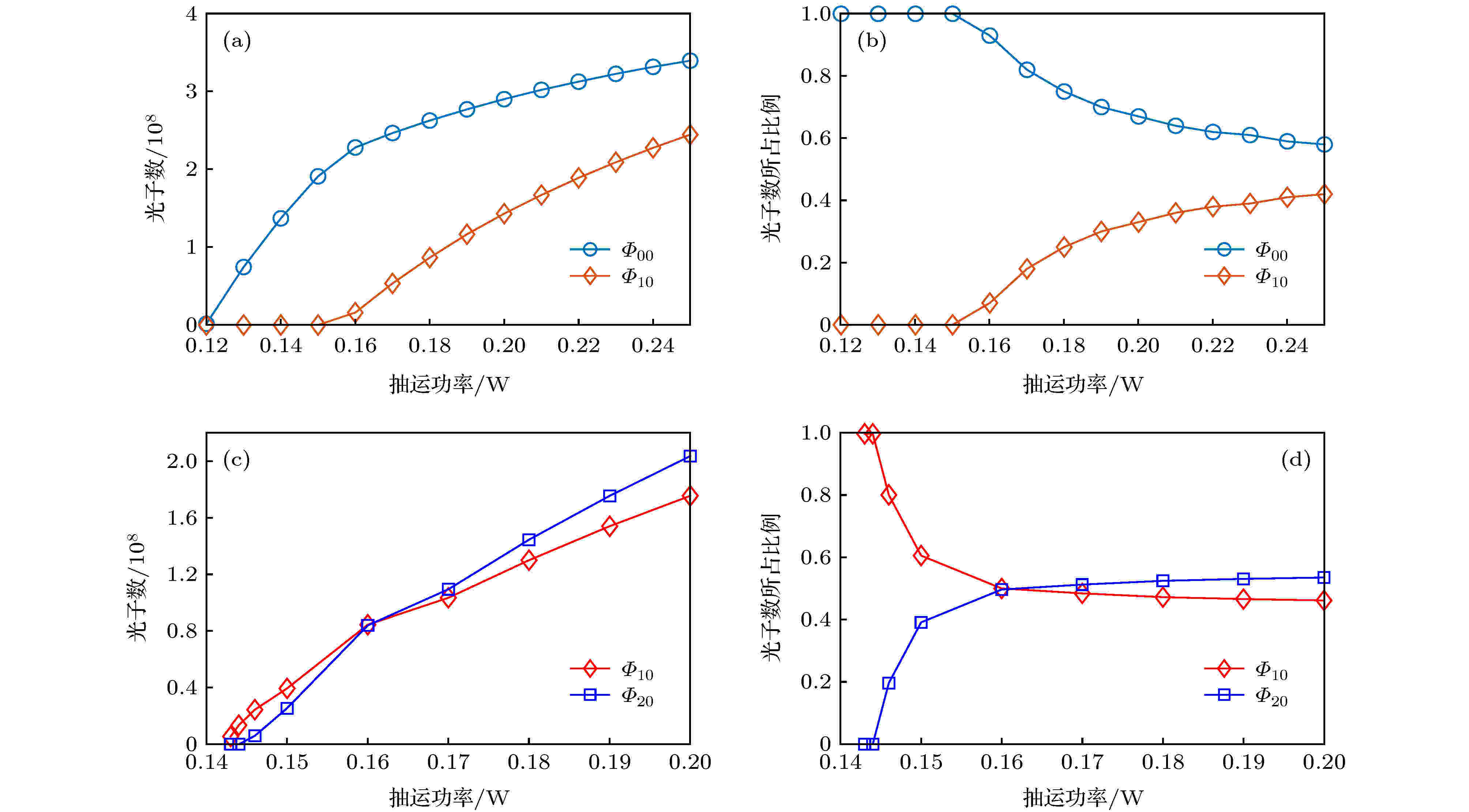图 3 在阈值附近, HG₀₀和HG₁₀模光子数(a), 光子数比例(b); HG₁₀和HG₂₀模光子数(c), 光子数比例(d)随抽运功率的变化
Figure3. Photon numbers of the mode HG₀₀ and HG₁₀ (a), and their percentages (b); photon numbers of the modes HG₁₀ and HG₂₀ (c), and their percentages (d) near the threshold.

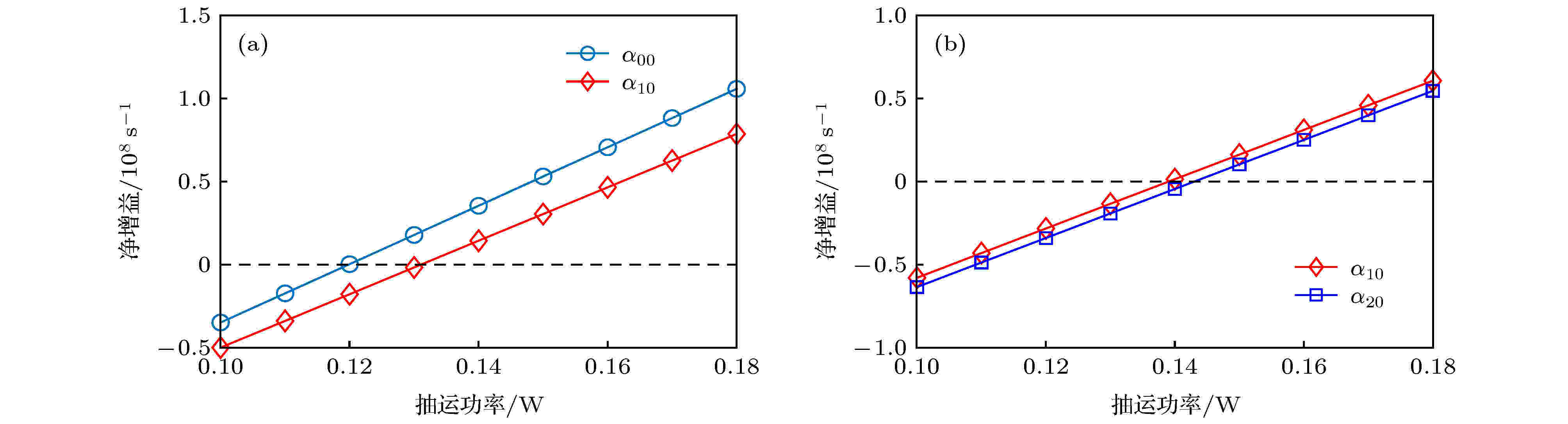图 4 净增益随抽运功率的变化　(a) 0.08 mm; (b) 0.155 mm
Figure4. Dependence of the net gains on the pump power: (a) 0.08 mm; (b) 0.155 mm.

图4(a)中, 抽运功率为0.13 W时, HG₁₀模的净增益开始大于0, 而一直到抽运功率增加为0.15 W时, 图3(a)中HG₁₀模的光子数才由0开始增加. 产生这一现象的物理原因是: 净增益反映了没有其他模式振荡情况下, 增益介质中属于这个模式的增益. 若谐振腔中没有其他的振荡模式, 某个模式的净增益大于0后, 该模式将达到阈值, 光子数将立即由0开始增加; 而当谐振腔中有其他模式振荡, 且其他模式与该模式空间上有交叠时, 原本属于该模式的一部分增益被其他模式消耗, 此时尽管计算出的净增益大于0了, 但实际上该模式并没有达到阈值条件. 这实际上反映了模式的空间交叉饱和效应, 是多模速率方程组(1)式或代数方程组(13)式中模式耦合效应的体现. 这里, 抽运功率为0.13 W时, HG₁₀模的净增益开始大于0, 但由于HG₀₀模消耗了二者交叠区域的增益, 使HG₁₀模直至抽运功率增加到0.15 W时才开始增加.
图3(c)是离轴量为0.155 mm时HG₁₀模和HG₂₀模光子数的变化情况. 当抽运功率超过0.14 W时, HG₁₀模和HG₂₀模的光子数几乎同时开始增长, 从图4(b)可以看出, 在此抽运功率下, 两个模式的净增益都由负变正, HG₁₀模的净增益略大于HG₂₀模的净增益. 而从光子数增加趋势看, 两个模式光子数的增加偏离线性, HG₁₀模呈现上凸的增长趋势, HG₂₀模呈现下凸的增长趋势, 当抽运功率增加到0.16 W时, 两个模式光子数相等, 随着抽运功率的进一步增加, 两个模式的光子数呈现近似线性增加的趋势, HG₂₀模的增长斜率要大于HG₁₀模的增长斜率. 从图3(d)看出, 在抽运功率在0.16 W以下时, HG₁₀模光子数所占比例大于HG₂₀模的光子数, 随抽运功率增加, 前者快速下降而后者上升, 然后逐渐趋于稳定, 最终HG₂₀模光子数所占比例要大于HG₁₀模的光子数.
2 -->

3.2.抽运光半径${\omega _{\rm{p}}} = {\omega _0}$时的输出模式

此时抽运光与振荡光的有效交叠变小, 若抽运功率继续保持为0.25 W, 计算发现离轴后各模式都不能达到阈值, 因此将抽运功率设定为0.5 W进行计算. 图5是这种情况下, 不同离轴量时的光斑. 可以看出, 在离轴量为0时, 仍然只有HG₀₀模输出; 当离轴量为0.05 mm时, 为HG₀₀模和HG₁₀模的叠加输出; 而当离轴量为0.1 mm时, 变为HG₀₀, HG₁₀和HG₂₀三个模式的叠加输出; 当离轴量增加到0.15 mm时, HG₀₀模不再出现, 变为HG₁₀, HG₂₀和HG₃₀三个模式的叠加; 当离轴量增加到0.175 mm时, HG₂₀模消失, 模式数目变少, 成为HG₁₀和HG₃₀两个模式的叠加; 当离轴量继续增加到0.2 mm时, 模式数目增加到四个, 成为HG₁₀, HG₂₀, HG₃₀, HG₄₀模的叠加; 而当离轴量进一步增加到0.25 mm时, 叠加的四个模式变为HG₂₀, HG₃₀, HG₄₀和HG₅₀模. 可见, 当抽运光半径与HG₀₀模的半径相等时, 随着离轴量的增加, 总有多个模式参与振荡, 整体上呈现低阶模被抑制、高阶模参与振荡的趋势, 但具体的演变过程又存在复杂性, 并不是低级模消失、高阶模出现这样的简单变化.
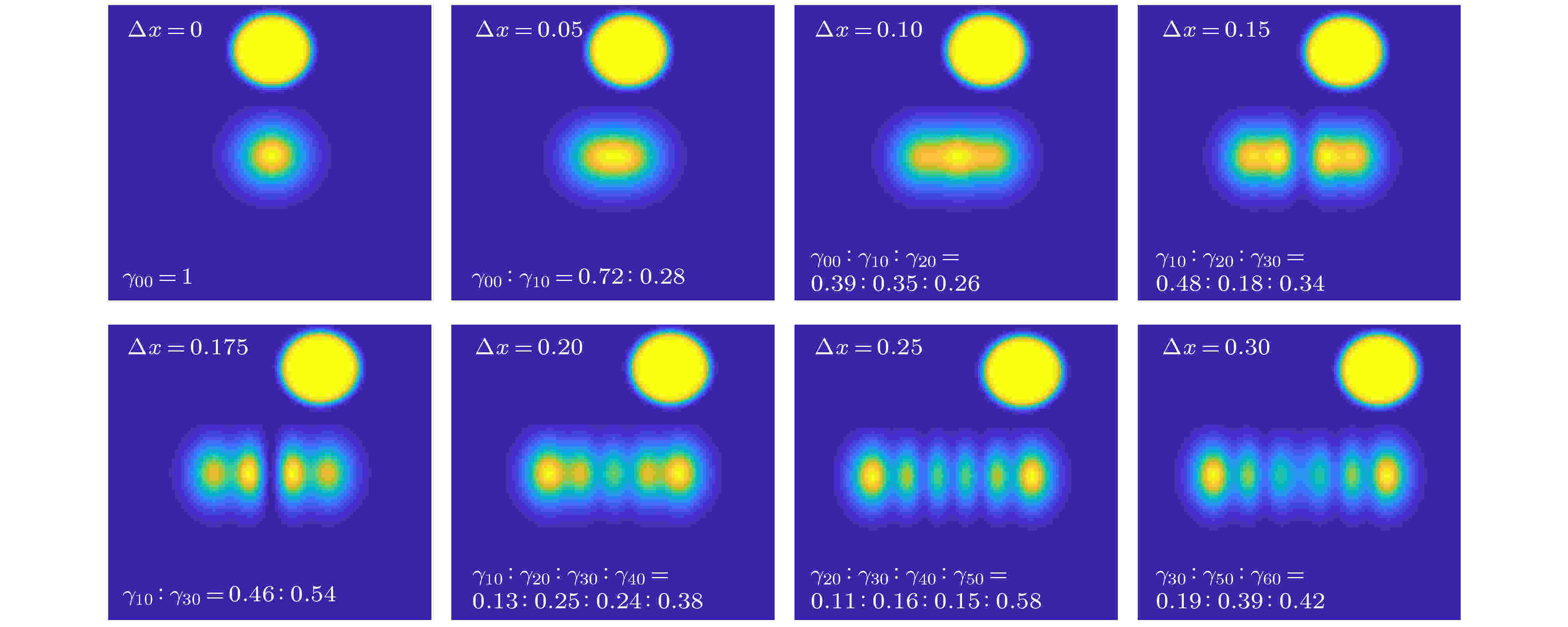图 5 抽运功率0.5 W、抽运光半径0.15 mm时, 8个离轴量下的光斑
Figure5. Laser beam profiles with different mode distributions in the eight transverse displacements when the pump power is 0.5 W and the pump beam radius is 0.15 mm.

图6是多个模式参与振荡时, 阈值附近各模式的光子数及光子数所占比例随抽运功率的变化, 为便于分析, 图7给出了模式的净增益随抽运功率的变化. 图6(a)和图6(b)是离轴量为0.1 mm下, HG₀₀, HG₁₀和HG₂₀模的光子数及其所占比例随抽运功率的变化, 结合图7(a)所示这种情况下净增益的变化可以看出, HG₀₀模的净增益最大, 随着抽运功率的增加, 其最先由负变正, HG₀₀模的光子数最先开始增加, 在其他模式光子数增加前, 其接近线性趋势增大. 当抽运功率增大到0.24 W时, HG₁₀模的净增益由负变正, 但此时HG₁₀模的光子数并未开始增加. 当抽运功率增大到0.25 W时, HG₂₀模的净增益由负变正, 但HG₂₀模的光子数也并不开始增加. 直至抽运功率增加到0.28 W时, HG₁₀模的光子数才开始增加, 到0.32 W时, HG₂₀模的光子数才开始增加. 随着后面两个模式的增加, HG₀₀模的曲线出现拐点, 增长趋势变缓; 当HG₂₀模的光子数开始增加后, HG₁₀模的增长趋势也变缓. 从三个模式光子数所占比例看, 随抽运功率的增加, 各自所占比例逐渐趋于稳定.
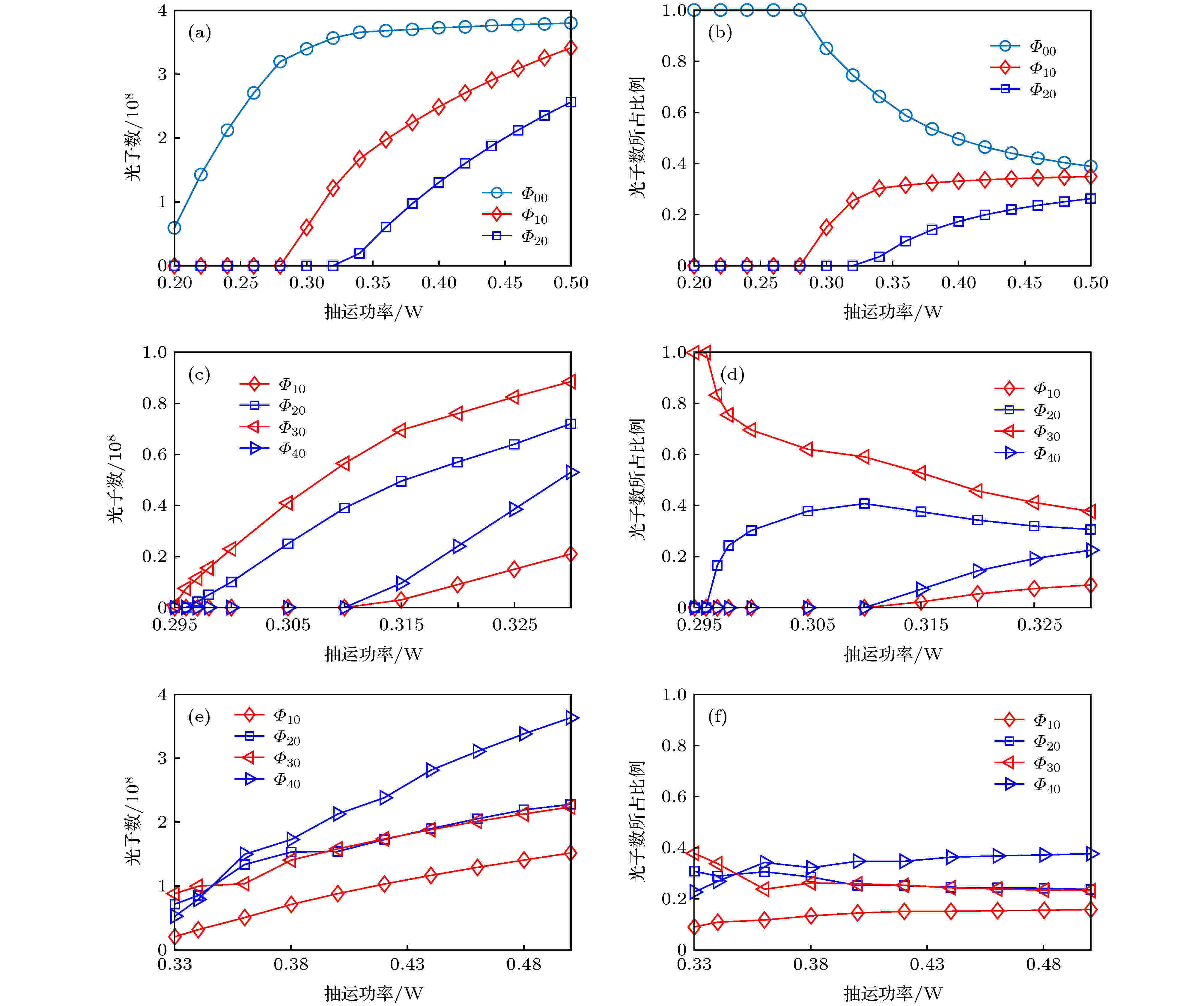图 6 在阈值附近, HG₀₀, HG₁₀和HG₂₀模光子数 (a), 光子数比例(b); HG₁₀, HG₂₀, HG₃₀和HG₄₀模光子数((c), (e)), 光子数比例((d), (f))随抽运功率的变化
Figure6. Photon numbers of the modes HG₀₀ , HG₁₀ and HG₂₀ (a) and their percentages (b); photon numbers of the modes HG₁₀, HG₂₀ and HG₃₀ ((c), (e)) and their percentages ((d), (f)) near the threshold.

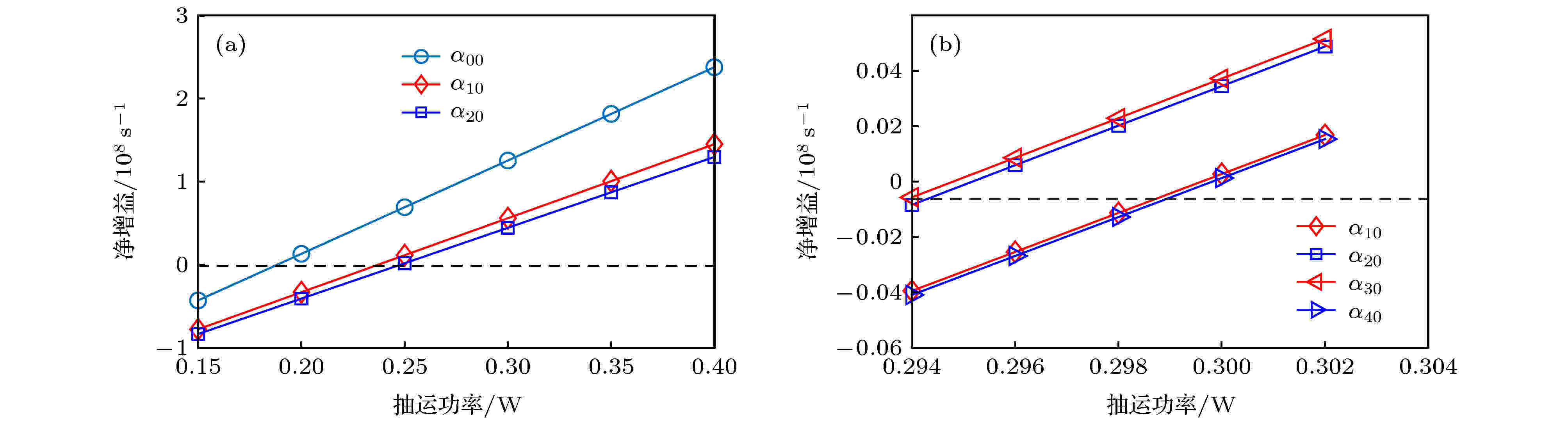图 7 净增益随抽运功率的变化　(a) 离轴量0.1 mm; (b) 离轴量0.2 mm
Figure7. Dependence of the net gains on the pump power: (a) 0.1 mm; (b) 0.2 mm.

图6(c)—图6(f)是离轴量为0.2 mm下, HG₁₀, HG₂₀, HG₃₀, HG₄₀模的光子数及其所占比例随抽运功率的变化, 图7(b)所示是这种情况下四个模式的净增益. HG₃₀模的净增益最大, 随抽运功率的增加, 其光子数最先开始增加, 然后HG₂₀模的光子数开始增加. 在抽运功率接近0.3 W时, HG₁₀模和HG₄₀模的净增益先后由负变正, 在抽运功率增加到0.31 W时, 这两个模式的光子数开始增加. 这时, 前两个模式光子数的增长趋势变缓. 另外我们看到, HG₄₀模要比HG₁₀模增加得快. 从图6(e)看出, 当抽运功率增加到约为0.35 W时, HG₂₀, HG₃₀和HG₄₀模的光子数增长曲线出现了一个交叉点, HG₄₀模的光子数变为最大, 之后逐渐过渡为稳定增长, HG₂₀和HG₃₀模的光子数变得十分接近. 从各模式光子数所占比例看, 随着抽运功率的增加, 经过一个复杂变化过程后, 比例逐渐趋于稳定.

第3节中讨论了阈值附近稳态时各个模式的光子数随抽运功率的变化情况. 本节通过直接数值求解速率方程(1)分析模式竞争的动态过程, 同时计算在较高抽运功率下各模式光子数所占的比例, 与阈值附近的计算结果进行比较. 计算了与上文对应的几个离轴抽运情况下的光子数动态变化, 结果如图8所示. 从图8(a)可以看出, 在抽运光半径为0.075 mm, 离轴量为0.08 mm, 抽运功率为0.25 W时, 有两个模式HG₀₀模和HG₁₀模参与振荡. HG₀₀模先进入了尖峰阶段, 经过数次尖峰后, HG₁₀模出现第一次尖峰, HG₁₀模尖峰的出现干扰了HG₀₀模的尖峰规律. 在200—600 μs, 两个模式呈现交叉尖峰. 在600 μs后两个模式出现了交叉弛豫振荡, 1000 μs后逐渐进入稳态. 从图8(b)可以看出当抽运功率增加为5 W时, 仍然为这两个模式振荡, 振荡的动态过程基本类似, 交叉尖峰和交叉弛豫振荡的时间缩短. 结合图4(a)可以看出, 先进入交叉尖峰的HG₀₀模的净增益较大. 抽运功率为5 W时, 数值计算得到的HG₀₀和HG₁₀模光子数所占的比例为0.59: 0.41, 与阈值附近计算的结果十分接近.
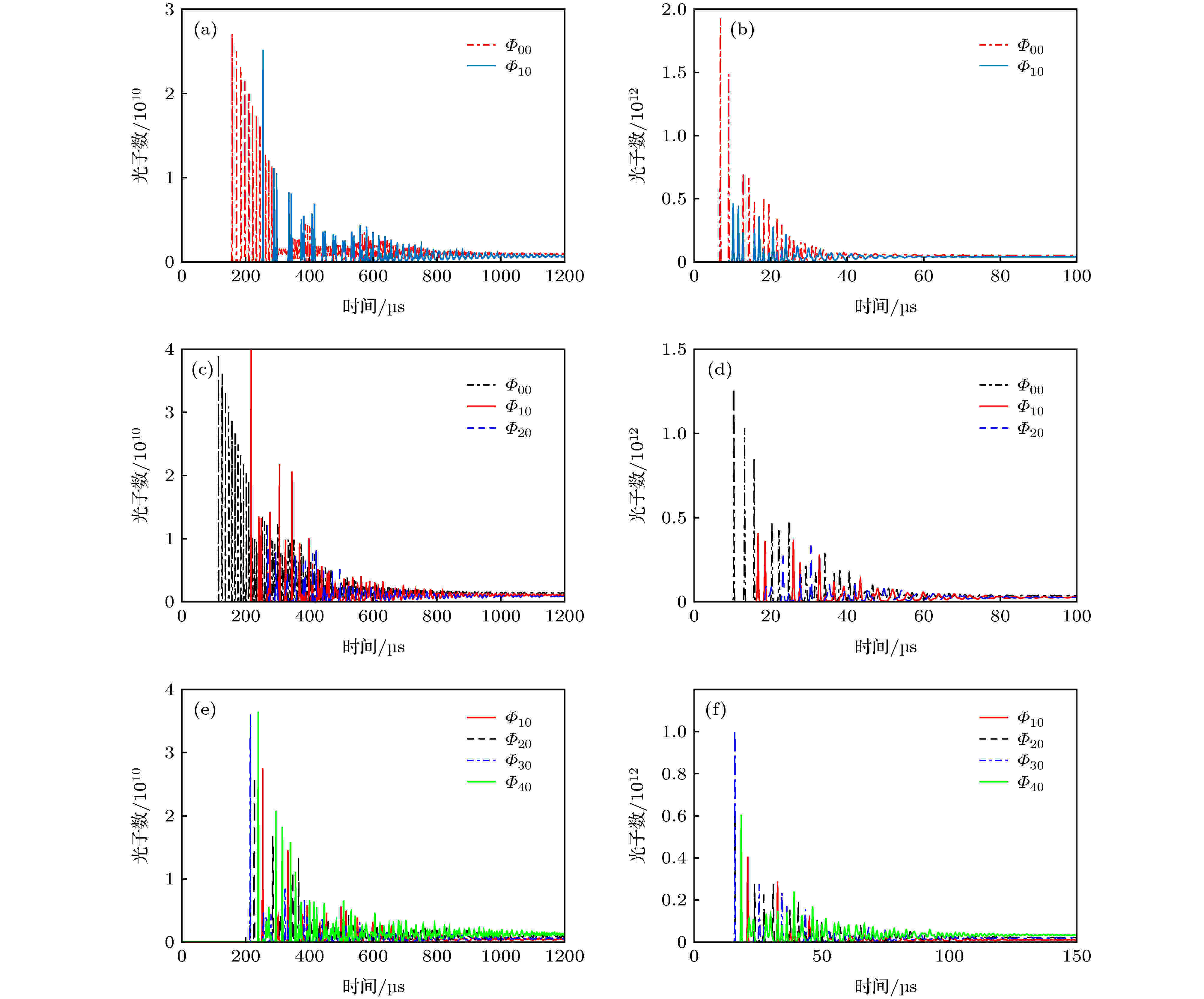图 8 光子数的动态变化过程　(a) ω_p = 0.075 mm, Δx = 0.08 mm, P_a = 0.25 W; (b) ω_p = 0.075 mm, Δx = 0.08 mm, P_a = 5 W; (c) ω_p = 0.15 mm, Δx = 0.1 mm, P_a = 0.5 W; (d) ω_p = 0.15 mm, Δx = 0.1 mm, P_a = 5 W; (e) ω_p = 0.15 mm, Δx = 0.2 mm, P_a = 0.5 W; (f)ω_p = 0.15 mm, Δx = 0.2 mm, P_a = 5 W
Figure8. Dynamics of the photon numbers: (a) ω_p = 0.075 mm, Δx = 0.08 mm, P_a = 0.5 W; (b) ω_p = 0.075 mm, Δx = 0.08 mm, P_a = 5 W; (c) ω_p = 0.15 mm, Δx = 0.1 mm, P_a = 0.5 W; (d) ω_p = 0.15 mm, Δx = 0.1 mm, P_a = 5 W; (e) ω_p = 0.15 mm, Δx = 0.2 mm, P_a = 0.5 W; (f) ω_p = 0.15 mm, Δx = 0.2 mm, P_a = 5 W.

当抽运光半径为0.15 mm, 离轴量为0.1 mm, 抽运功率为0.5和5 W时光子数的动态过程如图8(c)和图8(d)所示. 可以看出, 净增益最大的HG₀₀模最先进入了尖峰阶段, 经过数个衰减尖峰后, HG₁₀模出现了第一尖峰, HG₀₀模的尖峰规律被打乱, 二者交叉尖峰, HG₂₀模的尖峰出现后三者交叉尖峰, 尖峰的幅度逐渐衰减过渡到交叉弛豫振荡阶段, 最终进入稳定状态. 在5 W抽运功率下, HG₀₀, HG₁₀, HG₂₀三个模式的光子数所占比例为0.40:0.33:0.27, 与阈值附近计算的结果十分接近. 当抽运光半径为0.15 mm, 离轴量为0.2 mm, 抽运功率为0.5和5 W时光子数的动态过程如图8(e)和图8(f)所示. 同样也是这种情况下净增益最大的HG₃₀模最先出现尖峰, 其他几个模式的尖峰出现后互相干扰, 整体上呈现幅度减小趋势, 逐渐进入交叉弛豫阶段, 最后进入稳态. 抽运功率较大时, 进入稳态需要的时间大为缩短. 在5 W抽运功率下, HG₁₀, HG₂₀, HG₃₀和HG₄₀模稳态时光子数所占比例为0.12∶0.25∶0.24∶0.39, 与阈值附近计算的结果十分接近.
在较高抽运功率下, 计算得到的光子数比例与阈值附近小信号计算结果接近的原因在于当抽运功率升高, 各个模式光子数开始增加的初始阶段光子数随抽运功率的变化比较复杂, 但当抽运功率增加到一定值后, 各个模式的光子数随抽运功率进入线性增加阶段, 从此以后, 光子数的比例保持不变, 图3和图6中各种情况下的光子数比例变化图也说明了这一点. 大抽运功率下, 数值计算结果与阈值附近计算结果一致, 说明我们可以用阈值附近小信号的计算结果来估算大抽运功率下各个模式光子数的比例, 从而省去费时的数值计算.

设计了一台离轴抽运光纤耦合二极管端面抽运Nd: YAG激光器, 实验系统如图9所示. 抽运源为北京大族天成半导体技术有限公司的M808 ± 10-7-F105/22-R2型光纤耦合半导体激光器, 输出波长808 nm, 纤芯直径0.105 mm, 数值孔径0.22, 耦合透镜1和耦合透镜2的焦距分别为20和30 mm, 经耦合透镜变换后的抽运光直径约为0.15 mm. Nd:YAG晶掺杂浓度为1 at.%, 抽运端面镀1064 nm高反、808 nm高透膜. 输出耦合镜的曲率半径为200 mm, 透过率为10%. Nd: YAG晶体和输出耦合镜安装在精密位移台上, 实现抽运光的离轴. 用光斑分析仪(Cinogy公司, CinCam CMOS-1201)观察输出光斑. 实验中谐振腔长度取为15 cm.
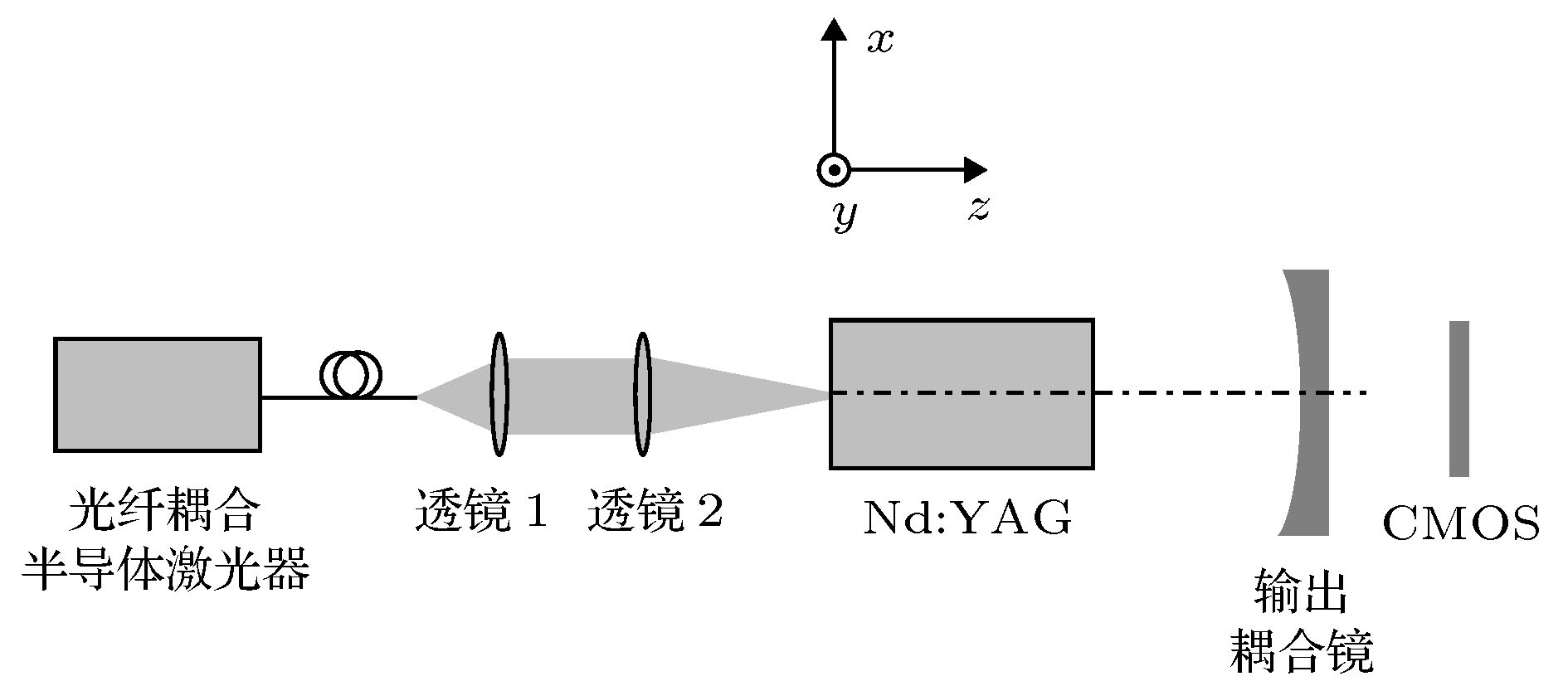图 9 离轴抽运实验装置图
Figure9. Schematic of the experimental setup.

在未离轴时, 激光器在0.4 W抽运功率下产生HG₀₀模激光输出, 将抽运功率增加到1 W, 增加离轴量观察输出光斑, 结果如图10所示. 随着离轴量的增加, 依次获得了HG₀₀—HG₅₀模式, 在两个单模之间, 出现了叠加模式输出. 本实验采用的输出耦合镜和谐振腔长度, 对应的Nd: YAG抽运端面处的HG₀₀模半径约为0.15 mm, 而抽运光半径约为0.075 mm. 从图10可以看出, 输出光斑随离轴量的变化与图2的理论计算结果符合很好. 选择一些离轴量, 研究光斑随激光功率的变化, 图11是离轴量为0.14 mm时, 光斑随激光功率的变化. 在该离轴量下, 输出光斑为HG₂₀模和HG₃₀模的组合, 当抽运功率在0.7—2.1 W变化时, 激光功率在50—400 mW变化, 而光斑基本保持不变.
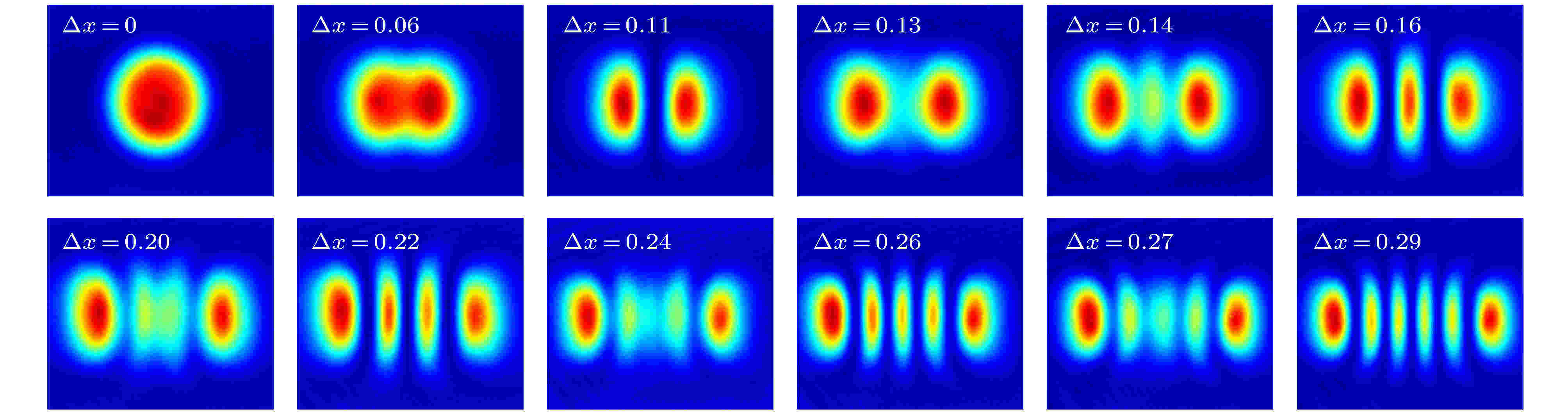图 10 不同离轴量下的输出光斑
Figure10. Output spots with different off-axis displacements.

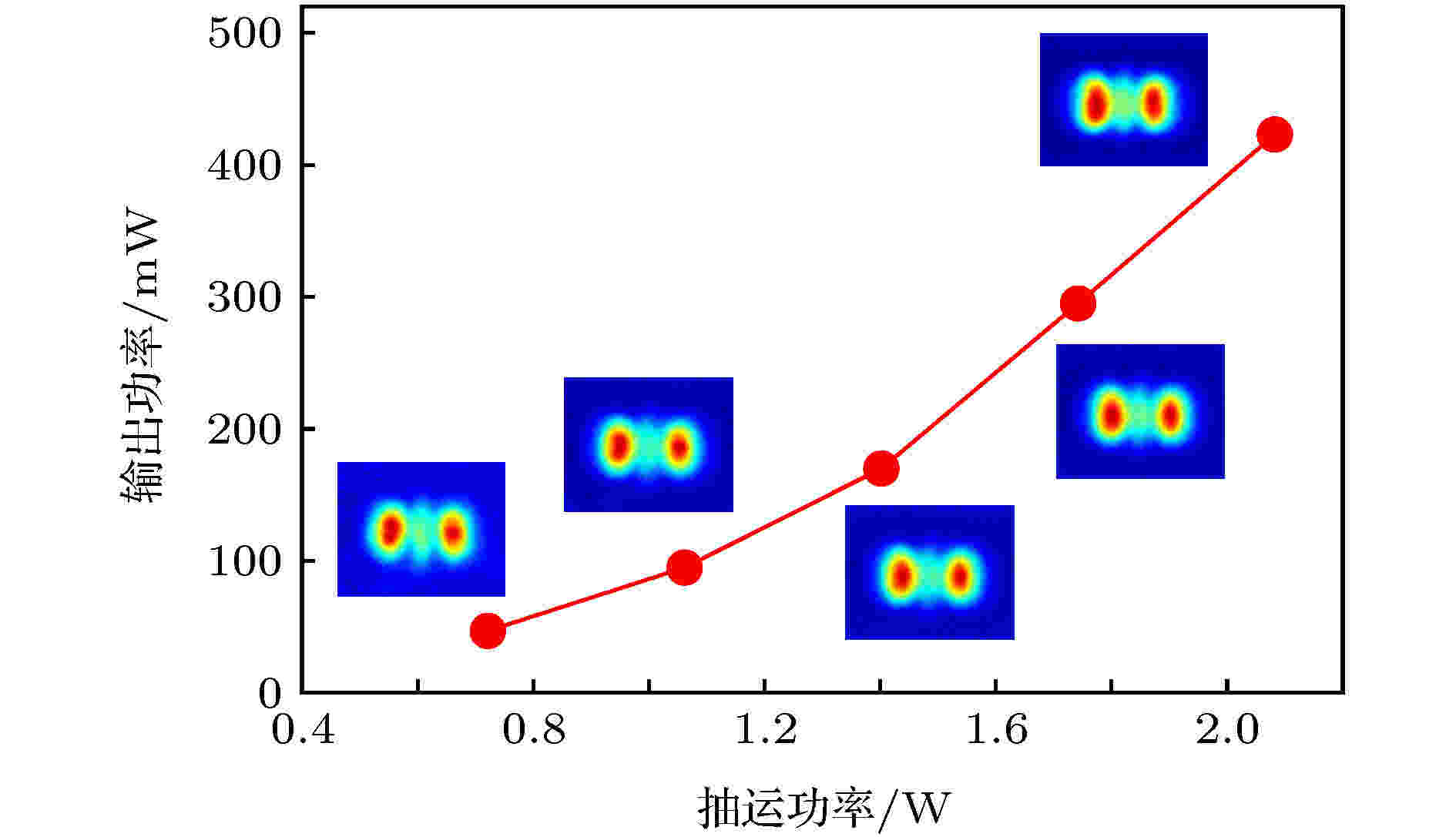图 11 光斑随激光功率保持不变
Figure11. The spot keeps unchanged with the variation of the laser power.

图10与图2的符合, 以及图11中光斑随功率保持不变的特点, 从实验上佐证了小信号方法计算的正确性. 图12(a)是在抽运功率为1 W时, 激光输出功率随离轴量的变化, 随着离轴量的增加, 输出功率出现接近线性的下降趋势. 图12(b)是各个模式的输出功率随抽运功率的变化. 激光功率随抽运功率的增加接近线性增加, 但模式阶数越高, 功率越小. 高阶模式的功率减小, 与实际谐振腔的衍射损耗及离轴抽运时非对称热效应形成的热致衍射损耗等因素有关.
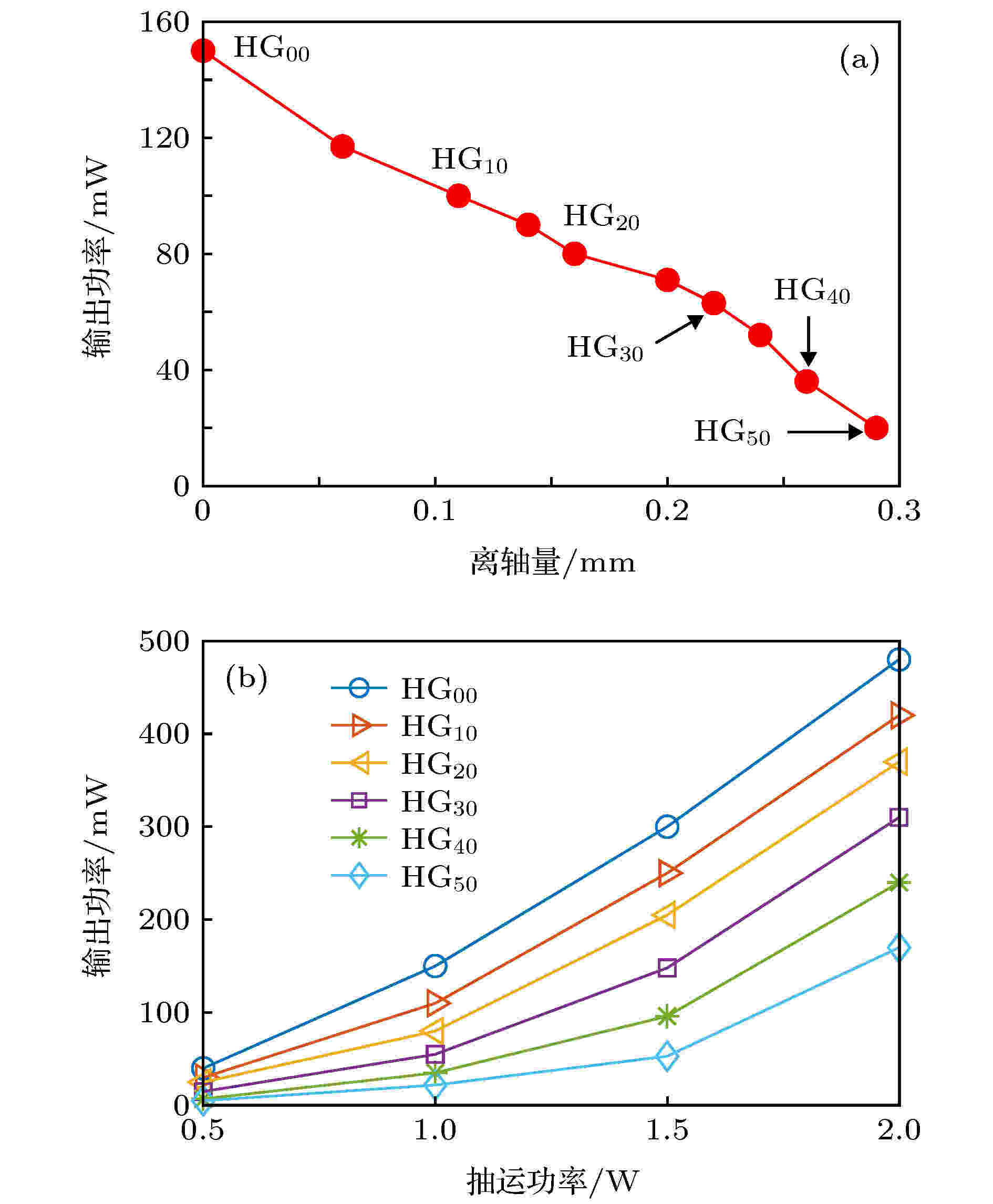图 12 (a)激光功率随离轴量的变化; (b)模式能达到的最大功率
Figure12. (a) Dependence of the output power on the displacement; (b) the maximum powers of the modes.

针对离轴抽运下固体激光器中多个HG模的竞争问题, 给出了阈值附近的小信号求解方法, 该方法把多模耦合的微分方程组化简为线性代数方程组. 用这种方法研究了输出光斑随离轴量的变化. 当抽运光半径在基模振荡光半径的一半以下时, 能选择出单一HG模; 当抽运光半径与基模振荡光半径相等时, 会出现三模以至四模输出. 随着离轴量的增加, 模式变化的整体趋势是高阶模工作, 低阶模抑制, 但具体过程呈现复杂性. 在多模竞争情况下, 在阈值附近随着抽运功率的增加, 第一个净增益由负变正的模式, 对应的模式光子数随即开始增加. 而第二个净增益由负变正的模式, 其光子数并不立即开始增加, 而要到抽运功率进一步增加后才开始增加, 其开始增加后第一个模式的增长趋势变缓, 这体现了模式竞争行为. 从动态过程看, 各个模式经过交叉尖峰和交叉弛豫振荡竞争过程后, 达到稳态. 较高抽运功率下的稳态光子数比例和小信号计算结果基本一致, 这使我们可以用小信号方法计算实际较高抽运功率激光器的输出模式, 方便这类激光器的研究. 实验获得了HG₀₀-HG₅₀模光束, 输出光斑随离轴量的变化与计算的结果符合很好.