摘要:研究了10 keV Cl^– 离子穿越Al₂O₃绝缘微孔膜的物理过程, 发现穿越的Cl^–其分布中心在初束中心即0°附近, Cl^–离子穿透率下降与几何穿透一致, 这是典型的直接几何穿越有一定角发散的微孔导致的结果; 而出射的Cl⁰和Cl⁺以微孔轴向为中心分布, Cl⁺和Cl⁰穿透率下降慢于几何穿透. 模拟计算发现沉积电荷会使出射粒子中Cl^–占主要成分, 并使出射Cl^–角分布中心移动到微孔轴向方向而随微孔膜倾角移动; 而在不考虑沉积电荷的情况下, 计算结果较好地符合了实验结果. 通过分析在不同倾角下散射过程对出射粒子的角分布和电荷态分布的影响, 发现绝大部分的Cl⁰是通过一次和两次散射出射的, 其中一次散射出射的Cl⁰占主要成分, 从而导致出射的Cl⁰沿微孔轴向出射而Cl⁺主要是经过一次碰撞出射. 这导致了随倾角增大, 出射的Cl⁰穿透率下降速度比Cl⁺小, Cl⁰所占比例相对增大较快, 从而导致观测到的Cl⁺/Cl⁰的比例下降. 本文结果更仔细地描述了低能离子穿越绝缘体微孔的物理机理, 印证了之前实验和理论工作的结果, 发现在10 keV以上能区的Cl^–离子穿越绝缘微孔膜的过程中, 沉积电荷并未起到主要作用, 其主要穿透特征是散射过程造成的.
关键词: Cl^–离子/
Al₂O₃绝缘微孔膜/
散射

English Abstract

全文HTML

--> --> -->

过去十来年, 带电粒子与绝缘纳米微结构的相互作用中的导向效应成为了离子束领域的热点问题^[1-22]. 导向效应是指离子穿越绝缘体微孔时, 在绝缘体微孔与离子入射方向的夹角大于其几何张角时, 能够观察到出射的离子, 出射离子的角分布中心随微孔相对于束流方向的倾角的改变而改变, 并且出射的离子保持其初始电荷态与能量^[1]. 大量的高电荷态离子穿越绝缘微孔膜的研究表明, 导向效应是由于入射离子在绝缘体微孔内部沉积的电荷形成一个排斥后续入射离子的库仑势导致的^{[1-6,9,12,13]}. 这种沉积电荷是通过相继有序形成电荷斑而形成一个使后续入射离子沿微孔轴向出射的导向电场达到的^[4,5]: 高电荷态离子会在微孔入口处形成第一块电荷斑; 后续入射离子在其电场的影响下, 一部分出射, 一部分在微孔中部第一块电荷斑的对面形成第二块电荷斑; 后续入射离子在第二块电荷斑的影响下, 会有更多的离子出射, 并会有一部分离子沉积在微孔的出口处形成第三块电荷斑, 从而建立完整的库仑场通道.
导向效应具有替代昂贵电磁设备使离子束进行准直和聚焦的潜力, 获得了离子束物理领域研究者的广泛关注^[1-22]. 后续, 离子穿越绝缘体微孔的成型效应被发现^[7-9]: 高电荷态离子穿越菱形和矩形微孔时, 出射束斑分别呈现矩形和菱形^[7]. 这是由于带电粒子在绝缘体微孔内部传输时的镜像电荷导致的^[7-9]. 成型效应的发现为控制离子束形状提供了新的技术手段. 基于导向效应, 采用锥形玻璃管可对离子束进行准直、聚焦到微米量级而形成微束, 其已成为一个研究热点, 微米量级的离子束已被用来进行针对生物细胞内部结构的辐照^[10,11].
高电荷态离子在绝缘微孔中的输运过程的研究已比较清楚^[12,13], 但是对带负电荷的粒子研究还很欠缺, 对负电荷粒子尤其是电子在微孔中是否有电荷斑产生以及电荷斑如何沉积等问题还未有定论^[14-18]. Milosavljevi?等^[14]通过低能电子穿过Al₂O₃微孔膜的实验, 发现电子的穿透强度随时间演化减小, 穿透电子仍沿微孔轴向出射, 没有明显能量损失. 此后, 在低能电子穿过PET (聚对苯二甲酸乙二醇酯)微孔膜的实验中, 观测到了穿透电子虽然沿轴向出射, 但是穿透率随倾角增加呈指数下降并且出现了能量损失, 这是一个非弹性散射过程造成的结果, 并由此电子在微孔中的输运过程中沉积电荷量不足以产生导向效应^[15]. 2009年, Schiessl等^[16]通过模拟计算500 eV电子穿过PET微孔膜的电子角分布和能量分布, 发现入射电子在微孔的入口处沉积的电荷沿微孔轴向输运达到平衡, 减弱了沉积电荷量. 并且由于二次电子发射的影响甚至有可能使入口处充正电, 而在与入射方向相反的一面会捕获电子沉积负电荷, 后续在微孔中发生的散射使微孔后部电场均匀分布, 从而导致电子在微孔中的输运是一个混合了散射过程和沉积电荷影响的穿透过程. 我们进行了电子穿越玻璃毛细管的实验测量, 发现了一个典型的几何穿透的过程: 出射电子角分布中心随着倾角变化发生微小移动, 并且穿透率和角分布宽度在几何容许角内基本不变^[17,18], 未发现如正离子那样的导向效应相关现象, 散射过程造成的电子出射份额和二次电子发射所占份额很小, 这些散射电子和二次电子角分布很发散, 没有像正离子那样沿微孔轴向出射的角分布. 电子的实验测量由于其质量轻而对电磁场非常敏感, 穿透电子的弹性散射部分与非弹性散射部分通常混合在一起, 在微孔中沉积电荷的影响、电子与微孔的表面原子的近距离散射过程以及二次电子的发射混合在一起无法进行清晰的分析, 导致了对电子的输运机制研究的困难. 为了避免电子实验测量中存在的问题, 我们采用了负离子进行实验, 发现在较大角度下穿透粒子角分布呈双峰结构, 一个峰在0°附近, 另一个峰与微孔轴向一致^[19]. 为了解释实验结果, 我们构筑了一个模型理论, 结合了穿透粒子散射过程和电荷交换过程的概率统计模型, 在Geant4 (Geometry and Tracking 4)的框架下模拟了16 keV的Cl^–穿透Al₂O₃微孔膜的过程, 计算了在不同沉积电荷下的穿透情况, 发现在无电荷沉积的情况下, 模拟结果与实验结果符合, 验证了之前的观测结果: 穿透的Cl^–离子主要通过几何穿透出射, 而Cl⁰及Cl⁺经表面近距离碰撞散射出射. 微孔中可能未形成足够的沉积电荷使得Cl^–离子无碰撞地通过微孔膜, 其输运过程主要以近距离碰撞为主^[20].
本文通过结合理论模拟和实验详细地研究了10 keV的Cl^–离子在Al₂O₃绝缘微孔膜中的输运的物理过程, 主要研究不同倾角下散射过程对出射粒子角分布和电荷态分布的影响. 对于10 keV的Cl^–离子, 实验特征和之前的其他能量是类似的, 穿透角分布呈现双峰结构, 出射的Cl^–沿初束方向分布, 而Cl⁰和Cl⁺沿微孔轴向分布^[20]. 而随着微孔膜倾角增大, 发现Cl^–离子所占比例在减小, Cl⁰和Cl⁺所占比例则在增大. 为了研究这些实验特征具体的物理原因, 采用自主研发的模拟程序计算了在沉积电荷和散射过程同时存在下出射粒子的角分布和电荷态分布, 发现沉积电荷会导致穿透Cl^–的角分布中心移动到微孔膜倾角位置, 双峰结构消失, 且出射粒子主要为Cl^–, 经过电荷交换产生的Cl⁰和Cl⁺的所占比例很小, Cl⁺/Cl⁰比例远小于实验值. 而在不考虑沉积电荷的影响下, 只考虑散射过程的模拟计算时, 得到的穿透粒子的角分布和电荷态分布较好地符合了实验结果. 结合模拟计算详细地分析了在不同倾角下散射过程对出射的Cl⁰和Cl⁺角分布和电荷态分布的影响. 发现随散射次数增加, 出射的Cl⁰向初束方向偏移. 随倾角增大, Cl⁰可以经过多次碰撞出射, 而Cl⁺是主要经过一次碰撞出射的, 使得 Cl⁰在倾角变大时相对Cl⁺减小较慢, 从而导致实验观测到的Cl⁺与 Cl⁰的比例下降.

2

-->

2.1.实验方法

本次实验在兰州大学核科学与技术学院的2 × 1.7 MeV串列加速器上进行. 实验所用Cl^–离子束由串列加速器上的铯溅射离子源提供, 经过两级间隔75 cm的四极狭缝准直之后, 形成束斑大小为3 mm × 3 mm, 角发散0.5°, 束流强度为几十个pA/mm²的Cl^–离子束. Al₂O₃纳米微孔膜安装在超高真空靶室的中心处. 微孔膜倾角ψ定义为微孔与初束垂直方向的夹角, 探测角?定义为出射束流与初束之间的夹角, 本次实验采用一维微通道板探测器(1D-MCP)来探测穿透粒子, 可以在探测角方向上分辨束流的穿透角分布. 沿着束流方向, 在微孔膜的后方安装了静电分析器, 用于分析穿透粒子的电荷态组成成分. 探测器的位置信号采用多参数数据获取系统进行提取. 实验装置简图见图1. 实验要求靶室的真空好于2.5 × 10^–5 Pa.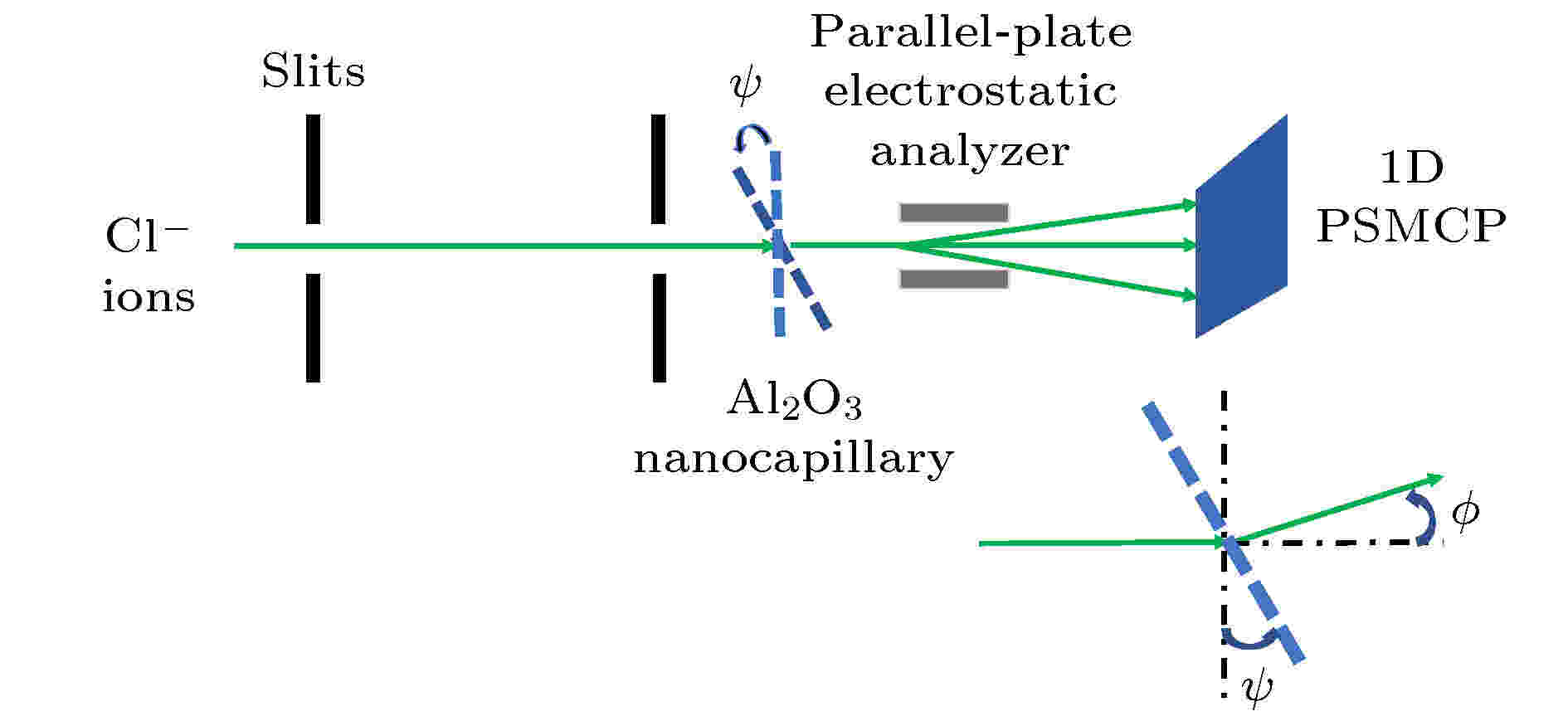
图 1 实验装置和探测角示意图
Figure1. Schematic diagram of experimental setup and the observation angle ?

实验采用的Al₂O₃微孔膜是通过二次阳极氧化法获得^[22-25]. 将预抛光的铝板放入按1∶4混合的65%的HClO₄溶液与99.5%的酒精溶液, 通入20 V的电压进行电化学抛光. 之后将铝板作为阳极放入0.3 mol/L的草酸溶液, 通上40 V的电压进行第一次阳极氧化, 然后放入含质量分数为1.8%的H₂CrO₄与质量分数为6%的H₃PO₄的混合溶液进行腐蚀去除阻挡层. 第二次阳极氧化与第一次步骤相同^[22]. 最终获得的微孔膜厚度为7 μm, 微孔直径为50 nm, 微孔密度为10¹⁰/cm². 微孔膜的光学穿透率为21%, 微孔轴向发散约1.0°. 为了排除微孔膜表面充电的影响, 在Al₂O₃微孔膜的前后表面镀有厚10 nm的金层. 图2为微孔膜的电子扫描显微镜图像.
图 2 Al₂O₃微孔膜的电子扫描显微镜图像
Figure2. Scanning electron microscope images of Al₂O₃ nanocapillaries.

2 -->

2.2.实验结果

在不同倾角下, 10 keV的Cl^–离子穿过厚度为7 μm的Al₂O₃微孔膜的穿透粒子角分布如图3(b)所示. 随着倾角的增大, 穿透粒子的计数率在下降, 并且角分布也随之展宽呈现出双峰的结构. 穿透粒子角分布的两个峰, 一个峰的峰位在0°附近, 另一个峰的峰位与微孔膜的倾斜角基本一致. 并且随着倾角的增大, 0°附近的峰所占比例在减小, 而与微孔膜倾斜角一致的峰所占比例在增大. 为了探究穿透粒子角分布的峰的组成成分, 我们在静电分析器加上了静电场, 得到了图4(b)所示的电荷态分布. 中性粒子保持原有角分布不变, 负离子向负角度方向移动了4°左右, 正离子向正角度方向移动了4°左右. 由此可以分析得到, 峰位在0°附近的峰成分主要为Cl^–离子, 峰位与倾角一致的峰主要成分为Cl⁰和Cl⁺. 其中Cl^–离子随倾斜角的增大所占比例在减小, 而Cl⁰和Cl⁺所占比例则在增大.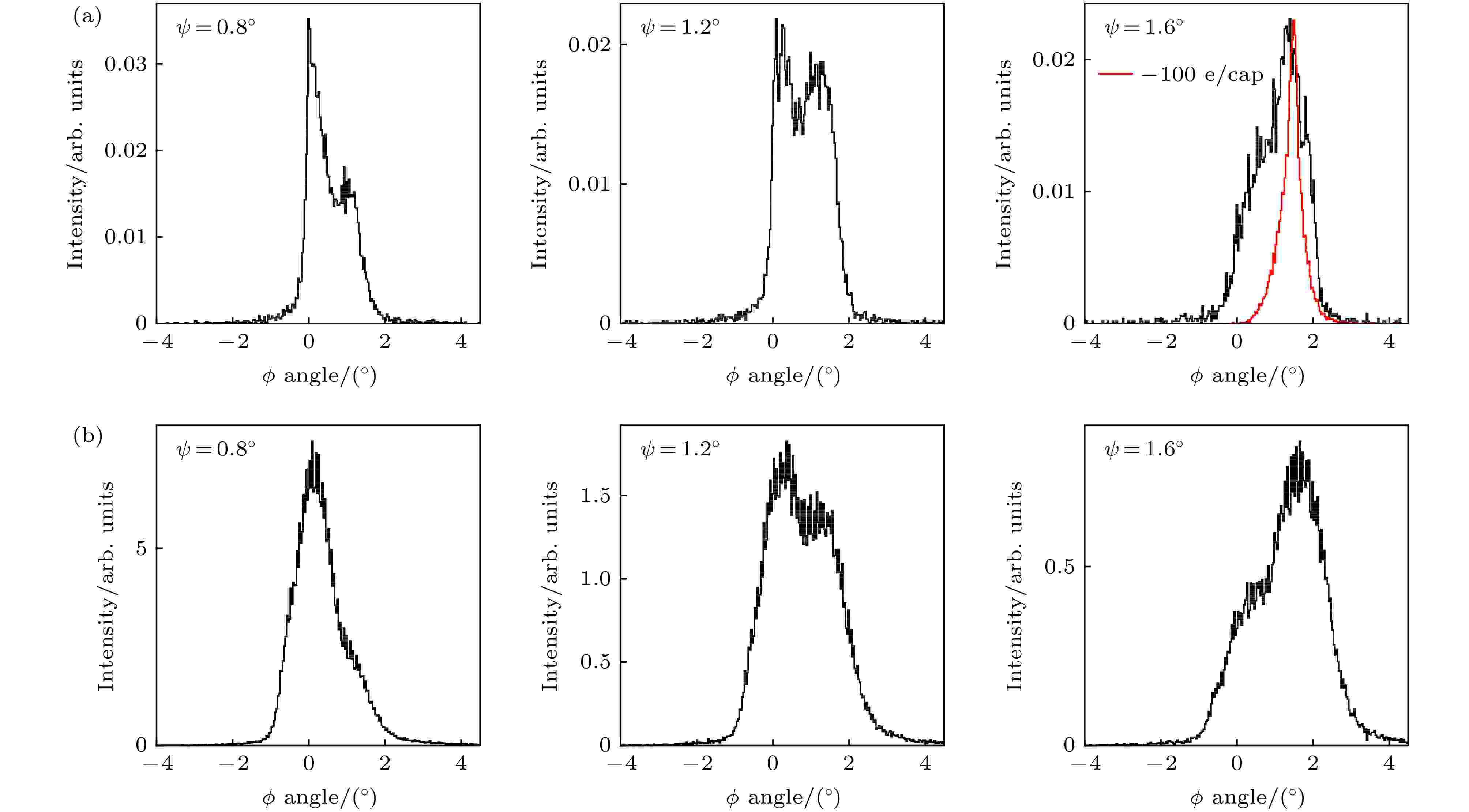
图 3 (a)不同倾角ψ下10 keV的Cl^–穿透角分布的计算结果(黑色为无沉积电荷的结果, 红色为沉积电荷为–100 e/capillary的结果); (b)不同倾角ψ下10 keV的Cl^–穿透角分布的实验结果
Figure3. (a) Calculated transmitted angular distributions for 10 keV-Cl^– ions at various tile angles ψ (black lines for no deposited charge and red line for deposited charge of –100 e/capillary); (b) the experimental transmitted angular distributions for 10 keV-Cl^– ions at various tile angles ψ.

图 4 加静电场后, (a)不同倾角ψ下10 keV的Cl^–穿透粒子的电荷态分布的计算结果(黑色为无沉积电荷的结果, 红色为沉积电荷为–100 e/capillary的结果); (b)不同倾角ψ下10 keV的Cl^–穿透粒子的电荷态分布的实验结果
Figure4. Exerting electrostatic field, (a) thecalculated charge state distributions of transmitted projectiles for 10 keV-Cl^– at various tilt angles ψ (black line for no deposited charge and red line for deposited charge of –100 e/capillary); (b) the experimental charge state distributions of transmitted projectiles for 10 keV-Cl^– at various tilt angles ψ.

在实验数据的电荷态分布 (图4(b))中可以看出Cl⁰峰的峰位随倾角变化而改变, 并与倾角基本形成图5所示的线性关系. 图5中实验结果的Cl⁰峰位与 Y = X 的直线只有微小歧离, X为倾角, Y是Cl⁰峰的峰位. 我们分析了不同角度下的模拟计算的Cl⁰出射峰位和实验结果的Cl⁰出射峰位角度与倾角的关系, 计算结果与实验结果基本符合, Cl⁰峰位以微孔轴向为中心分布. 不同角度下Cl^–和Cl⁰相对于0°的相对穿透强度与倾角的关系如图6(a) 所示. 由此可见穿透粒子的强度随倾角增大而减小. 可以看到, 与Cl⁰和Cl⁺相比, Cl^–的穿透强度随倾角下降得要快很多. Cl^–的穿透强度在小于1.2°时快速下降, 大于1.2°时, 其穿透相对强度与0°时相比保持在1.0 × 10^–3基本不变. 而Cl⁺和Cl⁰的穿透强度在大于1.2°时, 仍存在下降趋势. 主要原因在于, Cl^–穿透过程为几何穿透, 其穿透强度变化与沿束流方向的光学穿透率一致. 而Cl⁺和Cl⁰经过电荷交换产生, 因此需要经过一次或多次近距离碰撞后才能从微孔中出射. 为了清晰地看出Cl⁺和Cl⁰变化趋势的差别, 将其相对强度用以2为底的对数坐标表示在图6(b) 中. 结果发现Cl⁺较Cl⁰下降稍快.
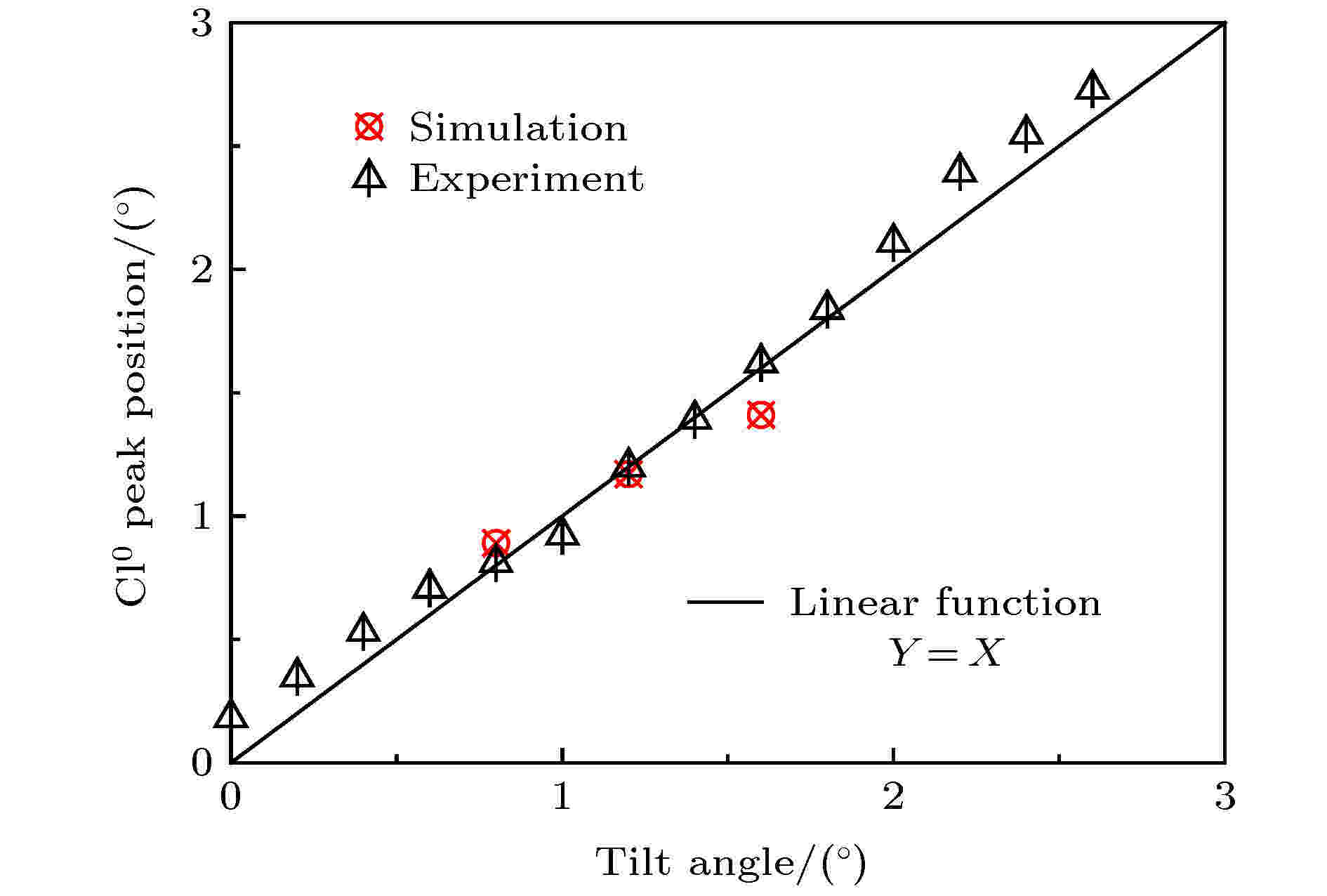图 5 实验与计算结果的中性穿透粒子(Cl⁰)角分布的峰位置随倾角的变化(实线是线性函数Y = X)
Figure5. Peak position of experimental and simulated angular distribution of transmitted neutrals (Cl⁰) as a function of the tilt angle. The solid line is the linear function that shows the peak position of transmitted neutral shifts according to the tilt angle.

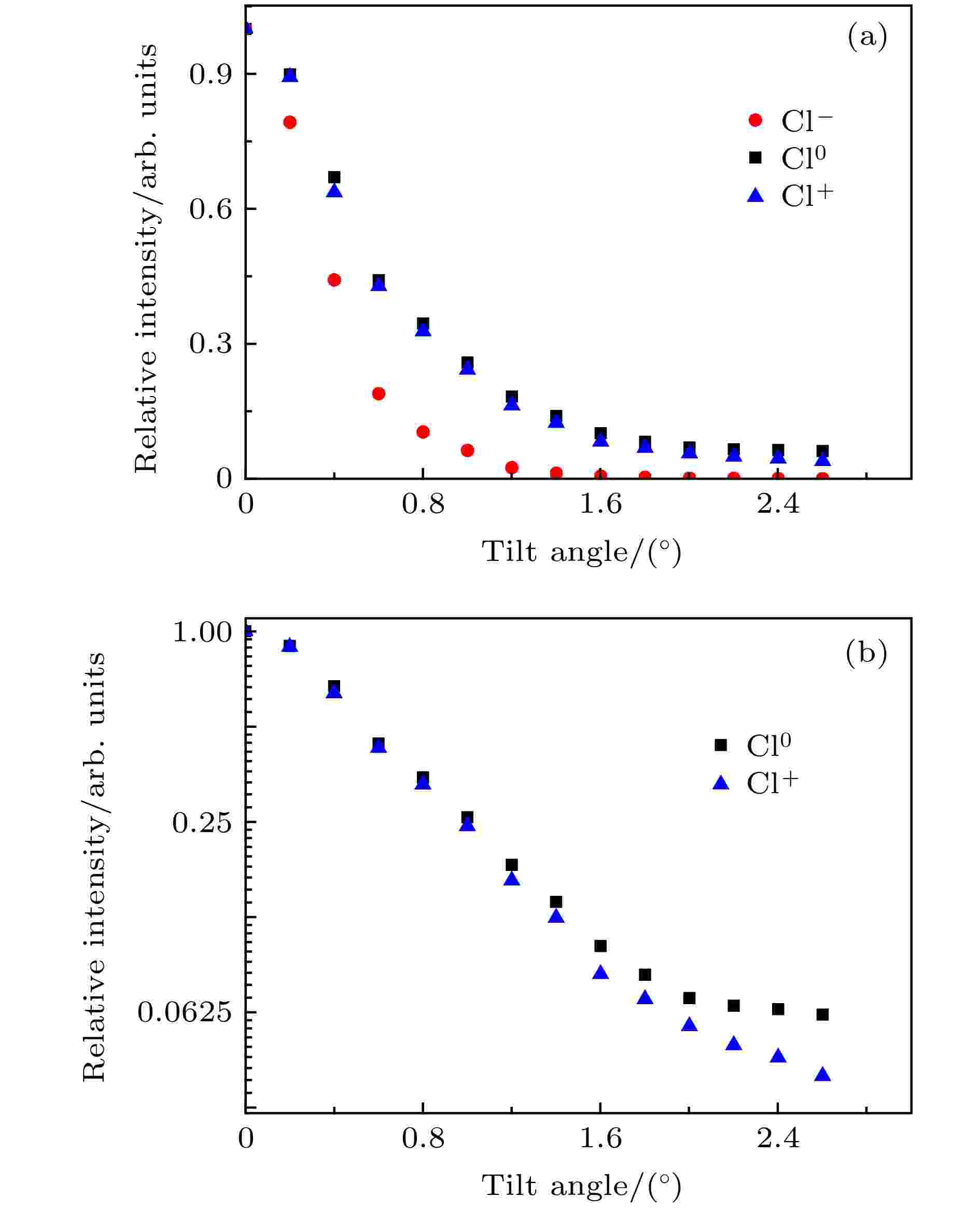图 6 (a)穿透的Cl^–, Cl⁰, Cl⁺粒子相对强度随倾角ψ变化; (b)穿透的Cl⁰和Cl⁺粒子相对强度随倾角ψ变化的对数坐标图
Figure6. (a) Relative intensity of transmitted Cl^–, Cl⁰ and Cl⁺ vs. the tilt angle ψ for 10 keV-Cl^– ions; (b) the logarithm scale of the relative intensity of transmitted Cl⁰ and Cl⁺ as a function of the tilt angle ψ

离子穿越微孔时可能的几何穿透角${\sigma _{{\rm{geot}}}} = $$\sqrt {{\sigma ^2}_{{\rm{asp}}} + {\sigma ^2}_{{\rm{beam}}} + {\sigma _{{\rm{axis}}}}} \approx {\rm{1}}{\rm{.}}{{\rm{2}}^ \circ }$, 其中, σ_asp, σ_beam和σ_axis分别代表微孔几何张角, 束流发散角和微孔轴向发散角^[20]. 穿透粒子中Cl⁺和Cl⁰的比值与倾角的关系如图7所示. 在倾角小于1.2°时, Cl⁺/Cl⁰的比值在0.16附近波动; 当倾角大于1.2°时, Cl⁺/Cl⁰的比值迅速减小. 实验的1.2°转折点与几何穿透角基本一致, 与之前16 keV的工作相似^[19]. 然而在相同角度下10 keV的Cl⁺/Cl⁰的比值小于16 keV的Cl^–的穿透结果.
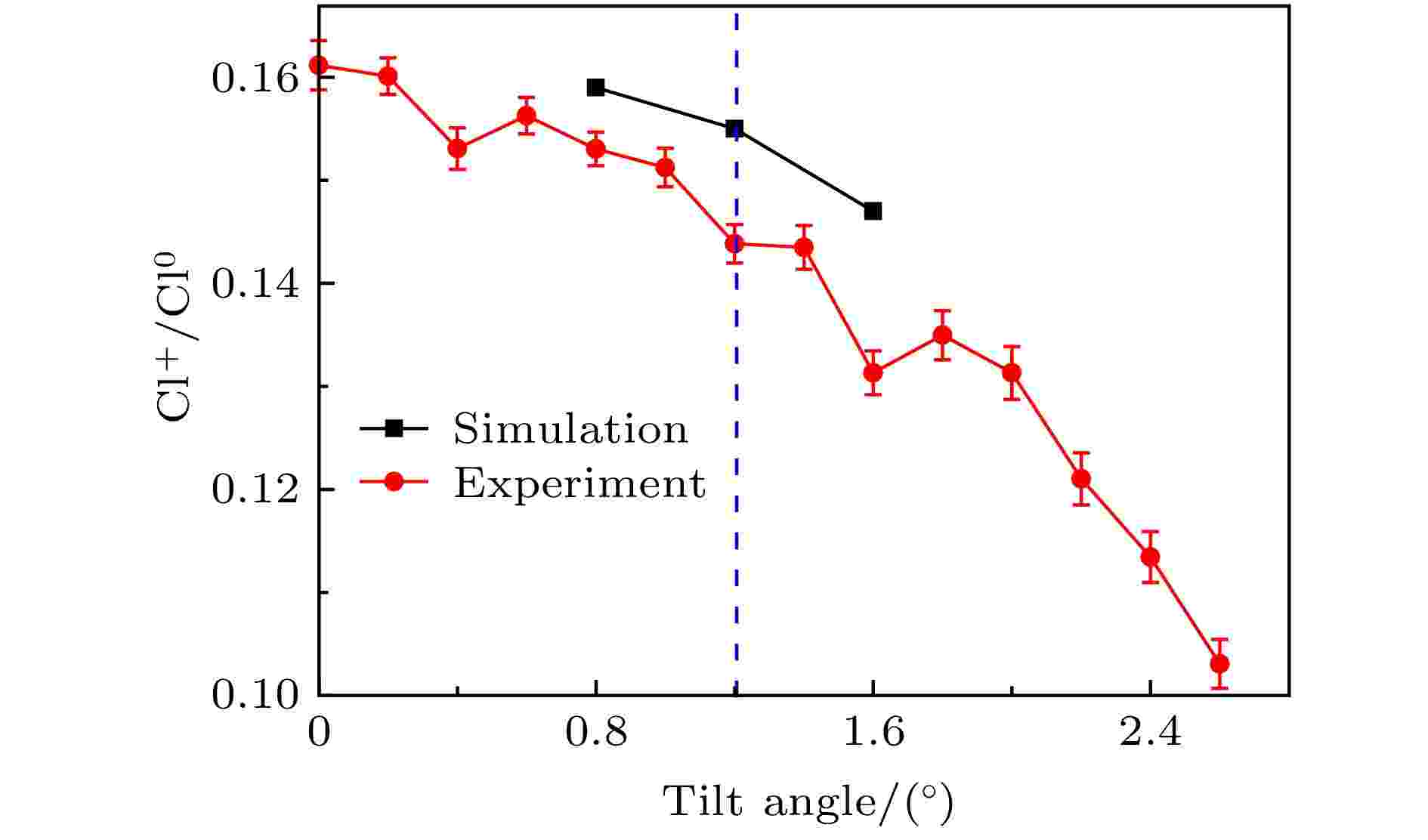图 7 在不同倾角ψ下10 keV的Cl^– 穿透的Cl⁺/Cl⁰的比值(红色实心圆是实验结果, 黑色实心矩形是计算结果, 蓝色虚线代表几何穿透角)
Figure7. Intensity ratio of transmitted Cl⁺ to Cl⁰ vs. the tilt angle ψ for the incident ions of 10 keV-Cl^–. The red solid circle corresponds to the experimental results; black solid square corresponds to the simulation results; blue dash line indicates the angle within which the geometrical transmission occurs.

为探究负离子在绝缘体微孔中的穿透过程, 我们构架了一个模型理论, 在Geant4框架下采用Runge-Kutta方法解牛顿方程来计算粒子在其中的径迹^[26]. 我们的模型理论中考虑了散射过程、电荷交换、镜像电荷力以及电荷沉积导致的库仑力, 详细内容见我们之前的工作^[20]. 计算中充分利用了Geant4中的标准模块: 径迹管理模块、时间管理模块、分步管理模块. 入射粒子轨迹主要受其引起的镜像力、沉积电荷作用以及离子与微孔内壁的近距离散射过程影响.
2

-->

3.1.初始化中的坐标变换

我们发展了一套坐标转换方法, 从而可以采用一个微孔来模拟实际束斑下百万量级的微孔. 在实验室坐标系下, 离子动量表示为

${{{p}}_l} = \left( {\begin{array}{*{20}{c}} {\sin {\theta _{\rm{m}}}\sin {\varphi _{\rm{m}}}} \\ {\sin {\theta _{\rm{m}}}\cos {\varphi _{\rm{m}}}} \\ {\cos {\theta _{\rm{m}}}} \end{array}} \right), $

其中θ_m描述束流发散, 束流发散遵循高斯分布, 其半高宽为0.5°; φ_m是在0—2π上的均匀分布函数. 考虑束流发散度的影响, 在实验室坐标系中, 将动量矢量(0, 0, 1)沿着${{{j}}_l}$旋转θ_m, 之后沿着${{{k}}_{\rm{l}}}$旋转φ_m. 从${{{p}}_{\rm{l}}}$到${{{p}}_{\rm{m}}}$沿着${j_{\rm{l}}}$旋转ψ. 然后${{{p}}_{\rm{m}}}$沿着${j_{\rm{m}}}$转动θ_d变为${{{p}}_{\rm{c}}}$.
最终在微孔坐标下的坐标表示为

${{{p}}_{\rm{c}}} = \left( {\begin{array}{*{20}{c}}{\cos {\varphi _{\rm{d}}}\cos {\theta _{\rm{d}}}\cos \psi - \cos {\varphi _{\rm{d}}}\sin {\theta _{\rm{d}}}\sin \psi }&{ - \sin {\varphi _{\rm{d}}}}&{\cos {\varphi _{\rm{d}}}\cos {\theta _{\rm{d}}}\sin \psi + \cos {\varphi _{\rm{d}}}\sin {\theta _{\rm{d}}}\cos \psi }\\{\sin {\varphi _{\rm{d}}}\cos {\theta _{\rm{d}}}\cos \psi - \sin {\varphi _{\rm{d}}}\sin {\theta _{\rm{d}}}\sin \psi }&{\cos {\varphi _{\rm{d}}}}&{\sin {\varphi _{\rm{d}}}\cos {\theta _{\rm{d}}}\sin \psi + \sin {\varphi _{\rm{d}}}\sin {\theta _{\rm{d}}}\cos \psi }\\{ - \sin {\theta _{\rm{d}}}\cos \psi - \cos {\theta _{\rm{d}}}\sin \psi }&0&{ - \sin {\theta _{\rm{d}}}\sin \psi + \cos {\theta _{\rm{d}}}\cos \psi }\end{array}} \right) \cdot {{{p}}_{\rm{l}}},$

其中$\psi $是相对于束流方向的微孔倾角, 沿着${{{j}}_{\rm{l}}}$旋转; θ_d是微孔轴向发散, 遵循高斯分布, 其半高宽为0.5°; φ_d是在0—2π上的均匀分布函数.
2 -->

3.2.内表面散射

当入射粒子与微孔内表面碰撞时会发生离子内表面散射, 离子从表面散射的概率如下^[27]: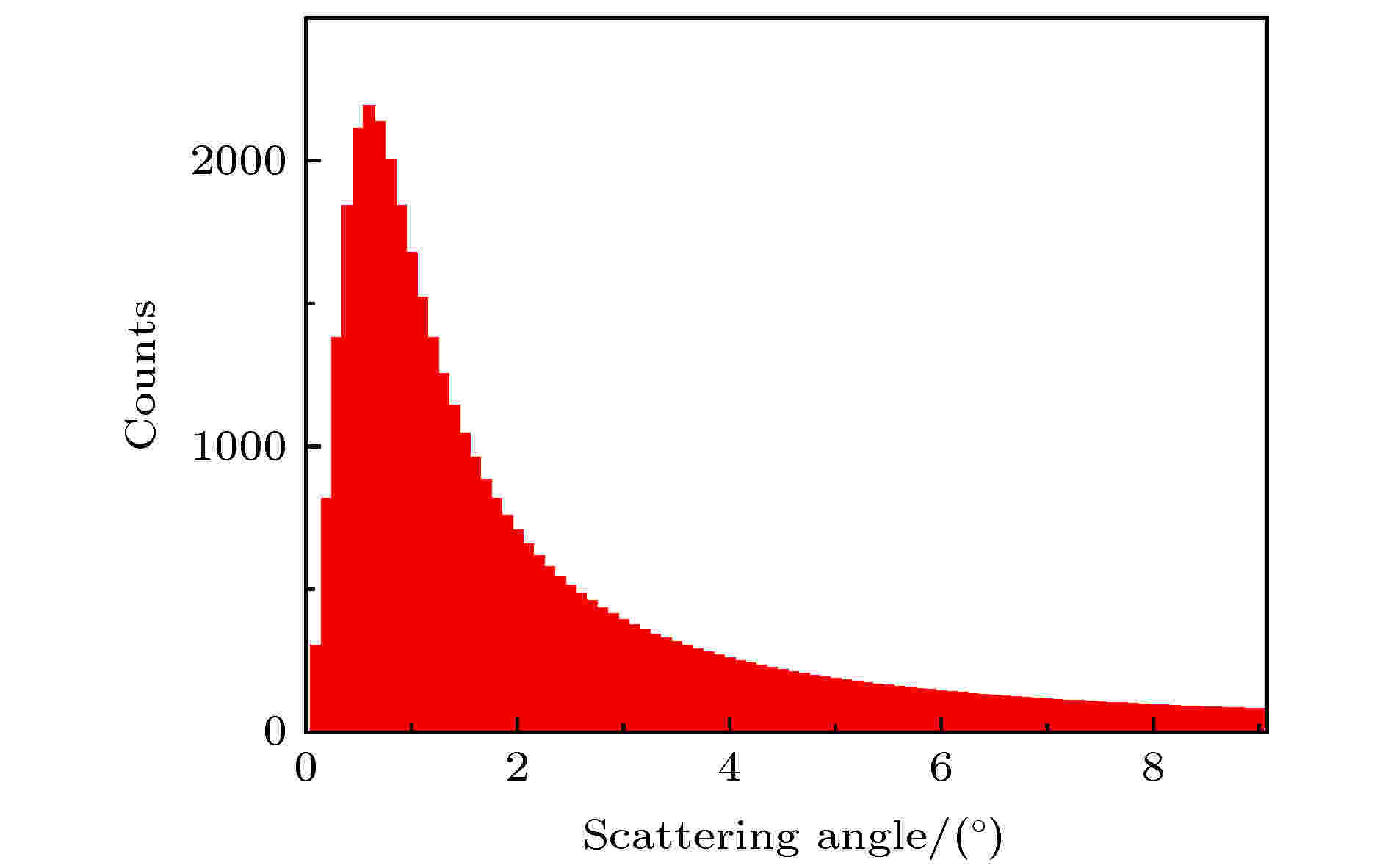

${P_{\rm{R}}} = {{\rm{e}}^{\frac{{ - E{{\sin }^2}{\theta }}}{{V(Z)}}}}, $

其中E是入射离子的动能; θ是离子碰撞到微孔内表面时的入射角度; V(z)为^[27]

$V(Z) = 2{\text{π }}{Z_{\rm{t}}}{Z_{\rm{p}}}{n_{\rm{a}}}{a_{\rm{s}}}\sum\limits_{{d_{\rm{i}}}}^3 {\frac{{{c_{\rm{i}}}}}{{{d_{\rm{i}}}}}} {{\rm{e}}^{ - Z{d_{\rm{i}}}/{a_{\rm{s}}}}}, $

Z是离子电荷态, Z_t和Z_p分别是靶原子和入射离子的核电荷数, n_a是微孔内表面的原子数密度, c_i和d_i是常数(c_i = {0.35, 0.55, 0.1}, d_i = {0.3, 1.2, 6}), a_s为

${a_{\rm{s}}} = {(\sqrt {{Z_{\rm{t}}}} + \sqrt {{Z_{\rm{p}}}} \,)^{ - 2/3}}.$

散射离子的出射角度用Firsov散射公式描述^[28]:

$N(\psi,\theta ) = \frac{{3{{(\psi \theta )}^{3/2}}}}{{2{\rm{\pi }}\psi ({\psi ^3} + {\theta ^3})}}, $

其中ψ是入射角度, θ是散射角度. 图8展示了在入射角为0.6°时根据Firsov散射公式计算的散射角分布, 可以看到散射粒子概率最大的出射角与入射角基本相同, 这具有镜面反射特征.
图 8 入射角为0.6°时, Firsov公式计算的散射粒子角分布
Figure8. Scattered angular distribution at the incident angle of 0.6° to the surface given by Firsov formula.

2 -->

3.3.电荷态交换

我们构筑了一个电荷态交换的唯像模型来定量地获得穿透粒子的电荷态分布^[19]. 在实验中, 微孔的倾斜角度比较小, 所以碰撞过程以一次和两次碰撞为主体, 还有部分Cl^–离子直接穿过微孔, 如图9所示. 当Cl^–离子与微孔内部发生碰撞时, 会发生图10中所示意的电荷态交换.
图 9 Cl^–离子穿过纳米微孔的原理简图(绿线为离子直接穿透的轨迹简图, 红线为一次碰撞散射的轨迹简图, 黑线为二次碰撞散射的简图)
Figure9. Schematic diagram of Cl^– ions transmitted through a nanocapillary. The green line is a schematic diagram of the direct transmission of ions, the red line is a schematic diagram of ions transmitted by single scattering, and the black line is a schematic diagram of ions transmitted by double scattering.

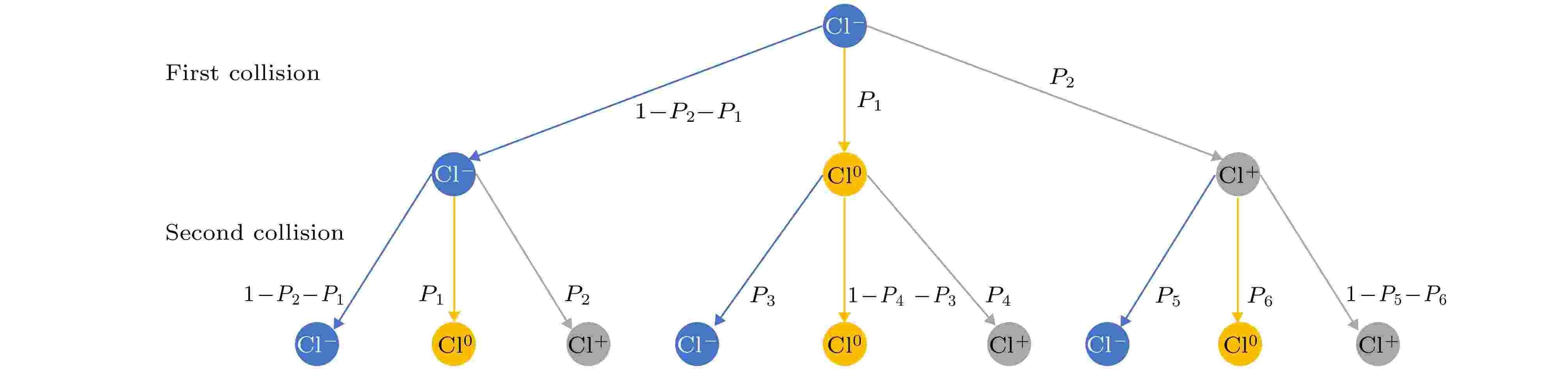图 10 传输过程的电荷交换简图
Figure10. Schematic diagram of charge state exchange during transmission.

我们定义一次碰撞过程中Cl^–变为 Cl⁰, Cl^– 变为 Cl⁺, Cl⁰ 变为 Cl^–, Cl⁰ 变为Cl⁺, Cl⁺ 变为 Cl^– 和 Cl⁺ 变为 Cl⁰的概率分别为P₁, P₂, P₃, P₄, P₅, P₆. 其中归一化条件为, Cl^– 转化为 Cl⁰和Cl⁺ 以及保持为 Cl^– 的总概率为 1, 同样地, Cl⁰和Cl⁺各自电荷交换总概率也为1.
在离子和微孔内壁的第一次碰撞中, Cl^– 转变为Cl⁺的概率为S₁ = P_RP₂; Cl^– 转变为Cl⁰的概率为S₂ = P_RP₁; Cl^– 转变为Cl^– 的概率为S₃ = P_R(1 – P₁ – P₂). 这里P_R是离子散射概率.
在第二次碰撞时, Cl^– 变为 Cl⁰ 的概率为S₄ = $ P_{\rm R}^2 $P₁(1 – P₂ – P₁); Cl^– 变为 Cl⁺ 的概率为S₅ = $ P_{\rm R}^2 $P₂(1 – P₂ – P₁); Cl^– 变为 Cl^– 的概率为S₆ = $ P_{\rm R}^2 $(1 – P₂ – P₁) (1 – P₂ – P₁); Cl⁰ 变为 Cl⁰的概率为 S₇ = $ P_{\rm R}^2 $P₁(1 – P₃ – P₄); Cl⁰ 变为 Cl⁺ 的概率为S₈ = $ P_{\rm R}^2 $P₁P₄; Cl⁰ 变为 Cl^– 的概率为S₉ = $ P_{\rm R}^2 $P₁P₃; Cl⁺变为Cl⁰的概率为 S₁₀ = $ P_{\rm R}^2 $P₂P₆; Cl⁺ 变为Cl⁺ 的概率为 S₁₁ = $ P_{\rm R}^2 $P₂(1 – P₅ – P₆); Cl⁺ 变为 Cl^– 的概率为 S₁₂ = $ P_{\rm R}^2 $P₂P₅.
将所有的碰撞事件相加, Cl^–变为Cl⁺的概率为
S₊ = P_RP₂ + $ P_{\rm R}^2 $(2P₂ – P₁P₂ – $ P_{2}^2 $ + P₁P₄ – P₂P₅ – P₂P₆)+高次项.
Cl^– 变为Cl⁰的概率为
S₀ = P_RP₁ + $ P_{\rm R}^2 $(2P₁ – P₁P₂ – $ P_{1}^2 $ + P₁P₃ – P₁P₄ – P₂P₆)+高次项.
受到Al₂O₃能带结构的影响^[29], 在一次单独的碰撞中, Cl^– 到Cl⁺的电荷态交换过程是两步过程: 首先Cl^– 变为Cl⁰, 其概率为 Q₁, 之后 Cl⁰ 变为Cl⁺, 其概率为Q₂. 这样在一次碰撞中, Cl^– 到 Cl⁺ 的转变概率为P₂ = Q₁Q₂, Cl^–到Cl⁰的转变概率为P₁ = Q₁(1 – Q₂). 因此得到S₊/S₀ ≈ P₂/P₁ = Q₂/(1 – Q₂). 由于二次以上散射出表面的概率呈数量级下降, 且在这个能区Cl⁺在近距离碰撞时中和为Cl⁰的概率接近为1^[30,31], 通过这个近似, 可以获得一次碰撞中的两步过程的其中一个过程即Cl⁰ 变为Cl⁺的概率Q₂以及由此可以得到其他可能电荷交换的概率^[20].
2 -->

3.4.镜像力

入射离子会极化绝缘微孔的内表面而产生镜像电荷力吸引离子靠近表面. 在圆柱内部, 镜像势可以被解析地表示为^[32,33]

$V(\rho ) = - \frac{{\varepsilon - 1}}{{\varepsilon + 1}}\frac{{q{\rho ^2}}}{{2a({a^2} - {\rho ^2})}}, $

其中a是圆柱半径, ρ是离子距圆柱轴心的距离, ε是介电常数, q是入射离子电荷数.
2 -->

3.5.沉积电荷

沉积电荷产生的库仑力与我们以前工作中的计算方式相同^[8]. 微孔内壁被切分为很多个微条. 对于每个带电微条, 可以得到其势能的解析表达式:

$U = {\sigma _0}a\ln \left[ {\frac{{z - {z_{\rm{s}}} + \sqrt {{{(x - {x_{\rm{s}}})}^2} + {{(y - {y_{\rm{s}}})}^2} + {{(z - {z_{\rm{s}}})}^2}} }}{{z - {z_{\rm{s}}} - {L_0} + \sqrt {{{(x - {x_{\rm{s}}})}^2} + {{(y - {y_{\rm{s}}})}^2} + {{(z - {z_{\rm{s}}} - {L_0})}^2}} }}} \right].$

根据我们之前的工作^[20], 1.6°下微孔内沉积的电荷达到–100 e/capillary时, 穿透角分布及电荷态分布会达到稳定状态, 因此本次工作在沉积电荷量为–100 e/capillary (图3(a) 1.6°红线、图4(a) 1.6°红线) 和无沉积电荷(图3(a) 1.6°黑线、图4(a) 1.6°黑线)的情况下, 对10 keV的Cl^–离子在1.6°下穿过的厚度为7 μm的Al₂O₃微孔膜进行了模拟计算, 为了直观地对比不同物理过程下对出射粒子角分布的影响, 将无沉积电荷计算结果的峰值与加入沉积电荷的计算结果进行了归一化. 发现沉积电荷将导致出射的Cl^–移动到微孔轴向方向, 双峰结构消失, 出射粒子中Cl^–占主要部分, 而Cl⁰和Cl⁺所占比例很小, Cl⁺/Cl⁰比例要比实验值小得多. 与实验结果的穿透角分布 (图3(b) 1.6°) 和电荷态分布 (图4(b) 1.6°) 不符. 而在无沉积电荷情况下的计算结果与实验结果符合得很好. 结合我们之前的模拟工作^[20], 发现沉积电荷并未在Cl^–离子穿越纳米微孔的过程中起明显作用, 其穿透过程的物理机理主要为散射过程.
结合无沉积电荷下1.6°的计算结果, 在不考虑沉积电荷的情况下, 又分别模拟了不同倾角0.8°和1.2°下离子的穿透角分布和电荷态分布. 计算得到的穿透粒子角分布(图3(a))和电荷态分布(图4(a))与实验的穿透粒子角分布(图3(b))和电荷态分布(图4(b)) 符合得很好. 计算结果的粒子角分布比实验穿透粒子角分布要窄一些, 双峰结构也更明显. 这是由于实际束流状况(角发散和束流轮廓)以及微孔的轴向发散、孔内壁表面粗糙度与理论模型之间的有差异^[20], 模型中的电荷交换和散射过程的物理描述也会与实际情况产生差异.
在1.2°下, 分析了模拟计算中出射的不同电荷态二维角分布 (图11(a))及对应的投影角分布(图11(b)), 出射的Cl^–以0°为中心分布, 出射的Cl⁰和Cl⁺粒子以微孔的轴向为中心分布. 出射的不同电荷态的粒子混合呈现出双峰结构.
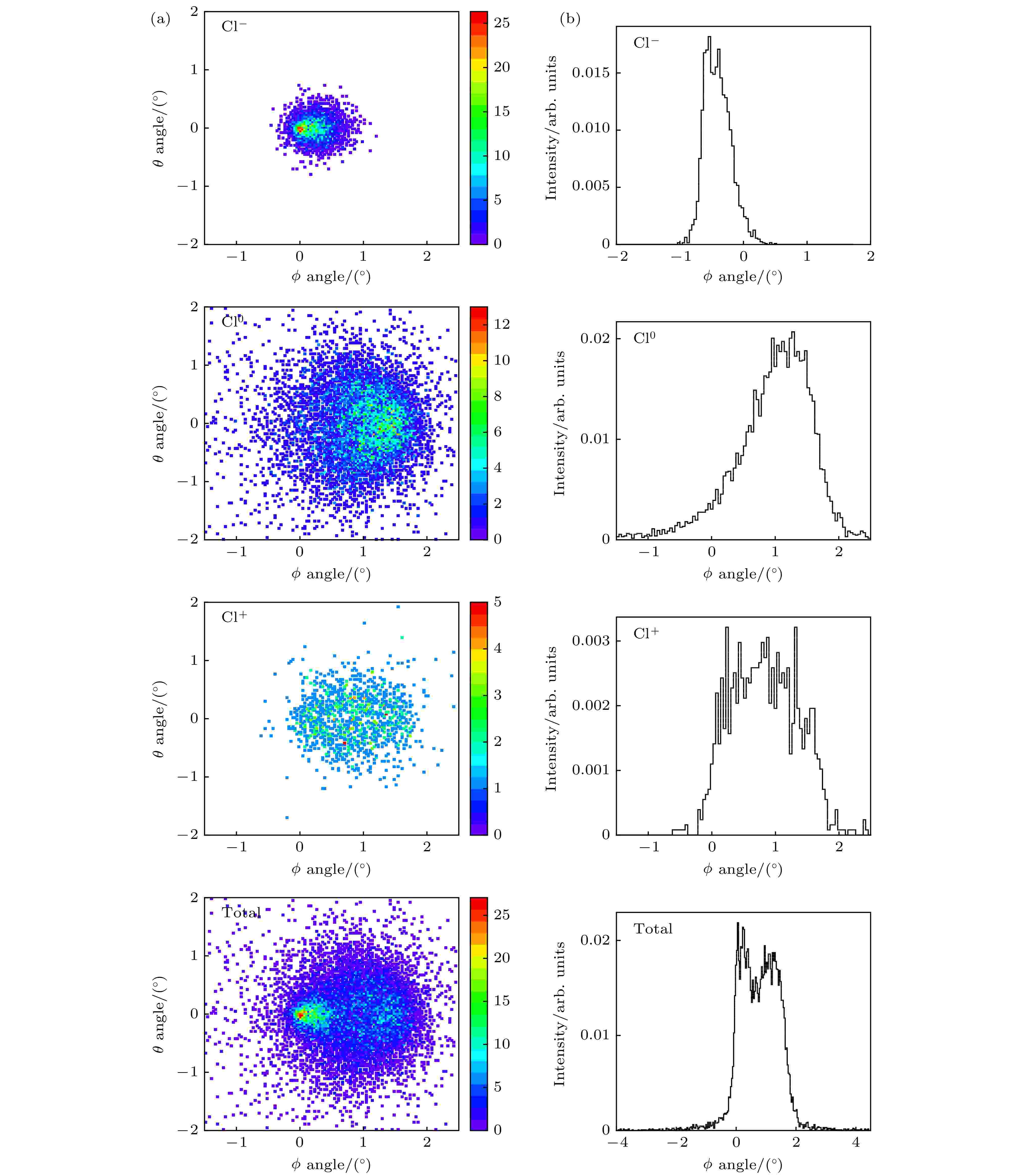图 11 模拟计算的倾角为1.2°时出射的不同电荷态粒子的二维角分布(a)及对应的投影角分布(b)
Figure11. Two dimensional transmitted angular distributions (a) and corresponding projections (b) of various charge states at tilt angle of 1.2° from simulations.

然后在1.2°下, 在经不同散射次数出射的Cl⁰的二维分布图景(图12(a))及对应的投影角分布 (图12(b)) 中. 发现经一次散射出射的Cl⁰出射方向以微孔轴向为中心; 经两次碰撞出射Cl⁰出射方向以1.0°为中心. 并且经不同散射次数出射的Cl⁰角分布在0°方向上都相对展宽较大.
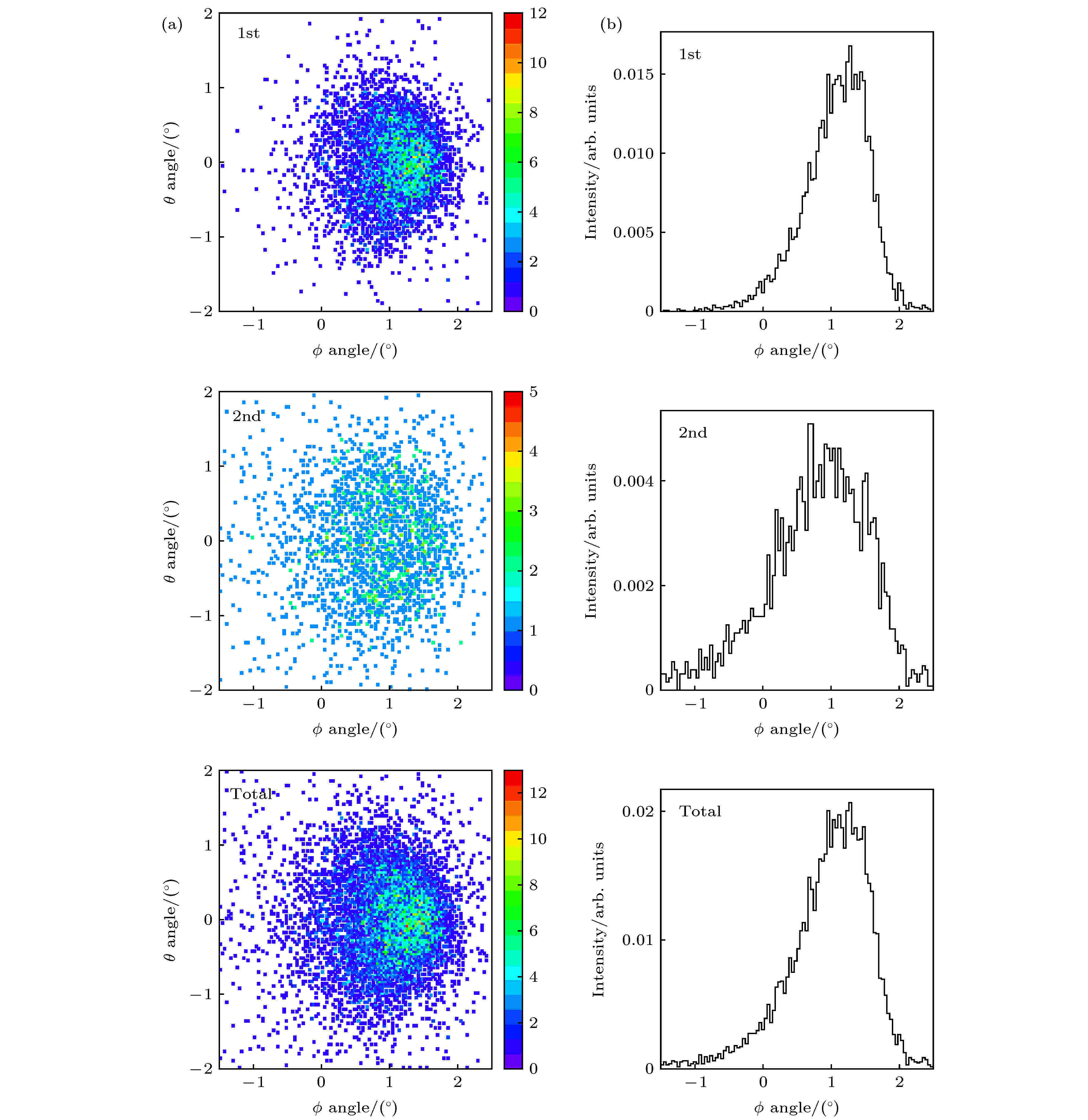图 12 模拟计算出的倾角为1.2°时经不同散射次数出射的Cl⁰二维角分布(a)及对应的投影角分布(b)
Figure12. (a) Two-dimensional transmitted angular distributions and (b) corresponding projections of transmitted Cl⁰ exited from the capillaries by single scattering and double scattering and the total of them at tilt angle of 1.2° from simulations.

计算出的Cl⁺与Cl⁰比例如图7所示, 计算的电荷比例随倾角变化的趋势与实验符合很好, 计算值略高于实验值. 不同倾角下的Cl^–, Cl⁰, Cl⁺所占比例如图13所示, 计算中不同电荷态所占的比例随倾角的变化趋势与实验结果基本相同. 出射的Cl^–穿透过程主要为几何穿透, 其所占比例随倾角增大而减小. 出射的Cl⁰和Cl⁺主要经微孔表面近距离碰撞出射, 其所占比例随倾角增大而增大. 从图13可以看出Cl⁰比Cl^–随倾角增长的快得多, 根据Al₂O₃的禁带宽度^[29], Cl^–转化为Cl⁰的概率要大很多. 而且在多次碰撞过程中, Cl⁰基本维持其电荷态不变, 而Cl⁺有很大概率转化为Cl⁰. 通过分析不同角度下经不同碰撞次数出射的Cl⁰比例, 得到了如图14所示的比例图, 发现随倾角增加, 经一次散射出射的Cl⁰比例基本不变, 而经多次碰撞出射的Cl⁰比例增大. 这是由于Cl⁺多为一次近距离碰撞出射, 多次碰撞很大概率转化为Cl⁰.
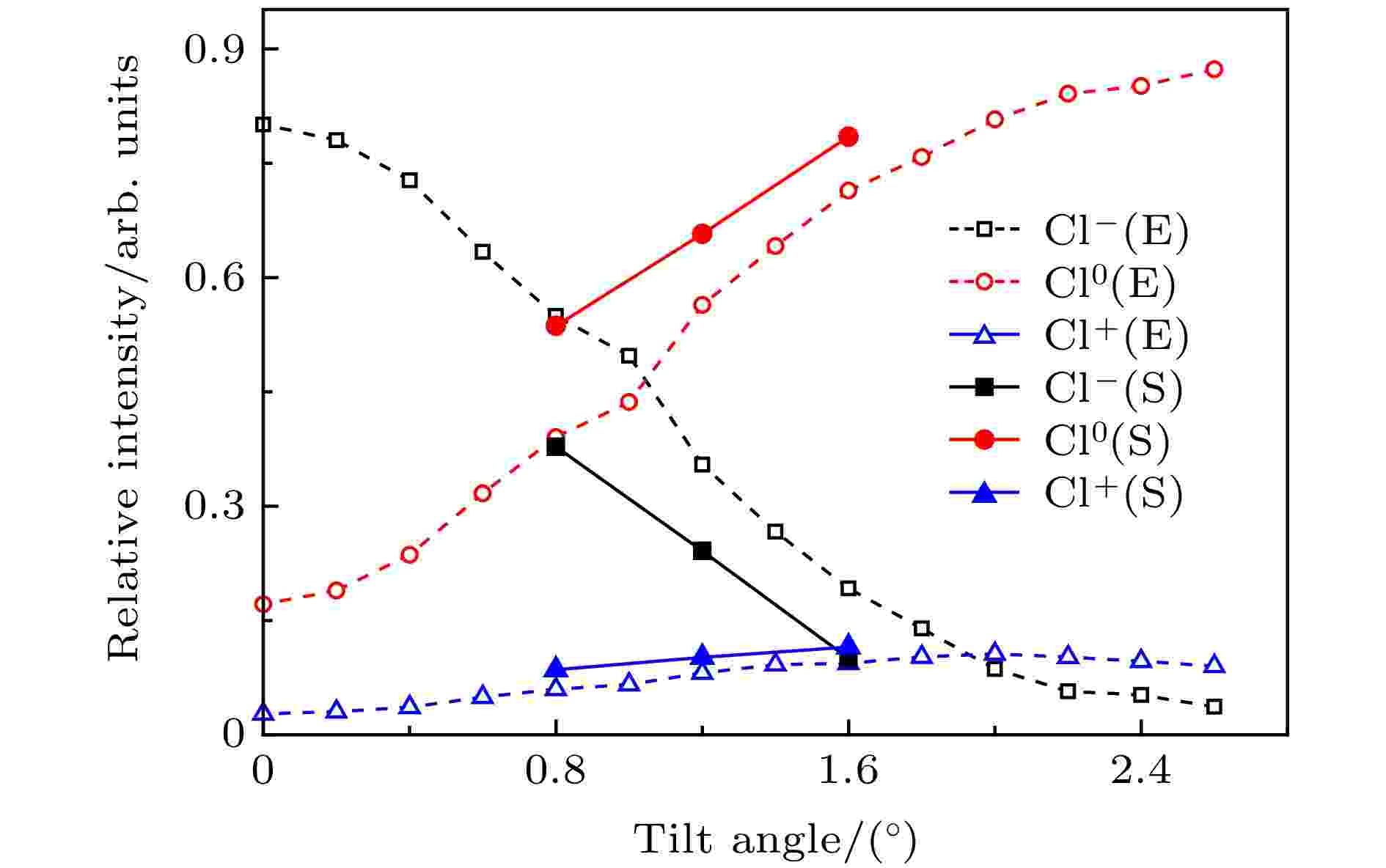图 13 出射粒子中不同电荷态所占比例随倾角的变化(E代表实验结果, S代表计算结果)
Figure13. Portions of various charge states in transmitted projectiles as a function of the tilt angle. E and S stand for the results from experiments and simulations, respectively.

图 14 模拟计算的不同角度0.8°, 1.2°, 1.6°下经过不同碰撞次数的出射的Cl⁰比例(黑色条形是经一次碰撞出射的, 红色条形是经两次散射出射的, 蓝色条形是经三次碰撞出射的)
Figure14. Portions of transmitted Cl⁰ for various scattering at the tilt angle of 0.8°, 1.2°, 1.6°. The black bars stand for single scattering, the red bars for double scattering, and the blue bars for those scattered three times from simulations.

本文结合实验和理论模拟研究了Cl^–离子在绝缘纳米微孔膜中的输运机制, 通过研究沉积电荷对出射粒子的影响以及随微孔膜倾角变化导致的不同散射过程对电荷交换和角分布的影响, 发现穿越的Cl^–离子穿透率下降与倾角变化一致, 穿透角分布沿初束方向分布, 为几何穿透结果; 而通过与微孔内表面的近距离碰撞出去的Cl⁰和Cl⁺经过一次或者多次散射出射, 其中经一次碰撞出射的粒子占主要成分, 出射角度与微孔膜倾角一致. 发现10 keV以上能区的Cl^–离子在穿越绝缘体微孔膜的过程中主要通过近距离碰撞作用散射射出, 沉积电荷对出射粒子末态并未起到明显作用.