摘要:介质阻挡放电被众多工业领域用作低温等离子体源, 柱状放电是介质阻挡放电的重要形式之一, 但其放电理论尚未掌握. 进行大气压氦气介质阻挡放电实验, 通过降低外施电压低于起始放电电压实现了柱状放电从单柱到多柱的斑图演化, 拍摄了电极底面放电图像, 测量了外施电压、放电电流、放电转移电荷、放电柱的柱直径和柱间距, 计算了放电柱受其他所有柱施加的库仑力与磁场力. 结果表明: 外施电压变化瞬间电极底面放电图像呈现出动态演化过程. 不同层放电柱的柱直径由中心向外层依次增大. 计算发现演化稳定后放电柱所受库仑力远大于磁场力, 推理存在一约束势平衡库仑力使放电柱稳定分布. 不同电压、位置的放电柱所受库仑力不同: 不同层的放电柱所受库仑力由最外层至中心柱依次减小, 中心柱受力为0, 最外层放电柱的约束势应最大而中心放电柱的约束势应该最小; 外施电压降低, 介质表面电荷和放电柱总数的共同作用导致库仑力增大, 约束势也应有所增大, 即约束势受介质表面电荷、放电柱总数与位置的共同影响.
关键词: 柱状斑图放电/
时空演化/
库仑力/
约束势

English Abstract

全文HTML

--> --> -->

介质阻挡放电(dielectric barrier discharge, DBD)是一种将绝缘介质插入放电空间的气体放电形式^[1], 常压下可以产生体积大、能量密度高的低温等离子体, 20世纪80年代以来, DBD被广泛应用于材料处理^[2]、环境治理^[3-5]、臭氧制备^[6]及生物医学^[4]等方面.
DBD涉及复杂的物理变化和化学反应, 存在复杂多变的时空非线性行为. 在不同放电条件下(电压峰值、工作气体、气体压强以及气隙距离等), DBD呈现出不同放电模式和特性^[1]. 交流电压激励下, 平板电极DBD常表现为丝状放电^[6]、均匀放电^[7,8]和斑图放电^[6,9]三种放电形式.
斑图放电(patterned discharge)是用介质阻挡电极产生斑图的气体放电形式, 常见的斑图主要有丝状(放电丝)^[10-12]、柱状(放电柱)^[13,14]、条形^[15]、螺旋^[16]等. 其中, 丝状斑图与柱状斑图的放电机理不同^[14,17], 但两种形式在一定的条件下均可稳定规律地排列在电极表面, 甚至呈现单点^[17,18]、同心圆^[13,16]、六边形^[9,16,19]等相同的空间自组织排列, 因此DBD斑图动力学行为研究中, 两种斑图形式可相互借鉴.
近年来, 国内外对斑图放电的形成机制、运动分析等斑图动力学行为做了大量研究, 发现在平板电极DBD系统中, 放电丝表现出类似粒子的行为^{[12,16,18,20]}, 为研究柱状斑图放电中柱间相互作用提供了参考.
有研究****推理存在外部约束势来平衡放电柱间的作用力. 2003年Radu等^[14]实验观察了不同频率、气隙宽度下放电柱的空间分布, 拍摄曝光时间1 s的放电图像, 计算氩气在8 kHz电压0.6 mm气隙宽度时相邻放电柱间的库仑力与磁场力, 发现库仑力远大于磁场力, 并将放电区域与“二维库仑模型”类比, 认为存在一种外部约束势来平衡库仑力. 2012年Dong等^[10]在空气-氦气混合气体中进行大气压DBD实验, 外施电压增加到一定值时, 放电丝的径向分布出现扭曲变形, 通过放电丝受力分析, 推断放电区域存在受外施电压影响的约束势影响了放电丝空间分布. 但这一外部约束势的影响因素还未进一步研究.
有****研究了影响放电斑图分布的主要因素. 2003年Shirafuji等^[20]实验发现外施电压升高过程中放电从一个丝变为6个丝呈环状分布的过程, 其分布并非1994年Bedanov和Peeters^[21]提出的1 + 5两层分布, 他们认为ITO涂层不均匀使放电间隙电场十分复杂, 约束势分布偏离纯抛物线类型, 从而导致了放电丝环状分布. 2012年Boeuf等^[22]用流体模型模拟了100个周期内放电丝的演化过程, 发现在复杂的自组织静态或动态结构的斑图中, 同一半周期产生的低电流的“侧放电”对周围放电丝的产生、消失和运动起着至关重要的作用. 2016年Mukaigawa等^[12]进行外施电压和阻挡介质厚度实验, 测量了放电丝的直径与间隔距离, 认为介质等效电容影响放电丝的间距. 2018年Hao等^[13]实验发现了外施电压由起始放电电压降低的过程中, 由均匀放电到单柱放电再到多柱斑图最后到局部均匀放电的演化现象. 对于柱状斑图分布的动态演化过程有待研究, 其形成机制仍有待得到科学的解释.
本文进行大气压氦气DBD实验, 降低外施电压实现柱状放电的单柱到多柱的斑图演化, 通过拍摄电极底面放电图像, 测量外施电压、放电柱的柱直径和柱间距, 计算放电电流峰值时刻放电柱的受力, 探讨外施电压由起始电压降低时柱状放电斑图的分布特性、动态演化过程和形成机制.

2

-->

2.1.放电柱间的库仑力

由于平板电极纵横比较大, 气体放电空间可以认为是准二维的, 放电柱可认为是准粒子, 具有“粒子”特性. 通过放电柱转移的电荷在介质表面存在累积作用, 且电流的相位会影响介质表面电荷的极性, 又因电荷在绝缘体表面迁移速度慢, 放电转移电荷被限定在放电柱的位置^[20], 不同放电柱的放电转移电荷极性相同, 产生相互排斥的库仑力. DBD中两放电单柱放电转移电荷间的库仑力可根据(1)式^[20]计算:

${{{F}}_Q}\left( {i,j} \right) = \frac{1}{{4{\text{π}}{\varepsilon _0}}}\frac{{{Q^2}}}{{{{\left| {{{{r}}_i} - {{{r}}_j}} \right|}^3}}}\left( {{{{r}}_i} - {{{r}}_j}} \right), $

其中, ${{{r}}_i}$, ${{{r}}_j}$为两放电单柱i, j中心的空间位置, ε₀为真空介电常数, ε₀ = 8.854188 × 10^–12 F/m, Q为放电阶段的每个放电柱转移的电荷, 为简便起见由介质表面电荷Q_d的绝对值按柱数平均分计算得到. 其中, Q_d根据图1等效电路^[19]由下列公式得到^[23]:
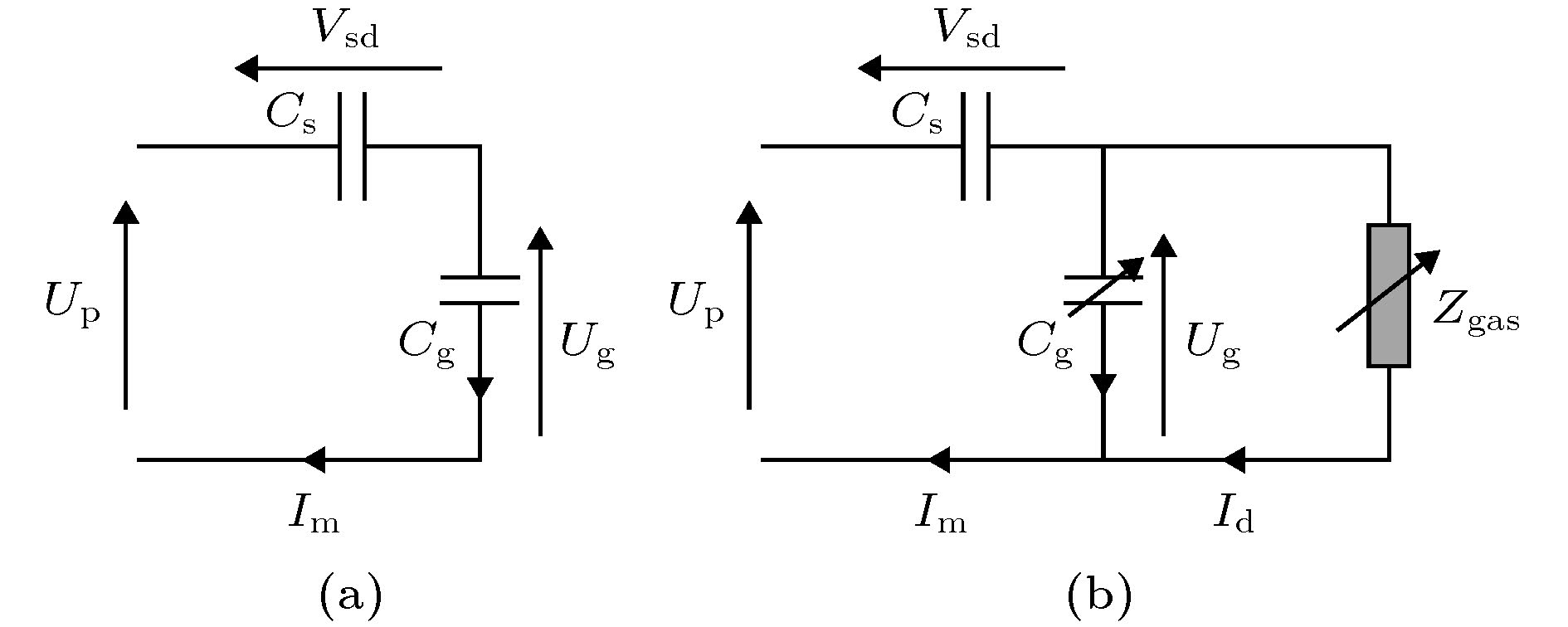图 1 DBD等效电路　(a)未放电阶段; (b)放电阶段
Figure1. The simplified electrical equivalent circuit: (a) Non-discharge; (b) discharges.

${U_{\rm{g}}}\left( t \right) = {U_{\rm{p}}}\left( t \right) - \frac{1}{{{C_{\rm{s}}}}}\int {{I_{\rm{m}}}\left( t \right)} \cdot {\rm{d}}t, $

${I_{\rm{d}}}\left( t \right) = {I_{\rm{m}}}\left( t \right) - {I_g}{\rm{ = }}{I_{\rm{m}}}\left( t \right) - {C_{\rm{g}}}\frac{{{\rm{d}}{U_{\rm{g}}}\left( t \right)}}{{{\rm{d}}t}}, $

${Q_{\rm{d}}}\left( t \right) = - \int {{I_{\rm{d}}}\left( t \right) \cdot {\rm{d}}t} + Q\left( {{t_0}} \right), $

式中, U_p是外施电压, C_s是阻挡介质等效电容, C_g是气隙等效电容, I_m是回路电流, 由电容电流I_g = C_gdU_g/dt和气隙放电电流I_d组成, 其中C_s由定义式^[24]求得, C_g是测量Lissajous图求得电极间总等效电容C后, 结合放电间隙的简化电路图, 通过电容的串联关系求得的^[25], Q(t₀)为介表电荷初始值, 负号是因为Q产生的电场与U_p产生的电场方向相反.
2 -->

2.2.放电柱间的磁场力

为实现放电柱的稳定分布, 放电柱之间必须存在对应的吸引作用, 来平衡库仑力的斥力. 电流的周围存在磁场, 相邻放电柱同一时刻电流方向一致, 电流产生的磁场力F_I是一种相互吸引的力, 可用(5)式计算^[14]: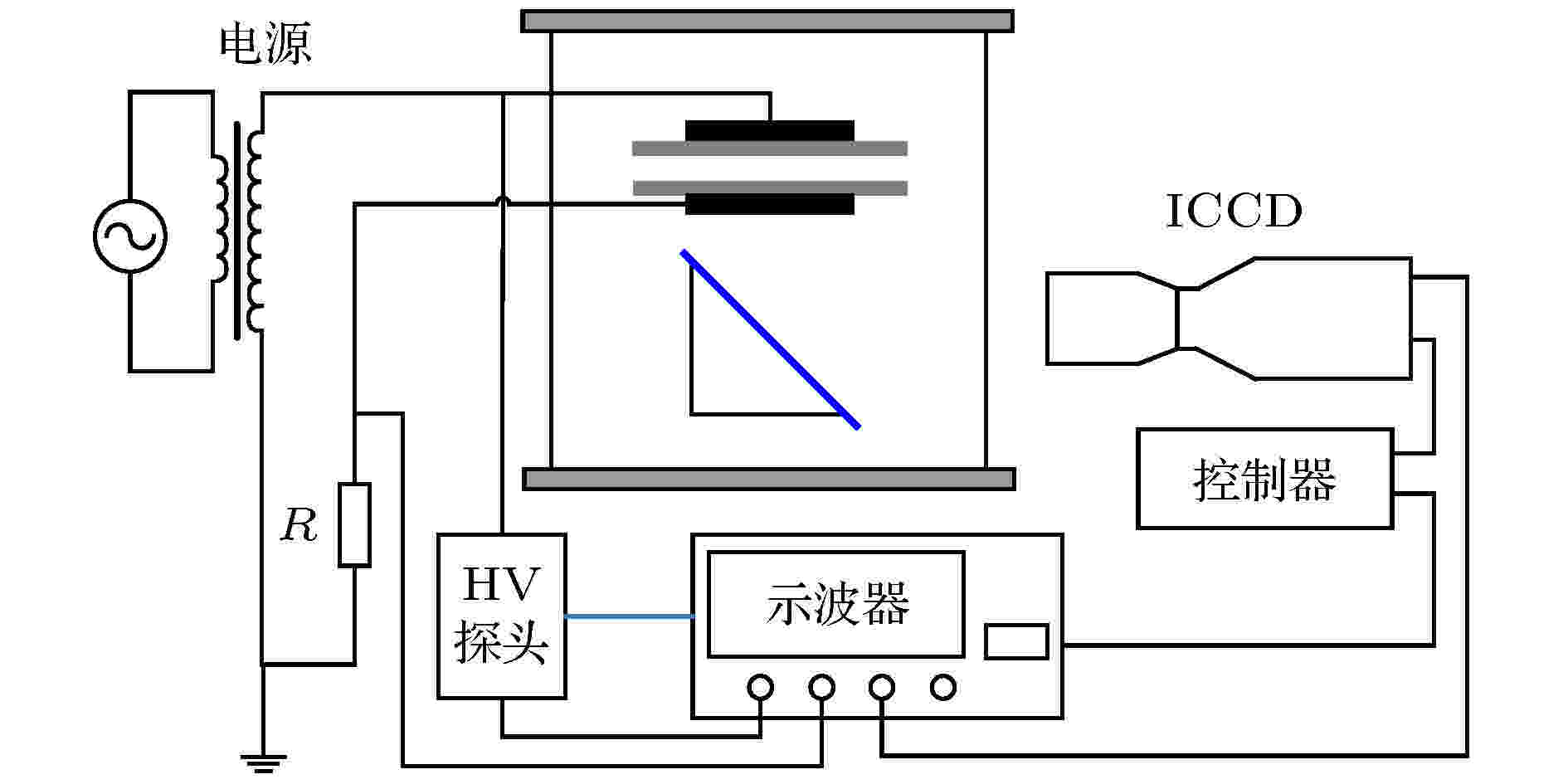

${{{F}}_{\rm{I}}}\left( {i,j} \right) = \frac{{{\mu _0}}}{{2{\text{π}}}}\frac{{I_{}^{^2}h}}{{{{\left| {{{r}} - {{{r}}_j}} \right|}^2}}}\left( {{{{r}}_i} - {{{r}}_j}} \right), $

式中, h为气体间隙宽度; I为放电单柱的电流, 为简便起见根据放电电流I_d平均分到每个放电柱计算得到; μ₀为真空磁导率, μ₀ = 4π × 10^–7 N/A².

DBD实验装置如图2所示. 电源输出电压频率为3—47 kHz、峰值为0—30 kV连续可调的正弦波. 工作时用真空机组将不锈钢放电室内空气排出达准真空状态, 再充入工作气体. 平行板电极放置于放电室内, 上电极为直径为60 mm的圆形铝电极, 表面覆盖100 mm × 100 mm × 1.4 mm的石英玻璃; 下电极通过下表面涂铟锡化物(indium-tin oxide, ITO)的100 mm × 100 mm × 1.1 mm石英玻璃与直径为60 mm的环形铜电极相互胶合构成. 环形电极下面安装一个与水平呈45°角的平面镜, 方便观察电极底面放电分布情况.
图 2 大气压DBD实验装置示意图
Figure2. Schematic diagram of experimental set-up for DBDs at atmospheric pressure.

外施电压U_p由高压探头(Tektronix P6015A, 分压比为1000∶1)测得, 回路电流通过放电回路串联的50 Ω的无感电阻R获得. 电阻的电流信号由数字示波器(Tektronix DPO4104, 采样频率为5 G/s)获得. 测量的Lissajous图形通过将电极两端外施电压U_p和测量电容两端电压U_c分别加在示波器的X轴和Y轴获得. 底部放电图像由ICCD相机(PI–MAX2, 像素为1024 × 1024, 最短曝光时间为2 ns)设置50 ns的曝光时间拍摄获得.

本文放电气体间隙为3 mm, 放电室空气抽至40 Pa后, 充入纯度为99.99%的氦气至1 atm ($ \rm 1~atm \!=\! 1.01\! \times\! 10^5\;Pa $). 外施电压频率为11.41 kHz.
2

-->

4.1.柱状斑图演化现象

3 -->

4.1.1.柱状斑图随外施电压的演化现象

外施电压峰值U_ps达2.34 kV时放电起始, 为覆盖整个电极的均匀放电. 此后不断降低U_ps出现了多种斑图的演化, 由布满整个电极的均匀放电过渡到2.23 kV的单柱放电, 再到2.22 kV的1 + 7两层多柱放电, 2.19 kV的1 + 6 + 12三层多柱放电, 2.14 kV的柱 + 均匀混沌放电, 最后到1.99 kV的局部均匀放电^[19], 外施电压与放电形式的关系见图3. 不同U_ps下放电电流峰值时刻的放电底部图像见图4.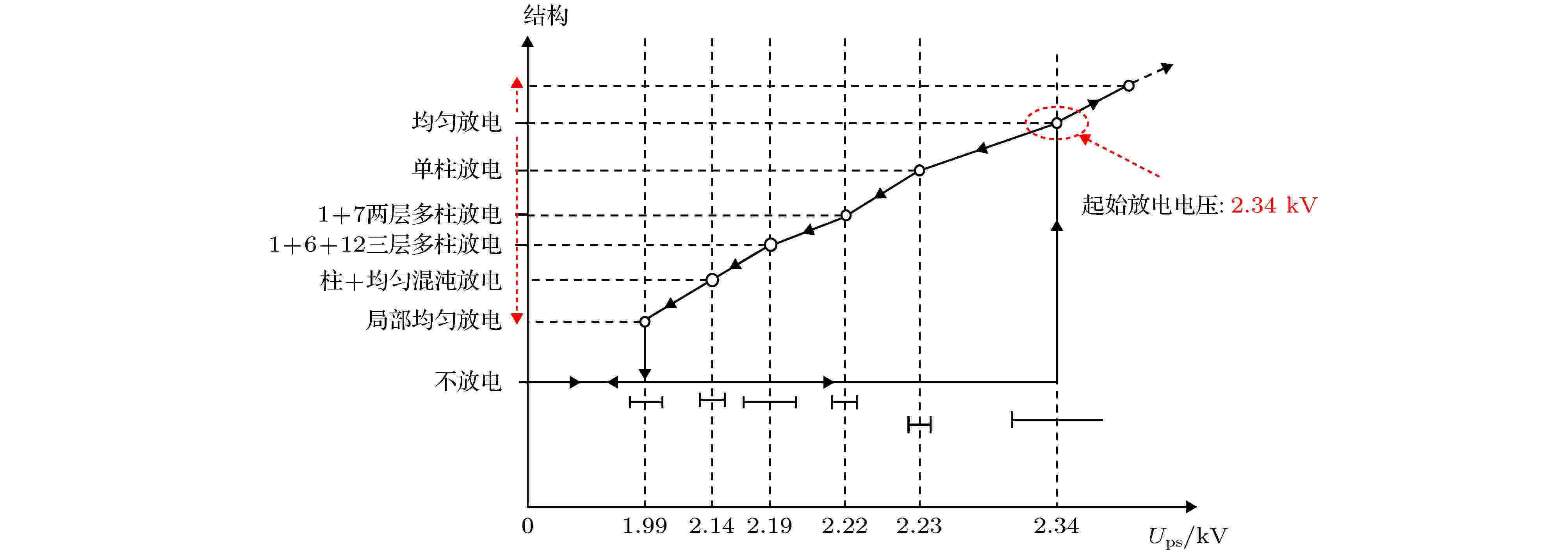
图 3 不同外施电压峰值下电极底面放电形式转化
Figure3. Evolution of end-view discharge under different U_ps.

图 4 不同外施电压下电极底面放电图像　(a) 2.34 kV; (b) 2.23 kV; (c) 2.22 kV; (d) 2.19 kV; (e) 2.14 kV; (f) 1.99 kV
Figure4. End-view discharge images under different U_ps: (a) 2.34 kV; (b) 2.23 kV; (c) 2.22 kV; (d) 2.19 kV; (e) 2.14 kV; (f) 1.99 kV.

3 -->

4.1.2.单柱到多柱动态演化过程

用60 fps普通相机拍摄了外施电压由2.23 kV瞬间降至2.22 kV放电由单柱变为1 + 7两层多柱的过程, 见图5的左列. 照片时间间隔为1/60 s =0.017 s, 用Matlab软件提取放电底面发光灰度值绘出光强径向分布, 见图5的右列. 把外施电压从2.23 kV降低至2.22 kV的时刻记为t = 0, 如图5(a)所示, 则呈稳定的1 + 7两层多柱放电的时刻t = 0.083 s, 如图5(f)所示.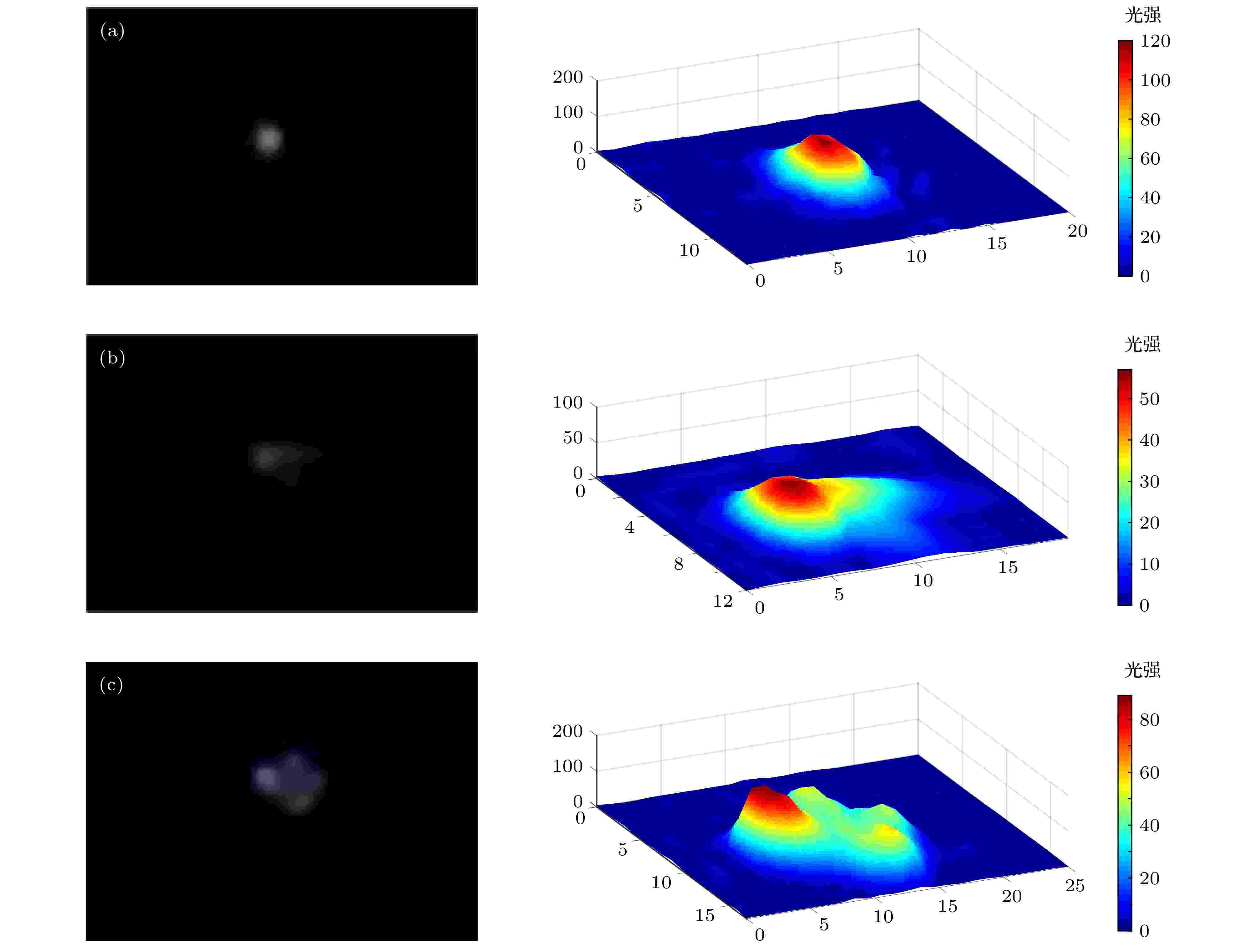


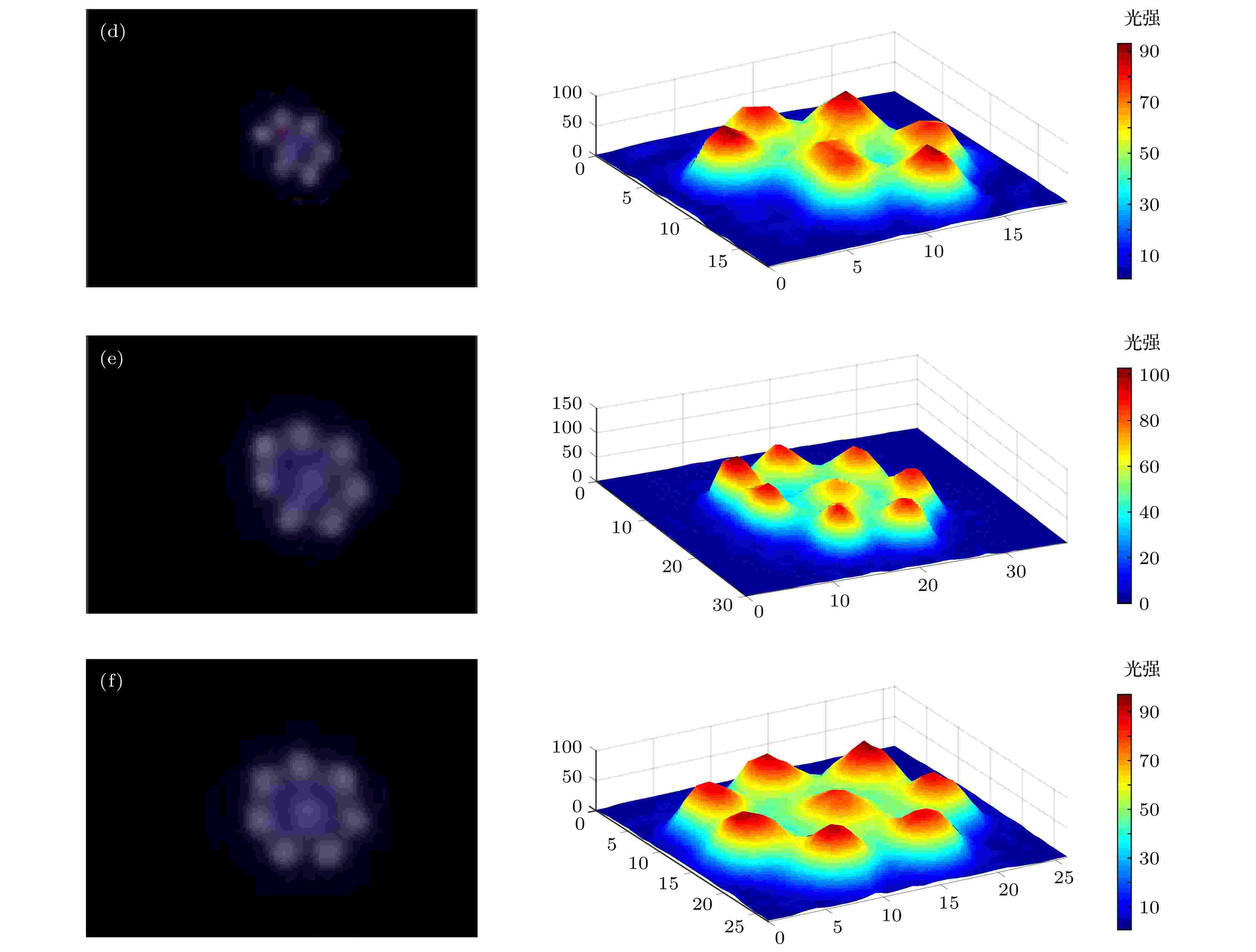图 5 外施电压峰值由2.23 kV降至2.22 kV过程中放电形式的径向演化与光强分布　(a) t = 0, U_ps = 2.23 kV → 2.22 kV; (b) t = 0.017 s; (c) t = 0.033 s; (d) t = 0.050 s; (e) t = 0.067 s; (f) t = 0.083 s
Figure5. Radial evolution of discharge pattern when U_ps reduce from 2.23 kV to 2.22 kV: (a) t = 0, Ups = 2.23 kV → 2.22 kV; (b) t = 0.017 s; (c) t = 0.033 s; (d) t = 0.050 s; (e) t = 0.067 s; (f) t = 0.083 s.

U_ps = 2.23 kV时为单柱放电, 见图5(a). 此时将U_ps迅速降低至2.22 kV, 外施电压仅为10 V的微小变化打破了单柱的平衡状态, 单柱右侧出现径向长度约为1.5 mm的新放电区, 见图5(b). 新放电区逐渐独立于原单柱, 好像逐渐分裂为3个放电较弱的“侧柱”, 见图5(c). 这3个侧柱与原单柱没有形成平衡状态, 位置不稳定, 相对于原单柱位置不断改变, 发光强度增大, 原单柱周围其余区域开始出现2—3个新柱, 如图5(d)所示. 由此可见, 新柱出现的时间并不相同, 它们围绕原放电单柱先后出现并形成7个清晰独立的柱, 见图5(e). 新柱的位置围绕原放电单柱不断调整, 最终达到平衡状态, 形成1 + 7两层多柱放电形式, 见图5(f).
2 -->

4.2.放电柱空间分布

用软件image j标出图4(a)放电区域, 根据电极直径为60 mm, 计算得到实际尺寸与图像尺寸的比例. 保持放电电极与图像拍摄位置的距离不变, 该比例可以用于柱状放电图像的尺寸计算. 测量图4(b)—(d)中放电柱的直径与间距, 根据图像尺寸比例计算实际的柱直径d和柱间距l.
由中心柱依次向外, 每层的柱直径依次为d₁, d₂, d₃, ···, d_x, x层的每个柱直径依次为d_xn, 其中n为x层放电柱的个数. 相邻层的柱间距依次为l_12n, l_23n, ···, l_xyn. 单柱放电、1 + 7两层多柱放电、1 + 6 + 12三层多柱放电形式的柱直径d_xn、柱间距l_xyn及平均值AVE、方差D见表1.

	Ups = 2.23 kV		Ups = 2.22 kV				Ups = 2.19 kV
n	d1n/mm		d1n/mm	d2n/mm	l12n/mm		d1n/mm	d2n/mm	l12n/mm	d3n/mm	l23n/mm
1	2.21		3.10	3.59	4.33		3.21	3.42	4.21	3.69	4.03
2	—		—	3.50	4.28		—	3.31	3.88	3.43	4.54
3	—		—	3.29	4.29		—	3.36	4.25	3.65	3.83
4	—		—	3.36	4.55		—	3.45	4.18	3.57	4.47
5	—		—	3.37	4.25		—	3.58	4.26	3.59	3.83
6	—		—	3.65	4.22		—	3.40	4.14	3.58	4.44
7	—		—	3.45	4.26		—	—	—	3.59	3.85
8	—		—	—	—		—	—	—	3.83	4.38
9	—		—	—	—		—	—	—	3.81	4.01
10	—		—	—	—		—	—	—	3.42	4.27
11	—		—	—	—		—	—	—	3.41	4.05
12	—		—	—	—		—	—	—	3.69	4.30
AVE	2.21		3.10	3.45	4.31		3.21	3.42	4.15	3.61	4.17
D	0		0	1.69%	1.22%		0	0.85%	1.99%	1.94%	6.94%

表1单柱放电(2.23 kV)、1 + 7两层多柱放电(2.22 kV)、1 + 6 + 12三层多柱放电(2.19 kV)的柱直径、柱间距
Table1.Diameters and spacing of discharge columns in single-column discharge (2.23 kV), two layers columnar discharge (2.22 kV), and three layers columnar discharge (2.19 kV).

由表1可知, 各层柱直径的方差均在2%以内, 除l₂₃外柱间距的方差均在2%以内, 各层的柱直径d和柱间距l可取其平均值表征. 当U_ps = 2.19 kV, 放电为1 + 6 + 12三层多柱呈正六边形分布时, 中心柱与中间层柱的柱间距l₁₂ = 4.15 mm和中间层与最外层的柱间距l₂₃ = 4.17 mm仅相差0.02 mm, 小于0.5%, 严格对称分布. 相同外施电压下不同层放电柱的柱直径由内向外依次增大, 外施电压降低中心柱的直径逐渐增加, 而中心柱与邻柱的柱间距减小.
2 -->

4.3.放电柱受力分析

本文对图4(c) 1 + 7两层多柱放电、图4(d) 1 + 6 + 12三层多柱放电计算了正半周期放电电流峰值时刻放电柱所受库仑力及放电柱间的磁场力.
由4.2节可知放电柱的直径与间距分散性很小, 可用平均值表征. 对图4(c), 位于同层的放电柱直径相同, 且均匀分布在以中心柱为圆心、柱间距为半径的圆上, 其受力分析见图6. 图6中Q₁为中心柱, 显然, 在放电柱受力分析中, Q₁所受的库仑力与磁场力均为零, 只需对其他柱进行受力分析. 因放电斑图分布呈中心对称, 其他柱Q_S, Q₂₂, Q₂₃, ···, Q₂₆的受力分析是相同的, 不失一般性, 图6中以Q_S柱为例.
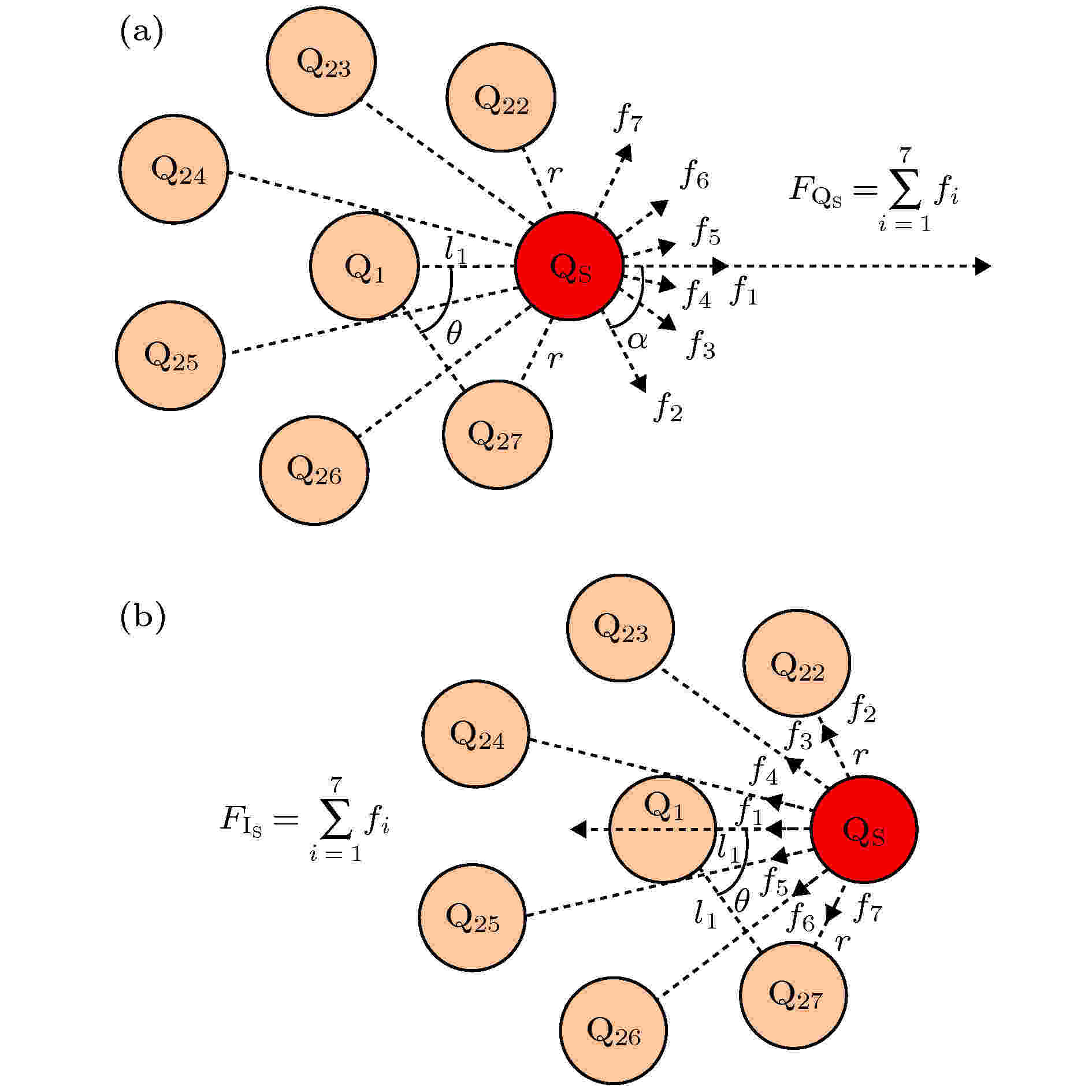图 6 1 + 7两层多柱放电中外层放电柱受力分析　(a)库仑力; (b)磁场力
Figure6. Force analysis diagram of discharge column of two layers distribution: (a) Coulomb force; (b) magnetic field force.

图6中外层两相邻柱与内层中心柱的中心所呈夹角∠Q_SQ₁Q₂₇为θ, Q₁Q_S延长线与Q₂₂Q_S延长线间的夹角为α, 同层邻柱的间距为r. 由对称性可知, θ = 360°/7, 并可由此计算出α和r的值. Q_S柱的库仑力和磁场力分析可以分别见图6(a)和(b). Q_S柱所受库仑力的大小用|F_Qs|表示, 方向与Q₁Q_S一致, 所受磁场力的大小用|F_Qs|表示, 方向与Q₁Q_S相反.
由图6可知库仑力与磁场力分析方法相同, 二者大小不同方向相反, 所以仅给出图4(d)的库仑力受力分析, 见图7. 对图4(d), 同层的放电柱直径相同, 且均匀分布在以中心放电柱为中心的正六边形顶点或边长中点上, 任意相邻三放电柱构成的锐角三角形均为正三角形, 图7中θ = α = 60°. 由表1可知l₁₂, l₂₃相等, r与l均取l₁₂, l₂₃的平均值4.16 mm.
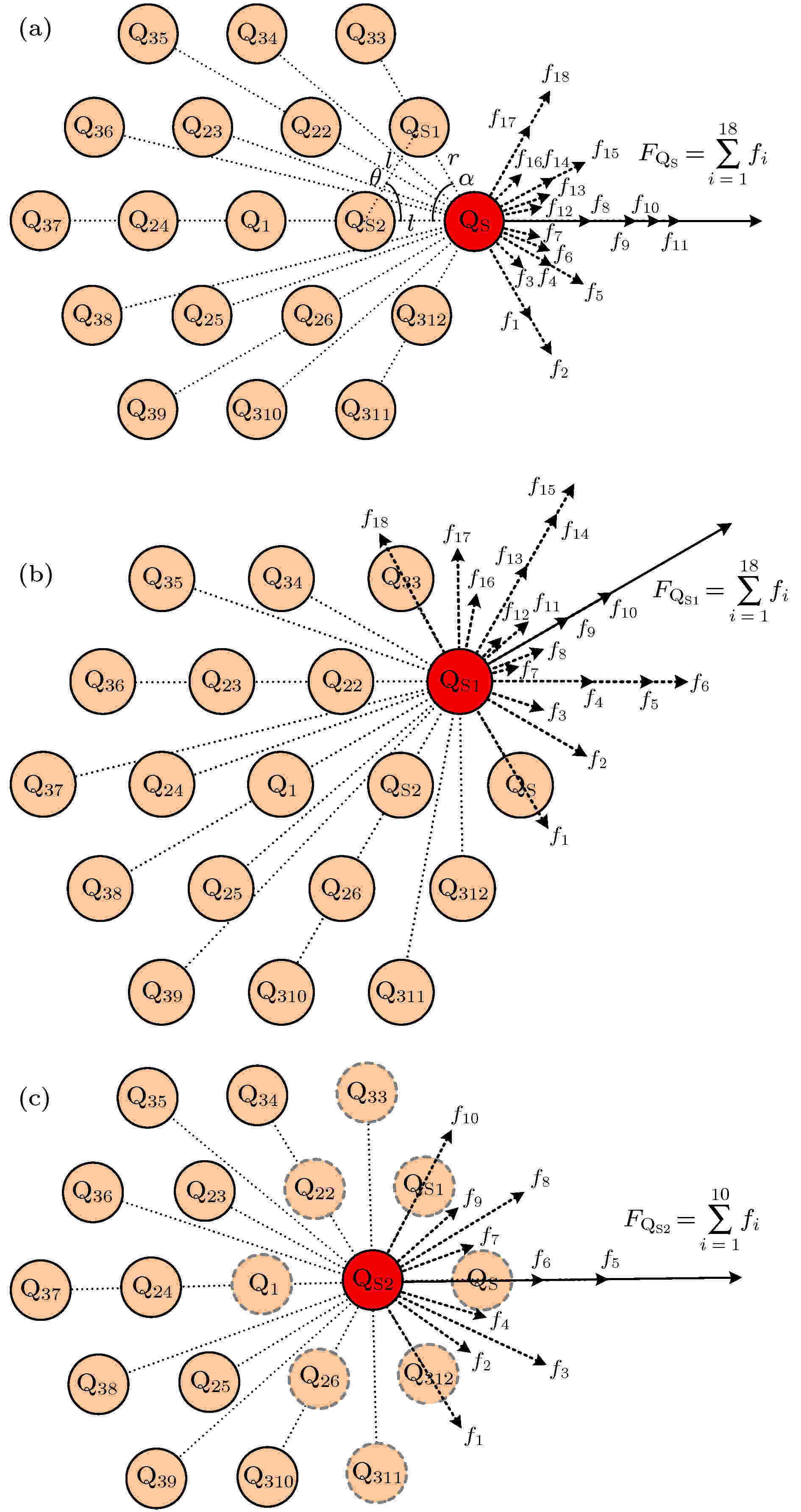图 7 1 + 6 + 12三层多柱放电中三类放电柱的库仑力分析　(a) Q_S; (b) Q_S1; (c) Q_S2
Figure7. Coulomb force analysis diagram of discharge column of 3 layers hexagon distribution: (a) Q_S; (b) Q_S1; (c) Q_S2.

显然, 中心柱Q₁所受的库仑力与磁场力均为0. 根据上述放电柱分布特点, 其他柱分为外层顶点柱Q_S、外层边长中点柱Q_S1、中层柱Q_S2三类, 库仑力受力分析分别见图7(a)—(c). 库仑力的大小用|F_Qs|表示. 对中层柱Q_S2, 发现柱Q_S2周围的柱(Q₁与Q_S、Q₂₂与Q₃₁₂、Q₃₃与Q₃₁₁、Q_S1与Q₂₆)产生的作用力两两抵消, 即Q_S2所受的库仑力和磁场力仅来自其余10个柱.
在1 + 7两层多柱放电、1 + 6 + 12三层多柱放电时的外施电压、回路电流^[19]基础上, 通过(2)式—(4)式求得放电电流、放电转移电荷波形, 如图8所示. 选取图4(c)和(d)对应时刻的放电电流和放电转移电荷的值, 并用(1)式、(5)式分别计算图6、图7中不同位置放电柱所受的库仑力与磁场力大小, 计算参数见表2, 结果见表3.

Ups/kV	θ/(°)	α/(°)	r/mm	l/mm	h/mm	用于计算FQ			用于计算FI
						Qd/nC	Q/nC		Id/mA	I/mA
2.22	51.43	64.29	3.74	4.31	3	0.12	0.015		2.95	0.37
2.19	60	60	4.16	4.16	3	0.31	0.016		5.40	0.28

表21 + 7两层多柱放电(2.22 kV)、1 + 6 + 12三层多柱放电(2.19 kV)的放电柱受力分析参数
Table2.Parameters used when calculating Lorentz force and Coulomb force under two layers columnar discharge (2.22 kV) and three layers columnar discharge (2.19 kV).

Ups/kV		FQ/10–7 N				FI/10–14 N
2.22		4.01				7.01
2.19		QS	QS1	QS2		QS	QS1	QS2
		5.35	4.82	2.25		4.69	4.22	1.97

表31 + 7两层多柱放电(2.22 kV)、1 + 6 + 12三层多柱放电(2.19 kV)的柱间库仑力与磁场力
Table3.Coulomb force and Lorentz force of discharge columns under two layers columnar discharge (2.22 kV) and three layers columnar discharge (2.19 kV).

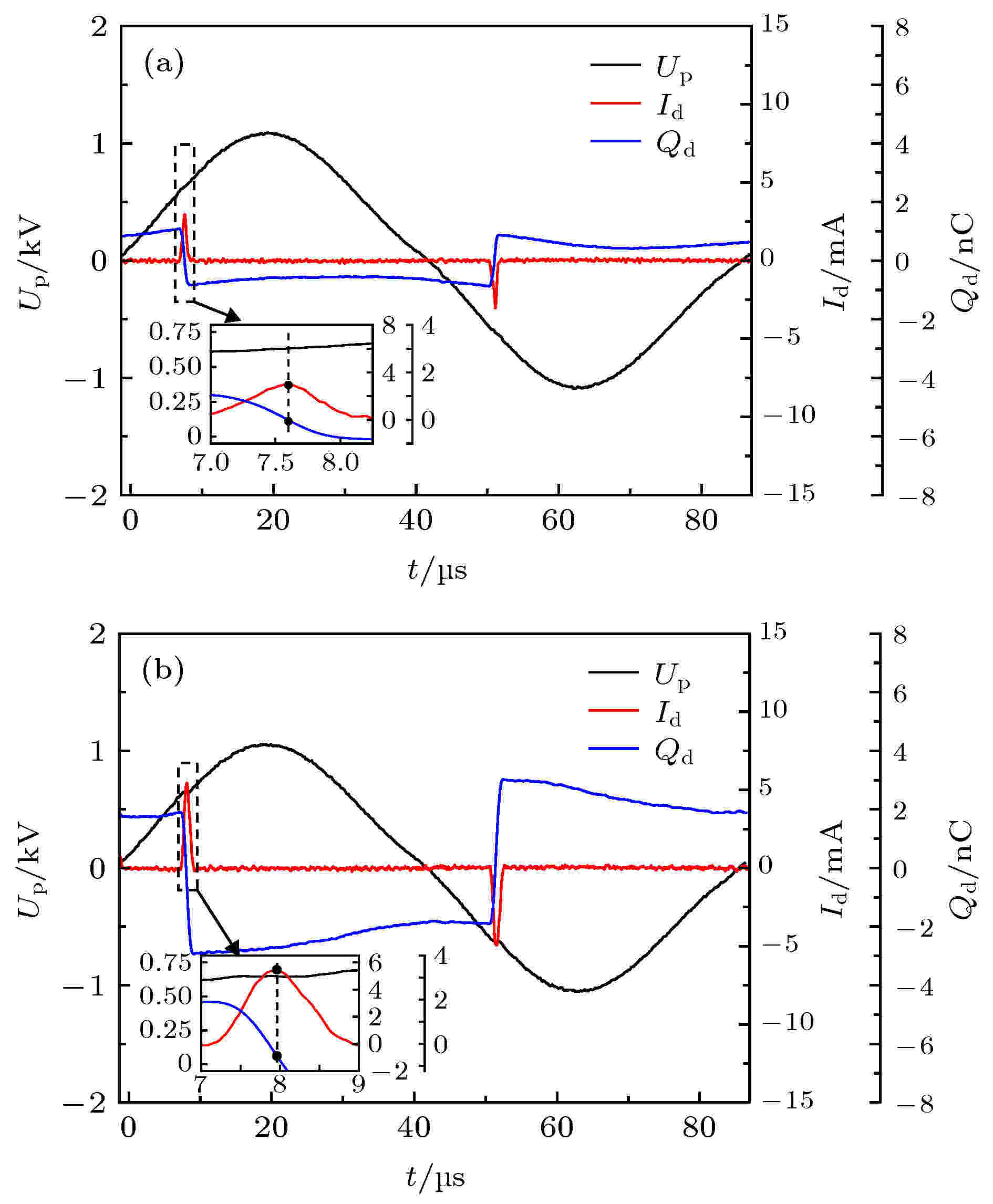图 8 1 + 7两层多柱放电(2.22 kV)、1 + 6 + 12三层多柱放电(2.19 kV)外施电压、放电电流、放电转移电荷波形(a) 2.22 kV; (b) 2.19 kV. 内插图为电流脉冲时期各波形的局部放大图
Figure8. Waves of applied voltage, discharge current and discharge transferred charge: (a) Two layers columnar discharge (2.22 kV); (b) three layers columnar discharge (2.19 kV). The inserted figure is a partial enlarged view of these waveforms during the current pulse period in both (a) and (b).

由表3可知, 两种放电形式下, 非中心柱所受的库仑力F_Q均比磁场力F_I大7个数量级, F_I远不足以平衡F_Q的效果, 推测放电柱还受到一个外部约束势来平衡库仑力, 从而维持稳定的斑图结构. 这一结果与文献[14,20]所得一致: 放电系统中放电通道所受库仑力远大于磁场力, 应存在一个外部的径向约束势U_conf来平衡库仑力, 以维持稳定斑图, 磁场力的作用可忽略. 同时, 由图8可知, 所选放电电流峰值时刻的Q_d趋近于0且I_d最大, 此时库仑力远大于磁场力, 其他时刻Q_d更大且I_d更小, 因此所得结果始终成立.
值得注意的是, 表3中, U_ps = 2.19 kV时, Q_S, Q_S1, Q_S2三种不同位置的放电柱所受力的大小也存在差异, 与1 + 7两层多柱放电一样, 最大受力出现在最外层顶点处, 中心放电柱Q₁受力为0. 且1 + 6 + 12三层多柱放电中, 外层放电柱所受的力明显大于中层放电柱的, 即不同层的放电柱所受的库仑力是由最外层至中心柱依次减小的, 由于库仑力与约束势在外部条件不变时相互平衡, 说明不同层的放电柱所受约束势的大小由最外层至中心柱也应依次减小, 中心柱处约束势为0.
另外, 计算中发现, 介质表面电荷Q_d和放电柱总个数对库仑力的大小有重要影响. 表3中, 外施电压降低, Q_d增大、放电柱总个数增加, 受二者变化的共同影响, 平均到每个放电柱的转移电荷Q略有增大, 放电柱所受F_Q的最大值变大, 同样地, 此时约束势强度也应发生变化, 且趋势相同, 推测约束势同样受介质表面电荷Q_d与放电柱总个数的共同影响. 也就是说, 放电柱所处位置的不同或介质表面电荷、放电柱总个数的不同均会使该约束势强度大小发生变化.
在此基础上, 对单柱放电演化为1 + 7两层多柱放电的过程给出解释. 单柱放电时, 没有其他的放电柱对其作用, 约束势强度为0^[21], 电压有微小降低后, 带电粒子径向扩散, 在激活-抑制作用下原单柱周围一定位置处形成新放电区^[22], 放电区之间开始存在相互排斥的库仑力, 且电压降低后介质表面电荷发生变化, 约束势强度改变, 不再为0, 在约束势与库仑力的共同影响下, 逐渐发展成1 + 7两层多柱的放电形式. 同理, 当外施电压进一步降低时, 约束势强度进一步增大, 并在与库仑力的相互影响下, 从1 + 7两层多柱放电转化为1 + 6 + 12三层多柱放电. 约束势作用的具体机制, 及其在不同位置、不同介质表面电荷、放电柱总个数下差异的原因有待进一步研究.

本文进行大气压氦气DBD实验, 通过降低外施电压得到了单柱与多柱放电的斑图演化现象, 拍摄了电极底面放电图像演化过程, 测量了柱直径、柱间距, 计算了放电柱所受的库仑力与磁场力.
1)在低于起始放电电压的较高电压下, 放电形式为柱状放电, 位于不同层的放电柱的柱直径由中心向外层依次增大. 外施电压降低, 中心柱的柱直径增加, 中心柱与相邻柱的柱间距减小.
2)拍摄了单柱放电向1 + 7两层多柱放电的变化过程, 当外施电压微小降低时, 放电单柱周围出现光强较弱的“侧柱”, 并逐渐演化成围绕原放电单柱排布的新的独立放电柱, 最终形成稳定的1 + 7两层多柱放电.
3)分别计算了1 + 7两层多柱放电、1 + 6 + 12三层多柱放电时不同层放电柱所受其他所有柱施加的库仑力与磁场力, 发现放电柱所受的总库仑力始终远大于总磁场力, 且不同位置、不同外施电压下的放电柱所受库仑力大小不同: 不同层的放电柱所受库仑力由最外层至中心柱依次减小, 中心柱受力为0, 最大值在最外层顶点处, 且随低于起始放电电压的外施电压的降低而增大.
4)结合受力分析, 推断存在一个约束势来平衡库仑力, 以维持放电柱稳定自组织分布, 根据库仑力在不同位置、不同电压下介质表面电荷和放电柱总个数的差异导致的库仑力大小的差异, 推测该约束势的强度在不同位置、介质表面电荷和放电柱总个数不同时, 存在与库仑力相同的变化趋势, 当然, 这种约束势的具体存在形式及其性质有待进一步研究.