摘要:为了提出性能优异的图像质量评价(IQA)模型, 本文基于人类视觉感知特性和图像的灰度梯度、局部对比度和清晰度特征, 提出了一种基于图像内容对比感知的IQA方法. 在该方法中, 首先结合视觉感知特性, 基于物理学中对比度定义, 提出一种图像质量定义及其值计算方法; 之后, 基于灰度梯度共生矩阵, 提出一种图像灰度梯度熵的概念及其值的计算方法, 并基于图像灰度梯度熵、局部对比度和清晰度, 提出一种图像内容及其视觉感知的描述方法; 最后, 基于图像内容特征和图像质量定义, 综合分析, 提出IQA方法及其数学模型. 并且采用5个开源图像数据库中的119幅参考图像和6395幅失真图像对其进行了仿真测试, 同时分析和探讨了52种失真类型对IQA的影响; 另外, 为了说明所提IQA模型的优势, 将其与现有的7个典型IQA模型, 从精度、复杂性和泛化性能上进行了对比分析. 实验结果表明, 所提IQA模型的精度PLCC值在5个数据库中最低可以实现0.8616, 最高可达到0.9622, 其性能综合效益优于7个现有IQA模型. 研究结果表明, 所提IQA方法是有效的、可行的, 所提IQA模型是一个性能优异的IQA模型.
关键词: 图像质量评价/
人类视觉特性/
图像内容/
对比度

English Abstract

全文HTML

--> --> -->

近些年, 随着图像、光电和电信技术的飞速发展和广泛应用, 各行各业对图像质量的要求也变得越来越高. 但随之而来的通信带宽限制要求更高的图像压缩技术和传输技术, 以实现在更低比特的条件下获得更高的图像视觉质量^[1,2]. 因此, 近些年对图像的压缩和传输技术进行了大量研究, 提出了较多方案, 诸如LTE, 4G和5G等. 相应的图像质量主要考虑外在因素, 即由于压缩和传输而产生的失真, 如模糊、块效应及振铃效应等^[2,3], 并以这些类型的失真作为主要特征来构建图像质量评价(image quality assessment, IQA)模型, 以评价图像的质量. 其中典型的IQA模型有PSNR (peak signal to noise ratio)^[4], VSNR (visual signal-to-noise ratio)^[4], SSIM (structural similarity)^[5], FSIMc (features similarity index)^[6], GMSD (gradient magnitude similarity deviation)^[7], VSI(visual saliency-based index)^[8]和MAD(most apparent distortion algorithm)^[9]等. 其中, PSNR是最早用于IQA的模型, 是基于失真图像与原始图像之间对应像素点的差值而构建的一种IQA模型, 该模型非常简单, 但精度不高, 在不同开源数据库中测试, 其主客观IQA分数之间的线性相关性参数一般为0.6左右; VSNR是主要针对自然图像提出的一种基于小波变换的视觉信噪比的IQA模型^[4], 其精度高于PSNR, 但算法比较复杂; SSIM是一种从图像亮度、对比度和结构三个方面入手, 基于结构相似性而构建的IQA模型^[5], 精度明显高于PSNR和VSNR, 由于其相对较高的精度和较低的计算复杂性, 目前被普遍接收; FSIMc是一种基于低层视觉特性相似的全参考IQA方法^[6], MAD是一种基于最明显失真统计的IQA模型^[9], 两模型的精度均较高, 但复杂性均是其致命弱点; GMSD是一种基于梯度幅值相似偏差的IQA模型^[7], VSI是主要依据视觉注意机制和掩蔽特性而提出的IQA测度^[8], GMSD和VSI模型精度均较高且简单, 但泛化性能稍欠佳. 对于这些IQA模型, 在实际应用中发现, 不同的图像经过相同的压缩或传输而产生的失真度, 其模型的客观IQA分数相差无几, 但人眼感知的主观IQA分数却常常大相径庭, 表现为主客观IQA分数之间的一致性比较差. 而目前均以人类感知的主观IQA分数为标准IQA分数^[5], 即MOS(mean opinion scores), 所以仍需要对IQA进行大量研究, 提出性能更好的模型. 通过对现有IQA模型的分析和研究, 发现不足主要表现在以下几个方面.
1) IQA模型中没有考虑图像内容. 现有的大部分IQA模型主要是依据压缩或传输等外在图像损伤因素引起的失真特征而构建的, 往往忽略图像内容对IQA的贡献, 包括上述的7个IQA模型. 而在实际生活中, 人类对图像的感知, 包括图像质量, 第一印象仍然是图像本身内容, 如图像画面中的人物、场景和具有特征的目标(感兴趣区域)等, 若图像的整体失真度较大, 但其中的主要场景、人物及特征等重点关注的图像内容没有产生较大失真, 当采用PSNR, SSIM和MAD等模型评价时, 客观IQA分数相对较低, 但人眼评估的主观IQA分数仍然比较高, 二者存在明显的差异. 因此图像内容对IQA具有重要的贡献, 如若不考虑, 则很难获得真正意义上的主客观IQA结果的一致性, 所以, 构建IQA模型时需要重点考虑图像内容^[10-12]. 这方面的工作, 近两年也引起了国内外极大的关注^[13,14], 本文亦是主要基于图像内容特征来研究IQA方法.
2)人眼复杂的感知特性因素. 就人类视觉系统(human visual system, HVS)而言, 人眼主观评价得出的IQA结果与较多因素有关, 对图像的内在画面(即图像内容), 人眼的评判标准、角度和结果往往存在较大的差异, 例如相同的压缩比特率不同的图像, PSNR, SSIM, MAD等IQA模型评价得出的分数可能完全一样, 但主观IQA结果可能差异较大^[12,15], 所以需要结合视觉特性.
3)构建模型的方法对IQA的影响. 在目前的IQA研究中, 往往采用数学建模和机器学习的方法, 而且由于机器学习方法的优点, 目前结合机器学习方法构建IQA模型的提案不在少数, 虽然其精度比较高, 但存在4个致命的性能缺陷, 即没有相关的物理意义解释、泛化性能较差、复杂性较高及训练样本有限^[16]. 而基于数学建模构建的IQA模型, 虽然精度稍差, 但可以解决机器学习方法构建模型的不足, 即可以较好地解释相应的物理意义、提升泛化性能和降低模型算法复杂性. 所以, 基于综合性能, 目前在实际应用中仍然采用数学建模方法构建的IQA模型^[17], 如PSNR和SSIM. 但其模型的精度、复杂性和泛化性能仍然不能满足实际需求, 需要在构建模型的方法上进行大量研究, 而且需要结合更相关的物理意义和生理、心理特征^[16-18].
4) HVS特性及其模型的结合. 目前, 为了提高IQA模型的精度, 一个有效的手段即是结合HVS及其模型, 如FSIMc和VSI模型. 但是, 当前存在两个问题, 一是在构建IQA模型时, HVS特性的引入在很大程度上增加了IQA模型的算法复杂性, 如何巧妙地结合HVS特性及其模型, 使得所提IQA模型简单而有效, 是目前的困境; 二是目前人类认知的HVS特性及其数学模型比较有限, 如何最大化且有效地利用它们同样是一个很大的难题^[18,19].
5) IQA模型的算法复杂性和泛化性能. 目前IQA模型构建的基本途径为: 通过提取一定数量的图像特征, 构建特征与图像质量之间的函数关系. 其中, 构建模型的性能主要取决于所提图像特征的数量和有效性. 为了提高模型精度, 一般需要提取更多的图像特征. 然而, 提取的特征越多, 模型的参数也越多, 模型也越复杂, 致使模型的泛化性能明显下降, 表现为模型精度、泛化性能和算法复杂性很难有效平衡^[3,16,17], MAD为典型的此类模型. 所以, IQA建模时, 需要综合考虑选取少量但有效的图像特征, 以实现模型性能的综合效益最大化.
基于以上对图像内容特征的重要性、HVS特性结合、模型构建方法、复杂性和泛化性能等方面的分析, 本文结合HVS特性, 利用图像亮度色度、纹理、局部对比度及清晰度等图像内容特征, 基于心理物理学中对比度的定义, 提出一种基于图像内容对比感知的IQA方法, 并构建其模型. 同时采用5个数据库中的6395幅失真图像对其进行了仿真测试, 且与7个现有的典型IQA模型进行了对比分析, 来探讨图像内容和HVS特征对IQA的影响.

目前, 人类获取信息的90%来自于视觉感知. 对于一幅图像, 人眼主要从4个方面感知其信息, 即图像的亮度和色度信息、画面(内部对象)信息、画面模糊程度、以及局部对比效果^[3,20]. 基于此, 可以将图像的内容表征为图像的亮度和色度信息、图像画面信息、图像清晰度、图像局部对比信息及其视觉感知结果之和, 用这些量共同描述.
2

-->

2.1.图像亮度色度信息和画面信息及其视觉感知

在人类感知图像时, 感知到的最主要信息即是图像的亮度和色度信息, 其信息一般采用亮度色度的灰度强弱来描述^[3,20], 而其强弱则可通过图像的灰度值及其分布来描述^[20]. 基于此, 可以采用图像的灰度值大小及其分布来表征图像亮度和色度信息.
就视觉感知特性而言, 图像的画面信息主要体现在图像内的场景、人物、目标对象等人眼感兴趣的信息, 即图像中纹理复杂的信息^[20]. 因此可以通过图像的纹理特征来表征图像的画面信息. 目前描述图像纹理特征的典型方法是梯度^[21], 因此可以采用图像的梯度大小及其分布来表征图像的画面信息.
基于以上两个方面的说明, 可以采取图像的灰度和梯度大小及其分布来描述图像的亮度和色度信息以及画面信息. 对于图像的灰度和梯度分布, 采用统计学中图像的灰度和梯度共生矩阵来计算, 但其结果只能说明灰度梯度的分布情况, 不能反映其强度值大小. 由此, 基于共生矩阵, 提出一个灰度梯度熵的概念, 其值用以表征图像的亮度色度信息、画面信息(即纹理复杂性)及其感知效果. 计算方法为: 首先计算图像的灰度梯度共生矩阵, 得到图像的亮度色度强度和梯度分布概率; 然后将所有梯度乘以共生矩阵中的对应概率值; 最后, 类似于霍夫曼编码中求熵的思想, 对所有值求和, 求和的结果称之为灰度梯度熵, 记为I_E (the entropy of the gray-gradient perception of image), 计算公式可表示为

${I_{\rm{E}}}=\sum\limits_{i = 0,~j = 0}^{i = 255,~j = 32} {\left\| {{\rm{gra}}{{\rm{d}}_j}} \right\| \cdot \frac{{{{H}}({\rm{gra}}{{\rm{y}}_i},{\rm{gra}}{{\rm{d}}_j})}}{{m \times n}}} ,$

其中, H是梯度和灰度共生矩阵, m × n是每幅图像的像素数, 梯度分为32个级别. I_E的取值范围为[0, 32], 可作为表征图像内容的特征参数之一.
2 -->

2.2.图像清晰度

在人类感知图像时, 人眼对图像的模糊程度非常敏感, 因此在IQA时, 图像画面的清晰度起到举足轻重的作用. 为此将计算的图像清晰度作为表征图像内容特征的第二个参数, 记为I_D (image definition), 其计算方法如下.
通过统计图像某一边缘方向的灰度变化来度量图像的清晰程度, 采用改进的点锐度算法^[22]来描述, 计算式为

${I_{\rm{D}}}=\frac1{{m \times n}}{{\sum\limits_{i = 1}^{m \times n} {\sum\limits_{N{\rm{p}} = 1}^8 {\left| {\frac{{{\rm{d}}I}}{{{\rm{d}}x}}} \right|} } }} ,$

式中, dx表示距离增量(像素间), dI表示灰度变化幅值, Np为最邻近的像素点数目. 其中, 由于像素一般以方格形式采样, 像元各向异性, 因此要求依据距离对方格上8邻域的灰度变化进行加权. 对于相邻的像元, 权值取法为: 0°和90°方向上, 权值为1; 对角45°和135°方向上, 权值为${1 / {\sqrt 2 }}$. 则图像清晰度的计算可描述为: 以每个点自身为中心, 分别求其与最邻近8个点之灰度差, 以不同方向上确定的权值为各差值的权重因子而加权求和, 再对图像上的所有像素点求和, 并按总像素数(m × n)求平均^[22]. 对于计算结果, I_D的取值范围为[0, 1], 其值越大, 表明点扩散程度越剧烈, 图像越清晰.
2 -->

2.3.图像局部对比度及其视觉感知

局部对比感知是人类识别和分辨图像的关键因素. 所提算法采用图像中每一点与其周围最邻近的8个点的对比度的平均值作为该点受局部环境影响的对比度, 然后再计算子块内所有像素点对比度的平均值, 并乘以对应中心的归一化亮度值, 其值可以表明人眼在该对比度下亮度的敏感结果, 记为I_C (local contrast of image), 计算表达式为:

${I_{\rm{C}}}=\frac{1}{{m \times n}}\sum\limits_{i = 1,j = 1}^{m,n} {\frac{{\rm{1}}}{{\rm{8}}}\left\{ {\sum\limits_{ {L_1} = - 1,0,1\atop{L_2} = - 1,0,1}{\frac{{I(i,j) - I(i - {L_1},j - {L_2})}}{{[I(i,j){{ + }}I(i - {L_1},j - {L_2})]}}} } \right\}} \cdot \frac{{I(i,j)}}{{255}},$

其中, I(i, j)为图像的灰度. I_C的取值范围为[0, 1], 其值越大, 表明图像局部对比及其视觉感知效果越好. 以此作为图像内容表征的第三个参数.
基于以上3个方面的说明和计算方法, 图像内容I_content可以表征为3个特征参数之和, 计算式为

${I_{{\rm{content}}}}={a_1}{I_{\rm{E}}} + {a_2}{I_{\rm{D}}} + {a_3}{I_{\rm{C}}},$

式中, a₁, a₂和a₃为参数, 依据主观实验分析人眼对图像的亮度色度、局部对比度、清晰度的感知对IQA的贡献(或重要性)、以及通过样本遍历测试分析得出, 其值分别取0.4, 0.3和0.3时所提IQA模型效果最佳. 另外, 由于不同的图像特征量, 其物理意义不同, 参数值范围也不一致, 则(4)式中特征参数值在合并之前需要进行归一化处理.

2

-->

3.1.图像质量定义

在目前的IQA方法中, 普遍的方法是采用失真图像与原始图像之间的某些特征参数之差来度量图像质量, 如目前普遍使用的PSNR是采用二者图像的灰度之差来描述, SSIM^[5]采用结构相似特征参数之差来描述, FSIM^[6]采用特征结构相似度之差来表征等. 采用特征之差来描述图像质量固然是一个比较好的方法, 但人眼判断图像的质量时, 不仅是判断其差值, 更多的是通过对比的方式得出图像质量, 而且由于对比是人类分辨事物的最佳判据^[17,20], 则分辨图像质量的优劣, 最好是将原始图像和失真图像按照子块一一对比, 最后综合所有子块的结果, 即为图像的质量, 即采用对比的形式来定义图像的质量. 目前, 目标对比的经典定义为物理学中明暗亮度光栅条纹的对比度定义, 在人眼对比敏感视觉特性的测量中亦采用该定义^[20], 其表达如(5)式. 基于此, 依据(5)式的对比度定义, 分别将原始图像和失真图像各子块的特征值代入其中的I_max和I_min, 如(6)式, 从而一一将两图像的子块特征进行对比, 得出各个子块的质量分数. 而且由于各个子块的质量分数存在差异, 人眼对差异的存在同样非常敏感, 为此, 对所有子块的质量分数采用池化(pooling)的形式进行综合处理, 计算如(7)式, 从而得到整个图像的质量.

$C=\frac{{\left| {{I_{\max }} - {I_{\min }}} \right|}}{{{I_{\max }} + {I_{\min }}}},$

其中I_max和I_min为光栅中明暗亮度条纹的亮度值.

${S_{{\rm{C}}\text{-} {\rm{block}}}}=\frac{{\left| {{\rm{Featur}}{{\rm{e}}_{{\rm{distorted }}- {\rm{image}}}} - {\rm{Featur}}{{\rm{e}}_{{\rm{original}}\;{\rm{image}}}}} \right|}}{{{\rm{Featur}}{{\rm{e}}_{{\rm{distorted}} \text{-} {\rm{image}}}} + {\rm{Featur}}{{\rm{e}}_{{\rm{original}}\; {\rm{image}}}}}},$

其中, Feature_{distorted-image}和Feature_{original-image}是为了IQA而提取的失真图像和原始图像的特征参数值, 在文中所提的方法中, 即为图像的灰度梯度熵、清晰度和局部对比度.

${\rm{Scores}} = \sqrt {\dfrac1{{{N_{{\rm{block}}}}}}{{\sum\limits_{i = 1}^{{N_{{\rm{block}}}}} {{{\left( {{{\rm{S}}_{{\rm{C}} \text{-} {{\rm{block}}}}}{{(}}i{{) }} - \overline {{{\rm{S}}_{{\rm{C}} \text{-} {{\rm{block}}}}}} } \right)}^2}} }}} ,$

其中N_block为图像子块的数量.
依据以上图像质量定义方法, 则度量规则为: 图像质量分数取[0, 1]之间的数值, 取0时, 表示两图像之间的对比差异最小, 失真图像与原始图像一样, 质量最好; 取1时, 两图像的对比差异最大, 表明失真图像的损伤非常严重, 质量最差; 取0—1之间的数值时, 其值越大, 表明失真图像与原始图像相比, 差异越大, 质量越差, 其值越小, 表明失真图像与原始图像越相近, 质量越好.
2 -->

3.2.图像质量客观评价方法及其模型

基于提出的图像内容表征方法和图像质量定义, 所提IQA方法的基本框架和流程如图1.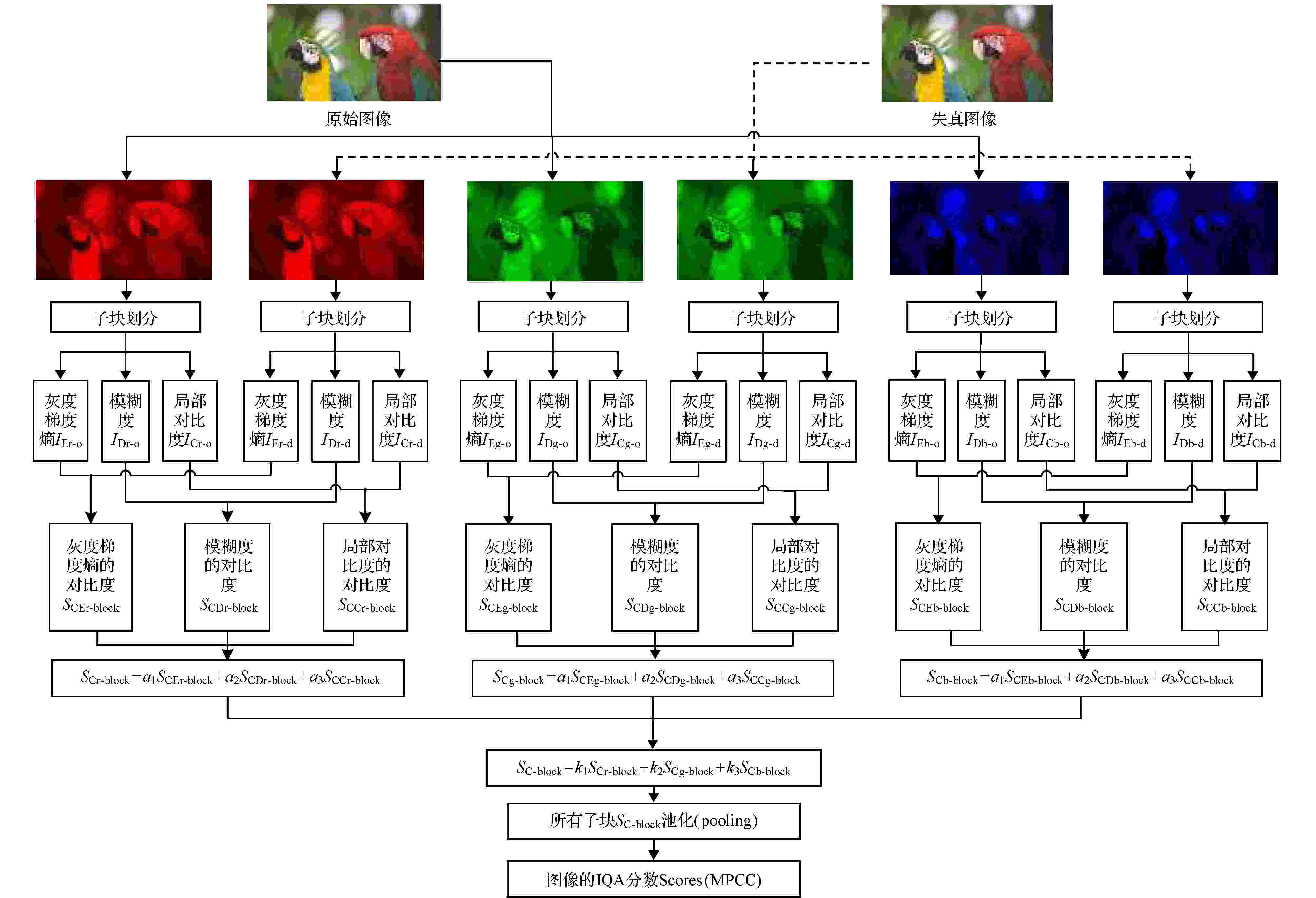
图 1 所提IQA方法的流程图
Figure1. The architecture of the proposed IQA method.

该IQA方法的基本思想为: 首先计算失真图像和原始图像的灰度梯度熵、清晰度和局部对比度, 以其作为图像内容的特征参数; 接着以上述提出的图像质量定义, 即采用失真图像和原始图像之间的内容特征对比度来定义图像的质量, 计算3个特征对比度, 并综合, 从而得出各子块的质量分数; 最后采用池化的方法进行综合处理, 得到整个图像的质量分数. 具体的方法和模型构建过程说明如下.
1) 子块划分
为了增加IQA模型的实时性和可操作性, 将原始图像和失真图像的R, G, B三分量图, 分别按照16像素 × 16像素大小进行子块划分, 并按照划分时的顺序进行排列.
2) 特征计算
结合上述灰度梯度熵、清晰度、局部对比度的理论和(1)式—(3)式的计算方法, 分别计算原始图像和失真图像的R, G, B三分量图的所有子块的灰度梯度熵I_E (即图1中的I_Er-o, I_Eg-o, I_Eb-o和I_Er-d, I_Eg-d, I_Eb-d), 和所有子块的图像清晰度I_D(即图1中的I_Dr-o, I_Dg-o, I_Db-o和I_Dr-d, I_Dg-d, I_Db-d), 以及所有子块的局部对比度I_C (即图1中的I_Cr-o, I_Cg-o, I_Cb-o和I_Cr-d, I_Cg-d, I_Cb-d).
3) 子块内容特征对比
① 将计算的原始图像和失真图像对应子块的灰度梯度熵, 即(I_Er-o, I_Er-d), (I_Eg-o, I_Eg-d)和(I_Eb-o, I_Eb-d)分别成对代入(6)式中, 实现对应子块熵的一一对比, 从而得到由灰度梯度熵的特征对比而贡献的图像质量, 对于R, G, B三分量图的子块, 其分数分别记为S_CEr-block, S_CEg-block, S_CEb-block. ② 同样方法, 计算得出由清晰度的图像内容特征对比而贡献的图像质量, 即将计算的清晰度按子块对应, 即(I_Dr-o, I_Dr-d), (I_Dg-o, I_Dg-d)和(I_Db-o, I_Db-d)分别成对代入(6)式中, 计算得出的分数分别记为S_CDr-block, S_CDg-block, S_CDb-block. ③ 按相同方法, 将计算的原始图像和失真图像对应子块的局部对比度, 按子块对应, 即(I_Cr-o, I_Cr-d), (I_Cg-o, I_Cg-d)和(I_Cb-o, I_Cb-d)分别成对代入(6)式中, 计算得出由局部对比度的图像特征对比而贡献的图像质量, 其分数分别记为S_CCr-block, S_CCg-block, S_CCb-block.
4) 子块的三分量图的图像质量
对每个子块的R, G, B三分量图的灰度梯度熵、清晰度、局部对比度对质量的贡献进行综合, 综合方法为将计算的R, G, B三分量的三个贡献分数分别代入(4)式中进行计算, 得到每个子块的三分量图的图像质量分数S_Cr-block, S_Cg-block和S_Cb-block, 计算公式为:

$\begin{split}&{S_{{\rm{Cr}} \text{-} {\rm{block}}}}={a_1}{S_{{\rm{CEr}} \text{-} {\rm{block}}}} + {a_2}{S_{{\rm{CDr}} \text{-} {\rm{block}}}} + {a_3}{S_{{\rm{CCr}} \text{-} {\rm{block}}}},\\&{S_{{\rm{Cg}} \text{-} {\rm{block}}}}={a_1}{S_{{\rm{CEg}} \text{-} {\rm{block}}}} + {a_2}{S_{{\rm{CDg}} \text{-} {\rm{block}}}} + {a_3}{S_{{\rm{CCg}} \text{-} {\rm{block}}}},\\&{S_{{\rm{Cb}} \text{-} {\rm{block}}}}={a_1}{S_{{\rm{CEb}} \text{-} {\rm{block}}}} + {a_2}{S_{{\rm{CDb}} \text{-} {\rm{block}}}} + {a_3}{S_{{\rm{CCb}} \text{-} {\rm{block}}}},\end{split}$

其中3个质量贡献值代入(4)式综合之前, 需要进行归一化处理.
5) 子块图像质量
按照RGB图中R, G, B颜色混合系数, 对三分量图的三子块的图像质量分数S_Cr-block, S_Cg-block和S_Cb-block进行组合, 得到每个子块的质量评价分数S_C-block, 计算式为

${S_{{\rm{C}} - {\rm{block}}}}={k_1}{S_{{\rm{Cr}} \text{-} {\rm{block}}}} + {k_2}{S_{{\rm{Cg}} \text{-} {\rm{block}}}} + {k_3}{S_{{\rm{Cb}} \text{-} {\rm{block}}}}.$

6) 图像质量
最后将所有子块的图像质量分数S_C-block代入(7)式中, 进行池化处理, 得到整个图像的客观IQA评价分数Scores.
记上述IQA方法的对应数学模型为MPCC (IQA model based on the perception of the contrast of image contents). 采用该模型评价图像得出的质量分数Scores记为MPCC, 其描述图像质量为: MPCC值越大, 表明失真图像与原始图像之间对比差异越大, 则失真图像的质量越差; 其值越小, 越接近于零, 表明失真图像与原图像的对比差异越接近于零, 则图像质量越好. 对于灰度图, 则只需按照(8)式中的一个表达式计算即可.

为了检验以上所提的IQA方法, 采用开源数据库LIVE^[23], CSIQ^[24], TID2008^[25]和TID2013^[26]中的共109幅参考图像和6345幅不同类型的失真图像进行仿真测试, 采用所提方法分别对其进行评价, 得出IQA分数MPCC. 同时, 为了更好地验证所提模型, 基于相关性参数和散点图, 将所提模型评价得出的客观IQA分数MPCC与数据库中提供的主观IQA分数MOS(或DMOS)进行相关性分析, 以说明模型的性能.
对于主客观IQA分数的相关性分析, 根据ITU质量评价专家组VQEG (video quality experts group)的建议, 一般包括主客观IQA分数之间的散点图, 以及4个相关性参数PLCC (Pearson linear correlation coefficient), SROCC (Spearman rank order correlation coefficient), RMSE (root mean squared error)和OR (outlier ratio)^[23,27]. 其中, 散点图可以直观地说明主客观IQA分数之间的离散程度、单调性和一致性; 对于相关性参数, PLCC和SROCC从两个IQA分数之间的一致性和单调性上直接定量说明所提模型的精度, 其值越大, 效果越好, 模型精度越高; RMSE和OR值从两分数之间的偏差和离散程度上定量描述模型精度, 在评估时, 一般配合直观散点图效果, 可以很好地描述所提模型的精度, 其值越小, 模型精度越高^[3,23,27]. 其中, OR采用(10)式的定义进行计算. 对于4个图像数据库, 均提供了每幅失真图像的主观IQA分数, 结合计算的客观IQA分数MPCC, 计算4个相关性参数和得出散点图, 结果如表1和图2. 其中, 图2中的曲线采用最小二乘法(least square method, LMS)拟合而成.

数据库	LIVE(779)	CSIQ(866)	TID2008(1700)	TID2013(3000)	加权
PLCC	0.9622	0.9586	0.8778	0.8616	0.8915
SROCC	0.9660	0.9569	0.8831	0.8452	0.8854
RMSE	7.4397	0.0747	0.6427	0.6293	—
OR	0.1531	0.2690	0.1287	0.1198	—

表14个数据库中的图像主客观IQA分数之间的相关性参数计算结果
Table1.Calculated 4 correlation parameters between the subjective and objective IQA scores of images in 4 databases.

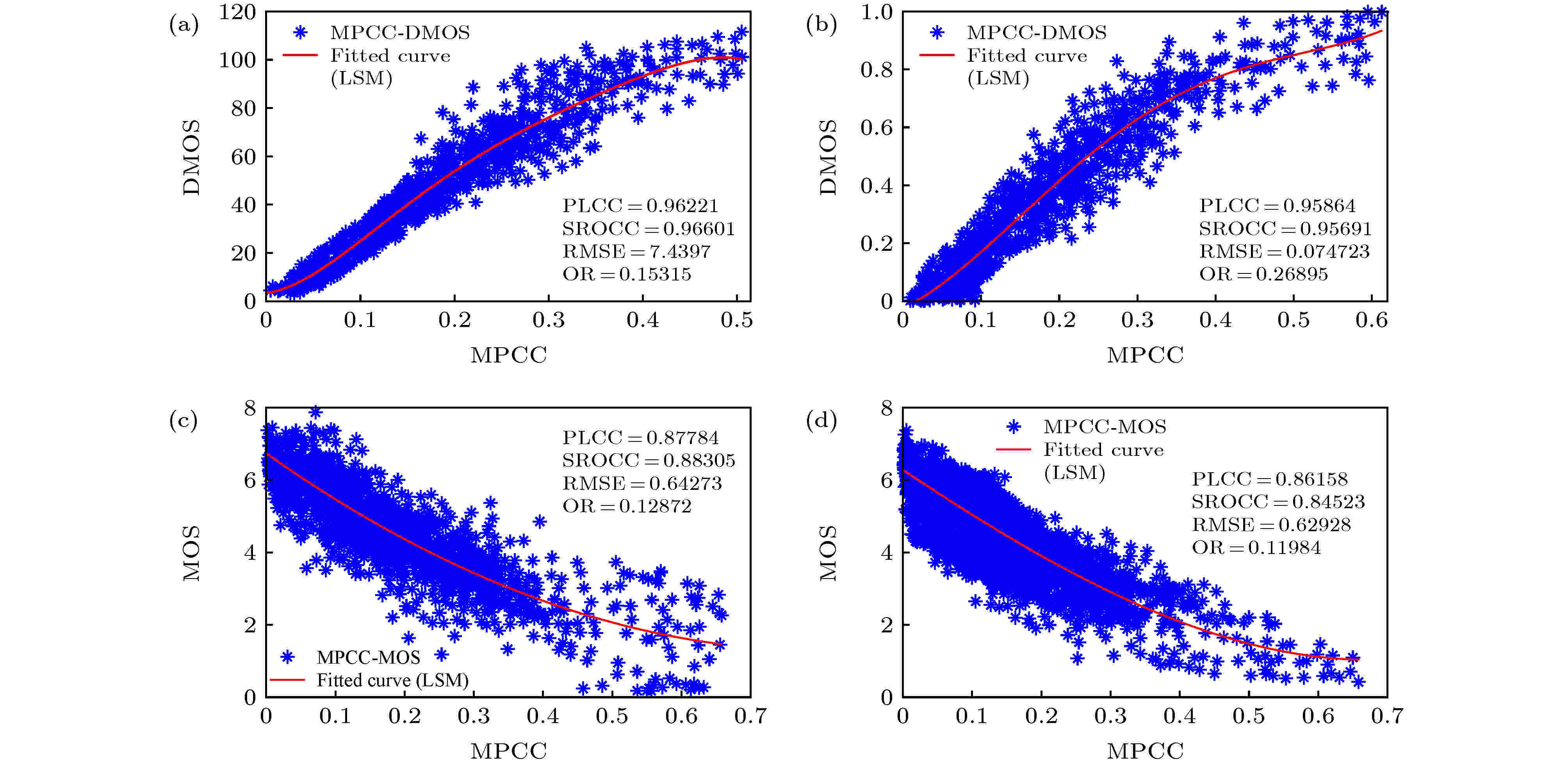图 2 4个数据库中的图像主客观IQA结果之间的散点图　(a) LIVE; (b) CSIQ; (c) TID2008; (d) TID2013
Figure2. Scatter plots between the subjective and objective IQA results of images in four databases: (a) LIVE; (b) CSIQ; (c) TID2008; (d) TID2013

${\rm{OR}} = \frac{1}{{{N_{{\rm{img}}}}}}\sum\limits_{i = 1}^{{N_{\rm img}}} {\frac{{\left| {{s_i} - {p_i}} \right|}}{{{p_i}}}} ,$

式中, N_img为被评价的失真图像数目, s_i为第i个失真图像的主观IQA分数, p_i为经拟合后预测的第i个失真图像的客观IQA分数.
从表1和图2的实验结果可得: 在4个图像数据库中, 无论从散点图的离散程度上, 还是从数值的定量结果上, 对于每个图像库, 所提IQA模型的IQA评价结果精度均较高, PLCC和SROCC值均在0.8452以上; 从模型对4个数据库的评价结果的加权来看, 精度上PLCC和SROCC值分别可达0.8915和0.8854; 对即使是24种失真类型、25幅不同内容的参考图像下TID2013数据库中的评价, 模型仍表现出较好的效果, 精度仍可达PLCC为0.8616. 实验结果表明所提模型既具有较高的评价精度, 又具有较好的泛化性能.

2

-->

5.1.单色和灰度图像的质量评价

对于单色和灰度图像的质量评价, 只需要采用(8)式中的一个分式即可, 为了说明其有效性, 采用IVC数据库^[28]中的10幅参考图像、单色和灰度图像各25幅进行仿真实验, 结果如图3.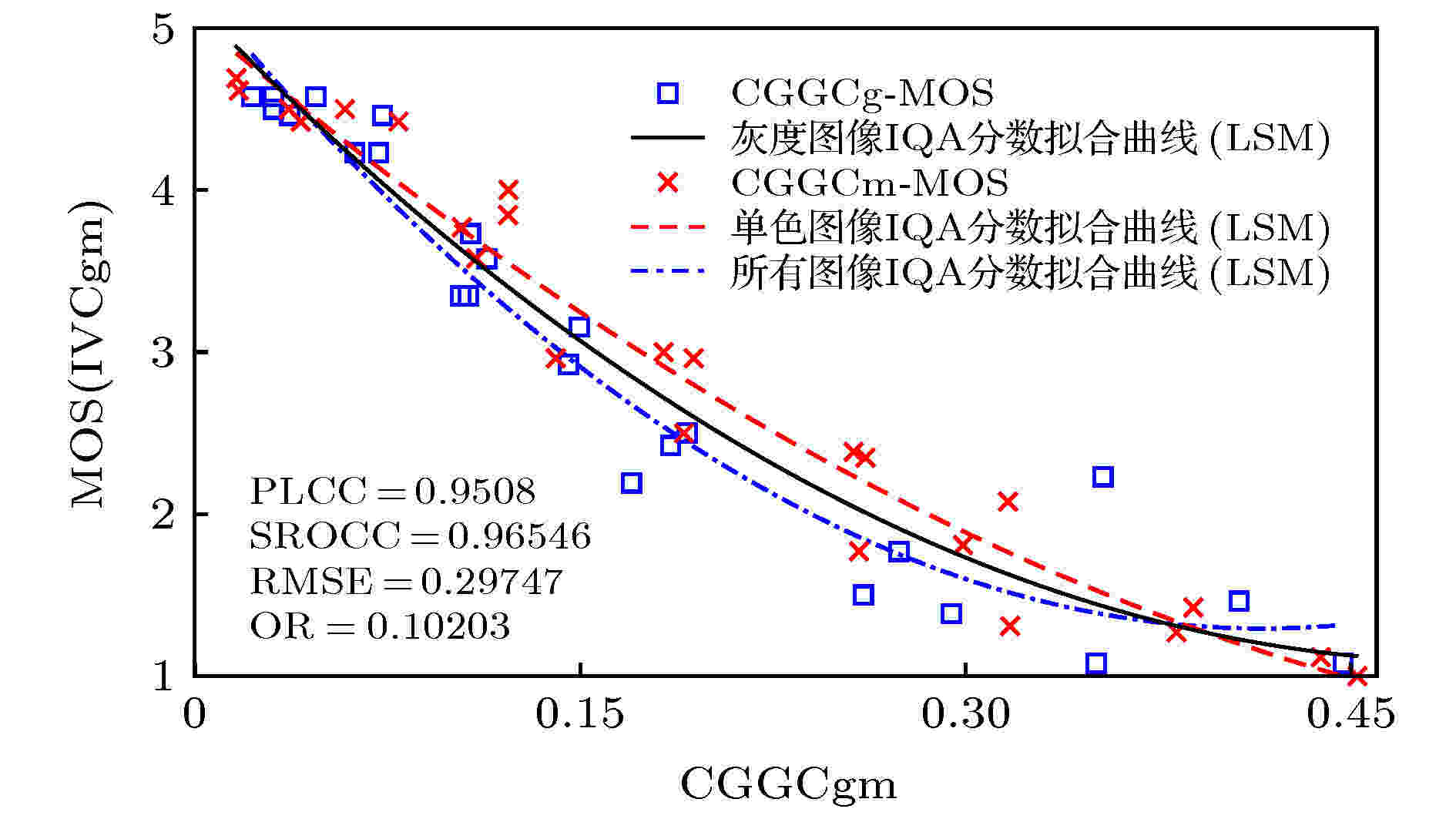
图 3 所提模型对IVC数据库中灰度和单色图像评价结果
Figure3. IQA results of the gray and monochrome images in IVC database by the proposed model.

图3所示的实验结果表明, 所提IQA模型对单色和灰度图像的质量评价效果同样具有较高的精度, 其PLCC和SROCC值均在0.95以上.
2 -->

5.2.模型性能分析

对于IQA模型, 最重要的属性为模型精度、泛化性和复杂性^[3,27]. 因此, 下面从此3个方面来分析和探讨所提模型的性能. 同时, 为了体现所提IQA方法的优势, 从此3个模型属性出发, 将其与7个典型IQA模型进行对比, 该7个模型为PSNR, VSNR, SSIM, FSIMc, GMSD, MAD和VSI^[4-9].
1) 模型精度和泛化性能对比. 对于IQA模型来说, 泛化性非常重要, 在不同的数据库中评价时均要求其有较高的精度. 其对比方法为: 采用上述实验测试中的4个开源数据库中的图像(即109幅参考图像和6345幅失真图像)作为评价对象, 采用此7个现有IQA模型对其进行质量评价, 得出其客观IQA分数; 同时基于数据库中提供的主观IQA分数, 进行主客观IQA分数相关性分析, 计算4个相关性参数, 并得出散点图. 将所得结果与所提模型的IQA结果进行对比, 见图4和表2. 其中, 图4是针对TID2008数据库中的图像的评价结果, 图中的曲线采用logistic函数拟合而成; 表2是针对CSIQ, LIVE和TID2013数据库中的图像的评价结果, 表中的PLCC, RMSE和OR的计算均采用了logistic函数拟合后的预测值.

数据库	参数	PSNR	VSNR	SSIM	FSIMc	VSI	GMSD	MAD	MPCC
CSIQ	PLCC	0.8000	0.8002	0.8613	0.9192	0.9279	0.9541	0.9502	0.9587
	SROCC	0.8058	0.8106	0.8756	0.9310	0.9423	0.9570	0.9466	0.9569
	RMSE	0.1575	0.1575	0.1334	0.1034	0.0979	0.0786	0.0818	0.0748
	OR	0.4220	0.3832	0.3535	0.3041	0.2873	0.2742	0.2829	0.2738
LIVE	PLCC	0.8723	0.9231	0.9449	0.9613	0.9482	0.9603	0.9675	0.9620
	SROCC	0.8756	0.9274	0.9479	0.9645	0.9524	0.9603	0.9669	0.9660
	RMSE	13.3597	10.5059	8.9455	7.5296	8.6816	7.6214	6.9073	7.4598
	OR	0.2179	0.2151	0.1865	0.1627	0.1853	0.1643	0.1529	0.1606
TID2013	PLCC	0.7062	0.7402	0.7895	0.8769	0.9000	0.8553	0.8267	0.8648
	SROCC	0.6917	0.7316	0.7417	0.8510	0.8965	0.8044	0.7807	0.8452
	RMSE	0.8887	0.8392	0.7608	0.5959	0.5404	0.6423	0.6975	0.6224
	OR	0.1636	0.1552	0.1427	0.1132	0.1045	0.1242	0.1323	0.1179

表2基于CSIQ, LIVE和TID2013数据库中的图像IQA结果比较所提模型与现有7个模型的精度
Table2.Comparing the accuracy of the proposed model with those of the existing 7 models based on the IQA results in CSIQ, LIVE, and TID2013 databases.

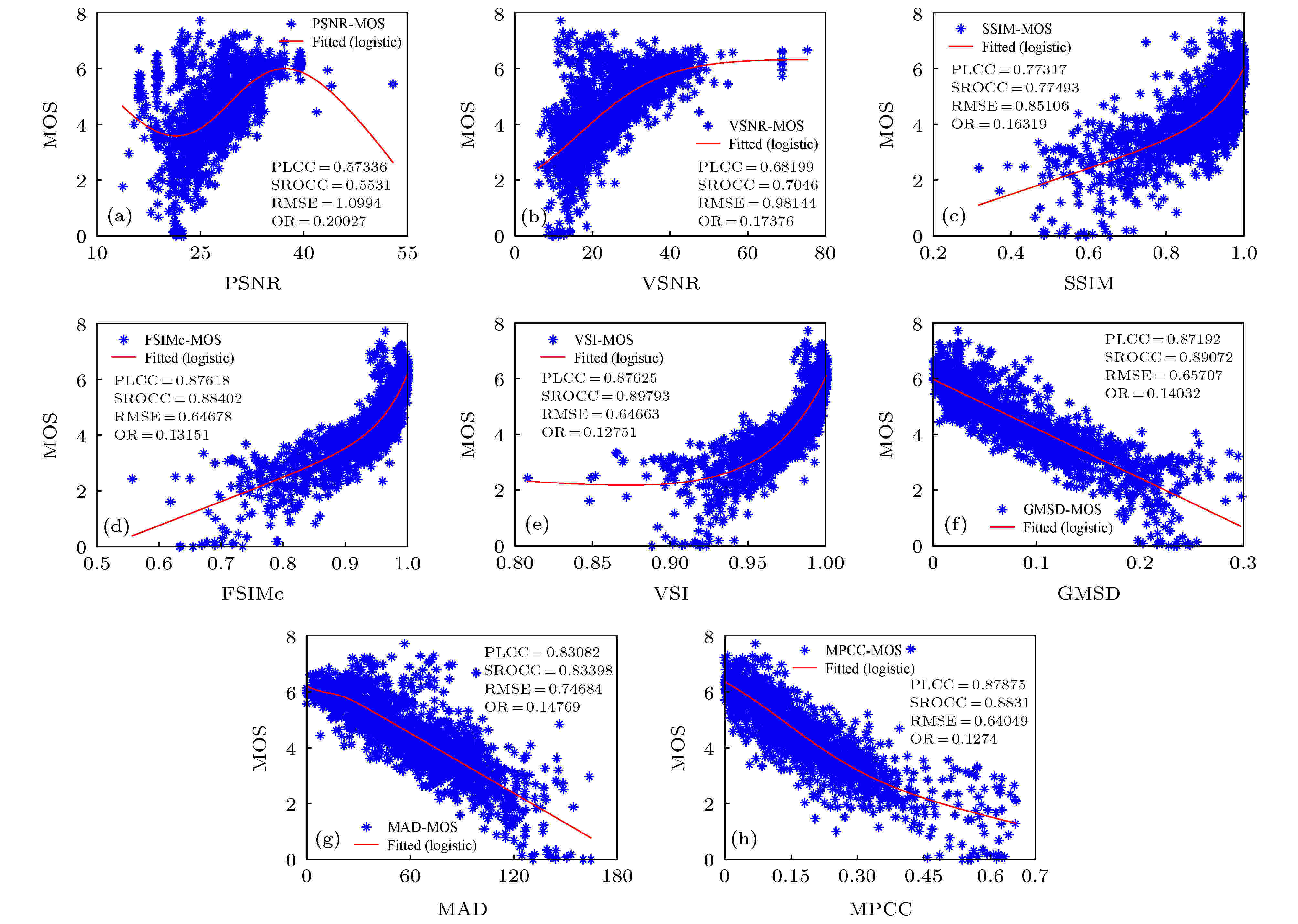图 4 基于TID2008数据库中的图像IQA结果比较所提模型与现有7个模型的精度　(a) PSNR-TID2008; (b) VSNR-TID2008; (c) SSIM-TID2008; (d) FSIMc-TID2008; (e) VSI-TID2008; (f) GMSD-TID2008; (g) MAD-TID2008; (h) MPCC-TID2008
Figure4. Comparing the accuracy of the proposed model with those of the existing 7 models based on the IQA results in TID2008 database: (a) PSNR-TID2008; (b) VSNR-TID2008; (c) SSIM-TID2008; (d) FSIMc-TID2008; (e) VSI-TID2008; (f) GMSD-TID2008; (g) MAD-TID2008; (h) MPCC-TID2008.

对比分析图4中的散点图及表2中4个相关性参数可得: ① 从散点图进行直观分析, 并配合RMSE, OR数值可以看出, 在TID2008数据库中, 所提模型评价结果的散点图中点的离散程度均比较小, 效果明显好于7个现有IQA模型的结果; ② 从4个相关性参数来说, 所提模型的PLCC和SROCC值在4个数据库中均可以达到该8个模型中的最大或次大, RMSE和OR达到最小或次小, 而且所提模型对所有数据库的评价结果的PLCC和SROCC值均超过了0.8452. 表明所提模型既具有较高的精度, 又具有较好的泛化性能.
分析原因主要有: 所提模型主要结合了HVS特性, 考虑了图像的亮度色度、纹理、清晰度、局部对比度等特征来构建IQA模型, 相对于7个现有IQA模型而言, 其更好地表征了图像, 而且特征参量相对比较少而有效, 所以其精度和泛化性能较好; 目前, 在图像失真的外在因素方面, 主要体现在图像的亮度色度失真、对比度失真、压缩失真和噪声失真等方面. 对于4个图像库中的图像失真基本亦是如此, 虽然4个数据库中有52种失真类型, 但基本是上述4个方面失真中的某一形式, 各失真类型之间有一定的相关度. 而所提模型在构建时, 基本将其失真因素悉数考虑在列, 即所提模型考虑失真因素较为宽泛, 所以所提模型的质量评价精度高, 散点图上点的离散程度较低, 而且泛化性能较好.
2) IQA模型算法复杂性对比. 算法复杂性问题关系到所提模型是否能实际应用, 所以同样非常重要. 在IQA模型研究中, 一般采用IQA模型评价图像的平均运算时间来定量描述其算法复杂性^[3,7,23]. 为此, 在仿真实验中, 采用所提模型和7个现有模型对4个数据库中的图像进行评价, 记录其算法运算时间, 并且将不同大小的图像的算法运算时间按照像素个数换算至512 × 512像素大小的图像评价时算法的运算时间, 最后计算其平均值, 从而比较各IQA模型的算法复杂性. 实验中, 采用处理器为Intel(R) Core(TM) i7-8550U cpu@1.80GHz 1.99GHz, 64位操作系统的笔记本电脑, MATLAB2018a编程环境进行仿真评价, 为了得到便于比较的结果, 其时间为平均每10幅图像的运行时间. 结果比较如图5所示.
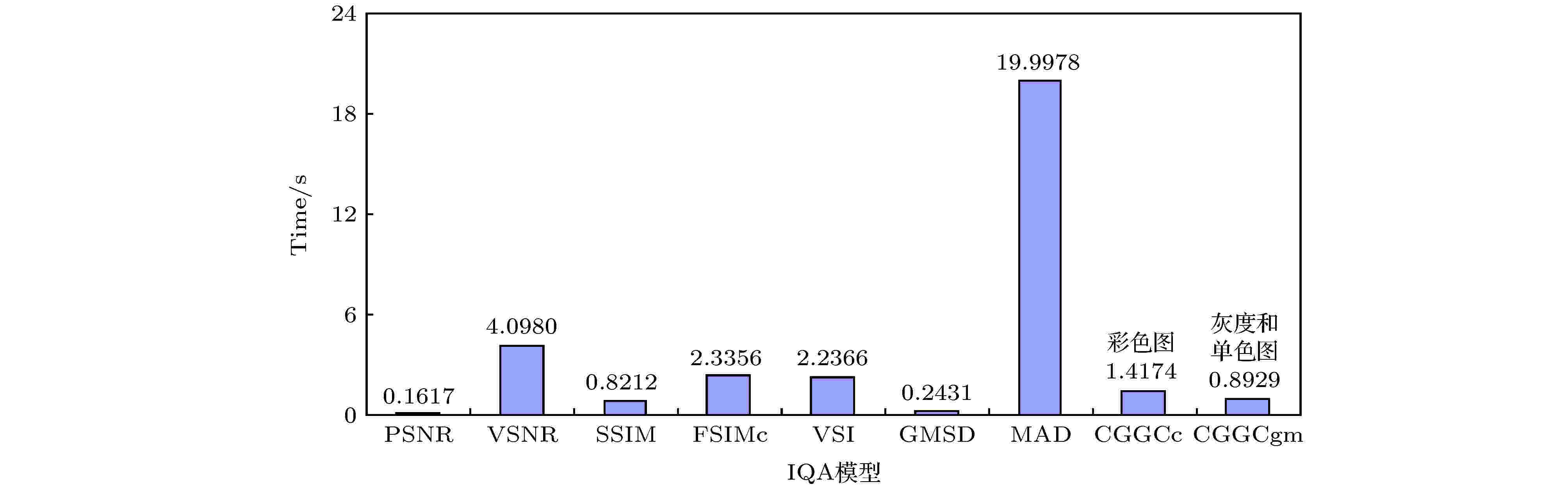图 5 基于平均每10幅图像的评价运行时间比较8个IQA模型的复杂性
Figure5. Comparison of the complexity of 8 IQA models based on the IQA running time per 10 images.

通过图5的算法运算时间的比较可以得出, 所提IQA模型的算法运算时间明显少于MAD, VSNR, VSI和FSIMc的算法运算时间, 而高于PSNR, SSIM和GMSD的算法运算时间; SSIM模型是目前国际上普遍接受和应用的典型IQA模型, 虽然所提模型的复杂性略高于SSIM模型, 但能与之相比拟, 而且从精度上, 所提模型较之高; 对于对灰度或单色图像的质量评价, 由于不考虑三分量图的原因, 其算法运算时间明显减少, 而且与SSIM的算法运算时间相接近. 综合复杂性和精度两方面可以看出, 所提模型是一个性能较好的IQA模型.
所提模型具有较低复杂性的主要原因为: 所提模型考虑了4个方面的图像特征, 其提取算法本身均不复杂, 且所提特征数量相对较少但有效; 另外, 不需要对图像进行任何相关的时空变换, 并且算法不需要反复循环运算, 所以其算法复杂性较低.
2 -->

5.3.IQA模型对不同失真类型的泛化性能分析

在目前的IQA研究中, 由于采取统计的方式测试IQA模型, 模型对大量图像的整体评价效果可能比较好, 但往往对不同失真类型的图像的质量评价效果有较大差异, 表现为较差的泛化性能, 以致在应用上存在较大的不确定性^[29-31]. 为此, 不仅需要探讨图像库中所有图像整体的质量评价效果, 而且需要分析各种失真类型的图像质量评价效果. 基于此, 对4个数据库中的每类失真类型的失真图像进行质量评价, 分析不同失真类型下质量评价效果. TID2013, TID2008, CSIQ和LIVE数据库中的所有图像分别采用了24, 17, 6和5种类型的失真. 探讨IQA模型对不同失真类型的泛化性能的方法为: 对每个数据库中的每一类失真类型的图像均采用上述现有的7个IQA模型和所提模型进行质量评价, 并计算其主客观质量评价分数之间的相关性参数, 并得出散点图, 基于相关性参数和散点图对各模型的精度和泛化性能进行对比和分析.
3 -->

5.3.1.相关性参数对比分析

相关性参数PLCC值能够较好地反映主客观IQA分数之间的一致性. 按照上述方法, 采用8个模型, 对4个数据库中的52种失真类型的所有失真图像进行评价, 计算每一类失真图像的客观IQA分数, 以及其与主观IQA分数之间的相关性参数PLCC; 基于PLCC值, 比较8个IQA模型对不同失真类型的失真图像的评价精度及其泛化性能, 结果见表3和图6.

失真类别	PSNR	VSNR	SSIM	FSIMc	VSI	GMSD	MAD	MPCC
1 Additive Gaussian noise(AGN)	0.9552	0.8319	0.8685	0.9152	0.9527	0.9503	0.8897	0.8706
2 Noise in color comp. (NCC)	0.9256	0.7814	0.8050	0.8873	0.9172	0.9118	0.8438	0.8324
3 Spatially correl. noise (SCN)	0.9525	0.8105	0.8621	0.8989	0.9472	0.9391	0.9008	0.7457
4 Masked noise (MN)	0.8707	0.7715	0.8219	0.8492	0.8203	0.7547	0.8009	0.6943
5 High frequency noise (HFN)	0.9731	0.9061	0.9081	0.9475	0.9655	0.9567	0.9233	0.9090
6 Impulse noise (IN)	0.8887	0.7442	0.7415	0.8171	0.8635	0.7572	0.3206	0.7408
7 Quantization noise (QN)	0.8880	0.8384	0.8702	0.8794	0.8747	0.9110	0.8571	0.8122
8 Gaussian blur (GB)	0.9169	0.9437	0.9634	0.9544	0.9551	0.9099	0.9357	0.9252
9 Image denoising (ID)	0.9640	0.9463	0.9589	0.9652	0.9707	0.9759	0.9645	0.9594
10 JPEG compression (JPEG)	0.9167	0.9386	0.9551	0.9754	0.9858	0.9843	0.9638	0.9509
11 JPEG2000 compression (JPEG2 K)	0.9170	0.9513	0.9658	0.9754	0.9845	0.9812	0.9740	0.9452
12 JPEG transm. errors (JPEG trans.)	0.8104	0.8597	0.9181	0.9176	0.9457	0.9079	0.9001	0.8805
13 JPEG2000 transm. errors (JPEG2K trans)	0.9002	0.8435	0.8801	0.8929	0.9192	0.9085	0.8838	0.8699
14 Non ecc. patt. noise (NEPN)	0.6746	0.6774	0.7773	0.8068	0.8162	0.8133	0.8608	0.8132
15 Local block-wise dist. (LBWD)	0.2410	0.3632	0.6022	0.5542	0.4984	0.6520	0.4187	0.6845
16 Mean shift (MS)	0.8056	0.5160	0.8019	0.7869	0.8021	0.7707	0.6934	0.7720
17 Contrast change (CC)	0.5811	0.4251	0.6026	0.7266	0.6974	0.7111	0.3199	0.8108
18 Change of color saturation (CSS)	0.3294	0.4184	0.4590	0.8228	0.8052	0.4234	0.2846	0.7583
19 Multipl. Gauss. noise (MGN)	0.9204	0.7730	0.7896	0.8660	0.9136	0.8911	0.8529	0.8759
20 Comfort noise (CN)	0.8702	0.9016	0.9022	0.9463	0.9546	0.9562	0.9444	0.8476
21 Lossy compr. of noisy (LCN)	0.9429	0.8960	0.9174	0.9564	0.9636	0.9703	0.9562	0.7889
22 Image color quant. w. dither (CQWD)	0.9308	0.8773	0.8619	0.8911	0.8963	0.9192	0.8779	0.8721
23 Chromatic aberrations (CA)	0.9556	0.9592	0.9770	0.9794	0.9748	0.9737	0.9696	0.9473
24 Sparse sampl. and reconstr. (SSR)	0.9296	0.9477	0.9667	0.9776	0.9808	0.9849	0.9766	0.9349
Max	0.9731	0.9592	0.9770	0.9794	0.9858	0.9849	0.9766	0.9594
Min	0.2410	0.3632	0.4590	0.5542	0.4984	0.4234	0.2846	0.6845
波动范围宽度	0.7321	0.5959	0.5181	0.4252	0.4873	0.5614	0.6920	0.2750
所有整体精度	0.7062	0.7402	0.7895	0.8769	0.9000	0.8553	0.8267	0.8648

表3基于TID2013库中24类失真图像评价结果的PLCC值以8个IQA模型的精度对比
Table3.Accuracy comparisons among 8 IQA metrics based on PLCC of IQA results from 24 types of distortion images in TID2013 database.

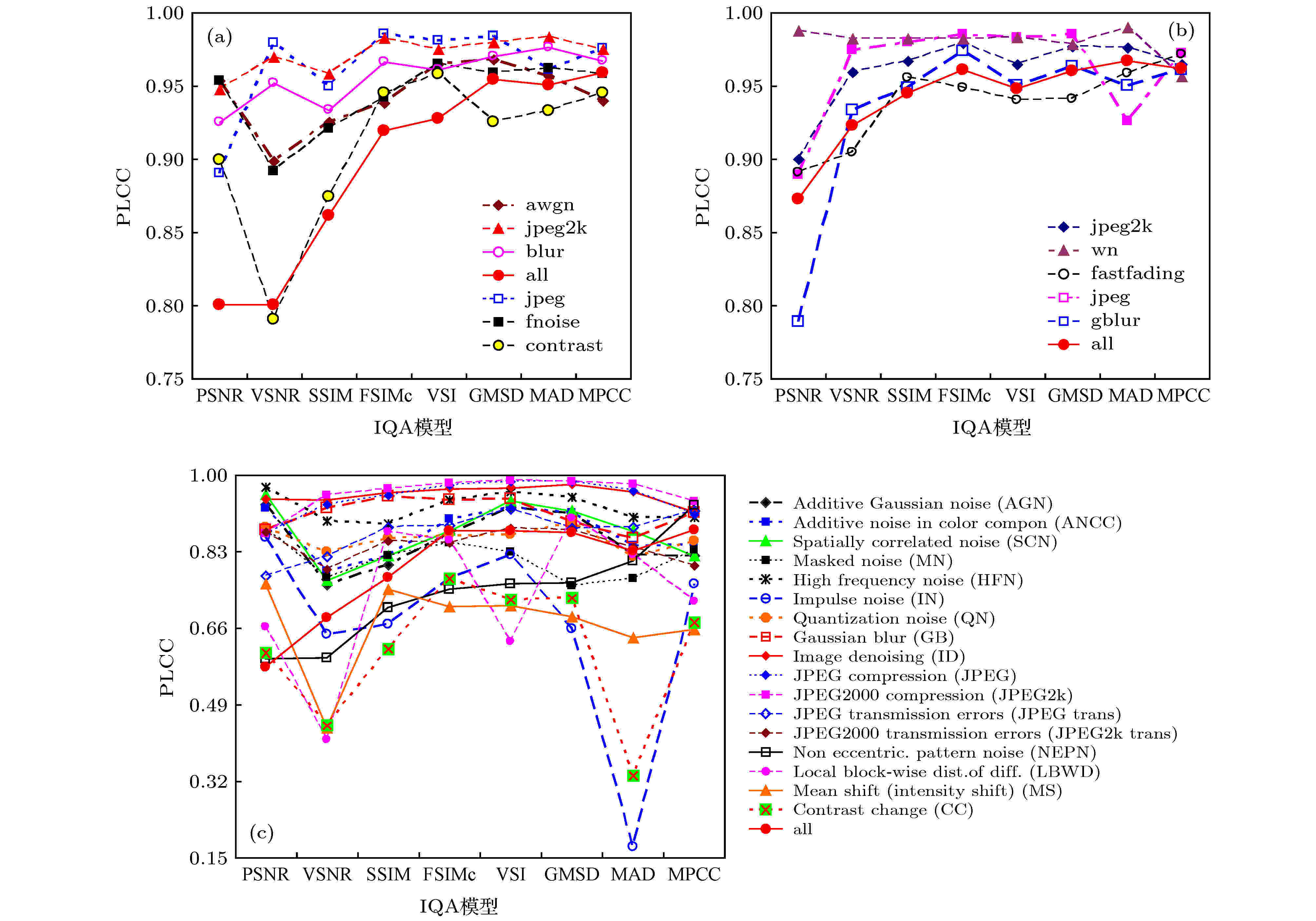图 6 基于3个数据库中28类失真图像评价结果的PLCC值以8个IQA模型的精度对比　(a) CSIQ; (b) LIVE; (c) TID2008
Figure6. Accuracy comparisons among 8 IQA metrics based on PLCC of IQA results from 28 types of distortion images in three databases: (a) CSIQ; (b) LIVE; (c) TID2008.

对比分析表3和图6中所提模型和7个现有IQA模型对4个数据库中52种失真类型的失真图像的质量评价结果, 可得: 从PLCC数值来看, 对于52种失真类型中的大部分类型, 所提模型的IQA精度均处在8个方法中的前一半; 从表3和图6中的最大和最小PLCC值及其波动范围可得, 52种失真类型中, 所提模型和7个现有模型的最高精度PLCC值均能达到0.95以上, 但精度最小值差别较大, 所提模型的最小精度PLCC值可达到0.6573, 而现有的7个IQA模型PSNR, VSNR, SSIM, FSIMc, VSI, GMSD和MAD的最小精度依次只有0.2410, 0.3632, 0.4590, 0.5542, 0.4984, 0.4234和0.1753, 波动较大, 表现了较大的不稳定性, 说明其对不同失真类型具有较差的泛化性能; 对52种失真类型, 7个现有IQA模型的评价效果各有优劣, 性能不一, 即在52种失真类型的IQA中, 7个模型和所提模型的精度PLCC值低于0.5的依次有2, 6, 1, 1, 1, 1, 6和0种类型, 这表明, 对不同失真类型, 所提模型具有较好的泛化性能, 而VSNR和MAD的泛化性能相对较差; 对于7个现有IQA模型, 在52种失真类型的IQA中, 对TID2013中的LBWD, CC和CCS失真类型, 以及TID2008中的NEPN, LBWD, MS, CC失真类型的评价效果均较差, 大部分的PLCC值在0.65以下. 但所提IQA模型对此7类失真类型的评价PLCC值均在0.65以上, 表明所提模型对这些类型的失真图像的评价效果有较好的提升. 5)从模型对数据库中所有图像的整体评价精度上看, 在4个数据库中, 所提模型的精度均能实现8个IQA模型中的最高或次高, 且精度对不同失真类型的波动较小, 表明所提模型不仅对不同失真类型具有较好的泛化性能, 而且还能兼顾不同失真类型间的差异, 使得整体评价精度同样较高.
3 -->

5.3.2.散点图结果分析

散点图上点的离散程度能够地直观地反映出所提IQA模型的精度, 其点的变化趋势能够较好地反映主客观IQA分数之间的单调性和一致性, 而且通过分析点的离散程度, IQA模型对不同失真类型的兼容性(即泛化性能)同样能较好地得到直观说明^[30]. 基于此, 为了说明所提模型对不同失真类型的泛化性能, 采用散点图来分析所提模型, 评价对每一类失真图像的评价性能, 即采用所提模型对4个数据库中的52种失真类型的图像进行评价, 得出其主客观IQA分数之间的散点图, 结果如图7—图10所示, 图中曲线采用最小二乘法LMS拟合而成.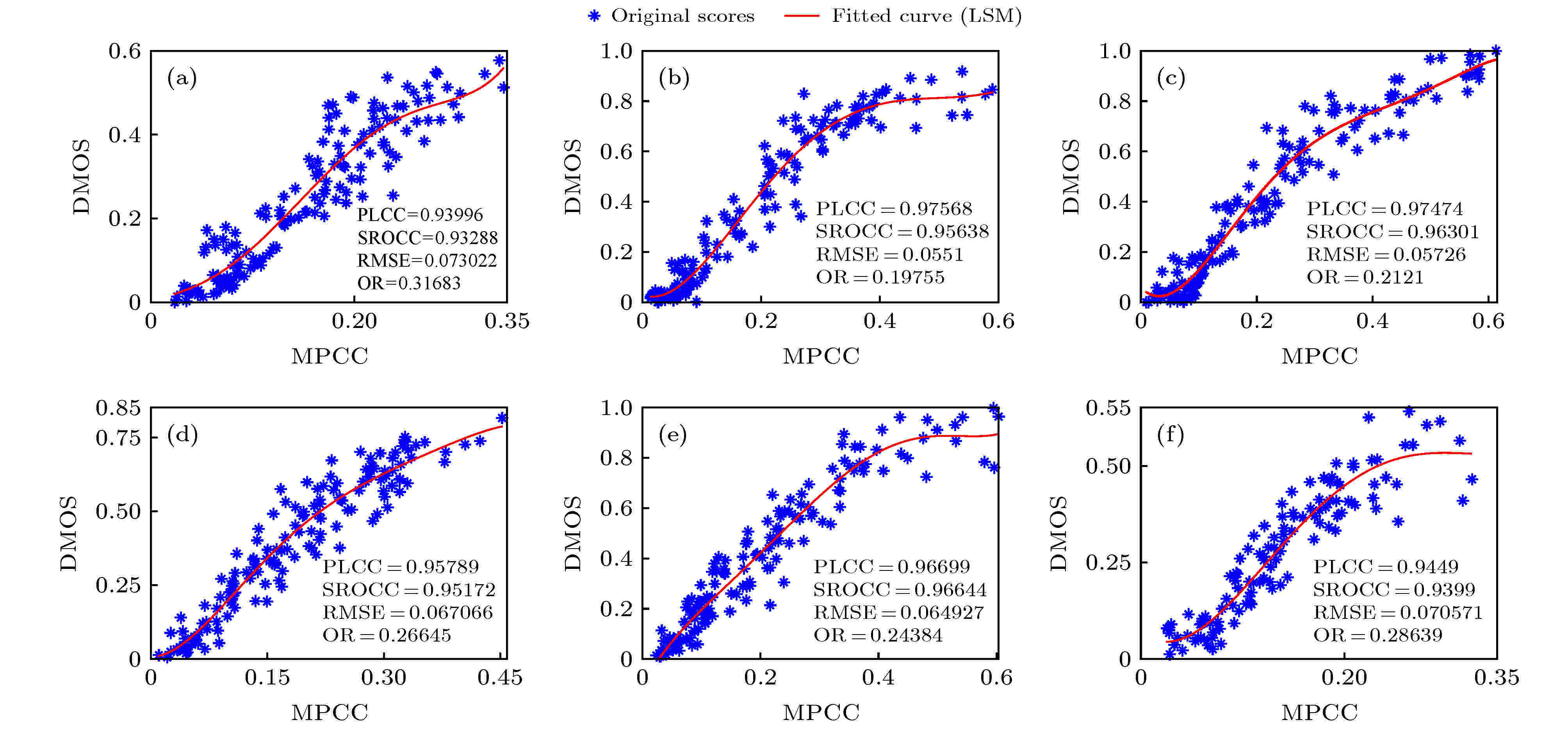
图 7 所提IQA模型对CSIQ库中6种失真类型的失真图像评价结果的散点图　(a) awgn; (b) jpeg; (c) jpeg2k; (d) fnoise; (e) blur; (f) contrast
Figure7. Scatter plots of the IQA results of 6 kinds of distorted images in CSIQ database evaluating by the proposed IQA model: (a) awgn; (b) jpeg; (c) jpeg2k; (d) fnoise; (e) blur; (f) contrast.

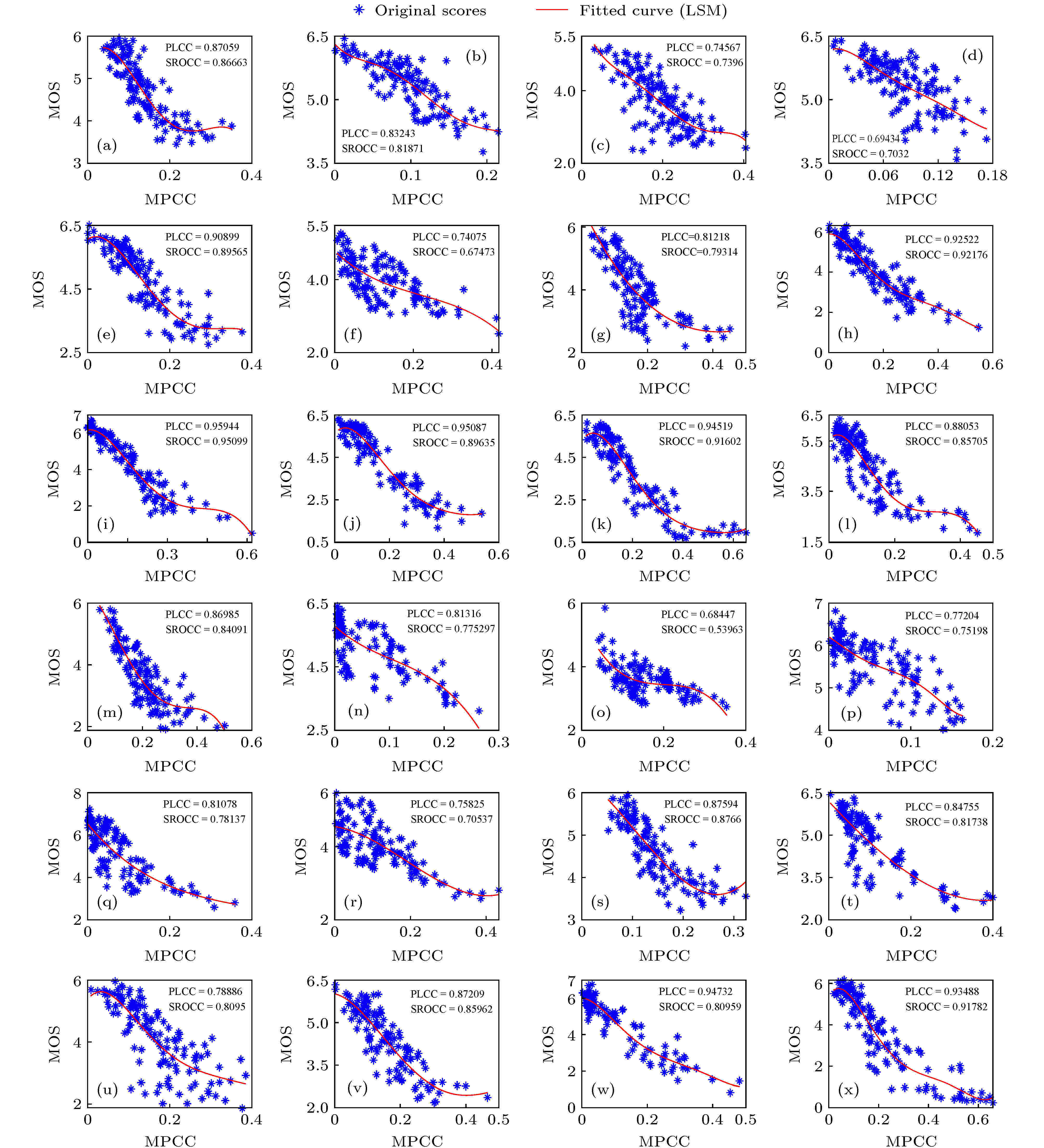图 10 所提IQA模型对TID2013库中24种失真类型的失真图像评价结果的散点图　(a) AGN; (b) NCC; (c) SCN; (d) MN; (e) HFN; (f) IN; (g) QN; (h) GB; (i) ID; (j) JPEG; (k) JPEG2k; (l) JPEGtrans; (m) JPEG2ktrans; (n) NEPN; (o) LBWD; (p) MS; (q) CC; (r) CCS; (s) MGN; (t) CN; (u) LCN; (v) CQWD; (w) CA; (x) SSR
Figure10. Scatter plots of the IQA results of 24 kinds of distorted images in TID2013 database evaluating by the proposed IQA model: (a) AGN; (b) NCC; (c) SCN; (d) MN; (e) HFN; (f) IN; (g) QN; (h) GB; (i) ID; (j) JPEG; (k) JPEG2k; (l) JPEGtrans; (m) JPEG2ktrans; (n) NEPN; (o) LBWD; (p) MS; (q) CC; (r) CCS; (s) MGN; (t) CN; (u) LCN; (v) CQWD; (w) CA; (x) SSR.

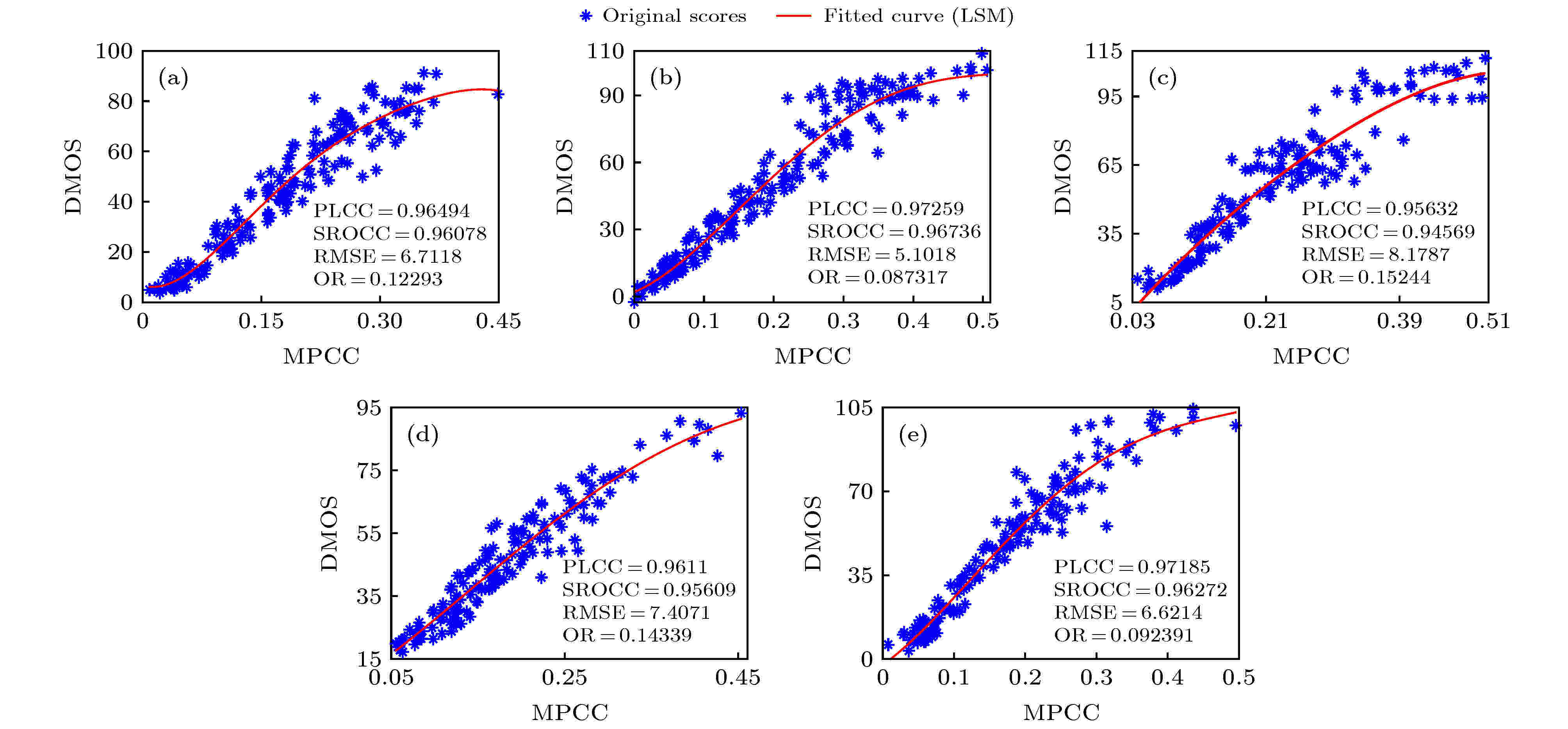图 8 所提IQA模型对LIVE库中5种失真类型的失真图像评价结果的散点图　(a) jpeg2k; (b) jpeg; (c) WN; (d) gblur; (e) fastfading
Figure8. Scatter plots of the IQA results of 5 kinds of distorted images in LIVE database evaluating by the proposed IQA model: (a) jpeg2k; (b) jpeg; (c) WN; (d) gblur; (e) fastfading.

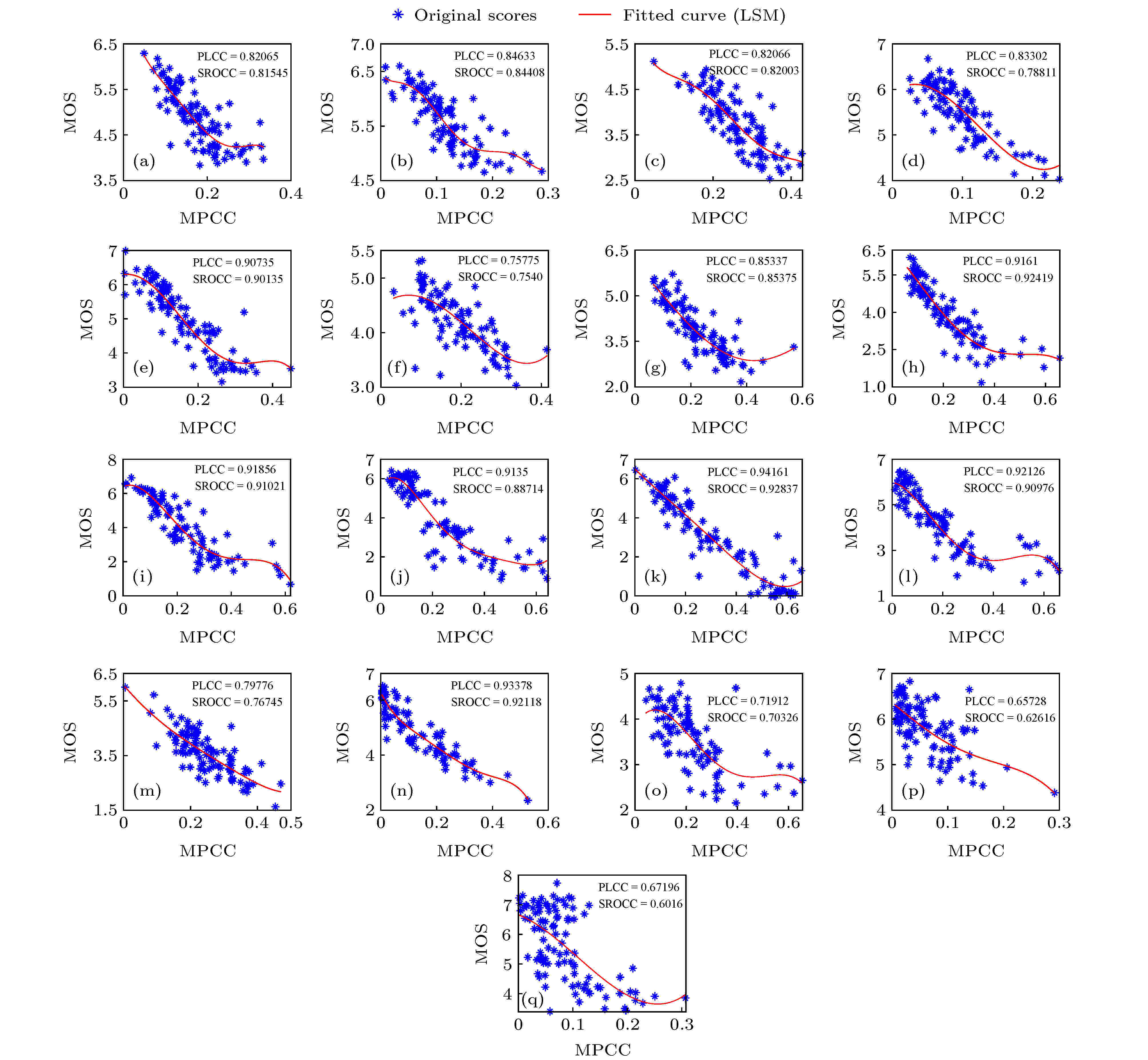图 9 所提IQA模型对TID2008库中17种失真类型的失真图像评价结果的散点图　(a) AGN; (b) ANCC; (c) SCN; (d) MN; (e) HFN; (f) IN; (g) QN; (h) GB; (i) ID; (j) JPEG; (k) JPEG2k; (l) JPEGtrans; (m) JPEG2ktrans; (n) NEPN; (o) LBWD; (p) MS; (q) CC
Figure9. Scatter plots of the IQA results of 17 kinds of distorted images in TID2008 database evaluating by the proposed IQA model: (a) AGN; (b) ANCC; (c) SCN; (d) MN; (e) HFN; (f) IN; (g) QN; (h) GB; (i) ID; (j) JPEG; (k) JPEG2k; (l) JPEGtrans; (m) JPEG2ktrans; (n) NEPN; (o) LBWD; (p) MS; (q) CC.

通过直观上分析图7—图10可得, 所提模型对CSIQ和LIVE中的11类失真图像的质量评价效果均比较好, 散点图上点的离散程度均较低; 对于TID2008数据库, 相对来说, 所提模型对HFN, GB, ID, JPEG, JPEG2k, JPEG trans.和NEPN类型的失真图像的评价效果较好, 散点图上点的离散程度较低, 对MS和CC类型的失真图像的质量评价效果稍差, 但其PLCC值仍然超过0.65; 对于TID2013数据库, 所提模型对其库中每一类失真图像的质量评价效果均较好, PLCC值均超过0.7, 对HFN, GB, ID, JPEG, JPEG2k, CA和SSR类型的失真图像质量评价效果更好, 散点图上点的离散程度较低, PLCC值均超过0.9. 结合在4个数据库中的整体评价精度和每类失真类型图像的评价精度(即表2,表3和图6中的PLCC值)及其散点图(图4), 连同图7—图10, 对比分析7个现有模型, 可以得出, 对于7个现有模型, 它们对单独某一类或几类的失真图像的质量评价效果可能非常好, PLCC值达0.95以上, 但也有不少失真类型的失真图像的IQA精度非常低, 导致数据库中所有图像的整体评价精度受到影响, 如PSNR, VSNR和MAD; 对于数据库中现有失真类型, 每类的IQA效果均比较好, 但总体评价精度不高, 如CSIQ数据库中PSNR和VSNR的结果.
分析以上实验结果的原因, 主要有: 所提模型在构建时, 考虑了图像的亮度色度及其视觉感知、纹理特性及其视觉感知、图像清晰度、以及图像的局部对比的影响, 在4个方面较好地囊括了图像内容及其视觉感知效果, 所以无论是每一类失真图像, 还是所有图像的整体评价, 其效果均表现出不错的性能; 而现有7个模型中, 提取的特征不能更有效地反映图像本身, 以致对部分失真类型无法涉及到, 所以其评价精度不高, 如在TID2013库中, PSNR, VSNR和MAD模型对MS, CC和CSS类型的失真图像的评价, 其评价的分数常常出现无穷大的情况, 这表明这些IQA模型中考虑该方面的因素较少; IQA模型单独对每一类失真的IQA效果均比较好, 但各类失真之间关联度较小, 各类失真图像评价的IQA分数之间离散程度较大, 如在TID2008库中, PSNR, VSNR和SSIM对各类失真的图像评价精度均较高, 但从散点图上可以明显看到, 各个类型的评价分数之间分散程度高, 从而导致整体评价精度不高; 而对于所提模型, 从图4和图7—图10中可以得到, 对每个类型的失真图像的IQA分数, 相互之间均表现为离散程度较低的效果.
以上对不同类型失真的图像质量评价精度、以及每个库中图像整体评价精度的对比分析, 表明所提模型无论在不同数据库之间, 还是对于不同失真类型之间, 均具有较好的泛化性能.

本文基于人类视觉感知特性和图像的灰度梯度、局部对比度和清晰度特征, 提出了一种基于图像内容对比感知的图像质量评价方法及其IQA模型. 在该方法中, 首先结合HVS特性, 采用对比度的定义描述两图像之间的差异, 从而提出一种图像质量定义方法; 再基于图像灰度梯度熵、局部对比度和清晰度, 提出了一种图像内容及其视觉感知的描述方法; 最后, 利用此两方法, 基于图像内容和图像质量定义, 提出了一种图像质量评价方法及其IQA模型. 同时采用CSIQ, LIVE, TID2008, TID2013和IVC共5个图像数据库中的119幅参考图像和6395幅失真图像进行了测试, 且探讨了52种失真类型对IQA的影响, 并与7个现有典型的IQA模型, 从精度、算法复杂性和泛化性能上进行了对比分析. 实验结果表明, 所提IQA模型的精度PLCC值在5个数据库中最低可以实现0.8616, 最高可达到0.9622, 其综合效益优于7个现有IQA模型. 通过综合分析和对比各模型的精度、泛化性能和复杂性, 表明所提模型是一个性能优异的IQA模型.