摘要:氟化镁(MgF₂)是工业用途广泛的重要碱土金属氟化物, 也是矿物质氟镁石的主要成分, 相比于电子结构和光学特性的研究, 人们从地球物理学的角度给予MgF₂高压热物性的研究明显不够, 而组成地球下地幔矿物的高压熔化、热膨胀等热物性预测对理解地球的结构、动力学、演化及起源至关重要. 本文利用基于密度泛函理论的第一性原理方法, 通过热力学、动力学、力学稳定性计算表明萤石结构为MgF₂高压结构, 根据等焓原理, 分别结合广义梯度近似和局域密度近似确定出了零温下MgF₂晶体从稳定金红石结构到高压萤石结构的相转变压力为19.26 GPa和18.15 GPa, 且萤石结构至少稳定到135 GPa (相当于下地幔压力); 利用基于有效势参数模型的经典分子动力学方法, 通过模拟特定压力下MgF₂体系的摩尔体积、总能随温度的变化确认了MgF₂萤石结构在300—6000 K温度范围内的高温稳定性. 在此基础上, 考虑选用能够提高密堆固体平衡特性的交换相关泛函形式的广义梯度近似方法且结合准谐德拜模型, 以及利用根据从头算Hartree-Fock方法获得的数据拟合得到的可靠经验势参数结合经典分子动力学方法, 共同预测了萤石结构的MgF₂在300—1500 K和0—135 GPa的温度和压力范围内的体积热膨胀系数、等温体模量、热弹性参数等重要热力学参量. 研究表明: MgF₂萤石结构基于体积热膨胀系数和等温体模量得到的热弹性参数并非物态方程研究中通常假定的常数, 但在高温高压条件下, 其值接近于常数.
关键词: 氟化镁/
结构相变/
热力学特性/
高温高压

English Abstract

全文HTML

--> --> -->

氟化物晶体材料是一类极其重要的功能晶体材料, 主要应用在激光固体发射器、通信、雷达、催化剂载体、光学棱镜及窗口材料等方面. 氟化镁(MgF₂)是典型的碱土金属氟化物晶体, 具有高抗腐蚀性、高热稳定性以及高硬度、高透过率、低折射率、宽带隙等优异性能, 可广泛应用于各个领域: 作为重要的固体激光器发光介质, MgF₂可用来制作光学棱镜、透镜和窗口等光学元器件, 大尺寸紫外级MgF₂单晶可用于光通信系统以及军工领域, 同时MgF₂是集成光学、光纤通信和激光元件等领域的重要光学镀膜材料^[1,2]; 作为催化剂载体, MgF₂在光催化中也起着重要的作用^[3]; MgF₂也是典型的地矿物质, 1968年在法国首次发现的矿物质氟镁石的主要成分是MgF₂^[4]. 氟化物相对于氧化物和硫化物更容易压缩, 人们可以在较窄的压力范围内观察到更大的晶格应变. 因此, 在很长的一段时间内, MgF₂晶体被看作为研究地幔中离子键型矿物(特别是含共价键的离子晶体)行为的矿物学模型, 也是高压下状态方程发展的实验材料^[5].
在环境压力下, MgF₂与二氧化钛(TiO₂)和二氧化硅(SiO₂)有着相同的相结构, 即以稳定金红石结构存在, 而碱土金属氟化物中的氟化钙(CaF₂)、氟化锶(SrF₂)和氟化钡(BaF₂)都是立方萤石型结构. 早期实验研究表明, 随着压力增加到30 GPa, MgF₂会发生从四角金红石结构到立方CaF₂型萤石结构的相转变^[6]; 2001年, Haines等^[5]的X射线粉末衍射实验结合密度泛函平面波方法的物相分析研究表明, MgF₂在高压下的结构相变行为非常复杂, 即在先于PdF₂型的萤石结构出现之前, MgF₂晶体在约9.1 GPa下会发生从四角金红石结构到正交氯化钙(CaCl₂)结构的相转变, 当压力达到35 GPa时, 出现了氯铅矿(α-PbCl₂)新结构, 由于该实验未能涉及到更高的压力, MgF₂高压CaF₂型萤石结构一直没有观察到; 2014年, ?ztürk等^[7]在关于MgF₂高压结构的从头算模拟研究中, 首次将压力上升到700 GPa, 发现当压力高达280 GPa时, 金红石结构才转变为CaF₂型立方萤石结构; 2017年, Nelson等^[8]利用密度泛函理论方法详细计算了MgF₂晶体压力达70 GPa时的结构相变, 但在0—70 GPa压力范围内未将CaF₂型萤石结构作为MgF₂的候选高压结构进行研究.
分子动力学关于多晶型MgF₂结构相变的研究, 20年前就已展开, 但由于MgF₂原子间相互作用势发展缓慢, 基于早期经验势模型的分子动力学方法一直难以得到合理的结果^[9-11]. Catti等^[11]拟合MgF₂金红石结构的实验晶格参数和弹性常数到两体Born-Mayer势函数形式, 确定出了一套经验势参数; Nga和Ong^[12]利用Catti等^[11]确定的经验势参数, 首次结合常压分子动力学方法研究了216个粒子组成的MgF₂体系从金红石结构到萤石结构的相转变压力, 结果表明MgF₂晶体在压力高达85 GPa的范围内均以稳定金红石结构存在, 之后随着压力的不断增加, 出现一模糊的亚稳结构, 一直到135 GPa (即地球下地幔边界条件的压力), 立方萤石结构才出现; 该结果是早期实验结果的4倍多^[6], 是最新从头算模拟结果的9倍多^[7]. Barrera等^[13]考虑到纯经验拟合势存在的问题, 曾尝试从第一性原理计算导出合适的有效势, 这样做不仅为计算机模拟提供了更为可靠的依据, 而且还可以反过来论证基于第一性原理的电子结构计算方法同有效势之间的联系. 根据从头算Hartree-Fock方法计算得到的MgF₂金红石结构的能量数值, Barrera等^[13]拟合得到了一套势参数, 并结合分子动力学重新估算了MgF₂晶体从金红石到萤石结构的相转变压力, 并和他们自己的从头算Hartree-Fock方法计算结果进行了比较. 分子动力学模拟得到的相变压力为12 GPa, 低于其从头算结果(约30 GPa), 但明显好于Nga和Ong^[12]的早期经典分子动力学模拟结果.
针对MgF₂高压萤石结构, Barrera等^[13]研究了压力达40 GPa时的热弹性参数αK_T随压力的变化, 由于热膨胀系数α是个不易测准的小量, 使得其和等温体模量K_T结合得到的热弹性参数αK_T在高压下完全不符合实际情况, 即αK_T远非物态方程中所假定的常数; Tian等^[14]利用分子动力学方法计算了立方萤石结构的MgF₂的熔化温度, 除了常压下的模拟熔化温度和早期实验数据可比拟外, 其高温高压下的P-V-T数据和基于密度泛函理论的第一性原理方法结合准谐德拜模型得到的最新结果在温度高于800 K时不相符合^[15]. 相比于电子结构和光学特性的研究, 人们从地球物理学的角度给予MgF₂高压热物性的研究明显不够, 而组成地球下地幔矿物在高压下的熔化、热膨胀等物性研究对理解地球的结构、动力学、演化及起源至关重要^[16].
本文采用精确的第一性原理计算方法, 对MgF₂稳定金红石结构和高压萤石结构的相变进行研究, 且通过热力学、动力学、力学稳定性分析来判断MgF₂高压萤石结构的稳定性, 通过经典分子动力学方法模拟MgF₂体系摩尔体积、总能随温度变化以判断萤石结构的高温稳定性. 在此基础上, 分别采用能够提高密堆固体平衡特性的交换相关泛函形式的广义梯度近似方法且结合准谐德拜模型, 以及利用通过筛选根据从头算Hartree-Fock方法获得的数据拟合得到的可靠经验势参数结合经典分子动力学方法, 共同预测萤石结构的MgF₂在300—1500 K和0—135 GPa的温度和压力范围内的体积热膨胀系数、等温体模量、热弹性参数等重要热力学参量, 给出这些热力学参量随温度和压力变化的规律性认识.

2

-->

2.1.第一性原理计算细节

本文采用密度泛函理论框架下的赝势平面波方法, 运用CASTEP软件包来预测MgF₂晶体的相关性质^[17]. 电子和电子之间的交换关联势分别采用CA-PZ形式的局域密度近似(LDA)^[18,19]以及2008年由Perdew等^[20]修订的Perdew-Burke-Ernzerhof形式的广义梯度近似方法(GGA), 芯电子与价电子间的相互作用势由超软赝势实现^[21]. 计算过程中Mg的2p⁶, 3s²和F的2s², 2p⁵电子均被看作价电子处理, 倒易空间布里渊区k点采用Monkhorst-Pack方法选取^[22], 针对四角金红石结构和立方萤石结构, 截断能均取600 eV, 分别采用9 × 9 × 12和15 × 15 × 15的k点网格, 就能很好保证所研究压力范围内的收敛精度. 零压和不同外压条件下MgF₂金红石结构和萤石结构的原子位置优化采用Broyden, Fletcher, Goldfarb和Shanno提出并发展起来的几何算法^[23]. 迭代过程中系统能量收敛标准为5 × 10^–6 eV/atom, 优化后作用在晶胞中每个原子上的力小于0.01 eV/?, 晶胞应力偏差低于0.02 GPa, 公差偏移小于5 × 10^–4 ?. 声子谱的计算采用线性响应方法^[24].
弹性常数是表征材料在微小应力作用下的形变能力的物理量, 可用来判断晶体结构的稳定性以及用来计算固体材料的其他力学性质, 本文采用应力-应变方法计算MgF₂萤石结构在静水压下的弹性常数C_ijkl, 其定义如下^[25]:

${C_{ijkl}} = {\left( {\frac{{\partial {\sigma _{ij}}(x)}}{{\partial {e_{kl}}}}} \right)_X}, $

式中, ${\sigma _{ij}}$和$\partial {e_{kl}}$是施加的应力和欧拉应变张量, X和x是变形前后的坐标. 在静水压P下有

${C_{ijkl}} = {c_{ijkl}} + \frac{P}{2}\left( {2{\delta _{ij}}{\delta _{kl}} - {\delta _{il}}{\delta _{jk}} - {\delta _{ik}}{\delta _{jl}}} \right), $

${c_{ijkl}} = {\left( {\frac{1}{{V(x)}}\frac{{{\partial ^2}E(x)}}{{{\partial _{eij}}{\partial _{ekl}}}}} \right)_X}, $

式中, ${c_{ijkl}}$表示无穷小应变的二阶导数, δ是有限应变变量. 由于应力和应变张量是对称的, 所以弹性刚度张量只有21个非零独立分量. 对于立方晶体, 如本文关注的MgF₂高压萤石结构, 有3个独立的弹性常数, 即C₁₁, C₁₂和C₄₄. 计算中最大应变振幅设置为0.003, 每个应变循环6步, 即产生6个扭曲结构.
2 -->

2.2.分子动力学模拟技术

分子动力学方法的出发点是物理系统的确定性微观描述, 是按照该体系内部的内禀动力学规律来确定位形的转变, 跟踪系统中每个粒子的运动, 然后根据统计物理规律, 给出微观量如分子的坐标、速度与宏观可观测量如温度、压力、弹性模量等的关系. 针对MgF₂立方萤石结构, 首先研究了不同压力下温度对该结构稳定性的影响, 接着预测了该结构在高温高压下的热力学特性. 立方萤石结构的MgF₂模拟体系由768个粒子(256个阳离子、512个阴离子)组成, 在使用有限粒子数来模拟实际体系中粒子的运动时, 需要考虑表面对体系中粒子运动的影响, 为避免这种影响, 通过施加三维周期性边界条件使处于模拟体系中的离子的运动空间成为赝无限. 粒子的初始速度根据模拟体系设定的温度赋值, 压力由维里定理得到, 模拟中长程静电力的处理采用Ewald求和技术^[26], 分别在实空间和倒空间中进行计算. 模拟过程中位能截断采用球形割去法, 截断半径为立方原胞边长的一半. 模拟选用等温等压系综, 即NPT系综. 模拟时间步长设为1 fs, 每个平衡态计算20000步, 前10000步使体系重新平衡到所要求的温度和压力, 然后再用10000步测量温度、体积和压力, 统计各种性质以供分析之用.
从原子层次上对具体材料的性质和过程进行计算机模拟, 其结果的准确性很大程度上依赖于原子间相互作用势的精度和复杂程度, 作用势函数确定后, 通过势函数对原子间的距离求导即可得到分子间的作用力. 本文中, MgF₂晶体各离子间的总相互作用能V_ij由长程库仑能和短程非库仑作用能组成, 短程相互作用取Born-Mayer形式:

${V_{ij}}({r_{ij}}) = \frac{1}{{4{\text{π}}{\varepsilon _0}}}\frac{{{Z_i}{Z_j}{e^2}}}{{{r_{ij}}}} + {A_{ij}}\exp \left( { - \frac{{{r_{ij}}}}{{{\rho _{ij}}}}} \right) - \frac{{{C_{ij}}}}{{r_{ij}^6}}, $

式中, 各项分别表示库仑能、排斥能项和范德瓦耳斯项(偶极-偶极项), 其中Z_i和Z_j为有效电荷, r_ij为原子之间的相互作用距离, A_ij和ρ_ij是排斥势参数, C_ij为范德瓦耳斯常数. 对许多离子材料来说, 短程相互作用取Born-Mayer势是一个十分传统而有效的模型, Born-Mayer势将排斥势与静电相互作用联合起来以描述离子晶体中的相互作用, 能够反映大部分典型二元金属化合物高温高压下的实际物性^[27-30]. 模拟中, 选用了两套势参数: Catti等^[11]拟合MgF₂金红石结构的实验晶格参数和弹性常数用到两体Born-Mayer势函数形式, 并确定出一套经验势参数, 记为模型I (Model 1); Barrera等^[13]根据从头算Hartree-Fock方法计算得到的MgF₂金红石结构的能量数值, 拟合得到了一套势参数, 记为模型II (Model 2). 这两套经验势参数很早被用来研究MgF₂晶体从四角金红石结构到立方萤石结构的相转变, 为后期第一性原理计算结果提供了可供比较的参考数据.

2

-->

3.1.萤石结构MgF₂的高压稳定性

常压下MgF₂以金红石结构存在, 早期研究表明, 随着压力的增加, MgF₂会发生从金红石结构到立方萤石结构的相转变. MgF₂金红石结构和萤石型结构如图1所示, 其中萤石结构具有较高的对称性, 存在两种配位体: 一种为以金属Mg原子为中心的Mg-8F立方体, 其中Mg原子位于立方体中心, 其余8个F原子分别位于立方体顶点; 另一种为以F原子为中心的F-4 Mg正四面体, F原子位于正四面体中心, Mg原子位于正四面体顶点. 图2(a)和图2(b)分别给出了利用GGA和LDA方法计算得到的MgF₂零温下的两种结构的焓与压力的关系, 内插图同时给出了它们的每个分子式的焓差随压力的变化, 以帮助准确地确定相变压力. 由图2可以看出, 零温下MgF₂金红石结构比萤石结构更稳定, 利用GGA和LDA两种不同交换相关函数计算得到的MgF₂从金红石结构到萤石结构的相变压力差别很小, 分别为19.26 GPa和18.15 GPa. 本文基于密度泛函理论的第一性原理计算结果给出的相变压力接近早期实验结果^[6]和最新从头算结果^[13], 但与?ztürk等^[7]、Nga和Ong^[12]的经典分子动力学模拟结果相比, 差别较大, 分析差别产生的原因, 除了早期分子动力学模拟给出的模拟体系太小容易忽略模拟背景之外, 主要是模拟采用的经验势参数模型引起的: 短程势采用通常处理离子晶体的两体Born-Mayer势, 显得过于简单; 拟合所用源数据是实验得到的基态结构参数, 不能反映高压情况; 势参数拟合用到了弹性常数, 而和晶格参数相比, 弹性常数是为对势函数所特别敏感的量, 从势函数拟合的角度讲, 弹性常数不是一个好量.
图 1 MgF₂晶体(a) 金红石结构和(b) 立方萤石结构示意图, 其中大球代表Mg原子, 小球代表F原子
Figure1. Crystal structures of MgF₂ with (a) the rutile-type phase and (b) the fluorite-type phase. The large and small spheres represent magnesium and fluorine atoms, respectively.

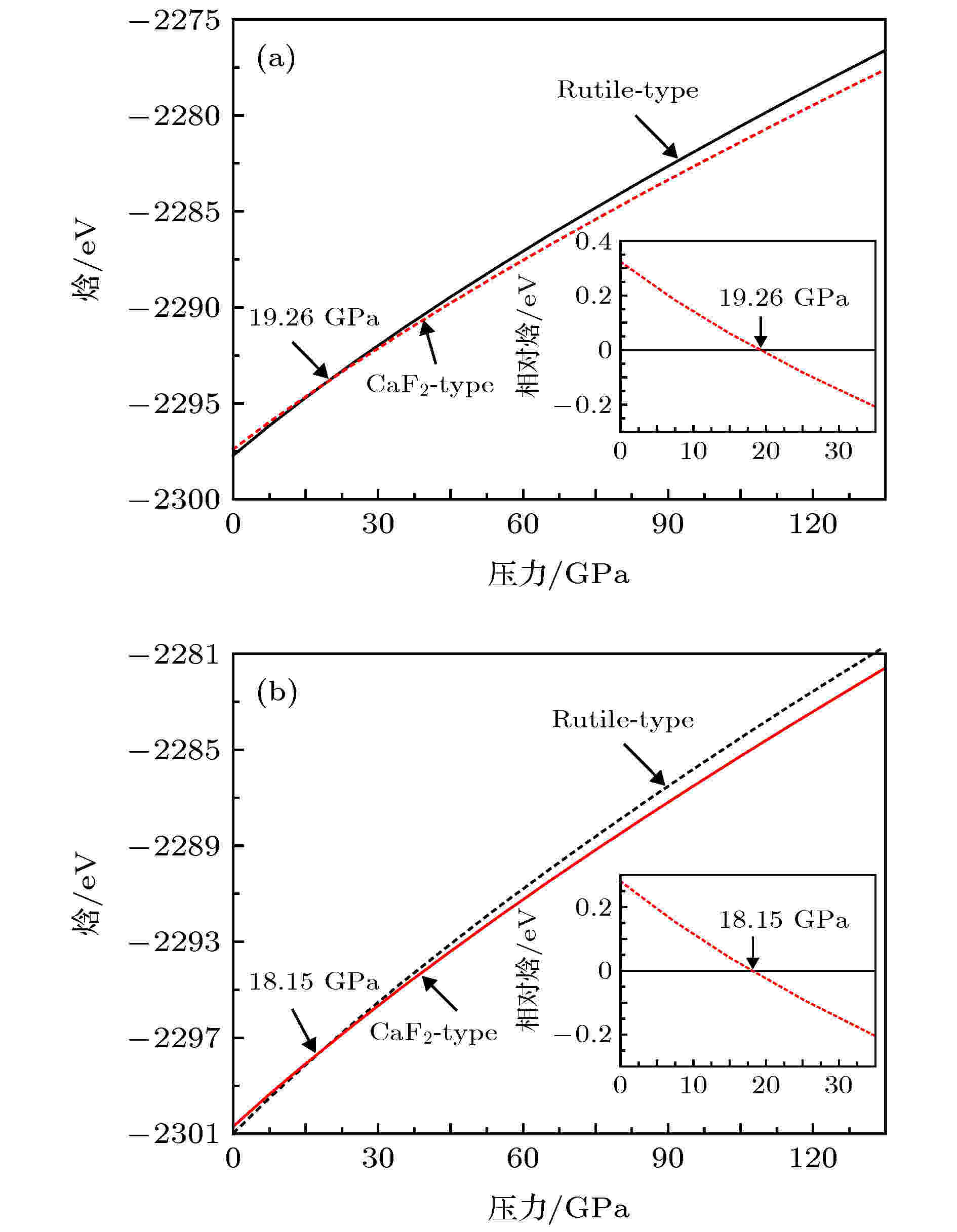图 2 利用(a) GGA和(b) LDA方法分别计算的MgF₂晶体金红石结构和萤石结构零温下的焓随压力的关系, 内插图分别为两种结构的MgF₂每个分子式的相对焓随压力的变化
Figure2. Calculated enthalpy as a function of pressure in the framework of (a) GGA and (b) LDA for MgF₂ with the rutile-type and fluorite-type structures at zero temperature. In the inset, the relative enthalpy versus pressure is presented.

在从微观角度分析材料的物理性质方面, 能带结构起着重要的作用. 利用GGA方法计算得到的MgF₂晶体金红石结构在零压和相变压力为19.26 GPa下的能带结构以及萤石结构在相变压力为19.26和135 GPa高压下的能带结构分别如图3(a)和图3(b)所示. 从图3(a)可以看出, MgF₂金红石结构的禁带宽度最窄的地方出现在G点处, 为直接带隙: 零压下, 导带与价带之间的带隙宽度为6.57 eV, 该值与文献结果6.97 eV^[31]相符合, 与实验值10.08 eV^[32]相比较偏小; 随着压力增加到19.26 GPa, 带隙宽度增加到7.59 eV. 从图3(b)可以看出, MgF₂萤石结构在相变压力为19.26和135 GPa下价带的顶点在X点, 而导带的底点在G点, 即价带的最高点与导带最低点不在同一点, 故属于间接带隙, 带隙宽度分别为6.89和9.71 eV. 本文的计算结果与实验值之间的差异是由于密度泛函理论计算的是基态近似的结果, 而在真实体系中的能隙属于激发态, 这在计算材料界是普遍存在的现象, 并不影响人们对MgF₂晶体电子结构的分析和研究.
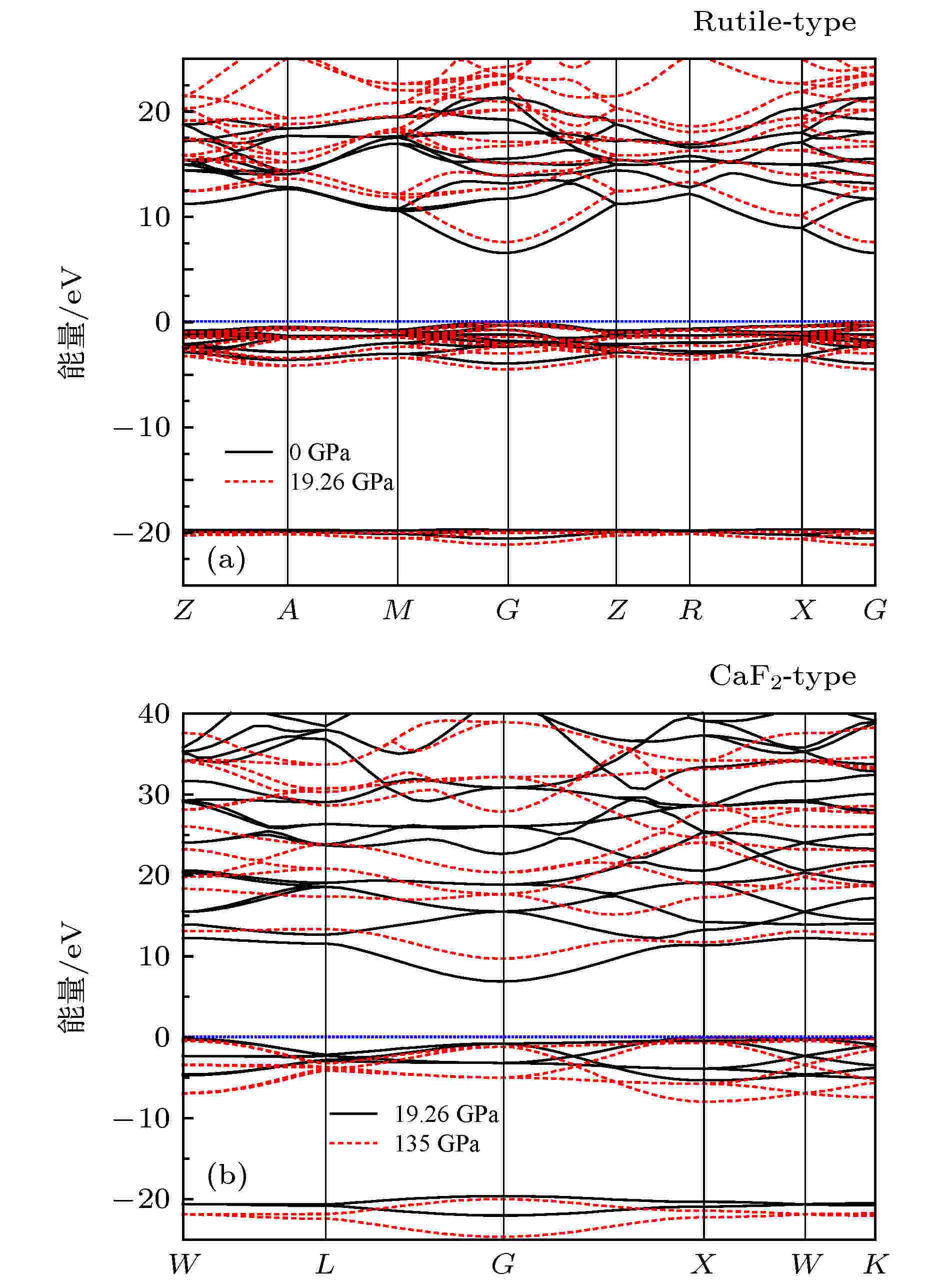图 3 利用GGA计算得到的MgF₂晶体(a) 金红石结构在零压和相变压力为19.26 GPa下的能带结构以及(b) 萤石结构在相变压力为19.26和135 GPa下的能带结构
Figure3. Calculated band structures of MgF₂ using GGA method: (a) The rutile-type phases at 0 and 19.26 GPa; (b) the fluorite-type phase at 19.26 and 135 GPa.

声子谱, 即格波的角频率与波矢量的关系曲线, 通过对晶体材料声子谱研究可以明确材料是否具有动力学稳定性特征. 为了检验MgF₂金红石结构和萤石结构的动力学稳定性, 在密度泛函理论框架下采用GGA近似、结合线性响应方法^[24]分别计算了金红石结构在零压和相变压力为19.26 GPa下的声子谱及萤石结构在下地幔压力135 GPa下的声子谱: MgF₂四角金红石结构的原胞共有6个原子, 立方萤石结构的原胞共有3个原子, 因此从理论上而言MgF₂晶体的两种结构应各有18和9种色散关系, 即应各有18和9条声子谱计算曲线, 在波矢的某些取值范围内, 这些声子谱曲线有些是重叠的, 如图4所示. 由图4可以看出, 零压下MgF₂晶体金红石结构为稳定结构, 当压力达到相变压力19.26 GPa时, 金红石结构的声子谱有虚频存在, 说明该结构在这种状态下是不稳定的, 即有相变发生, 符合前面热力学稳定性计算结果; 高压萤石结构当压力达到地球下地幔压力135 GPa时, 其声子谱在整个布里渊区没有虚频出现, 这意味着在该压力下, 它是动力学稳定的.
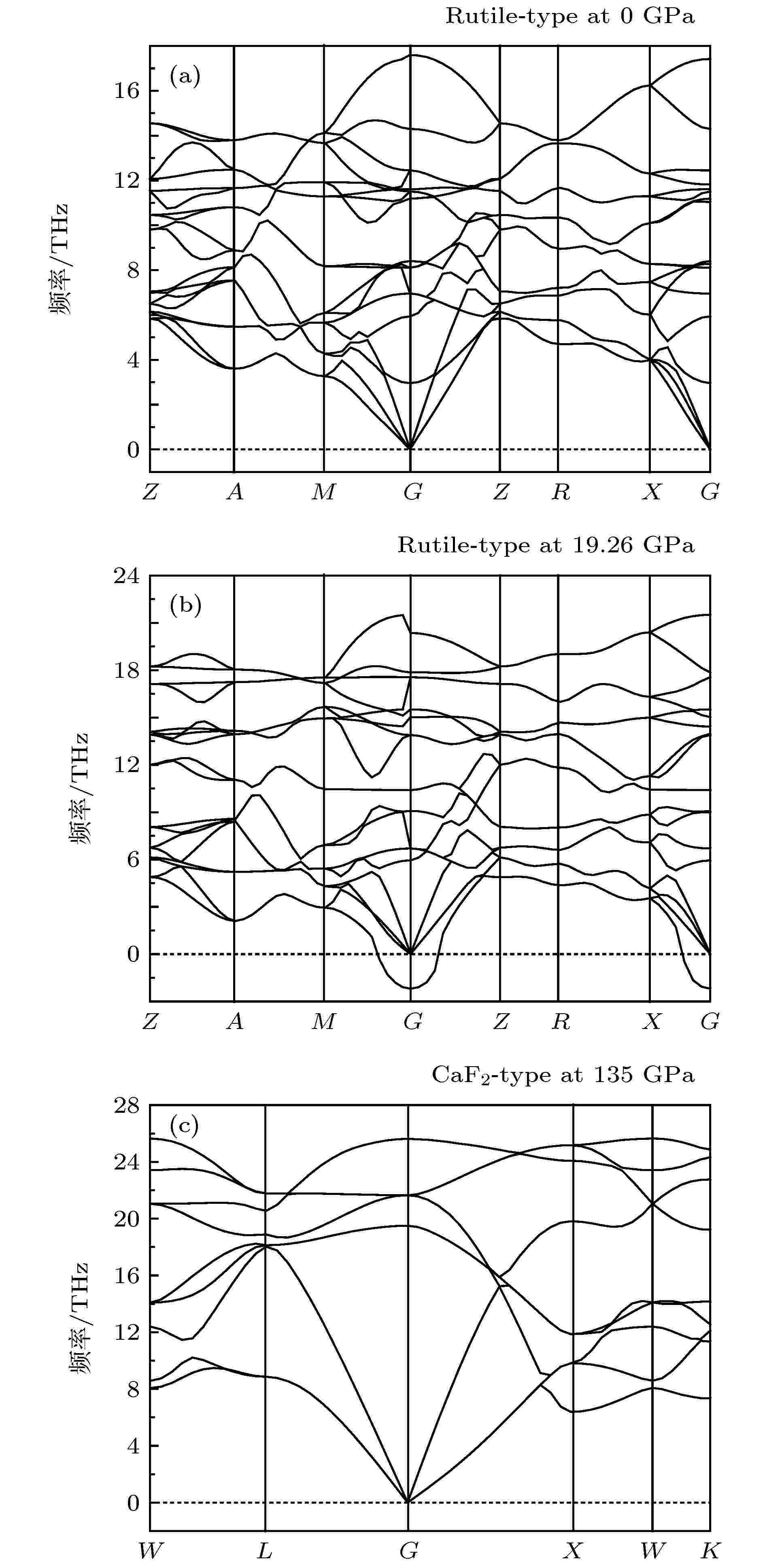图 4 利用GGA计算得到的MgF₂晶体金红石结构在(a)零压、(b)相变压力为19.26 GPa下的声子谱和(c)萤石结构在135 GPa下的声子谱
Figure4. Calculated phonon spectra of MgF₂ with the rutile-type phases at (a) 0 GPa and (b) 19.26 GPa and with (c) the fluorite-type phase at 135 GPa using GGA method.

弹性常数是反映固体对弹性形变的抵抗能力的物理量, 通过弹性常数可以了解晶体的脆性破坏、屈曲、弹性波的传播及德拜温度等方面的信息, 也可以判断晶体结构的稳定性. 对于立方晶系的晶体, 比如MgF₂萤石结构, 由于其应变能必须为正, 因此晶体的力学稳定性必需满足下列条件^[33]:

${C_{11}} + 2{C_{12}} > 0,\;{C_{44}} > 0,\;{C_{11}} - {C_{12}} > 0.$

本文利用GGA方法计算得到的MgF₂萤石结构在下地幔压力135 GPa下的弹性常数C₁₁, C₁₂和C₄₄分别为945.34 GPa, 368.99 GPa和53.98 GPa. 图5给出了利用GGA计算得到的MgF₂萤石结构的弹性常数随外加静压的变化, 这里未考虑其和金红石结构之间的相变. 在研究的0—135 GPa的压力范围内, 可以发现代表弹性尺度的弹性常数C₁₁受压力的影响要比表征在晶体形状方面的弹性的弹性常数C₁₂和C₄₄都要大. 弹性常数C₁₁和C₁₂随压力的增加而增加, 但C₁₁随压力的变化比C₁₂更为明显, 而弹性常数C₄₄随压力的增加逐渐减小. 在本文研究的压力范围内, 弹性常数均满足以上力学稳定性判据, 这表明MgF₂萤石结构是力学稳定的.
图 5 利用GGA近似计算的MgF₂萤石结构的弹性常数C_ij随外加压力的变化
Figure5. Pressure dependence of the elastic constants C_ij for MgF₂ with the fluorite-type structure.

2 -->

3.2.萤石结构MgF₂的高温稳定性

本节拟利用分子动力学模拟方法预测MgF₂晶体萤石结构的高温稳定性. 为了检验所选取的两体势函数和势参数模型I、模型II在高温高压下的可靠性, 在判断MgF₂晶体金红石和萤石结构相变的基础上, 比较了分子动力学模拟方法和第一性原理计算方法得到的MgF₂萤石结构压力达135 GPa、温度达1000 K下的压力(P )-体积(V )-温度(T )数据即物态方程计算结果, 如图6所示, 其中图6(a)给出了分子动力学方法结合经验势参数模型I和模型II预测的MgF₂萤石结构在300 K温度下的体积比率随压力的变化, 图6(b)给出了50 GPa压力下利用两种势参数模型得到的MgF₂萤石结构的体积比率随温度的变化, 内插图为0.1 MPa下利用模型II计算得到的MgF₂萤石结构的体积比率随温度的变化, 以上结果均和密度泛函理论框架下的GGA及LDA近似结合准谐德拜模型(QHD)^[34]计算的结果进行了比较, QHD计算所要求的MgF₂萤石结构的总能与体积的关系由图7给出.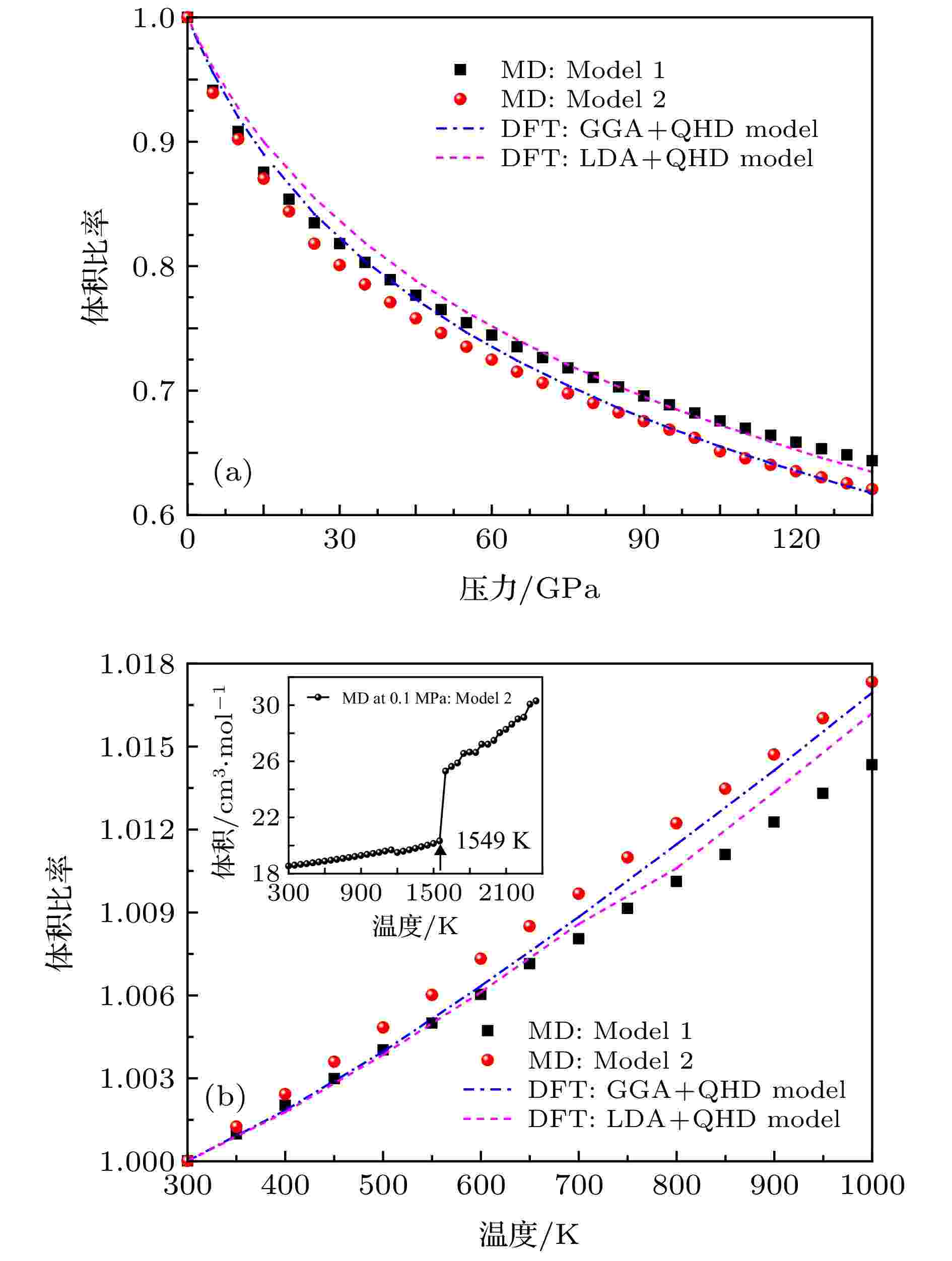
图 6 利用分子动力学模拟和第一性原理计算得到的MgF₂萤石结构 (a) 在300 K下的体积比率随压力的变化和(b) 在50 GPa下的体积比率随温度的变化, 内插图为0.1 MPa下的模拟结果
Figure6. Volume ratios of MgF₂ with the fluorite-type structure obtained from molecular dynamics simulations and first-principles calculations: (a) Volume ratios under different pressures at 300 K; (b) volume ratios under different temperatures at 50 GPa, where in the inset, the data at 0.1 MPa is presented.

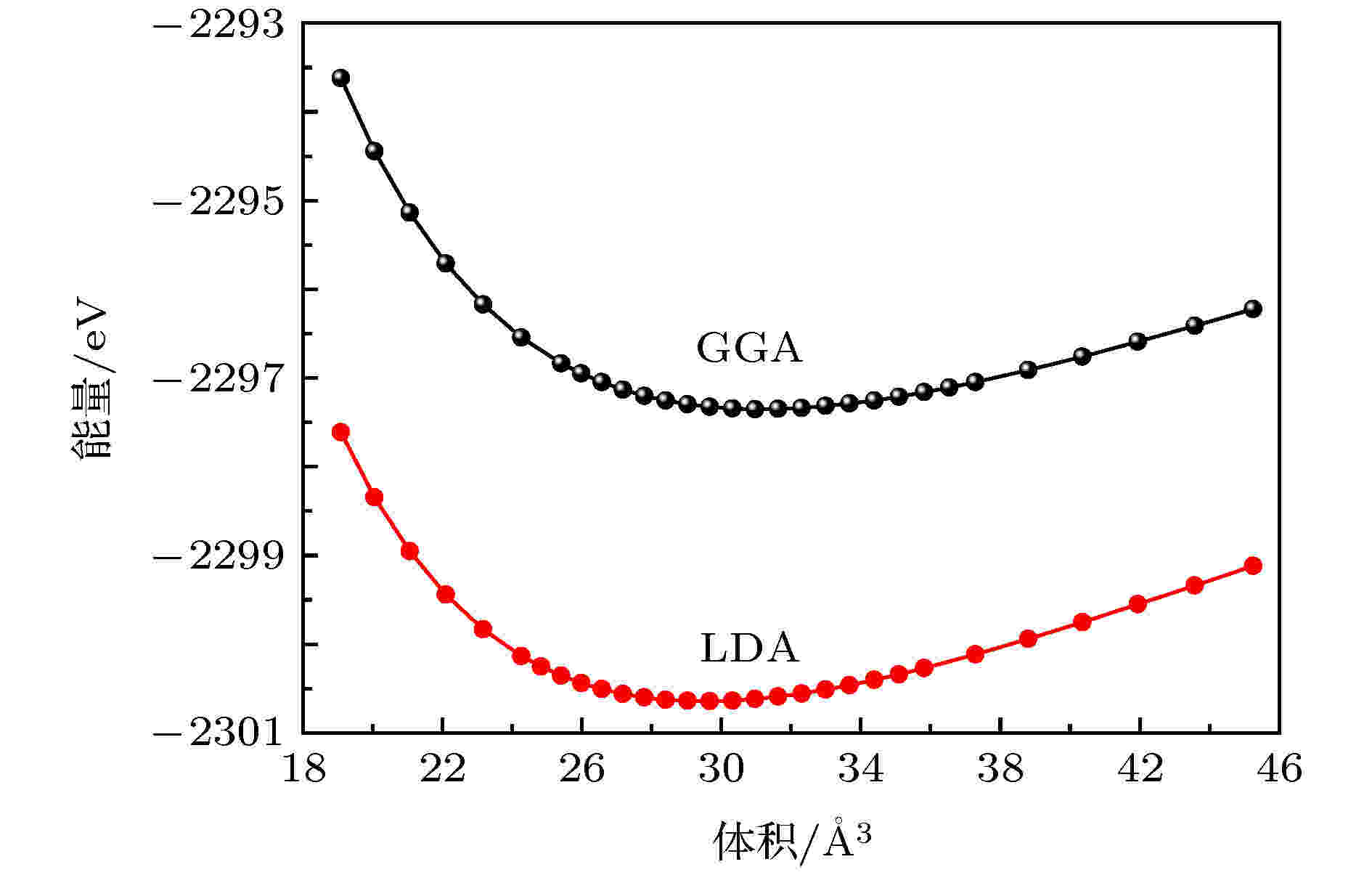图 7 利用GGA和LDA计算得到的MgF₂萤石结构的原胞总能随体积的变化
Figure7. Energy as a function of primitive cell volume for MgF₂ with the fluorite-type structure using GGA and LDA calculations.

在密度泛函理论框架内, 由于GGA和LDA方法上的差别, 使得基于LDA第一性原理计算往往低估晶格常数从而低估模拟体积, 所以在整个研究的压力范围内, 两种近似关于MgF₂晶体萤石结构的体积比率随压力变化的模拟结果存在差别, 这由图6(a)可以看出. 低压下, 分子动力学方法结合经验势参数模型I和模型II预测的结果和GGA结合QHD计算结果符合, 随着压力的增加, 两套势参数得到的分子动力学模拟结果差异逐渐变大, 其中模型II得到的结果更符合GGA结合QHD计算的结果, 这在图6(b)中特定压力下MgF₂萤石结构的体积比率随温度的变化关系中也得到了体现. 本工作GGA计算中的交换相关泛函采用修订的Perdew-Burke-Ernzerhof形式^[20], 目的是提高研究对象在高压下作为密堆固体的平衡特性, 同时GGA在处理电子与电子之间的交换关联作用时考虑了局域及非均匀效应, 能得到比LDA方法更精确的结果, 而分子动力学模拟中, 选取的模型II势参数由Barrera等^[13]根据从头算Hartree-Fock方法得到, 和模型I采用的拟合实验晶格参数和弹性常数得到的结果^[11]相比要更为准确, 所以两种方法, 即GGA方法和基于模型II的分子动力学方法得到的MgF₂萤石结构的P-V-T数据在研究的整个温度和压力范围内相互吻合符合我们的预期. 后文中, 高温高压下MgF₂萤石结构的熔化温度及体积热膨胀系数、等温体模量等热力学参量随温度和压力的变化, 利用GGA结合QHD模型或基于模型II的分子动力学方法来进行可靠预测.
萤石结构MgF₂晶体的高温稳定性, 通过其熔化特性来判断. 从晶体结构的观点来看, 熔化现象是固体在高温作用下原子的热振动使晶体结构从长程有序到无序转变造成的结果. 固体发生熔化时, 固、液两相的吉布斯自由能相等, 而体积发生突变, 且伴随着熵增, 因此, 属于一级相变. 在熔化过程中, 其抗剪切能力消失, 在结构上由长程有序结构变为无序结构, 固、液两相之间在晶体学上没有任何明确的位向关系, 因此属于重构性相变. 物质在极端压力条件下的熔化行为非常复杂, 需涉及复杂的离子间的相互作用问题, 本文选用检验可靠的经验势参数模型, 结合分子动力学方法模拟了不同压力下(0.1 MPa, 10 GPa, 50 GPa, 100 GPa和135 GPa)萤石结构MgF₂体系在300—6000 K温度范围内的摩尔体积和总能随温度的变化, 如图8所示. 由图8可以看出, 萤石结构MgF₂晶体在加热到一定温度时, 对应的摩尔体积和总能发生了明显的跃变: 在0.1 MPa (即环境压力)下, 得到的跳变温度为1549 K (见图6(b)内插图); 在10, 50, 100和135 GPa压力下, 得到的跳变温度分别为2149, 3583, 4395和4699 K. 随着压力不断增加, 熔化温度的增加速率逐渐变得缓慢.
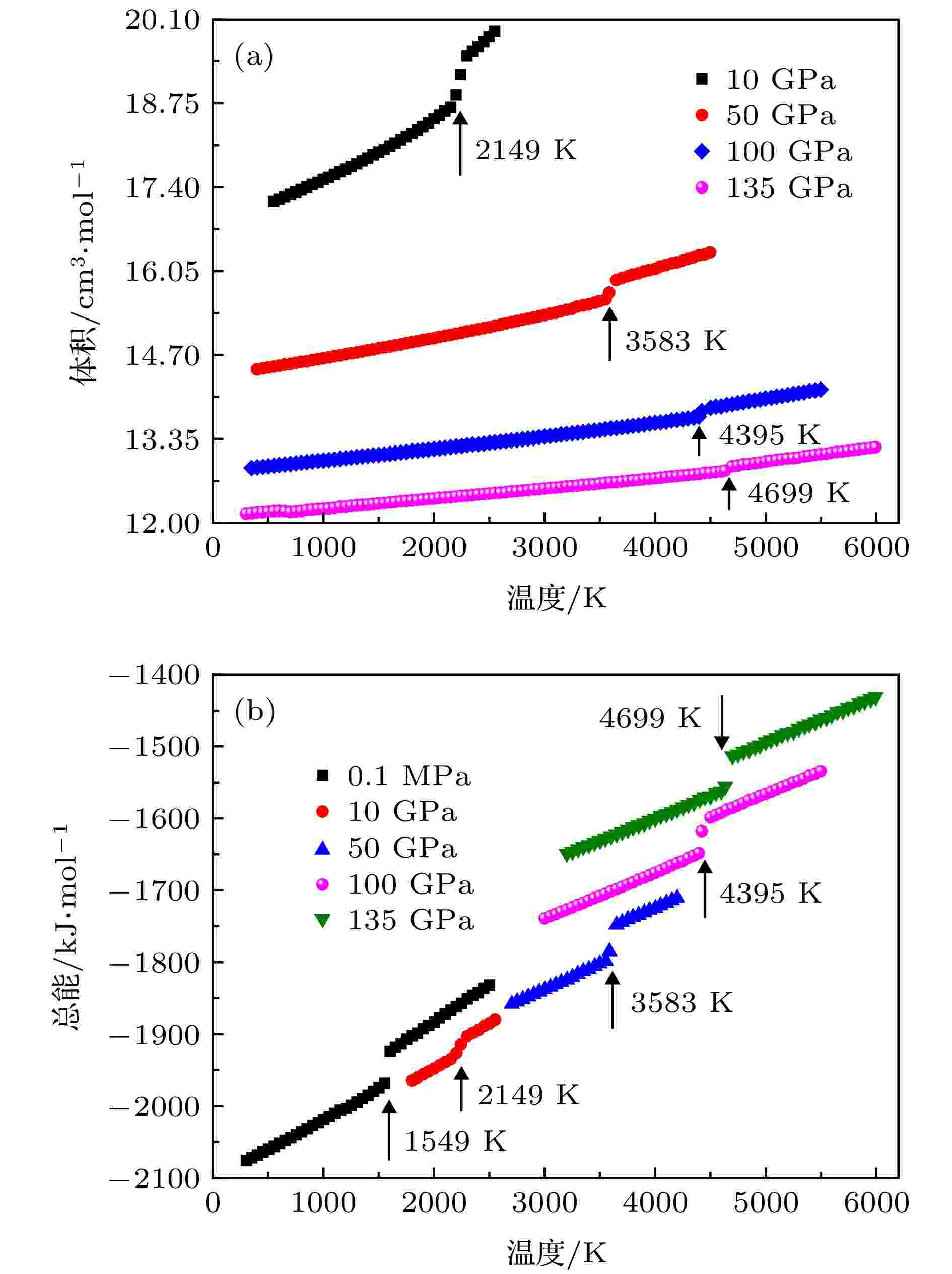图 8 利用分子动力学模拟得到不同压力下的MgF₂萤石结构的(a) 摩尔体积随温度的变化和(b) 总能随温度的变化
Figure8. (a) Molar volume and (b) total energy of MgF₂ with the fluorite-type structure as a function of temperature under different pressures calculated by molecular dynamics.

利用单相分子动力学模拟熔化时, 宏观现象会出现摩尔体积、自由能、熵、焓等物理量的不连续性变化, 所以可以初步地判断为常压下萤石结构MgF₂体系在约1549 K时发生了熔化. 一般认为体积突变对应的温度不是被模拟晶体的真正熔化温度, 因为模拟温度通常要高于实验得到的熔化温度, 其和实验熔化温度的差异被归结为过热所致, 过热率的多少, 与所采用的原子间作用势参数模型的影响很大. 本文中, 所采用的分子动力学优选势参数模型给出的萤石结构的MgF₂的体积跃变对应的温度接近实验熔化温度1539 K^[35], 所以可作为参考熔化温度, 显然MgF₂晶体在低于该温度时, 皆能保持其立方萤石结构直至135 GPa.
图9给出了单相分子动力学模拟得到的MgF₂晶体萤石结构压力达135 GPa的熔化相图. 碱土金属氧化物MgO和碱土金属氟化物MgF₂同属重要地矿物质, 同时提供了经典分子动力学方法结合描述离子极化特性的壳层模型(shell model)和描述离子压缩效应的呼吸壳层模型(breathing shell model)得到的MgO岩盐结构的高压熔化相图以作比较^[27]. 可以看出: 在零压下, MgO的熔化温度高于MgF₂的熔化温度; 随着压力的增加, 同为立方结构的MgF₂和MgO熔化温度均逐渐增加; 在高压下, 它们的熔化温度随压力的增加逐渐变得缓慢; 在所研究的整个压力范围内, MgF₂和MgO的熔化曲线具有相同的趋势.
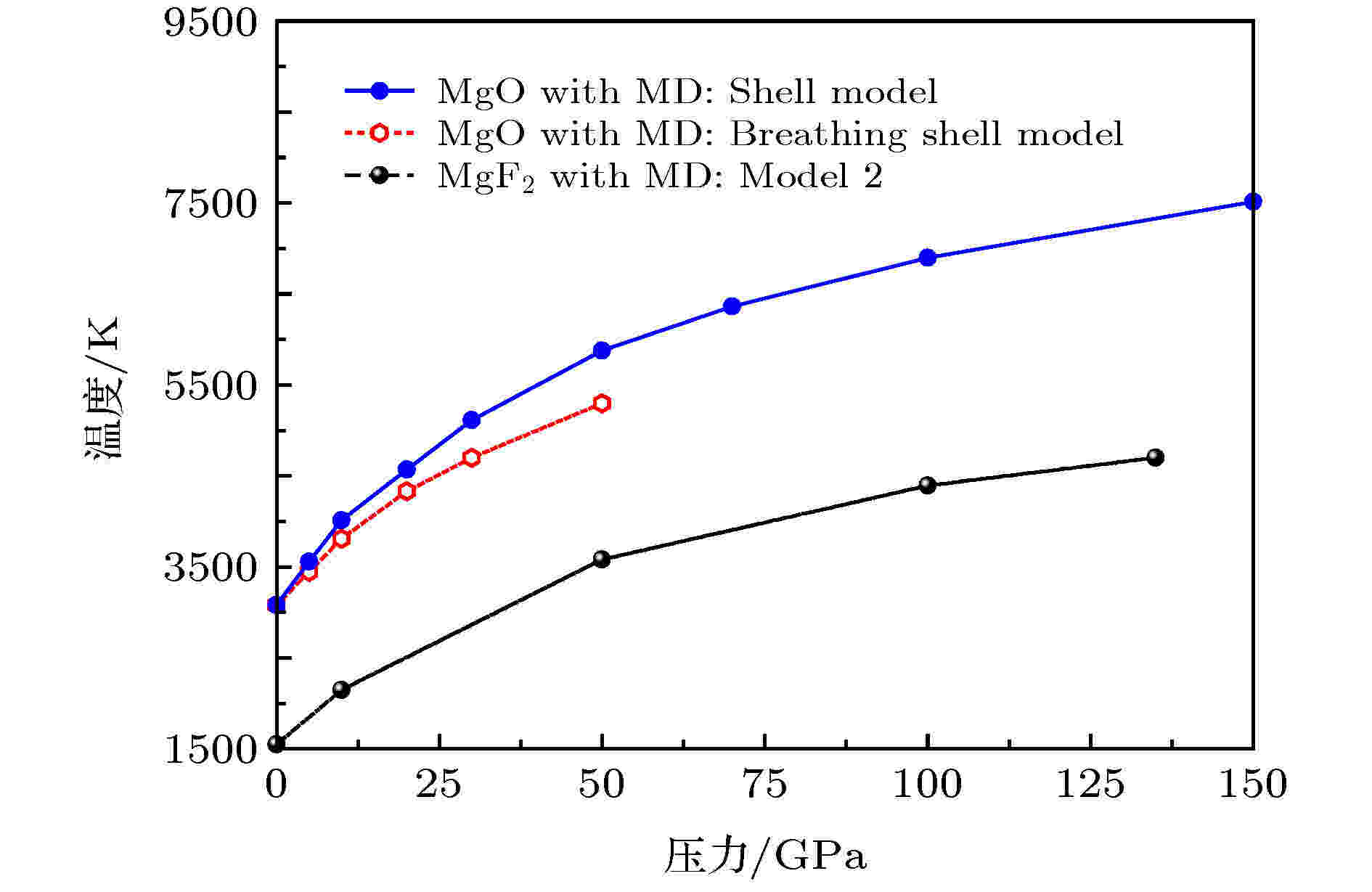图 9 分子动力学模拟得到MgF₂晶体萤石结构的熔化相图及和MgO岩盐结构熔化相图的比较
Figure9. Melting phase diagram of MgF₂ with the fluorite-type structure obtained from molecular dynamics (MD) simulations, in comparison with the calculated melting phase diagram of the rocksalt phase of MgO.

2 -->

3.3.萤石结构MgF₂的高压热物性可靠预测

热力学性质是晶体材料最重要的性质, 它们对压强P、温度T和体积V的导数描述了晶体在各种热力学变化条件下的行为、状态方程和响应函数. 材料热力学特性涉及到的重要热力学参量有热膨胀系数、体弹性模量、热弹性参数等. 这些固体非线性参量是固体内组成原子(或分子)作非简谐振动的表征, 它们在物理学、材料科学、地球物理等的研究中有着重要的意义和作用, 尤其对物质系统的物态方程研究有着不可忽视的地位^[36]. 比如要计算矿物质的热力学函数, 就必须对热膨胀系数、体弹性模量和比容在整个感兴趣的压力和温度范围内都有准确的认识. 再如为了解决固体材料在高温物理方面的应用, 就需要掌握固体从室温到熔化温度的热膨胀数据, 这也正是研究地球内部一定深度处的温度、组成物质密度等地球物理、地球化学理论的基础知识和必要条件; 同时热膨胀系数与状态方程参量有着密切关系, 是研究状态方程的一个重要内容与途径: 如果已知物质系统的状态方程, 就可以利用其定义对膨胀系数在理论上进行预测计算, 反之如果掌握热膨胀系数与其他状态参量之间的函数关系或与其相关的实验数据, 就可以根据数学处理或作图分析等方法来研究物质系统的状态方程及其相关的热力学性质. 相比于电子结构和光学特性的研究, 人们从地球物理学的角度给予MgF₂高压热物性的研究明显不够, 本文在系统研究MgF₂高压萤石结构稳定性的基础上, 利用可靠的计算机模拟手段对其热物性进行了研究.
图10和图11分别给出且比较了环境温度和压力下(300 K, 0.1 MPa)利用不同方法模拟得到的MgF₂萤石结构的体积热膨胀系数α、等温体弹性模量K_T、热弹性参数αK_T随压力和温度的变化, 同时给出了利用优选的分子动力学经验势参数模型和GGA结合QHD方法可靠预测的不同温度(500, 1000, 1500 K)和压力(50, 100, 135 GPa)下的MgF₂萤石结构的体积热膨胀系数、等温体弹性模量、热弹性参数随压力和温度的变化, 模拟的整个温度和压力范围为300—1500 K和0—135 GPa.
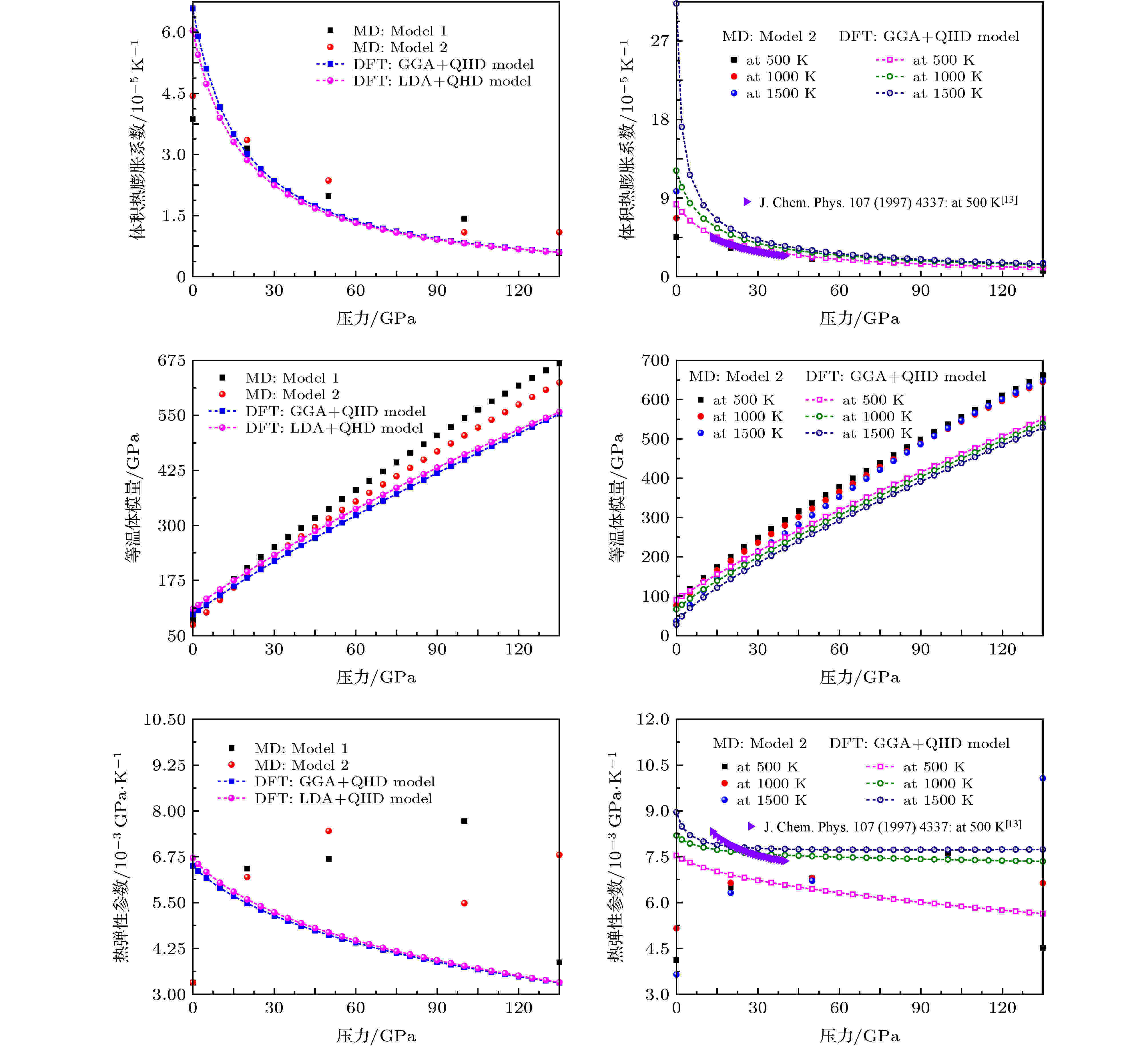图 10 模拟得到的300 K及其他不同高温(500, 1000和1500 K)下的MgF₂萤石结构的体积热膨胀系数、等温体模量、热弹性参数随压力的变化
Figure10. Predicted volume thermal expansion coefficient α, isothermal bulk modulus K_T, and thermoelastic parameter αK_T of MgF₂ with the fluorite-type structure as a function of pressure at 300 K and other different temperatures (500, 1000 and 1500 K).

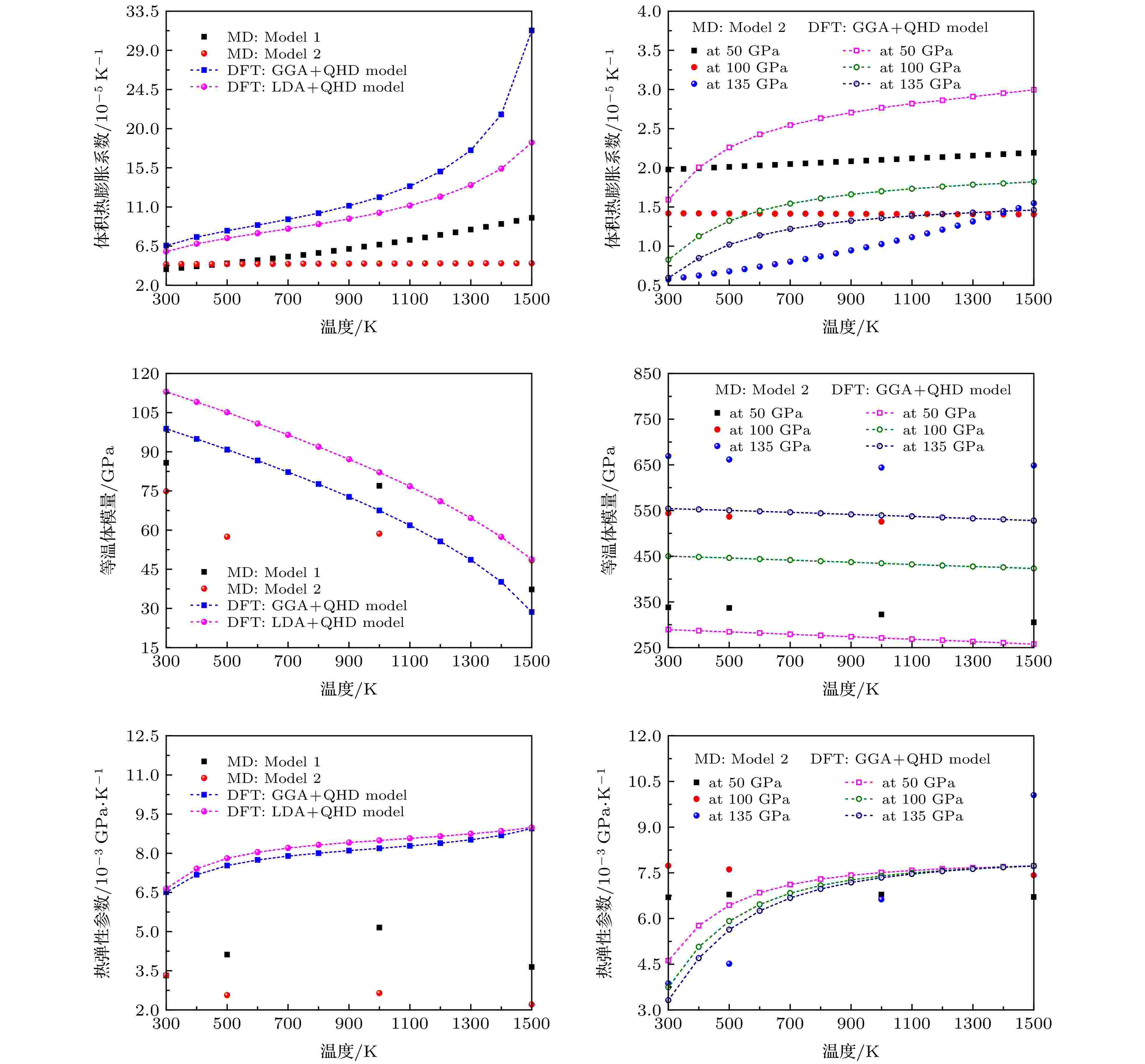图 11 模拟得到的环境压力下及其他不同高压(50, 100和135 GPa)下的MgF₂萤石结构的体积热膨胀系数、等温体模量、热弹性参数随温度的变化
Figure11. Predicted volume thermal expansion coefficient α, isothermal bulk modulus K_T, and thermoelastic parameter αK_T of MgF₂ with the fluorite-type structure as a function of temperature at 0.1 MPa and other different pressures (50, 100 and 135 GPa).

体积热膨胀系数是一个小量, 其在高温和高压条件下的数值很难通过实验方法测量, 环境条件下, 利用分子动力学模型II和GGA结合QHD计算得到的MgF₂萤石结构的体积热膨胀系数分别为4.435 × 10^–5和6.583 × 10^–5 K^–1. 从图10可以看出: 体积热膨胀系数随压力的增加逐渐减小, 低压情况下随温度的升高而增加的趋势很明显, 但压力达到一定数值时其随温度的增加逐渐变得缓和; 在低温下MgF₂萤石结构的热膨胀系数随着T ³增加, 在高温下逐渐线性增加, 接着增加的趋势变得缓和, 符合材料热膨胀的普遍行为. 同时, 利用分子动力学模型II和GGA结合QHD计算得到的MgF₂萤石结构在500 K温度下的体积热膨胀系数随压力的变化和Barrera等^[13]结合周期Hartree-Fock理论、准谐晶格动力学和分子动力学方法得到的计算结果十分符合.
体模量是表征物体体积弹性的模量, 它是反映物体体积反抗外压变化而产生形变的一个物理量. 物体的体模量越大, 物体所受的压力改变时, 其形变越小. 环境条件下, 利用分子动力学模型II和GGA结合QHD计算得到的MgF₂萤石结构的等温体模量分别为85.76和98.82 GPa; 标准条件下, Haines等^[5]的密度泛函平面波理论模拟结果为106 GPa. 当温度保持一定时, 等温体模量随着压力的增加而增加, 当压力为一定值时, 等温体模量随着温度的增加逐渐减小, 高压下减小逐渐变得缓慢. 在整个研究的温度和压力范围内, 利用分子动力学模型II得到的结果和利用GGA结合QHD计算得到的结果相比, 在低压段符合程度更好.
热物性研究中, 晶体体积随温度和压力变化而变化的行为是常见的物理现象, 表征晶体膨胀和压缩行为的热膨胀系数和体积弹性模量是晶体的两个基本物理参量, 体积热膨胀系数α和等温体弹性模量K_T的乘积αK_T被定义为热弹性参数, 热弹性参数在物态方程研究中具有重要意义. 利用计算机模拟方法得到的MgF₂萤石结构在不同温度和压力下的热弹性参数如图10和图11所示, 可以看出, 其随温度和压力的变化主要由α和K_T的变化决定, 可以看出该值在高温高压下趋近于一常数, 符合物态方程研究中假定的常数. 在低压下, αK_T随压力的增加减小; 在低温下, αK_T随温度的增加而增加.

采用先进的计算机模拟手段, 对典型碱土金属氟化物MgF₂萤石相的结构稳定性及热物性在宽广的温度和压力范围内进行了可靠预测研究. 首先基于密度泛函理论, 计算了MgF₂金红石和萤石相的吉布斯自由能随压力的变化、声子谱和萤石相弹性常数, 判断了MgF₂高压萤石结构的热力学、动力学和力学稳定性, GGA和LDA计算表明其从相变压力19.26和18.15 GPa可一直稳定到下地幔压力135 GPa; 接着利用经典分子动力学方法, 对MgF₂高压萤石结构的高温稳定性进行了模拟研究, 发现利用优选势参数模型的分子动力学模拟给出的MgF₂萤石结构在环境压力下的参考熔化温度约为1549 K, 接近实验熔化温度1539 K, 从更高压力下得到的参考熔化温度可以看出在低于本文所预测热物性给出的1500 K温度时, MgF₂晶体皆能保持其立方萤石结构直至135 GPa. 在此基础上, 发现MgF₂萤石结构的体积热膨胀系数随压力的增加逐渐减小, 低压情况下随温度的升高而增加的趋势很明显, 但压力达到一定数值时其随温度的增加逐渐变得缓和; 在低温下热膨胀系数随着T ³增加, 在高温下增加的趋势变得缓和. 等温体模量当温度保持一定时随着压力的增加而增加, 当压力保持一定值时随着温度的增加逐渐减小, 高压下减小逐渐变得缓慢. 热弹性参数在低压下随压力的增加减小, 在低温下随温度的增加而增加, 在高温高压下趋近于一常数.