摘要:在使用大涡模拟方法获得超声速混合层流场的基础上, 利用拉格朗日相干结构法和涡核位置提取方法, 得到了涡结构的边界和涡核的位置坐标, 并由此提出了涡结构内部流体密度分布的表示方法. 通过分析涡结构内部流体的密度在不同情况(如涡结构的空间尺寸、混合层流场的压缩性和涡结构的融合过程)下的变化, 揭示出超声速混合层涡结构内部流体的密度分布特性: 在弱和中等压缩性的超声速混合层流场中, 其涡结构内部流体的密度分布既关于流向(x轴)对称又关于纵向(y轴)对称, 涡核处的流体密度最低而涡边界处的流体密度最高, 流体密度在连接涡核与涡边界的射线上单调且近似均匀地增加; 在强压缩性的超声速混合层流场中, 其涡结构内部流体的密度分布不再具有对称性, 而且流体密度呈现波动变化的特点; 随着涡结构空间尺寸和流场压缩性的增加, 涡核处的流体密度降低(最大减少量约为31%—56%), 而涡边界的流体密度变化量约为6%—27%; 在相邻两个涡结构的融合过程中, 涡结构内部流体密度的变化较轻微, 表明融合过程很可能是两个涡结构内部流体的对等组合过程.
关键词: 密度分布/
涡结构/
超声速混合层/
大涡模拟

English Abstract

全文HTML

--> --> -->

红外制导技术以其分辨率高、隐身性好、抗干扰能力强以及适用于夜间和烟雾环境等优点而被广泛应用于多种飞行器上, 以实现对目标的精确搜索、跟踪和攻击^[1]. 然而, 对于高速/超高速飞行的红外制导飞行器而言, 其光学窗口周围复杂的流动结构会使穿越其中的光束产生如目标图像偏移、模糊和抖动等现象的气动光学效应^[2]. 其中, 为消除气动热效应对光学窗口的影响而使用的制冷射流与外部主流形成的超声速混合层是产生气动光学效应的主要流动因素^[3], 如图1(a)所示.
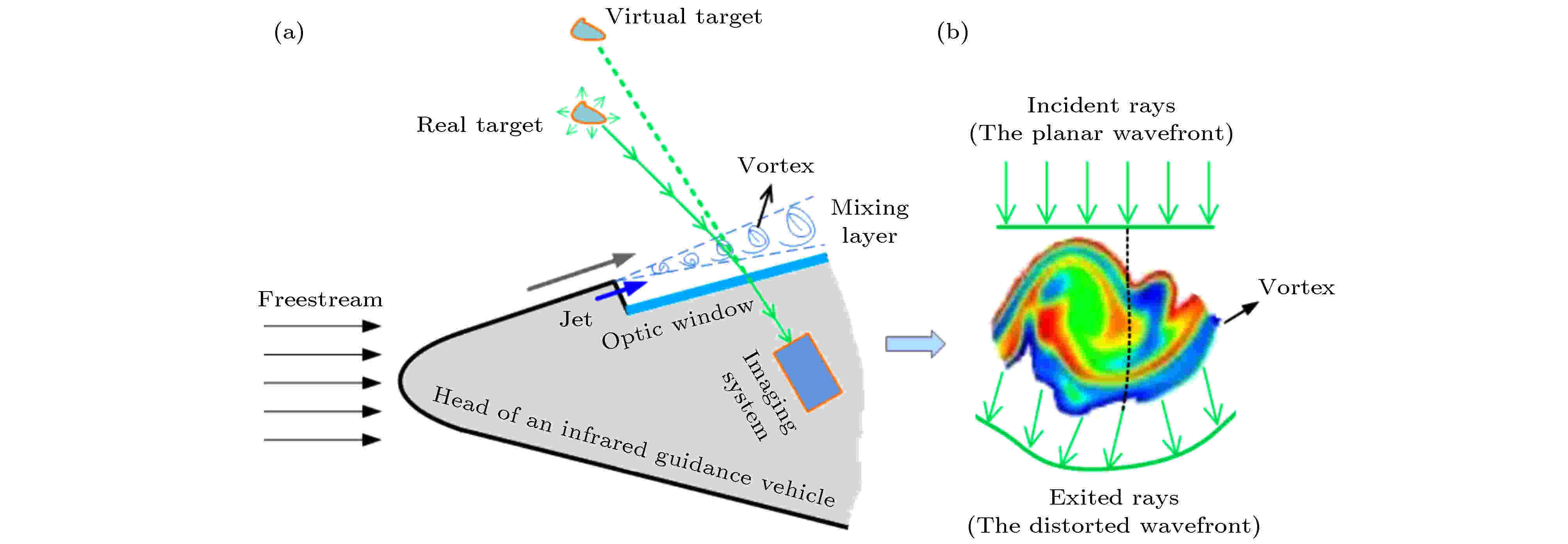图 1 (a)红外制导飞行器的气动光学效应; (b)涡结构引起光束波前畸变的示意图
Figure1. (a) Schematic of aero-optic effects of an infrared guidance vehicle; (b) wavefront distortion caused by a vortex.

关于混合层流场中的流动结构, Rogers和Moser^[4]首次采用直接数值模拟的方法证明了混合层流场中存在涡结构; Mungal等^[5]的研究进一步表明无论来流的初始边界层是层流还是湍流, 雷诺数在一定范围内的混合层中仍然存在涡结构. Brown和Roshko^[6]发现涡结构是混合层发展过程中的主要表现形式, 涡结构主导了混合层流动的动力学行为. 近年来, 国内的****们在混合层涡结构的可视化、稳定性和流动控制等方面进行了卓有成效的工作, 取得了较大的进展. 通过风洞试验, 易仕和团队^[7,8]使用其开发的基于纳米示踪的平面激光散射技术清晰展示了超声速混合层流场中的涡结构, 并对涡结构的流动特点及时间演化规律进行了研究. 沈清等^[9]指出混合层流动的失稳特性和失稳结构与流动转捩过程密切相关, 并根据流动失稳特性研究了可压缩混合层的混合增强控制方法. Wang等^[10]对超声速混合层厚度和混合效率的影响因素, 如对流马赫数、来流速度和密度比等进行了较详细的研究, 发现混合层厚度和混合效率都随对流马赫数的增加而减小. Zhang等^[11]研究了强迫振动下超声速混合层的流动特性, 与无振动相比, 强迫振动使混合层的失稳位置提前, 卷起的展向涡尺度变大, 能加快上下两层流动的混合. 郭广明等^[12]采用大涡模拟方法对脉冲激励下超声速混合层流场中涡结构的演化机理进行了研究, 发现涡结构的生长不再是依靠相邻两个涡结构之间的相互融合, 而是通过涡核外围的一串小涡旋结构被依次吸进涡核来实现; 总结出涡结构的平均对流速度与脉冲周期的乘积近似等于涡结构的空间尺寸. 最近, 张冬冬等^[13]通过直接数值求解Navier-Stokes方程, 研究了入流激励下可压缩混合层中涡结构的响应特性, 得出了与文献[12]中相似的研究结论. ****们的研究成果表明: 不同尺度的涡结构是混合层流场中的主要流动结构, 它们决定了混合层的流动特性. 因此, 光束穿越混合层产生的气动光学效应也就与流场中涡结构的动力学特性紧密相关^[14,15]. 混合层流场中, 涡结构导致入射光束的波前畸变示意图如图1(b)所示.
在涡结构尺寸与混合层流场气动光学效应的关系方面, Chew和Christiansen^[16]实验测量了光束穿越混合层不同位置产生的气动光学畸变, 发现光束穿越涡结构卷起之前的流场区域产生的气动光学畸变最小, 而光束的气动光学畸变在涡结构线性生长的流场区域随流向距离的增加而增加. 甘才俊等^[17]利用量级分析和风洞实验研究了超声速混合层流场气动光学效应的规律性, 讨论了混合层涡结构的空间尺寸与光束穿越流场引起的视线误差(图像偏移)之间的关系. 除了涡结构的空间尺寸能够直接影响混合层的气动光学效应之外, 涡结构的对流速度也会对气动光学效应的频率有影响^[18]. 近年来, 基于涡结构的流动特性决定着混合层气动光学效应的认识, 研究人员开始从抑制混合层涡结构生长和通过流动控制调制混合层涡结构的角度来探索降低和消除混合层气动光学效应的有效方法^[19-22].
尽管****们从涡结构的角度对混合层气动光学效应进行了较全面的研究, 获得了光束穿越混合层(涡结构)产生的气动光学畸变图像随涡结构空间尺寸、对流速度、来流条件等参数的变化规律; 提出了抑制涡结构生长和调制涡结构等控制混合层气动光学效应的策略和方法. 然而, 目前的研究大多把混合层涡结构视为一个“黑箱”, 没有揭示光束在其内部的传输特性, 难以从根本上阐明混合层涡结构产生气动光学效应的机理. 从几何光学的角度来讲, 涡结构产生气动光学效应在本质上是由于涡结构内部流体密度的不均匀分布导致的折射率脉动, 使得光束中的光线在涡结构内部传输时所历经的光程和光线出射角等都不相同. 因此, 要阐明混合层涡结构产生气动光学效应的机理, 获得光线在涡结构内部的传输规律, 首先要对混合层涡结构内部流体的密度分布特性有一定的认识.
本文使用大涡模拟方法实现超声速混合层涡结构的可视化, 采用拉格朗日相干结构法和涡核位置提取方法获取涡结构的边界和涡核的位置坐标。通过分析涡结构内部流体的密度在不同情况(如涡结构的空间尺寸、混合层流场的压缩性和涡结构的融合过程)下的变化, 初步揭示了超声速混合层涡结构内部流体的密度分布特性, 为阐明混合层气动光学效应的产生机理提供了基础.

2

-->

2.1.大涡模拟

大涡模拟(large eddy simulation, LES)是介于直接数值模拟和雷诺平均方法之间的一种流体运动模拟方法, 其基本思想是通过精确求解某个尺度以上所有湍流尺度的运动, 以捕捉流场中出现的大尺度效应和拟序结构. 本文使用的LES程序是由上海交通大学航空航天学院刘洪教授课题组开发, 其可靠性和准确性已被多次验证^[12,23,24], 此处不再对其进行介绍.
图2是使用LES方法得到的超声速混合层流场, 它清晰展示了流场中不同空间尺寸的涡结构以及涡结构的生长过程, 从中能看到涡结构的生长是通过相邻两个涡结构的互相融合实现的^[23]. 需要说明: 尽管LES计算时使用的是三维网格, 但考虑到研究的方便和各流向平面内的流场具有相似性, 本文以二维超声速混合层流场为研究对象. 如图2所示, 超声速混合层流场的几何尺寸为0.3 m (流向, x) × 0.048 m (纵向, y), 坐标原点(0, 0)也是混合层的源点; 随着流向距离的增加, 涡结构的空间尺寸也逐渐增加.
图 2 超声速混合层的涡量等值面
Figure2. The vorticity contour of a supersonic mixing layer simulated by LES.

2 -->

2.2.拉格朗日相干结构法

拉格朗日相干结构(Lagrangian coherent structures, LCS)法是一种流场后处理方法, 它与基于欧拉法的如Q准则作用相似, 用于展示流场中的流动结构. 与欧拉法不同的是, LCS是通过计算流场空间中粒子的运动轨迹来显示流场中流动结构的物质界面.
通过计算流场的有限时间李雅普诺夫指数(finite-time Lyapunov exponent, FTLE)可获得流场的LCS. FTLE是一个标量, 它表征从t → t + T的一段时间内, 流场中某一流体质点和它周围流体质点运动轨迹之间的平均分离程度. FTLE的计算公式如下^[25]:

$\sigma _t^T\left( x \right) = \frac{1}{{\left| T \right|}}\ln \sqrt {{\lambda _{\max }}\left( \Delta \right)},$

其中, $ {\sigma }_{t}^{T}\left(x\right) $表示流场空间点x处的质点在从t → t + T时间内的李雅普诺夫指数, ${\lambda _{\max }}\left( \varDelta \right)$表示在t → t + T时间内空间点x附近所发生的最大拉伸. 在计算了流场所有空间点的FTLE之后, 该流场FTLE场中的脊线即表示流场中的LCS. 在以下的研究中, 混合层流场的LCS和混合层流场的涡量等值面(如图2所示)共同用于确定混合层流场中涡结构的边界.
2 -->

2.3.涡核位置提取方法

混合层流场中的涡结构在向下游移动的同时其自身也在进行着高速的旋转运动, 导致涡结构内部的流体往涡边界聚集, 使得涡核位置的流体密度较低而涡边界处的流体密度较高. 涡核位置提取方法就是基于这个物理实际, 采用光线追踪方法计算入射光线垂直穿越整个混合层流场的光程(optical path length, OPL). 由于每条光线的OPL与其在混合层流场中所历经的流体密度密切相关, OPL的大小就能够反映该条光线所历经流体的密度大小. 因此, 通过提取OPL分布上局部最小值所在的位置坐标就能获得各个涡结构涡核位置的信息, 该方法的具体介绍请参考文献[12,23].

为获得混合层涡结构内部流体的密度分布特性, 首先要确定流场中涡结构的边界. 其次, 涡核是涡结构内部流体的密度最低点, 可作为密度参考点来分析涡结构内部流体的密度分布特性.
2

-->

3.1.涡结构的边界

从混合层流场的涡量等值面(见图2)能够看到流场中存在一系列不同空间尺寸的涡结构, 它们或独立“漂浮”在流场中, 或与周围的涡结构进行融合. 尽管从图2中能够辨识出每个涡结构的大致轮廓, 但较难准确地勾画出每个涡结构的边界. 为获得涡结构的边界, 使用2.2节提出的LCS法. 以图2中白色矩形框所标识的两个涡结构为例(见图3(a)), 通过计算它们所在区域的FTLE以获得该区域的李雅普诺夫指数场, 场中的脊线即表示该段流场中的LCS, 如图3(b)所示. 从所得到的LCS发现, 它能够较清晰地勾画出涡结构的边界, 但有时并不能给出一个封闭的涡边界; 给出的涡边界形状不是十分规整, 较难用一个简单的几何图形来描述. 因此, 在确定涡结构边界的过程中, 把混合层流场的LCS和其涡量等值面结合起来使用, 并用一个椭圆来近似表示涡结构的边界, 如图3(c)所示.
图 3 涡边界椭圆模型的建立过程示意图　(a)两个涡结构; (b) LCS; (c)涡边界的椭圆模型
Figure3. Process of establishing an elliptic model for the vortex boundary: (a) Two vortices; (b) LCS; (c) elliptic model of vortex boundary

参数a和b分别表示椭圆的长半轴和短半轴, 同时也表征了涡结构在流向和纵向的空间尺寸. 为了定量化分析混合层流场中的涡结构在不同情况下的形状变化, 使用数学上椭圆扁率(记为e)的计算公式,

$e = ({{a - b}})/{a},$

从(2)式能够看到, e的值在0和1之间; e的值越大, 表明涡的形状越扁, e的值越小, 表明涡的形状越接近圆形.
2 -->

3.2.涡核的位置坐标

涡核是涡结构内部的一个特殊位置, 它既是涡结构内部流体的密度最低点也是涡结构的中心. 对于所建立的涡结构边界椭圆模型而言, 涡核的位置也就是椭圆的中心点. 基于涡核位置提取方法, 获取涡核位置坐标(x_c, y_c)的过程如图4所示, 阐述如下: 在纵向(即y方向)布置光线垂直入射混合层流场, 使用光线追踪计算每条出射光线的OPL, 进而得到所有光线穿越混合层流场之后的OPL分布. 由于涡核的流体密度最低, 则经过涡核的出射光线的OPL最小, 即OPL最小值的流向坐标就是涡核位置所对应的流向坐标x_c; 同理, 在流向(即x 方向)布置光线垂直入射混合层流场, 则所有出射光线的OPL分布中最小值的纵向坐标就是涡核位置所对应的纵向坐标 y_c. 通过使用两次涡核位置提取方法, 最终获得涡核的位置坐标(x_c, y_c), 也即是涡结构椭圆模型的中心点坐标.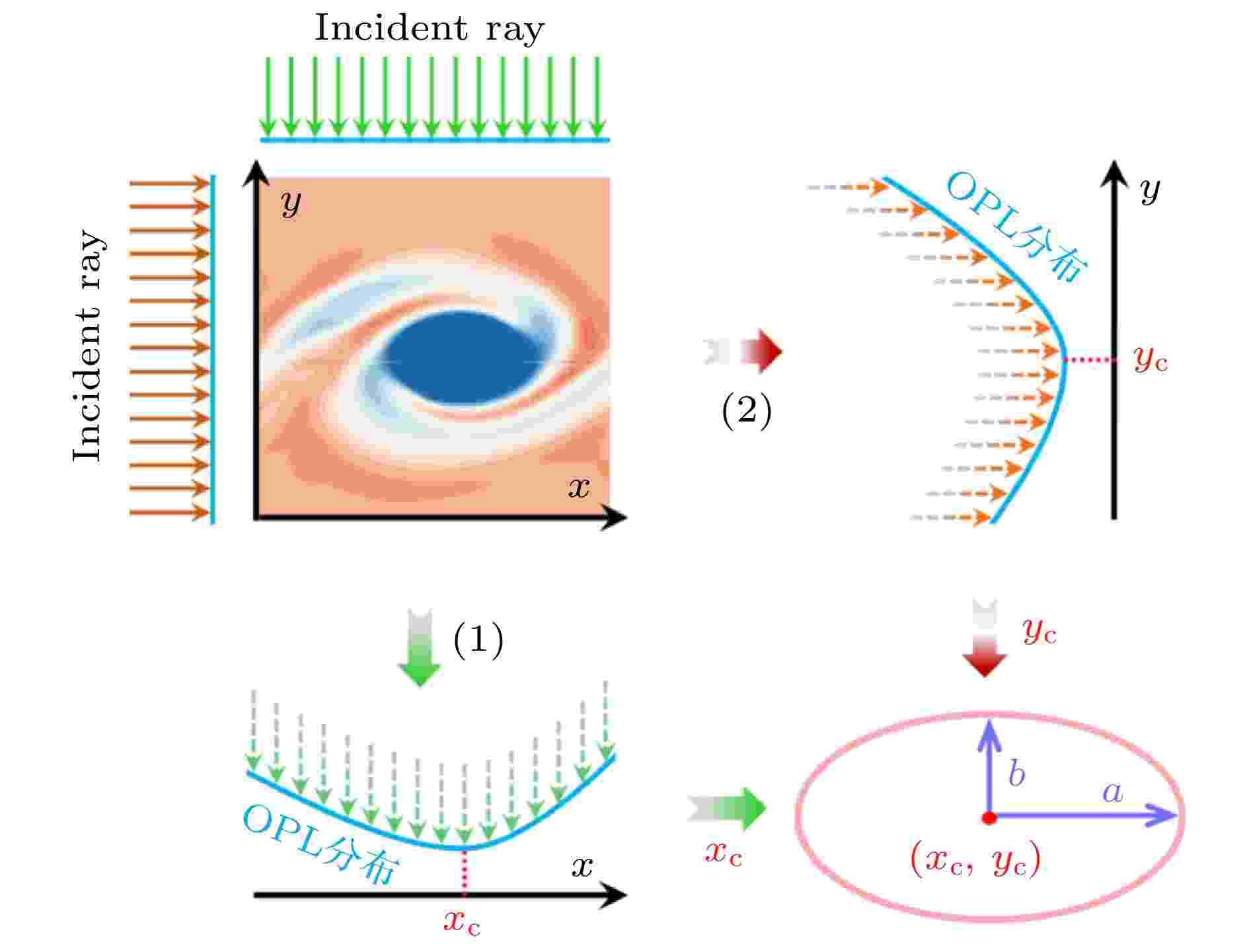
图 4 计算涡核位置坐标的原理图
Figure4. Schematic of calculating position coordinates of a vortex core.

2 -->

3.3.涡结构内部流体的密度分布表示方法

涡结构的高速旋转使其内部流体往涡边界聚集, 即涡结构内部流体密度分布的总体特征是涡边界处的流体密度大, 而涡核处的流体密度小. 因此, 获取涡核至涡边界路径上的流体密度数据对揭示涡结构内部流体的密度分布特性至关重要.
基于3.1节和3.2节获得的涡结构边界和涡核位置坐标, 从涡核到涡边界引出一系列射线, 如图5所示. 其中, 中间的红点表示涡核的位置, 是每条射线的起点; 射线Line 1和Line 7的长度即为涡边界椭圆模型的长半轴a, 射线Line 4和Line 10的长度即为涡边界椭圆模型的短半轴b; 其他各条射线的长度介于长半轴a和短半轴b之间. 此外, 每条射线之间的夹角都是30°, 即12条射线是从流向开始沿着逆时针方向均匀布置在整个涡结构内部.
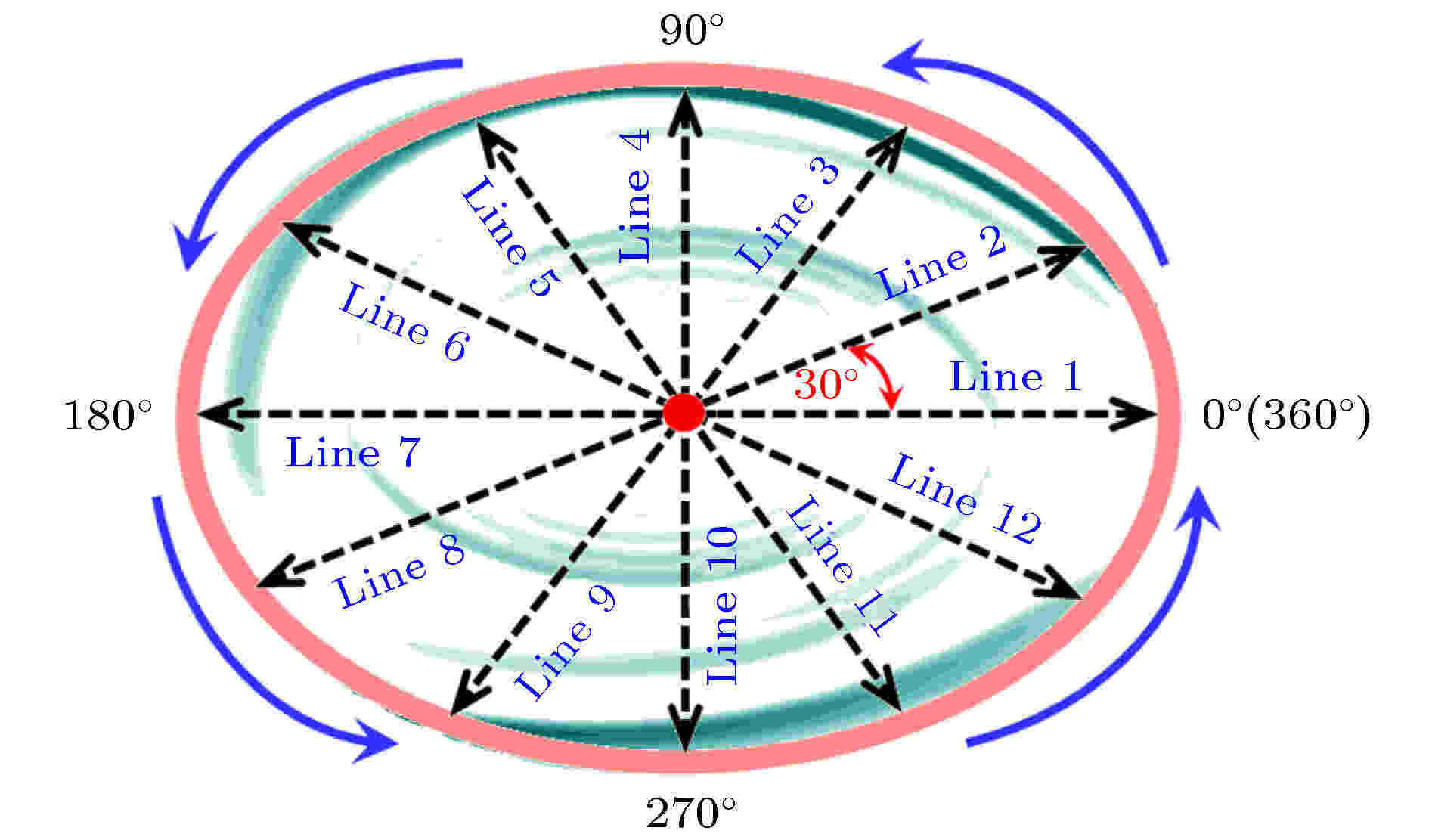图 5 基于涡边界和涡核位置的涡结构内部流体密度分布表示方法
Figure5. Method of representing fluid density distribution inside a vortex based on its boundary and core location.

沿着图5中的每条射线提取涡结构内部流体的密度数据, 经过数据处理得到反映涡结构内部流体密度随着离涡核的距离和相对涡核的方位等参数变化的曲线图, 用于分析涡结构内部流体的密度分布特性. 理论上来讲, 从涡核位置引出更多的射线并提取沿着它们的流体密度数据用于分析会更详细地反映涡结构内部流体的密度分布特性. 然而, 考虑到涡结构在几何上近似具有对称性, 而且图5中射线所在的位置已经涵盖了涡结构内部的典型位置, 因此通过对这12条射线上流体密度数据的提取和分析能够获得涡结构内部流体的密度分布特性.

对超声速混合层而言, 涡结构的空间尺寸和形状不仅与其所在的流向位置和所处的演化状态有关, 还会受到流场压缩性的影响. 因此, 为了较全面地揭示涡结构内部流体的密度分布特性, 考虑的涡结构情况有不同空间尺寸的涡结构、不同压缩性流场中的涡结构和处于两涡融合过程中的涡结构等. 三种不同压缩性的超声速混合层入流条件如表1所示, 其中T_∞, P_∞, ρ_∞和Mc分别表示混合层入流的温度、压强、密度和混合层流场的对流马赫数; 混合层流场的压缩性可以使用参数Mc表征, Mc越大表明混合层流场的压缩性越强^[26].

序号	混合层入流速度/m·s–1		T∞/K	P∞/kPa	ρ∞/kg·m–3	Mc
	上层流体(U1)	下层流体(U2)
1	605.6	403.7	281	89.9	1.107	0.3
2	740.2	403.7	281	89.9	1.107	0.5
3	1009.3	403.7	281	89.9	1.107	0.9

表1超声速混合层的入流参数
Table1.Inflow parameters of three supersonic mixing layers.

2

-->

4.1.不同空间尺寸的涡结构

涡结构的空间尺寸是表征其几何特征的一个重要参数, 本节以不同空间尺寸的涡结构为对象, 研究涡结构空间尺寸变化对其内部流体密度分布的影响. 以Mc = 0.5的超声速混合层为例, 其某个瞬间的流场涡量等值面如图6(a)所示, 其中黑色虚线箭头表示两个涡结构互相围绕着高速旋转的融合状态. 从图6(a)看到, 尽管流场中各个涡结构的空间尺寸不同而且形态各异, 但它们可近似分为两类: 一类是单个涡结构自由“漂浮”状态, 如黑色虚线矩形框内的涡结构; 另一类是涡结构与其相邻涡结构互相围绕着高速旋转的融合状态.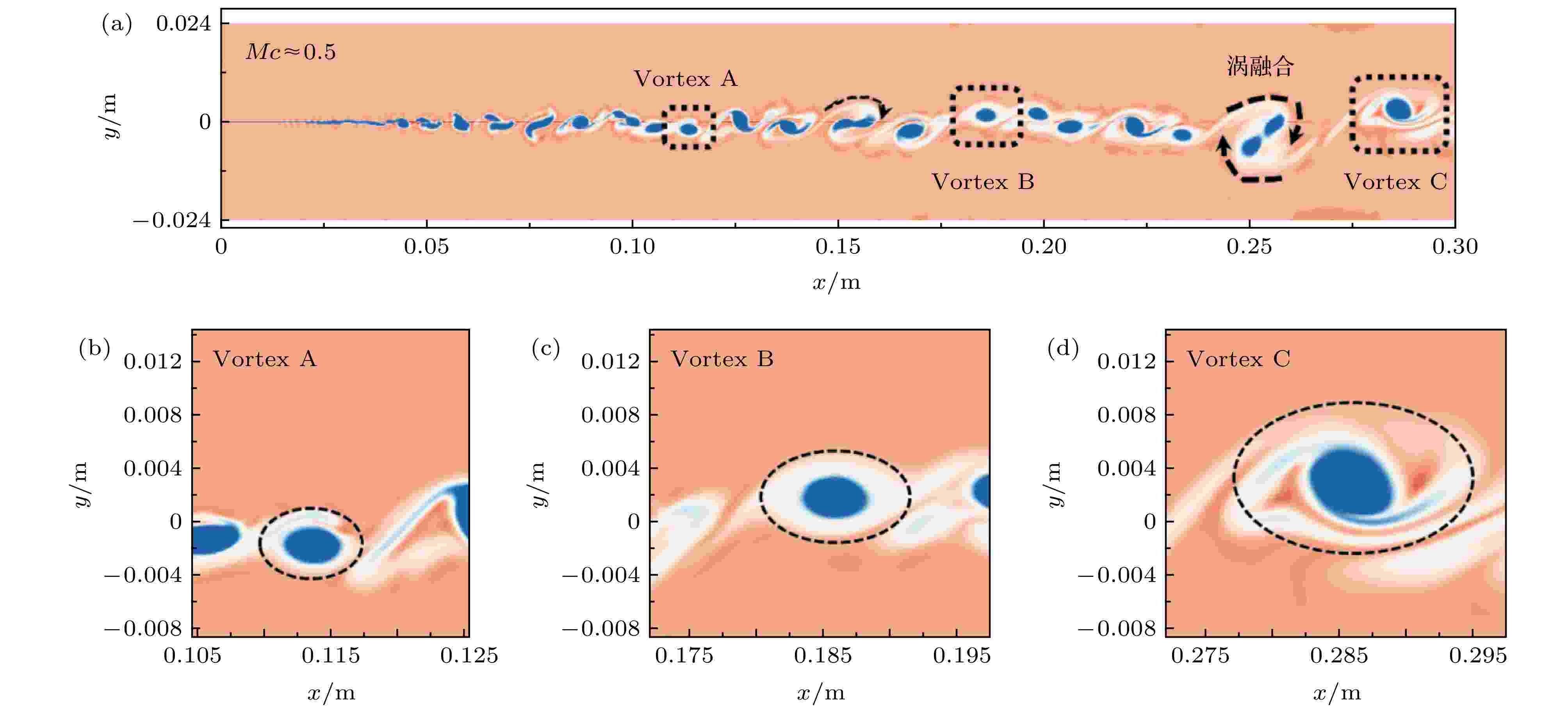
图 6 (a)对流马赫数0.5的超声速混合层; (b)涡结构 A; (c)涡结构B; (d)涡结构C
Figure6. (a)The supersonic mixing layer with Mc = 0.5; (b) Vortex A; (c) Vortex B; (d) Vortex C.

选取三个处于独立状态且空间尺寸不同的涡结构, 分别记为Vortex A、Vortex B和Vortex C, 局部放大如图6(b)—(d)所示. 其中, 黑色虚线表示的椭圆为LCS法和涡量等值面共同确定的涡结构边界. 各个涡结构的涡核位置坐标(x_c, y_c)由涡核位置提取方法获得. 这三个涡结构的相关几何参数列于表2, 从中发现: 涡结构的空间尺寸在随着流向距离的增加而增加的同时, 其扁率e也在逐渐增加. 这表明涡结构在生长的过程中, 其形状也在发生变化. 具体来说, 涡结构的扁率e由0.1844增加到0.5221, 即涡结构的形状变得越来越扁, 这表明涡结构在流向的生长速度要快于其在纵向的生长速度.

涡结构	中心点		长半轴a/m	短半轴b/m	扁率e
	xc/m	yc/m
Vortex A	0.1136	–0.001762	0.003314	0.002703	0.1844
Vortex B	0.1858	0.001635	0.006231	0.003877	0.3778
Vortex C	0.2863	0.003296	0.010652	0.005091	0.5221

表2不同空间尺寸涡结构的几何参数
Table2.Geometric parameters of three vortices with different sizes.

图7为三种不同尺寸涡结构的内部流体密度在射线Line 1到Line 12上的数据随流向(x)和纵向(y)距离变化的曲线图, 其中ρ_c, ρ_b和ρ_a分别表示涡核、短半轴和长半轴与涡边界交点处的密度, 图7的流体密度值已经使用混合层入流密度进行了无量纲化. 以Vortex A为例, 容易发现其涡核处的密度(ρ_c = 0.577)最低, 流体密度随着离开涡核的距离增加而近似单调均匀地增加. 短半轴与涡边界交点处的密度ρ_b = 0.946, 而长半轴与涡边界交点处的密度ρ_a = 1.091, 这表明涡结构在流向边界处的密度要稍大于其在纵向边界处的密度. 这个现象的物理原因是涡结构的流向边界近似位于相邻两个涡结构的中间位置, 那里的流体因相邻涡结构的高速旋转而处于被挤压的状态. 同时也能够发现, 相对于x轴(流向)和y轴(纵向)对称的射线, 例如相对于x轴对称的Line 3和Line 11及相对于y轴对称的Line 3和Line 5, 流体密度在这些射线上的数据曲线近似重合(注:在涡结构的边界附近, 曲线的重合性稍差), 表明流体密度在射线Line 3、Line 5和Line 11上的分布近似相同. 进一步观察发现, 这个特点对于剩下的射线也是成立的, 这表明涡结构内部流体的密度分布具有既关于流向(x轴)对称又关于纵向(y轴)对称的特点.
图 7 不同尺寸涡结构内部流体的密度分布曲线　(a) Vortex A内部流体的密度随流向(x)距离变化的曲线图; (b) Vortex A内部流体密度随纵向(y)距离变化的曲线图; (c) Vortex B内部流体密度随流向(x)距离变化的曲线图; (d) Vortex B内部流体密度随纵向(y)距离变化的曲线图; (e) Vortex C内部流体密度随流向(x)距离变化的曲线图; (f) Vortex C内部流体密度随纵向(y)距离变化的曲线图
Figure7. Density distribution of fluid inside three vortices: (a) Density distribution of fluid inside Vortex A along the flow direction (x-axis); (b) density distribution of fluid inside Vortex A along the longitudinal direction (y-axis); (c) density distribution of fluid inside Vortex B along the flow direction (x-axis); (d) density distribution of fluid inside Vortex B along the longitudinal direction (y-axis); (e) density distribution of fluid inside Vortex C along the flow direction (x-axis); (f) density distribution of fluid inside Vortex C along the longitudinal direction (y-axis).

随着涡结构空间尺寸的逐渐增加(见Vortex B和Vortex C的密度数据曲线), 涡核处的流体密度ρ_c逐渐降低(分别为0.543和0.398), 减少量依次约为5.9%和31.0%; 短半轴与涡边界交点处的流体密度ρ_b也逐渐降低(分别为0.927和0.894), 减少量依次约为2.0%和5.5%; 而长半轴与涡边界交点处的流体密度ρ_a有轻微增加(分别为1.132和1.104), 增加量依次约为3.8%和1.2%. 这种现象的物理原因可解释如下: 随着涡结构空间尺寸的逐渐增加, 涡结构边界处的流体更有机会“深入”到混合层主流中, 而主流能量的输入会使涡结构的旋转速度增加, 进而使涡核及其附近的流体被往涡边界的方向输运; 涡结构旋转速度的增加也会使相邻两个涡结构之间的流体被更强烈的挤压.
随着涡结构空间尺寸的增加, 涡结构内部流体的密度分布仍然近似具有既关于流向(x轴)对称又关于纵向(y轴)对称的特点. 从密度曲线的重合性方面观察, 能够发现涡结构内部流体的密度分布关于流向(x轴)的对称性要好于关于纵向(y轴)的对称性. 需要指出的是: 所选的Vortex A、Vortex B和Vortex C是混合层流场中处于独立状态的涡结构, 它们受相邻涡结构的影响较小. 对处于融合状态的涡结构, 其内部流体密度的分布特性将在4.3节论述.
2 -->

4.2.不同压缩性流场中的涡结构

流场压缩性是影响混合层涡结构流动特性的一个重要参数, 必然也会影响涡结构内部流体的密度分布. 本节以不同压缩性流场中的涡结构为对象, 研究压缩性对涡结构内部流体密度分布的影响. 为了与4.1节得到的结论相比较, 以Mc = 0.5的超声速混合层为参考, 依次减弱(Mc = 0.3)和增强(Mc = 0.9)混合层流场的压缩性, 它们的涡量等值面如图8所示. 容易看到: 压缩性较弱的混合层流场中的涡结构形状较规整, 能够清晰地看到相邻两个涡结构的融合过程; 而强压缩性混合层流场中的涡结构在流向的空间尺寸显著大于纵向, 流场中也没有明显的相邻涡结构融合现象.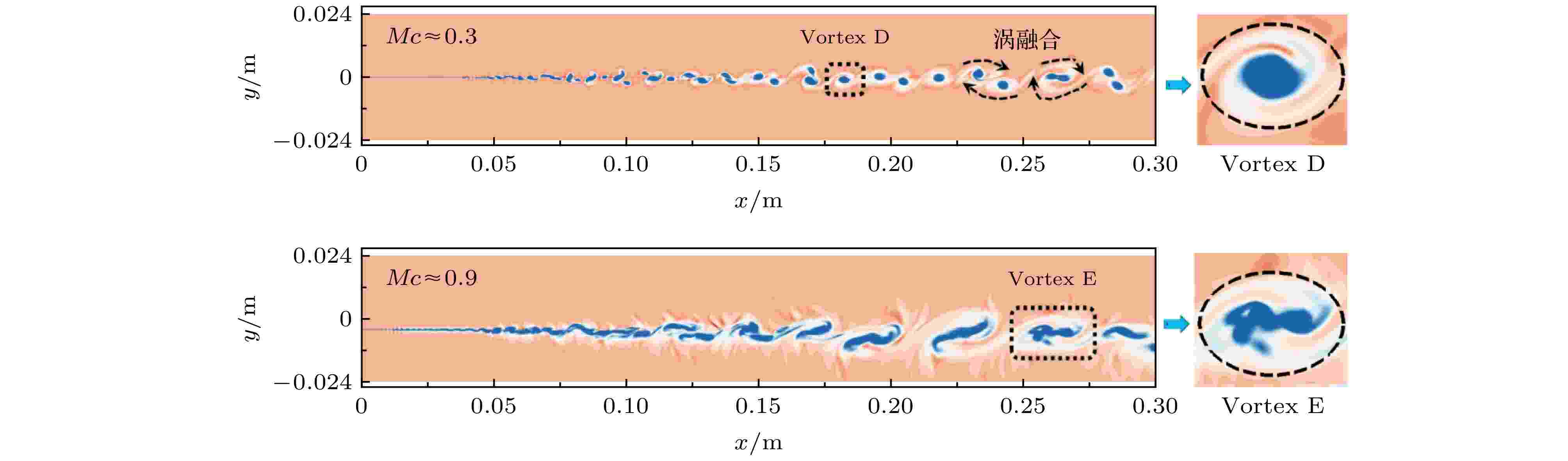
图 8 不同压缩性的超声速混合层
Figure8. Supersonic mixing layers with different compressibilities

同样地, 选取流场中处于独立状态的涡结构, 记为Vortex D和Vortex E, 局部放大如图8右半部分所示. 其中, 黑色虚线表示的椭圆为LCS法和涡量等值面共同确定的涡结构边界, 涡结构的涡核位置坐标(x_c, y_c)由涡核位置提取方法获得. 这两个涡结构的相关几何参数列于表3, 从中发现: 强压缩性混合层流场中涡结构的空间尺寸远大于弱压缩性混合层流场中涡结构的空间尺寸, 而且形状也更加扁平. 需要指出: 对于强压缩性的混合层, 其流场中涡结构的形状已不规则, 其内部流体排列的规律性变差, 使得涡核位置偏离其几何中心. 对于Vortex E, 表3括号里的数据为使用涡核位置提取方法获得的涡核位置坐标, 它与椭圆几何中心之间的距离约为长半轴a的15.5%.

涡结构	中心点		长半轴a/m	短半轴b/m	扁率e
	xc/m	yc/m
Vortex D (Mc = 0.3)	0.1824	–0.0008203	0.004854	0.003128	0.3556
Vortex E (Mc = 0.9)	0.2607(0.2589)	–0.0012338(–0.0001429)	0.013673	0.006051	0.5574

表3不同压缩性超声速混合层涡结构的几何参数
Table3.Geometric parameters of two vortices in the fields with different compressibilities.

图9为不同压缩性超声速混合层流场中涡结构的内部流体密度在射线Line 1到Line 12上的数据随流向(x)和纵向(y)距离变化的曲线图, 其中ρ_c, ρ_b和ρ_a分别表示涡核、短半轴和长半轴与涡边界交点处的密度, 流体密度值已经使用混合层入流密度进行了无量纲化. 对于弱压缩性混合层流场中的涡结构(见Vortex D的密度曲线图), 其涡核处的密度(ρ_c = 0.786)最低, 流体密度随着离开涡核的距离增加而近似单调均匀地增加. 短半轴与涡边界交点处的密度ρ_b = 0.975, 而长半轴与涡边界交点处的密度ρ_a = 1.038, 即涡结构在流向边界处的密度稍大于其在纵向边界处的密度. 对于强压缩性混合层流场中的涡结构(见Vortex E的密度曲线图), 其涡核处的密度(ρ_c = 0.343)最低, 流体密度随着离开涡核的距离增加而非单调地增加, 表明涡结构内部流体密度的变化不均匀且有波动性. 短半轴与涡边界交点处的密度ρ_b = 0.711, 而长半轴与涡边界交点处的密度ρ_a = 1.159, 即涡结构在流向边界处的密度显著大于其在纵向边界处的密度. 对比图7和图9能够得出如下的结论: 随着混合层流场压缩性的增加, 涡结构涡核位置的流体密度减小(Mc = 0.9时的密度值相对于Mc = 0.3减小约56.4%); 短半轴与涡边界交点处的流体密度也减小(Mc = 0.9时的密度值相对于Mc = 0.3减小约27.1%); 长半轴与涡边界交点处的流体密度有少量增加(Mc = 0.9时的密度值相对于Mc = 0.3增加约11.6%). 分析表1中的混合层入流速度能够发现这个结论背后的物理原因: 压缩性增加(由U₁增加引起)能够让更多的主流能量进入涡结构, 使其旋转速度增加, 进而使涡结构内部更多的流体往边界方向聚集; 另一方面, 主流往下游移动的速度越高, 涡结构纵向边界附近的流体就更多地被“挟裹”着堆积在涡结构的流向边界.
图 9 不同压缩性流场中涡结构内部流体的密度分布曲线
Figure9. Density distribution of fluid inside two vortices in the supersonic mixing layers with different compressibilities.

从Vortex D内部流体密度数据曲线能够看到, 其内部相对于x轴(流向)和y轴(纵向)对称的射线, 例如相对于x轴对称的Line 3和Line 11及相对于y轴对称的Line 3和Line 5、Line 8和Line 12, 流体在这些射线上的密度数据曲线近似重合, 表明流体密度在这些射线上的分布近似相同. 实际上, 对于剩下的射线这个结论也是成立的, 这表明涡结构内部流体的密度分布具有既关于流向(x轴)对称又关于纵向(y轴)对称的特点. 同时也注意到, 涡结构内部流体的密度分布相对于流向(x轴)的对称性好于其相对于纵向(y轴)的对称性. 然而, 从Vortex E内部流体密度数据曲线发现, 此时涡结构内部流体的密度分布已经不具有关于流向(x轴)对称或关于纵向(y轴)对称的特点. 对比图7和图9能够得出如下的结论: 对于弱压缩性(Mc = 0.3)和中等压缩性(Mc = 0.5)的混合层流场, 其涡结构内部流体的密度分布具有既关于流向(x轴)对称又关于纵向(y轴)对称的特点; 而对于强压缩性(Mc = 0.9)的混合层流场, 其涡结构内部流体的密度分布不具有关于流向(x轴)对称或关于纵向(y轴)对称的特点.
2 -->

4.3.融合过程中的涡结构

从图2能够观察到超声速混合层流场中相邻涡结构之间的融合过程, 它是推动混合层生长的内在动力, 也是涡结构在演化过程中的一个典型环节. 本节以相邻两个涡结构的融合过程为例, 研究涡结构内部的流体密度在融合过程中的变化特性. 弱压缩性的超声速混合层在某时刻的流场等值面如图10(a)所示, 选取黑色虚线矩形框中配对完成的两个相邻涡结构(记为涡a和涡b), 它们在融合过程中的几个典型时刻(t₁ → t₆)如图10(b)所示.
图 10 (a)弱压缩性的超声速混合层, Mc = 0.3; (b)其流场中相邻两个涡结构的融合过程
Figure10. (a) Supersonic mixing layer with Mc = 0.3; (b) two adjacent vortices during their merging process.

相邻两个涡结构的融合过程是一个动态的过程, 每个涡结构在不同时刻的空间尺寸和形状都会发生变化(见图10). 考虑到涡融合是两个涡结构的互相作用过程, 在建立涡结构的边界模型时, 把这两个涡结构视为一个整体. 具体来说, 涡a和涡b的涡核连线作为涡边界椭圆模型的长轴, 这两个涡核之间连线的中点作为涡边界模型的中心点, 椭圆短轴垂直长轴且过中心点; 在t₁时刻建立的涡边界椭圆模型随涡融合的进程而保持同步旋转. 提取涡a和涡b在椭圆模型长轴和短轴上对应的流体密度数据, 它们在涡融合过程中的变化曲线如图11所示. 其中, 横坐标表示长轴和短轴上的流体质点离中心点(红色小圆点)的距离, 负号表示方向相反; 纵坐标是使用混合层入流密度进行无量纲化处理之后的流体密度值.
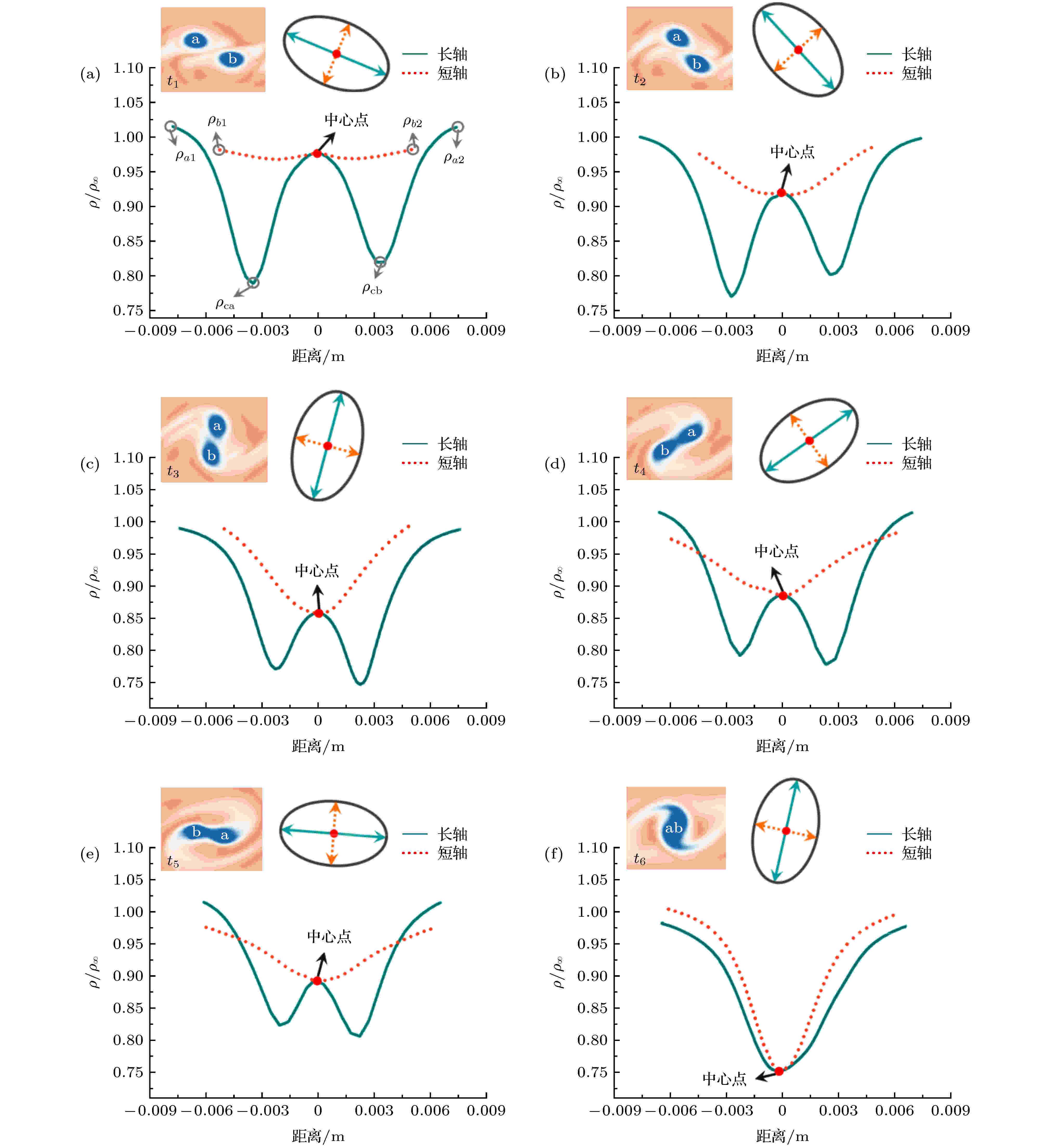图 11 涡a和涡b在长轴和短轴上的流体密度在涡融合过程中的变化曲线
Figure11. Variation curve of the fluid density inside the vortex a and b during their merging process.

在两个涡结构融合的起始时刻(见t₁时刻), 能够看到流体密度在短轴上的变化较平缓, 波动较小; 中心点处的流体密度值(约为0.98)与短轴两个端点处的密度值(ρ_b1和ρ_b2)大小相当, 稍小于长轴两个端点处的密度值(ρ_a1和ρ_a2). 此外, 涡a和涡b的涡核密度(ρ_ca和ρ_cb)远小于中心点、短轴及长轴两端点的密度. 这表明t₁时刻涡a和涡b之间的界面还没有被打破, 涡a内部的流体与涡b内部的流体还未发生融合. 在涡融合的过程中(见t₂ → t₅时刻), 中心点处流体密度依次约为0.924, 0.863, 0.881和0.894, 其密度值的小幅变化正是涡融合动态过程的体现. 同时也发现, 中心点附近长轴和短轴上的流体密度值都随着涡融合的发展而减小, 表明中心点附近的空间逐渐被来自涡a和涡b内部的流体所填充, 也是涡融合逐渐深入的体现. 在t₆时刻, 长轴和短轴上的流体密度分布都只有一个共同的最小值, 而且它们的分布曲线都是关于中心点近似对称, 这表明此时刻涡a和涡b的融合几乎完成, 它们融合成了一个完整且更大的涡结构.
为了定量化分析涡结构内部流体的密度在融合过程中的变化特性, 以涡a和涡b的涡核密度、短轴和长轴端点密度为特征点密度, 它们在融合过程中的变化曲线如图12所示. 整体上, 它们在涡融合过程中均表现出小幅度波动的变化特性. 以涡融合开始的t₁时刻为参考, 两涡融合形成新涡的涡核密度相对于涡a和涡b的涡核密度分别降低约4.6%和8.2%. 在相邻两个涡结构的融合过程中, 短轴和长轴端点处的流体密度变化量不超过3.0%. 从上述分析能够发现: 在涡结构的融合过程中, 涡a和涡b内部流体的密度变化比较轻微, 这表明相邻两涡的融合过程很可能是涡a和涡b内部流体的对等组合过程(即涡核与涡核的流体组合、边界与边界的流体组合), 没有看到较强的流体挤压和涡结构内部流体重新分配等现象.
图 12 特征点密度在涡融合过程中的变化
Figure12. Variation of fluid density at several characteristic points during their merging process.

在以上的研究中, 超声速混合层上下两层来流的密度相同. 然而, 对于图1所示的由制冷射流和外部主流形成的超声速混合层, 射流和主流的密度可能并不相同, 这里简要讨论此情况下涡结构内部流体的密度分布特性. 以文献[23]中表1描述的超声速混合层为例(Mc ≈ 0.46), 其流场某时刻的涡量等值面如图13(a)所示. 选取一个处于独立状态的涡结构(记为Vortex F), 其内部流体的密度在射线上沿纵向(y)和流向(x)的变化曲线分别如图13(b)和(c)所示, 其中ρ_c, ρ₁和ρ₂分别表示涡核、上层来流和下层来流的密度.
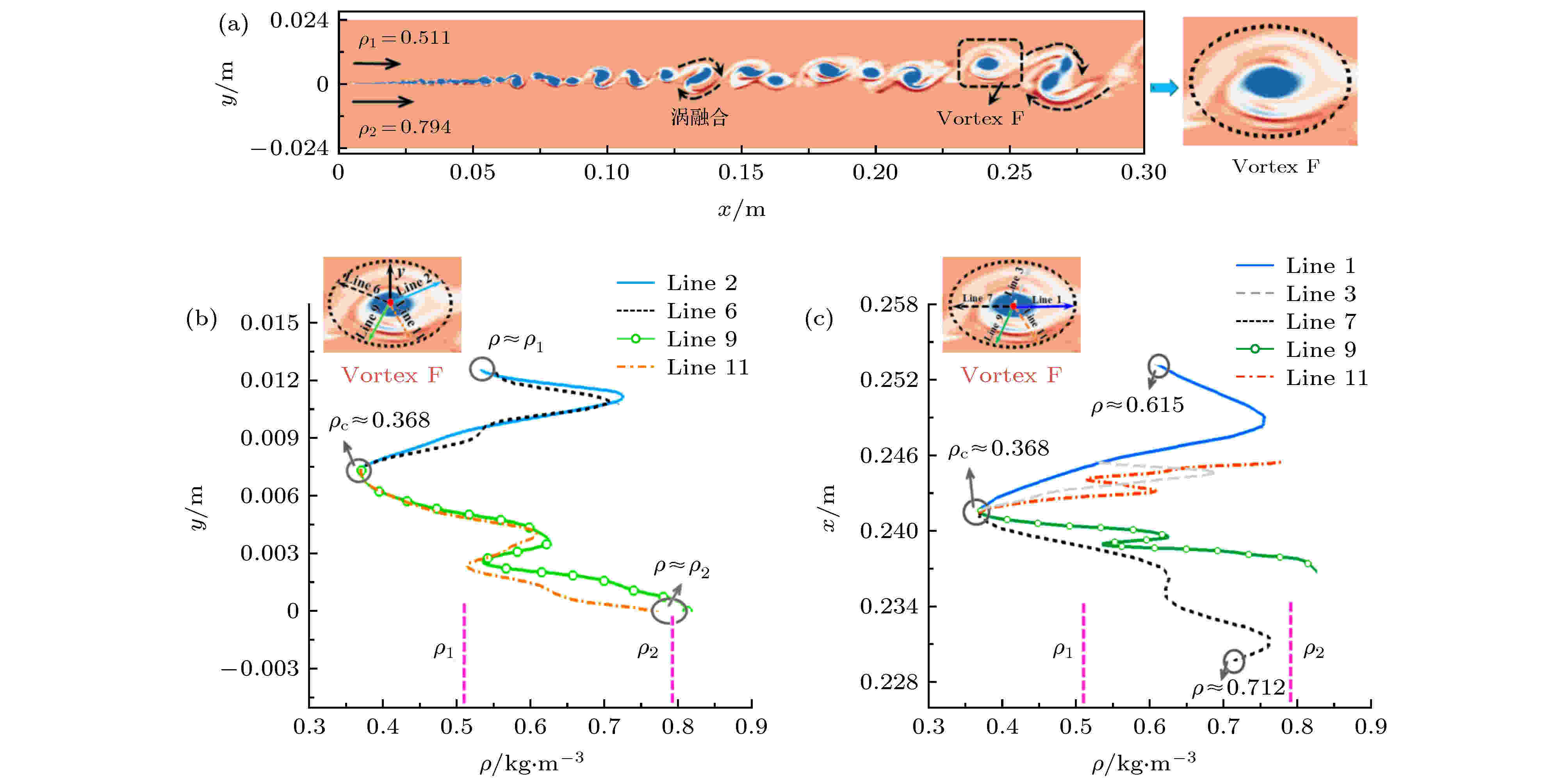图 13 (a)上下层来流密度不同的超声速混合层; (b)涡结构内部流体的密度沿纵向(y)分布曲线; (c)涡结构内部流体的密度沿流向(x)分布曲线
Figure13. (a) The supersonic mixing layer with different inflow density of its upper and lower layers; (b) density distribution of fluid inside the vortex along the longitudinal direction (y-axis); (c) density distribution of fluid inside the vortex along the flow direction (x-axis).

以关于纵向(y)对称的两组射线(Line 2、Line 6和Line 9、Line 11)为例, 涡核位置的流体密度约为0.368, 射线Line 2和Line 6上的流体密度沿纵向(y)的变化曲线具有较好的重合性, 射线Line 9和Line 11上的流体密度变化也具有相似的特性. 具体来说, 随着离开涡核距离的增加, 射线Line 2和Line 6上的流体密度先逐渐增加后逐渐减小, 端点(涡边界)位置的流体密度约等于ρ₁; 射线Line 9和Line 11上的流体密度整体上逐渐增加(中间部分的流体密度有小幅波动), 端点(涡边界)位置的流体密度约等于ρ₂. 上述分析表明: 涡结构内部流体的密度分布仍近似具有关于纵向(y)对称的特性; 涡核附近流体的密度线性增加, 而远离涡核的流体密度受上层或下层来流的影响较大, 即涡结构上边界附近的流体密度趋近于上层来流的密度, 而涡结构下边界附近的流体密度趋近于下层来流的密度, 这种现象的原因可能是涡结构高速旋转使混合层的上层和下层流体被不断地“卷吸”进涡结构内部. 因此, 涡结构内部流体的密度分布也就不再具有关于流向(x)对称的特性(见Line 3和Line 11上的流体密度变化曲线).
此外, 对比图7和图13中的密度变化曲线能够发现, 超声速混合层上层和下层来流密度的差异会使涡结构内部流体的密度变化出现波动. 能够推测, 上层和下层来流密度的差异越大, 涡结构内部流体的密度波动就会越剧烈. 因此, 从降低超声速混合层气动光学效应的角度, 制冷射流的密度应尽可能地接近外部主流的密度.

对红外制导的高速飞行器来说, 外部主流与光学窗口上方制冷射流形成的超声速混合层是其产生气动光学效应的主要来源, 而其流场中涡结构内部流体密度的时空变化则是光束产生偏移、模糊和抖动等现象的最根本物理原因. 在使用LES方法获得超声速混合层流场的基础上, 借助LCS法和涡核位置提取方法, 得到了涡结构的边界及其涡核的位置坐标, 并由此提出了涡结构内部流体密度分布的表示方法. 通过对不同空间尺寸、不同压缩性混合层和融合过程等情况下涡结构内部流体密度数据的分析, 初步揭示了超声速混合层涡结构内部流体的密度分布特性. 从本文的工作中, 总结出以下结论.
1)涡结构的涡核和纵向边界处的流体密度都随涡结构空间尺寸的增加而降低, 而涡结构流向边界处的流体密度随之有轻微增加. 以超声速混合层(Mc = 0.5)的大尺度涡结构相对小尺度涡结构而言, 涡核处的流体密度减少约31.0%, 涡结构纵向边界处的流体密度减少约5.5%, 而流向边界处的流体密度增加约3.8%.
2)随着超声速混合层流场压缩性的增加(Mc = 0.3, 0.5, 0.9), 以中等尺度的涡结构为例, 其涡核处的流体密度依次约为入流密度的0.79, 0.54和0.34; 其纵向边界处的流体密度依次约为入流密度的0.98, 0.93和0.71; 其流向边界处的流体密度依次约为入流密度的1.04, 1.13和1.16.
3)对于弱(Mc = 0.3)和中等压缩性(Mc = 0.5)的超声速混合层, 其流场中涡结构内部流体的密度分布既关于流向(x轴)对称又关于纵向(y轴)对称, 流体密度在连接涡核与涡边界射线上单调且近似均匀地增加. 对于强压缩性(Mc = 0.9)的超声速混合层, 其流场中涡结构内部流体的密度分布不再具有对称性, 且流体密度呈现波动变化的特点.
4)在相邻两个涡结构的融合过程中, 融合后的涡核密度相对于融合前减少约8.2%, 涡边界密度的变化量约为3.0%. 这表明融合过程很可能是两个涡结构内部流体的对等组合过程(即涡核与涡核的流体组合、涡边界与涡边界的流体组合).
5)涡结构在生长的过程中, 其几何形状逐渐趋于扁平, 表明涡结构在流向的生长速度快于其在纵向的生长速度.
6)超声速混合层上层和下层来流密度的差异会使涡结构内部流体的密度变化出现波动, 从降低超声速混合层气动光学效应的角度, 制冷射流的密度应尽可能地接近外部主流的密度.
感谢上海交通大学高性能计算中心的“π”超级计算机为本研究提供的计算支持.