全文HTML
--> --> -->由于单元结构的亚波长尺度特征, 超材料可由连续的(均匀或非均匀)等效媒质参数来描述. 过去二十余年, 超材料领域一直以等效媒质为基础, 根据几何光学、物理光学、变换光学等物理原理, 通过定制等效媒质参数及其分布而控制电磁波, 产生一系列奇特的物理现象并推动其应用[1-50]. 然而在工程实际中, 超材料器件往往需要由大量的结构单元构成阵列才能实现预定功能, 因此基于等效媒质的功能器件体积较为庞大、构型复杂, 难以应用于微波电路领域. 同时超材料器件一旦制备, 其功能即被固化, 很难用来实时地操控电磁波, 以实现众多不同的功能, 也难以和信息理论及数字信号处理方法相结合. 因此, 亟待突破超材料现有的研究体系, 探索超材料新的表征方法. 近年来出现的数字编码超材料、现场可编程超材料和信息超材料是其中的典型代表, 有望解决上述瓶颈问题.
2.1.数字编码和现场可编程超材料
由于单元结构的亚波长特征, 超材料可由连续的等效媒质参数来描述. 类比于电路, 具有连续媒质参数的超材料可称为模拟超材料. 模拟系统的缺点是, 当系统结构变得复杂时, 其分析与设计难度也随之提高. 以二值数字逻辑为基础的数字系统不仅在多个方面展现出独特优势(例如受噪声干扰小、允许较大的器件参数容差等), 而且具有逻辑运算和处理功能, 通过逻辑上的组合便可形成不同功能的器件与系统. 为了实现“数字版”的超材料, 本研究组和美国宾夕法尼亚大学Engheta研究组于2014年相互独立地提出了数字超材料的概念[51,52]. Engheta研究组[51]提出通过空间混合的“数字超材料位”来构建“超材料字节”的方法, 以实现所需的媒质参数, 其中“数字超材料位”由不同媒质参数(例如正介电常数和负介电常数)的材料粒子构成(图1). 因此Engheta工作的核心是用数字位的手段来描述等效媒质, 仍属于等效媒质超材料的范畴. 由于负介电常数媒质实现的复杂性, 该数字化概念很难推广应用. 实际上, 早在2009年(二维情况)和2010年(三维情况)已经有****提出类似的观念[21-23], 用空气(折射率为1)和某种介质(折射率为n)的不同配比(不同尺寸的空气孔)即可实现介于1和n之间的任意折射率. 与需要负的介电常数相比, 这种方法更容易实现, 因此已经广泛应用于宽带地面隐身斗篷[21,22]、三维变换光学透镜[23]、渐变折射率平板透镜[24-26]、以及放大透镜[27,28]等新现象的实验验证和新器件的研制. 而在同一时间段, 本研究组也独立地提出了数字超材料的概念. 与Engheta研究组的表征方法不同, 本研究组[52]从信息科学的角度研究超材料, 摒弃了等效媒质的表征方法, 提出用数字编码来表征超材料的新思想, 通过改变数字编码单元的空间排布来控制电磁波, 进而实现了可编程超材料. 该思想不但被实验所证实, 而且开拓出超材料新领域, 并被其他****推广到了声学超材料和力学超材料[53,54].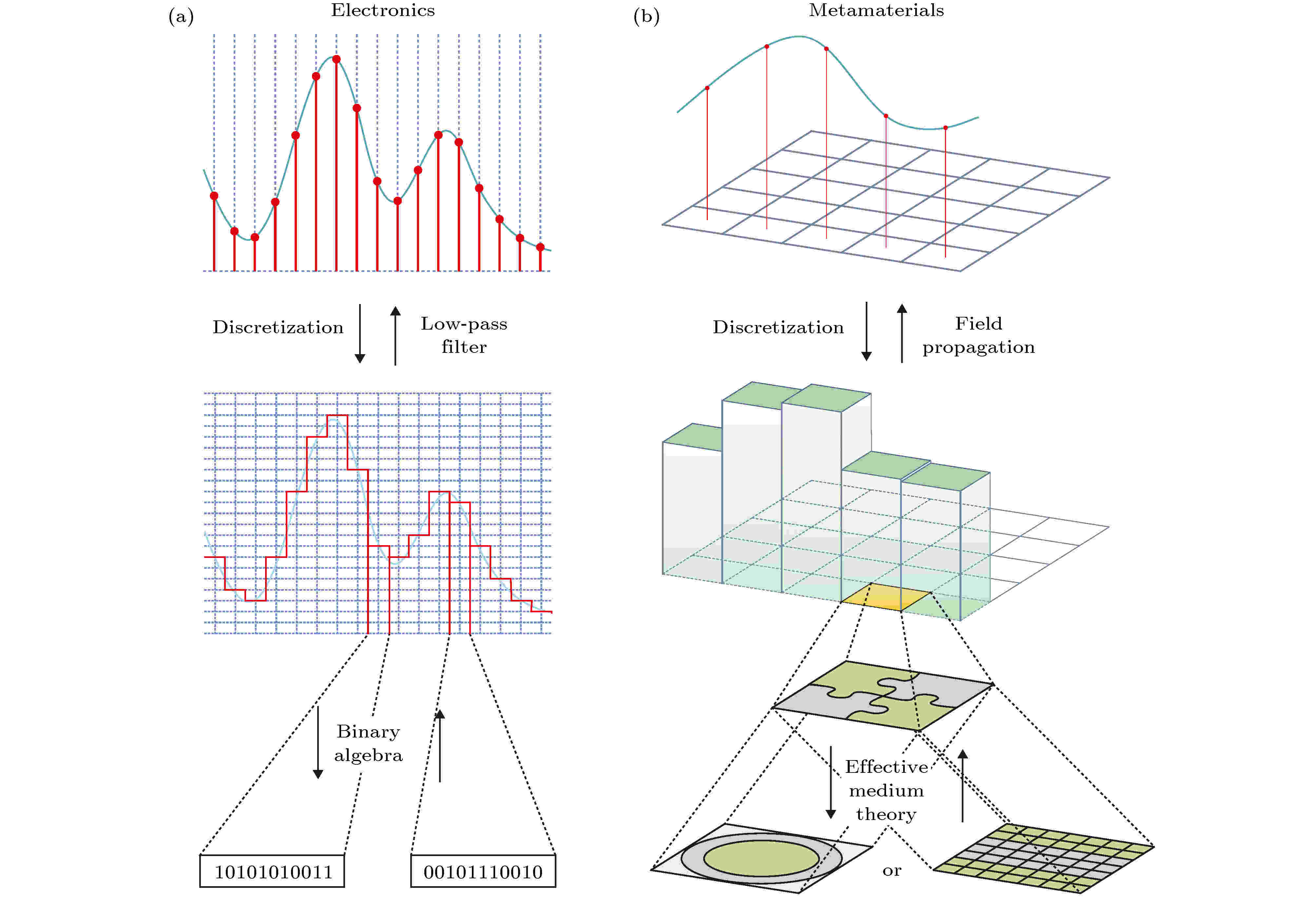
图 1 等效媒质超材料的数字化[51] (a) 等效媒质超材料的离散化和数字化过程; (b) 给定介电常数函数的取样和离散化, 并用两个超材料单元来设计Figure1. Digitization of effective-medium metamaterial[51]: (a) Discretizing and digitizing processes of effective-medium metamaterial; (b) sampling, discretizing, and digitizing a required permittivity function using two metamaterial bits as building blocks.
为了突破超材料惯用的等效媒质表征方式, 本研究组[52]提出以电磁响应相位差为180°的两个超材料粒子构建1比特数字编码超材料的0和1单元, 应用0和1编码单元的空间排列来控制电磁波, 以获得所需的物理功能, 实现超材料的全数字化设计(图2). 例如, 在电磁波垂直入射的情况下, 全0或者全1单元数字编码超材料能产生高增益的单波束反射; 0和1单元一维交错分布的数字编码超材料可产生超越斯涅耳定律的双波束反常反射(图2(c)); 而0和1单元二维交错分布的编码超材料可实现四波束的反常反射(图2(d)), 其中波束偏折角度可由0和1的排列数目周期所确定. 如果超材料共由N个基本单元构成, 则1比特编码超材料0和1的不同排列数将有2N种, 因此可以实现2N种调控功能, 进而产生可设计的任意多波束反常反射. 当0和1数字编码呈随机分布(或码元数目较少情况下呈现某种优化编码序列)时, 该超材料可以激励起电磁波的随机漫散射, 将入射电磁波打散到很多方向, 每个方向的散射电平很低, 实现了电磁波在宽频带和宽角域的隐身. 上述物理现象和功能均得到全波数值仿真和实验结果的验证[52].
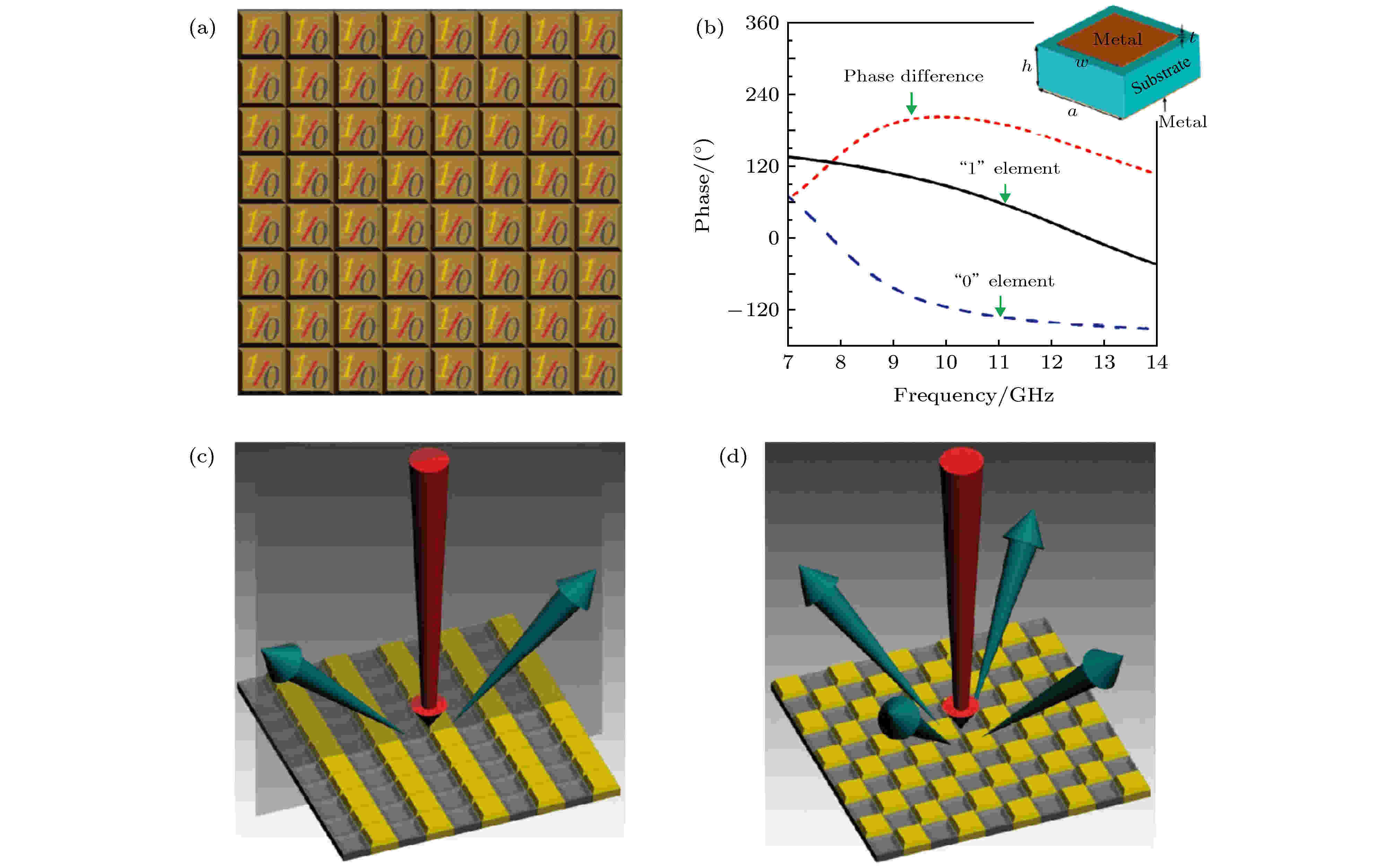图 2 超材料的数字编码表征及数字编码超材料[52] (a) 数字编码超材料; (b) 数字0和1单元的物理实现及其相位响应; (c), (d) 不同数字编码序列下的电磁响应, 展示出完全不同的功能Figure2. Digital coding representation of metamaterials[52]: (a) Digital coding metamaterial; (b) the physical implementations of digital units 0 and 1 and their phase responses; (c), (d) electromagnetic responses under different digital coding sequences, showing different functions.
数字编码超材料的概念可由1比特编码推广到2比特和多比特, 其中2比特编码超材料由相位差为90°的00, 01, 10, 11四个编码单元构成; 3比特编码超材料由相位差为45° 的000, 001, 010, 011, 100, 101, 110, 111八个编码单元构成; n比特编码超材料由相位差为360°/2n的2n个编码单元构成[52]. 文献[55]提出了一种Minkovski分形结构, 根据结构的不同尺度可实现所需比特的数字编码单元, 进而灵活地调控太赫兹波. 一般说来, 数字编码超材料的比特数越高, 其调控电磁波的能力越强. 例如, 2比特编码超材料可实现广义斯涅耳定律的反常反射、缩减雷达散射截面更显著的漫散射[52,55]以及产生轨道角动量涡旋波等[56,57].
超材料的数字编码表征建立起超材料物理世界和数字世界的桥梁, 因此很多物理概念可以引入数字世界, 例如各向异性数字编码[58]和张量数字编码[59]. 文献[58]通过设计一种非对称结构, 能对不同极化的入射电磁波呈现出不同的数字编码状态(水平极化时为数字0, 垂直极化时为数字1), 这样可将1比特的数字编码0和1扩展为各向异性数字编码0-0, 0-1, 1-0和1-1四个态; 同理, 2比特各向异性编码拥有16个数字态. 因此, 各向异性数字编码超材料可将数字编码超材料的功能扩充一倍. 类似地, 张量数字编码超材料可进一步扩充数字编码超材料的功能并提高调控电磁波的能力, 例如将空间电磁波转换为表面波等[59]. 与此相对应, 数字领域的很多概念和方法也可用于物理调控.
上述编码超材料中, 数字0和1单元由不同的物理结构实现, 因此还不能称为数字超材料. 真正的数字超材料的数字0和1单元应该由包含某种有源器件的同一超材料结构构成, 通过有源器件的工作状态来实现编码单元的0和1状态的调控. 为此, 我们设计了图3(a)所示的超材料单元[52], 其编码状态受控于偏压二极管的状态, 当二极管导通时(对应于控制电压高电平), 该单元表现为数字编码1状态; 当二极管断开时(对应于控制电压零电平), 该单元表现为数字编码0状态; 二者对应的相位响应相差180° (图3(b)). 而控制电压的高电平和零电平恰好是基带数字领域的1和0, 因此这个结构是一个真正的数字化超材料单元, 可实时调控数字编码的0和1状态, 并将超材料物理世界和数字世界有机地联系起来.
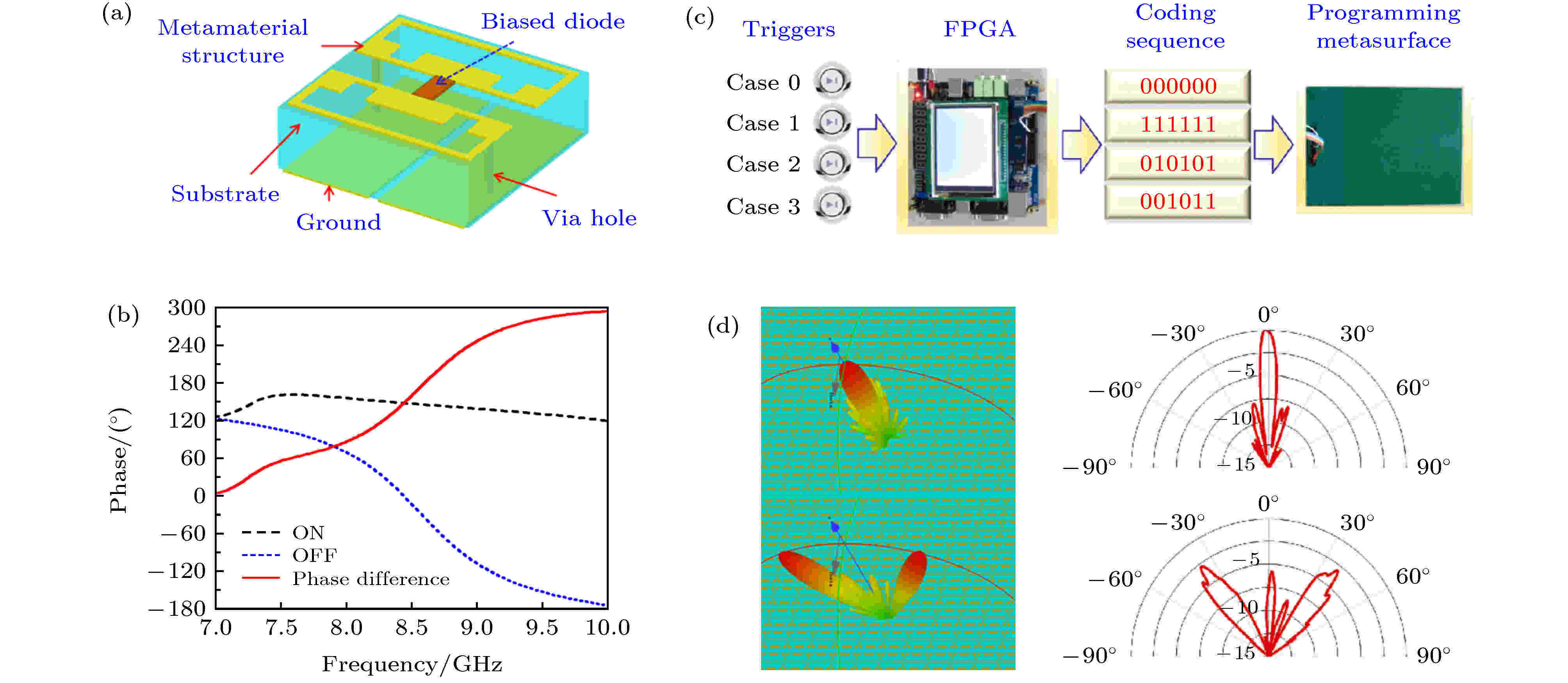图 3 数字超材料与现场可编程超材料[52] (a) 动态可调的数字编码超单元; (b) 数字0和1状态下的相位响应; (c) FPGA驱动下的现场可编程超材料; (d) 不同编码序列下的可编程功能Figure3. Digital metamaterial and programmable metamaterial[52]: (a) An active digital meta-atom; (b) the phase responses of the active digital meta-atom under the 0 and 1 states; (c) a programmable metamaterial controlled by FPGA; (d) the measured programmable functions under different digital coding sequences.
图3(a)为第一个数字化超材料的单元结构, 作为单一的数字超材料平台, 其每个单元的0和1状态可独立调控, 拥有2N个编码组合(其中N是超材料的总单元数). 对应于不同电磁响应的编码序列提前设计好并存储在现场可编程门阵列(field programmable gate array, FPGA)之中, 用FPGA实时触发数字超材料实现对电磁波的动态调控, 形成了首个现场可编程超材料(图3(c))[52]. 通过预加载的切换编码序列, 可完成多种不同的功能, 例如单波束辐射、多波束辐射(波束数目可选择), 如图3(d)所示; 也可实现涡旋波辐射、波束扫描以及漫散射雷达缩减等[52,55,60].
2
2.2.信息超材料
本研究组[61]于2017年在Journal of Materials Chemistry C的特邀论文中提出信息超材料的概念, 涵盖了数字编码超材料、现场可编程超材料以及未来的软件化超材料和可认知超材料, 是物理学与信息科学的有机融合. 信息超材料采用数字化方式对超材料的人工原子进行表征与标定, 从而使人们可以从信息的角度来分析与设计超材料, 它能直接处理数字编码信息, 并可进一步对信息进行感知、理解, 甚至记忆、学习, 为基于超材料的电磁波调控提供了一个全新的物理平台, 从而实现对信息更加灵活、实时和智能地控制. 信息超材料的核心是在超材料的物理空间上建立起数字空间, 可将电磁学和信息科学有机地结合起来, 开拓新的学科方向, 产生一系列具有新体制新机理的信息系统.2
3.1.信息熵
对于信息超材料, 不同的数字编码图案导致不同的物理性能. 例如, 全0或者全1编码超材料产生单波束辐射, 而图4(a)所示的0和1随机编码产生大量的多波束辐射(图4(b)和图4(c)), 后者的信息量明显高于前者. 为了定量地评估信息超材料所辐射的信息量大小, 本研究组[62]提出利用香农信息熵来表征具有不同数字编码图案的信息超材料所携带的信息量, 由此可通过设计不同的数字编码图案来操控信息超材料所辐射的信息量. 数值仿真与理论计算表明, 香农信息熵可用来准确评估信息超材料所携带信息量的大小. 数字编码图案越随机, 其几何熵与远场方向图的物理熵就越大, 并且两者之间存在近似正比关系, 如图4(d)所示. 这恰好与熵在热力学中的原始定义相吻合, 也与香农提出的信息熵定理相一致. 基于信息熵, 可准确地实现具有任意信息量的远场方向图, 为新体制微波成像等奠定基础.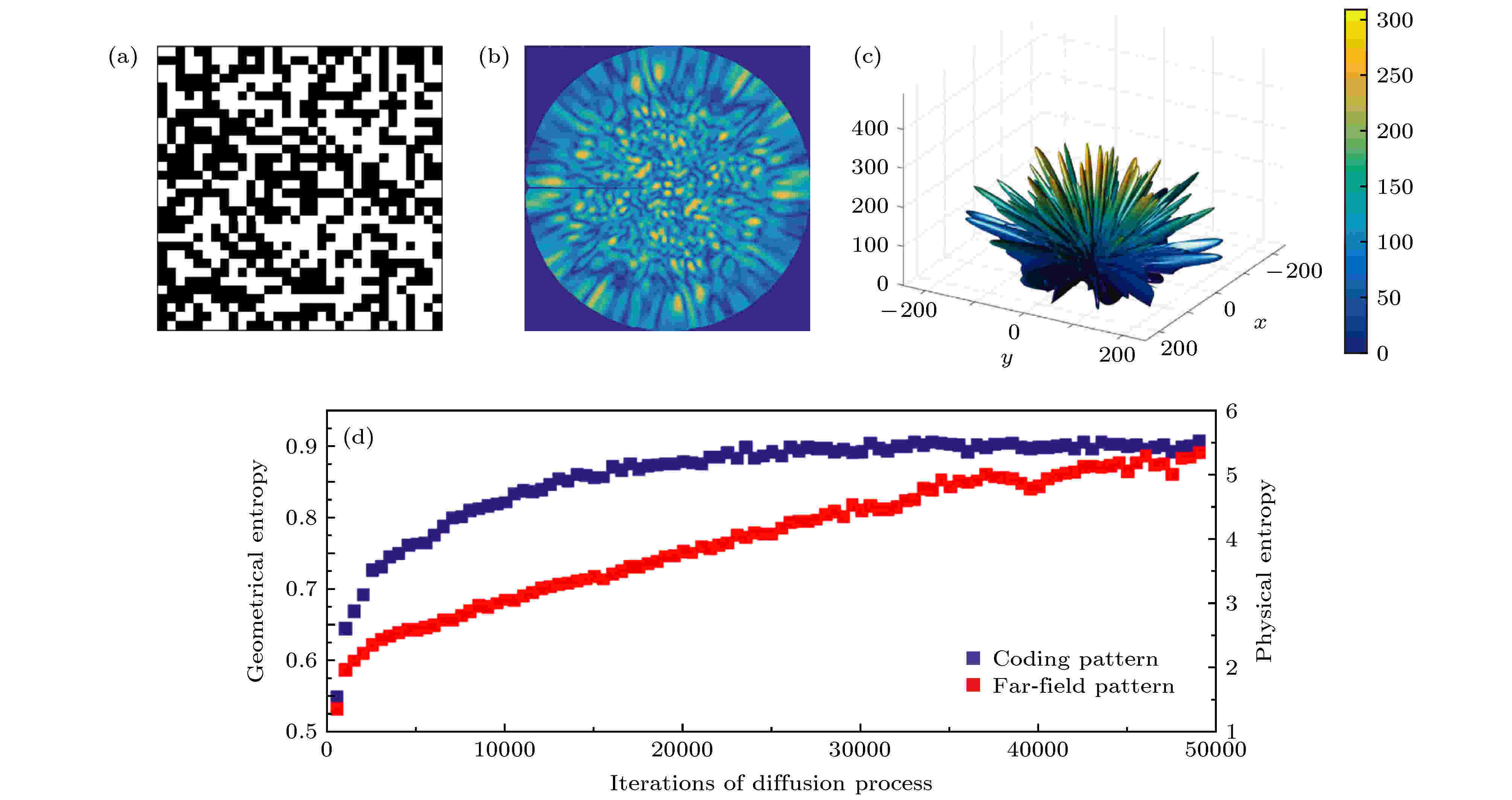
图 4 信息超材料的信息熵[62] (a) 随机0和1数字编码; (b), (c) 随机0和1数字编码超材料的远场方向图; (d) 数字编码序列由有序到无序时的几何信息熵和物理信息熵Figure4. Information entropy of information metamaterials [62]: (a) The random 0 and 1 coding pattern; (b), (c) the far-field radiation patterns of the random 0 and 1 digital coding metamaterial; (d) the geometric information entropy and physical information entropy of the digital coding sequences from order to disorder.
2
3.2.数字卷积定理
信息超材料因其海量的数字编码图案可产生异常丰富的电磁波束, 但如何生成特定的电磁波束是信息超材料设计的核心. 一般说来, 若实现任意角度的波束扫描, 需要采用优化算法根据远场方向图来反演数字编码图案, 将消耗大量的计算资源和计算时间. 为解决这一难题, 本研究组[63]提出在信息超材料物理空间上进行数字卷积的新方法, 仅采用有限个状态的数字编码单元即可实现连续的波束扫描. 得益于信息超材料的数字编码与其远场方向图之间的傅里叶变换关系, 可将数字信号处理中的卷积定理应用于远场方向图的偏转, 在已有编码图案上叠加一个梯度编码序列(图5(a)—(c)), 就能将方向图朝着任意设计的方向无失真地偏转(图5(d)—(f)), 其机理类似于傅里叶变换中将基带信号搬移到高频载波的过程(图5(g)—(i)). 分析与实验结果证明, 应用信息超材料的数字卷积运算能将电磁波辐射到上半空间的任意设定方向, 或实现全半空间的波束扫描.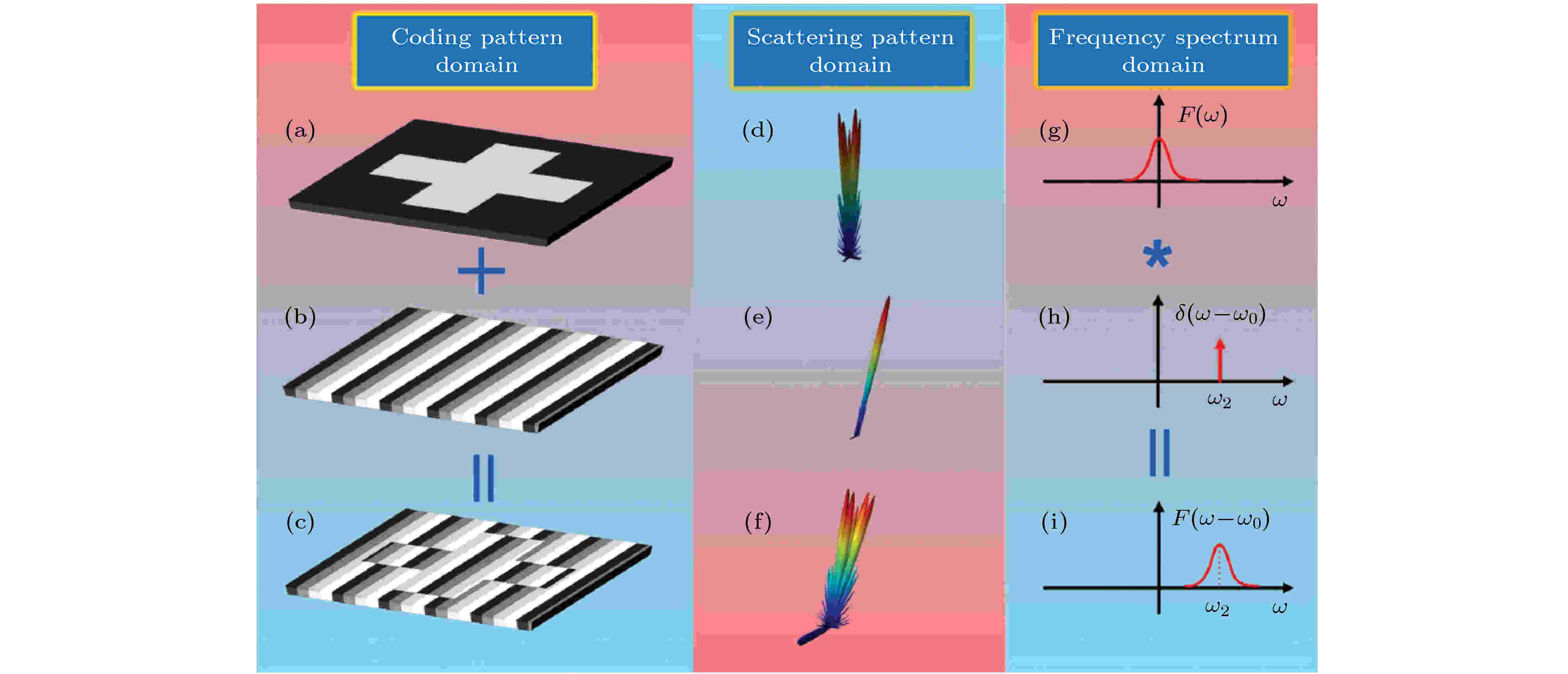
图 5 基于信息超材料的数字卷积定理[63] (a)?(c) 三种不同的数字编码图案, 其中(a)与(b)相加得到(c); (d)?(f) 相应数字编码图案的远场方向图, 实现方向图搬移; (g)?(i) 类比于信号处理中的频谱搬移Figure5. Digital convolution theorem based on the information metamaterials[63]: (a)?(c) Three different digital coding patterns, where (c) is obtained by adding (a) and (b); (d)?(f) the far field patterns of the corresponding digital coding patterns, showing the shift property of radiation beam; (g)?(i) the spectrum shift property in the digital signal processing.
2
3.3.加法定理
信息超材料的数字卷积定理保障了单波束任意方向扫描或多波束的任意方向联动辐射. 为了实现多波束相互独立的任意辐射, 本研究组[64]进一步提出了信息超材料的加法定理. 加法定理的基础是复数数字编码, 复数编码从电磁波的本质出发, 将相位信息所在的复数部分整体作为数字编码, 从而推广到了复数域. 加法定理的物理意义可从微观和宏观两方面来解释. 在微观层面, 加法定理揭示了不同比特编码之间的相互联系, 即两个N比特编码相叠加将产生N+1比特的数字编码, 所以不同比特位的数字编码可通过加法定理相互转换; 从宏观角度来说, 加法定理可将两种或多种不同的功能进行叠加, 例如实现多波束的独立调控, 进一步拓展了信息超材料的信息处理能力, 提高了设计自由度.2
4.1.可编程全息成像系统
全息成像是一种利用干涉和衍射原理记录并再现物体三维图像的技术, 一般说来, 全息图案设计好之后, 其所对应的全息图像也随之确定. 近年来, 人们将超材料和超表面用于设计太赫兹、红外和光频段的全息成像器件, 把不同极化或不同位置处的全息图案写在同一个超表面上, 获得了两个或多个固定的全息图像[33-36]. 为了使同一个超表面能实时地呈现千变万化的全息像, 本研究组和北京大学李廉林研究组[65]合作, 利用1比特现场可编程超材料首次实现了实时动态可调的微波全息成像(图6). 根据改进的Gerchberg-Saxton算法, 可计算出不同的图像所对应的0/1编码图案, 将这些预先计算好的编码图案存储到FPGA中, 用FPGA驱动数字编码超材料, 即可实时地产生所对应的全息像. 该成像系统不仅能生成可编程的全息微波图像, 而且由于超材料单元的亚波长特点, 所生成的全息图像具有更高的空间分辨率、更低的噪声和更高的准确性. 另外, 亚波长尺度的可编程超材料单元可减小衍射效应, 从而提高成像效率.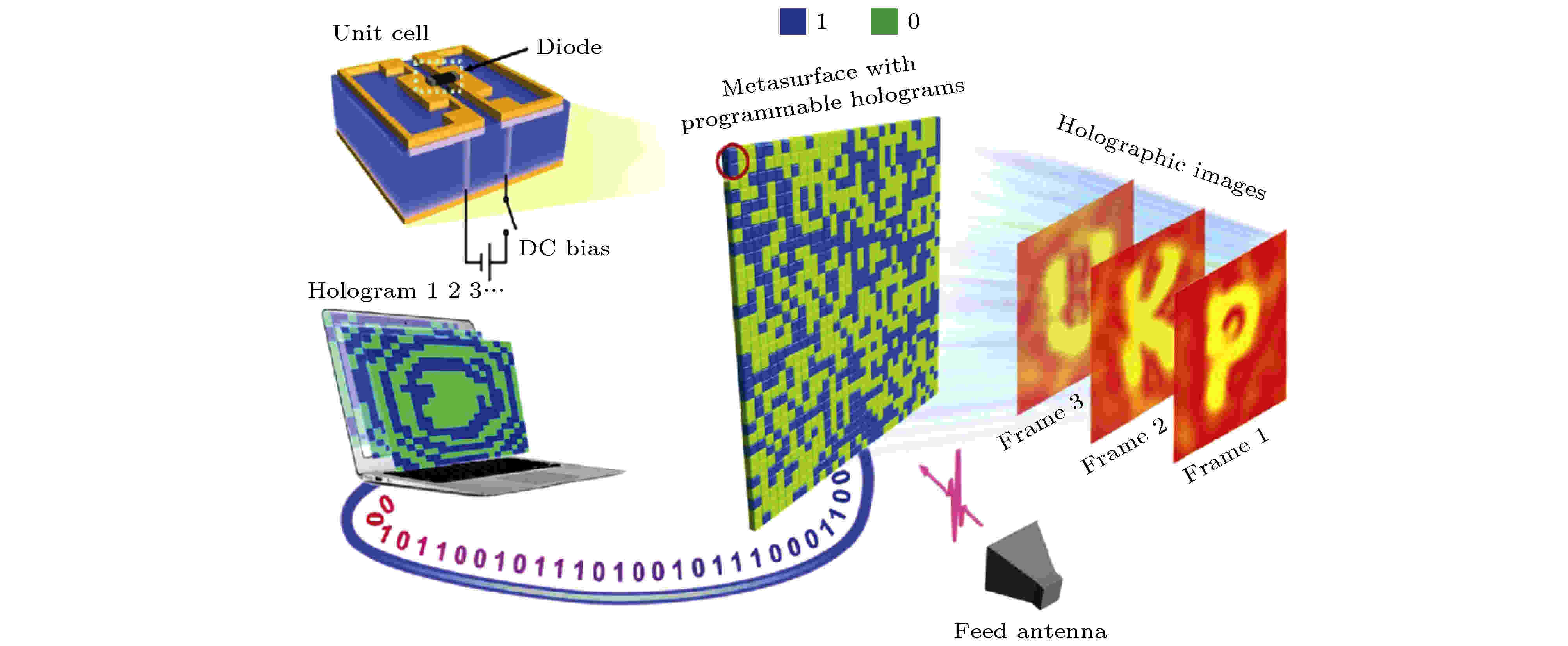
图 6 基于1比特现场可编程超材料的可编程微波全息成像系统(FPGA控制不同的数字编码图案, 实时地产生不同的全息像)[65]Figure6. A reprogrammable microwave holographic imaging system based on 1-bit programmable metamaterial. Different binary holograms are controlled by FPGA to generate different holographic images[65].
2
4.2.新体制微波成像系统
传统的微波成像分为相控阵体制和合成孔径体制. 相控阵体制需要多个发射天线和接收天线, 价格昂贵; 合成孔径体制仅包含单个发射和接收天线, 但需要机械扫描, 数据获取效率低. 基于现场可编程超材料, 本研究组[66]提出一种新体制微波成像系统原型, 在单频点情况下, 使用单天线、不需机械扫描即可实现微波成像, 大大简化了成像系统架构, 降低了成像成本. 该成像系统的核心原理是利用2比特现场可编程超材料, 在喇叭天线的激励下, 通过切换预先设计的不同的数字编码图案, 产生大量、相对独立的随机波束照射待成像目标, 并接收其回波信号; 然后通过逆散射算法或者压缩感知技术处理所获取的独立多波束测量数据, 以恢复最终目标像[67].上述微波成像系统虽然简化了系统架构, 降低了成像成本, 但通过可编程超材料的数据获取和通过压缩感知的数据处理过程是割裂的, 且高度依赖于高运算量的优化算法(例如稀疏增强优化算法), 因而严重制约了成像系统实时感知的需求. 为了解决这一难题, 本研究组与北京大学李廉林研究组[68]合作, 基于现场可编程超材料提出了机器学习驱动的智能电磁感知方法, 实现了人体目标的实时动态成像. 如图7所示, 该感知方法将可编程数字超材料和卷积神经网络机器学习方法相结合, 采用机器学习方法对超材料进行在线训练, 实现了数据获取和数据处理的一体化操作. 实验证明, 可编程超材料具有物理域特征提取和数据降维的能力, 因此能同时进行机器学习驱动的波束扫描和自适应数据获取. 更进一步, 实验验证了该成像系统能以大约百赫兹级别的帧率进行高分辨率微波成像和目标识别, 为解决现有的成像体制在成本、效率和精度等方面的难题提供了新途径.
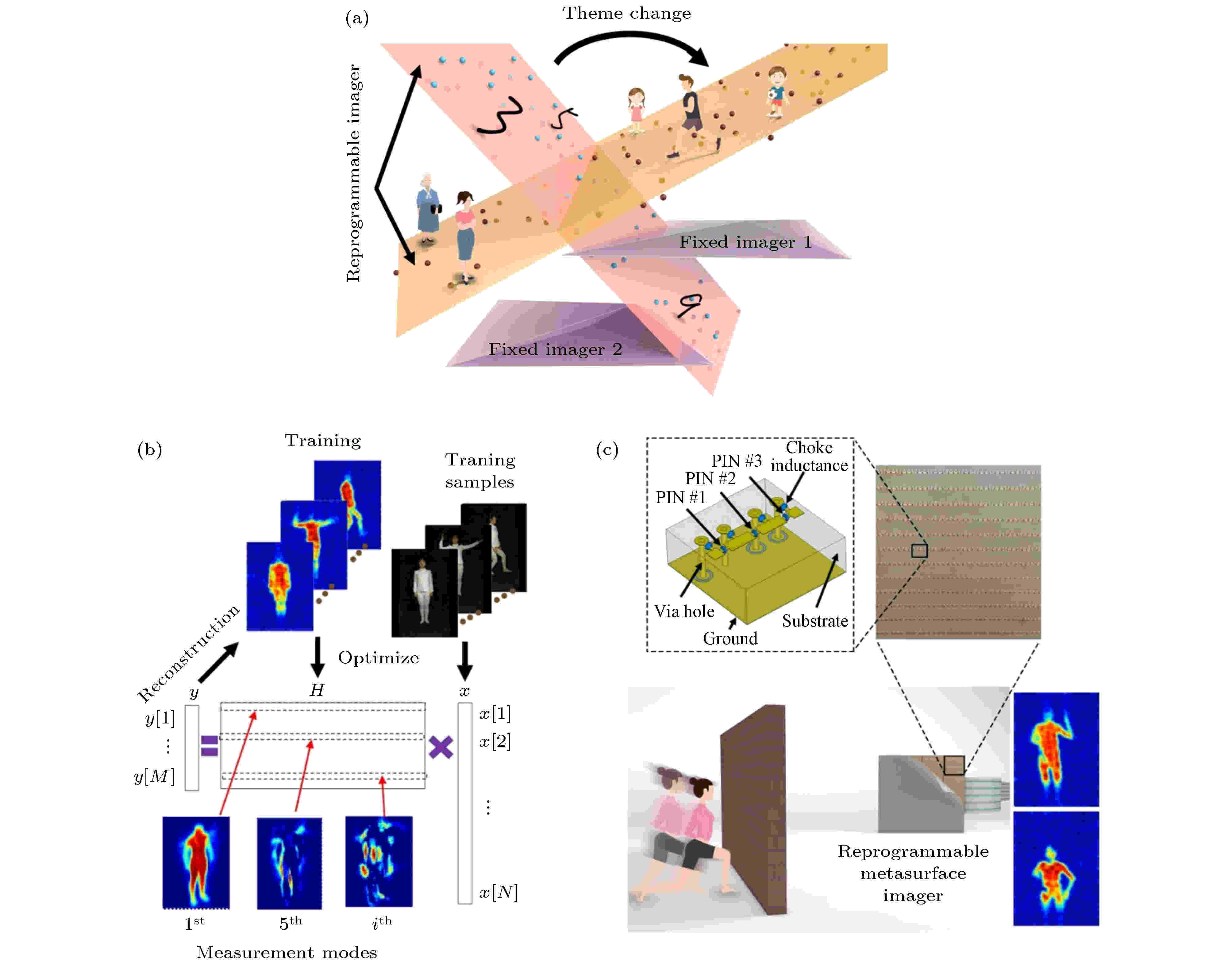图 7 可编程实时微波成像系统[68] (a)机器学习成像系统可根据不同场景进行优化; (b)训练可编程成像系统示意图; (c) 2比特数字编码超材料及其对一个运动目标的实时成像示意图和测量结果Figure7. Real-time digital-metasurface imager[68]: (a) The machine-learning metasurface imager can be optimized for different kinds of scenes; (b) the illustration of training the reprogrammable imager; (c) the map of 2-bit coding digital metasurface, and the illustration of real-time imaging a moving person behind a wall, as well as measurement results.
2
4.3.新构架无线通信系统
现代无线通信系统的工作原理是, 先将所要传递的信息转换为数字形式的二进制码, 通过数字/模拟转换, 将数字信号变成中频模拟信号, 再将中频模拟信号进行调制, 加载到载波, 经过放大和微波射频链路后通过发射天线发送出去. 基于信息超材料, 本研究组[69]提出了一种全新的直接辐射无线数字通信系统, 极大地简化了传统通信构架, 发射系统所传递的信息被加载到可编程超材料上, 在馈源天线的照射下以不断变换的远场方向图的形式直接辐射到自由空间中; 接收系统将处于远场区域不同位置处的接收天线所接收到的电场值汇总得到远场方向图, 并通过对比远场方向图与编码序列之间的映射关系而恢复出所发送的原始信息. 除此之外, 该通信系统还集成了状态检测算法以及状态优化算法, 能够实时地提取远场的可用状态信息, 并保证在电磁环境恶劣的情况下能有效地检索到可用的状态进行通信. 未来可在系统发射端和接收端引入基于机器学习的智能算法, 从而进一步提高系统通信容量和鲁棒性. 本工作提供的直接通信系统省去了数模转换以及混频的模块, 极大地简化了通信系统的复杂度, 降低了通信系统的成本, 且具有与生俱来的保密特性, 能够从物理层保证所传递的信息无法从单点或者非关键点被截获. 近来, 这一方法已经推广到近场的多通道通信[70].除了使用空间数字编码进行直接通信, 本研究组[71]进一步提出了时间编码超材料的概念, 通过在时间域引入数字编码来控制超材料周期单元, 以可编程方式实现了超材料对电磁频谱的实时动态调控, 以及对不同谐波的精确控制, 并可实现入射能量从载波至高阶谐波的高效转换. 根据2比特梯度时间编码对正负一次谐波的高效产生和实时切换特征, 本研究组基于时间编码超材料构建了一种新的二进制频移键控(binary frequency shift keying, BFSK)无线通信系统构架. 在该构架中, 传统通信系统发射机中所必须的数模转换、混频器、射频链路、天线等部件被超表面和FPGA所取代, 基带信号直接映射为超表面反射系数, 实现了对入射波载波频率的调制. 该系统能够在多角度、有干扰等情形下实现信息的低误码率、高速传输, 极大简化了通信系统的复杂度, 为新一代通信、雷达系统的发展提供了新思路. 由于BFSK通信系统的数据传输速率较低, 又进一步提出和研制了基于时间编码超材料的正交相移键控(quadrature phase shift keying, QPSK)[72,73]、8移相键控(8-phase shift keying, 8 PSK)[74,75]以及多种机制混合[76]的无线通信系统. 其中, QPSK超材料无线通信系统架构如图8所示, 在主频为4 GHz的情况下, 其数据传输速率已达1.6 Mbps, 可实时、无误码地传输视频电影[73].
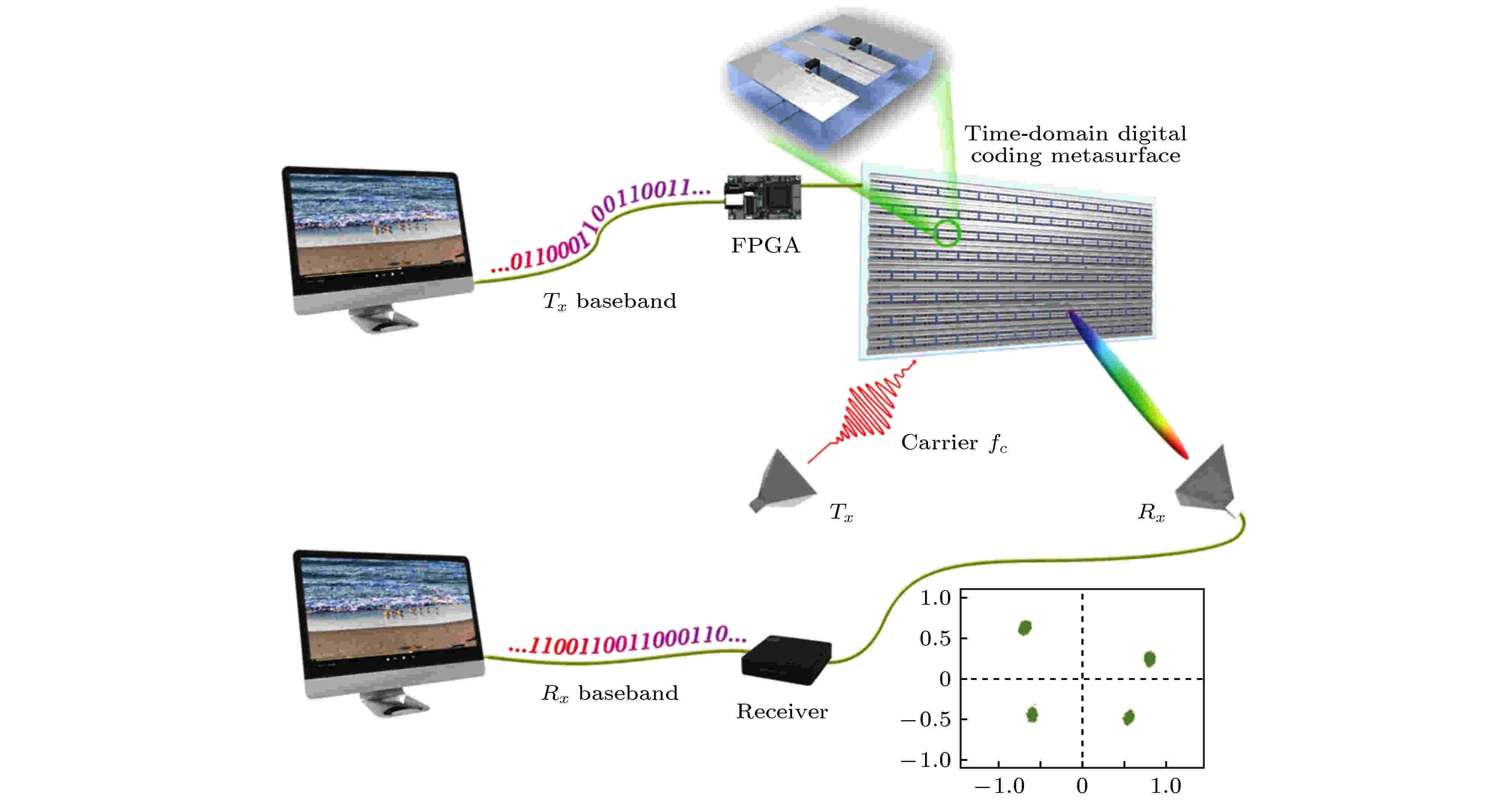图 8 基于时间编码数字超材料的新架构QPSK无线通信系统, 可实时地传输视频信号, 其中右下图为测量的星座图[73]Figure8. Schematic description of the new-architecture QPSK wireless communication system based on the time-domain digital coding metasurface, which can transmit movies in real time[73].
基于信息超材料的无线通信系统新架构也引起了国内外通信领域****的极大关注, 从接收机、信道模型、路径损耗模型、能耗等多种不同角度对新机制无线通信进行了大量研究, 被视为下一代无线通信的候选技术之一[77-80]. 由于篇幅关系, 这里不再详述.
本文对信息超材料的概念、基本原理、对电磁波和信息的调控能力、以及几个系统级应用做了简单概述. 这一全新领域近几年展现出迅猛的发展势头, 最近半年就涌现出很多新方法和新应用. 下面从信息维度、控制维度、智能维度和应用维度四个方面展望信息超材料的进一步发展方向.
2
5.1.信息维度
现有可编程超材料均是对相位进行数字编码的, 数字信息也仅编码在相位之上. 为了提高对电磁波的控制能力、增加信息维度, 相位编码应该推广到幅相联合编码, 以便在超材料上进行更广泛的数字信号处理运算. 目前虽然已经做了初步的幅相编码超材料工作[81,82], 但都基于静态编码单元, 尚未研制出幅相调控的可编程超材料.空间相位编码可调控电磁波的空间波束, 而时间编码可控制电磁波的频谱分布. 将二者结合起来, 空间-时间联合编码不但可同时调控电磁波的空间波束和频谱分布, 还可以极大地增加信息容量. 目前, 已对空间-时间联合编码数字可编程超材料进行了初步研究[83,84], 实验证明了其对电磁波强大的调控能力, 并打破电磁波的时空互易性, 实现了电磁波空间非互易和频率非互易传输[84]. 但空间-时间联合编码超材料的研究才刚刚起步, 有很多新物理特征和信息特征值得进一步挖掘.
2
5.2.控制维度
目前, 大部分数字编码单元的实时切换是基于偏压二极管的动态调控来实现的, 为了进一步增加控制维度, 本研究组在超材料单元中引入三极管, 不但实现了能量控制的数字编码超材料, 对能量进行编码, 还可以对电磁波进行放大[85-87]. 另外, 微机电系统也可作为一种新的候选调控方案. 在以二极管、三极管和微机电系统等为主导的电控方案中, 存在着控制电路复杂及控制布线密集等问题. 为了解决这个问题, 本研究组[88-90]提出了光控数字编码和可编程超材料及红外控制的数字编码和可编程超材料, 体现出了它们各自的独特优势. 然而, 能量控制的数字编码超材料、红外及光控制的数字编码超材料的研究还处于初步阶段, 仅能实现简单的编码图案调控, 更复杂的调控需要进一步研究.2
5.3.智能维度
超材料(乃至材料)的智能化是研究人员追求的目标. 超材料的数字编码表征已经能使超材料以可编程的方式动态、任意地操纵电磁波, 但是, 目前的可编程超材料还需要人工控制来切换不同的功能. 为了实现智能超材料, 本研究组[91]提出了一个简化版本—自适应超材料, 它能根据不同环境自适应地调整编程功能, 而无需人工参与. 自适应超材料可通过集成在超材料上的传感器来感测周围环境, 并通过传感反馈系统自适应地调整其电磁操作功能. 图9展示了一个自适应超材料的示意图, 将一个三轴陀螺仪集成到运动的超材料上, 可实时侦测超材料的高度及方位角. 在不同的方位角度下, 根据超材料内嵌算法自适应地调整超材料的数字编码图案, 可使其电磁波束恒定指向卫星方向[91]. 该工作提出了一种在线反馈算法作为控制软件, 使超材料可自适应地实现单波束及波束转向. 自适应超材料还可利用其他传感器, 以检测环境的湿度、温度、照度等, 实现更多、功能更广的自适应超材料.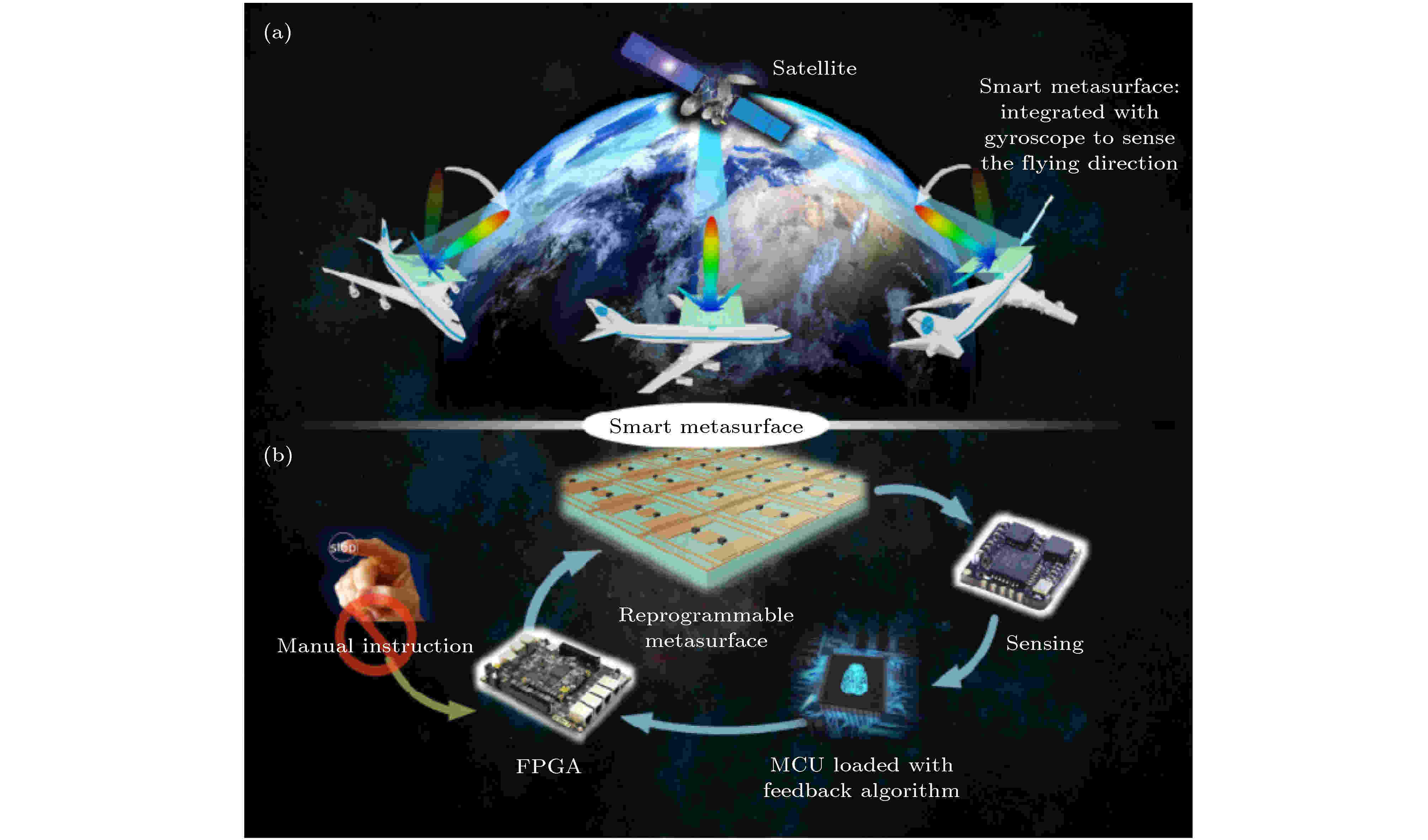
图 9 自适应超材料[91] (a) 自适应超材料的示意图; (b) 自适应超材料的闭环系统, 由现场可编程超材料、FPGA、传感器和自适应算法所组成Figure9. . The self-adaptive metamaterial[91]: (a) An illustrative example; (b) the closed-loop system of the self-adaptive metamaterial, which includes a programmable metamaterial, an FPGA, a sensor, and a microcontroller unit loaded with the fast feedback algorithm.
超材料的智能化还体现在其与人工智能算法的结合. 本文4.2节所介绍的基于机器学习算法驱动的动态成像系统是超材料智能化的应用之一[67], 该工作最近又取得新进展. 通过在可编程超材料中嵌入三种机器学习算法所研制的智能超材料, 不仅实现了非合作人体目标生命体征的探测, 而且完成了非合作人体目标的自动微波手语识别, 为解决智慧家庭人机交互、语言障碍人群交流等问题提供了新的途径[92,93]. 相信在不久的将来, 会有更多的深度学习算法和极端学习算法应用于可编程超材料, 以实现更先进的功能.
但是, 上面所述的自适应超材料和智能超材料还不具备自主学习的功能, 通过将二者的有机融合并结合大数据训练集, 将有望在未来实现更智能的可认知超材料[61,94,95], 即在陌生环境下可实现超材料的自主学习, 并智能地完成相关功能性操作.
2
