摘要: 本文基于库仑耦合双量子点复合系统, 研究了自发非平衡过程中熵产生率与信息流的基本关系. 从玻恩马尔科夫近似下的量子运动主方程出发, 获得稳态时总系统和子系统的熵产生率. 利用Schnakenberg网络理论, 揭示了各种熵产生率与基本环流的密切联系, 发现全局环流决定了双量子点间的能量和信息交换, 从而证明了化学势差驱动电子流动以及子系统间能量和信息交换是子系统熵产生的关键要素, 信息交换引起的熵产生保证了电子输运的持续进行. 结果表明在不违背热力学第二定律的基本条件下, 信息可作为驱动力使电子从低化学势流向高化学势.
关键词: 熵增加原理 /
双量子点系统 /
能流 /
信息流 English Abstract The entropy production rate of double quantum-dot system with Coulomb coupling Lin Zhi-Yuan Shen Wei Su Shan-He Chen Jin-Can College of Physical science and technology, Xiamen University, Fujian 361005, China Received Date: 12 December 2019Accepted Date: 24 April 2020Available Online: 09 May 2020Published Online: 05 July 2020Abstract: In thermodynamics of irreversible processes, the entropy production rate (EPR) is usually generated by the rate of the entropy change of the system due to its internal transitions and the entropy flows due to the interactions between the system and the environment. For the bipartite system, in addition to the factors mentioned above, the energy and information exchanges between the two subsystems will generate an additional entropy production in the EPR of a subsystem. To reveal the essence and role of the information flow, we build an open dissipative quantum system coupled to multiple electronic reservoirs with the same temperature and different chemical potentials. Based on the thermal and electron transport properties of a double quantum-dot system with Coulomb coupling, the EPR of each quantum dot and the information flow between subsystems are studied. Starting from the quantum master equation under the Born, Markov, and rotating-wave (or secular) approximations, we derive the EPRs of the total system and subsystems at the steady state. For purposes of relating the thermodynamic properties to the fundamental fluxes and affinities, a graph representation of the dynamics of the four-state model is introduced. Selecting a directed graph and a complete set of basic cycles by using Schnakenberg’s network theory, we show how the EPRs of the total system and the subsystems relate to global and local cycle fluxes. It is found that the energy and information exchanges between the quantum dots depend on the global cycle flux. The EPRs induced by the electron flows due to the chemical potential difference as well as the energy and information exchanges between the subsystems are the key elements of thermodynamic irreversibilities. The EPRs caused by the information exchange guarantee the continuous electron transports. The EPRs and the coarse-grained EPRs of the subsystems varying with the Coulomb coupling strength are obtained numerically. The results demonstrate that the information flows in the process of internal exchange become important to fully understand the operation mechanism of the bipartite system. Without violating the second law of thermodynamics, the information can be regarded as a driving force to move electrons from low to high chemical potential.Keywords: principle of entropy increase /double quantum-dot system /energy flow /information flow 全文HTML --> --> --> 1.引 言 物质的相互作用, 伴随着能量交换和信息交换[1 ,2 ] . 特别是在一些热力学过程中, 信息交换对全面理解整个系统的运行机制十分重要. 研究表明信息认知和提取可辅助物理系统更有效地做功[3 ,4 ] . Cottet等[5 ] 利用超导电路观察信息驱动热机做功, 实现热力学量的自由控制和测量. Park等[6 ] 提出双原子分子模型, 认为Szilard热机可完全由量子互信息驱动. Paneru等[7 ] 建立了一类无损信息引擎, 它能结合无错误反馈机制将所有可用的信息转换成机械能. 国内****Dong等[8 ] 和Cai等[9 ] 讨论了量子推广的Szilard热机模型, 发现在操作结束之后, 系统与Maxwell妖之间存在纠缠, 信息擦除的功耗使得热力学第二定律不会被破坏. 这些研究均利用一系列传递热量并做功的热力学过程组成完整的热力学循环, 需要利用外部辅助改变宏观参量来驱动循环运转, 测量结果记录在辅助物理系统中, 测量信息将反馈到系统影响功率输出[10 -17 ] .[18 -21 ] 和半导体量子点系统的电热输运[22 ,23 ] , 其中信息交换以稳恒流动的形式存在, 从实际出发建立有效理论研究信息稳定流动在热力学系统变化过程中的作用就变得尤为重要. Horowitz和Esposito[24 ] 首先从随机热力学出发统一描述了自发非平衡过程中信息如何产生并在系统内部传递. Barato等[25 ] 利用条件熵表示在已知内部随机变量的条件下外部随机变量的不确定性, 量化大肠杆菌感应网络处理信息的效率. 结合线性不可逆热力学, Yamamoto等[26 ] 发现Onsager互易性在信息驱动引擎中依然成立. Ptaszyński和Esposito[27 ] 又将随机热力学的研究成果推广到了多热源的自发非平衡量子开放系统, 发现系统内部信息交换引起的能流是非平衡自由能的重要组成部分. Strasberg等[28 ] 考虑系统与多热源的反复相互作用, 建立了量子与信息热力学理论的统一框架, 并讨论如何在其所建立的框架内分析非平衡系统的热力学特性. 由量子点和生物感应系统构成的自发过程具有共同的非平衡特性, 而非平衡系统的物质流、信息流和能量流与系统的熵产生率紧密相关. 对于开放系统, 熵产生率不仅包含系统本身熵的变化率还包含从系统到环境的熵流. 开放系统熵的变化率可由冯诺依曼熵定义. 开放系统与环境间物质和能量交换引起的熵变化则被称为热力学熵. 总结文献[24 -28 ]的研究发现, 信息的产生和交换依赖于内部子系统间的相互作用.[29 ] , 引入基本环流, 探讨局域电子环流和全局环流所导致的能流、信息流与子系统熵产生率的关系. 从子系统熵产生率中分解出粗粒化熵和信息熵, 揭示信息流对应的热力学力如何保证电子输运的持续进行, 并驱动电子从低化学势流向高化学势.2.库仑耦合双量子点输运模型 如图1 所示, 系统由两个单能级量子点X 和Y 通过库仑耦合力U 相互作用组成. 量子点X (Y )可与左右两个电子热库XL 和XR (YL 和YR )交换电子. ${T_v}$ 和${\mu _v}$ 分别表示电子热库v (v = $ XL, XR, YR $ 和YL )的温度和化学势. $\varGamma _{{x_i}}^{(v)}$ 和$\varGamma _{{y_i}}^{(v)}$ 是量子点与热库之间电子的隧穿几率. 系统的哈密顿量为图 1 库仑耦合双量子点非平衡系统Figure1. The nonequilibrium double quantum-dot system with Coulomb coupling.$d_{X(Y)}^\dagger $ ($d_{X(Y)}^{}$ )为能量${\varepsilon _{X(Y)}}$ 的量子点的产生(湮灭)算符. 电子热库的哈密顿量$c_{k\alpha \chi }^\dagger $ (${c_{k\alpha \chi }}$ )表示热库$\chi $ 中能级为${\varepsilon _{k\alpha \chi }}$ 电子的产生(湮灭)算符. 各个库的电子能量满足费米-狄拉克分布. 系统与热库的相互作用哈密顿量为${t_{k\alpha \chi }}$ 是在能级为${\varepsilon _{k\alpha \chi }}$ 的量子点$\alpha $ 与热库$\chi $ 的耦合强度. 系统的态空间可表示成各个量子点系统的本征态的张量积. 用下标0和1表示其中一个量子点位置有无被电子占据(0表示没有占据, 1表示有占据), 则系统可分解出四种状态(记为集合z ). 因此, 双量子点系统的能量本征态为$\left| z \right\rangle = \left| {\left( {x, y} \right)} \right\rangle =\left| x \right\rangle \otimes \left| y \right\rangle $ , 其中, $x \in \left\{ {{x_0}, \;{x_1}} \right\}$ 和$y \in \left\{ {{y_0}, \;{y_1}} \right\}$ 分别表示量子点X 和Y 的本征态. 图2 给出了各种状态之间的跃迁关系, 顶点(即节点)代表四种状态, 双向边缘线代表任意两个状态的向前和向后跃迁. 用$W_{z, z'}^{\left( v \right)}$ 表示由热库v 引起的状态$z' = \left( {x', y'} \right)$ 到状态$z = \left( {x, y} \right)$ 的跃迁速率, 用有方向的边$e: = \left( {z'\mathop \to \limits^v z} \right)$ 表示. 假设图中规定了所有边的正方向, 则可定义集合$\xi $ , 且$\left( {z'\mathop \to \limits^v z} \right) \in \xi $ , $\left( {z\mathop \to \limits^v z'} \right) \notin \xi $ . 因为系统包含两部分, 每一条边代表量子点X 或Y 的状态改变. $\left( {\left( {x', y} \right)\mathop \to \limits^v \left( {x, y} \right)} \right)\left( {x' \ne x} \right)$ 表示X 的状态变化, Y 的状态不变. 而$\Big( \left( {x, y'} \right)\mathop \to \limits^v \left( {x, y} \right) \Big) \left( {y' \ne y} \right)$ 表示Y 的状态变化, X 的状态不变. 因此, 集合$\xi $ 可归纳成两个子集图 2 库仑耦合双量子点系统的状态点和跃迁模式Figure2. The states and transition modes of the double quantum-dot system with Coulomb coupling.$p(z, t)$ 为t 时刻状态z 出现的概率, 在玻恩-马尔科夫近似下[30 ,31 ] , 状态z 随时间的变化可用如下运动主方程表示:[26 ,30 ,31 ] :$f_{{x_i}}^{\left( v \right)} = {\left( {1 + \exp \left\{ {{\beta _v}\left( {{\varepsilon _Y} + {\rm{i}}U - {\mu _v}} \right)} \right\}} \right)^{ - 1}}$ , $f_{{y_i}}^{(v)} \!=\! {({1 \!+\! \exp \{ {{\beta _v}( {{\varepsilon _X} \!+\! {\rm{i}}U \!-\! {\mu _v}} )} \}} )^{-1}}$ $({i \!=\! 0, 1})$ . ${\beta _v} \!=\! 1/ {k_{\rm{B}}}{T_v}$ , 而${k_{\rm{B}}} = 1.3806 \times {10^{ - 23}}~{\rm{J/K}}$ 为玻尔兹曼常数. 在(4 )式中, 可用$J_e^{(v)} = W_{zz'}^{(v)}p\left( {z', t} \right) - W_{z'z}^{(v)}p(z, t)$ 表示通过热库v 从状态$z'\mathop \to \limits^v z$ 跃迁对应的流. 则系统通过所有路径从状态$z' \to z$ 跃迁对应的流为$J_{xx'|y}^{\left( v \right)} = W_{xx'|y}^{\left( v \right)}p\left( {x', y} \right) - W_{x'x|y}^{\left( v \right)}p\left( {x, y} \right)$ 表示量子点Y 状态不变时, 量子点X 状态通过热库v 从$x'\mathop \to \limits^v x$ 跃迁引起的流. 同理可定义$J_{yy'|x}^{\left( v \right)}$ 表示量子点X 状态不变时, 量子点Y 状态通过热库v 从$y'\mathop \to \limits^v y$ 跃迁引起的流. 结合(5 )式, 可证3.热力学第二定律和信息流 系统的熵S 可用香农熵表示[32 ,33 ] :9 )式对时间求导, 在稳态时可得${a_i} \!\geqslant \!0$ 和${b_i} \!\geqslant\! 0$ , $\sum\limits_{i = 1}^n {{a_i}} \ln\!\Big(\!{\dfrac{a_i}{b_i}}\!\Big) \!\geqslant\! \sum\limits_{i = 1}^n {{a_i}} \ln\! \left({\sum\limits_{i = 1}^n {{a_i}} \Big/\!\!\sum\limits_{i = 1}^n {{b_i}} }\! \right)$ , 可证明${\dot S_{\rm{T}}} \geqslant {\rm{0}}$ , 满足热力学第二定律, 即熵产生率必须是非负的. (9 )式—(12 )式给出了双量子点作为总系统的各种熵流和熵产生率, 但并未明确给出子系统之间的能量和信息交换以及各子系统的熵产生率. 因此, 需要结合(7 )式, (8 )式和(12 )式, 可将总熵产生率分解成子系统X 和Y 的熵产生率之和, 即${\dot S_{X(Y)}} \geqslant {\rm{0}}$ . 为了比较直观地分析(14 )式和(15 )式的物理意义, 可通过图论方法, 采用Schnakenberg网络理论[29 ] , 将其进一步拆分.[34 ] . 下面根据求解需要选定了一组完备的基本循环$C = \left\{ {C_1^X, C_2^X, C_1^{\rm{G}}, C_1^Y, C_2^Y} \right\}$ :$C_1^X$ 表示系统从初态$\left( {{x_0}, {y_0}} \right)$ 出发通过与热库$XL$ 相互作用跃迁到状态$\left( {{x_{\rm{1}}}, {y_{\rm{0}}}} \right)$ , 又通过与库$XR$ 耦合回到初态$\left( {{x_0}, {y_0}} \right)$ 的一个闭合路径, 如图3 所示. 图中每一条边代表量子点X 或Y 的跃迁, 箭头规定了跃迁的正方向. ${C^X}: = {\rm{\{ }}C_1^X, \;C_2^X{\rm{\} }}$ 构成一个局域循环的子集, 并且每个元素表示只有量子点X 状态发生变化的环. 同理可定义与量子点Y 有关的局域循环构成的子集${C^Y}: = {\rm{\{ }}C_1^Y, \;C_2^Y{\rm{\} }}$ . ${C^{\rm{G}}}: = \{ C_1^{\rm{G}}\} $ 表示全局循环, 跟X 和Y 的变化同时关联.图 3 四态模型的有向图及其基本循环Figure3. The directed graph of the four-state model and its cycle basis.$e: = \left( {z'\mathop \to \limits^v z} \right)$ , 可定义驱动这种跃迁的热力学力11 )式中的总熵产生率可改写为$\Xi $ 为[29 ] ${e^\dagger }: = \left( {z\mathop \to \limits^v z'} \right)$ 表示与e 方向相反的跃迁. $e\left( {{e^\dagger }} \right) \in {C_k}$ 表示$e\left( {{e^\dagger }} \right)$ 属于环${C_k}$ 上的一条边. 由函数$\Xi $ , 可定义环${C_k}$ 所对应的热力学力${J_e}$ 可表示为与跃迁e 相关的所有环流的代数和, 且7 )式和(21 )式, 基本循环对应的环流为:14 )式和(15 )式, 稳态时子系统X 和Y 的熵产生率可分解成三部分:$\Delta {\mu _X} = {\mu _{XR}} - {\mu _{XL}}$ , $\Delta {\mu _Y} = {\mu _{YR}} - {\mu _{YL}}$ , ${\dot S_{{\mu _i}}}\left( {i = X, Y} \right)$ 表示化学势差驱动子系统与电子热库交换电子引起的熵产生率, 只与局域的环流${C^X}$ 和${C^Y}$ 有关. ${\dot S_{{U_i}}}$ 为两个量子点间库仑力产生耦合能量导致的熵产生率. 值得注意的是, ${\dot I_i}$ 表示子系统间信息交换所引起的熵增加.X 和Y 信息交换所对应的热力学力, 在这里简称信息力. ${\dot S_{{U_i}}}$ 和${\dot I_i}$ 都与全局循环${C^{\rm{G}}}$ 紧密相关, 全局循环决定系统内部的能量交换和信息交换.23 )式, 从XL 到XR 的粒子流为$YL$ 到$YR$ 的粒子流为24 )式, (25 )式和(29 )式, 可发现信息熵只有在子系统X , Y 的熵产生率中起作用, 而对总熵的效果为0. 这是因为信息熵是由于两个子系统的相互作用而产生的, 当研究其中一个子系统时, 信息熵的影响就体现出来, 而对于总系统, 这一对信息熵所对应的信息力就好比是一对“作用力”与“反作用力”, 互相制约. 考虑信息熵后, 子系统的熵产生率大于零, 符合熵增加原理的基本规律.4.结果与讨论 为了讨论方便且不失一般性, 引进参数$\delta $ 和$\varDelta $ , 并令各隧穿速率为图4(a) 中的熵产生率${\dot S_{\rm{T}}}$ , ${\dot S_X}$ 和${\dot S_Y}$ 取值均为非负, 符合熵增加原理, 即不可逆热力过程中熵的微增量总大于零. 由于量子点X 两端电子热库化学势差较大, 电子流${J_X}$ 相对较大, 总熵产生率${\dot S_{\rm{T}}}$ 主要来自电子通过量子点X 输运导致的不可逆熵产生率${\dot S_X}$ . 由图4(b) 可发现, 当$\beta U \geqslant \beta {U_0}$ 时, 通过量子点Y 的电子流${J_Y}$ 方向出现了翻转. 因为量子点Y 两端电子热库的化学势差较小, 当库仑耦合强度增大到一定程度时, 量子点间的相互作用足够强, 量子点X 和电子热库XL 和XR 构成热机将推动电子通过量子点Y 从低化学势流向高化学势. 由图4(b) 还可观察到电子流${J_Y}$ 的方向一旦出现翻转, 将一直保持这个方向. 同时因为量子点Y 对X 的反馈作用, 电子流${J_X}$ 大小也会随着$\beta U$ 的增大而减小. 当库仑耦合强度足够大时, 两个子系统间的相互作用, 导致${J_X}$ 和${J_Y}$ 下降, 熵产生率${\dot S_{\rm{T}}}$ , ${\dot S_X}$ 和${\dot S_Y}$ 也逐渐趋于0. 说明库仑耦合足够强时, 库仑耦合的作用远远大于化学势差对系统的驱动作用, 将抑制电子流的产生.图 4 (a)熵产生率${\dot S_{\rm{T}}}$ , ${\dot S_X}$ 和${\dot S_Y}$ 及(b)电子流${J_X}$ 和${J_Y}$ 随库仑耦合强度的变化曲线. 其中$\beta \Delta {\mu _X} = 2$ , $\beta \Delta {\mu _Y} = 1$ , $ \delta =\varDelta =1 $ , ${\varepsilon _X} = \dfrac{{\left( {{\mu _{XR}} + {\mu _{XL}}} \right)}}{2} - \dfrac{U}{2}$ , ${\varepsilon _Y} = \dfrac{{\left( {{\mu _{YR}} + {\mu _{YL}}} \right)}}{2} - \dfrac{U}{2}$ Figure4. (a) The entropy production rates ${\dot S_{\rm{T}}}$ , ${\dot S_X}$ , and ${\dot S_Y}$ , and (b) the curves of the electron flows ${J_X}$ and ${J_Y}$ varying with the Coulomb coupling strength, where $\beta \Delta {\mu _X} = 2$ , $\beta \Delta {\mu _Y} = 1$ , $\delta \!=\!\varDelta \!=\!1$ , ${\varepsilon _X} \!=\! \dfrac{{\left( {{\mu _{XR}} + {\mu _{XL}}} \right)}}{2} \!-\! \dfrac{U}{2}$ , and ${\varepsilon _Y} \!=\! \dfrac{{\left( {{\mu _{YR}} + {\mu _{YL}}} \right)}}{2} - \dfrac U2$ ${\dot S_X}$ 和${\dot S_Y}$ 具体分解, 可观察化学势差、库仑耦合和信息力三者的作用. 从图5 可看出, 化学势差驱动电子流对量子点X 的熵产生率起主导作用. 库仑耦合对系统热力学不可逆性的影响具体体现在: 1) 当$\left| {\beta U} \right|$ 较小时, 化学势差驱动电子通过量子点X 和Y 从高化学势流向低化学势, 单位时间不可逆熵增主要来自${\dot S_{{\mu _i}}}\left( {i = X, Y} \right)$ ; 2) $\left| {\beta U} \right|$ 增大使两个子系统的熵产生率${\dot S_X}$ 和${\dot S_Y}$ 减小, 降低了热力学过程的不可逆性; 3) 库仑耦合伴随着信息熵的产生, 且${\dot I_X}$ 和${\dot I_Y}$ 绝对值相等, 符号相反; 4) 存在${\dot S_{{U_i}}}=0$ 而${\dot I_i} \ne 0$ , 这时相互作用以信息交换为主导机制, 同时存在${\dot I_i}=0$ 而${\dot S_{{U_i}}} \ne 0$ , 这时相互作用以能量交换为主导机制; 5) 当$\beta U \geqslant \beta {U_0}$ 时, 电子流反向${J_Y} < 0$ 导致${\dot S_{{\mu _Y}}} < 0$ , 量子点X 利用库仑耦合推动电子流${J_Y}$ 逆向流动.图 5 部分熵产生率${\dot S_{{\mu _i}}}$ , ${\dot S_{{U_i}}}$ 和${\dot I_i}\left( {i = X, Y} \right)$ 随库仑耦合强度的变化曲线.Figure5. The curves of the partial entropy production rates ${\dot S_{{\mu _i}}}$ , ${\dot S_{{U_i}}}$ , and ${\dot I_i}\left( {i = X, Y} \right)$ varying with the Coulomb coupling strength.X , Y 两个子系统并不是独立变化的.(24 )式和(25 )式可进一步整理成两部分30 )式右边第一项表示量子点X 的粗粒化熵产生率${\dot \sigma _X}$ 表示观测者只能时时监测到X 的状态, 而没有意识或观察到子系统Y 的存在. 同理可定义量子点Y 的粗粒化熵产生率${\dot \sigma _Y}$ . 如图6 所示, 当X 和Y 相互作用不存在($U=0$ )时, ${\dot \sigma _X} \geqslant 0$ . 当库仑耦合强度不为零时, 由于量子点Y 的影响, ${\dot \sigma _X}$ 可能出现负值[35 -37 ] . 从信息的角度理解, 两个子系统库仑耦合除了能量交换还存在信息交换, 如量子点Y 可根据量子点X 的状态, 及时改变自身状态对X 做出相应的反馈. 根据图5 和图6 , 当U 较小时, ${\dot \sigma _Y} < 0$ , ${\dot I_Y} > 0$ , 子系统X 从其两端热源获取能量并通过监测子系统Y 的状态产生信息流${\dot I_X}\left( { = - {{\dot I}_Y}} \right)$ , 这部分信息流被注入到子系统Y , 驱动电子通过子系统Y . 当U 较大时, ${\dot \sigma _X} \!<\! 0$ , ${\dot I_X} \!>\! 0$ , 子系统Y 从其两端热源获取能量并通过监测子系统X 的状态产生信息流${I_Y}\left( { = - {I_X}} \right)$ , 这部分信息被注入到子系统X , 驱动电子通过子系统X . 这说明信息交换在非平衡热力学过程中起关键作用, 保证热力学过程可持续进行.图 6 粗粒化熵产生率${\sigma _i}\left( {i = X, Y} \right)$ 随库仑耦合强度变化曲线Figure6. The curves of the coarse-grained entropy production rates ${\sigma _i}\left( {i = X, Y} \right)$ varying with the Coulomb coupling strength.5.总 结 本文基于库仑耦合的双量子点复合系统, 结合量子开系统理论和图论的分析方法, 研究了自发非平衡系统物质流、能量流与信息流间的协同关系. 根据状态变化所经历的不同闭合路径, 区分全局循环和局域循环, 从各子系统熵产生率中分解出基本循环对应的热力学流与热力学力. 发现子系统间的能量和信息交换依赖于全局环流, 相互作用可能以信息或能量交换为主导, 由库仑耦合强度决定. 最终揭示了信息驱动引起的熵产生保证了电子输运的持续进行. 




 图 1 库仑耦合双量子点非平衡系统
图 1 库仑耦合双量子点非平衡系统

























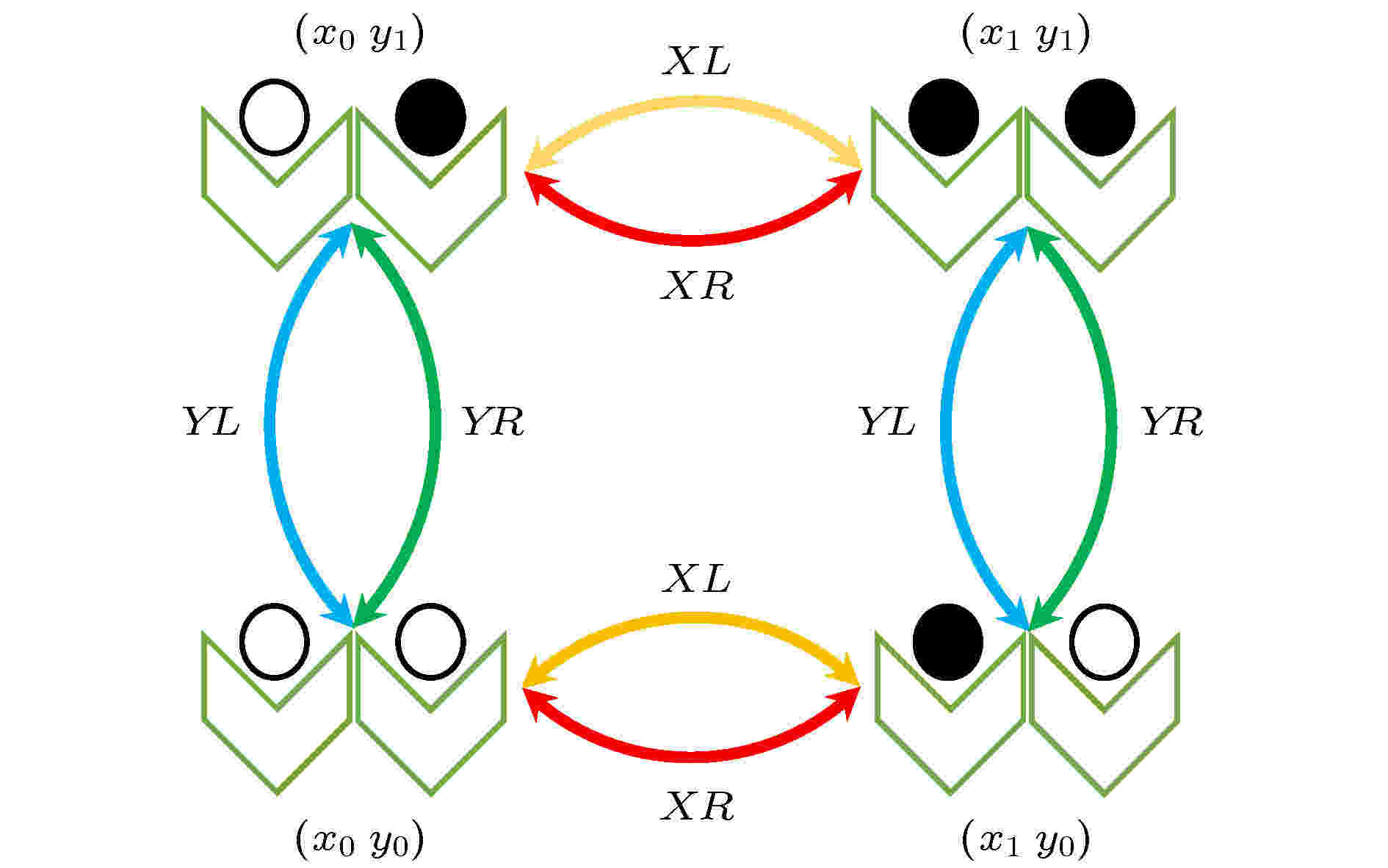 图 2 库仑耦合双量子点系统的状态点和跃迁模式
图 2 库仑耦合双量子点系统的状态点和跃迁模式





























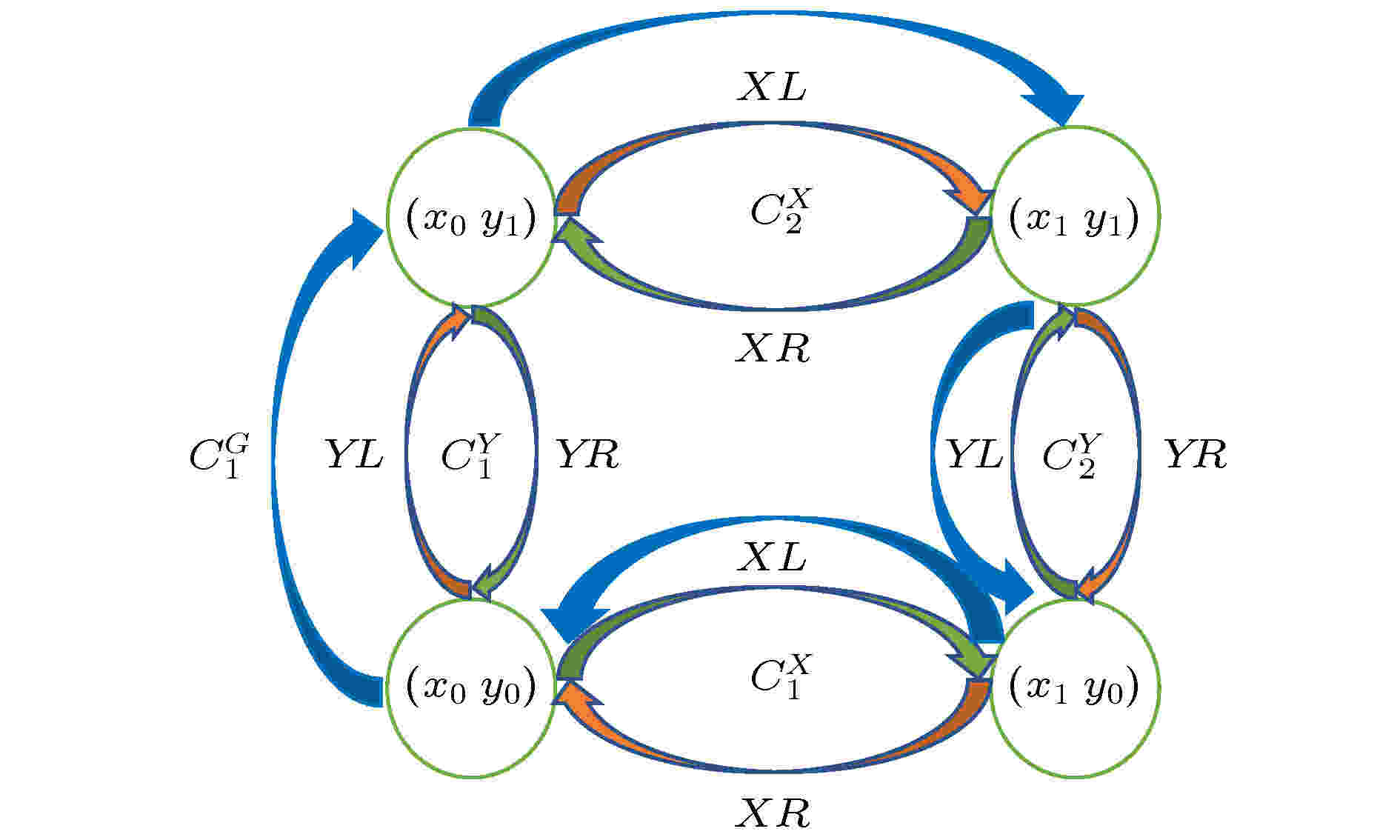 图 3 四态模型的有向图及其基本循环
图 3 四态模型的有向图及其基本循环


































































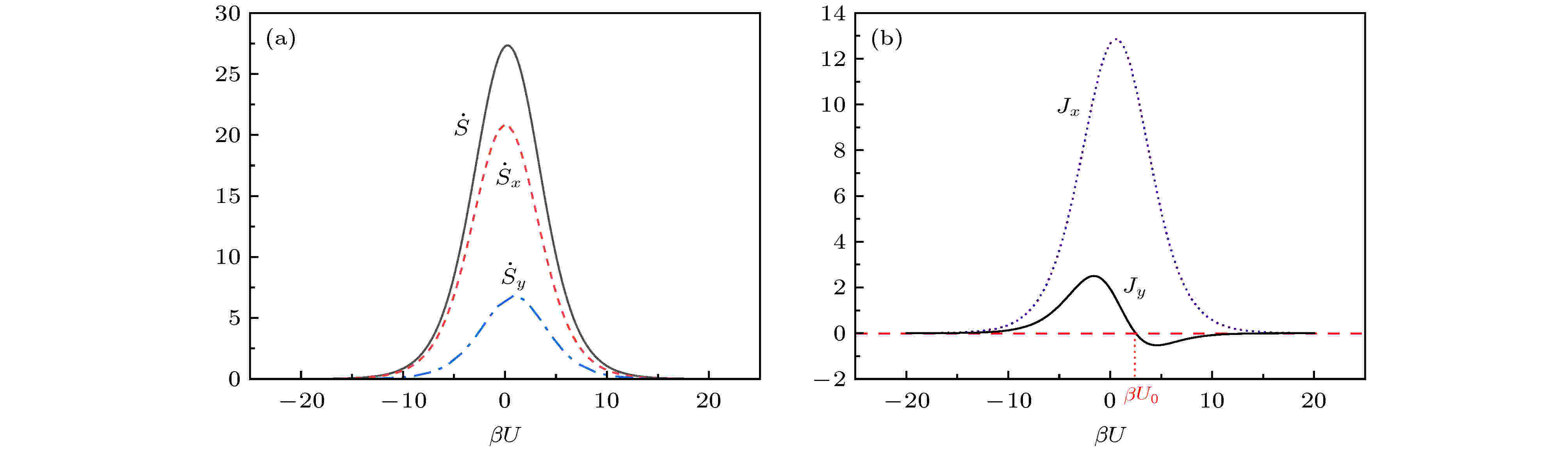 图 4 (a)熵产生率
图 4 (a)熵产生率










































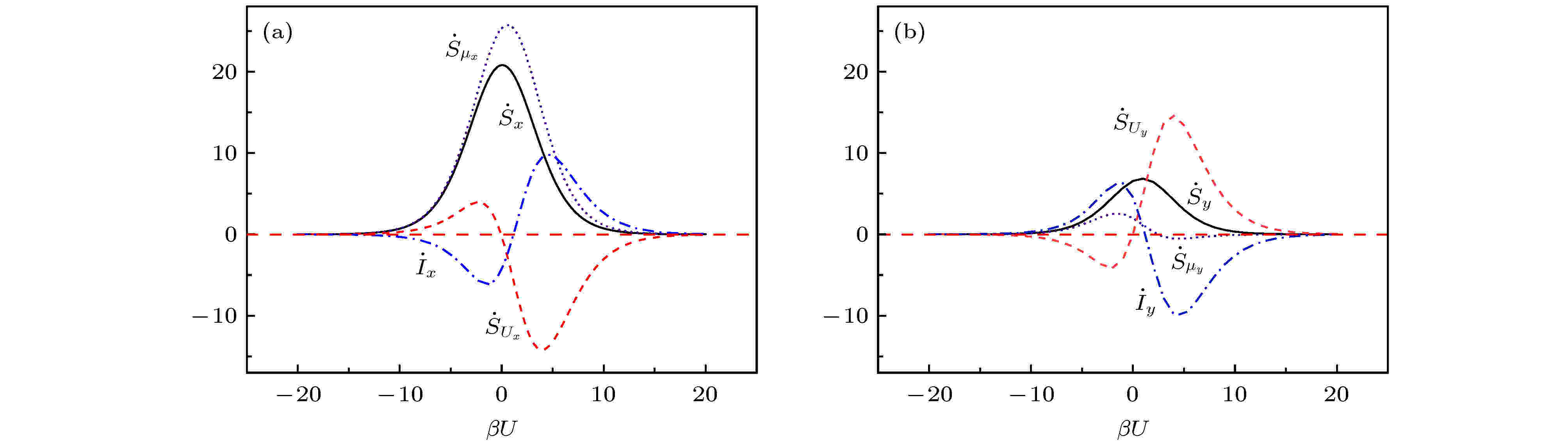 图 5 部分熵产生率
图 5 部分熵产生率


















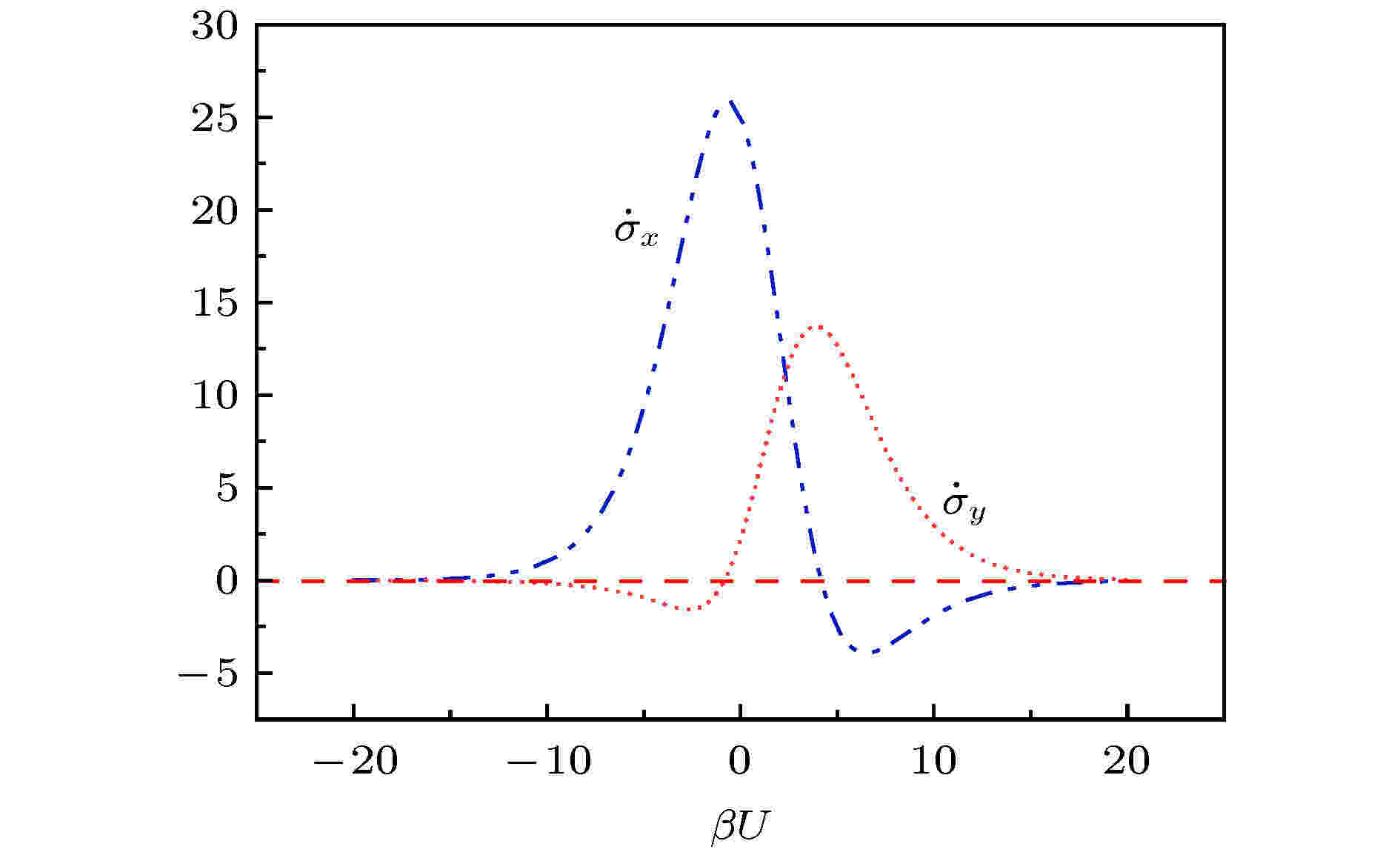 图 6 粗粒化熵产生率
图 6 粗粒化熵产生率

