全文HTML
--> --> -->本文将表面等离极化激元(surface plasmon polariton)简称为SPP. 表面等离激元(surface plasmon, SP)一般仅指由于电子相干的集体振动在金属表面处形成的元激发. 电子的振动必定伴随着表面附近电磁场的产生, 两者耦合在一起总称SPP. 在纳米颗粒体系中, 由于这种元激发的电磁场在三个维度都是局域的, 一般称为局域表面等离激元(localized surface plasmon), 简称LSP.
图 1 具有等离激元能带的结构示意图和扫描电子显微镜(scanning electron microscope, SEM)照片 (a), (b) 金属薄膜刻蚀周期性的孔洞[61]; (c), (d) 金属纳米颗粒周期性排列[62]; (e), (f) 金属表面覆盖介质光子晶体[63]; (g), (h) 金属表面覆盖自组装介质小球[64]Figure1. Schematic views and SEM images of structures possessing plasmonic band structures: (a), (b) Metal films with periodic arrays of sub-wavelength holes[61]; (c), (d) periodic arrays of metal particles[62]; (e), (f) metallic substrate coated with dielectric photonic crystal[63]; (g), (h) metallic substrate coated with self-assembled dielectric spheres[64].
对应于上述不同的结构, 其所支持的SPP模式, 尽管相互类似但其成因和空间分布却不尽相同, 如图2所示[65]. 对于平金属情况, 根据麦克斯韦方程组和边界条件, 可以计算得到SPP的色散公式为:
图 2 (a) 表面等离极化激元、(b) 局域表面等离激元和(c) 人工表面等离激元[65]的场分布Figure2. Field distributions of (a) SPP, (b) localized SPP and (c) spoof SPP[65].
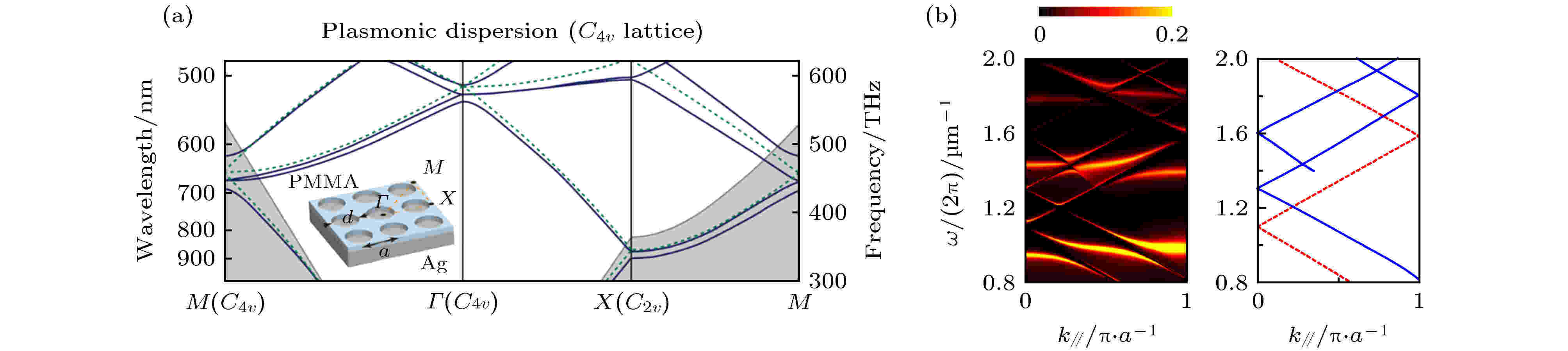图 3 (a) 金属表面覆盖光子晶体的能带[63]; (b) 银光栅两侧覆盖介质层的透射光谱(左)和对应结构的介质层中的波导模式(实线)和银表面的SPP(虚线)的折叠能带(右)[67]Figure3. (a) Plasmonic band structure of flat metallic substrates coated with two-dimensional dielectric photonic crystal layer[63]. (b) Left panel: transmission spectra of Ag grating coated symmetrically with dielectric layers; right panel: folded dispersion of guided (solid lines) and SPP (dashed lines) modes of Ag grating coated symmetrically with dielectric layers[67].
对于金属颗粒阵列的情况, 由于金属纳米颗粒存在的LSP, 当金属纳米颗粒周期性排列时, 颗粒之间的LSP共振会相互作用, 从而产生能带结构. 金属颗粒阵列可以看作耦合的谐振子体系, 当只考虑金属纳米颗粒的电偶极子共振时, 能带可以通过耦合电偶极子方程[68]计算得到. 方程的形式如下:
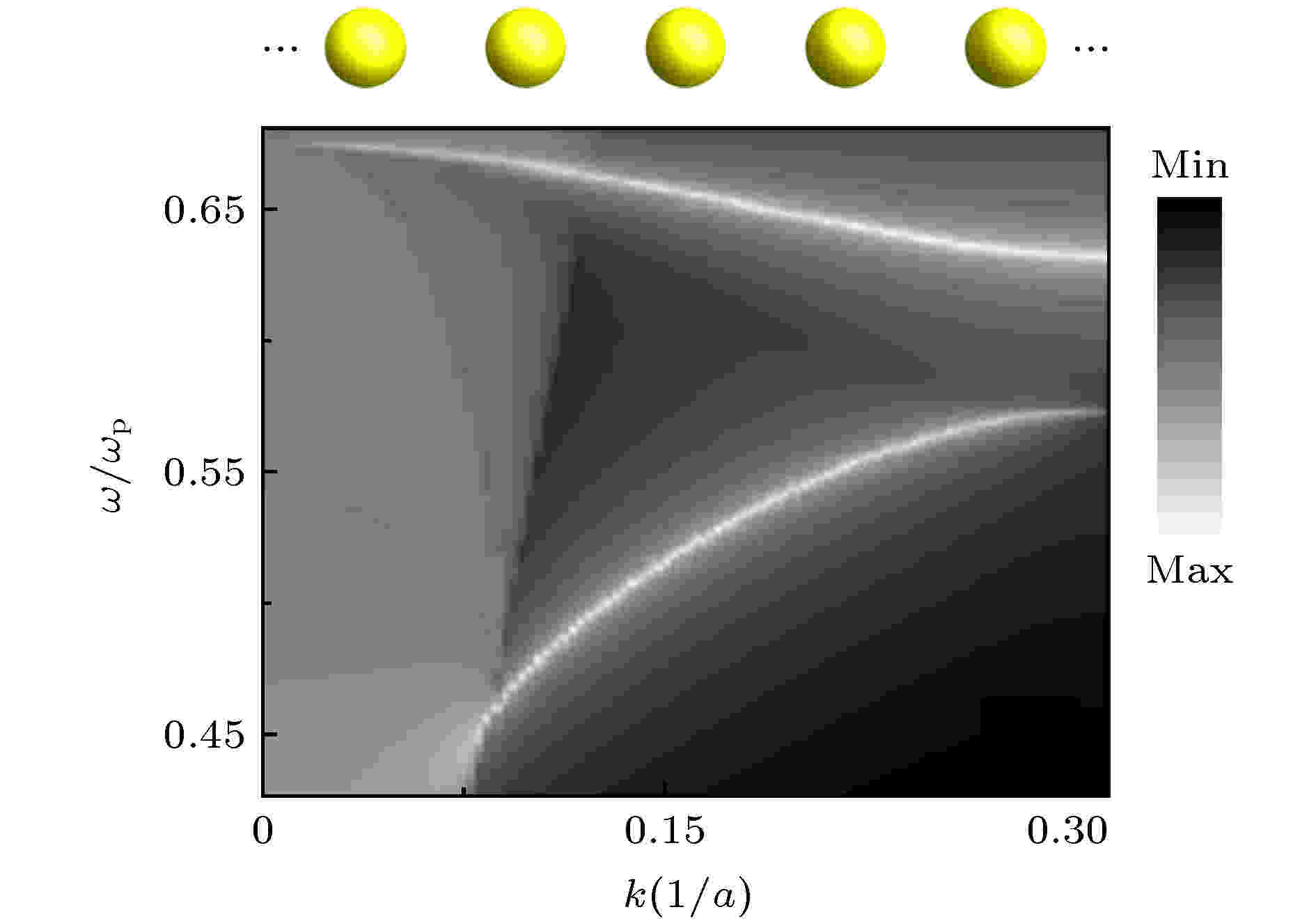图 4 金属纳米颗粒链的能带[69]Figure4. Band structure of metal nanoparticle chain[69].
2
3.1.能带在光线以上的性质
与电子体系中的布里渊区不同, 如前所述, SPP系统(也适用于其他光子体系)的布里渊区可以被光线划分为两个区域, 分别是光线以上和光线以下. 光线以上的能带又分为两种: 一种在真空光线k = ω/c以上; 另外一种是当折射率为n的介质覆盖在系统表面时, 能带在介质光线k = nω/c以上, 但在真空光线之下. 在真空光线以上的能带中的模式的波矢能够与真空中的波矢匹配, 因此其能够泄漏到自由空间中, 这些模式被称为漏波模式(leaky mode). 利用这些漏波模式, 人们可以在很大自由度上实现SPP模式的耦合与操控. 对于这些漏波模式, 即使不考虑金属内部的本征损耗, 由于辐射损耗的存在, 模式的频率或者波矢也是一个实部和虚部都不为零的复数. 反映在能带上, 如图5(a)所示, 其实际的能带不再是由曲线构成, 而是具有一定的宽度[62,63]. 其中, 模式本征频率的虚部对应于能带在频率轴上的展宽, 如红色线段所示. 考虑频域与时域的对应关系, 频域上的展宽对应于模式的振幅在时域上的衰减. 同理, 能带在波矢轴上的展宽, 如蓝色线段所示, 对应于模式波矢的虚部, 反映了模式在空间上的传播距离. 从频域和时域角度, 这些漏波模式就像是一个谐振腔, 具有可以严格定义的品质因子(Q factor). 从空间传播的角度, 这些SPP漏波模式的辐射场具有一定的空间相干性, 如图5(b)所示[62,63]. 其相干性可以被双缝干涉的干涉条纹验证, 相干程度也可由干涉条纹的明暗对比所反映. 利用SPP能带中的漏波模式的高品质因子和辐射场的空间相干性好的特性, SPP晶体结构已经广泛地被应用于光-物质强耦合、定向辐射、激射和光传感器等方面. 对于被介质覆盖的金属系统来说, 虽然SPP的色散始终在介质光线以下. 但是当系统被周期性结构调制, 能带发生折叠, SPP能带的一部分会出现在介质光线以上、真空光线以下. 这一部分能带上的模式能够与介质中的波导模式耦合, 使得透射增强[67]. 在图3(b)右图中, 给出了银光栅两侧覆盖600 nm厚的介质层的SPP能带, 其中实线为介质层中的波导模, 虚线为银光栅和介质之间的SPP折叠能带. SPP能带经过折叠后与介质中的波导模交叠, 即此时两种模式的波矢匹配, 模式之间发生耦合. 反映到图3(b)左图的透射图中, 可以明显地观察到在两种模式色散交叉的频率处, 透射强度有明显增强. 最后, 需要注意的是, 如果在SPP模式的两侧覆盖厚金属, 由于金属的限制, 光线以上的态也不能向外泄漏, 此时系统更接近于二维体系. 同时表面等离极化激元模式也可以与金属边界内的腔模耦合, 形成较为复杂的杂化模式[71].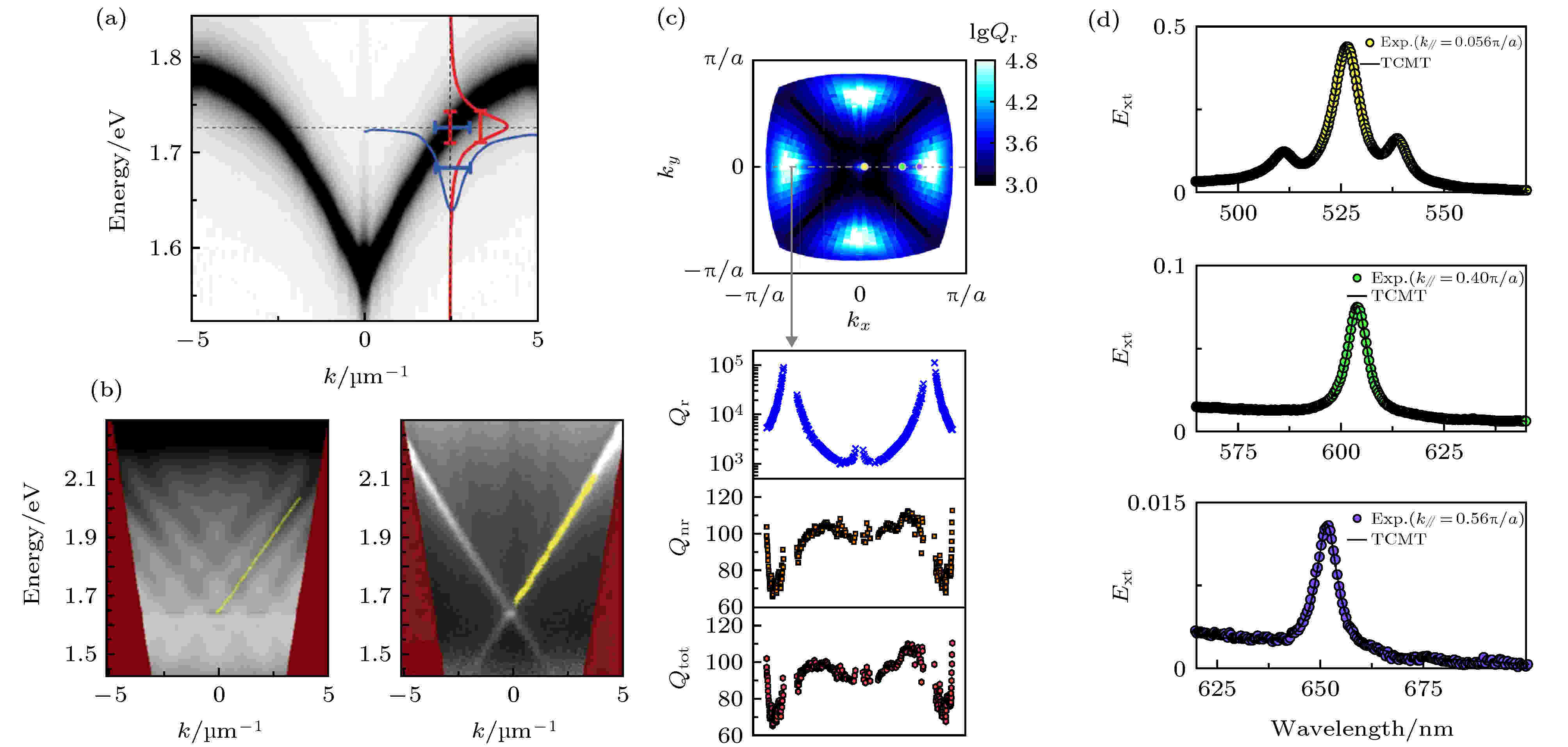
图 5 光线以上能带的性质包括连续体中的束缚态、时间相干性和空间相干性[62,63]Figure5. Properties of band which inside light cone including BIC, time and spatial coherence[62,63].
最近, 在光线以上的漏波模式中, 一些辐射品质因子趋近于无限大的模式(如图5(c)和图5(d)所示[62,63])越来越受到关注. 由于落在光线以上的漏播模式能够与自由空间的某些传播模式满足波矢匹配条件, 它们的频率必然落入自由空间连续谱范围之内, 其原本是可以, 如上所述, 辐射到远场的. 但其品质因子发散, 意味着这些处于自由空间连续谱范围内的模式被束缚在周期性结构的近场范围, 从而该模式的辐射为0. 由于这些模式的反常性质, 被称为连续谱中的束缚态 (bound state in the continuum, BIC)[72]. BIC在很多物理系统中都能被找到, 例如光子系统[73-76]、声学系统[77,78]、甚至在水波[79]中. BIC具有无穷大的Q因子, 这使得很多应用成为可能[80-82], 包括SPP激射和矢量光发射等.
对于BIC的成因, 当前主要有三类相互自洽的解释. 第一类解释主要针对布里渊区中具有旋转对称性的高对称点[83-85], 例如布里渊区中心的Γ点. 在Γ点, SPP晶体的本征模式具有在旋转操作下的+1 (对称)和–1 (反对称)本征值. 其中的+1本征值对称情况由于与自由空间的对称性不匹配, 因此会出现无法辐射的BIC模式. 随着最近非Γ点BIC的情况越来越多的被发现(如图5(c)和图5(d)所示), 第二类基于结构内部多种模式的互相干涉导致总的辐射场的相干相消的机制被广泛的研究[73-75,86,87]. 除了上面两类解释以外, 第三类基于动量空间(波矢空间)的拓扑性的偏振涡旋[88-90]解释BIC的成因是这三类解释中最形象直观的. 对于光线以上的漏波模式, 其远场部分对应于辐射到环境介质中的平面波. 光波在自由空间的横波条件要求在远场下, 平面波必须具有确定的偏振态. 当将这些漏波模式在远场的偏振态投影到动量空间时, 远场偏振态在第一布里渊区中就构成了一个二维的矢量场. 对于任意一个矢量场, 其一个最值得关注的特征就是在矢量场中是否存在场的奇点. 如果存在奇点, 该奇点的邻域偏振场就构成了矢量场的涡旋结构. 在涡旋的中心, 偏振态无法定义, 也就意味着, 该模式在远场无法满足光波的横波条件, 从而对应上述的BIC. 为了基于动量空间偏振场的拓扑奇点描述BIC, 引入了“拓扑荷”的定义, 即偏振态(一般为椭圆偏振)的长轴对于奇点的绕数. 对于二维系统来说, 当研究问题限定在第一布里渊区时, 根据第一布里渊区的环面(torus)的整体拓扑特性, 所有的奇点, 或者所有的BIC, 应满足整个第一布里渊区的“拓扑荷”的求和等于二维布里渊区环的欧拉示性数χ = 0. 如图6(a)所示, 其为模拟计算得到的图3(a)中第二条能带上各模式远场辐射的偏振, 实线表示不同的偏振方向, 蓝色和红色的点分别表示“拓扑荷”为+1和–1的核, 灰色的区域为不辐射的态. 因此, 可以预测图中灰色的区域的“拓扑荷”为–3. 图6(b)和图6(c)分别为Zhang等[63]通过研制的偏振分辨动量空间成像光谱仪实验测得的远场辐射的偏振态和其主轴角度在平金属覆盖介质光栅体系中的第一布里渊区中的分布. 动量空间中的偏振场不仅有效地解释了BIC的成因, 而且还揭示了隐藏在SPP能带结构中的新的自由度—偏振态. 基于偏振态这个新的自由度, 研究者能够将奇点光学、拓扑光学与SPP晶体的辐射共振态中的偏振场建立起了联系. 通过对动量空间偏振场加以一些独特的调控, 可能会产生出新奇的辐射效应和面内传输效应.
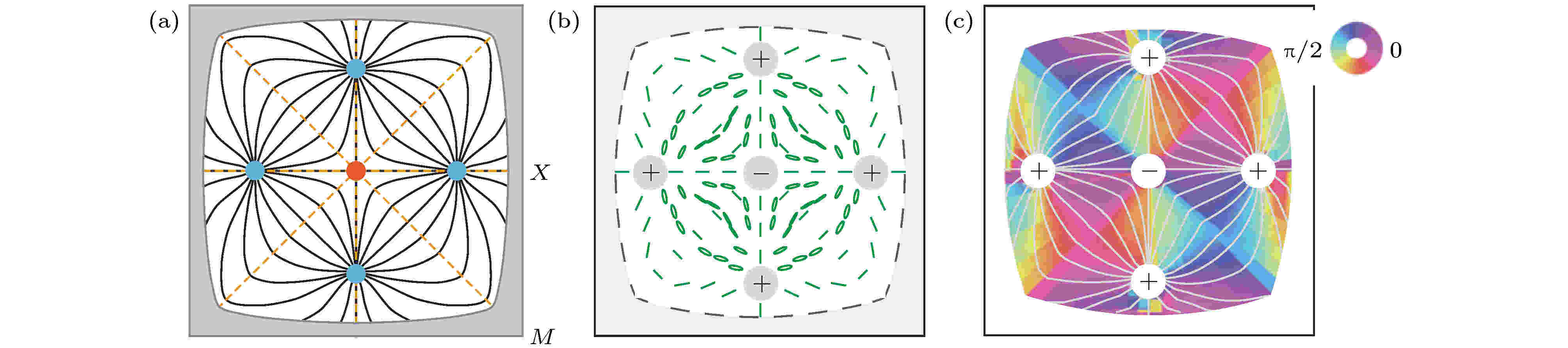图 6 连续体中的束缚态的拓扑解释[63]Figure6. Topological nature of BICs[63].
2
3.2.能带在光线以下的性质
能带在光线以下的部分, 由于其模式无法辐射到真空中, 其模式天然的适合导波[91,92]. 例如, Maier等[93]基于金属纳米颗粒链在光线以下的能带的模式在实验上实现了在衍射极限以下的电磁波的传输(图7(a)). 这种波导的尺寸为亚波长, 对于在纳米尺度上的光学器件实现光与物质的相互作用来说至关重要. 例如, Li等[94]提出了利用这种波导作为纳米透镜进行聚焦的可能性. 但是由于这种波导模式发生在金属的等离激元共振频率处, 金属的内禀损耗则大大降低了模式的传输距离, 限制了这种波导的应用. 除了通带里面的传导模式, 具有完全禁带的SPP结构对于光学器件来说同样重要. Wu等[95]在平金属表面覆盖二维的周期性排列的介质柱实现SPP的全禁带. 基于这种SPP全禁带, 可以实现对通信波段的电磁波传输的调控. 负折射是最近十几年研究的一个热点, 从微波波段到红外波段的负折射率材料一般是由开口谐振环组成的. 但是到了光频段, 开口谐振环无法再支持强烈的磁共振. 通过设计六角晶体摆放的同轴金属-介质-金属波导结构可以实现在光频段的负折射(图7(d))[96], 这种结构并不需要特殊的偏振和角度激发, 且相比于多层“渔网结构”更加容易制备. 拓扑是最近研究的另一个热点. 使用金属纳米颗粒, 将其在平面内摆放成六角晶格的结构, 则能够在等离激元能带中实现Dirac点(图7(c))[97,98]. 不同于石墨烯和二维光子晶体中的Dirac点, 在等离激元能带中的Dirac点不仅能够支持标量波还能够矢量波. 同时, 等离激元能带中的Dirac点产生的边界态的一些行为也完全不同于石墨烯[97]. 在微波波段, 利用局域spoof SPP, 打破结构单元的镜面对称, 则能够实现“谷”极化的拓扑边界态(图7(e))[46]. 最后介绍一种在微波波段工作的spoof SPP波导, 这种波导的能带同样在光线以下. 上文中提到的spoof SPP因其结构厚度大且加工不易, 限制了它在实际中的应用. 实际上, 具有锯齿结构的金属薄膜也可以支持spoof SPP, 其结构如图7(f)中的插图. 金属薄膜的厚度越小, 其模式的色散越往蓝移, 也即模式局域性更高[99]. 这种spoof SPP的能带受结构的影响很大, 可以通过改变锯齿的形状、深度有效的调节其能带[100,101]. 由超薄金属构成的spoof SPP波导的能带同样在真空光线以下, 并不与真空中的电磁波相互作用, 因此具有很强的抗干扰性. 其次场分布相比于三维的人工表面等离极化激元具有更加高度的局域性, 在传输电磁波过程中能够更加有效地避免串扰. 同时由于其结构超薄、具有柔性、便于制造, 因此可以被设计成集成光路中的各类功能器件中, 例如环形谐振器、功分器[102,103]等. 在未来, 这种spoof SPP波导在通信、集成光路等可能有更广泛的应用.
图 7 等离激元能带在光线以下的一些性质 (a) 导波[93]; (b) 全禁带[95]; (c) 狄拉克点[97,98]; (d) 负折射[96]; (e) 拓扑边界态[46]; (f) spoof SPP波导[99]Figure7. Properties of plasmonic bands inside the light cone: (a) Wave guiding[93]; (b) complete band gap[95]; (c) Dirac point[97,98]; (d) negative refraction[96]; (e) topological edge state[46]; (f) spoof SPP waveguide[99].
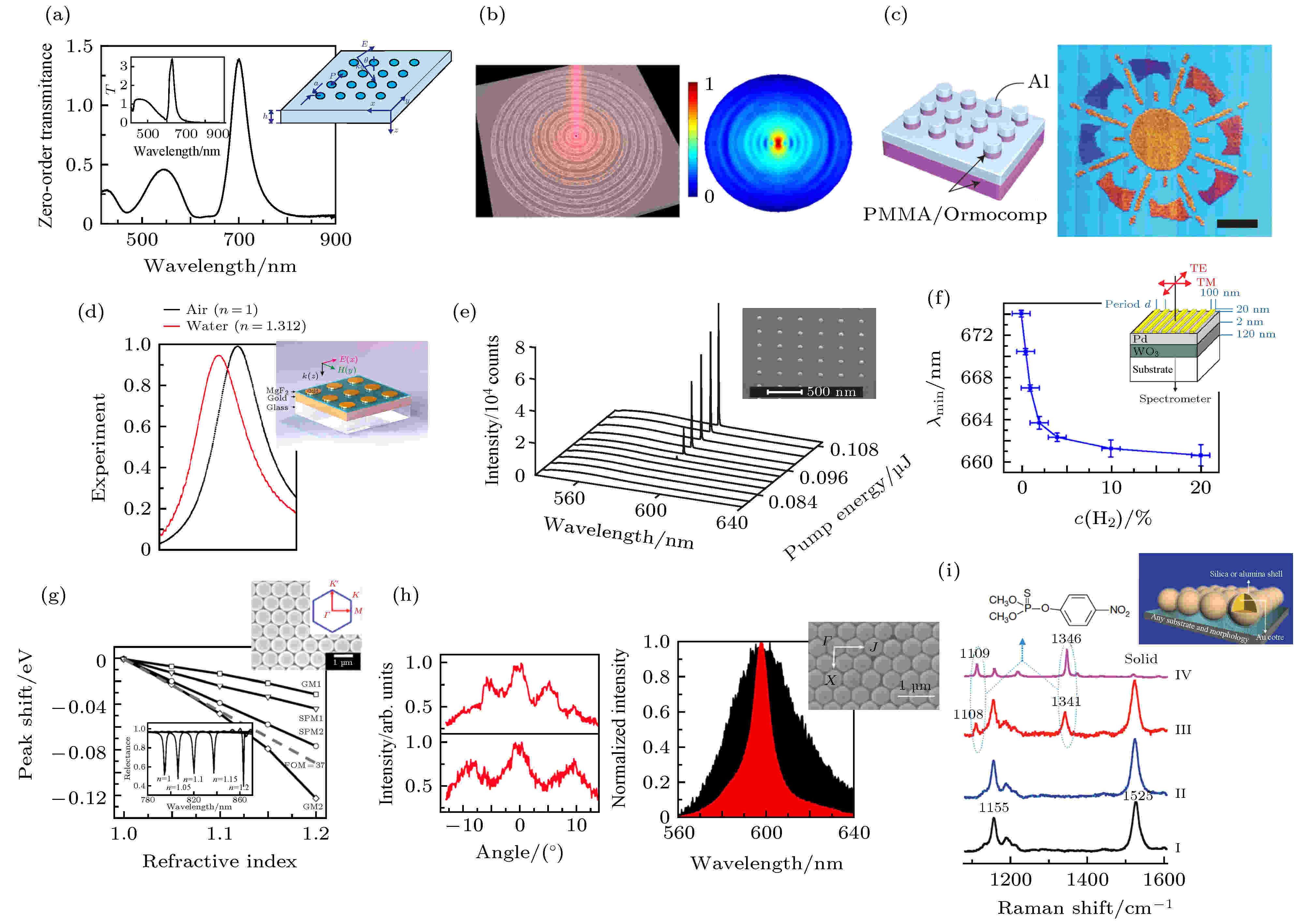图 8 等离激元的一些应用 (a) 光学异常透射[104]; (b) 利用“牛眼”结构实现光的汇聚[105]; (c) 结构色[106]; (d) 红外光的完美吸收器[108]; (e) 以银颗粒阵列为基底的分布式激光器[110]; (f) 基于金属棒阵列的氢气浓度探测器[112]; (g) 基于混合光子与等离激元晶体的传感器[64]; (h) 基于混合光子与等离激元晶体的荧光相干辐射[113]; (i)利用金属颗粒增强拉曼光谱[114]Figure8. Applications of plasmonics: (a) Extraordinary optical transmission[104]; (b) beaming light with a bull’s eye structure[105]; (c) structural colors[106]; (d) infrared perfect absorber[108]; (e) distributed feedback laser based on silver particle array[110]; (f) hydrogen sensor based on metallic photonic crystal slabs[112]; (g) sensor based on hybrid plasmonic-photonic crystal[64]; (h) coherent fluorescence emission by hybrid photonic-plasmonic crystals[113]; (i) enhance Raman spectroscopy by using metal nanoparticles[114].
2
5.1.石墨烯等离激元能带
石墨烯与介质表面也存在SPP共振. 不同于金属与介质表面产生的SPP, 石墨烯只有一层原子的厚度, 所以上下表面都会产生表面等离激元共振, 通过石墨烯的介电常数公式结合边界条件与麦克斯韦方程组可计算出其TM模的色散的公式为
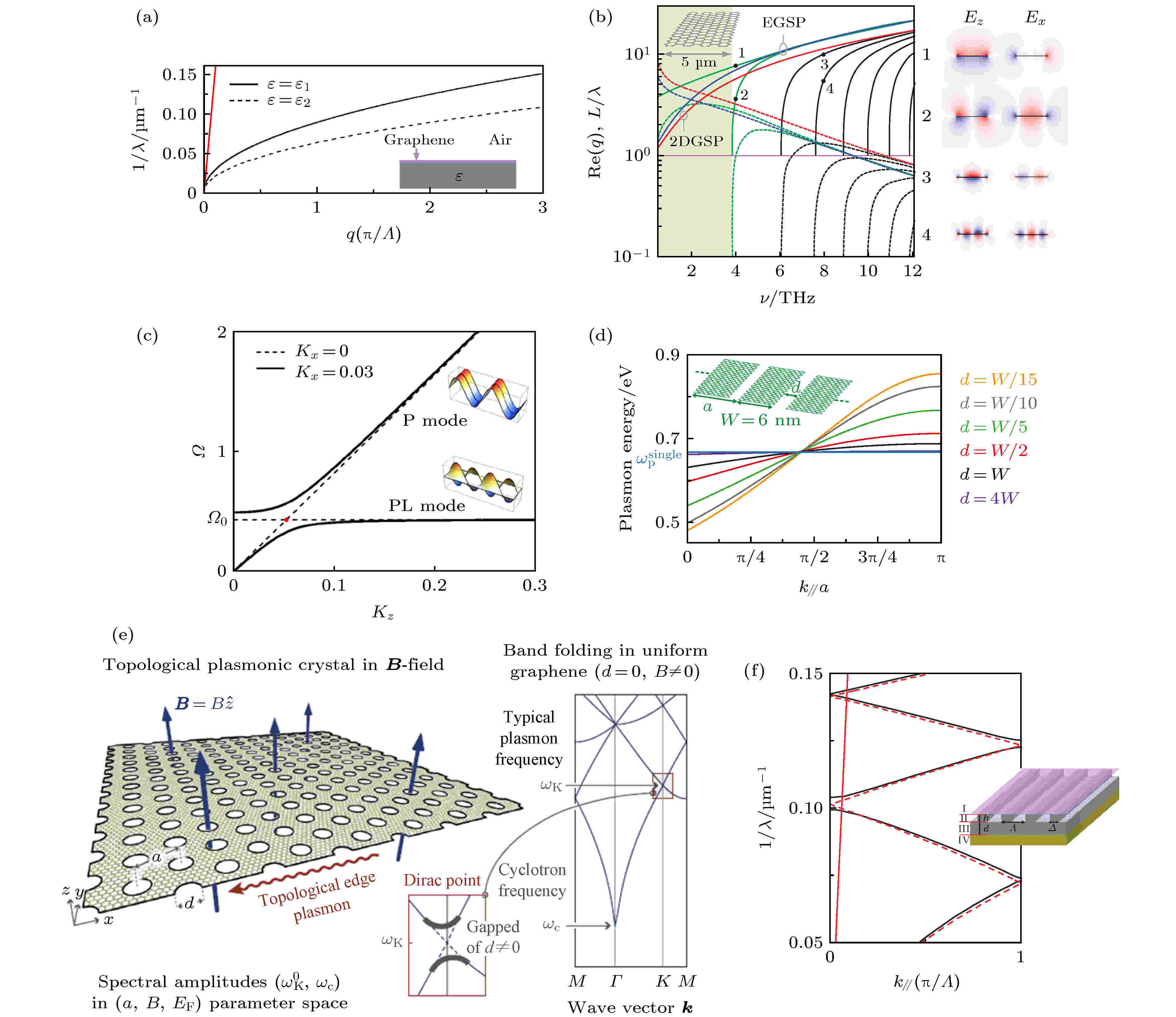图 9 (a) 石墨烯等离激元色散[125]; (b) 石墨烯条的等离激元色散[129]; (c) 单层石墨烯周期性排布TM模式的能带[126]; (d) 石墨烯条周期性排布的能带[130]; (e) 石墨烯刻蚀六角晶格孔洞的能带[128]; (f) 石墨烯覆盖在一维介质光栅上的能带[125]Figure9. (a) Dispersion of graphene-based plasmons[125]; (b) dispersion of graphene ribbon based plasmons[129]; (c) TM band structure for monolayer graphene sheet array[126]; (d) band structure for graphene ribbon array[130]; (e) band structure for graphene-based plasmonic crystal[128]; (f) band structure for one-dimensional dielectric grating coated with monolayer grapheme sheet[125].
2
5.2.石墨烯等离激元的应用
对于石墨烯等离激元的色散的调控存在很多可能的应用[132]. 例如, Zhao等[133]设计了一种基于石墨烯等离激元的太赫兹切伦科夫辐射的结构(图10(a)). 其基本过程为: 首先使用电子束激发石墨烯的SPP, 而后SPP经过略微的衰减穿过缓冲层达到缓冲层与基板的界面, 最后转化为基底中的切伦科夫辐射. 主要原理在于, 利用缓冲层使石墨烯SPP的色散蓝移以越过在基底中的光线, 只要缓冲层的厚度小于石墨烯在垂直方向上的衰减长度, 在基底中的光线以上的石墨烯的SPP就越过缓冲层转化为基地中的切伦科夫辐射(如图10(a)下部所示). 相比于金属圆盘, 石墨烯圆盘具有更强的LSP, 将石墨烯圆盘周期性地摆放[134,135], 利用其强烈的LSP了同样可实现完美吸收(图10(b)). 石墨烯等离激元的可调性也存在一定的应用, 例如Lu等[136]将石墨烯覆盖在齿深逐渐增大的介质光栅上实现了石墨烯等离激元的慢光效应, 并且通过改变石墨烯电压控制光的释放与束缚(图10(c)). Wang等[137]则通过利用周期性排列的多层石墨烯之间的SPP的耦合实现了光的分束与定向传播(图10(d)).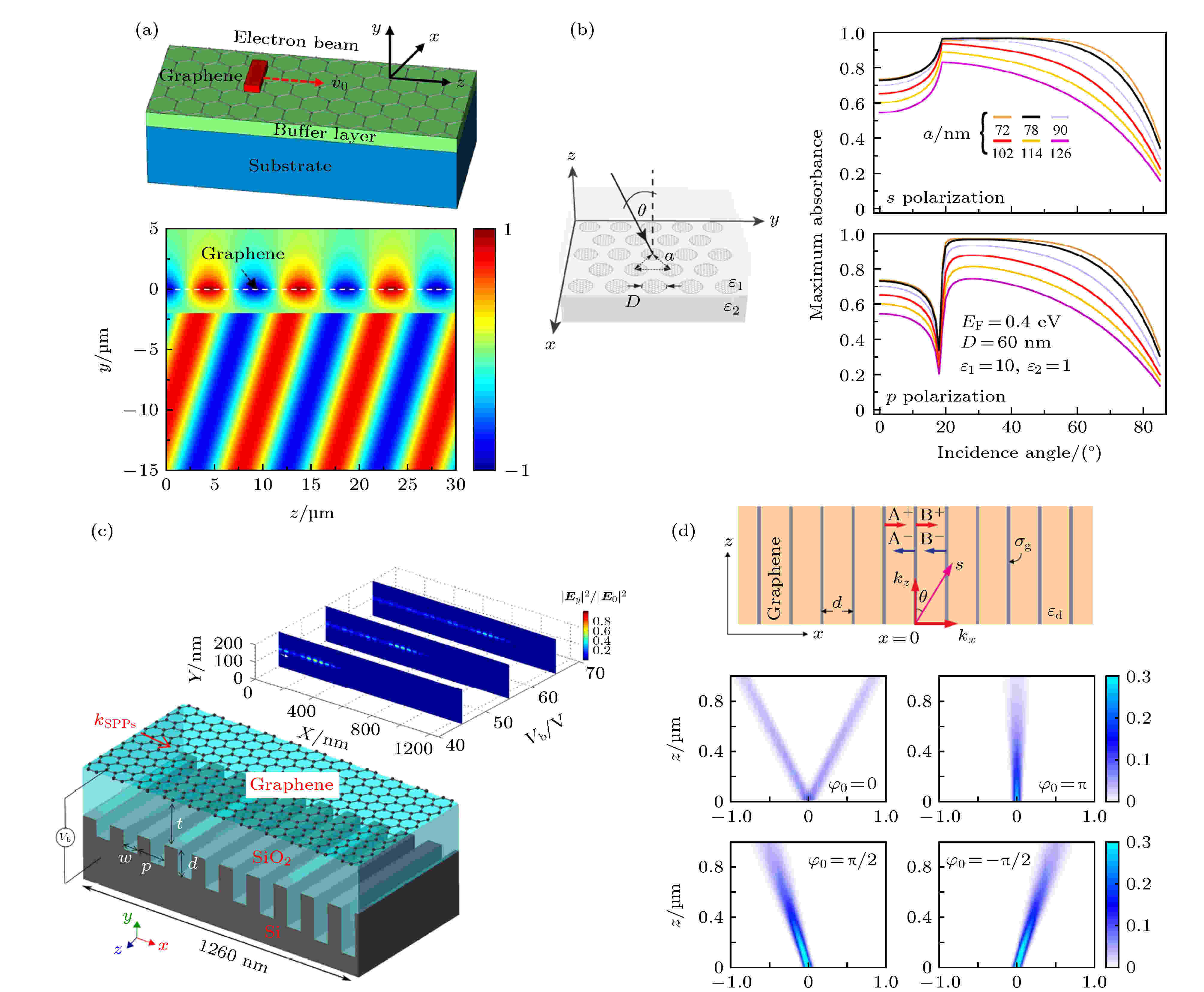
图 10 石墨烯的一些应用 (a) 基于石墨烯SPP的太赫兹切伦科夫辐射[133]; (b) 基于周期性摆放的石墨烯圆盘的宽角度的全吸收[134]; (c) 在槽深逐渐变化的介质光栅上覆盖石墨烯, 实现光在特定位置的束缚与释放[136]; (d) 利用周期性摆放的石墨烯实现对光的分束与定向辐射[137]Figure10. Applications of graphene-based plasmonic: (a) Cherenkov terahertz radiation viagraphene plasmons[133]; (b) complete absorption by periodic array of graphene nanodisks[134]; (c) slow and release light based on graphene plasmons[136]; (d) beam splitting and direction control of light based on monolayer graphene sheet array[137].
1)支持SPP的导体材料由于其具有自由电子, 实际上理应具有很强的非线性系数. 但对于无结构的平导体材料, 其在光波段的负介电常数导致电磁波无法深入穿透样品, 因此实际的非线性效应很小. 由于SPP的强场强效应, 具有SPP模式的材料理应能够极大地增强光与物质的非线性相互作用[138,139]. 不过, 需要注意的是, 高效率的非线性过程不仅与场强相关, 而且也需要满足相位匹配条件[140]. 考虑到SPP本身能带的强色散特性, 绝大部分报道的与SPP有关的非线性工作是基于LSP的[138,141]. 为了在长的作用距离上能够实现高效的非线性转换, SPP的能带结构设计就显得尤其重要. 如能再结合当前光子晶体中近零折射率等概念, 使相位匹配设计简化, 基于SPP的片上高效非线性操控有可能成为未来片上光学和片上光计算的重要组成部分.
2)利用SPP实现材料的激射, 一直都是领域中的重要发展方向. 在其中, 由于具有能带结构的SPP模式具有高品质因子和长程的空间相干性, 周期性金属颗粒阵列结构最近被广泛地报道其有利于实现物质的激射[142,143]. 尽管如此, 可实现激射的物质绝大多数均分散在溶液环境中, 极大地限制了这类SPP激光的应用范围. 如何有效地实现基于SPP的固态物质激射, 甚至电注入下激射是SPP研究领域中的一个关键问题. 这个问题的回答不仅依赖于研究人员对SPP的能量耗散机制[144,145]和SPP与物质相互作用机制[146]更深刻的理解, 而且也与金属等材料的微加工工艺的提升密切相关. 如何能够在适合现有发光光电半导体的工艺制程中大面积的加工金属结构？如何在不破坏原有固态材料本身内量子效率的情况下, 实现在发生电荷转移和跃迁的关键位置加工金属结构？如何能够使提供SPP局域强场的金属结构不成为激射材料或者发光器件中电子的捕获体或“陷阱”？这些制造工艺问题仍有待于深入的研究.
3)无论上述的非线性过程或光抽运下的激射应用, 均需要强功率的入射激光. 由于金属材料在光频段的强吸收特性, 热效应对器件的损伤极大. 如果通过传统的导热材料导出热量, 在实际的SPP能带结构的设计中有必要考虑这方面的具体影响.
4)最后, SPP作为一个与实际联系紧密的应用物理研究方向, 其设计有必要具有一定的范式. 该范式需满足工业根据具体目标效能构筑SPP结构的需求. 这有赖于多物理场与光场耦合的模拟手段有效配合遗传和粒子群等的优化算法. 同时, 在算法中引入能够积累设计经验的人工智能甚至无监督人工智能算法也可以进一步加速设计.
本文主要讨论了金属和石墨烯等离激元的能带, 介绍了产生等离激元能带的微结构、能带的产生机制, 能带在光线以上和光线以下的各种性质. 基于等离激元能带上的各类性质, 等离激元在波导、传感器、光的定向辐射等方面显示了一定的应用. 随着人们对等离激元能带的深入研究, 有望推动等离激元在广泛的领域有更多的应用.
