全文HTML
--> --> -->另一方面, 包括光子晶体、超构材料以及光子晶格(倏逝波耦合的光学波导阵列)等在内的人工光子微结构为模拟和探究凝聚态物理、材料科学、量子力学和光子学交叉领域的重要前沿物理问题提供了一个可调控的实验平台. 其中光子晶格更是成为光学系统类比研究其他物理问题的典型例子. 利用光子晶格平台, 不仅可以精确控制实验系统初始条件, 而且可以操控入射波函数(包括振幅与相位等), 这些为用经典光波传输类比实现凝聚态系统中电子的新奇现象提供了可能. 例如, 在过去二十年, 很多有趣的现象都在光子晶格体系得到了实现, 包括空间光孤子[22-24]、动态光局域[25,26]以及无序晶格中的安德森局域[27,28]等.
伴随着凝聚态系统中平带物理的蓬勃发展, 平带在光子微结构中的研究也得到突破性的进展, 一系列新颖的现象得到了理论预言与实验证实. 本综述中, 首先回顾平带光子微结构的最新研究进展, 并聚焦讨论光诱导光子晶格中新颖的平带光局域与实空间拓扑 (real-space topology) 现象. 第二部分, 介绍几种典型的平带结构、平带理论以及相关的研究进展, 这些平带晶格是目前研究的热点. 第三部分, 总结光诱导/光直写方式制备平带光子晶格的两种方法. 随后, 第四部分具体介绍在光诱导Lieb, Kagome以及菱形光子晶格中常规的紧凑平带局域态 (compact localized states)的实验研究. 在第五部分, 总结在Lieb与超级蜂窝光子晶格中非常规平带线形态 (unconventional line states) 的实验研究. 这种新型平带模式由系统的实空间拓扑特性引起, 且无法通过常规紧凑平带局域态的叠加得到. 新的线形模式可以看作是不可压缩环形态(noncontractible loop states)在有限的平带晶格中的展现. 进一步, 第六部分讨论在Kagome光子晶格中两种实现不可压缩环形态的方法: 一种是在有限晶格中观察环绕整个晶格的稳定边界模 (robust boundary modes, RBM), 可看作是不可压缩环形态的间接实现; 另一种是在特殊设计的Corbino型Kagome晶格中实现对不可压缩环形态的直接观察, 使得二维无限Kagome晶格或是能满足周期边界条件的三维圆环面(torus)上的环形态在一个维度上等效实现, 讨论其形成机制和实空间拓扑特性. 最后第七部分是总结和展望.
本文着重介绍几种典型平带晶格结构, 包括准一维菱形晶格、二维Lieb晶格、Kagome晶格以及超级蜂窝型晶格. 紧束缚近似下, 只考虑最近邻格点之间的耦合时, 这些结构的能带(见下文)中均包含狄拉克锥形能带以及至少一个完全无色散的平带. 平带意味着波包的群速度为零或者粒子有效质量无穷大, 其宏观简并特性使得利用布洛赫波的叠加能够构建局域化的平带模式—紧凑局域模式, 这些局域模式在实空间中能量束缚在有限数目的格点上[6]. 如图1所示, 一维菱形晶格的平带模式占据A与B两个格点, 振幅大小相同, 相位相反; 对于Lieb结构, 其平带模式则占据四个格点, 所有格点振幅相同, 相邻格点相位相反; 而对于Kagome与超级蜂窝型晶格, 平带局域模式均占据六个格点, 仍然为振幅相同的反相位结构. 由于特殊的几何排列, 这些模式的能量在向近邻格点耦合时, 波函数之间相干相消而保持局域. 比如, 一维菱形结构中, 紧凑局域模式在传播过程中能量由A与B两个格点向近邻的C点耦合时, 由于相干相消导致C点能量始终为0, 因此该模式能量始终局域在A与B格点上.
图 1 几种典型的平带晶格结构 (a) 菱形晶格; (b) Lieb晶格; (c) Kagome晶格; (d) 超级蜂窝型晶格; 彩色点为常规紧凑排列的局域本征模式示意图, 灰色点振幅为0, 红色点代表振幅为1, 蓝色点为–1, 即两者振幅大小相同而相位差为πFigure1. Typical examples of flatband lattices: (a) Quasi-one-dimensional (1D) rhombic lattice; (b) Lieb lattice; (c) Kagome lattice; (d) super-honeycomb lattice (sHCL). Compact localized states (CLSs) are depicted as colored sites, where zero amplitudes are denoted by gray color, and those with non-zero amplitudes of opposite phase are denoted by red and blue colors.
不同晶格结构的平带性质不同. Flach等[43]根据紧凑局域模式所占据的晶格原胞数U对平带模式进行区分. 例如, 菱形结构的平带局域本征模式只占据一个原胞, 因而U = 1. 对于Lieb等结构则U ≥ 2, 其局域模式更加复杂. 根据平带本征模式性质可以将平带分为三类: “对称保护”(symmetry-protected)平带、“偶然”(accidental)平带与“拓扑保护”(topologically protected)平带. 菱形晶格中, 所有紧凑局域态(U = 1)构成平带模式完备正交基, 这样的平带属于“对称保护”平带. “偶然”平带可以看成通过调整系统参数形成的占据超过两个原胞(U ≥ 2)的本征模式构成. 这种平带系统中能带并不总是平坦的, 只是“偶然”出现于特殊参数条件下, 例如出现在Mielke[32]提出的一系列一维线状排列结构以及Tasaki[35]提出的具有次近邻耦合时的结构. 而“拓扑保护”平带是稳固的平带, 完全由晶格的拓扑结构决定, 比如具有二分(bipartite)结构的Lieb晶格的平带, 即使在一些特殊微扰下带隙打开, 但平带仍然能够很好的保持[31,44].
随着平带物理研究日益深入, 在光子晶体、超构材料与光子晶格等光学系统中平带也得到了广泛研究并观察到了许多新颖的物理效应. 特别地, 平带光子微结构的最新研究进展为光场调控打开了新的大门. 例如, 平带对应波函数群速度为零, 可以用来实现整个布里渊区的慢光效应. 理论上, 通过调整系统结构参数可以在多种不同结构的光子晶体波导中实现平带慢光效应[45-47]. 在超构材料系统, Nakata等[48]利用金属棒与金属圆盘构建了Kagome结构并直接观察到了太赫兹波等离激元平带. 从图 2(a)所示的透射谱中可以看到, 平带所在的共振频率透射最小并且与入射角度无关. 该研究组在二维Lieb结构中也观察到类似的性质[49]. 与此同时, Huang等[50]在介质棒构建的四方光子晶体中实现了等效零折射率超构材料并观察到了微波波段的隐身效应(图2(b)). 在该结构中, 通过改变参数调整偶极与单极模式的简并性, 得到了与Lieb结构相似的能带, 即一个锥形能带以及中间的平带. 2016年, Baboux等[51]构建了基于微柱光学腔的一维“枕”型结构并直接观察到无色散的平带(图2(c)), 同时, 实验实现了平带对应的激子-极化激元凝聚态. 类似地, 在最新研究中, Whittaker等[52] 与Harder等[53]理论与实验实现了 Lieb结构中的平带激子-极化激元. 更有趣的是, Mili?evi?等[54]研究发现, 在蜂窝型排列的极化激元耦合微米柱结构中, 当引入拉伸形变时, 其P轨道能带中的平带与抛物线能带交叉点会变成两个倾斜的狄拉克锥, 当形变为特定值时会产生第三类狄拉克锥, 因而在该系统中同时存在平带与多种形式的狄拉克锥. 近期的综述文章中, Leykam等[55,56]对人工平带系统中的一些理论模型和实验研究进行了总结讨论.
图 2 光子系统中平带研究的典型实例 (a) 左图为表面等离激元平带的金属Kagome超构材料, 右图为对应的太赫兹波透射图, 存在一个全角度的无辐射平带(水平虚线所示)[48]; (b) 左图为四方结构的全介质零折射率超构材料实现隐身效应实验装置, 右图为适当介质参数时得到的四方结构色散关系, 含有一个狄拉克锥与一个无色散平带[50]; (c) 一维“枕”型结构的微柱光学腔及其色散关系, 中间为平带[51]Figure2. Examples of photonic flatband structures: (a) Kagome lattice for terahertz spoof plasmons, displaying an omnidirectional minimum in the transmission at the flatband frequency (dashed line) in the right panel[48]; (b) experimental setup exposing the zero-refractive-index all-dielectric metamaterials with a square lattice to realize cloaking inside a channel with the Dirac point, and the right panel shows corresponding three-dimensional dispersion diagrams consisting of a Dirac cone and a flatband[50]; (c) structured microcavity forming a 1D stub lattice and its photoluminescence spectrum, revealing a flatband in the middle[51].
2004年以来, 飞秒激光直写技术成为制备介质波导的重要手段[57,58], 采用该方法制备了多种结构的耦合波导阵列, 即光子晶格, 这使得在光子晶格中研究新颖物理现象有了更加便利的平台. 利用该技术, 二维蜂窝型光子晶格(光子石墨烯)及其形变结构得以实现[59,60]. 更重要的是, 还可以进一步构建螺旋型的光子石墨烯晶格, 从而实现光子拓扑绝缘体[61,62], 进而在拓扑激光器等方面得以应用[63]. 得益于飞秒激光直写技术的进步, 平带光子晶格研究也取得飞速进展. 2015 年, 两个独立的研究组分别制备了Lieb光子晶格(图3(a)), 并首次实验观察到局域的平带本征模式[64,65]. 最新的研究中, EI Hassan等[66]利用飞秒激光直写技术在玻璃样品中成功构建了有限周期的Kagome光子晶格(图3(b)), 并实现了新颖的拓扑角态, 这为进一步研究Kagome晶格中的平带性质和平带拓扑现象提供了平台. 另一方面, Mukherjee等[67]与Kremer等[68]分别利用飞秒激光直写技术制备了纵向弯曲的菱形结构(图3(c)), 引入了人工(artificial)磁场, 在该结构中实验类比实现了Aharonov-Bohm效应. 此外, 近几年, 非厄米系统中平带也取得了一系列进展[69-75], 然而相关的研究均局限于理论研究. 2019年, Biesenthal等[76]通过在纵向加入散射体在波导中引入损耗成功实现了非厄米的晶格哈密顿量, 在实验上首次实现了宇称时间 (parity-time, PT) 对称平带.
图 3 利用飞秒激光直写技术制备的平带光子晶格 (a) 用于研究平带局域模式的Lieb光子晶格[64,65]; (b) 用于研究拓扑角态的Kagome光子晶格[66]; (c) 用于实现Aharonov-Bohm效应的纵向弯曲菱形光子晶格[67,68]Figure3. Examples of femtosecond laser-writing flatband photonic lattices: (a) A photonic Lieb lattice for demonstration of flatband compact localized states[64,65]; (b) a photonic Kagome lattice established for demonstration of topological corner states[66]; (c) a driven photonic rhombic lattice for experimental observation of Aharonov-Bohm cages[67,68].
2
3.1.多光束干涉光诱导技术
Segev与Christodoulides课题组[22,23]提出多光束干涉光诱导的方法并利用该方法首次实验观察到二维光学离散孤子. Chen等[77,78]进一步提出了部分相干光干涉技术, 该技术克服了相干光的调制不稳定性, 能够产生折射率调制均匀的波导阵列. 目前, 该方法被广泛应用到关于光子晶格的研究中, 其实验装置如图4 所示. 高斯光经过旋转散射器调制后形成部分相干光, 入射到振幅掩膜板上并在傅里叶面滤波后叠加形成无衍射光场. 将该光场入射到铌酸锶钡(strontium barium niobite, SBN)晶体中, 在非线性条件下诱导产生波导阵列结构. 多光束干涉光诱导技术不仅可以用来产生多种周期性光子晶格, 同时也可以用来制备具有缺陷和特定边界等配置的晶格. 例如, 在最近的研究中, 该方法作为非常有效的实验手段被用来制备光子石墨烯, 并进一步来研究该结构的边缘态[59]与赝自旋[79-81]等物理现象.
图 4 多光束干涉光诱导技术制备光子晶格[80,83], 其中第一排为实验光路图(PBS, 偏振分光棱镜; Mask, 掩膜板; SBN, 铌酸锶钡晶体); 第二排为实验制作的典型光子晶格 (a) 蜂窝型光子晶格; (b) 对称破缺的蜂窝型光子晶格; (c) 涡旋晶格; (d) Kagome晶格Figure4. Examples of photonic lattices created by multiple-beam optical induction method[80,83]. Top panel shows schematic of experimental setup. PBS, polarized beam splitter; SBN, strontium barium niobite. Bottom panel shows typical examples of photonic lattices realized in experiment: (a) A “perfect” honeycomb lattice; (b) an inversion-symmetry-breaking honeycomb lattice; (c) a vortex lattice; (d) a Kagome lattice.
制备光子晶格时要求诱导晶格的光场在传播方向上不变, 因而使用该技术时首先需要利用多光束干涉产生相应的无衍射光场. Boguslawski等[82]通过特殊滤波系统, 给出了平面波叠加产生的多种离散无衍射光场. 以六边形结构为例, 利用振幅掩膜板和相位调制器在傅里叶频谱面上进行振幅和相位调制能够产生不同结构的衍射图样, 如蜂窝型结构、Kagome与涡旋型结构等[83]. 它们均可以通过波矢大小相同的六束平面波叠加产生, 不同点在于初始相位调制不同. 理论上, 在光折变晶体中这些无衍射光场均可以诱导产生对应的光子晶格结构.
除了Kagome晶格, 其他平带结构同样可以利用多光束干涉光诱导技术制备. Lieb晶格是最简单的二维平带系统之一[31,64,65,84], 由于该结构不属于布拉维格子, 想要通过多光束干涉振幅调制来制备Lieb光子晶格, 需要在实验装置中加入新的设计. Xia等[85]利用两个或者多个简单光场的非相干叠加实现了该结构. 该实验中, 首先通过四束平面波叠加分别构建一个“蛋托”(egg-crate)型晶格与一个四方结构对应的光场. 随后, 将两个干涉图样非相干叠加, 光强暗点构成Lieb结构对应的无衍射光场. 最终, 利用自散焦非线性效应在晶体中诱导实现了Lieb光子晶格. 这种多个光场非相干叠加的方法也被用来制备一维与二维超晶格[86-88].
2
3.2.连续激光直写技术
利用多光束干涉光诱导的方法可以很方便地制备多种无边界的晶格结构. 然而, 实际研究中往往需要一些具有特殊边界的晶格. 例如, 对于石墨烯结构, 不同边界支持不同的边界态, 同时带来不同的物理效应[59]. 而在研究延展的线形平带局域态时, 就需要制备具有特定边界的平带光子晶格. 这里介绍一种逐点写入的连续激光直写技术[89], 实验装置如图5所示. 一束532 nm的激光入射到空间光调制器上, 通过调制得到出射位置可控的高斯光. 经4f系统滤波后, 高斯光在10 mm 长的SBN晶体内传输可认为是接近无衍射的. 在外加电场作用下, 由于非瞬时的自聚焦效应, 高斯光在晶体内形成近似孤子态并诱导形成波导. 通过计算机调控加载的相位, 可以灵活改变入射光的位置进而调整写入波导的位置, 在逐个写入波导后最终形成沿传播方向不变的波导阵列结构. 这种点对点的写入技术与多光束干涉方法完全不同, 不仅可以用来制备有限周期Lieb光子晶格[89], 也可以用来产生任意边界的Kagome[90]、超级蜂窝型晶格[91]与菱形晶格[92]等. 当然, 该方法有它的局限性, 由于相邻波导之间相互影响, 晶格的周期不能过小, 实验中采用周期不小于26 μm. 在平带的研究中, 往往要求所制备的晶格结构满足紧束缚模型, 此时周期无需过小, 因此这种方法恰好能实现平带物理现象的相关实验. 类似地, 无衍射的贝塞尔光也可以用来诱导制备波导阵列, 然而贝塞尔光具有多个旁瓣, 在构建波导的过程中各个贝塞尔光的旁瓣之间相互影响导致其同样不能用来制备小周期的晶格结构[93].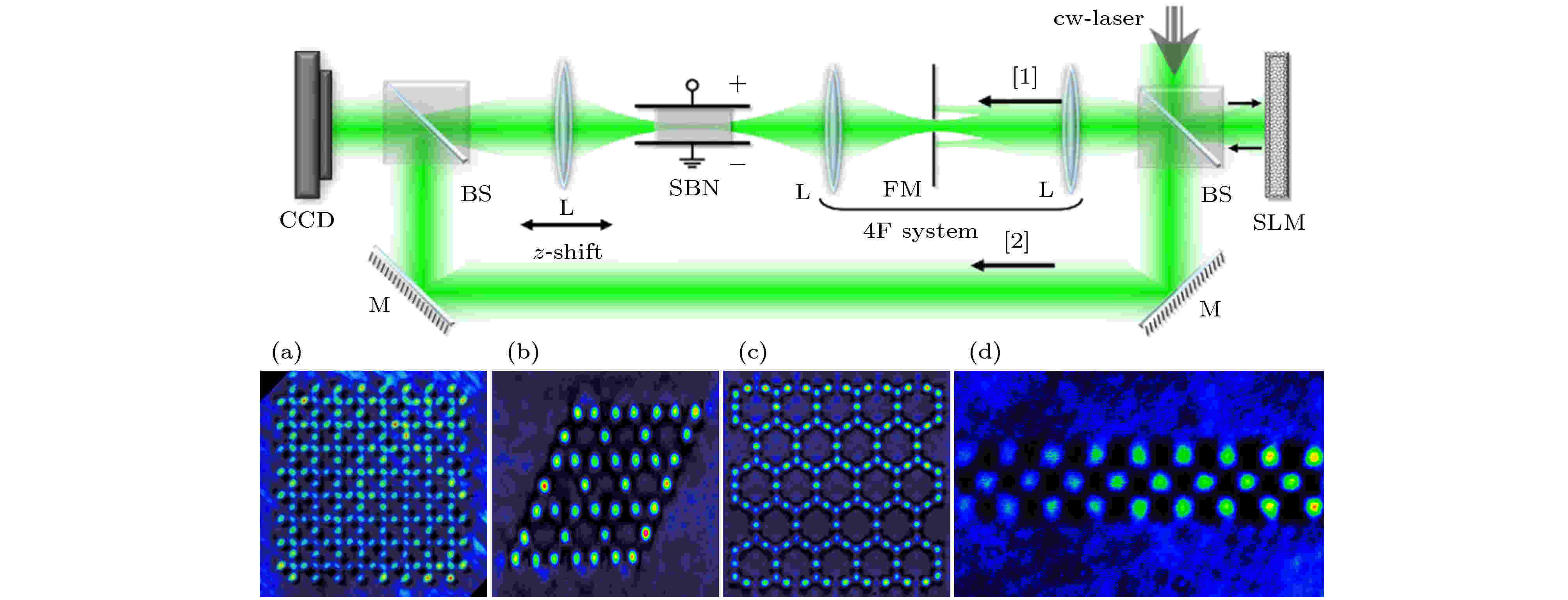
图 5 连续激光直写技术制备不同平带光子晶格, 其中, 第一排为实验光路图(SLM, 空间光调制器; BS, 分光棱镜; FM, 傅里叶掩膜板); 第二排为典型的直写光子晶格 (a)“胡须”边界(“bearded” edges)的Lieb光子晶格[89]; (b) 平滑边界的Kagome光子晶格[90]; (c) 超级蜂窝晶格[91]; (d) 横向折射率梯度变化的菱形光子晶格[92]Figure5. Examples of photonic lattices created by direct cw-laser-writing technique in a nonlinear bulk crystal. Top panel shows illustration of experimental setup. SLM, spatial light modulator; BS, beam splitter; FM, Fourier mask. Bottom panel shows typical examples of photonic lattices created by direct cw-laser-writing method: (a) A photonic Lieb lattice with “bearded” edges[89]; (b) a photonic Kagome lattice with flat boundary[90]; (c) a photonic sHCL[91]; (d) a driven photonic rhombic lattice with refractive index gradient parallel to the ribbon[92].
Lieb结构是最简单也是研究最多的二维平带结构之一. 如图6(a)所示, 紧束缚近似下, 其能带包括三部分: 两个锥形能带以及中间的一个无色散平带, 三个能带对称排列且在高对称点M点(kx = ky = π)处交叉. 与蜂窝型晶格类似, 色散带构成的狄拉克锥带来很多有趣的现象. 例如, 锥形衍射[94]、赝自旋[95]以及拓扑边缘态[96]等. 与其他具有锥形能带的结构相比, Lieb晶格明显不同在于其锥形能带中间存在一个完全无色散的平带. 2014年, Guzmán-Silva等[41]首次实现了Lieb光子晶格, 该研究讨论了在拉伸的晶格中实现边界模式. 2015年, Mukherjee等[64]与Vicencio等[65]分别在飞秒激光直写的Lieb光子晶格中首次实验报道了局域的平带模式. Lieb光子晶格中平带是手性对称保护的, 其与色散带之间的交叉受到实空间拓扑的保护[6]. 研究表明, 该系统的平带在无序条件下能够保持稳定[97-101].
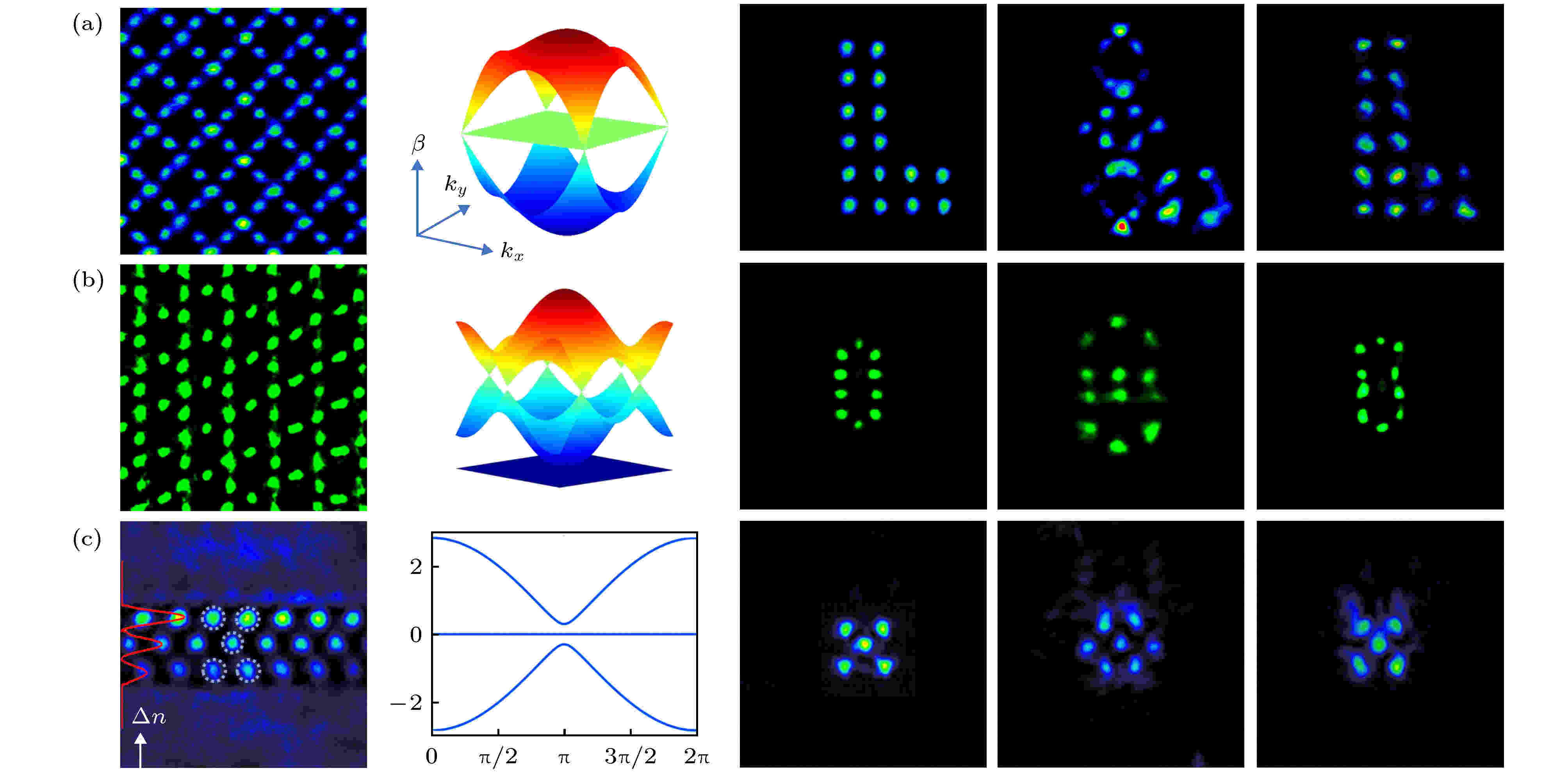图 6 平带光子晶格常规紧凑局域模式的实验结果(从左至右: 实验制备的光诱导光子晶格结构、紧束缚近似下能带结构、入射面探测光、同相位输出以及反相位输出) (a) Lieb光子晶格中基于平带模式的图像传输[85]; (b) Kagome光子晶格中的平带局域模式[104]; (c) 折射率梯度场下菱形光子晶格中U = 2的局域本征模式[92]Figure6. Experimental results of CLSs in flatband lattices: (a) Linear image (formed by CLSs) propagation through an optically induced Lieb photonic lattice[85]; (b) a bound-state transmission in a Kagome photonic lattice[104]; (c) observation of a quincunx-shaped (U = 2) compact localized state which spans over two-unit cells in a photonic rhombic lattice[92]. From left to right: shown are the lattices, calculated band structures in the tight-binding approximation, probe beam inputs, and their in-phase and out-of-phase outputs.
前文提到, Xia等[85]提出了一种简单有效的光诱导Lieb光子晶格的方法. 在其构建的光诱导Lieb光子晶格中, 不仅实验观察到了局域的本征模式, 同时还实现了文本的传输. 如图6(a)所示, 利用平带本征模式的叠加, 构建了文本“L”作为探测光. 当探测光相邻点保持反相位入射到晶体前表面时, 平带局域模式被激发, 探测光在晶体出射面能够很好的保持局域. 而当探测光所有点同相位时, 在出射面则表现为离散衍射现象. 该研究表明平带在图像传输方面具有潜在的应用前景.
与此同时, Kagome光子晶格中的研究也取得了快速发展. 该结构可以看成是蜂窝结构与“沙漏”(sandglass)结构构成, 其能带结构中同样包括狄拉克锥与平带. 2013年, Vicencio和Johansson[102]理论预言了非线性Kagome晶格模型中平带孤子的存在. 随后, 在该结构中理论证实利用平带可实现无衍射图像传输[103]. 2016年, Zong等[104]利用多光束干涉诱导的方法制备了Kagome晶格结构, 并首次观察到了局域本征模式, 实验结果如图6(b)所示. 由于局域本征态的叠加仍然为系统本征模式, 实验中可以看到, 由两个简单局域模式叠加构成的探测光入射到晶格内后可以保持局域传输. 同样, 在该结构中利用多个平带本征模式的叠加也可以实现无衍射的图像传输, 而且Kagome 晶格的局域本征态是六边形结构, 更利于构建环形或者链状的图像进行传输.
近来, 平带与外场的相互作用也同样受到了关注. 外场作用下的平带展现出许多新颖的物理效应. 例如拓扑平带绝缘体[105-110]、平带朗道-齐纳布洛赫振荡(Landau-Zener Bloch oscillations)[111,112]以及磁场作用下Aharonov-Bohm效应[67,68]. 在这些研究中存在一个重要的基本物理问题: 外加磁场下, 平带及其本征模式是如何变化的? Mukherjee和Thomson[113]研究发现, 外场作用下的一维菱形结构的平带局域模式是稳定的. Khomeriki和Flach[111]理论研究表明该局域本征模式在外加电场与磁场作用下同样也能稳定存在. 而Kolovsky对二维dice晶格的研究表明, 在外加场作用下其平带模式由紧凑的局域态变为指数衰减的形式[114]. 可以看到, 相关的物理机制仍然不清晰且缺少实验证实. 为了解决这个问题, Xia等[92]以一维菱形结构为例, 在理论与实验上阐明了在具有水平或垂直方向折射率梯度的光子晶格中平带及其本征模式的变化, 并且首次在实验上实现了U = 2的局域本征态. 实际上, 一维菱形结构及其平带模式在多种系统中都得到了广泛讨论[111,113,115-117]. Xia等[92]利用连续激光写入波导的方式, 通过改变诱导光的相对光强制备了具有折射率梯度的一维菱形波导阵列. 实验结果如图6(c)所示, 此时的折射率梯度可等效于外加的直流电场. 在具有水平方向(x方向)梯度时, 菱形结构的能带转化为瓦尼尔-斯塔克势阶 (Wannier-stark ladders) 的形式, 但平带本征模式保持不变, 仍为图1(a)所示. 在垂直方向(y方向)梯度时, 能带间带隙打开且平带能够很好的保持. 更重要的是, 平带本征模式此时发生了根本的改变: 由U = 1的局域模式转变为占据两个原胞的U = 2形式. 此外, 当施加y方向折射率梯度场时, 平带模式在传输过程中也能够保持局域. 在x方向折射率梯度作用下, 虽然平带模式的叠加仍是系统的本征模式且传输过程中能够保持局域, 然而其在动量空间能量分布却表现为周期性振荡形式.
不可压缩环形态理论上存在于无限的晶格中, 在实验上是不可能实现的, 因而平带实空间拓扑性质提出以后, 相关的实验研究开展较少. 最近研究发现, 不可压缩环形态可存在于具有特殊边界的有限周期晶格内, 表现为依赖于边界的线形模式并且满足平带模式相干相消的条件. 2018年, Xia等[89]通过连续激光直写技术制备了Lieb光子晶格并首次在实验报道了这种非常规的平带模式. 如图7(a)所示, Lieb光子晶格紧凑局域本征模式之间是线性独立的并且不能形成完备平带模式, 因此需要不可压缩环形态的参与才能构成整个平带. Lieb晶格中对应的是在一个方向延展的平带线形态. 该研究中, 首先利用连续激光写入方式构建了具有胡须状边界的Lieb光子晶格(图5(a)). 随后将由多个高斯光构成且具有反相位结构的探测光入射到晶体内(图7(b1)). 没有晶格存在时, 探测光各个点在传输方向上衍射(图7(b2)). 有晶格作用时, 入射光的光强能够很好地保持局域而不产生衍射效应(图7(b3)). 作为对比, 将输入的探测光改为同相位的形式, 可以看到在出射面探测光表现为离散衍射的形式(图7(c3)), 即能量耦合到邻近波导中. 更重要的是, 同相位与反相位入射时具有完全不同的频谱能量分布. 反相位时, 频谱能量分布在布里渊区边界(图7(b5)), 该点即为能带交叉的位置, 而同相位入射时, 出射光的能量分布在布里渊区中心(图7(c5)). 这种非常规线形平带模式不能通过常规紧凑型的局域本征模式叠加得到而是来源于系统实空间拓扑特性.
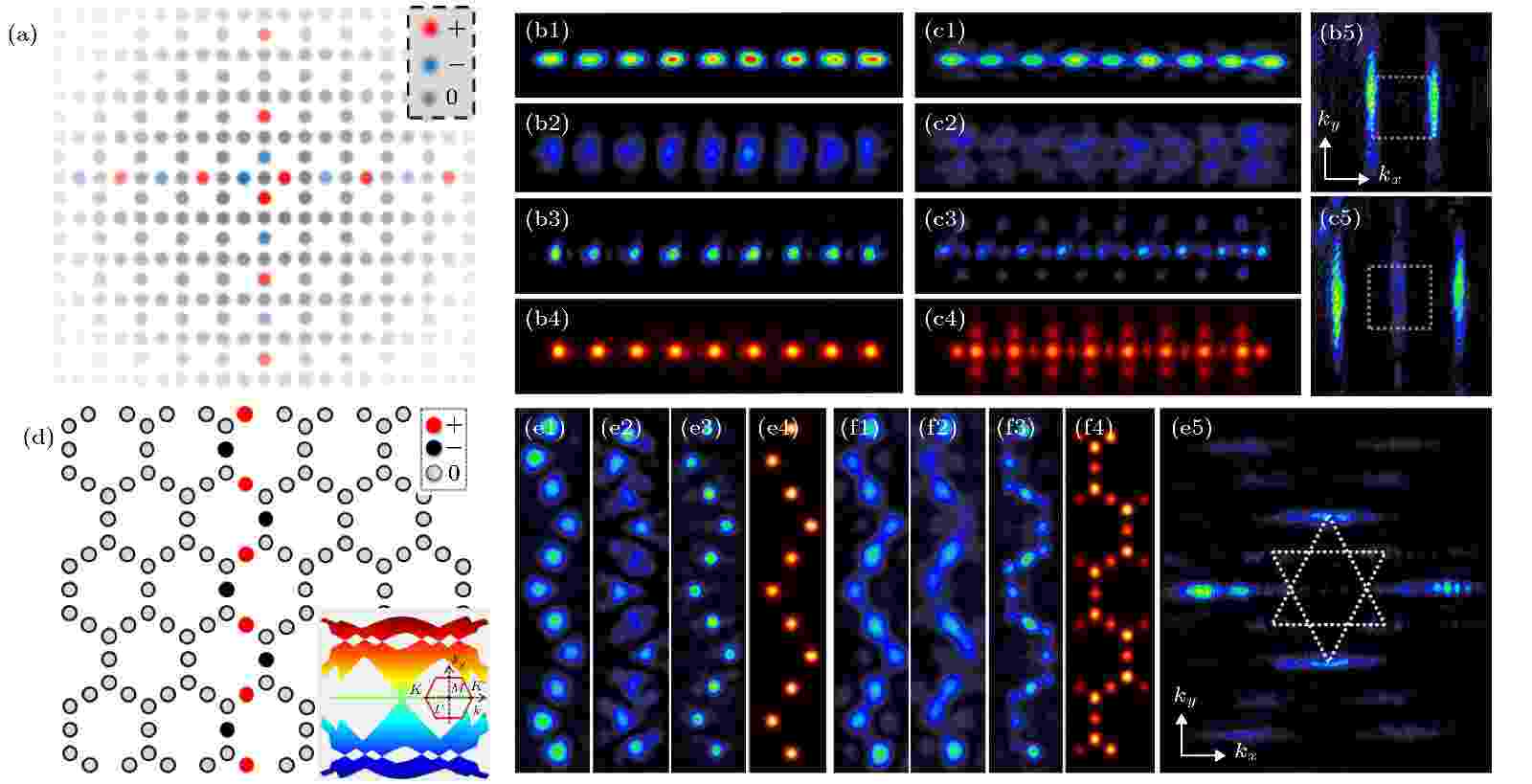图 7 Lieb与超级蜂窝光子晶格中非常规线形平带模式的实验结果[89,91] (a), (d)非常规线形平带局域模式的示意图, 其中图(d)右下插图为能带结构; (b1), (e1) 反相位入射的探测光; (b2), (e2) 无晶格时的输出; (b3), (e3) 有晶格时的输出; (b4), (e4) 长距离传输的数值模拟结果; 图(c1)?(c4)完全对应(b1)?(b4), 但为探测光同相位入射时的结果; 图(f1)?(f4)对应(e1)?(e4), 但为探测光同相位入射时的结果; (b5), (c5)为对应(b3), (c3)的k空间能谱, 虚线框为第一布里渊区边界; (e5) 为对应于图(e3)的k空间能量分布, 其中虚线框表示第一与第二布里渊区边界Figure7. Demonstration of unconventional line state in photonic Lieb and super-honeycomb lattices[89,91]: (a), (d) Schematic of flatband line states in infinite lattices, and insect in (d) shows the band structure of sHCL; (b1), (e1) out-of-phase input line beam; (b2), (e2) out-of-phase output without the lattice; (b3), (e3) out-of-phase output through the lattice; (b4), (e4) simulation results showing the out-of-phase line beam remains intact but the in-phase line deteriorates after propagating a long distance through the lattice; (b5) measured k-space spectrum of (b3) with a dashed square marking the first Brillouin zone (BZ); (c1)?(c5) the same as in (b1)?(b5), and (f1)?(f4) the same as in (e1)?(e4) except that the line beam is in in-phase excitation condition; (e5) momentum space spectrum of (e3), where the white dashed lines outline the first and second BZs.
Lieb结构中平带与色散带在布里渊区边界相交叉, 还有一些平带结构的能带交叉点发生在其他高对称点. 例如超级蜂窝型晶格, 这也是一种同时具有狄拉克锥与平带的晶格结构. 在冷原子与光学系统中, 人们已经理论研究了该结构中的狄拉克锥以及锥形衍射现象[119,120], 但缺少相关的实验研究. 如图7(d)所示, 超级蜂窝型晶格单个原胞包含五个不同的格点, 在紧束缚模型近似下, 其能带包含五个带, 一个完全平坦的能带与两个锥形带在第一布里渊区中心交叉, 这与Lieb晶格中赝自旋为1的狄拉克锥相似. 更有趣的是, 该晶格中同样存在赝自旋为–1/2 的狄拉克锥. 由于平带与狄拉克锥在布里渊区中心交叉, 在超级蜂窝型晶格中也存在线形平带模式. Yan等[91]研究发现, 在具有特定边界的有限周期晶格中, 线形平带模式存在两种不同类型的形式: x方向的直线排列的线形模式, 即局域模式的各点排列在一条直线上; y方向的锯齿型模式, 即局域模式的各点按锯齿形排列. 两种模式在实空间表现出不同的形状, 占据不同的子晶格并且都不能通过常规紧凑排列的局域本征模式叠加得到. 图7(e)为连续激光直写技术制备的胡须边界的蜂窝超晶格中锯齿型局域态的实验结果. 为了激发这种局域模式, 入射的探测光设计成锯齿状并垂直入射到晶格中. 当反相位入射的探测光激发晶格时, 探测光演化为锯齿型平带模式并在传输过程中保持局域(图7(e3)). 值得注意的是, 这种锯齿状排列的局域态在Lieb与Kagome晶格中均不存在, 是超级蜂窝型晶格所独有的. 更有趣的是, 线形平带模式的空间频谱分布在高阶布里渊区中心, 这与Lieb晶格也明显不同. 这些结果再次表明非常规线形局域模式的存在与平带和色散带之间的能带接触/交叉有关.
是否能够找到其他观察Kagome结构中不可压缩环形态的方法呢? 最近, Ma等[90]的实验中给出了两种不同的方式来解决这个问题. 一方面, 实验上在特定边界的有限周期晶格中实现了环绕到整个晶格的稳定边界模. 这种边界模式可以对应三维圆环面展开到二维平面时不可压缩的环形本征态叠加产生, 在有微扰时能够稳定存在, 并能在传输过程中消除边界缺陷的影响, 产生“自愈”效应. 另一方面, 通过构建Corbino型的Kagome结构来实现晶格至少一个方向的周期性, 在该晶格中直接观察到不可压缩环形态.
首先看方式一. 图8(a)与图8(b)表示在无限周期的Kagome晶格或者圆环中不可压缩的平带本征模. 图8(c)为揭示不可压缩的平带本征模的两种模式, 其中橘黄色线代表模式一, 用RBM1表示, 绿色线代表模式二, 用RBM2表示. RBM1可以认为是沿着圆环面和径向两个方向切断圆环形成的四个不可压缩环形态的叠加. 如图8(b)所示, 这如同沿着圆环上的两条线截断圆环, 如果在这个环内有两对不可压缩环形态, 那么沿着这两对模式切断这个圆环, 将其展开可以形成一个四边打开的有限周期的晶格. 在有限周期晶格边界存在的这个态RBM1, 就被认为是四个不可压缩环形态叠加. 为了观察这种局域边界模式, Ma等[90]在实验上首先构建了具有平坦边界的Kagome光子晶格, 见图5(b). 一束由多个高斯光构成的探测光被调制成反相位排列的平行四边形形状, 当探测光入射到晶格边界时, 可以看到在出射面探测光能够很好的保持局域(图8(e1)). RBM2可以看成是RBM1和一个常规紧凑局域模式的叠加, 因而相对于RBM1有两个缺陷点. 很明显, 反相位激发形成的RBM2在晶格中传输仍然可以很好地保持局域(图8(e3)). 该研究表明, 在有特殊边界的Kagome晶格中, 可以实现由不可压缩环形态引起的稳定边界局域模式. 此外, 该研究也进一步说明这样的边界局域模式不仅在传输时能够保持局域, 并且具有抵抗微扰的能力.
图 8 (a) Kagome晶格中两种不可压缩环形态示意图; (b) 模拟无限Kagome晶格两个不可压缩环形态的圆环面; (c) 在平滑边界的Kagome晶格中两种稳定的平带边界局域模, 橘黄色线代表模式一, 绿色虚线代表模式二; (d) Corbino-Kagome结构示意图, 橘黄色圆环代表不可压缩的局域环形态; (e) 从左至右, (e1), (e2) 边界模式一的反相位输出与对应数值模拟结果; (e3), (e4) 边界模式二的反相位输出与对应数值模拟结果; (f1) 实验制备的Corbino-Kagome光子晶格; (f2), (f3)反相位激发的不可压缩环形态及其对应数值模拟结果; (f4) 40 mm传输时数值模拟结果; 图中所有插图均代表输入探测光; 同相位激发破坏所有平带局域模式的形成[90]Figure8. (a) Illustration of the noncontractible loop states (NLSs) in an infinitely extended Kagome lattice; (b) a torus showing two NLSs mimicking the 2D infinite lattice; (c) two robust boundary modes (RBMs) in a Kagome lattice with flat cutting edges, where black sites are of zero-amplitude, while blue and red ones distinguish non-zero sites with opposite phase; (d) schematic diagram of the Corbino-shaped Kagome lattice, where the NLS is illustrated by the orange circle; (e) from left to right (e1), (e3) experimental results of RBM1 and RBM2 under out-of-phase condition; (e2), (e4) simulation result corresponding to (e1) and (e3); (f1) experimentally established finite-sized Kagome lattice in a Corbino-geometry; (f2)－(f4) the NLS observed in (f2) experiment and (f3) simulations after propagation to 10 mm and (f4) 40 mm under out-of-phase condition. All insets are from input ring necklace of the probe beam. In-phase excitation destroys all localized states[90].
另一种直接实现不可压缩环形态的方法为设计和制备如图8(d)所示的Corbino-Kagome晶格. 这种特殊设计的结构等效于沿着Kagome晶格的一个方向实现了周期性边界条件, 因而可以实现沿着一个圆环曲面方向的不可压缩环形态. 该结构中, 每一环的B, C子晶格距离是相等的, 并且随着半径增加而增加. A与B (C)的间距同样相同, 但每个环是不同的. 实验中, 可以通过连续激光直写方式制备该光子晶格, 如图8(f1)所示. 为了观察环形局域模式, 一个反相位的环形链状探测光入射到晶格内激发相应的平带局域模式, 对应的实验结果如图8(f2)所示, 可以观察到, 链状探测光在晶体内传输后能够很好地局域在入射格点上. 对应的数值模拟结果如图8(f3)与图8(f4)所示, 与实验结果能够很好的吻合.这一结果可以认为是首次直接实验观测到由实空间拓扑决定的平带系统中不可压缩环形态.
近来, 关于光学微结构中平带物理效应的研究越来越多. 很多新颖的物理效应有待进一步探究. 例如, PT对称平带的实现为非厄米系统中平带的实验研究提供了平台[76], 该研究可以进一步拓展到二维平带结构同时探讨非线性相互作用等. Lim等[122]在对Lieb与Kagome晶格研究中发现, Lieb晶格转换成Kagome晶格过程中平带能够演变产生狄拉克点. 这表明Lieb与Kagome晶格, 平带与狄拉克点之间存在潜在的关联[123], 相关的物理机制值得进一步探索. 此外, 最新的研究中, Wang等[124]利用光诱导的方法成功制备了二维摩尔光子晶格(photonic Moiré lattices), 并且能够选择旋转的角度. 摩尔晶格的实现表明, 任意几何结构的变化与子晶格之间的对称性有关, 同时该研究中还发现了在特定旋转角度时平带的存在, 为摩尔晶格中的平带现象的进一步研究提供了条件[125].
总之, 对平带人工光子学微结构与平带局域和拓扑特性的研究为理解相关的基本物理概念和现象提供了新的视角. 可以断定, 对凝聚态物理、冷原子系统、超构材料与光子学系统中平带物理引发的新颖现象的研究及相关应用的开拓方兴未艾, 有着诱人的前景.
衷心感谢Leykam D, Flach S, Rhim J W, Yang B J, Danieli C与Vicencio R A等的合作和对本文的帮助.
