摘要:图像质量评价(IQA)方法需要考虑如何从主观视觉度量结果出发, 设计出符合该结果的客观图像质量评价方法, 应用到相关实际问题中. 本文从视觉感知特性出发, 量化色度和结构特征信息, 提出了基于色貌和梯度两个图像特征的图像质量客观评价模型. 两个色貌新指标(vividness和depth)是色度特征信息提取算子; 梯度算子用来提取结构特征信息. 其中, vividness相似图一方面作为特征提取算子计算失真图像局部质量分数, 另一方面作为图像全局权重系数反应每个像素的重要程度. 为了量化所提模型的主要参数, 根据通用模型性能评价指标, 使用Taguchi实验设计方法进行优化. 为了验证该模型的性能, 使用4个常用图像质量数据库中的94幅参考图像和4830幅失真图像进行对比测试, 从预测精度、计算复杂度和泛化性进行分析. 结果表明, 所提模型的精度PLCC值在4给数据库中最低实现0.8455, 最高可以达到0.9640, 综合性能优于10个典型和近期发表的图像质量评估(IQA)模型. 研究结果表明, 所提模型是有效的、可行的, 是一个性能优异的IQA模型.
关键词: 图像质量评价/
人类视觉特性/
色貌/
梯度

English Abstract

全文HTML

--> --> -->

随着各种多媒体通信系统中彩色图像内容和成像设备的迅速发展, 传统的灰度传输方式被彩色传输所取代. 在这种转变下, 感知图像质量评估(image quality assessment, IQA)在众多的视觉数据处理应用中发挥了重要的作用, 特别是针对由于压缩和传输而产生的失真评价, 如模糊、块效应和白噪声等^[1]. 在过去的几十年里, 人们设计了多种客观的IQA模型来评估图像质量^[2]. 人眼视觉系统(human visual system, HVS)是一种理想的视觉信息接收系统, 也是用主观判断^[3]评价图像质量最可靠的方法. 通常, 主观评价的结果由平均意见分数(mean opinion scores, MOS)和差异意见分数(differential mean opinion scores, DMOS)表示, 且这两种主观评分是图像质量客观评价性能的评估依据.
目前, 典型的图像客观质量评价方法主要有: 1) 基于数学统计的方法, 如MSE (mean squared error)和PSNR (peak signal to noise ratio)等; 2) 基于HVS感知特性的方法, 如SSIM (structural similarity), IFC (information fidelity criterion), FSIM (feature similarity)等; 3) 基于机器学习的方法^[4], 该方法计算精度较高, 但需要长时间样本训练, 且计算结果过度依赖训练样本, 难以应用到实际问题中. 上述基于数学统计的方法拥有较好的运行效率, 但准确性较基于HVS感知特性的方法存在不足. 在基于HVS感知特性的方法中, 具有代表性的SSIM^[5]方法假设人类对于一个场景的视觉感知可以用提取结构信息进行表征, 其主要提取信息包括亮度、对比度和结构. 该方法因其设计思路的新颖性和特征信息的计算方式, 为后续相关研究提供很多启发和思路. 这种基于SSIM计算方式的图像质量评价模型也被叫做全参考图像质量评价模型. Sheikh和Bovik^[6]提出IFC^[7]及其衍生方法VIF (visual information fidelity), 这两个方法通过原始图像和失真图像的交互信息保真度进行比较和计算, 虽然其性能较SSIM有所提升, 但计算效率较差, 难以广泛应用. 基于SSIM模型, 其他研究者又提出很多扩展模型. 其中具有代表性的模型有: 加入HVS多尺度特性的MS-SSIM(multi-scale SSIM)方法^[8]; 根据图像全局信息分布, 通过信息加权的方式得到的IW-SSIM(information content weighted SSIM)方法^[9]. Larson和Chandler^[10]基于最明显失真统计提出MAD(most apparent distortion algorithm)方法, 该方法的不足是计算复杂性较高. Zhang等^[11,12]针对人类视觉系统对图像的理解主要依赖于图像的底层特征的特点, 提出了两种新的基于特征相似度的全参考图像质量评价指标RFSIM (riesz transforms based feature similarity index)和FSIM (feature similarity). 在FSIM中, 作者针对灰度图像将相位一致性(phase congruency)和梯度幅值(gradient magnitude)结合, 并使用权重系数获得单位质量分数; 此外, 为解决彩色图像评价问题, 加入色度算子, 引申出FSIMc模型. 基于梯度结果, Liu等^[13]提出GSM (gradient similarity metric)方法. 上述提到的RFSIM, FSIMc和GSM方法的精度较好, 但计算泛化性能欠佳. 近年, 基于对比度和视觉显著性, Jia等^[14]提出CVSS (contrast and visual saliency similarity)方法, 该方法评价灰度图像的性能较好, 但是针对日常生活在的彩色图像, 性能仍有不足. Yao等^[15]基于图像内容对比度感知特性, 提出MPCC (IQA model based on the perception of the contrast of image contents)方法.
一般来说, 上述较好的模型在空间和频率域描述了结构信息、亮度信息、对比度信息和颜色信息. 通过上述分析, 可以发现目前的IQA模型在设计方法、复杂性和泛化性能仍有不足. 所以, 本文选择基于HVS感知特性构建图像质量客观评价模型, 以基本物理理论为基础, 构建具有较高的精度、泛化性和较低计算复杂度模型. 目前常见的全参考模型在进行特征相似计算时(如前文中提到的IW-SSIM, RFSIM, FSIMc, GSM、CVSS等模型), 多参照SSIM的计算方式, 本文也是参考SSIM进行相似计算全参考图像质量评价模型.
通常情况下, 彩色图像的质量可以通过在单个RGB通道上使用灰度模型, 然后连接通道分数来评估. 由于这种方法的精度有限, 因此需要提出更精细的利用颜色感知特性的模型. 此外, 彩色图像的质量可以用类似于比色法的方法来评估. 均匀的颜色空间(如CIELAB)可以描述成对颜色之间感知到的颜色差异^[16,17]. CIELAB中的圆柱极坐标与刺激的颜色属性相关. 因此, 利用该公式可以更好地在像素级表征彩色图像的感知失真. 虽然这些公式对比较均匀色块很有用, 但需要通过优化, 与复杂的真实图像数据保持一致. 随着人眼对色彩表象的感知能力的不断提高, 一些新的模型被提出, 并利用相似计算公式对这些模型进行修正. Lee和Plataniotis^[18,19]提出了基于正常三通道色貌指标的IQA方法(即亮度、色调和色度), 从而获得较好的彩色图像评价性能. 因为色貌指标可以代表彩色图像在HVS感知方式下的颜色偏差, 所以为了获得与主观评价更高的一致性, 可以考虑选择色貌指标评价图像的色彩信息.
前文已提到多种图像特征信息, 为了获得图像的质量分数, 需要选择合适的特征. 本文提出了一种新的基于相似性的IQA模型, 该模型主要提取图像的色彩信息和结构信息两个部分. 结合HVS对于色彩感知和图像轮廓特征的机理, 选择色貌和梯度两个指标提取上述两个特征信息, 并量化得到对应的图像质量分数. 目前, 彩色图像已应用于很多领域, 所以色彩信息需要在图像质量评价时重点考虑. 色貌新指标(vividness和depth)^[20]考虑色度和亮度的同步变化, 更符合人眼视觉感知的机理, 可以体现图像质量的色彩特征变化. 除此之外, 选择vividness指标作为所提模型的权重系数, 进一步突出所提模型对于色彩信息的重视. 梯度是目前常用的图像结构特征的提取算子, 作为补充特征, 可以完善所提模型对于图像质量的评价. 通过仿真测试, 与其他典型的模型相比, 所提模型具有更低的复杂度和更好的预测效果.

本节提出基于色貌和梯度相似(color appearance and gradient similarity, CAGS)方法来量化彩色图像的感知视觉质量. 该模型是具有通用性, 对于常见的彩色和灰度图像始终表现良好的评价效果. 该模型的输入图像是两个具有相同空间分辨率的RGB图像(X和Y), 分别称为原始图像和失真图像. 同时, 它们在尺寸上匹配并且正确对齐. 输出质量评分记为CAGS(X, Y), 其范围在0到1之间(当两幅图像完全相同时, 1表示最佳质量评分).
该模型包含两个相似图, 一个是利用CIELAB颜色空间中的色貌相似图来测量颜色失真, 色貌分布图可以在像素级上表示两幅图像之间的颜色差异, 与HVS感知更加兼容^[20]. 对于结构失真, 由于梯度具有的优越性^[12,13], 所以可以利用梯度推导出另一个相似图. 最后, 基于文献^[12,21]提到的权重系数方法, 将上述两个相似图进行合并和池化.
2

-->

2.1.色貌相似图

为了更好地表征HVS感知到的图像色貌, 可以将原始的RGB图像转化为更符合人类视觉的颜色空间, 使用CIELAB色空间. 由于CIELAB色空间和孟塞尔系统之间紧密联系, 同时分离成亮度(L^*)和色度(a^*, b^*或$C_{ab}^*$, $ H_{ab}^* $), 限制了CIELAB在实际应中描述颜色在明度和色度共变时的有效性, 例如在艺术、设计、比较着色剂效果和彩色图像评估等领域. 因此, 两个新的CIELAB色貌指标被提出, 即vividness和depth, 来扩展CIELAB作为色貌变量的有效性, 如图1所示^[20]. 从图1中可以发现, 为了区分两个颜色, 需要对两个颜色的对应参数进行比较, 上述两个色貌指标除了可以表征亮度和色度特性以外, 还可以作为色貌坐标, 计算颜色差别. 经过色空间从RGB到CIELAB变换后, X的每个像素包含三个颜色分量: 亮度通道L*、红绿通道a*和蓝黄通道b*, 并通过(1)式和(2)式计算得到vividness($ V_{ab}^* $)图和depth($ D_{ab}^* $)图.
图 1 颜色1和2的vividness($ V_{ab}^* $)和depth($ D_{ab}^* $)维度表征, 线段长度定义对应属性^[20]
Figure1. Dimensions of vividness, $ V_{ab}^* $, and depth, $ D_{ab}^* $ for colors 1 and 2. Line lengths define each attribute^[20].

$V_{ab}^* \!=\! \sqrt{(L^*)^2 \!+\! (a^*)^2 \!+\! (b^* )^2} \!=\! \sqrt{(L^*)^2 \!+\! (C_{ab}^*)^2}, $

$\begin{split}D_{ab}^ * =\;& \sqrt {{{\left( {100 - {L^ * }} \right)}^2} + {{\left( {{a^ * }} \right)}^2} + {{\left( {{b^ * }} \right)}^2}} \\=\;& \sqrt {{{\left( {100 - {L^ * }} \right)}^2} + {{\left( {C_{ab}^ * } \right)}^2}} .\end{split}$

为了量化颜色分量中的视觉失真, 使用了两个色度描述符: vividness相似图S_V和depth相似图S_D. 根据(1)式和(2)式, 原始图像X和失真图像Y的局部色貌分布图由V₁和D₁, V₂和D₂表示. 图2是一个选自LIVE数据库的例子, 图2(a)为参考图像, 图2(b)为高斯模糊失真后的图像. 图2(c)、图2(d)、图2(e)和图2(f)分别是对应参考图像和失真图像的V₁, V₂, D₁和D₂图像. 然后, 根据SSIM相似计算的方式将被比较的两幅图像的色貌相似图定义为
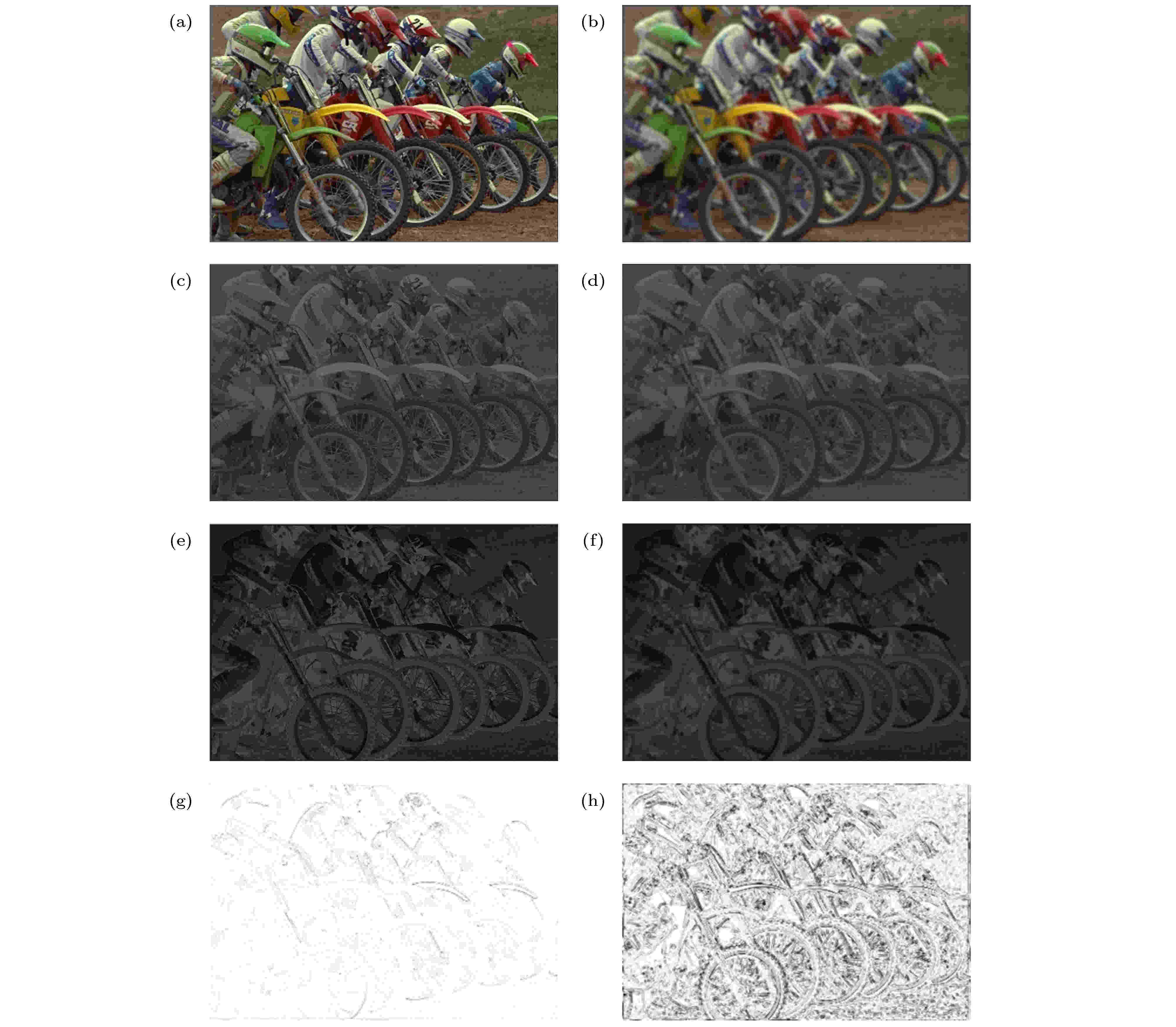图 2 从LIVE数据库中提取的典型图像　(a)为参考图像; (b)为高斯模糊畸变类型的失真图像; (c)和(e)分别是参考图像的Vividness和Depth图; (d)和(f)分别是失真图像的Vividness和Depth图; (g)是色貌相似图; (h)为梯度相似图
Figure2. Typical images extracted from LIVE: (a) The reference image;(b) the distorted vision of it by Gaussian blur distortion type; (c) and (e) are the vividness and depth map of the reference image, respectively; (d) and (f) are the vividness and depth map of the distorted image; (g) the color appearance similarity map by connecting the vividness and depth similarity map; (h) the gradient similarity map.

${S_V} = \frac{{2{V_1} \cdot {V_2} + {K_V}}}{{V_1^2 + V_2^2 + {K_V}}}, $

${S_D} = \frac{{2{D_1} \cdot {D_2} + {K_D}}}{{D_1^2 + D_2^2 + {K_D}}}, $

其中K_V和K_D都是常量, 增加模型的稳定性, 保证分母不为0 ^[5]. 将vividness相似图S_V和depth相似图S_D通过简单幂函数相乘的方式结合, 可以得到原始图像X和失真图像Y的色貌相似图S_CA, 如下式所示:

${S_{{\rm{CA}}}} = {\left( {{S_V}} \right)^\alpha } \cdot {S_D}, $

其中α表征两个色貌指标在色貌相似计算中的相对权重, 区间是[0, 1]. 较大的α值, 表示vividness在色貌相似计算中的相对权重越高. 为了说明色貌指标的有效性, 图2(g)是连接vividness相似图和depth相似图的色貌相似图. 图2(g)中颜色较深的点, 表征该区域的图像色彩差别越大. 从图2(g)中可以清楚地看到, 色貌相似图可以有效表征失真图像与参考图像之间的差别.
2 -->

2.2.梯度相似图

目前, 有几种不同的算子可以计算图像梯度, 如Prewitt算子^[22]、Sobel算子^[22]、Roberts算子^[23]和Scharr算子^[23]. 离散域梯度幅值的计算通常是基于上述算子, 并利用差值表示图像函数. 图像X的垂直梯度G_y和水平梯度G_x计算方式是利用卷积得到: $G_x=h_x \ast X$和$G_y={{h}}_{{y}} * {{X}}$(参见(6)式和(7)式), 其中h_x和h_y分别为水平和垂直梯度算子, *表示卷积. 则梯度的定义是$G\left(x\right)= \sqrt{{G}_{x}^{2}+{G}_{y}^{2}}$. 在提出的IQA模型中, 这些计算方式的执行效果是相同的. 梯度表征结构信息的原理是通过梯度算子的卷积处理图像, 保留包含显著边缘区域的信息, 去除平滑区域的信息.

${G_x} = \frac{1}{{16}}\left[ {\begin{array}{*{20}{c}} 3&0&{ - 3} \\ {10}&0&{ - 10} \\ 3&0&{ - 3} \end{array}} \right] * X, $

${G_y} = \frac{1}{{16}}\left[ {\begin{array}{*{20}{c}} 3&{{\rm{1}}0}&3 \\ 0&0&0 \\ { - 3}&{ - {\rm{1}}0}&{ - 3} \end{array}} \right] * X.$

在本文中, 经过前期梯度算子的比较, 发现Scharr在本文模型中可以更大程度地提取结构信息, 获得较好的结果. 因此, Scharr算子被选择用来计算参考图像和失真图像CIELAB色空间亮度(L^*)通道的梯度(G₁和G₂). 通过这两个梯度, 可以得到两个图像的梯度相似图S_G, 其计算公式如下所示:

${S_G} = \frac{{2{G_1} \cdot {G_2} + {K_G}}}{{G_1^2 + G_2^2 + {K_G}}}, $

其中参数K_G为控制数值稳定性的常数. 梯度相似图(S_G)在文献[24—26]中被广泛应用, 并研究了它在图像失真测量中的作用. 如图2(h)所示, 图中颜色较深的点, 表征该区域的图像结构差别越大. 因此, 梯度相似图是对HVS结构信息的一种有效表征.
2 -->

2.3.CAGS方法

根据前文提取的色貌相似和梯度相似图, 在IQA任务中定义一个新的模型—色貌和梯度相似指标(color appearance and gradient Similarity index, CAGS), 其程序代码请参见https://github.com/AlAlien/CAGS, 计算公式如下所示:

${\rm{CAGS}} = \frac{{\displaystyle\sum\nolimits_\varOmega {{S_G} \cdot {S_{CA}} \cdot {V_m}} }}{{\displaystyle\sum\nolimits_\varOmega {{V_m}} }}, $

其中Ω表示空间域; V_m (V_m = max (V₁, V₂))用于表征两个图像的局部重要性权重.
人们普遍认为, 不同的位置对HVS图像质量的视觉感知有不同的贡献, 因此, 在得到最终质量分数时可以考虑视觉系统的注视点. 由于人类视觉皮层对亮度和色度很敏感, 所以某个位置的vividness值可以反映出它是一个可感知的重要点的权重大小. 由于上述原因, 在提出的模型中选择色貌分布图(V_m)来描述局部区域的视觉重要性. CAGS的计算过程如图3所示. 本文所提模型, 以色貌特征为基础, 结合梯度特征, 表征图像质量. 色貌特征处理图像颜色信息差别, 梯度特征计算图像结构信息的不同, 通过颜色信息和结构信息的综合计算, 得到图像的客观评分.
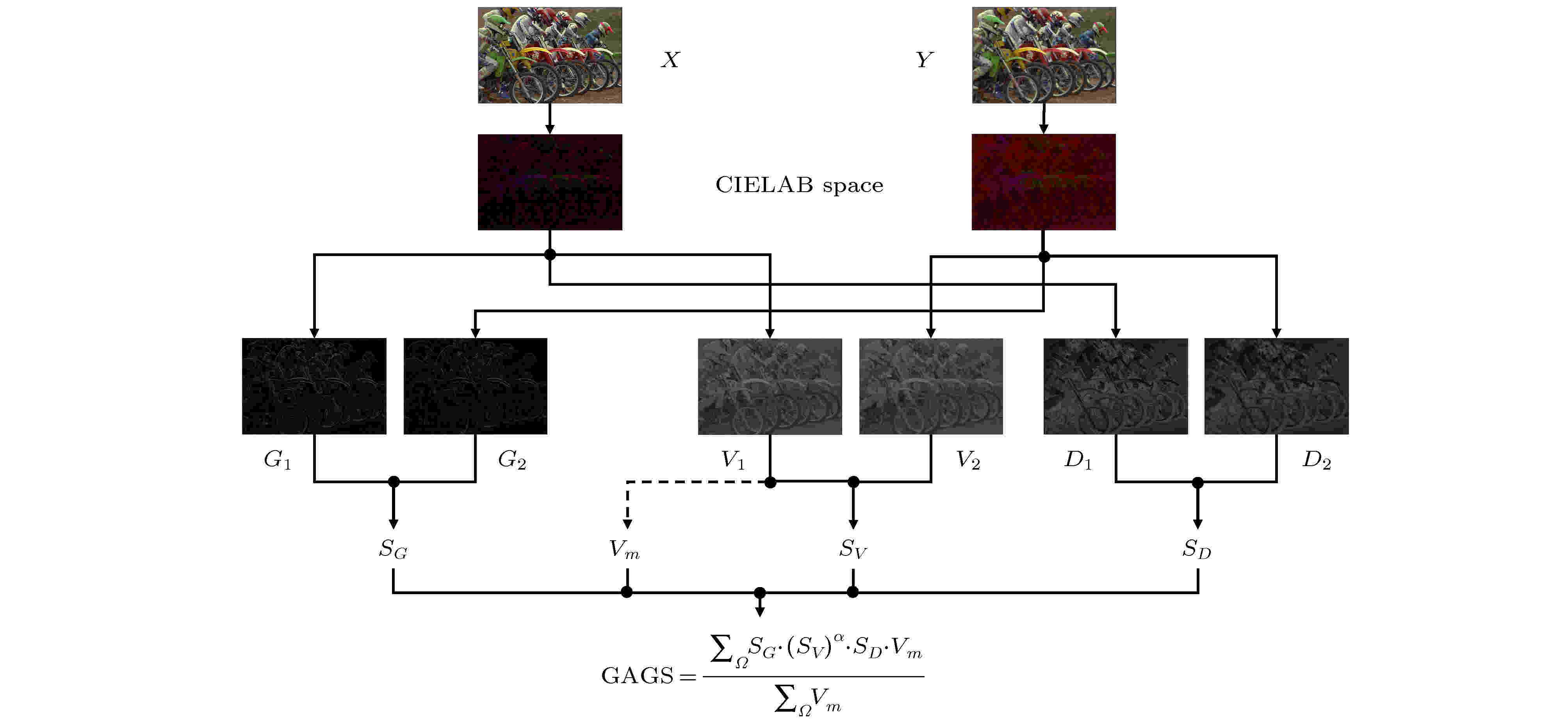图 3 本文提出的IQA模型CAGS的计算过程
Figure3. Illustration for the computational process of the proposed IQA model CAGS.

在本文中, K_V, K_D, K_G均为常数, 可以方便地应用于所有数据库. 此外, α为了应用于所有数据库也需要确定. 在以往的研究中, 试错法是处理这类问题的一种常用方法, 但在时间和消耗上都不现实. 近年来, Taguchi等^[27]实验设计方法被广泛应用于解决多参数寻优问题. 后续, 将使用Taguchi方法优化模型中的相关参数.

2

-->

3.1.性能评价标准和参考数据库

在我们的研究中, 选择4个公共数据库进行模型验证和比较, 即TID2013^[28], CSIQ^[29], LIVE^[30]和IVC^[31], 表1列出了上述每个数据库的基本信息. 这4个数据库是IQA研究中最常用的集合, 涵盖了现实应用中常见的各种失真. 它们用主观的评价来表征图像质量(MOS或DMOS), 可以作为设计的模型进行合理的基准测试. 上述数据库中的失真图像是从一组原始图像处理得到的, 这些原始图像反映了足够的颜色复杂性和边缘/纹理细节的多样性, 包括人类、自然场景和人造物体的图片.

数据库	原始图像数量	失真图像数量	失真类型	观察者
TID2013	25	3000	24	971
CSIQ	30	866	6	35
LIVE	29	779	5	161
IVC	10	185	4	15

表1IQA数据库基本信息
Table1.Benchmark test databases for IQA.

为了评估一个模型是否能够预测人类观察者的感知, 将使用客观评价模型计算出的图像质量分数与观察者所评定的值进行拟合. IQA模型常用的四个评价标准是: Spearman秩序相关系数(Spearman rank-order correlation coefficient, SROCC)、Pearson线性相关系数(Pearson linear correlation coefficient, PLCC)、Kendall秩序相关系数(Kendall rank-order correlation coefficient, KROCC)和均方根误差(root mean squared error, RMSE)^[2,32].
为了计算PLCC和RMSE指标, 采用logistic回归得到与主观判断相同的量表值:

$p\left( s \right) = {\beta _1}\left[ {\frac{1}{2} - \frac{1}{{1 + \exp \left( {{\beta _2}\left( {s - {\beta _3}} \right)} \right)}}} \right] + {\beta _4}s + {\beta _5}, $

其中β₁, ···, β₅都是拟合参数, s代表原始IQA分数, p(s)是回归后的IQA分数^[30].
2 -->

3.2.参数优化

Taguchi方法是Taguchi和Konishi共同开发的一种有效的实验设计工具^[33]. 根据前文的分析, 为了适用于所有数据库, K_V, K_D, K_G和α是CAGS模型优化的主要变量参数. 根据相关研究, 将各影响因素的水准数及各水准的值选取在适当的范围内, 如表2所列. 对于每个参数, 都选择了3个值. 两个色貌相似度对应参数应该确定相同的水准值, 这些值的选择基于文献[34]. 为了得到梯度相似图的最佳相关系数, 可以在[0, 100]中设置K_G^[26], 因此定义水准值为10, 50和100. 相对权重参数α, 应该限制在[0, 1], 所以选择0.1, 0.5, 1作为水准值.

代号	参数表述	水准数	水准一	水准二	水准三
A	KV	3	0.002	0.02	0.2
B	KD	3	0.002	0.02	0.2
C	KG	3	10	50	100
D	α	3	0.1	0.5	1

表2变量参数及其控制水准
Table2.Influence factors and level setting for CAGS.

选取参数和水准后, 在直交表中进行组合实验, 如表3所列. 采用试错法进行实验需要3⁴次, 而利用Taguchi方法设计实验只需进行9次即可, 大大减少了实验时间. 直交表配置为L₉(3⁴)型. 选择IVC数据库作为优化参数的参考集, 表征量化质量特征的SROCC, RMSE值及其S/N(signal to noise)值均包含在表3中. 较大的S/N值表征其对应的水准具有较好评价效果. 对于SROCC来说, 性能具有望大性, 即数值越大表征效果越好. 因此, SROCC的S/N值(ε₁)可以根据(11)式计算. 相反, RMSE应该越少越好. 因此, RMSE的S/N值(ε₂)可以根据(12)式计算.

实验序号	A	B	C	D	SROCC	SROCC的S/N	RMSE	RMSE的S/N
1	1	1	1	1	0.9300	–0.6303	0.4113	7.7168
2	1	2	2	2	0.9192	–0.7318	0.4533	6.8723
3	1	3	3	3	0.9096	–0.8230	0.4825	6.3301
4	2	1	2	3	0.9171	–0.7517	0.4596	6.7524
5	2	2	3	1	0.9173	–0.7498	0.4672	6.6099
6	2	3	1	2	0.9291	–0.6388	0.4142	7.6558
7	3	1	3	2	0.9114	–0.8058	0.4735	6.4936
8	3	2	1	3	0.9279	–0.6500	0.4174	7.5890
9	3	3	2	1	0.9195	–0.7290	0.4481	6.9725

表3采用L₉(3⁴)直交表的实验设计及IVC数据库测试结果
Table3.Design with a L₉(3⁴) orthogonal array for IVC database.

${\varepsilon _{\rm{1}}} = {\rm{ - 10}}\log \frac{{\displaystyle\sum\nolimits_{i = 1}^t {\left( {{{\rm{1}} / {{q_i}^2}}} \right)} }}{t}, $

${\varepsilon _{\rm{2}}} = {\rm{ - 10}}\log \frac{{\displaystyle\sum\nolimits_{i = 1}^t {\left( {{q_i}^2} \right)} }}{t}, $

其中q_i表示与第i次试验对应的SROCC和RMSE的值; t为每次试验的总数.
特定的参数组合对SROCC和RMSE两个评价标准的影响可以通过计算该特定参数的水准三次实验相应的平均S/N值来评估. 不同水准值对应的S/N值可以在图4中清晰地识别出来, 其值越高表明该水准对应的评价效果越好.
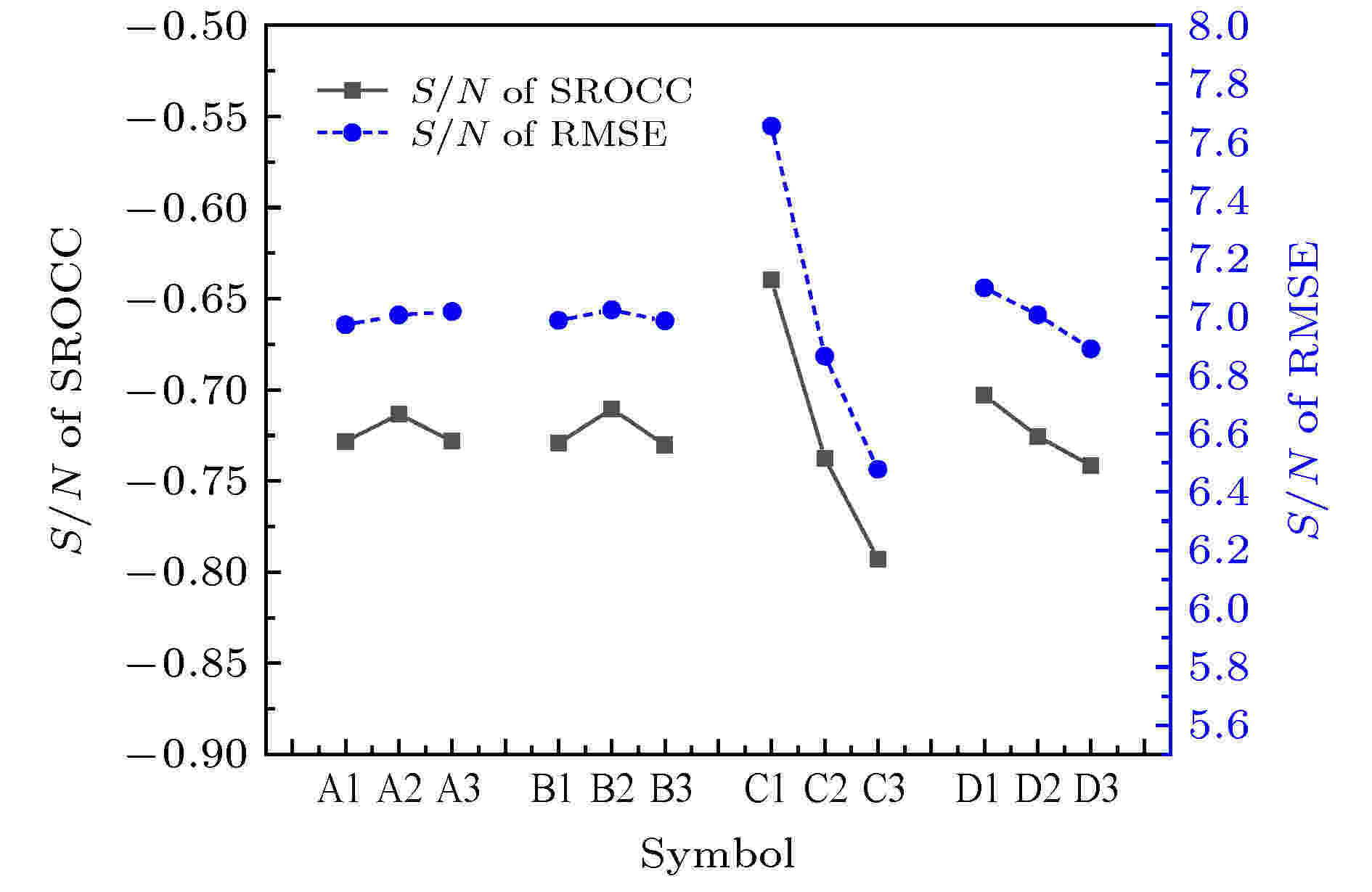图 4 SROCC和RMSE对应的不同水准的S/N值
Figure4. S/N ratio of different levels for SROCC and RMSE.

从图4可以得到下述直观合理的结果. 例如, 较小的参数C值, 可以获得较大的S/N值; 同时因其对应的S/N值变化幅度最大, 表明其影响程度也是最大的. 对于其他3个参数, 最佳组合为A2-B2-D1. 对于参数C, 由于其影响程度最大, 需要将其进一步调整为更合适的值, 以达到更好的拟合程度.
使用本文提出的CAGS方法, 通过计算四种数据库在不同K_G下SROCC, PLCC和KROCC的加权平均值(根据每个数据库中失真图像的数量分配不同的权重)和直接平均值, 确定K_G值, 如图5所示. 从图5中可获得最佳的K_G值, 所以最终CAGS模型的最佳参数是K_V = K_D = 0.02, K_G = 50, α = 0.1.
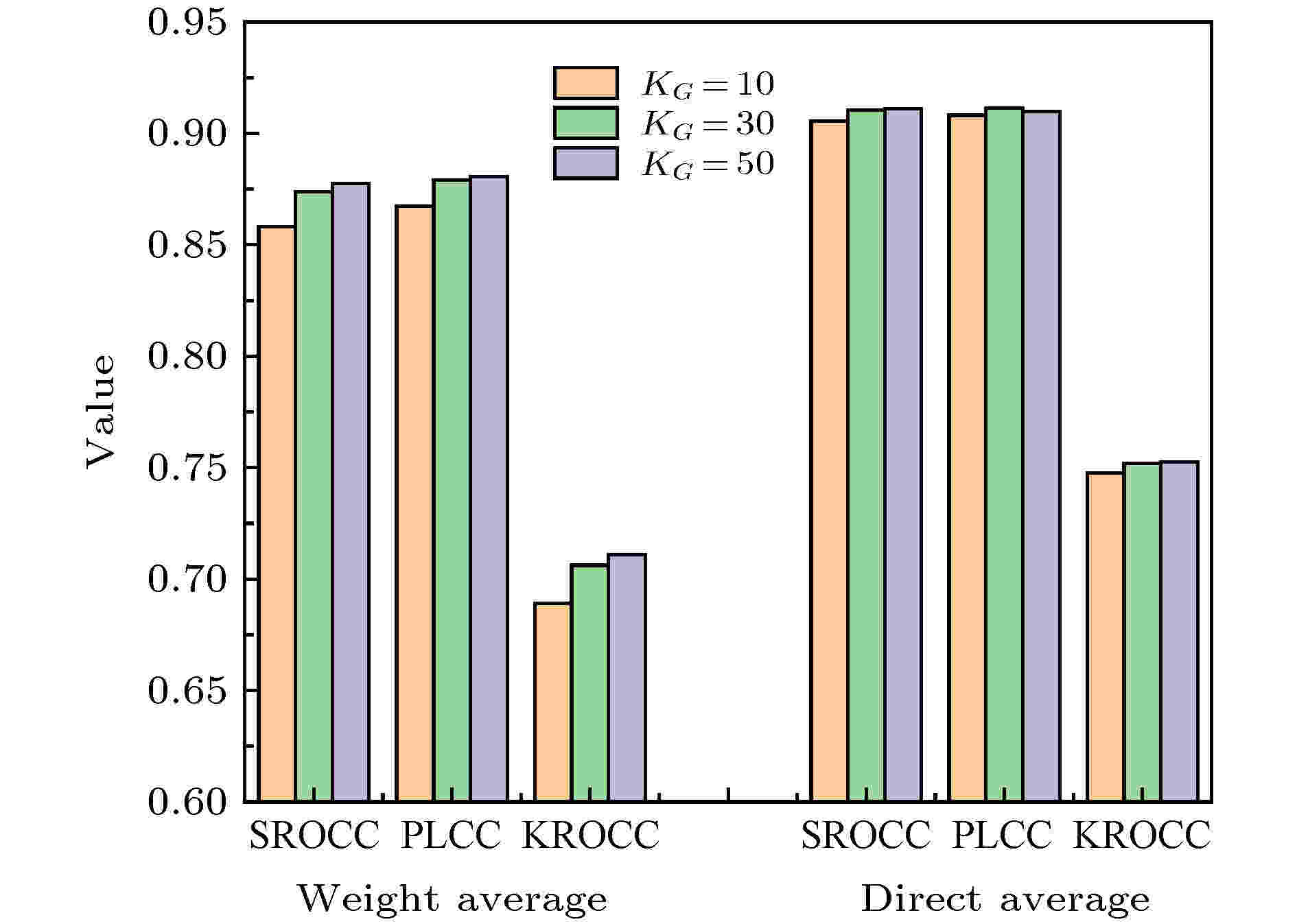图 5 不同K_G值对模型性能的影响
Figure5. Performance of different K_G values.

2

-->

4.1.IQA模型的性能对比

一个理想的IQA模型应该具有良好的性能, 并且在不同类型的失真情况下具有良好的一致性. 本节将所提出的模型与其他典型的模型进行了比较, 包括SSIM^[5], IW-SSIM^[9]、IFC^[6], VIF^[7], MAD^[10], RFSIM^[11], FSIMc^[12]和GSM^[13], 以及近年提出的方法CVSS(2018)^[14]和MPCC(2020)^[15]. 表4中, 4个数据库中每个评价指标对应最好的3个结果使用粗体突出显示. 此外, 根据Wang和Li^[9], 4个数据库的SROCC, PLCC和KROCC结果的加权和直接平均值也如表4所列, 以评估整体性能. 每个数据库的权值是根据数据库中包含的失真图像的数量确定的.

数据库		SSIM	IW-SSIM	IFC	VIF	MAD	RFSIM	FSIMC	GSM	CVSS	MPCC	Proposed
TID2013	SROCC	0.7417	0.7779	0.5389	0.6769	0.7807	0.7744	0.8510	0.7946	0.8069	0.8452	0.8316
	PLCC	0.7895	0.8319	0.5538	0.7720	0.8267	0.8333	0.8769	0.8464	0.8406	0.8616	0.8445
	RMSE	0.7608	0.6880	1.0322	0.7880	0.6975	0.6852	0.5959	0.6603	0.6715	0.6293	0.6639
	KROCC	0.5588	0.5977	0.3939	0.5147	0.6035	0.5951	0.6665	0.6255	0.6331	—	0.6469
CSIQ	SROCC	0.8756	0.9213	0.7671	0.9195	0.9466	0.9295	0.9310	0.9108	0.9580	0.9569	0.9198
	PLCC	0.8613	0.9144	0.8384	0.9277	0.9502	0.9179	0.9192	0.8964	0.9589	0.9586	0.9014
	RMSE	0.1334	0.1063	0.1431	0.0980	0.0818	0.1042	0.1034	0.1164	0.0745	0.0747	0.1137
	KROCC	0.6907	0.7529	0.5897	0.7537	0.7970	0.7645	0.7690	0.7374	0.8171	—	0.7487
LIVE	SROCC	0.9479	0.9567	0.9259	0.9636	0.9669	0.9401	0.9599	0.9561	0.9672	0.9660	0.9734
	PLCC	0.9449	0.9522	0.9268	0.9604	0.9675	0.9354	0.9503	0.9512	0.9651	0.9622	0.9640
	RMSE	8.9455	8.3473	10.2643	7.6137	6.9073	9.6642	7.1997	8.4327	7.1573	7.4397	8.3251
	KROCC	0.7963	0.8175	0.7579	0.8282	0.8421	0.7816	0.8366	0.8150	0.8406	—	0.8658
IVC	SROCC	0.9018	0.9125	0.8993	0.8964	0.9146	0.8192	0.9293	0.8560	0.8836	—	0.9195
	PLCC	0.9119	0.9231	0.9093	0.9028	0.9210	0.8361	0.9392	0.8662	0.8438	—	0.9298
	RMSE	0.4999	0.4686	0.5069	0.5239	0.4746	0.6684	0.4183	0.6088	0.6538	—	0.4483
	KROCC	0.7223	0.7339	0.7202	0.7158	0.7406	0.6452	0.7636	0.6609	0.6957	—	0.7488
权重平均	SROCC	0.8051	0.8376	0.6560	0.7750	0.8456	0.8306	0.8859	0.8438	0.8628	—	0.8737
	PLCC	0.8321	0.8696	0.6786	0.8353	0.8752	0.8650	0.8987	0.8730	0.8820	—	0.8772
	KROCC	0.6270	0.6662	0.5002	0.6158	0.6819	0.6575	0.7160	0.6775	0.7020	—	0.7044
直接平均	SROCC	0.8668	0.8921	0.7828	0.8641	0.9022	0.8658	0.9178	0.8794	0.9039	—	0.9111
	PLCC	0.8769	0.9054	0.8071	0.8907	0.9164	0.8807	0.9214	0.8901	0.9021	—	0.9099
	KROCC	0.6920	0.7255	0.6154	0.7031	0.7458	0.6966	0.7589	0.7097	0.7466	—	0.7526

表4对比不同IQA模型的4个数据库性能
Table4.Performance comparison of IQA models on four databases.

从表4可以看出, 我们提出的模型对所有数据库的性能都较好. 特别是, CAGS模型在LIVE和IVC数据库的排名前三名. 对于TID2013, CAGS模型具有竞争性, 与前三的差距很小. 对于CSIQ, CAGS模型仅比前三模型表现稍差. 虽然MAD, CVSS和MPCC可以从CSIQ中得到最好的结果, 但是它们的性能对其他三个数据库不如我们提出的模型的性能. 此外, CAGS模型还是三个指标加权和直接平均值的前三名. 综上, 获得前三数量最多的模型是FSIM (16次), CAGS (15次)和CVSS(14次). 而且, 对于所有数据库的SROCC和PLCC值均大于0.8316, 所以可以认为CAGS模型既具有较高的性能, 又具有较好的泛化性. 特别的, 由于MPCC模型代码未开源, 相关数据有所缺失, 所以表4仅提供可查阅的MPCC相关数据. 但与MPCC模型性能的比较中可以发现, CAGS模型与MPCC模型的性能差距较小, 与当前最新的研究结果相比具有竞争性.
为了更好地说明所提出的IQA模型在不同类型的失真情况下具有更好的性能, 使用TID2013数据库的散点图进行比较, 如图6所示. 从图6中可以看出, 与其他模型相比, CAGS模型的客观评分与主观评分之间存在着高度的相关性.
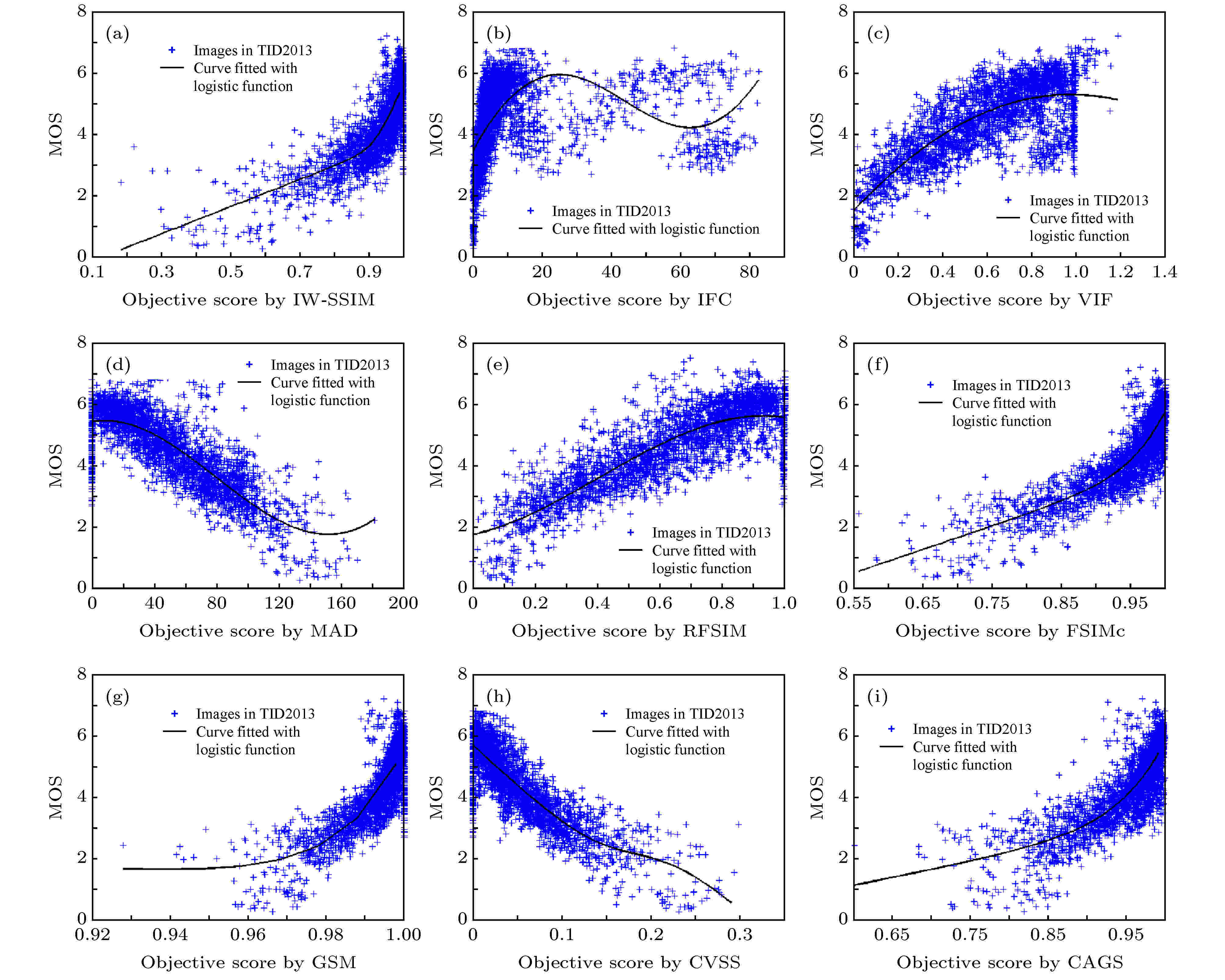图 6 基于TID2013数据库的主观MOS与IQA模型计算结果拟合对比　(a) IW-SSIM; (b) IFC; (c) VIF; (d) MAD; (e) RFSIM; (f) FSIMc; (g) GSM; (h) CVSS; (i) CAGS
Figure6. Scatter plots of subjective MOS against scores calculated by IQA models’ prediction for TID2013 databases: (a) IW-SSIM; (b) IFC; (c) VIF; (d) MAD; (e) RFSIM; (f) FSIMc; (g) GSM; (h) CVSS; (i) CAGS.

出现上述结果的原因主要有: 1) CAGS模型结合HVS特性, 同时提取色度信息和结构信息, 并利用权重系数表征局部重要性, 所以其较其他模型具有较好的性能和泛化性; 2) 在颜色信息提取方面, 考虑亮度和色度的协同变化, 提高了颜色信息提取的准确性, 更好的表征图像失真程度.
2 -->

4.2.IQA模型对不同失真类型的性能对比

一个稳定IQA模型需要产生良好的性能, 才能对每种失真类型进行一致的预测. 在本节中, 对每种失真类型的模型性能进行了对比, 结果如表5所列. 选择SROCC作为评价指标, 因为其他指标(PLCC, RMSE和KROCC)具有类似的效果. 由于IVC数据库中每种失真类型的失真图像的数量太少, 无法用统计的方式表达结果. 因此, 选取了三个主要数据库中的35组失真图像. 对于每个数据库和每种失真类型, 排名前三SROCC值的IQA模型的结果用粗体突出显示. 进一步, 对于最新MPCC模型, 与CAGS对比TID2013数据库PLCC的结果, 如图7所示.

数据库	失真类型	SSIM	IW-SSIM	IFC	VIF	MAD	RFSIM	FSIMC	GSM	CVSS	MPCC	Proposed
TID2013	AGN	0.8671	0.8438	0.6612	0.8994	0.8843	0.8878	0.9101	0.9064	0.9401	0.8666	0.9359
	ANC	0.7726	0.7515	0.5352	0.8299	0.8019	0.8476	0.8537	0.8175	0.8639	0.8187	0.8653
	SCN	0.8515	0.8167	0.6601	0.8835	0.8911	0.8825	0.8900	0.9158	0.9077	0.7396	0.9276
	MN	0.7767	0.8020	0.6932	0.8450	0.7380	0.8368	0.8094	0.7293	0.7715	0.7032	0.7526
	HFN	0.8634	0.8553	0.7406	0.8972	0.8876	0.9145	0.9094	0.8869	0.9097	0.8957	0.9159
	IN	0.7503	0.7281	0.6208	0.8537	0.2769	0.9062	0.8251	0.7965	0.7457	0.6747	0.8361
	QN	0.8657	0.8468	0.6282	0.7854	0.8514	0.8968	0.8807	0.8841	0.8869	0.7931	0.8718
	GB	0.9668	0.9701	0.8907	0.9650	0.9319	0.9698	0.9551	0.9689	0.9348	0.9218	0.9614
	DEN	0.9254	0.9152	0.7779	0.8911	0.9252	0.9359	0.9330	0.9432	0.9427	0.9510	0.9466
	JPEG	0.9200	0.9187	0.8357	0.9192	0.9217	0.9398	0.9339	0.9284	0.9521	0.8964	0.9585
	JP2 K	0.9468	0.9506	0.9078	0.9516	0.9511	0.9518	0.9589	0.9602	0.9587	0.9160	0.9620
	JPTE	0.8493	0.8388	0.7425	0.8409	0.8283	0.8312	0.8610	0.8512	0.8613	0.8571	0.8644
	J2 TE	0.8828	0.8656	0.7769	0.8761	0.8788	0.9061	0.8919	0.9182	0.8851	0.8409	0.9250
	NEPN	0.7821	0.8011	0.5737	0.7720	0.8315	0.7705	0.7937	0.8130	0.8201	0.7753	0.7833
	Block	0.5720	0.3717	0.2414	0.5306	0.2812	0.0339	0.5532	0.6418	0.5152	0.5396	0.6015
	MS	0.7752	0.7833	0.5522	0.6276	0.6450	0.5547	0.7487	0.7875	0.7150	0.7520	0.7441
	CTC	0.3775	0.4593	0.1798	0.8386	0.1972	0.3989	0.4679	0.4857	0.2940	0.7814	0.4514
	CCS	0.4141	0.4196	0.4029	0.3009	0.0575	0.0204	0.8359	0.3578	0.2614	0.7054	0.3711
	MGN	0.7803	0.7728	0.6143	0.8486	0.8409	0.8464	0.8569	0.8348	0.8799	0.8766	0.8700
	CN	0.8566	0.8762	0.8160	0.8946	0.9064	0.8917	0.9135	0.9124	0.9351	0.8174	0.9168
	LCNI	0.9057	0.9037	0.8160	0.9204	0.9443	0.9010	0.9485	0.9563	0.9629	0.8095	0.9574
	ICQD	0.8542	0.8401	0.6006	0.8414	0.8745	0.8959	0.8815	0.8973	0.9108	0.8596	0.9060
	CHA	0.8775	0.8682	0.8210	0.8848	0.8310	0.8990	0.8925	0.8823	0.8523	0.8094	0.8768
	SSR	0.9461	0.9474	0.8885	0.9353	0.9567	0.9326	0.9576	0.9668	0.9605	0.9178	0.9580
CSIQ	AWGN	0.8974	0.9380	0.8431	0.9575	0.9541	0.9441	0.9359	0.9440	0.9670	0.9329	0.9652
	JPEG	0.9543	0.9662	0.9412	0.9705	0.9615	0.9502	0.9664	0.9632	0.9689	0.9564	0.9573
	JP2 K	0.9605	0.9683	0.9252	0.9672	0.9752	0.9643	0.9704	0.9648	0.9777	0.9630	0.9545
	AGPN	0.8924	0.9059	0.8261	0.9511	0.9570	0.9357	0.9370	0.9387	0.9516	0.9517	0.9492
	GB	0.9608	0.9782	0.9527	0.9745	0.9602	0.9643	0.9729	0.9589	0.9789	0.9664	0.9574
	CTC	0.7925	0.9539	0.4873	0.9345	0.9207	0.9527	0.9438	0.9354	0.9324	0.9399	0.9273
LIVE	JP2 K	0.9614	0.9649	0.9113	0.9696	0.9676	0.9323	0.9724	0.9700	0.9719	0.9608	0.9822
	JPEG	0.9764	0.9808	0.9468	0.9846	0.9764	0.9584	0.9840	0.9778	0.9836	0.9674	0.9836
	AWGN	0.9694	0.9667	0.9382	0.9858	0.9844	0.9799	0.9716	0.9774	0.9809	0.9457	0.9837
	GB	0.9517	0.9720	0.9584	0.9728	0.9465	0.9066	0.9708	0.9518	0.9662	0.9561	0.9641
	FF	0.9556	0.9442	0.9629	0.9650	0.9569	0.9237	0.9519	0.9402	0.9592	0.9627	0.9633

表5IQA模型的不同失真类型SROCC值对比
Table5.SROCC values of IQA models for different types of distortions.

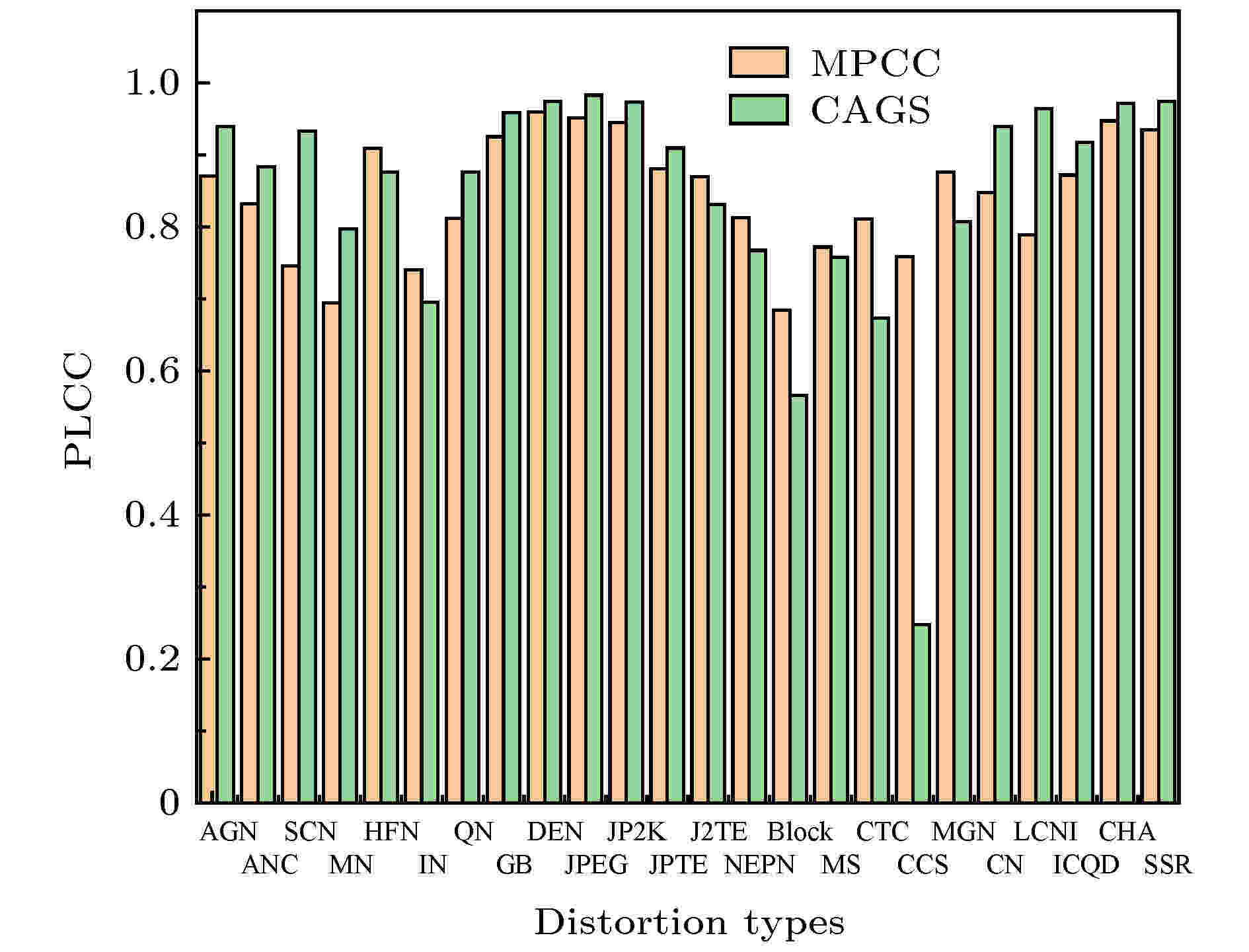图 7 CAGS与MPCC在TID2013数据库种不同失真类型PLCC值对比
Figure7. PLCC comparison of different distortion types between CAGS and MPCC on TID2013.

对比分析表5和图7中不同模型对于不同失真类型的失真图像评价结果, 可得: 1) CAGS模型与其他典型IQA模型相比具有明显的统计优势, 总体效果最好. 特别是, CAGS模型在TID2013和LIVE数据库的排名前三的数量较多. 而对于CSIQ, CAGS模型具有竞争性, 与前三的差距很小. 获得前三数量最多的模型是CAGS (21次), CVSS (19次)和FSIM (14次). 2) 对于35种失真类型, 每个模型的评价结果各有优势, 其中SROCC值大于0.95的数量最多模型是CAGS(14次)和CVSS(14次). 对于上述两个模型, 其最小SROCC值分别是0.3711和0.2614, 且SROCC值小于0.5都是2个类型(CTC和CCS). 所以, CAGS模型的波动程度更小, 性能更加稳定, 具有较好的泛化性. (3)对比CAGS和MPCC模型, SROCC值排名前三次数分别是21次和6次; SROCC值大于0.95次数分别是14次和9次; 在TID2013数据库不同失真类型的PLCC值, 在24种失真类型中, CAGS在15种失真类型中具有较高的精度; CAGS和MPCC的最小SROCC值分别是0.3711和0.5396; 对比结果表明CAGS比最新的MPCC模型具有明显的精度优势, 而MPCC具有更好的泛化性. 综上可以得出结论, 与其他IQA模型相比, CAGS模型预测的客观评分与主观评价高度相关.
通过以上对于不同失真类型的图像质量评价精度的对比分析, 表明CAGS模型在不同数据库中和在不同失真类型中都具有较好的精度和泛化性.
2 -->

4.3.不同模型间计算复杂性对比

IQA模型的运行效率也是一个重要的考虑因素. 使用2.5 GHz Intel Core i5 CPU和8 G RAM的型号电脑比较不同模型的运行时间, 软件平台为MATLAB R2013b. 表6列出了每个模型用于比较一对彩色图像的时间, 分辨率为512 × 512(选自IVC数据库). 由此表6结果可知, CGGS模型具有适中的计算复杂度. 具体来说, 它比一些具有良好预测性能的现代IQA模型运行得更快, 如IW-SSIM, IFC, VIF和MAD. 由于CAGS模型仅包含色度信息和结构信息两个方面的内容, 即可有效评价图像质量, 同时无需循环计算, 所以CAGS模型计算复杂度较低.

IQA模型	运行时间/s	IQA模型	运行时间/s
PSNR	0.0186	RFSIM	0.1043
SSIM	0.0892	FSIMc	0.3505
IW-SSIM	0.6424	GSM	0.1018
IFC	1.1554	CVSS	0.0558
VIF	1.1825	MPCC	—
MAD	2.7711	CAGS	0.4814

表6计算复杂度对比
Table6.Time cost comparisons.

我们提出了一种新颖且性能良好的IQA模型, 即CAGS模型. 该模型由色貌相似图和梯度相似图组成, 分别表征了颜色失真和结构失真. 其中, 色貌相似图由vividness和depth两部分组成, 这两部分是表征颜色特征的两个新指标. 同时, 选取vividness图作为权重系数, 定义局部图像的重要性. 最后, 根据权重关系将上述两个相似图合并得到所提模型. 模型中的主要参数通过Taguchi方法确定, 使用该方法可大大减少实验时间. 为了证明所提出的模型的优异性能, 使用4个常用的IQA数据库共94幅参考图像和4830幅失真图像进行测试, 与另外10个最典型的或被近期发表的IQA模型的结果进行了比较. 结果表明, CAGS模型的精度PLCC在4给数据库中最低实现0.8455, 最高可以达到0.9640, 综合性能优于其他IQA模型. 与其他计算复杂度适中的模型相比, CAGS模型具有更好的预测精度和泛化性. 未来, 我们将进一步优化模型, 提升预测精度和泛化性能.