摘要: 标度拓展经典负半阶分抗逼近电路, 可实现具有任意分数阶微积算子运算功能的分抗逼近电路, 但牺牲了运算恒定性. 从电路网络的角度分析具有恒定运算性能的负半阶Carlson分形格分抗逼近电路. 根据标度分形格分抗逼近电路的等效无源双口网络, 探讨该双口网络右侧端口的运算有效性, 设计具有高运算恒定性的任意阶标度分形格分抗逼近电路. 结合负实零极点对基元系统的零极点分布及其局域化特性, 阐述具有任意实数阶微积算子运算功能的标度分形格分抗逼近电路运算振荡现象的物理本质, 并从理论上分析有效抑制频域运算振荡现象的方法. 结合对称阻容T型节电路优化理论及方法, 对任意阶对称格型级联双口网络的频域逼近性能进行优化, 获得具有高逼近效益的任意阶标度分形格分抗逼近电路. 具有低振荡幅度的任意阶对称格型级联双口网络为高运算恒定性的分抗逼近电路设计及应用提供了一种新方法及思路.
关键词: 分数微积分 /
标度拓展 /
分数阶元件 /
运算恒定性 English Abstract Arbitrary-order high-operation constant fractance approximation circuit—lattice cascaded two-port network Zhang Yue-Rong Yuan Xiao College of Electronics and Information Engineering, Sichuan University, Chengdu 610065, China Received Date: 03 September 2020Accepted Date: 02 October 2020Available Online: 05 February 2021Published Online: 20 February 2021Abstract: Fractional calculus is widely used in the analysis and description of various nonlinear and non-integer dimensional physical phenomena and processes in nature, and it gradually becomes a research hotspot. The order value of fractional-order system is more flexible, and fractional-order system is more accurate for analysis of non-integer dimensional physical phenomena and processes. In recent years, various negative half-order fractance approximation circuits and rational approximation algorithms for negative half-order fractional operators have been proposed and aroused people's research interest. The scaling extension of classic negative half-order fractance approximation circuits can facilitate the design of fractance approximation circuits with arbitrary-order fractional operators, but the operational constancy is sacrificed. The typical arbitrary-order fractance approximation circuits have operational oscillating phenomena in frequency domain, both the order-frequency characteristic curves and the phase-frequency characteristic curves have obvious oscillating waveforms. The operational oscillating phenomena will inevitably affect the fractional operator operational performance of the fractance approximation circuits, and result in errors in physical application. In this paper, the negative half-order Carlson fractal-lattice fractance approximation circuit with constant operational performance is analyzed from perspective of circuit network, the symmetry for equivalent two-port network of Carlson fractal-lattice fractance approximate circuit is analyzed. The equivalent two-port network of scaling fractal-lattice fractance approximation circuit is explored, Operational validity for the right port of scaling lattice cascaded two-port network is studied. A symmetrical lattice cascaded passive two-port network after scaling extension is designed through cascade of the ports on both sides of two-port network, and an arbitrary-order scaling fractal-lattice fractance approximation circuit with high-operation constancy is designed. By studying the zero-pole distribution and localization characteristics of the negative real zero-pole pair elemental unit, the physical nature of operational oscillating phenomenon for scaling fractal-lattice fractance approximation circuit with the operational performance of arbitrary-order fractional operator is explained theoretically, the methods and ideas to effectively suppress frequency-domain operational oscillating phenomenon are theoretically analyzed. The physical nature of operational oscillating amplitude reduction is explained by contrastively analyzing the pole-zero distributions of scaling fractal-lattice fractance approximation circuit and symmetrical lattice cascaded two-port network. According to the optimization principle of arbitrary-order fractance approximation circuits, the symmetrical resistor-capacitor T-section circuit optimization methods are used to optimize the frequency-domain approximation performance of any real-order symmetrical lattice cascaded two-port network, and it contributes to obtain any real-order scaling fractal-lattice fractance approximation circuit with high benefit of approximation. Arbitrary-order symmetrical lattice cascaded two-port network provides methods and ideas for the design of fractance approximation circuits with high-operation constancy.Keywords: fractional calculus /scaling extension /fractional order element /operational constancy 全文HTML --> --> --> 1.引 言 分数阶微积分适用于描述自然界中大多数非线性, 非整数维物理现象及过程. 由于阶次取值更加灵活, 分数阶系统更能准确刻画非线性问题及其物理本质, 例如电化学分析[1 ,2 ] 、扩散过程[3 –5 ] 、信号处理[6 –8 ] 等. 分数阶微积分广泛应用于非线性控制系统[9 ,10 ] 、分数阶混沌系统[11 ,12 ] 及神经网络[13 ] 等各种非整数维物理过程的研究. 分数阶微积分用于扩散、概率、粘弹性动力学、遗传结构等非整数维物理现象的建模分析等. 分数阶电路元件或分抗逼近电路是实现分数阶电路与系统的关键组成部分, 现有的非整数阶分抗逼近电路几乎都具有不恒定的运算性能, 这势必会影响分数阶电路等物理系统的理论与应用研究的真实性[14 ] .[15 ] . 理想$ \mu $ 阶分抗元的阻抗函数为s 表示复频率变量也称运算变量, $ {F}^{\left(\mu \right)} $ 为理想分抗元的集总特征参量, 简称分抗量. 理想分抗元的具体实现还存在困难, 目前常用的方法是设计一个物理可实现的有理阻抗函数序列$ \left\{{Z}_{k}\left(s\right)\right\} $ 逼近理想分抗元的阻抗函数$ {I}^{\left(\mu \right)}\left(s\right) $ . 即k 表示分抗逼近电路的规模或迭代逼近次数, $ {n}_{k} $ 和$ {d}_{k} $ 分别为阻抗函数$ {Z}_{k}\left(s\right) $ 的分子分母多项式的次数, $ {\beta }_{ki} $ 和$ {\alpha }_{ki} $ 分别表示分子分母多项式系数. 现有的经典分抗逼近电路如负半阶Oldham分形链分抗逼近电路[16 ,17 ] , 任意阶梯形分抗逼近电路[18 ] , Liu-Kaplan分形链分抗逼近电路[19 ] 等, 都能在一定频段近似实现理想分抗的运算性能[20 ] . 这些电路都来自于自然界、科学与实验研究、工程实践中的各种物理现象与过程的分析和电路建模.$ {Z}_{k}(s) $ 进行归一化处理. 对于$ RC $ 分抗逼近电路取归一化复频率变量$ w=\tau s $ , 其中$ \tau =RC $ 表示时间常数. 对(2 )式中的$ {Z}_{k}\left(s\right) $ 进行归一化, 得到归一化阻抗函数$w= {\rm{j}}{10}^{\varpi }$ , 其中$ {\rm{j}}=\sqrt{-1} $ , $ \varpi \in {\mathbb R} $ 表示归一化频率指数变量, 简称频率变量. 将$ w={\rm{j}}{10}^{\varpi } $ 代入归一化阻抗函数$ {y}_{k}\left(w\right) $ , 得到幅频、相频、阶频、F频特征函数分别为:$ {s}^{-1/n} $ 的正则迭代逼近法. 袁晓[14 ] 将Carlson正则迭代法推广为任意阶分数算子的有理逼近, 何秋燕等[21 –23 ] 对其运算性能与逼近性能做了详细分析. 结合标度拓展[24 ] 理论, 负半阶Carlson分形格分抗标度拓展后可获得具有任意实数阶微积算子运算功能的标度分形格分抗逼近电路[25 ,26 ] , 袁晓[14 ] 、He等[23 ] 和Pu等[27 ] 提出任意阶格型标度分忆抗元等新概念及模拟电路实现. 这些成果表明, Carlson格型结构的分抗逼近电路具有许多优良的物理性质. 分析任意阶标度分形分抗逼近电路的频域特征, 发现标度拓展后的电路在频域存在固有运算振荡现象[27 ] . 这些典型的任意阶分抗的阶频特征曲线、相频特征曲线都有明显的振荡波形. 运算特征曲线的波动反映分抗逼近电路的分数阶运算性能的不恒定性, 振荡现象势必会影响分抗电路的分数算子逼近性能, 在物理应用上造成误差, 因此必须寻找有效方法克服或抑制分抗逼近电路的运算振荡现象.2.无源双口网络—标度分形格分抗逼近电路 经典Carlson分形格分抗逼近电路具有负半阶运算性能, 归一化后的Carlson分形格分抗逼近电路(图1 )是由k 个基本对称格型节级联而成的双口网络.图 1 有限k 节Carlson格型分抗逼近电路 (a) 归一化原型电路; (b) 等效双口网络Figure1. Finite k -stage Carlson Lattice fractance approximation circuit: (a) Normalized prototype circuit; (b) equivalent two-port network图1 中虚线方框中表示单个基本对称格型节. 根据网络的传输参量矩阵特点, 级联后的分抗逼近电路仍然是对称的双口网络. 该分抗逼近电路的运算特征曲线如图2 . 取$ k=32 $ , 当频率指数$ -2.5 < \varpi < 2.5 $ 时, 其中的阶频特征曲线和相频特征曲线几乎为一条直线, 表现为恒定的运算阶与恒定的相位. 因此, Carlson分形格分抗具有恒定的运算性能.图 2 Carlson分形格分抗逼近电路的运算特征曲线 (a) 阶频特征曲线; (b) 相频特征曲线Figure2. Operational characteristic curves of Carlson fractal-lattice fractance approximation circuit: (a) Order-frequency characteristic curves; (b) phase-frequency characteristic curves.25 ]根据标度拓展理论, 获得可构建具有任意实分数阶微积算子运算性能的标度化的Carlson分形格分抗逼近电路—标度分形格分抗逼近电路(图3 ). 图3 中, $ \alpha $ 与$ \beta $ 分别是电阻递进比与电容递进比, 统称为标度特征参量, $ \sigma =\alpha \beta $ 是该电路的标度因子. 当$ 1 < \alpha, \beta < \infty $ 时为正比标度拓展, 当$ 0 < \alpha, \beta < 1 $ 时为反比标度拓展. 标度分形格分抗逼近电路归一化电路原理图及等效的标度双口电路网络如图3 . 图3(b) 中分抗元$ {F}_{1}, {F}_{2} $ 表示分抗逼近电路的迭代次数$ k\to {\infty } $ 时的近似等效理想分抗元, 因此使用区别于相关文献中的理想分抗元的电路符号.图 3 k 节标度分形格分抗逼近电路 (a) 归一化原型电路; (b) 等效双口网络Figure3. k -stage scaling fractal-lattice fractance approximation circuit: (a) Normalized prototype circuit; (b) equivalent two-port network图3 中归一化阻抗$ {y}_{{\rm{L}}k}\left(w\right) $ , $ {y}_{{\rm{R}}k}\left(w\right) $ 分别表示网络的左右侧输入阻抗函数. 由标度分形格分抗逼近电路的结构形式, 其左侧分抗的归一化阻抗函数$ {y}_{{\rm{L}}k}\left(w\right) $ 的代数迭代方程为$ 1 < \alpha, \beta, \sigma < \infty $ . 在甚低频条件$ 0\leftarrow \left|w\right|\ll 1 $ 下, 方程(5 )可简化为正则标度方程$ {F}_{1} $ 具有任意Liu氏运算阶, 反比拓展时甚高频条件下具有相同的近似解结果. 根据迭代方程(5 )可数值求解该分抗逼近电路的阻抗函数$ {y}_{{\rm{L}}}\left(w\right) $ 及其运算特征曲线. 标度拓展后的单节格型电路是对称的双口网络, 但每一节都是不同参量的无源双口网络, 第i 节对称格型基本节的传输参量矩阵k 节标度格形分抗逼近电路双口网络的传输参量矩阵为k 节标度格形分抗逼近电路双口网络的右侧端口传输参量矩阵为$ {{T}}_{{\rm{L}}k}\ne {{T}}_{{\rm{R}}k} $ . 标度分形格分抗逼近电路的等效双口网络为非对称的, 左侧端口特性与右侧端口特性不同. 理论分析和数值仿真表明左侧端口作为输入端口时, 该分抗逼近电路能够逼近任意实数阶微积算子. 当初始阻抗$ {y}_{0}\left(w\right)=\infty $ , 正比拓展时, 根据传输参量矩阵数值求解阻抗函数, 获得$ {y}_{{\rm{L}}k}\left(w\right) $ 与$ {y}_{{\rm{R}}k}\left(w\right) $ 的运算特征曲线如图4 . 图中黑色为左侧端口分抗$ {F}_{1} $ 的运算特征曲线, 蓝色为右侧端口分抗$ {F}_{2} $ 的运算特征曲线.图 4 正比拓展时左侧端口分抗与右侧端口分抗的运算特征曲线($ k=12, \sigma =5 $ ) (a) 阶频特征曲线; (b) 相频特征曲线Figure4. Operational characteristic curves of left-side port fractance and right-side port fractance in direct proportion extension (k = 12, σ = 5): (a) Order-frequency characteristic curves; (b) phase-frequency characteristic curves.图4 中的运算特征曲线表明, 图3 中的等效双口网络两侧端口都能够逼近任意阶分数算子, 且具有相同的运算阶$ {\mu }_{{\rm{L}}{\rm{iu}}} $ 和有效运算频段. 当运算阶$ {\mu }_{{\rm{L}}{\rm{iu}}}=-0.5 $ 时, 两侧端口分抗的运算特征曲线重合. 当运算阶$ {\mu }_{{\rm{L}}{\rm{iu}}}\ne -0.5 $ 时, 两侧端口具有不同的运算特征曲线. 选择不同端口作为输入端口, 可以得到不同的任意阶分抗逼近电路. 标度拓展后, 标度分形格分抗$ {F}_{1} $ 的运算特征曲线在有效运算频段内产生了振荡. 该双口网络的右侧分抗$ {F}_{2} $ 同样具有运算振荡现象, 两侧分抗具有相同的运算振荡强度与周期$ W=\left|{\lg}\sigma \right| $ . 该振荡现象势必影响由分抗元件F 构成的分数阶电路与系统的运算恒定性. 因此, 要提高分数阶电路与系统的运算性能, 应当消除或抑制分抗元F 的运算振荡现象, 从而提高理论分析与实践测试的真实性与准确性.3.高运算恒定性对称格型级联双口网络 23.1.对称格型级联双口网络 3.1.对称格型级联双口网络 对称的负半阶Carlson分形格原型分抗逼近电路(图1 )的运算特征曲线在有效运算频段内无振荡现象, 运算特征曲线呈现恒定的负半阶运算性能. 电路的等效双口网络具有对称性, 左右侧端口完全等价. 标度拓展后的等效双口网络(图3 )为非对称的, 两侧端口虽然能够有效逼近分数算子, 但在有效频段内运算特征不恒定. 由此自然想到, 如果能够构成标度拓展后的对称无源双口网络, 是否可以有效抑制频域的运算振荡现象, 获得具有恒定运算性能的任意阶分抗逼近电路.$ k\to {\infty } $ . 根据图3(b) 中的等效双口网络, 将两个相同的标度分形格分抗逼近电路的左侧与右侧端口级联, 级联后新的等效格型双口网络如图5 .图 5 等效格型级联双口网络NFigure5. Equivalent lattice cascaded two-port network N.$ {\rm{N}}_{1} $ 的传输参量矩阵$ {\rm{N}}_{2} $ 的传输参量矩阵为图5 中级联形成的新网络N的传输参量矩阵为图6 中红色曲线, 相比于标度分形格分抗(黑色曲线), 级联后的新网络N的运算振荡幅度明显减小.图 6 标度分形格分抗与新网络N的运算特征曲线($ k\to {\infty }, \sigma =5 $ ) (a) 阶频特征曲线; (b) 相频特征曲线Figure6. Operational characteristic curves of scaling fractal-lattice fractance and new network N ($ k\to {\infty }, \sigma =5 $ ): (a) Order-frequency characteristic curves; (b) phase-frequency characteristic curves.3.2.数值仿真与实验结果分析 -->3.2.数值仿真与实验结果分析 设计数值仿真实验, 对比分析新网络N的运算性能与标度分形格分抗的运算性能. 取k 节标度分形格分抗逼近电路, 级联后的归一化电路原理图如图7 . 当初始阻抗$ {y}_{0}\left(w\right)=\infty $ , 电路节数$ k=8 $ 时, 正比拓展条件下, 由传输参量矩阵数值求解的新网络N与标度分形格分抗的运算特征曲线对比如图8 . 红色曲线表示新网络N的运算特征曲线, 黑色为标度分形格分抗的运算特征曲线.图 7 新网络N的归一化电路原理图Figure7. Normalized circuit schematic diagram of new network N.图 8 新网络N与标度分形格分抗运算特征曲线对比图($ k=8, \sigma =5 $ ) (a) 阶频特征曲线; (b) 相频特征曲线Figure8. Comparison diagram of operational characteristic curves of new network N and scaling fractal-lattice fractance (k = 8, σ = 5): (a) Order-frequency characteristic curves; (b) phase-frequency characteristic curves.4.运算振荡现象及分抗逼近电路的优化 24.1.运算振荡现象的理论分析 4.1.运算振荡现象的理论分析 考虑零点频率指数与极点频率指数分别为$ {\varpi }_{{\rm{Z}}i} $ , $ {\varpi }_{{\rm{P}}i} $ 的零极点对组成的一次子系统$ {E}_{i}\left(\varpi \right) $ , 其归一化阻抗函数为[14 ] :图9 .图 9 一次子系统的运算特征曲线Figure9. Operational characteristic curves of primary sub-system.图9 中的运算特征曲线表明, 每个一次子系统都具有产生波峰的局域化特性, 频域的运算振荡现象正是由零点与极点的共同作用导致的. 由运算特征函数表达式(18 )式可知, $ {\lg}{\alpha }_{i} $ 取值越大, 一次子系统的运算振荡幅度越大. 标度分形格分抗同样可以看成由多个负实零极点对基元系统$ {E}_{i}\left(\varpi \right) $ 组成, 频域的运算振荡现象正是这些一次子系统的集体行为.$ {\lg}{\alpha }_{i} $ , 理论上便可有效抑制运算振荡幅度, 实现恒定的运算性能. 正比拓展$ \sigma =5 $ , 迭代逼近次数$ k=4 $ 时, 不同运算阶下, 标度分形格分抗逼近电路等效双口网络的左侧端口分抗$ {F}_{1} $ 与右侧端口分抗$ {F}_{2} $ 的零极点频率指数分布如图10(a) . 左侧端口分抗$ {F}_{1} $ 与新网络N的单侧端口分抗的零极点指数分布对比如图10(b) .图 10 (a) 正比拓展左侧分抗零极点指数(黑色)与右侧分抗的零极点指数(绿色)分布对比图; (b) 正比拓展左侧分抗零极点指数(黑色)与新网络N的零极点指数(红色)对比图Figure10. (a) The distribution comparison diagram of zero-pole exponents (black) of left-side fractance and zero-pole exponents (green) of right-side fractance in direct proportion extension; (b) the distribution comparison diagram of zero-pole exponents (black) of left-side fractance and zero-pole exponents (red) of new network N.图10(a) 可以看出, 标度分形格分抗等效双口网络的左侧分抗$ {F}_{1} $ 与右侧分抗$ {F}_{2} $ 在相同运算阶下的极点频率指数重合, 当运算阶$ {\mu }_{{\rm{L}}{\rm{iu}}}=-0.5 $ 时, 零点频率指数也重合. $ {\mu }_{{\rm{L}}{\rm{iu}}}\ne -0.5 $ 时, 零点频率指数位置不同, 且运算阶为$ {\mu }_{{\rm{L}}{\rm{iu}}} $ ($ -0.5 < {\mu }_{{\rm{L}}{\rm{iu}}} < 0 $ )时, 左侧分抗$ {F}_{1} $ 与右侧分抗$ {F}_{2} $ 的相邻两个零点频率指数间距与运算阶为($ {-1-\mu }_{{\rm{L}}{\rm{iu}}} $ )时对应的相邻零点频率指数间距近似相等. 图10(b) 表明, 通过双口网络的左右侧端口级联, 新的分抗的零极点频率指数个数增加了一倍, 从而导致相邻的零极点频率指数间距变小. 特别是当$ {\mu }_{{\rm{L}}{\rm{iu}}}=-0.5 $ 时, 相比于标度分形格分抗, 相邻零点与极点频率指数间距减小了一半. 因此, 级联后的新网络N的分数阶运算振荡幅度大幅减小.4.2.对称格型级联双口网络N的电路优化 -->4.2.对称格型级联双口网络N的电路优化 分析图8 中对称标度格型级联双口网络的运算特征曲线, 在有效逼近频段内, 当频率指数变量$ \varpi \to 0 $ 时, 分抗逼近电路的运算特征曲线偏离理想分抗元的运算特征直线. 正比拓展时, 有效逼近频段内较高频率侧的逼近效果有待优化. 当运算阶$ -1 < {\mu }_{{\rm{L}}{\rm{iu}}} < -0.5 $ 时, 运算特征曲线向上偏移. 此时分抗逼近电路的运算性能偏向电阻的运算特性(电阻元可视为0阶分抗元件), 整个电路中电阻元件的作用强于电容元件的作用, 因此需在原分抗逼近电路中加入电容. 当运算阶$ -0.5 < {\mu }_{{\rm{L}}{\rm{iu}}} < 0 $ 时, 运算特征曲线向下偏移. 此时分抗逼近电路的运算性能偏向电容的运算特性(电容元可视为$ -1 $ 阶分抗元件), 即电容元的作用强于电阻元的作用, 因此需加入电阻. 考虑较高频段串联电容的容抗较小, 对电路的性能影响较小, 因此电容选择并联, 电阻选择串联. 反比拓展时运算特征曲线的待优化侧为较低频段, 电路的优化原理与正比拓展时类似.图11 为级联后的高运算恒定性分抗的电路优化原理图.图 11 新双口网络N的电路优化原理图 (a) 正比拓展优化; (b) 反比拓展优化Figure11. Circuit optimization principle diagram of new two-port network N: (a) Optimization in direct proportion extension; (b) optimization in inverse proportion extension.19 )式, (19a )式为正比拓展时的电路优化参数, (19b )式为反比拓展优化参数. 以阶频特征曲线为例, 正比拓展和反比拓展下优化前后的新双口网络N的运算特征曲线对比如图12 , 实验结果表明相频特征曲线具有相同的优化效果.图 12 阶频特征曲线优化对比图 (a) 正比拓展优化 ($ k=8, \sigma =5 $ ); (b) 反比拓展优化 ($ k=8, \sigma =1/5 $ )Figure12. Optimization comparison diagram of order-frequency characteristic curves: (a) Optimization in direct proportion extension ($ k=8, \sigma =5 $ ); (b) optimization in inverse proportion extension ($ k=8, \sigma =1/5 $ ).$ {\mu }_{{\rm{L}}{\rm{iu}}}=-0.5 $ 时, 级联的低振幅分抗有效逼近带宽最大, 此时不需优化. 当运算阶${\mu }_{{\rm{L}}{\rm{iu}}}\ne -0.5$ 时, 在频率$ w=1 $ 附近(频率指数$ \varpi =0 $ )运算特征曲线偏离目标运算阶的理想分抗频域曲线, 此时优化后的阶频特征曲线显然比优化前的新双口网络N的阶频特征曲线具有更高的逼近效益.5.实例应用—信号的分数阶微分运算 选用负半阶对称格型级联双口网络N, 构建半阶微分运算电路. 取标度因子$ \sigma =5 $ , 运算阶${\mu }_{{\rm{L}}{\rm{iu}}}= -0.5$ , 由(7 )式求解的标度特征参量$ \alpha =\beta =2.2361 $ . 取电路节数$ k=5 $ , 电阻阻值$ R=1\;\mathrm{k}{\Omega } $ , 电容容值$ C=1$ μF, 对称格型级联双口网络N逼近的理想分抗元的阻抗值为$ 2 k=10, \sigma =5 $ )的频域曲线与负半阶标度分形格分抗($ k=5, \sigma =5 $ )及Carlson原型分形格分抗($ k=10 $ )的频域曲线对比如图13 .图 13 模拟电路仿真的频域曲线对比图 (a) 幅频特征曲线; (b) 相频特征曲线Figure13. Frequency-domain curves comparison diagram of analog circuits: (a) Amplitude-frequency characteristic curves; (b) phase-frequency characteristic curves.[26 ] 图13 的新网络N作为理想分抗元F , 构建半阶微分运算电路(图14 ). 其中$ {R}_{2}=1\;\mathrm{k}{\Omega } $ , $ {R}_{\mathrm{f}}=10\;\mathrm{k}{\Omega } $ , $ {R}_{\mathrm{i}\mathrm{n}}=1\;\mathrm{k}{\Omega } $ , ${R}_{\mathrm{b}1}={R}_{\mathrm{b}2}= 820\;{\Omega }$ , $ {R}_{1} $ 使用$ k=5 $ 时的负半阶新网络N, 放大芯片A和B选择Multisim14.0中的运算放大器OP37AZ. 该分数阶微分运算电路的电压传输函数为(22 )式.图 14 半阶微分运算电路原理图Figure14. Schematic diagram of half-order differential operational circuit.图13 中的有效逼近频率范围, 选择基波角频率$ {\Omega }_{0}=1\mathrm{H}\mathrm{z} $ , 峰峰值$ E=0.5\;\mathrm{V} $ 的周期对称方波为输入信号$ {u}_{\mathrm{i}\mathrm{n}}\left(t\right) $ . 由周期对称方波信号的半阶微分运算表达式22 )式), 求解半阶微分后的信号$ {u}_{\mathrm{o}\mathrm{u}\mathrm{t}}\left(t\right) $ 如图15(a) , Multisim14.0中模拟电路仿真的运算结果如图15(b) .图 15 周期对称方波的半阶微分运算 (a) 理论结果; (b) 模拟电路仿真结果Figure15. The half-order differential operation of a periodic symmetrical square wave: (a) Theoretical result; (b) analog circuit simulation result$ k=5 $ 时的负半阶新网络N, 可设计分数阶维恩桥振荡器. Multisim14.0中的模拟负半阶微分运算电路仿真结果, 证实了设计的具有高运算恒定性新网络N的有效性.6.结 论 本文提出一种实现具有高运算恒定性分抗逼近电路的设计新方法. 从电路网络的角度分析经典的标度分形格分抗逼近电路, 发现该分抗的等效双口网络的两侧端口都可实现任意实数阶理想分抗元的运算性能. 结合双口网络的传输参量矩阵, 构造标度拓展后的对称格型级联无源双口网络, 并有效抑制了任意阶标度分形格分抗逼近电路的运算振荡现象. 根据零极点频率指数的分布情况, 理论分析任意阶标度分形格分抗运算振荡现象产生的原因, 从理论上分析抑制运算振荡幅度的方法. 结合分抗逼近电路优化理论, 实现具有恒定运算性能、高逼近效益的任意分数阶格型级联双口网络. 后续有待研究的问题是: 四类具有负半阶运算性能的Oldham分形链类分抗逼近电路同样具有恒定的运算性能, 且同样可等效为无源级联双口网络, 因此, 是否可以构造标度拓展后链式结构的对称级联双口网络, 这种结构的分抗逼近电路是否也具有任意实数阶恒定的运算性能. 



















 图 1 有限k节Carlson格型分抗逼近电路 (a) 归一化原型电路; (b) 等效双口网络
图 1 有限k节Carlson格型分抗逼近电路 (a) 归一化原型电路; (b) 等效双口网络

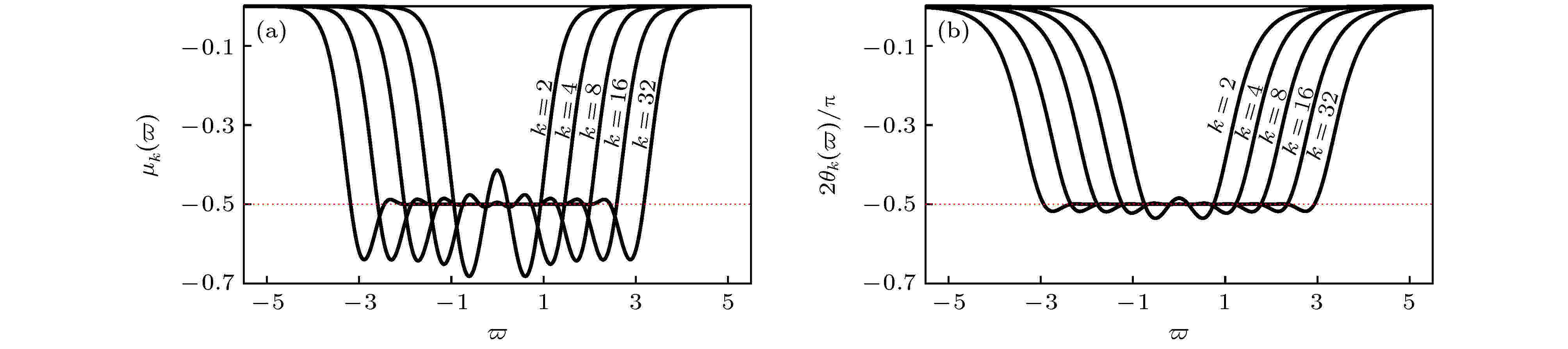 图 2 Carlson分形格分抗逼近电路的运算特征曲线 (a) 阶频特征曲线; (b) 相频特征曲线
图 2 Carlson分形格分抗逼近电路的运算特征曲线 (a) 阶频特征曲线; (b) 相频特征曲线






 图 3 k节标度分形格分抗逼近电路 (a) 归一化原型电路; (b) 等效双口网络
图 3 k节标度分形格分抗逼近电路 (a) 归一化原型电路; (b) 等效双口网络














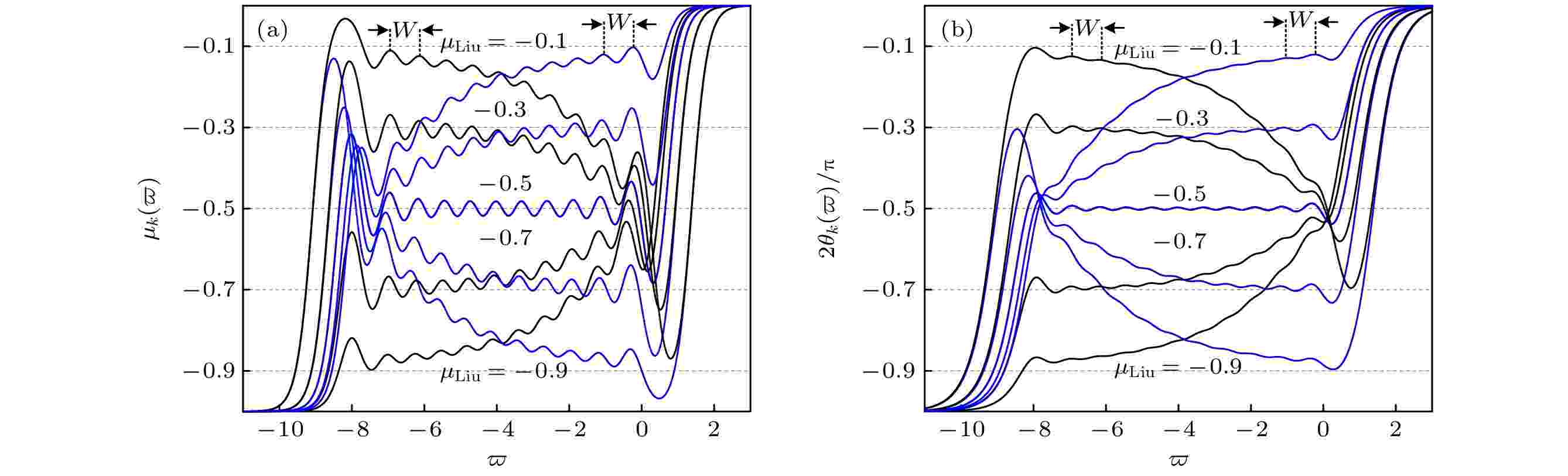 图 4 正比拓展时左侧端口分抗与右侧端口分抗的运算特征曲线(
图 4 正比拓展时左侧端口分抗与右侧端口分抗的运算特征曲线(







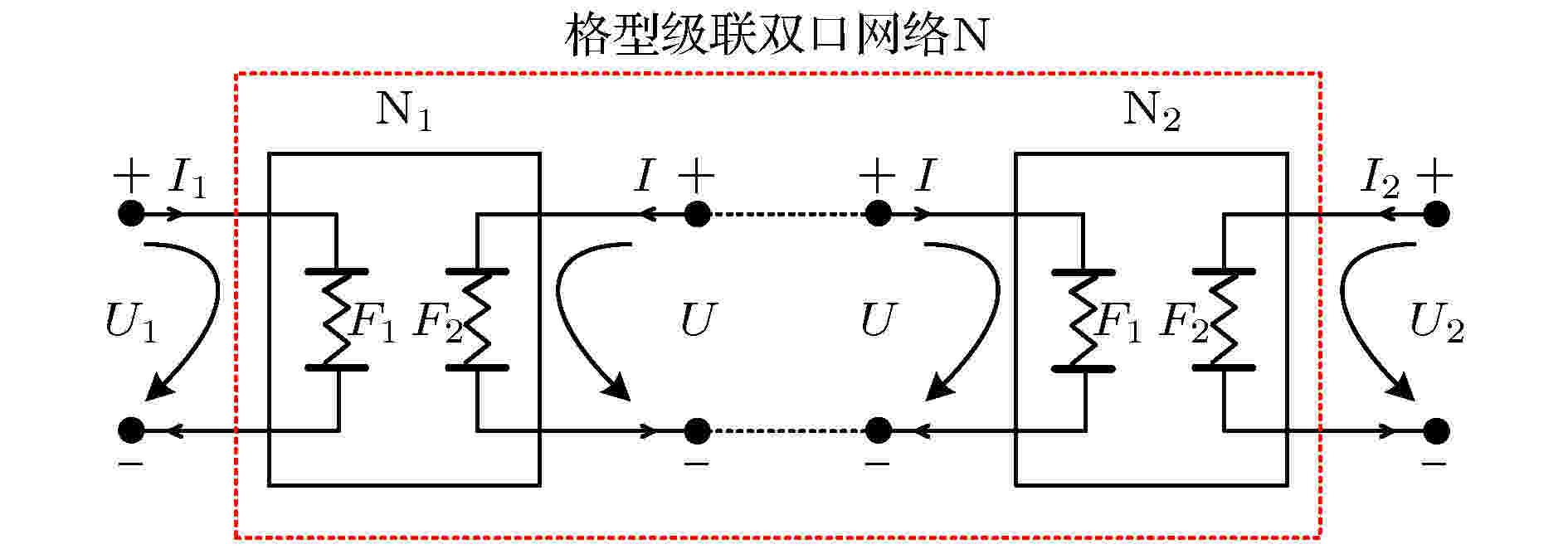 图 5 等效格型级联双口网络N
图 5 等效格型级联双口网络N

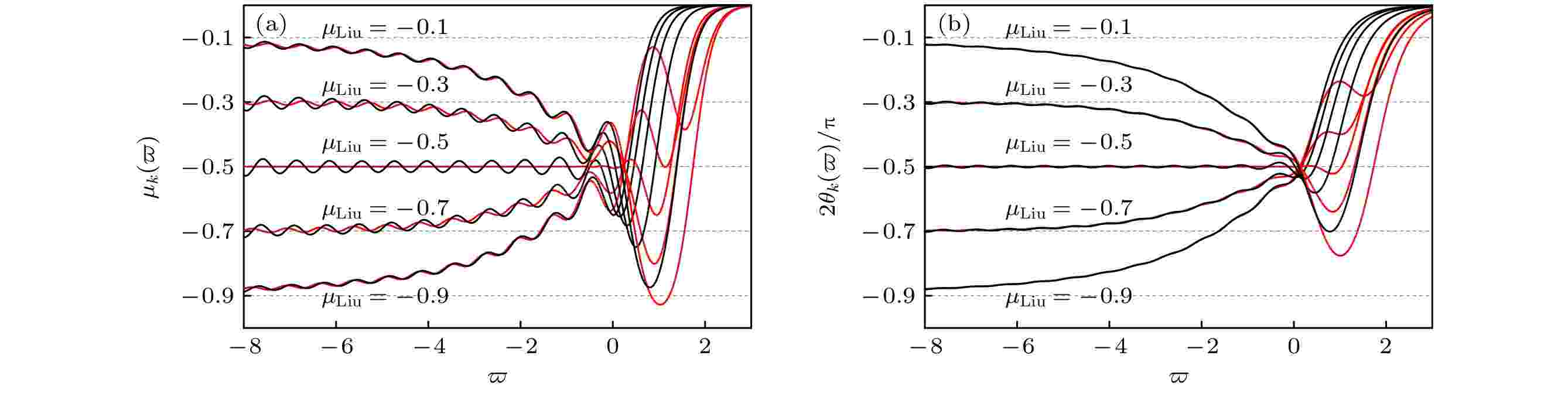 图 6 标度分形格分抗与新网络N的运算特征曲线(
图 6 标度分形格分抗与新网络N的运算特征曲线(



 图 7 新网络N的归一化电路原理图
图 7 新网络N的归一化电路原理图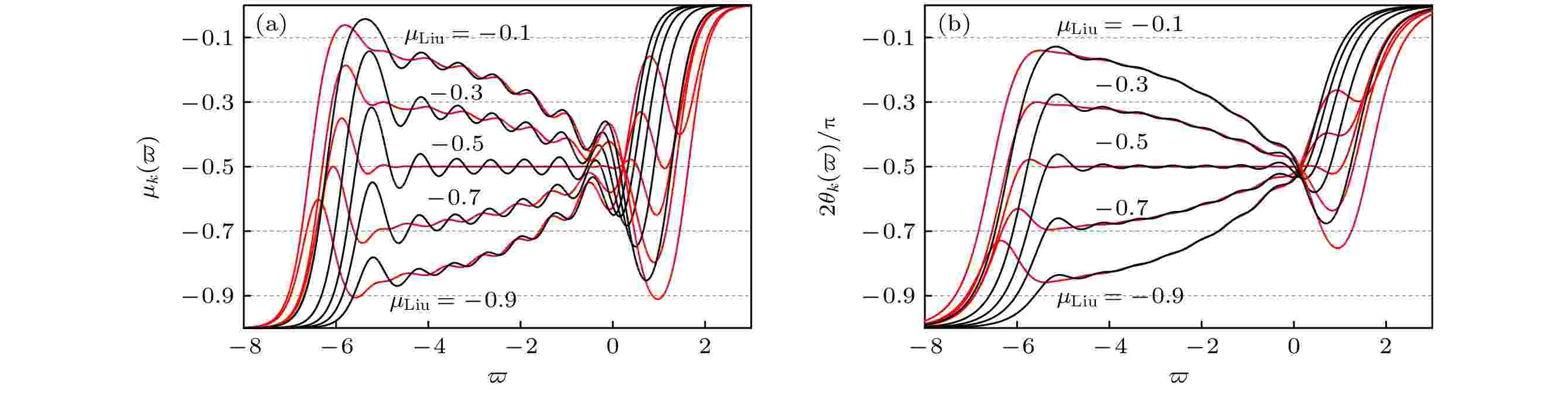 图 8 新网络N与标度分形格分抗运算特征曲线对比图(
图 8 新网络N与标度分形格分抗运算特征曲线对比图(



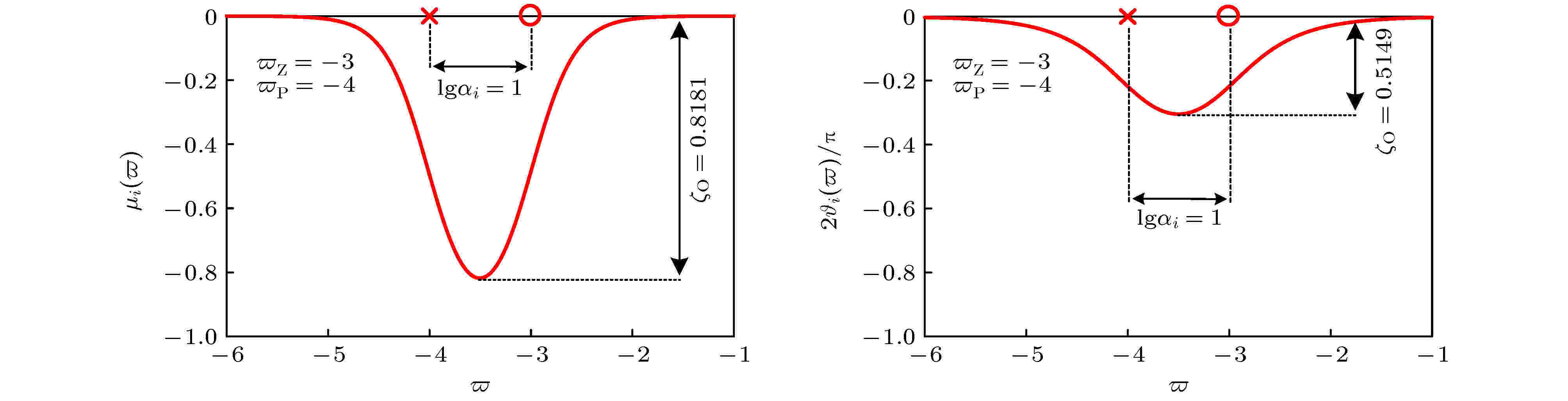 图 9 一次子系统的运算特征曲线
图 9 一次子系统的运算特征曲线









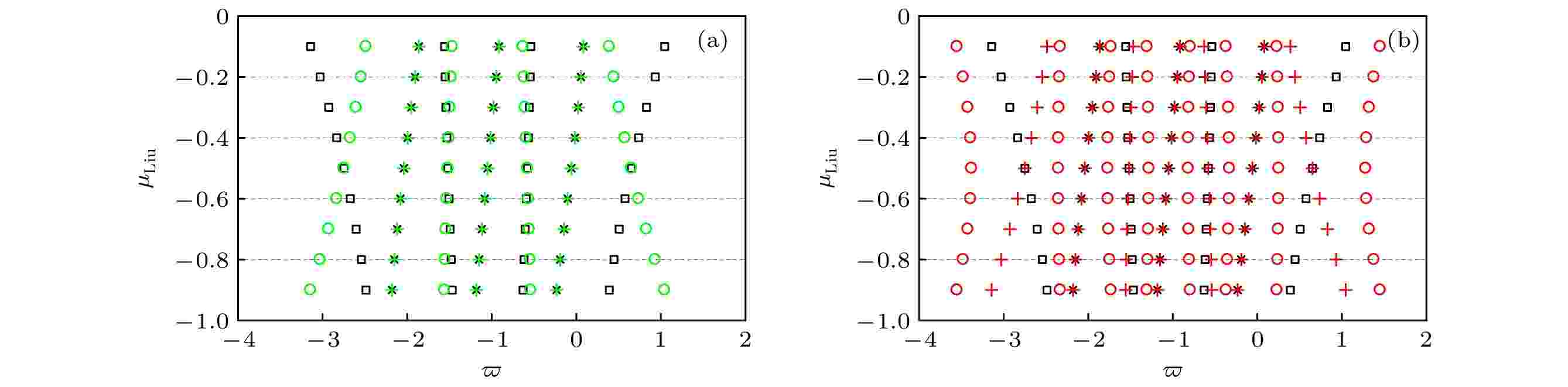 图 10 (a) 正比拓展左侧分抗零极点指数(黑色)与右侧分抗的零极点指数(绿色)分布对比图; (b) 正比拓展左侧分抗零极点指数(黑色)与新网络N的零极点指数(红色)对比图
图 10 (a) 正比拓展左侧分抗零极点指数(黑色)与右侧分抗的零极点指数(绿色)分布对比图; (b) 正比拓展左侧分抗零极点指数(黑色)与新网络N的零极点指数(红色)对比图



















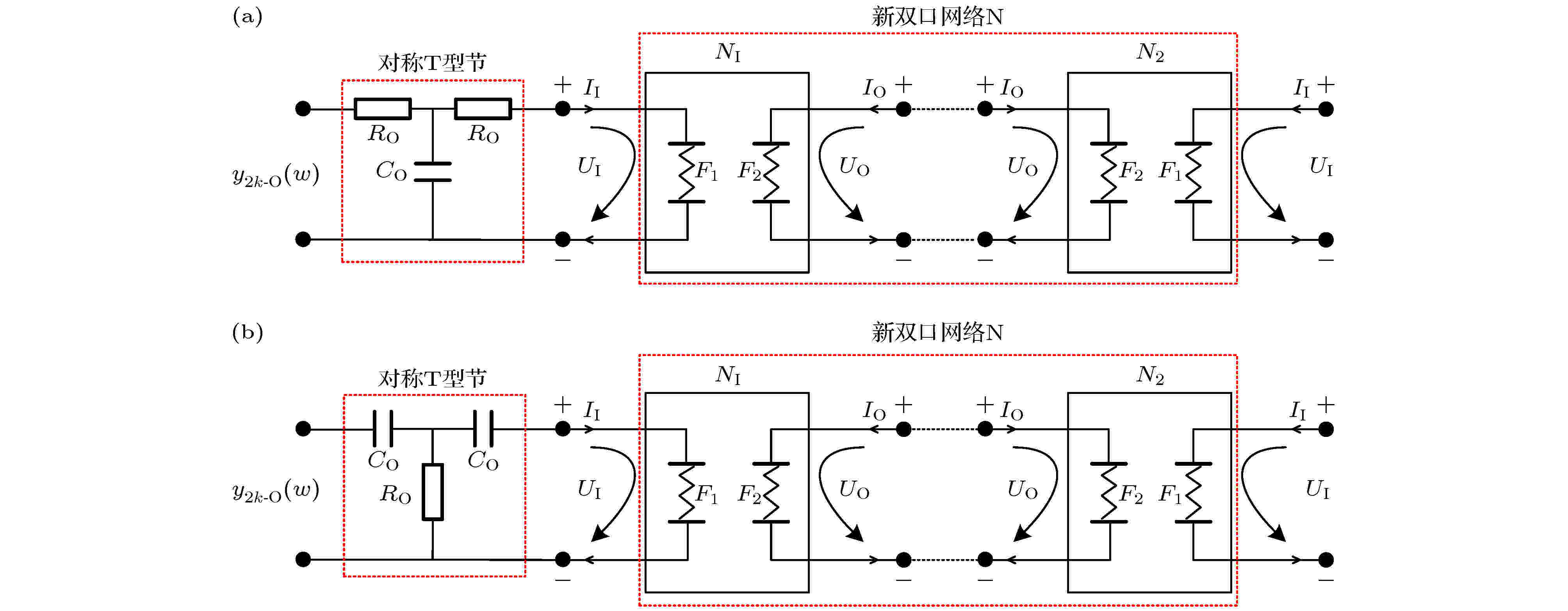 图 11 新双口网络N的电路优化原理图 (a) 正比拓展优化; (b) 反比拓展优化
图 11 新双口网络N的电路优化原理图 (a) 正比拓展优化; (b) 反比拓展优化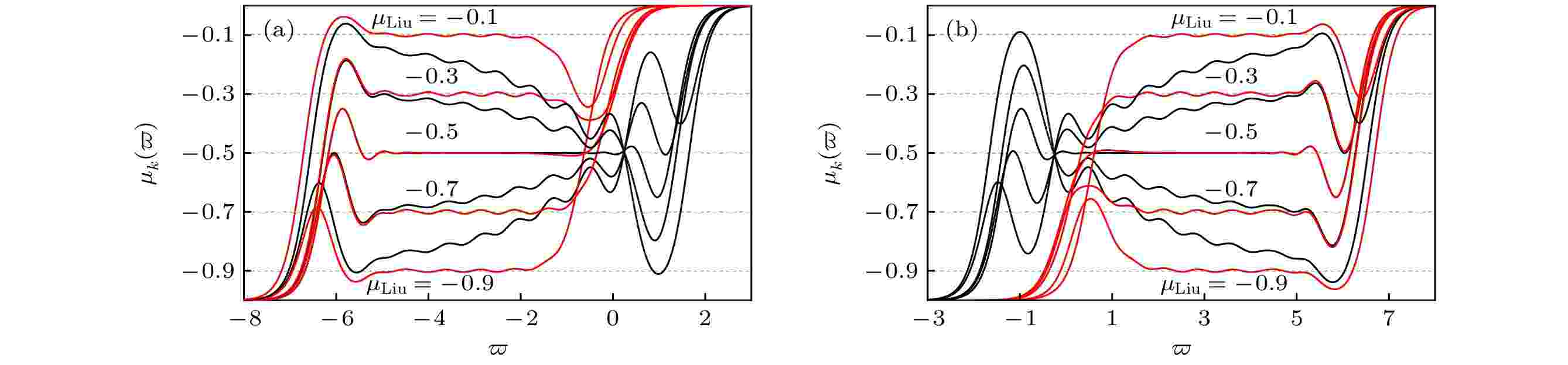 图 12 阶频特征曲线优化对比图 (a) 正比拓展优化 (
图 12 阶频特征曲线优化对比图 (a) 正比拓展优化 (
















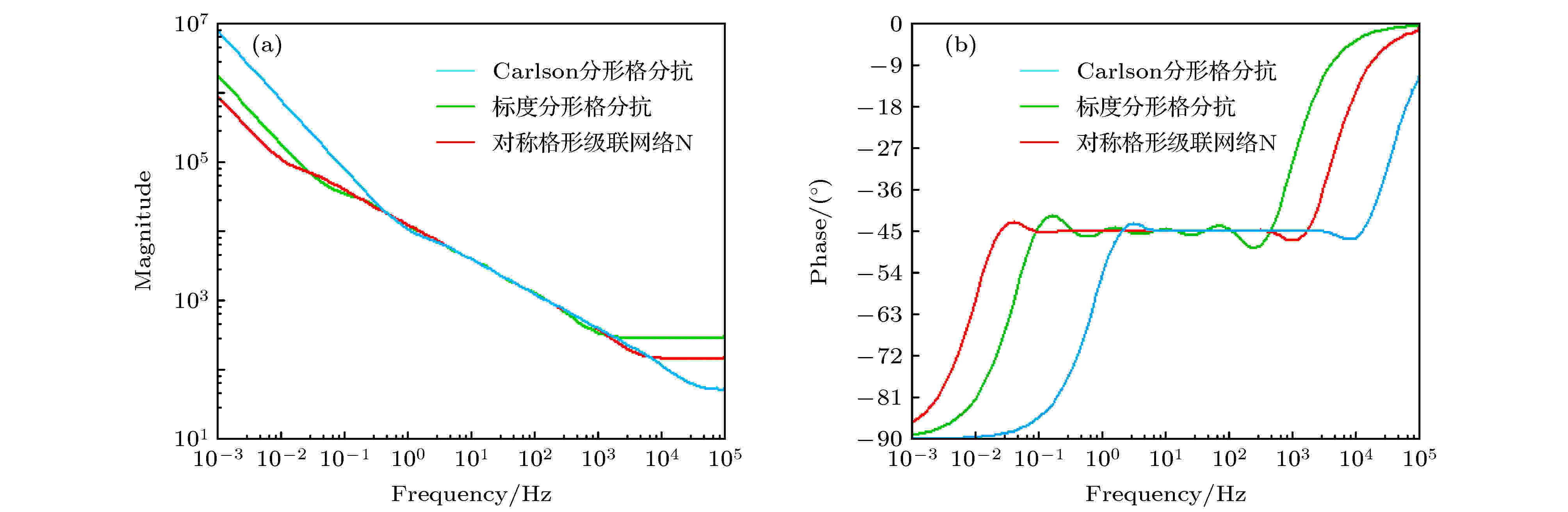 图 13 模拟电路仿真的频域曲线对比图 (a) 幅频特征曲线; (b) 相频特征曲线
图 13 模拟电路仿真的频域曲线对比图 (a) 幅频特征曲线; (b) 相频特征曲线





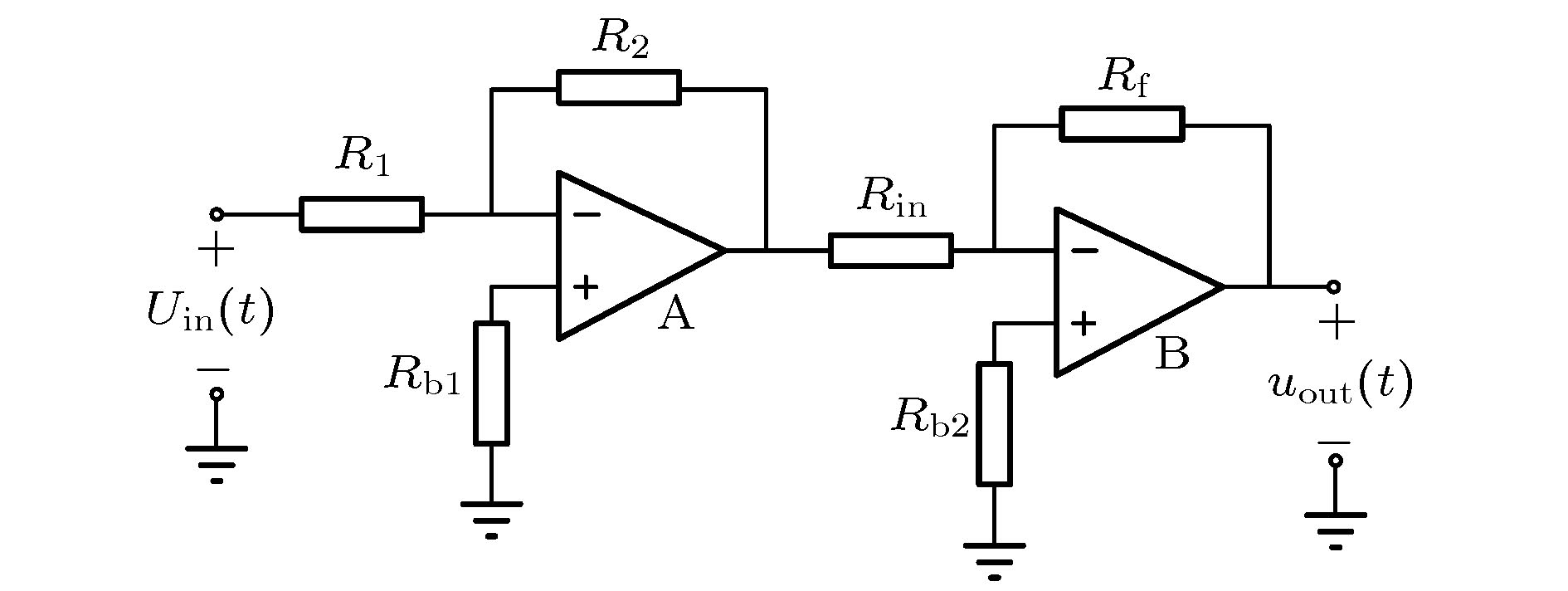 图 14 半阶微分运算电路原理图
图 14 半阶微分运算电路原理图



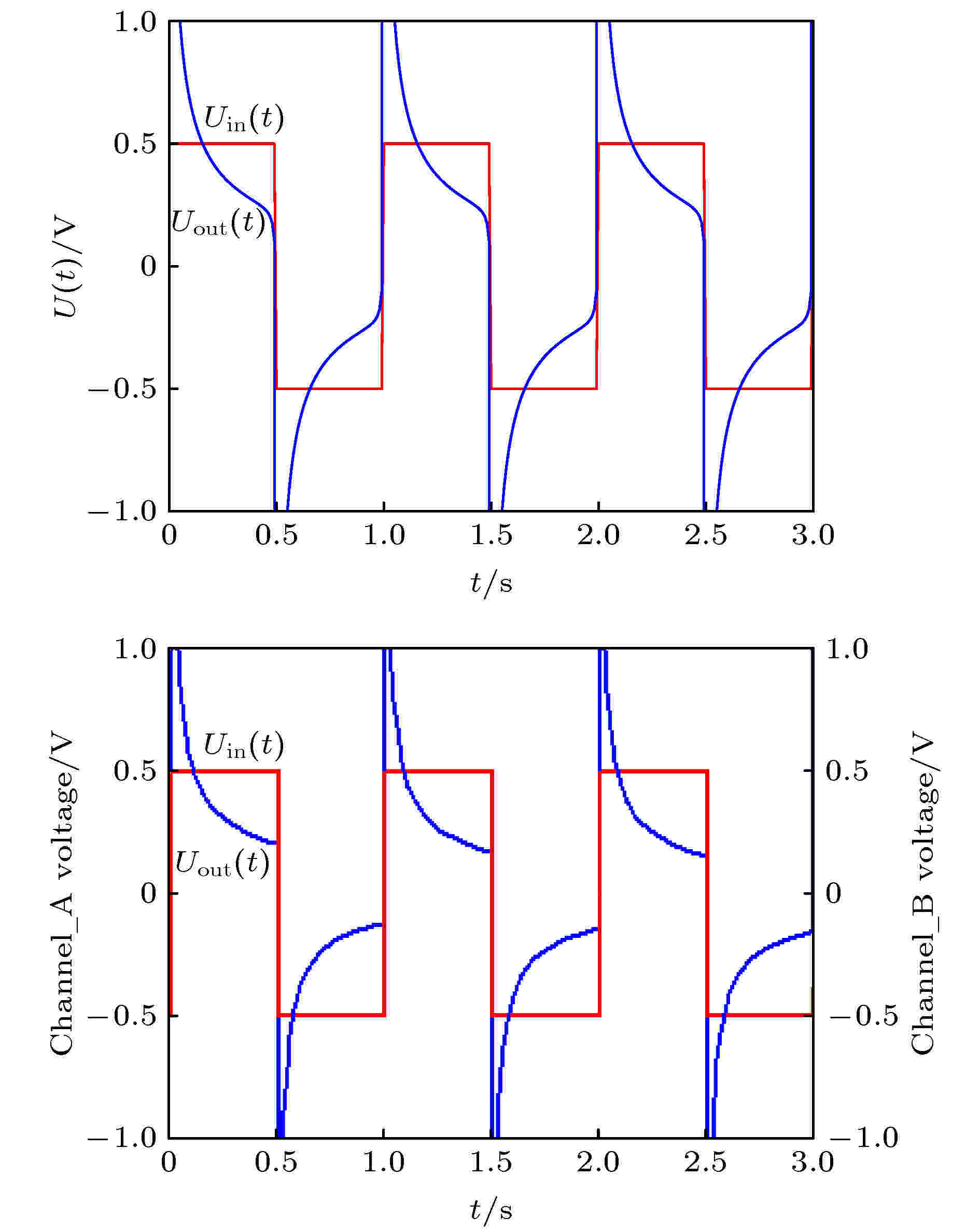 图 15 周期对称方波的半阶微分运算 (a) 理论结果; (b) 模拟电路仿真结果
图 15 周期对称方波的半阶微分运算 (a) 理论结果; (b) 模拟电路仿真结果
