摘要:大量动物实验表明, 生物神经系统中存在着不规则的混沌现象. 混沌神经网络是一种高度非线性动力系统, 它可以实现一系列复杂的动力学行为, 能够优化全局搜索和神经计算, 还可产生伪随机序列进行信息加密. 基于脑波由不同频率的正弦信号叠加理论, 为使神经网络更具生物特性, 提出了一种基于多频-变频正弦函数和分段型函数的非单调激活函数. 分析表明, 通过调节参数可使该激活函数拥有不同状态的脑电信号, 能够模拟频率不同、类型不同的脑电波同时工作时丰富多变的脑部活动. 基于该激活函数设计了一种新型混沌细胞神经网络. 采用基于结构复杂度的SE复杂度算法和C0复杂度算法分析了神经网络的复杂度; 利用Lyapunov指数谱、分岔图和吸引盆等方法, 详细分析了激活函数参数变化对其动力学特性的影响, 发现此混沌神经网络模型出现了一系列的复杂现象, 如多种不同类型的混沌吸引子、共存混沌吸引子、共存极限环等, 提升了混沌神经网络的性能, 证明了多频正弦混沌神经网络具有丰富的动力学特性, 使得其在信息处理、信息加密等方面也具有较好的前景.
关键词: 细胞神经网络/
混沌/
多频正弦激活函数

English Abstract

全文HTML

--> --> -->

人工神经网络是一种新型信息处理体系, 也是一种高度的非线性动力学系统. 通过****们的不懈研究探索, 已有数百种人工神经元和神经网络的模型被开发利用. 由于人工神经网络的快速发展, 许多领域都逐渐出现它的身影. 人工神经网络可以有效地解决许多问题, 并且在许多领域都能发挥巨大的作用. 比如在图像识别领域中, 孙为民等^[1]提出将人工神经网络和Adaboost相结合可提高绝缘子图像识别的准确率. 在信息加密领域中, Wang和Li^[2]基于Hopfield混沌神经网络提出了一种彩色图像加密算法. 该算法提高了加密效率, 具有良好的安全性能, 可以抵抗常见的攻击方法. 由于人工神经网络强大的处理信息能力, ****们纷纷研究可以有效模拟人工神经网络的方法. 比如董哲康等^[3]基于纳米级别的忆阻器, 设计了一种多通道忆阻脉冲耦合神经网络模型, 能够有效模拟网络中连接系数的动态变化, 解决神经网络中固有的参数估计问题. Bao等^[4]建立了具有整体隐藏振荡的3D忆阻HR神经元模型, 并进行了相应的数值模拟, 该模型展示了实际神经元电活动的复杂动力学. 一个混沌系统, 其状态不仅依赖于当前状态, 也依赖于系统的初始状态, 这也恰恰反映了大脑本身的特点. 因此, 神经动力学中的混沌动力学研究逐步成为国际学术界关注的热点问题^[5].
1987年, Freeman等^[6]在研究兔子嗅觉系统时, 发现在生物神经系统中存在着不规则的混沌现象, 进而提出了混沌神经网络(chaotic neural network, CNN)的概念. 随后, Chua和Yang^[7]基于Hopfield神经网络和细胞自动机首次提出细胞神经网络的概念. 1990年, Aihara等^[8]通过在经典的McCulloch-Pitts神经元中引入时间延迟, 从而提出一个混沌神经网络模型. 生物神经系统之所以出现混沌现象, 是因为它是一个强非线性系统. 为了在人工神经网络中实现这一行为, 通常采用非线性函数作为其激活函数, 由此构成的混沌神经网络作为一种高度非线性动力学系统, 它可以实现一系列复杂的动力学行为, 在全局搜索优化、信息加密及伪随机序列发生器等方面有着广泛的应用. Chen等^[9]提出了一种左Caputo离散增量意义上的三维分数阶(FO)离散Hopfield神经网络(FODHNN), 研究了一种基于混沌FODHNN的图像加密系统的相关问题. 而Jiang和Chen^[10]构建了基于混沌神经网络的超分辨率图像盲恢复模型, 主要用于解决神经网络的传统超分辨率图像盲恢复模型容易陷入局部极小问题.
神经网络中的激活函数可采取多种形式, 其整体呈现单调性, 如常见的Sigmoid激活函数、tanh(x)函数、分段型函数等. 但Potapov和Ali^[11]指出, 激活函数采用非单调的函数可以使神经元更容易产生混沌动力学特性. 例如, Yi等^[12] 提出的I-TCNN模型, 将正弦函数与Sigmoid函数的复合作为非单调激励函数; Zhang和Xu^[13] 提出了Morlet小波混沌神经网络(MWCNN)和墨西哥帽小波混沌神经网络(MHWCNN)模型, 将Morlet或Mexican Hat小波函数代替Sigmoid函数作为其细胞神经网络的激活函数. 这些激活函数整体单调递增而局部非单调, 都能使得神经网络具有更加复杂的动力学行为, 但都不具有生物机制, 因为脑波不是单一频率的正弦波^[14].
在不同的场景下脑电波具有不同的频率和幅度. 基于频率和幅度不同可以将脑波分为五种类型, 分别为α, β, δ, γ和θ, 其频率随着活跃度因子x的增大而增大, 而幅度则随着活跃度因子x的增大而减小. 为了更加适应人脑的生物机制, 胡志强等^[15]提出了一种变频混沌神经网络(FCS-CNN)模型, 其激活函数由一个变频正弦函数与Sigmoid函数加和组成. 这虽然在混沌神经元模型中加入了生物机制, 但FCS函数却只有单个变频正弦波信号.
脑电波来源于锥体神经元顶端树突的突触后电位. 人的大脑有上百亿个神经元, 所产生的脑电波并非单一存在的, 而应该由同时作用的不同频率的多个正弦信号叠加而成^[16]. 为使混沌神经网络更贴近人脑工作状态, 本文提出了一种多频-变频混沌神经网络模型, 建立了一种更具生物特性的非单调激活函数, 该激活函数由一种多频-变频正弦函数(multifrequency-frequency conversion sinusoidal, MFCS)与一个分段线性函数加和而成. 其中, MFCS由多个频率不同, 相位不同的正弦函数波叠加而成, 通过调节相关参数使得这些正弦函数分别拥有不同状态的脑电信号, 从而更好地模拟频率不同、类型不同的脑电波同时工作时丰富多变的脑部活动. 在MFCS函数激励下神经网络产生了更为复杂的混沌运动, 使其具有更丰富的生物特性, 更加贴近智能的人类行为.

脑电波是一些自发的有节律的神经电活动, 其频率变动范围可划分为四个波段, 即δ(1—3 Hz), θ(4—7 Hz), α(8—13 Hz), β(14—30 Hz). 除此之外, 在觉醒并专注于某一事时, 常见一种频率较β波更高的γ波, 其频率为30—80 Hz, 波幅范围不定^[16]. 脑电波是一种随机性很强的非平稳信号, 具有混沌动力学特性^[17].
在生活中人们经常处在不同的状态, 相应的脑电波类型也不尽相同. 脑电波中的正弦波信号并不是单一存在的, 频率越低其幅值越低, 反之越高. 考虑到大脑活动的生物学特性, 将脑波信号引入到混沌神经网络中, 使其更加贴近大脑真实的动力学特性. 多频正弦信号是一种周期性的信号^[18-20], 它是由幅度、相位和频率不同的多个正弦信号叠加而成, 多频正弦信号的数学表达式如下:

$x(t) = \sum\limits_{i = 1}^N {{A_i}\sin ({\omega _i}t + {\varphi _i})} $

其中, ${A_i}$, ${\omega _i}$和${\varphi _i}$分别为幅度、角频率和初相位.
为了分析方便本文将其简化, 使用频率和初相不同的两个正弦信号的叠加组成一个多频正弦信号, 并引入至细胞神经网络的激活函数中, 进而定义MFCS为

$\begin{split} S(x) =\;& {A_1}\sin \left( {\frac{x}{{{\varepsilon _1}}} + {\varphi _1}} \right) + {A_2}\sin \left( {\frac{x}{{{\varepsilon _2}}} + {\varphi _2}} \right) \\ =\;& A{{\rm{e}}^{ - q\left| x \right|}}\!\left[ {\sin\! \left(\! {\frac{{x{\rm{\pi }}}}{{{\varepsilon _1}{{\rm{e}}^{ - m\left| x \right|}}}}} \!\right) \!+\! \sin\! \left(\! {\frac{{2x{\rm{\pi }}}}{{{\varepsilon _2}{{\rm{e}}^{ - n\left| x \right|}}}} \!+\! {\varphi _2}} \!\!\right)} \!\right]\!,\\{A_1}=\;&{A_{\rm{2}}},\\[-10pt]\end{split} $

式中x为自变量, 表示脑部活动的强弱; A, A₁和A₂为幅值, 且区间为$0 \leqslant A \leqslant 1$, 取${A_1} = {A_2} = A$; q, m, n为正值参数, ${\varepsilon _1}$, ${\varepsilon _2}$分别为两个不同正弦函数的陡度参数; φ₁, φ₂为初相位. 当参数取值为A = 0.3, ${\varepsilon _1}$ = 0.04, ${\varepsilon _2}$ = 0.02, ${\varphi _1}$ = 0, ${\varphi _2}$ = $ {{\text{π}}}/{4}$, m = 6.8, n = 1.8, q = 7时, MFCS的波形如图1所示.
图 1 MFCS图像
Figure1. Graph of MFCS function.

由图1可以看出, 由两种不同频率的正弦函数叠加而成的MFCS, 其幅度和频率的变化都更加复杂. 相比单一的变频正弦函数, 使用两个不同频率和相位的正弦函数进行叠加, 使整个函数更加贴近脑电波的生物机制.
将MFCS与分段线性函数$g(x) \!=\!\dfrac { {| {x\! +\! 1} | \!-\! | {x \!-\! 1} |} }2$相加构成了本文的激活函数:

$\begin{split}f(x) =\;& S(x)+g(x) \\=\;& {{\rm{e}} ^{ - q\left| x \right|}}\!\left[ {\sin \left( {\frac{{x{\rm{\pi }}}}{{{\varepsilon _1}{{\rm{e}}^{ - m\left| x \right|}}}}} \right) \!+\! \sin \left(\! {\frac{{2x{\rm{\pi }}}}{{{\varepsilon _2}{{\rm{e}}^{ - n\left| x \right|}}}} \!+\! {\varphi _2}}\! \right)}\! \right]\\&+\frac{1}{2}\left( {\left| {x + 1} \right| - \left| {x - 1} \right|} \right).\\[-12pt]\end{split}$

如图2所示, 新的激活函数整体成单调性, 但局部是非单调的, 这一特征可以使神经元更加容易产生混沌动力学特性, 同时也使MFCS激活函数依然具有激活函数的动力学特性.
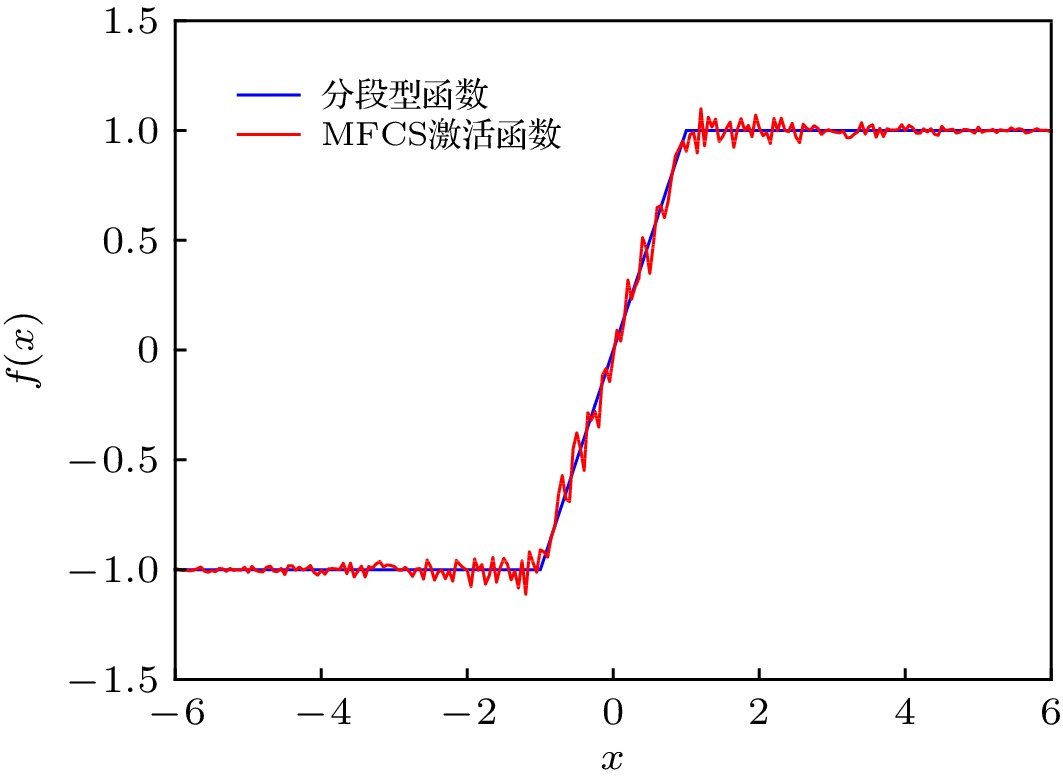图 2 分段型函数+0.15 MFCS激活函数
Figure2. Piecewise function + 0.15 MFCS activation function.

和FCS一样, MFCS也能通过参数的调节来控制其频率和幅度, 如图3所示. 通过对A, ${\varepsilon _1}$, ${\varepsilon _2}$, $\varphi $, m, n, q 进行调节, 可以看出q决定着函数的幅值宽度, m和n决定着频率的变化. 当q越大时, 幅值宽度越小; m和n越大, 频率陡度越大, 且随着n变化的频率陡度是随着m变化的频率陡度的两倍. 在参数值相同的情况下, 图3(c)中的频率陡度比图3(b)中更加明显. 这模拟了脑电信号中, 两个不同频率的正弦波叠加工作的一种状态.
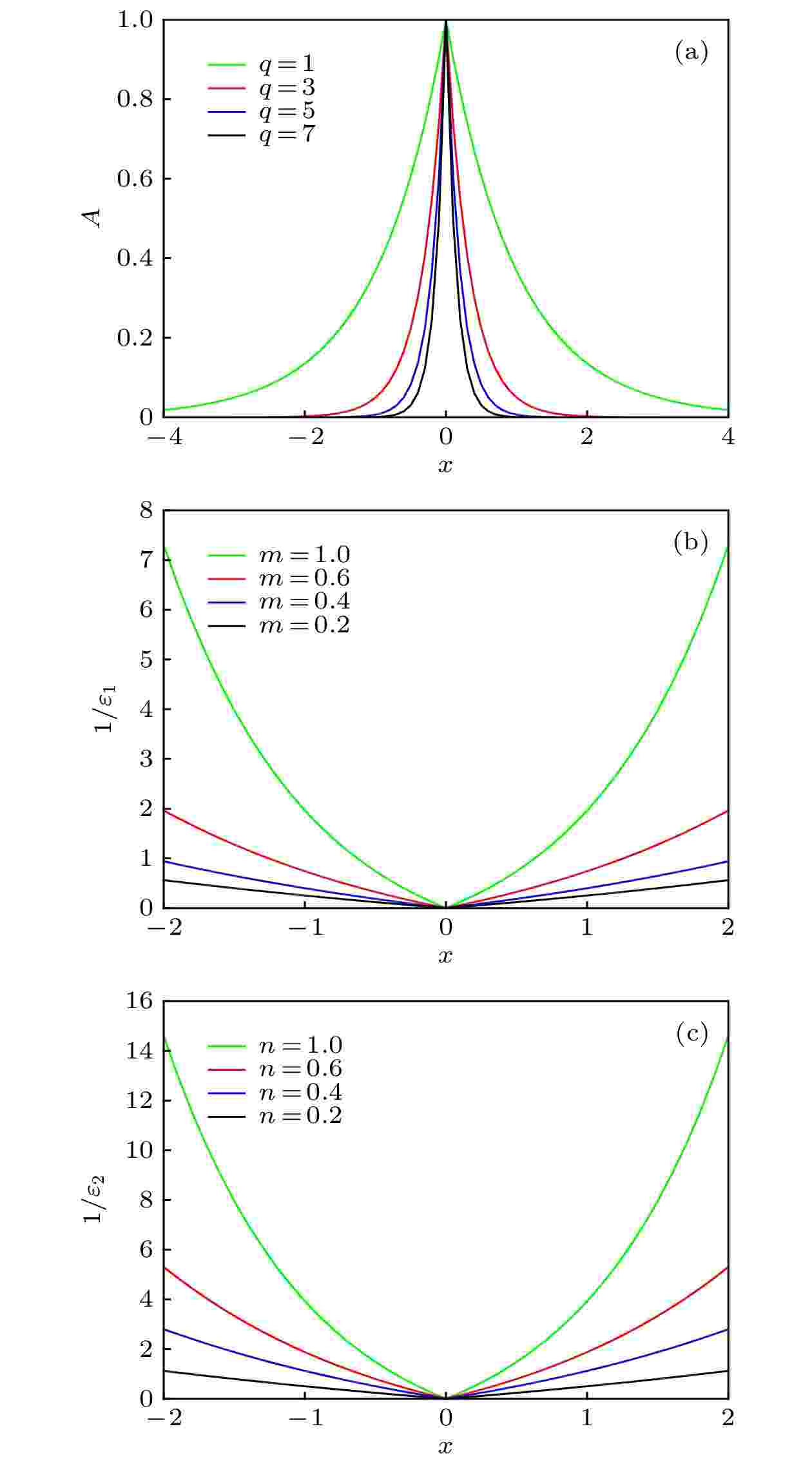图 3 幅值和频率随q, m, n的变化　(a)幅值A随q的变化; (b)频率1/${\varepsilon _1}$随m的变化; (c)频率1/${\varepsilon _2}$随n的变化
Figure3. Change characteristic of the amplitude and frequency with q, m, n: (a) The change characteristic of the amplitude A with q; (b) the change characteristic of the frequency 1/${\varepsilon _1}$ with m; (c) the change characteristic of the frequency 1/${\varepsilon _2}$ with n.

同时, m, n和x决定了MFCS的频率范围, 具体关系可见表1.

类型	频率/Hz	${\varepsilon _1}$(0)	${\varepsilon _2}$(0)
$\delta $	0.50—3.01	0.32	0.64
$\theta $	3.98—6.97	0.04	0.08
$\alpha $	7.96—15.09	0.02	0.04
$\beta $	15.92—30.18	0.01	0.02
$\gamma $	36.17—100.31	0.0044	0.0088

表1频率${\varepsilon _1}, {\varepsilon _2}$随n的变化
Table1.Change characteristic of the frequency ${\varepsilon _1}$ and ${\varepsilon _2}$ with n.

由表1可知, 通过调整参数, MFCS产生的频率${\varepsilon _1}$, ${\varepsilon _2}$都能够很好地模拟脑电波的频率, 进而可以模拟多种不同频率脑电信号同时工作的状态, 其中$\left| x \right| \leqslant 1$. 为了更加直观地看出参数m, n对MFCS的影响, 固定自变量x为1, 画出MFCS随参数m, n改变的三维立体图, 如图4所示. 由此看出, 多频正弦函数相比单一的正弦函数有着更加复杂的动力学特性, 且更加贴合脑电信号的工作状态.
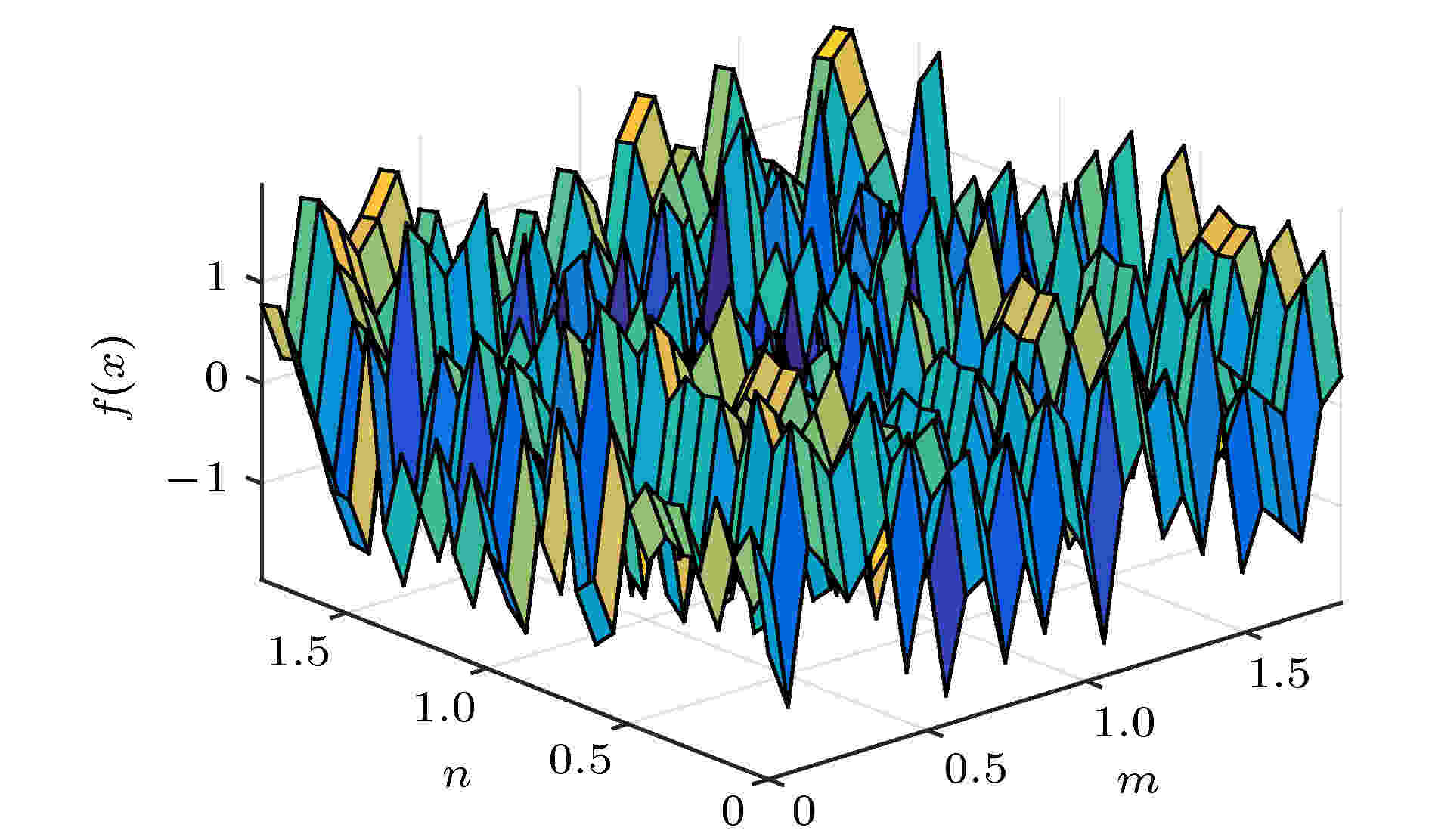图 4 MFCS随参数m, n变化图像
Figure4. Change characteristic of the MFCS with m and n.

激活函数对神经元上层级与下层级之间传递的信息进行处理, 使神经网络具备了分层的非线性映射学习能力, 对整个神经网络是至关重要的. 传统的Sigmoid激活函数存在软饱和性^[21]的缺陷, 使它在向后传递的过程中出现梯度消失问题, 会导致训练速度降低. 而且它的输出不是以0为中心, 这会使它收敛速度较慢, 导致逼近最优解的能力大大降低. 本文提出的激活函数由多频-变频正弦函数与分段型函数加和组成, 它不但加入了生物机制, 也克服了软饱和性的缺陷. 对分段线性函数g(x)和多频-变频函数S(x)分别求导得:

$g'(x) = \frac{1}{2}\left[ {{\rm{sign}}(x + 1) - {\rm{sign}}(x - 1)} \right],$

$\begin{split} S(x)=\;&\left\{ \begin{aligned} & A{{\rm{e}}^{ - qx}}\left\{ - q\left[ {\sin \left( {\frac{{x{\rm{\pi }}}}{{{\varepsilon _1}{{\rm{e}}^{ - mx}}}}} \right) + \sin \left( {\frac{{2x{\rm{\pi }}}}{{{\varepsilon _2}{{\rm{e}}^{ - nx}}}} + {\varphi _2}} \right)} \right] + \cos \left( {\frac{{x{\rm{\pi }}}}{{{\varepsilon _1}{{\rm{e}}^{ - mx}}}}} \right)\frac{{{\rm{\pi }}{{\rm{e}}^{mx}}}}{{{\varepsilon _1}}}(1 + mx)\right. \\ &\!\!\qquad\qquad\left.+ \cos \left( {\frac{{2x{\rm{\pi }}}}{{{\varepsilon _2}{{\rm{e}}^{ - nx}}}} + {\varphi _2}} \right)\frac{{2{\rm{\pi }}{{\rm{e}}^{nx}}}}{{{\varepsilon _2}}}(1 + nx) \right\}, &{(x > 0)}, \\& A{{\rm{e}}^{qx}}\left\{q\left[ {\sin \left( {\frac{{x{\rm{\pi }}}}{{{\varepsilon _1}{{\rm{e}}^{mx}}}}} \right) + \sin \left( {\frac{{2x{\rm{\pi }}}}{{{\varepsilon _2}{{\rm{e}}^{nx}}}} + {\varphi _2}} \right)} \right] + \cos \left( {\frac{{x{\rm{\pi }}}}{{{\varepsilon _1}{{\rm{e}}^{mx}}}}} \right)\frac{{{\rm{\pi }}{{\rm{e}}^{mx}}}}{{{\varepsilon _1}}}(1 + mx) \right.\\&\qquad\qquad\left.+ \cos \left( {\frac{{2x{\rm{\pi }}}}{{{\varepsilon _2}{{\rm{e}}^{nx}}}} + {\varphi _2}} \right)\frac{{2{\rm{\pi }}{{\rm{e}}^{ - nx}}}}{{{\varepsilon _2}}}(1 - nx) \right\}, &{(x < 0)}, \\ \end{aligned} \right. \\ =\;& - A{{\rm{e}}^{ - q\left| x \right|}}\left\{ q\left[ {\sin \left( {\frac{{\left| x \right|{\rm{\pi }}}}{{{\varepsilon _1}{{\rm{e}}^{ - m\left| x \right|}}}}} \right) + \sin \left( {\frac{{2\left| x \right|{\rm{\pi }}}}{{{\varepsilon _2}{{\rm{e}}^{ - n\left| x \right|}}}} + {\varphi _2}} \right)} \right] + \cos \left( {\frac{{\left| x \right|{\rm{\pi }}}}{{{\varepsilon _1}{{\rm{e}}^{ - m\left| x \right|}}}}} \right)\frac{{{\rm{\pi }}{{\rm{e}}^{m\left| x \right|}}}}{{{\varepsilon _1}}}(1 + m\left| x \right|)\right. \\ &\;\;\;\qquad\qquad\left.+ \cos \left( {\frac{{2\left| x \right|{\rm{\pi }}}}{{{\varepsilon _2}{{\rm{e}}^{ - n\left| x \right|}}}} + {\varphi _2}} \right)\frac{{2{\rm{\pi }}{{\rm{e}}^{n\left| x \right|}}}}{{{\varepsilon _2}}}(1 + n\left| x \right|) \right\}. \end{split} $

通过调节MFCS激活函数的幅度参数q, 可以改变MFCS激活函数是否以0为中心输出. 分别画出分段型函数、MFCS和MFCS激活函数及其导数, 如图5所示.
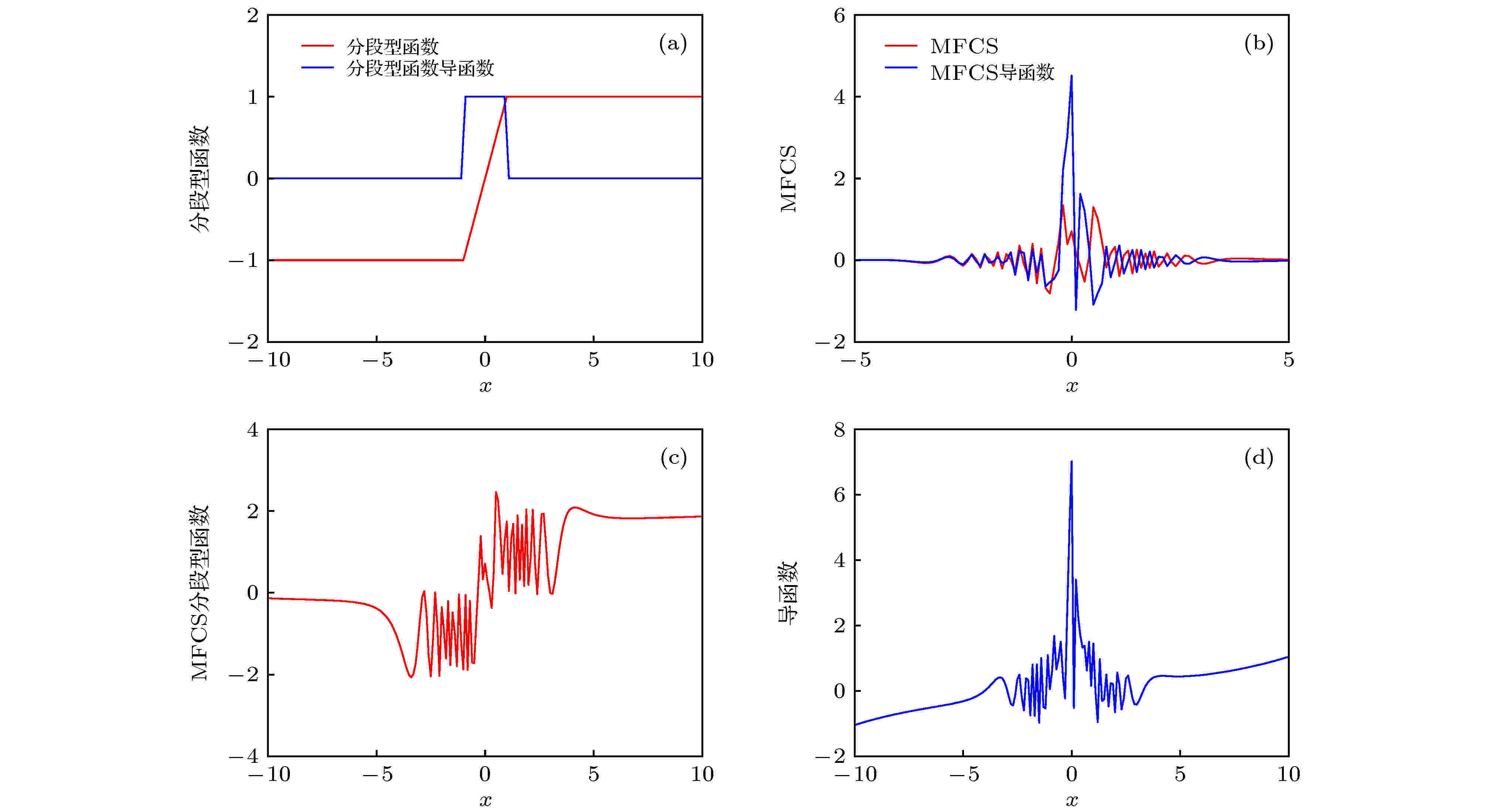图 5 分段型函数、MFCS和MFCS激活函数及其导数图像　(a)分段型函数及其导函数; (b) MFCS及其导函数; (c) MFCS激活函数; (d) MFCS激活函数导函数.
Figure5. Piecewise function, MFCS and MFCS activation function and its derivative image: (a) Piecewise function and its derivative function; (b) MFCS and its derivative function; (c) MFCS activation function; (d) MFCS activation function and its derivative function.

分析可知, 分段型函数和MFCS都可以以0为中心输出. 虽然分段型函数的导函数最终趋于0, 但由于MFCS可通过调节幅度参数q来控制其自身的导函数最终是否趋近于0, 因此MFCS激活函数的导函数也可通过调节参数q来控制其是否具有软饱和度, 故而不存在梯度消失的问题. 由图5(c)可知, 虽然MFCS激活函数的斜率最终趋近0, 但在x趋于正无穷和负无穷时, MFCS激活函数的导函数(图5(d))却分别大于零和小于零. 因此, MFCS激活函数不仅具有生物特性, 而且不容易发生梯度消失, 且其输出以0为中心(图5(c)). 本文提出的基于MFCS和分段函数的激活函数相比于传统的激活函数具有更好的特性.

采用本文设计的具有生物特性的函数与原激活函数相结合作为其非线性激活函数. 细胞神经网络模型可以描述为

$\begin{split} \frac{{{\rm{d}}{x_j}}}{{{\rm{d}}t}} =\; & - {x_j} + {a_j}f({x_j}) + \sum\limits_{ k = i,~ k \ne j }^n {A_{jk}}f({x_k}) \\ & + \sum\limits_{ k = i,~ k \ne j }^n {{S_{jk}}{x_k} + } {I_j}, \end{split}$

其中, a_j, A_jk和S_jk取常数, f (x_j)为MFCS和激活函数加和而成的MFCS激活函数. 当a_j, A_jk和S_jk取一些特定的值时, 可以呈现具有丰富动力学特性的混沌现象. 设六阶细胞神经网络的细胞参数为

$ \left\{ \begin{aligned}&{{{S}}_{{{jk}}}}\!=\!\left\{ \!\!{\left. {\begin{array}{*{20}{c}}0&0&{{S_{13}}}&{{S_{14}}}&0&0\\0&{{S_{22}}}&{{S_{23}}}&0&0&0\\{{S_{31}}}&{{S_{32}}}&0&0&0&0\\{{S_{41}}}&0&0&{{S_{44}}}&0&0\\{{S_{51}}}&{{S_{52}}}&0&0&{{S_{55}}}&0\\0&{{S_{62}}}&0&0&{{S_{65}}}&{{S_{66}}}\end{array}}\!\!\right\}} \right.,\\&{{{a}}_{{i}}} = [\;\begin{matrix}0 & 0 & 0 & 0 & 0 &0 \end{matrix}\;],\\&{I_1} = {I_2} = {I_3} = {I_4} = {I_5} = {I_6} = 0,\\&{A_{24}} = 4,\;{\text{其余}}{A_{jk}}=0.\end{aligned} \right.$

则此MFCS混沌细胞神经元模型可以描述为

$\left\{ \begin{aligned} &{{\dot x}_1} = {S_{13}}{x_3} + {S_{14}}{x_4}, \\ &{{\dot x}_2} = {S_{22}}{x_2} + {S_{23}}{x_3} + {A_{24}}f({x_4}), \\ &{{\dot x}_3} = {S_{31}}{x_1} + {S_{32}}{x_2}, \\ &{{\dot x}_4} = {S_{41}}{x_1} + {S_{44}}{x_4}, \\& {{\dot x}_5} = {S_{51}}{x_1} + {S_{52}}{x_2} + {S_{55}}{x_5}, \\ &{{\dot x}_6} = {S_{62}}{x_2} + {S_{65}}{x_5} + {S_{66}}{x_6}, \end{aligned} \right.$

其中,

$\begin{split} f({x_4}) =\;& Ac{{\rm{e}}^{ - q\left| {{x_4}} \right|}}\left[ \sin \left( {\frac{{{x_4}{\rm{\pi }}}}{{{\varepsilon _1}{{\rm{e}}^{ - m\left| {{x_4}} \right|}}}}} \right) \right.\\ &\left.+ \sin \left( {\frac{{2{x_4}{\rm{\pi }}}}{{{\varepsilon _2}{{\rm{e}}^{ - n\left| {{x_4}} \right|}}}} + \varphi } \right) \right] + g({x_4}), \\ g({x_4}) =\;& \frac{1}{2}\left( {\left| {{x_4} + 1} \right| - \left| {{x_4} - 1} \right|} \right). \end{split} $

此处, 参数S_jk, A₂₄, A, c, q, m, n, ${\varepsilon _1}$, ${\varepsilon _2}$, φ均为常数; g(x)为原激活函数. 当参数取适当的值时, 将会产生混沌现象. 例如参数取值如表2所列, 系统产生的混沌吸引子相图见图6, 图中的x, y, z, w, u和v分别对应(8)式中的x₁, x₂, x₃, x₄, x₅和x₆.

参数	参数值		参数	参数值		参数	参数值		参数	参数值
S13	–1.0		S41	98		S65	4.0		m	10.6
S14	–1.0		S44	–105		S66	–4.0		n	0.1
S22	–1.3		S51	1.0		A24	5.0		${\varepsilon _1}$	0.04
S23	2.0		S52	18		A	0.5		${\varepsilon _2} $	0.02
S31	13.0		S55	–1		c	0.25		φ	$ - {{\text{π}} / {{4}}} $
S32	–14.0		S62	100		q	–1.0

表2与图6相对应的参数取值
Table2.Values of parameters corresponding Fig. 6

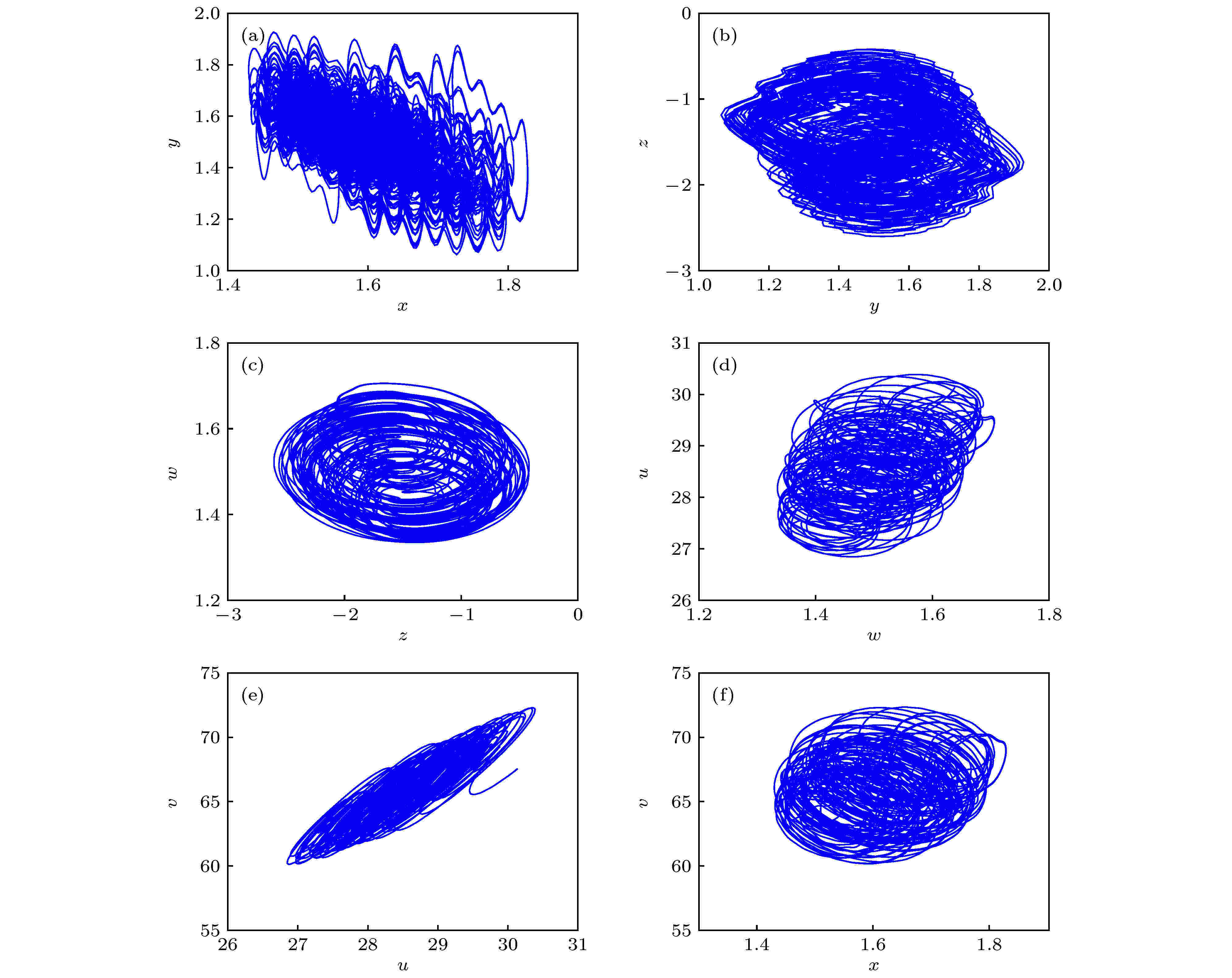图 6 混沌吸引子相图
Figure6. Chaotic attractors of the MFCS chaotic cell neuron model.

Lyapunov指数可以表征系统运动的特征, 通过计算得到该混沌神经元系统的Lyapunov指数为LE1 = 5.2631, LE2 = –0.0005, LE3 = –0.9956, LE4 = –4.0100, LE5 = –7.5025, LE6 = –104.0340, Lyapunov维数DL = 2.2986.
2

-->

3.1.MFCS混沌细胞神经网络复杂性分析

由于本文采用的混沌细胞神经元模型使用的是MFCS激活函数, 这使生成的MFCS混沌细胞神经网络系统具有复杂的动力学行为.
为了更加深入分析MFCS混沌细胞神经元模型特性, 以及它相对于传统的细胞神经网络所表现出的更为复杂的动力学特性, 画出其随参数m变化的Lyapunov指数谱图, 同时使用一种基于结构复杂度的算法——SE复杂度算法^[22]和C0复杂度算法^[23,24]. 这种基于结构复杂度的算法, 时间序列复杂性越大, 随机性越大, 序列能够恢复成原序列越困难. 对于SE复杂度算法, 当序列的功率谱变化越稳定, 相对应的结构则越简单, 振幅越不明显; 对于C0复杂度算法, 不规则的部分越多, 其对应时域信号越接近随机序列, 而序列的复杂性也越大. 图7为画出的三维SE图与C0图.
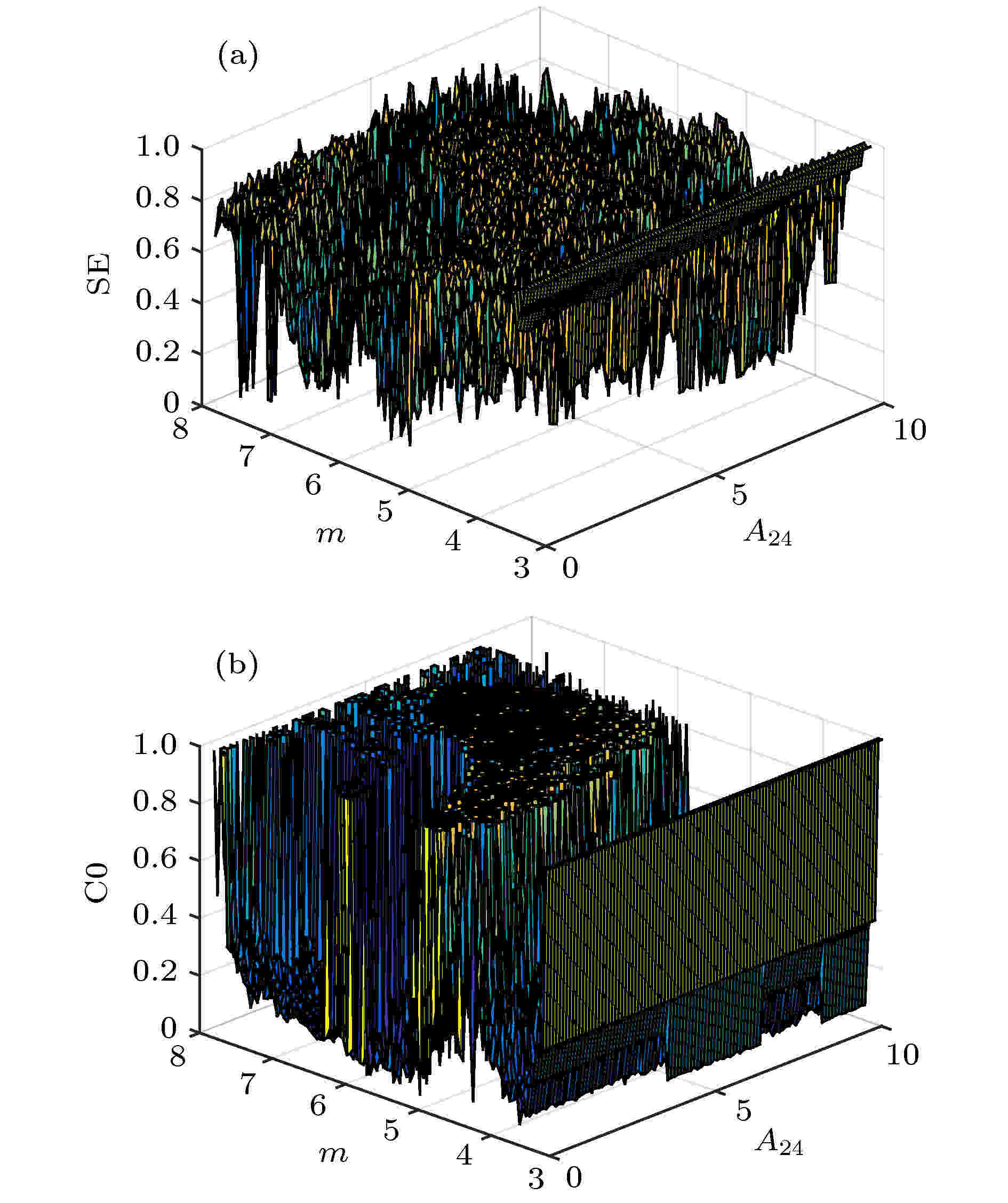图 7 系统的三维复杂度　(a) SE图; (b) C0图
Figure7. Three-dimensional complexity of the system: (a) The complexity of the SE; (b) the complexity of the C0.

从SE图和C0图可知, 当系统处于周期态时, 其SE和C0复杂度最小, 反之系统处于混沌态时, 其SE和C0复杂度大. 为清楚起见截取A₂₄ = 5时随m变化的SE图和C0图, 如图8所示. 可以看出, 在m = 3.5与m = 7.8等窗口处, 系统处于周期状态, 对应的SE与C0的值也比较小. 当处于m = 4.7与m = 6.5等窗口处时, 其SE与C0的值比较大, 说明此时系统处于混沌状态.
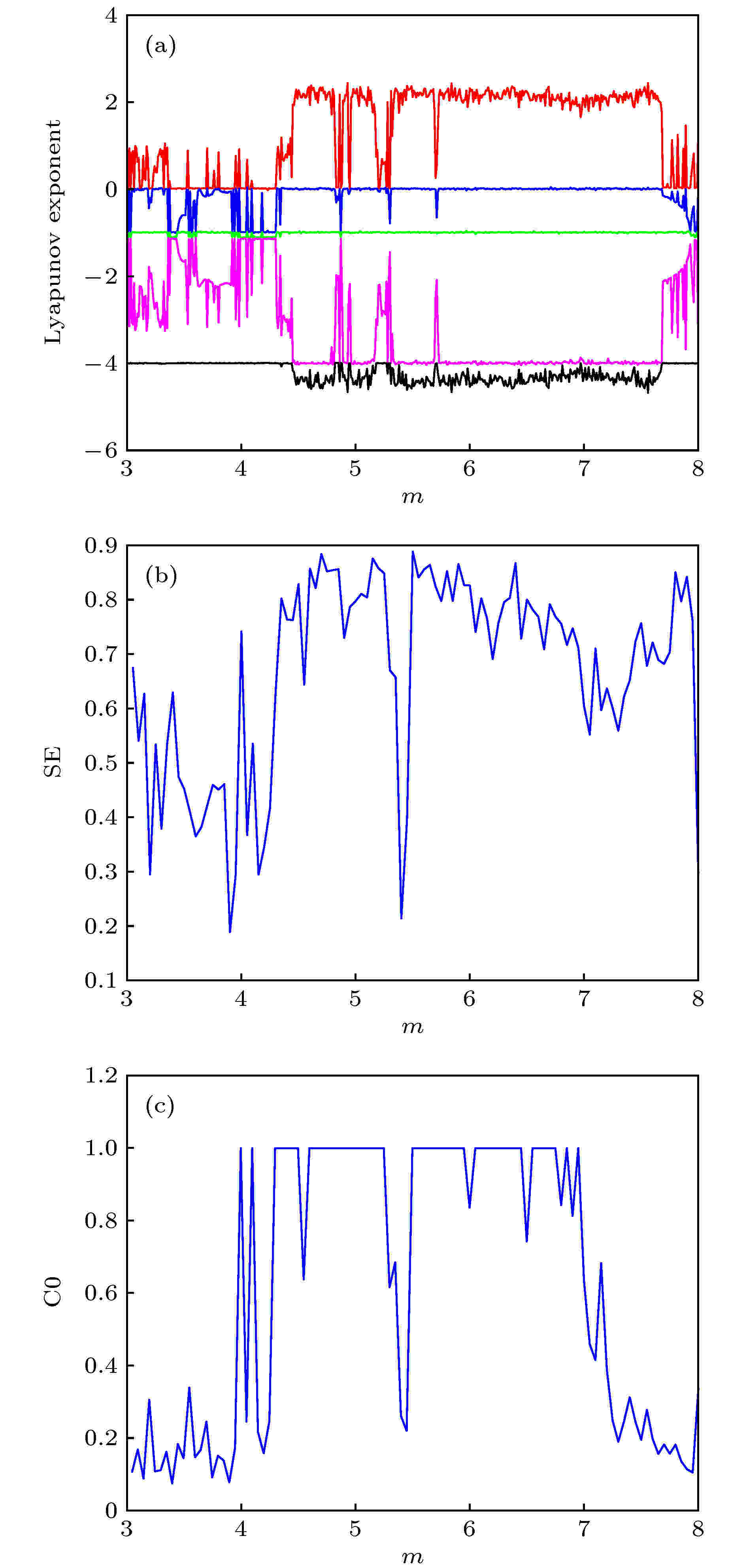图 8 系统的二维复杂度　(a) Lyapunov指数谱; (b) SE图; (c) C0图
Figure8. Two-dimensional complexity of the system: (a) Lyapunov exponents; (b) the complexity of SE; (c) the complexity of C0.

2 -->

3.2.MFCS激活函数对系统动力学特性影响

本文取MFCS激活函数中几个具有代表性的参数c, q和n, 分析MFCS激活函数对细胞神经网络的影响. 其中c代表着MFCS激活函数的比例系数, q为控制幅度A的参数, n为控制频率变化的参数. 随着参数c, q, n的改变, 系统也将处于不同的状态. 固定初始条件(0.1, 0.2, 0.3, 0.4, 0.5, 0.6), 令参数c, q, n分别在一定区间内变化, 其他参数的取值如表3所列, 对应的系统的分岔图与Lyapunov指数谱如图9、图11和图13所示, 相应的相图如图10、图12和图14所示.

参数	参数值		参数	参数值
A24	5		${\varepsilon _1}$	0.04
A	0.5		${\varepsilon _2}$	0.02
m	10.6		φ	$ - {{\text{π}} / {\rm{4}}}$

表3参数c, q, n取不同值时, 其他参数的取值
Table3.Values of other parameters when changing c, q, n.

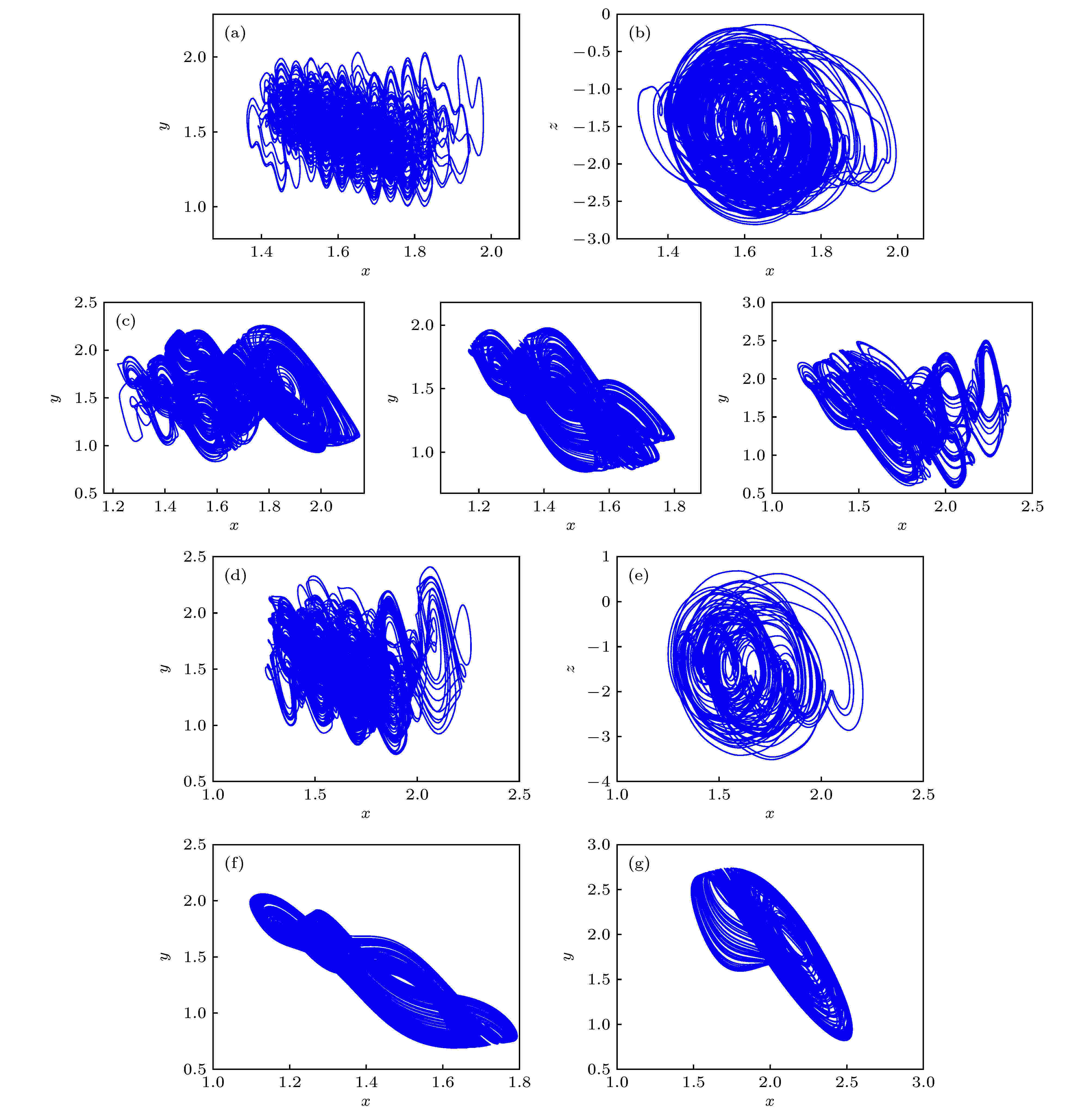图 10 系统随参数n变化的相图　(a) n = 0.2; (b) n = 0.53; (c) n = 0.61; (d) n = 0.7; (e) n = 1.62; (f) n = 2.98; (g) n = 3.16
Figure10. Chaotic attractors of the system changing with parameter n: (a) n = 0.2; (b) n = 0.53; (c) n = 0.61; (d) n = 0.7; (e) n = 1.62; (f) n = 2.98; (g) n = 3.16.

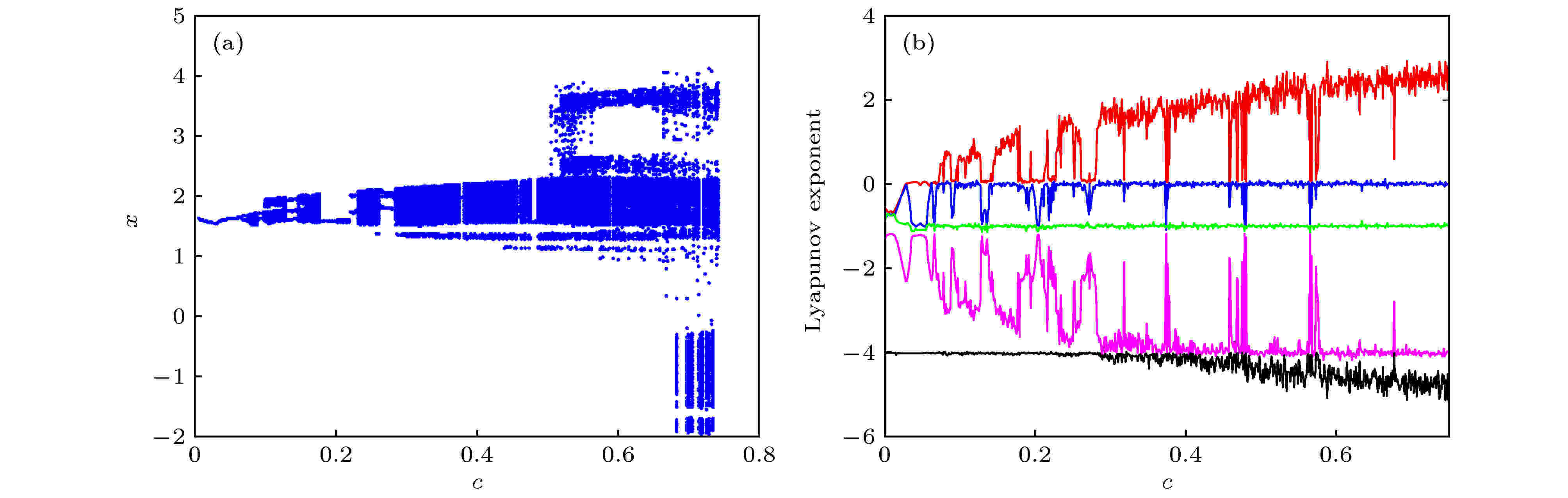图 11 系统随参数c变化的分岔图和Lyapunov指数谱　(a)分岔图; (b) Lyapunov指数谱
Figure11. Bifurcation diagram and Lyapunov exponential spectrum of the system varying with c: (a) Bifurcation diagram; (b) Lyapunov exponents.

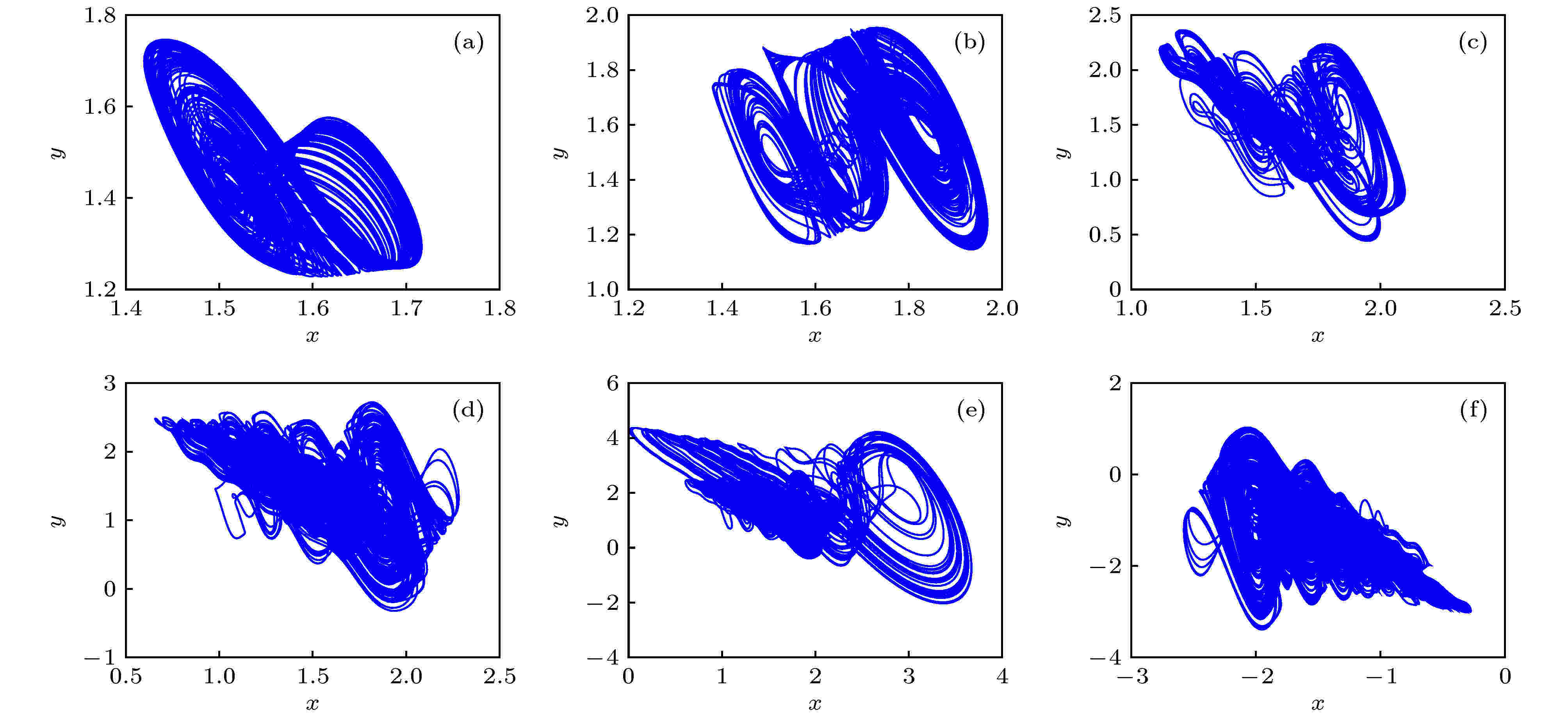图 12 系统随参数c变化的相图　(a) c = 0.08; (b) c = 0.118; (c) c = 0.25; (d) c = 0.50; (e) c = 0.52; (f) c = 0.73
Figure12. Chaotic attractors of the system changing with parameter c: (a) c = 0.08; (b) c = 0.118; (c) c = 0.25; (d) c = 0.50; (e) c = 0.52; (f) c = 0.73.

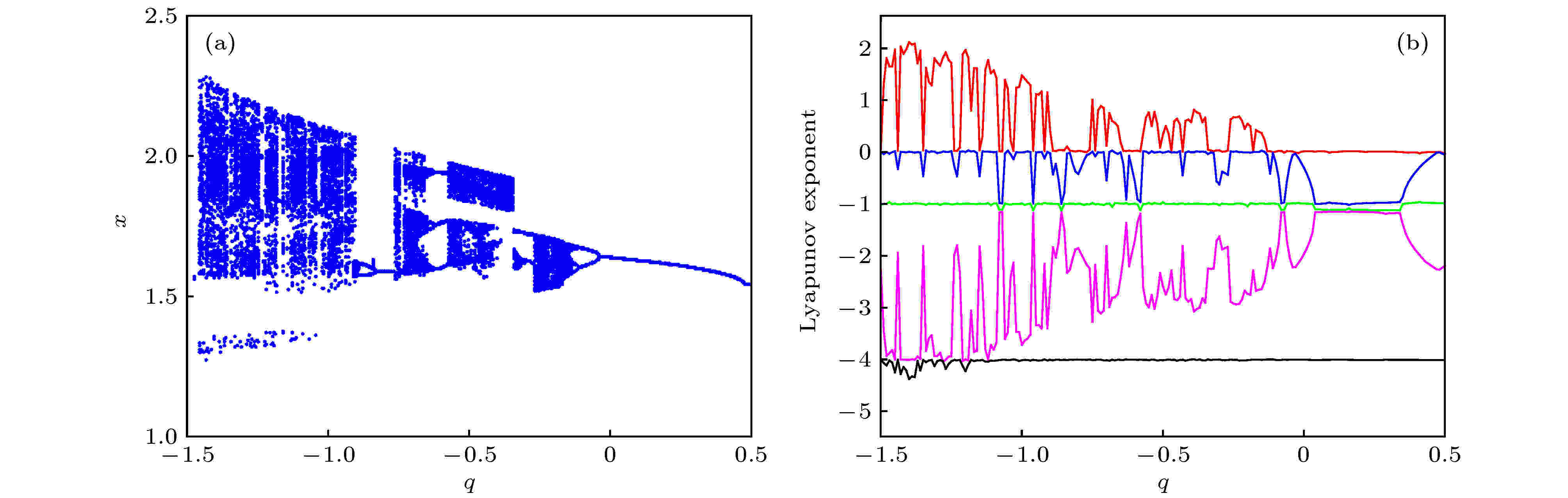图 13 系统随参数q变化的分岔图和Lyapunov指数谱　(a)分岔图; (b) Lyapunov指数谱
Figure13. Bifurcation diagram and Lyapunov exponential spectrum of the system varying with q: (a) Bifurcation diagram; (b) Lyapunov exponents.

图 14 系统随参数q变化的相图　(a) q = –1.26; (b) q = –0.75; (c) q = –0.38; (d) q = –0.25
Figure14. Chaotic attractors of the system changing with parameter q: (a) q = –1.26; (b) q = –0.75; (c) q = –0.38; (d) q = –0.25.

3 -->

3.2.1.MFCS激活函数参数n对系统动力学特性的影响

当n在区间[0, 5]变化时, c和q的取值分别为c = 0.25和q = –1, 其余参数如表3所列, 系统的分岔图及Lyapunov指数谱如图9所示.
图 9 系统随参数n变化的分岔图和Lyapunov指数谱　(a)分岔图; (b) Lyapunov指数谱
Figure9. Bifurcation diagram and Lyapunov exponential spectrum of the system varying with n: (a) Bifurcation diagram; (b) Lyapunov exponents.

在MFCS激活函数中, n为控制频率变化的参数. 从图9看出, 随着参数n的增大, 系统处于混沌状态而后又通过逆倍周期分岔逐渐演变为周期状态. 因此, 在n > 3.2的频率范围内, 系统不出现复杂现象.
另外, 在此演化过程中还出现了多次阵发混沌现象. 其分岔图整体可以分为4个部分: [0, 0.5], [0.5, 0.8], [0.8, 2.75]和[2.75, 4]. 当n处于[0, 0.5]时, 系统处于混沌状态, 其吸引子形状较为复杂, 如图10(a)所示; 当n处于[0.5, 0.8]时, 系统处于周期与混沌交替的状态, 此时系统分岔图的结构相对于区间[0, 0.5]比较简单, 区间也比较小, 反映至相图上, 即相图呈现出较第一部分更为简单的吸引子相图交替出现, 如图10(b)—(d)所示; 当n处于区间[0.8, 2.75]时, 系统又处于一个较为复杂的阶段, 此时系统的混沌吸引子以更复杂的线轨呈现出来, 如图10(e)所示; 当n处于区间[2.75, 4]时, 系统的分岔图逐渐趋于简单化最终演变为周期, 期间的混沌吸引子如图10(f)和图10(g)所示.
3 -->

3.2.2.MFCS激活函数参数c对动力学特性的影响

当c在区间[0, 1]变化时, q和n的取值分别为q = －1和n = 2.5, 其余参数如表3所列, 可画出系统的分岔图及Lyapunov指数谱如图11所示.
由图11可知, 系统逐渐由周期轨道通过周期分岔演变为混沌状态. 参数c为MFCS激活函数的比例系数, 当c越大时, MFCS函数在细胞神经网络中所占的比例也就越大. 随着参数c逐渐增大, 变量x的混沌映射区间(幅值)也逐渐增大. 当c运行至0.51与0.7时, 出现混沌映射区间突然增大的现象, 此时系统的吸引子也变得更为复杂. 这一现象也验证了参数c越大, MFCS函数所占的比重越大, 系统变量的混沌映射区间也越大, 其动力学特性也更为丰富多变. 其典型的混沌吸引子见图12.
3 -->

3.2.3.MFCS激活函数参数q对动力学特性的影响

当q在区间[–1.5, 0.5]变化时, c和n的取值分别为0.25和2.5, 其余参数如表3所列, 系统的分岔图及Lyapunov指数谱如图13所示.
MFCS激活函数中, q为控制幅度A的参数. 可以看出, 随着参数q的增大, 系统通过几个逆倍周期分叉窗口逐渐从混沌演变至周期, 在整个演化过程中有多次周期轨道与混沌轨道的切换, 这对系统激活函数的幅度提出了一定的限制. 例如当q∈[–0.7, –0.63]系统处于混沌轨道, 当q∈[–0.63, –0.58]系统处于周期轨道. 类似地, 在区间[–0.5, 0]内, 系统经历了多次混沌轨道与周期轨道切换的过程, x-y相平面吸引子随q变化的几种典型相图如图14所示.
从图9、图11和图13看出, 当系统分别随参数c, q和n变化时, 所产生的混沌吸引子的Lyapunov指数都较大, 其中随参数n变化时, 最大Lyapunov指数为5.263, 随参数c变化时, 最大Lyapunov指数为2.5211, 而随参数q变化时最大Lyapunov指数也有2.0655. 大的Lyapunov指数反映了系统在初值变化时其轨道之间的分离程度, 即具有更好的初值敏感性. 这说明在MFCS激活函数作用下系统会产生更为复杂的混沌动力学行为, 其吸引子相图较一般的混沌神经网络系统也显得更为丰富, 如图15所示.
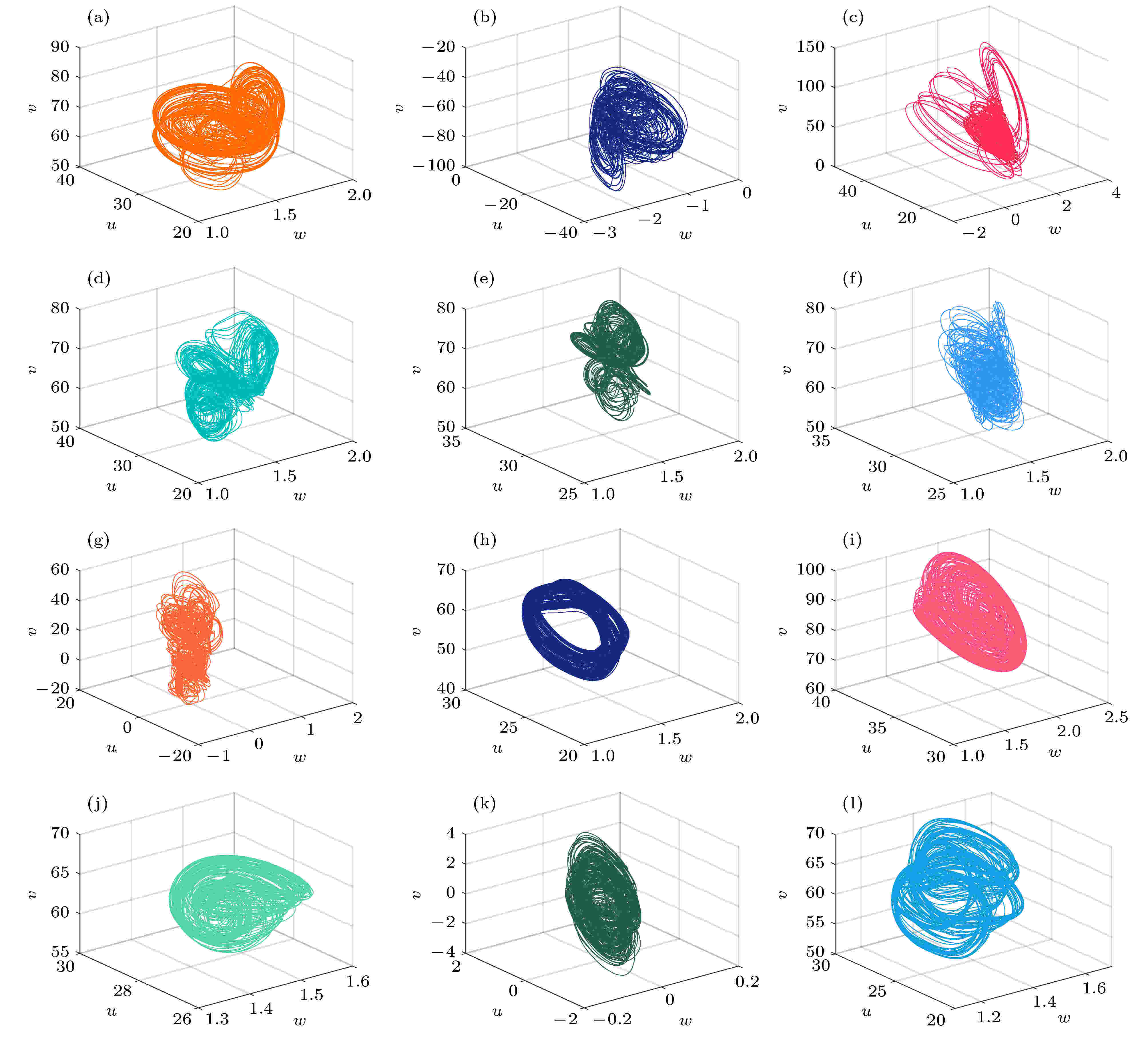图 15 系统随参数c, q, n变化的几种典型相图　(a) c = 0.25, q = –1, n = 2.5; (b) c = 0.73, q = –1, n = 2.5; (c) c = 0.52, q = –1, n = 2.5; (d) c = 0.25, q =–1, n = 0.715; (e) c = 0.118, q = –1, n = 2.5; (f) c = 0.25, q = –1, n = 0.2; (g) c = 0.73, q = –0.9, n = 2.5; (h) c = 0.25, q = –1, n = 2.98; (i) c = 0.25, q = –1, n = 3.16; (j) c = 0.08, q = –1, n = 2.5; (k) c = –0.25, q = –0.9, n = 2.5; (l) c = 0.25, q = –1, n = 0.61
Figure15. Several typical chaotic attractors of the system changing with parameter c, q, n: (a) c = 0.25, q = –1, n = 2.5; (b) c = 0.73, q = –1, n = 2.5; (c) c = 0.52, q = –1, n = 2.5; (d) c = 0.25, q =–1, n = 0.715; (e) c = 0.118, q = –1, n = 2.5; (f) c = 0.25, q = –1, n = 0.2; (g) c = 0.73, q = –0.9, n = 2.5; (h) c = 0.25, q = –1, n = 2.98; (i) c = 0.25, q = –1, n = 3.16; (j) c = 0.08, q = –1, n = 2.5; (k) c = –0.25, q = –0.9, n = 2.5; (l) c = 0.25, q = –1, n = 0.61.

2 -->

3.3.非线性系统的共存动力学行为

当系统设置参数A₂₄ = 5, A = 0.5, c = 0.25, m = 5.6, n = 2.5, q = –1, ${\varepsilon _1}$ = 0.02, ${\varepsilon _2}$ = 0.04和φ =$ - {{\text{π}} {\text{/}}{\rm{4}}} $时, 状态变量x随着初始条件[0.1, y(0), 0.3, 0.4, 0.5, 0.6]中$y(0) \in [ - 2, \;2]$的变化, 系统的Lyapunov指数谱和分岔图如图16所示.
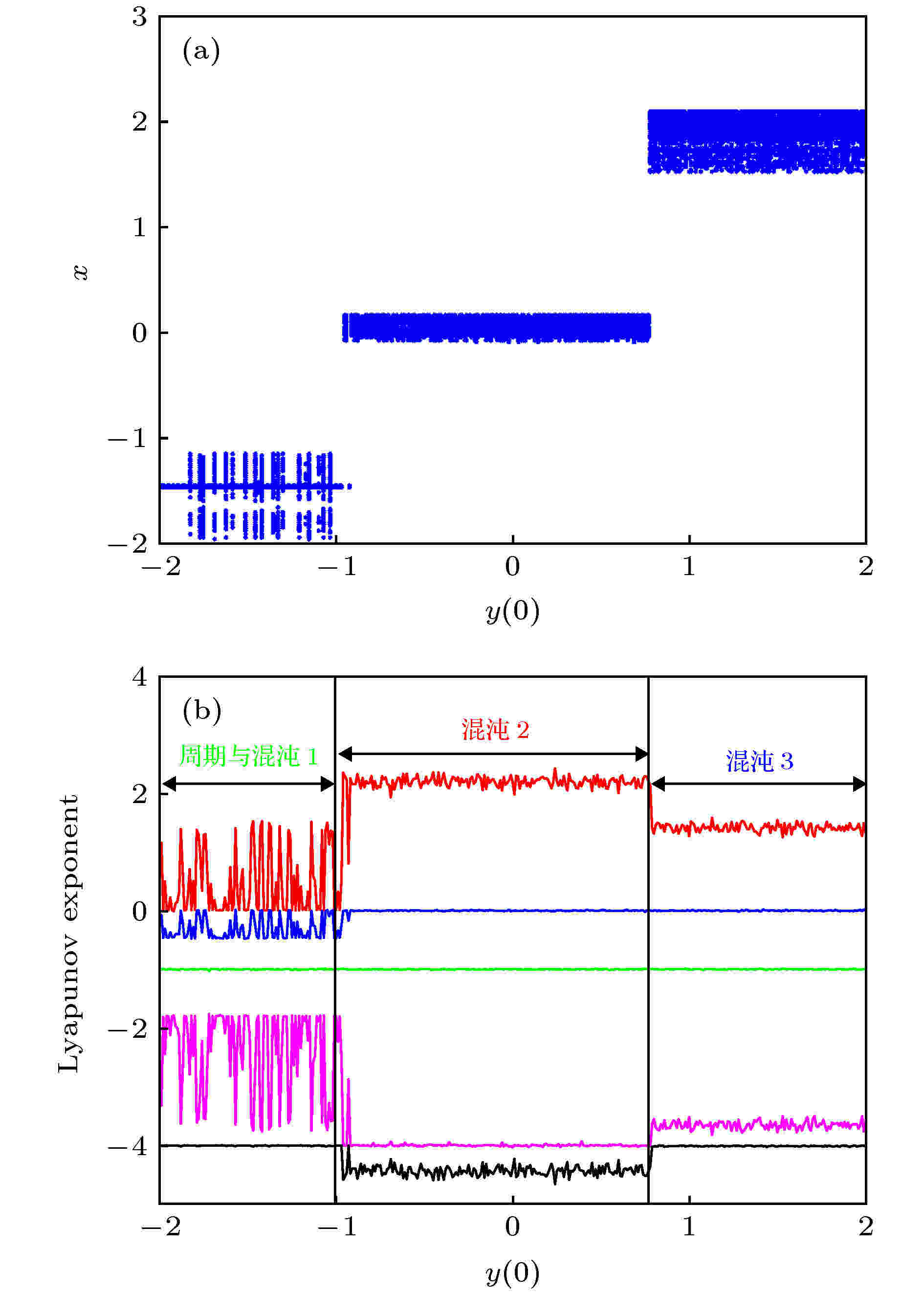图 16 系统随初始值y(0)变化的分岔图和Lyapunov指数谱　(a)分岔图; (b) Lyapunov指数谱
Figure16. Bifurcation diagram and Lyapunov exponential spectrum of the system varying with the initial value y(0): (a) Bifurcation diagram; (b) Lyapunov exponents.

可以看出, 系统大多数时间都处于混沌状态, 其运动轨迹大致分为三部分. 第一部分处于周期轨道和混沌轨道相互切换的状态; 第二部分和第三部分处于混沌状态, 且在y(0)等于–1和0.8的情况下, 系统的混沌轨道发生了两次跳变, 其吸引子类型与形状随之改变, 如图17所示. 当y(0)处于区间[–2, –1]时, 系统大部分时间处于周期状态, 但期间存在多次周期轨道与混沌轨道的切换. 当y(0)处于区间[–1, 2]时, 系统处于混沌状态, 但是当y(0)处于0.8时, 混沌发生了跳变如图16所示.
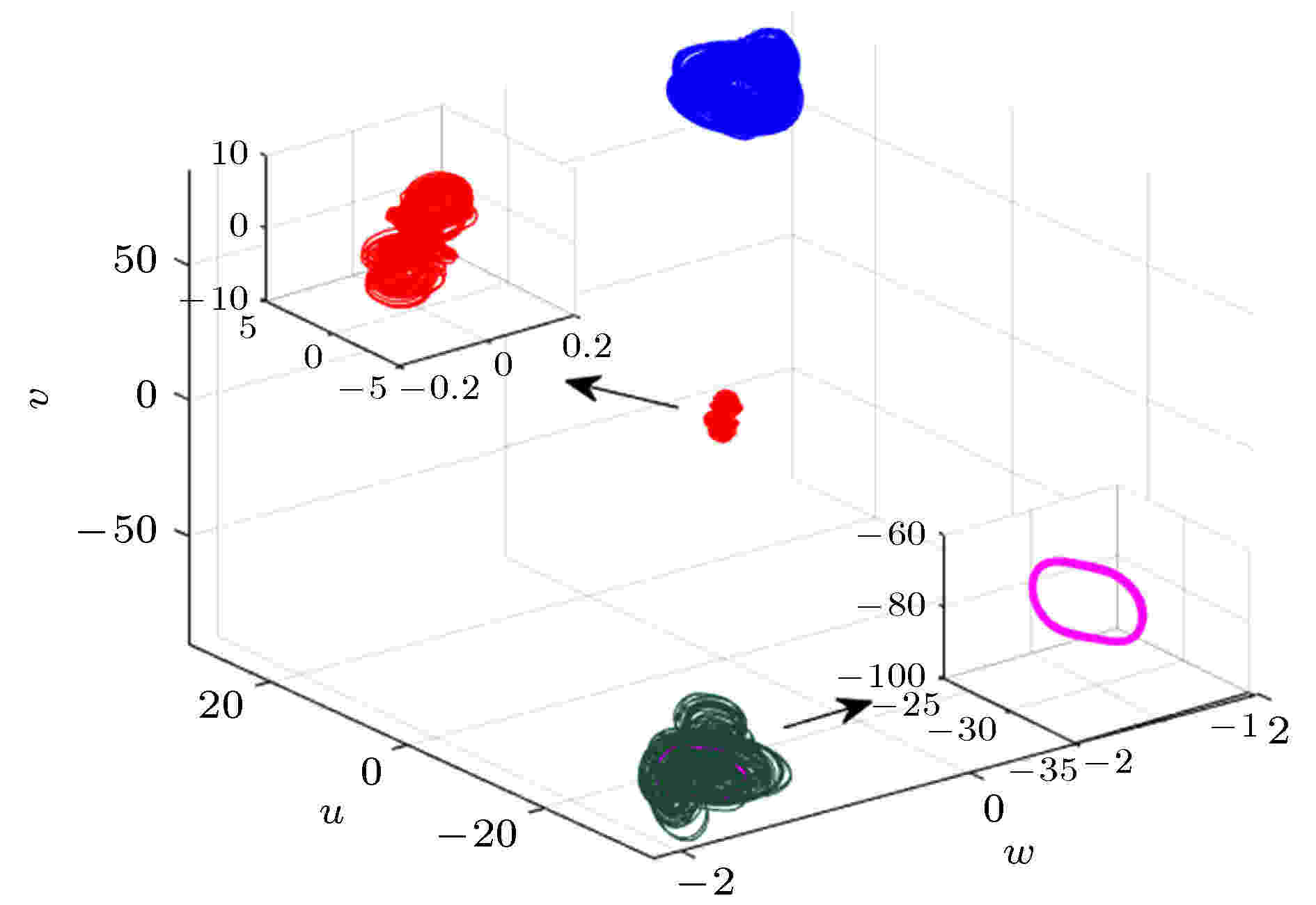图 17 系统随初始值y(0)变化的相图-共存吸引子
Figure17. Chaotic attractors of the system changing with the initial value y(0)-coexistence attractor.

共存吸引子是系统参数固定时, 初值变化引起的不同动力学行为, 其本质反映论文系统的敏感性, 但与传统的初值敏感性有所不同. 传统的初值敏感性一般指在同一个混沌吸引子中, 由于初值的微小扰动而引起混沌轨道的快速分离. 而共存吸引子是指初值变化时系统产生的不同动力学特性的吸引子, 如混沌、周期和点吸引子等, 或具有系统动力学特性但特征不同的吸引子. 因此也把共存吸引子分为两类, 一类是具有相同动力学行为的不同吸引子, 称之为同质共存吸引子; 另一类是具有不同动力学行为的不同吸引子, 称之为不同质的共存吸引子. 若一个混沌系统具有共存吸引子, 说明该混沌系统对初值更为敏感, 也具有更复杂的动力学行为, 系统在信息加密和保密通信等方面也具有更好的应用价值.
一个系统在不同的参数下, 具有很多不同的共存吸引子不算特别, 但本文所述的MFCS混沌细胞神经网络在固定参数数值的情况下, 依然具有十分丰富的共存吸引子. 不同类型的吸引子共存在一起是系统多稳定性的体现. 多稳定性可用于图像处理等领域, 因此在许多保密工程中, 它被视为另一个随机序列的来源. 如果取表4中的参数值, 系统可产生多种共存吸引子, 几个典型的例子如图18所示. 可以看出, 随着初值的变化, 系统将会产生多种共存现象. 其中有I_c型、II_c型和III_c三种类型的共存混沌吸引子, 如图18(a)和表4所列. 此外还存在混沌吸引子与极限环共存的情况, 如图18(b)所示; 也存在I_p型和II_p两种极限环的共存现象, 如图18(c)所示. 每种共存吸引子的性质与初值条件如表5所列.

参数	参数值		参数	参数值
A24	5		q	–1
A	0.5		${\varepsilon _1}$	0.04
m	5.6		${\varepsilon _2}$	0.02
n	2.5		φ	$ - {{\text{π}} / {\rm{4}}}$

表4与图18相对应的参数的取值
Table4.Values of parameters corresponding Fig. 18.

性质	类型	初始条件
混沌吸引子与 混沌吸引子	Ic型、 IIc型	(0.2, 0.2, 0.3, 0.4, 0.5, 0.6), (0.52, 0.2, 0.3, 0.4, 0.5, 0.6)
	Ic型、 IIIc型	(0.2, 0.2, 0.3, 0.4, 0.5, 0.6), (–0.5, –1.2, 0.3, 0.4, 0.5, 0.6)
	IIc型、IIIc型	(0.52, 0.2, 0.3, 0.4, 0.5, 0.6), (–0.5, –1.2, 0.3, 0.4, 0.5, 0.6)
混沌吸引子 与极限环	IIc型、Ip型	(0.82, 1.5, 0.3, 0.4, 0.5, 0.6), (5.5, 5.81, 0.305, 0.4, 0.5, 0.6001)
	IIIc型、IIp型	(–0.8, –1.5, 0.3, 0.4, 0.5, 0.6), (0.1, –1.51, 0.3, 0.4, 0.5, 0.6)
极限环与 极限环	Ip型、IIp型	(5.5, 5.81, 0.305, 0.4, 0.5, 0.6001), (0.1, –1.51, 0.3, 0.4, 0.5, 0.6)

表5初始条件的取值
Table5.Values of initial conditions.

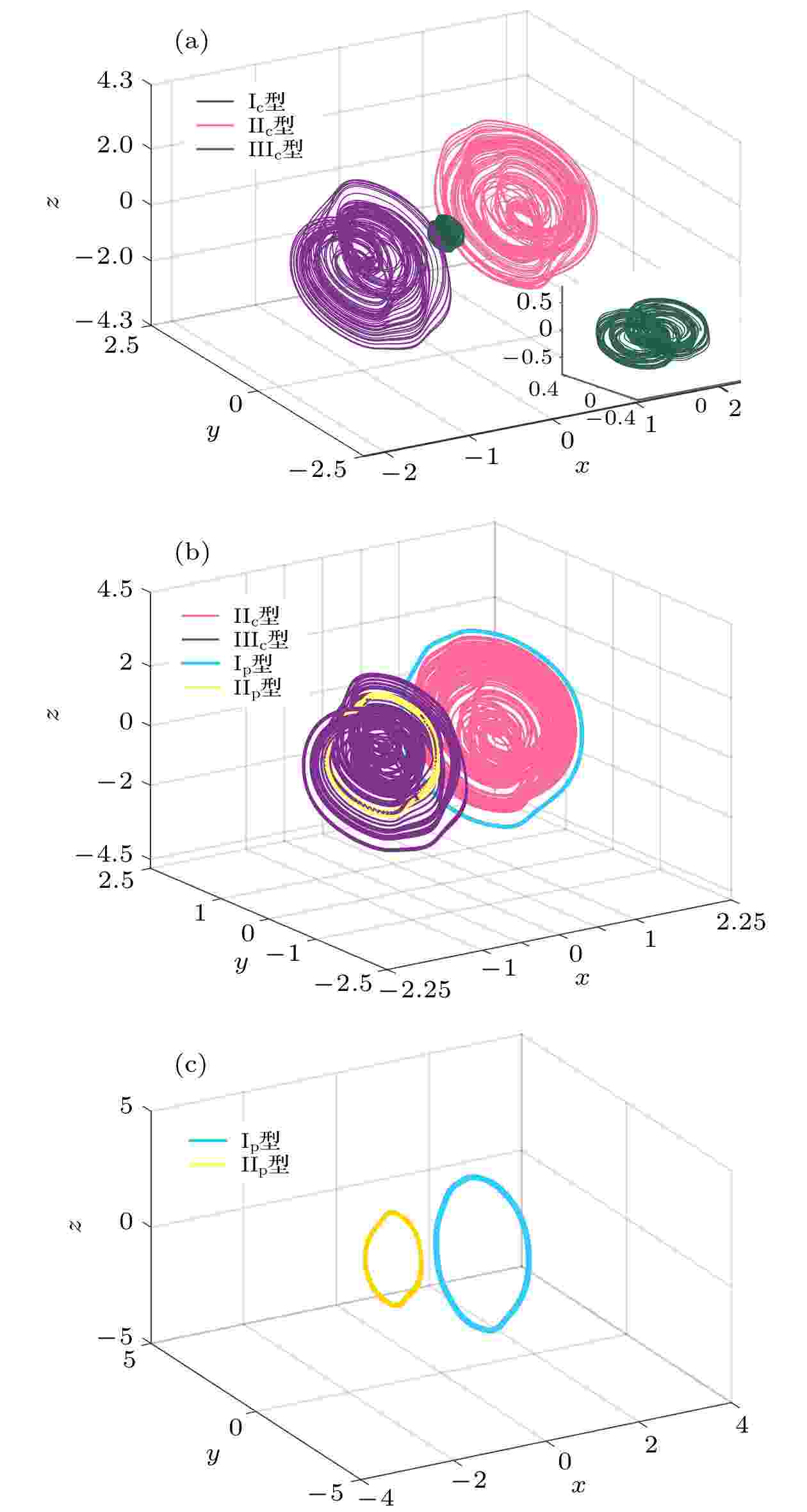图 18 系统在x-y-z平面的共存吸引子　(a) 混沌吸引子共存; (b) 混沌吸引子与极限环共存; (c) 极限环共存
Figure18. Coexistence attractor of the system in the x-y-z plane: (a) Chaotic attractors coexist; (b) chaos attractors coexist with limit cycles; (c) limit cycles coexist.

从图17、图18和表5看出, 系统产生的II_c型、III_c型吸引子相互对称, 分别从初始状态(0.52, 0.2, 0.3, 0.4, 0.5, 0.6)和(–0.5, –1.2, 0.3, 0.4, 0.5, 0.6)出发, 但这两种吸引子的初始条件并不对称, 显然其对称性来自系统本身. 系统关于初值x(0)-y(0)和x(0)-z(0)的吸引盆如图19所示, 其中不同的颜色区域代表不同种类的共存吸引子. 图19(a)中橙色代表II_p型, 红色代表II_c型, 蓝色代表I_p型; 图19(b)中橙色代表I_c型, 红色代表II_c型, 蓝色代表I_p型.
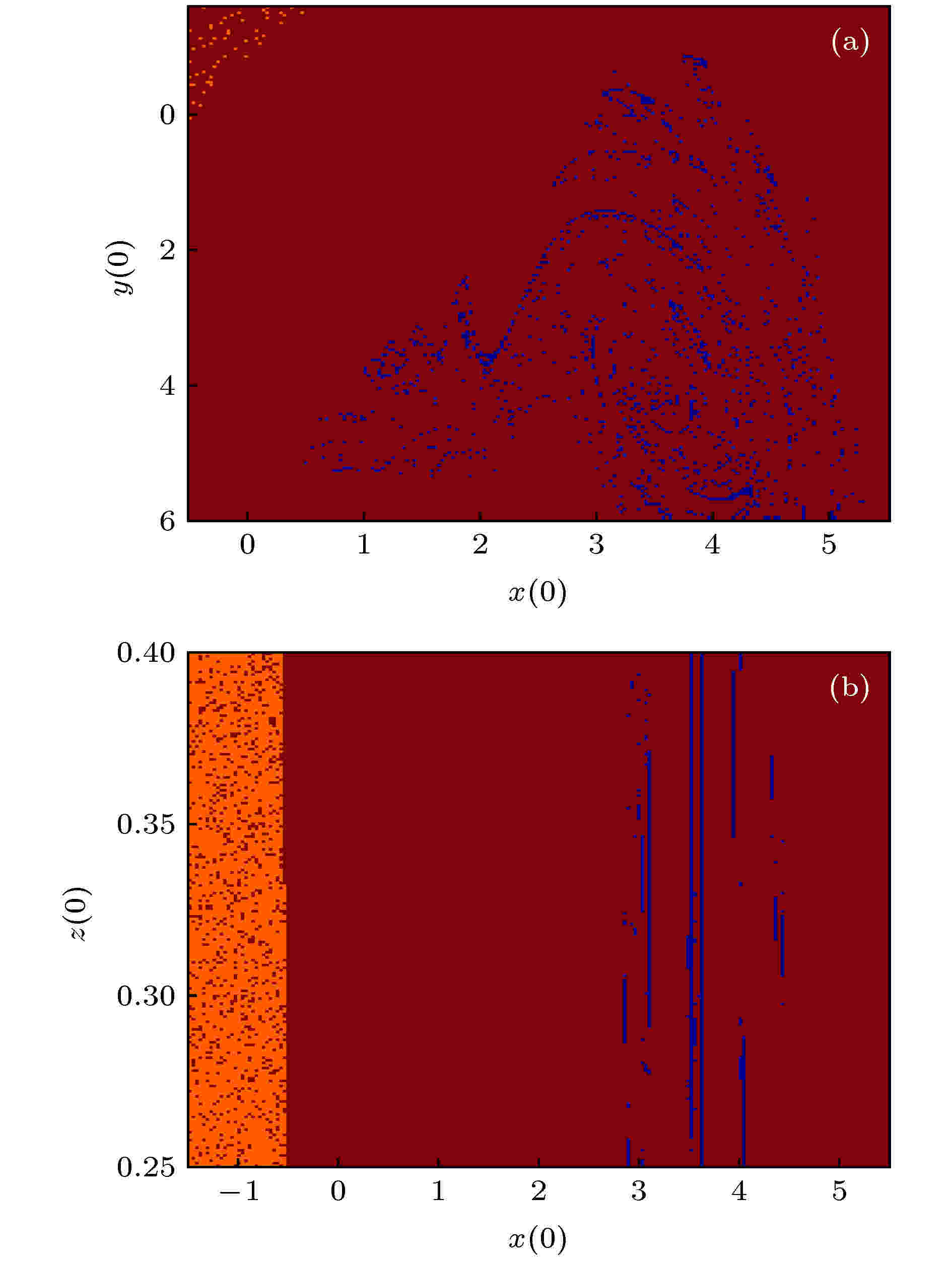图 19 系统随x(0), y(0), z(0)变化的吸引盆　(a)系统随x(0), y(0)变化的吸引盆; (b)系统随x(0), z(0)变化的吸引盆
Figure19. Suction basin of the system varying with x(0), y(0) and z(0): (a) The suction basin of the system varying with x(0), y(0); (b) the suction basin of the system varying with x(0), z(0).

本文基于多频-变频正弦函数设计了一种新的激活函数, 此激活函数不仅具有激活函数的特性, 而且还具有一定的生物特性. 将此激活函数应用于细胞神经网络中, 提出了一种基于多频-变频正弦激活函数的混沌细胞神经网络. 分析发现激活函数中的参数显著影响系统的动力学特性, 使混沌细胞神经网络产生了系列复杂动力学行为, 包括各类混沌吸引子和周期吸引子, 以及各类共存吸引子等, 提升了混沌神经网络的性能, 使得其在信息处理、信息加密等方面具有较好的前景.