摘要:因为在生物安全性和导入效率等方面的优势, 基于力学方法实现基因导入日益得到学术界的重视. 本文提出了一种基于零质量射流, 对微管道中运动的细胞施加流体作用力, 引起其发生变形, 进而促使细胞膜上力敏通道开启的方法, 并通过数值模拟进行了理论验证. 本文采用浸没有限元法, 对红细胞在微管道内运动过程中受到零质量射流作用的变形情况进行数值模拟, 探讨了如何高效地实现小分子物质导入细胞. 数值模拟的重要参数有微管道内压力梯度Δp, 零质量射流的振幅A_m和频率f. 经过对流场特征和红细胞受力情况的分析, 发现当细胞某处表面张力T₀大于临界表面张力 τ _c时, 细胞表面力敏通道打开, 并得到每一时刻细胞力敏通道打开的百分比P_open. 本文定义了通道开启积分I, 以衡量在不同的流动参数情况下, 细胞膜力敏通道的开启程度, 进而探讨了压力梯度和射流振动频率、振幅对I值的影响, 以寻找优化的工艺参数. 该方法具有微制造工艺简单易行, 在保证高通量导入的同时, 便于对所施加的流体作用力进行精确控制的特点, 这使得蛋白质、基因等物质实现跨膜输运, 进入细胞并发生重编程成为可能.
关键词: 浸没有限元法/
零质量射流/
力敏通道/
跨膜输运

English Abstract

全文HTML

--> --> -->

细胞重编程(cell reprogramming)是细胞生物学领域的一项关键技术, 在再生医药、疾病模型和药物筛选等方面有着广泛应用. 以往的研究表明^[1], 诱导多功能干细胞(induced pluripotent stem cells, IPSCS)可由特定转录因子的异位表达使躯体干细胞发生细胞重编程得到. 基因递送(gene delivery)技术通过将目的基因导入细胞, 也可以诱导细胞重编程发生.
实现基因跨细胞递送主要有生物和物理方法. 生物方法包括基因转化(transformation)、接合(conjugation) 和转导(transduction)等^[2-4]. 物理方法包括显微注射(microinjection)、粒子轰击(particle bombardment)、基因枪、电穿孔(electroporation)和光学方法等^[5-7]. 目前应用比较广泛的递送方法是病毒转导. 病毒载体能保证诱导多功能干细胞中转基因的稳定表达, 但其存在发生肿瘤等生物安全性方面的风险^[8]. 一些****因而致力于利用蛋白质诱导得到多功能干细胞的研究^[9]. 蛋白质导入细胞常见方法之一是电穿孔. 该方法产生电渗透作用的同时, 可能会随机地使细胞膜发生破裂而导致细胞死亡^[10,11], 而且转染范围也受到电场方向的限制^[12]. 因此, 现有的生物、物理方法, 或者可能会对细胞造成永久性损坏, 甚至死亡; 或者由于病毒转染和基因插入使得细胞发生癌变可能而存在生物安全性方面的隐患; 或者因只能适用于少数种类或者少数数量的细胞等原因而被限制其广泛应用.
运用力学方法使细胞膜发生变形, 可以引起物质跨细胞膜输运, 同时在生物安全性方面具有一定的优势. 通过精确地控制细胞膜的受力, 有可能实现高效的物质输运, 并保证细胞的存活率. 麻省理工大学(MIT)Fetterman等^[13]提出了细胞挤压(cell squeezing)技术, 即驱使细胞通过小于其直径30%—80%的收缩通道, 使其受到挤压发生变形, 促使细胞膜上力敏通道(mechano-sensitive channel)打开^[14]. 目前的研究已证实该方法可运用于很多种类的细胞, 具有应用的广泛性. 但有两个因素制约该方法的发展: 一方面, 该技术需要制备直径仅为数微米的变截面微管道, 对微制造技术要求比较高; 另一方面细胞尺寸制约了输送效率^[15], 且对于非同步群体(asynchronous population), 尺寸过大的细胞可能堵塞通道, 而对于尺寸过小的细胞, 由于细胞膜变形不充分会降低物质的输运效率. 为了处理大小和力学性质不同的细胞种类, 需要设计不同规格的收缩通道^[14], 这导致制造成本变高, 阻碍了该项技术的大规模发展和应用.
近年来, 基于超声波空化(ultrasonic cavitation)效应的声致穿孔(sonoporation)成为基因递送技术中一个相当活跃的领域^[16-20]. 在该方法中, 系统中传播的超声波在液体中产生气泡, 气泡进一步生长并破裂, 在破裂过程中气泡形成射流, 对细胞膜施加一定的流体作用力, 使细胞膜破裂或细胞膜上力敏通道^[21-23]开启, 容许大分子从周围介质进入细胞, 从而实现物质跨细胞输运, 进而诱导细胞发生重编程. 细胞膜上的孔道打开一段时间(毫秒至数秒)后, 外部作用力消失, 基于自修复机理, 细胞膜上的孔道自愈合. 该方法虽然可以同时作用于大量细胞, 导入效率较高, 但由于外部压力对细胞的作用很难均匀控制, 所以难以保证大批量细胞的存活率. 为了克服该方法的不足, Duke大学 Zhong课题组^[24,25]利用激光在介质中的局部加热效应, 形成两个串联的气泡, 二者之间的相互作用引起二次Bjerknes力^[26]产生离开串行气泡中心的射流(速度可达50 m/s)作用于细胞膜. 该方法的射流速度和流体剪切力可以精确控制, 在细胞膜上形成的孔洞直径较大(几百纳米乃至微米量级), 而且保证了细胞的生理功能. 但同样由于装置比较复杂, 目前还只适用于单细胞操作.
近期发展的导入方法有Modaresi等^[27]提出的利用细胞悬浮通过微流控芯片作为破坏细胞膜所需的驱动力来实现物质导入细胞, 该方法提供了一种即插即用(plug-and-play)的新平台技术来实现基因载体和纳米颗粒的胞内传递. 另外, Kizer等^[28]开发了一种基于单纯细胞剪切快速机械变形的无堵塞惯性微流控平台来实现物质跨细胞输运的方法.
本文提出一种基于零质量射流, 对细胞膜施加射流作用, 促使细胞在微管道中发生应力变形, 以打开细胞膜表面力敏通道的方法. 1950年Ingard和Labate^[29]提出了零质量射流(zero-net-mass-flux, ZNMF)的概念, 又被称作合成射流(synthetic jet). 零质量射流通常采用活塞或压电薄膜的往复运动吹/吸流体, 在狭小孔口外形成一系列涡环/对, 向外扩展的过程中这些涡环/对相互融合形成一种动量射流^[30,31]. 自Wiltse和Glezer^[32]于1994年首次将零质量射流方法运用于流动主动控制以来, ZNMF受到了流体力学领域的广泛关注^[33-37].
本文运用浸没有限元(immersed finite element method, IFEM)方法, 研究零质量射流作用于微管道中红细胞运动的过程, 分析不同流动参数下细胞变形和细胞膜力敏通道开启的情况, 以验证该方法的可行性, 为进行该装置的制造和优化设计提供了理论支撑.

2

-->

2.1.浸没有限元法

浸没边界法(immersed boundary method, IBM)由Peskin^[38]于1972年提出, 并运用于模拟心脏受力和周围血流的问题^[39]. 此后, 浸没边界法吸引了大量关注, 并且被广泛地应用在流固耦合问题的数值模拟中. 在该方法中, 运动流体用欧拉网格表示, 固体部分则看作在流体网格上的运动和变形, 用拉格朗日方法描述. 固体和流体的相互作用由光滑离散的Dirac δ函数, 通过差值速度和分布节点力得到^[40]. 在浸没边界法中, 假定浸没的固体是一维的, 并不占据流体区域体积, 因此不能精确反映固体部分的真实情况; 其次, 由于Dirac δ函数连续性的局限性, 其处理几何形状不规则的固体和复杂边界条件不够准确^[41,42]. 为了弥补这些不足, Wang和Liu^[42], Zhang等^[43]提出了浸没有限元法(immersed finite element method, IFEM), 并将其运用于生物流体力学计算中^[44,45].
在浸没有限元法中, 整个计算域Ω由不可压三维可变形固体结构$ \varOmega ^{\rm{s}} $和不可压流体$ \varOmega ^{\rm{f}} $组成(上标s和f分别代表固体和流体). 采用有限元法离散计算网格, 固体部分完全浸没在流体部分之中, 即${\varOmega ^{\rm{f}}} \cup {\varOmega ^{\rm{s}}} = \varOmega, {\varOmega ^{\rm{f}}} \cap {\varOmega ^{\rm{s}}} = \emptyset $. 整个计算区域Ω的流体网格用与时间无关的位置矢量x表示. 位置矢量X^s和x^s(X^s, t)分别表示初始构型$\varOmega _0^{\rm{s}}$和当前构型$ \varOmega ^{\rm{s}} $下的固体物质点. 对于流体的计算, 未知量是速度v和压力p; 对于固体部分$ \varOmega ^{\rm{s}} $, 需要求解的是节点位移u^s, 定义为u^s = x^s – X^s, 即当前构型和初始构型下的位移差. 速度v^s = du^s/dt是位移的物质导数. IFEM的控制方程^[43]如下:

${\rho ^{\rm{f}}}\left(\frac{{\partial {{v}}}}{{\partial t}} + {{v}} \cdot \nabla {{v}}\right) = \nabla {{{\sigma}} ^{\rm{f}}} + {{{F}}^{\rm{FSI}}} + {{F}}_{\rm{ext}}^{\rm{f}} ,~{{X}} \in \varOmega,$

$\nabla \cdot {{v}} = 0,$

${{{v}}^{\rm{s}}}({{{X}}^{\rm{s}}},t) = \int\nolimits_\varOmega {{v}} ({{x}},t)\delta ({{x}} - {{{x}}^{\rm{s}}}({{{X}}^{\rm{s}}},t)){\rm{d}}\varOmega ,$

$ \begin{split}{{{F}}^{{\rm{FSI}},{\rm{s}}}} =\;& \left({\rho ^{\rm{f}}} - {\rho ^{\rm{s}}}\right)\left(\frac{{\partial {{v}}}}{{\partial t}} + {{v}} \cdot \nabla {{v}}\right) + \nabla {\sigma ^{\rm{s}}} - \nabla {\sigma ^{\rm{f}}} \\&+ {{F}}_{\rm{ext}}^{\rm{s}} - {{F}}_{\rm{ext}}^{\rm{f}} , \;\;\; {{x}} \in {\varOmega ^{\rm{s}}}, \end{split}$

${{{F}}^{\rm{FSI}}}({{x}},{{t}}) \!=\! \int\nolimits_{{\varOmega ^{\rm{s}}}} {{{{F}}^{{\rm{FSI}},{\rm{s}}}}({{{X}}^{\rm{s}}},{{t}})} {\rm{\delta}} ({{x}} - {{{x}}^{\rm{s}}}({{{X}}^{\rm{s}}},{{t}})){\rm{d}}\varOmega ,$

式中$ \rho^{\rm f}, \rho^{\rm s} $分别表示流体密度和固体密度; t是时间; 速度场变量v^s表示固体区域Ω^s的速度; v表示整个计算域Ω的速度; $ {F}^{\rm FSI, s} $表示固体区域Ω^s的流固相互作用力(fluid solid interaction); ${{F}}_{\rm{ext}}^{\rm{s}}$, ${{F}}_{\rm{ext}}^{\rm f}$分别是作用于固体和流体上的外力; σ^f是流体压力; σ^s是固体压力. 对于数值方法的详细介绍可参考文献[43-47].
IFEM采用流线迎风/Petrov Galerkin (streamline upwind/Petrov Galerkin, SUPG)和压力稳定/Petrov Galerkin (pressure-stablizing/Petrov-Galerkin, PSPG)算法以减小数值振荡和耗散^[48-50], 利用分布算子和差值算子实现固体边界和周围流体力与速度的信息交换, 采用重构核粒子法(reproducing kernel particle method, RKPM)形函数^[51]来近似Dirac δ 函数. 离散的Dirac δ 函数更加高阶和光滑, 有助于流固相互作用的计算和复杂边界条件的处理.
方程(3)中速度插值和方程(5)中力的分布表达成如下离散形式:

${{v}}_{iI}^{\rm{s}} = {\displaystyle\sum _J}{{{v}}_{iJ}}(t){\varPhi _J}({{{{X}}}_J} - {{{X}}}_I^{\rm{s}}){{, }}~{{{{X}}}_J} \in {\varOmega _{{\varPhi }I}} ,$

${{F}}_{iJ}^{\rm{FSI}} \!=\! {\sum _I}{{F}}_{iI}^{{\rm{FSI}},{\rm{s}}}({{{X}}^{\rm{s}}},t){\varPhi _I}({{{X}}_J} - {{X}}_I^{\rm{s}}){{, }}~{{X}}_I^{\rm{s}} \!\in\! {\varOmega _{\varPhi J}},$

式中, ${\varPhi _I}$, ${\varPhi _J}$是由RKPM得到的Dirac δ函数的离散重构形式; Ω_ФI, Ω_ФJ是固体节点的影响域, 其他变量是在节点I和J的离散形式^[35]. 关于速度插值和力分布的详细处理可参考文献[43,51].
2 -->

2.2.零质量射流

零质量射流通常由空腔振荡膜或活塞迫使流体通过孔口交替性地进出外流场形成(图1). 该射流的特点在于, 它完全由流动系统的工作流体形成, 确保动量传递到流动系统中而不需要通过外界流体的质量注入. 吹气冲程中, 喷出的流体在喷孔的尖锐边缘分离并向上滚动形成一对涡对或涡环; 吸气冲程中, 涡对或涡环离孔口较远, 由于其自诱导速度而不断向外传播. 因此, 涡对或涡环会结合在一起形成具有动量传递的射流^[52,53].
图 1 零质量射流示意图. D_c表示空腔直径, H表示空腔高度, D₀表示孔口直径, h表示孔口高度. 典型的合成射流流场可划分为三个明显流动区域, 即近场区域、过渡区域和远场区域
Figure1. Schematic diagram of ZNMF jet flow. D_c stands for the cavity diameter, H for the cavity height, D₀ for the orifice diameter, and h for the orifice height. The typical flow field of synthetic jet can be divided into three flow zones: Near field zone, transition zone, and far field zone.

本文的数值模拟考虑在微通道中引入零质量射流, 计算区域如图2所示. 微通道尺寸为40 μm × 400 μm × 40 μm, 射流小孔位于通道底部中间, 尺寸为2 μm × 2 μm.
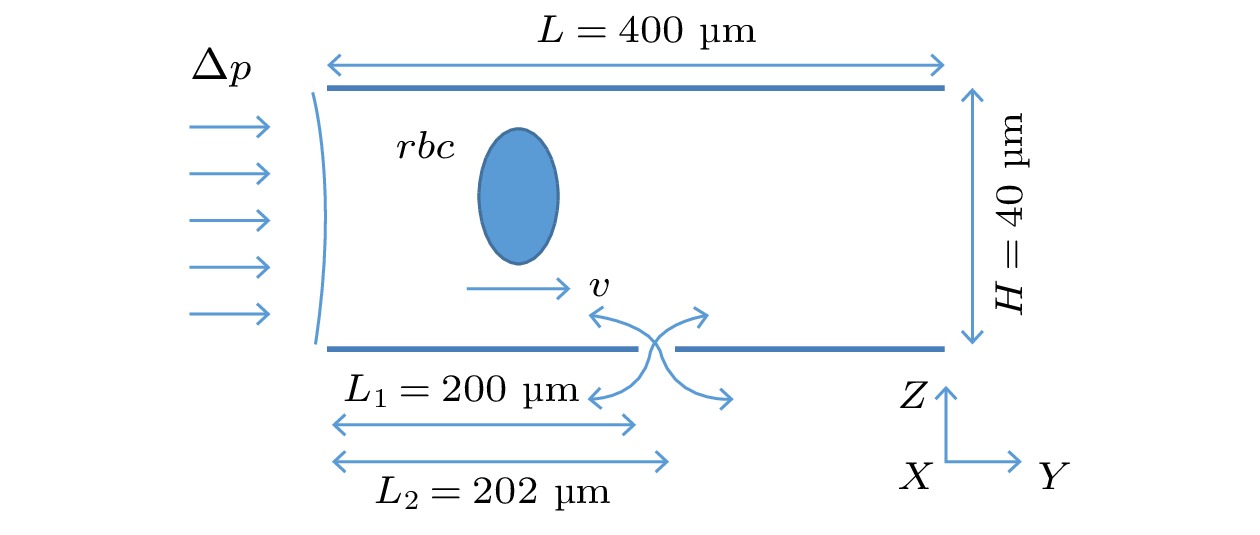图 2 数值模拟物理模型示意图, 其中L₁表示射流小孔左端距离入口距离, L₂表示射流小孔右端距离入口距离, L₂–L₁ = 2 μm, H表示管道的高度, v示意红细胞运动方向, 速度单位为 mm/s. 红细胞(red blood cell, rbc)在压力梯度作用下通过射流上方
Figure2. Physical model of numerical simulation, in which L₁ stands for the distance between the left end of the jet hole and the inlet, while L₂ for the distance between the right end of the jet hole and the inlet, L₂–L₁ = 2 μm, H is the height of the channel, v is the movement direction of the red blood cells, the units of velocity is mm/s, which passes above the synthetic jet driven by pressure gradient.

本文研究重点是射流对红细胞的影响, 忽略了空腔内部流动细节的模拟, 只考虑由于空腔内薄膜运动引起流体在孔口处的速度边界条件的变化. 参考Lee 等^[44]给出的薄膜运动规律得到孔口速度:

${{v}}(t) = {A_{\rm{m}}} \cos(2\pi ft),$

其中, A_m是射流振幅, f是振动频率. 该公式视为计算模型中空腔出口处小孔的速度边界条件, 其方向沿着Z轴竖直向上.
零质量通量射流中振幅A_m改变射流速度大小, 较大的射流速度可能致使细胞受到过大射流作用影响而死亡, 较小的振幅则可能造成细胞膜打开不充分. 因此, 通过调整射流的振幅, 可以比较便捷地实现对细胞施加不同大小的作用力.
2 -->

2.3.红细胞的本构关系

本文采用Mooney-Rivlin模型描述以三维超弹性材料构成的红细胞的本构关系. 该模型已经应用于众多研究领域^[54,55], 例如微喷射^[56]、细胞气穴现象^[57]和新型软执行器材料-离子液体凝胶(material-ionic liquid gel)的性能研究^[58]等.
细胞的弹性势能W表示为

$W = {c_1}({J_1} - 3) + {c_2}({J_2} - 3) + \frac{{\rm{\kappa}} }{2}{({J_3} - 1)^2} , $

式中, c₁, c₂和κ是材料常数; ${J_1} = {I_1}I_3^{ - 1/3}$, ${J_2} = {I_2}I_3^{ - 2/3}$, ${J_3} = I_3^{1/2}$, ${I_1} = {C_{kk}}$, ${I_2} = (I_1^2 - {C_{ij}}{C_{ij}})/2$, ${I_3} = {\rm{det}}({{C}})$, 柯西-格林变形张量C定义为C = F^TF, 变形梯度张量F_ij = ?x_i/?X_j, 对于不可压缩材料来说J₃ = 1.
柯西应力和弹性势能W之间的关系是

${{{\sigma}} ^{\rm{s}}} = {J^{ - 1}}{{F}}\frac{{\partial W}}{{\partial {{E}}}}{{{F}}^{\rm{T}}} ,$

式中J = det(F)是雅可比矩阵.
2 -->

2.4.数值实现

本文数值模拟中, 流体是六面体网格, 红细胞是双面凹结构, 采用四面体网格. 经过网格和时间步长无关性测试, 流体和红细胞节点数分别为674081和3266, 单元数分别为640000和9908, 计算时间步长dt = 2.5 × 10^–5 s. 流体和红细胞的密度相同, ρ^f = ρ^s = 1 g/cm³, 流体黏性μ = 1 g/(m·s). 微管道出、入口采用压力边界条件, 入口、出口压力差为Δp. 在本文的模拟中, 选取的压力梯度值分别是Δp = 20, 30, 40, 50, 60 Pa, 其他边界采用无滑移边界条件, 零质量通量射流作为速度边界条件作用于图2的微通道小孔处.
数值计算中, 红细胞在压力梯度Δp作用下从入口处运动, 速度达到稳定匀速后进入射流作用区域. 本文进行了不同参数的模拟, 通过调整压力梯度Δp, 射流振幅A_m和频率f来分析流动参数对红细胞运动变形和力敏通道开启的影响.

2

-->

3.1.零质量射流

首先分析微管道中没有红细胞时的流场特征. 当零质量射流单独作用于微通道时, 流场是对称分布的, 其具体的分析可参阅文献[59]. 若沿着Y轴正方向施加压力梯度Δp, 零质量射流将与管道横流发生互相影响, 图3是射流振动频率f = 625 Hz, 射流振幅A_m = 78.125π mm, 压力梯度Δp = 60 Pa时的流场图.
图 3 压力梯度作用下零质量射流流场分布(A_m = 78.125π mm, f = 625 Hz, Δp = 60 Pa), 其中速度的量纲为mm/s. 截取的截面Y轴坐标范围170 μm ≤ Y ≤ 230 μm, 小孔位于截面正中心Y = 200 μm. 图中箭头表示速度方向, 颜色表示速度大小, 颜色越深, 则速度值越大. 四幅图描述了流场运行稳定后, 一个周期(T = 1.6 × 10^–3 s)内沿着流动方向截面上的流场分布情况　(a) t = T/4; (b) t = 2T/4; (c) t = 3T/4; (d) t = T
Figure3. Flow field distribution under the action of ZNMF jet and pressure gradient (A_m = 78.125π mm, f = 625 Hz, Δp = 60 Pa), in which the unit for velocity magnitude is mm/s. The cross-section depicted ranges 170 μm ≤ Y ≤ 230 μm in Y coordinate, and the hole is in the center of the cross-section Y = 200 μm. The arrow in the figure represents the direction of velocity vectors, and the color represents the magnitude of velocity. The darker the color, the greater the velocity magnitude. The four figures describe the distribution of flow field in a period: (a) t = T/4; (b) t = 2T/4; (c) t = 3T/4; (d) t = T.

结果显示, 压力梯度的施加对通道内零质量射流引起的流场有较大的影响, 导致了其中涡结构的变化. 如图3(a)所示, 在吹气半冲程刚开始(t = T/4)时, 由于左侧压力较大, 导致孔口两侧速度场结构的对称性遭到破坏, 孔口附近流体偏向右边, 下游的速度值也稍大; 如图3(b)所示, 当t = T/2时, 吹气冲程达到最大, 主流的动量因射流的加入有所增加, 有助于抑制下游回流区的出现, 因此并没有出现明显的涡结构; 在图3(c)所示的吸气冲程(t = 3T/4)中, 由流体速度方向可知, 此时流体是回流进孔口, 说明在孔口附近射流对流体吸力作用大于压力梯度的影响, 孔口左侧速度值总体大于右侧; 如图3(d)所示, 当t = T时, 吹气冲程达到最大, 此时下游由于孔口的吸气作用, 主流的动量有所减少, 导致在孔口右侧出现了两个旋涡.
2 -->

3.2.红细胞在微管道中的运动

本节研究零质量射流对微管道中红细胞的运动和变形的影响. 当红细胞在压力梯度Δp作用下运动一段距离, 达到稳定速度, 即速度达到匀速状态后, 进入射流作用的区域发生变形. 图4绘制了红细胞的质心坐标在YZ平面随运动时间变化的规律, 此时压力梯度Δp = 30 Pa, 射流振动频率f = 625 Hz, 射流振幅A_m = 78.125π mm.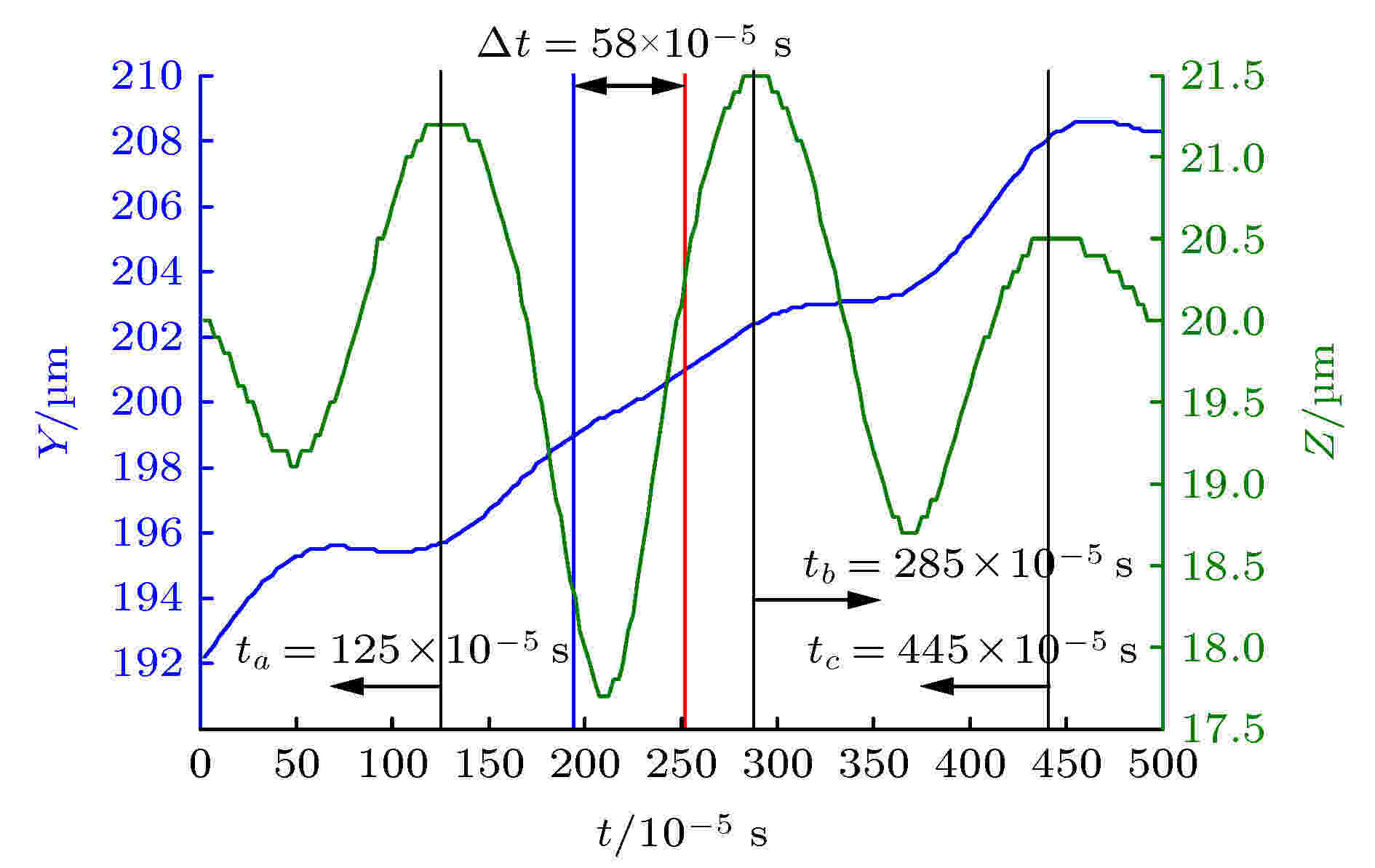
图 4 红细胞经过射流作用区域时, 质心的Y轴和Z轴坐标随时间t变化规律(A_m = 78.125π mm, f = 625 Hz, Δp = 30 Pa). 图中绿线表示质心Z轴坐标变化, 蓝线表示Y轴坐标变化, 三条黑线分别表示红细胞被拉伸到最长时的时刻, 对应为t_a = 125 × 10^–5 s, t_b = 285 × 10^–5 s, t_c = 445 × 10^–5 s, 任意两条黑线之间时间间隔为一个振动周期, T = 1.6 × 10^–3 s. 红蓝两条垂直线表示红细胞进入孔口正上方的时刻, 红细胞经过射流孔口的时间Δt = 58 × 10^–5 s
Figure4. The variation of Y-axis and Z-axis coordinates of cell centroid with time (A_m = 78.125π mm, f = 625 Hz, Δp = 30 Pa). The green line represents for the change of Z-axis coordinate of the centroid, while the blue line represents for the change of its Y-axis coordinate. The three black lines represent the moment when red blood cells are stretched to the maximum, corresponding to t_a = 125 × 10^–5 s, t_b = 285 × 10^–5 s, t_c = 445 × 10^–5 s, and any two black lines represent a jet period, T = 1.6 × 10^–3 s. The red and blue vertical lines indicate the moment when the red blood cells enter the orifice directly above, the interal of the red blood cells pass through the orifice Δt = 58 × 10^–5 s.

在图4中, 红细胞起始质心坐标Y = 192 μm, Z = 20 μm. 由于射流的作用方向是沿着Z轴正方向, 所以红细胞持续地受到射流吸力和推力作用, 在竖直方向(Z轴方向)上发生伸长和收缩的变形, 其质心位置随着射流周期性地变化. Z坐标的最小值为17.6 μm, 对应吸气冲程, 此时红细胞位于孔口上方, 吸力最大; Z坐标的最大值为21.5 μm, 对应吹气冲程. 红细胞在Y方向大致表现出稳定的线性变化, 其运动范围为192 μm ≤ Y ≤ 208 μm, 但压力梯度和射流的共同作用显著地影响着红细胞向前的运动速度大小. 红细胞经过孔口区域的时间Δt = 58 × 10^–5 s, 因孔口长度为2 μm, 红细胞速度大约为v_s = 3.5 mm/s.
为了更好地观察红细胞变形时的流场信息, 分析在一个射流振动周期内红细胞变形和应力以及流场的压力分布图(图5).
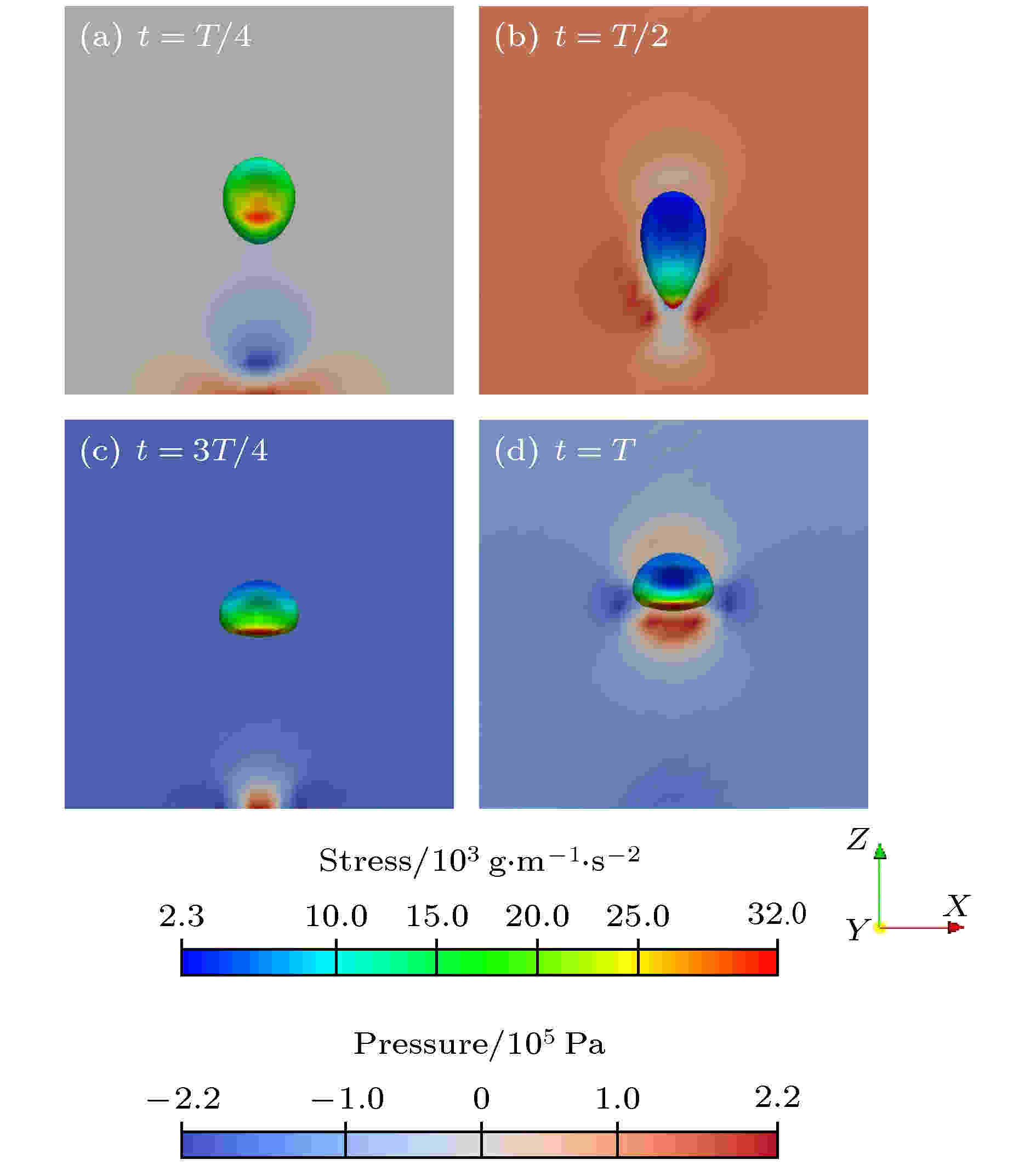图 5 一个射流周期内(T = 1.6 × 10^–3 s)红细胞变形所受应力和流体压力场(A_m = 78.125π mm, f = 625 Hz, Δp = 30 Pa)　(a)?(d)分别表示不同时刻红细胞质心所在XZ截面的流体压力分布以及红细胞受到的压力 (a) t = T/4 (Y = 197.7 μm); (b) t = T/2 (Y = 199.5 μm); (c) t = 3T/4 (Y = 200.8 μm); (d) t = T (Y = 202.4 μm)
Figure5. Diagram of stress of red blood cell and fluid pressure field in one peroid for A_m = 78.125π mm, f = 625 Hz, Δp = 30 Pa. (a)?(d) represents the fluid pressure distribution in the XZ section of the RBC center of mass at different times and the stress on the RBC membrane: (a) t = T/4 (Y = 197.7 μm); (b) t = T/2 (Y = 199.5 μm); (c) t = 3T/4 (Y = 200.8 μm); (d) t = T (Y = 202.4 μm).

图5是一个流动周期内, 在不同时刻红细胞质心Y轴坐标截取的XZ截面上流体压力分布和红细胞受到的应力变化, 图5中红细胞应力范围为2.3 Pa ≤ σ ≤ 32.0 Pa, 流体压力范围为–220 Pa ≤ p ≤ 220 Pa, 压力值为负说明流体对红细胞是吸力作用, 其中图5(a),(b)对应吸气冲程, 红细胞处于伸长状态, 图5(c),(d)对应吹气冲程, 红细胞处于压缩状态. 在图5(a)中, 射流在吸气上半冲程, 吸力作用不是很明显, 红细胞受到的应力左右对称. 在图5(b)中, 射流吸气冲程中射流吸力达到最大, 红细胞拉伸到最长状态, 红细胞几乎位于射流小孔正上方, 此时整个流场区域压力达到最大. 在图5(c)中, 射流吹气冲程刚刚开始, 尽管红细胞也几乎位于小孔正上方, 但此时红细胞附近流体速度较大, 所以压力较小, 红细胞所受应力也较小, 压缩程度未达到最大. 在图5(d)中, 射流吹气冲程吹力达到最大, 红细胞周围流体压力较大, 而且下方压力大于上方, 红细胞继续向上压缩变形达到最大程度, 而流场除了细胞周围以外其他区域速度大小差不多, 压力值大小也几乎相同, 均远小于红细胞周围的压力值.
为了研究在流体作用力下细胞膜力敏通道的打开情况, Sabass等^[60-64]通过构建细胞膜变形能的解析模型, 得到了细胞膜力敏通道开启的临界表面张力τ_c, 即当细胞膜表面局部表面张力T₀大于τ_c时, 认为此处力敏通道开启. 参照该解析模型^[60-64]的公式推导, 临界细胞膜张力${{{\tau}} _{\rm{c}}} \approx \dfrac{{2 K{U^2}}}{{{R_{\rm{closed}}} + {R_{\rm{open}}}}}, \;K \!=\! \dfrac{{\sqrt 2 {{(K_{\rm{t}}^{\rm{3}}{K_{\rm{b}}})}^{1/4}}}}{{{\varepsilon ^{3/2}}}}$, 其中R_closed = 2.3 nm和R_open = 3.5 nm分别代表力敏通道封闭和开启时的半径, 疏水错位(hydrophobic mismatch)U = 0.015 μm, K_t和K_b为细胞磷脂双分子层物性参数, ε为细胞膜厚度. 对于本文的算例, 红细胞半径为3.9 μm, 膜厚度为0.05 μm, 可计算得到τ_c ≈ 79.7 mN/m. 本文根据已有文献的方法^[65], 计算得到了细胞膜上受到的表面张力分布, 由此得到每一时刻细胞膜力敏通道打开的百分比P_open (percentage of mechanosensitive channel to open).
图6显示了当射流频率f = 625 Hz, Δp = 30 Pa时, 不同射流振幅值下细胞膜力敏通道随着时间变化的开启情况. 如图6所示, 力敏通道的打开百分比随着射流振幅呈现周期性变化的趋势. 当细胞接近射流空腔时, 细胞膜的变形已经引起了通道的开启; 当其位于空腔上方时, 开启百分比达到最大值, 此后P_open 则随着细胞远离空腔而逐渐减小, 并趋向于零. 如所预期的, 零质量射流振幅A_m 越大, 红细胞受到的射流作用力也越大, 更容易导致力敏通道的打开. 这个结果也验证了本文提出的基于零质量射流的物质导入技术在理论上的可行性.
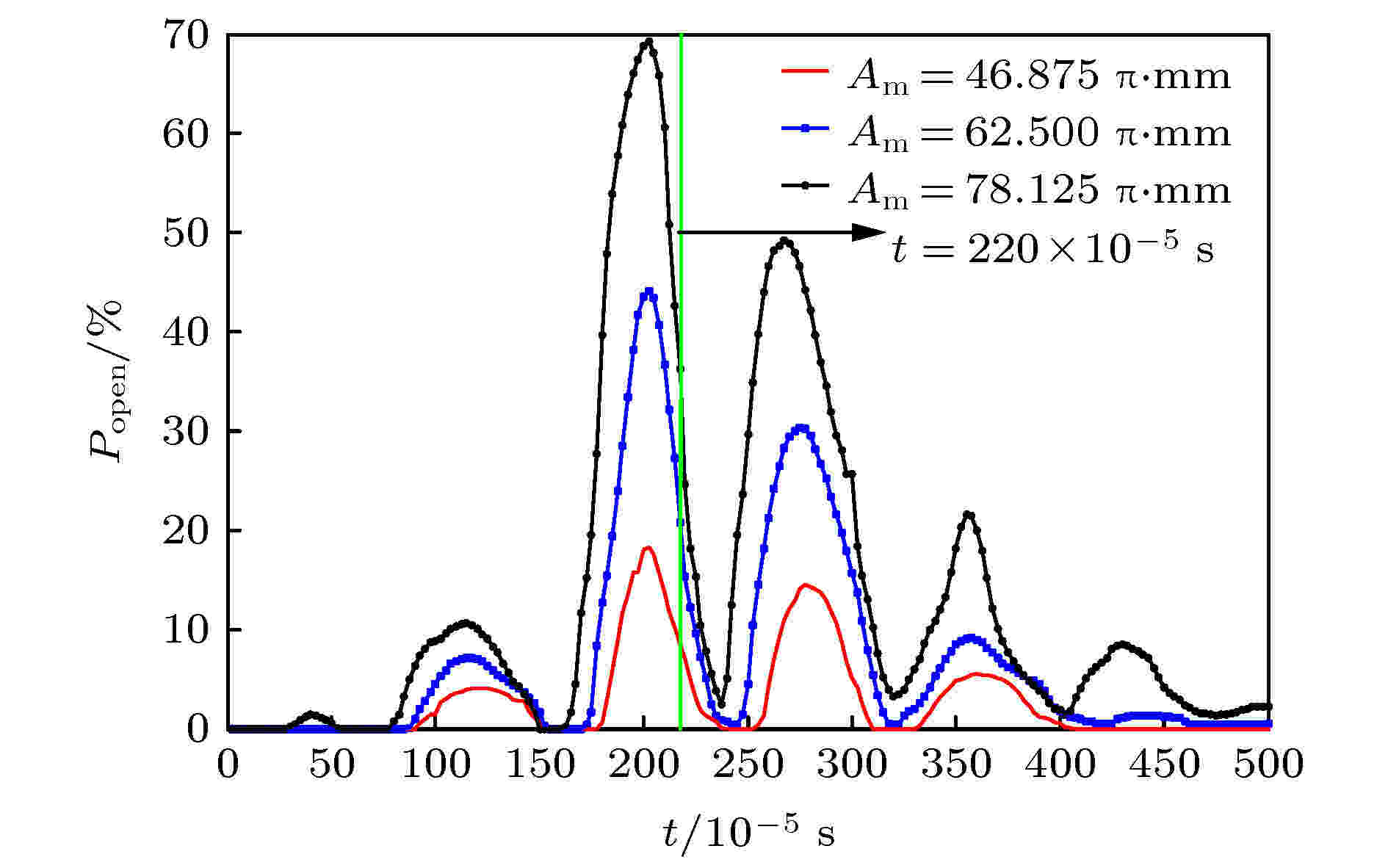图 6 不同振幅A_m 作用下红细胞变形时力敏通道开启百分比P_open随运动时间t的变化(f = 625 Hz, Δp = 30 Pa), 图中竖直绿线表示红细胞刚好经过孔口正中心位置的时刻
Figure6. Variation of P_open for mechano-sensitive channel gating in cell deformation with time t under different amplitude A_m (f = 625 Hz, Δp = 30 Pa). The green line in the figure stands for the moment when the cell passes above the orifice.

2 -->

3.3.流动参数的影响

在实施物质跨膜输运的实际过程中, 往往希望在力敏通道开启百分比P_open尽可能大的同时, 也保持较长的持续开启时间t_s = t₂ – t₁ (t₁为细胞进入射流作用区域开始发生变形的时刻, t₂为细胞离开射流作用区域停止发生变形的时刻). 因此, 本文构造一个参数, 即通道开启积分(channel gating integral)$I =\displaystyle \int_{{{\rm{t}}_1}}^{{{\rm{t}}_2}} {{P_{{\rm{open}}}}{\rm{d}}t} $来综合衡量二者共同决定的力敏通道的开启程度, 并在此基础上, 分析外加压力梯度、射流频率等参数如何对力敏通道开启程度产生的影响.
为此, 本文在压力梯度和射流频率($ \Delta p\text{-}f $)平面, 绘制了射流振幅A_m = 78.125π mm时通道开启积分的变化情况(图7). 对于较小的压力梯度, 细胞受到的流体剪切力较小, 但细胞运动速度较慢, 在管道中滞留时间较长; 而压力梯度较大时, 虽然细胞受到的剪切应力较大, 但细胞滞留时间较短. 因此存在一个压力梯度的优化值, 使得通道开启程度I达到较大值. 结果表明(图7), 在本文计算参数下, 对于不同的振动频率, 当Δp = 30 Pa时, 通道开启程度总能达到最优值.
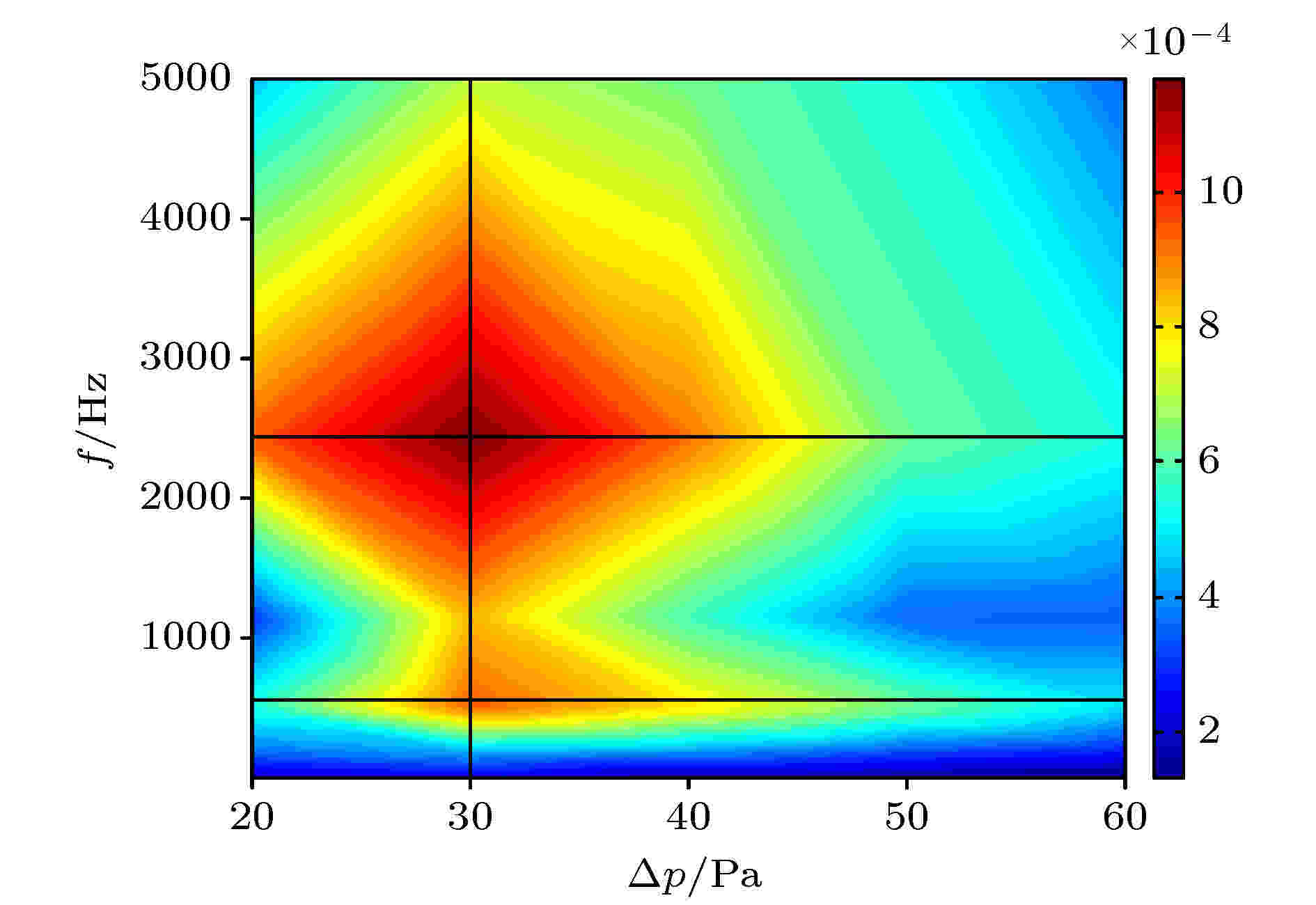图 7 通道开启程度I随着压力梯度Δp和射流振动频率f的变化. 颜色代表I的大小, 颜色越深, I值越大. 图中竖直黑线表示Δp = 30 Pa, 两条水平横线分别代表f = 2500 Hz和f = 625 Hz
Figure7. The variation of channel gating integral I with the pressure gradient Δp and the jet vibration frequency f. The color represents the magnitude of I, the darker the color, the greater of I. The black line stands for Δp = 30 Pa, while the two horizontal lines for f = 2500 Hz and f = 625 Hz, respectively.

射流频率的高低对细胞的变形也有重要的影响, 这与细胞膜对流动剪切作用的响应时间有关. 频率过高, 可能导致细胞膜来不及对外加剪切作用产生响应, 进而影响其发生变形, 导致蛋白质跨膜输运效率低下. 因此, 需要寻找理想的射流振动频率. 在本文计算参数下, 图7 表明, 通道开启积分I的最大值对应于振动频率f = 2500 Hz, 同时在f = 625 Hz处I出现了另一个较低峰值. 导致出现两个峰值的原因是否与细胞膜的本征振动频率有关, 是将来工作中希望进一步研究的问题.

在生物医学研究中, 为更好实现蛋白质、基因、药物等小分子物质导入细胞内, 研究细胞膜变形和力敏通道开启的机理, 进而探索高效、安全的基因导入技术至关重要. 本文提出了一种基于零质量射流的方法, 通过其作用于微管道中运动的细胞, 希望实现高通量、易于控制的细胞跨膜输运技术. 因为人们对红细胞的本构关系结构比较熟悉, 本文运用浸没有限元方法, 数值模拟了红细胞在零质量射流作用下的变形和运动, 分析了其力敏通道的开启情况. 本文分析了在周期射流作用下, 红细胞在流场中的运动、变形和力敏通道开启的情况, 通过调节压力梯度以及射流的振幅和频率, 使红细胞膜表面力敏通道打开百分比更大, 且打开时间更长, 并构造参数I来衡量力敏通道开启的总体效果. 数值模拟结果表明, 在本文的计算参数下, 使I最大的压力梯度是Δp = 30 Pa, I值最大的振动频率是f = 2500 Hz. 射流振幅的增大有助于细胞膜力敏通道的开启, 这使得人们可以方便地调节此振幅值, 既保证了细胞的存活率, 又充分地保证了细胞导入的效率. 这些结果也说明了该技术在理论上的可行性. 基于零质量射流的细胞跨膜输运技术具有微制造工艺简单, 流动参数便于精确控制的特点, 有望高效、安全地实现对不同种类细胞的物质导入. 因此, 本文的工作为进一步制作和优化该基因递送装置打下了理论基础.