摘要:生物阻抗谱是一种非侵入式、免标记、能够定量分析的检测技术, 将其应用于生物细胞及组织的生理、病理分析中具有很大优势. 本文采用数值仿真的方法研究了单细胞电学特性与其结构之间的关系, 并通过实验进行了验证. 根据细胞的生理特征, 依据细胞的双壳模型与单壳模型理论分别建立了不同种类细胞的电学模型, 研究了细胞种类、细胞膜、细胞核对细胞电学特性的影响. 数值分析结果表明: 1)细胞结构尺寸的变化引起细胞电学特性的改变, 因此, 依据细胞电学特性能够准确实现细胞分类; 2)柯尔-柯尔(Cole-Cole)图上高频与低频的两个半圆弧分别是由细胞质或细胞外液的离子极化、细胞膜与细胞外液之间的界面极化引起的; 3)细胞核大小对测量阻抗的影响主要在低频段, 是由细胞核与细胞内液的界面极化引起的, 当存在细胞膜且当细胞核的核质比小于0.25时可忽略其影响. 为验证仿真结果, 对20%不同活性的酵母菌进行了实验. 实验结果表明, 运用本文建立的细胞电学模型, 可以准确检测细胞的不同活性. 该方法对实现细胞的精准电阻抗检测提供了理论依据, 具有重要的应用价值.
关键词: 生物阻抗谱/
单细胞模型/
数值仿真/
电学特性

English Abstract

全文HTML

--> --> -->

免疫细胞化学法^[1]、流式细胞术^[2]以及核酸检测法^[3]是细胞生理、病理分析中常用的方式, 但是这些方法存在检测速度慢、需要标记等问题. 生物阻抗谱(biological impedance spectroscopy, BIS)方法是一种利用生物组织的电阻抗特性提取相应生理、病理信息的检测技术^[4], 该方法通过对被测物体施加幅值较小的交流激励, 使用扫频的方式测量每种频率下检测目标对应的阻抗值^[5]. BIS技术通过交流电阻抗技术检测生物细胞的电导率和介电常数, 并引入电介质物理模型的数值计算, 获得细胞外液、细胞膜和细胞质的电学信息, 由此来区分不同种类的细胞^[6]. 生物细胞作为非均匀结构(细胞外、细胞膜和细胞质), 其电学特性具有异质性. 当交流电场作用于细胞时, 细胞的介电响应出现α色散和β色散的弛豫现象^[7], 可以利用该弛豫现象对细胞的不同结构特征进行检测识别. 因此, BIS成为研究细胞结构特性及细胞分类识别的一种新方式.
BIS方法具有操作简单、信息丰富等特点, 国内外已经有大量****在BIS的细胞检测方面做了大量研究. 1989年Hodgkin和Huxley^[8]根据细胞膜选择通透性的特点, 提出了细胞膜等效电路模型, 而后1983年Kanai等^[9]结合细胞膜、细胞质、细胞外液等特性建立起单细胞等效电路模型. 2014年宁波大学方云等^[10]建立了细胞单壳模型, 对肝癌细胞电阻抗特性的频响特性进行分析, 采用生物阻抗谱、Bode 图和Nyquist 图观察了细胞体积分数对肝癌细胞电阻抗特性的影响. 2010年空军军医大学王威等^[11]根据相关文献建立椭圆细胞模型, 用于COMSOL仿真来研究细胞变形引起的阻抗变化. 2016年Nahin Amin等^[12]通过建立细胞模型以及等效电路得出细胞尺寸、膜厚以及内部细胞核的大小和细胞质的密度对阻抗的影响, 同时提出采用混合电极法以消除测量时接触阻抗的影响. 2010年Sun等^[13]建立了细胞的单壳模型, 通过调整细胞膜及细胞质等结构的变化参数对单细胞的生物阻抗谱进行了数值分析, 探索了细胞在不同生长阶段的电学特性规律. 2015年Guo等^[14]提出一款可降低接触阻抗的微流控芯片用以单细胞阻抗测量, 而后通过对该芯片获得阻抗数据分析获取细胞的电学特性. 2016年东南大学Zhu等^[15]利用有限元建模方式研究微流控BIS的几何相关传感特性.
目前大多数****普遍采用建立等效电路模型拟合的方式获得所测物体的各个成分的电学特性(导电率、介电常数), 这种方式获得细胞的电学特性是可行的, 但在解释细胞结构所引起的电阻抗变化的内在机理方面仍然存在局限性. 因此, 本文采用数值仿真的方法对细胞引起的电阻抗变化的内在机理进行分析, 研究细胞内在结构与其电学特性之间的关系. 首先, 建立双壳模型(two shell model, TS)^[16,17]、单壳模型(single shell model, SS)^[18]以及无壳模型, 作为细胞的仿真模型. 其次, 基于电学仿真理论, 研究细胞各组成成分结构的变化对其电阻抗的影响. 最后, 使用20%不同活性的酵母菌进行实验, 对仿真结果进行验证.

2

-->

2.1.仿真模型

为研究细胞各结构对阻抗谱的影响, 建立多种不同结构、尺寸的细胞模型. 包括TS模型(图1(a))、SS模型(图1(b))、“无壳模型(no shell model, NS)”(图1(c)). 由于大部分细胞内部都具有细胞核, TS模型即是考虑细胞核的情况下建立的细胞模型; 成熟的红细胞(内部无细胞器、细胞核)这类细胞则不需考虑细胞核的影响而建立起SS模型, 通过建立的TS, SS模型的比较, 还可以很好地反映出细胞核的大小对生物阻抗的影响; NS模型则是为了与SS模型进行比较以研究细胞膜对生物阻抗谱的影响而建立的细胞模型.
图 1 仿真模型 (a)?(c)细胞模型; (d), (e)仿真区域模型
Figure1. Simulation model (a)?(c) Model of cell; (d), (e) model of simulation area.

采用不同细胞半径(正常B细胞R₁ = 3.3 μm, 癌B细胞R₁ = 5.2 μm)^[19]以及细胞核半径(正常B细胞R₂ = 2.8 μm, 癌B细胞R₂ = 4.4 μm)的方式模拟正常细胞和癌细胞两种类别. 基于SS模型将膜的双层框架改为单层以模拟“无膜”状态, 并将此模型与SS模型进行对比以分析细胞膜对阻抗谱的影响. 细胞核的半径分别定为R₂ = 2.8, 1.9, 1.5 μm以及R₂ = 0以探索细胞核对电阻抗的影响. 本文设定仿真区域(L × L = 20 μm × 20 μm), 其中测量电极(l = 4 μm)对称地放置在仿真边界的两侧, 如图1(d)和图1(e)所示.
2 -->

2.2.仿真理论

本文基于Maxwell理论进行有限元仿真, 忽略电极与细胞外液间的界面极化以及外界噪声和电磁影响, 仿真中满足如下公式^[20,21]:

$\nabla \cdot {{J}} = - \frac{{\partial \rho }}{{\partial t}},$

${{E}} = - \nabla \varphi ,$

${{J}} = (\sigma + {\rm{j}}\omega \varepsilon ){{E}} = \sigma {{E}} + {\rm{j}}\omega {{D}},$

式中J (A/m²)为全电流密度, E (V/m)为场强, φ (V)为电势, $\sigma $ (S/m)为导电率, ${\rm{j}} = \sqrt { - 1} $, $\omega $ (Hz)为角频率, D (C/m²)为电位移矢量. 根据Maxwell-Wager理论, 细胞的复介电常数按如下公式表示^[22]:

$\varepsilon _{{\rm{sp}}}^*{\rm{ = }}\varepsilon _{\rm{m}}^{\rm{*}}\frac{{2\left( {1 - {\nu _{{\rm{in}}}}} \right)\varepsilon _{{\rm{in}}}^{\rm{*}} + \left( {1 + 2{\nu _{{\rm{in}}}}} \right)\varepsilon _{{\rm{in}}}^*}}{{\left( {2 + {\nu _{{\rm{in}}}}} \right)\varepsilon _{{\rm{in}}}^{\rm{*}} + \left( {1 - {\nu _{{\rm{in}}}}} \right)\varepsilon _{{\rm{in}}}^*}},$

$\varepsilon _{\rm{m}}^{\rm{*}} = {\varepsilon _{\rm{m}}} - {\rm{j}}\frac{{{k_{\rm{m}}}}}{{w{\varepsilon _v}}},$

$\varepsilon _{{\rm{in}}}^{\rm{*}} = {\varepsilon _{{\rm{in}}}} - {\rm{j}}\frac{{{k_{{\rm{in}}}}}}{{w{\varepsilon _v}}},$

${\nu _{{\rm{in}}}} = {(1 - d/R)^3},$

式中$\varepsilon _{{\rm{sp}}}^*$为细胞复介电常数, $\varepsilon _{\rm{m}}^{\rm{*}}$为细胞膜复介电常数, ${\nu _{{\rm{in}}}}$为细胞内体积分数, $\varepsilon _{{\rm{in}}}^*$为细胞内复介电常数, ${\varepsilon _{\rm{m}}}$为细胞膜介电常数, ${k_{\rm{m}}}$为细胞膜导电率, ${\varepsilon _{{\rm{in}}}}$为细胞内介电常数, ${k_{{\rm{in}}}}$为细胞内导电率, d为细胞膜厚度, R为细胞半径.
根据(4)式—(7)式, 在仿真过程中选定细胞各结构电学特性参数, 如表1所列. 根据BIS测量原理, 在有限元仿真中还需选定相应的扫描频率及扫描点来完成对细胞的仿真检测. 本研究中使用的激励源赋值为1 mA, 频域范围f为4 Hz—1 GHz.

	参数	正常细胞	癌细胞
导电率σ/S·m–1	环境	0.6	0.6
	细胞膜	5.6 × 10–5	9.1 × 10–6
	细胞质	1.31	0.48
	核膜	1.11 × 10–2	4.4 × 10–3
	核质	2.04	1.07
相对介电常数	环境	80	80
	细胞膜	12.8	9.8
	细胞质	60	60
	核膜	106	60.3
	核质	120	120
几何参数/μm	仿真区域(L × L)	20 × 20	20 × 20
	电极$ (l) $	2 × 4	2 × 4
	细胞半径(R1)	3.3	5.2
	细胞核半径(R2)	2.8	4.4
	细胞膜厚(d1)	0.007	0.007
	核膜厚(d2)	0.04	0.04

表1正常B细胞及病变B细胞的仿真参数
Table1.Simulation parameters of normal and malignant (farage) onsillar B-cells^[19].

2

-->

3.1.细胞种类与细胞电学特性

目前典型的三类细胞有: 正常细胞(有细胞核、细胞器)、成熟红细胞(无细胞核、无细胞器)和肿瘤细胞(尺寸较大、表面粗糙). 为研究不同种类细胞的电学特性差异, 本文以B细胞各结构成分为研究基础, 建立无核细胞(图1(b))、带核细胞(图1(a))以及细胞半径、细胞核半径有所增大的癌细胞模型进行仿真研究, 通过研究这三类细胞电学特性参数对生物阻抗谱的影响, 获得细胞类别与其电学特性之间的内在机理.
由于在低频时细胞膜呈现高阻值状态, 因此从图2(a) (1-1), (2-1), (3-1)可看出在f = 10.5 kHz时, 电场线均绕过细胞从细胞外液中流过. 由图2(a)可看出细胞内的电势随频率的增加而升高. 频率f = 3 MHz时, 图2(a)中的(1-2), (2-2), (3-2)中细胞内有大量的电场线流过, 细胞内同位置的电势φ_1-2 < φ_2-2 < φ_3-2; f = 1 GHz时, 细胞已经被完全击穿, 虽然图2(a) (1-3), (2-3)内部无电场线, 图2(a) (3-3)细胞内部依旧有大量的电场线, 但是细胞内的电势φ_1-3 ≈ φ_2-3 ≈ φ_3-3.
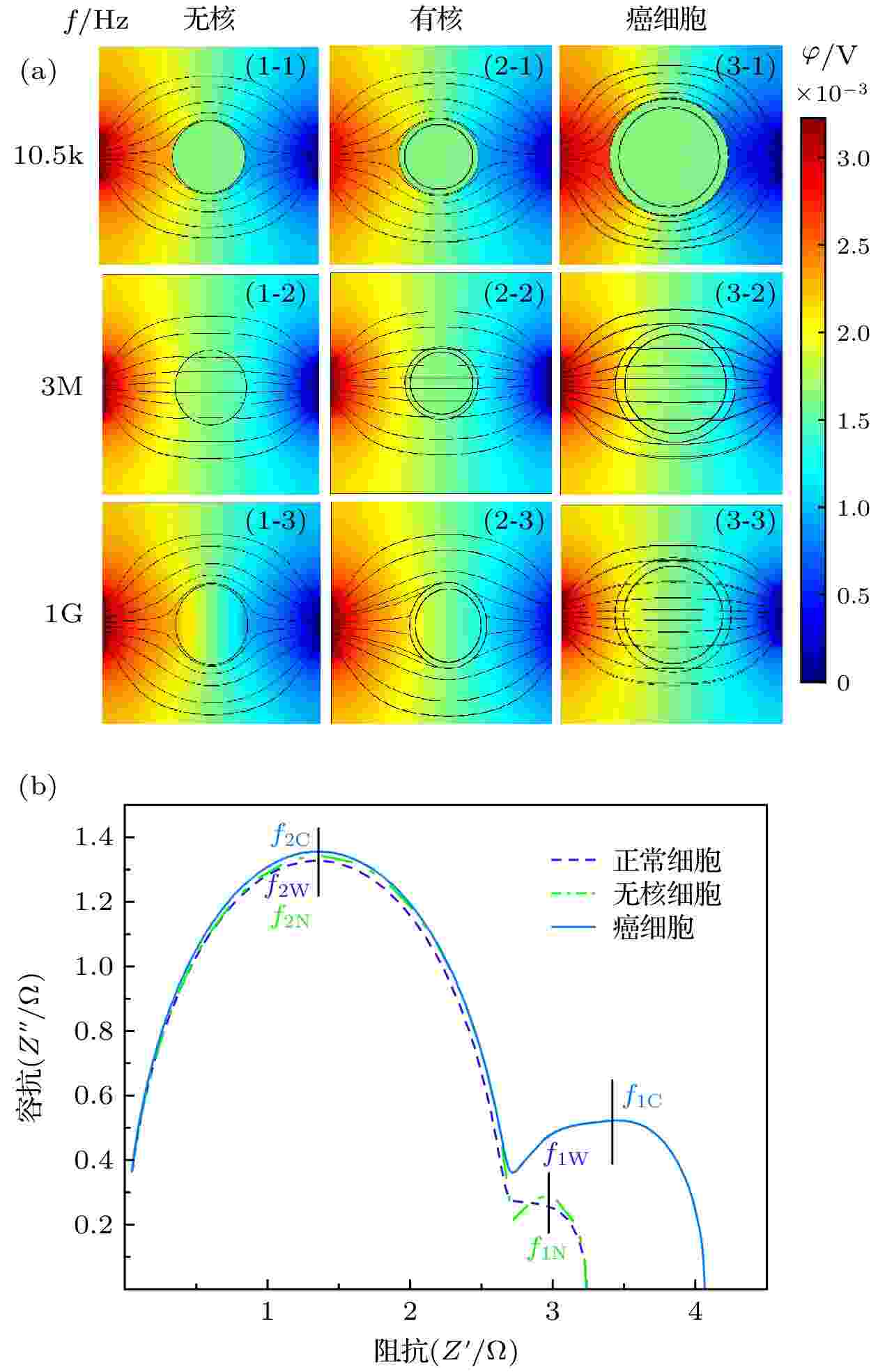图 2 不同细胞的仿真结果及Cole-Cole Plot　(a)不同细胞在不同频率下的仿真结果; (b)不同细胞的Cole-Cole Plot
Figure2. Simulation results of different cells and Cole-Cole Plot: (a) Simulation results of different frequencies of different cells; (b) Cole-Cole Plot of different cells.

由图2(b)可看出这三类细胞Cole-Cole Plot都有两个半圆弧. 但是在低频段(4 Hz—3 MHz)有较大的区别: 癌细胞在该频段的圆弧面积明显大于无核细胞与有核细胞的圆弧面积, 并且在该频段癌细胞的驰豫频率f_{1 C} = 7.08545 × 10⁵ Hz, 无核与带核的驰豫频率f_1N = f_1W = 1.251258 × 10⁶ Hz. 高频段(3 MHz—1 GHz)三类细胞的圆弧曲线基本重合, 细胞的驰豫频域f_2N = f_2W = f_2C = 1.3687 × 10⁸ Hz.
由此可得出以下结论: 1)细胞半径越大(正常细胞R₁ = 3.3 μm, 癌细胞R₁ = 5.2 μm)则低频段的驰豫频率越低; 2)细胞膜导电率越高(正常细胞导电率σ = 5.6 × 10^–5 S/m, 癌细胞σ = 9.1 × 10^–6 S/m)则低频段的Cole-Cole Plot的面积越小. 因此, 细胞结构尺寸的变化引起细胞电学特性的改变, 依据细胞电学特性能够准确地进行细胞分类.
2 -->

3.2.细胞膜对细胞电学特性的影响

由图2(b)中Cole-Cole图可看出三类细胞在都呈现出两个半圆弧, 这也就意味着细胞产生了两种介电弛豫. 因此为了探索这两种介电弛豫产生的内在机理, 本文基于SS模型, 对其进行仿真分析.
图3(a)细胞内的电势随频率的升高逐渐增大, 由于细胞膜具有低频高阻抗性, 因此在频率f = 10.5 kHz时, 图3(a) (1-1)细胞内基本无电场线穿过, 而(2-1) 细胞内已经有大量的电场线穿过; f = 3 MHz时, 细胞膜的阻抗降低, 图3(a) (1-2) 细胞内有电场线通过, 且细胞内同位置的电势与图3(a) (2-2)近似相等. f = 1 GHz时, 细胞已经完全被击穿, 此时的细胞已经处于完全导通状态. 图3(b)中SS模型有无膜在Cole-Cole Plot已经有很大的区分: 有膜的SS细胞模型依旧在Cole-Cole 图上呈现出高频低频两个半圆弧, 而无膜的SS细胞模型在Cole-Cole图上只剩下一个大半圆弧且与有膜状态下的大半圆弧重合.
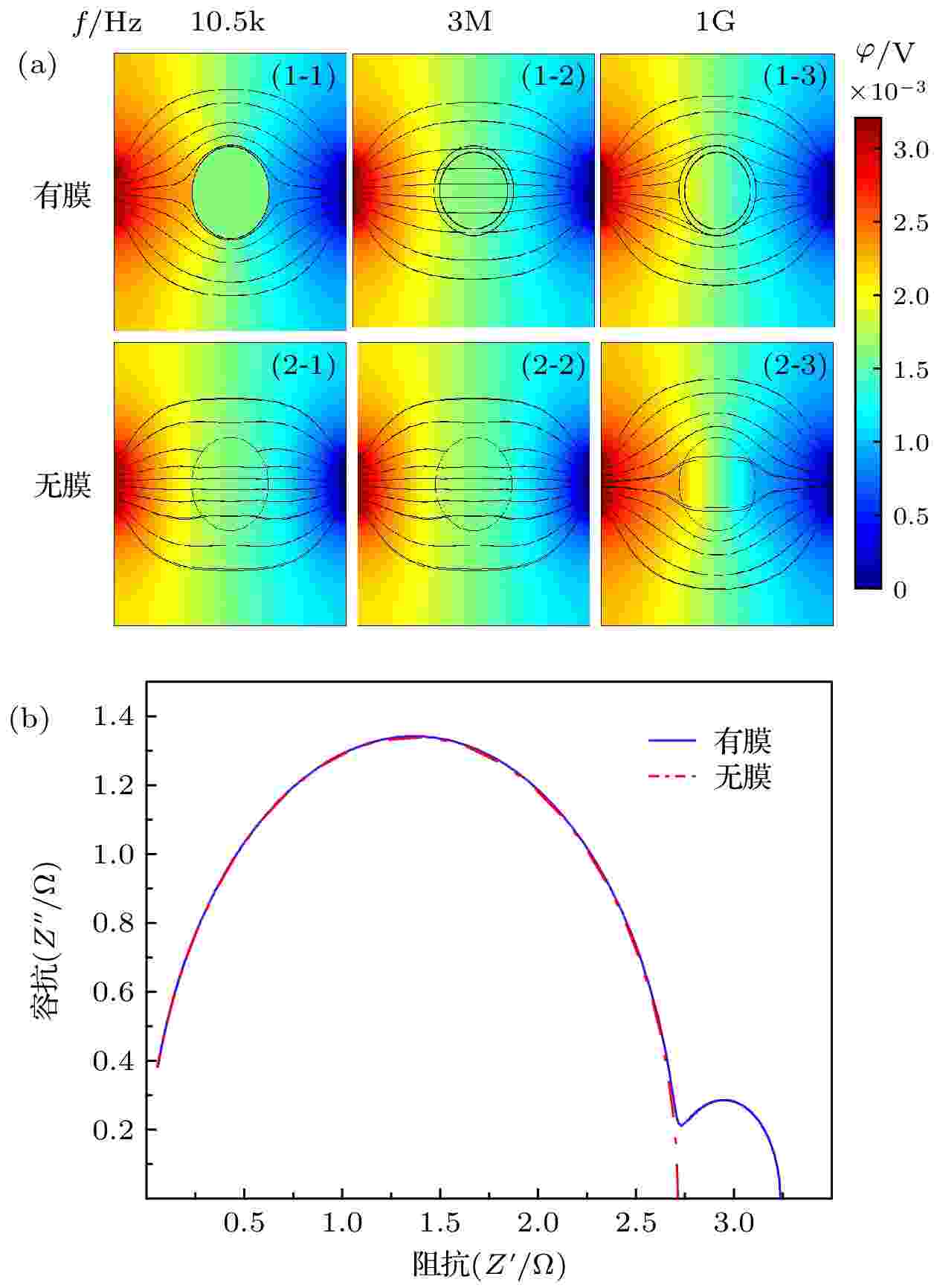图 3 无核细胞在有无膜下的仿真结果　(a)不同频率下无核细胞的仿真结果; (b)仿真结果对应的Cole-Cole Plot
Figure3. Simulation results of no-nuclear cells with or without membrane: (a) Simulation results of non-nucleated cells with different frequencies; (b) the Cole-Cole Plot corresponding to the simulation results.

由于“无膜”状态下的SS细胞模型内部只有细胞质的存在, 因此, 得出以下结论: 1)无核无膜下Cole-Cole图中的高频圆弧为细胞质与细胞外液的离子极化引起的; 2)有膜无核细胞较无膜细胞多出的小半圆弧为细胞外液与细胞膜的界面极化引起的.
2 -->

3.3.细胞核对细胞电学特性的影响

如2.1节所述, 目前大多数研究者普遍认同只考虑细胞膜结构的SS模型, 这说明细胞核及其他细胞器对阻抗谱分析无影响. 但是在图2(b)中可看出无核细胞模型与带核细胞模型在低频处的小半圆弧还是有所差距, 这说明细胞内部的细胞核会对细胞的阻抗造成影响. 因此, 为了探索细胞核的影响, 本文采用TS模型探索其影响因素.
仿真采用的TS细胞模型的核径分别为R₂ = 2.8 μm, R₂ = 1.9 μm, R₂ = 1.5 μm, R₂ = 0 (即无核). 首先在它们都带有细胞膜的情况下对其进行仿真分析, 而后去膜仿真加以验证.
频率f = 10.5 KHz时, 由于在该频率下细胞膜呈现出高阻态, 电流未进入细胞内, 因此图4(a)中的(1-1), (2-1), (3-1), (4-1)无明显区别, 细胞核对其无影响. 在相同频率下, 图4(a)无膜状态下的(1-4), (2-4), (3-4), (4-4)呈现较大的不同, 细胞内同一位置的电势随细胞核半径的减小而逐渐增加, 这表明细胞在无膜状态下核半径越大阻值越大. 在f = 3 MHz时, 虽然图4(a)中(1-2), (2-2), (3-2), (4-2)中已经有电场线通过, 但是在细胞内同位置的电势φ_1-2 < φ_2-2 < φ_3-2 < φ_4-2, 表明当细胞透过细胞膜后细胞核越大细胞阻值越大. 当频率高达f = 1 GHz时细胞已经被完全击穿, 因此图4(a) (1-3), (2-3), (3-3), (4-3)无明显区别, 图4(a)中的(1-6), (2-6), (3-6), (4-6)也没明显差别.
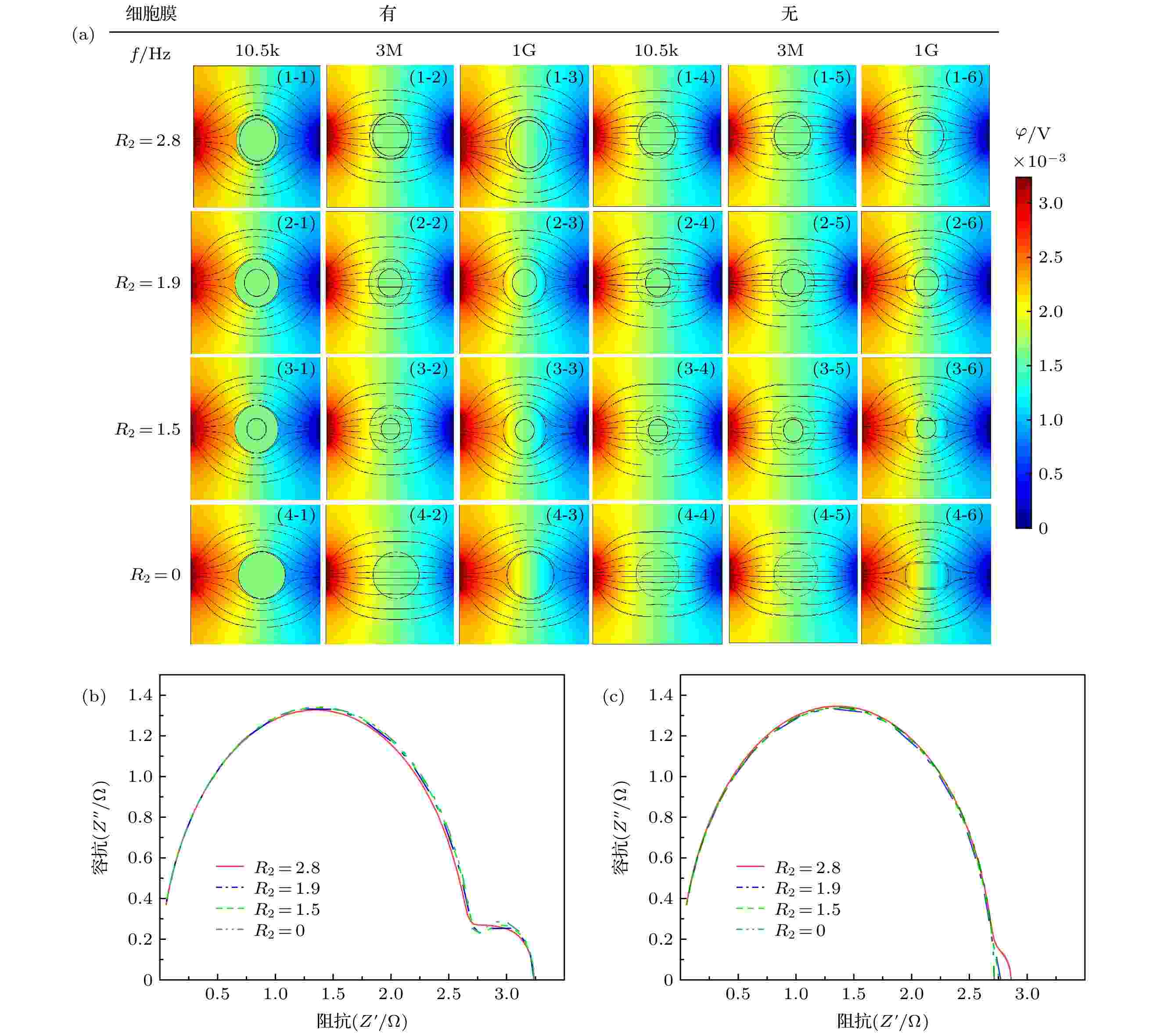图 4 不同核径细胞的仿真结果　(a)不同频率下的仿真结果; (b), (c)相应的Cole-Cole图
Figure4. Simulation results of cells with different nuclear radius: (a) Simulation results of cells at different frequencies; (b), (c) Cole-Cole Plot of different nuclear radius.

图4(b)显示, 在低频处的小半圆弧在不同细胞核半径下, 先是基本重和而后出现核径R₂ = 2.8 μm 时阻抗值 大于 R₂ = 1.9 μm的阻抗值, 并且后者的阻抗值与 R₂ = 1.5 μm 和 R₂ = 0时近似相同. 在图4(c)中不考虑细胞膜的影响时, 同样在低频处R₂ = 2.8 μm, R₂ = 1.9 μm, R₂ = 1.5 μm, R₂ = 0对应的小半圆弧先分散而后逐渐与高频处的大圆弧基本重合. 由此, 可判断并验证在低频小半圆弧出现的分散是由细胞核半径大小引起.
此外, 由图4(b)和图4(c)可看出, 在细胞核半径R₂ = 1.9 μm, R₂ =1.5 μm, R₂ = 0时的阻抗基本相等, 由此看出当细胞核半径R₂ ≤ 1.9 μm时可将细胞核的影响忽略. 细胞核质比计算公式为:

$N = {V_{\rm{n}}}/{V_{\rm{c}}},\tag{8a}$

${V_{\rm{n}}} = \frac{4}{3}{\text{π}}R_2^3,\tag{8b}$

${V_{{\rm{cell}}}} = \frac{4}{3}{\text{π}}R_1^3,\tag{8c}$

${V_{\rm{c}}} = {V_{{\rm{cell}}}} - {V_{\rm{n}}},\tag{8d}$

其中V_n为细胞核的体积, V_cell为细胞体积, V_c为细胞质体积. 计算可知此时细胞核质比约为1∶4, 且当细胞的核质比小于0.25时可忽略其影响. 正常细胞的核质比为1∶4—6, 因此****普遍将细胞内核以及其他细胞器忽略视为单壳模型(SS).

2

-->

4.1.实验设备

本实验以酵母悬液为被测对象. 图5给出了实验设备原理图: 一台PC机、一台阻抗分析仪(IM7581)、一个四端开尔文卡子、一个降噪屏蔽和一个小试管. 试管是一个方柱状容器, 长d_c = 10 mm, 宽w_c = 2 mm, 高h_c = 20 mm. 测量电极由对侧平行的一对金属板组成, 面积为A = 20 mm×10 mm. 将小试管置于降噪罩中进行测量, 隔离环境中的电磁干扰. 小试管通过一个四端开尔文卡子连接到阻抗分析仪上. 阻抗分析仪捕获探头发出的信号后, 将测量数据传输给PC机进行后续的拟合. 测量频率范围为f = 100 kHz—300 MHz, 测量点数量为1500个. 提取20%体积分数的死活酵母悬浮液的阻抗信息, 并作出相应的Cole-Cole图.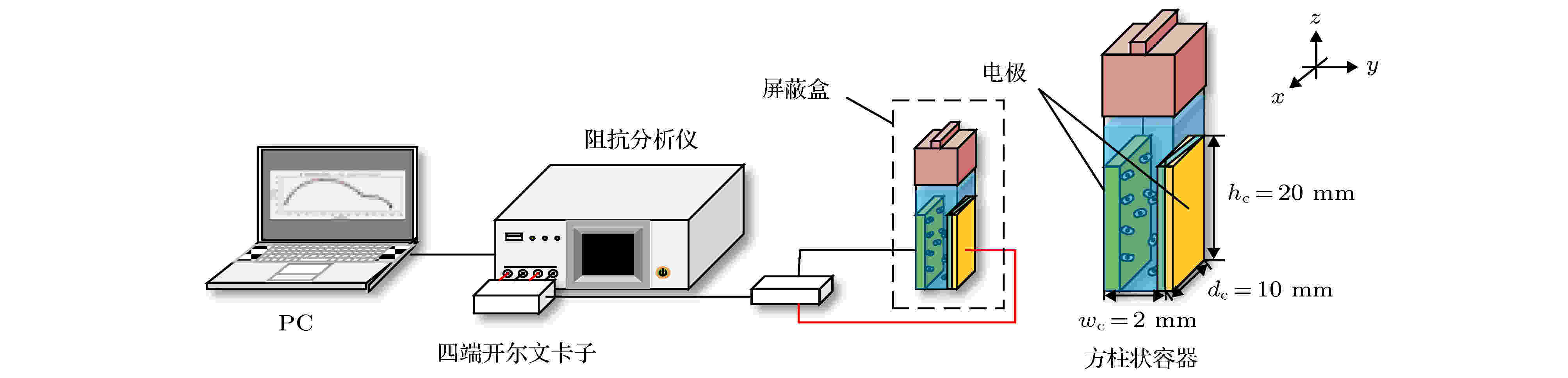
图 5 实验设备
Figure5. Experimental set-up.

2 -->

4.2.实验结果

图6(a)给出了实验中酵母的显微结构及模型图. 其中将酵母菌粉置于37 ℃ ± 2 ℃的温水中浸泡30 min, 获得活酵母菌, 死酵母菌则在70 ℃ ± 2 ℃的热水中浸泡30 min获取. 可以看出, 活酵母菌的细胞膜光滑平整, 而死酵母菌的细胞膜出现收缩皱裂, 由此可知酵母菌经热水处理后细胞膜已完全被破坏, 处于“无膜”状态. 由图6(b)可看出, 20%活酵母菌在Cole-Cole图中显示出大小两个半圆弧, 而经过热水处理后的同体积分数的酵母菌在Cole-Cole图只有一个半圆弧, 且该半圆弧处于高频段. 图6(b)中两个样品的Cole-Cole图对应比较, 可推断出死酵母菌(无膜)在此时呈现的圆弧即为细胞质与细胞外液形成的介电驰豫, 而活酵母菌低频段出现的小圆弧正是细胞膜与细胞外液间极化形成的介电驰豫. 在忽略阻抗值大小后, 可看出图6(b)中 Cole-Cole图的基本趋势与图3 (b)无核细胞的有无膜的Cole-Cole图基本趋势一致. 因此, 20%体积分数的酵母菌实验验证了3.2节中的仿真内容.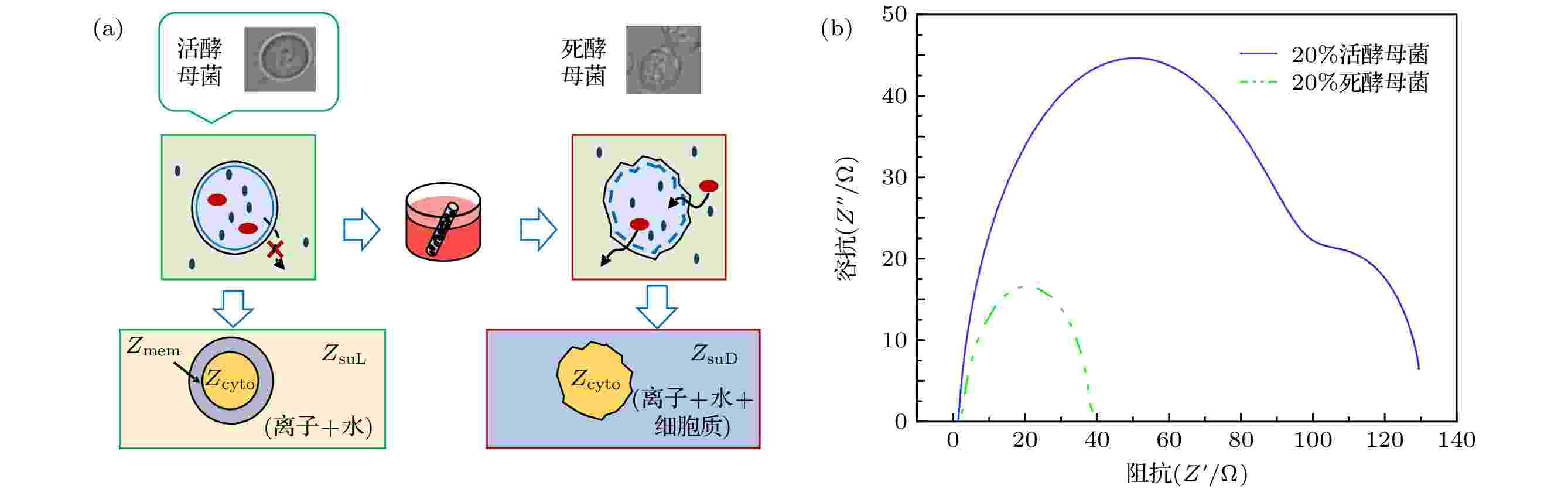
图 6 实验图　(a)死活酵母菌实物与模型图; (b)20%死活酵母菌Cole-Cole图
Figure6. Experiment: (a) Object and model of dead and alive yeast; (b) Cole-Cole Plot of 20% dead and alive yeast.

图3(b)阻抗数值比图6(b)中的数值小是由以下原因造成的: 1)实验中使用的细胞外液为纯水导电率σ_0e = 5.5 × 10^–6 S/m, 而仿真中使用的导电率σ_0i = 0.6 S/m, 这将导致仿真中所获得的数据远低于实验的阻抗值; 2)实验中的电极尺寸与待测区域的比值d_e为

${d_{\rm{e}}} = \frac{l}{L}$

其中l为电极长, L为测量区域的边长. 实验中d_e = 14.14/550 = 0.026, 而仿真的d_e = 4/20 = 0.2. d_e越小则压降越严重, 这将会使得所测的阻抗数值偏大.
此外图3(b)中无膜状态下的大圆弧与有膜下的大圆弧基本重合, 而图6(b)中的死酵母菌对应的圆弧与活酵母并未重合. 这是由于仿真中无膜细胞区域与外界区域已经被划开, 两者之间不产生离子的流动(即导电率较为稳定). 而实验中, 酵母菌一旦失去活性, 细胞膜破裂, 细胞内的离子无障碍地流向细胞外液中, 如图6(a)所示, 从而导致细胞外液的导电率升高, 阻抗较低.

本文采用数值仿真的方式研究了单细胞电学特性与其结构之间的关系, 并通过实验进行验证, 得出以下四个结论.
1) 细胞结构尺寸的变化引起细胞电学特性的改变, 依据细胞电学特性能够准确进行细胞分类;
2) Cole-Cole图上高频与低频的两个半圆弧分别是由细胞质与细胞外液的离子极化、细胞膜与细胞外液之间的界面极化引起的;
3) 细胞核大小对测量阻抗的影响主要在低频段, 是由细胞核与细胞内液的界面极化引起的, 但当细胞核质比小于0.25时可忽略其影响;
4) 对20%不同活性的酵母菌进行实验, 实验结果和仿真结果一致, 验证了Cole-Cole图中高频与低频两个圆弧分别是由细胞质或细胞外液的离子极化、细胞膜与细胞外液之间的界面极化引起的.
感谢西安理工大学刘夏移博士和日本千叶大学武居昌宏教授提供的技术支持.