删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

含双曲超构材料的复合周期结构的带隙调控及应用

本站小编 Free考研考试/2021-12-29
摘要:等频面的拓扑结构强烈影响光在材料中的行为. 通常组成光子晶体原胞的材料都是介电材料, 其等频面都具有相同的封闭拓扑结构. 结构最为简单的光子晶体是由两种介电材料交替组成的一维光子晶体. 然而, 这种传统的光子晶体在横磁和横电偏振下的光子带隙将随着入射角的增大而向短波方向移动, 既不利于全向带隙的产生与展宽, 又使得基于光子带隙的一些应用限制在很窄的入射角度范围内. 本综述利用双曲超构材料对电磁波相位的独特调控作用, 在由具有开放的等频面的双曲超构材料和具有封闭的等频面的普通介电材料交替组成的复合周期结构中实现了随入射角零移以及红移的特殊带隙, 为研制具有新型功能的光学器件提供了新机理. 基于零移带隙, 可设计具有固定带宽的全向反射器和宽角度的近完美光吸收器. 基于红移带隙, 可设计宽角度的偏振选择器和超灵敏折射率传感器.
关键词: 双曲超构材料/
光子晶体/
光子带隙

English Abstract


全文HTML

--> --> -->
1.引　言
光在材料中的行为强烈依赖于材料的色散关系$\omega ({{k}})$, 特别是等频面$\omega ({{k}}) = {\omega _0}$的拓扑结构. 对于通常的介电材料而言, 其等频面为封闭的球面或椭球面. 近年来, 利用人工微结构调控等频面的拓扑结构引起了国内外研究人员的极大兴趣, 一个典型的例子便是双曲超构材料[1-6]. 双曲超构材料是指介电张量或磁导率张量中的三个分量既有正值又有负值的一种超构材料[1-6]. 不同于通常介电材料封闭的等频面, 双曲超构材料的等频面为开放的双曲面[1-6]. 双曲超构材料特殊的等频面形态, 极大地丰富了人们对光的调控. 各种基于双曲超构材料的新现象和应用不断地涌现了出来, 例如负折射[7-9]、自发辐射调控[10,11]、表面等离激元调控[12,13]、远距离电磁感应透明[14]和电磁波定向传播[15-17]等. 近年来, 研究人员还利用双曲超构材料实现了对光学波阵面的灵活调控[18,19], 如波束偏转[18]、波束聚焦[18]和宽带的艾里光束产生[19]等.
双曲超构材料可进一步分为电双曲超构材料和磁双曲超构材料, 二者的区别在于是介电张量还是磁导率张量的三个分量中既有正值又有负值. 由于光波段的磁响应比较难以实现, 所以位于光波段的电双曲超构材料比磁双曲超构材料更为普遍. 对于单轴的电双曲超构材料, 在主轴坐标系下, 其介电张量可以表示为$\overline{\overline \varepsilon } = {\rm{diag(}}{\varepsilon _x}, {\varepsilon _y}, {\varepsilon _z}{\rm{)}}$, 其中${\varepsilon _x}= {\varepsilon _y}$[2-5]. 将介电张量代入麦克斯韦方程组中, 可得在横磁(transverse magnetic, TM)偏振下的等频面方程为[2-5]
$\frac{{k_x^2+k_y^2}}{{{\varepsilon _z}}} + \frac{{k_z^2}}{{{\varepsilon _{x,y}}}} = \frac{{{\omega ^2}}}{{{c^2}}}.$
从方程(1)可以看出, 当${\varepsilon _{x, y}}$和${\varepsilon _z}$的符号相反, 即${\varepsilon _{x, y}}{\varepsilon _z} < 0$时, 等频面为开放的双曲面, 这就是双曲超构材料名称的由来. 根据${\varepsilon _{x, y}}$和${\varepsilon _z}$的具体正负情况, 双曲超构材料可以进一步分为第一类(介质型)和第二类(金属型)双曲超构材料[2-5]. 若${\varepsilon _{x, y}} > 0$而${\varepsilon _z} < 0$, 称为第一类双曲超构材料, 其等频面为双叶双曲面, 可支持具有任意切向波矢的模式[2-5]. 由于其介电张量中有两个分量为正, 具备更多介质的特征, 因此又被称为介质型双曲超构材料[2-5]. 近年来, 介质型双曲超构材料被应用于超分辨成像[20]、角度选择器[21]、光的自旋霍尔效应增强[22]、亚波长谐振腔[23]、超灵敏传感器[24]、光吸收器[25]以及热辐射增强[26]等领域. 若${\varepsilon _{x, y}} < 0$而${\varepsilon _z} > 0$, 则称为第二类双曲超构材料, 其等频面为单叶双曲面, 只能支持具有较大切向波矢的模式, 即具有截止切向波矢[2-5]. 由于其介电张量中有两个分量为负, 具备更多金属的特征, 反射较强, 因此又被称为金属型双曲超构材料[2-5]. 近年来, 金属型双曲超构材料被应用于非对称传输[27]、亚波长谐振腔[28]、超灵敏传感器[29,30]和光吸收器[31]等方面.
另一方面, 由不同材料周期性排列而成的光子晶体的光传输特性的调控引起了研究人员的广泛关注, 涵盖了带隙调控、通带调控和群速度调控等各个方面[32-35]. 近年来, 宇称-时间(parity-time, PT)对称的光子晶体也引起了人们的关注[36-39]. 基于PT对称的光子晶体, 可以实现多种新奇的光学现象, 包括奇异点(exceptional point)劈裂[36]、奇异点合并[37]、各向异性的反射振荡[38]和单方向隐身[39]等. 光子带隙是光子晶体的一个核心特征, 对光子晶体的带隙调控是目前光物理的一个活跃领域[32-35]. 频率落在带隙中的光, 将无法在光子晶体中稳定传播, 从而被光子晶体强烈反射[40,41]. 三十多年来, 光子晶体的带隙被广泛地应用在各个方面[42,43], 如激光器[44-46]、滤波器[47-49]、传感器[50,51]、偏振分束器[52,53]、光波导[54,55]、光纤[56-58]、高方向性天线[59]、单向传输[60-62]和自发辐射调控[63]等. 目前, 通常组成光子晶体原胞的材料的等频面都具有相同的封闭拓扑结构, 其中结构最为简单的是由两种各向同性介质交替组成的一维光子晶体. 然而, 这种传统的光子晶体的带隙强烈依赖于光的入射方向[64-68]. 在TM和横电(transverse electric, TE)偏振下, 各向同性的电介质的等频线均为封闭的圆. 因此, 在固定频率下, 光子晶体原胞内的总传播相位将随着入射角的增大而减小. 为了维持布拉格反射条件(即原胞内的总传播相位等于π的整数倍)的成立, TM和TE偏振的带隙随着入射角的增大将会向高频(短波)方向移动(即蓝移)[64-68]. 传统的全介质一维光子晶体带隙的蓝移特性, 将使得全向带隙的宽度小于正入射时的带隙宽度, 从而不利于全向带隙的产生和展宽[64-68]. 此外, 对于TM和TE偏振, 传统带隙都是随入射角蓝移的, 这将导致带隙对不同偏振的区分度不明显, 从而限制了偏振选择的工作角度范围. 此外, 光子晶体带隙的蓝移特性还将导致金属/光子晶体异质结中的光学界面态的蓝移特性[69,70], 从而使得基于光子带隙的一些应用(如近完美光吸收[71-73]和超灵敏传感[74-76])限制在很窄的入射角度范围内. 综上所述, 由具有相同拓扑结构的等频面的材料组成的光子晶体具有一系列的缺点. 因此, 一个很有趣的问题是, 由具有不同拓扑结构的等频面的材料组成的复合周期结构对光子带隙的形成机制有何影响?
本文将介绍本研究组近年来在含双曲超构材料的复合周期结构的带隙调控及其应用方面的研究情况. 这种新型的复合周期结构如图1所示. 目前, 双曲超构材料主要可由两种方式实现. 一种方式是由二维金属柱阵列实现[77,78]. 此时, 复合周期结构是由一个层状介电材料和二维金属柱阵列杂化而成的复合光子晶体. 另一种方式是由金属/介质亚波长多层膜实现[78-80]. 此时, 复合周期结构就是一个由多层膜构成的一维光子晶体. 一维结构的制备只需用到镀膜技术[81,82], 比二维和三维结构简单许多[43,83], 且更容易进行大面积的制备[84]. 此外, 一维光子晶体的应用十分广泛, 包括宽带反射镜[64,85-90]、宽带透明[91,92]、宽带波片[93]、窄带滤波器[94-98]、窄带吸收器[71-73,99,100]、非互易传输[101-103]和辐射制冷[84]等. 因此, 本文将主要介绍课题组在这方面的研究情况.
图 1 含双曲超构材料的复合周期结构的示意图
Figure1. Schematic of the compound periodic structure containing hyperbolic metamaterials.

2.传统的全介质一维光子晶体带隙的蓝移特性
图2为由两种各向同性的普通电介质交替组成的一维光子晶体的示意图. 一维光子晶体的第一个(最低频)带隙位置可由如下的布拉格反射条件决定:
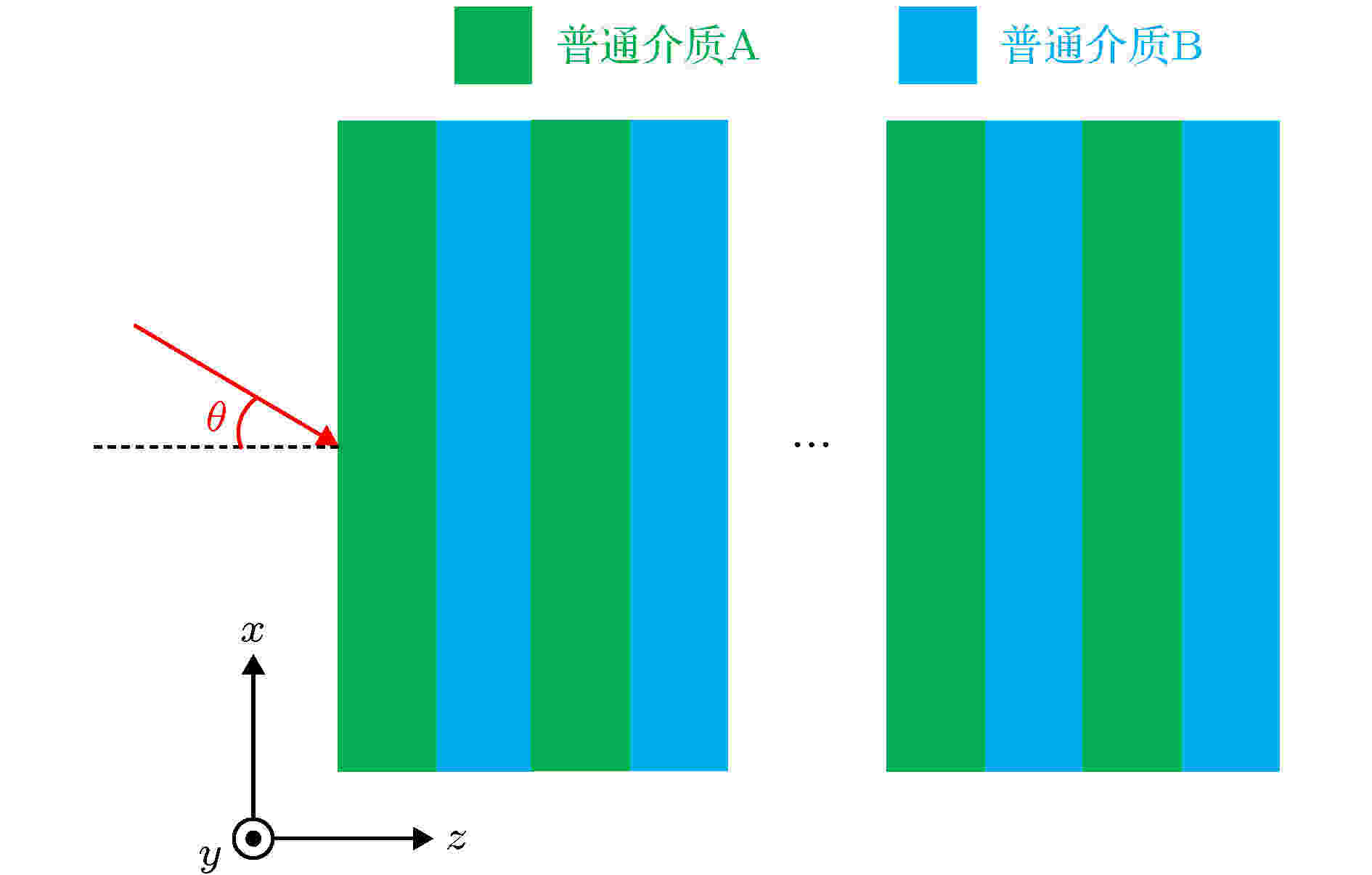图 2 传统的全介质一维光子晶体(AB)N的示意图
Figure2. Schematic of the conventional all-dielectric one-dimensional photonic crystal (AB)N.

${\left. \varPhi \right|_{{\omega _{{\rm{Brg}}}}}} = {\left. {{k_{{\rm{A}}z}}{d_{\rm{A}}} + {k_{{\rm{B}}z}}{d_{\rm{B}}}} \right|_{{\omega _{{\rm{Brg}}}}}} = {\rm{\text{π}}}.$
其中, Φ为光子晶体原胞的总传播相位, ${k_{{\rm{A}}z}}$和${k_{{\rm{B}}z}}$为介质A和B中的波矢的z分量, ${d_{\rm{A}}}$和${d_{\rm{B}}}$为介质A和B的厚度, ${\omega _{{\rm{Brg}}}}$为布拉格频率. 将介质A或B的介电常数代入麦克斯韦方程组, 可得其等频线(TM和TE偏振)方程为
$k_x^2 + k_{{\rm{A(B)}}z}^2 = {\varepsilon _{{\rm{A(B)}}}}\frac{{{\omega ^2}}}{{{c^2}}}.$
由方程(3)可知, 各向同性介质A和B的等频线均为封闭的圆, 如图3所示.
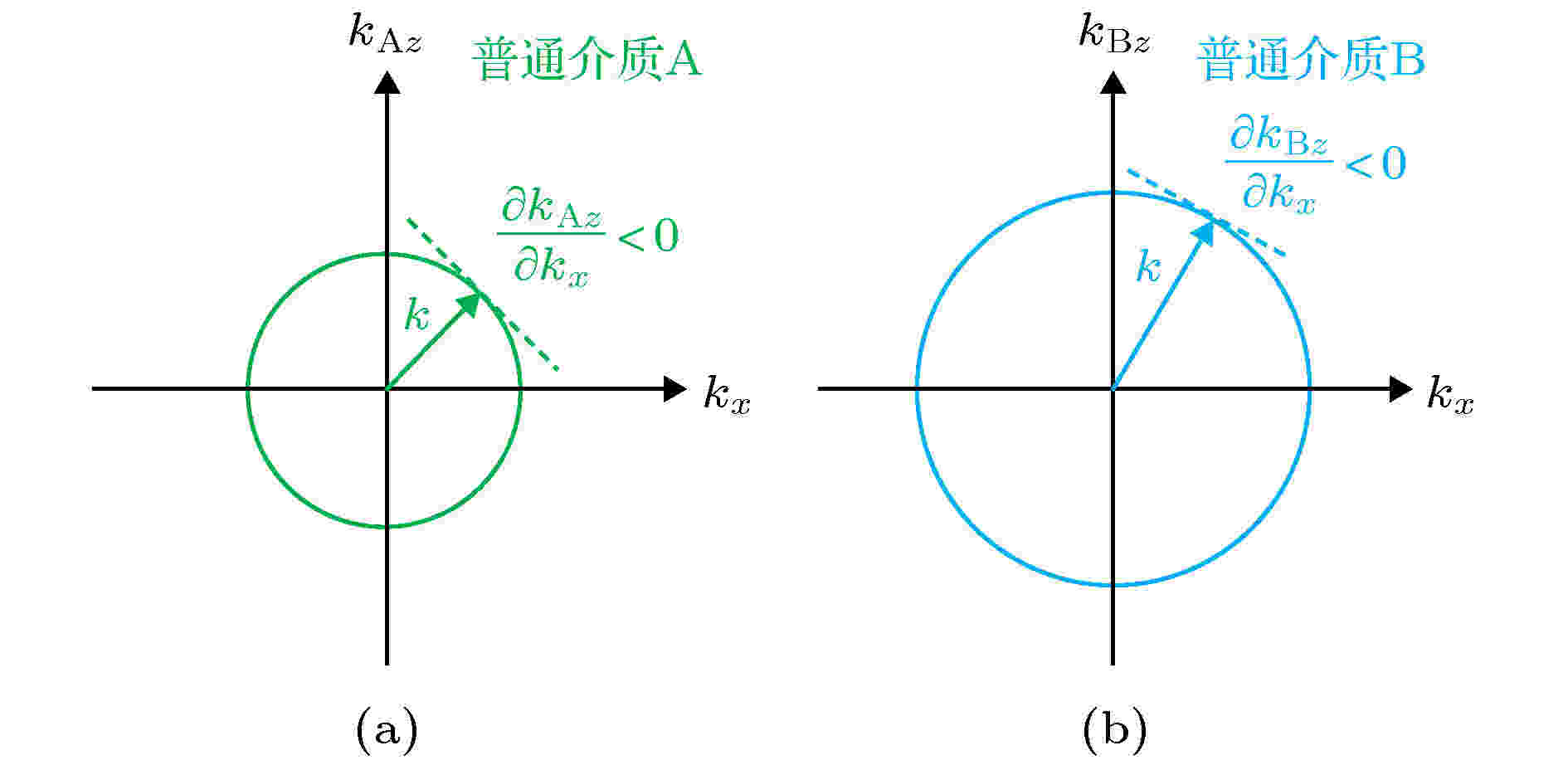图 3 普通介质A和B的等频线(TM和TE偏振)
Figure3. Iso-frequency curves of isotropic dielectrics A and B (TM and TE polarizations).

因此, $\dfrac{{\partial {k_{{\rm{A}}z}}}}{{\partial {k_x}}}$和$\dfrac{{\partial {k_{{\rm{B}}z}}}}{{\partial {k_x}}}$均小于0. 在频率不变时, 随着入射角$\theta $的增大, 介质A和B中的波矢的z分量${k_{{\rm{A}}z}}$和${k_{{\rm{B}}z}}$将减小. 为了维持布拉格条件的成立, 此时频率必须增大, 带隙将向短波方向移动. 此即传统一维光子晶体带隙蓝移的物理原因.
下面给出一个具体的例子. 图4给出了数值计算的一维光子晶体(AB)10的反射谱(TM和TE偏振)随入射角的变化, 其中蓝色虚线为带隙的两个边缘, 由最靠近带隙的反射极小值提取. A和B层的材料分别为SiO2和TiO2, 折射率分别为1.43和2.12[104]. A和B层的厚度满足四分之一波堆条件${n_{\rm{A}}}{d_{\rm{A}}} = {n_{\rm{B}}}{d_{\rm{B}}} = {{{\lambda _0}} / 4}$, 其中, ${\lambda _0} = 410$ nm. 入射和衬底介质分别为空气和BK7玻璃(折射率为1.52). 数值计算方法为传输矩阵法[105].
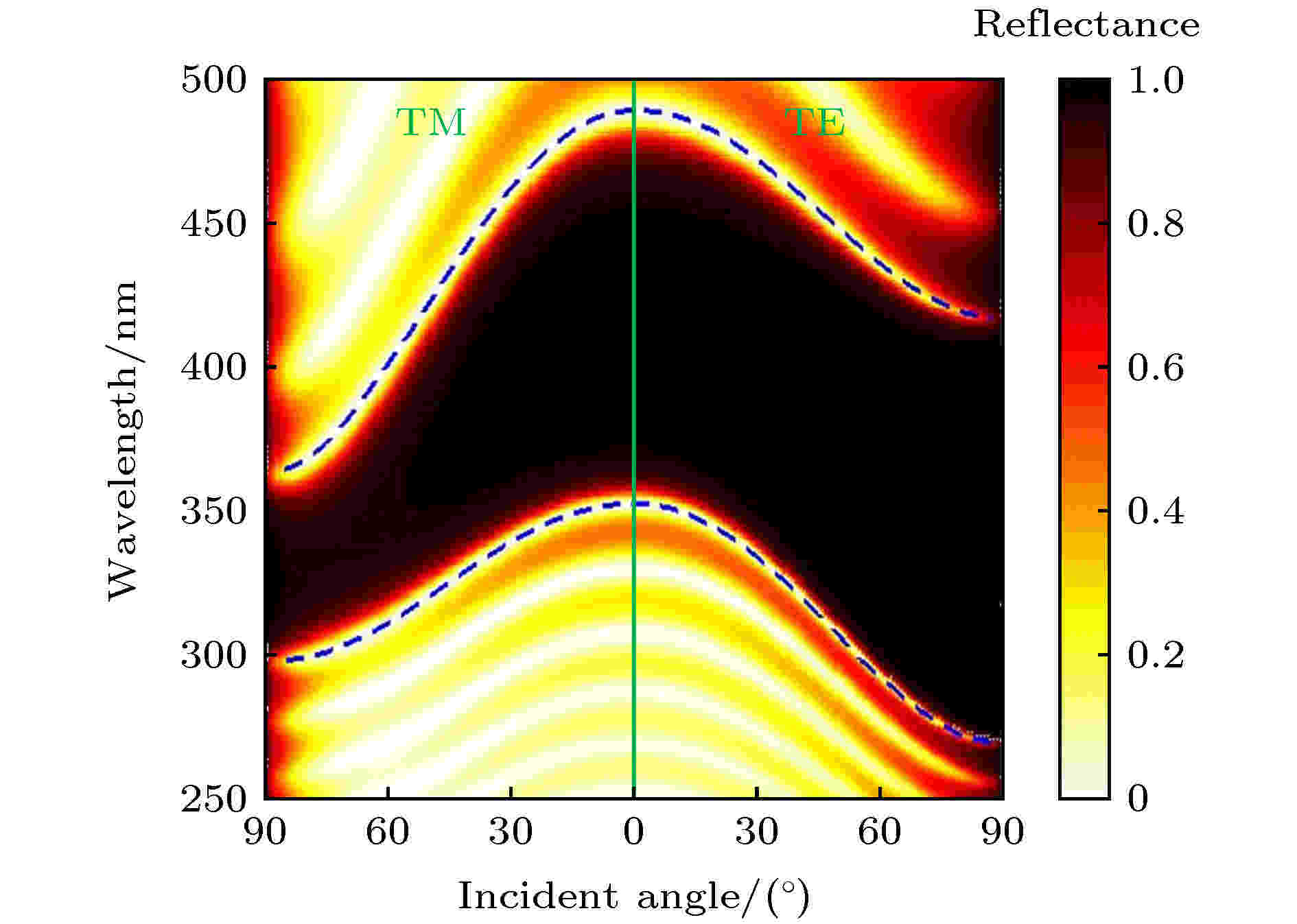图 4 数值计算的一维光子晶体(AB)10的反射谱(TM和TE偏振)随入射角的变化
Figure4. Calculated reflectance spectrum of (AB)10 as a function of incident angle (TM and TE polarizations).

由图4可知, 无论是对于TM还是TE偏振而言, 传统的全介质一维光子晶体的带隙均随着入射角的增大而蓝移. 如引言所述, 传统一维光子晶体TM和TE偏振带隙的蓝移特性, 不仅不利于全向带隙的产生和展宽, 还大大限制了偏振选择、近完美光吸收以及超灵敏传感的工作角度范围.
3.含双曲超构材料的一维光子晶体的零移带隙和红移带隙
2
3.1.带隙调控的理论基础
-->

3.1.带隙调控的理论基础

为了克服传统的全介质一维光子晶体的物理限制, 构造了由双曲超构材料和介质交替组成的一维新型光子晶体, 如图5所示. 其中, 双曲超构材料由金属/介质亚波长多层膜等效而成. 根据等效介质理论, 金属/介质亚波长多层膜在某个特定的频段可等效为单轴的电双曲超构材料, 其等效相对介电张量的两个分量为[2-5]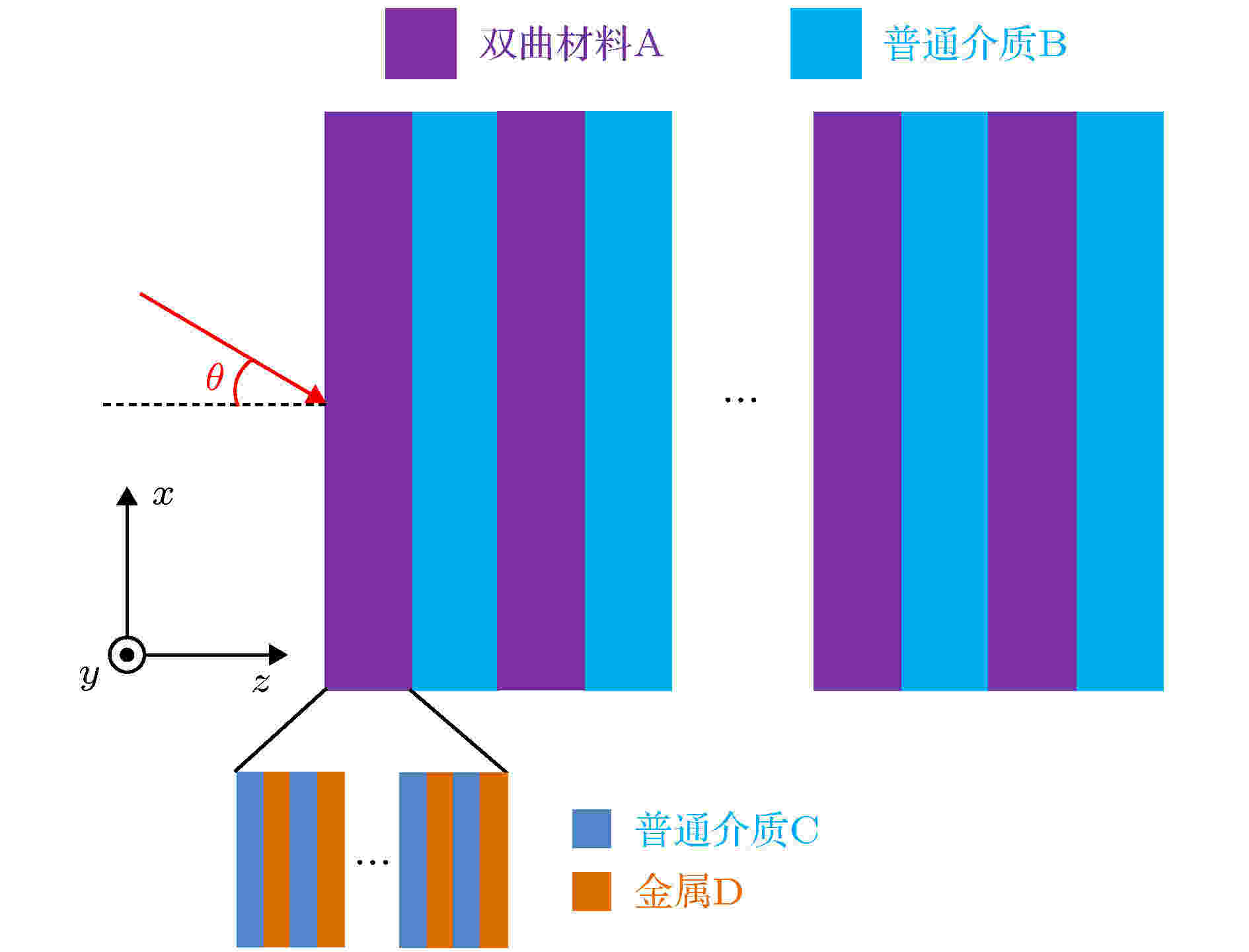
图 5 含双曲超构材料的一维光子晶体[(CD)SB]N的示意图
Figure5. Schematic of the one-dimensional photonic crystal containing hyperbolic metamaterials [(CD)SB]N.

${\varepsilon _{{\rm{A}}x}} = f{\varepsilon _{\rm{C}}} + (1 - f){\varepsilon _{\rm{D}}},\tag{4a}$
$\frac{1}{{{\varepsilon _{{\rm{A}}z}}}} = \frac{f}{{{\varepsilon _{\rm{C}}}}} + \frac{{1 - f}}{{{\varepsilon _{\rm{D}}}}},\tag{4b}$
其中$f = {d_{\rm{C}}}/({d_{\rm{C}}} + {d_{\rm{D}}})$为亚波长介质层的填充比. 在第一类双曲的频段内, 有$\operatorname{Re} ({\varepsilon _{{\rm{A}}x}}) \!>\! 0, \operatorname{Re} ({\varepsilon _{{\rm{A}}z}}) \!<\! 0$. 这里只考虑第一类双曲的频段而不考虑第二类双曲的频段的原因是, 第二类双曲在TM偏振下的等频线存在截止切向波矢, 在入射光的切向波矢小于截止切向波矢的情况下, 入射光将被双曲材料强烈反射[4]. 因为要研究由两种透明材料(在任何入射角度下)组成的周期结构的能带特性, 因此使用第一类全角度透明的双曲超构材料. 在TM偏振下, 双曲超构材料A的等频线方程为[2-5]
$\frac{{k_x^2}}{{{\varepsilon _{{\rm{A}}z}}}} + \frac{{k_{{\rm{A}}z}^2}}{{{\varepsilon _{{\rm{A}}x}}}} = \frac{{{\omega ^2}}}{{{c^2}}}.$
由方程(5)可知, 双曲超构材料A在TM偏振下的等频线为开放的双曲线, 如图6(a)所示. 这里需要指出的是, 在TE偏振下, 双曲超构材料A中传播的是正常光(ordinary wave), 其等频线为封闭的圆而不是双曲线[5]. 因此, 本文中只考虑TM偏振. 对于普通介质B, 在TM偏振下, 其等频线也为封闭的圆, 如图6(b)所示.
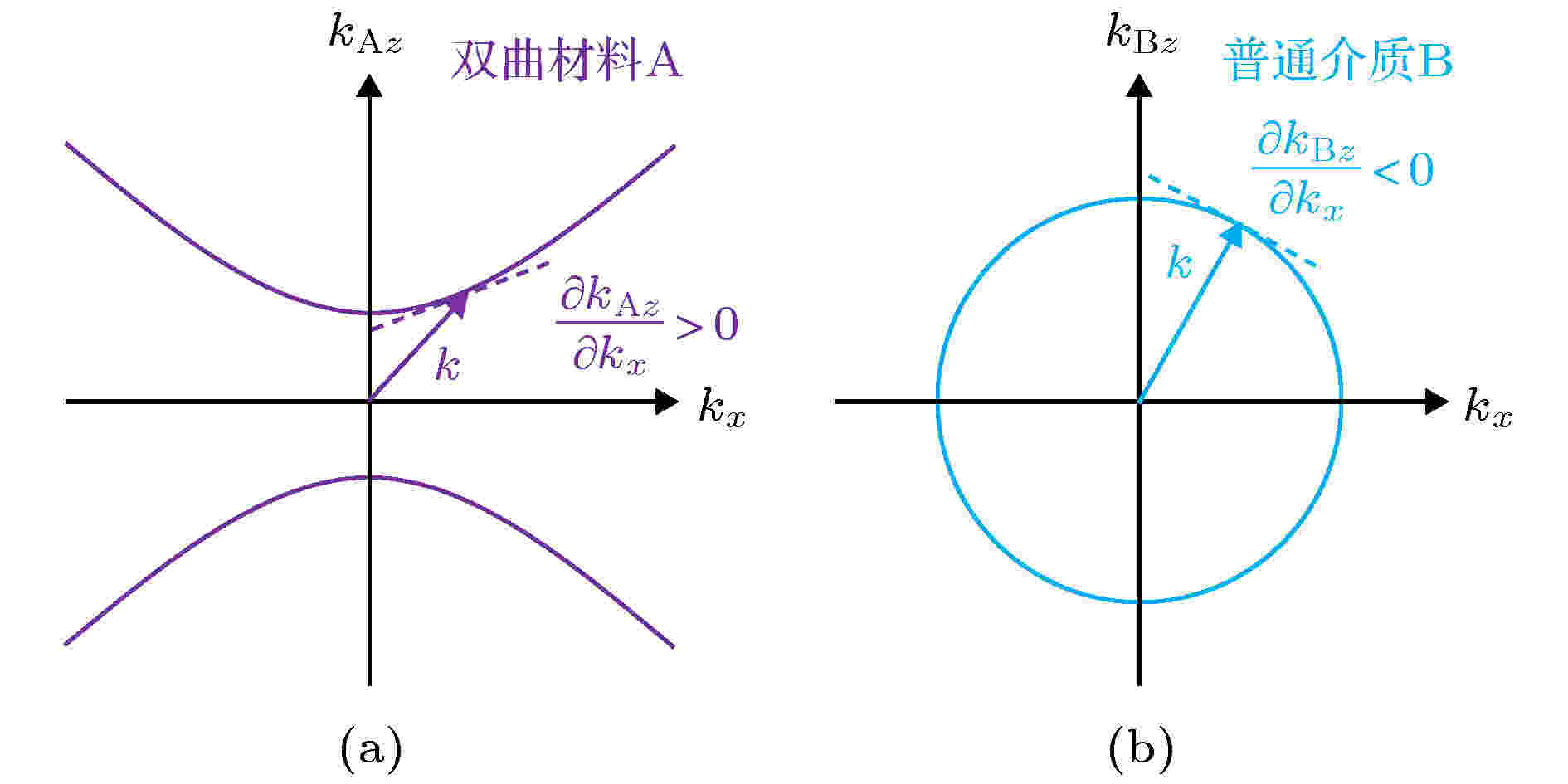图 6 (a)双曲材料A和(b)普通介质B的等频线(TM偏振)
Figure6. Iso-frequency curves of (a) hyperbolic metamaterial A and (b) isotropic dielectric B (TM polarization).

由图6可知, $\dfrac{{\partial {k_{{\rm{A}}z}}}}{{\partial {k_x}}} > 0$而$\dfrac{{\partial {k_{{\rm{B}}z}}}}{{\partial {k_x}}} < 0$. 也就是说, 随着入射角的增大, 在双曲材料层中的波矢的z分量${k_{{\rm{A}}z}}$将增大, 而在普通介质层中的波矢的z分量${k_{{\rm{B}}z}}$将减小. 因此, 在TM偏振下, 光子晶体原胞的总传播相位$\varPhi = {k_{{\rm{A}}z}}{d_{\rm{A}}} + {k_{{\rm{B}}z}}{d_{\rm{B}}}$随入射角增大的变化规律可以灵活调节. 基于以上的理论基础, 可以实现TM偏振的零移带隙以及红移带隙.
2
3.2.零移带隙
-->

3.2.零移带隙

零移带隙即与角度无关的带隙, 这种带隙不随入射角的增大而移动. 因此, 根据布拉格条件, 光子晶体原胞的总传播相位$\varPhi $必须与入射角$\theta $(或${k_x}$)无关, 即[106]
$\frac{{\partial \varPhi }}{{\partial {k_x}}} = \frac{{\partial {k_{{\rm{A}}z}}}}{{\partial {k_x}}}{d_{\rm{A}}} + \frac{{\partial {k_{{\rm{B}}z}}}}{{\partial {k_x}}}{d_{\rm{B}}} = 0.$
将方程(6)和布拉格条件(即方程(2))联立, 在近似条件$ \left| {{\varepsilon _{{\rm{A}}z}}} \right| \gg 1$和${\varepsilon _{\rm{B}}} \gg 1$下, 可得TM偏振的零移带隙的两个解析条件[106]:
${d_{\rm{A}}} = \frac{{{\lambda _{{\rm{Brg}}}}}}{2}\frac{1}{{\sqrt {{\varepsilon _{{\rm{A}}x}}} \left(1 - {{{\varepsilon _{\rm{B}}}}}/{{{\varepsilon _{{\rm{A}}z}}}}\right)}},\tag{7a}$
${d_{\rm{B}}} = \frac{{{\lambda _{{\rm{Brg}}}}}}{2}\frac{1}{{\sqrt {{\varepsilon _{\rm{B}}}} \left(1 - {{{\varepsilon _{{\rm{A}}z}}}}/{{{\varepsilon _{\rm{B}}}}}\right)}},\tag{7b}$
其中${\lambda _{{\rm{Brg}}}}$为选取的正入射时的布拉格波长. 根据方程(7), 设计了具体的多层膜结构, 结构式为[(CD)2B]3. 根据等效介质理论(即方程(4)), 金属/介质亚波长多层膜(CD)2在波长309— 430 nm的范围内满足$\operatorname{Re} ({\varepsilon _{{\rm{A}}x}}) > 0$和$\operatorname{Re} ({\varepsilon _{{\rm{A}}z}}) < 0$, 可等效为第一类双曲超构材料[107]. 选取的正入射时的布拉格波长为${\lambda _{{\rm{Brg}}}} = 373$ nm. 其中C和B层的材料为TiO2, D层的材料为Ag. 入射和衬底介质分别为空气和BK7玻璃. 数值计算和实验测量的不同入射角下的反射谱(TM偏振)分别如图7(a)和7(b)所示. 其中实心圆点代表最靠近带隙的反射极小值(即带隙边缘的标定位置), 灰色阴影区域代表带隙的边缘随入射角的波动范围.
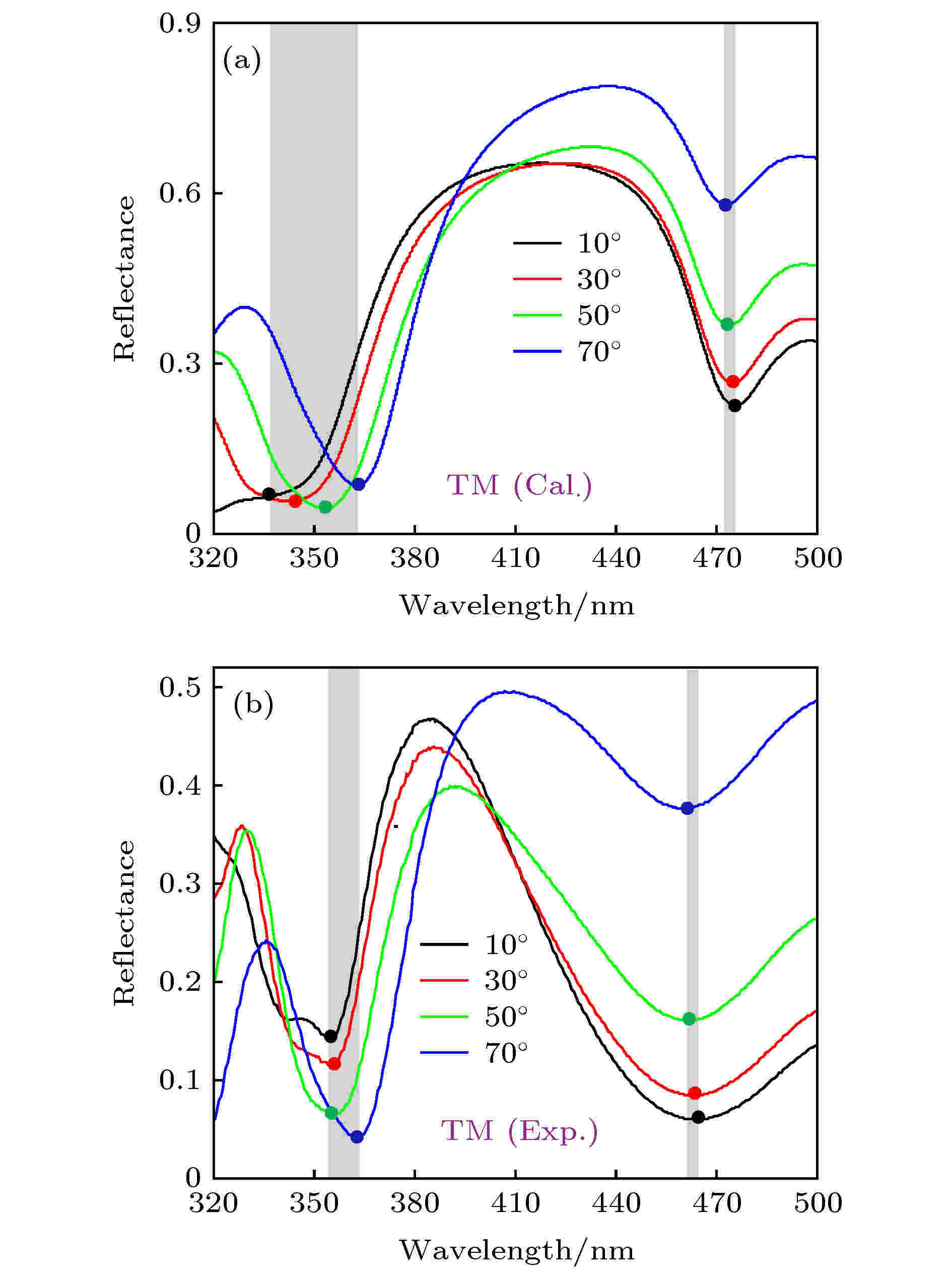图 7 含双曲超构材料的一维光子晶体[(CD)2B]3在不同入射角下的反射谱(TM偏振) 　(a) 数值计算结果[107]; (b) 实验测量结果[107]
Figure7. Reflectance spectra of [(CD)2B]3 under different incident angles (TM polarization): (a) Simulated result[107]; (b) experimental result[107].

由数值计算结果可知, 带隙的长波长边缘几乎与入射角无关, 然而短波长边缘随入射角有轻微的移动, 这是由于在设计中, 近似条件$ \left| {{\varepsilon _{{\rm{A}}z}}} \right| \gg 1$和${\varepsilon _{\rm{B}}} \gg 1$没有被很好地满足引起的[107]. 若这两个条件能在具体设计中被很好地满足, 带隙的两个边缘均与入射角几乎无关[106]. 由实验测量结果可知, 该结果与数值计算结果符合得较好, 带隙的两个边缘随入射角的移动幅度都比较小. 最后, 图8给出了数值计算结果和实验测量结果的进一步对比[107]. 其中彩色背景代表数值计算的反射谱(TM偏振)随入射角的变化; 黑色空心圆圈代表实验测量的带隙边缘波长, 由最靠近带隙的反射极小值提取.
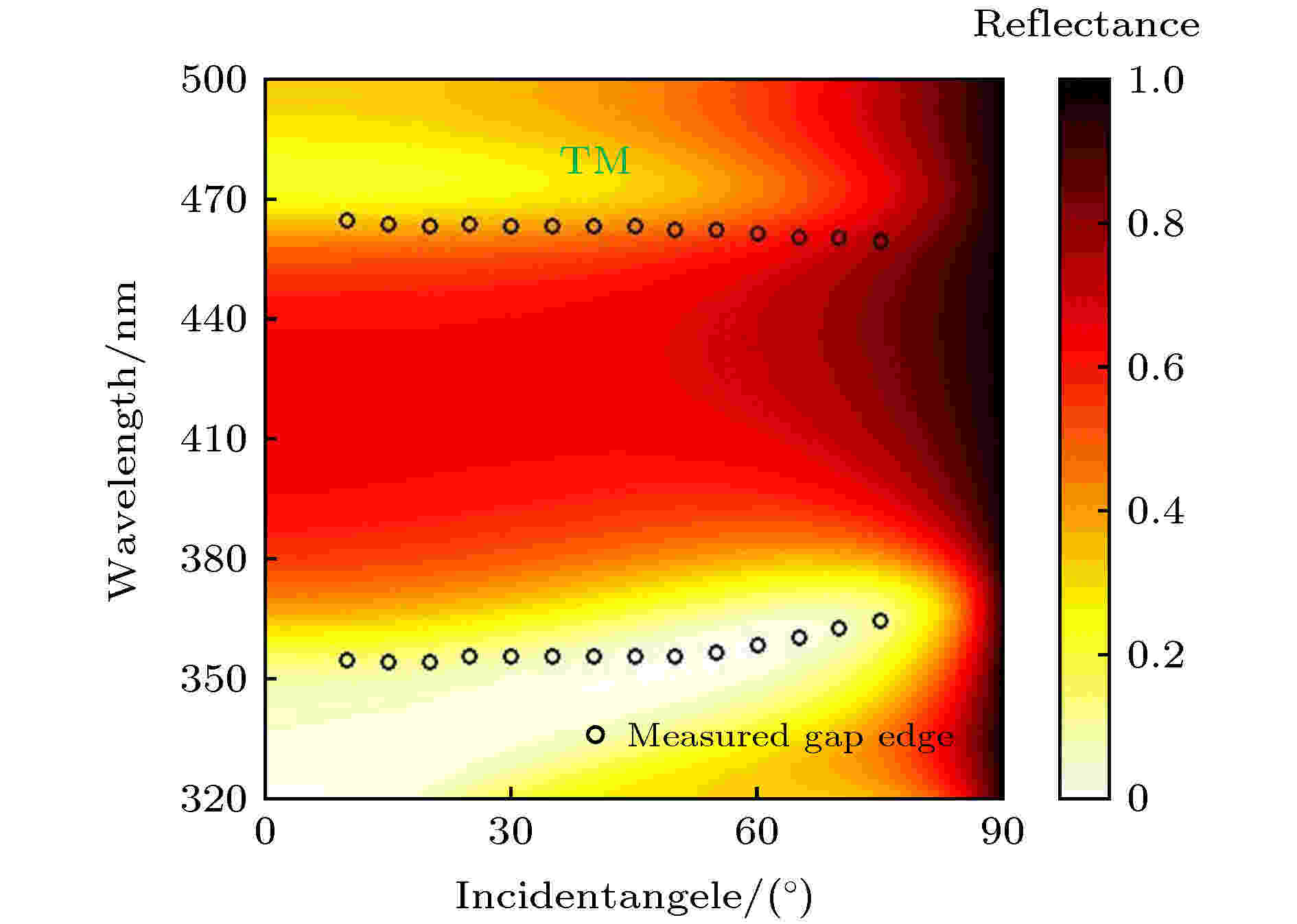图 8 含双曲超构材料的一维光子晶体[(CD)2B]3的反射谱(TM偏振)随入射角的变化[107], 其中彩色背景代表数值计算结果, 黑色空心圆圈代表实验测量的带隙边缘(由最靠近带隙的反射极小值提取)
Figure8. Reflectance spectrum of [(CD)2B]3 as a function of incident angle (TM polarization)[107]. Background color represents the calculated result. Black hollow circle represents measured gap edge extracted from the reflectance dip.

由图8可知, 当入射角从10°增大到75°时, 测量的带隙短波长边缘从355 nm轻微移动到了365 nm, 长波长边缘始终位于462 nm附近. 因此, 得到了一个位于可见光波段的近乎零移的全向带隙, 其范围约为365—460 nm. 这一与入射角无关的带隙为我们设计具有固定带宽的全向反射器提供了新的机理.
2
3.3.红移带隙
-->

3.3.红移带隙

红移带隙即随入射角的增大而红移的带隙. 要获得红移带隙, 根据布拉格条件, 光子晶体原胞的总传播相位$\varPhi $必须随着入射角$\theta $的增大而增大[108]. 因此, 总传播相位$\varPhi $也必须随着${k_x}$的增大而增大, 即有[108]
$\frac{{\partial \varPhi }}{{\partial {k_x}}} = \frac{{\partial {k_{{\rm{A}}z}}}}{{\partial {k_x}}}{d_{\rm{A}}} + \frac{{\partial {k_{{\rm{B}}z}}}}{{\partial {k_x}}}{d_{\rm{B}}} > 0.$
将方程(8)和布拉格条件(即方程(2))联立, 在近似条件$ \left| {{\varepsilon _{{\rm{A}}z}}} \right| \gg 1$和${\varepsilon _{\rm{B}}} \gg 1$下, 可得TM偏振红移带隙的两个解析条件[108]:
${d_{\rm{A}}} > {d_{{\rm{Amin}}}} = \frac{{{\lambda _{{\rm{Brg}}}}}}{2}\frac{1}{{\sqrt {{\varepsilon _{{\rm{A}}x}}} \big(1 - {{{\varepsilon _{\rm{B}}}}}/{{{\varepsilon _{{\rm{A}}z}}}}\big)}},\tag{9a}$
${d_{\rm{B}}} = ({{ {{{\lambda _{{\rm{Brg}}}}}}/{2} - \sqrt {{\varepsilon _{{\rm{A}}x}}} {d_{\rm{A}}}}})/{{\sqrt {{\varepsilon _{\rm{B}}}} }},\tag{9b}$
其中, ${\lambda _{{\rm{Brg}}}}$为选取的正入射时的布拉格波长. 然而, 上述推导都是在TM偏振的情形下进行的. 在TE偏振下, 由金属/介质亚波长多层膜等效而成的电双曲超构材料的等频线不再是开放的双曲线, 而与普通介质一样, 都是封闭的圆, 其等频线方程如下[5]:
$k_x^2 + k_{{\rm{A}}z}^2 = {\varepsilon _{{\rm{A}}x}}\frac{{{\omega ^2}}}{{{c^2}}}.$
因此, 含双曲超构材料的一维光子晶体的TM偏振带隙虽然可被设计成红移的, 但其TE偏振带隙仍然是蓝移的. 由于两种偏振的带隙随入射角增大的走向相反, 在带隙的边缘波长处, 可用于实现宽角度的偏振选择. 在4.2节中, 将宽角度的偏振选择作为红移带隙的一个具体应用进行介绍.
根据方程(9), 设计了具体的多层膜结构, 结构式为[(CD)2B]3. 选取的正入射时的布拉格波长${\lambda _{{\rm{Brg}}}} = 386$ nm. 其中C和B层的材料均为TiO2, D层的材料为Ag. 入射和衬底介质分别为空气和BK7玻璃. 图9给出了数值计算的含双曲超构材料的一维光子晶体[(CD)2B]3的反射谱(TM和TE偏振)随入射角的变化, 其中蓝色虚线为带隙的两个边缘, 由最靠近带隙的反射极小值提取[108].
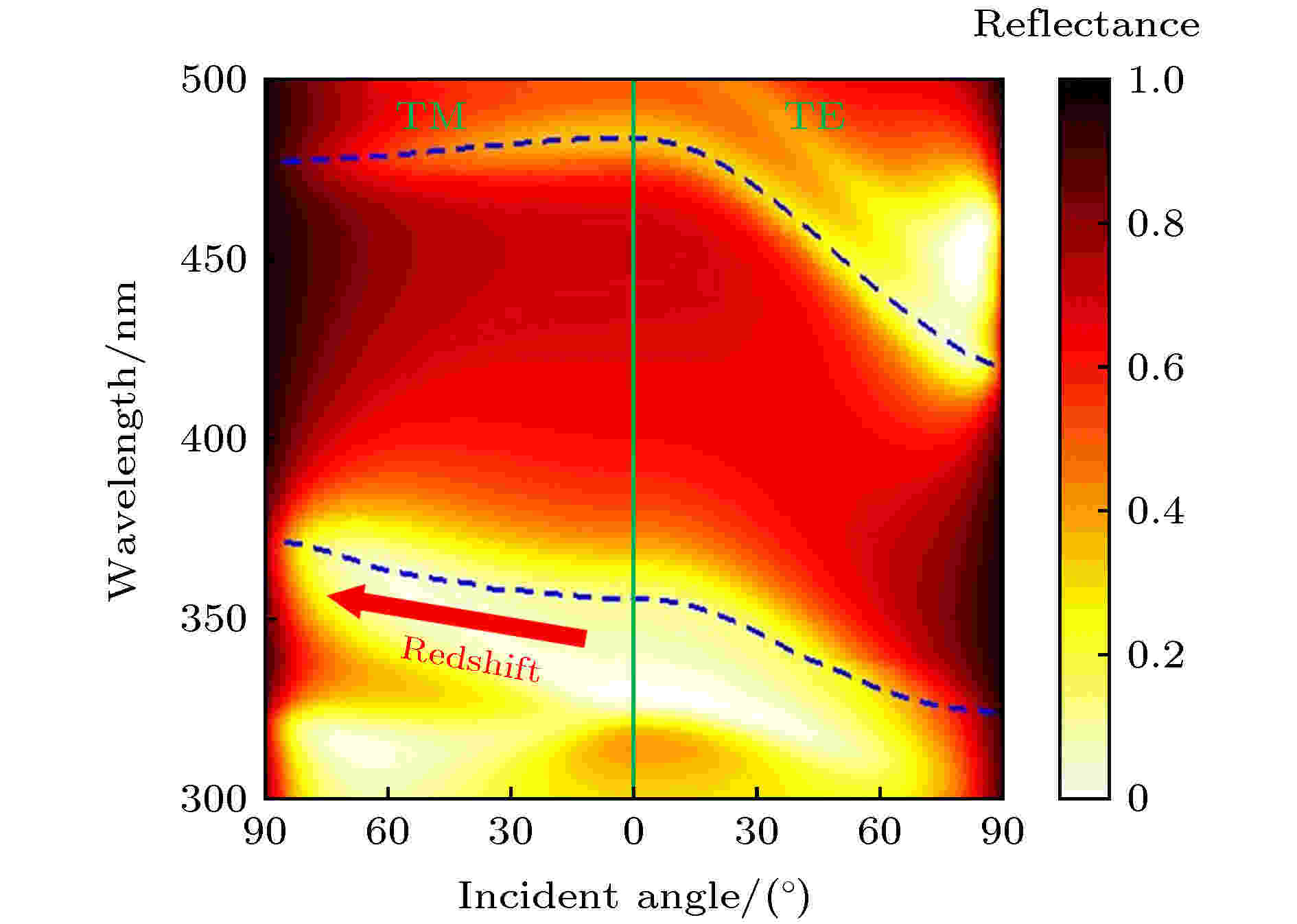图 9 数值计算的含双曲超构材料的一维光子晶体[(CD)2B]3的反射谱(TM和TE偏振)随入射角的变化[108]
Figure9. Calculated reflectance spectrum of [(CD)2B]3 as a function of incident angle (TM and TE polarizations)[108].

由图9可知, 对于TM偏振而言, 带隙的短波长边缘随着入射角的增大而红移, 这与我们的理论设计相符. 然而, 带隙的长波长边缘并没有随着入射角的增大而红移, 这是由于长波长边缘落在了(CD)2的第一类双曲区域之外[108]. 对于TE偏振而言, 带隙的两个边缘均随着入射角的增大而蓝移. 因此, 在短波长边缘处, 两种偏振的带隙随入射角增大的走向相反. 这一特性可用于实现宽角度的偏振选择, 详见4.2节.
图10给出了相应的实验测量结果[108]. 其中图10(a)和图10(b)分别代表TM和TE偏振的反射谱测量结果. 实心圆点代表最靠近带隙的反射极小值(即带隙边缘的标定位置), 灰色阴影区域代表带隙的短波长边缘随入射角的波动范围.
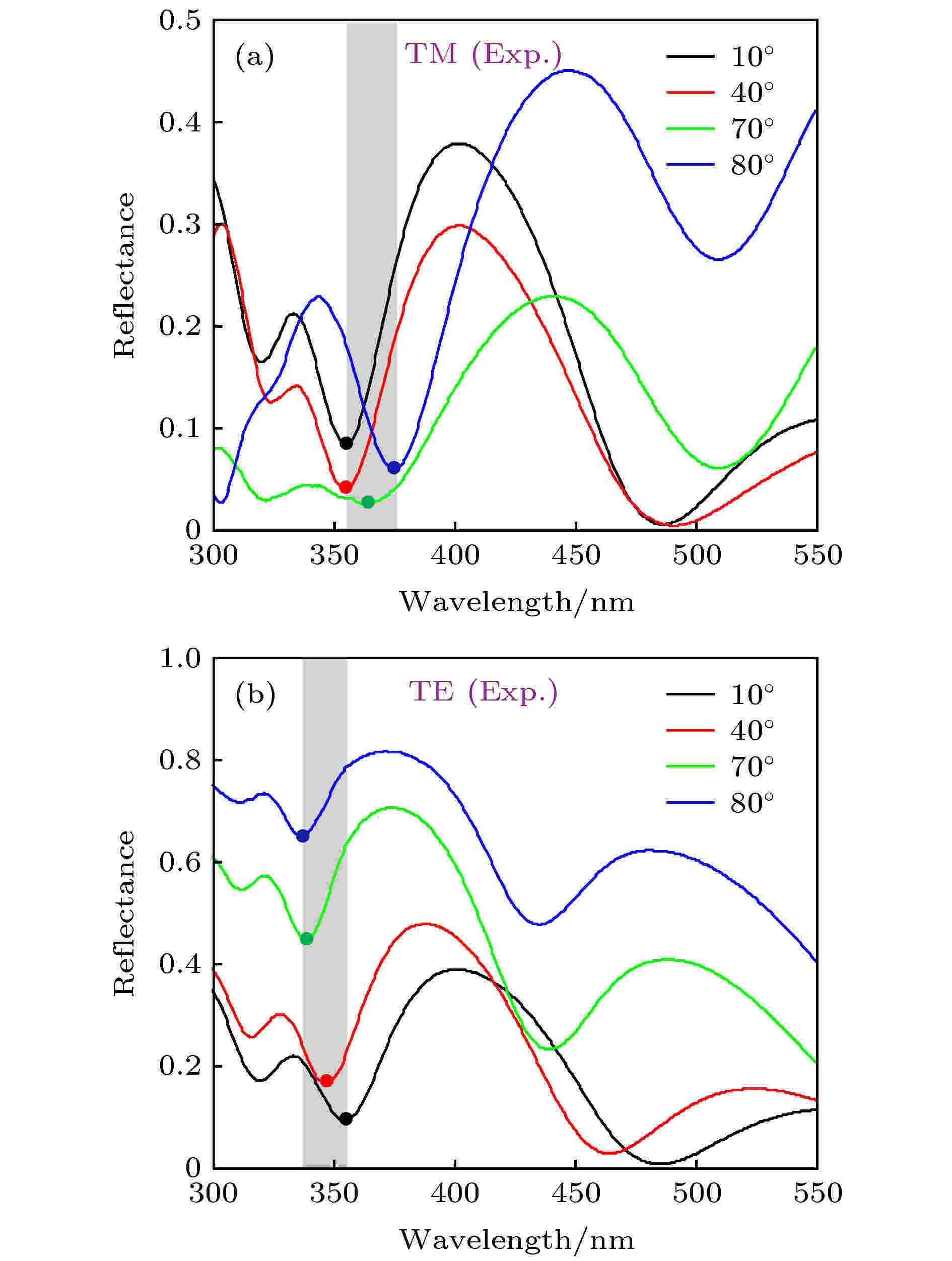图 10 实验测量的含双曲超构材料的一维光子晶体[(CD)2B]3在不同入射角下的反射谱　(a) TM偏振[108]; (b) TE偏振[108]
Figure10. Experimental reflectance spectra of [(CD)2B]3 under different incident angles: (a) TM polarization[108]; (b) TE polarization[108].

由图10可知, 随着入射角的增大, 实验测得的TM偏振下的带隙的短波长边缘是红移的, 而TE偏振下的带隙的短波长边缘则是蓝移的. 在第4节中, 将介绍上述两种新型带隙—零移带隙和红移带隙的三个具体应用.
4.零移带隙和红移带隙的应用
2
4.1.基于零移带隙的宽角度近完美光吸收器
-->

4.1.基于零移带隙的宽角度近完美光吸收器

利用金属/全介质一维光子晶体异质结中的光学界面态的场局域特性, 可实现近完美的光吸收[71-73]. 然而, 由于全介质一维光子晶体带隙随入射角蓝移的特性, 异质结中的界面态也将随着入射角的增大而蓝移, 这大大限制了近完美光吸收的工作角度范围[71-73]. 在3.2节中, 利用含双曲超构材料的一维光子晶体实现了随入射角零移的带隙. 若将金属和具有零移带隙的光子晶体组成新型的异质结, 将可实现对入射角不敏感的光学界面态, 从而大大拓宽近完美光吸收的工作角度范围[109].
异质结的结构式为M[(CD)2B]3, 结构示意图如图11(a)所示[109]. 其中M为金属层, 其材料为Ag. [(CD)2B]3为含双曲超构材料的一维光子晶体, 其中C和B层的材料为TiO2, D层的材料为Ag. 入射和衬底介质分别为空气和BK7玻璃. 图11(b)给出了实验测量的异质结在不同入射角下的吸收谱(TM偏振)[109].
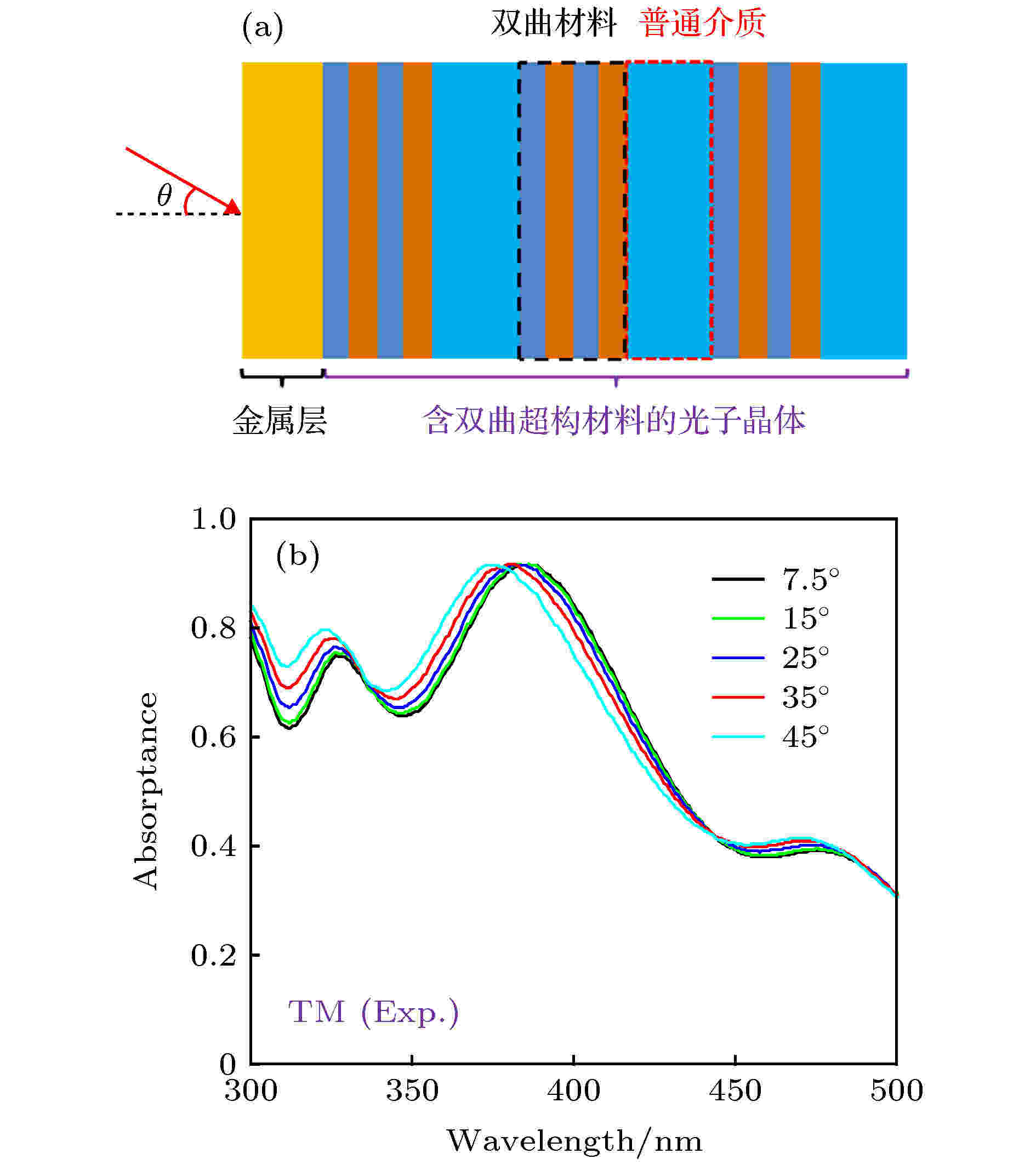图 11 (a) 异质结M[(CD)2B]3的结构示意图[109]; (b) 实验测量的异质结M[(CD)2B]3在不同入射角下的吸收谱(TM偏振)[109]
Figure11. (a) Schematic of the heterostructure M[(CD)2B]3[109]; (b) experimental absorptance spectra of M[(CD)2B]3 under different incident angles (TM polarization)[109].

从图11(b)可以看出, 近完美吸收峰对入射角不敏感. 当入射角从7.5°增大到45°时, 吸收峰从386.5 nm轻微移动到了376 nm, 较好地继承了带隙对入射角不敏感的特性. 图12进一步给出了实验测量的在波长380 nm处的吸收率随入射角的变化(TM偏振)[109].
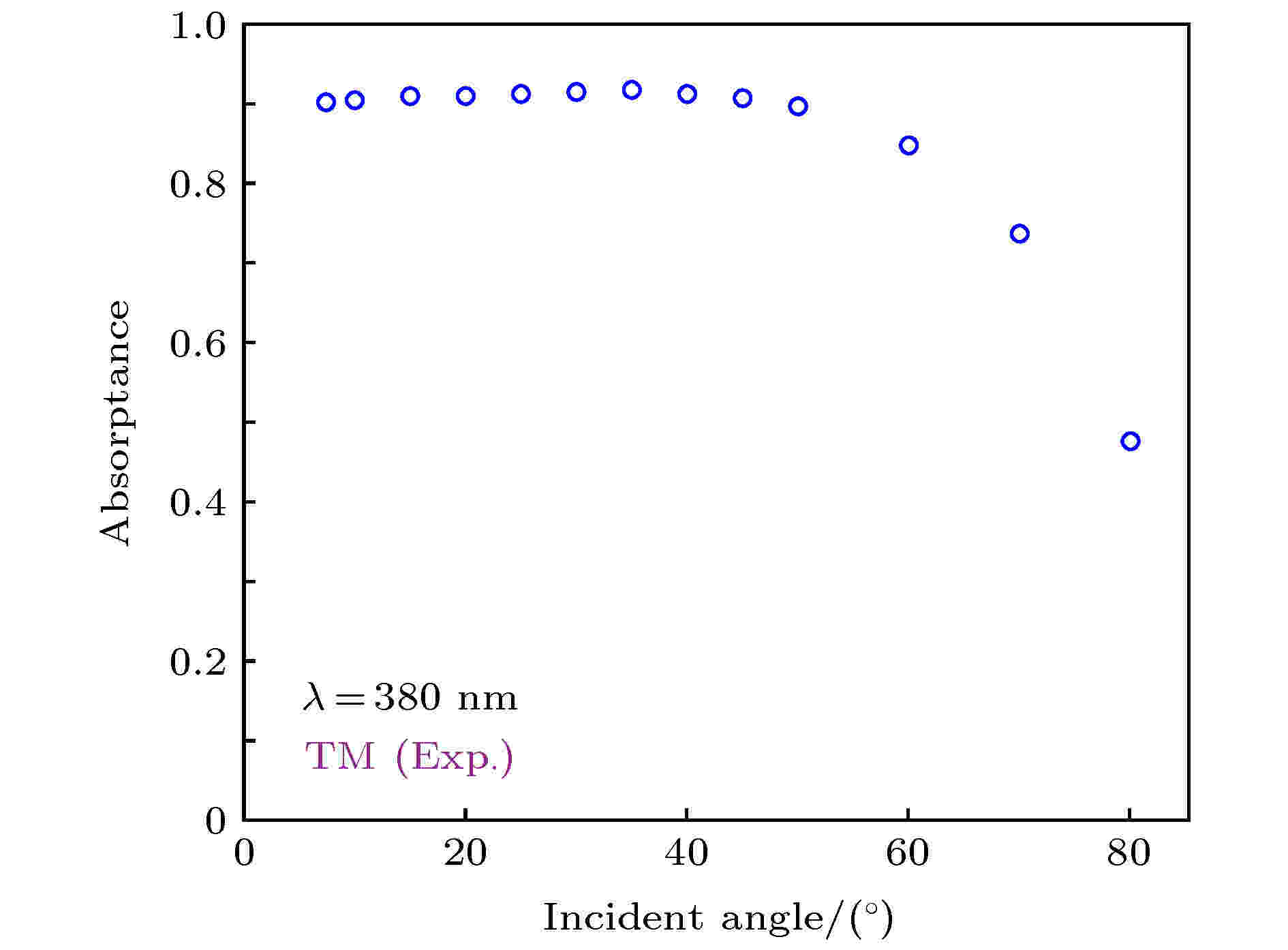图 12 实验测量的异质结M[(CD)2B]3在波长380 nm处的吸收率随入射角的变化(TM偏振)[109]
Figure12. Experimental absorptance of M[(CD)2B]3 as a function of incident angle at $\lambda = 380$ nm (TM polarization)[109].

由图12可知, 在波长380 nm处, 随着入射角从7.5°增大到45°, 吸收率始终保持在90%以上. 因此, 基于零移带隙, 我们有效地拓宽了金属/一维光子晶体异质结的近完美光吸收的工作角度范围, 实现了宽角度的近完美光吸收.
从应用来看, 基于金属/介质亚波长多层膜的单个双曲超构材料也可实现近完美光吸收, 但它只能工作在很窄的角度范围内[110]. 有研究人员利用双曲超构材料阵列结构, 例如将由金属/介质亚波长多层膜金字塔结构等效而成的双曲超构材料排成一维阵列, 实现了宽角度的近完美光吸收[31,111]. 这种阵列结构对制备技术的要求较高. 而我们利用一维复合周期结构实现了宽角度的近完美光吸收. 相比阵列结构, 这种多层膜复合结构更容易制备.
2
4.2.基于红移带隙的宽角度偏振选择器
-->

4.2.基于红移带隙的宽角度偏振选择器

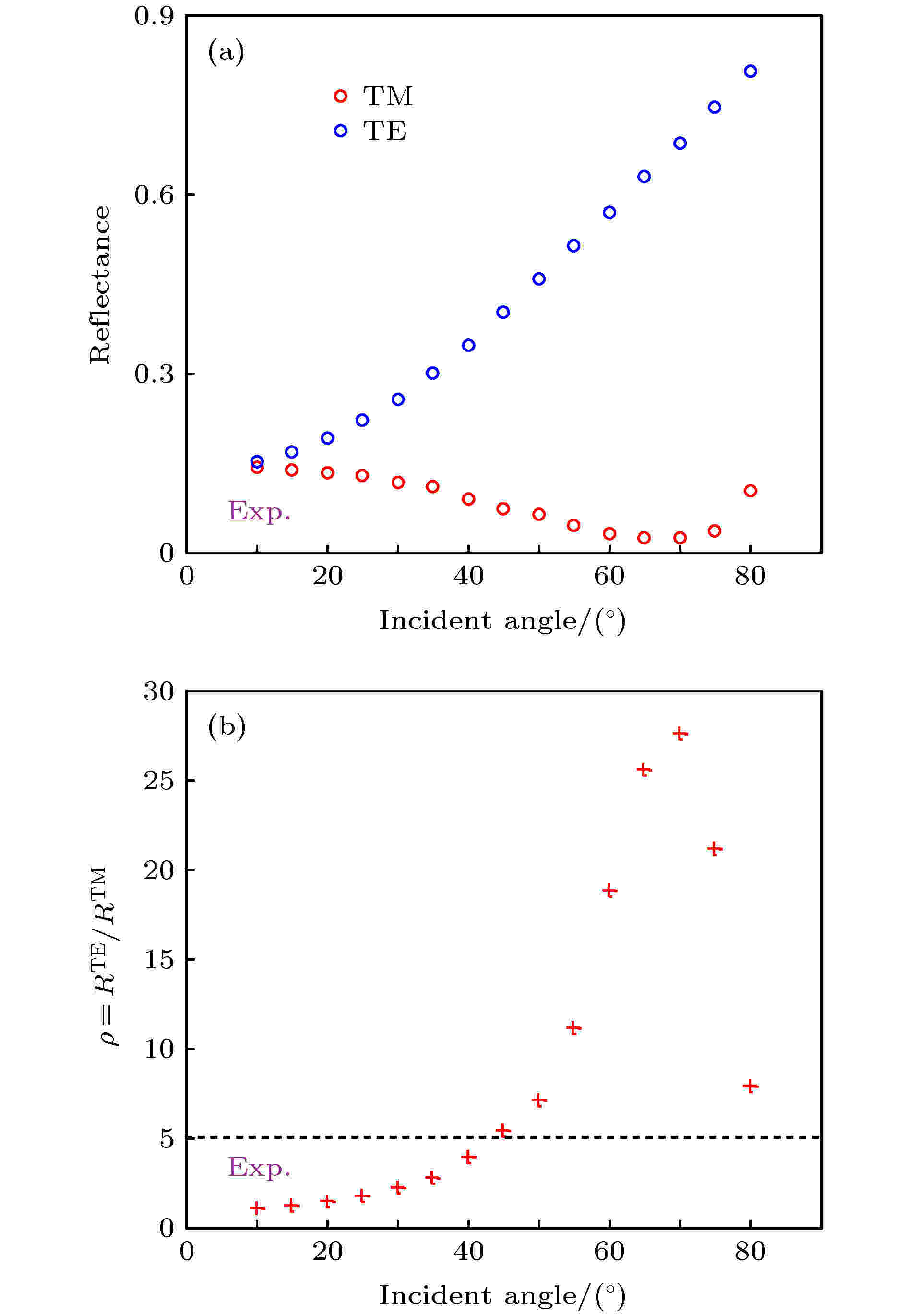如引言所述, 对于TM和TE偏振, 传统的全介质一维光子晶体的带隙都是随入射角的增大而蓝移的, 这将导致带隙对不同偏振的区分度不明显, 从而限制了偏振选择的工作角度范围. 在3.2节, 在含双曲超构材料的一维光子晶体中实现了TM偏振的红移带隙和TE偏振的蓝移带隙. 因此, 在带隙的短波长边缘处, 由于两种偏振的带隙随入射角增大的走向相反, 可用于实现宽角度的偏振选择. 图13(a)给出了实验测量的含双曲超构材料的一维光子晶体[(CD)2B]3的TM和TE偏振在带隙的短波长边缘$\lambda = 365$ nm处的反射率随入射角的变化[108]. 光子晶体的材料和几何参数同3.2节.
图 13 (a) 实验测量的含双曲超构材料的一维光子晶体[(CD)2B]3在波长365 nm处的TM和TE偏振的反射率随入射角的变化[108]; (b) 相应的偏振选择比随入射角的变化[108]
Figure13. (a) Experimental reflectance of M[(CD)2B]3 as a function of incident angle for TM and TE polarizations at $\lambda = 365$ nm[108]; (b) corresponding polarization selection ratio as a function of incident angle[108].

由图13(a)可知, 随着入射角的增大, 波长365 nm处TE偏振的反射率逐渐增大而TM偏振的反射率始终维持在较低的水平. 图13(b)给出了相应的偏振选择比$\rho = {R^{\rm TE}}/{R^{\rm TM}}$随入射角的变化[108]. 可以看到, 在入射角位于45°到80°的范围内, 偏振选择比均高于5. 因此, 基于红移带隙, 可有效地拓宽偏振选择的工作角度范围, 实现宽角度的偏振选择.
从实现偏振分光的功能而言, 已有研究人员从理论上利用双曲超构材料的等频面的偏振依赖特性实现了宽角度的偏振选择[112]. 尽管这个工作中用到的结构是金属/介质亚波长多层膜, 但其偏振选择机制决定了膜的界面方向与入射波矢的切向分量垂直, 即光需要从多层膜的侧面入射. 由于侧面的尺寸限制, 实验上测量分光将有一定的困难. 虽然我们的结构也是多层膜结构, 但是膜的界面方向与入射波矢的切向分量平行, 即光从多层膜的正面入射. 这在实验上易于测量分光. 当然, 由于我们的结构含有多层双曲超构材料, 结构对光的吸收比较多, 会在一定程度上降低偏振选择比.
2
4.3.基于红移带隙的宽角度折射率传感
-->

4.3.基于红移带隙的宽角度折射率传感

近年来, Tsurimaki等[75]研究人员利用金属/全介质一维光子晶体异质结的光学界面态, 实现了基于椭偏相位(TM和TE偏振的反射相位之差)的超灵敏温度传感. 在斜入射下, 异质结在TM和TE偏振下的界面态波长将会不同, 从而导致椭偏相位在TM或TE偏振的界面态波长附近发生剧变, 进而导致了传感的高灵敏性[75]. 然而, 由于全介质一维光子晶体在TM和TE偏振下的带隙都是随入射角的增大而蓝移的, 导致异质结在TM和TE偏振下的界面态也是蓝移的[74-76]. 在小角度入射下, 异质结在TM和TE偏振下的界面态的波长差别很小, 从而降低了传感的灵敏度[74-76]. 因此, 对于传统的异质结, 具有高灵敏度的传感的工作角度范围较小. 在集成光学系统中, 入射光源往往具有一定的波束宽度和角发散性, 这将导致传感的灵敏度的进一步降低[113]. 在3.2节, 我们在含双曲超构材料的一维光子晶体中实现了TM偏振的红移带隙和TE偏振的蓝移带隙. 因此, 若将金属和这种特殊的光子晶体组成新型的异质结, 将可实现在TM偏振下红移而在TE偏振下蓝移的光学界面态, 从而大大拓宽具有高灵敏度的传感的工作角度范围[114].
新型异质结的结构式为M[(CD)2B]9, 其中M为金属层, 其材料为Cu. [(CD)2B]9为含双曲超构材料的一维光子晶体, 其中C和B层的材料为Si, D层的材料为ITO (氧化铟锡). 入射和衬底介质分别为空气和BK7玻璃. 图14给出了数值计算的异质结M[(CD)2B]9的反射谱(TM和TE偏振)随入射角的变化[114]. 其中蓝色虚线为带隙的两个边缘, 由最靠近带隙的反射极小值提取. 红色虚线代表界面态, 由带隙中的反射极小值提取.
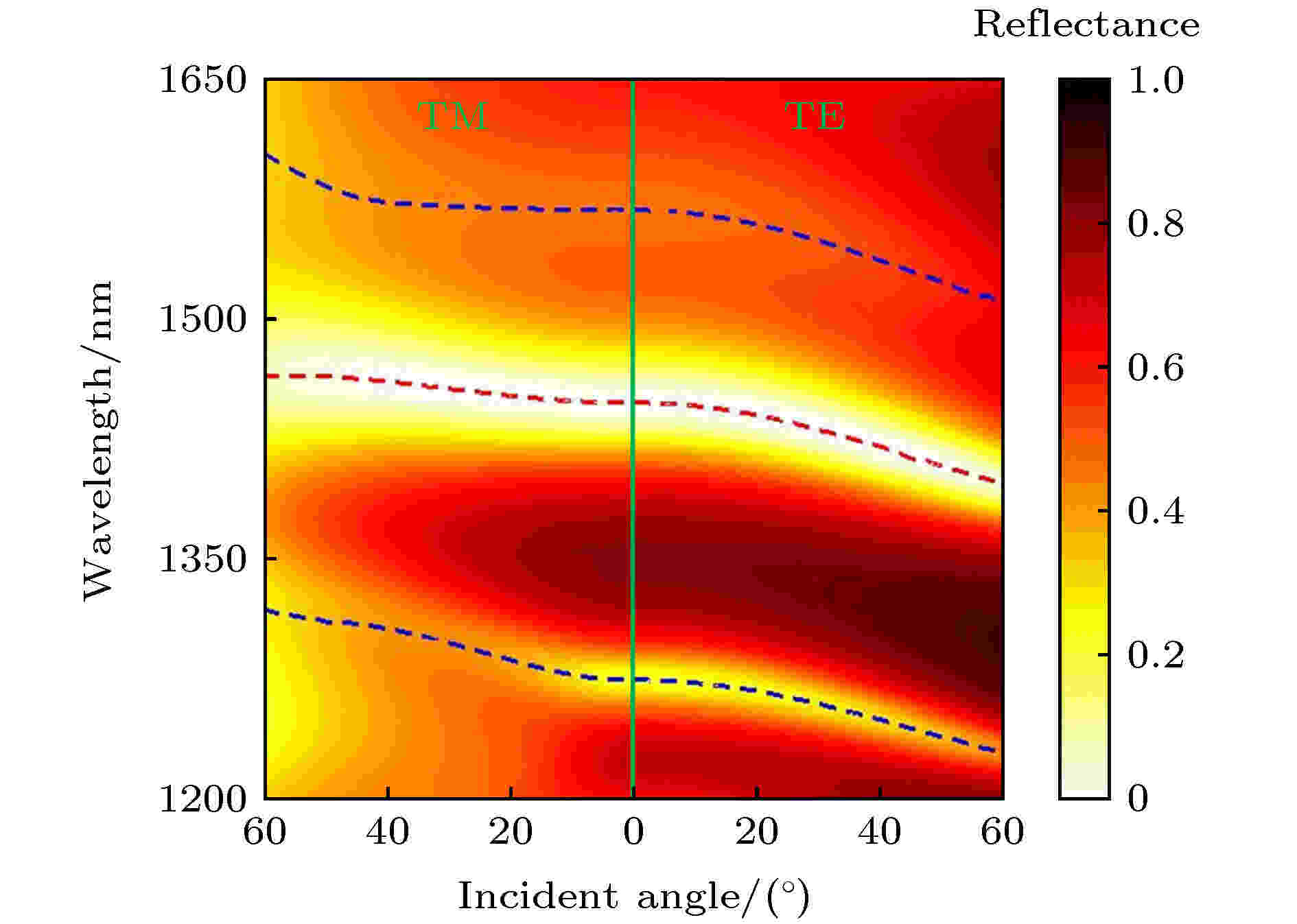图 14 数值计算的异质结M[(CD)2B]9的反射谱(TM和TE偏振)随入射角的变化[114]
Figure14. Calculated reflectance spectrum of M[(CD)2B]9 as a function of incident angle (TM and TE polarizations)[114].

由图14可知, 对于TM偏振而言, 界面态随着入射角的增大是红移的, 而对于TE偏振而言, 界面态则是蓝移的. 因此, 即使在小角度入射下, TM和TE偏振的界面态的波长差别也比较显著, 传感的灵敏度可以得到保证[114]. 我们在异质结的下方放置了一个溶液池, 溶液池中放置折射率待测的溶液, 如图15(a)所示[114]. 图15(b)给出了数值计算得到的传感器的最佳折射率分辨率随入射角的变化[114]. 由图15(b)可知, 传感器在入射角从5°到84°的范围内的最佳折射率分辨率均小于${10^{ - 4}}$ RIU (refractive index unit). 因此, 基于红移带隙, 我们有效地拓宽了具有高灵敏度的折射率传感的工作角度范围, 实现了宽角度的折射率传感.
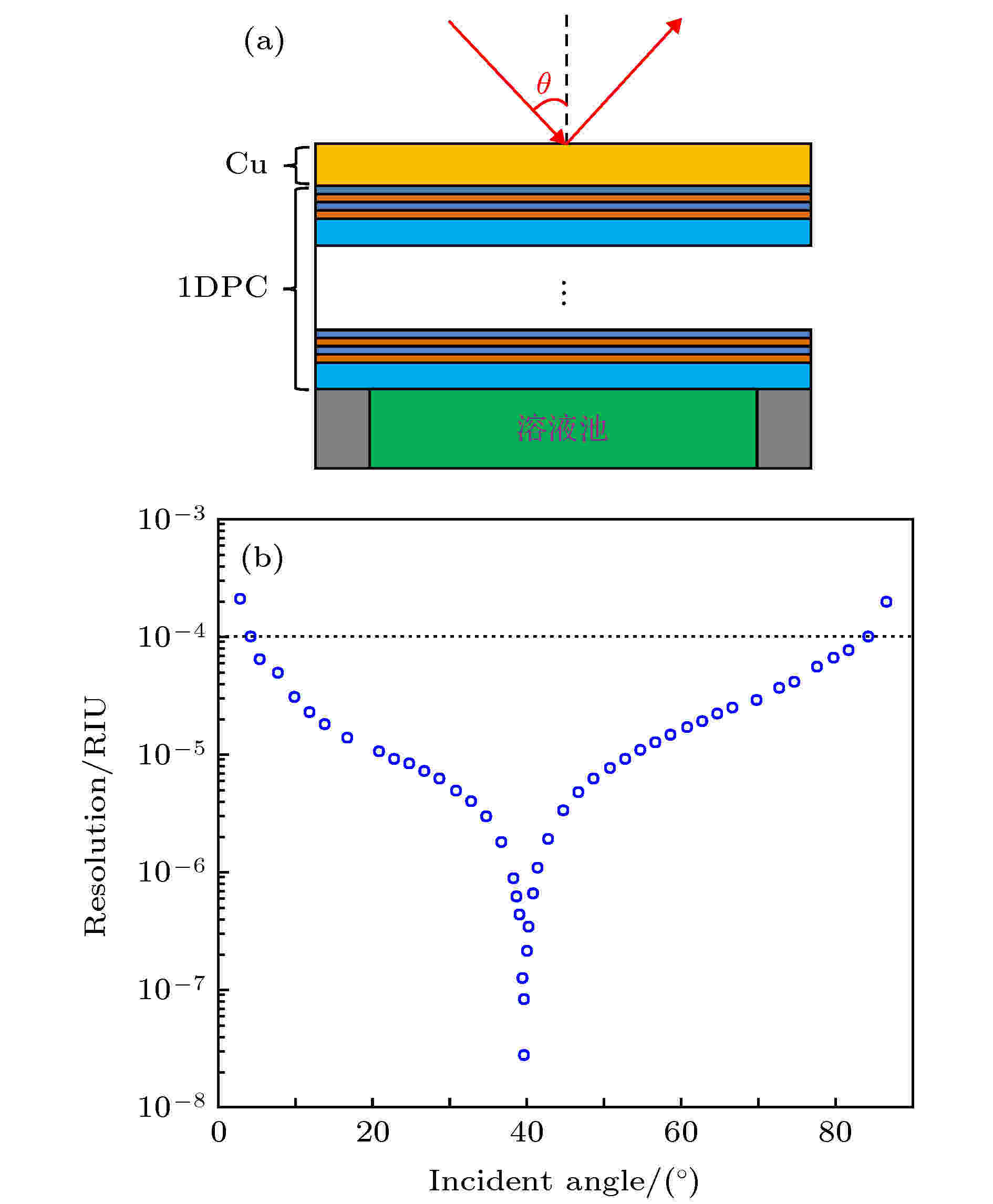图 15 (a) 折射率传感器的示意图[114]; (b) 数值计算的传感器的最佳折射率分辨率随入射角的变化[114]
Figure15. (a) Schematic of the refractive index sensor[114]; (b) calculated minimal refractive index resolution as a function of incident angle[114].

从应用来看, 利用双曲超构材料的大波矢模式也可实现宽角度的超灵敏折射率传感[29]. 但是大波矢模式的激发需要用到光栅耦合[29]或棱镜耦合[30]. 而我们结构的传感机制则是利用了光学界面态, 其色散关系位于光锥线以上, 可直接被从空气中入射的平面波激发. 当然, 我们的结构含有多层双曲超构材料, 双曲超构材料中的损耗会在一定程度上降低传感的灵敏度.
5.结　论
本综述介绍了含双曲超构材料的复合周期结构的光子能带工程及其应用. 利用双曲超构材料特殊的等频线形态, 可实现传统的全介质一维光子晶体所不能实现的两种新型带隙—随入射角零移和红移的带隙. 基于零移带隙, 可设计具有固定带宽的全向反射器和宽角度的近完美光吸收器. 基于红移带隙, 可设计宽角度的偏振选择器和超灵敏折射率传感器. 我们的研究为研制具有新型功能的光学器件提供了新的机理和设计方法. 在后续的研究中, 可进一步将主动可调的材料引入到双曲超构材料中[115], 并利用这种可调的双曲超构材料实现功能更加丰富的光学器件.
相关话题/材料 光子 结构 金属 测量
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 平带光子微结构中的新颖现象:从模式局域到实空间拓扑
    摘要:近年来,凝聚态物理中平带局域与拓扑等概念与光学体系的有机结合,使得平带光子学系统的研究迎来了极为快速的发展,催生了一系列新颖的光物理现象与潜在的应用前景.目前,平带结构在光子晶体、光学超构材料以及光子晶格(倏逝波耦合的光学波导阵列)等多种人工光子微结构中得到了实现,并在其中观察到了很多凝聚态系 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 光学超构材料芯片上类比引力的研究进展
    摘要:光学超构材料是一种人工设计的微结构材料,它的出现打破了传统材料设计思维的局域性,为在微纳尺度上人为调控电磁波提供了新的范式,实现了具有超越自然界常规材料的光学性质.尤其是超构材料具有将光和电磁辐射耦合到亚波长尺度的能力,满足了高速发展的现代科学技术对光学元器件的高性能、微型化以及集成化的新要求 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 等离激元能带结构与应用
    摘要:近些年来,表面等离激元因其具有强局域、亚波长和高场强等特殊的光学性质而备受关注,在化学、生物、通信、纳米能源等各领域得到了广泛的研究.为了更好地控制表面等离激元的激发、传播和辐射,具有能带结构的周期性表面等离激元结构被广泛的研究.本文全面综述了具有等离激元能带的微纳结构、能带的产生机制与其特殊 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 信息超材料研究进展
    摘要:超材料是物理和信息领域的研究热点之一,本文主要介绍信息超材料的研究进展.不同于传统超材料的等效媒质参数表征,信息超材料由物理单元的数字编码来描述,通过控制不同的编码序列来实时地调控电磁波,进而实现超材料的现场可编程功能.由于在超材料的物理空间上构筑起数字空间,因此可在超材料的物理平台上直接处理 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 偏置磁场方向对磁性光子晶体能带结构的影响及其在构建拓扑边界态中的作用
    摘要:光子晶体中的拓扑相变源自于其能带结构中带隙的打开-闭合-再打开,其中伴随着能带结构中带序(或本征态)之间的交换.本文探讨了偏置磁场方向对磁性光子晶体能带结构的影响,它在构建拓扑边界态中的作用以及对边界态特性的影响.结果表明:反转偏置磁场方向会导致能量不同但宇称相同的本征态之间的交换,这种交换为 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 绝缘体上铌酸锂薄膜片上光子学器件的研究进展
    摘要:铌酸锂晶体具有卓越的电光和非线性光学性质,一直以来都被认为是最有前景的集成光子学基质材料之一.也正是由于铌酸锂晶体多方面优良的光学性能,近年来新兴的铌酸锂薄膜技术在集成光子学的研究中受到了极大的关注.借助于先进的微纳加工技术,许多高性能的铌酸锂集成光子学器件已经得以实现.本文总结了几种微纳加工 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 外尔超构材料里频率分离外尔点的数值设计
    摘要:外尔半金属是指三维能带结构具有手性拓扑点简并特征的无能隙固体材料,并且简并点附近的色散关系遵从外尔方程的描述.它具有很多独特的电子输运性质,比如:费米弧表面态、负磁阻效应、手性朗道能级等.类比电子系统的外尔半金属材料,人们设计出理想外尔超构材料,在电磁波体系里实现了频率一致的外尔点简并.本文打 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • SeH<sup>+</sup>离子低激发态的电子结构和跃迁性质的理论研究
    摘要:采用内收敛多组态相互作用及Davidson修正方法精确地计算了SeH+离子能量最低的3个离解极限对应的12个Λ—S态的势能曲线.计算中考虑了芯-价电子关联、标量相对论修正和自旋-轨道耦合效应.结果表明在30000—40000cm–1处Ω态的曲线存在许多避免交叉,导致a2,b0+,A12,A21 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 氟化镁高压萤石结构稳定性及热物性的数值模拟
    摘要:氟化镁(MgF2)是工业用途广泛的重要碱土金属氟化物,也是矿物质氟镁石的主要成分,相比于电子结构和光学特性的研究,人们从地球物理学的角度给予MgF2高压热物性的研究明显不够,而组成地球下地幔矿物的高压熔化、热膨胀等热物性预测对理解地球的结构、动力学、演化及起源至关重要.本文利用基于密度泛函理论 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于驻极体材料的机械天线式低频/甚低频通信磁场传播模型
    摘要:低频/甚低频电磁波的频率极低,趋肤深度较深,可以以很小的损耗穿透海水和地下来进行通信.传统的低频发射天线存在尺寸和功耗较大的问题,本文采用驻极体材料设计了一种机械天线式低频/甚低频发射天线结构.利用激励装置驱动驻极体所带极化电荷进行机械运动,从而产生交变的电磁场,并激发出电磁波携带能量和信息, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.