摘要:提出一种适用于灰度图像与RGB格式彩色图像的通用图像加密算法. 利用双线性插值Bilinear与卷积神经网络对图像进行压缩, 再使用二维云模型与Logistic组成的复合混沌系统对压缩图像加解密(滑动置乱与矢量分解), 最后对解密图像进行重构. 重构网络中, 由卷积神经网络与双线性插值Bilinear主要负责重构轮廓信息, 全连接层主要负责重构颜色信息. 实验结果表明, 该基于深度学习压缩感知与复合混沌系统的通用图像加密算法在数据处理质量和计算量上有着很大优势. 由于复合混沌系统有着足够大的密钥空间且将明文哈希值与密钥关联, 可实现一图一密的加密效果, 能有效抵抗暴力攻击与选择明文攻击, 与对比文献相比, 相关系数更接近理想值且信息熵与明文敏感性指标也都在临界值范围内, 其加密算法有着更高的安全性.
关键词: 深度学习/
压缩感知/
加密/
复合混沌系统

English Abstract

全文HTML

--> --> -->

随着互联网技术的飞速发展, 数字图像已成为信息传输的重要载体. 由Candes, Romberg, Tao和Donoho等^[1-3]提出的压缩感知理论, 利用信号在某些变换中满足稀疏性的特点, 使采样率在远低于奈奎斯特采样率的情况下对信号进行压缩与重构. 传统压缩感知重构方法基于稀疏先验知识, 从一个欠定方程组中寻找到最优解来重构图像, 然而真实图像在某些变换中并不精确满足稀疏性, 使得重构质量不高且多次迭代求解, 耗时长. 而基于深度学习的压缩感知算法采用纯数据驱动的方式提取测量值并重构, 放宽了对图像信号稀疏性的假设条件. Mousavi等^[4]利用堆降噪自编码模型设计了两种网络, 第一种采用线性的重构方法, 耗时短但重构质量较低; 第二种采用非线性端到端的方法, 耗时略长但重构质量提高明显. MSRNet^[5], ReconNet^[6], DR²-Net^[7]也是基于深度学习的压缩感知算法, 与传统压缩感知算法相比, 耗时短且重构质量高, 但他们的重点都放在重构网络上, 使用随机高斯矩阵压缩的图像质量差, 限制了图像的重构质量.
混沌学是在非线性动力学的基础上发展起来的, 在确定性系统中做不可预测的随机运动, 细微的改变就能造成巨大误差. 混沌系统由于具有伪随机性、遍历性和非周期性等特点, 在图像加密中被广泛运用^[8-10], 虽能获得很好的加密效果, 但存在着耗时长且不便于传输等问题. 有研究^[11-13]将压缩感知与图像加密结合, 便于图像的存储、传输且安全性也得到保证, 但使用的都是传统压缩感知, 总耗时比在原图上直接加密的时间还长, 且都只适用于灰度图像.
本文提出一种通用的图像压缩加密算法, 在压缩与加密的性能上都有所提升. 贡献有如下5点: 首先在压缩网络上使用双线性插值Bilinear对图像的宽高压缩, 再通过卷积神经网络将3通道压缩为1通道, 使压缩网络对采样率没有限制并获得高质量的压缩图像. 第二, 在重构网络上使用双线性插值Bilinear与卷积神经网络组成的模型(bilinear convolutional neural network, BCNN)重构图像的轮廓信息, 使用全连接层重构图像的颜色信息, 可得到高质量的重构图像. 第三, 压缩重构网络默认使用的是RGB格式彩色图像, 可将灰度图复制为3通道后再压缩, 重构后求3通道对应位置的平均值, 变为1通道, 使整个网络也适用于灰度图像. 虽然网络训练使用的是彩色图像, 但灰度图像重构质量依然优于其他算法. 第四, 加密算法上复合混沌系统由二维云模型与Logistic级联产生, 密钥空间大且序列更随机. 第五, 置乱方法使用滑动置乱, 与像素点置乱、行列置乱相比, 置乱次数与置乱效果能达到很好的平衡.

2

-->

2.1.压缩感知

对于$h \times w$维的原始图像x, 取测量矩阵${{\varPhi }}$对原始图像x进行采样:

${{y}} = {{\varPhi}}{{x}},$

(1)式中, ${{\varPhi }}$为$n \times h$维的矩阵且n $\ll $ h, y为$n \times w$维的矩阵, 所以矩阵x的元素个数远大于矩阵y的元素个数, 方程组有无数解, 需将x转化为

${{x}} = {{\varPsi}}{{s}},$

其中, ${{\varPsi }} \in {{\rm{R}}^{h \times h}}$和${{s}} \in {{\rm{R}}^{h \times w}}$分别是稀疏表示矩阵和k稀疏矩阵, k稀疏矩阵是指矩阵s中每列最多有k个非零值且k $\ll $ h. 根据(2)式, 可将(1)式转化为

${{y}} = {{\varPhi}}{{\varPsi}}{{s}},$

(3)式中, 已知测量值y、测量矩阵${{\varPhi }}$和稀疏表示矩阵${{\varPsi }}$, 可通过${{{l}}_1}$范数来近似逼近${{{l}}_0}$范数求解s:

$\min {\left\| {{s}} \right\|_1}~\begin{array}{*{20}{c}} {{\rm{s}}.{\rm{t}}{{.}}} \end{array}~ \begin{array}{*{20}{c}} {{{y}} = {{\varPhi}}{{\varPsi}}{{s}}.} \end{array}$

传统压缩感知方法需要对(4)式多次迭代求解, 运算时间长, 而基于深度学习的压缩感知方法不需要迭代优化且有GPU硬件条件的支持, 运算时间得到保障.
2 -->

2.2.复合混沌系统构造

本文利用二维云模型的期望值$(Ex_1, Ex_2)$, 熵$(En_1, {{En}}_2)$, 超熵$({{He}}_1, {{He}}_2)$这6个数字特征来产生一组具有随机性的隶属度${{{u}}_{i}}$. $(Ex_1, Ex_2)$反映了云滴群的重心位置, $(En_1, {{En}}_2)$反映了云滴群的随机性, $({{He}}_1, {{He}}_2)$反映了$(En_1, {{En}}_2)$的不确定性度量. 二维云模型正向发生器算法如下所示.
生成两组正态随机数, 以${{En}}_1$与${{En}}_2$为期望值, ${{He}}_1$与${{He}}_2$为标准差:

$\left\{ \begin{aligned}& {{{y}}_{1{i}}} = {{\rm{R}}_{{n}}}({{En}}_1,{{He}}_1), \\ &{{{y}}_{2{i}}} = {{\rm{R}}_{{n}}}({{En}}_2,{{He}}_2), \end{aligned} \right.$

其中n为云滴生成个数. 再生成两组正态随机数, 以${{Ex}}_1$和${{Ex}}_2$为期望值, ${{{y}}_{1{i}}}$和${{{y}}_{2{i}}}$为标准差:

$\left\{ \begin{aligned}& {x}_{1{i}} = {{\rm{R}}_{{n}}}({{Ex}}_1,{{{y}}_{1{i}}}), \\& {x}_{2{i}} = {{\rm{R}}_{{n}}}({{Ex}}_2,{{{y}}_{2{i}}}), \end{aligned} \right.$

最后计算隶属度:

${{{u}}_{i}} = \exp \!\left[ \!{ \!-\! \frac{{{{({x}_{1{i}} \!-\! {{Ex}}_1)}^2}}}{{2 \times {{{y}}_{1{i}}}^2}} \!-\! \frac{{{{({x}_{2{i}} \!-\! {{Ex}}_2)}^2}}}{{2 \times {{{y}}_{2{i}}}^2}}} \!\right],~ 0 < {{{u}}_{i}} \!<\! 1.$

Logistic序列表达式为

${{z}_{i}} = {r} \times {{z}_{i}} \times (1 - {{z}_{i}}),~ 0 < {{z}_{i}} < 1.$

将隶属度${{{u}}_{i}}$与Logistic级联得到C-L混沌序列:

${{c}_{i}} = \left[ {({{{u}}_{i}} + {{z}_{i}})od 1} \right] \times 2\pi, ~ 0 < {{c}_{i}} < 2\pi .$

2 -->

2.3.滑动置乱

置乱方法中, 像素点置乱虽能很好地打乱图像信息分布, 但处理时间较长. 行列置乱耗时虽短, 但置乱效果不好. 滑动置乱弥补了像素点置乱与行列置乱的缺点, 耗时短且置乱效果好. 本文滑动置乱分两步, 先行滑动再列滑动, 公式如下所示:

$\left\{ \begin{aligned} &{r}{{s}_{i}} = {\rm{int}} ({{{u}}_{i}}[0:{{h}}] \times {{w}}), \\ &{c}{{s}_{i}} = {\rm{int}} ({{{u}}_{i}}[{{h}}:{{h}} + {{w}}] \times {{h}}), \end{aligned}\right.$

其中, h和w表示图像高宽, ${r}{{s}_{i}}$和${c}{{s}_{i}}$表示行列滑动距离.

$\left\{ \begin{aligned} &{{{\rm{img}}\_}}rs{{[}}{h_i},\;{{:]}} = {{{\rm{roll}}({\rm{img}}[}}{h_i}{{,\;:],\;}}r{s_i}{{),}} \\& {{{\rm{img}}\_}}cs{{[:}},\;{w_i}{{]}} = {{{\rm{roll}}({\rm{img}}\_}}rs{{[:,\;}}{{{w}}_{i}}{{],\;}}c{s_i}{{)}}{{.}} \end{aligned}\right.$

img是通过压缩网络得到的压缩图像, 具体流程如图1所示.
图 1 滑动置乱流程图
Figure1. Flow chart for scrambling.

2 -->

2.4.矢量分解

将置乱后的图像${{{\rm{img}}\_}}{cs} $进行矢量分解^[14], 公式可表示为

${\rm{img}}{{\_cs}} = \left| {\exp ({\rm{i}}\phi )\left. { + \exp [{\rm{i}}(\phi + \varphi )]} \right|} \right.,$

令${M_1} \!=\! \exp ({\rm{i}}\phi )$, ${M_2} \!=\! \{ {{\rm{angle}}[ {\exp[ { {{\rm{i}}(\phi \!+\! \varphi )} ]} \!+\! {{\pi }}} ]} \}{{/}}(2\pi )$, $0 < {M_2} < 1$, ${\rm{angle}}\left[ \cdot \right]$表示相位角. $\phi $是$[0, 2{\text{π}} ]$上均匀分布的随机序列, 本文使用C-L级联混沌序列来代替. $\varphi $的计算公式如下所示:

$\varphi = \pi - {\rm{arccos}}\left(1 - \frac{{{\rm{img}}{{\_cs}}}}{2}\right),$

将分解后的${M_2}$作为密文.

本文压缩重构网络(fully connected layer and bilinear convolutional neural network, FCLBCNN)在压缩前需将原图分割为多个大小为3 × 33 × 33且不重叠的原始图像块, 重构后再拼接成大图. 彩色图像采样率MR = 0.18的压缩重构网络如图2所示.
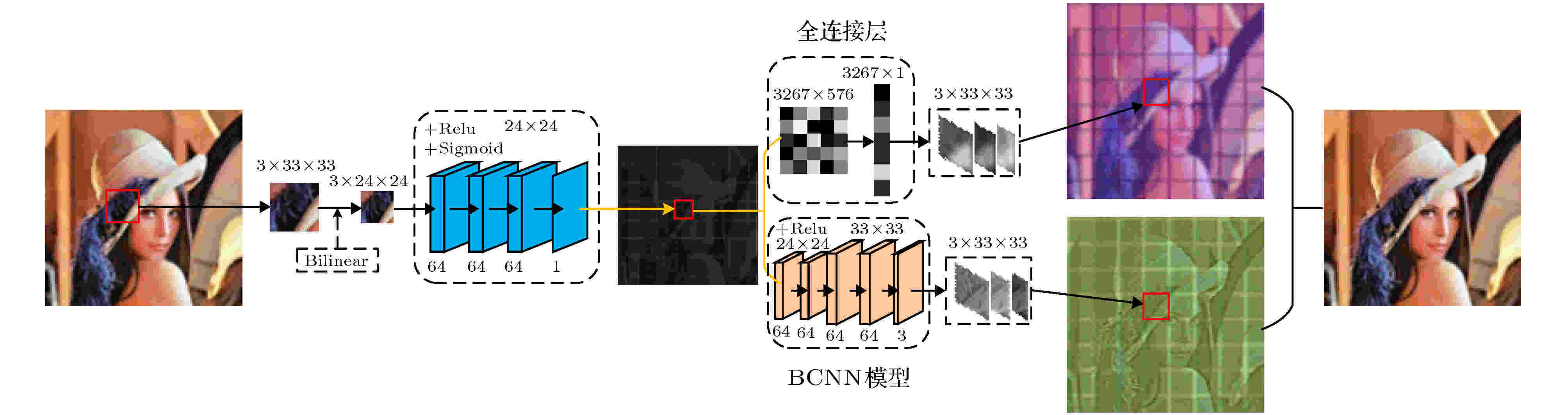图 2 彩色图像的压缩重构网络(采样率MR = 0.18)
Figure2. Color image compression and reconstruction network, sampling rate MR = 0.18.

2

-->

3.1.压缩网络

压缩网络由双线性插值Bilinear与卷积神经网络组成, 双线性插值Bilinear将图像的宽高压缩, 卷积神经网络将图像3通道合并为1通道, 卷积核大小分别为9 × 9, 3 × 3, 3 × 3, 1 × 1. 彩色图像在采样率MR = 0.08, 0.03, 0.01, 0.003与灰度图像在MR = 0.25, 0.10, 0.04, 0.01时, 压缩图像大小皆为1 × 17 × 16, 1 × 10 × 11, 1 × 6 × 7, 1 × 3 × 3. 网络中使用Relu激活函数^[15]来提高网络表达能力, 最后一层使用Sigmoid激活函数将值映射到0—1之间. 压缩网络${{{F}}^{\rm{c}}}( \cdot )$的输入值为原始图像块${{{x}}_{{i}}}$, 卷积层权重${{{W}}^{\rm{c}}}$和压缩图像${{{y}}_{{i}}}$通过Adam方法训练得到, 公式如下:

${{{y}}_{{i}}} = {{{F}}^{\rm{c}}}({\rm{Bilinear}} ({{{x}}_{{i}}}),{{W}}^{\rm{c}}).$

2 -->

3.2.重构网络

3 -->

3.2.1.BCNN模型

BCNN模型也是由卷积神经网络与双线性插值Bilinear方法组成. 双线性插值Bilinear负责上采样, 将网络层宽高放大到33 × 33. 卷积神经网络的卷积核大小分别为5 × 5, 3 × 3, 3 × 3, 1 × 1. 压缩图像${{{y}}_{{i}}}$通过BCNN模型${F^{\rm{b}}}( \cdot )$重构出原始图像块${{{x}}_{{i}}}$的轮廓信息${{x}}_{{i}}^{\rm{b}} $, 公式如下:

${{x}}_{{i}}^{\rm{b}} = {{{F}}^{\rm{b}} }({{{y}}_{{i}}},{{{W}}^{\rm{b}}}) = {{{F}}^{\rm{b}}}({{{F}}^{\rm{c}} }({\rm{Bilinear}} ({{{x}}_{{i}}}),{{{W}}^{\rm{c}} }),{{{W}}^{\rm{b}} }).$

${{{W}}^{\rm{b}}}$是BCNN模型权重参数.
3 -->

3.2.2.全连接层

与轮廓信息相比, 颜色信息更加复杂, 需要更多的权重参数. 卷积神经网络虽能很好地重构图像轮廓信息, 但权重参数有限, 过多的网络层又会造成重构时间增长. 全连接层有足够多的参数, 以彩色图像MR = 0.18为例, 将1 × 24 × 24 = 576的向量放大到3 × 33 × 33 = 3267, 共有1881792个权重参数可以用来重构颜色信息. 压缩图像${{{y}}_{{i}}}$通过全连接层${F^{\rm{l}} }( \cdot )$重构出原始图像块${{{x}}_{{i}}}$颜色信息${{x}}_{{i}}^{\rm{l}} $, 公式如下:

${{x}}_{{i}}^{\rm{l}} = {{{F}}^{\rm{l}}}({{{y}}_{{i}}},{{{W}}^{\rm{l}}}) = {{{F}}^{\rm{l}}}({{{F}}^{\rm{c}} }({\rm{Bilinear}} ({{{x}}_{{i}}}),{{{W}}^{\rm{c}} }),{{{W}}^{\rm{l}}}).$

${{{W}}^{\rm{l}}}$是全连接层权重参数. BCNN模型与全连接层重构出的图像如图3所示.
图 3 BCNN模型与全连接层分别重构的Lena和Sea图像　(a) Lena (灰度); (b) Lena (彩色); (c) Sea (灰度); (d) Sea (彩色)
Figure3. Lena and Sea images reconstructed from BCNN model and fully connected layer respectively: (a) Lena (gray); (b) Lena (color); (c) Sea (gray); (d) Sea (color).

由于BCNN模型与全连接层重构的图像很多像素值不在0—1之间, 为了能直观展示出来, 对图像像素值进行归一化处理. 从图3可知, BCNN模型重构出的图像颜色虽然单调, 但轮廓非常清晰. 全连接层重构出的图像较模糊, 但颜色更加丰富.
3 -->

3.2.3.损失函数

压缩图像${{{y}}_{{i}}}$通过BCNN模型和全连接层后, 合并颜色信息${{x}}_{{i}}^{\rm{l}} $和结构信息${{x}}_{{i}}^{\rm{b}} $, 得到图像块的近似解${{{x}}'_{{i}}}$:

$ {{x}}_{{i}}^{\prime} = {{x}}_{{i}}^{\rm{l}} + {{x}}_{{i}}^{\rm{b}},$

损失函数使用均方误差函数:

$\begin{split}&{{L}}({{{W}}^{\rm{c}} },{{{W}}^{\rm{l}}},{{{W}}^{\rm{b}} }) = \frac{1}{{{N}}}\sum\limits_{i = 1}^N {\left\| {{{x}}_{{i}}^{\prime} - {{{x}}_{{i}}}} \right\|} _2^2 \\&= \frac{1}{{{N}}}\sum\limits_{i = 1}^N {\left\| {{{{F}}^{\rm{l}} }({{{y}}_{{i}}},{{{W}}^{\rm{l}}}) + {{{F}}^{\rm{b}} }({{{y}}_{{i}}},{{{W}}^{\rm{b}} }) - {{{x}}_{{i}}}} \right\|} _2^2.\end{split}$

2 -->

3.3.网络训练数据集与配置

先将91张彩色图像^[5]按0.75, 1和1.5的比例缩放, 再将图像分块, 大小为3 × 33 × 33且取步长为14, 共87104块小图像, 作为训练数据集. 使用Pytorch开源工具训练网络, 设备主要配置为Intel Core i5-8500 CPU, 内存16 GB, 显卡GTX 2080ti.
2 -->

3.4.网络训练参数设置

全连接层${F^{\rm{l}}}( \cdot )$使用默认的初始化权重. 压缩网络${F^{\rm{c}}}( \cdot )$和BCNN模型${F^{\rm{b}} }( \cdot )$使用Xavier方法初始化权重. 使用Adam方法训练整个网络, 学习率设为0.001, 每100000次学习率降低为原来的1/2, 共训练500000次. 为了提高网络的抗噪能力, 训练时可在压缩图像上添加强度$\sigma = 0.10$的高斯噪声.

2

-->

4.1.加　密

本文的通用图像压缩加密方案, 详细流程如图4所示.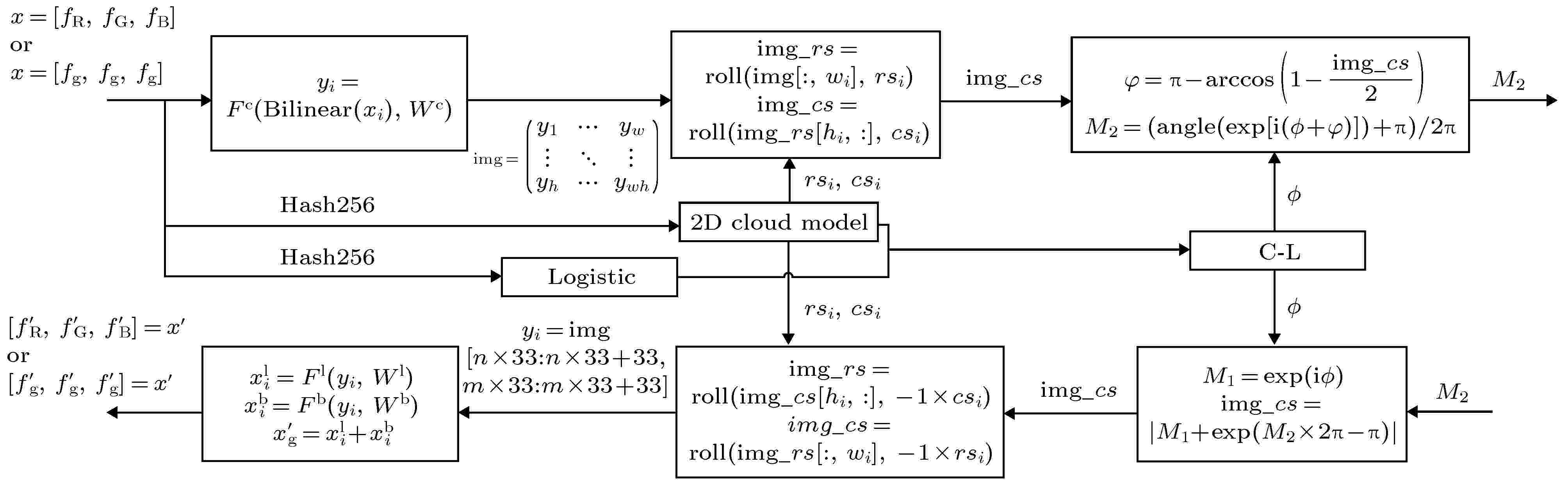
图 4 整个算法流程图
Figure4. Entire algorithm flow chart.

详细的加密步骤如下所示.
步骤1: 将彩色图像设置成RGB格式, 灰度图可以先转成3通道且对应位置的值相同. 经过压缩网络压缩后, 压缩图像块${{{y}}_{{i}}}$是4维的, 在加密之前需拼接并转成2维的图像img.
步骤2: 先根据SHA256算法计算原始图像的哈希值, 将哈希值按步长为2切割并转十进制, 得到32个范围在1—256的值, 再从前往后进行异或处理, 最后除以256, 得到0—1之间的一个小数作为原始图像的密钥${k_1}$.
步骤3: 根据原始图像的密钥${k_1}$再产生与压缩图像img大小一样的二维云模型序列、Logistic序列和C-L序列. 二维云模型初始值$({{Ex}}_1, {{Ex}}_2) = (11, 22)$, $({{En}}_1, {{En}}_2) \!=\! (33, 44)$, $({{He}}_1, {{He}}_2) \!=\! (10, 30)$, 生成正态随机数之前, 先分别产生$({{Ex}}_1, {{Ex}}_2)$, $({{En}}_1, {{En}}_2)$, $({{He}}_1, {{He}}_2)$的哈希值, 将这3组哈希值相加, 再按步长为2切割并转十进制, 然后求平均值, 与原始图像密钥${k_1}$结合作为随机种子. Logistic序列的参数${r} = 3.999$, 初始值为原始图像的密钥${k_1}$.
步骤4: 将二维云模型产生的随机序列放大取整后, 对压缩图像img进行行和列的滑动置乱, 得到置乱后的图像${\rm{img}} \_cs$.
步骤5: 将C-L序列作为矢量分解的夹角$\phi $, 与图像${\rm{img}} \_cs$进行矢量分解得到相位分布矩阵${M_2}$, 并将${M_2}$作为密文.
2 -->

4.2.解　密

解密过程是加密过程的逆过程, 具体公式图4中已给出, 详细步骤如下所示.
步骤1: 通过C-L级联混沌序列求出${M_1}$. 已知${M_1}$与密文${M_2}$, 根据(12)式得到置乱后的图像${\rm{img}} \_cs$.
步骤2: 根据(10)式产生的序列对图像${\rm{img}} \_cs$进行列和行的逆向滑动, 得到2维的压缩图像img, 再拼接成4维的图像块${{{y}}_{{i}}}$.
步骤3: 得到图像块${{{y}}_{{i}}}$后, 再通过重构网络重构出图像.

2

-->

5.1.重构质量分析

在重构质量上与TVAL3^[16], NLR-CS^[17], D-AMP^[18], ReconNet, DR²-Net, MSRNet这些算法比较. 前三种是基于传统的压缩感知算法, 后三种是基于深度学习的压缩感知算法. 本节通过引入一些指标来衡量图像重构质量的高低. 峰值信噪比(peak signal to noise ratio, PSNR)作为重构质量的评估指标, 值越大表示图像重构的质量越高. PSNR的公式如下:

${\rm{PSNR \!=\! 10 \!\times\! lg}}\left( {\frac{{{\rm{MA}}{{\rm{X}}^{\rm{2}}}}}{{{\rm{MSE}}}}} \right){\rm{ \!=\! 20 \times lg}}\left( {\frac{{{\rm{MAX}}}}{{\sqrt {{\rm{MSE}}} }}} \right){{,}}$

其中, MAX表示图像像素可取的最大值, MSE表示均方差. 均方差的公式如下:

${\rm{MSE}} = \frac{1}{{{{mn}}}}\sum\limits_{{i} = 0}^{{{m}} - 1} {\sum\limits_{{{j}} = 0}^{{{n}} - 1} {{{\left[ {{{f}}\left( {{i},{{j}}} \right) - {{f'}}\left( {{i},{{j}}} \right)} \right]}^2}} } .$

式中, m和n表示图像的宽高, ${{f}}\left( {{i}, {{j}}} \right)$表示原始图像像素值, ${{f'}}\left( {{i}, {{j}}} \right)$表示重构图像像素值. 结构相似性(structural similarity, SSIM)从亮度、对比度和结构3个层次比较是否相似, 值在0—1之间, 越接近1表示两幅图像越相似. SSIM的公式如下:

${\rm{SSIM}}\left( {{{X}},{{Y}}} \right) = {{L}}\left( {{{X}},{{Y}}} \right) \times {{C}}\left( {{{X}},{{Y}}} \right) \times {{S}}\left( {{{X}},{{Y}}} \right),$

其中, X与Y表示对比的两张图像, ${{L}}\left( {{{X}}, {{Y}}} \right)$表示亮度的对比结果, ${{C}}\left( {{{X}}, {{Y}}} \right)$表示对比度的对比结果, ${{S}}\left( {{{X}}, {{Y}}} \right)$表示结构的对比结果.

$\left\{ \begin{aligned} &{{L}}\left( {{{X}},{{Y}}} \right) = \frac{{2{{{u}}_{{X}}}{{{u}}_{{Y}}} + {{{C}}_1}}}{{{{u}}_{{X}}^2 + {{u}}_{{Y}}^2 + {{{C}}_1}}}, \\ &{{C}}\left( {{{X}},{{Y}}} \right){{ = }}\frac{{2{{{\sigma }}_{{X}}}{{{\sigma }}_{{Y}}}{{ + }}{{{C}}_2}}}{{{{\sigma }}_{{X}}^2{{ + \sigma }}_{{Y}}^2{{ + }}{{{C}}_2}}}, \\ &{{S}}\left( {{{X}},{{Y}}} \right){{ = }}\frac{{{{{\sigma }}_{{{XY}}}}{{ + }}{{{C}}_3}}}{{{{{\sigma }}_{{X}}}{{{\sigma }}_{{Y}}}{{ + }}{{{C}}_3}}}, \end{aligned} \right.$

其中${{{u}}_{{X}}}$和${{{u}}_{{Y}}}$分别是图像X和图像Y的均值, ${{{\sigma }}_{{X}}}$和${{{\sigma }}_{{Y}}}$分别是图像X和图像Y的方差, ${{{\sigma }}_{{{XY}}}}$是图像X和图像Y的协方差, ${{{C}}_1} = {\left( {{{{k}}_1} \times {{j}}} \right)^2}$, ${{{C}}_2} = {\left( {{{{k}}_2} \times {{j}}} \right)^2}$, ${{{C}}_3} = {{{{{C}}_1}} / 2}$, ${{{k}}_1} = 0.01$, ${{{k}}_2} = 0.03$, ${{j}} = 255$.

$\left\{ \begin{aligned}& {{{u}}_{{X}}} = \frac{1}{{{{m}} \times {{n}}}}\sum\limits_{{i} = 0}^{{{m}} - 1} {\sum\limits_{{{j}} = 0}^{{{n}} - 1} {{{X}}\left( {{i},{{j}}} \right)} }, \\ &{{\sigma }}_{{X}}^2 = \frac{1}{{{{m}} \times {{n}} - 1}}\sum\limits_{{i} = 0}^{{{m}} - 1} {\sum\limits_{{{j}} = 0}^{{{n}} - 1} {{{\left( {{{X}}\left( {{i},{{j}}} \right) - {{{u}}_{{X}}}} \right)}^2}} }, \\ &{{{\sigma }}_{{{XY}}}} \!=\!\! \frac{1}{{{{m}}\! \times\! {{n}} \!\!-\!\! 1}}\!\sum\limits_{{i} = 0}^{{{m}} - 1} {\sum\limits_{{{j}} = 0}^{{{n}} - 1} \!{\left( {{{X}}\!\left( {{i},{{j}}} \right) \!-\! {{{u}}_{{X}}}} \right)\!\left( {{{Y}}\!\left( {{i},{{j}}} \right) \!-\! {u_{{Y}}}} \right)} } , \end{aligned} \right.$

其中m和n表示图像的宽高.
使用11张灰度图像^[5]进行测试, 表1列出了采样率MR = 0.25, 0.10, 0.04, 0.01的重构结果.

采样率	算法	Lena	Monarch	Flinstones	平均PSNR
0.25	TVAL3	28.67	27.77	24.05	27.84
	NLR-CS	29.39	25.91	22.43	28.05
	D-AMP	28.00	26.39	25.02	28.17
	ReconNet	26.54	24.31	22.45	25.54
	DR2-Net	29.42	27.95	26.19	28.66
	MSRNet	30.21	28.90	26.67	29.48
	FCLBCNN	31.09	29.97	27.57	29.71
0.10	TVAL3	24.16	21.16	18.88	22.84
	NLR-CS	15.30	14.59	12.18	14.19
	D-AMP	22.51	19.00	16.94	21.14
	ReconNet	23.83	21.10	18.92	22.68
	DR2-Net	25.39	23.10	21.09	24.32
	MSRNet	26.28	23.98	21.72	25.16
	FCLBCNN	26.93	24.58	22.08	25.41
0.04	TVAL3	19.46	16.73	14.88	18.39
	NLR-CS	11.61	11.62	8.96	10.58
	D-AMP	16.52	14.57	12.93	15.49
	ReconNet	21.28	18.19	16.30	19.99
	DR2-Net	22.13	18.93	16.93	20.80
	MSRNet	22.76	19.26	17.28	21.41
	FCLBCNN	23.33	19.59	17.17	21.51
0.01	TVAL3	11.87	11.09	9.75	11.31
	NLR-CS	5.95	6.38	4.45	5.30
	D-AMP	5.73	6.20	4.33	5.19
	ReconNet	17.87	15.39	13.96	17.27
	DR2-Net	17.97	15.33	14.01	17.44
	MSRNet	18.06	15.41	13.83	17.54
	FCLBCNN	18.12	15.63	13.90	17.62

表1重构的灰度图像在不同算法、不同采样率下的PSNR
Table1.PSNR of reconstructed gray images under different algorithms and different sampling rates.

表1列出了3张灰度图像的PSNR与11张灰度图像的平均PSNR. 从表1可以看出, 基于深度学习的算法ReconNet在MR = 0.25时, 重构质量低于前三种传统压缩感知算法, 但DR²-Net, MSRNet和FCLBCNN的重构质量高于传统的3个算法, 且FCLBCNN在4个采样率上的重构图像平均PSNR值最高.
在数据集BSD500上测试算法的泛化能力, 共500张图像. 测试结果如表2所列.

算法	MR = 0.08			MR = 0.10			MR = 0.18			MR = 0.25			MR = 0.53
	PSNR	SSIM		PSNR	SSIM		PSNR	SSIM		PSNR	SSIM		PSNR	SSIM
ReconNet	—	—		23.28	0.6121		—	—		25.48	0.7241		—	—
DR2-Net	—	—		24.26	0.6603		—	—		27.56	0.7961		—	—
MSRNet	—	—		24.73	0.6837		—	—		27.93	0.8121		—	—
FCLBCNN (gray)	—	—		24.83	0.7056		—	—		28.19	0.8400		32.87	0.9392
FCLBCNN (color)	27.94	0.8252		—	—		32.07	0.9279		—	—		—	—

表2在BSD500测试集上不同算法、不同采样率下的平均PSNR和平均SSIM
Table2.Mean PSNR and SSIM of different algorithms and different sampling rates on the BSD500 test set.

表2为各算法在数据集BSD500上的PSNR与SSIM值(“—”表示空). 采样率MR = 0.25, 0.10时, FCLBCNN (gray)的PSNR和SSIM值都是最高的, 重构性能优于基于深度学习的ReconNet, DR²-Net和MSRNet. FCLBCNN (color)的采样率MR = 0.08, 0.18对应FCLBCNN(gray)的采样率MR = 0.25, 0.53, 且他们的PSNR和SSIM值相差不大, 说明FCLBCNN通过彩色图像训练的网络也适用于灰度图像, 不需要重新训练网络. 实验表明, 本文FCLBCNN与其他算法相比, 重构质量更高且有着很好的泛化能力.
256 × 256的Lena图像在各阶段效果如表3所列.

原图	采样率	压缩图像	置乱图像	密文图像	重构图像	PSNR	SSIM
	0.53					36.4387	0.9715
	0.18					32.5516	0.9456

表3Lena图像在各阶段的效果(采样率MR = 0.53 (灰度), 0.18 (彩色))
Table3.Lena image effects at various stages, sampling rate MR = 0.53 (gray), 0.18 (color).

从表3可以看出, Lena在采样率MR = 0.53 (灰度), 0.18 (彩色)时, 密文图像已看不出原图轮廓, 重构出的图像也与原始图像非常接近, 具有良好的视觉效果, 所以下列的性能分析皆使用这两个采样率.
2 -->

5.2.密钥空间分析

一般情况下, 密钥空间足够大时, 图像加密算法才能有效抵御暴力破解. 本文使用的混沌系统中, Logistic序列的密钥有r与${z}[0]$, 二维云模型的密钥有随机种子${k_1}$, $({{Ex}}_1, {{Ex}}_2)$, $({{En}}_1, {{En}}_2)$和$({{He}}_1, {{He}}_2)$, 共9个密钥. 仿真设备精度为${10^{15}}$, 精确位数为15位, 密钥空间为${10^{15 \times 9}} = {10^{135}}$, 而密钥空间$ \geqslant {2^{100}} \approx {10^{30}}$就能满足安全要求^[19], 所以本文加密算法的密钥空间足够大, 暴力破解无法对加密图像进行有效解密.
2 -->

5.3.相关性分析

一般来说, 原始图像相邻像素值的相关性会比较高, 但对于一个理想的密文图像, 相邻像素值的相关性应该为0. 因此, 密文图像的相邻像素值的相关系数是加密算法优劣的一个重要指标. 相关系数分为水平、垂直和斜线3个方向, 计算公式如下:

$r = \frac{{ \sum\nolimits_{i = 1}^N {({{x}_{i}} - \overline x ) \times ({{y}_{i}} - \overline y )} }}{{\sqrt { \sum\nolimits_{i = 1}^N {{{({{x}_{i}} - \overline x )}^2}} } \times \sqrt { \sum\nolimits_{i = 1}^N {{{({{y}_{i}} - \overline y )}^2}} } }}.$

其中, $\overline x $和$\overline y $分别为${{{x}}_{{i}}}$和${{{y}}_{{i}}}$的平均值. 表4所列为本文与文献[20, 21]在3个方向上的相关系数, 密文图像上的绝对值最小值已用粗体标出.

测试图像	方向	明文(gray)	密文
			本文(gray)	本文(color)	文献[20]	文献[21]
Lena	水平	0.9396	0.0010	–0.0024	–0.0048	0.0011
	竖直	0.9639	–0.0066	0.0012	–0.0112	0.0098
	斜线	0.9189	–0.0039	0.0035	–0.0045	–0.0227
Peppers	水平	0.9769	–0.0004	–0.0023	–0.0056	0.0071
	竖直	0.9772	0.0089	0.0063	–0.0162	–0.0065
	斜线	0.9625	–0.0077	0.0004	–0.0113	–0.0165
平均值	水平	—	0.0003	–0.0024	–0.0052	0.0041
	竖直	—	0.0012	0.0038	–0.0137	0.0017
	斜线	—	–0.0058	0.0020	–0.0079	–0.0196

表4不同加密算法的相关系数比较
Table4.Comparison of correlation coefficients of different encryption algorithms.

从表4可以看出, 本文算法在相关系数的平均值上更接近0, 优于其他算法. 同时, 为了更直观的展现图像相邻像素值的相关性, 引入Lena (gray)的明文图像与密文图像在3个方向上的相关性分布图如图5所示.
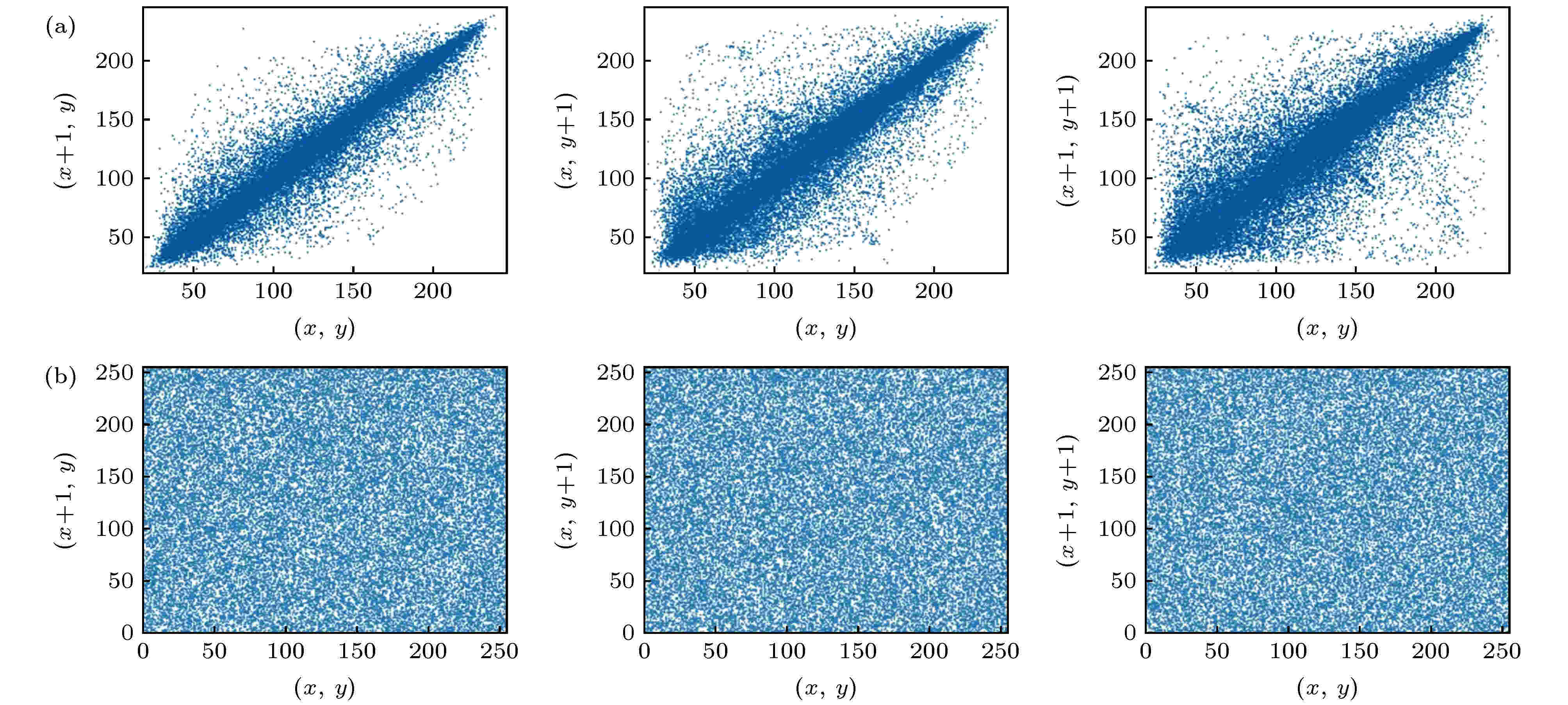图 5 Lena (gray)图像明文与密文在水平、竖直、斜线3个方向的相关分布图　(a) 明文图像的相关分布图; (b)密文图像的相关分布图
Figure5. Correlation distribution of the plaintext and ciphertext in the horizontal, vertical and oblique directions of Lena (gray) images: (a) Correlation distribution of plaintext; (b) correlation distribution of ciphertext.

从图5上可以看出, 本文算法得到的密文图像在3个方向上的像素点成随机性分布, 已显著破坏了相邻像素点的相关性, 增强了保密性.
2 -->

5.4.信息熵分析

全局信息熵反映了整个图像像素值的混乱程度, 其信息熵越大, 表示图像所包含的信息越混乱, 全局信息熵的公式如下所示:

${\rm{en}} = - \sum\limits_{i = 1}^L {p(i){{\log }_2}p(i)} .$

其中, L表示图像的灰度等级, 本文使用的图片灰度级皆为256, $p(i)$表示像素值出现的概率, en的理想值为8. 本文与其他算法在Lena, Peppers上的全局信息熵如表5所列, 密文图像的全局信息熵最大值已用粗体标出.

测试图像	明文(gray)	密文
		本文(gary)	本文(color)	文献[12]
Lena	7.3035	7.9949	7.9944	7.9544
Peppers	7.4344	7.9956	7.9952	7.9633

表5不同加密算法得到的信息熵的比较
Table5.Comparison of the entropy obtained by different encryption algorithms.

基于局部信息熵的图像随机性统计检验方法^[22]是对全局信息熵的扩展, 通过计算多个非重叠且随机选择的图像块上信息熵的样本均值来衡量图像的随机性. 使用共30个大小为44 × 44的不重叠图像块, 本文算法在Lena, Peppers上密文的局部信息熵如表6所列.

测试图像	局部信息熵(gray/color)	临界值
		$\begin{array}{l} u_{0.05}^{* - } = 7.9019 \\ u_{0.05}^{* + } = 7.9030 \end{array}$	$\begin{array}{l} u_{0.01}^{* - } = 7.9017 \\ u_{0.01}^{* + } = 7.9032 \end{array}$	$\begin{array}{l} u_{0.001}^{* - } = 7.9015 \\ u_{0.001}^{* + } = 7.9034 \end{array}$
Lena	7.9024/7.9027	Pass	Pass	Pass
Peppers	7.9027/7.9023	Pass	Pass	Pass

表6不同加密算法得到的局部信息熵比较
Table6.Comparison of the local entropy obtained by different encryption algorithms.

从表5可以看出, 本文算法的全局信息熵更接近8. 表6中, 局部信息熵的值也都在临界范围内. 因此, 可以认为本文算法得到的密文像素值分布非常混乱, 能更好地掩盖明文图像信息.
2 -->

5.5.明文敏感性分析

本文加密算法使用的密钥与明文有关且明文对密文非常敏感, 使轻微修改明文后得到的密文与原密文相差很大, 无法破译密码系统. 本节引入像素改变率(number of pixels change rate, NPCR)和一致平均改变密度(unified average changing intensity, UACI)来评估加密算法抵抗差分攻击的能力, 公式如下所示:

$\begin{split}{\rm{NPCR}} =\;& \frac{1}{{MN}}\sum\limits_{i = 1}^M \sum\limits_{j = 1}^N \big[\left| {\rm{sign}} \big({P_1}(i,j)\right.\\&\left. { - {P_2}(i,j)\big)} \right| \times 100\% \big] ,\end{split}$

${\rm{sign}}(x) = \left\{\begin{aligned} &1, &x \geqslant 0, \\& 0, & x = 0, \\&- 1, & x \leqslant 0. \end{aligned} \right.$

${\rm{UACI}} = \frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {\frac{{|{P_1}(i,j) - {P_2}(i,j)|}}{{255 - 0}}} \times 100\% },$

其中, ${P_1}(i, j)$为密文图像${P_1}$的像素值, ${P_2}(i, j)$为密文图像${P_2}$的像素值.
本文与其他算法在Lena, Peppers密文上的NPCR与UACI对比如表7和表8所列.

测试图像	NPCR (gray/color)	NPCR理论临界值
		$N_{0.05}^* = 99.5693\% $	$N_{0.01}^* = 99.5527\% $	$N_{0.001}^* = 99.5341\% $
Lena	0.9960/0.9961	Pass	Pass	Pass
Lena[12]	0.9954/—	Fail	Fail	Pass
Lena[20]	0.9962/—	Pass	Pass	Pass
Peppers	0.9959/0.9957	Pass	Pass	Pass
Peppers[12]	0.9944/—	Fail	Fail	Fail
Peppers[20]	0.9963/—	Pass	Pass	Pass

表7不同加密算法得到的NPCR比较
Table7.Comparison of NPCR obtained by different encryption algorithms.

测试图像	UACI (gray/color)	UACI理论临界值
		$\begin{array}{l} u_{0.05}^{* - } = 33.2824\% \\ u_{0.05}^{* + } = 33.6447\% \end{array}$	$\begin{array}{l} u_{0.01}^{* - } = 33.2255\% \\ u_{0.01}^{* + } = 33.7016\% \end{array}$	$\begin{array}{l} u_{0.001}^{* - } = 33.1594\% \\ u_{0.001}^{* + } = 33.7677\% \end{array}$
Lena	0.3352/0.3357	Pass	Pass	Pass
Lena[12]	0.3303/—	Fail	Fail	Fail
Lena[20]	0.3370/—	Fail	Pass	Pass
Peppers	0.3333/0.3331	Pass	Pass	Pass
Peppers[12]	0.3305/—	Fail	Fail	Fail
Peppers[20]	0.3369/—	Fail	Pass	Pass

表8不同加密算法得到的UACI比较
Table8.Comparison of UACI obtained by different encryption algorithms.

从表7和表8可以看出, 本文算法在NPCR与UACI上都处于临界范围内, 说明本文加密算法能够更好地抵御差分攻击.
2 -->

5.6.鲁棒性分析

为了验证本文算法的压缩重构网络在训练时添加高斯噪声能提高鲁棒性, 网络在训练时添加了强度$\sigma = 0.10$的高斯噪声与网络在训练时没有添加高斯噪声的算法, 对高斯噪声、椒盐噪声和剪切攻击的对比如图6和图7所示.
图 6 在密文图像上添加高斯噪声或椒盐噪声后重构出的Lena图像　(a), (b)使用的网络在训练时没有添加高斯噪声; (c), (d)使用的网络在训练时添加了强度为0.10的高斯噪声
Figure6. Lena image reconstructed by adding Gaussian noise or salt and pepper noise to the ciphertext image: The networks used in (a) and (b) did not add Gaussian noise during training; the networks used in (c) and (d) are trained with Gaussian noise with an intensity of 0.10.

图 7 Lena图像的密文被剪切后的重构结果　(a)剪切不同大小后的密文; (b), (c)使用的网络在训练时没有添加高斯噪声; (d), (e)使用的网络在训练时添加了强度为0.10的高斯噪声
Figure7. Reconstruction result after ciphertext cut of Lena image: (a) Cut ciphertexts of different sizes; the networks used in (b) and (c) did not add Gaussian noise during training; the networks used in (d) and (e) are trained with Gaussian noise with an intensity of 0.10.

图6中, 由于重构(a)和(b)图像的网络在训练时没有添加高斯噪声, 解密与重构后图像已看不清轮廓. 重构(c)和(d)图像的网络在训练时添加了高斯噪声, 解密与重构后图像依然能看清轮廓. 图7中, 密文图像被剪切后, 重构出的(d)和(e)图像质量优于(b)和(c)图像质量. 从图6和图7可以看出, 训练网络时在压缩图像上添加高斯噪声, 能抵抗一定程度的噪声污染与剪切攻击.
2 -->

5.7.选择明文攻击分析

选择明文攻击是指通过特殊的明文与对应的密文推导出中间密钥, 本节通过一个简单的实验来验证本文算法能抵御选择明文攻击. 定义一个像素点全为0的灰度图P₁, 图像P₂与P₁只有一个像素值不一样, C₁, C₂分别为P₁, P₂的密文图像. 定义P₃ = |P₁ – P₂|, C₃ = |C₁ – C₂|. 在明文上找一个像素点并修改像素值, P₁, P₂, P₃与C₁, C₂, C₃如图8所示.
图 8 选择明文攻击效果图
Figure8. Effect pictures of chosen plaintext attack.

从图8可知, 外界无法从C₃上获得任何有效信息, 说明本文加密算法能有效抵御选择明文攻击.
2 -->

5.8.直方图分析

直方图反映了图像中每种灰度级的像素个数, 越均匀说明加密效果越好, 本节通过明文和密文的直方图对本文算法进行评估, Lena, Peppers在灰度图像和彩色图像上的直方图如图9所示.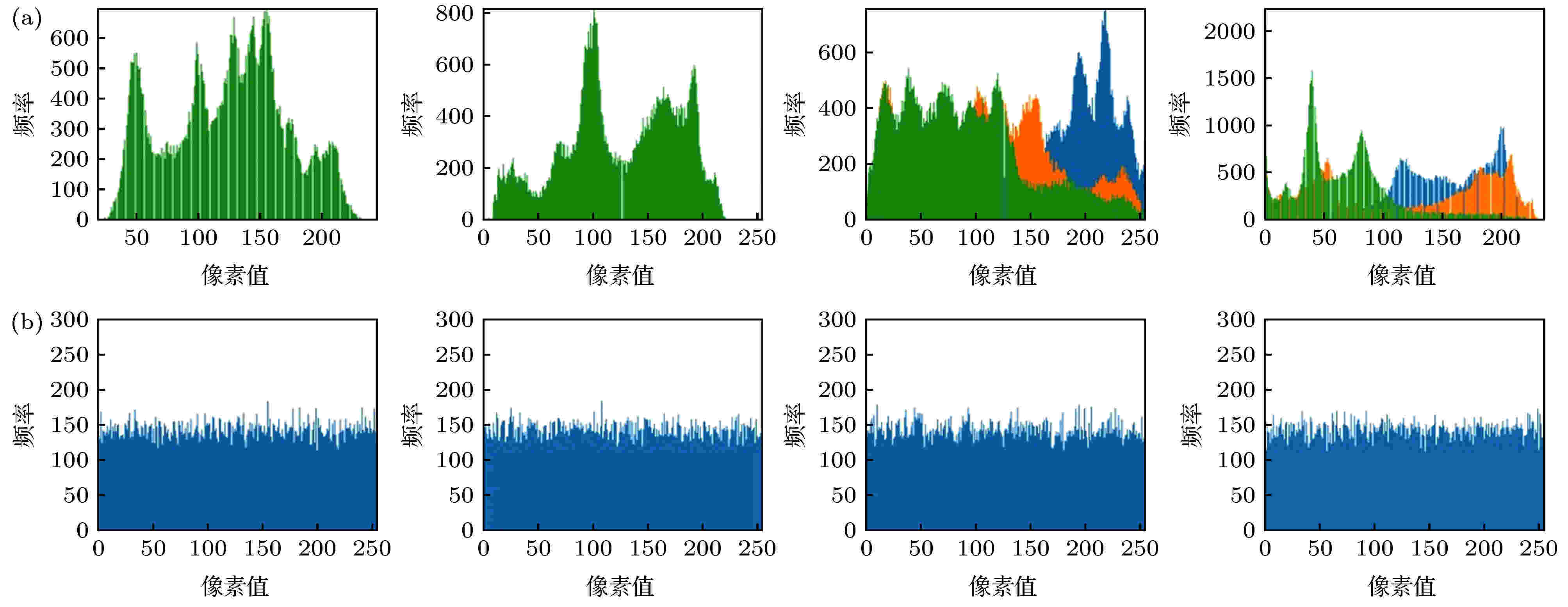
图 9 Lena (gray), Peppers (gray), Lena (color), Peppers (color)图像在明文与密文上的直方图　(a)明文直方图; (b)密文直方图
Figure9. Histograms of Lena (gray), Peppers (gray), Lena (color), Peppers (color) images in plain text and ciphertext: (a) Plain text histogram; (b) ciphertext histogram.

图9中, Lena和Peppers的明文图像直方图有着明显的像素值分布特性, 而密文图像的直方图非常均匀, 很好地隐藏了明文图像的像素值分布特性. 说明本文算法可以很好地抵抗统计攻击.
2 -->

5.9.时间复杂度分析

时间复杂度也是衡量算法性能的一个重要指标. 为了验证本文基于深度学习的压缩重构网络能降低整个算法的耗时, 与在原图上直接使用本文加密算法的耗时对比如表9所列, 最快时间已用粗体标出.

图像大小	压缩重构(gray/color)	加解密(gray/color)	总时间(gray/color)	编程工具	平台
256 × 256	0.21/0.20	0.66/0.65	0.87/0.85	Pycharm + Pytorch	i5-8500 CPU
	—	0.93/2.81	0.93/2.81
512 × 512	0.91/0.89	2.51/2.51	3.42/3.40
	—	3.89/11.96	3.89/11.96
1024 × 1024	4.81/4.62	9.40/9.42	14.21/14.04
	—	15.84/48.51	15.84/48.51

表9本文压缩加密算法与在原图上直接使用本文加密算法的耗时对比
Table9.Time-consuming comparison that the compression encryption algorithm of this article and the encryption algorithm of this article directly used on the original image.

从表9可以看出, 本文压缩加密算法比在原图上直接使用本文加密算法的总耗时更短, 特别是彩色图像, 说明本文压缩加密算法在时间上有着很大优势.

本文提出了一种基于深度学习的压缩感知与复合混沌的通用图像加密方案, 利用深度学习方法来压缩重构图像, 适用于灰度图像与RGB格式的彩色图像, 不需要单独训练网络, 使用复合混沌系统、滑动置乱与矢量分解组成的加密算法对压缩后的图像进行加解密. 通过实验与性能分析, 验证了本文压缩加密算法在图像存储与传输方面的优势, 耗时短、重构质量高、抗噪能力强且安全性高.