摘要:传输线电缆是一种生活中很常见的一维波导, 除了在工程上有广泛应用外, 也可以被应用于基础研究领域的一些理论验证性实验中. 例如, 因为传输线和量子电路具有相同的波动方程形式, 传输线被广泛应用于量子图的研究中. 另一方面, 传输线网络方程还和零能紧束缚模型的方程形式相似, 所以可以用传输线网络来验证基于紧束缚模型理论所预言的物理性质, 例如安德森局域化、能带结构、拓扑性质等. 本文从传输线网络方程出发, 回顾传输线在上面提到的几个研究方向中的具体应用. 这些研究方向分别为: 一维、二维、三维网络中的安德森局域化研究; 周期性以及准周期性网络中的能带结构; 传输线网络中角动量依赖的拓扑传输的验证. 本文详细阐述了这些工作的研究思路以及结果, 展现了传输线在基础研究领域的广泛应用潜力.
关键词: 传输线/
紧束缚模型/
拓扑材料/
安德森局域化

English Abstract

全文HTML

--> --> -->

传输线是一种一维波导, 以横向电磁模式从一个节点向另一个节点传输电磁波. 其结构形式有双导线、同轴线、带状线、微带线等, 而其中最常见的结构是同轴电缆, 比如我们家里的电视信号线都经常用到. 以同轴电缆为例, 其横截面从内到外有四层结构, 分别是: 中心导体、电介质绝缘体、外层导体、外层绝缘体. 电磁波被限制在电介质绝缘体中传播, 而在中心导体和外层导体上有着方向相反、大小相同的交变电流, 从而构成了交变电流回路; 同时两层导体之间存在着电压差值, 这个电压差值即为同轴电缆在某一点位置的电压; 而对于一列行波, 电压和电流的比值即为电缆的阻抗, 这是传输线的一个重要参数. 一般同轴电缆的阻抗为50 Ω或者75 Ω, 50 Ω电缆通常为基带同轴电缆^[1], 而75 Ω电缆为宽带同轴电缆^[1]. 因为电压和电流的比值是固定的, 所以无论是电压或者电流值都可以当作电磁波的波函数, 也就是说这里的电磁波可以当作标量波处理.
虽然传输线被大量应用在工程中, 但人们很少探讨其在基础学科研究中的应用. 在一些数学和基础物理的研究中, 传输线电缆可以被用来连成网络, 继而进行一些理论验证性的工作. 由于电缆波动方程和量子电路中的薛定谔方程十分相似, 所以电缆可以被用于一些量子图以及随机矩阵理论^[2-8]的研究当中, 从而在宏观的电缆网络中非常直观地模拟量子图. 另外电缆网络方程和零能紧束缚模型的方程结构也十分相似, 因此其还可被用于一些基于紧束缚模型的研究中, 例如安德森局域化^[9,10]、晶体以及准晶^[11-15]、拓扑材料^[16]等. 除了用于模拟物理模型, 一些电缆网络本身也具有独特的能带性质, 例如无色散平带^[15,17]、强衰减带隙^[18,19]等, 如果进一步在电缆中引入增益和损耗, 还可用于研究宇称-时间对称的非厄密系统^[20-23]. 而且考虑到电缆的连接十分灵活, 一些在实际材料中较难实现的模型, 甚至超过三维空间的高维模型, 在电缆网络中都可以被轻松实现. 通常在电缆网络的理论计算中, 网络的大小、形状可以随意选取; 但如果要在实验中实现, 由于空间以及传输损耗的限制, 一般不会搭建过于庞大的网络.
本文介绍了一些基于传输线网络的研究工作, 并了解其在不同研究领域的具体应用. 整篇文章内容如下: 第2节首先介绍传输线网络的方程, 并且用了几个具体例子来讲解计算方法; 第3节介绍一些用传输线网络研究安德森局域化的工作; 第4节介绍一些关于周期性以及准周期性网络的能带研究; 第5节介绍一项关于在电缆网络中实现拓扑传输的研究; 第6节进行总结.

对于一个由传输线电缆连接构成的网络, 传输线上除节点外的任意一点的波函数满足波动方程^[9]:

$\frac{{{\partial ^2}}}{{\partial {s^2}}}{\psi _{jk}}(s) + \frac{{{\varepsilon _{\rm{r}}}{\omega ^2}}}{{{c_0}^2}}{\psi _{jk}}(s) = 0,$

其中${\psi _{jk}}(s)$为在连接节点j和节点k的电缆上、和节点j距离长度s的位置的波函数, 而$\omega $, ${c_0}$, ${\varepsilon _{\rm{r}}}$分别是角频率、真空光速、电缆中电介质的相对介电常数. (1)式的通解形式为^[9,24]

${\psi _{jk}}(s) = {\psi _j}\frac{{\sinh [z({l_{jk}} - s)]}}{{\sinh (z{l_{jk}})}} + {\psi _k}\frac{{\sinh (z \cdot s)}}{{\sinh (z{l_{jk}})}},$

其中${\psi _j}$和${\psi _k}$分别是节点j和节点k处的波函数, l_jk是连接节点j和节点k的电缆长度, $z \!=\! ({\rm{i}}\omega / {c_0})\sqrt {{\varepsilon _{\rm{r}}}} $. 另外在每个节点上运用基尔霍夫电流守恒方程^[9,24]:

$\sum\limits_k {{{\left. {\frac{\partial }{{\partial s}}{\psi _{jk}}(s)} \right|}_{s = 0}}} = 0,$

其中对k求和是对所有连接节点j的其他节点的求和. 通过(2)式和(3)式, 可以推导出各个节点上的波函数满足方程^[9,24]:

$ - {\psi _j}\sum\limits_k {\coth \left( {z{l_{jk}}} \right)} + \sum\limits_k {\frac{1}{{\sinh \left( {z{l_{jk}}} \right)}}{\psi _k}} = 0,$

(4)式是一个关于各个节点的方程, 被称为网络方程或者耦合方程, 大部分关于传输线网络的计算也都基于该方程. 其方程形式和能量为零的紧束缚模型十分相似, 第一项可以看作是节点的本地能量, 第二项则可视为不同节点之间的耦合项.
首先考虑一个图1(a)中的开放网络. 该网络有两个节点A和B, 由两条长度l₁的电缆连接而成. 另外在输入和输出线上分别增加了额外端点“in”和“out”, 分别距离A, B点l₂长度. 对于节点A, B, 分别写下其网络方程:
图 1 传输线网络中透反射谱和能带的计算　(a) 有输入输出的开放性传输线网络; (b) 一维的周期性传输线网络; (c) 二维的周期性传输线网络; (d) 三维的周期性传输线网络; (e)?(g) 分别对应(b)?(d)中三种网络的能带图
Figure1. Transmission/reflection spectra and band structures in transmission line network: (a) The transmission line network with input and output (open boundary); (b) one-dimensional (1D) periodic transmission line network; (c) two-dimensional (2D) periodic transmission line network; (d) three-dimensional (3D) periodic transmission line network; (e)?(g) correspond to the band structures of the networks shown in (b)?(d) respectively.

$\begin{split} &\left[ { - 2\coth \left( {z{l_1}} \right) - \coth \left( {z{l_2}} \right)} \right]{\psi _A} + \frac{2}{{\sinh \left( {z{l_1}} \right)}}{\psi _B}\\ & + \frac{1}{{\sinh \left( {z{l_2}} \right)}}{\psi _{{\rm{in}}}} = 0,\\ &\frac{2}{{\sinh \left( {z{l_1}} \right)}}{\psi _A} + \left[ { - 2\coth \left( {z{l_1}} \right) - \coth \left( {z{l_2}} \right)} \right]{\psi _B} \\ &+ \frac{1}{{\sinh \left( {z{l_2}} \right)}}{\psi _{{\rm{out}}}} = 0.\end{split}$

对于入射和出射波, 还可以再列四个等式:

$\begin{split}&{\psi _{{\rm{in}}}} - r = 1,\\&{\psi _A} - r \cdot \exp ( - z{l_2}) = \exp (z{l_2}),\\&{\psi _B} - t = 0,\\&{\psi _{{\rm{out}}}} - t \cdot \exp (z{l_2}) = 0,\end{split}$

其中r和t分别是反射和透射系数, 入射信号设为1, 从端点“in”输入, 从节点B流出. 联立(5)式和(6)式, 可以得到矩阵形式:

$ \left(\!\!\begin{array}{*{20}{c}} {\textstyle -2\coth (zl_1) \atop \textstyle -\coth ( zl_2)} & 2/\sinh(zl_1) & 1/\sinh(zl_2) & 0 & 0 & 0 \\ 2/\sinh(zl_1) & {\textstyle -2\coth (zl_1) \atop \textstyle -\coth (zl_2)} & 0 & 0 & 1/\sinh (zl_2) & 0 \\ 0 & 0 &1 & {-1} & 0 & 0 \\ 1 & 0 & 0 & -\exp(-zl_2) & 0 & 0 \\ 0 &1 & 0 & 0 & 0 & -1 \\ 0 & 0 & 0 & 0 &1 & -\exp(zl_2) \end{array}\!\!\right)\!\!\left(\!\!\begin{array}{*{20}{c}} \psi _A \\ \psi _B \\ \psi_{\rm in} \\ r \\ \psi_{\rm out} \\ t\end{array}\!\!\right) \!=\! \left(\!\!\!\!\begin{array}{*{20}{c}}\!\! 0 \\ 0 \\ 1 \\ \exp(zl_2) \\ 0 \\ 0 \!\!\end{array}\!\!\!\!\right),$

这个方程具有${{M\psi}} = {{\eta}} $的形式. 通过${{\psi}} = {{{M}}^{ - 1}}{{\eta}} $, 可以得到所有节点上的波函数.
上述是开放网络透射率、反射率的计算, 接下来讲周期性网络的能带计算. 考虑图1(b)中的一维周期性网络, 红虚线框中是选中的一个元胞, 长度为a. 元胞内有A, B两个节点, 用两条长度l₁的电缆连接. 不同元胞之间用长度l₂的电缆连接. 根据布洛赫周期性条件, 在A点左侧的另一个B点波函数表示为${\psi _B}\exp ( - {\rm{i}}{k_x}a)$, 所以A点的网络方程表示为

$\begin{split} & \left[ { - 2\coth \left( {z{l_1}} \right) - \coth \left( {z{l_2}} \right)} \right]{\psi _A} + \left[ \frac{2}{{\sinh \left( {z{l_1}} \right)}} \right.\\ &+\left. \frac{1}{{\sinh \left( {z{l_2}} \right)}} \cdot \exp ( - {\rm{i}}{k_x}a) \right]{\psi _B} = 0.\end{split}$

B点的方程也可以用类似的方法得到:

$\begin{split} &\left[ { - 2\coth \left( {z{l_1}} \right) - \coth \left( {z{l_2}} \right)} \right]{\psi _B} + \left[ \frac{2}{{\sinh \left( {z{l_1}} \right)}} \right.\\ &+\left. \frac{1}{{\sinh \left( {z{l_2}} \right)}} \cdot \exp ({\rm{i}}{k_x}a)\right]{\psi _A} = 0.\end{split}$

联立(8)式和(9)式, 方程可以用矩阵形式表示:

$\left( {\begin{array}{*{20}{c}} { - 2\coth (z{l_1}) - \coth (z{l_2})}&{\dfrac{2}{{\sinh (z{l_1})}} + \dfrac{1}{{\sinh (z{l_2})}} \cdot \exp ( - {\rm{i}}{k_x}a)} \\ {\dfrac{2}{{\sinh (z{l_1})}} + \dfrac{1}{{\sinh (z{l_2})}} \cdot \exp ({\rm{i}}{k_x}a)}&{ - 2\coth (z{l_1}) - \coth (z{l_2})} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {{\psi _A}} \\ {{\psi _B}} \end{array}} \right) = 0.$

对于每一个固定的k_x, 当(10)式中的矩阵行列式等于0时, 正好对应着网络的本征频率和本征模式. 历遍k_x, 就可以得到该周期性系统的能带. 令l₁ = 1, l₂ = 1, 计算出一维能带如图1(e)所示. 用类似的方法, 可以计算出二维、三维以及更高维度的传输线网络的能带. 图1(c)是六角蜂巢网络, 可以作为二维情况的一个例子, 电缆长度a = 1, 其对应的布洛赫能带如图1(f)所示. 这里在K点我们能看到有狄拉克点的存在. 同时需要注意到, 和紧束缚模型不同, 除了最低阶模式外, 传输线网络还有更高频模式的存在. 图1(d)给出了一个三维的例子, 用二维六角蜂巢晶格在z方向层间距为h重复堆叠, 同层电缆长度a = 1, 并且在A, B亚晶格上的跨层连接电缆具有不同的长度l₁, l₂. 令l₁ = 1, l₂ = 1.1, 相邻层之间的布洛赫相位差固定在${k_z}h = 2{\text{π}}/3$, 得到图1(g)中的能带. 这里由于A, B亚晶格之间的宇称对称性被打破, K点的简并被打开. 值得注意的是, 电缆网络的能带在频率方向上有周期重复性, 这一点在图1(e)和图1(f)中能明显看到, 不过在图1(g)中没能看到. 这是因为例子中的一维和二维网络中所用的电缆长度l都是相同的, 所以其频率周期满足$zl = {\rm{i}} \cdot 2{\text{π}}$; 而在三维网络的例子里, 用到了两种不同长度的电缆, 虽然在图1(g)中看不到其频率周期性, 但实际上是因为其频率周期较大, 为两种电缆各自频率周期的最小公倍数, 所以在有限的频率范围内没能显现出来.
上述的情况是开放系统和周期性的系统, 如果是有限的封闭系统, 只需要对所有的节点列出耦合方程, 最后让耦合矩阵的行列式等于0, 即可得到本征能级图以及对应的本征模式. 和周期性系统一样, 封闭系统的本征能级同样具有频率周期性.

安德森局域化是一个研究了几十年的经典问题, 其描述的现象是无序引入的多重散射会导致原本向远处传导的波被局域在一个范围里. 本节就对一维、二维、三维传输线网络中安德森局域化的一些研究工作进行回顾介绍^[9,10].
首先介绍一维网络的研究^[9], 研究的对象如图2(a)所示. N个节点沿一个方向一字排开, 相邻节点之间用若干根电缆进行连接, 而无序性可以通过不同的电缆数目(配位数)和长度来引入. 当所有电缆取一样的长度l, 则(4)式变形为
图 2 一维和二维传输线网络中安德森局域化的研究^[9]　(a) 一维的随机传输线网络, 通过配位数和电缆长度的变化来引入随机性; (b) 二维的随机传输线网络, 通过在正方格子网络中随机移除结点之间的电缆来引入随机性
Figure2. Anderson localization in 1D and 2D transmission line networks^[9]: (a) 1D random transmission line network, the randomness is introduced by changing the coordination numbers and cable lengths; (b) 2D random transmission line network, the randomness is introduced by removing the cables randomly in the square lattice network.

$- {\psi _j}\sum\limits_k {\cos \left( \theta \right)} + \sum\limits_k {{\psi _k}} = 0,$

其中$\theta = - {\rm{i}} \cdot zl$. 当$\theta = 0$或者$2 m{\text{π}}$时(注意对于无耗散系统, 这里的z是一个纯虚数), 无论配位数如何随机改变, 总存在一个稳定的本征模式. 在该模式下, 各个节点的波函数都相等, 所以这个态被称作均一态. 随后Zhang和Sheng^[9]对配位数以及$\theta $如何影响局域长度分别作了数值计算研究. 数值结果显示, 当$\theta $值固定, 局域长度$\xi $和$\Delta n$成反比^[9]: $\xi \propto 1/\Delta n$, 其中

$\Delta n \!=\! {\Bigg\langle {\sum\limits_{j = 2}^{N - 1} {n(j) - 1} } \Bigg\rangle _{{\rm{conf}}}}\Bigg/(N \!-\! 2),$

用于表征缺陷的密度. 这里的$n(j)$为节点j和节点j + 1之间的电缆数目, 下标“conf”表示对大量组态作了平均. 当$\Delta n = 0$, 一维网络退化成了一根电缆, 所以不存在散射, 局域长度为无穷大; 当$\Delta n$不等于0, 增加的额外电缆等概率地随机分布于各个节点之间, 形成缺陷. 因为局域长度正比于平均自由程, 而平均自由程又反比于缺陷密度, 所以局域长度也反比于缺陷密度, 符合数值计算结果. 另一方面, 数值结果表明, 当$\Delta n$固定, 在均一态附近改变$\theta $, 局域长度$\xi $和$\theta $成平方反比^[9]: $\xi \propto 1/{\theta ^2}$. 这与声子系统中$\xi \propto 1/{\omega ^2}$也是一致的.
接下来介绍二维网络中的局域, 研究的对象是图2(b)所示的正方格网络, 所用的电缆长度相同, 而连接相邻格点的电缆有1－p的概率被拆除. Zhang和Sheng^[9]从两种情况出发进行数值研究, 分别是有序网络极限$(p \to 1, \theta \ne 0)$和均一态极限$(p \!\ne 1, \theta \!\to 0)$. 研究所用方法是有限尺寸标度法^[25], 将宽为M、长为L的样品在横向加上周期性边界条件, 纵向两端接上有序样品构成的外接引线, 通过标准递归格林函数法算出透射率, 进而算出该长条形样品的局域长度$\xi (M)$. 当$M \to \infty $, $\xi (M)$就可以逼近二维体样品的局域长度$\xi $. 通过数值计算并取系综平均, 可以验证在有序网络极限和均一态极限情况下, 局域长度的规律分别符合函数形式^[9]:

$\xi (p) = a{\left( {\frac{p}{{1 - p}}} \right)^{1/2}}\exp \left[ {b{{\left( {\frac{p}{{1 - p}}} \right)}^{1/2}}} \right],$

$\xi (\theta ) = \frac{c}{\theta }\exp \left( {\frac{d}{\theta }} \right),$

其中a, b是不依赖于p的系数; c, d是不依赖于$\theta $的系数. 不过, Zhang和Sheng^[9]认为这个拟合结果并不十分准确, 根据紧束缚模型给出的形式应为

$\xi (p,\theta ) = \frac{a}{{{\theta ^2}}}\left( {\frac{p}{{1 - p}}} \right)\exp \left[ {\frac{{bp}}{{{\theta ^2}\left( {1 - p} \right)}}} \right],$

其中a, b为不依赖于p, $\theta $的系数. 数值结果偏离这个形式比较大, 这也许是因为精确度不够造成的. 当$p \to 1$, 局域长度$\xi $会变得非常大, 如果想得到更精确的结果, 所需计算的样品长度也需要随之增大, 会非常耗时, 所以文献[9]没有做进一步计算.
为了进一步确认电缆网络模型的普适性类别, Zhang和Sheng^[9]计算了$\xi (M)/M$和$\xi /M$的关系曲线. 根据有限尺寸标度理论^[25], 假如电缆网络模型和无序紧束缚模型同属一个普适性类别, 则$\xi (M)/M$是以$\xi /M$为单一变量的函数, 和其他任何参数都无关. 计算结果显示, 当M分别取值M = 32, 64和128时, 改变p和$\theta $的值得到基本重合的三条曲线, 证明网络模型和紧束缚安德森模型同属于一个普适性类别^[9].
在另一项研究中, Zhang等^[10]在三维网络中实验观测到了安德森局域化, 其研究的三维网络见图3(a), 网络在z方向为AB层交替堆叠的结构, 相邻层之间重叠的节点直接用0.5 m单根电缆相连. A和B层的结构如图3(a)所示, 水平方向的直线代表单根0.5 m电缆, 垂直方向的直线代表两根长度分别为0.5和2 m电缆连接(如虚线框所示). 在该研究中, x和y方向分别有5个和6个节点, z方向共有ABABA五层, 所以样品尺寸为5 × 6 × 5. 第一层左下角的节点坐标标注为(x, y, z) = (1, 1, 1), 其他位置坐标依次类推. 首先, 他们数值计算并实验测量了该有序网络的透射频谱(见图3(b)左图), 信号输入点为(x, y, z) = (1, 4, 3), 输出点为(x, y, z) = (5, 3, 3), 这里计算中考虑进了真实电缆的损耗, 实验和模拟结果符合得很好. 从透射谱中可以看到一个41—60 MHz的带隙(通过能带计算, 将这个带隙更加精确地确定在了44—59 MHz). 在这个带隙中52 MHz的位置上有一个尖峰, 对应着表面态.
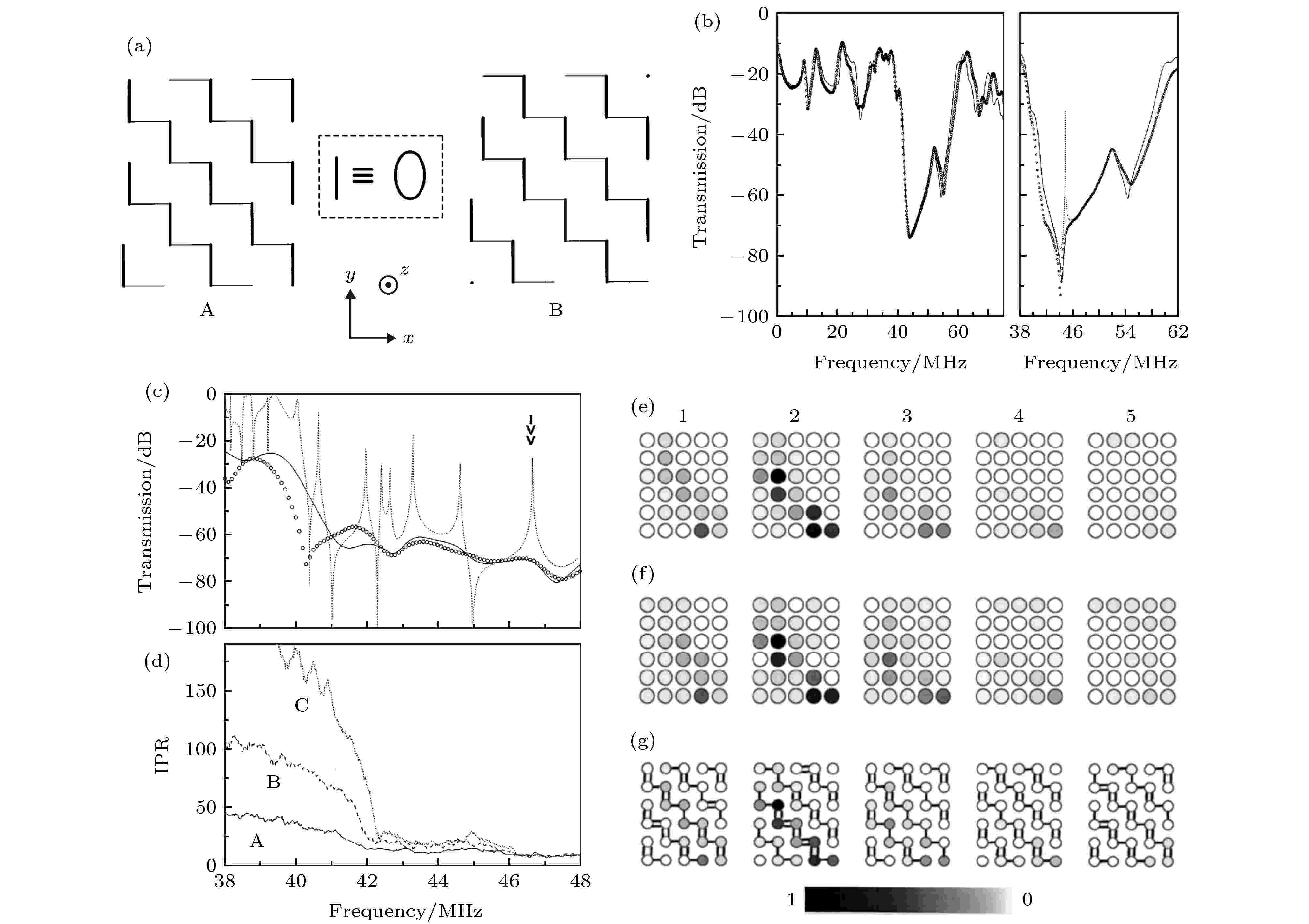图 3 在三维传输线网络中实验观测安德森局域态^[10]　(a) 样品结构示意图, 样品为AB层交替堆叠的结构; (b) 左图为(a)所示的样品测量得到的透射频谱, 圆点虚线和实线分别为实验测量和模拟结果; 右图为引入缺陷后得到的透射频谱, 圆点虚线和实线分别为实验和模拟结果, 细虚线为不考虑传输线损耗的模拟结果; (c) 引入随机性后的透射频谱, 圆点虚线和实线分别为实验和模拟结果, 细虚线为不考虑损耗的模拟结果; (d) 在不同的样品尺寸下计算IPR来评测态的延展程度; (e) 当频率为46.66 MHz时的散射波函数强度场图; (f), (g) 分别为实验测量和模拟得到的安德森局域态的强度场图, (g)图中还给出了该随机样品的电缆连接情况
Figure3. Experimental observation of Anderson localization in 3D transmission line network^[10]: (a) The structure of the sample (it is the AB alternatively stacked structure); (b) the left panel is the transmission spectrum measured for the sample in (a), the circles and solid curves are the measured and calculated results respectively; the right panel is the transmission spectrum after introducing a defect, the circles and solid curves are the measured and calculated results respectively, the dotted curve is the calculated result without dissipation; (c) the transmission spectrum after introducing randomness, where the circles and solid curves are the measured and calculated results, and the dotted curve is the calculated result without considering dissipation; (d) inverse participation ratios (IPRs) for different sample scales; (e) the field intensity pattern of the scattered wave function at 46.66 MHz; (f) and (g) are measured and calculated field intensity pattern of localized states respectively, (g) also shows the connections of the random network sample.

接下来, 他们将三维网络正中心((3, 3, 3)和(3, 4, 3)之间)的双电缆连接处的一根2 m的电缆换成了1.6 m, 以此引入了一个缺陷, 再重复透射频谱的测量. 如图3(b)右图所示, 点虚线和实线分别为实验和模拟结果. 除了这两条曲线, 还有一条细虚线为不考虑耗散存在的模拟结果, 可以见到一个尖峰在45 MHz附近显现出来, 正是对应了缺陷态的频率. 由此可见, 耗散的存在会抹平缺陷态和局域态在频谱上的尖峰, 从而导致其现象十分不明显. 为了解决此问题, 文献[26, 27]直接从局域态的中心位置点入射信号, 以此来激发起十分明显的局域波.
随后, 在原本有序网络的基础上引入随机性. 随机选取20%的单根电缆连接被替换为双电缆连接, 同时也随机选取20%的双电缆连接变为单根电缆连接. 相应的透射谱如图3(c)所示, 圆点虚线和实线分别为实验和有耗散的模拟结果, 细虚线为不考虑损耗的模拟结果. 为了避开表面态的影响, 这里选取了38—48 MHz的频率范围. 从细虚线频谱中可以看到, 随机性的引入导致了在带隙中产生了很多局域态. Zhang等^[10]选取了最右边位于46.66 MHz的局域态(双箭头所指), 画出了对应的模拟(无耗散)散射波函数强度场图(如图3(e)所示). 从左到右分别是1—5层, 在(2, 4, 2)处的波函数最强, 因此这一点被确定为观测安德森局域态的信号入射点. 从(2, 4, 2)点入射46.66 MHz的信号后, 所对应的实验以及考虑耗散的模拟场图分别如图3(f)和图3(g)所示, 图3(g)还给出了这一个组态下的电缆连接方式. 可以看到实验和模拟符合得很好, 而且安德森局域态也清晰可见.
还有一个问题是, 损耗衰减、缺陷态、局域态这三者都是指数型衰减, 如何区分它们? 首先, 在这个研究中的频率范围内, 吸收长度的量级大约在150 m左右, 远大于所观测到的局域态的尺寸, 所以可以排除耗散衰减的影响. 另一方面, 缺陷态是由于有序环境中的一个或若干缺陷产生的, 而局域态是由无序环境产生的, 相比起来, 局域态的有效干涉效应不像缺陷造成的那么强, 所以局域态会有更长的衰减长度. 为了展示这种区别, Zhang等^[10]在有序网络的第一层和第二层制造了几个缺陷以此产生了多重缺陷态. 统计所有节点的波强度, 计算得到其衰减长度为0.52, 另外又计算了图3(b)右图中的单一缺陷态的衰减长度为0.48. 而图3(f)和图3(g)中的局域态衰减长度为0.76, 远大于前面两个缺陷态. 另外Zhang等^[10]通过波函数的平均位置及其标准偏差计算了局域态在实空间的中心位置和体积大小. 图3(c)中46.66和43.29 MHz对应的局域态中心位置只相差了0.26, 比其平均线性尺寸2.1要小很多. 同时图3(c)中所有局域态的平均占据体积为9.2, 比该网络中平均一个缺陷占据的体积3.6大很多. 这些数据都证明了所观测到的局域态是一个单一的安德森局域态, 由无序环境中的各个缺陷多重散射形成.
最后, 计算了逆参与率(inverse participation ration, IPR)来评估一个态的空间延展程度^[10]:

${\rm{IPR}} = {\left( {\sum\nolimits_j {{{\left| {{\psi _j}} \right|}^2}} } \right)^2}\Big/\sum\nolimits_j {{{\left| {{\psi _j}} \right|}^4}} .$

在N个节点的网络中, 对于一个延展态, IPR和N是一个量级的, 并且随着样品尺寸增大而变大; 对于一个局域态, IPR远小于N, 并且和样品尺寸无关. 图3(d)给出了三种尺寸样品的IPR: $\left( {5 \times 6 \times 5} \right)$, $\left( {7 \times 8 \times 7} \right)$, $\left( {9 \times 10 \times 9} \right)$, 分别对应曲线A, B, C. 可以看到, 在带隙外, IPR很大并且和样品尺寸有关, 说明此范围的态是延展态; 在带隙内, IPR很小并且和样品尺寸无关, 这个范围的态已经被局域.

除了被用来研究安德森局域化, 传输线网络还经常被用来研究周期性和非周期性结构的传输特性、能带结构等, 这一节将介绍这方面的部分理论工作.
首先介绍一个关于分形网络的能带结构研究^[11]. 研究对象是Sierpinski分形^[28]网络, 通过在三角形内部细分出更小的三角形而成. 图4(a)所示是一个四阶Sierpinski分形网络, 三个顶点连着输入输出线. 图4(b)给出了两种测量透射率的方式: 单输出(上图)和双输出(下图). 图4(d)—(f)分别对应一阶、二阶、三阶Sierpinski网络的透射频谱, 上排的图对应单输出的情况, 下排的图对应双输出, 其中虚线和实线分别对应无损耗和有损耗的情况. 从这一系列频谱可以发现, 随着分形网络的阶数增加, 其透射谱和能带也呈现出更精细的分形结构. 以单透射为例, 无论是否考虑损耗, 一阶Sierpinski网络的透射率在200 MHz附近都有三个明显的尖峰; 增加到二阶以后, 中间的尖峰进一步分裂为三个尖峰; 增加到三阶以后, 这三个新尖峰中最中间的那个又分裂出三个尖峰, 依此类推. 为了说明透射频谱和能带的对应关系, 图4(c)给出了封闭的一阶Sierpinski分形网络对应的耦合矩阵的行列式绝对值. 同时我们已经论证过行列式绝对值为零的频率对应着闭合网络的本征频率. 对比图4(d)的透射频谱, 可以看到图4(c)对应本征频率的位置都是透射峰值, 从而验证了透射频谱和本征频率的对应关系.
图 4 Sierpinski分形传输线网络的透射谱和能带结构^[11]　(a) 四阶Sierpinski网络, 三个顶点连着输入输出线; (b) 有输入输出的一阶Sierpinski网络, 上图对应单输出, 下图对应双输出; (c) 求解封闭一阶Sierpinski网络的本征频率, 纵坐标为矩阵M的行列式绝对值, 横坐标为频率, 当行列式绝对值为零时, 对应着网络的本征频率; (d)—(f) 分别对应一阶、二阶、三阶Sierpinski网络的透射频谱, 上排的图对应单输出的情况, 下排的图对应双输出
Figure4. Transmission spectra and band structures of Sierpinski fractal transmission line networks^[11]: (a) A 4^th-generation Sierpinski network with three input/output cables on its three vertices; (b) the 1^st-generation Sierpinski network with input/output cables, the upper panel corresponds to the single-exist case while the lower one to the double-exist case; (c) the eigen-frequencies of an isolated first-generation Sierpinski network, the vertical axis corresponds to the absolute value of the determinant of matrix M, the horizontal axis corresponds to frequency. When the absolute value of determinant equals to zero, the corresponding frequency is an eigen-frequency; (d)?(f) correspond to the transmission spectra of the 1^st, 2^nd, 3^rd Sierpinski networks respectively, the upper rows correspond to the single exit channel case and the lower rows correspond to the double exit channel case.

接下来一个研究是关于基础构造单元对整体网络能带带隙的影响^[12]. 图5(a)给出了三种闭合环网络的透射频谱: 正三角形(实线)、正方形(细虚线)、正六边形(粗虚线). 注意到因为电缆网络可以随意变形, 所以这里所说的正多边形只是要求各个边长上的电缆长度相同, 其节点之间的物理距离和形成角度并不重要. 输入信号从闭合环多边形的一个顶点进入, 把所有其他顶点的透射强度加起来得到该透射频谱, 从图5可见只有三角形闭合环网络出现了明显的带隙结构. 接下来Cheung等^[12]计算了正方形晶格网络的能带(图5(b)左)和透射频谱(图5(b)右), 没有出现带隙; 然而在正方形晶格网络的一组对角线上加上和原本正方形边长相同的电缆(图5(c)), 能带和透射频谱上都能看到出现了带隙, 对应的频率位置和三角形闭合环的带隙频率位置一致. 前者(图5(b))的基础单元是正方形, 后者(图5(c))为正三角形, 这启示了我们整个网络的能带带隙似乎是和基础构造单元一致的. 为了验证这个猜想, Cheung等^[12]计算了各种网络结构的透射率, 其中包括周期性以及准周期性结构、二维以及三维(在这些结构中, 设定所使用的电缆长度全部相同). 计算结果表明, 在二维和三维的周期性结构中, 只有当基础构造单元包含有正三角形时, 全带隙才存在, 并且对应的频率正好和正三角形的带隙频率相同, 否则就不存在带隙; 在二维和三维的准周期性结构中, 类似的结论也成立. 不过当网络尺寸不是很大时, 不含有正三角形的网络也有较大的带隙; 而随着尺寸增大, 这个带隙中会出现局域态, 最后会让整个带隙消失; 而含有正三角形的准周期网络带隙就十分稳定. 这里要指出, 这些结论都是基于所用的电缆长度是相同的基础上. 最后Cheung等^[12]还指出, 这种存在于正三角结构中的反共振现象(闭合环内两列相向行波相消干涉)只有当闭合环上的节点数为奇数时才会出现. 这是因为, 如果闭合环上有偶数个节点数(为简单起见, 假设有2N个节点), 信号从一个节点1进入, 正好会在对面的节点N + 1处干涉加强. 这个物理图像很好地解释了为什么图5(a)三种多边形的透射频谱中只有三角形闭环存在带隙.
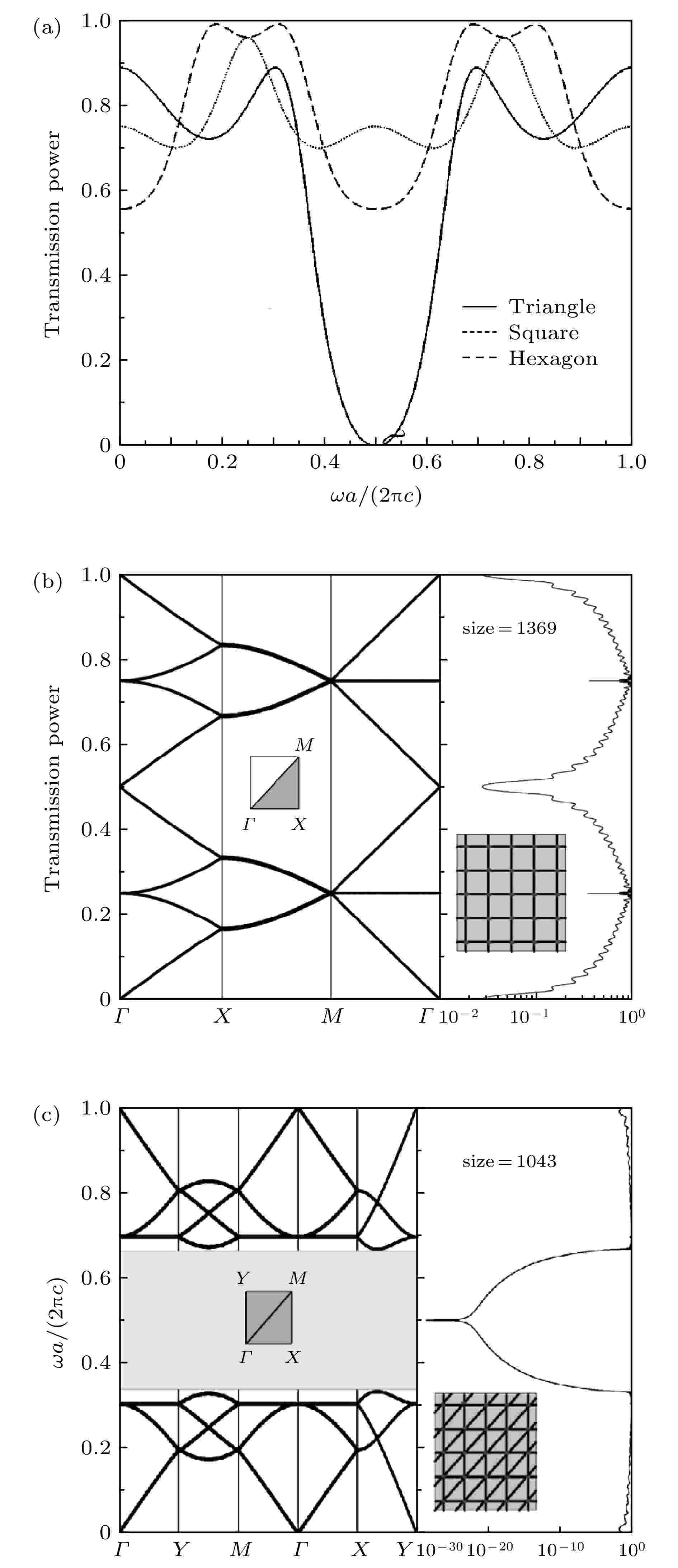图 5 不同基础构造单元对周期性及准周期性网络的能带带隙的影响^[12]　(a) 三角形(实线)、正方形(细虚线)、六边形(粗虚线)单环网络的透射频谱; (b) 正方形晶格网络的能带(左图)和透射频谱(右图); (c) 和(b)一样, 但是在(b)的方格网络中的对角线位置加入传输线(见右下角插图)
Figure5. Influence of the fundamental loop on the band gaps of the periodic and quasiperiodic networks^[12]: (a) The transmission spectra of the triangle (solid curve), square (dotted curve), hexagon (dash curve) loop networks; (b) the band structure (left panel) and the transmission spectrum (right panel) of the square lattice; (c) the same as (b), but for the lattice network which add cables on the diagonals of the square lattice (see the inset at the right lower corner).

近些年来拓扑材料成为了研究热点, 而传输线网络可灵活连接的特点为研究拓扑材料提供了很好的研究平台. 通过将电缆连接成具有特定拓扑性质的网络结构, 就可以直接在这个网络中观测到拓扑传输. 这一节将介绍一项这方面的研究^[16].
首先介绍该研究中所用的紧束缚模型^[16]. 图6(a)所示为具有轨道角动量涡旋的元原子构成的六角蜂巢晶格结构. 最简化的模型下面, 每个元原子可由三个离散化的节点表示(图6(b)), 这里要求: 节点上的波函数幅值相等, 彼此之间的相位差可取$2{\text{π}}/3$, 0, $ - 2{\text{π}}/3$, 分别对应m = 1, m = 0, m = –1三个轨道角动量. 在图6(b)中离散模型的基础上, Jiang等又通过图6(c)所示的模型来引入轨道角动量和波矢之间的耦合. 一个元原子中的三个节点被分别置放在三层中的同一个亚晶格A或者B上. 例如图中A₁, A₂, A₃为一个位于A亚晶格上的元原子的三个节点. 图6(c)中蓝线表示了层内节点之间的耦合, 黄线表示了不同层节点之间的耦合, 并且第一层被要求以同样的连接方式连回第三层. 随后, 用紧束缚模型可以在$K( {0, 4{\text{π}}/3\sqrt 3 a})$和 $K' \left( {0, - 4{\text{π}}/3\sqrt 3 a} \right)$点展开得到有效哈密顿量:
图 6 具有拓扑性质的传输线网络^[16]　(a) 由具有轨道角动量涡旋的元原子构成六角蜂巢晶格结构; (b) 将(a)中的元原子离散化为三个节点; (c) 在(b)的基础上引入轨道角动量和波矢之间的耦合, 这里只画出了晶格中的一个六边形; (d), (e) 计算(c)所示的传输线网络能带, 分别对应m = 0和m = 1; (f), (g)分别是m = 1情况下沿着x和y方向的投影能带, 红色和蓝色分别代表位于两个相对边界的边界态
Figure6. Transmission line network possessing topological properties^[16]: (a) A hexagonal ring formed by the meta-atoms which possess angular momentum; (b) discretizing the meta-atom into three nodes; (c) shows how to introduce the coupling between the angular momentum and wave vector to the model in (b). Here we only show a hexagon of the honeycomb lattice; (d), (e) calculated band structures of the model in (c) for the m = 0 and m = 1 sectors respectively; (f), (g) projected band structures along x and y directions for m = 1 modes, the red and blue curves represent the edge states at the opposite boundaries respectively.

$\begin{split}H\left( {{p}} \right) =\;& \frac{9}{2}{t_1}\left( {\left| m \right| - \frac{2}{3}} \right){{{\sigma}} _0} - \frac{3}{2}a{t_2}\left( {{p_x}{{{\sigma}} _y} + \tau {p_y}{{{\sigma}} _x}} \right) \\ &+ \frac{9}{2}{t_1}m\tau {{{\sigma}} _z},\\[-15pt]\end{split}$

其中$\tau = 1$和$\tau = - 1$分别对应 K点和K'点, ${{{\sigma}} _0}$是2 × 2单位矩阵, ${{{\sigma}} _x}$, ${{{\sigma}} _y}$, ${{{\sigma}} _z}$是泡利矩阵, ${{p}} = ({p_x}, {p_y})$是以 K点和K′点附近作展开的动量, a是相邻亚晶格的间距, ${t_1}$和${t_2}$分别对应层间和层内节点间的耦合强度. 从(16)式可以看到, 其第二项对应着狄拉克点, 而最后一项就是轨道角动量和波矢之间的耦合项, 称之为“角动量-轨道耦合”. 当$m = \pm 1$时, 这一耦合项类似量子自旋霍尔效应中的自旋-轨道耦合, 因而在单独一个角动量的子空间中, 存在非平庸的拓扑能带带隙; 当$m = 0$时, 耦合项消失, 两条能带在K (K')点简并为狄拉克点.
得到紧束缚模型后, Jiang等^[16]选择用电缆网络来实现该模型. 节点和节点之间的耦合可以直接用电缆连接两个节点来实现, 并且将第一层连回第三层的头尾连接也可以轻松实现. 虽然电缆网络和紧束缚模型并不完全等价, 但其能带的拓扑性质并不会改变. 研究中, 层内节点之间的耦合电缆长度被定为0.43 m, 不同层节点之间的耦合电缆长度为2.06 m. 图6(d)和图6(e)给出了计算得到的周期性传输线网络能带, 分别对应m = 0和m = 1. 可以看出, 当m = 0时, 两条能带在K点形成狄拉克点; 当m = 1时, 出现了拓扑非平庸带隙(灰色区域); m = –1的能带和m = 1形状相同, 但陈数符号相反. 这些结果都和紧束缚模型给出的定性结果是完全一致的. 图6(f)和图6(g)分别是m = 1情况下沿着x和y方向的投影能带, 红色和蓝色分别代表位于两个相对边界的边界态, 这些单向边界态也佐证了所对应能带的非平庸拓扑.
计算完周期性网络能带后, Jiang等^[16]又用有限尺寸网络来测试边界态的鲁棒性. 图7(a)为用来测试边界态鲁棒性的网络平面示意图, 三个红色六边形是缺陷, 其内部用于连接不同层的2.06 m电缆全部被移除(注意这里缺陷没有破坏角动量守恒), 信号从左侧输入, 右侧输出. 计算得到的m = 1透射频谱(紫线)如图7(b)所示, 和没有缺陷的同尺寸网络的透射谱(黑线)进行对比, 发现两个频谱在带隙外差别很大, 但在拓扑带隙内差别很小, 这说明该缺陷没有引起边界态的反方向散射, 单向边界态非常稳定. 接下来Jiang等在实验上观测了边界态. 实验中的样品尺寸如图7(c)所示, 右上角的红线是外加的散射缺陷, 在该点处的三层节点上都连上额外的三根2.06 m电缆, 所以没有破坏角动量的守恒性, m = 1的信号从箭头所示的点输入. 图7(d)为实验网络的照片, 红点和红线标出了样品的大致框架. 图7(e)和图7(f)分别是实验和模拟得到的m = 1边界态场图, 频率为34.5 MHz, 在拓扑带隙中. 由于传输线有损耗, 所以边界态沿着传播方向逐渐衰减. 当m = –1, 边界波会反方向传播, 由此实现了边界态波矢和角动量的锁定. 对于m = 0, 则没有观测到任何拓扑边界态.
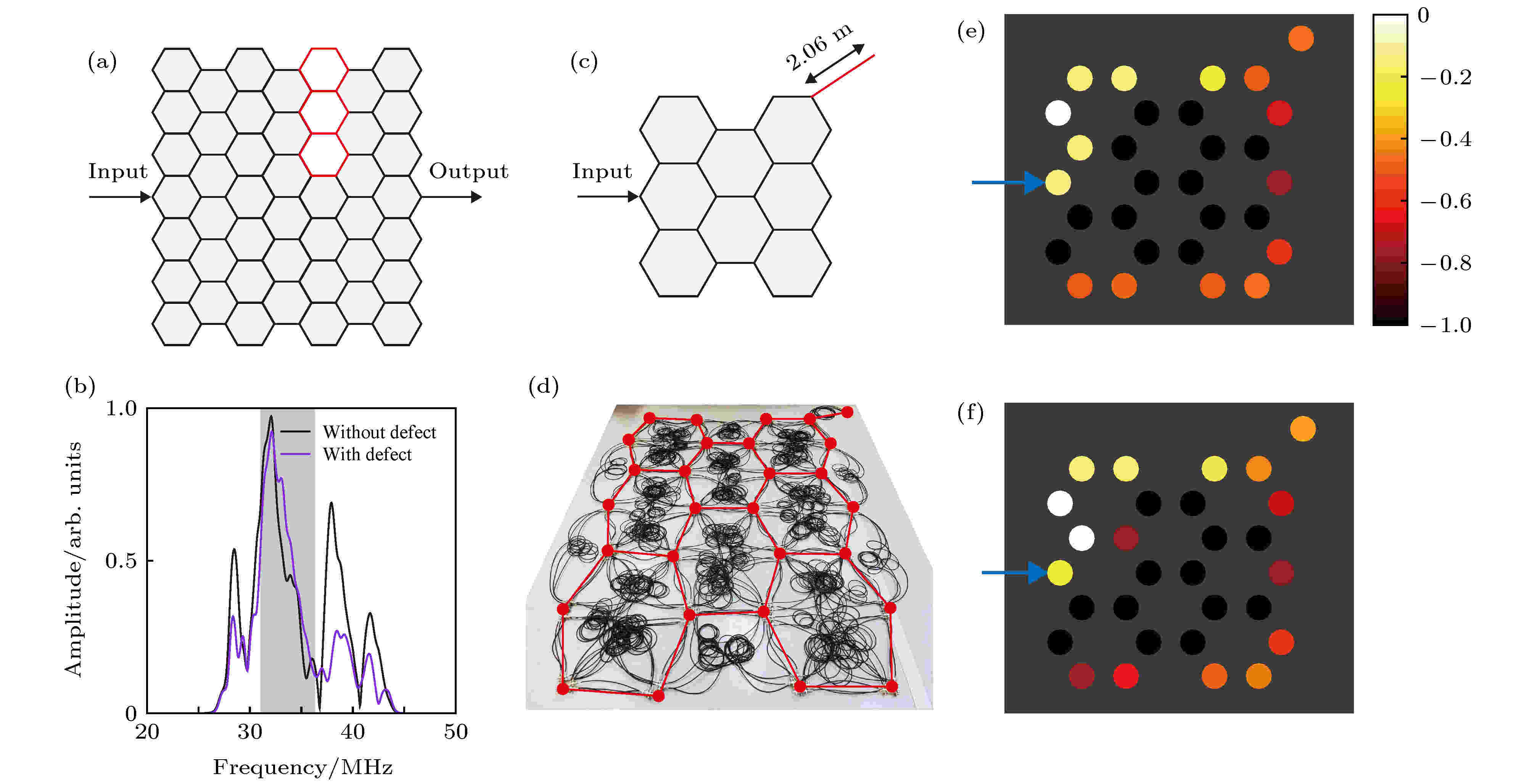图 7 拓扑边界态的鲁棒性和实验观测拓扑边界态^[16]　(a) 用来模拟测试边界态鲁棒性的样品示意图; (b) 对(a)中的样品进行模拟得到的m = 1透射频谱(紫线), 并且和没有缺陷的同尺寸样品(黑线)进行对比; (c) 用来实验观测边界态的样品示意图; (d) 实验样品的照片, 红点和红线标出了样品的大致框架; (e), (f) 分别是实验和模拟得到的m = 1边界态场图, 频率为34.5 MHz
Figure7. Robustness of topological edge states and its experimental observation^[16]: (a) The sample configuration to verify the robustness of edge states in simulations; (b) the simulated transmission spectrum of m = 1 modes (purple curve) for the sample in (a), compared with the one without defect (black curve); (c) the experimental configuration used to observe the edge states; (d) the photo of experimental sample, red dots and lines are used to highlight its underlying honeycomb structure; (e), (f) the experimental and simulated field intensity patterns of the edge state for m = 1 modes at 34.5 MHz.

因为实验中的样品尺寸很小, 周期性能带理论预测结果可能有偏差, 所以这里进一步引入局域陈数^[29,30]的概念来表征有限大系统的拓扑特性. 而局域陈数由投影算符的反对称乘积来定义^[29,30]:

$\nu (P)\!=\! 12{\text{π}}{\rm{i}}\sum\limits_{j \in A} {\sum\limits_{k \in B} {\sum\limits_{l \in C} {({P_{jk}}{P_{kl}}{P_{lj}}\!-\! {P_{jl}}{P_{lk}}{P_{kj}})} } } ,$

其中$P = \displaystyle\sum\nolimits_{f \leqslant {f_{\rm{c}}}} {\left| {{u_f}} \right\rangle \left\langle {{u_f}} \right|} $是将截止频率${f_{\rm{c}}}$以下的所有本征态$\left| {{u_f}} \right\rangle $全部累加起来得到的投影算符, 而${P_{ij}} = \left\langle {{x_i}} \right.\left| P \right.\left| {{x_j}} \right\rangle $为实空间波函数在位置x_i和x_j之间的空间关系. 计算局域陈数前, 先选取一块计算区域, 并且将其分成A, B, C三个子区域, 分别对应图8(a)所示的红、蓝、绿三个区域. 最后(17)式的计算结果标记的是计算区域中心处的局域陈数. 需要注意这个计算区域的尺寸需要大小合适, 如果选取得过大或过小都会导致计算结果变为零.
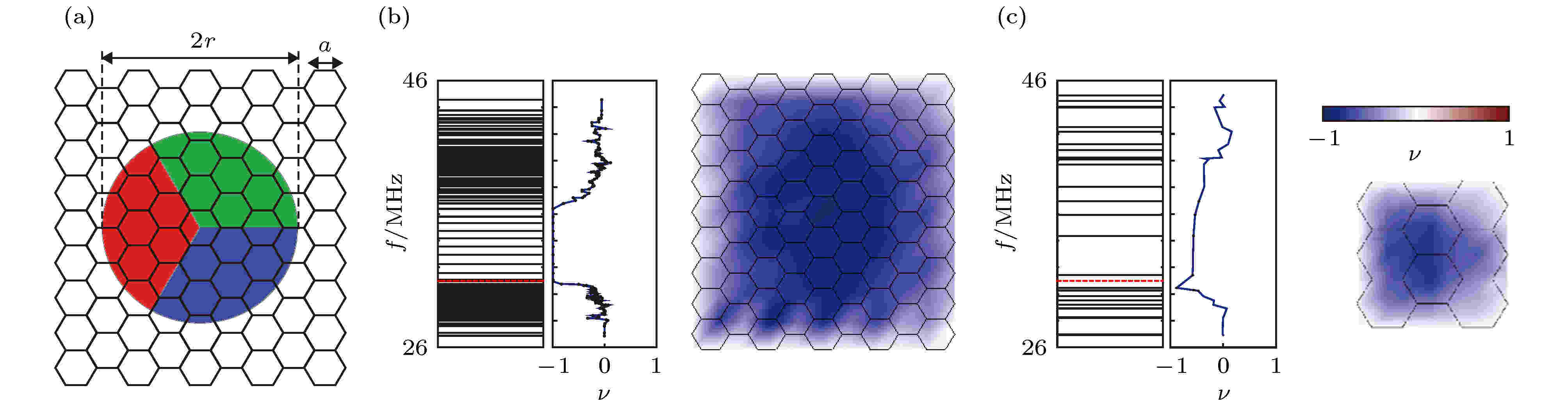图 8 有限样品中局域陈数的计算^[16]　(a) 计算局域陈数的方法; (b) 从左至右分别为能级图、局域陈数和截止频率的关系、局域陈数场图, 研究的样品尺寸如右图所示; (c) 和(b)图相同, 但所计算的样品尺寸和实验样品尺寸相同
Figure8. Calculation of local Chern number in the finite samples^[16]: (a) The computation domain for local Chern number calculations; (b) from left to right: energy level, the relation between local Chern number and cutoff frequency, local Chern number patterns. The size of sample can be seen in the right panel; (c) the same as (b), but the sample size equals to the size in experiments.

要将局域陈数的计算公式应用到传输线网络上, 要将网络看成由一堆一维波导, 而不是一堆节点. 通过节点上的已解波函数, 连接节点j和节点k的波导上每一点波函数可以通过(2)式求解. 同时有正交关系:

$\sum\limits_{{\text{所有电缆}}} {\int_0^{{l_{jk}}} {\psi (s;\;{f_m}) \cdot {\psi ^*}(s;\;{f_n}) \cdot {\rm{d}}s} } = {\delta _{mn}}.$

在数值计算中, 首先需要将网络中所有电缆离散化为相同长度$\Delta l$的小分段, 分段中点的波函数被近似当作该分段整体的波函数$\psi (s;\;{f_m})$. 在归一化之后, 波函数满足离散化的正交关系:

$\sum\limits_{{\text{所有分段}}} {\;\psi (s;\;{f_m}) \cdot \psi _{}^*(s;\;{f_n}) \cdot \Delta l} = {\delta _{mn}}.$

于是关联两个位置的投影算符${P_{ij}}$可以用各个分段上的波函数表示为

${P_{ij}} = \sum\limits_{f \leqslant {f_{\rm{c}}}} {\psi (i;\;f) \cdot {\psi ^*}(j;\;f) \cdot \Delta l} .$

将(20)式代入(17)式, 即可得到计算区域中心处的局域陈数.
接下来将局域陈数应用到该研究中的电缆网络上. 图8(b)左图所示为求解封闭$9 \times 9$样品的能级图, 可以看到中间有段频率范围能级较为稀疏, 对应的正是边界态. 图8(b)中图为局域陈数和截止频率的关系图, 这里选取了样品中心的局域陈数, 可以看到局域陈数在体态的频率范围接近0, 但在边界态的频率范围内接近–1, 正好和周期性能带的拓扑带隙相对应. 图8(b)右图为局域陈数的分布图, 通过平移计算区域(图8(a)中的有色区间)来扫描整个样品得到, 并且选取带隙边界31 MHz作为截止频率(能级图中红线位置), 可以看到局域陈数在样品内部分布比较均匀并且接近–1, 而在接近边界的位置会逐渐变为0. 图8(c)和图8(b)相同, 只不过将样品尺寸换成了实验中的尺寸3 × 3, 可以看到虽然样品尺寸非常小, 但其局域陈数依然接近–1, 所以实验中仍能观察到拓扑边界态.

本文详细介绍了该如何计算一个由传输线电缆构成的网络. 通过对比其网络方程和紧束缚模型方程发现, 其方程形式和零能紧束缚模型的非常相似, 因此网络节点可以类比为紧束缚模型中的原子, 而原子之间的耦合就通过电缆来实现. 因此电缆网络是实现一些紧束缚模型的理想物理平台.
我们列举了一部分电缆网络被应用于研究一维、二维、三维安德森局域化的研究, 其中一维和二维网络的理论模拟结果表明这两个维度的电缆网络在临界点附近的局域行为和紧束缚模型里的安德森局域是同属一类普适性类别的, 而在三维的网络中则实验观测到了光子晶体能带带隙中的安德森局域态. 除了被用来研究安德森局域化, 电缆网络也可以被用来研究晶体以及准晶的能带问题. 在一项Sierpinski分形网络的研究中发现, 准晶能带结构会随着网络阶数增加而产生更多精细的分形结构. 另一项对很多种周期性及准周期性网络的模拟研究则表明, 网络的能带带隙取决于其基础构造单元的带隙. 而随着拓扑领域的新兴, 电缆网络又可以被用来实现拓扑传输的模型. 在一项关于角动量依赖的拓扑传输研究中, 具有拓扑特性的电缆网络被实验搭建起来, 随后在其中测量到了传播方向和轨道角动量相互锁定的拓扑边界态, 并且计算了局域陈数来证明了其拓扑非平庸性质.
可以看到, 本文介绍的几项研究工作分别属于几个不同的领域, 但是都在传输线网络模型上得到了较好的理论以及实验验证, 可见其在数学、物理等基础研究上具有非常广泛的应用前景. 事实上, 传输线中的波动方程属于最普遍的一类标量波一维波动方程, 所以只要由符合这种波动方程的一维波导组成的物理体系, 基本上都可以由传输线网络来模拟, 例如其在量子图领域的应用正是基于量子电路具有相同的波动方程形式. 而对于紧束缚模型, 虽然传输线网络并不能严格与之对应, 但因为没有改变其拓扑结构, 所以仍然可以保持紧束缚模型中的一些性质, 比如局域性质、能带结构、拓扑性质等. 总而言之, 传输线网络在基础研究中还有更多的潜在应用等待我们发掘, 相信其今后会在更多的新兴研究领域中找到用武之地.