摘要:结合机器学习的湍流模型是流体力学领域的研究热点之一. 现有方法主要将实验/数值的数据用于重构或修正湍流涡黏性和雷诺应力, 鲜有针对转捩问题的研究. 本文利用深度残差网络(ResNet)重构了间歇因子与流场平均量间的映射函数, 并与Spallart-Allmaras (SA)模型耦合, 发展了一种类代数转捩模型. 结合高精度加权紧致非线性格式(WCNS-E6E5)在转捩平板和S809翼型算例中进行了验证, 并与四方程的SST-γ-Re_θ转捩模型进行了对比, 结果表明: 纯数据驱动的ResNet模型能够准确预测间歇场, 很大程度上改善了SA模型对自然转捩流动的模拟能力; 训练数据仅基于两个零压力梯度转捩平板, 模型能够应用于S809翼型不同迎角的情况, 预测的升阻力特性和摩擦系数分布接近SST-γ-Re_θ转捩模型的结果; 在此基础上, 相较SST-γ-Re_θ模型节省了超过30%的计算成本. 本研究显示了机器学习方法在转捩模型构建中的强大潜力.
关键词: 转捩流动/
神经网络/
间歇因子/
加权紧致非线性格式

English Abstract

全文HTML

--> --> -->

边界层转捩普遍存在于流体机械内部或其表面, 是经典物理学中亟待解决的挑战性问题. 在飞行器的运行过程中, 流体受到包括来流湍流度、物面粗糙度、马赫数等诸多因素的影响, 易由分层稳定流动向混沌湍流转变. 这一转捩过程同时伴随着壁面摩阻和传热特性的急剧变化^[1]. 因此, 对转捩流动进行快速准确的计算流体力学(computational fluid dynamics, CFD)模拟对飞行器性能和设计效率的提升有重要意义.
转捩预测可以采用求解全尺度湍流脉动的直接数值模拟(direct numerical simulation, DNS)或仅求解大尺度脉动的大涡模拟(large-eddy simulation, LES)方法, 但其计算量随雷诺数Re呈指数型增长(相当于Re^9/4), 当前计算机技术的发展仍旧难以满足其工程应用的计算需求^[2]. 结合湍流模型的雷诺平均数值模拟(Reynolds averaged Navier-Stokes, RANS)方法凭借其易用性及高效性, 在工程实践中仍占有举足轻重的地位^[3,4].
转捩流动中, 流场在同一空间位置会间歇性地呈现层流或湍流状态, 称为间歇现象. 若采用函数$I\left( {x, y, z, t} \right)$描述这一现象, 并定义层流时函数值为0, 湍流时为1, 那么间歇因子γ即为该函数的时间平均值^[5],

$\gamma \left( {x,y,z,t} \right) = \dfrac{1}{T}\int_0^T {I\left( {x,y,z,t} \right){\rm{d}}t} . $

考虑间歇性的转捩模式通过引入“间歇因子”定量描述湍流生成, 是目前工程转捩预测中最流行的一类方法. 模式通过显式方程或求解额外的输运方程得到所需的间歇因子. 早期, Dhawan等^[6]采用经验公式描述间歇因子的流向分布, 但得到的间歇因子仅取决于来流及物面条件, 不考虑流场结构, 仅适用于简单流动. Libby^[7]首先引入带有间歇因子的输运方程计算湍流, 其后许多研究工作聚焦于改善输运方程对多种流动例如自由剪切流^[8]、边界层^[9]转捩的预测效果. 然而, 这些模式往往通过非局部变量判断转捩起始, 难以在并行计算和非结构网格中得到应用. Menter等^[10-12]采用应变率为底的雷诺数代替动量厚度雷诺数Re_θ, 发展了完全基于局部变量的四方程SST-γ-Re_θ转捩模型. 其中无量纲的γ, Re_θ输运方程的守恒形式为

$\begin{split}\dfrac{{\partial \left( {\rho \gamma } \right)}}{{\partial t}} + \dfrac{{\partial \left( {\rho \gamma {u_j}} \right)}}{{\partial {x_j}}} =& \frac{1}{{{ {Re}} }}\dfrac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\sigma _\gamma }{\mu _t}} \right)\dfrac{{\partial \gamma }}{{\partial {x_j}}}} \right]\\&+ {P_\gamma } - {E_\gamma }, \end{split}$

$\begin{split}&\frac{{\partial \left( {\rho \tilde R{e_{\theta t}}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \tilde R{e_{\theta t}}{u_j}} \right)}}{{\partial {x_j}}}\\ =\;& \frac{1}{{{ {Re}} }}\frac{\partial }{{\partial {x_j}}}\left[ {{\sigma _{\theta t}}\left( {\mu + {\mu _t}} \right)\frac{{\partial \tilde R{e_{\theta t}}}}{{\partial {x_j}}}} \right] + {P_{\theta t}}, \end{split}$

其中, P_γ, E_γ分别为γ方程的生成项和耗散项, ${P_{\theta t}}$为$\tilde R{e_{\theta t}}$方程的源项. 上述输运方程仅用于获取间歇因子, 还需耦合SST湍流模型以模拟转捩过程. 国内外许多研究^[13-15]表明该模型对转捩流动有较好的预测能力. Bas等^[16,17]提出了一种基于当地平均量的代数转捩模型(或称为B-C模型), 提高了计算效率, 但不适用于湍流度在(0.5, 2.0)区间内的情况^[17]. 另外, 传统转捩模型受经验公式束缚, 对计算平台敏感, 往往不具备很好的通用性.
要解决上述问题, 关键在于找到流场当地平均量与间歇因子之间的映射关系, 而机器学习方法则提供了一种新的途径. He等^[18]于2015年提出残差网络(deep residual network, ResNet), 这种新的结构在前馈神经网络的基础上引入跨层连接, 解决了深层网络的训练问题, 受到广泛应用. ResNet凭借其复杂的网络结构, 具备从大量数据中描述复杂非线性映射的能力且易于训练, 已经在各领域取得了举世瞩目的成就.
有研究已经将神经网络这类机器学习技术应用于CFD领域. 许多研究者将机器学习方法应用于重构或修正涡黏系数或雷诺应力. Ling等^[19,20]构建了张量基神经网络模型(TBNN) 以预测雷诺应力各向异性张量, 改善了对管流角涡和波形壁流动分离的预测, 但其与求解器间的迭代收敛性还有待验证. Zhu等^[21]直接构建了湍流涡黏性的纯数据驱动“黑箱”代数模型, 但其对标SA湍流模型, 不具备对转捩的预测能力. Duraisamy等^[22,23]基于Ge等^[24]的k-ω-γ转捩模型, 利用神经网络(NN)和高斯过程(GP)重构了γ输运方程中的源项, 改善了模型对于T3系列平板算例的预测精度. 该研究证明了机器学习方法在转捩模型构建中的可行性, 但没有进一步探究模型对于新几何外形和来流条件的泛化能力.
与以往研究不同, 本文基于SST-γ-Re_θ模型的计算数据, 利用深度残差网络ResNet重构了当地平均量与间歇因子γ之间的纯数据驱动“黑箱”映射模型, 并与SA模型相耦合, 发展了一种数据驱动的转捩模型. 模型需要求解的微分方程数量仅为一, 相比于四方程的SST-γ-Re_θ模型具有更高的计算效率. 采用满足伽利略不变性的当地流场平均特征量作为输入特征, 便于与现代CFD求解器耦合, 同时保证良好的泛化性能.
在相同网格条件下, 高精度格式相比于传统二阶格式能够获得更准的气动力结果^[25,26]. 本文中将基于高阶精度的加权紧致非线性格式(weighted compact nonlinear scheme, WCNS)^[27,28]对RANS方程和模型方程进行数值离散.

2

-->

2.1.整体思路

本文结合深度残差网络技术与SA全湍流模型^[29], 参考基于局部变量的间歇转捩模型构造思路, 发展了一种数据驱动的转捩预测方法. 模型的构建过程可分为两个部分: 数据学习和耦合求解. 数据学习部分主要包括训练数据选择, 神经网络模型框架和参数优化. 在耦合求解部分, 首先将流场中间歇因子γ的初值设为1(即采用全湍流模型), 利用二阶格式快速得到初始收敛场; 接着将流场的平均特征量(q₁, q₂, …, q_n)代入神经网络模型得到γ的预测结果; 最后利用γ修正SA模型, 采用WCNS高精度格式计算收敛, 使其具有预期的转捩预测效果. 具体过程如图1所示.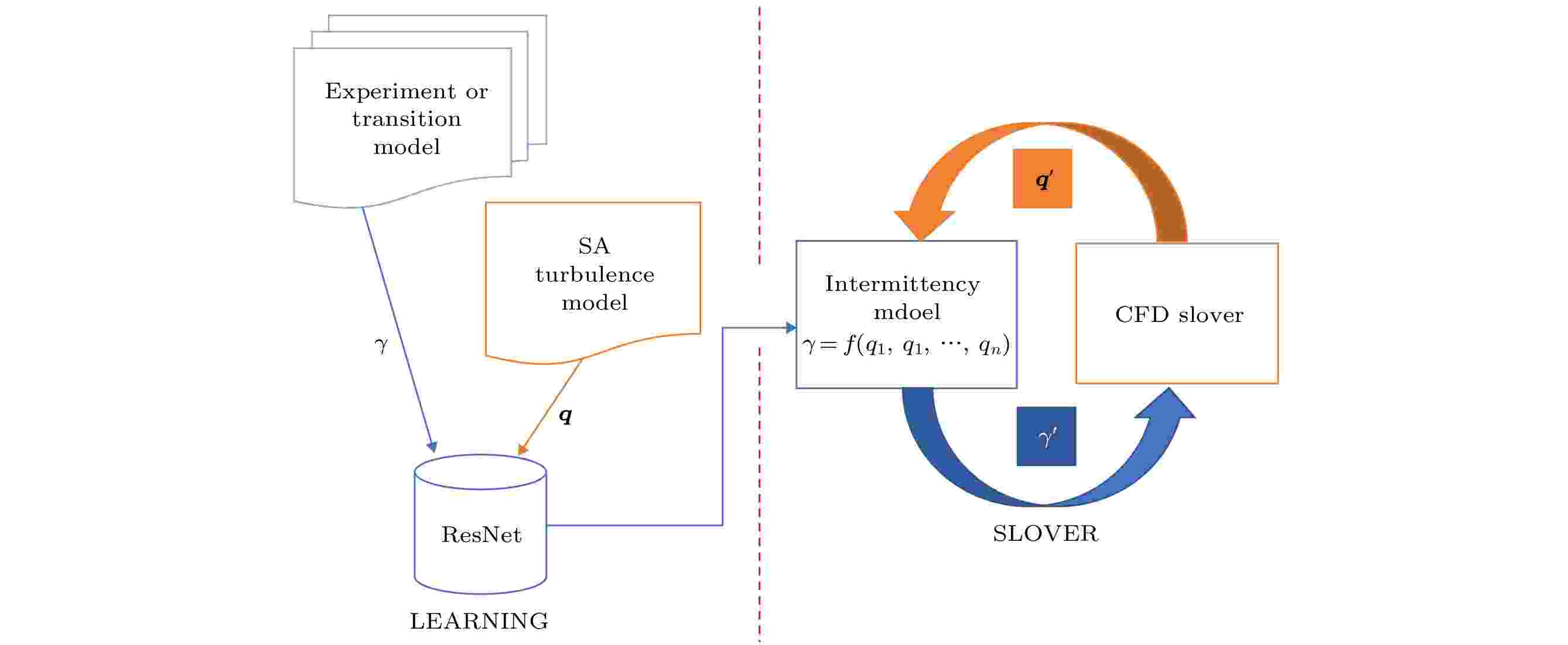
图 1 整体框架
Figure1. Overall framework

2 -->

2.2.训练数据集的构建

本文选择间歇因子γ作为残差网络的预测对象. 相较于直接预测雷诺应力或涡黏性, 这样做的好处在于避免神经网络这类模糊预测方法产生的结果直接作为最终结果, 降低极端异值和非物理解的影响, 结果更具可信度. 然而γ并非流场中实际存在的物理量, 无法从DNS, LES等高精度数据中直接获得其真实分布. 即便通过贝叶斯反演等方法利用高精度数据能够反算出一组间歇因子γ, 这种结果导向型的方法不能得到唯一确定的解^[30]. 消耗大量计算代价得到的γ场并不一定反映了真实的流动状态. Zhu等^[21]基于SA模型的计算数据训练NN模型, 取得了不错的效果. 鉴于此, 可采用更易获得的γ-Re_θ转捩模型得到的间歇因子γ分布作为真值, 同时训练数据集中还包含了二阶SA湍流模型的结果作为输入特征.
本文主要针对自由流湍流强度远小于1.0%的自然转捩. 传统转捩模型中, 函数或函数中的参数总是通过一系列零压力梯度平板算例标定得到. 在本工作中, 零压力梯度自然转捩平板(S&K和T3A-)扮演智能算法训练数据来源的角色.
2 -->

2.3.湍流模型

一方程SA模型控制方程为

$\frac{{D\widetilde \nu }}{{Dt}} = {P_\nu } \!-\! {D_\nu } \!+\! \frac{1}{\sigma }\left[ {\nabla \cdot \left( {\left( {\nu \!+\! \widetilde \nu } \right)\nabla \widetilde \nu } \right) \!+\! {C_{b2}}{{\left( {\nabla \widetilde \nu } \right)}^2}} \right], $

其中$\nu $为分子运动黏性系数, $\widetilde \nu $表示与湍流涡黏系数${\nu _t}$相关的修正涡黏系数, 具体关系由下式定义:

${\nu _t} = \widetilde \nu {f_{v1}},\;{f_{v1}} = \frac{{{\chi ^3}}}{{{\chi ^3} + C_{v1}^3}},\;\chi = \frac{{\widetilde \nu }}{\nu }.$

生成项${P_\nu }$与破坏项${D_\nu }$定义为

${P_\nu }{\rm{ = }}{C_{b1}}\widehat S\widetilde \nu,\;{D_\nu }{\rm{ = }}{C_{w1}}{f_w}{\left( {\frac{{\widetilde \nu }}{d}} \right)^2}, $

其中, d为最小壁面距离. $\widehat S$为涡量Ω的函数:

$\widehat S = \varOmega + \dfrac{{\widehat \nu }}{{{\kappa ^2}{d^2}}}{f_{v2}},\;{f_{v2}} = 1 - \dfrac{\chi }{{1 + \chi {f_{v1}}}}, $

$\begin{split}&{f_w} = g{\left( {\dfrac{{1 + C_{w3}^6}}{{{g^6} + C_{w3}^6}}} \right)^{\textstyle\frac{1}{6}}},\;g = r + {C_{w2}}\left( {{r^6} - r} \right),\;\\& \qquad \quad \qquad r = \min \left( {\dfrac{{\widetilde \nu }}{{\widehat S{\kappa ^2}{d^2}}},10} \right).\end{split}$

上述方程中, 常数取值如下:

${C_{b1}} = 0.1355,~{C_{b2}} = 0.622,~\sigma = \frac{2}{3},~\kappa = 0.41,$

${C_{w2}} = 0.3,~{C_{w3}} = 2,~{C_{v1}} = 7.1,~{C_{t3}} = 1.2,$

${C_{t4}} = 0.5,~{C_{w1}} = \frac{{{C_{b1}}}}{{{\kappa ^2}}} + \frac{{1 + {C_{b2}}}}{\sigma }.$

参考相关性间歇转捩模型的思想, 本文将间歇因子作用于湍流模型以抑制转捩前和转捩过程中的湍流生成, 使得原全湍流结果向转捩流场修正. 考虑间歇因子描述流场某点处间歇状态的客观性定义, 通过神经网络描述其潜在函数关系并与SA湍流模型结合具备合理性. 对于SA湍流模型的输运方程, 间歇因子用于抑制涡黏的生成项与破坏项:

$\frac{{D\widetilde \nu }}{{Dt}} \!=\! {\widetilde P_\nu } \!-\! {\widetilde D_\nu } \!+\! \frac{1}{\sigma }\left[ {\nabla \cdot \left( {\left( {\nu \!+\! \widetilde \nu } \right)\nabla \widetilde \nu } \right) \!+\! {C_{b2}}{{\left( {\nabla \widetilde \nu } \right)}^2}} \right]\!,$

${\widetilde P_\nu } = {\gamma _{{\rm{pre}}}} \cdot {P_\nu },$

${\widetilde D_\nu } = \min \left[ {\max \left( {{\gamma _{{\rm{pre}}}},\beta } \right),1.0} \right] \cdot {D_\nu },\;\beta {\rm{ = }}0.3,$

其中, P_ν和D_ν分别是原SA模型的生成项和破坏项, β为破坏项修正系数.
SA 模型不计算当地湍动能, 进而无法考虑湍流度的影响. Medida等^[31]将γ-Re_θ模型耦合至SA 模型时, 假定湍流度在整个流场中不改变. 本工作同样采取这种方式, 并将自由流湍流度作为ResNet的输入特征之一.
在上述修改的基础上, 为保证间歇因子与SA模型的兼容性, 需要对破坏项系数β和SA模型流场变量远场值ν_t∞做相应调整. 对于新的几何外形和来流条件, 训练完成的ResNet模型能够快速给出所需的γ值, 而不需要再借助其他转捩模型.
用于数值模拟的转捩平板网格见图2, 大小为324 × 108 (流向 × 法向), 平板上分布291网格单元. 如图3(a)所示, 在自然转捩情况下, 过大的ν_t∞会导致摩阻曲线提早过渡到湍流状态, 因此远场值最终设置为1.0 × 10^–8. 如图3(b)所示, 原全湍流结果(β = 1)在湍流区域较实验值整体偏低, 破坏项修正系数β的作用就在于控制湍流区域的摩阻系数涨幅, 本文取β = 0.3.
图 2 转捩平板计算网格
Figure2. Computing mesh for transition plate.

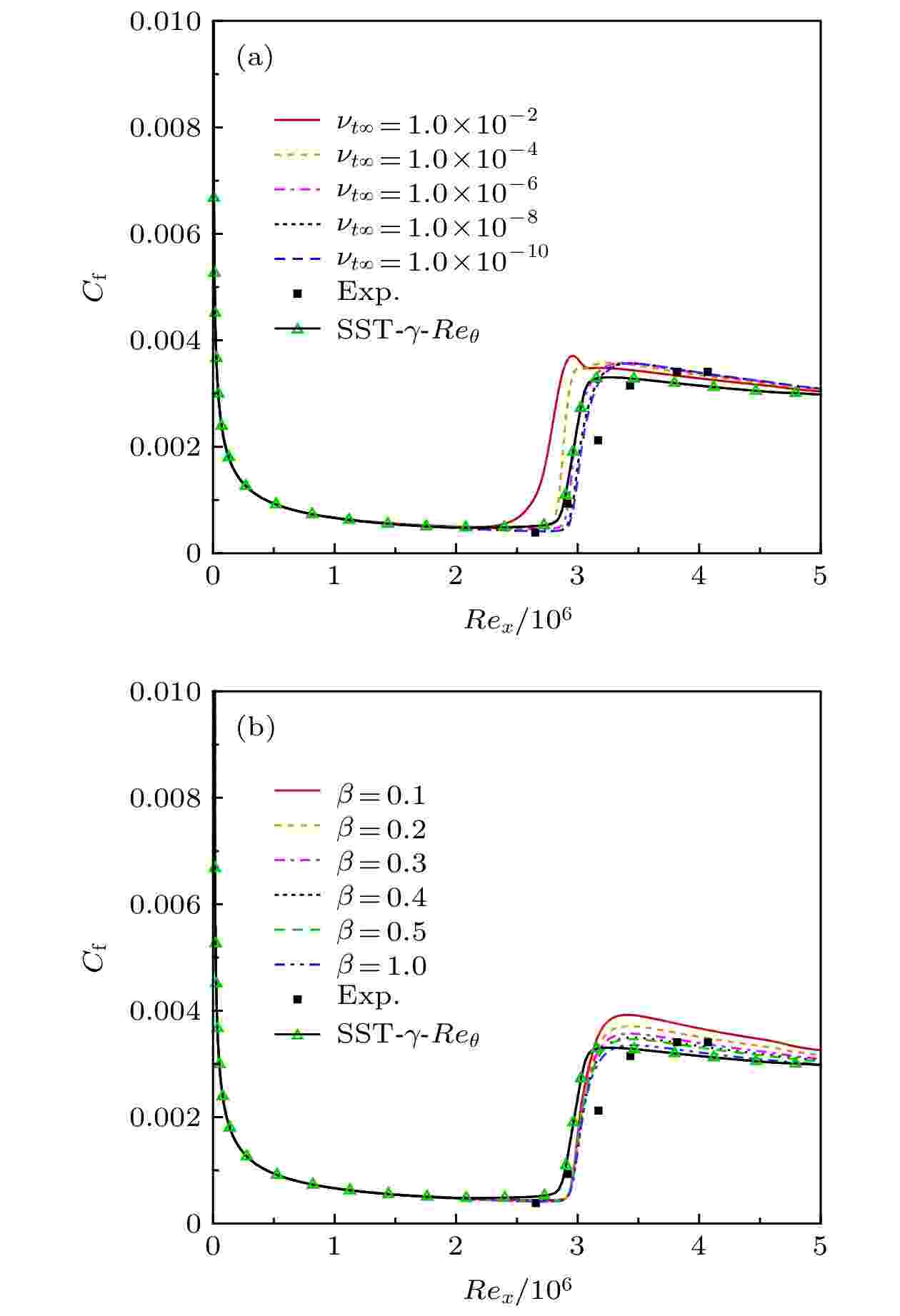图 3 模型参数对壁面摩阻的影响　(a) ν_t∞; (b) β
Figure3. The influence of model parameters on wall friction: (a) ν_t∞; (b) β.

上述过程通过引入间歇因子赋予SA模型预测转捩的能力. 其中的关键在于, 对于一个全新的几何外形和自由来流条件, 能否快速通过某种算法或模型给出足够准确的间歇因子预测场. 本节利用自由来流条件和局部无量纲特征量等信息, 试图建立一种具备理想泛化能力的间歇因子模型.
2

-->

3.1.模型选择

在转捩问题中, 流场某一空间位置的间歇状态与当地的平均变量间存在复杂的映射关系, 且这种关系是非线性的, 难以建立解析的表达式. 为了满足工程需求, 往往需要建立数学模型以近似描述这类映射.
传统间歇转捩模型的构建往往基于将转捩的起始与某个或某些特征量相关联, 最终也都证明模型具有良好的效果. 这些设计的关键特征与流场转捩行为的关联性直接影响到模型的准确程度和适用范围. Bas等^[16]就在此类工作上付出过努力, 他们构建的局部量Term₁比较了当地动量厚度Re_θ是否达到转捩的临界动量厚度Re_θc, 以判断转捩起始位置; Term₂控制边界层内的间歇因子生成; 最后, 通过指数函数生成间歇因子. 这种简单的代数模型在部分情况下能够达到接近γ-Re_θ模型的效果, 但对于湍流度在(0.5, 2.0)区间内的转捩问题并不适用. 不过该研究足以表明, 构建合适的局部特征对转捩预测起到关键作用.
由于转捩问题的复杂性和混沌性, 人工构建普适的相关特征量以构建模型绝非易事. 幸运的是, 当前高性能计算的发展使得神经网络模型的训练更加高效, 能够借助其强大的特征学习和表示能力构建模型. 具体来说, 神经网络的每一层都对上一层传递来的信号进行加工, 这些本与转捩不直接相关的初始特征经过多隐藏层的处理, 逐步转换为与转捩密切相关的特征量. 输入层和所有隐藏层可看成“特征学习”的过程, 而最后一层的输出层仅仅是以生成的特征量为输入的简单模型^[32], 最终完成间歇因子的预测. 这种多层激活函数嵌套的结构普遍存在于深层的网络结构之中. 这便是深度神经网络为什么适合于本研究的重要原因.
本工作希望能够利用已有高精度计算数据中的信息, 通过深层次的网络结构和辅助优化算法提取到与转捩密切相关的流场特征, 从而构建出当地特征量与流场间歇性之间的类代数映射模型, 以获得高精度和高效性并存的效果.
2 -->

3.2.残差神经网络

深度学习作为机器学习技术的典型代表, 能够挖掘数据集中潜藏的深层次非线性映射并建立模型, 实现判断和预测. 残差神经网络在一般神经网络的基础上引入跨层连接(skip connection), 使得误差梯度得以跨层传递, 是一种典型的深度学习算法. 为保证理论的完整性, 引入跨层连接的优势将在附录中展开说明. 基本网络结构可由一个输入层、若干隐藏层、一个输出层和跨层连接组成, 如图4所示.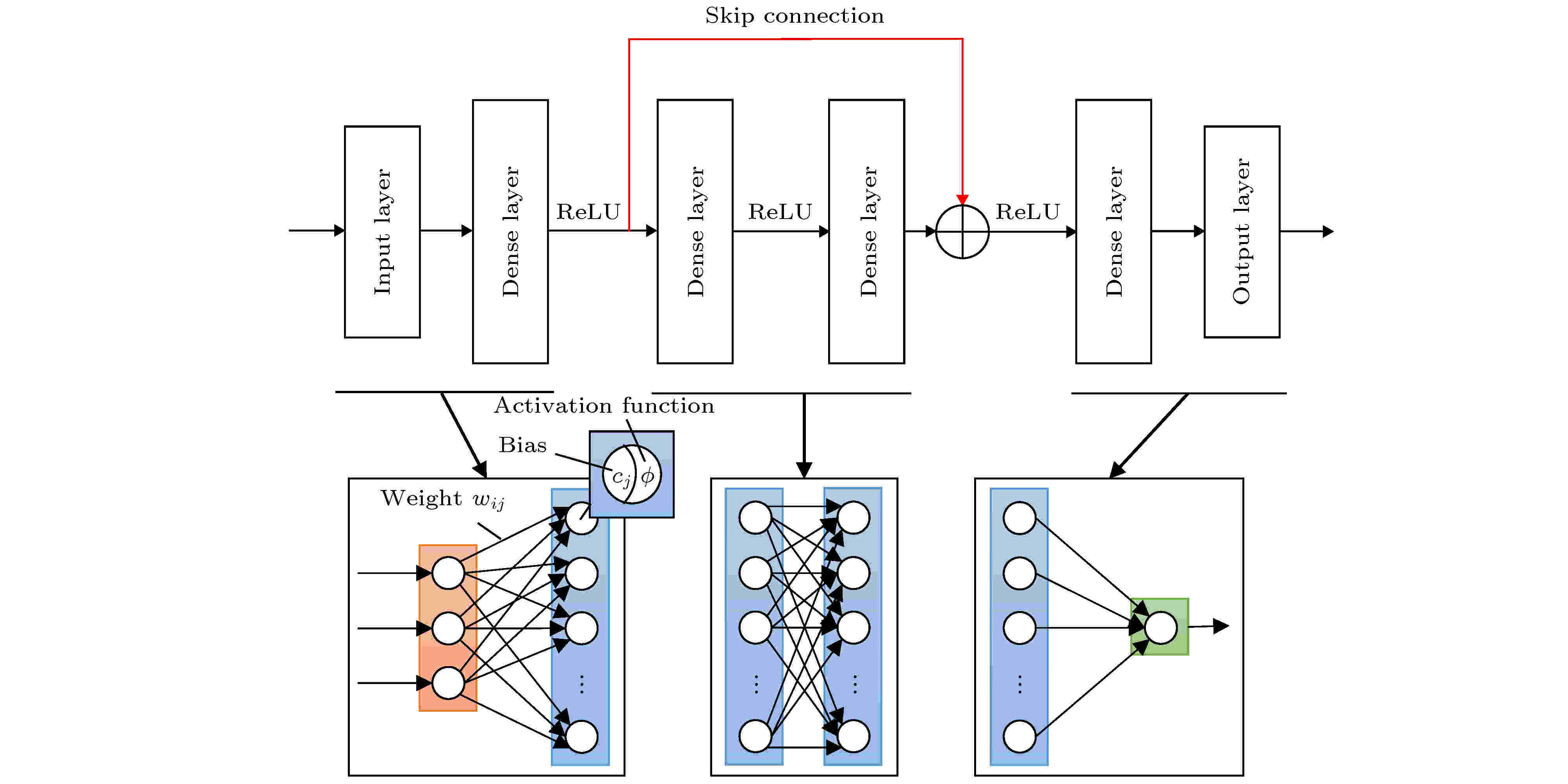
图 4 残差神经网络结构示意图
Figure4. Structure of residual neural network

输入层由一组代表流场不同属性的当地平均量q = (q₁, q₂, …, q_n)组成. 这些输入量经历带权重的连接到达下一隐藏层, 新的输入值在层中节点将与阈值比较, 然后通过非线性激活函数转换. 特征信息每经过一个隐藏层都会被变换到新的特征空间, 直到输出结果. 以图4所示的神经网络模型为例, 对于一个新的输入${x_i}$, 第一隐藏层的输出分量$z_j^{(1)}$可表示为

$z_j^{(1)} = {\phi ^{(1)}}\left( {\sum\limits_{i = 1}^3 {w_{ij}^{(1)}{x_i} - c_j^{(1)}} } \right), $

其中, 上标(m)表示第m个隐藏层, $\phi $为非线性激活函数, 本文采用ReLU函数; $w_{ij}^{}$为上层与本层间的连接权; $c_j^{}$为神经元节点处的阈值. 同样, 第二、三隐藏层的输出分量可分别写为

$z_j^{(2)} = {\phi ^{(2)}}\left( {\sum\limits_{i = 1}^{{m_1}} {w_{ij}^{(2)}z_j^{(1)} - c_j^{(2)}} } \right), $

$z_j^{(3)} = \sum\limits_{i = 1}^{{m_2}} {w_{ij}^{(3)}z_j^{(2)} - c_j^{(3)}}, $

其中${m_1}$, ${m_2}$分别表示第一、二隐藏层的神经元节点数. 可以看到, 第一隐藏层的输出通过跨层连接与第三隐藏层未经激活的输出相加, 合并的数据流经过激活函数后向下传递, 这种跨层连接实际上就是在层间增加一个恒等映射, 最终第四隐藏层的输出分量可表示为

$\begin{split} z_k^{(4)} =\;& {\phi ^{(4)}}\bigg[ \sum{j = 1}^{m_3} w_{jk}^{(4)}{\phi ^{(3)}} \\&\times \bigg( {z_j^{(1)} + \sum\limits_{i = 1}^{{m_2}} {w_{ij}^{(3)}z_i^{(2)}} - c_j^{(3)}} \bigg) - c_k^{(4)} \bigg]. \end{split}$

得益于上述多层次、非线性的激活变换, 网络得以具备描述输入特征与输出量间的深层次非线性映射的能力. 常用的非线性变换函数(或称激活函数)有Sigmoid, ReLU和TANH等, 具体形式如下.
Sigmoid函数定义为

${\rm{Sigmoid}} (x) = \dfrac{1}{{1 + {{\rm{e}}^{ - x}}}}, $

ReLU函数定义为

${\rm{ReLU}} \left( x \right) = \max \left( {0,x} \right), $

Tanh函数定义为

$\begin{split} {\rm{Tanh}} \left( x \right) ={}& \frac{{{{\rm{e}}^x} - {{\rm{e}}^{ - x}}}}{{{{\rm{e}}^x} + {{\rm{e}}^{ - x}}}} = 2 \cdot {\rm{Sigmoid}} \left( {2x} \right) - 1. \end{split}$

激活函数能够在网络中引入非线性变换, 且连续可导, 便于后续采用梯度下降等优化算法训练神经网络, 曲线如图5所示. 对于回归预测, 输出层往往不需添加非线性函数, 直接按照一定权值将特征矢量线性组合并输出结果.
图 5 激活函数曲线　(a) Sigmoid; (b) ReLU; (c) Tanh
Figure5. Activation function curves: (a) Sigmoid; (b) ReLU; (c) Tanh.

损失函数是直接反映模型精度的重要指标, 本文采用损失函数设置为

${\rm{Loss = }}\dfrac{1}{N}\sum\limits_{k = 1}^N {{{\left( {\overline {{\gamma _k}} - {\gamma _k}\left( {{{{q}}_i}} \right)} \right)}^2}}, $

其中, $\overline {{\gamma _k}} $表示训练集中对应的真实标签, ${\gamma _k}\left( {{{{q}}_i}} \right)$表示神经网络的输出结果, N为用于训练的数据点总数.
对于给定的训练数据集, 可以通过梯度下降法对网络节点的权重w_ij与阈值c_j进行优化:

$\begin{split}& w_{i,j}^{(l)} \!=\! w_{i,j}^{(l)} - f\left( {\frac{{\partial {\rm{Loss}}}}{{\partial w_{i,j}^{(l)}}}} \right), \\& c_j^{(l)} \!=\! c_j^{(l)} - f\left( {\frac{{\partial {\rm{Loss}}}}{{\partial c_j^{(l)}}}} \right), \end{split}$

其中f由不同优化算法决定, 这里采用Adam算法, 具体可参考文献[33]. 一旦确定了网络节点的最优参数, 模型的预测效果则完全取决于隐藏层、每层节点数、激活函数、权重与阈值等超参数, 而与训练数据的规模无关.
本研究的神经网络部分基于TensoFlow框架. 输入层由自由来流条件、当地流场平均量及其导数等特征构成, 输入特征量的详细描述列于表1. 此外, 经过反复的实验权衡计算成本与损失函数之间的平衡, 采用的网络结构由浅到深依次由6个全连接层、两个内含8个隐藏层的残差块和8个全连接层组成, 每个隐藏层有24个神经元节点, 激活函数为ReLU. 输出层为无激活的单一变量γ.

Feature	Sign	Feature	Sign
Density	$\rho $	Scalar function 3[19]	${\rm Tr}({ {{S} }^3})$
Nearest wall distance	${d_w}$	Scalar function 4[19]	${\rm Tr}({ {{\varOmega } }^2}{{S} })$
Turbulence intensity	Tu	Scalar function 5[19]	${\rm Tr}({ {{\varOmega } }^2}{ {{S} }^2})$
Kinematic viscosity	$\nu $	Normalized strain rate	${{\left\| {{S}} \right\|} / {\left( {\left\| {{S}} \right\|{\rm{ + }}\left\| {{\varOmega }} \right\|} \right)}}$
Eddy viscosity	${\nu _t}$	Vortex Reynolds number (strain rate)	${{\rho d_w^2 S} / \mu }$
Reciprocal of local velocity	$1/U$	Vortex Reynolds number (vorticity)	${{\rho d_w^2\Omega } / \mu }$
Scalar function 1[19]	${\rm Tr}({ {{S} }^2})$	Q criterion[34]	$\dfrac{ {\dfrac{1}{2}\left( { { {\left\| {{\varOmega } } \right\|}^2} - { {\left\| {{S} } \right\|}^2} } \right)} }{ {\dfrac{1}{2}\left( { { {\left\| {{\varOmega } } \right\|}^2} - { {\left\| {{S} } \right\|}^2} } \right) + { {\left\| {{S} } \right\|}^2} } }$
Scalar function 2[19]	${\rm Tr}({ {{\varOmega } }^2})$
Ratio of modified viscosity to kinematic viscosity (χ)	${{\widetilde \nu } / \nu }$	Dimensionless quantity similar to turbulent viscosity	${{{\nu _t}} / {\left( {U{d_w}} \right)}}$

表1作为神经网络输入的流场局部平均特征量
Table1.The local average flow features used as the inputs of neural network.

神经元和隐藏层数的增加伴随着过拟合的风险, 研究通过5次交叉验证确定超参数, 确保模型没有出现过拟合. 训练数据被随机地均分为5组, 其中一组作为验证集, 剩余的分组作为训练集, 5次验证的平均绝对误差列于表2. 输入特征采用当地无量纲量以保证泛化性. 为了降低各特征间的相关性, 降低输入冗余, 在网络训练前将输入数据进行了白化(whiting)处理, 使得其均值为0, 方差为1.

Fold	Training error	Validation error
1	0.011719	0.013654
2	0.012549	0.010681
3	0.015313	0.018738
4	0.012985	0.015888
5	0.015822	0.014451

表25次交叉验证结果
Table2.Results of fivefold cross validation.

计算基于自主研发的WCNS软件平台. WCNS格式于2000年由Deng等^[28]提出, 其优势在广泛的流动问题中得到证明. 本文采用的WCNS-E6E5格式具备良好的涡保持特性和很强的鲁棒性, 在各类工程流动问题中得到广泛应用. 其中, 王圣业等^[35]将WCNS-E6E5格式应用于三角翼的分离涡模拟中, 并和传统基于线性涡黏模型的分离涡模拟方法进行了对比, 证明了格式在分离湍流模拟的精细度方面更加优秀.
2

-->

4.1.T3系列平板

T3系列低速平板实验将用于测试上述数据驱动间歇因子模型对流场间歇性的预测能力并结合SA模型验证最终的预测效果. 实验包括S&K, T3A, T3A-和T3B, 通常用于标定转捩模型中的经验系数和经验关系式. 本文主要关注于低湍流度自然转捩实验S&K 和T3A-的模拟. 采用的计算网格见图1, 网格为324 × 108(流向 × 法向), 平板上分布291 网格单元. 为适应低速流动条件, 计算采用预处理技术^[36]. 设置的进口条件如表3.

Case	U/m·s–1	Re∞	Tu∞/%
S&K	50.1	3.4 × 106	0.179
T3A-	19.8	1.4 × 106	0.843

表3平板算例入口条件
Table3.The entry condition of plate cases.

湍流边界层具有更大的摩阻, 由此能够通过摩阻曲线判断边界层的转捩情况. 图6给出了壁面摩阻的对比结果, 可以发现SA-ResNet模型和SST-γ-Re_θ模型能够较好地预测自然转捩, 而SA模型未能预测出转捩, 且全湍流计算的壁面摩阻与实验值相差很大. BC模型能够预测到转捩现象, 但过早地预测了T3A-平板算例的转捩位置. 原因在于模型很大程度上依赖人为标定的经验公式, 这在一定范围内增加了模型的不确定度, 影响了适用性. 同为一方程的SA-ResNet模型在保证了求解效率的同时, 避免了上述问题.
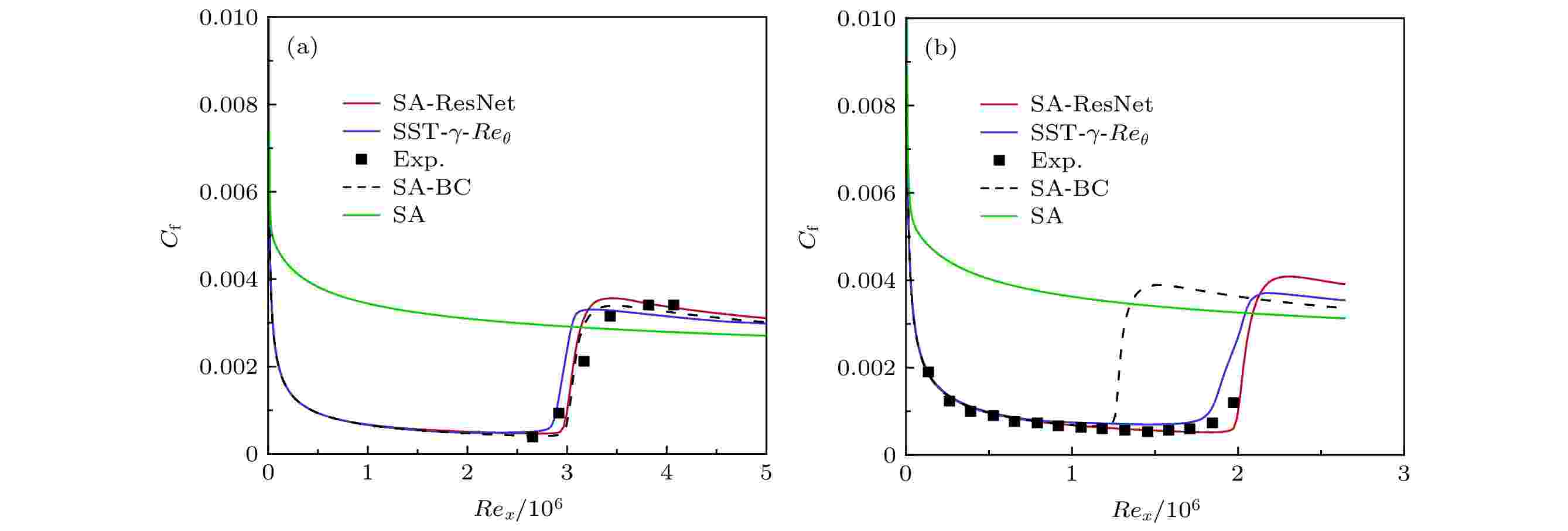图 6 转捩平板壁面摩阻曲线　(a) S&K; (b) T3A-
Figure6. Wall friction curve of transition plate cases: (a) S&K; (b) T3A-.

值得注意的是, ResNet模型完全基于SST-γ-Re_θ的计算数据进行学习, 但预测结果并不完全相同. 这是由于两者基于的全湍流模型存在原理上的差异, 再者SA-ResNet模型中的破坏项系数和流场变量初值对转捩位置、转捩区长度和湍流区的摩阻幅值存在些许影响, 这在第2节中进行过说明.
图7(a),(b)比较了SA-ResNet模型和SST-γ-Re_θ模型对于T3A-转捩平板间歇因子预测结果. 两模型结果的差异见图7(c). 可以看出, ResNet模型能够模拟出平板表面的层流边界层发展和转捩的过程, 模拟得到的边界层厚度和转捩位置与SST-γ-Re_θ模型基本一致. 在全湍流区上游壁面附近ResNet模型的预测结果出现不光滑的情况. 原因在于壁面附近网格较为密集, 同时层流与湍流的分界区域间歇因子急剧变化, 这种情况下, 神经网络这类模糊预测方法有时难以清晰地给出分界线. 但这并没有影响结果的正确性, 间歇因子正确地控制了流场中湍流的生成, 如图7(d). 这正是不直接以涡黏性或雷诺应力作为神经网络预测对象的优势所在.
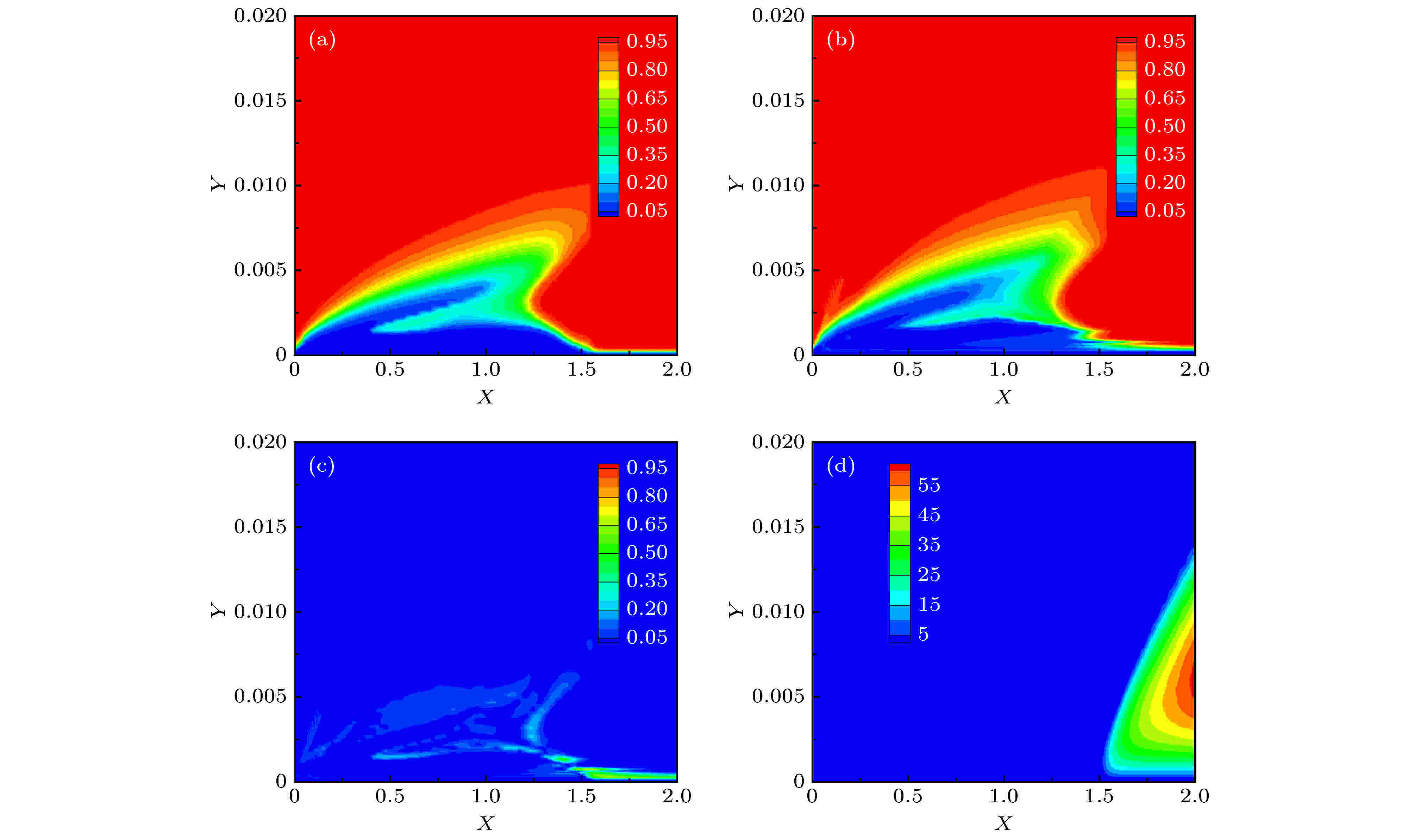图 7 T3A-平板间歇因子和湍流黏性分布　(a) SST-γ-Re_θ预测γ场; (b) SA-ResNet预测γ场; (c) SST-γ-Re_θ和SA-ResNet预测γ的差异; (d) SA-ResNet预测的湍流黏性
Figure7. Intermittency and turbulent viscosity distribution of T3A- case: (a) γ from SST-γ-Re_θ; (b) γ from SA-ResNet; (c) discrepancy of γ between SST-γ-Re_θ and SA-ResNet; (d) turbulent viscosity from SA-ResNet.

2 -->

4.2.S809翼型

S809翼型的亚声速定常绕流模拟将作为验证模型泛化性能的典型算例. 该翼型为厚度21%c的层流翼型, 专门为横轴风力涡轮机设计. 翼型的低速试验在戴尔福特科技大学(Delft University of Technology)的低湍流度风洞中进行^[37]. 计算网格如图8所示, 采用C 型拓扑结构, 共划分约6.6 万网格单元, 壁面首层网格距离达到1 × 10^–6c, 远场边界取120c, 进口马赫数为0.1, 雷诺数为2.0 × 10⁶, 翼型前缘湍流度设为0.2%.
图 8 S809翼型计算网格
Figure8. Computing mesh for S809 airfoil.

图9对比了S809翼型气动特性计算值和实验值的结果. 由图中可以看出, 结合了ResNet的SA模型与SST-γ-Re_θ模型在升阻力特性上都与实验值更加相符. 不考虑转捩的原SA模型预测的升力系数偏小, 且总是过多地预测了阻力. 结合ResNet的SA模型则很大程度上修正了这一情况.
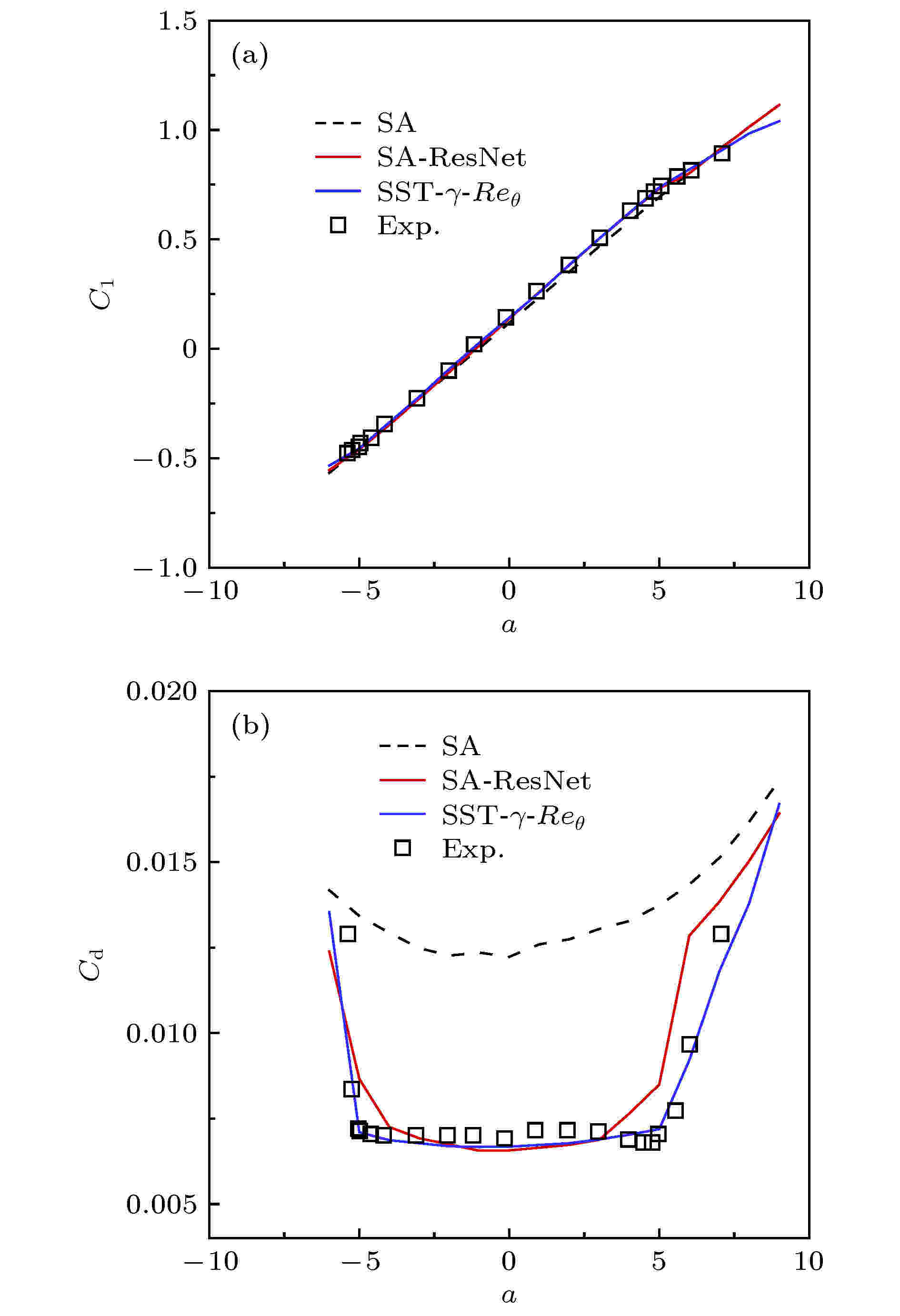图 9 S809翼型气动特性曲线　(a) C_l; (b) C_d
Figure9. Aerodynamic characteristics of the S809 airfoil: (a) C_l; (b) C_d.

由于训练集中不包含逆压梯度和大分离的例子, 这里仅讨论S809翼型迎风面的转捩位置情况. 转捩位置随迎角变化曲线见图10, 计算中的自然转捩位置取摩阻最小值点, 分离转捩的位置取摩阻由负值变正值时摩阻为零点. 由图中可以看出, 在0°—3°范围内SA-ResNet模型的转捩位置较实验略微靠前, 其他迎角下计算值与实验值符合较好.
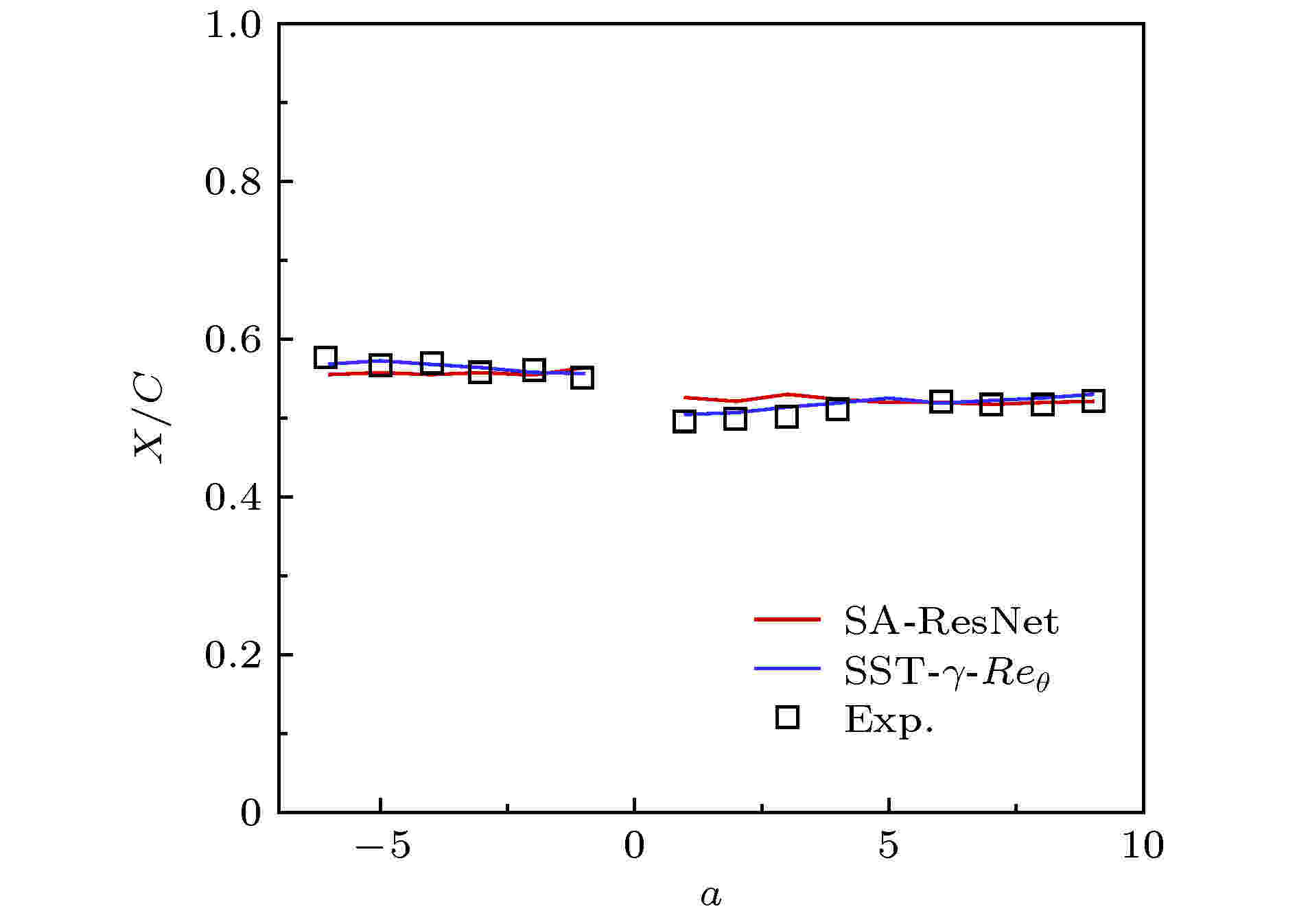图 10 S809翼型迎风面转捩位置随迎角变化曲线
Figure10. S809 airfoil transition position changes with the angle of attack.

图11给出了不同迎角下翼型表面的摩阻系数分布, 由图可以看出SA模型在1°, –6°和9°迎角下都未能预测出转捩. 而SA-ResNet模型与SST-γ-Re_θ转捩模型的结果十分贴近. 在1°迎角下, 翼型上下翼面分别在0.550和0.526附近发生分离转捩. 上翼面转捩位置随迎角增大不断前移, 在9°迎角时转捩位置到达0.01附近, 壁面摩阻沿流动方向不断下降, 流动再度层流化. 下翼面转捩位置随迎角不断向后缘移动.
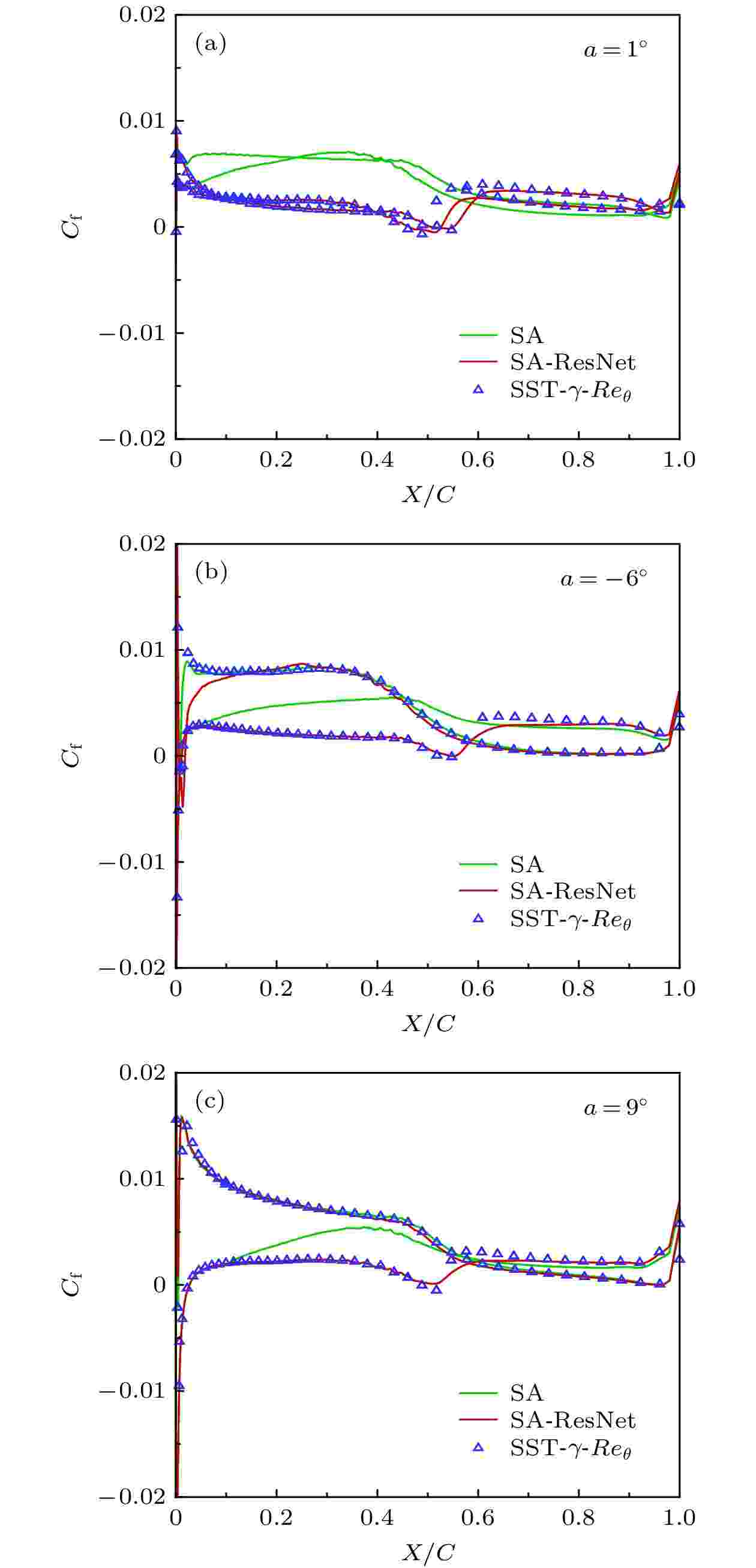图 11 S809翼型不同迎角下的摩阻系数曲线
Figure11. Friction coefficient of S809 airfoil at different angles of attack.

上述结果验证了SA-ResNet模型的转捩预测能力. 在此基础上, 模型的另一优势在于求解效率. 相较于四方程SST-γ-Re_θ转捩模型, SA-ResNet模型通过代数“黑箱”模型给出间歇因子分布, 不需引入额外的微分方程, 降低了计算耗时. 效率提升在大网格量的算例上更为明显. 表4列出了S&K、T3A-转捩平板和S809翼型3°迎角下的计算时间. 对于S&K平板算例, SA-ResNet模型的计算耗时为SST-γ-Re_θ转捩模型的85.6%, 然而在网格量更大的S809翼型上, 前者所需CPU时间仅为后者的67.2%. Wang等^[38]结合了BC代数转捩模型和WALE子网格模型对三维圆柱绕流问题进行了模拟, 结果发现每次迭代所需CPU时间不到SST-γ-Re_θ转捩模型的30%. 这表明在流动拓展到三维后, 代数转捩模型带来的效率优势十分可观.

ComputingTime	SA	SA-ResNet	SST-γ-Reθ
S&K	1.0	1.11	1.30
T3A-	1.0	1.33	1.49
S809 (α = 3°)	1.0	1.20	1.78

表4模型计算时间对比(残差收敛至O(10^–4))
Table4.Comparison of transition model’s compu-ting time.

本文基于WCNS-E6 E5格式, 结合深度残差神经网络方法和SA湍流模型, 参考基于当地流场变量的相关性间歇模型的构造思路, 重构了间歇因子映射模型, 发展了一种基于数据驱动的SA-ResNet高精度转捩模型. 对S&K、T3A-转捩平板试验和S809翼型不同迎角下的亚声速定常绕流进行了模拟, 并与SST-γ-Re_θ转捩模型计算值和实验值进行了对比.
转捩平板算例表明, 深度残差网络方法能够通过计算数据描述流场平均量与间歇因子间的复杂非线性映射; 得到的间歇因子能够较好地与SA模型兼容, 准确捕捉流场中的转捩现象. 在有限训练数据的情况下, SA-ResNet对于未包含于训练集的S809翼型的不同迎角情况能够得出较为准确的预测. 这表明深度残差网络能够做到的并不仅仅是对数据进行简单的插值, 其具备探索流场变量与转捩过程间复杂关系的强大潜力.
在S809翼型亚声速定常绕流的模拟中, SA-ResNet的性能接近SST-γ-Re_θ, 但收敛到同一精度时节省了超过30%的计算成本. 下一步工作在于向多种转捩机理的流动和不同来源的计算数据拓展, 强化模型的工程应用能力.

一般而言, 更多的神经元单元和隐藏层能够提升网络性能同时加速训练收敛. 然而, 网络增加到一定层数后, 在利用反向传播算法训练网络的过程中容易出现梯度消失/爆炸问题^[39,40], 导致训练无法收敛. 例如对于一般的全连接神经网络, 有

$ \small{{{z}}^{(l{\rm{ + }}1)}} = {\phi ^{(l)}} ( {{{{s}}^{(l)}}} ), \tag{A1}$

$ \small{{{s}}^{(l)}} = {{z}}_{}^{(l)}{{w}}_{}^{(l)} - {{c}}_{}^{(l)}, \tag{A2}$

其中${{w}}$为连接权, ${{c}}$为偏差, ${{z}}$为网络层的输出, ${{s}}$为激活函数输入值, $\phi $为激活函数. 因此, 在误差梯度反向传播过程中, 对权重有

$ \small\frac{{\partial {\rm{Loss}}}}{{\partial w_{i,j}^{(l)}}} = z_i^{(l)}\frac{{\partial {\rm{Loss}}}}{{\partial s_j^{(l)}}} = z_i^{(l)}\phi ' ( {s_j^{(l)}} )w_j^{(l + 1)} \cdot \frac{{\partial {\rm{Loss}}}}{{\partial s_{}^{(l + 1)}}}, \tag{A3}$

对阈值有

$ \small\frac{{\partial {\rm{Loss}}}}{{\partial c_j^{(l)}}} = - \frac{{\partial {\rm{Loss}}}}{{\partial s_j^{(l)}}} = - \phi ' ( {s_j^{(l)}} )w_j^{(l + 1)} \cdot \frac{{\partial {\rm{Loss}}}}{{\partial s_{}^{(l + 1)}}}, \tag{A4}$

对于多层网络:

$ \small\frac{{\partial {\rm{Loss}}}}{{\partial w_{i,j}^{(l)}}} = z_i^{(l)}\prod\limits_{l' = l}^{d - 1} {\phi ' ( {s_j^{(l')}} )w_j^{(l' + 1)}} \cdot \frac{{\partial {\rm{Loss}}}}{{\partial s_{}^{(d)}}}, \tag{A5}$

$ \small\frac{{\partial {\rm{Loss}}}}{{\partial c_{i,j}^{(l)}}} = - \prod\limits_{l' = l}^{d - 1} {\phi ' ( {s_j^{(l')}} )w_j^{(l' + 1)}} \cdot \frac{{\partial {\rm{Loss}}}}{{\partial s_{}^{(d)}}}. \tag{A6}$

误差梯度中存在激活函数导数和权重的连乘, 当网络层数增长到一定规模以后, 浅层隐藏层接收到的梯度由于一系列连乘而剧烈衰减/增长, 从而引发梯度消失或梯度爆炸问题. 这种问题的出现阻碍了训练的收敛, 甚至导致网络退化. 这种退化是由过多的隐藏层造成而非过拟合.
由于跨层连接的存在, 被连接包围的网络层(残差块)仅学习连接前后的残差映射(因此称为残差网络), 误差梯度能够越过残差块反向传播, 减少传播路径, 从而降低梯度消失或梯度爆炸的风险.