摘要: 本文提出了一种通过压缩驱动放置一个YIG小球的腔量子电动力学(QED)系统产生两体和三体纠缠的理论方案. 微波腔场与铁磁共振(FMR)模和静磁(MS)模的强耦合导致腔内光子、FMR模和MS模之间互相产生纠缠. 稳态情况下, 腔内光子、FMR模和MS模之间可以产生三体纠缠, 其三体纠缠的最小剩余共生纠缠度随非线性增益的增加而增大. 进一步研究发现, 该三体纠缠与MS模式的耗散系数有关, 最小剩余共生纠缠随MS模耗散系数的减小而增大. 同时还发现, 压缩驱动导致的三体纠缠对温度不敏感, 具有很好的鲁棒性. 结果表明磁-腔QED系统是研究宏观量子现象的一个强有力平台.
关键词: 压缩驱动 /
负值度 /
最小剩余共生纠缠 English Abstract Bipartite and tripartite entanglement caused by squeezed drive in magnetic-cavity quantum electrodynamics system Zhou Ying 1,2 ,Xie Shuang-Yuan 1 ,Xu Jing-Ping 1 1.Key Laboratory of Advanced Micro-Structured Materials, Ministry of Education, School of Physics Science and Engineering, Tongji University, Shanghai 200092, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11874287, 11774262, 61975154) and the Science and Technology Commission of Shanghai, China (Grant No. 18JC1410900)Received Date: 03 June 2020Accepted Date: 30 June 2020Available Online: 10 November 2020Published Online: 20 November 2020Abstract: Utilizing optical nonlinearity for generating the entanglement is still a most widely used approach due to its quality and simplicity. Here in this paper, we propose a theoretical scheme to generate bipartite and tripartite entanglement in a cavity quantum electrodynamics (QED) system with one Yttrium iron garnet (YIG) sphere by using a squeezed drive. In such a system, the parametric down-conversion process is used to generate the nonlinearity and further increase the coupling between cavity and YIG. Thus, the enhanced coupling between the microwave cavity photons and the ferromagnetic resonance (FMR) mode/magnetostatic (MS) mode results in bipartite entanglements. By using the mean field theory, we show that the bipartite entanglements strongly depend on the detuning of the cavity and magnon mode. When the driving field is tuned to be resonant with the FMR mode, but the MS mode is far off-resonant, the entanglement between photons and the FMR mode reaches its maximum. However, when the driving field is tuned to be resonant with the MS mode, but the FMR mode is detuned very well, the entanglement between photons and the MS mode reaches its maximum. We show that the dissipation of the FMR/MS mode affects the entanglement greatly, and the bipartite entanglement decreases as the dissipation rate of the FMR/MS mode increases. Under the steady-state approximation, we also show that the tripartite entanglement can be generated, and the minimum residual contangle increases with the enhancement of the nonlinear gain coefficient. With the nonlinearity induced by the parametric down conversion process, the interaction between the driving field and the magnetic-cavity QED system leads to the tripartite entanglement involving the cavity photons, FMR mode and the MS mode. Likewise, we show that the tripartite entanglement also strongly depends on the dissipation rate of MS mode, and the minimum residual contangle increases as the dissipation rate of the MS mode decreases. We also show that the squeezed field induced tripartite entanglement is insensitive to the temperature and has good robustness. Our results suggest that the magnetic-cavity QED system could provide a promising platform for studying the macroscopic quantum phenomena, and the squeezing field opens a new method of generating the entanglement.Keywords: squeezed drive /logarithmic negativity /minimum residual contangle 全文HTML --> --> --> 1.引 言 强耦合与超强耦合是腔量子电动力学(cavity quantum electrodynamics, 腔QED)的研究热点, 其可以在单粒子水平上研究光与粒子之间的相互作用[1 ] , 在量子信息科学、量子计量等方面具有广阔的应用前景[2 -4 ] . 基于强耦合与超强耦合的腔QED系统, 人们可以产生非经典光源[5 ,6 ] 、超灵敏探测和控制[7 ] 、超辐射现象[8 ,9 ] 以及光子阻塞效应[10 -12 ] 等. 近年来, 钇铁石榴石(yttrium iron garnets, YIG)材料因出色的亚铁磁性质而备受关注. YIG材料的居里温度为559 K, 因此, 其在低温[13 -15 ] 和室温[16 ] 下皆呈现出铁磁性. 同时, YIG材料不仅具有较高的自旋密度(约为2.1 × 1022 cm–3 ), 而且自旋之间存在较强的交换相互作用, 这使得集体自旋激发具有较低的耗散率(约为1 MHz). 已有研究表明, YIG小球中波矢为零的Kittel模[17 ] 可与微波腔光子实现强耦合[13 -16 ,18 ,19 ] 和超强耦合[20 ,21 ] , 从而导致腔磁极化子. 由于腔内光子与YIG小球之间的强耦合使不同载体之间的信息传递成为可能, 故而促发了一系列有趣的研究, 例如: 双稳态[22 ] 、腔自旋电子学[18 ,23 ] 、磁暗态模[24 ] 、以及磁诱导透明[25 ] 等. 同时, 可磁控的慢光[26 ] 以及Kittel模与单个超导比特(qubit)之间的耦合[27 ] 也正在深入研究.[28 ] 在放置一个YIG小球的谐振腔磁力机械系统中, 由磁场直接驱动YIG小球, 腔内光子和磁子通过磁偶极相互作用耦合, 磁子和声子则是通过磁致伸缩相互作用耦合. 在稳态情况下, 该系统实现了腔内光子、磁子和声子的三体纠缠. 同时, 他们还发现, 在腔中放置两个YIG小球时, 也可利用YIG小球内磁子和声子之间磁致伸缩提供的非线性作用, 实现两个YIG小球内磁子间的纠缠[29 ] . 之后, Zhang等[30 ] 提出, 磁晶各向异性产生的Kerr非线性作用可以替代YIG小球因磁致伸缩而产生的非线性效应. 当采用蓝失谐的微波场驱动磁-腔QED系统时, 可以实现两个相同YIG小球内磁子间的纠缠. Nair和Agarwal[31 ] 则提出, 即使磁-腔QED系统没有任何非线性, 采用压缩真空场[32 ,33 ] 注入的方式, 同样可以产生非线性效应, 使两个相同的YIG小球内磁子之间产生很大的纠缠.[19 ,34 ] 同时与腔内光子产生强耦合. 通过光参量放大过程压缩驱动腔模, 使腔内光子、FMR模和MS模之间互相产生纠缠. 在一定的参数范围内, 它们还可以产生三体纠缠. 进一步研究发现, 纠缠的强弱与光参量放大的非线性增益系数和MS模的耗散系数有关, 同时, 压缩驱动导致三体纠缠对温度不敏感, 具有很好的鲁棒性.2.理论模型 本文采用文献[19 ]的微波腔. 在微波腔中产生TE102 模式, 为了使YIG小球与微波腔场之间产生强耦合, 将YIG小球放置在矩形微波腔短边(y 方向)的中心处(如图1(a) 所示). 这是因为TE102 模式在这个位置具有较强的微波磁场, 且与微波腔短边平行. 同时, 外加一个x 方向的静磁场, 则该静磁场与YIG小球处的微波磁场垂直. 调节静磁场可使YIG小球中的磁子与微波腔的TE102 模式共振. YIG小球内大量自旋的集体运动表现为铁磁共振模(FMR模), 在FMR模共振频率附近还存在另一种集体自旋激发的模式, 即为静磁模(MS模)[19 ] . FMR模和MS模都是集体自旋激发的长波模式, 其中FMR模是均匀磁化的Kittel模[13 -16 ] , 而MS模则是非均匀磁化模, 其磁化情况与样本尺寸有关.图 1 (a) 磁-腔QED系统示意图. YIG小球位于腔中短边中心处, 该处微波腔的TE102 模式的磁场沿y 轴方向, 静磁场沿x 轴方向; (b) 利用Comsol模拟微波腔TE102 的网格划分示意图; (c) 微波腔TE102 模式的磁场方向和磁场强度Figure1. (a) Schematic diagram of a magnetic-cavity QED system. A YIG sphere is located at the center of one short edge in the cavity, where magnetic field of microwave cavity mode TE102 is along y -axis direction, and static magnetic field is along x -axis direction; (b) schematic diagram of grid of microwave cavity mode TE102 by Comsol simulation; (c) magnetic field direction and magnetic field intensity of the microwave cavity mode TE102 .${\omega _{\rm{c}}}$ 表示腔模的频率, $a({a^\dagger })$ 表示腔模中微波光子的湮灭(产生)算符, g 为朗德g 因子, ${\mu _{\rm{B}}}$ 为玻尔磁子, ${B^{({\rm{FMR}})}}$ 和${B^{({\rm{MS)}}}}$ 分别表示YIG小球所处位置FMR模和MS模的有效磁场. FMR模的集体自旋算符${{{S}}^{({\rm{FMR}})}} = (S_x^{({\rm{FMR}})}, S_y^{({\rm{FMR}})}, S_z^{{\rm{(FMR}})})$ , MS模的集体自旋算符${{{S}}^{({\rm{MS}})}} = (S_x^{({\rm{MS}})}, S_y^{({\rm{MS}})}, S_z^{({\rm{MS}})})$ , 其中$S_ \pm ^{({\rm{FMR}})} = S_x^{({\rm{FMR}})} \pm {\rm{i}}S_y^{({\rm{FMR}})}$ , $S_ \pm ^{({\rm{MS}})} = S_x^{({\rm{MS}})} \pm {\rm{i}}S_y^{({\rm{MS}})}$ , 为FMR模和MS模的升降算符. 利用Holstein-Primakoff变换[35 ] 可以将磁子的集体自旋算符用磁子湮灭(产生)算符表示, 即$S_z^{({\rm{FMR}})} = m_1^{{\dagger _{}}}{m_1} - {S^{{\rm{(FMR}})}}$ ,${S^{{\rm{(FMR)}}}}$ (${S^{{\rm{(MS)}}}}$ )为FMR(MS)模的总自旋数, ${m_1}\big( {m_1^\dagger }\big)$ 为FMR模的湮灭(产生)算符, ${m_2}\big( {m_2^\dagger } \big)$ 为MS模的湮灭(产生)算符. 对于低激发情况, ${{\big\langle {m_1^{{\dagger _{}}}{m_1}} \big\rangle }/{2{S^{({\rm{FMR}})}} \ll 1}}$ , ${{\big\langle {m_2^{{\dagger _{}}}{m_2}} \big\rangle }/{2{S^{({\rm{MS}})}} \ll 1}}$ , 可以得到$S_ + ^{({\rm{FMR}})} \approx {m_1}\sqrt {2{S^{({\rm{FMR}})}}} $ , $S_ - ^{({\rm{FMR}})} \approx m_1^{{\dagger _{}}}\sqrt {2{S^{({\rm{FMR}})}}} $ 以及$S_ + ^{({\rm{MS}})} \approx {m_2}\sqrt {2{S^{({\rm{MS}})}}} $ , $S_ - ^{({\rm{MS}})} \approx m_2^{{\dagger _{}}}\sqrt {2{S^{({\rm{MS}})}}} $ . 令${\omega _{{m_1}}} = g{\mu _{\rm{B}}}{B^{({\rm{FMR}})}}$ 和${\omega _{{m_2}}} = g{\mu _{\rm{B}}}{B^{({\rm{MS}})}}$ 分别表示FMR和MS模的角频率, ${g_1} = {g_{{\rm{FMR}}}}\sqrt {2{S^{({\rm{FMR}})}}}$ (${g_2} = {g_{{\rm{MS}}}} \sqrt {2{S^{({\rm{MS}})}}}$ )表示腔内光子与FMR(MS)模的耦合强度. 利用旋波近似, 哈密顿量(1 )式可以写成${\omega _0}$ 、拉比频率为${\varepsilon _{\rm{p}}}$ 的微波场沿x 方向入射. 另一束角频率为$2{\omega _0}$ 的泵浦场沿y 方向驱动一块二阶非线性晶体, 利用二阶非线性过程产生压缩的腔模, 其光参量放大的非线性增益系数为$\varOmega $ . 此时, 系统的总哈密顿量可写成$a\left( {{a^\dagger }} \right)$ , ${m_1}({m_1^\dagger } )$ 和${m_2} ( {m_2^\dagger } )$ 满足$\left[ {O, {O^\dagger }} \right] = 1$ , $O = a, {m_1}, {m_2}$ . 对微波场频率${\omega _0}$ 作旋转坐标变换, 系统的哈密顿量可简化为${\varDelta _{\rm{c}}} \!=\! {\omega _{\rm{c}}} \!-\! {\omega _0}$ 为腔模的失谐量, ${\varDelta _{{m_1}}} \!=\! {\omega _{{m_1}}} \!-\! {\omega _0}$ 为FMR模的失谐量, ${\varDelta _{{m_2}}} = {\omega _{{m_2}}} - {\omega _0}$ 为MS模的失谐量.${\kappa _a}, \; {\kappa _1}$ 和${\kappa _2}$ 分别为微波腔、FMR模和MS模的损耗, ${a^{{\rm{in}}}}$ , $m_1^{{\rm{in}}}$ 和$m_2^{{\rm{in}}}$ 则表示输入的热噪声, 其平均值为零, 并且具有如下关系[36 ] :${N_l}\left( {{\omega _l}} \right) = {\left[ {\exp \left( {\hbar {\omega _l}/{k_{\rm{B}}}T} \right) - 1} \right]^{ - 1}}$ $\left( {l = a, {m_1}, {m_2}} \right)$ 分别代表平衡态情况下腔内平均热光子数、YIG小球中FMR模的平均热磁子数以及MS模的平均热磁子数.5 )式—(7 )式, 即将算符写成$O = \langle O\rangle + {\rm{\delta }}O$ $\left( {O = a, {m_1}, {m_2}} \right)$ , 可以得到算符期望值的方程组:$P = {\varDelta _{\rm{c}}} - \dfrac{{g_1^2}}{{{\varDelta _{{m_1}}} + {\rm{i}}{\kappa _1}}} - \dfrac{{g_2^2}}{{{\varDelta _{{m_2}}} + {\rm{i}}{\kappa _2}}} + {\rm{i}}{\kappa _a}$ . 由此可求得系统的平均光子数、FMR模的平均磁子数和MS模的平均磁子数.[19 ] , ${\omega _{\rm{c}}}/2{\text{π}} = 10.306\;{\rm{ GHz}}$ , ${\kappa _a}/2{\text{π}} = 2.4\;{\rm{ MHz}}$ , ${\kappa _1}/2{\text{π}} = 1.3\;{\rm{ MHz}}$ , ${\kappa _2}/2{\text{π}} \!=\! 3.3\;{\rm{ MHz}}$ , ${g_1}/2{\text{π}} \!=\! 7.5\;{\rm{ MHz}}$ , ${g_2}/2{\text{π}} \!=\! 8.3\;{\rm{ MHz}}$ , ${\omega _{{m_1}}}/2{\text{π}} = 10.306\;{\rm{ GHz}}$ , ${\omega _{{m_2}}}/2{\text{π}} = 10.265\;{\rm{ GHz}}$ . 其中 $g_1^2 \gg {\kappa _a}{\kappa _1}$ , $g_2^2 \gg {\kappa _a}{\kappa _2}$ , 表明腔内光子与FMR模和MS模之间的耦合为强耦合. 对磁-腔QED系统注入一束拉比频率${\varepsilon _{\rm{p}}} = \gamma $ $(\gamma /2{\text{π}} = $ $1.0\;{\rm{MHz}})$ 的微波光场和另一束非线性增益$\varOmega = 1.5\gamma $ 的泵浦光, 系统的平均光子数、FMR模的平均磁子数和MS模的平均磁子数如图2 所示. 显然, 在${\varDelta _{\rm{c}}} \approx 0$ , ${\varDelta _{{m_1}}} \approx 20\gamma $ 附近, 微波腔内平均光子数、FMR模和MS模的平均磁子数出现极大值, 其物理原因可以通过分析(14 )式的极值点获得. 取$P = 0$ 且忽略所有耗散项, 可以得到(14 )式的极值点位于${\varDelta _{\rm{c}}} = 0$ , 且${{g_1^2}}/{{{\varDelta _{{m_1}}}}} = - {{g_2^2}}/{{{\varDelta _{{m_2}}}}}$ . 当${g_1} = {g_2}$ , ${\varDelta _{{m_1}}} = - {\varDelta _{{m_2}}}$ , 即${\varDelta _{{m_1}}} \approx ({{{\omega _{{m_1}}} - {\omega _{{m_2}}}}})/{2} \approx 20\gamma$ 时, 驱动场与磁-腔QED系统的耦合最强, 从而可以观察到较多的光子数和磁子数.图 2 (a) 平均光子数、(b) FMR模的平均磁子数和 (c) MS模的平均磁子数随失谐量${\varDelta _{{m_1}}}$ 和${\varDelta _{\rm{c}}}$ 的变化关系, 其中$\gamma /2{\rm{\pi = 1}}{\rm{.0\;MHz}}$ . 取${\varepsilon _{\rm{p}}} = \gamma $ , $\varOmega = 1.5\gamma $ , 其他参数已在正文中给出Figure2. (a) Average photon number, (b) FMR mode average magnon number, and (c) MS mode average magnon number versus detunings ${\varDelta _{{m_1}}}$ and${\varDelta _{\rm{c}}}$ , where, $\gamma /2\rm{\pi} = 1{\rm{.0\;MHz}}$ . We take${\varepsilon _{\rm{p}}} = \gamma $ , $\varOmega = 1.5\gamma $ . Other parameters are given in the text.3.磁-腔QED系统中的两体纠缠 这里研究该系统中的两体纠缠. 忽略二阶涨落项, 腔内光子和两个磁模的正交涨落项可由下式给出: ${\rm{\delta }}X = $ $\left( {{\rm{\delta }}a + {\rm{\delta }}{a^\dagger }} \right)/\sqrt 2 $ , ${\rm{\delta }}Y = $ ${\rm{i}}\left( {{\rm{\delta }}{a^\dagger } - {\rm{\delta }}a} \right)/\sqrt 2 $ , ${\rm{\delta }}{x_1} = \left( {{\rm{\delta }}{m_1} + {\rm{\delta }}m_1^\dagger } \right)/\sqrt 2 $ , ${\rm{\delta }}{y_1} = $ ${\rm{i}}\left( {{\rm{\delta }}m_1^\dagger \!-\! {\rm{\delta }}{m_1}} \right)/\sqrt 2$ , ${\rm{\delta }}{x_2} = $ $\left( {{\rm{\delta }}{m_2} + {\rm{\delta }}m_2^\dagger } \right)$ $/\sqrt 2 $ , ${\rm{\delta }}{y_2} = {\rm{i}}\left( {{\rm{\delta }}m_2^\dagger - {\rm{\delta }}{m_2}} \right)/\sqrt 2 $ . 因此, 描述系统正交涨落项的线性朗之万方程$\left( {{\rm{\delta }}X, {\rm{\delta }}Y, {\rm{\delta }}{x_1}} \right.\left. {, {\rm{\delta }}{y_1}, {\rm{\delta }}{x_2}, {\rm{\delta }}{y_2}} \right)$ 可以写成:${{f}}(t) \!\!=\!\! [{\rm \delta }X(t),{ \rm\delta }Y(t), {\rm\delta }{x}_{1}(t), {\rm\delta }{y}_{1}(t), {\rm\delta }{x}_{2}(t), {\rm\delta }{y}_{2}(t)]^{\rm{T}}, {{\eta }}(t)$ $\!=\! [ {\sqrt {2{\kappa _a}} {X^{{\rm{in}}}}(t)}$ , $\sqrt {2{\kappa _a}} {Y^{{\rm{in}}}}(t)$ , $\sqrt {2{\kappa _1}} x_1^{{\rm{in}}}(t)$ , $\sqrt {2{\kappa _1}} y_1^{{\rm{in}}}(t)$ , $\sqrt {2{\kappa _2}} x_2^{{\rm{in}}}(t)$ , ${\sqrt {2{\kappa _2}} y_2^{{\rm{in}}}(t)} ]^{\rm{T}}$ . 特征矩阵A V ${V_{ij}} = \left\langle {{f_i}(t){f_j}\left( {{t^\prime }} \right)} \right.$ $\left. { + {f_j}\left( {{t^\prime }} \right){f_i}(t)} \right\rangle /2$ $(i, j = 1, 2, \cdots , 6)$ .V [37 ,38 ] , 即${D_{ij}}\delta \left( {t - {t^\prime }} \right) = \left\langle {{\eta _i}(t){\eta _j}\left( {{t^\prime }} \right) + {\eta _j}\left( {{t^\prime }} \right){\eta _i}(t)} \right\rangle /2$ . 利用Lyapunov方程可解得协方差矩阵V ${E_N}$ [39 ,40 ] . 采用负值度来度量两体纠缠的强弱.${E_N}$ [39 ,40 ] 定义为${\hat v_ - } = \min [ {{\rm{eig}} | {{\rm{i}}{{{\varOmega }}_2}{{{{\tilde V}}}_4}} |} ]$ 为协方差矩阵的最小辛矩阵特征值, ${{{\varOmega }}_2} = \oplus _{j = 1}^2{\rm{i}}{{{\sigma }}_y}$ 是辛矩阵, ${{{{\tilde V}}}_4} = {{{P}}_{1 |2}}{{{V}}_4}{{{P}}_{1 |2}}$ , 其中, ${{{P}}_{1 |2}} = {\rm{diag}} (1, - 1, 1, 1)$ , ${{{V}}_{\rm{4}}}$ 是三体系统中任意两体子系统的协方差矩阵. ${E_N} > 0$ 表示系统存在两体纠缠.20 )式计算了腔内光子-FMR模, 腔内光子-MS模和FMR模-MS模之间的两体纠缠, 分别用${E_{a{m_1}}}$ , ${E_{a{m_2}}}$ 和${E_{{m_1}{m_2}}}$ 表示. 图3(a) —图3(c) 分别表示${E_{a{m_1}}}$ , ${E_{a{m_2}}}$ 和${E_{{m_1}{m_2}}}$ 随失谐量${\varDelta _{{m_1}}}$ 和${\varDelta _{\rm{c}}}$ 的变化关系, 系统参数与图2 一致. 显然, 腔内光子、FRM模和MS模之间均产生两两纠缠(${E_{ij}}$ 始终大于零, $i, j = a, {m_1}, {m_2}$ ). 比较图3(a) 和图3(b) 可知, ${E_{a{m_1}}}$ 与${E_{a{m_2}}}$ 几乎关于点(${\varDelta _{\rm{c}}} \approx 0$ , ${\varDelta _{{m_1}}} \approx 20\gamma $ )对称. 当驱动光和FMR模共振, 和MS模非共振时(即${\varDelta _{{m_1}}} = 0$ ), 光子和FMR模的纠缠最大. 当驱动光和MS模共振, 和FMR模非共振时(即${\varDelta _{{m_1}}} \approx 40\gamma $ ), 光子和MS模的纠缠最大. 同时, ${E_{a{m_1}}}$ 的最大值略大于${E_{a{m_2}}}$ 的最大值, 这是因为FMR模的耗散系数略小于MS模的耗散系数. 如图3(c) 所示, 在${\varDelta _{\rm{c}}} \approx 0$ , ${\varDelta _{{m_1}}} \approx 20\gamma $ 附近, FMR模-MS模纠缠的负值度${E_{{m_1}{m_2}}}$ 出现极大值, 这是因为此时${\varDelta _{{m_1}}} \approx ({{{\omega _{{m_1}}} - {\omega _{{m_2}}}}})/{2} \approx 20\gamma$ , FMR模与MS模具有相同的激发强度, 非线性效应最强, 从而导致该处负值度较大.图 3 两体纠缠的负值度 (a) ${E_{a{m_1}}}$ , (b) ${E_{a{m_2}}}$ 和(c) ${E_{{m_1}{m_2}}}$ 随失谐量${\varDelta _{{m_1}}}$ 和${\varDelta _{\rm{c}}}$ 的变化关系. 其中${\varepsilon _{\rm{p}}} = \gamma $ , $\varOmega = 1.5\gamma $ . (d)负值度${E_{a{m_1}}}$ (实线)、${E_{a{m_2}}}$ (虚线)和${E_{{m_1}{m_2}}}$ (点划线)随非线性增益$\varOmega $ 的变化. 其中${\varepsilon _{\rm{p}}} = \gamma $ , ${\varDelta _{\rm{c}}} = - 2.5\gamma $ , ${\varDelta _{{m_1}}} = 23\gamma $ . 其他参数与图2 一致Figure3. Density plot of logarithmic negativity related to bipartite entanglement (a) ${E_{a{m_1}}}$ , (b) ${E_{a{m_2}}}$ , and (c) ${E_{{m_1}{m_2}}}$ versus detunings ${\varDelta _{{m_1}}}$ and ${\varDelta _{\rm{c}}}$ , where ${\varepsilon _{\rm{p}}} = \gamma $ , $\varOmega = 1.5\gamma $ . (d) Logarithmic negativity ${E_{a{m_1}}}$ (solid), ${E_{a{m_2}}}$ (dashed), and${E_{{m_1}{m_2}}}$ (dot-dashed) versus the nonlinear gain coefficient $\varOmega $ , we take ${\varepsilon _{\rm{p}}} = \gamma $ , ${\varDelta _{\rm{c}}} = - 2.5\gamma $ and${\varDelta _{{m_1}}} = 23\gamma $ . The other parameters are the same as in Fig.2 .${\varDelta _{{m_1}}} = 23\gamma $ , ${\varDelta _{\rm{c}}} = - 2.5\gamma $ , 腔内光子、FMR模和MS模之间的两体纠缠如图3(d) 所示, 其中横坐标为非线性增益系数$\varOmega $ . 当$\varOmega = 0$ 时(即只有线性驱动光), 腔内光子、FMR模和MS模之间的两体纠缠度皆为零, 表明在没有非线性效应时, 系统不会产生两体纠缠. 利用参量下转换提供的非线性压缩驱动腔模产生纠缠, 这与利用压缩真空场[31 ] 和磁晶各向异性的Kerr材料[30 ] 中的非线性产生纠缠的做法类似. 如图3(d) 所示, 两体纠缠的负值度${E_{ij}}$ 随非线性增益系数$\varOmega $ 的增加而增大.4.磁-腔QED系统中的三体纠缠 最后, 考虑该磁-腔QED系统的三体纠缠. 度量三体纠缠的最小剩余共生纠缠$R_\tau ^{{\rm{min}}}$ [41 ,42 ] 满足:$R_\tau ^{i|jk} \equiv {C_{i|jk}} - {C_{i|j}} - {C_{i|k}}{\rm{ }}\left( {i, j, k = a, {m_1}, {m_2}} \right)$ 为剩余共生纠缠, ${C_u}_{|v}$ 为子系统u 和$\nu $ ($\nu $ 包含一个或两个模式)的负值度的平方. 当$\nu $ 包含两个模时, ${{{\varOmega }}_{\rm{3}}} = \oplus _{j = 1}^3{\rm{i}}{{{\sigma }}_y}$ 替换${{{\varOmega }}_{\rm{2}}} = \oplus _{j = 1}^2{\rm{i}}{{{\sigma }}_y}$ , ${{{\tilde V}}_{\rm{6}}} = {{{P}}_{i|jk}}{{V}}{{{P}}_{i|jk}}$ 替换${{{\tilde V}}_{\rm{4}}} \!=\! {{{P}}_{{\rm{1 |2}}}}{{{V}}_{\rm{4}}}{{{P}}_{{\rm{1 |2}}}}$ , 其中${{{P}}_{{\rm{1 |23}}}} \!=\! {\rm{diag}} (1, \!-\! 1, 1, 1, 1, 1)$ , ${{{P}}_{{\rm{2 |13}}}} = {\rm{diag}} (1, 1, 1, - 1, 1, 1)$ 以及${{{P}}_{{\rm{3 |12}}}} \!=\! {\rm{diag}} (1, 1, 1, 1, 1, - 1)$ . 一般地, 当$R_\tau ^{\min } > 0$ 时系统存在三体纠缠.${\varDelta _c} = - 2.5\gamma $ , 图4(a) 给出了三体纠缠的最小剩余共生纠缠$R_\tau ^{{\rm{min}}}$ 随失谐量${\varDelta _{{m_1}}}$ 的变化关系. 显然, 当$\varOmega = 0$ 时, $R_\tau ^{{\rm{min}}} = 0$ , 系统不存在三体纠缠. 当$\varOmega > 0$ 时, $R_\tau ^{{\rm{min}}} > 0$ , 非线性效应导致系统出现三体纠缠, 且$R_\tau ^{{\rm{min}}}$ 在${\varDelta _{{m_1}}} \approx 20\gamma $ 附近存在极大值, 表示具有最强的三体纠缠度. 这是因为该处驱动场与磁-腔QED系统的耦合最强, 非线性效应也最强, 从而激发了最大的三体纠缠. 随着非线性增益$\varOmega $ 的增加, 最小剩余共生纠缠$R_\tau ^{{\rm{min}}}$ 的极大值也随之变大. 取${\varDelta _{{m_1}}} = 23\gamma $ , 图4(b) 给出了三体纠缠随温度T 的变化关系. 显然, 最小剩余共生纠缠$R_\tau ^{{\rm{min}}}$ 对温度不敏感, 具有很好的鲁棒性. 同时发现, 非线性增益$\varOmega $ 越大, 三体纠缠的鲁棒性越好. 当$\varOmega = 1.5\gamma $ 时, $R_\tau ^{{\rm{min}}}$ 的温度鲁棒性可达到200 mK. 同时还注意到, 在非线性增益系数$\varOmega = 0$ 时, 系统没有非线性, 所以没有纠缠. 当$\varOmega > 0$ 时, 非线性效应导致三体纠缠的产生. 同时, 非线性导致的量子扰动和温度导致的量子扰动相互干涉, 从而导致图4(b) 中出现一个小峰. 并且当T 很小的时候, $\varOmega $ 导致的三体纠缠占主导, 当温度增大到一定程度后, 热扰动使三体纠缠度变小. 所以图4(b) 中最小剩余共生纠缠随温度的变化不是单调减小, 并且在温度增大到一定程度后才出现显著下降.图 4 (a) 不同非线性增益情况下, 三体纠缠的最小剩余共生纠缠$R_\tau ^{{\rm{min}}}$ 随失谐量${\varDelta _{{m_1}}}$ 的变化关系; (b) 最小剩余共生纠缠$R_\tau ^{{\rm{min}}}$ 随温度T 的变化, 其中${\varepsilon _{\rm{p}}} = \gamma $ , ${\varDelta _{\rm{c}}} = - 2.5\gamma $ . 虚线、实线、点线和点划线分别对应非线性相互作用强度$\varOmega = 1.65\gamma $ , $\varOmega = 1.5\gamma $ , $\varOmega = 1.0\gamma $ 和$\varOmega = 0.5\gamma $ 的情况. 在图4(b) 中, 取${\varDelta _{{m_1}}} = 23\gamma $ , 其他参数与图2 一致Figure4. (a) Tripartite entanglement in terms of the minimum residual contangle $R_\tau ^{{\rm{min}}}$ versus detuning ${\varDelta _{{m_1}}}$ ; (b) robust against temperature of the minimum residual contangle $R_\tau ^{{\rm{min}}}$ , Where ${\varepsilon _{\rm{p}}} = \gamma $ , ${\varDelta _{\rm{c}}} = - 2.5\gamma $ . The dashed line, solid line, dotted line, and dash-dot line indicate nonlinear interaction strength $\varOmega = 1.65\gamma $ , $\varOmega = 1.5\gamma $ , $\varOmega = 1.0\gamma $ , and $\varOmega = 0.5\gamma $ , respectively. At the same time, we take ${\varDelta _{{m_1}}} = 23\gamma $ for Fig. 4 (b). The other parameters are the same as in Fig. 2 .图5 所示, 减小MS模的耗散系数, 系统的最小剩余共生纠缠$R_\tau ^{{\rm{min}}}$ 增大, 从而可以获得更大的三体纠缠.图 5 三体纠缠的最小剩余共生纠缠$R_\tau ^{{\rm{min}}}$ 随失谐量${\varDelta _{{m_1}}}$ 和耗散系数${\kappa _2}$ 的变化关系; 设定${\varepsilon _{\rm{p}}} = \gamma $ , $\varOmega = 1.5\gamma $ , ${\varDelta _{\rm{c}}} = - 2.5\gamma $ , 从左到右, ${\kappa _2}$ 所取的数值分别为$1.7\gamma $ , $2.1\gamma $ , $2.5\gamma $ , $2.9\gamma $ 以及$3.3\gamma $ . 其他参数与图2 一致Figure5. Tripartite entanglement in terms of the minimum residual contangle $R_\tau ^{{\rm{min}}}$ versus detuning ${\varDelta _{{m_1}}}$ and dissipation rates ${\kappa _2}$ , setting ${\varepsilon _{\rm{p}}} = \gamma $ , $\varOmega = 1.5\gamma $ and ${\varDelta _{\rm{c}}} = - 2.5\gamma $ , the lines denote $1.7\gamma $ , $2.1\gamma $ , $2.5\gamma $ , $2.9\gamma $ , a nd $3.3\gamma $ for ${\kappa _2}$ from left to right. The other parameters are the same as in Fig. 2 .5.结 论 本文提出一种利用新的非线性机制在磁-腔QED系统中产生两体和三体纠缠的理论方案. 该磁-腔QED系统中只含有一个YIG小球, 腔内光子耦合YIG小球中集体自旋激发的FMR模和MS模, 通过注入泵浦光, 利用参量下转换使系统产生非线性, 从而压缩驱动腔模, 使系统产生纠缠. 采用实验可行的参数, 稳态情况下, 腔内光子、FMR模和MS模之间互相实现两体纠缠. 当关闭泵浦光的输入($\varOmega = 0$ ), 系统不产生纠缠. 同时, 该稳态系统还可以实现三体纠缠, 度量三体纠缠的最小剩余共生纠缠随非线性增益的增加而增大. 进一步研究发现, 该三体纠缠与MS模式的耗散系数有关, 减小MS模的耗散系数, 系统的最小剩余共生纠缠$R_\tau ^{{\rm{min}}}$ 增大, 从而可以获得更大的三体纠缠. 研究同时得出三体纠缠对温度不敏感, 具有很好的鲁棒性.  图 1 (a) 磁-腔QED系统示意图. YIG小球位于腔中短边中心处, 该处微波腔的TE102模式的磁场沿y轴方向, 静磁场沿x轴方向; (b) 利用Comsol模拟微波腔TE102的网格划分示意图; (c) 微波腔TE102模式的磁场方向和磁场强度
图 1 (a) 磁-腔QED系统示意图. YIG小球位于腔中短边中心处, 该处微波腔的TE102模式的磁场沿y轴方向, 静磁场沿x轴方向; (b) 利用Comsol模拟微波腔TE102的网格划分示意图; (c) 微波腔TE102模式的磁场方向和磁场强度




































































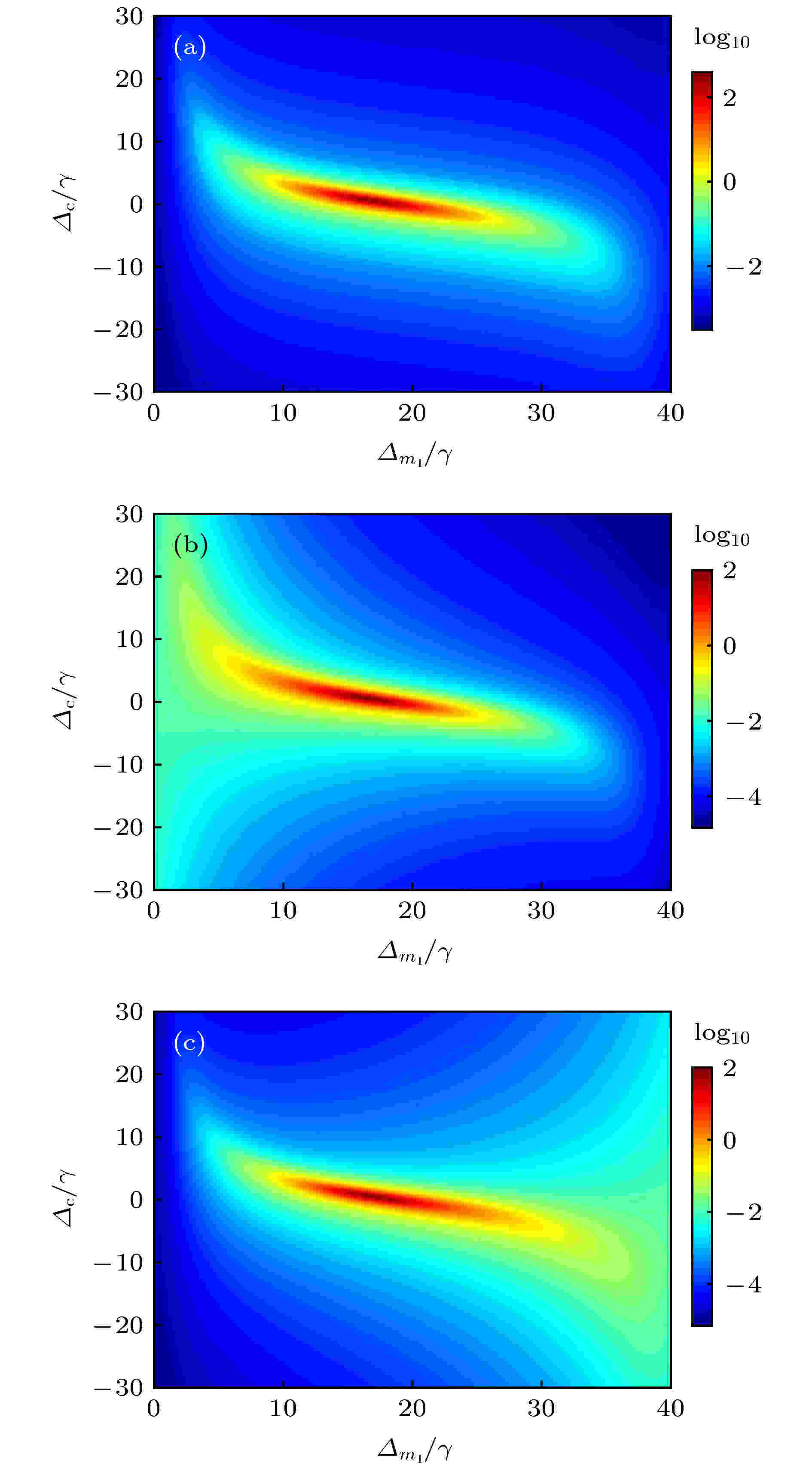 图 2 (a) 平均光子数、(b) FMR模的平均磁子数和 (c) MS模的平均磁子数随失谐量
图 2 (a) 平均光子数、(b) FMR模的平均磁子数和 (c) MS模的平均磁子数随失谐量
































































































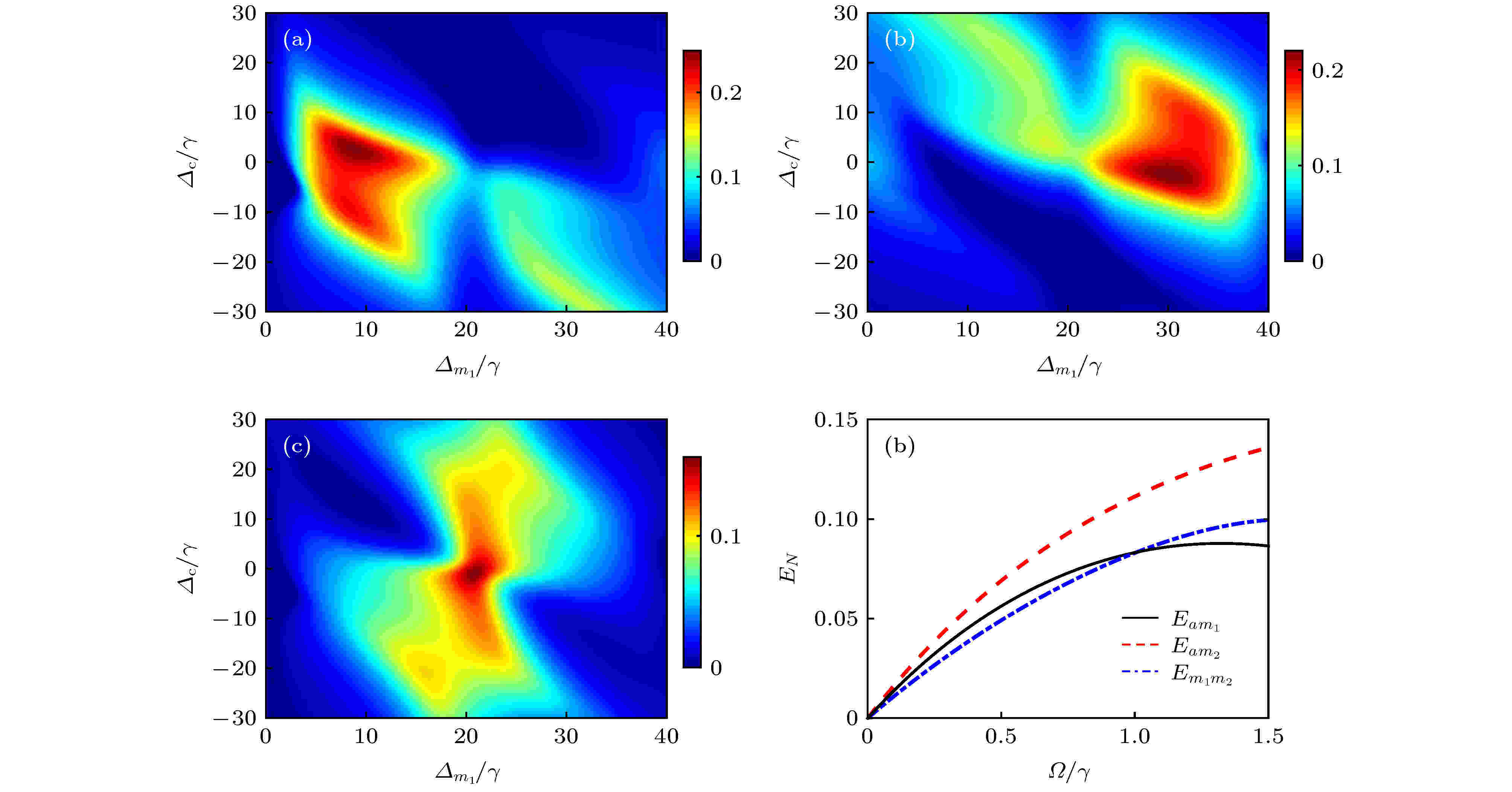 图 3 两体纠缠的负值度 (a)
图 3 两体纠缠的负值度 (a) 
























































































































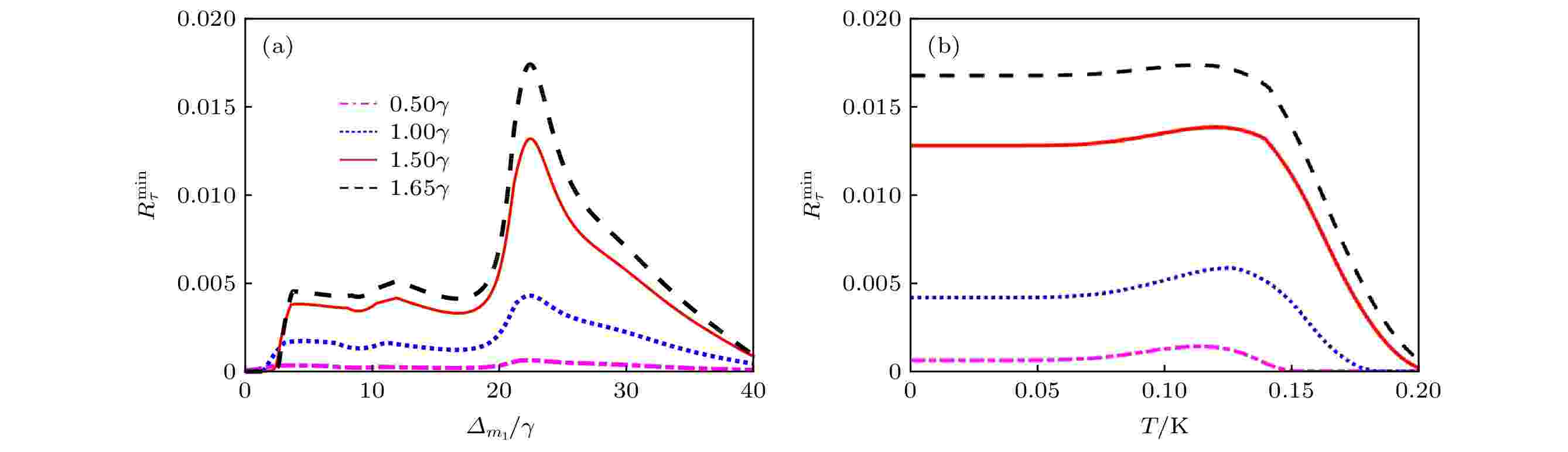 图 4 (a) 不同非线性增益情况下, 三体纠缠的最小剩余共生纠缠
图 4 (a) 不同非线性增益情况下, 三体纠缠的最小剩余共生纠缠
























 图 5 三体纠缠的最小剩余共生纠缠
图 5 三体纠缠的最小剩余共生纠缠





























