摘要: Fokas系统是最简单的二维空间非线性演化模型. 本文首先研究一种相似变换将该系统转换为长波-短波共振模型形式; 然后基于该相似变换和已知的长波-短波共振模型的有理形式解, 通过选择空间变量
y 的待定函数为Hermite函数, 得到了Fokas系统的一个有理函数表示的严格解析解; 进而选定合适自由参数给出了Fokas系统丰富的二维怪波激发, 并可对二维怪波的形状和幅度进行有效控制; 最后借助图示展现了二维怪波的传播特征. 本文提出的构造Fokas系统二维怪波的途径可以作为一种激发二维怪波现象的潜在物理机制, 并推广应用于其他(2 + 1)维非线性局域或非局域模型.
关键词: 二维怪波 /
Fokas系统 /
(2 + 1)非线性演化模型 /
相似变换 English Abstract Excitation of rogue waves of Fokas system Zhang Jie-Fang 1,2 ,Jin Mei-Zhen 3 1.Institute of Intelligent Media Technology, Communication University of Zhejiang, Hangzhou 310018, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 61877053)Received Date: 12 May 2020Accepted Date: 11 June 2020Available Online: 30 October 2020Published Online: 05 November 2020Abstract: Rogue wave (RW) is one of the most fascinating phenomena in nature and has been observed recently in nonlinear optics and water wave tanks. It is considered as a large and spontaneous nonlinear wave and seems to appear from nowhere and disappear without a trace. The Fokas system is the simplest two-dimensional nonlinear evolution model. In this paper, we firstly study a similarity transformation for transforming the system into a long wave-short wave resonance model. Secondly, based on the similarity transformation and the known rational form solution of the long-wave-short-wave resonance model, we give the explicit expressions of the rational function form solutions by means of an undetermined function of the spatial variable y , which is selected as the Hermite function. Finally, we investigate the rich two-dimensional rogue wave excitation and discuss the control of its amplitude and shape, and reveal the propagation characteristics of two-dimensional rogue wave through graphical representation under choosing appropriate free parameter. The results show that the two-dimensional rogue wave structure is controlled by four parameters: ${\rho _0},\;n,\;k,\;{\rm{and}}\;\omega \left( {{\rm{or}}\;\alpha } \right)$ . The parameter $ {\rho _0}$ controls directly the amplitude of the two-dimensional rogue wave, and the larger the value of $ {\rho _0}$ , the greater the amplitude of the amplitude of the two-dimensional rogue wave is. The peak number of the two-dimensional rogue wave in the $(x,\;y)$ and $(y,\;t)$ plane depends on merely the parameter n but not on the parameter k . When $n = 0,\;1,\;2, \cdots$ , only single peak appears in the $(x,\;t)$ plane, but single peak, two peaks to three peaks appear in the $(x,\;y)$ and $(y,\;t)$ plane, respectively, for the two-dimensional rogue wave of Fokas system. We can find that the two-dimensional rogue wave occurs from the zero background in the $(x,\;t)$ plane, but the two-dimensional rogue wave appears from the line solitons in the $(x,\;y)$ plane and $(y,\;t)$ plane. It is worth pointing out that the rogue wave obtained here can be used to describe the possible physical mechanism of rogue wave phenomenon, and may have potential applications in other (2 + 1)-dimensional nonlinear local or nonlocal models. Keywords: two-dimensional rogue wave /Fokas system /(2 + 1) nonlinear wave model /similarity transformation 全文HTML --> --> --> 1.引 言 怪波又称畸形波, 是一种罕见且极端的自然现象, 以大振幅和突然性为特征, 并在空间和时间上呈代数方式衰减的双重局域. 二十多年来对怪波的实验观测和理论分析涉及海洋动力学、非线性光学、等离子体物理、物质波、超流体、毛细管波、法拉第表面波纹、电传输线、大气和金融等领域[1 -16 ] . 2007年Solli等[2 ] 在超连续光谱的产生中观察到怪波事件, 并命名“光学怪波”. 因光学怪波现象具有重要的物理意义和潜在的应用价值, 近年取得了重大的进展[17 -36 ] .[37 ] u 是表征某个物理量的非线性波, x 和 y 是空间坐标, t 是时间坐标. 当$x = y$ 时其约化为非线性薛定谔方程. 它可以通过逆散射方法求解, 其各类孤子、lump、dromion、线怪波、各阶呼吸子及混合解等已由文献[38 -44 ]分别使用不同的方法得到, 但时空双重局域的怪波解还未见文献报道. Yan[45 ] 通过相似变换将(2 + 1)维非局域非线性薛定谔方程变换为(1 + 1)维聚焦非线性薛定谔方程, 进而构造出它的二维怪波. 受此驱动, 本文首先研究Fokas系统(1 )式的一个相似变换, 将其转化为长波-短波共振模型形式, 然后通过选择合适的待定函数和自由参数, 得到了它的丰富二维怪波激发.2.Fokas系统的相似变换 为了寻找(1 )式的怪波解, 引入下列相似变换$\rho \left( y \right),\; \phi \left( {\xi, \tau } \right),\; \varphi \left( {x, y, t} \right)$ 和$\xi = \xi \left( {x, t} \right),\; \tau = \tau \left( t \right)$ 分别是指定变量的待定函数.2 )式可以得到3 )—(6 )式代入(1 )式导出$\xi \left( {x, t} \right),\; \tau \left( t \right),\; \varphi \left( {x, y, t} \right)$ 和$\rho \left( y \right)$ 满足下列关系:7 )式约化为下列形式:8 )式得到$\rho \left( y \right)$ 满足下列积分关系:${\left| {\rho \left( y \right)} \right|^2}$ 的积分在整个坐标$\left( { - \infty, \infty } \right)$ 是一个有界的实常数, 其中${\xi _0},\; {\tau _0},\; \alpha$ 和k 为任意实常数, $\beta \left( y \right)$ 是空间变量y 的任意非零函数.$\psi \left( {x, y, t} \right)$ , 而且满足1 )化为15 )式具有长波-短波共振模型的形式. 我们知道当物理系统的长波相速度与短波群速度相匹配时, 会产生长波与短波共振的自然现象, 并由下列方程描述:$L\left( {\xi, \tau } \right),\; S\left( {\xi, \tau } \right)$ 分别表示短表面波包和长界面波. 长波-短波共振模型首先从底层流体动力学方程的多尺度渐近展开得到[46 ] , 后在非线性光学[47 ,48 ] 和等离子体物理[49 ] 中得到验证. 在流体动力学中, 由于毛细波和重力波之间的相互作用, 也可以产生长波短波共振[50 -52 ] . 文献[53 , 54 ]分别通过取呼吸子的非奇异极限和借助Darboux变换得到了长波-短波共振模型的一类怪波解.3.Fokas系统的二维怪波构造 下面从长波-短波共振模型的怪波解出发, 通过选择满足(14 )式的特定函数$ \rho \left(y\right) $ , 并借助变换(3 )式及关系(11 )—(13 )式, 讨论Fokas系统(1 )式的二维怪波激发.46 ]已经得到(16 )式的怪波解$\phi \left( {\xi, \tau } \right)$ 为$ {\varOmega _0}$ 满足${\rho _0}$ 是一个可选实数. 作为应用, 选择函数$\rho \left( y \right)$ 为Hermite (也称Hermite-Gaussian) 函数[55 ] ${{\rm{H}}_n}\left( {\omega y} \right)$ 为Hermite多项式, $\omega \ne 0$ 是常数. 联合(13 )式和(19 )式导出参数a 和$\omega $ 的关系17 )式、(18 )式、(2 )式, (10 )—(12 )式, 可得$\beta \left( y \right) = 0, {\xi _0} = {\tau _0} = 0$ .22 )式可知怪波结构由4个参数${\rho }_{0},\; n,\; \omega ({\text{或}}\;\alpha )$ , k 进行控制. 图1 和图2 分别为当${\rho _0} = 1.5, \alpha = {\left| \omega \right|^{ - 1}} = 1,\;n = 0$ 和$k = 0,\; 1$ 时在$\left( {x,\; t,\; y = 0} \right)$ , $\left( {x, \;y,\; t = 0} \right)$ 和$\left( {y,\; t,\; x = 0} \right)$ 平面上二维光学怪波结构; 图3 和图4 分别为当${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1, n = 1$ 和$k = 0,\; 1$ 在$\left( {x,\; t,\; y = 1} \right)$ , $\left( {x,\; y,\; t = 0} \right)$ 和$( y,\; t,\; x = 0 )$ 平面上的二维怪波结构; 图5 为当${\rho _0} = 1.5,\; a = {\left| \omega \right|^{ - 1}}\! = \!1,\;n = 2$ 和$k = 2$ 在$(x,\; t,\; y = 0)$ 平面上二维怪波结构.图 1 ${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 0$ , $k = 0$ 时, 由(22 )式所确定的二维怪波激发 (a), (d) $y = 0$ 时在$\left( {x, t} \right)$ 平面上的演化图和相应的等高线图; (b), (e) $t = 0$ 时在$\left( {x, y} \right)$ 平面上的演化图和相应的等高线图; (c), (f) $x = 0$ 时在$\left( {y, t} \right)$ 平面的演化图和相应的等高线图Figure1. Cross-sections of two-dimensional rogue wave propagations (top row) and contour plots (bottom row) for the density distribution ${\left| {u\left( {x, y, t} \right)} \right|^2}$ given in Eq. (22 ) for ${\rho _0} = 1.5,\; \alpha =$ ${\left| \omega \right|^{ - 1}} = 1,\; n = 0$ with $k = 0$ : (a), (d) $\left( {x, t} \right)$ -plan with $y = 0$ ; (b), (e) $\left( {x, y} \right)$ -space with $t = 0$ ; (c), (f) $\left( {y, t} \right)$ -plane with $x = 0$ .图 2 ${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 0$ , $k = 1$ 时, 由(22 )式所确定的二维怪波激发 (a), (d) $y = 0$ 时在$\left( {x, t} \right)$ 平面上的演化图和相应的等高线图; (b), (e) $t = 0$ 时在$\left( {x, y} \right)$ 平面上的演化图和相应的等高线图; (c), (f) $x = 0$ 时在$\left( {y, t} \right)$ 平面的演化图和相应的等高线图Figure2. Cross-sections of two-dimensional rogue wave propagations (top row) and contour plots (bottom row) for the density distribution ${\left| {u\left( {x, y, t} \right)} \right|^2}$ given in Eq. (22 ) for ${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 0$ with $k = 1$ : (a), (d) $\left( {x, t} \right)$ -plane with $y = 0$ ; (b), (e) $\left( {x, y} \right)$ -space with $t = 0$ ; (c), (f) $\left( {y, t} \right)$ -plane with $x = 0$ .图 3 ${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 1$ , $k = 0$ 时, 由(22 )式所确定的二维怪波激发 (a), (d) $y = 1$ 时在$\left( {x, t} \right)$ 平面上的演化图和相应的等高线图; (b), (e) $t = 0$ 时在$\left( {x, y} \right)$ 平面上的演化图和相应的等高线图; (c), (f) $ x=0 $ 时在$ (y, t) $ 平面的演化图和相应的等高线图Figure3. Cross-sections of two-dimensional rogue wave propagations (top row) and contour plots (bottom row) for the density distribution ${\left| {u\left( {x, y, t} \right)} \right|^2}$ given in Eq. (22 ) for ${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 1$ with $k = 0$ : (a), (d) $\left( {x, t} \right)$ -plane with $y = 1$ ; (b), (e) $\left( {x, y} \right)$ -space with $t = 0$ ; (c), (f) $\left( {y, t} \right)$ -plane with $x = 0$ .图 4 ${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1$ , $n = 1$ , $k = 1$ 时, 由(22 )式所确定的二维怪波激发 (a), (d) $y = 1$ 时在$\left( {x, t} \right)$ 平面上的演化图和相应的等高线图; (b), (e) $t = 0$ 时在$\left( {x, y} \right)$ 平面上的演化图和相应的等高线图; (c), (f) $x = 0$ 时在$\left( {y, t} \right)$ 平面的演化图和相应的等高线图Figure4. Cross-sections of two-dimensional rogue wave propagations (top row) and contour plots (bottom row) for the density distribution ${\left| {u\left( {x, y, t} \right)} \right|^2}$ given in Eq. (22 ) for ${\rho _0} = 1.5$ , $\alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 1$ with $k = 1$ : (a), (d) $\left( {x, t} \right)$ -plane with $y = 1$ ; (b), (e) $\left( {x, y} \right)$ -space with $t = 0$ ; (c), (f) $\left( {y, t} \right)$ -plane with $x = 0$ .图 5 ${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 2,\; k = 2$ 时, 由(22 )式所确定的二维怪波激发 (a), (d) $y = 0$ 时在$\left( {x, t} \right)$ 平面上的演化图和相应的等高线图; (b), (e) $t = 0$ 时在$\left( {x, y} \right)$ 平面上的演化图和相应的等高线图; (c), (f) $x = 0$ 时在$\left( {y, t} \right)$ 平面的演化图和相应的等高线图Figure5. Cross-sections of two-dimensional rogue wave propagations (top row) and contour plots (bottom row) for the density distribution ${\left| {u\left( {x, y, t} \right)} \right|^2}$ given in Eq. (22 ) for ${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 2$ with $k = 2$ : (a), (d) $\left( {x, t} \right)$ -plane with $y = 0$ ; (b), (e) $\left( {x, y} \right)$ -space with $t = 0$ ; (c), (f) $\left( {y, t} \right)$ -plane with $x = 0$ .图1 —5 中, 选取${\rho _0}$ 和$\alpha = {\left| \omega \right|^{ - 1}}$ 是固定的, 但n 和k 选取为不同的值, 可以发现参数${\rho _0}$ 直接决定二维怪波的振幅的大小, ${\rho _0}$ 越大二维怪波的振幅越大. ${\rho _0}$ 确定后当$n = 0$ 和$k = 0$ 时二维怪波的振幅最大值$A = 5.08$ 发生在($x = y = t = 0$ )位置. 当固定参数n 时, 参数k 影响在$\left( {x,\; t} \right)$ , $\left( {x,\; y} \right)$ , $\left( {y,\; t} \right)$ 平面上观测二维怪波的振幅大小. 参数n 决定$\left( {x,\; y} \right)$ 和$\left( {y,\; t} \right)$ 平面上观测二维怪波的波峰个数, 与参数k 取值无关; 当$n = 0, \;1, \;2,\; \cdots $ 时, 在$\left( {x,\; t} \right)$ 平面上观测怪波保持只呈现一个波峰, 但在$\left( {x,\; y} \right)$ 和$\left( {y,\; t} \right)$ 平面上观测二维怪波分别呈现为1个波峰、2个波峰到3个波峰, 依次类推.图1 —5 分别给出在$( x,\; t, \; y = 0 )$ 、$( x,\; y,\; t = 0)$ 和$\left( {y,\; t,\; x = 0} \right)$ 平面上观测的二维怪波的演化过程. 下面考察不同时间的二维怪波演化, 考虑二维怪波演化的时间对称性. 这里列出(a) $t = - 7$ , (b) $t = - 3$ , (c) $t = 0$ , (d), (e) $t = 5$ , (f) $t = 10$ 的六种情形, 如图6 所示. 表明在$t = - 7$ 时二维怪波还湮灭在一个振幅$A = 1.29$ 的稳定线孤子背景波中; 在$t = - 3$ 时二维怪波有些隆起, 但还是一个振幅$A = 1.34$ 的稳定线孤子; 在$t = 0$ 时二维怪波嵌入在一个线孤子上, 其振幅达到最大值$A = 5.08$ ; 在$t = 0.5$ 时二维怪波开始消失, 还嵌在线孤子背景波中, 其最大幅度$A = 1.34$ ; 在$t = 5$ 时二维怪波已经消失在一个振幅$A = 1.29$ 的稳定线孤子背景波中; 在$t = 10$ 时二维怪波则完全消失成一个振幅$A = 1.27$ 的稳定线孤子. 这很好地说明了怪波的“来无影去无踪”特征.图 6 由(22 )式确定的二维怪波在$\left( {x, t} \right)$ 平面上的演化(这里取${\rho _0}{{ = 1}}{{.5}}$ , $\alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 0$ , $k = 3$ ) (a) $t = - 7$ ; (b) $t = - 3$ ; (c) $t = 0$ ; (d)$t = 0.5$ ; (e) $t = 5$ ; (f) $t = 10$ Figure6. Cross-sections of two-dimensional wave propagations (top row) for the density distribution ${\left| {u\left( {x, y, t} \right)} \right|^2}$ given in Eq. (22 ) for ${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 0$ with $k = 3$ : (a) $t = - 7$ ; (b) $t = - 3$ ; (c) $t = 0$ ; (d) $t = 0.5$ ; (e) $t = 5$ ; (f) $t = 10$ .图1 —6 可知, 当$n\! =\! 0$ , 在$\left( {x,\; t} \right),\left( {x,\; y} \right),\left( {y,\; t} \right)$ 平面上观测二维怪波呈现的都是一个波峰, 而且在$\left(x,\; t\right)$ 平面上观测二维怪波非常类似非线性薛定谔方程的一阶怪波. 为了说明二维怪波在$\left( {x,\; t} \right)$ 平面上的“来无影去无踪”特征, 下面考察其随坐标y 值变化的演化情况. 考虑到时间对称性, 这里列出(a) $y = - 3$ , (b) $y = - 1$ , (c) $y = 0$ , (d) $y = 0.5$ , (e) $y = 2$ , (f) $y = 3$ 的六种情形, 如图7 所示. 表明在$y = - 3$ 时二维怪波不存在, 其幅度基本为零; 在$y = - 1$ 时二维怪波的振幅已达到$A = 1.87$ ; 在$y = 0$ 时二维怪波的振幅达到最大值$A = 5.08$ ; 在$y = 0.5$ 时二维怪波的振幅降到$A = 3.95$ ; 在$y = 2$ 时二维怪波的振幅衰减到$A = 0.09$ ; 在$y = 3$ 时二维怪波开始消失, 其幅度趋于零, 随后完全消失.图 7 由(22 )式确定的二维怪波在$\left( {x, t} \right)$ 平面上的演化(这里取${\rho _0}{{ = 1}}{{.5}}$ , $\alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 0$ , $k = 3$ ) (a) $y = - 3$ ; (b) $y = -1$ ; (c) $y = 0$ ; (d) $y = 0.5$ ; (e) $y = 2$ ; (f) $y = 3$ Figure7. Cross-sections of two-dimensional rogue wave propagations (top row) for the density distribution ${\left| {u\left( {x, y, t} \right)} \right|^2}$ given in Eq. (22 ) for ${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 0$ with $k = 3$ : (a) $y = - 3$ ; (b) $y = - 1$ ; (c) $y = 0$ ; (d) $y = 0.5$ ; (e) $y = 2$ ; (f) $y = 3$ .$\rho \left( y \right)$ 为双曲函数形式24 )式和(14 )式得到N 是整数; ${a_i} = \left( {i = 1,\; 2,\; \cdots,\; N} \right)$ 是正的任意参数; ${b_i},\; {c_i}\left( {i = 1,\; 2,\; \cdots,\; N} \right)$ 是任意实数, 它们一起控制二维怪波的结构. 限于篇幅, 这里不做进一步讨论.4.结 论 综上所述, 选择一个相似变换, 可将Fokas系统转化为长波短波模型形式, 并给出了构造它的二维怪波的一种途径. 由于得到的怪波解包含空间y 的Hermite-Gaussian函数, 导致怪波具有丰富的结构和传播特性. 将这种方法推广到其他(2 +1)维非线性波动模型, 并寻找更有意义的二维怪波激发, 值得更深入研究. 如何把本文的二维怪波应用到实际情况中去, 也有待进一步思考. 




































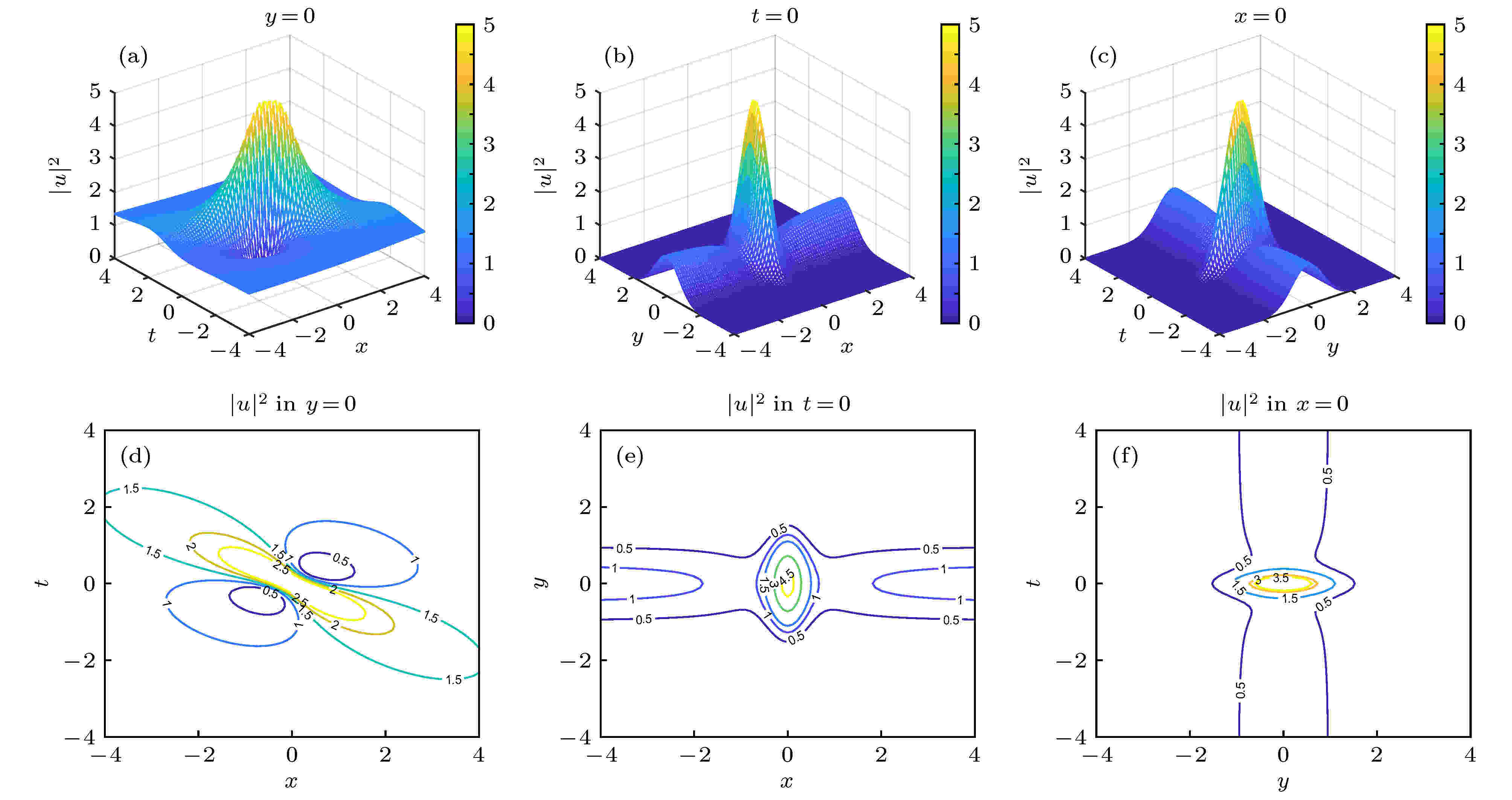 图 1
图 1 

















 图 2
图 2 
















 图 3
图 3 
















 图 4
图 4 


















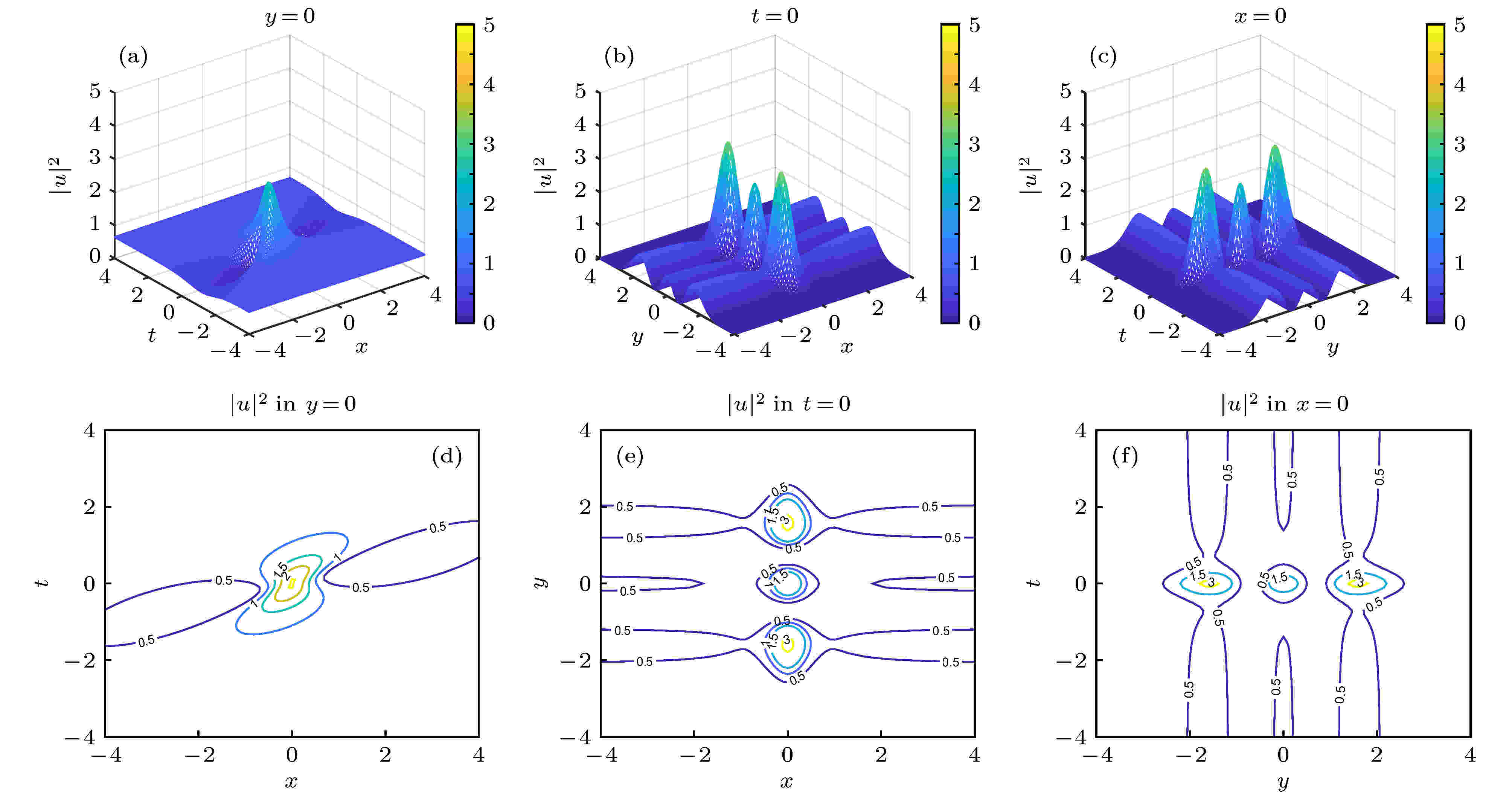 图 5
图 5 





























































































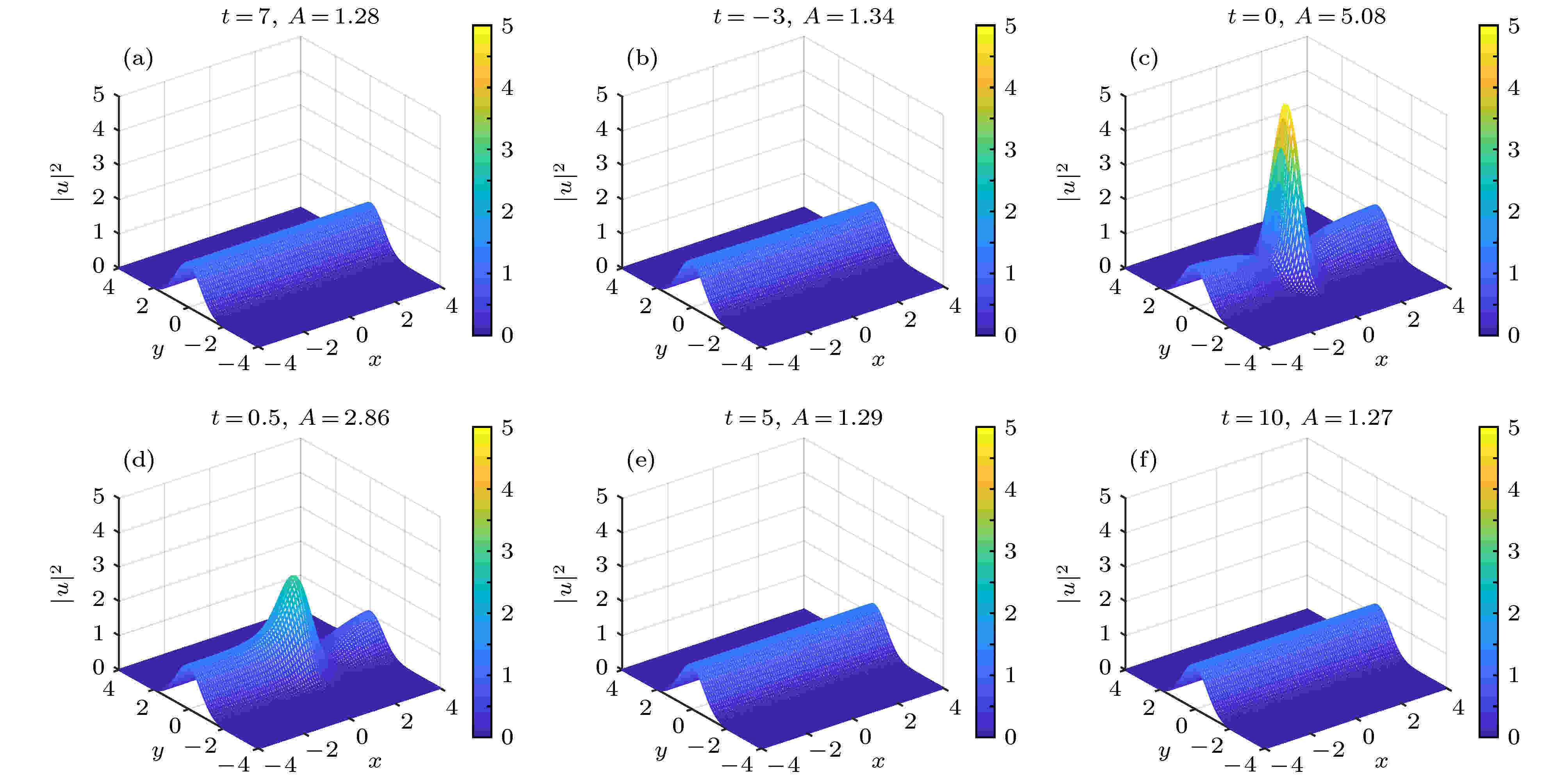 图 6 由(22)式确定的二维怪波在
图 6 由(22)式确定的二维怪波在


















































 图 7 由(22)式确定的二维怪波在
图 7 由(22)式确定的二维怪波在



























