摘要:作为一种紧凑型高功率微波器件, 磁绝缘线振荡器在起振过程中容易出现模式竞争现象, 如果不能对其进行有效抑制, 可能导致器件的最终输出性能下降. 由于磁绝缘线振荡器中波束互作用区通常采用同轴盘荷波导作为其慢波结构, 因此本文从同轴盘荷波导中几个可能被相对论电子束激发的低阶本征模与电子束之间的色散关系入手, 分析了三种类型的模式竞争的特点、产生的可能原因以及削弱方法. 基于以上分析, 给出了一种高功率紧凑型L波段磁绝缘线振荡器的物理模型, 并利用全电磁三维粒子程序对其进行了冷腔和热腔的数值模拟. 结果表明, 由于结构不完全对称和电子发射可能存在一定的非均匀性, 器件运行初期互作用区有竞争模式HEM₁₁模出现, 与理论分析一致；起振一小段时间后(10 ns左右), 互作用区基模增长加快, 高阶模被抑制. 进一步优化后器件在基模获得了高效率和高功率微波输出, 饱和时输出功率约为8.1 GW, 输出效率达到了18%, 模式纯度约为97%. 本文研究结果可为磁绝缘线振荡器运行过程中出现的竞争模式的识别和输出性能优化提供理论参考和依据.
关键词: 磁绝缘线振荡器/
模式竞争/
数值模拟

English Abstract

全文HTML

--> --> -->

磁绝缘线振荡器(magnetically insulated transmission line oscillator, MILO)是一种紧凑型高功率微波器件, 它不需要外加引导磁场聚焦电子束, 输出功率可达吉瓦量级, 在许多领域有着良好的应用前景^[1]. 为进一步提高MILO输出性能, 如提高其输出功率和效率, 增加模式稳定性等, 研究人员一直在进行相关研究和探索^[2-21].
为了获得高效稳定的高功率微波输出, MILO工作点一般设计在基模(TM₀₀模)的π模, 但器件运行初期仍然容易有不同程度的模式竞争现象出现^[11-21]. 由于MILO中波束互作用区通常采用同轴盘荷波导作为其慢波结构, 因此, 从同轴盘荷波导中几个可能被相对论电子束激发的低阶模式(TM₀₀, TM₀₁和HEM₁₁模)与电子束之间的色散关系入手, 简要分析了三种类型的模式竞争的特点、产生的可能原因以及削弱方法, 具体包括基模TM₀₀模相邻纵向模式之间的竞争、高阶对称模TM₀₁与基模之间的竞争以及非对称模式HEM₁₁与基模之间的竞争, 为磁绝缘线振荡器运行过程中出现的竞争模式的识别和输出性能的优化提供参考. 在此基础上, 给出了一种稳定紧凑型L波段MILO的物理模型并利用全电磁三维粒子程序进行了数值模拟, 重点对起振阶段的模式竞争问题进行了分析.

由于MILO中波束互作用区通常采用同轴盘荷波导作为其慢波结构, 下面从同轴盘荷波导中几个可能被电子束激发的低阶模式与电子束之间的色散关系入手, 对MILO中模式竞争问题进行物理分析.
同轴盘荷波导的纵向中心截面(即过轴线的纵向截面, 以下简称纵向截面)和横截面如图1所示, 包括阴极、阳极叶片和阳极外壳, 它们均为金属导体, 其中p为慢波结构的周期长度, 整个结构为轴对称的圆柱结构.
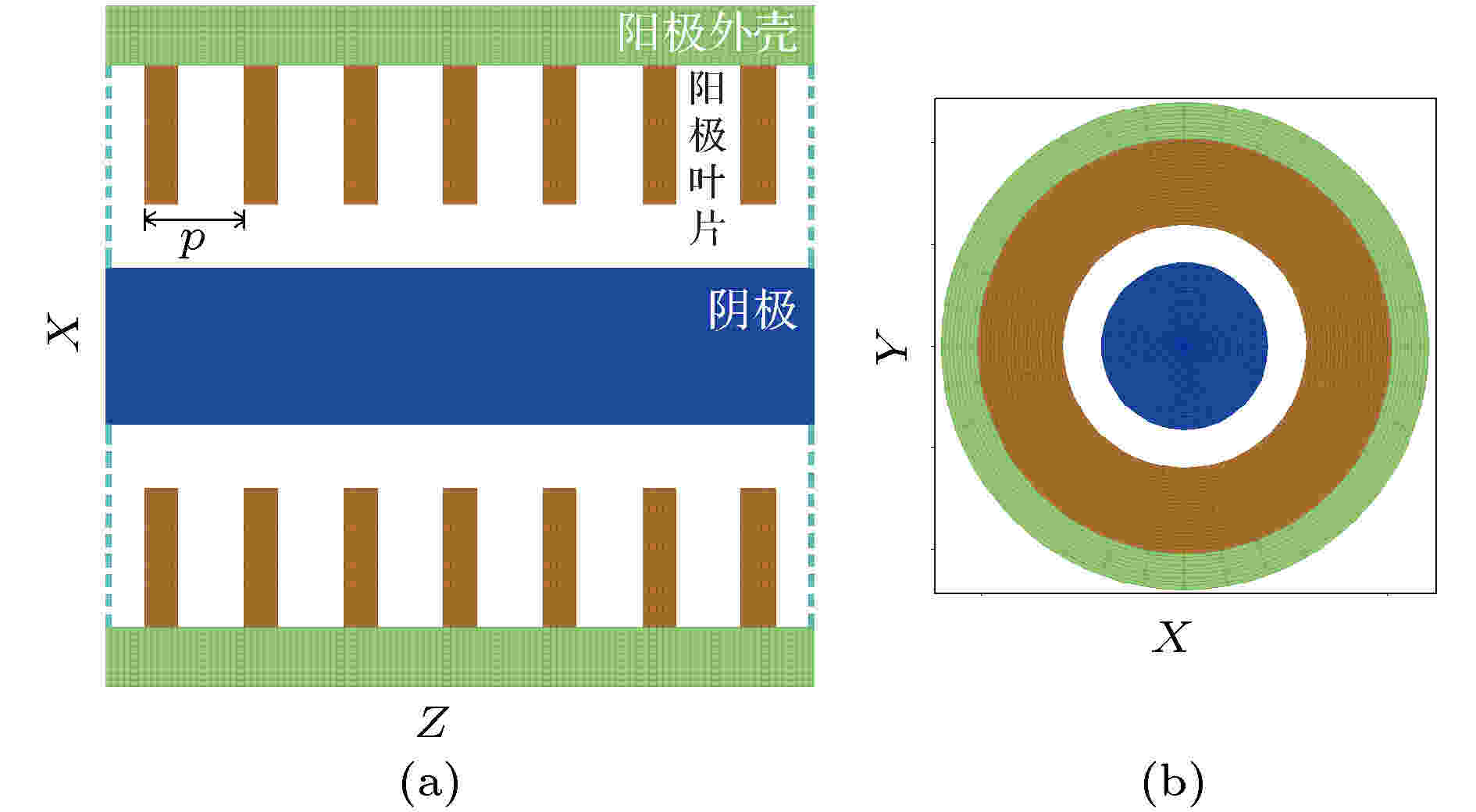图 1 同轴盘荷波导的结构示意图　(a) 纵向中心截面; (b) 横截面
Figure1. Schematic drawings of the coaxial disk-loaded waveguide in (a) Axial and (b) radial cross section

利用电磁场模拟程序, 计算了上述同轴盘荷波导中TM₀₀模、TM₀₁模和HEM₁₁模的色散曲线, 具体计算方法可参考文献[4,20,22], 其中阴极半径为4.0 cm, 阳极叶片和阳极外壳的内半径分别为6.0 cm和10.0 cm, 周期长度p为3.0 cm, 电子束电压为500 kV, 具体结果如图2所示. 图2中还给出了电子束和真空中光束的色散曲线, ${v_{\rm{e}}}$和${v_{{\rm{drift}}}}$分别为电子可能达到的最大速度和达到磁绝缘时的漂移速度. 图2中A, B和C所对应的点分别为电子束与TM₀₀模, HEM₁₁模和TM₀₁模色散曲线的交点. MILO工作点一般设计在基模(TM₀₀模)的π模, 即点A处, 对应的纵向电场在纵向和横向截面分布的等高图如图3(a)和图3(b)所示.
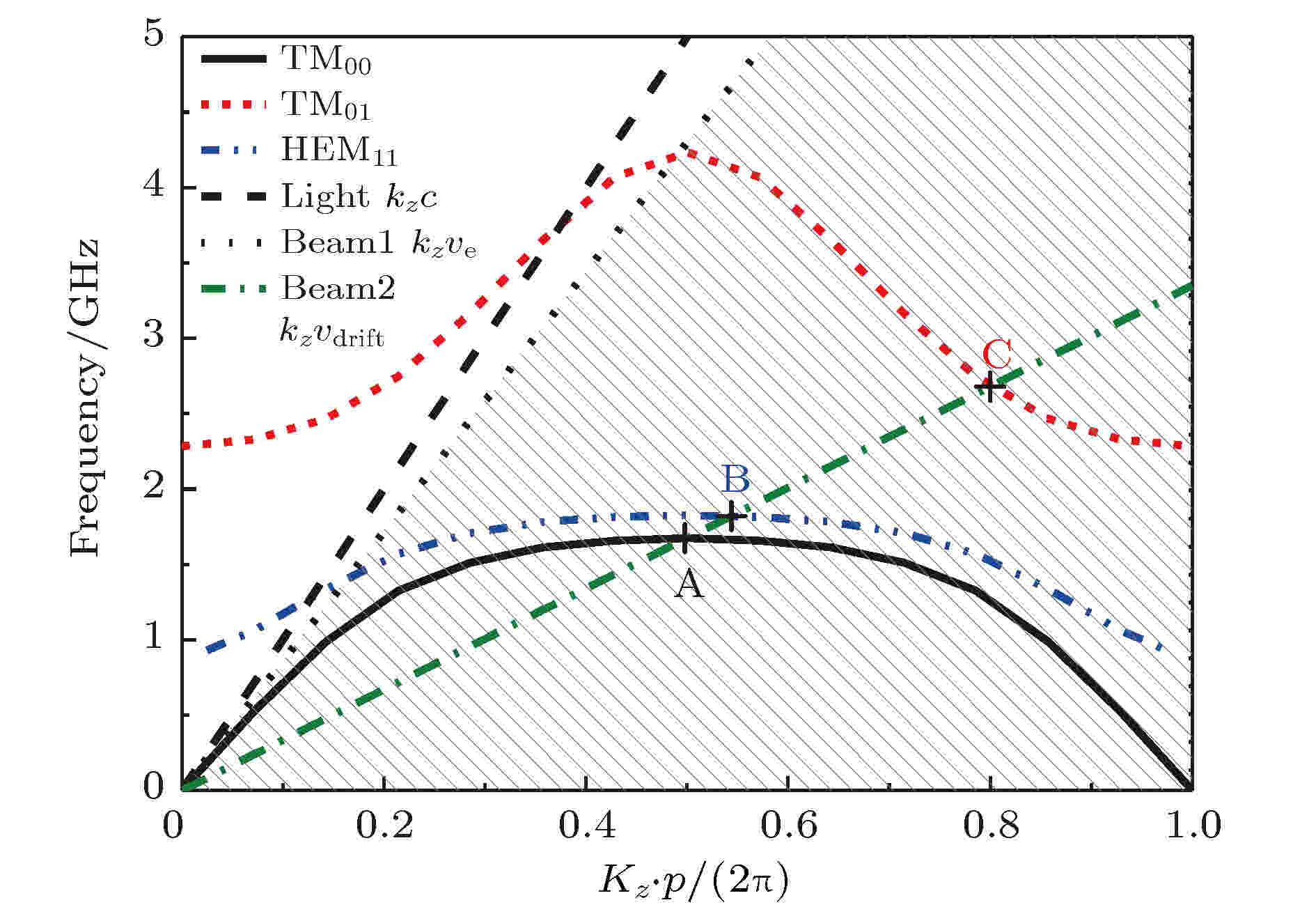图 2 同轴盘荷波导中TM₀₀模、TM₀₁模、HEM₁₁模以及电子束和光束的色散关系图
Figure2. The uncoupled dispersion curves of the coaxial disk-loaded waveguide (TM₀₀, TM₀₁ and HEM₁₁), and the dispersion lines of the electron and light beam.

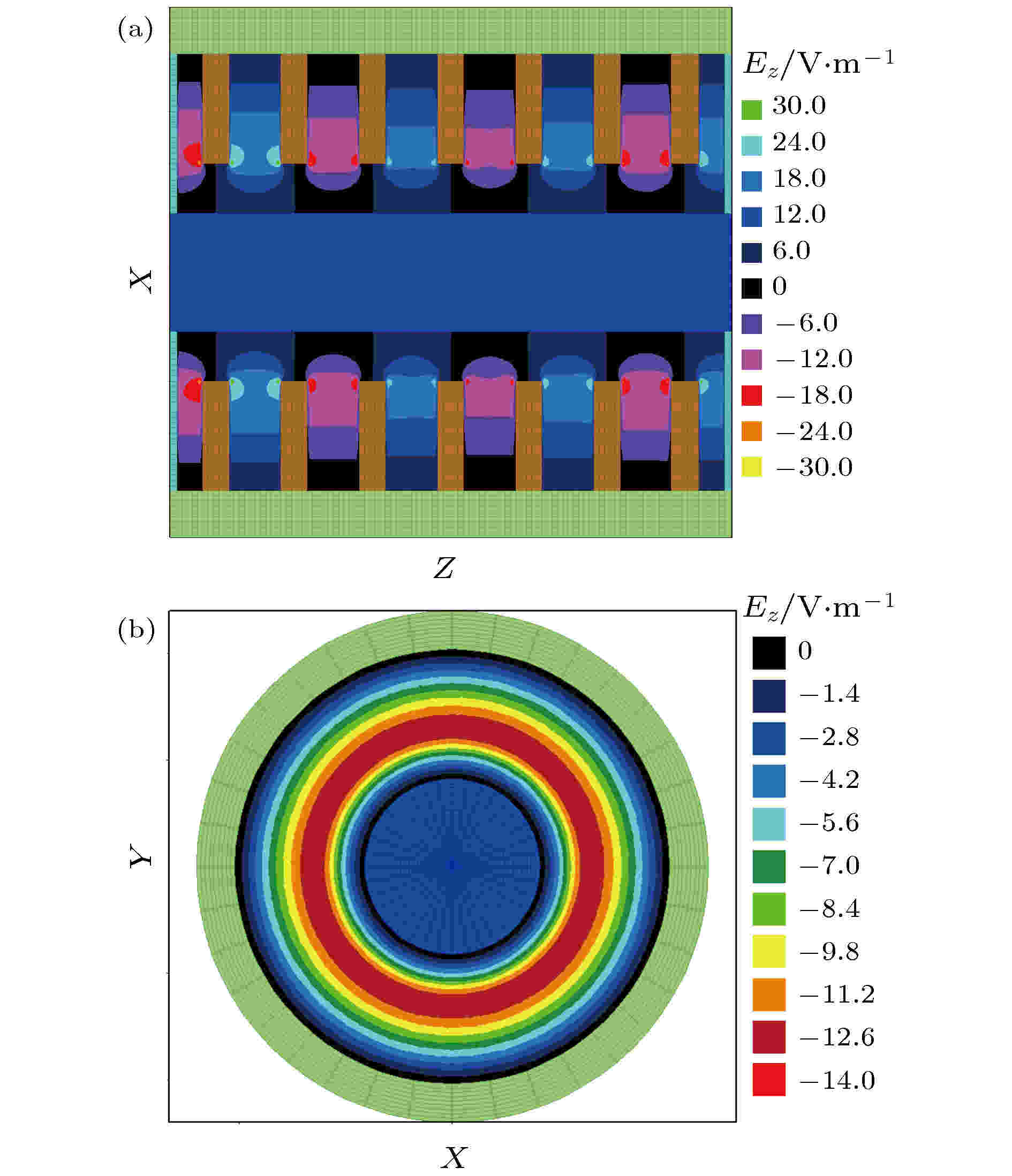图 3 同轴盘荷波导中TM₀₀(π模)的轴向电场在(a) 纵向中心截面和(b) 横截面的等高图
Figure3. The contour plots of E_z of the TM₀₀ (π mode) in the coaxial disk-loaded waveguide in the (a) Axial and (b) radial cross section.

2

-->

2.1.基模TM₀₀不同纵向模式的竞争

对于来自基模(TM₀₀)非π模的竞争, 由图2可以看到, 可能参与竞争的纵向模式一般是与π模(点A)较接近的模式, 如(N–1)π/N, N为互作用区阳极腔的个数, 即慢波结构的周期数. 由于是基模之间的竞争, 因此竞争模式的电磁场分布仍然具有轴对称性(图3(b)), 共振频率略低于工作点π模对应的频率. 该竞争模式初期可能先于π模被激发, 一段时间后, 可能被π模抑制.
已经知道, 在MILO中, 从阴极发射的电子束的能量分配到了径向和轴向两个方向. MILO设计时, 要求电子的平均漂移速度约等于基模TM₀₀模的相速度. 但由于电子的动能与径向位置相关, 因此, 磁绝缘尚未完全形成前, 电子速度沿径向连续变化, 电子束色散线可扫过如图2的阴影部分^[15,16]. 电子束色散线与TM₀₀模的色散曲线将产生一系列交点, 从而可能激发起TM₀₀模的含π模在内的其他纵向模式. TM₀₀模的纵向模式之间的竞争已经在实验上观察到且被证实^[17,18].
通过合理选取阳极腔的个数来控制模式隔离度, 或者选取合适的阳极叶片半径, 尤其是提取腔叶片的半径来调整束波互作用腔的品质因数, 可以削弱或者抑制TM₀₀模的纵向模式之间的竞争.
2 -->

2.2.高阶模TM₀₁与基模的竞争

对于基模与高阶模TM₀₁之间的竞争, 此时竞争模式TM₀₁的电磁场分布也具有轴对称性, 只是轴向电场沿径向正负交替一次, 如图4所示. 由色散关系图2可以看到, 点C为电子束和TM₀₁模色散曲线的交点, 其对应的共振频率远高于点A对应的频率, 且交点位置随电子束纵向速度(电压)变化相对较为敏感, 因此激发难度相对较大. 但由于此时束波共振点对应的本征模的群速度小于零, 如果器件品质因数较高或者互作用区较长, 器件运行初期有可能被激发.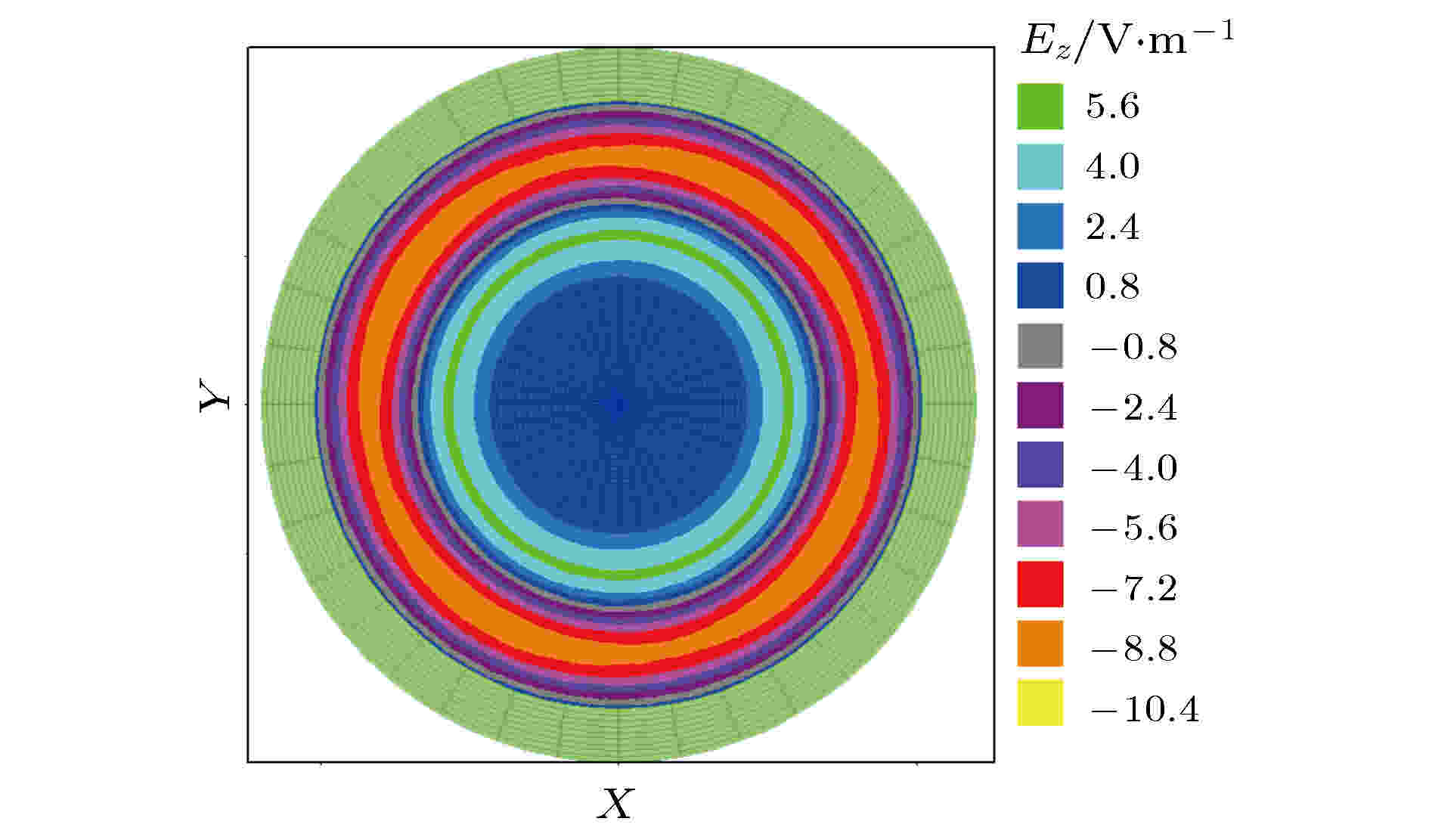
图 4 同轴盘荷波导中TM₀₁的轴向电场在横截面的等高图
Figure4. The contour plots of E_z of the TM₀₁ mode in the coaxial disk-loaded waveguide in the radial cross section.

通过调节阳极叶片的半径进而降低束波互作用腔的品质因数, 或者通过增加负载电流强度缩短MILO达到磁绝缘状态的时间, 都可能有效抑制TM₀₁模式的起振和放大.
2 -->

2.3.非对称模式HEM₁₁模与基模的竞争

对于非对称模式HEM₁₁模与基模的竞争, 由图2可以看到, HEM₁₁各纵向模式的频率仅略高于与之对应的TM₀₀模的频率, π模附近的频率相差最小(图中点A和点B). 其中, HEM₁₁模在点B处对应的纵向电场在纵向和横向截面分布的等高图如图5(a)和图5(b)所示. 可以看到, HEM₁₁模的轴向电场E_z不再具有轴对称性, 而是沿角向正负交替一次.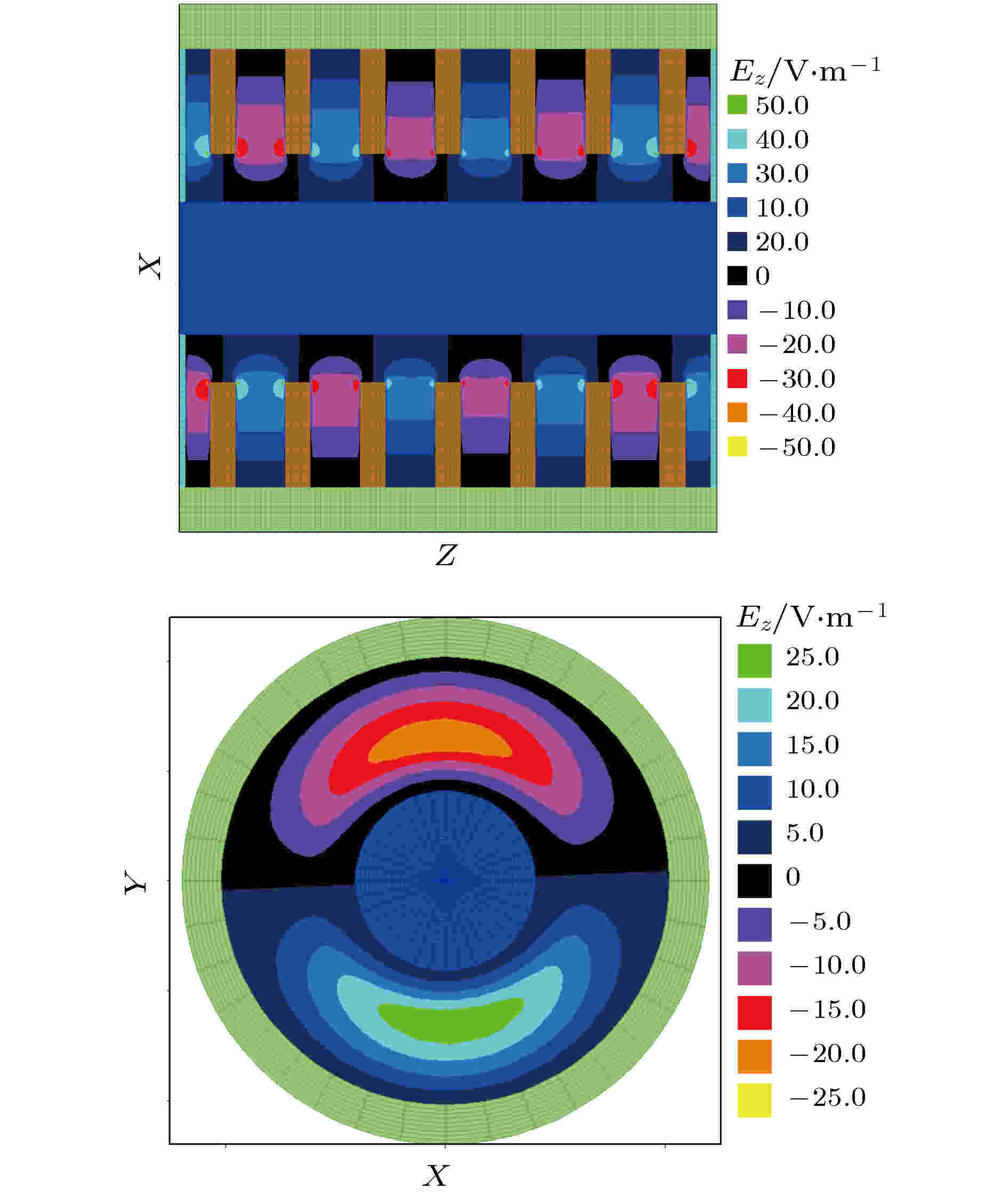
图 5 同轴盘荷波导中HEM₁₁(π模)的轴向电场在　(a) 纵向中心截面和(b)横截面的等高图
Figure5. The contour plots of E_z of the HEM₁₁(π mode)in the coaxial disk-loaded waveguide in the (a) Axial and (b) radial cross section.

已有研究表明: 任何小的结构非对称或者电子发射的非均匀, 都可能在器件运行初期激发HEM₁₁模, 且起振较快, 在器件运行初期很难完全抑制^[19-21]. 由于MILO慢波结构包括反射区、互作用区和提取输出区, 在这些区域, 阳极叶片半径各有差异, 加上输出区还有支撑杆, 导致与TM₀₀模的频率接近的HEM₁₁模容易被激发
尽量保证器件结构的对称性和阴极电子发射的均匀性, 尽管不能够完全消除这种竞争模式, 但可以最大程度地缩短模式竞争的时间和减小竞争模式的强度.

为了获得稳定的高功率微波输出, 基于以上分析和认识, 结合已有工作基础^[3-6,13,14], 设计了一种紧凑型L波段MILO, 其结构示意图如图6所示, 除支撑杆沿角向以90°夹角均匀排列外, 整个结构为轴对称结构, 其中波束互作用区采用的慢波结构为前面部分讨论过的同轴盘荷波导, 点D为后面的模拟计算中在互作用区中设置的观察点. 下面我们对上述MILO中的模式竞争问题和其输出特性进行模拟和分析.
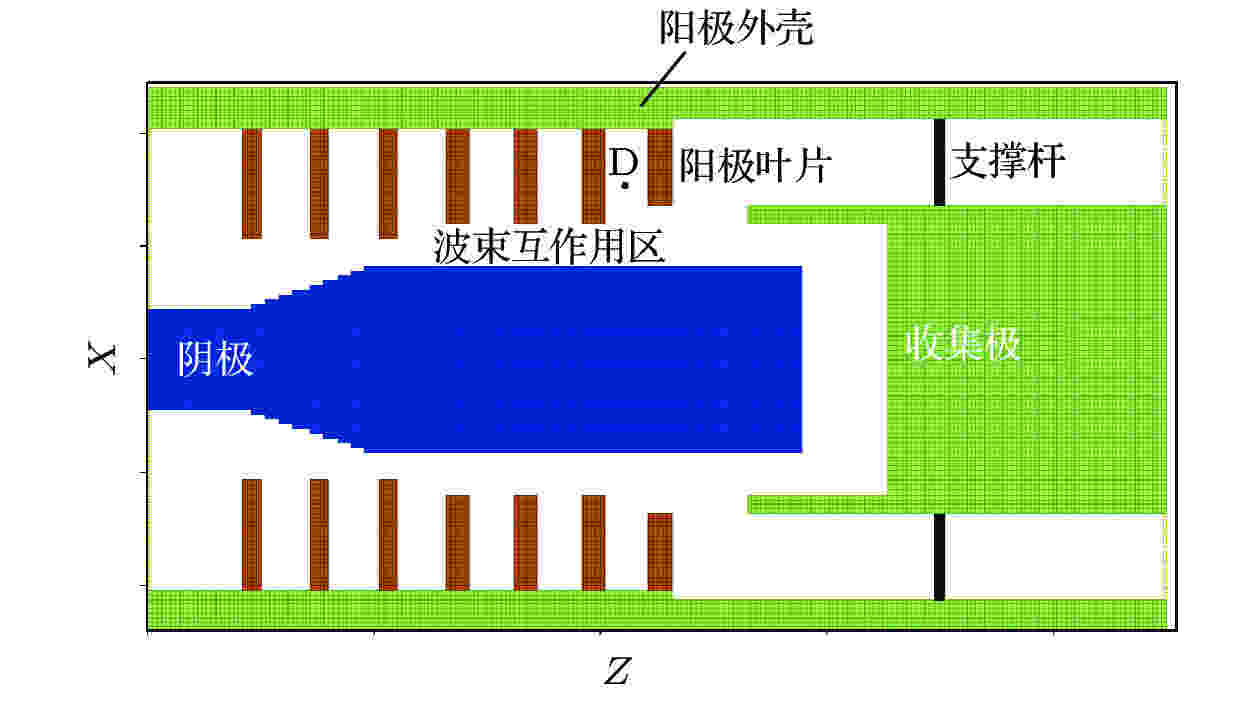图 6 紧凑型MILO纵向截面示意图
Figure6. Schematic drawing of the compact MILO in the axial cross section.

2

-->

3.1.冷腔模拟和分析

为了计算波束互作用区中的共振频率, 将上述MILO的互作用区两端封闭, 同时沿z方向在第四和第五叶片之间加载一个短脉冲宽频信号来激励电磁场振荡. 图7给出了上述激励信号在MILO互作用区中点D的位置激发出的电场频谱图. 由图7可以看到: 在容易被激发的频率中, 较低的两个频率分别为1.61和1.77 GHz.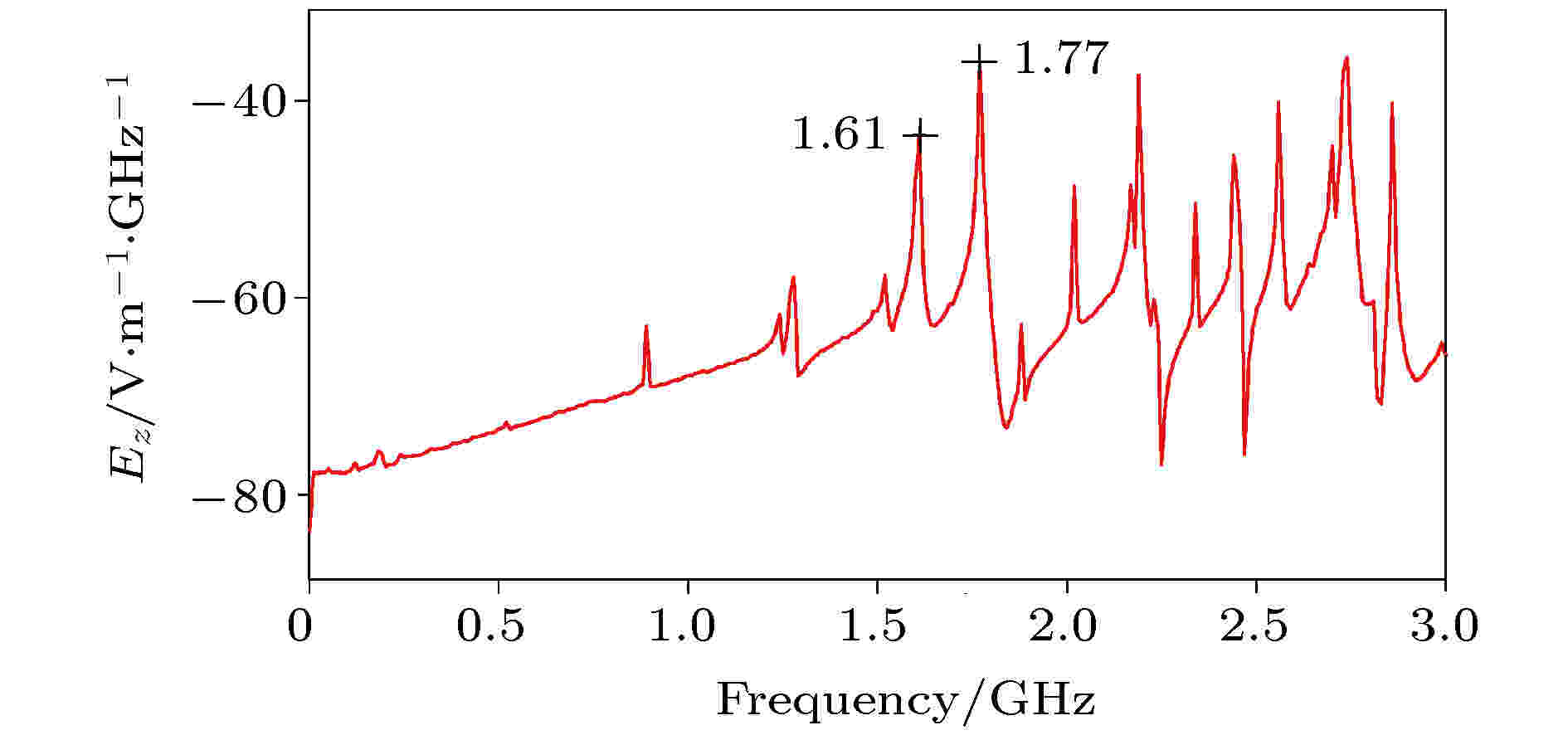
图 7 短脉冲宽频信号激发后MILO互作用区中点D处电场的频谱图
Figure7. The oscillation frequency of the E_z stimulated in cold cavity at point D.

图8(a)、图8(b)和图9(a)、图9(b)分别给出了频率分别为1.61和1.77 GHz时对应的纵向电场在XZ和XY两个截面分布的等高图. 结合前面的分析, 可知这两个频率对应的电磁场模式分别是TM₀₀模和HEM₁₁模的π模. 由此可见, 与基模TM₀₀模相同, 对于HEM₁₁模, 与电子束容易产生相互作用的模式也是π模.
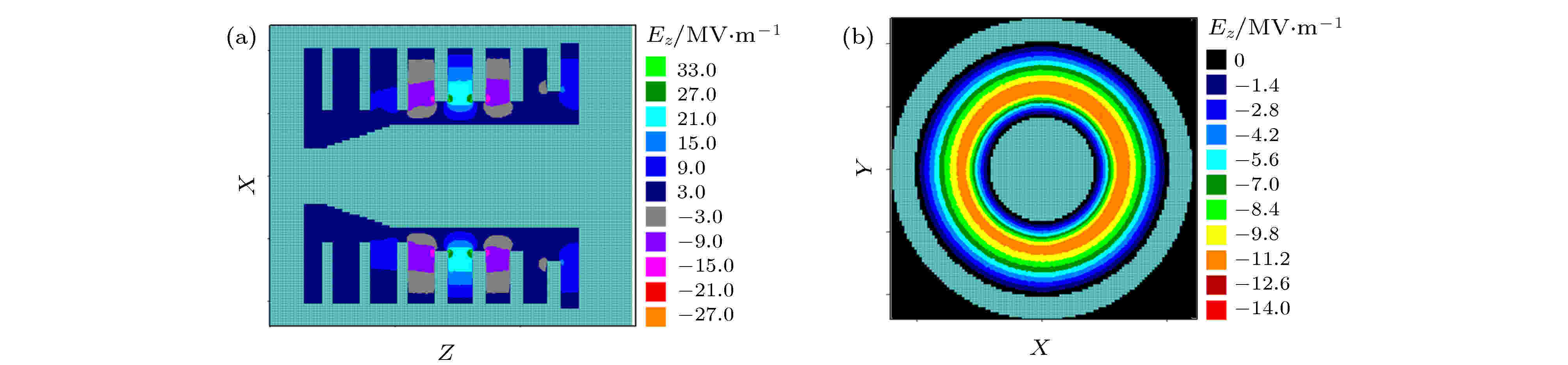图 8 频率为1.61 GHz的纵向电场在　(a) 纵向和(b) 横向截面等高图
Figure8. The contour plots of E_z with the frequency of 1.61 GHz in (a) The axial and (b) the radial cross section.

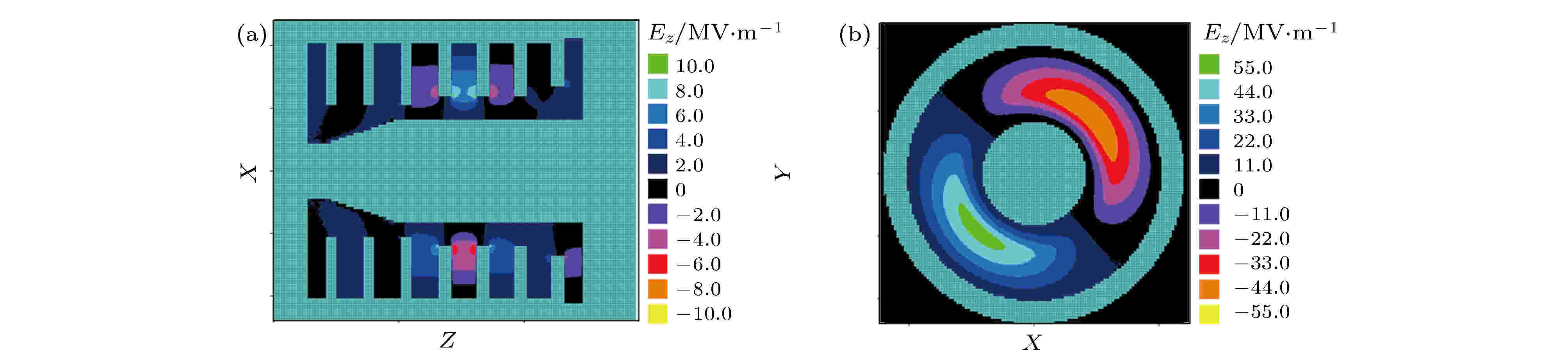图 9 频率为1.77 GHz的纵向电场在　(a) 纵向和(b) 横向截面的等高图
Figure9. The contour plots of E_z with the frequency of 1.77 GHz in (a) The axial and (b) the radial cross section.

2 -->

3.2.热腔的数值模拟及物理分析

下面, 我们利用全电磁三维粒子模拟程序对给出的如图6所示的L波段MILO的输出性能进行数值模拟, 同时考察初始阶段的模式竞争情况, 其中注入的电子束的平均电压约为510 kV, 对应的电功率约为32.8 GW.
图10(a)—(d)和图11(a)—(d)给出了阳极腔内D点电场和磁场随时间的变化曲线及针对不同时段的FFT变换图. 由图10(a)和11(a)可以看到, 辐射场8.0 ns左右开始起振, 大约22.0 ns达到饱和, 其中在8.0至14.0 ns之间, 存在一个小的峰值. 对电磁场按时间分段做FFT变换, 可以得到, 全时段(0—50 ns)的电磁场的中心频率约为1.6 GHz, 但是可以看到有略高于该频率的小峰值, 提示有一定强度的竞争模式; 初期(8—14 ns)的电磁场的频率约为1.7 GHz, 稳定后(> 14 ns), 电磁场的频率约为1.6 GHz, 频谱比较纯, 略高于该频率的小峰值没有出现. 可见, 在起振后的初始阶段, 存在明显的模式竞争; 大约过10 ns左右, 竞争模式被抑制.
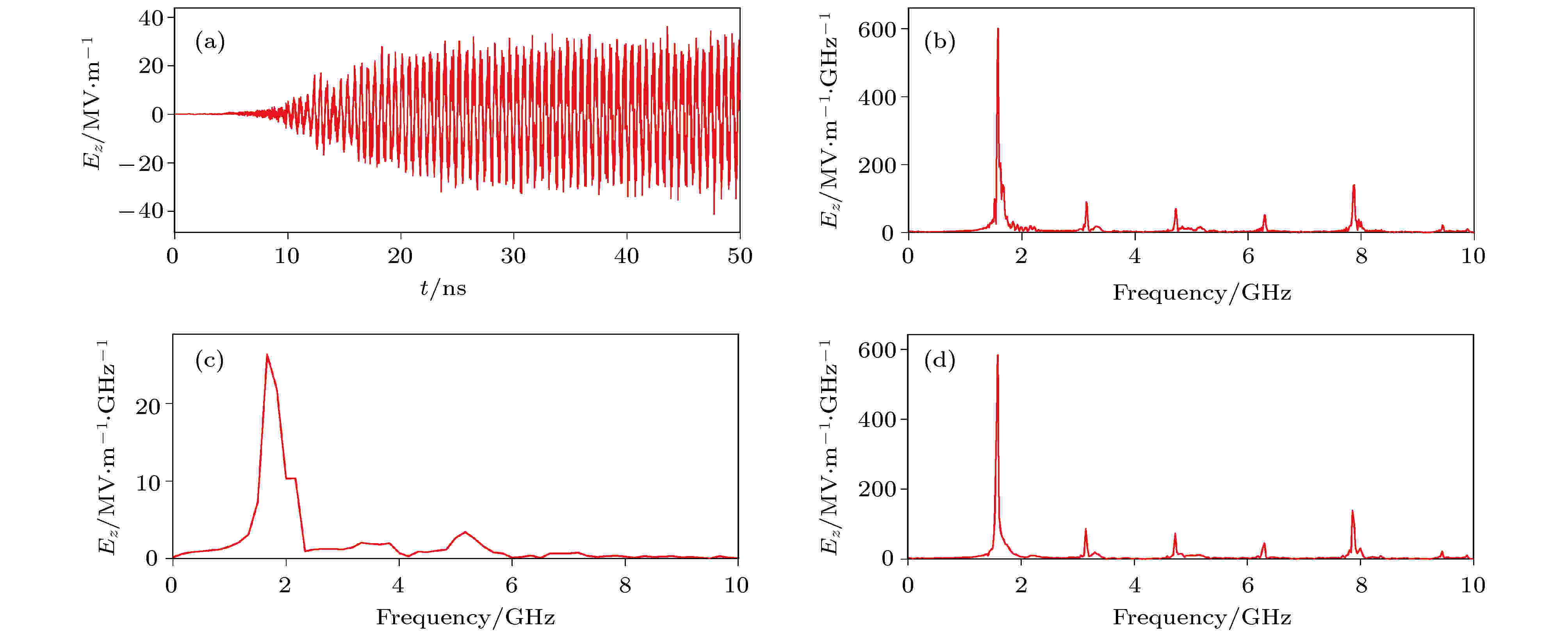图 10 (a) 阳极腔内观察点D的电场E_z随时间的变化曲线及不同时间窗口(b) 0?50 ns, (c) 8?14 ns和(d) 14?50 ns的FFT变换图
Figure10. (a) Variations of E_z with time at the observation point D in the anode cavity; the corresponding Fourier transform with different time intervals: (b) 0?50 ns; (c) 8?14 ns; (d) 14?50 ns.

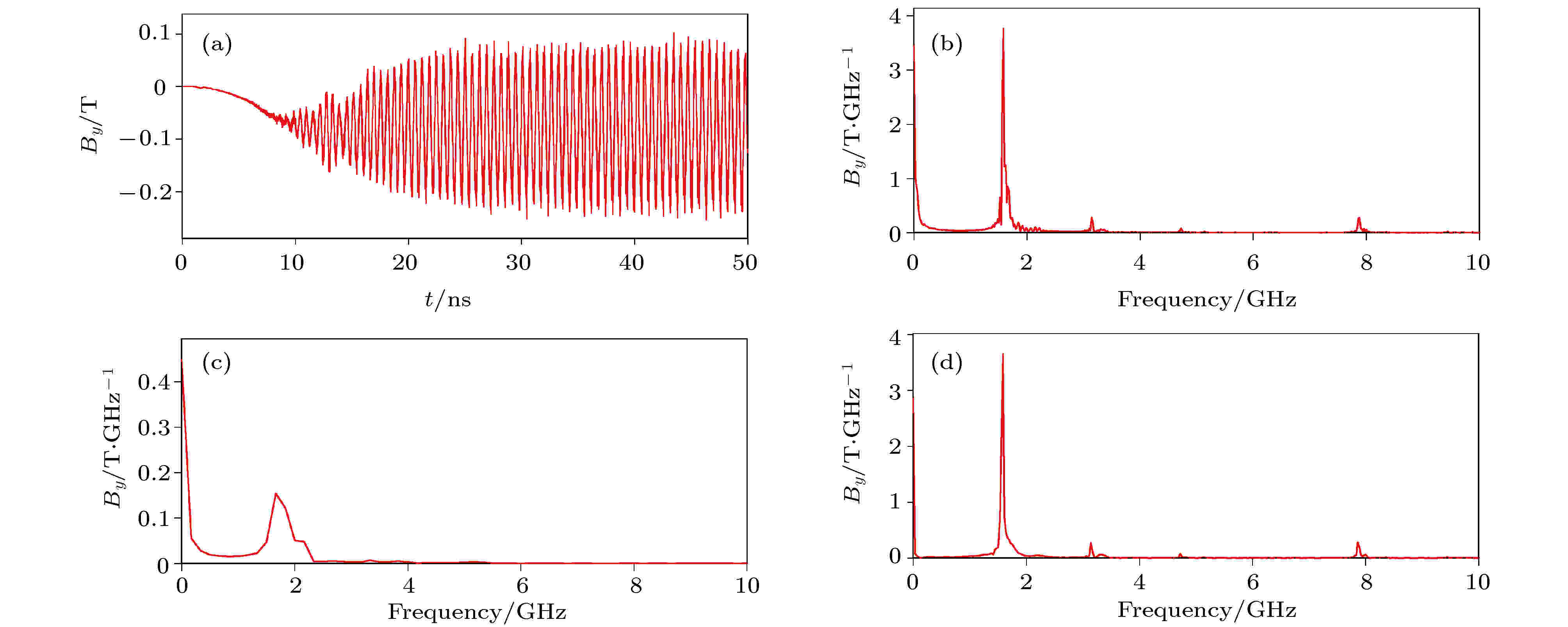图 11 (a) 阳极腔内观察点D磁场B_y随时间的变化曲线及不同时间窗口(b) 0?50 ns, (c) 8?14 ns和(d) 14?50 ns的FFT变换图
Figure11. (a) Variations of B_y with time at the observation point D in the anode cavity, and the corresponding Fourier transform with different time intervals: (b) 0?50 ns, (c) 8?14 ns (d) 14?50 ns.

图12(a)—(d)给出了初始阶段不同时刻互作用区D点所在横截面轴向电场的等高图. 可以看到, 轴向电场沿角向的分布由初期的非轴对称分布, 逐渐转变为轴对称分布. 由轴向电场的分布特征和共振频率, 结合冷腔计算结果, 可以确定, 在初始阶段, 非对称模式HEM₁₁模与TM₀₀模产生竞争; 由于加载了电子束, 因此与冷腔分析时的结果进行比较, TM₀₀模和HEM₁₁模的频率由冷腔时的1.61和1.77 GHz分别降为1.6和1.7 GHz.
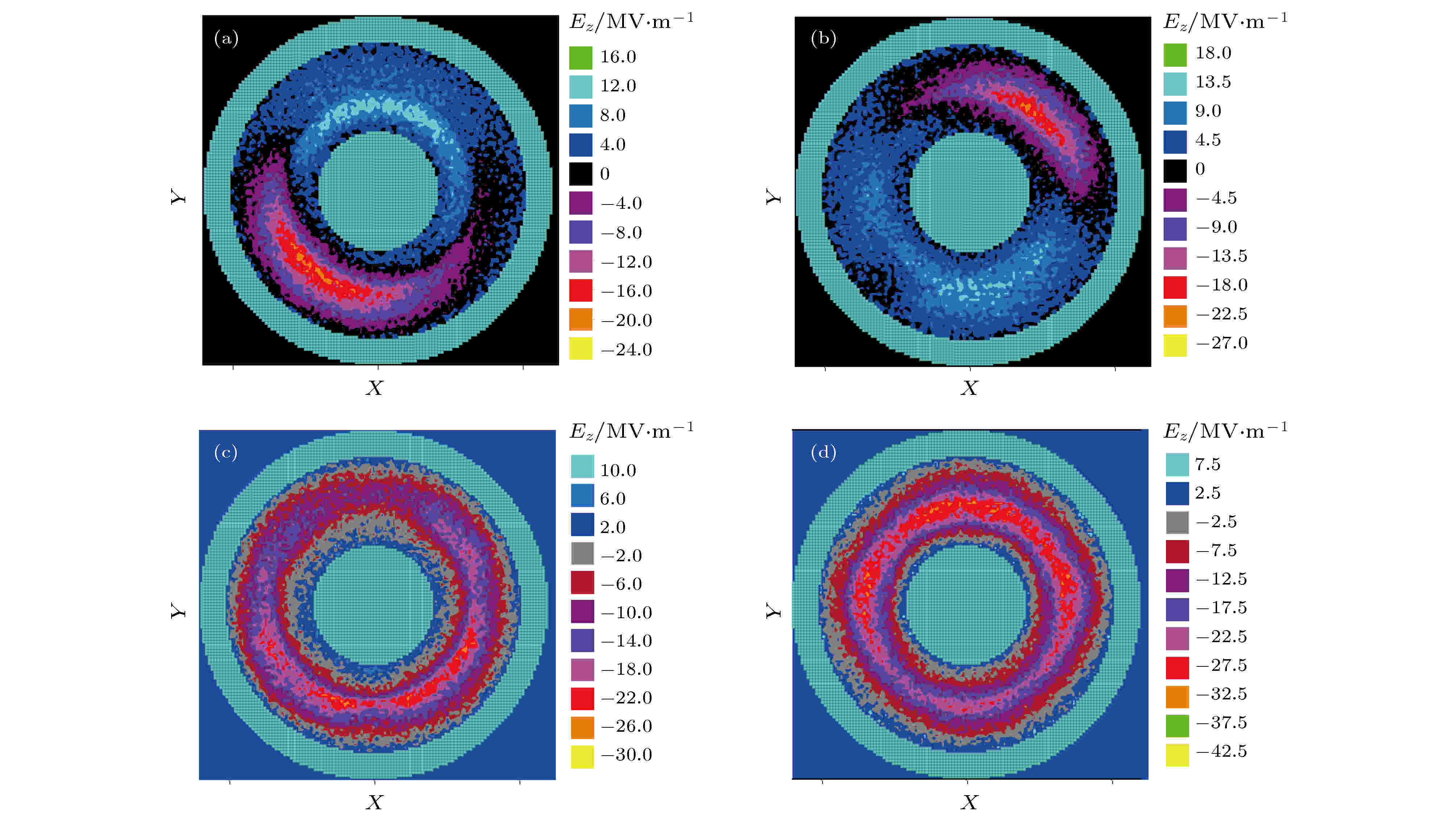图 12 初始阶段不同时刻互作用区横截面轴向电场的等高图　(a) t = 12.171 ns; (b) t = 13.094 ns; (c) t = 14.944 ns; (d) t = 16.793 ns
Figure12. Contour plots of E_z in the interaction region at different times at the initial stage.

由图13(a)和图13(b)给出了饱和时互作用区中轴向电场在纵向和横向截面的等高图, 可以看到, 饱和时轴向电场在互作用区的阳极腔中正负交替排列(π模场分布), 沿角向呈轴对称分布, 与TM₀₀模的场分布完全一致, 因此, 可以确定器件稳定后互作用区的工作模式为TM₀₀模的π模.
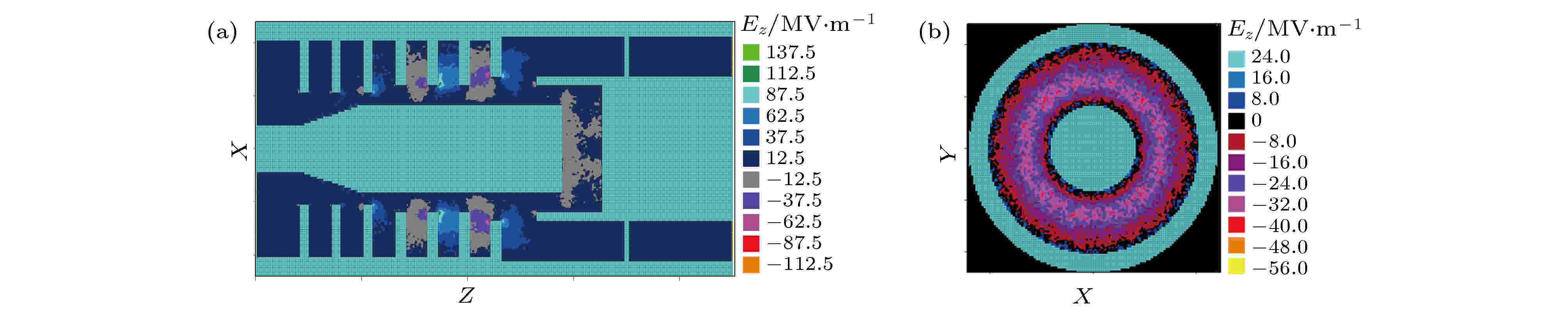图 13 饱和时互作用区轴向电场在(a) 纵向截面和(b) 横向截面的等高图, t = 45.727 ns
Figure13. Contour plots of E_z in the (a) Axial and (b) radial cross section in the interaction region at saturation.

由于是在直角坐标系中建立的三维计算模型, 加上输出区还有支撑杆, 因此互作用区很难实现完全轴对称. 同时, 由于阴极电子发射面大, 电子发射也存在一定的非均匀性, 这些因素使得器件运行初期容易激发HEM₁₁模, 且很难完全抑制. 起振一小段时间后(10 ns左右), 互作用区基模增长加快, 高阶模被抑制.
基于以上分析, 为了提高器件的输出功率和效率, 对器件的参数进行了进一步的优化, 主要调节了互作用区的周期长度和电子束电压, 其他参数保持不变. 模拟结果表明, 当周期长度p为3.1 cm, 注入的电子束的平均电压约为600 kV, 对应电功率约为45 GW时, 器件的输出效率达到了18%.
图14(a)和图14(b)给出了MILO输出周期平均功率随时间的变化曲线以及稳定后输出口电场的FFT变换图. 由图14可以看到, 饱和时输出功率高达8.1 GW, 输出频谱比较纯, 中心频率约为1.552 GHz. 由于MILO的输出区为同轴波导, 输出模式应为同轴TEM模. 图15(a)和图15(b)给出了输出口横截面电磁场分布的箭矢图, 可以看到, 计算所得的电磁场分布确与理想同轴TEM模的分布一致. 利用文献[23]给出的方法, 计算得到了模式纯度约为97%.
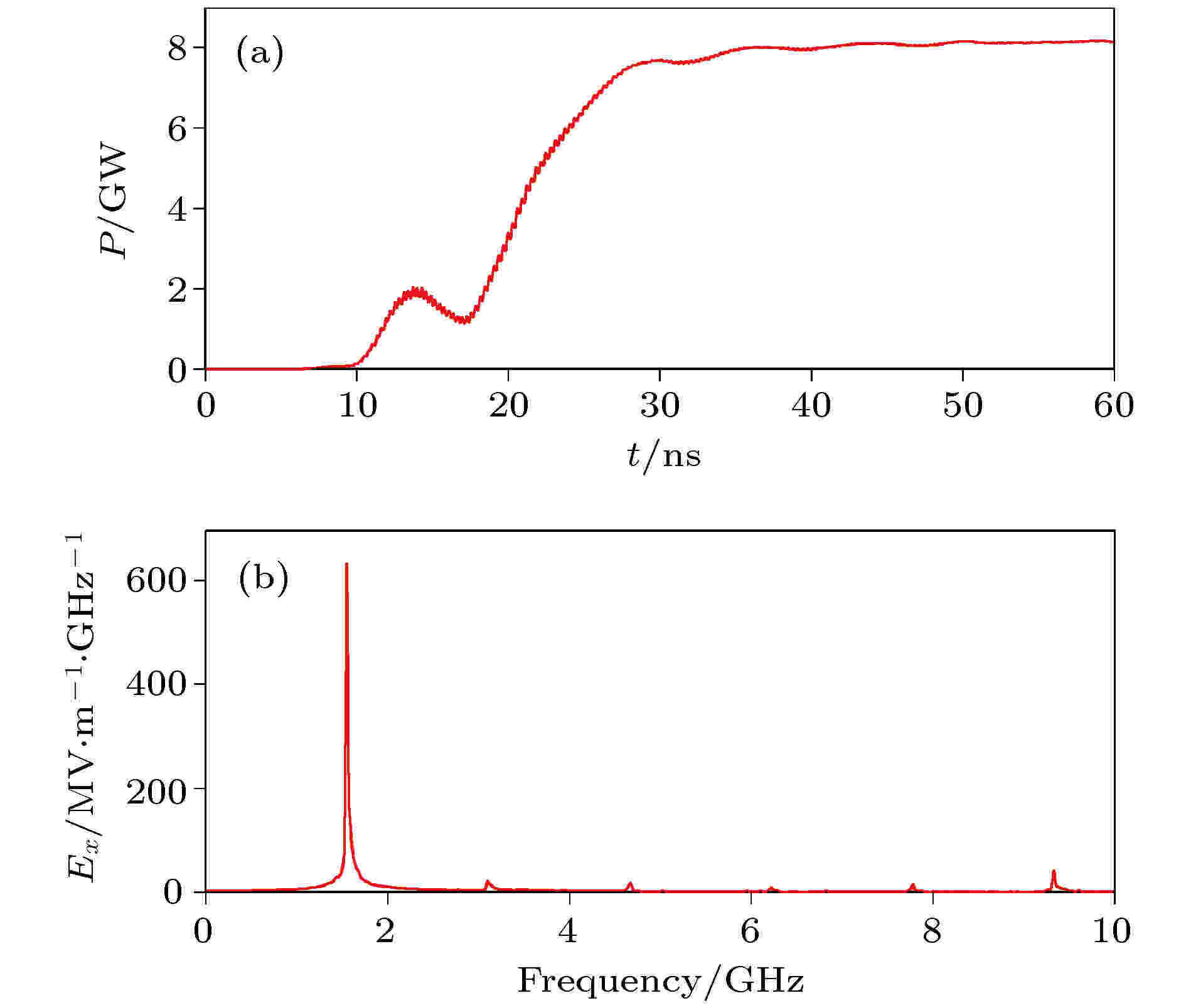图 14 (a) MILO输出周期平均功率随时间的变化曲线; (b)稳定后输出口电场的FFT变换图
Figure14. (a) Time plots of the periodic-average output power of the MILO; (b) the Fourier transform of E_x at the output port.

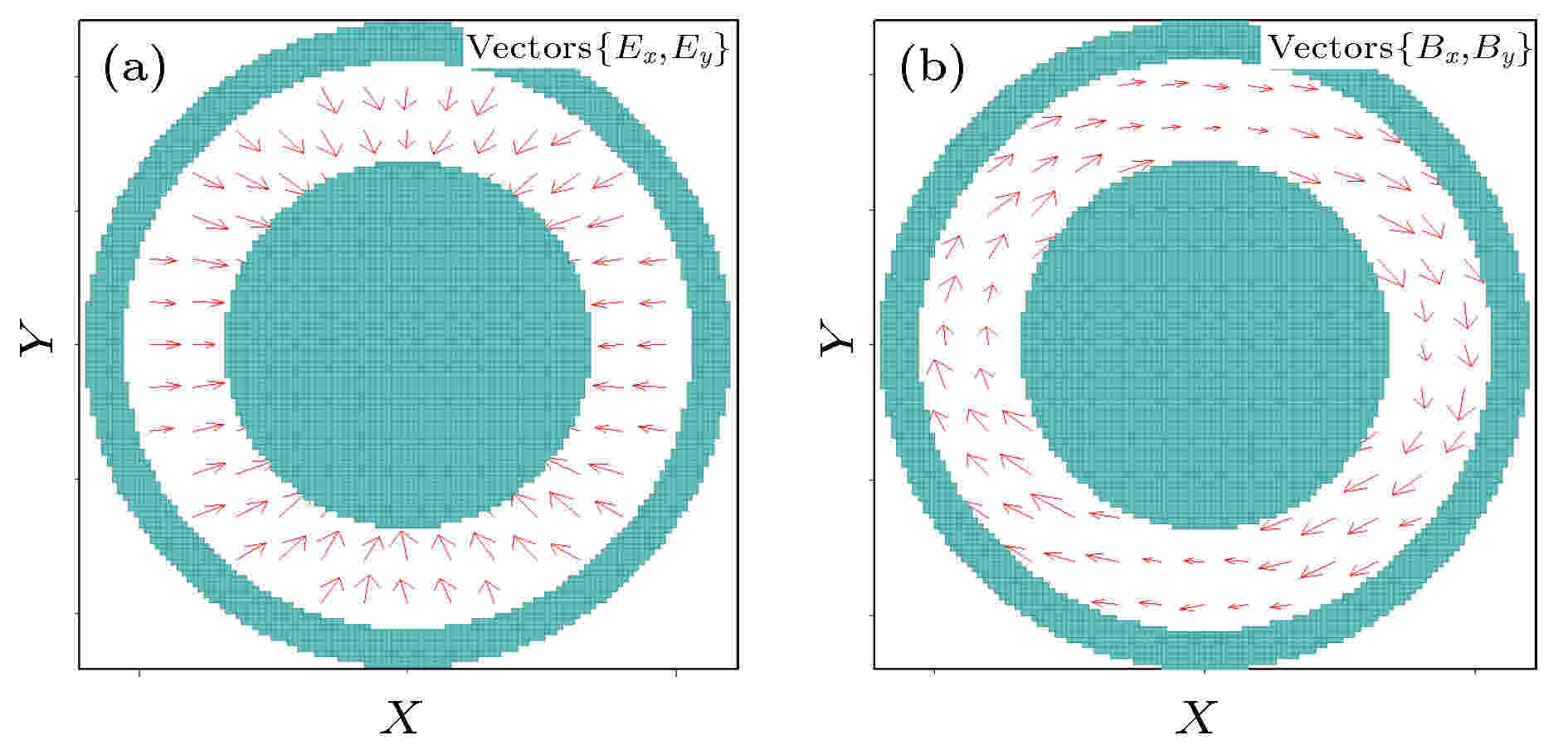图 15 电磁场在输出口横向截面分布的箭矢图　(a) 电场; (b)磁场
Figure15. The vector plots of the (a) Electric field and (b) magnetic field in the radial cross section at the output port.

从同轴盘荷波导中几种可能被电子束激发的低阶模式 (TM₀₀, TM₀₁和HEM₁₁模)的色散曲线与电子束色散曲线关系入手, 简要分析了三种类型的模式竞争的特点和产生的可能原因以及削弱方法, 具体包括基模TM₀₀模相邻纵向模式之间的竞争、高阶对称模TM₀₁与基模之间的竞争以及非对称模HEM₁₁与基模之间的竞争. 在此基础上, 给出了一种稳定紧凑型L波段磁绝缘线振荡器的物理模型, 并利用全电磁三维粒子程序对其中的模式竞争问题进行了数值模拟. 冷腔分析表明: 在容易被激发的本征模式中, 对应频率较低的模式分别是TM₀₀和HEM₁₁的π模, 对应的频率分别为1.61 GHz和1.77 GHz. 热腔的模拟结果表明, 该器件运行初期主要竞争模式是HEM₁₁模, 起振约十个ns后, 竞争模式基本被抑制. 进一步优化后器件在基模获得了高效率和高功率微波输出, 饱和时输出功率约8.1 GW, 输出效率达到了18%, 模式纯度约为97%. 研究结果可为磁绝缘线振荡器运行过程中出现的竞争模式的识别和输出性能优化提供理论参考和依据. 下一步将在控制好模式竞争的基础上改进和优化器件结构, 以进一步提高器件的输出功率和效率.