摘要: 提出并验证了一种高灵敏度复合环形腔结构的激光拍频位移传感技术方案. 该方案采用环形腔复合直腔的谐振腔结构, 利用激光拍频传感原理实现传感系统信号的解调. 该结构通过掺饵光纤放大器提供增益, 采用光纤布拉格光栅作为传感头兼直腔反射镜, 利用π相移光栅进行窄带滤波. 理论分析结果表明激光拍频频率随传感头应变的增加线性减小; 实验结果显示, 当监测频率为1.7483 GHz时, 传感器的灵敏度达到了86.19 kHz/mm, 线性拟合度为0.9973, 最小可分辨位移为10 μm左右, 该系统同时具有空间位置分辨的潜力. 结果表明所提出的新型位移传感方案是可行的, 结构紧凑、简单实用、灵敏度高, 为将来实现高精度、微型化以及分布式传感系统打下基础.
关键词: 光纤激光传感 /
复合环形腔 /
拍频 /
掺饵光纤放大器 English Abstract High sensitivity fiber displacement sensor based compound ring laser cavity with linear variation of beat frequency signal Tian Jing Hou Mei-Jiang Jiang Yang Zhang Hong-Xu Bai Guang-Fu Feng Hao College of Physics, Guizhou University, Guiyang 550025, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 61801134, 61835003, 61965004), the Science and Technology Plan of Guizhou Province, China (Grant No. [2019]1127), and the SRT Program of Guizhou University, China (Grant No. SRT No.20)Received Date: 15 March 2020Accepted Date: 05 May 2020Available Online: 07 June 2020Published Online: 20 September 2020Abstract: A novel fiber sensor based compound ring laser cavity with linear variation of frequency is proposed and demonstrated experimentally. The compound ring laser cavity is comprised of a ring cavity and a straight cavity. This system can generate the beat frequency spectrum by employing an erbium doped fiber amplifier, a fiber Bragg grating is used as a sensor head and the straight cavity reflector, a π phase shifted fiber Bragg grating serves as a microwave photonic passband filter. The principle of the proposed sensor is theoretically analyzed, showing that as the displacement increases the beat frequency decreases, and there exists a linear relationship between displacement change and beat frequency shift. In experiment, it is shown that the sensor has a high sensitivity of about 86.19 kHz/mm and can achieve a good linear response (R 2 = 0.9973), and that the minimum monitored displacement is about 10 μm. The measurement results demonstrate that the sensor is accurate, sensitive, and the proposed sensor system has a compact and simple structure, which makes it convenient for more applications in future.Keywords: fiber laser sensor /compound ring laser cavity /beat frequency /erbium doped fiber amplifier 全文HTML --> --> --> 1.引 言 光纤传感因具有检测灵敏度高、耐腐蚀、抗电磁干扰、成本低廉等特性, 在近几十年中不断完善发展, 被广泛应用于工业自动化和系统监测中[1 -5 ] . 光信号在光纤中传输时可能受到外界诸如温度、应变、压力、电流、位移、振动等因素的影响, 从而对光波的特征参量如光强、频率、波长、相位、偏振态产生调制作用. 光纤传感就是根据这些参量随外界因素的变化关系来检测各相应物理量的变化[6 -12 ] . 近年来基于光纤激光器构成的有源拍频传感系统因频率响应灵敏、信噪比高、线宽窄、结构简单紧凑, 在超声传感和大型结构监测等领域[13 -18 ] 受到了广泛关注. 光学谐振腔作为该传感系统的重要组成部分, 具有高分辨率的频率响应特性和腔内光场增强效应[19 ] , 是提升光纤激光传感灵敏度和测量精度的关键, 若要提高激光传感器的性能, 就需要对光学谐振腔结构以及整个传感系统进行优化和设计.[11 ,12 ] , 该结构采用了环形腔中嵌套直腔的复合环形腔结构, 既便于对位移变化量进行准确监测, 还具有空间位置分辨的潜力, 结构简单紧凑, 灵敏度高. 同时该结构采用的EDFA集成了传统的抽运激光和掺饵光纤功能, 简化了传感系统结构, 可为系统提供稳定增益.2.系统结构与原理 位移传感系统方案如图1 所示, 该系统由激光复合环形腔和观测系统两大部分构成, 其中激光复合环形腔由环形谐振腔和直腔嵌套组成, 观测系统主要由光谱仪(optical spectrum analyzer, OSA)和电频谱仪 (electrical spectrum analyzer, ESA)等组成. EDFA为系统提供稳定增益, 光在腔内顺时针传播并相互干涉, 得到不同模式的纵模激光. 当谐振腔内增益大于损耗时, 在滤波器 (Filter) 和π-FBG的选模作用下, 激光器会输出多个离散的激光拍频模式. 这些激光模式经耦合器后, 70%的光场在复合谐振腔环路中振荡, 另外30%接入观测系统. 该传感器结构中, 偏振片 (polarization controller, PC) 用于调节光信号的偏振态, 光隔离器 isolator, ISO) 用于保持光的单向传输, 检偏器 (polarizer, POL) 使得光路保持线偏振. 光场由环形器 (circulator, Cir) 1端口进入传输到2端口, 2端口接传感头和π-FBG, 其中FBG与π-FBG构成直腔, 最后经FBG与π-FBG反射的信号光经由环形器3端口输出, Filter对反射的光波进行带宽限制和杂波滤除. 利用微位移平台对传感头进行水平拉伸使光纤产生水平轴向位移变化, 从而改变复合谐振腔的腔长, 导致拍频信号发生漂移. 激光拍频模式经光电探测器 (photodetector, PD)光电转换后通过ESA进行频谱监测, 根据监测频率的漂移量与位移的变化关系即可实现位移变化监测和预警.图 1 位移传感方案原理图Figure1. Schematic diagram of the proposed fiber laser displacement sensor.图2 ), 多纵模激光信号在光路中两两拍频, 不同的拍频频率$\nu,\; 2\nu,\; 3\nu,\; 4\nu,\; \cdots,\; (n - 1)\nu,\; \cdots, N\nu$ 可由激光的任意j 模式或i 模式拍频产生, 只要分别满足$j - i = 1,\;2,\;3,\;4,\; \cdots,\; \left( {n - 1} \right), \cdots, N$ 即可. 由于光电探测器不能响应高频信号, 只响应低频信号, 因此探测后信号强度可以表示为[20 ] 图 2 π-FBG反射谱与激光器纵模关系Figure2. Fiber laser cavity’s excited longitudinal modes controlled by π-FBG’s bandwidth.${\alpha _i}$ , ${\alpha _j}$ 是频率为${\nu _i}$ , ${\nu _j}$ 的激光模式的振幅; ${\varphi _i}$ , ${\varphi _j}$ 是两激光模式的原始相位; ${\nu _i} \!-\! {\nu _j}$ ($i, j \!=\! 1, 2, 3, 4, {\rm{ }} \cdots ; \;N = j - i$ ), 是两个纵模模式光的差频, 称为拍频, 可用${\nu _N}$ 表示,2 )式推导得到相邻纵模频率间隔${\nu _1},\;{\nu _2},\; \cdots ,\; {\nu _i}, \;{\nu _j}$ 都是激光的纵模模式, 当$j - i = 1$ , $\nu = c/nL$ 称为基频, 是所有相邻模式的两两拍频, 除此之外都是基频的高倍频. c 是真空中的光速, n 是光纤的折射率, L 是光在谐振腔内完成一次循环走过的几何路程, 对于复合环形腔系统$L = {L_1} + 2{L_2}$ (图1 ). 对于直腔而言, 光完成一次循环走过的几何路程是直腔腔长的2倍. 可见对于一个确定的激光器, 只要腔长L 不变, 其拍频间隔ν 恒定. 当谐振腔中放入π-FBG或FBG时, 由于它们的带宽限制, 只有在带宽范围内的激光模式才能振荡, 因此系统中使用π-FBG滤波将会大大提高拍频模式的强度.${\nu _N}$ 与轴向位移变化的关系为${P_{\rm{e}}}$ 是光纤的有效弹光系数, $\Delta L$ 是轴向位移. 从(4 )式可见, 拍频信号$\Delta {\nu _N}$ 与$\Delta L$ 轴向位移呈线性关系.3.实验结果与分析 实验使用了3 dB带宽为50 pm的π-FBG, 其反射率为99%, 中心波长为1550.452 nm; 采用的FBG的反射率为85%, 中心波长为1550.4 nm. 实验过程中调节滤波器的中心波长, 三者光谱如图3(a) 所示. 实验使用OSA测量出射激光的光谱, 如图3(b) 所示, 其出射的峰值波长与π-FBG的反射中心基本一致, 该复合环形腔产生的激光线宽比较窄, 激光强度为–10 dB左右. 将此激光导入PD, 经光电转换后被ESA观测.图 3 (a) Filter, FBG与π-FBG的光谱; (b) 激光复合谐振腔光谱Figure3. (a) Optical spectra of Filter, FBG and π-FBG; (b) optical spectrum of the compound ring laser sensor cavity.图4 所示, 可以看出拍频范围达到了4 GHz, 由(4 )式可知, 选取的拍频监测频率越高, 得到的拍频频率变化量越大. 图5(a) 和图5(b) 所示是两套频率不同的拍频观测信号, 显示有两套谐振腔, 其中图5(a) 的拍频间距为27 MHz, 根据(3 )式能计算出对应的光纤激光谐振腔长度为3.7 m, 与实测该传感结构中直腔的腔长一致; 图5(b) 的拍频间距为3 MHz, 同理计算得到腔长大致为67.7 m, 结合实际情况, 该拍频间距可对应为图1 中复合环形腔的拍频间距. 由于直腔与环形腔腔长不同, 对应的拍频间距不同, 如果其中一个腔长发生拉伸位移, 与其相应腔的拍频间距就会发生变化, 根据不同腔长拍频间隔的变化情况, 就可以对位移发生的空间位置进行分辨, 因此该传感器系统具有空间位置分辨的潜力. 若系统中多加几个相同中心波长的FBG, 并形成不同长度的直腔, 就能更有效地分辨传感的空间位置, 进而实现传感器的大范围分布式监测.图 4 电频谱仪输出的拍频信号Figure4. Beat frequency spectra of BFS.图 5 (a) 直腔拍频频谱图; (b) 复合环形腔拍频频谱图Figure5. (a) Beat frequency spectrum of straight cavity; (b) beat frequency spectrum of compound ring laser cavity.图6 所示, 频率范围从1.74824 GHz到1.74834 GHz(即100 kHz). 为验证传感器的线性拟合度和灵敏度, 传感器两端分别固定在两个微位移平台上, 当对平台进行微调移动时, 应变就加载在传感头上, 位移变化可由平台自带的千分尺读出. 由于实验所用传感光纤较短, 根据传感光纤的拉伸极限, 实验中将位移测试范围定在0—0.18 mm范围内. 为了验证理论与实验的一致性和实验方案的可行性, 用微位移平台对传感头在其可承受范围内进行随机位移长度拉伸, 如拉伸位移为0.01, 0.05, 0.09 和0.11 mm等, 总共11个位移变化量, 得到的位移与频率的关系如图7 所示, 随着拉伸位移的增加, 频率线性减小, 其线性拟合斜率为–86.189, 线性拟合度高达0.9973, 灵敏度达到了86.19 kHz/mm, 最小可分辨位移为10 μm左右(图6 ). 由数据分析可见实验结果与理论推导基本一致. 实验过程中, 传感器暴露在室温环境下, 由于实验耗时较短, 室内温度变化不明显, 所以温度对传感器腔长变化的影响可不予考虑, 实验中光纤的双折射、色散等效应都会对传感系统具有一定的增敏作用. 如果想同时探测温度的变化, 只需要在此结构基础让FBG处于自由状态, 利用波长监测设备同时监测传感器的波长变化信息即可.图 6 位移与频移关系图Figure6. Beat signal spectra shifts as a function of displacement variations.图 7 位移传感实验结果分析Figure7. Measured results analysis of the displacement sensor.4.结 论 本文主要提出了一款新型高灵敏度复合环形腔结构的激光拍频位移传感方案, 采用了环形腔中嵌套直腔的复合环形腔结构, 便于对位移变化量进行准确监测, 具有对传感的空间位置进行分辨的潜力, 结构简单紧凑, 灵敏度高. 同时该结构使用EDFA为光纤激光谐振腔提供增益, 替代了以往的利用抽运激光和掺饵光纤分别为激励源和增益介质的光路焊接传感系统, 简化了传感系统结构. 最终利用EDFA结合FBG、π-FBG的高反射率、窄带滤波功能成功搭建了一款复合腔结构的激光纵模拍频传感器系统. 通过实验验证, 该款传感器的线性拟合度达到了0.9973, 当监测频率为1.7483 GHz时灵敏度达到了86.19 kHz/mm, 最小可分辨位移为10 μm左右. 结果表明所提出的新型位移传感方案是可行的, 结构设计简单、实用、灵敏度高, 为进一步实现高精度、微型化、分布式传感器系统打下基础. 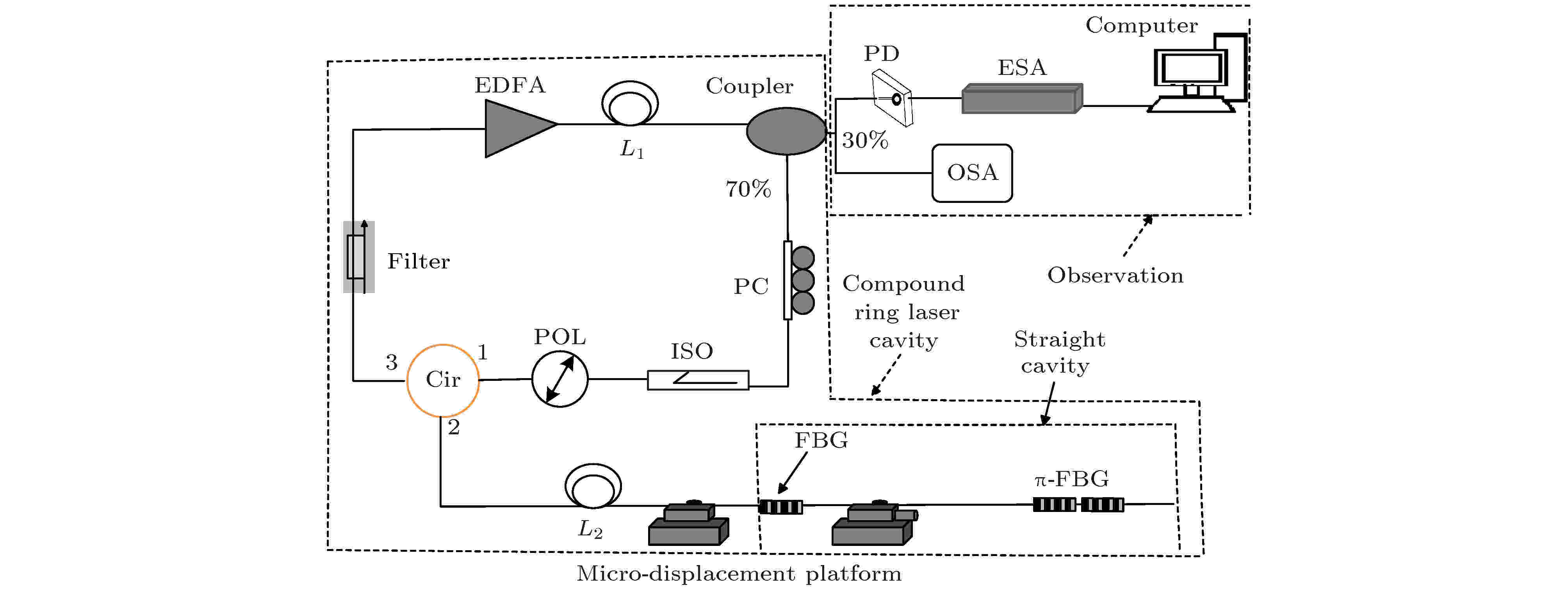 图 1 位移传感方案原理图
图 1 位移传感方案原理图

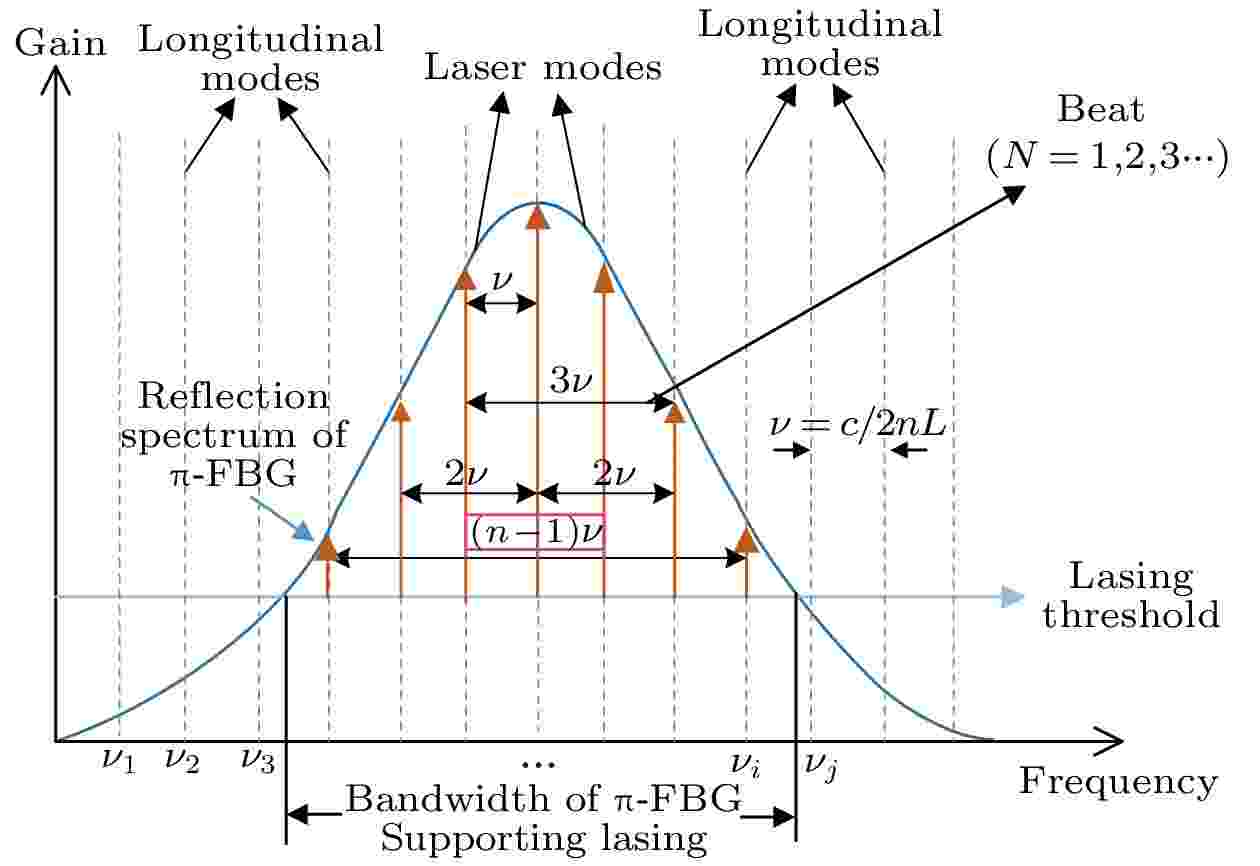 图 2 π-FBG反射谱与激光器纵模关系
图 2 π-FBG反射谱与激光器纵模关系



















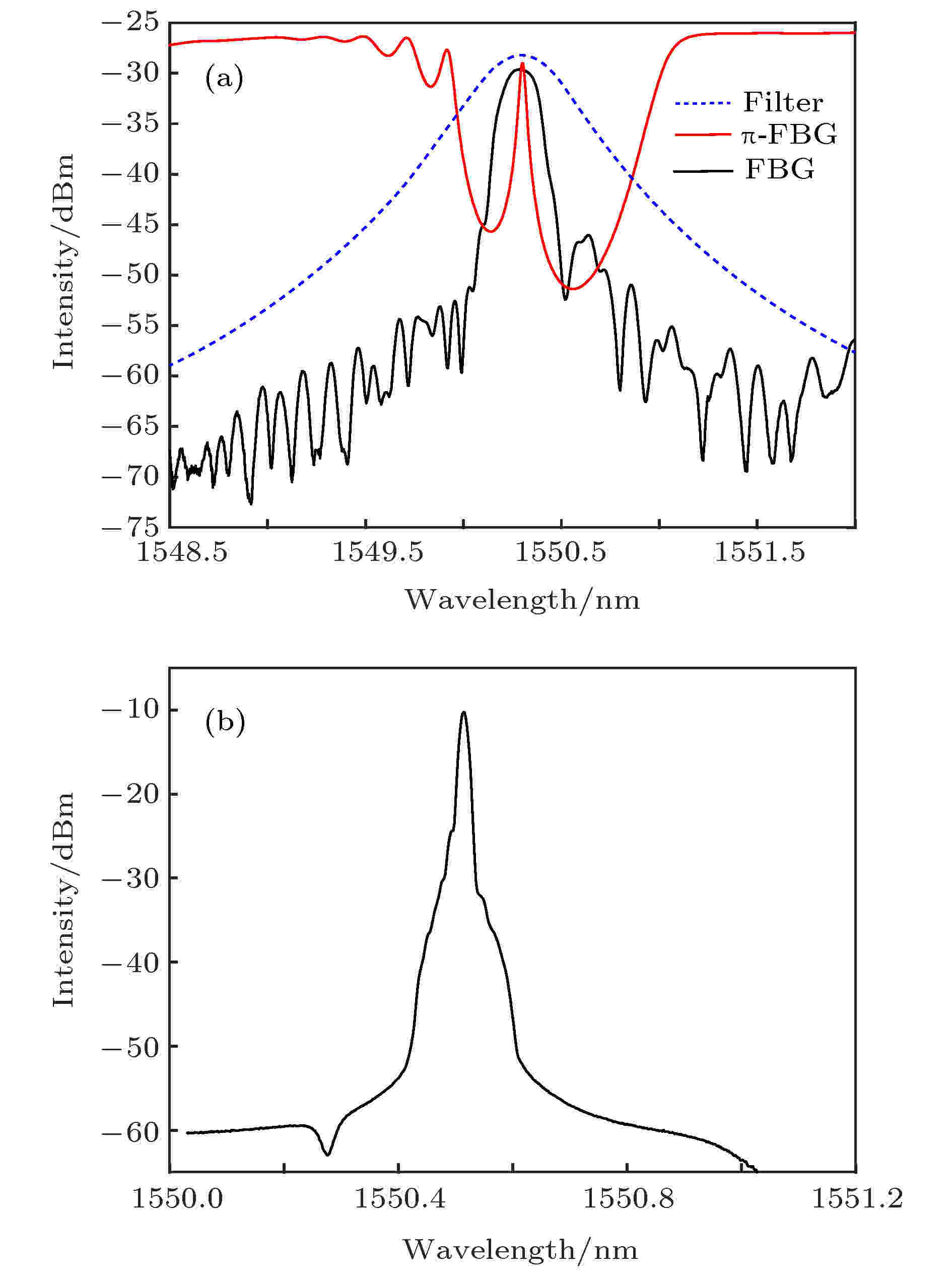 图 3 (a) Filter, FBG与π-FBG的光谱; (b) 激光复合谐振腔光谱
图 3 (a) Filter, FBG与π-FBG的光谱; (b) 激光复合谐振腔光谱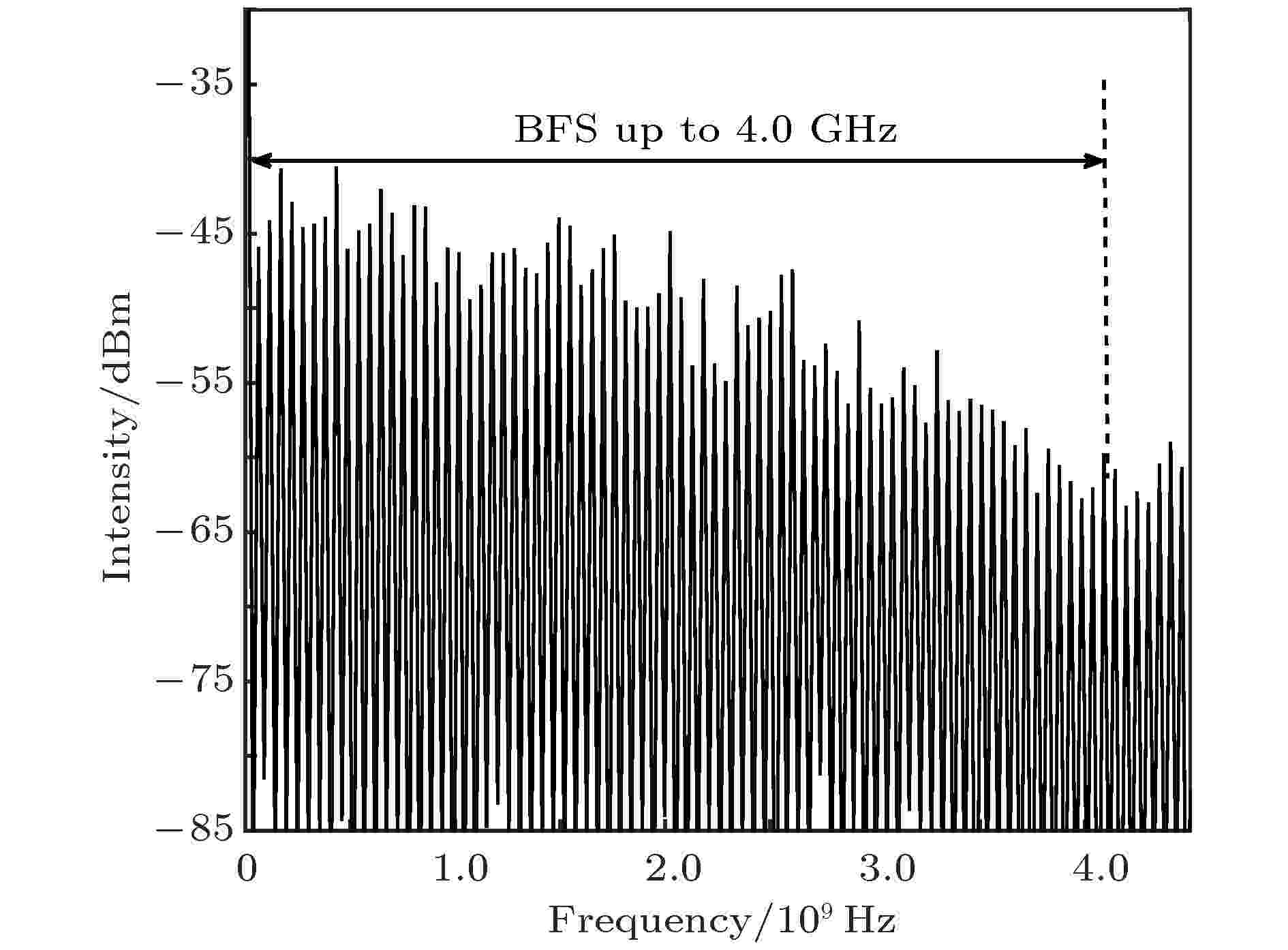 图 4 电频谱仪输出的拍频信号
图 4 电频谱仪输出的拍频信号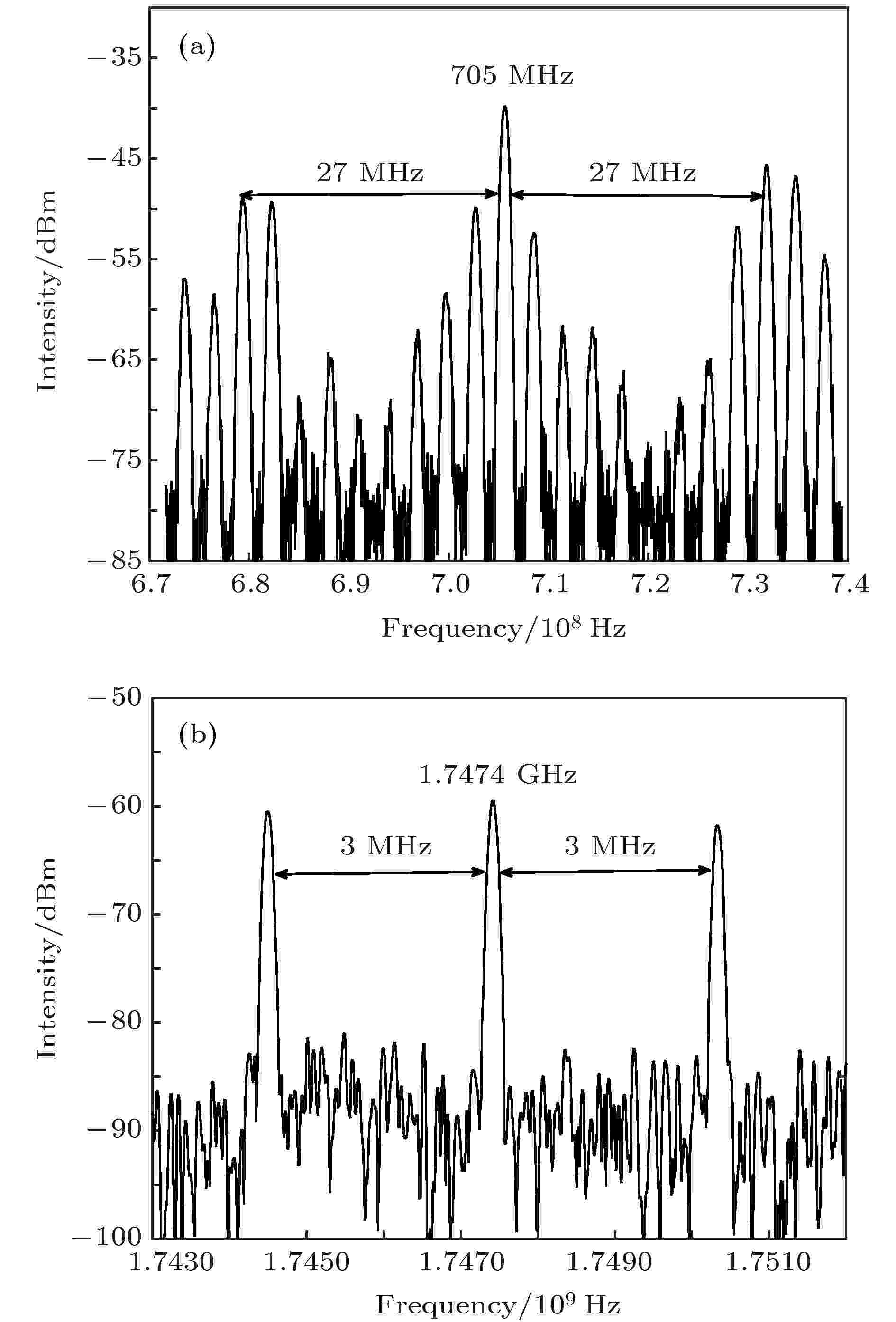 图 5 (a) 直腔拍频频谱图; (b) 复合环形腔拍频频谱图
图 5 (a) 直腔拍频频谱图; (b) 复合环形腔拍频频谱图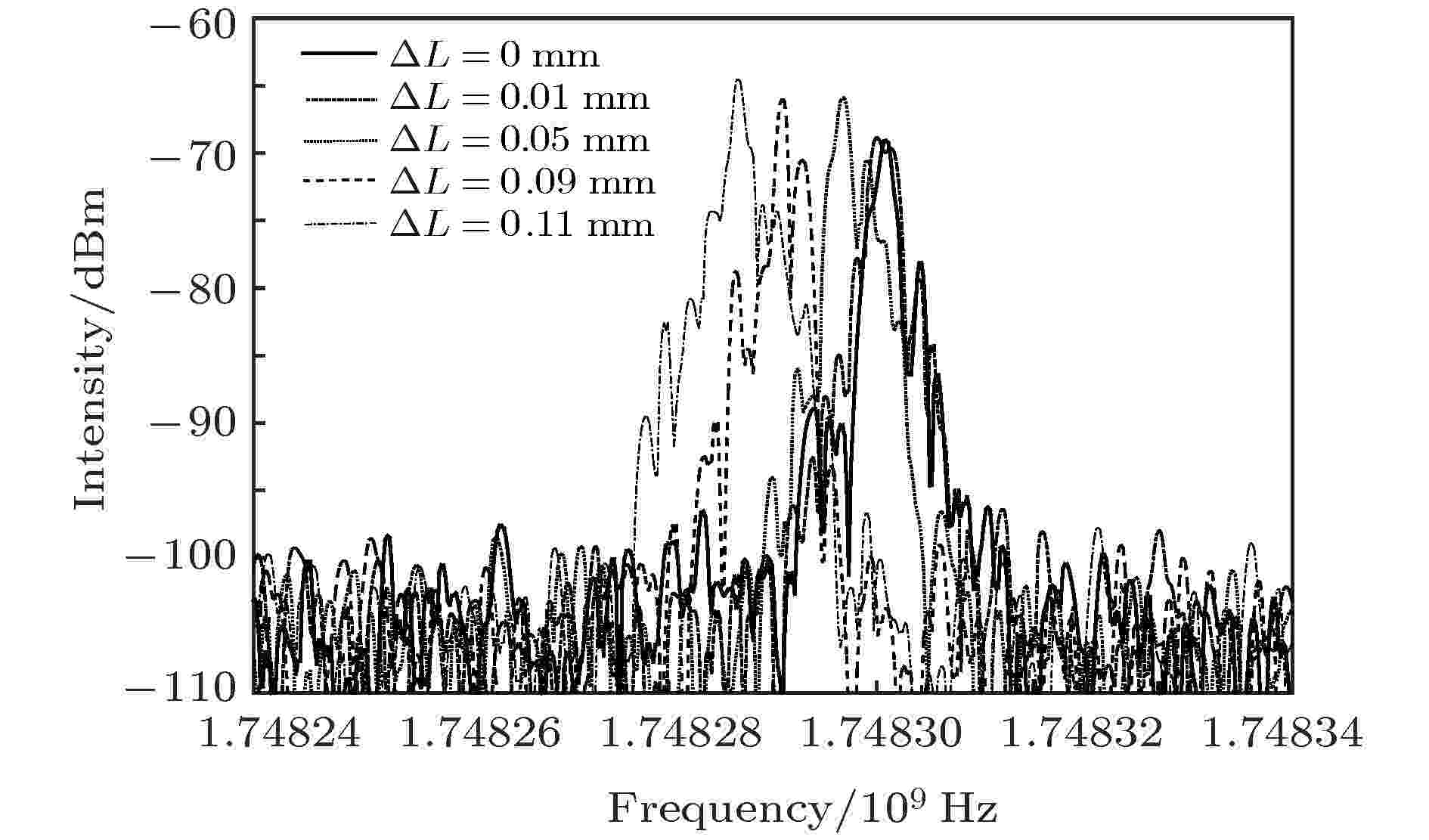 图 6 位移与频移关系图
图 6 位移与频移关系图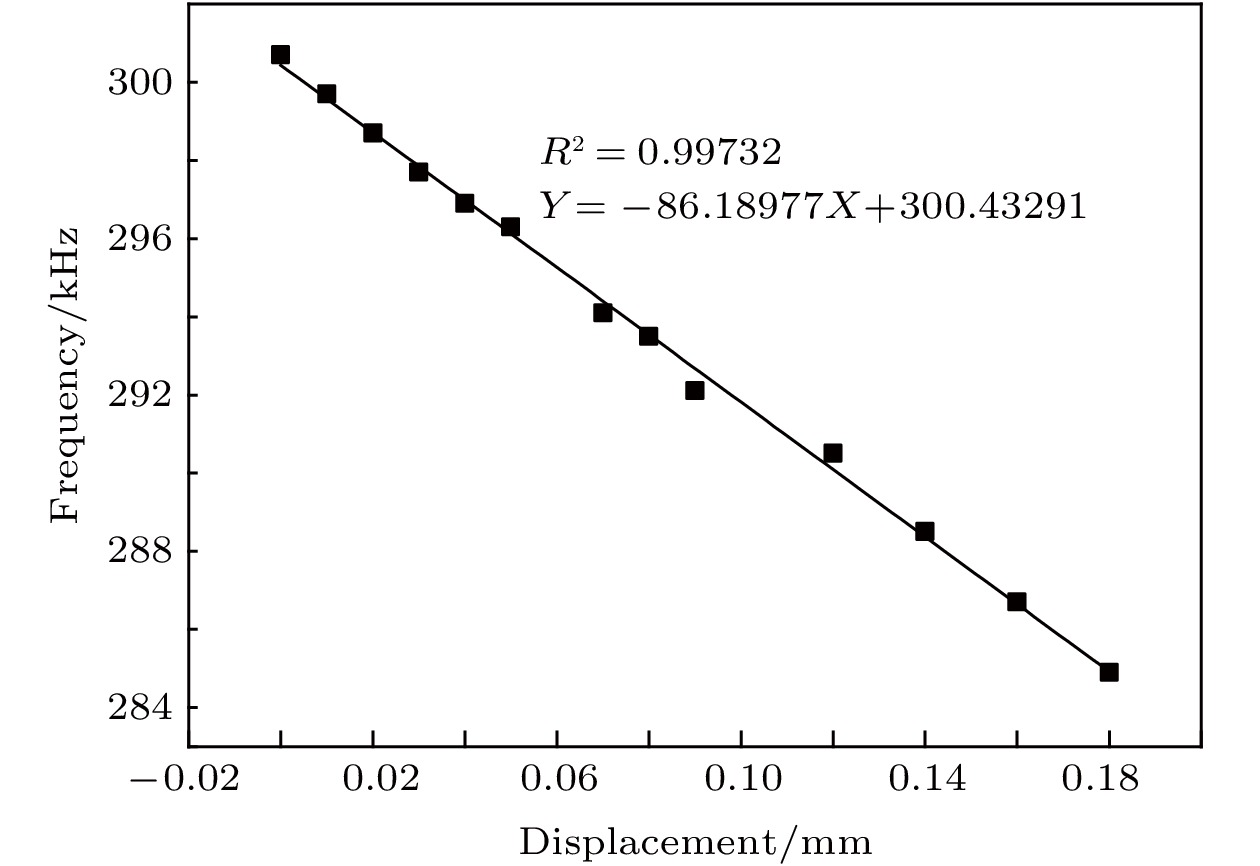 图 7 位移传感实验结果分析
图 7 位移传感实验结果分析