摘要:为了有效改善二维工具头辐射面振幅分布不均匀的问题, 对二维超声塑料焊接系统进行了优化设计研究: 首先, 利用横向位错在大尺寸长条形工具头上构造近周期声子晶体同质位错结, 调节带隙的宽度和位置, 使得二维超声塑料焊接系统的工作频率位于工具头的横向振动的带隙内, 进而有效地控制工具头X方向的横向振动; 其次, 利用近周期声子晶体斜槽结构进一步优化辐射面的振幅分布均匀度, 并分析了斜槽结构参数对超声塑料焊接系统纵向共振频率和振幅分布均匀度的影响规律. 模拟仿真结果表明, 近周期声子晶体同质位错结和斜槽结构能够实现对二维超声塑料焊接系统的优化, 为横向振动抑制理论的进一步研究提供了基础.
关键词: 近周期声子晶体/
同质位错结/
斜槽结构/
振幅分布均匀性

English Abstract

全文HTML

--> --> -->

超声塑料焊接工具头是超声塑料焊接系统中一个非常重要的部件, 其设计的好坏直接影响到焊接的质量, 工具头需要根据焊件进行专门的设计, 常见的有长方体、圆柱体等^[1,2]. 当工具头的横向尺寸小于四分之一纵波波长时, 可以忽略横向振动对振动工具头的影响, 通常只考虑工具头的一维振动^[3]; 但是当工具头的横向尺寸接近或大于四分之一纵波波长时, 工具头会产生严重的横向振动, 横向振动和纵向振动相互耦合使得工具头辐射面的振幅分布不均匀, 使得振动能量不能均匀的传递到焊件的表面, 严重时甚至可以引起塑料产品漏焊或局部溢料, 影响焊接质量. 为了使大尺寸工具头纵向振动时辐射面的振幅分布均匀, 必须对工具头的横向振动进行抑制^[4-7].
针对上述问题, 国内外****都进行了相关研究. Adachi和Ueha ^[8]利用附加振动器实现了工具头辐射面上均匀的振幅分布. Mori等^[9]从工程应用的角度出发, 提出了表观弹性法理论, 应用该理论可以得到大尺寸振动工具头耦合振动的基频解; Lucas和Smith等^[10]提出了利用电子散斑图案干涉法和激光多普勒测速法的工具头设计方法, 可以通过对有限元模型的修改来成功完成垫铁的重新设计; Lee等^[11]通过在变幅杆的两侧开槽的方法, 一定程度上改善了振动系统的振幅均匀性; Nguyen等^[12]提出了一种利用阶梯式宽叶片工具头来实现焊接面振幅均匀的方法; Kumar等^[13]使用MINITAB软件分析了槽参数对振幅的影响, 并确定了槽的最佳尺寸; Rani等^[14]通过实验设计分析, 确定开槽对模态频率和振幅均匀性的影响, 从而得到使振幅分布更加均匀的变幅杆最佳设计参数. 国内, 林书玉等^[15]、周光平等^[16]、赵甜甜等^[17]、林基艳等^[18]都进行了抑制矩形工具头耦合振动的研究. 以上这些研究用到的主要方法是附加振动器、调整变幅杆的形状、或工具头上加工若干平行于工具头高度方向的垂直槽, 以减弱横向振动的干扰, 但抑制效果有时并不理想. 基于此, 本文提出了基于声子晶体位错理论的二维超声塑料焊接系统的研究, 运用近周期声子晶体同质位错结和斜槽结构有效控制工具头的横向振动, 进一步改善工具头辐射面的纵向振动位移分布的均匀度, 并分析了斜槽高度、宽度、倾斜角度与工具头纵向共振频率、振幅分布均匀度变化的关系, 为二维超声塑料焊接系统的优化设计提供更多的理论依据.

2

-->

2.1.大尺寸二维工具头的耦合振动理论

设大尺寸二维长条形工具头沿X, Y及Z方向的长、宽、高分别为l, w, h, 其辐射面为长条形的工具头, 即l, h $ \gg $ w, l与h接近. 根据弹性力学原理, 振动工具头内任意一点的轴向应力σ_x, σ_y, σ_z与轴向应变ε_x, ε_y, ε_z之间的关系为^[9]

${\varepsilon _x} = [{\sigma _x} - \upsilon ({\sigma _y} + {\sigma _z})]/E, $

${\varepsilon _y} = [{\sigma _y} - \upsilon ({\sigma _x} + {\sigma _z})]/E, $

${\varepsilon _z} = [{\sigma _z} - \upsilon ({\sigma _x} + {\sigma _y})]/E, $

其中, E表示材料的杨氏模量, 而$\upsilon $则代表材料的泊松系数. 设E_x, E_y, E_z为工具头的表观弹性系数, λ₁, λ₂, λ₃为工具头轴向间的耦合系数, 则${E_x} = $${\sigma _x}/{\varepsilon _x},\; {E_y} = {\sigma _y}/{\varepsilon _y}$, ${E_z} = {\sigma _z}/{\varepsilon _z},\; {\lambda _1} = {\sigma _x}/{\sigma _y},\; {\lambda _2} =$${\sigma _y}/{\sigma _z},\; {\lambda _3} = {\sigma _z}/{\sigma _x}$. 由(1)—(3)式可得

${E_x} = E{\rm{/[1}} - \upsilon {\rm{(}}{\lambda _{\rm{3}}}{\rm{ + 1/}}{\lambda _1}{\rm{)]}}, $

${E_y} = E{\rm{/[1}} - \upsilon {\rm{(}}{\lambda _1}{\rm{ + 1/}}{\lambda _2}{\rm{)]}}, $

${E_z} = E{\rm{/[1}} - \upsilon {\rm{(}}{\lambda _2}{\rm{ + 1/}}{\lambda _3}{\rm{)]}}, $

${\lambda _1}{\lambda _2}{\lambda _3} = {\rm{1}}. $

根据日本****森荣司提出的表观弹性法理论^[9]和文献[15], 在大尺寸工具头边界自由时, 其3个轴向的频率方程为

${k_x}l = i{\rm{\pi }}\;\;(i = 1,2,3, \cdots ), $

${k_y}w = j{\rm{\pi }}\;(j = 1,2,3, \cdots ), $

${k_z}h = m{\rm{\pi }}\;(m = 1,2,3, \cdots ), $

式中, k_x, k_y, k_z为工具头3个轴向的表观波数, ${k_n} = \omega /{c_n}~(n = x, y, z)$, 其中$\omega $为大尺寸工具头的振动圆频率, c_n为声速, ${c_n} \!=\! {({E_n}/\rho )^{1/2}}~(n \!=\! x, y, z)$; ρ为材料的密度; i, j, m为不同的振动模式. 令i, j, m = 1, 将(4), (5), (6)式和k_n的表达式代入(8), (9), (10)式, 并使$c_n^2\text{π}^2/\omega^2 = A$, 经过代换, 可得大尺寸工具头的谐振频率方程:

$ \begin{split}&\frac{{{i^2}{j^2}{m^2}}}{{{l^2}{w^2}{h^2}}}{A^3} - \left(\frac{{{i^2}{j^2}}}{{{l^2}{w^2}}} + \frac{{{j^2}{m^2}}}{{{w^2}{h^2}}} + \frac{{{i^2}{m^2}}}{{{l^2}{h^2}}}\right){A^2} \\&+\left(1 - {\upsilon ^2}\right)\left(\frac{{{i^2}}}{{{l^2}}} + \frac{{{j^2}}}{{{b^2}}}\frac{{{m^2}}}{{{h^2}}}\right)A + 2{\upsilon ^3} \\& +3{\upsilon ^2} - 1 = 0. \end{split}$

从(11)式可以看出, 大尺寸工具头的频率方程是关于A的三次方程, 3个解分别对应工具头X, Y, Z方向的谐振频率. 对于长条形矩形工具头, 两个横向尺寸l和w中有一个远小于其纵向尺寸h, 但另一个却接近或超过其纵向尺寸. 由于Y方向的横向共振频率远高于系统的纵向共振频率, 而X方向的横向共振频率接近于系统的纵向共振频率, 因此, 在超声塑料焊接振动系统发生纵向共振时, X方向的横向振动也基本上处于谐振状态, 对系统的纵向振动产生影响. 此时, 系统的振动为二维耦合振动, X方向振动和Z方向的纵向振动相互耦合, 导致辐射面输出的振幅不均匀. 因此为了保证二维大尺寸长条形工具头辐射面的纵向位移均匀度, 必须对其长度X方向的横向振动进行抑制^[15].
2 -->

2.2.近周期声子晶体位错理论

近周期声子晶体指的是为满足实际需求, 在完美周期结构上设计一些不完整结构, 比如, 缺陷态、近周期结构、失谐结构等^[19]. 弹性波在近周期结构中传播时, 同样会有禁带的产生, 且带隙内存在丰富的局域模式^[20-22].
位错是在晶体结构上的拓扑缺陷, 引入位错缺陷的声子晶体称为同、异质位错结^[23]. 同质位错结是一种拓扑缺陷, 根据不同的位错方向, 可以将同质位错结分成两类: 横向位错结和纵向位错结, 横向位错结指的是将位错线左、右两边的全部散射子沿横向整体向左或右移动一定距离; 纵向位错结则指的是沿着位错线将左、右两边的散射子整体向上或者向下移动一定距离^[24]. 利用同质位错结, 可以调节带隙的宽度和位置, 产生传导模和局域模, 可以更加灵活地调控弹性波的传播行为和频带特征^[25,26].
根据2.1节可知, 二维大尺寸工具头X方向会产生严重的横向振动, 导致工具头辐射面振幅分布不均匀, 为了对X方向横向振动进行抑制, 可以设计基于近周期声子晶体同质位错结的二维大尺寸工具头, 将超声塑料焊接系统的工作频率设计在工具头的横向振动的带隙内, 进而有效地控制工具头X方向的横向振动.

图1为二维超声塑料焊接系统, 主要包括夹心式超声换能器、复合变幅杆和二维大尺寸工具头3个部分.
图 1 二维超声塑料焊接振动系统结构示意图
Figure1. Structural diagram of two-dimensional ultrasonic plastic welding vibration system.

将二维超声塑料焊接系统的工作频率设定在20 kHz附近, 为了达到谐振, 一般将换能器、变幅杆、工具头均设计为一个半波长结构. 二维超声塑料焊接系统选用纵向夹心式压电陶瓷复合换能器, 压电陶瓷晶堆选择Piezoelectric ceramic crystal stack-4 (PZT-4), 半径设为25 mm, 厚度为6 mm, 2 片, 前后盖板的高度均为56 mm, 等截面圆柱, 半径与压电陶瓷片相同, 即换能器的总高度为124 mm. 为了得到较大的振幅增益, 系统选择圆柱和圆锥型复合型变幅杆. 其中, 圆柱端高度为77 mm, 圆锥段高度为45 mm, 即复合变幅杆的总高度为122 mm. 二维工具头的长度为240 mm, 宽度为46 mm, 高度为115 mm. 除压电陶瓷晶堆外, 其他模块均选择硬铝, 换能器沿Z轴方向激励. 由于二维工具头的l, h $ \gg $ w, l与h接近, 由于泊松效应, 工具头在X方向会产生严重的横向振动. 利用Comsol Multiphysics计算并绘制二维不开槽超声振动系统焊接面沿X (长度)方向的振幅分布图, 图2给出了振动系统的振型图, 图3给出了二维工具头沿辐射面X方向的纵向位移分布图.
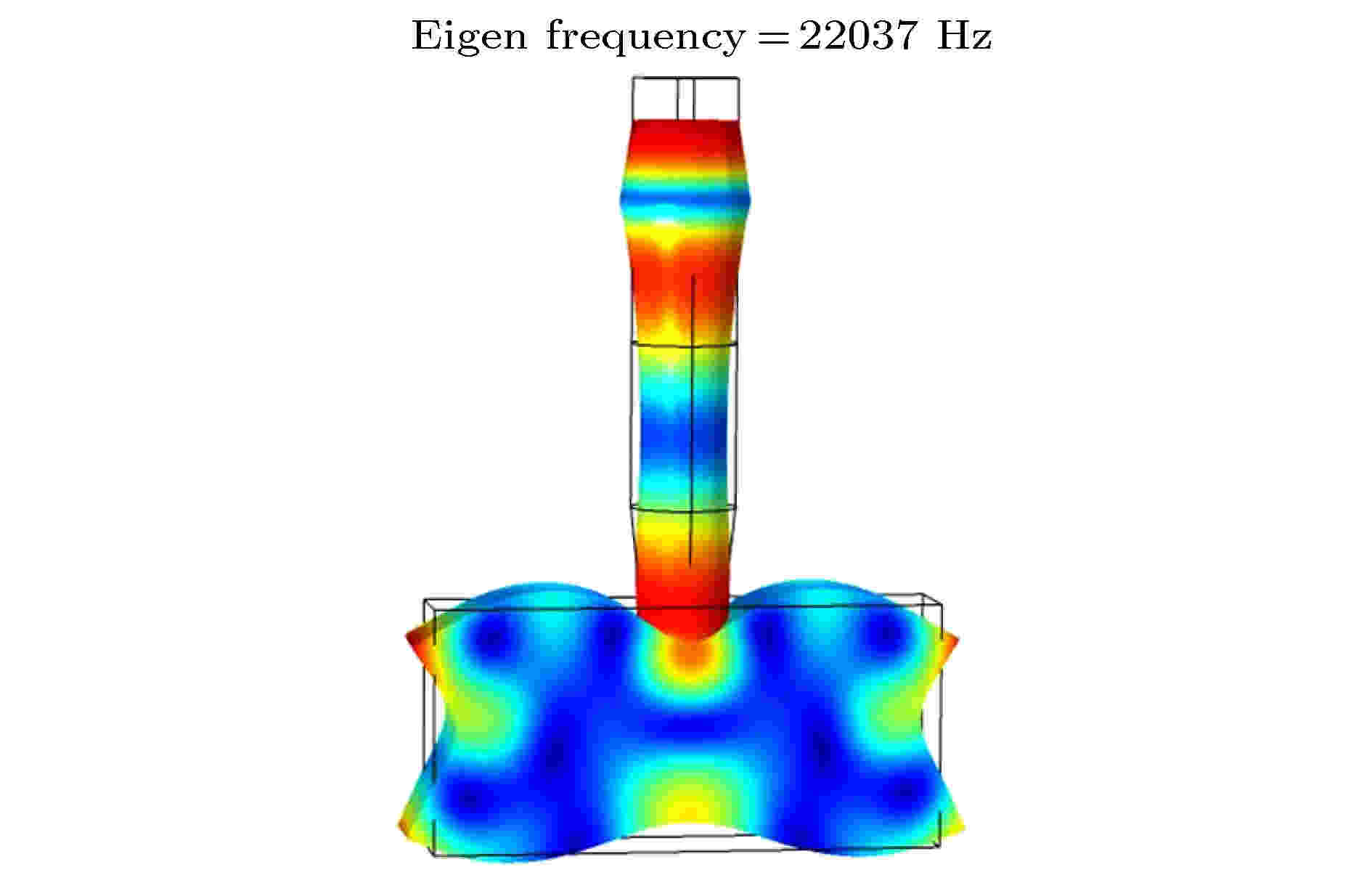图 2 二维超声塑料焊接振动系统的振型图
Figure2. Modal diagram of two-dimensional ultrasonic plastic welding vibration system.

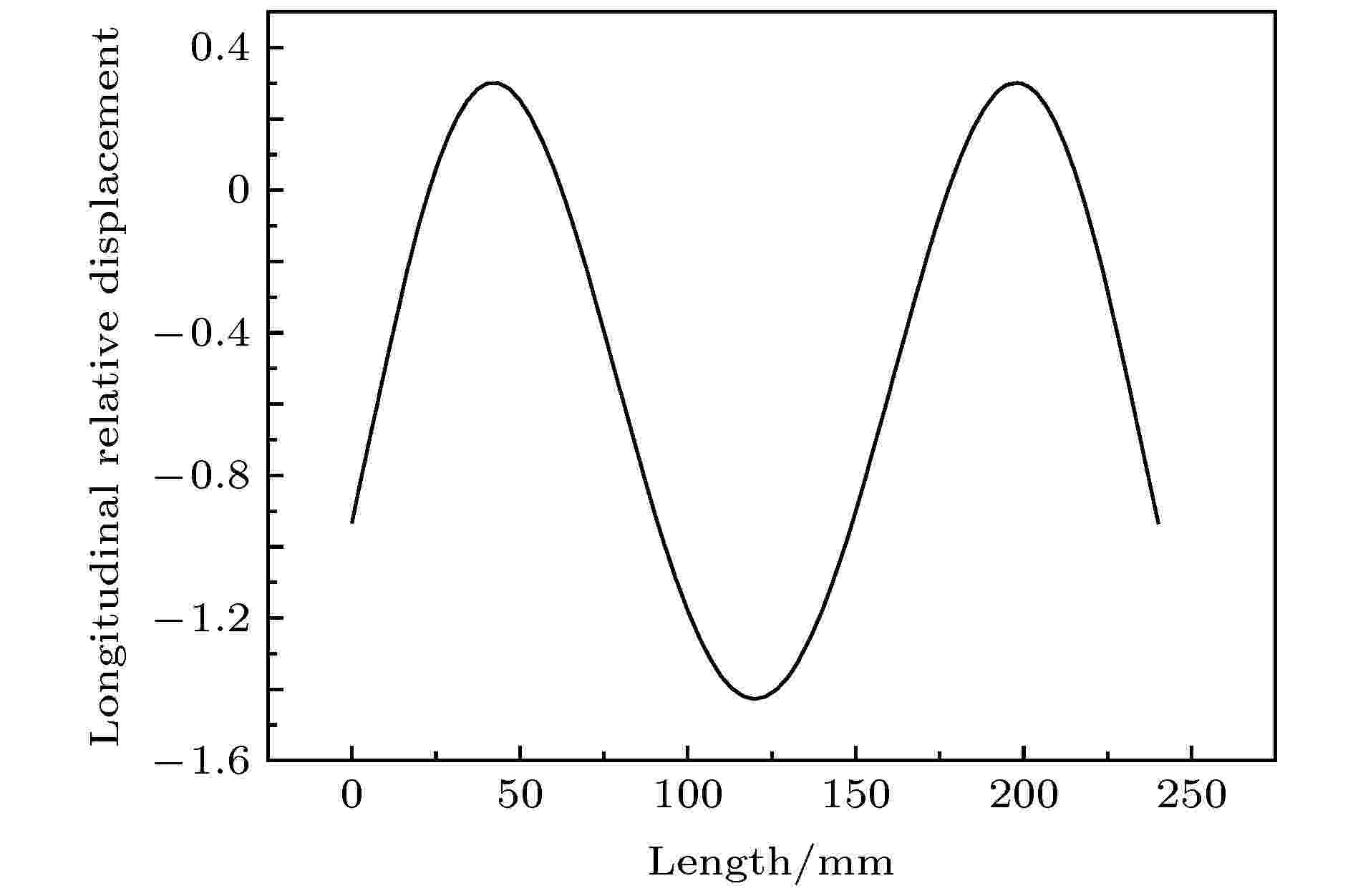图 3 工具头辐射面X方向纵向相对位移分布
Figure3. X-direction longitudinal relative displacement distribution of radiating surface of tool head.

从图2和图3可以看出, 未优化的二维大尺寸超声塑料焊接系统工具头表面的振幅分布非常不均匀, 相对位移变化范围从0.3至–1.5, 振幅分布不均匀且振幅增益较小, 为了对X方向的横向振动进行有效控制, 使辐射面振幅分布更加均匀, 提高振幅增益, 本文对二维超声塑料焊接系统的工具头进行改进.
近年来, 由周期性排列的孔构成的声子晶体受到了越来越多的关注^[27,28]. 基于此, 本设计沿二维工具头的X方向, 加工4个均匀的周期性直孔槽, 构造如图4所示的基于近周期声子晶体多槽结构的二维工具头和各部分的尺寸图以及工具头的原胞模型, 其中, a为晶格常数, 槽的几何参数为b, c, d. 为了使二维超声振动工具头的辐射面位移分布更加均匀, 可以将超声塑料焊接振动系统的纵向谐振频率设计在工具头的方向带隙内, 以实现对长度X方向振动的有效控制, 使振动模态变得更加单一.
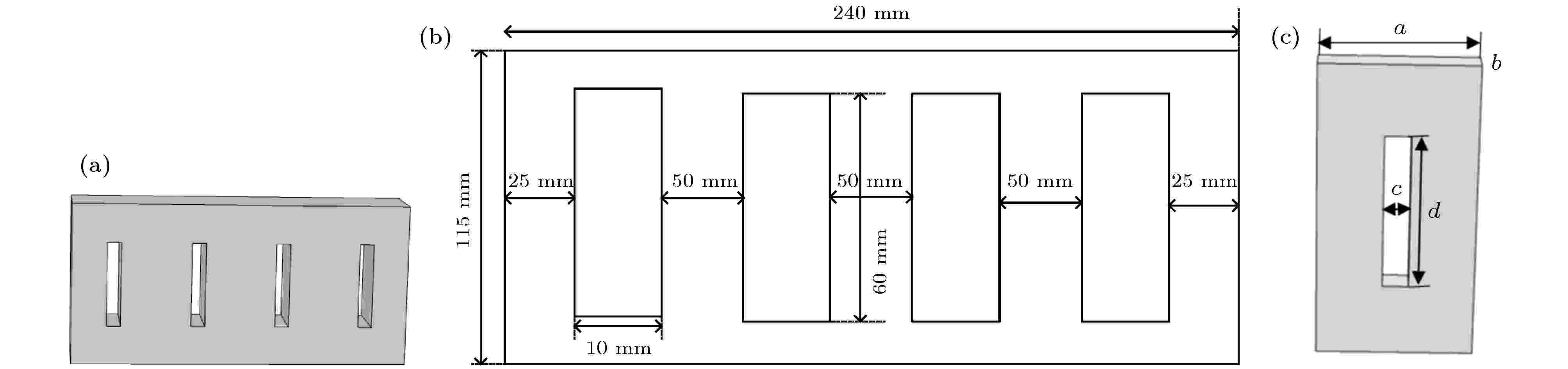图 4 基于近周期声子晶体多槽结构的二维工具头　(a)结构; (b)尺寸; (c)原胞模型
Figure4. Two-dimensional tool head based on near-period phononic crystal multiple-grooves: (a) Structure; (b) dimensions; (c) cell model diagram.

图4所示的工具头的长度、宽度、高度尺寸均与未优化前保持相同, 其中, 工具头原胞的晶格常数a = 60 mm, 基体的高度为115 mm, 宽度b = 11.5 mm; 槽的长度c = 10 mm, 宽度b = 11.5 mm, 高度d = 60 mm. 在COMSOL Multiphysics建立工具头的原胞模型, 利用COMSOL结构力学和声学模块对原胞的加速度响应曲线进行求解, 以确定模型的带隙范围, 结果如图5所示, 图中, 加速度幅值小于1的频率范围即为所求解的模型在X方向的振动带隙^[17].
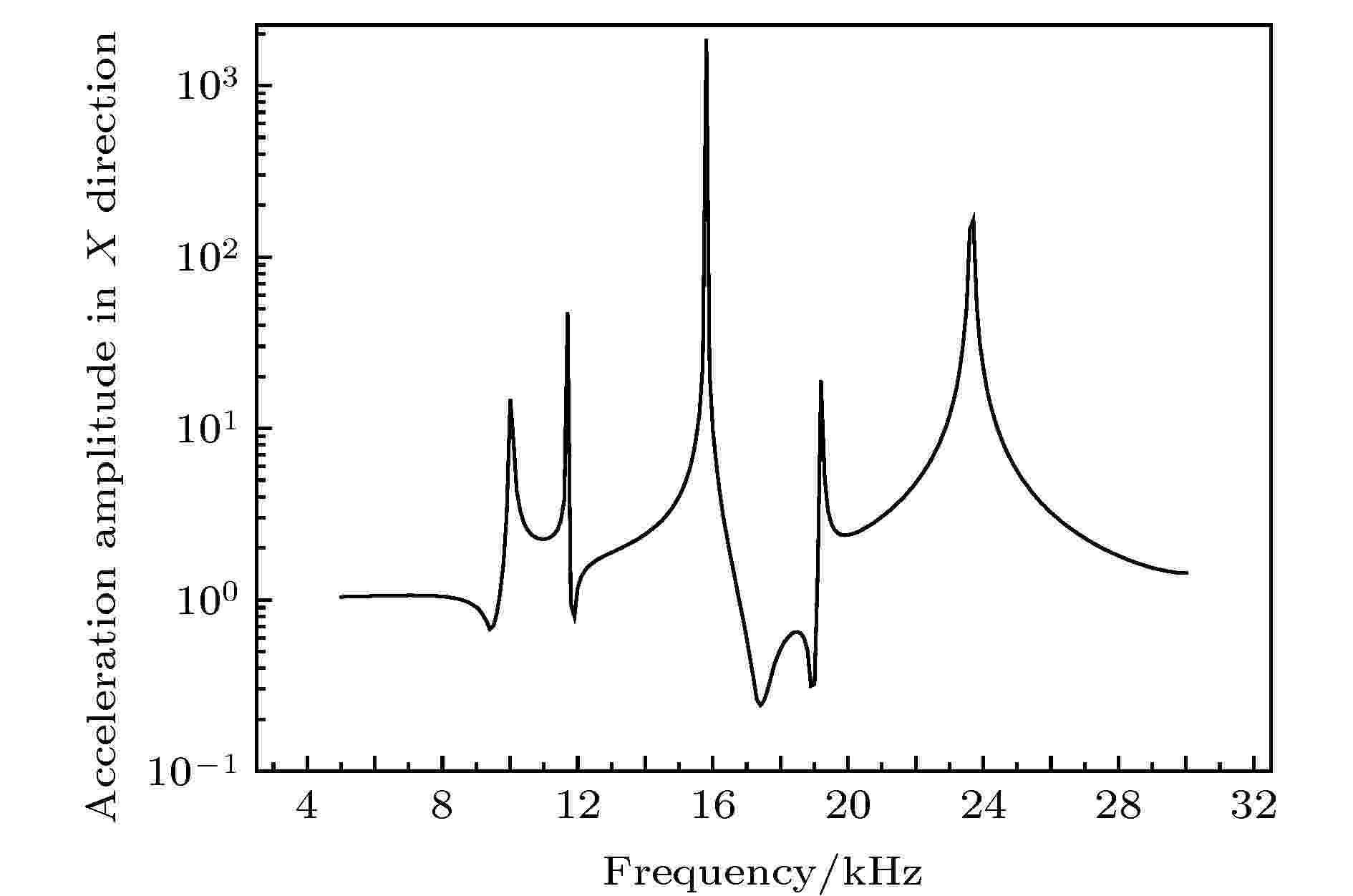图 5 原胞结构在X方向的加速度响应曲线
Figure5. Acceleration response curve of the cell structure in the X direction.

从图5可以看出, 基于近周期声子晶体多槽结构的二维工具头在17—19 kHz之间存在方向带隙, 但是本文设计的焊接系统的纵向共振频率在20 kHz附近, 为了使二维超声塑料焊接系统的工作频率位于工具头的横向振动带隙内, 必须调整基于近周期声子晶体多槽结构的工具头的带隙位置或者带隙宽度.
由2.2节可知, 利用同质位错结, 可以改变声子晶体结构规则的晶格排列, 起到控制带隙特性的作用. 因此, 本研究利用横向位错效应构造了基于近周期声子晶体同质位错结的二维工具头, 以达到调整带隙位置和增大带隙宽度的目的, 最终实现对工具头横向耦合振动的有效控制, 优化工具头辐射面的振幅均匀度, 提高振幅增益.
2

-->

3.1.基于近周期声子晶体同质位错结的二维超声塑料振动系统

由2.2节可知, 横向位错是指将位错线左(右)两边所有的散射子沿着横向整体向左(右)移动${{\left| {\Delta x} \right|} / {\rm{2}}}$的距离, 如图6所示. 可知, 同质位错结是一种非周期结构, 不具备平移对称性, 因此不能再将系统简化为单原胞计算, 而要在位错线两边选取相同数量的原胞以构造超胞计算模型^[19]. 图6中, 使用虚线勾勒出的矩形便是一个工具头的超胞模型.
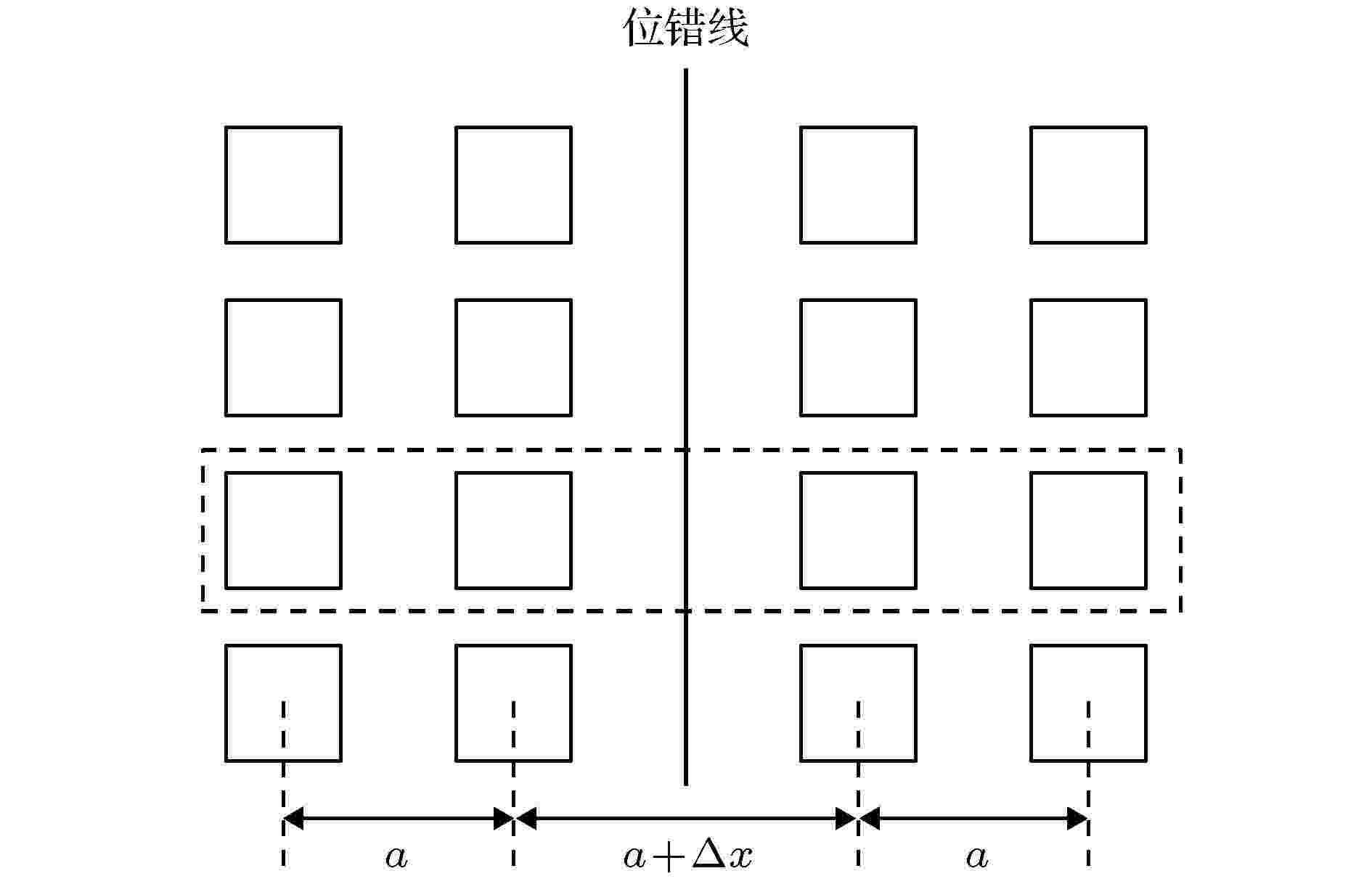图 6 基于近周期声子晶体同质位错结的二维工具头的超胞模型
Figure6. Supercell model of a two-dimensional tool head based on near-period phononic crystal homogenous dislocation junction.

计算时, 超胞数选为4 (左右两边各选取2个原胞), 原胞结构与图4相同, 以Δx = 10 mm为例, 构建如图7所示的工具头超胞结构示意图, 并计算该超胞模型在X方向的加速度响应曲线, 结果如图8所示, 基于近周期声子晶体多槽结构和基于近周期声子晶体同质位错结结构的对比结果如图9所示.
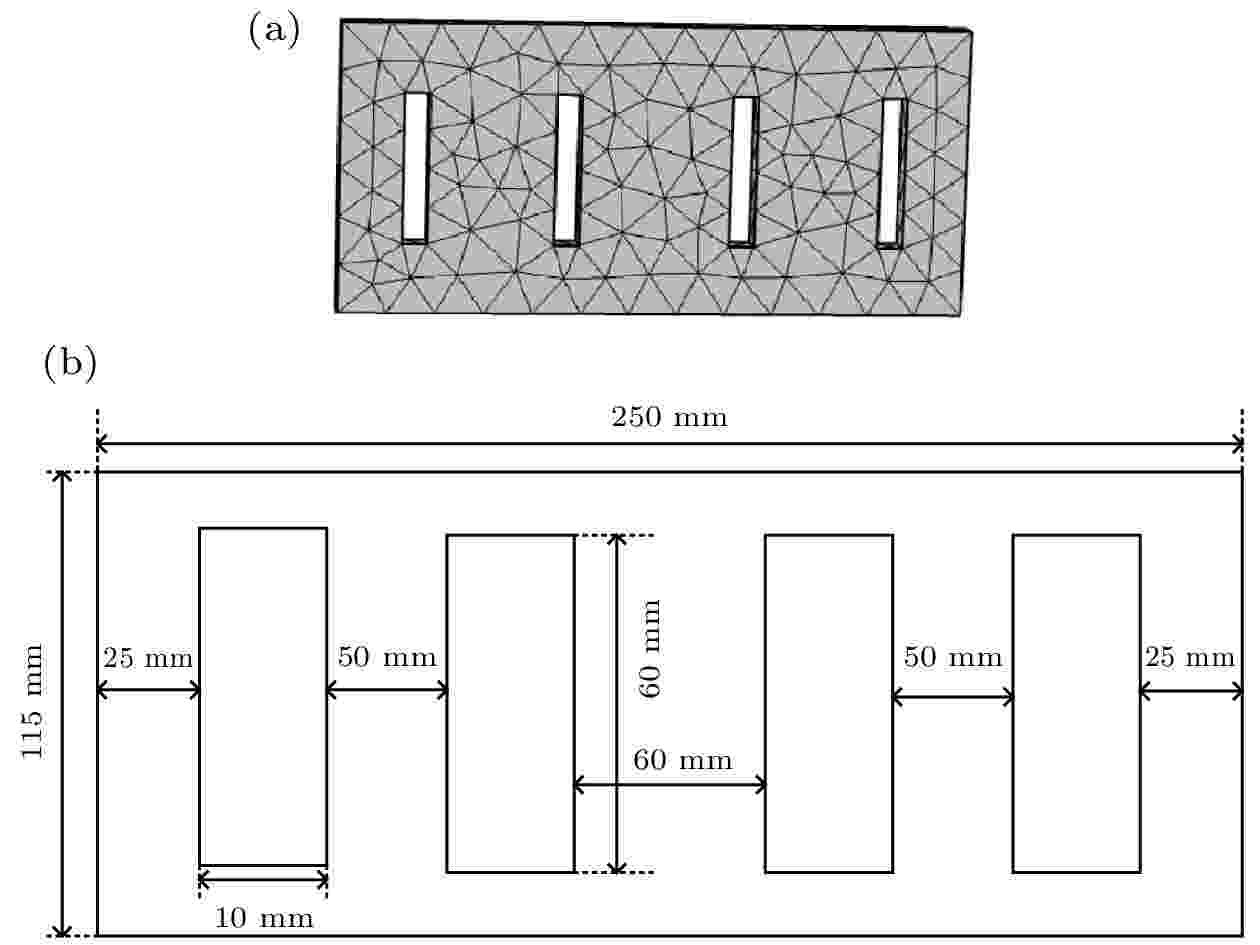图 7 近周期声子晶体同质位错结的超胞示意图
Figure7. Schematic diagram of near-period phononic crystal supercell based on homogenous dislocation junction.

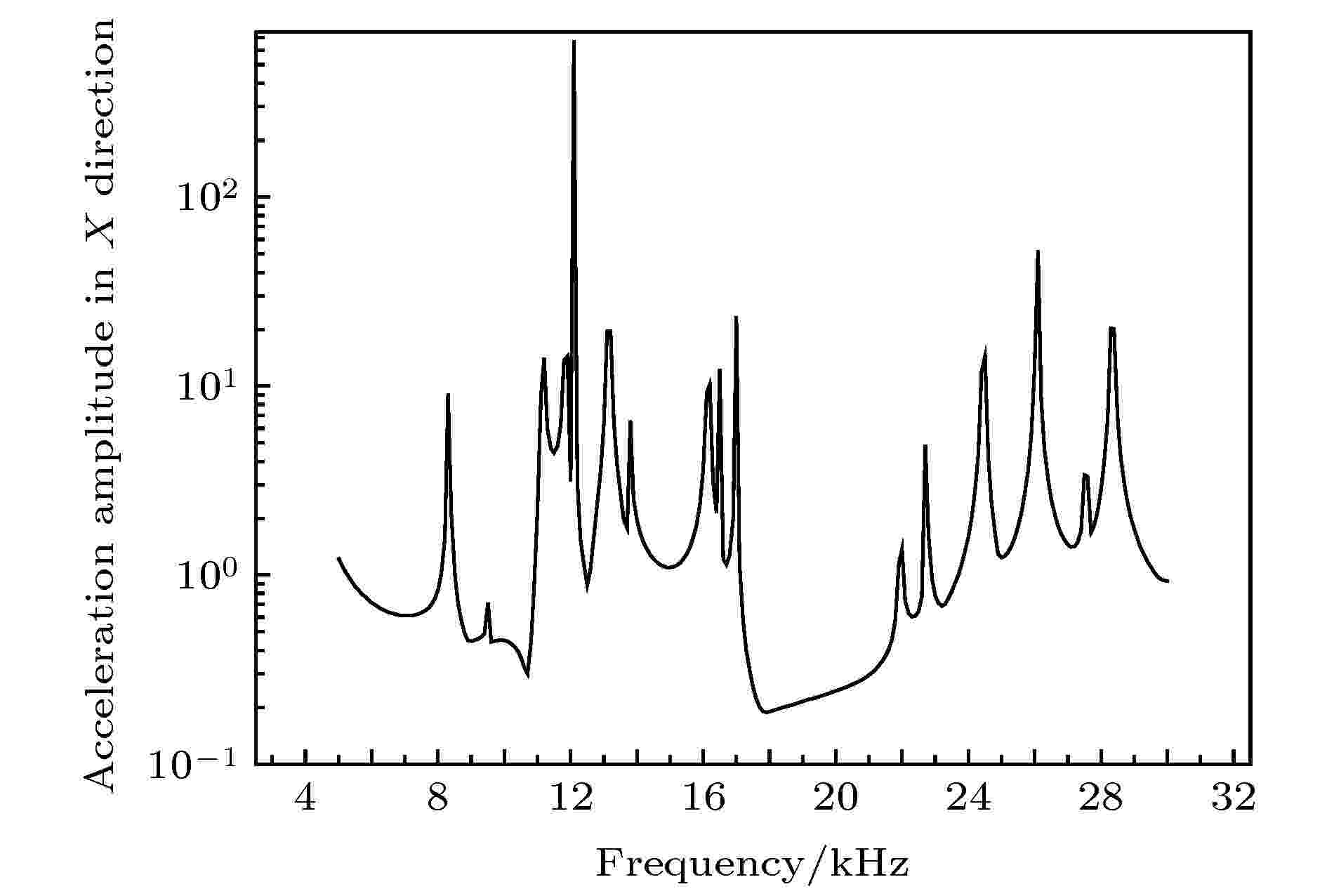图 8 基于近周期声子晶体同质位错结的超胞结构在X方向的加速度响应曲线
Figure8. X-direction acceleration response curve of supercell structure based on near-period phononic crystal homogenous dislocation junction.

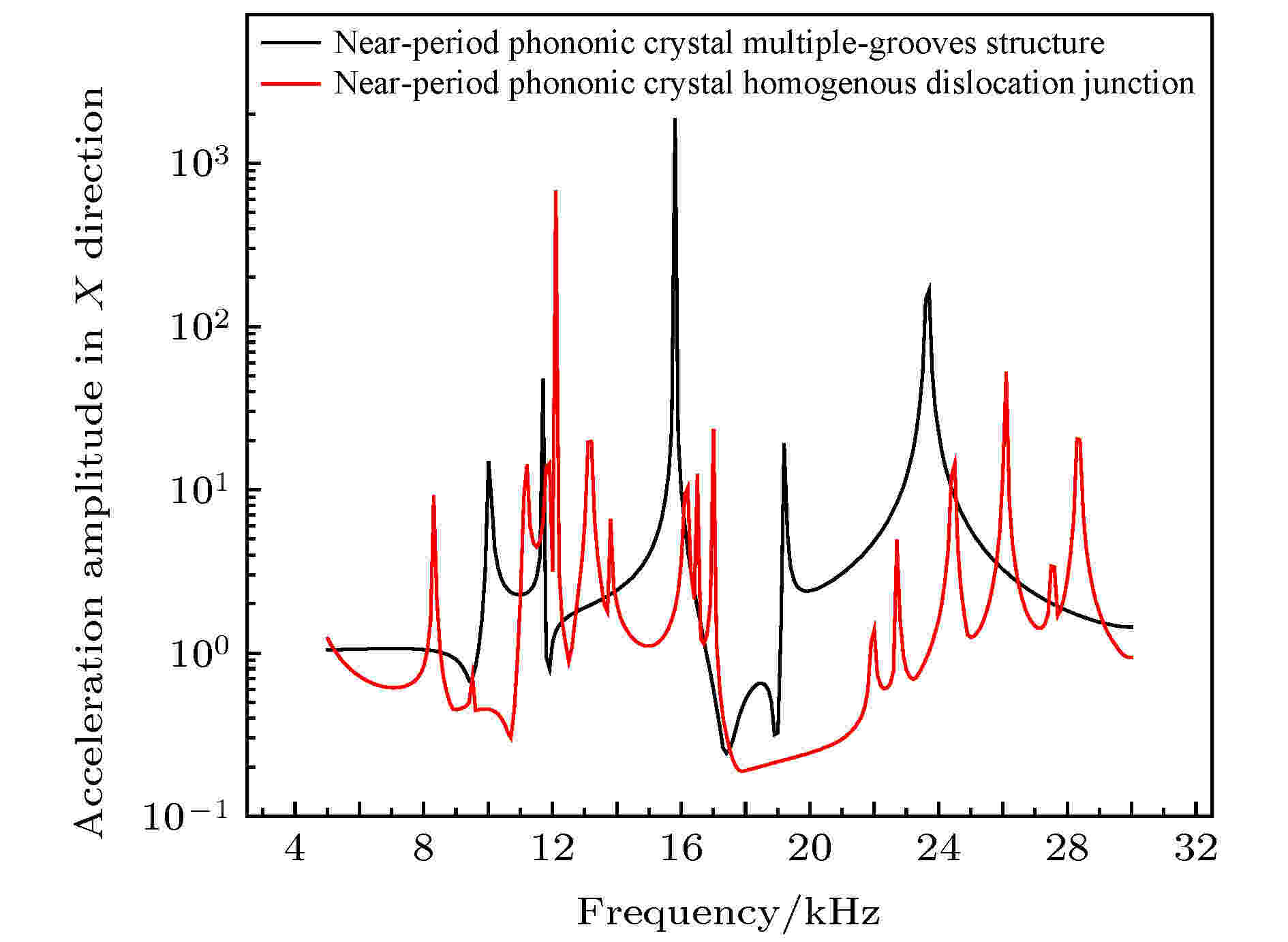图 9 两种结构在X方向的加速度响应曲线对比图
Figure9. Comparison of acceleration response curves of the two structures in the X direction.

从图9可以看出, 通过同质位错结可以产生更丰富的局域模态, 并能有效地改变带隙的上、下限频率, 其中, 对下限频率的影响更为明显, 带隙宽度也因此得到了显著拓展, 比如近周期声子晶体多槽结构在X方向最宽的振动带隙为16.8 —19 kHz, 而近周期声子晶体同质位错结的结构在X方向最宽带隙为17.2—21.8 kHz, 带隙宽度明显增大, 而且恰好在20 kHz附近, 因此, 可以利用此带隙, 实现对X方向振动的抑制, 有效改善工具头辐射面的纵向振动位移分布的均匀度.
在COMSOL Multiphysics中建立基于近周期声子晶体同质位错结的二维超声塑料焊接振动系统模型, 计算模型的特征频率, 获得图10所示的系统振型图, 可以看出, 基于近周期声子晶体同质位错结的超声塑料焊接振动系统的纵向谐振频率为20.674 kHz, 恰好位于工具头X方向的振动带隙内, 因而对系统X方向的横向振动进行有效的抑制, 改善了工具头辐射面的纵向振动位移分布的均匀程度. 图11给出了基于近周期声子晶体同质位错结结构的工具头辐射面位移分布及其与基于近周期声子晶体多槽结构的位移分布对比情况, 可以看出, 近周期声子晶体同质位错结能从一定程度上控制横向振动, 提高工具头辐射面振幅分布均匀度, 且振幅增益明显提高.
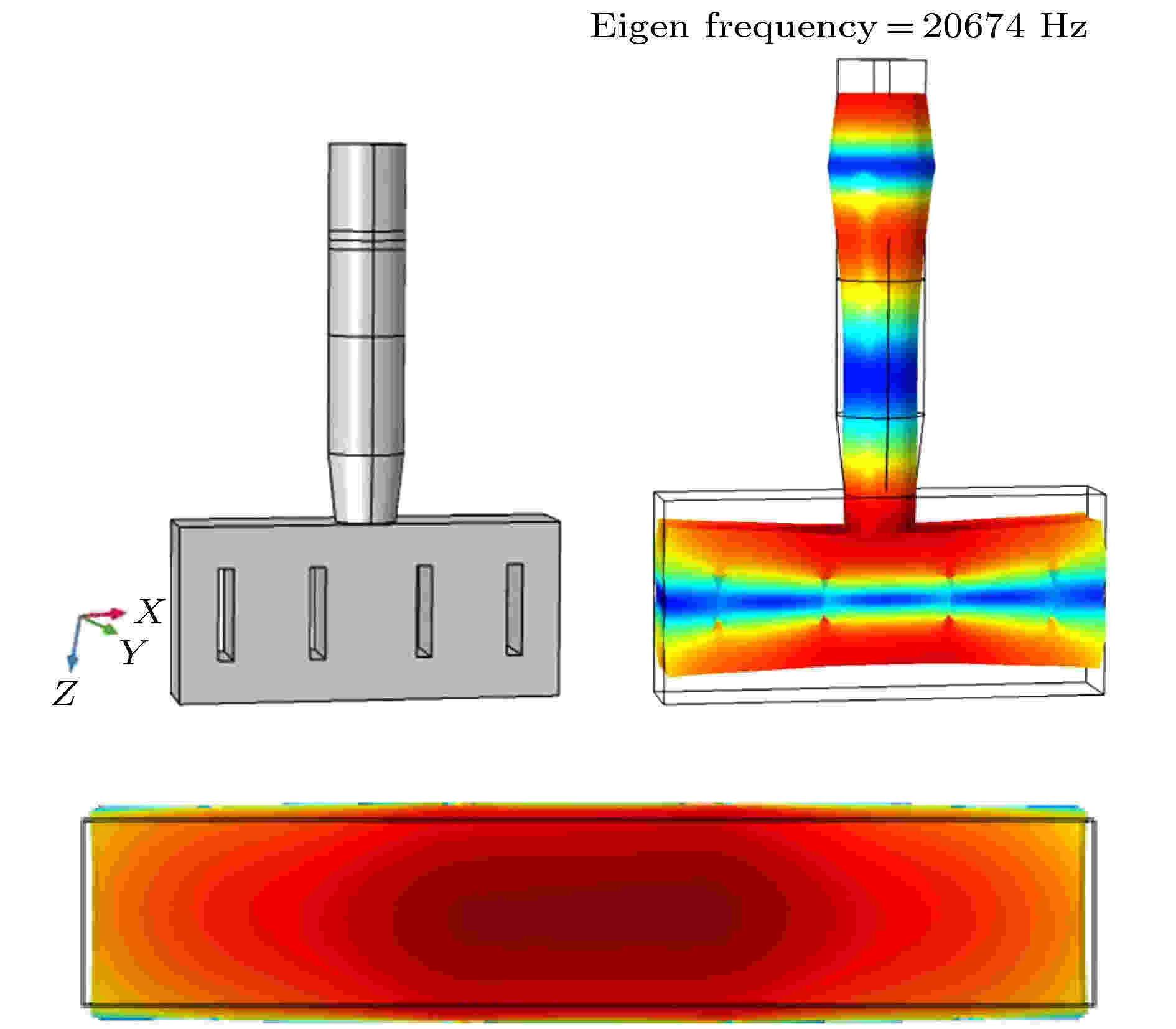图 10 基于近周期声子晶体同质位错结的二维超声塑料焊接振动系统的结构图和振型图
Figure10. Structure diagram and modal diagram of two-dimensional ultrasonic plastic welding vibration system based on near-period phononic crystal homogenous dislocation junction.

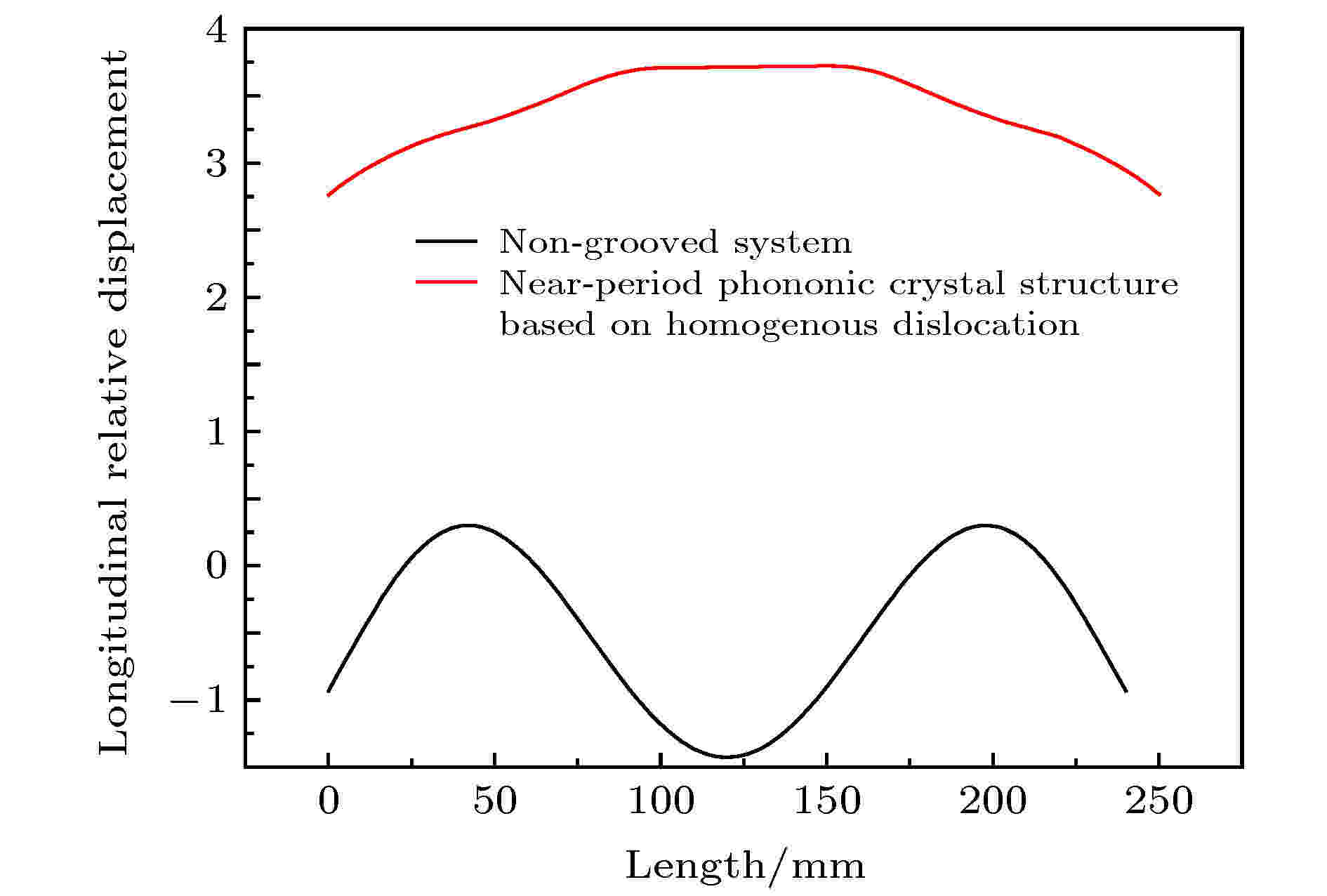图 11 基于近周期声子晶体同质位错结系统的工具头辐射面位移分布图及与不开槽系统的位移分布对比图
Figure11. Displacement distribution diagram of tool head radiating surface of system based on near-period phononic crystal homogenous dislocation junction and its comparison with radiation surface displacement distribution with non-grooved system and system.

但从图11中也能发现, 基于近周期声子晶体同质位错结系统的工具头辐射面振幅变化范围为2.8—3.7, 仍然偏大, 因为横向位错效应可以使位于带隙频率范围内的声波沿着该位错通道传播, 而位错线通道位于工具头中部, 这就导致了工具头辐射面中间部分的位移较大, 而两边位移较小, 如图10和图11所示, 因此, 还需要进一步优化二维超声塑料焊接系统.
2 -->

3.2.基于近周期声子晶体斜槽结构的二维工具头

为了进一步提高二维超声塑料焊接系统焊接面纵向位移的均匀度, 沿工具头的X方向加工了4个斜槽(换能器、复合变幅杆、工具头的长度、宽度、高度以及槽子的高度和宽度尺寸均保持不变), 构造基于近周期声子晶体斜槽结构的大尺寸二维工具头, 优化后的工具头结构和各部分尺寸如图12所示, 工具头长、宽、高均不变, 斜槽的宽度和高度也不改变, 仅把中间两个槽沿槽的中心法线倾斜4°, 外侧两个槽沿槽的中心法线倾斜5°.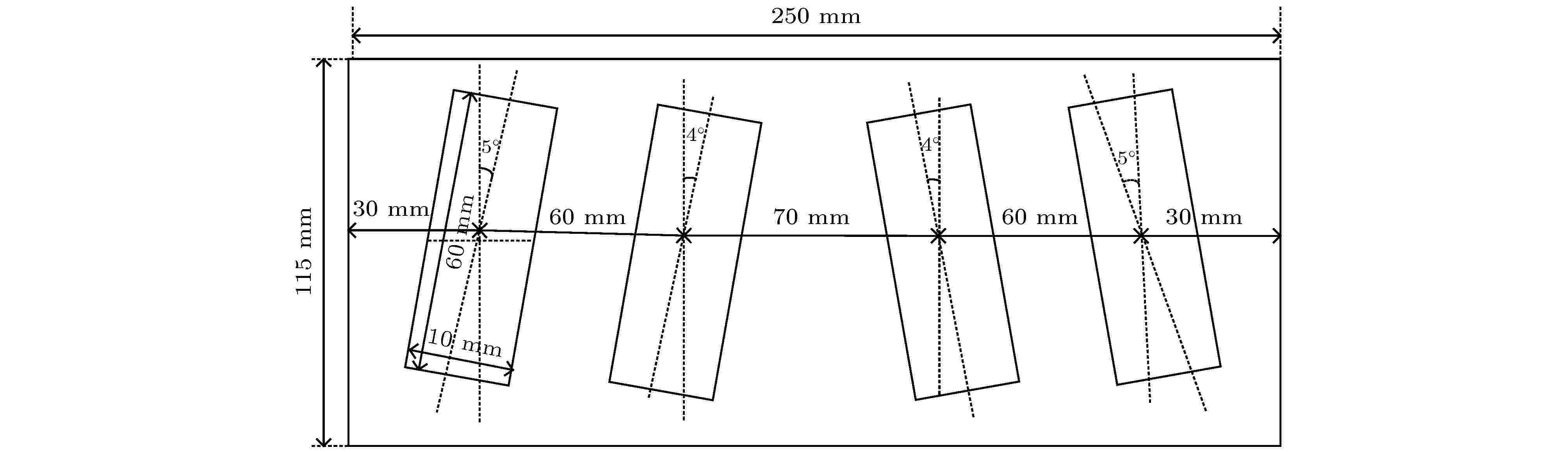
图 12 基于近周期声子晶体斜槽结构的工具头的结构尺寸图
Figure12. Dimensional diagram of tool head based on near-period phononic crystal inclined groove structure.

同样利用COMSOL Multiphysics获得图13所示的系统振型图和图14所示的位移分布图. 为了更清晰地看到近周期斜槽结构对工具头辐射面振幅分布均匀度的优化, 图14给出了两种结构的纵向位移分布对比图. 从图14可以看出, 相比近周期声子晶体同质位错结结构, 近周期声子晶体斜槽结构能更好地控制横向振动, 有效地提高辐射面振幅分布均匀度.
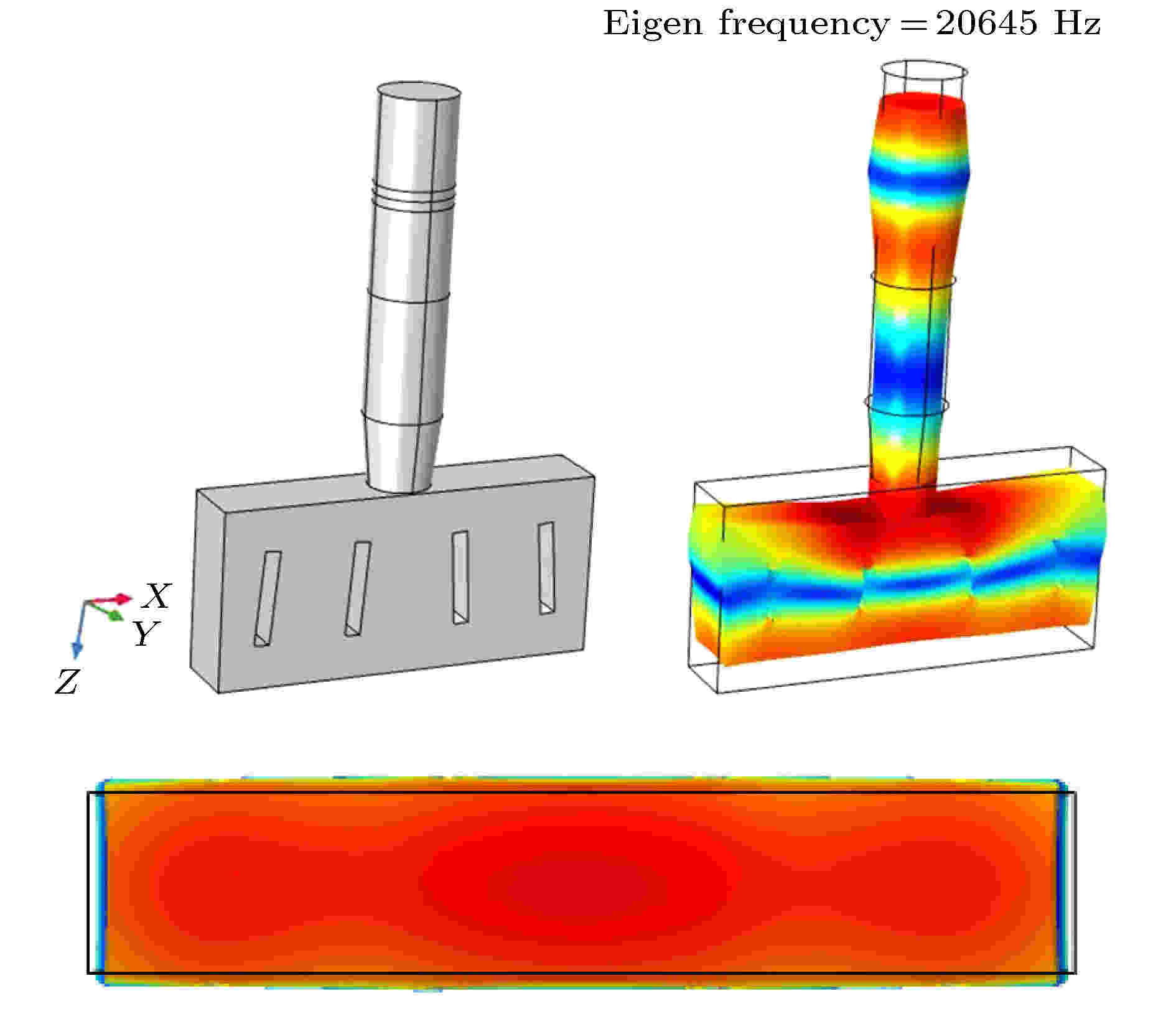图 13 基于近周期声子晶体斜槽结构的二维超声塑料焊接振动系统的结构图和振型图
Figure13. Structural diagram and modal diagram of two-dimensional ultrasonic plastic welding vibration system based on a near-period phononic crystal inclined groove structure.

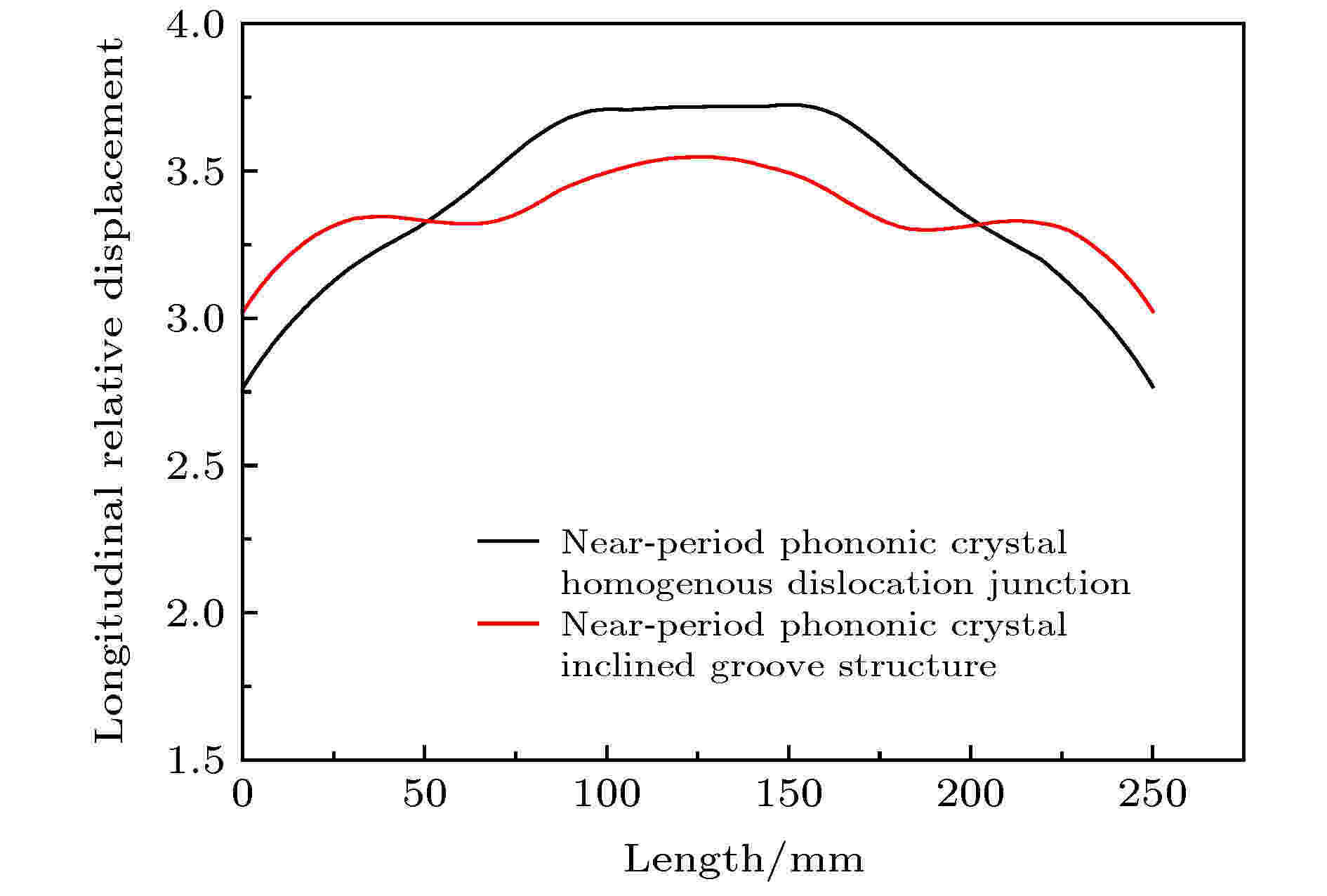图 14 基于近周期声子晶体斜槽结构的工具头辐射面位移分布及其同近周期声子晶体同质位错工具头辐射面位移分布对比图
Figure14. Displacement distribution diagram of tool head radiating surface of system based on near-period phononic crystal inclined groove structure and its comparison with the displacement distribution of radiating surface of tool head with homogenous dislocation in near-period phononic crystal

2 -->

3.3.斜槽结构参数对基于近周期声子晶体斜槽结构的超声塑料焊接振动系统纵向谐振频率和纵向相对位移分布的影响

由3.2节可知, 斜槽的引入使得系统工具头辐射面的振幅分布更加均匀, 即斜槽的结构参数是决定振幅均匀度的一个重要因素, 为了找到最佳的斜槽结构参数, 方便设计, 本研究利用COMSOL Multiphysics仿真分析了斜槽结构参数对基于近周期声子晶体斜槽结构的超声塑料焊接振动系统纵向谐振频率和振幅分布的影响规律, 这里的斜槽结构参数主要包括斜槽高度、斜槽宽度和斜槽倾角, 仿真结果如图15和图16所示. 图16中的dr表示振幅变化范围, 即辐射面纵向位移最大值减去辐射面纵向位移最小值, 即dr越大, 辐射面纵向位移的变化范围越大, 振幅分布越不均匀, dr越小, 辐射面纵向位移的变化范围越小, 振幅分布越均匀; 图中的θ₁是外侧斜槽倾斜角度, θ₂是内侧斜槽倾斜角.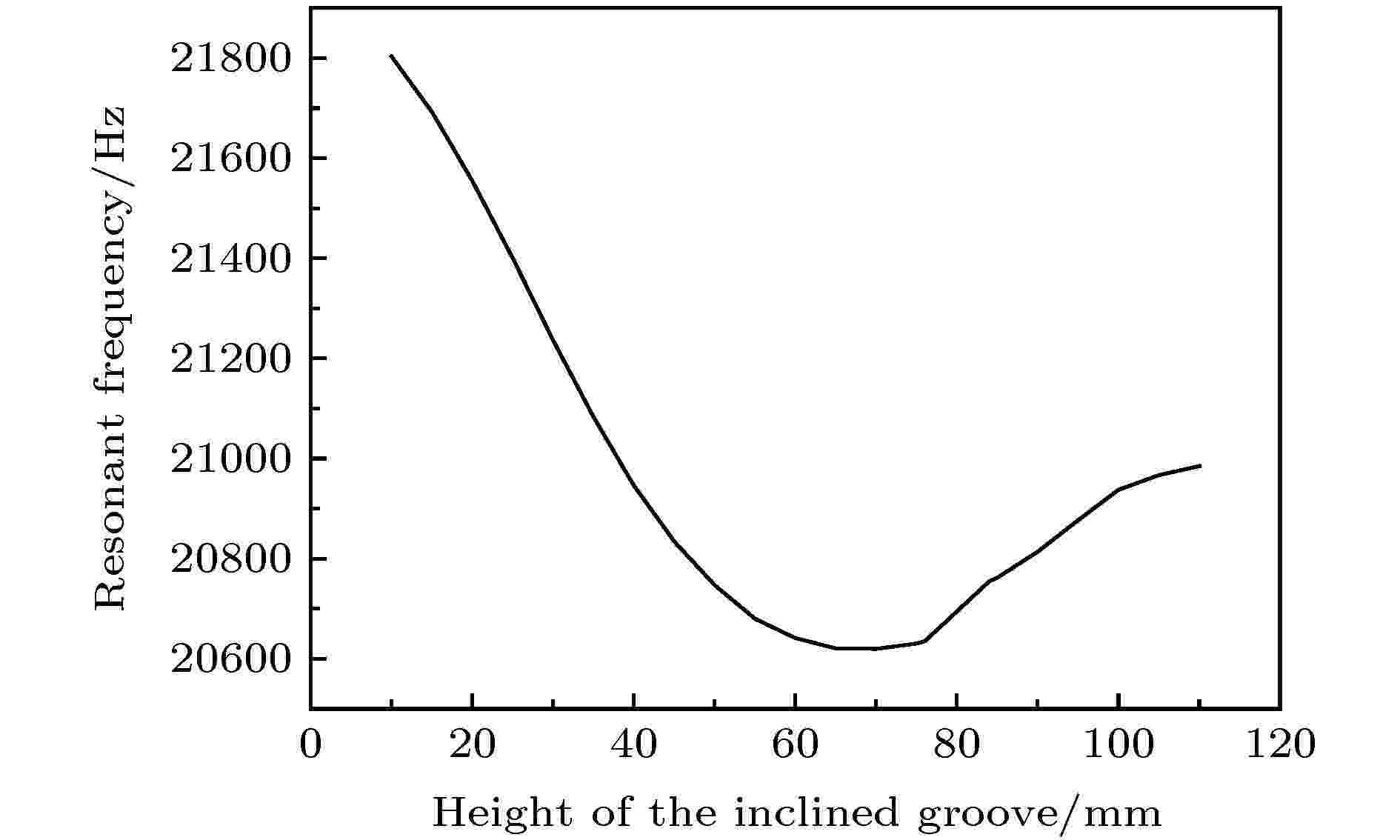
图 15 斜槽高度对系统谐振频率的影响
Figure15. Influence of the height of the inclined grooves on the resonance frequency of the system.

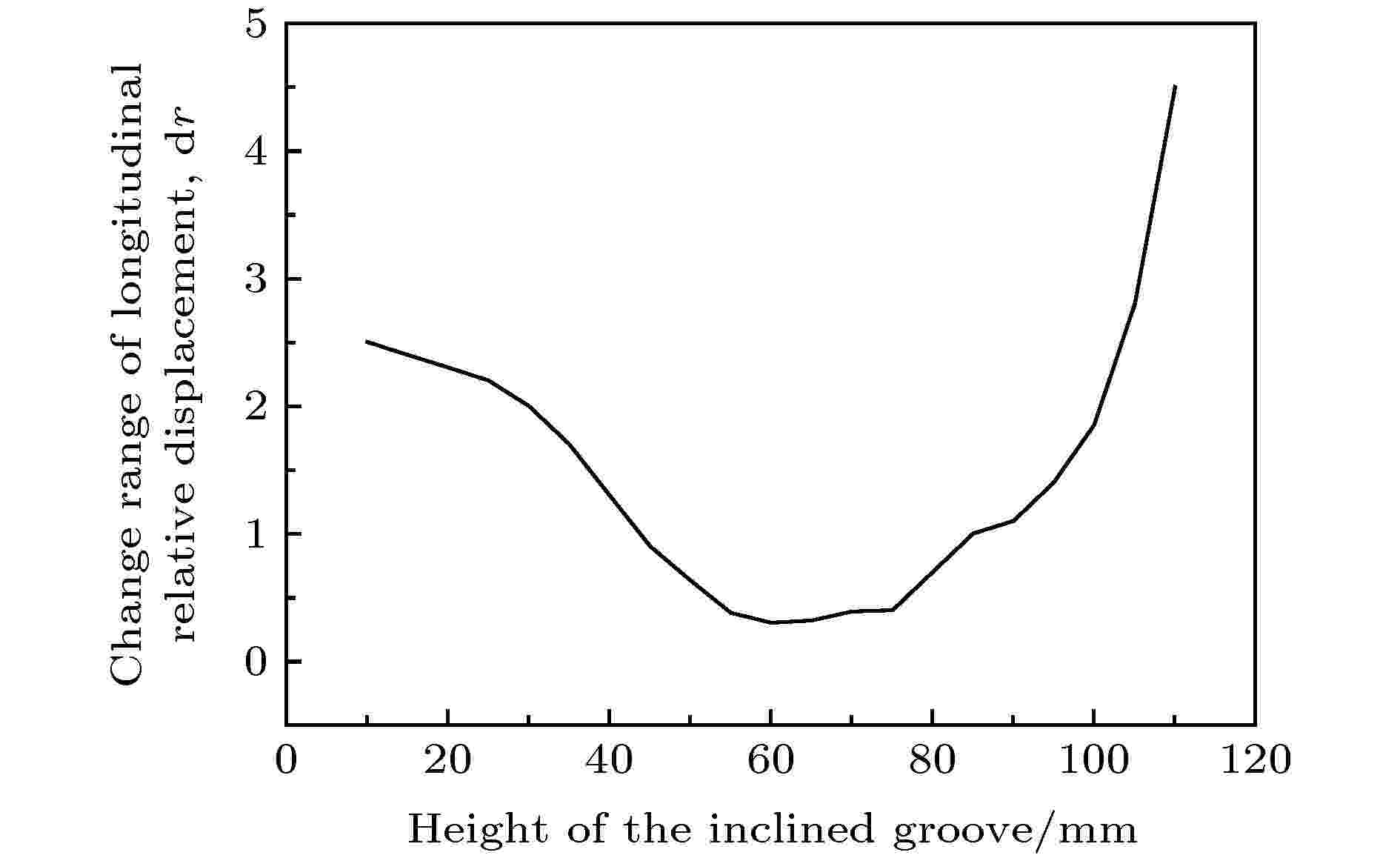图 16 斜槽高度对振幅变化范围的影响
Figure16. Influence of the height of the inclined grooves on the range of amplitude variation

图15和图16分别反映了系统谐振频率和振幅变化范围dr与斜槽高度的关系. 从图15可以看出, 当其他参数不变时(斜槽宽度、外侧斜槽倾角和内侧斜槽倾角固定, 斜槽宽度固定为10 mm, 斜槽外侧倾角为5°, 内侧倾角为3°), 随着斜槽高度的增大, 二维超声塑料焊接系统的谐振频率先减小, 然后再逐渐增大. 从图16可以看出, dr随着斜槽高度的增大先减小, 再增大, 即辐射面的振幅分布均匀度随斜槽高度的增加先越来越均匀, 而后越来越不均匀, 由此可以看出, 斜槽高度的取值要在合适的范围内, 高度太小或者太大, 都会导致系统的振幅分布不均匀, 在此系统中, 斜槽的高度在60—75 mm之间时, 振幅均匀度最佳.
从图17可以看出, 当其他参数不变时(斜槽高度、外侧斜槽倾角和内侧斜槽倾角固定, 斜槽高度固定为60 mm, 斜槽外侧倾角为5°, 内侧倾角为3°), 随着斜槽宽度的增大, 二维超声塑料焊接系统的谐振频率逐步减小. 从图18可知, 当其他参数不变时, dr随着斜槽宽度的增大先减小, 再增大, 即系统的振幅分布均匀度随斜槽宽度的增加先越来越均匀, 而后越来越不均匀, 由此可以推出, 斜槽宽度的取值也要在合适的范围内, 宽度太小或者太大, 都会导致系统的振幅分布不均匀, 在此系统中, 斜槽的宽度在10—12 mm之间时, 振幅均匀度最佳.
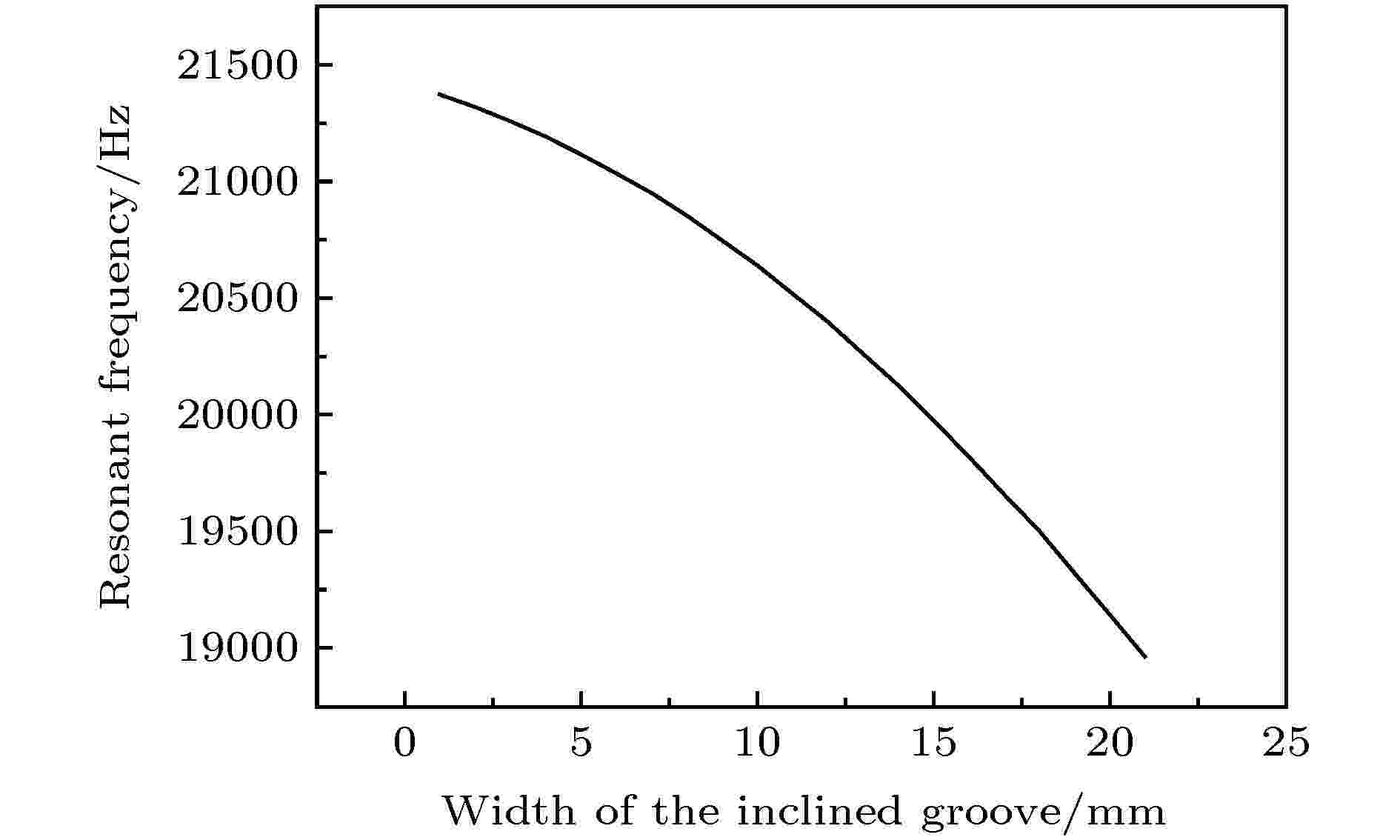图 17 斜槽宽度对系统谐振频率的影响
Figure17. Influence of the width of the inclined grooves on the resonance frequency of the system.

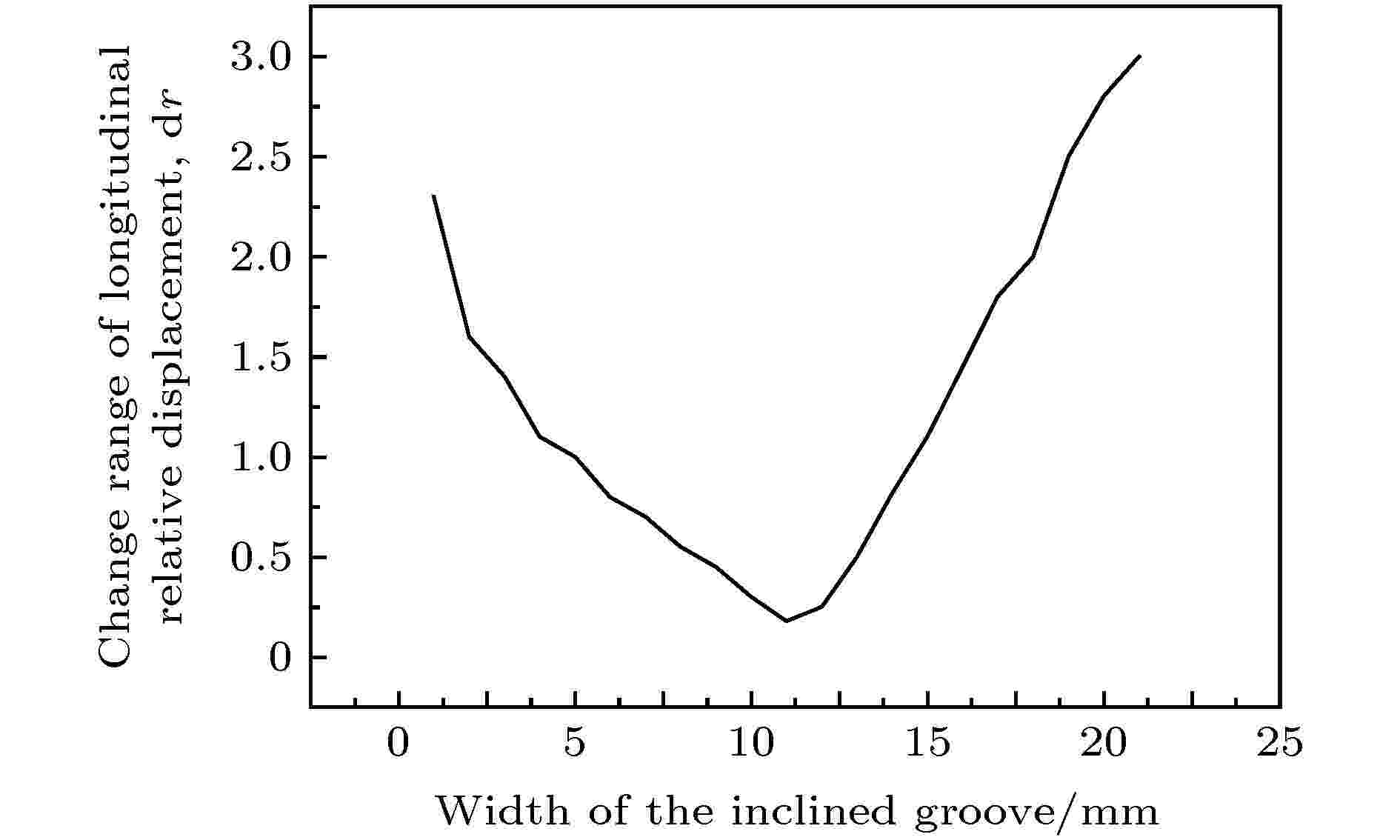图 18 斜槽宽度对振幅变化范围的影响
Figure18. Influence of the width of the inclined grooves on the range of amplitude variation.

图19是系统谐振频率随两个变量—θ₁外侧斜槽倾斜角度以及θ₂内侧斜槽倾斜角的变化关系. 当θ₂ = 1°时, θ₁从1°变化到20°的过程中, 系统谐振频率与两者的关系可以用图19中的黑色线条表示; 同理, θ₂ = 2°时, θ₁从1°变化到20°的过程中, 系统谐振频率与两者的关系可以用图19中的红色线条, 以此类推. 图20是辐射面的振幅变化范围随两个变量θ₁, θ₂的变化关系, 其中, 上图反映了dr和θ₁随θ₂的变化曲线, 由于点过多, 将上图分成了图20(a)和图20(b)两部分, 图(a)显示了θ₂从1°变化到5°时, dr和θ₁随θ₂的变化曲线, 同理, 图(b)显示了θ₂从6°变化到10°时, dr和θ₁随θ₂的变化曲线; 下图反映了dr和θ₂随θ₁的变化曲线, 图(c)显示了θ₁从1°变化到5°时, dr和θ₂随θ₁的变化曲线, 图(d)显示了θ₁从6°变化到10°时, dr和θ₂随θ₁的变化曲线.
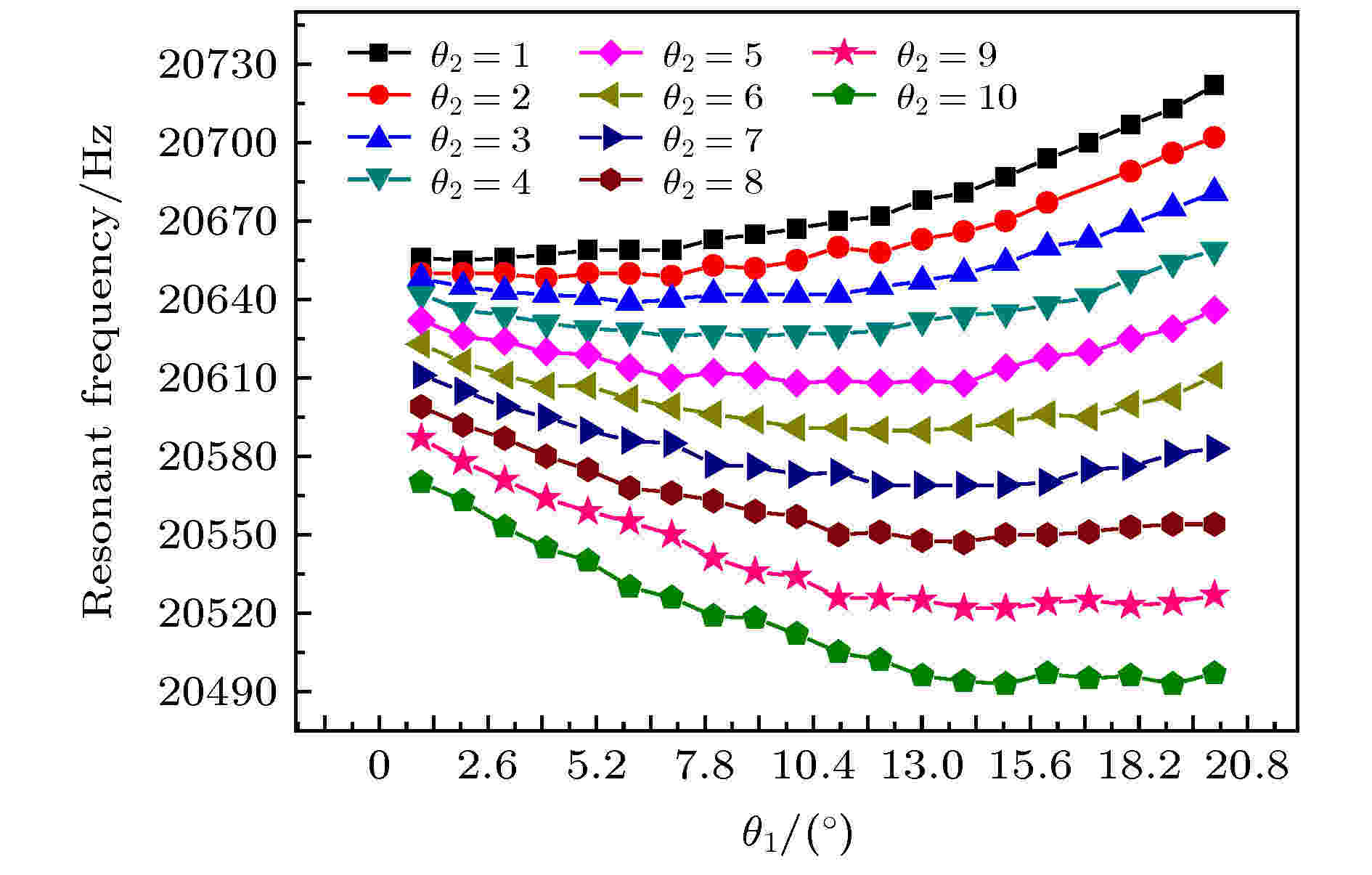图 19 斜槽角度对系统谐振频率的影响
Figure19. Influence of the angle of the inclined grooves on the resonance frequency of the system

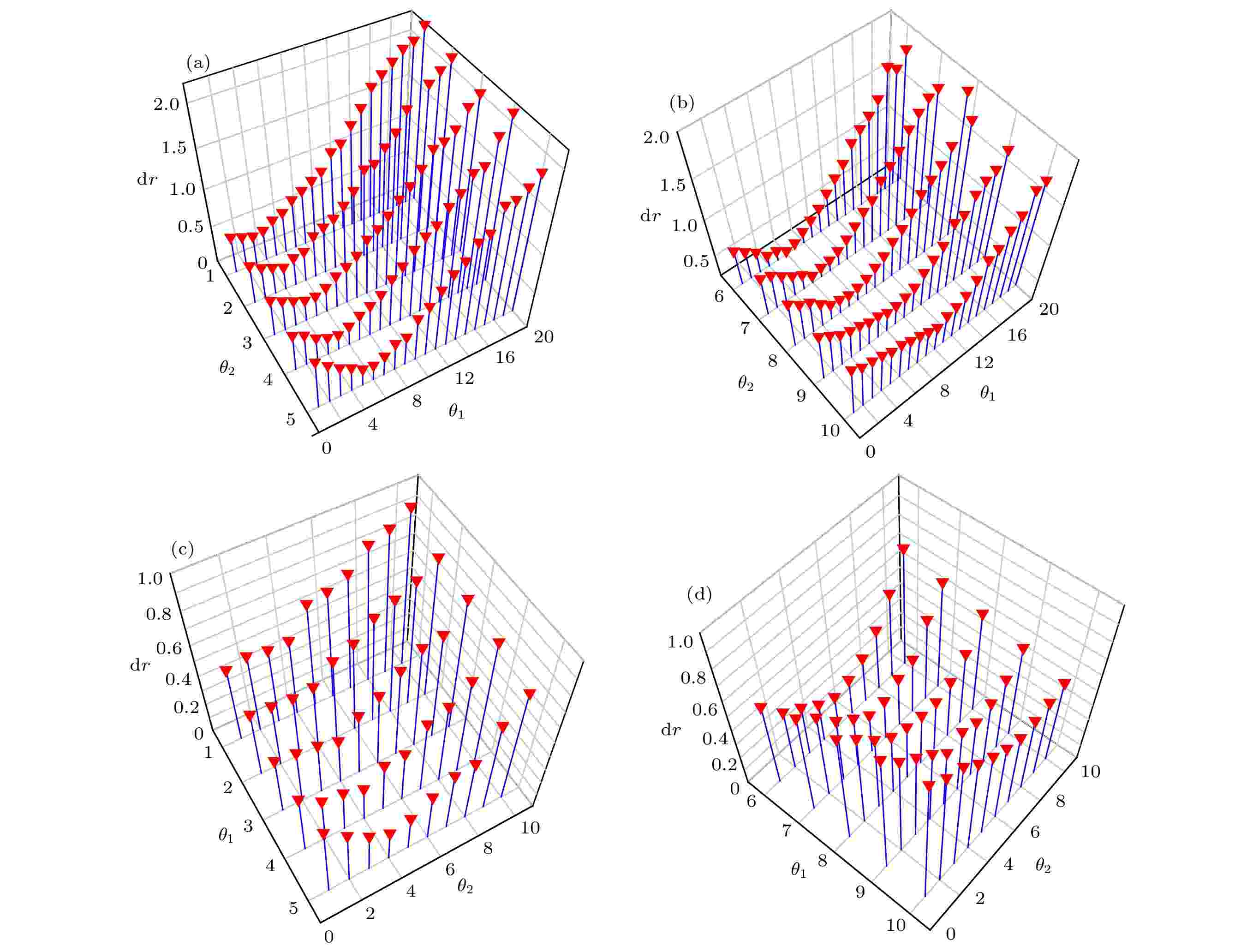图 20 斜槽角度对振幅变化范围的影响
Figure20. Influence of the angle of the inclined grooves on the range of amplitude variation

从图19可以看出, 当其他参数不变时, 随着斜槽倾斜角度的增大, 二维超声塑料焊接系统的谐振频率整体呈先减小后增大的趋势. 从图20可知, 当其他参数不变时, 二维超声塑料焊接系统的dr取值随着斜槽倾斜角度的增大先减小, 再增大, 即系统的振幅分布均匀度随斜槽倾角的增加先越来越均匀, 而后越来越不均匀, 且:
1)外侧和内侧斜槽倾角均不宜过大, 外侧和内侧斜槽倾角越大, dr值越大, 系统振幅分布均匀度越差. 从图20可以看出, 本系统内、外侧斜槽倾角最佳范围为3°—6°.
2)外侧和内侧斜槽倾角二者角度相差也不宜过大, 外侧和内侧斜槽倾角相差越大, 系统振幅分布越不均匀, 图21给出dr较小时对应的内外倾角. 从图20和图21可以看出, 本系统内、外侧斜槽倾角角度相差0°—2°为最佳.
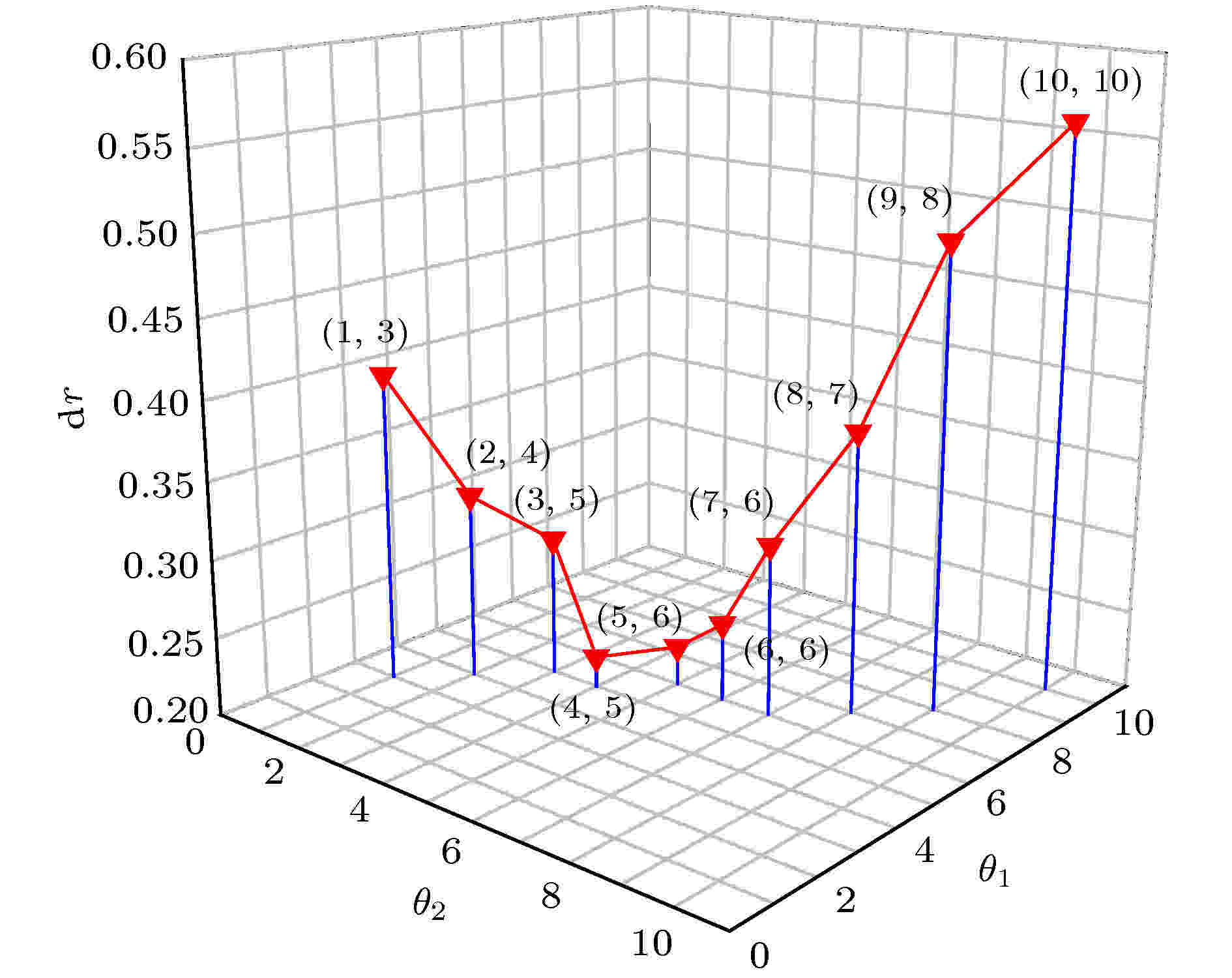图 21 dr和内外侧斜槽角度差值的关系
Figure21. Relationship between dr and the angle difference of outer and inner inclined grooves.

从以上结论可以得出, 开槽后, 系统的频率会降低, 合适的槽子高度、宽度会改善辐射面的纵向位移分布, 而不合理的开槽却会使得系统的纵向位移分布更不均匀; 斜槽比直槽能更好地改善振幅分布均匀度, 但内外斜槽倾斜角度不宜过大, 内外斜槽倾斜角度的差值也不宜过大.

振幅分布均匀度是影响超声塑料焊接系统焊接质量的一个关键因素, 本文对二维超声塑料焊接系统进行了优化设计, 通过近周期声子晶体同质位错结和斜槽结构, 有效地抑制了二维长条形工具头X方向的横向耦合振动, 并分析了斜槽高度、斜槽宽度和斜槽角度对焊接面振幅分布的影响规律; 仿真结果表明, 利用近周期声子晶体同质位错结、带隙理论, 同时结合耦合振动理论, 可以实现二维超声塑料焊接系统的优化设计.