摘要: 耦合相振子的同步研究对理解复杂系统自组织协同的涌现具有重要的理论意义. 相比于传统耦合振子的两体成对耦合, 多重耦合近年来得到广泛的关注. 当相振子间的多重耦合机制起主要作用时, 系统会涌现一系列去同步突变, 这一新颖的动力学特性对理解复杂系统群体动力学提供了重要的理论启示. 本文研究了平均场的三重耦合Kuramoto系统的同步动力学, 发现了去同步转变具有不可逆性, 并利用平均场自洽方法和无序态线性稳定性分析揭示了不可逆去同步突变的动力学机制. 进一步研究发现, 随着振子自然频率分布半宽度的变化, 系统会经历一系列去同步驻波态的转变. 在相变临界点, 系统在高维相空间会通过鞍结分岔导致同步态失稳而塌缩至稳定的低维不变环面. 本文的研究揭示了多重耦合函数作用的振子系统的各种协同态及其相变机制, 同时可为理解其他复杂系统(如超网络结构)协同态的动力学转变提供理论借鉴.
关键词: 同步 /
多重耦合 /
爆炸性去同步 /
去同步驻波态 English Abstract Synchronization in coupled oscillators with multiplex interactions Wang Xue-Bin 1,2 ,Xu Can 1,2 ,Zheng Zhi-Gang 1,2 1.Institute of Systems Science, Huaqiao University, Xiamen 361021, China Received Date: 15 March 2020Accepted Date: 14 May 2020Available Online: 25 May 2020Published Online: 05 September 2020Abstract: The study of synchronizations in coupled oscillators is very important for understanding the occurrence of self-organized behaviors in complex systems. In the traditional Kuramoto model that has been extensively applied to the study of synchronous dynamics of coupled oscillators, the interaction function among oscillators is pairwise. The multiplex interaction mechanism that describes triple or multiple coupling functions has been a research focus in recent years. When the multiplex coupling dominates the interactions among oscillators, the phase oscillator systems can exhibit the typical abrupt desynchronization transitions. In this paper, we extensively investigate the synchronous dynamics of the Kuramoto model with mean-field triple couplings. We find that the abrupt desynchronization transition is irreversible, i.e. the system may experience a discontinuous transition from coherent state to incoherent state as the coupling strength deceases adiabatically, while the reversed transition cannot occur by adiabatically increasing the coupling. Moreover, the coherent state strongly depends on initial conditions. The dynamical mechanism of this irreversibility is theoretically studied by using the self-consistency approach. The neutral stability of ordered state is also explained through analyzing the linear-stability of the incoherent state. Further studies indicate that the system may experience a cascade of desynchronized standing-wave transitions when the width of the distribution function of natural frequencies of oscillators is changed. At the critical coupling, the motion of coupled oscillators in high-dimensional phase space becomes unstable through the saddle-node bifurcation and collapses into a stable low-dimensional invariant torus, which corresponds to the standing-wave state. The above conclusions and analyses are further extended to the case of multi-peak natural-frequency distributions. The results in this work reveal various collective synchronous states and the mechanism of the transitions among these macroscopic states brought by multiplex coupling. This also conduces to the in-depth understanding of transitions among collective states in other complex systems.Keywords: synchronization /multiple coupling /abrupt desynchronization transitions /desynchronized standing wave transition 全文HTML --> --> --> 1.引 言 同步的涌现作为一类具有代表性的自组织协同行为广泛存在于自然界诸多系统中, 它对于理解复杂系统诸多看似不同或无关联的集体行为的物理机制及其某些功能的实现至关重要[1 -3 ] . 例如, 超导耦合约瑟夫森结、激光阵列和电网中的各种集体行为、非平衡化学反应中各种形式的化学斑图、大脑中的神经元集体放电、萤火虫的同步闪烁、蟋蟀的集体鸣叫, 以及社会系统中人群拥塞、踩踏、鼓掌、流行病的传播等行为在一定条件下都会表现出同步或与同步密切相关的特性[4 -6 ] . 因此, 深入探索这些自组织协同态的涌现, 揭示其内在的动力学机制不仅对理解复杂系统群体动力学行为有着重要的理论意义, 同时也可为开展相关实验以及潜在应用研究起到积极的推动作用[7 -9 ] .[10 ] 在20世纪60年代敏锐地认识到振子的相位自由度在同步研究中扮演着重要角色, 并通过构造相位的响应函数来刻画弱耦合极限环振子的同步. Kuramoto[11 ,12 ] 在此基础上做了进一步简化, 假设相振子之间的相互作用为相位差正弦函数的平均场耦合. Kuramoto模型形式简洁, 在统计物理的意义上可解, 对于大量振子的同步相变给出了丰富的物理内涵. 研究表明, 当振子的自然频率分布满足单峰对称且振子之间的耦合强度超过某一临界值时, 系统会自发的经历从无序(非同步态)到有序(同步态)的二级相变[13 -15 ] . 基于该模型的解析可解性, 人们将Kuramoto模型作为研究同步问题的经典范例, 并在其基础上提出了一系列的改进和推广, 并在实验研究和实际应用的多个方面取得了重要进展.[16 -19 ] . 然而人们也发现, 对于很多实际系统, 每一个振子可以同时与多个振子产生相互作用, 而耦合函数是多个振子之间相差的函数, 称为多重耦合函数[20 ,21 ] . 因此, 考虑耦合函数包含多重耦合的高阶简谐项, 并研究多重耦合函数的效应具有重要的理论和现实意义. 最近的研究表明, 多重耦合机制对许多动力学系统的行为至关重要. 例如, 神经网络中神经元之间的信号传递以及大脑中某些结构和功能的关联等都与多重耦合有着密不可分的关系[22 -24 ] . 另外, 当引入多重耦合机制时, Skardal和Arenas[25 ] , Tanaka和Aoyagi[16 ] , Komarov和Pikovsky[17 ] 的研究发现, 相振子系统会涌现出多稳态和爆炸性去同步(abrupt desynchronization transitions, ADT), 即系统在去同步临界点处的转变是不连续、突变的. 这一动力学特性为大脑中的记忆和信息存储提供了潜在的应用[26 ,27 ] . 进一步的研究表明, ADT是多重高阶耦合系统的一类固有性质, 但是如何理解ADT的动力学转变机制尤其是刻画其在相空间的分岔属性及特征依然不清楚.2 节引入三重耦合的动力学模型及其序参量的定义. 在第3 节, 介绍爆炸性去同步现象, 并证明系统的无序态对于任意的耦合强度总是稳定的. 在第4 节, 运用自洽方程理论分析爆炸性去同步的转变机制, 并给出相应的临界耦合强度和临界序参量. 在第5 节, 分析系统由爆炸性去同步到去同步驻波态的过渡机制, 并利用线性稳定性分析计算系统处于驻波态时的稳定性. 在第6 节将得到的结论推广至对称多峰自然频率分布. 在第7 节对全文给出总结, 并对进一步的研究给出展望.2.三重耦合Kuramoto模型 考虑由N 个相振子组成的系统, 振子之间的相互作用函数为三重团簇的耦合函数. 为简便起见, 类似于经典Kuramoto模型, 考虑全局的平均场耦合, 则系统满足如下的动力学方程:${\theta _i}$ 代表第i 振子的相位$i = 1, \cdots, N$ ; N 为系统尺寸; ${\omega _i}$ 为第i 个振子的自然频率, 满足概率分布$g(\omega )$ ; $K > 0$ 为耦合强度. 不失一般性, 假设分布函数$g(\omega )$ 为偶函数, 即$g(\omega ) = g( - \omega )$ . (1 )式与经典Kuramoto模型的不同之处在于振子之间的相互作用并非成对出现, 而是通过一个三元组合($m, n, i$ )即每一个振子i 同时与另外两个振子m 和n 通过单一作用函数产生作用. 这样的相互作用等价于赋予耦合振子系统全连接的超网络拓扑结构[28 -30 ] . 另外, (1 )式的三重耦合函数是相位的高阶正弦函数, 因而三重作用及其高阶耦合会带来新奇的集体动力学与同步行为. (1 )式中的耦合函数$\sin ({\theta _m} + {\theta _n} - 2{\theta _i})$ 使得(1 )式具有相位旋转不变性, 即如果将所有的相振子做相位的平移变换, 则方程(1 )的形式保持不变, 这一点与经典Kuramoto模型一致, 可为后续的理论处理带来便利.k 为整数. 当$k = 1$ 时, 上述定义的${Z_1}$ 即为经典的Kuramoto序参量, 而$k = 2$ 定义的${Z_2}$ 称为Daido序参量[31 ] . 各阶序参量${Z_k}$ 为复参量, 其中${R_k}$ 和${\varTheta _k}$ 分别代表序参量的振幅和相位. 各阶序参量${Z_k}$ 具有明确的物理意义, 可以刻画大量振子的不同整体有序性. 由(2 )式可以看到, $0 \leqslant {R_k} \leqslant 1$ . ${R_k} = 0$ 时, 振子相位在$[0, 2{\text{π}} ]$ 间呈无序分布, 系统整体处于无序态. 当${R_k} = 1$ 时, 振子相位呈现集团分布. ${R_1} = 1$ 描述所有振子处于相同相位$\{ {\theta _i}(t) = \theta (t), \;i = 1, 2, \cdots, N\}$ 的单集团态, ${R_2} = 1$ 则对应于振子分裂为两个相位差为${\text{π}} $ 即$\{ {\theta _i}(t) \!=\! \theta (t)$ , $ {\theta _j}(t) = \theta (t) + {\text{π}}, \;i = 1, 2, \cdots, M, \;j = M\! + 1, \cdots, N\}$ 的双集团态. 推而广之, ${R_k} = 1$ 代表振子处于相位差为$2{\text{π}} /k$ 的k 集团态. ${R_k}$ 处于0和1之间时表示振子处于k 集团态的部分同步态, 即有一定比例的振子会游离在k 个同步集团之外. 对于以下重点讨论的三重耦合情形, k 取到2即可.3.不可逆爆炸性去同步与无序态的稳定性 下面首先通过数值模拟来研究动力学方程(1 )式的集体行为. 在以往的研究中, 自然频率分布$g(\omega )$ 通常被选取为一个单峰对称函数(典型的如Gauss分布和Lorentz分布等[16 ,17 ,25 ] ). 在这种情况下, 当振子之间的耦合强度从大到小越过某一临界值时, 系统会自发地经历从部分同步态到无序态的一级相变, 而当耦合强度从小到大变化时则不会出现该一级相变. 下面考虑一类双峰对称分布函数, 为简便选取如下的双峰Lorentz分布:$ \pm {\omega _0}$ 代表分布函数双峰的位置; $\gamma $ 表示分布的半宽度. 通过调整${\omega _0}$ 和$\gamma $ 的相对大小, $g(\omega )$ 可以从双峰分布过渡到单峰分布.$N = {10^5}$ 个振子进行计算, 这样的振子数可以得到较好的统计结果. 振子自然频率满足上述的双峰Lorentz分布$g(\omega )$ , 其中${\omega _0} = 1$ , $\gamma = 1$ . 考虑不同的不对称初始条件, 将振子不同的初始相位即初始态按比例$\eta $ 和$1 - \eta $ 分别设置为$0$ 和${\text{π}} $ . 考虑耦合强度的绝热变化, 从较大的耦合强度$K = 20$ 开始模拟, 绝热地将耦合强度K 降低到0, 每次耦合强度变化幅度为$\Delta K = 0.01$ (注意, 只要变化幅度足够小, 该取值不会影响结论). 这里参数K 的绝热变化是指对该参数改变的时间尺度远远小于振子系统的动力学弛豫时间尺度, 实际模拟中对每一个给定的耦合强度K , 以前一个耦合强度$K + \Delta K$ 时振子系统的末态作为其初态. 类似地, 再以绝热增加的方式将K 从0逐渐恢复到$K = 20$ . 对于每一个耦合强度, 通过计算序参量${R_{1, 2}}$ 来考察振子系统的有序行为.图1 给出了不同$\eta $ 时序参量${R_{1, 2}}$ 随耦合强度K 的变化. 由图1 可以看到, 取决于耦合强度K 绝热改变的方向, 系统动力学会展现出两种有趣的转变过程. 当K 绝热减小时, 系统从由$\eta $ 决定的不同初始态演化, 序参量${R_{1, 2}}$ 可以遍历各种不同的部分同步态, 每个分支在不同的临界耦合强度从一个最小非零$R_{1, 2}^{\min }$ ($R_{1, 2}^{\min } > 0$ )不连续地跃迁到无序态${R_{1, 2}} = 0$ . 不同的初始态比例$\eta $ 对应于不同的有序态分支, 这种有趣的现象表明, 多重耦合系统在大耦合强度时会有多重的稳定性, 不同的$\eta $ 会存在不同的分支, 在热力学极限$N \to \infty $ 下系统会存在无限个有序分支, 它们对应于在不同的临界耦合强度下产生不连续转变, 我们称其为ADT[21 ] . 上述结果表明, 部分同步态多分支的特征取决于系统的初态, 在本文中以不对称参数$\eta $ 来描述. 另一方面, 尽管绝热减小耦合强度会导致有序态向无序态的不连续转变, 但逆过程却不会发生. 从图1 可以看到, 当耦合强度K 从$0$ 绝热地增加时, 弱耦合时处于无序态的系统并没有随耦合强度增加而自发地跳变到部分同步态, 序参量${R_{1, 2}}$ 一直保持为零, 即系统会维持在无序态, 不存在产生跃迁至有序态的临界耦合强度. 这表明随着绝热增加耦合强度, 系统不会产生与ADT对应的爆炸性同步转变. 我们将上述行为称为不可逆ADT. 这一结果非常有趣, 它在经典的二体作用Kuramoto系统中并没有观察到, 与经典的一级相变有着本质的区别.图 1 系统序参量随耦合强度K 的变化曲线, 箭头表示耦合强度绝热变化的方向 (a)${R_1}$ ; (b)${R_2}$ Figure1. Relation between the order parameter ${R_{1, 2}}$ ((a), (b)) and the coupling strength K . Arrows denote the direction of the adiabatic change of the coupling K : (a)${R_1}$ ; (b)${R_2}$ .2 )式, 动力学方程(1 )式可以改写为平均场形式:4 )式给出了诸振子在平均场下“解耦”的独立方程, 振子之间的相互作用等价于所有振子都与一个耦合强度为$KR_1^2$ 的有效平均场${\varTheta _1}$ 耦合. (4 )式与经典Kuramoto模型相比较有两个显著特点: 1) 非线性耦合强度正比于$R_1^2$ , 这与经典Kuramoto模型中的耦合强度正比于${R_1}$ 明显不同; 2) 耦合项为高阶简谐函数$\sin (2{\varTheta _1} - 2{\theta _i})$ . 这种非线性高阶耦合机制会导致多重耦合相振子系统呈现一系列非平庸动力学特性.$N \to \infty $ 下, 引入振子的状态概率密度分布函数$\rho (\omega, \theta, t)$ , 其中$\rho (\omega, \theta, t){\rm{d}}\omega {\rm{d}}\theta $ 代表在t 时刻自然频率介于$\omega $ 到$\omega + {\rm{d}}\omega $ 之间、相位介于$\theta $ 到$\theta + {\rm{d}}\theta $ 之间振子的比例. 考虑到分布函数$\rho (\omega, \theta, t)$ 中相位变量具有$2{\text{π}} $ 周期性, 可以将$\rho (\omega, \theta, t)$ 做傅里叶分解为$\rm c.c.$ 代表前面复数求和部分的复共轭. 分布函数$\rho (\omega, \theta, t)$ 的时间演化满足连续性方程:$v = \dot \theta $ . 将(5 )式和相速度表达式代入(6 )式, 可以得到各阶系数的演化方程为$Z_1^*$ 是${Z_1}$ 的复共轭. 值得注意的是, ${\rho _n} = 0\; (n \ne 0)$ 总是(7 )式的平庸解, 它对应于系统的无序态${Z_1} = {Z_2} = 0$ .7 )式不难看出, 如果对无序态(${\rho _n} = 0\;$ )施加微扰$\Delta {\rho _n}$ 并只保留线性项, 则此时(7 )式右边第二项为高阶扰动项, 对系统的线性稳定性分析无贡献, 因此可以得到线性方程组:$n = 1, 2, \cdots, \infty$ . 可以发现, 线性模只存在纯虚本征值谱(连续谱, 因为$\omega $ 定义在整个实轴上)而没有非零实部的本征值谱, 在这种情况下无序态总是中性稳定的. 无序态的中性稳定性会导致系统随着耦合强度的变化, 无序态不会自动失稳. 这解释了图1 中的ADT不可逆的原因, 即对于任意耦合强度系统都不可能自发地从无序态失稳而产生向有序态(如果存在的话)的相变. 作为对比, 对于经典Kuramoto模型, 当对无序态做稳定性分析时, 会得到其线性算子本征值谱既包含连续谱又包含离散谱, 其中离散谱的实部随着耦合强度增加会在某一临界耦合强度由负变正, 此时无序态失稳, 这为系统从无序态向同步态的自发相变(二级或一级)提供了可能.4.爆炸性ADT的自洽方程分析 上面的分析只是通过对无序态的线性稳定性分析研究了无序-同步转变的不可逆性. 要分析有序态的出现及其动力学特征, 可以采用自洽方程的方法来研究系统长时间演化的宏观动力学行为. 考虑到$g(\omega )$ 为偶函数, 并且(1 )式具有相位旋转不变性, 因而可以通过选取适当坐标系而设${\varTheta _k} = 0$ [32 ,33 ] , 此时对平均场(4 )式做变量平移变换得${Z_k} = {R_k}$ . 从(9 )式可以看到, 不同的振子由于其自然频率不同而最终会演化到如下两类不同的动力学状态.$\left| {{\omega _i}} \right| \leqslant KR_1^2$ 时, (9 )式${\dot \theta _i} = 0$ . 自然频率满足该条件的振子会被平均场锁定到定态解$\{ \theta _i^0\} $ , 该解满足$\theta _i^0$ 的振子与相位为$\theta _i^0 + {\text{π}} $ 的振子均满足上述条件, 这将导致处于锁相态的振子中会有一部分处于$\theta _i^0$ 状态, 而另一部分处于$\theta _i^0 + {\text{π}} $ 状态[28 ,34 ] , 它们的相位差为${\text{π}} $ . 这意味着锁相振子可能形成两个相差为${\text{π}} $ 的同步集团. 可以通过引入${p_i} = \pm 1$ 来标记两个集团, 于是,${p_i}$ 随机取值, 两种取值满足$\eta ({\omega _i})$ 和$1 - \eta ({\omega _i})$ 分别代表锁相的振子中处在$\theta _i^0$ 和$\theta _i^0 + {\text{π}} $ 两个集团的比例, 反映系统的不对称度. 不失一般性, 设$\eta ({\omega _i})$ 为一个偶函数, 且${1}/{2} \leqslant \eta ({\omega _i}) \leqslant 1$ . 注意, 图1 给出的是当$\eta (\omega )$ 为常数时的结果.$\left| {{\omega _i}} \right| > KR_1^2$ 的振子, 这部分振子不能够被平均场锁住, 因而处于非同步的漂移状态, 它们以非零角速度${\omega _i} - KR_1^2\sin (2{\theta _i})$ 做非匀速周期运动.$\left\langle \cdot \right\rangle$ 代表对振子相位的统计平均. 当系统达到稳态时, 漂移振子相位形成的分布反比于振子的漂移速度. 由于系统具有相位旋转对称性和频率反演对称性, 因此处于漂移态的振子对系统序参量的实部和虚部均无贡献[35 ,36 ] , 即${\left\langle {{{\rm{e}}^{{\rm{i}}k\theta }}} \right\rangle _{\rm{drift}}} = 0$ . 所以在热力学极限下($N \to \infty $ ), 求出序参量(15 )式只需要计算锁相态振子的统计平均. 利用(14 )式, (15 )式可以写成如下积分形式:$g\left( \omega \right)$ 为自然频率的偶函数, 根据(9 )式有${\left\langle {\sin k\theta } \right\rangle _{\rm{lock}}} = 0$ , 所以${R_2}$ 为17 )式和(18 )式构成了描述系统稳态行为的自洽方程组, 两阶序参量${R_1}$ 和${R_2}$ 可以通过这组闭合方程自洽求解.$q = KR_1^2$ , 则(17 )式变为q 不难看出, (17 )式—(19 )式建立起了序参量${R_k}$ 和耦合强度K 之间的隐函数关系.$\eta (\omega )$ 为常数且$g(\omega )$ 为双峰Lorentz分布(参数为${\omega _0}$ 和$\gamma $ )的情形, 此时$F(q) = (2\eta - 1)f(q)$ , 其中函数图2(a) 给出了几组不同自然频率分布半宽度$\gamma $ 时的$f(q)$ 曲线. 由图2(a) 可以看出, 对于不同的分布半宽度$\gamma $ , 函数$f(q)$ 都有$f(0) = 0$ , $f( + \infty ) = 0$ , 且所有曲线$f(q)$ 都在0到$ + \infty $ 之间有惟一的极大值点. 另外可以看到, 曲线$f(q)$ 的极大值随着自然频率峰的半宽度$\gamma $ 增加而降低. 这说明曲线$f(q)$ 的值有一个上限.图 2 (a) 当${\omega _0} = 1$ 时不同自然频率分布半宽度$\gamma $ 对应的$f(q)$ 曲线; (b) 当${\omega _0} = 1$ , $\gamma = 0.2$ , $\eta = 1$ 时, $F(q) = (2\eta - 1) f(q)$ 和$G(q) = 1/\sqrt K $ 两条曲线的交点随着耦合强度K 变化的示意图Figure2. (a) $f(q)$ curves when ${\omega _0} = 1$ ; (b) the intersection of curves $F(q) = (2\eta - 1)f(q)$ and $G(q) = 1/\sqrt K $ for different couplings K , where ${\omega _0} = 1$ , $\gamma = 0.2$ , $\eta = 1$ .19 )式的解可以通过寻找曲线$G(q) = 1/\sqrt K $ 与曲线$F(q) = (2\eta - 1)f(q)$ 的交点得到. 当耦合强度K 很小时, 曲线$G(q)$ 对应的值很大, 以至于$G(q)$ 总在曲线$F(q)$ 上方, 因而两条曲线无交点, 系统没有非零的${R_k}$ 解. 随着耦合强度K 的增加, 曲线$G(q) = 1/\sqrt K $ 逐渐降低. 当K 增加至临界值${K_{\rm{c}}}$ 时, 曲线$G(q)$ 与曲线$F(q)$ 会在图2(a) 中$f(q)$ 的极值点${q_{\rm{c}}}$ 处发生相切. 这表明可以通过上述方法来确定系统发生同步转变的临界耦合强度值. 当K 进一步增加时, 对于给定的$\eta $ , 曲线$G(q)$ 与曲线$F(q)$ 会有两个交点, 即(18 )式有两组解, 设分别为${q_ \pm }$ . 利用稳定性分析很容易发现${q_ - } < {q_{\rm{c}}}$ 对应于非稳定解, ${q_ + } > {q_{\rm{c}}}$ 对应于稳定解[37 ] . 对于不同的耦合强度K , $G(q)$ 和$F(q)$ 两条曲线的交点如图2(b) 所示. 另一方面, 不管耦合强度K 多大, 无序态(${R_k} = 0$ )作为系统的一类平庸解总是存在. 考虑到上述无序态的稳定性, 系统在${q_{\rm{c}}}$ 处会发生一连串ADT, 对应的临界耦合强度为$R_1^{\rm{c}}$ 和${K_{\rm{c}}}$ 满足如下标度行为:22 )式—(24 )式可以看出, 当给定临界参数${q_{\rm{c}}}$ 时, ADT发生的临界耦合强度与系统的非对称函数$\eta $ 成平方反比, 与之相对应的临界Kuramoto序参量$R_1^{\rm{c}}$ 则与非对称函数$\eta $ 成正比. 有趣的是, 临界Daido序参量$R_2^{\rm{c}}$ 与$\eta $ 无关, 它只依赖于系统的临界耦合参数${q_{\rm{c}}}$ . 特别地, 当取极端情形$\eta = 1/2$ 时(即锁相振子在两个团簇之间取相同的概率), ${K_{\rm{c}}} = \infty $ , $R_1^{\rm{c}} = 0$ 而$R_2^{\rm{c}} > 0$ . 因此, 对于高阶耦合相振子系统有必要用两类序参量${Z_{1, 2}}$ 共同刻画系统的协同行为.5.从ADT到DSWT 图3 给出了不同频率分布半宽度$\gamma $ 时系统序参量${R_{1, 2}}$ 随耦合强度K 变化的分岔行为. 可以看到, 当$\gamma \ne 0$ 时, 系统会经历一连串的ADT, 且临界耦合强度${K_{\rm{c}}}$ 随着$\eta $ 的增加而单调降低, 而$R_1^{\rm{c}}$ 随着$\eta $ 的增加而单调增加, $R_2^{\rm{c}}$ 则始终保持不变. 当$\gamma = 0$ 时, 发现系统不会经历ADT, 当减小耦合强度使得$K < {K_{\rm{c}}}$ 时, 可以发现${R_{1, 2}} \ne 0$ . 进一步数值模拟发现, ${R_{1, 2}}$ 并非处于定态解, 即序参量会随时间表现出周期振荡行为. 图4 给出了不同耦合强度下序参量的时间行为. 从图4 可以看到, 序参量是一种大幅振荡, 表明系统的集体态在单集团同步态和双集团同步态之间来回跃迁. 我们将这一族周期振荡态定义为驻波态. 研究驻波态在集体行为上的具体表现是一个重要问题. 下面重点分析系统从ADT到DSWT的转变机制.图 3 自然频率为双峰Lorentz分布且${\omega _0} = 1$ 时不同分布半宽$\gamma $ 对应的系统序参量${R_1}$ , ${R_2}$ 随耦合强度K 的变化 (a), (d) $\gamma = 0$ ; (b), (e) $\gamma = 0.5$ ; (c), (f) $\gamma = 1$ . 图中实线和符号标记分别对应于理论预测和数值结果($N = {10^5}$ 个耦合相振子), 对于每一个$\eta $ , 系统的初始相位分别按概率$\eta $ 和$1 - \eta $ 随机设置为$0$ 和$\pi $ Figure3. The order parameters ${R_1}$ [(a)—(c)] and ${R_2}$ [(d)—(f)] varying against the coupling strength K for different γ and ${\omega _0} = 1$ , when the natural frequency obeys a bimodal Lorentz distribution: (a), (d) $\gamma = 0$ ; (b), (e) $\gamma = 0.5$ ; (c), (f) $\gamma = 1$ . Theoretical predictions and numerical results are labeled as solid lines and symbols, respectively ($N = {10^5}$ ). For every η , the initial phase is set as 0 and π for η and 1–η .图 4 当$\eta = 1$ , ${\omega _0} = 1$ , $\gamma = 0$ 时不同耦合强度K 对应的序参量${R_{1, 2}}(t)$ 的周期振荡图像($N = {10^5}$ 个耦合振子) (a), (b) $K = 1.5 < {K_{\rm{c}}}$ ; (c), (d)$K = 0.5 < {K_{\rm{c}}}$ Figure4. Oscillatory behaviors of the order parameter ${R_{1, 2}}(t)$ for different coupling strengths K , where $\eta = 1$ , ${\omega _0} = 1$ , $\gamma = 0$ , and $N = {10^5}$ : (a), (b) $K = 1.5 < {K_{\rm{c}}}$ ; (c), (d) $K = 0.5 < {K_{\rm{c}}}$ .$\gamma $ 趋于零时, 自然频率分布$g(\omega )$ 退化为双峰Dirac分布:$\eta $ 为与自然频率无关的常数时, $f(q)$ 可以解析给出:$f(q)$ 的极大值可通过$\dfrac{{{\rm{d}}f}}{{{\rm{d}}q}} = 0$ 求出, 它位于${q_{\rm{c}}} = \dfrac{{2{\omega _0}}}{{\sqrt 3 }}$ , 相应地,$\gamma = 0$ 时, 所有振子只有大小相等、方向相反的两种自然频率, 整个振子系统通常会分裂成4个团簇$ \pm \theta $ 和${\text{π}} \pm \theta $ , 其中每一个振子选择$ \pm \theta $ 团簇的概率分别为$\eta /2$ , 选择${\text{π}} \pm \theta $ 的概率分别为$(1 - \eta )/2$ . 与系统达到稳态不同的是, 此时$ \pm \theta $ 两个团簇的相差会随时间做周期变化, 从而导致了DSWT的出现.${R_1}(t) = (2\eta - 1)\left| {\cos \theta (t)} \right|$ , ${R_2} = \left| {\cos 2\theta (t)} \right|$ , 平均场(9 )式可以简写为K 很小时, $ \pm \theta $ 以及${\text{π}} \pm \theta $ 团簇均不能够被平均场锁住, 它们分别在单位圆上做非均匀周期旋转, 从而导致如图4 所示的${R_{1, 2}}(t)$ 的周期振荡.28 )式计算得到. 做变量分离, 在相位的$2{\text{π}} $ 周期内对两边做积分可以得到所需要的时间为${T_\eta }$ 即对于给定$\eta $ 时每个团簇的运动周期. 序参量${R_{1, 2}}(t)$ 在一个周期的平均值为图3(a) 和图3(d) 给出的平均值结果表明, 理论与数值模拟完全一致.27a )式给出的临界耦合强度${K_{\rm{c}}}$ 可知, 当$K > {K_{\rm{c}}} = \dfrac{{8{\omega _0}}}{{3\sqrt 3 {{(2\eta - 1)}^2}}}$ 时, (28 )式有定态解, 振荡解DSWT失稳, 此时4个团簇$ \pm \theta $ 和${\text{π}} \pm \theta $ 均被平均场锁住. 对该定态解施加扰动, 代入(1 )式中, 并忽略高阶扰动项, 可以得到线性扰动方程, 其雅可比矩阵J $\sin (2{\theta _i}) \!=\! \pm \dfrac{{{\omega _0}}}{{KR_1^2}}$ (当$i \!=\! 1, \cdots, {N}/{2}$ 时为正, $i = {N}/{2} \!+\! 1, \cdots, N$ 时为负), $\cos (2{\theta _i}) \!=\! \sqrt {1 \!-\! {{\left( {\dfrac{{{\omega _0}}}{{KR_1^2}}} \right)}^2}}$ . 进一步分析雅可比矩阵(31 )式可以发现, J N 个本征值分别为1 )式的旋转不变性;J $N - 2$ 重简并, 对应于雅可比矩阵J $N - 2$ 重根. 利用锁相条件可以发现, 当$q > {q_{\rm{c}}} = 2{\omega _0}/\sqrt 3 $ 时$\theta < {\text{π}}/6$ , 相对应的本征值为${\lambda _{2, 3}} < 0$ , 这意味着四团簇锁相态稳定; 而当$q < {q_{\rm{c}}}$ 时$\theta > {\text{π}} /6$ , 此时本征值中${\lambda _2} > 0, {\lambda _3} < 0$ , 这意味着四团簇锁相态失稳, 系统发生去同步驻波态转变.$\theta $ 随时间周期变化, 这就意味着雅可比矩阵J ${\lambda _2}, \;{\lambda _3}$ 都含时(周期), 根据Floquet定理, DSWT的稳定性由含时本征值在一个周期内的时间平均来确定:$i = 2$ , 3. 当${I_i} < 0$ 时, 周期解DSWT稳定, 反之则不稳定. 计算发现, 对于任意的$\eta $ 有$\gamma $ 趋于零的极限情况, 一方面, 相应的频率分布概率测度为零, 此时系统无序态的连续谱退变成几对离散的纯虚本征值, 标志无序态将不再具有吸引性, 这为系统打破ADT提供了可能; 另一方面, 对锁相态的稳定性分析表明, 系统在高维相空间经历了一个鞍结分岔, 此时${\lambda _2}$ 由负变正, 整个高维相空间塌缩到一个四维不变环面上, 导致了DSWT的形成.6.多峰自然频率分布时的爆炸性去同步 第5 节中的结论可以推广到振子自然频率为多峰分布的情况. 当自然频率分布半宽度$\gamma = 0$ 时, 分布函数可写为如下形式:$2 m$ 为分布函数峰值的个数. 对于给定$\eta $ , $f(q)$ 可写成如下积分形式:图5 给出了当${\omega _0} = 1$ 时几组不同m 情况下的$f(q)$ 曲线. 可以发现, 对于不同的m , $f(0) = 0$ , $f( + \infty ) = 0$ . 与双峰情况不同的是, 对于不同的m , $f(q)$ 在0到$ + \infty $ 上会有m 个不同的极值点, 将最大极值点所对应的横坐标标记为$q_m^{\rm{c}}$ . 根据等式关系${1}/{{\sqrt K }} = (2\eta - 1)f(q)$ , 可以求出对于每个m 系统所对应的ADT临界值为图 5 当${\omega _0} = 1$ 时, 不同m (2m 为分布函数峰值的个数)对应的$f(q)$ 曲线Figure5. $ f\left(q\right) $ curves where 2m is the number of peaks of the distribution function for ${\omega _0} = 1$ .图6 给出了当${\omega _0} = 1$ , $m = 2, \;3$ 时, 系统序参量${R_{1, 2}}$ 随耦合强度K 变化的数值模拟结果($N = {10^5}$ 个振子)与理论预测ADT临界值的对比, 结果表明数值模拟与理论预测完全一致.图 6 当${\omega _0} = 1$ 时, 不同m 对应的序参量${R_{1, 2}}$ 随耦合强度K 的变化 (a), (b) m = 2; (c), (d) m = 3. 标记有图形的实线表示数值模拟结果, 黑色虚线表示ADT临界值理论预测结果(40 )式Figure6. The order parameters ${R_1}$ [(a), (c)] and ${R_2}$ [(b), (d)] varying against the coupling strength K for different m and ${\omega _0} = 1$ : (a), (b) $m = 2$ ; (c), (d) $m = 3$ . Theoretical predictions and numerical results are labeled as solid lines and symbols, respectively. The dotted lines are the theoretical predictions of the critical values of ADT given in (40 ).7.总 结 本文探讨了多重耦合机制对相振子集体动力学的影响. 研究发现, 随着振子自然频率分布半宽度的改变, 系统会经历从ADT到DSWT的转变. 利用平均场自洽理论, 解析地给出了系统发生ADT的临界耦合强度以及相应临界序参量的一般表达式. 当振子自然频率分布的半宽度减小到零时, 系统的无序态线性模的连续本征谱会退变为若干对纯虚本征值, 这使得无序态解不再具有吸引性, 从而导致ADT不再出现. 系统锁相态的本征谱结构表明, 当耦合强度小于临界耦合强度时, 系统在高维相空间会经历一个鞍结分岔导致同步态的失稳而塌缩至稳定的低维不变环面, 该环面对应于DSWT. 上述现象和理论分析可以推广到多峰自然频率分布的情形. 



































































































 图 1 系统序参量随耦合强度K的变化曲线, 箭头表示耦合强度绝热变化的方向 (a)
图 1 系统序参量随耦合强度K的变化曲线, 箭头表示耦合强度绝热变化的方向 (a)























































































































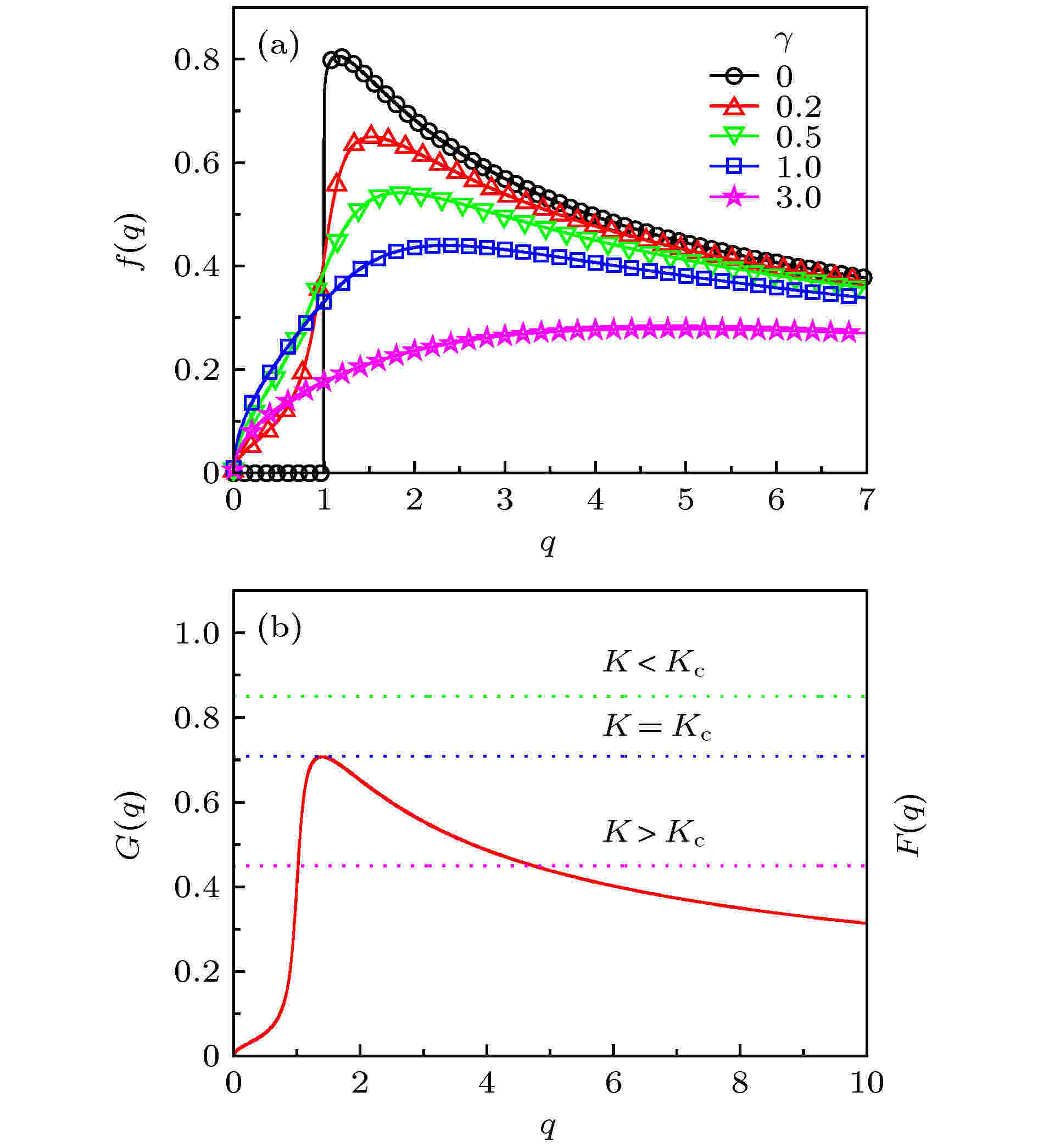 图 2 (a) 当
图 2 (a) 当


















































































































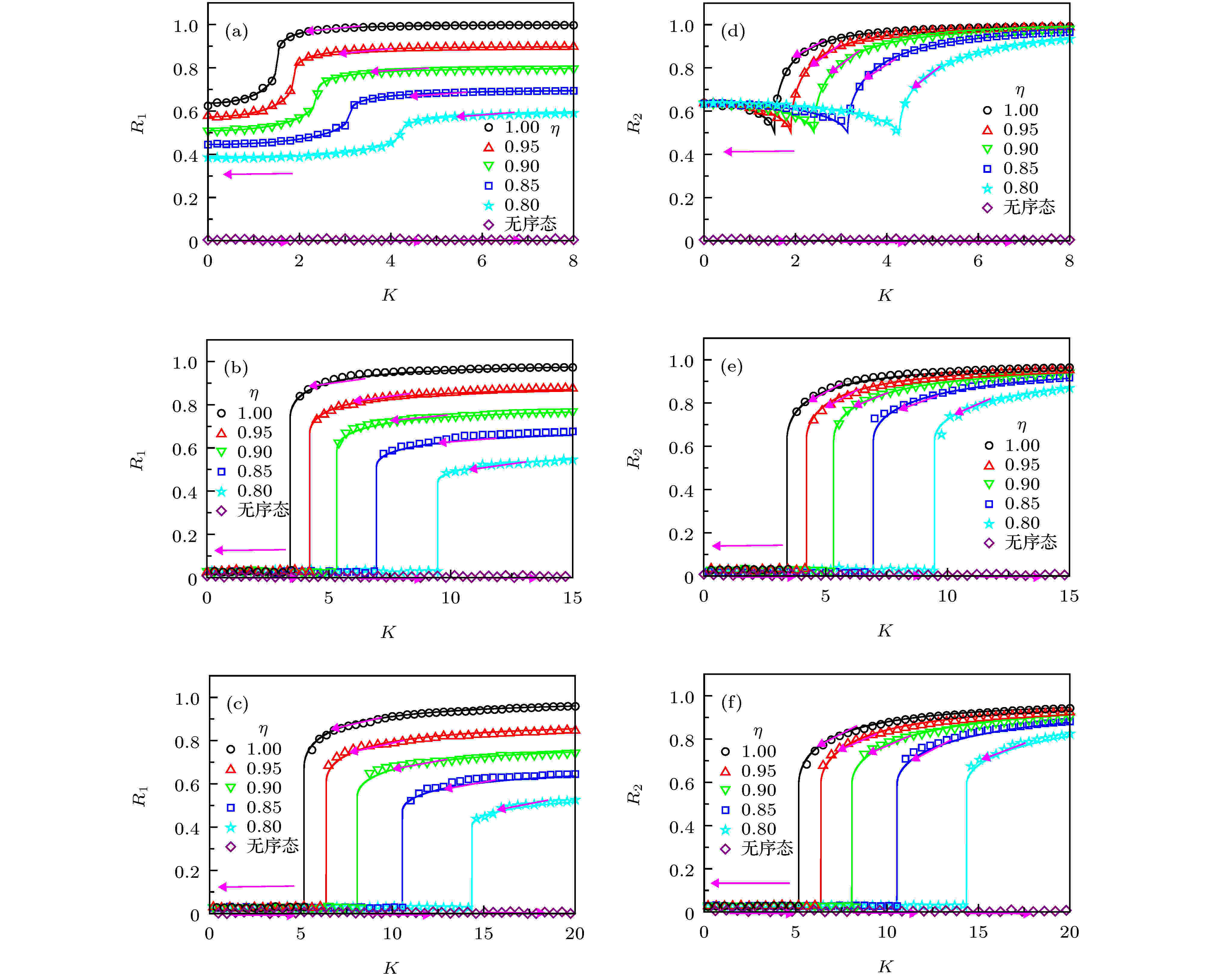 图 3 自然频率为双峰Lorentz分布且
图 3 自然频率为双峰Lorentz分布且





















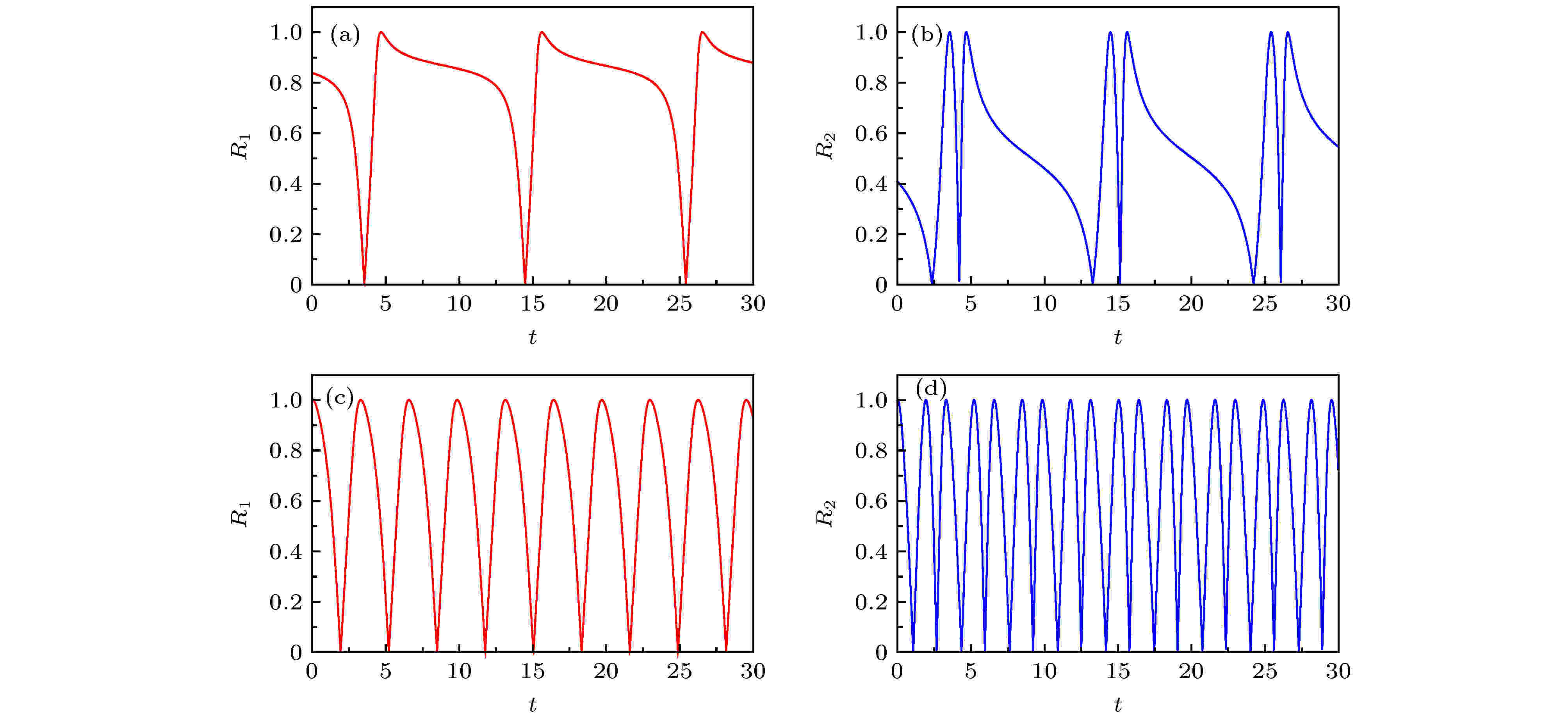 图 4 当
图 4 当




















































































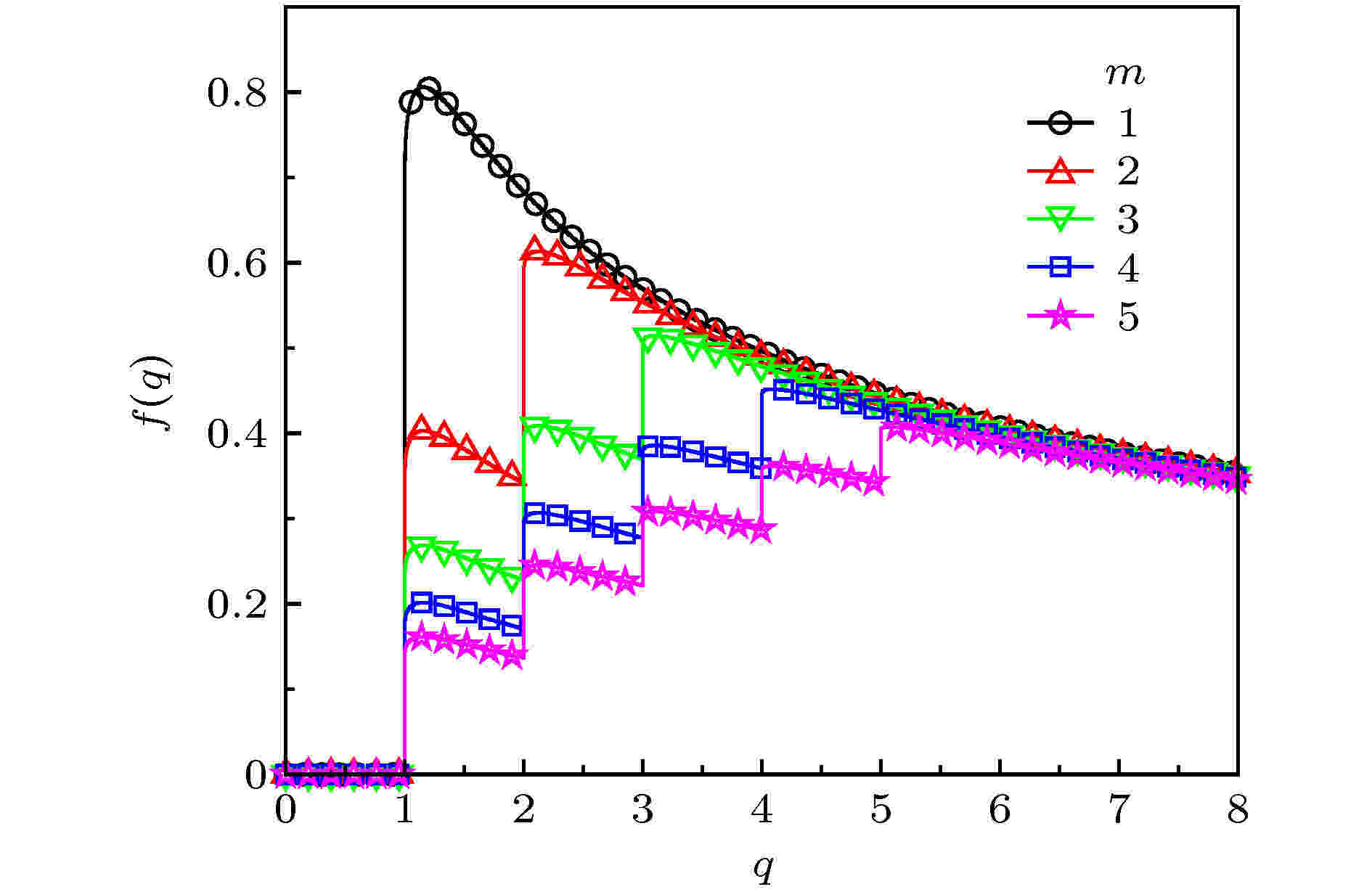 图 5 当
图 5 当







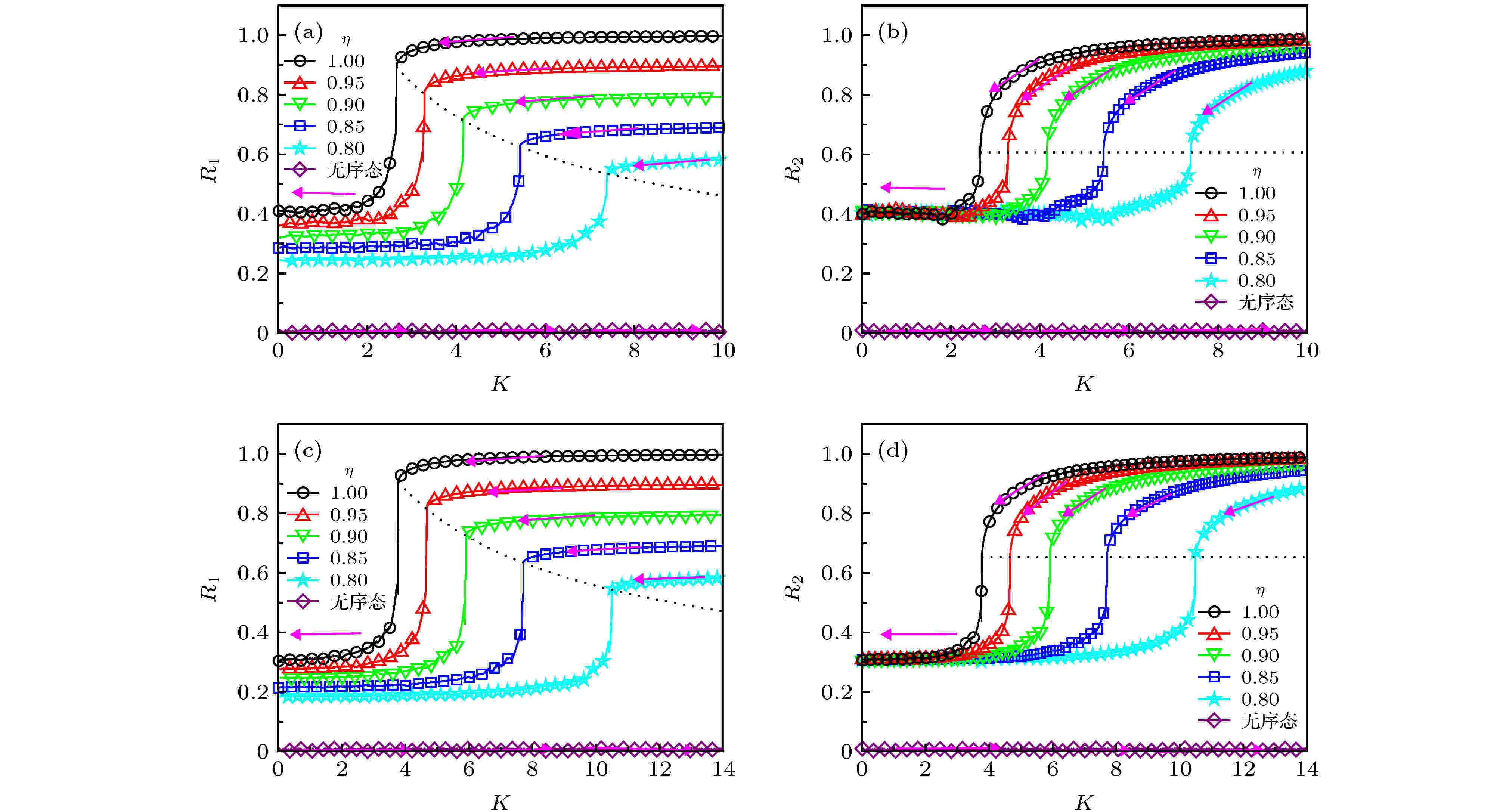 图 6 当
图 6 当






