摘要:研究了使用垂直线列阵情况下, 浅海环境中的模态空间检测器(modal space detector, MSD)的检测性能. 推导了MSD的处理增益, 结果表明其处理增益随波导环境中传播模态数的增多而减小, 进而其检测性能也随之下降. 利用各阶模态深度函数之间的正交性, 将MSD分解为若干阶模态子空间检测器(modal subspace detector, MSSD). 推导了各阶MSSD的处理增益, 发现其随各阶模态衰减系数的增大而减小. 根据各阶模态的衰减规律设计加权系数, 提出一种加权模态子空间检测器(weighted modal subspace detector, WMSSD). 以处理增益作为比较参量, 通过理论和仿真实验分析了声源位置和声速剖面对WMSSD检测性能的影响. 结果表明: 1) 当声源位于负梯度声速波导的近海面区域和正梯度声速波导的近海底区域时, 由于低阶模态深度函数存在反转点, WMSSD的处理增益弱于MSD, 而当声源位于其他大部分观测区域时, WMSSD的处理增益都优于或显著优于MSD; 2) 在等声速梯度波导中, 各阶模态深度函数不存在反转点, 在所有观测区域WMSSD的处理增益都显著优于MSD.
关键词: 模态空间检测/
模态衰减系数/
处理增益/
模态函数反转点

English Abstract

全文HTML

--> --> -->

水下声源检测是水声信号处理所要解决的重要问题之一, 它通过对接收数据进行一定的处理来判断声源是否存在. 对于被动声源检测, 最优检测器为匹配模型检测器(matched model detector, MMD)^[1,2]. 在求解MMD的检测统计量时, 要求环境参数和声源位置已知. 然而实际的浅海水声环境存在不确定性, 声源位置又是未知的, 因此MMD并不能实现, 而是作为一般检测器的性能上限参考.
针对浅海波导环境中的声源检测问题, 相关研究人员提出了诸多解决方法. 一类是根据海洋环境和声源位置的不确定信息建模, 提出MMD的改进的方法, 如贝叶斯检测器^[2,3](Bayes detector, BD)、基于主成分分析(principle component analysis, PCA)的检测器^[4]和基于蒙特卡罗优化的广义似然比(Monte Carlo generalized likelihood ratio test, MC-GLRT)检测器^[5]等. BD利用贝叶斯原理通过对不确定的环境参数和未知的声源位置进行积分, 最终得到一种平均意义上的最优检测器, 但它需要复杂的指数和积分运算. 为减小运算复杂度, 刘宗伟等相继提出了PCA检测器和MC-GLRT检测器, 以较低的运算代价实现了性能几乎接近于BD的稳健检测. 这两种检测器都需要利用不确定海洋环境中的信号波前采样与接收数据做匹配相关处理. 当声源位置可能的区域范围增大时, 为得到充分的声场信息, 需要大量信号波前采样及相应的相关运算, 这将带来较大的运算负担. 另一类方法是利用子空间检测^[6]的思想来解决声源位置未知的问题. 子空间检测器通过将接收数据能量正交投影到信号子空间来获得检测统计量, 应用到水下波导环境时, 不同文献^[7-13]中的命名有所差异, 但实际上它们都是同一种检测器. 由于信号子空间通常由阵列采样模态信息^[14]所张成, 本文中将其称为模态空间检测器^[12](modal space detector, MSD). 受限于阵列孔径尺寸和环境不确定性, MSD常会遭遇模态信息非完备采样和不确定采样的问题. 对于前者, 文献[11]通过对模态相关矩阵特征分解给出了一种有效谱检测器; 而对于后者, 文献[12]利用模态采样矩阵之间的近似“包含关系”提出了一种稳健检测方法.
子空间检测不需要信号波前采样, 运算量较小且具有较好的稳健性. 对于相同的输入信噪比(下简称信噪比), MSD的检测性与模态空间(即信号子空间)维度成负相关, 而波导中的传播模态数增多将引起模态空间维度增大. 当频率升高、波导环境深度变大等无可避免的因素造成传播模态数增多时, 相应MSD的检测性能也随之下降. 这对于水下声源检测, 尤其是远距离传播的低信噪比声源检测十分不利. 为改善MSD的检测性能, 文献[9,10]提出截断子空间检测器(truncated subspace detector, TSD), 通过截断部分传播模态构造更低维度的信号子空间以提高其检测性能, 截断子空间的求取依赖于信噪比; 然而实际中信噪比是未知的, 导致TSD难以实现. 另外, PCA检测器实际上是一种加权子空间检测器, 其各阶主成分分量张成了信号子空间, 但其加权系数与各子空间的信号分量并不匹配, 尤其是当传播模态数增多时反而会造成检测器性能的下降.
根据简正波理论^[15], 声信号以若干阶简正波模态的形式在水下传播, 传播过程中伴随海水吸收、海底反射等过程, 各阶简正波模态系数在传播过程中会发生不同程度的衰减, 衰减程度与各阶模态衰减系数和传播距离成正相关. 对于远距离传播的声信号, 衰减系数一定程度上反映了各阶简正波模态对声源信号的贡献. 因此可考虑利用各阶简正波模态的衰减规律对MSD进行改进. 本文研究发现, 使用垂直线列阵(vertical linear array, VLA)时, 利用各阶模态函数采样的近似正交性, 可将MSD分解为若干阶独立的模态子空间检测器(modal subspace detector, MSSD), 各阶MSSD的处理增益与模态系数成正比. 根据模态系数与衰减系数之间的关系设计加权系数, 提出一种加权的模态子空间检测器(weighted modal subspace detector, WMSSD). 相同信噪比下, 检测器的处理增益越大, 其最终的输出信噪比也越大, 进而其检测性能也越好. 利用模态衰减规律设计的加权系数反映了各阶MSSD对最终得到检测器的贡献, 使WMSSD可获得高于MSD的处理增益, 从而WMSSD可实现更优的检测性能.
本文所采取的加权方式反映了模态衰减对各阶MSSD处理增益的影响, 而各阶MSSD的处理增益还与声源位置处模态深度函数^[16,17](下简称模态函数)的值有关. 声源位置处模态函数值由声源位置和模态函数共同决定. 模态函数形状与相应模态反转点^[17,18]密切相关, 模态反转点一般位于若干低阶模态函数, 其深度由波导中的声速决定. 因此, 声源位置和声速剖面将影响WMSSD的检测性能.
本文其他部分安排如下. 第二节推导了浅海环境中的MSD, 给出了其处理增益的计算公式, 并分析了波导环境中传播模态数对MSD检测性能的影响; 第三节给出了本文所提出WMSSD的推导过程, 并从理论上分析了影响其检测性能的因素; 第四节通过仿真实验给出了WMSSD的检测性能及其相较于MSD的性能提高效果, 深入探究了声源位置和声速剖面对WMSSD检测性能的影响, 以及导致这种影响的物理机理, 并归纳了WMSSD的适用场景; 第五节给出了本文得出的相关结论.

2

-->

2.1.浅海环境中的声场模型

考虑浅海波导环境中远距离窄带声源, 假设声源位置未知、中心频率f已知. 根据简正波理论, 声源辐射到接收点$\left( {r, z} \right)$处的声压传递函数可表示为各阶简正波之和的形式

$g\left( {r,z} \right) = \sum\limits_{m = 1}^M {{a_m}\left( {r,{z_{\rm{s}}}} \right) \cdot {\phi _m}\left( z \right)} , $

式中, M为波导环境中传播的简正波阶数, r, ${z_{\rm{s}}}$和z分别为接收点与声源的水平距离、声源深度和接收点的深度, ${\phi _m}\left( \cdot \right)$为第m阶模态深度函数(下简称模态函数), ${a_m}\left( {r, {z_{\rm{s}}}} \right)$为第m阶模态系数. 模态系数是声源位置的函数, 其表达式为

${a_m}\left( {r,{z_{\rm{s}}}} \right) = \frac{{{\rm{i}}{{\rm{e}}^{ - {\rm{i}}\left( {{\text{π}}/4 - {k_{rm}}r} \right) - {\delta _m}r}}}}{{\rho \left( {{z_{\rm{s}}}} \right)\sqrt {8{\text{π}}r{k_{rm}}} }}{\phi _m}\left( {{z_s}} \right), $

模态系数下文简写为${a_m}$. 模态函数是深度的函数, 且满足正交性

$\int_0^H {\frac{{{\phi _m}\left( z \right){\phi _n}\left( z \right)}}{{\rho \left( {{z_{\rm{s}}}} \right)}}{\rm{d}}z} = \delta \left( {m - n} \right), $

式中, H为波导深度.
利用(1)式, 声信号传播到垂直线列阵(vertical linear array, VLA)的传递函数可表示为模态矩阵和模态系数向量乘积的形式

${{g}} = \left( {\begin{array}{*{20}{c}} {{\phi _1}\left( {{z_1}} \right)}& \ldots &{{\phi _M}\left( {{z_1}} \right)} \\ \vdots & \ddots & \vdots \\ {{\phi _1}\left( {{z_N}} \right)}& \cdots &{{\phi _M}\left( {{z_N}} \right)} \end{array}} \right)\left[ \begin{gathered} {a_1} \\ \vdots \\ {a_M} \\ \end{gathered} \right] = {{\varPhi }}\cdot {{a}}, $

式中, N为阵元个数, ${z_1}, \cdots , {z_N}$为各阵元深度, ${{\varPhi }}$为$N \times M$维的实矩阵, 记作${{\varPhi }}\in {\mathbb{R}^{N \times M}}$, 由各阵元采样的各阶模态函数构成, 下文简称模态矩阵; ${{a}} \in {\mathbb{R}^M}$为M维列向量, 由各阶简正波的模态系数构成.
2 -->

2.2.模态空间检测器

假设VLA覆盖全水深, 且阵元数足够采集完备的模态信息. 将阵列接收数据变换到频域进行处理, 可得如下频域信号检测模型,

$\begin{split} \; &{H_0}: {r} = {n}{\rm{,}}\\\; &{H_1}: {r} = {s} + {n}.\end{split}$

式中, $\left( {{r}, {s}, {s}} \right) \in {\mathbb{R}^N}$为列向量, 分别表示阵列接收数据、声源辐射信号和背景噪声. 声源信号可用声场传递函数表示为

${s} = \mu \cdot {g}, $

式中, $\mu $为表示声源幅度和相位的未知复变量. 假设背景噪声为空间白噪声, 服从均值为零、协方差矩阵为$\sigma _{\rm{n}}^2{{I}_N}$(${{I}_N} \in {\mathbb{R}^{N \times N}}$为单位矩阵)的多维复高斯分布. (5)式描述了一个二元假设检验问题, 零假设${H_0}$表示声源信号不存在, 备选假设${H_1}$表示声源信号存在.
将(4)式和(6)式代入(5)式中, 并记${\theta } = \mu \cdot {a}$, 则两种假设下接收数据的概率密度函数分别为^[19],

$\begin{split}& p\left( {{r}|{H_0}} \right) = \dfrac{1}{{{{\left( {{\text{π}}\sigma _{\rm{n}}^2} \right)}^N}}}\exp \left( { - {{r}^{\rm{H}}}{r}{\rm{/}}\sigma _{\rm{n}}^2} \right),\\& p\left( {{r}|{H_1},{\theta }} \right) \!=\! \dfrac{1}{{{{\left( {{\text{π}}\sigma _{\rm{n}}^2} \right)}^N}}}\exp \left( {\! -\! {{\left( {{r}\! -\! {\varPhi \theta }} \right)}^{\rm{H}}}\!\left( {{r} \!-\! {\varPhi \theta }} \right)/\sigma _{\rm{n}}^2} \right)\!.\end{split}$

式中, 上标‘H’表示共轭转置运算. 由于声源位置未知, ${\theta }$为未知变量, 进而$p\left( {{r}|{H_1}, {\theta }} \right)$为条件概率密度函数. 令$\partial p\left( {{r}|{H_1}, {\theta }} \right)/\partial {\theta } = 0$, 可得${\theta }$的最大似然估计为

${\hat \theta } = {{\varPhi }^{\rm{T}}}{\left( {{\varPhi }{{\varPhi }^{\rm{T}}}} \right)^{ - 1}}{r}.$

式中, 上标‘T’表示转置运算. 利用(7)式和(8)式, 可得两种假设下的条件似然比为

$L\left( {r} \right) = \frac{{p\left( {{r}|{H_1},{\hat \theta }} \right)}}{{p\left( {{r}|{H_0}} \right)}}.$

对(9)式做化简运算并取自然对数, 可得相应的检测统计量为,

$T\left( {r} \right) = \ln L\left( {r} \right) = \frac{{{{r}^{\rm{H}}}{\varPhi }{{\left( {{{\varPhi }^{\rm{T}}}{\varPhi }} \right)}^{ - 1}}{{\varPhi }^{\rm{T}}}{r}}}{{\sigma _{\rm{n}}^2}}.$

由(10)式可知, 该检测统计量$T\left( {r} \right)$(以下简写为T)为接收数据在模态矩阵张成空间(以下简称模态空间)上的正交投影能量与噪声功率之比, 因此将该检测器称为模态空间检测器(modal space detector, MSD).
由其检测统计量可知, MSD是一种二次型检测器, 根据统计信号处理的知识^[19]可得其服从的统计分布为,

$\left\{ \begin{aligned}& {H_0}:2T \sim \chi _{2M}^2,\\& {H_1}:2T \sim \chi _{2M}^2\left( \lambda \right).\end{aligned} \right.$

式中, $\chi _{2 M}^2$表示自由度为$2 M$的卡方分布, 非中心参量为

$\lambda = 2{{s}^{\rm{H}}}{s}/\sigma _{\rm{n}}^2.$

$\chi _{2 M}^2\left( \lambda \right)$表示非中心参量为$\lambda $的非中心卡方分布. 根据(11)式描述的统计分布可求得MSD的检测概率为

${P_{\rm{D}}} = Q_{\chi _{2M}^2\left( \lambda \right)}^{}\left( {2\gamma } \right), \gamma = Q_{\chi _{2M}^2}^{ - 1}\left( {{P_{{\rm{FA}}}}} \right)/2.$

式中, $Q_{\chi _{2 M}^2\left( \lambda \right)}^{}\left( \cdot \right)$表示$\chi _{2 M}^2\left( \lambda \right)$的右尾概率函数, $Q_{\chi _{2 M}^2}^{ - 1}\left( \cdot \right)$表示$\chi _{2 M}^2$右尾概率函数的逆函数, $\gamma $为检测门限, ${P_{{\rm{FA}}}}$为虚警概率. 由(13)式可知, 给定虚警概率下, 检测概率与非中心参量和自由度有关; 根据函数关系可知, 检测概率随非中心参量$\lambda $的增大而增大, 随自由度2M的增大而减小. 由(12)式可知, 非中心参量表征的是信号能量与噪声功率之比, 进而容易理解, 非中心参量越大, 检测概率越大. 自由度由传播模态数决定, 这表明对于相同的信噪比和虚警概率, 当波导环境中传播模态数增多时, 对应MSD的检测概率将减小.
2 -->

2.3.MSD的处理增益

使用处理增益来定量地描述检测器的检测性能, 其定义为输出信噪比与输入信噪比之比,

$G = OSNR/SNR, $

式中, G为处理增益, OSNR和SNR分别表示输入信噪比和输出信噪比. 定义输入信噪比(下简称信噪比)为各阵元接收信号平均能量与阵元噪声功率的比值,

$SNR = \frac{{{{s}^{\rm{H}}}{s}/N}}{{\sigma _{\rm{n}}^2}} = \frac{{{{s}^{\rm{H}}}{s}}}{{N\sigma _{\rm{n}}^2}}.$

由(12)式和(15)式可知, 非中心参量与信噪比存在关系$\lambda = 2 N \cdot SNR$. 输出信噪比可使用检测器的偏移系数来近似计算^[20], 其定义为

$OSNR = \frac{{{\rm{E[}}T|{H_1}{\rm{]}} - {\rm{E[}}T|{H_0}{\rm{]}}}}{{{{\left\{ {{\rm{E[}}{T^2}|{H_0}{\rm{]}} - {{\rm{E}}^2}{\rm{[}}T|{H_0}{\rm{]}}} \right\}}^{1/2}}}}, $

式中, ${\rm{E[}} \cdot {\rm{]}}$表示求期望运算. 利用(15)式和(16)式可得MSD的处理增益(推导过程见附录)为

$G = N/\sqrt M .$

由(17)式可知, MSD的处理增益与传播模态阶数的平方根成反比, 与阵元个数成正比, 这与2.2节根据统计分布规律得出的结论一致.
检测器的处理增益衡量的是检测器本身对噪声的抑制能力, 由其表达式也可看出, 它与输入信噪比无关. 容易理解, MSD对噪声的抑制能力随阵元个数的增多而增强. 而对于相同的信噪比, 当传播模态数增多时, MSD将接收数据投影到更高维度的模态空间以获取所有声源辐射信号的能量, 但同时也引入了更多维的噪声分量, 最终导致输出信噪比减小, 处理增益降低. 因此当声源频率增加或波导深度增大而使得波导中传播的模态数增多时, MSD的处理增益降低造成检测性能变差, 这对水下声源信号检测尤其是低信噪比的情况极为不利.

为提高MSD的处理增益进而改善其检测性能, 本节先对MSD做子空间分解, 然后分析各子空间检测器的处理增益, 并提出一种加权子空间检测器.
2

-->

3.1.MSD的子空间分解

考虑模态深度函数采样完备的情况, 各阶采样模态向量之间近似满足正交性, 即${{\varPhi }^{\rm{T}}}{\varPhi } \approx {{I}_M}$(${{I}_M} \in {\mathbb{R}^{M \times M}}$为单位矩阵), 将其代入(10)式中可得简化的检测统计量,

$T = \frac{{{{r}^{\rm{H}}}{\varPhi }{{\varPhi }^{\rm{T}}}{r}}}{{\sigma _{\rm{n}}^2}}, $

分别记

${\varPhi } = \left[ {{{\phi }_1}, \cdots ,{{\phi }_M}} \right],{{\phi }_m} = {\left[ {{\phi _m}\left( {{z_1}} \right), \cdots ,{\phi _m}\left( {{z_N}} \right)} \right]^{\rm{T}}}, $

式中, ${{\phi }_{ m}}$为第m阶采样模态函数构成的列向量, 则MSD可写为M个模态子空间检测器(mode subspace detector, MSSD)之和的形式,

$\begin{split}\; &T = \sum\limits_{m = 1}^M {{{r}^{\rm{H}}}{{\phi }_m}{\phi }_m^{\rm{T}}{r}/\sigma _{\rm{n}}^2} = \sum\limits_{m = 1}^M {{T_m}} ,\\&{T_m} = {{r}^{\rm{H}}}{{\phi }_m}{\phi }_m^{\rm{T}}{r}/\sigma _{\rm{n}}^2. \end{split}$

式中, ${T_m}$为第m阶MSSD的检测统计量. 容易得到, ${T_m}$服从如下分布

$\left\{ \begin{aligned}&{H_0}:2{T_m} \sim \chi _2^2,\\&{H_1}:2{T_m} \sim \chi _2^2\left( {{\lambda _m}} \right).\end{aligned} \right.$

式中, ${\lambda _m}$为非中心参量

${\lambda _m} = 2{{s}^{\rm{H}}}{{\phi }_m}{\phi }_m^{\rm{T}}{s}/\sigma _{\rm{n}}^2.$

由(21)式可知, 各阶MSSD的自由度都为2, 因此其检测性能仅由对应的非中心参量(${\lambda _m}$)唯一决定. 而各阶非中心参量的大小迥异, 因而相应的各阶MSSD具有不同的检测性能.
为更直观地考量各阶MSSD的检测性能, 推导了第m阶MSSD的处理增益为(推导过程见附录)

${G_m} = l{a_m} \cdot a_m^ * , $

式中, 上标‘*’表示复数共轭运算, l为常系数. (23)表式明第m阶MSSD的处理增益与相应的模态系数成正比. 将(2)式代入(23)式中可得,

${G_m} = l\frac{{\phi _m^2\left( {{z_{\rm{s}}}} \right){{\rm{e}}^{ - 2{\delta _m}r}}}}{{{\rho ^2}\left( {{z_{\rm{s}}}} \right)8{\text{π}}r{k_{rm}}}}.$

由(24)式可知, 由于各阶相异的模态衰减系数${\delta _m}$、声源深度上的模态函数值${\phi _m}\left( {{z_{\rm{s}}}} \right)$以及水平波数${k_{rm}}$, 导致各阶MSSD具有不同的处理增益, 进而表现出不同的检测性能. 浅海波导中的各阶水平波数在数值上相差较小, 因此造成各阶MSSD不同检测性能的主要因素是声源深度上的模态函数值和模态衰减系数.
2 -->

3.2.基于模态衰减加权的子空间检测器

MSD为各MSSD非相干叠加之和, 由于各MSSD的处理增益实际上大不相同, 因此对MSD最终检测性能的贡献也各不相同. 处理增益较大的MSSD为MSD贡献更多的信号能量, 处理增益较小的MSSD则为MSD主要引入噪声分量. 如果根据各阶处理增益的变化规律设计权值对各阶MSSD进行加权求和, 使得到的检测器具有更大的输出信噪比, 则最终获得的检测器将获得更好的检测性能. 基于此, 我们提出一种加权的模态子空间检测器(weighted modal subspace detector, WMSSD). 结合(20)式, 构造WMSSD的检测统计量为

${T_{\rm{w}}} = \sum\limits_{m = 1}^M {{w_m}{T_m}} = {{r}^{\rm{H}}}{\varPhi W}{{\varPhi }^{\rm{T}}}{r}/\sigma _{\rm{n}}^2, $

式中, ${W} = {\rm{diag}}\left( {{w_1}, \cdots , {w_M}} \right)$, ${w_m}$为第m阶MSSD的加权系数. 将(25)式代入(16)式和(14)式中, 可得WMSSD的处理增益为

${G_{\rm{w}}} = \frac{{{\rm{tr}}\left( {{{g}^{\rm{H}}}{\varPhi W}{{\varPhi }^{\rm{T}}}{g}} \right)}}{{{\rm{t}}{{\rm{r}}^{1/2}}\left( {{WW}} \right)}}, $

式中, ${\rm{tr}}\left( \cdot \right)$表示矩阵求迹运算. 显然, 当加权系数等于各阶MSSD的处理增益时, 即权值${w_m} = {G_m}$, WMSSD可以获得最优的处理增益, 将相应的检测器称为最优加权的模态子空间检测器(optimal weighted modal subspace detector, OWMSSD). 然而由于实际上声源位置未知, 无法直接计算得到各阶处理增益作为加权系数, OWMSSD并不能实现. 为此, 需要寻求其他次优的加权系数.
根据3.1节分析可知, 各阶MSSD的处理增益与声源深度处的模态函数值和模态衰减系数成正比. 简正波的各阶模态函数随波导深度变化. 在等声速波导中, 各阶模态函数随深度振荡变化, 振荡频率随阶数的增大而增大. 在非等声速波导中, 模态函数存在反转点. 由文献[16]可知, 各阶模态函数在反转点之间是振荡变化的, 在反转点之外呈指数规律迅速衰减. 因此, 不同声源深度上的各阶模态函数值的变化较为复杂. 而各阶模态衰减系数的变化规律较为简单, 随模态阶数的增大而增大. 虽然模态衰减系数在数值上相对于水平波数较小, 但对于远距离传播的声信号, 在指数衰减规律(${{\rm{e}}^{ - 2{\delta _m}r}}$)的作用下, 各阶MSSD的处理增益呈现明显的衰减, 且衰减程度随阶次增大而增大.
基于上述分析, 可以考虑利用模态衰减系数来设计加权系数. 假设目标声源位于观测区域, 观测区域在距离上的范围为$R - {R_1}$(单位为km), 利用衰减指数设计各阶MSSD的加权系数为

${w'_m} = {{\rm{e}}^{ - 2{\delta _m}R \times {{10}^3}}},{W'} = {\rm{diag}}\left( {{{w}'_1}, \cdots ,{{w}'_M}} \right).$

将(27)式代入(26)式中计算可得WMSSD的处理增益. 对于本文考虑的远距离传播的声信号, 模态衰减系数对处理增益的作用较为强烈, 该加权方式能反映各阶处理增益的变化趋势, 因此得到的WMSSD预期可获得更大的处理增益, 并实现一定的检测性能提升.
各阶MSSD的最优加权为其相应的处理增益, 各阶处理增益由声源的深度和距离共同决定, 由于本文在设计加权系数时仅考虑了模态衰减系数的影响, 因此得到的WMSSD的处理增益与声源深度和距离有关. 声源深度主要影响的是模态函数值$\phi _m^{}\left( {{z_{\rm{s}}}} \right)$, 模态函数在波导深度上的分布规律主要与声速剖面有关, 因此WMSSD的处理增益在声源深度上的分布规律将受到声速剖面的影响.

本节将通过仿真实验验证WMSSD的检测性能相较于MSD的提升效果, 同时探究WMSSD的检测性能随相关参数的变化规律及造成这种变化的物理机理, 并通过与MSD的处理增益对比归纳WMSSD的适用场景. 仿真使用的波导环境模型和VLA如图1所示, 图中标注了相关的海洋环境参数. VLA覆盖整个水深, 阵元个数$N = 120$, 起始阵元深度为1 m, 阵元间距为1 m. 假设目标位于观测区域范围15— 30 km. 仿真中的信噪比为对数信噪比(即$10\lg SNR $), 单位为dB. 声场与模态深度函数由Kraken程序计算.
图 1 浅海波导环境及其相关参数
Figure1. The shallow water waveguide and its environmental parameters.

2

-->

4.1.MSD与WMSSD的检测性能

假设声源位于距离为18 km、深度为50 m处, 仿真中通过提高声源频率来增大波导中的传播模态数. 图2给出了MSD的检测概率随信噪比和虚警概率变化的曲线, 即检测性能曲线, 其中窄带声源中心频率f分别为50, 100, 300, 500和700 Hz时在波导中激发的传播模态数分别为3, 5, 16, 27和37. 从图2可以看出, 相同信噪比条件下, 随着传播模态数的增多, 对应MSD的检测概率随之下降, 下降幅度逐渐减缓.
图 2 不同传播模态数下MSD的检测性能曲线　(a) 检测概率随输入信噪比的变化, ${P_{{\rm{FA}}}} = 0.1$; (b) 检测概率随虚警概率的变化, $SNR = - 15\;{\rm{ dB}}$
Figure2. Detection performance curves of the MSD under various numbers of normal modes: (a) Probabilities of detection versus SNRs, ${P_{{\rm{FA}}}} = 0.1$; (b) probabilities of detection versus probabilities of false alarm, $SNR = - 15\;{\rm{dB}}$.

为进一步探究MSD检测性能变化的原因, 图3给出了不同模态数下MSD的处理增益, 对图中处理增益取对数表示, 即10lgG, 单位为分贝(dB). 由图3可知, 随着模态个数增多, MSD的处理增益逐渐减小. 这是由于随着传播模态数的增多, 引入了更多的噪声分量, 而信号能量保持不变, 从而导致MSD的处理增益下降. 同时也注意到随模态数的增加处理增益下降的速度在减缓, 这与检测性能曲线呈现的结果相一致.
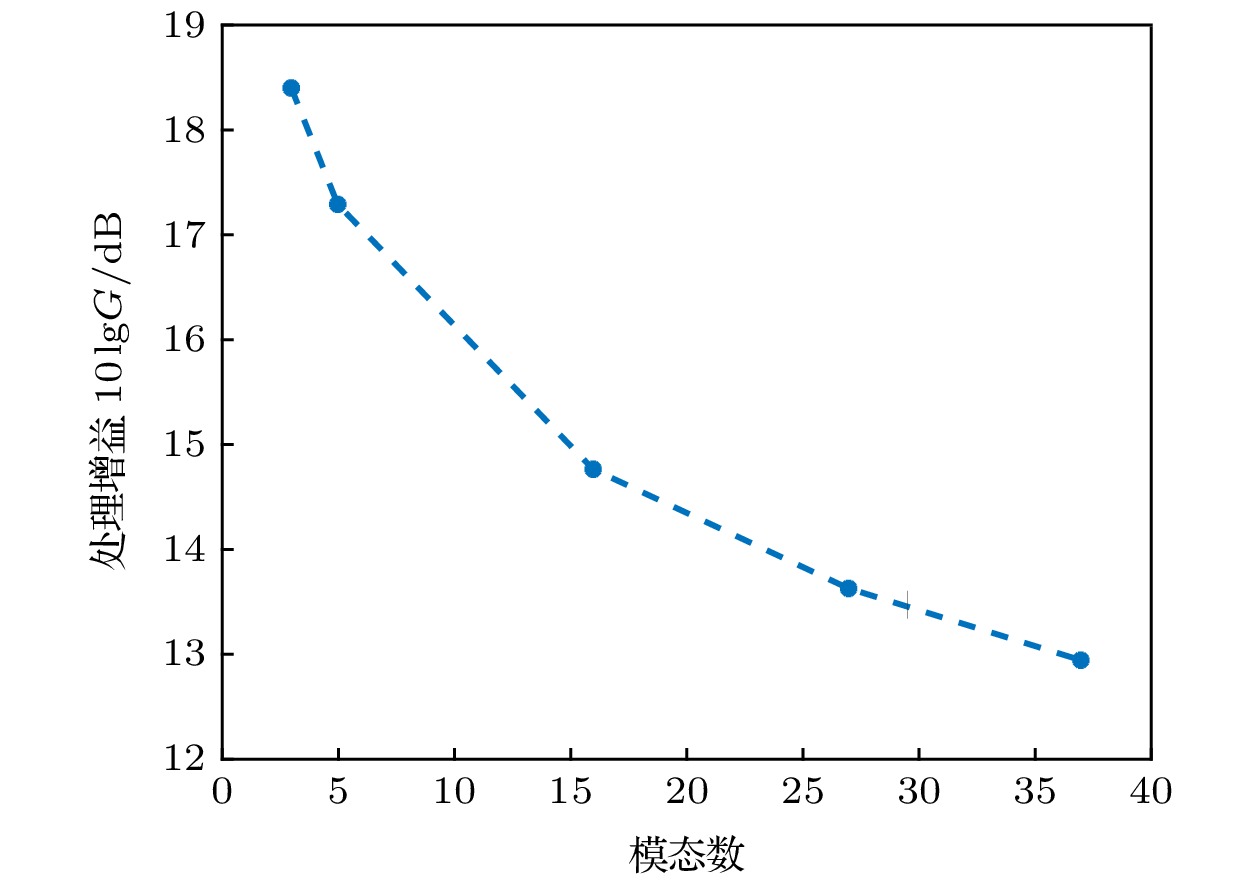图 3 MSD的处理增益随模态数的变化曲线
Figure3. The processing gains of the MSD versus the numbers of normal modes.

声源位置同上, 图4给出了不同传播模态数下归一化的各阶MSSD处理增益(这里为便于展示${G_m}$的变化趋势未对其取对数)的分布, 其中阶数大于8的处理增益都近似为零, 图中未予展示. 由图4可知, 尽管模态数增多, 处理增益仍主要集中在少数几阶MSSD, 且各阶MSSD的分布呈现随阶数的增大逐渐减小的趋势; 此外, 还观察到当传播模态数较多时, 各阶MSSD的处理增益分布存在起伏. 由文中(24)式可知, 第m阶MSSD的处理增益不仅与模态衰减系数有关, 它使得MSSD的处理增益随阶数呈下降趋势; 此外, 第m阶MSSD的处理增益还与声源深度上的模态函数幅值$\phi _m^{}\left( {{z_{\rm{s}}}} \right)$有关, 由于$\phi _m^{}\left( {{z_{\rm{s}}}} \right)$随阶数振荡变化, 尤其是当传播模态数较多时, $\phi _m^{}\left( {{z_{\rm{s}}}} \right)$随阶数振荡变化的更剧烈, 进而使得各阶MSSD的处理增益存在起伏; 例如当M = 37时, 此时$\phi _1^{}\left( {{z_{\rm{s}}}} \right) < \phi _2^{}\left( {{z_{\rm{s}}}} \right)$使得第一阶MSSD的处理增益小于第二阶MSSD.
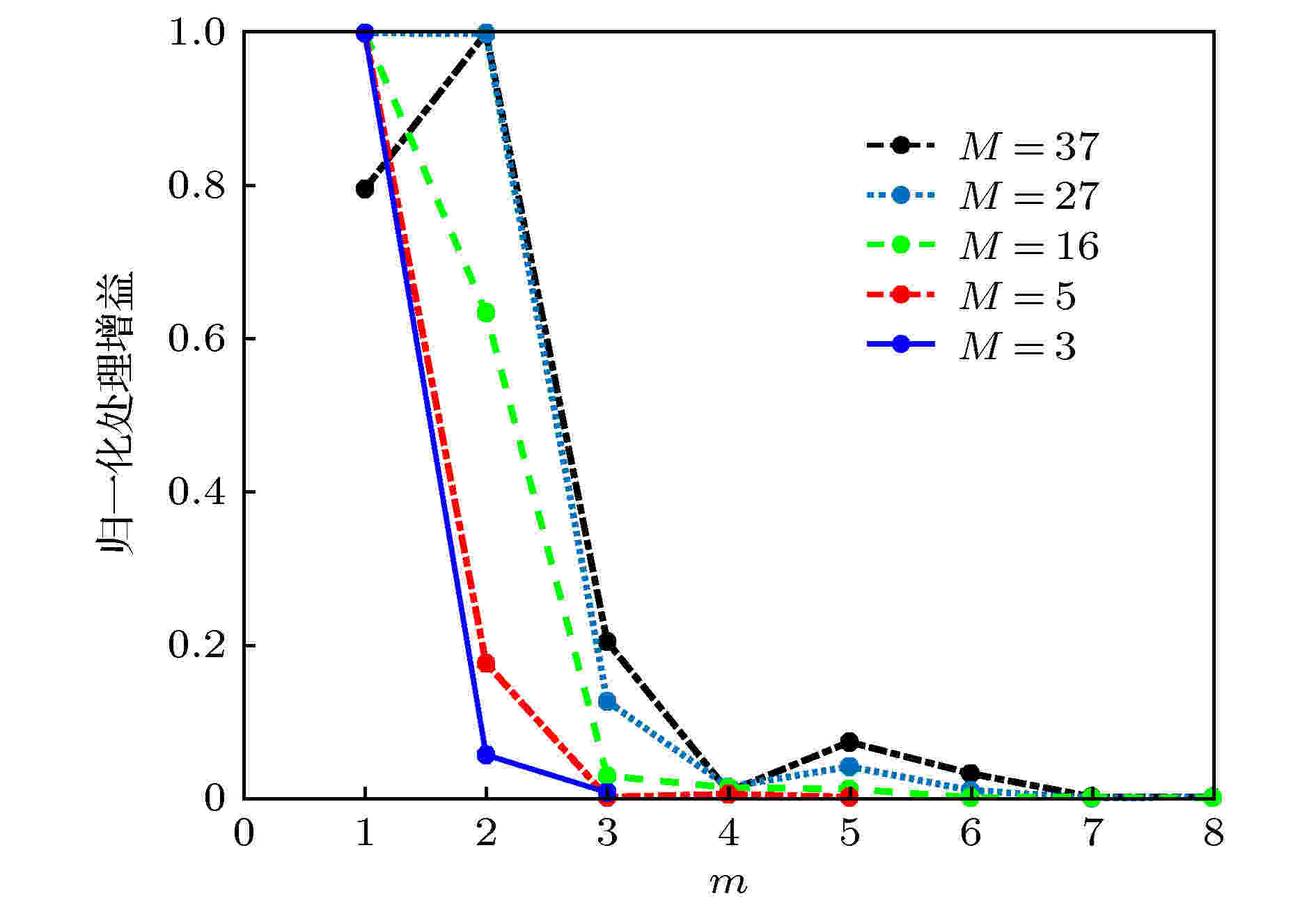图 4 各阶MSSD处理增益随阶数的变化
Figure4. The processing gains of MSSD versus the orders of normal modes.

声源位置同上. 利用(17)式和(26)式分别计算了该声源位置处MSD, WMSSD和OWMSSD的处理增益, f = 100 Hz时对应的处理增益分别为17.41 dB, 20.10 dB和20.11 dB, f = 300 Hz时对应的处理增益分别14.90 dB, 19.18 dB和19.25 dB. 可以看出, WMSSD的处理增益相较于MSD有很大幅度的提升, 并且接近于OWMSSD. 图5和图6分别给出了这两种频率(100和300 Hz)下相应的MSD, WMSSD和OWMSSD的检测性能曲线. 由图5和图6可知, 对于该位置的声源, WMSSD与OWMSSD的检测性能曲线几乎重合, 即WMSSD实现了理论上所能达到的最优检测性能, 相较于MSD有了显著的提升; 取检测概率为0.5时所需的信噪比门限为比较对象(下同), 对于100和300 Hz的声源, WMSSD的信噪比门限分别下降了1.5和3 dB. 对比图5和图6也可看出, 虽然WMSSD对较高频率声源的性能提升幅度较大, 但当频率增大时其检测性能仍有所下降, 这由传播模态数增多导致.
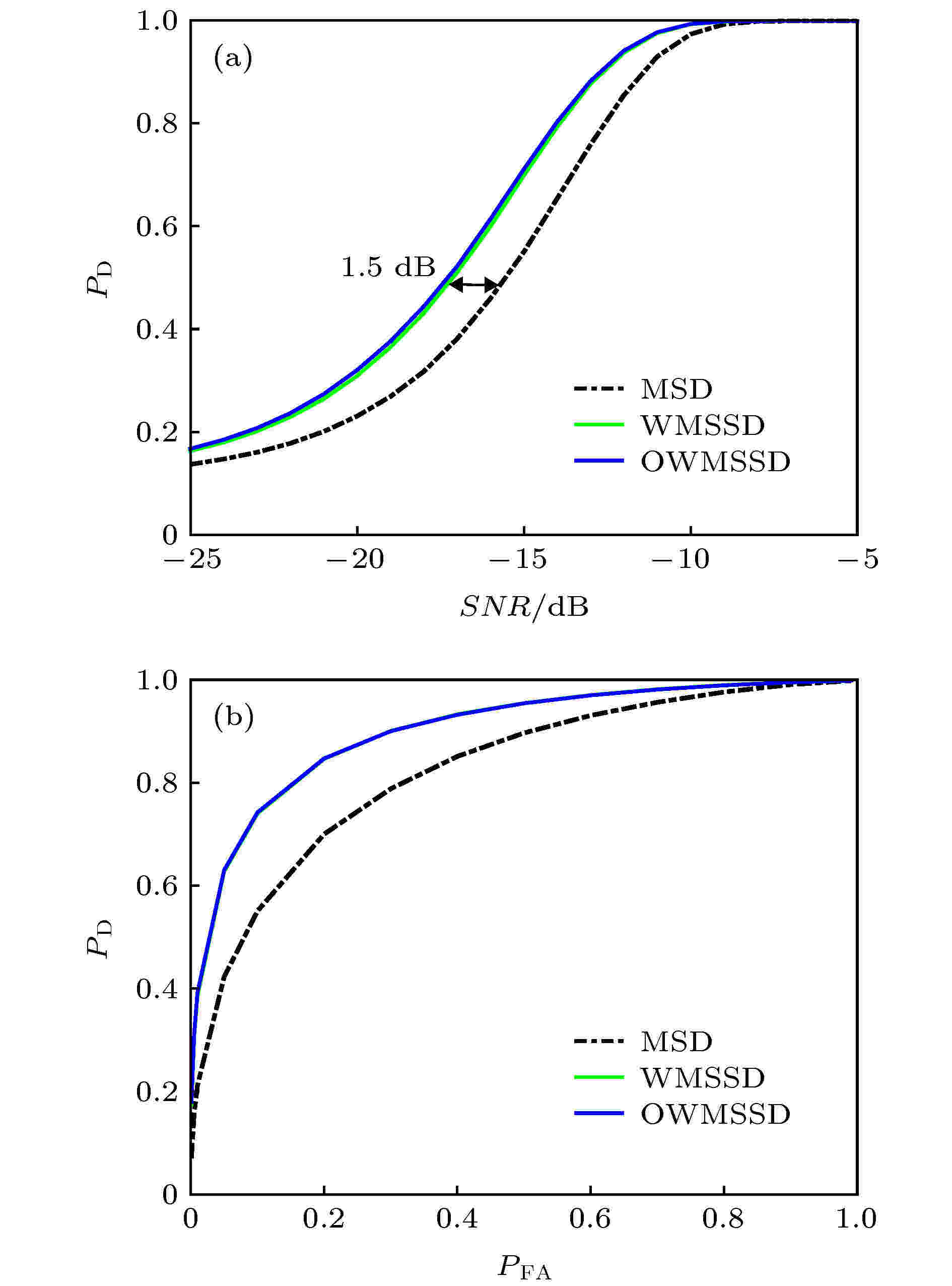图 5 MSD, WMSSD, OWMSSD的检测性能曲线, f = 100 Hz　(a) 检测概率随输入信噪比的变化, ${P_{{\rm{FA}}}} = 0.1$; (b) 检测概率随虚警概率的变化, $SNR = - 15\;{\rm{dB}}$
Figure5. Detection performance curves of the MSD, WMSSD and OWMSSD with f = 100 Hz: (a) Probabilities of detection versus SNR, ${P_{{\rm{FA}}}} = 0.1$; (b) probabilities of detection versus probabilities of false alarm, $SNR = - 15\;{\rm{dB}}$.

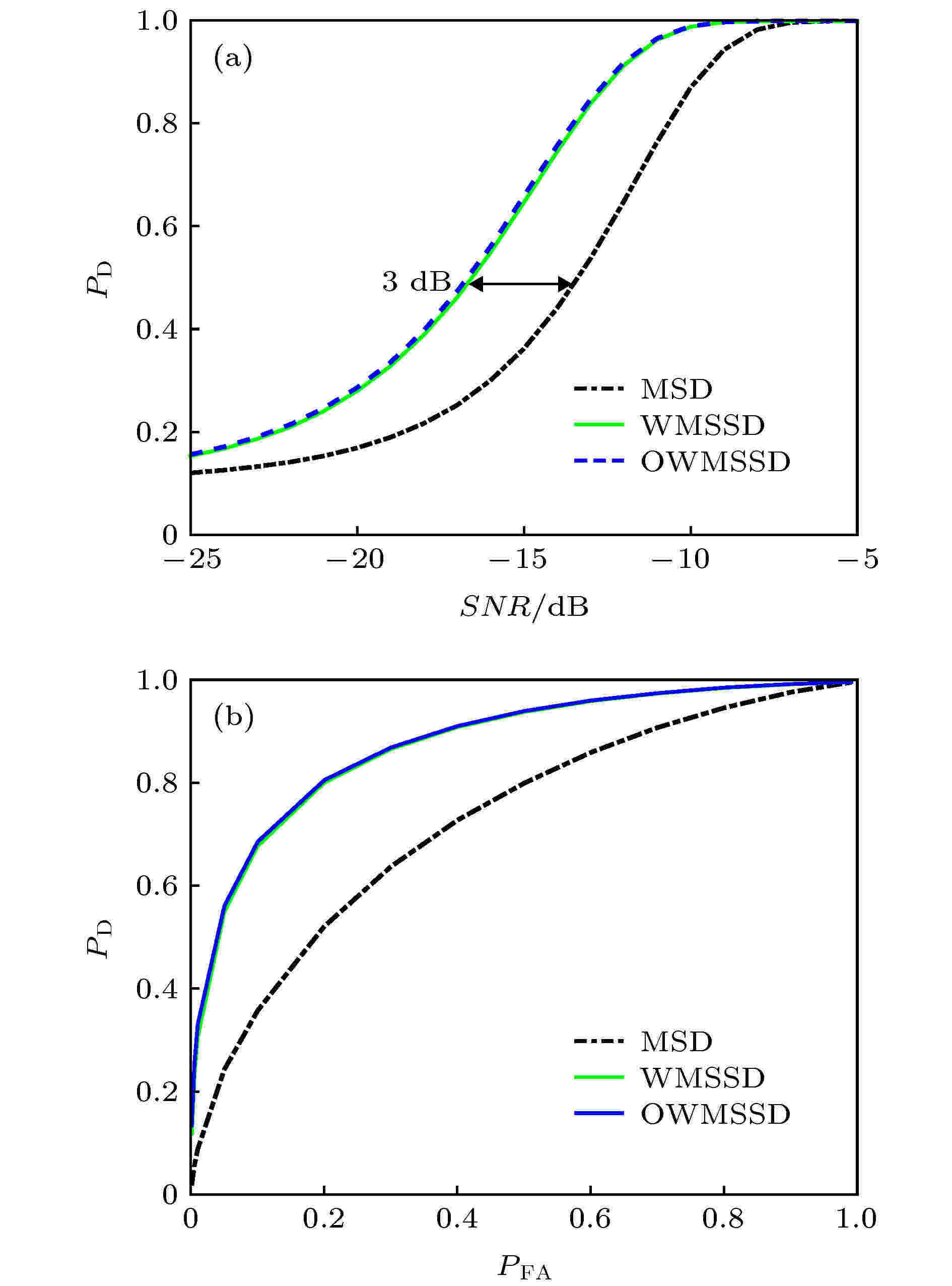图 6 MSD, WMSSD, OWMSSD的检测性能曲线, f = 300 Hz　(a) 检测概率随输入信噪比的变化, ${P_{{\rm{FA}}}} = 0.1$; (b) 检测概率随虚警概率的变化, $SNR = - 15\;{\rm{dB}}$
Figure6. Detection performance curves of the MSD, WMSSD and OWMSSD with f = 300 Hz: (a) Probabilities of detection versus SNR, ${P_{{\rm{FA}}}} = 0.1$; (b) probabilities of detection versus probabilities of false alarm, $SNR = - 15\;{\rm{dB}}$.

2 -->

4.2.声源位置对WMSSD检测性能的影响

对于相同的信噪比, 处理增益越大, 检测器的输出信噪比就越大, 进而检测器将获得更优的检测性能, 因而检测器处理增益的大小直接反映了其检测性能的优劣. 各阶MSSD的处理增益与声源位置(深度和水平距离)直接相关, 而加权系数与声源位置无关, 因此加权系数并不与各阶MSSD的处理增益完全一致, 这就使得WMSSD的处理增益会受到声源位置的影响.
为充分了解WMSSD的检测性能, 我们给出了当声源(频率为300 Hz)位于不同深度和距离时WMSSD的处理增益(单位为dB), 同时作为对比也给出了MSD和OWMSSD的处理增益随声源位置的变化, 如图7所示. 由图7(a)和图7(b)可知, MSD的处理增益基本稳定在14.85 dB左右, 随声源位置波动很小, WMSSD的处理增益变化范围较大, 在5—20 dB之间波动. 但同时也注意到, 事实上只有一小块区域WMSSD的处理增益较小(小于MSD), 而大部分区域上的处理增益都在较大数值范围内波动. 图7(b)中标示出了处理增益小于MSD的区域, 将该区域称为WMSSD的弱探测区域, 即黑色实线左上角部分, 在其他区域WMSSD的处理增益均大于MSD. 记WMSSD与MSD处理增益相同的深度为临界深度, 可以看出临界深度随距离增大而减小, 到24 km处时减小为零, 即当声源距离大于24 km时, WMSSD的弱探测区域消失. 同时注意到在深度为60—80 m范围内, WMSSD的处理增益达到最大, 都在18 dB以上, 且随距离的波动较小. 由图7(c)可知, OWMSSD的处理增益总是大于MSD和WMSSD, 且它在不同位置的变化规律与WMSSD类似.
图 7 MSD, WMSSD, OWMSSD的处理增益随声源位置的变化, f = 300 Hz　(a) MSD; (b) WMSSD; (c) OWMSSD
Figure7. The processing gains of the MSD, WMSSD and OWMSSD versus acoustic source locations with f = 300 Hz: (a) MSD; (b) WMSSD; (c) OWMSSD.

图7中的数值结果表明, 在大部分情况下, WMSSD的检测性能明显优于MSD, 但当声源深度位于临界深度以浅时, 其检测性能要差于MSD, 同时临界深度随距离的增大而减小. 这是由WMSSD的加权方式造成的. 在设计加权系数时只考虑了模态衰减的影响, 而各阶MSSD的处理增益不仅与模态衰减系数有关, 还与声源深度上的模态函数值${\phi _m}\left( {{z_{\rm{s}}}} \right)$有关, 声源深度上的各阶模态函数值使得WMSSD的处理增益随声源位置的改变而改变.
2 -->

4.3.WMSSD处理增益变化机理分析

波导环境中的模态函数主要取决于声速剖面. 在非等声速波导中, 各阶模态函数以反转点深度为临界, 在波导垂直尺度上呈现不同的分布规律, 而反转点的位置主要与波导中的声速有关, 因此WMSSD的处理增益还受到声速剖面的影响. 反转点深度处的声速满足如下关系式^[16]

$c\left( {{z_{{\rm{rev}}}}} \right) = 2{\text{π}}f/{k_{rm}}.$

式中, ${z_{{\rm{rev}}}}$为反转点处深度. 由(28)式可知, 由于各阶水平波数不同, 各阶模态深度函数具有迥异的反转点深度. 由于各阶水平波数随阶数增大而逐渐减小, 高阶模态函数的反转点处声速更大. 因此对于负梯度声速剖面, 各阶模态函数的反转点深度将随阶数增大而变小. 以图1中的负梯度声速波导为例, 各阶模态函数及其反转点深度如图8所示. 由图8(b)可知, 反转点深度随阶数增大而逐渐变小. 结合图8(a)可知, 在反转点以浅, 模态函数呈指数迅速衰减, 相应的模态函数值很小; 在反转点以深, 模态函数呈周期性的振荡变化. 对于较高阶模态函数, 若$c\left( z \right) < 2{\text{π}}f/{k_{rm}}$对所有深度都成立, 此时不存在反转点或者说反转深度为零, 如图8(b)中第8阶及以后的模态函数不再存在反转点.
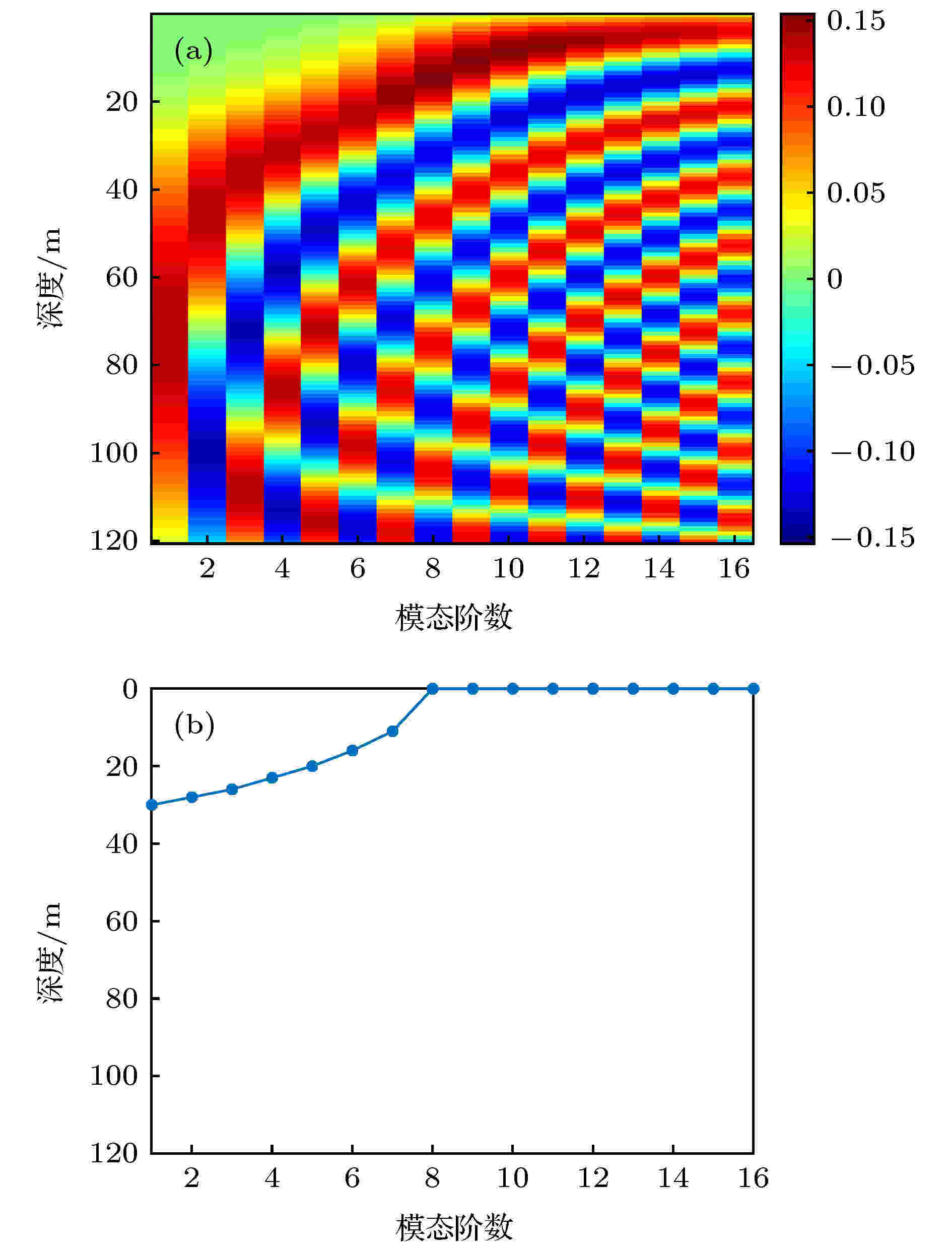图 8 各阶模态函数及其反转点深度, f = 300 Hz　(a) 波导环境中的各阶模态函数分布; (b) 各阶模态函数的反转点深度
Figure8. The modal depth functions and their turning-depths with f = 300 Hz: (a) Each modal depth function in the waveguide; (b) the turning-depth of each modal depth function.

当声源位于若干阶模态函数的反转深度以浅时, 相应的声源模态幅值${\phi _m}\left( {{z_{\rm{s}}}} \right)$很小, 这种情况下由于声源模态幅值的作用, 各阶MSSD处理增益的变化趋势为低阶和高阶较小, 中阶较大, 这与加权系数的变化趋势不一致, 如图9(a)所示, 导致WMSSD的处理增益较差并小于MSD. 当声源位于各阶反转深度以深时, 加权系数较大程度地刻画了各阶MSSD处理增益的变化趋势, 如图9(b)所示, 进而WMSSD的处理增益较大并大于MSD. 当声源位于某一深度上时, WMSSD的处理增益与MSD相等, 该深度即为图7(b)中的临界深度.
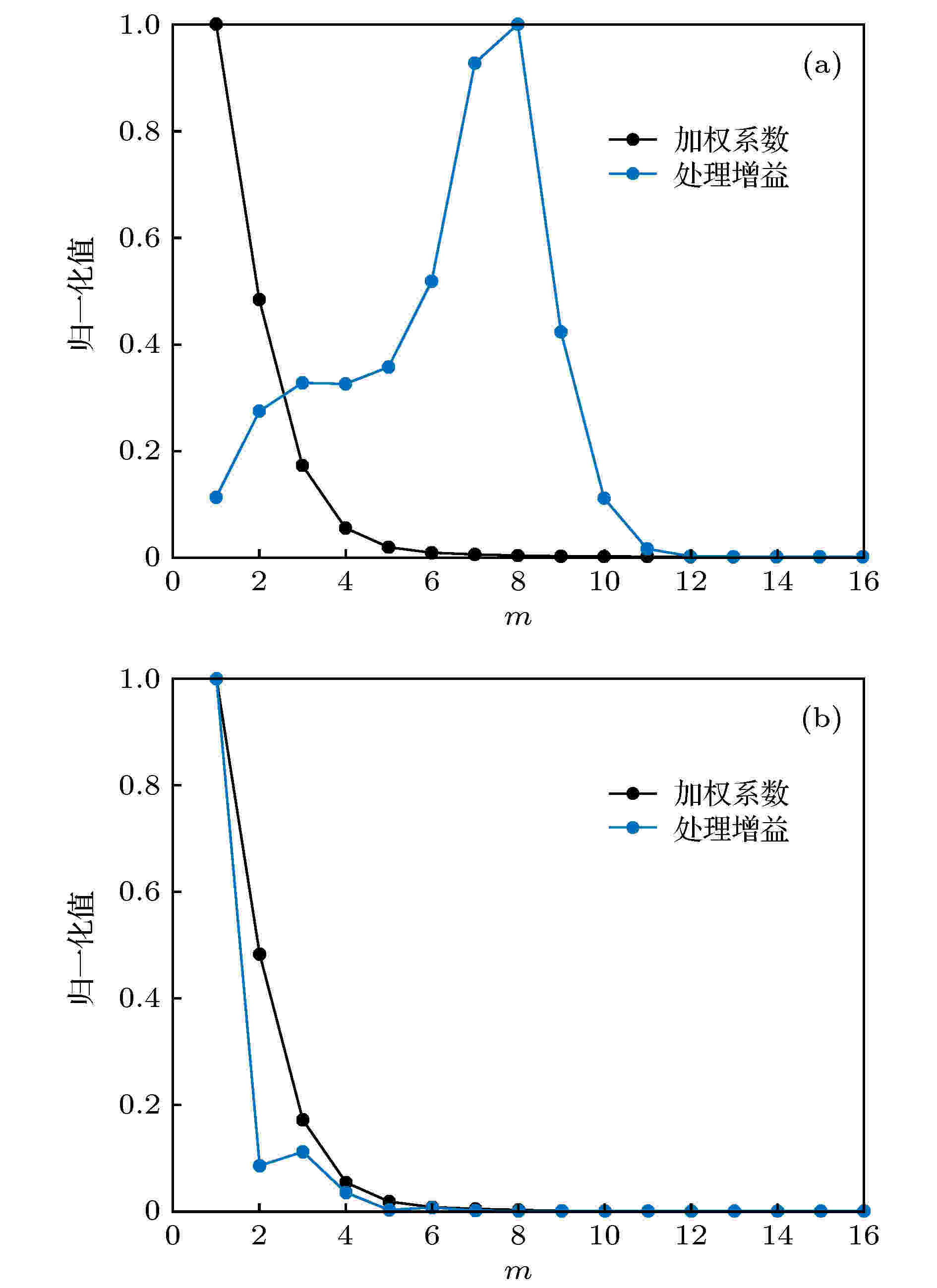图 9 各阶MSSD的加权系数与处理增益, f = 300 Hz, 声源距离15 km　(a)声源深度10 m; (b) 声源深度80 m
Figure9. The weighting coefficients and the processing gains of the MSSD with f = 300 Hz and source range of 15 km: (a) Source depth of 10 m; (b) source depth of 80 m.

对于不同频率的声源, 临界深度随声源距离的变化如图10所示. 由图10可知, 临界深度随声源距离的增大而减小. 这是由于当声源距离增大时, 衰减指数的作用更加剧烈, 信号能量更多的集中在低阶MSSD, 相较于图9(a), 图11所示的各阶MSSD归一化的加权系数与处理增益的变化趋势更加一致, 进而WMSSD的处理增益提高, 临界深度变浅. 同时由图10可以看出, 随声源距离增大低频声源临界深度更快减小为零. 这是由于当声源频率增大时, 模态个数增加, 存在反转点的模态数也增多, 因而声源模态幅值的影响增大, 最终导致临界深度随声源距离的变化速率减缓.
图 10 不同频率时临界深度随距离的变化图
Figure10. The critical depths versus ranges under various frequencies.

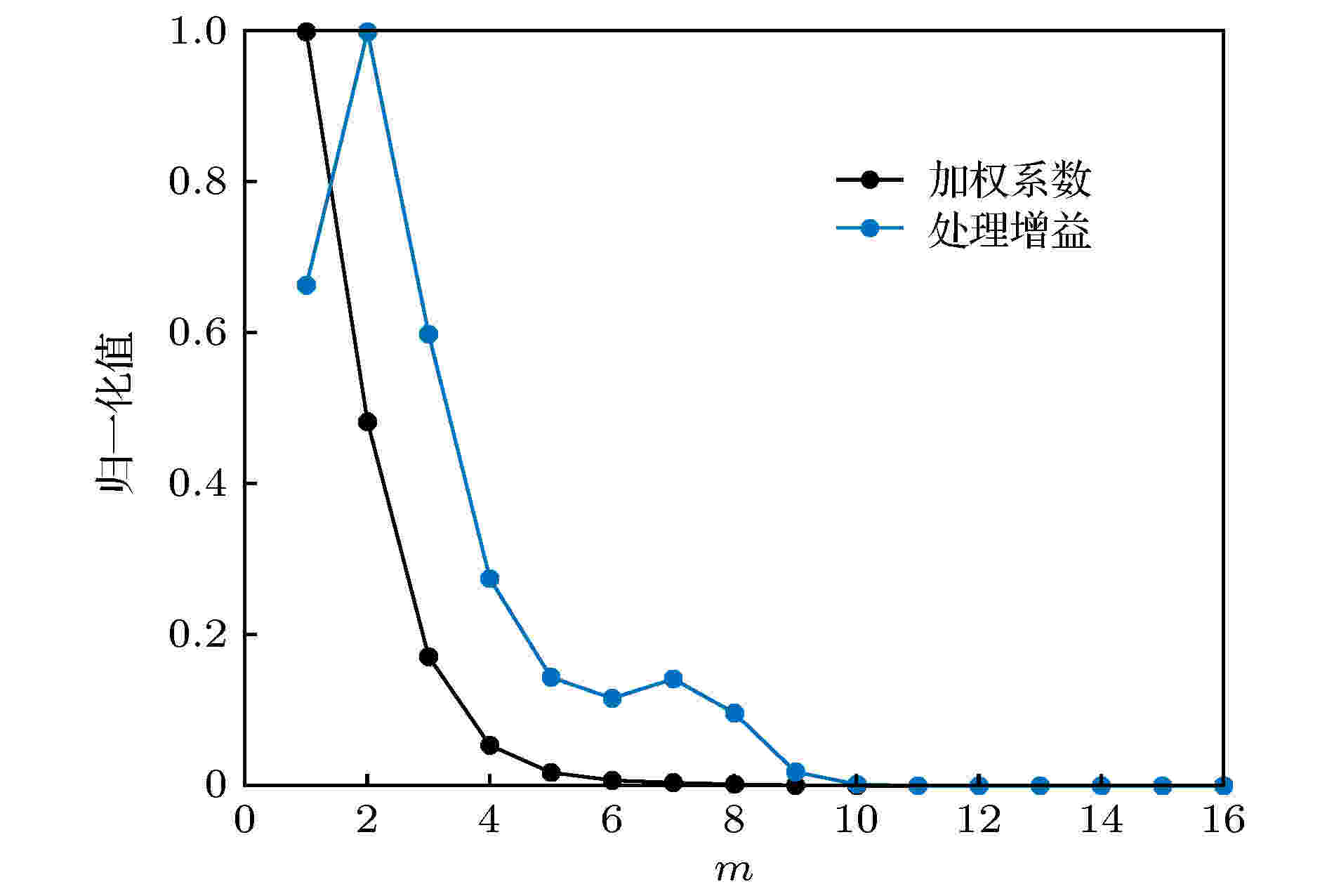图 11 各阶MSSD归一化的加权系数与处理增益, f = 300 Hz, 声源深度10 m, 声源距离25 km
Figure11. The weighting coefficients and the processing gains of the MSSD with f = 300 Hz, source depth of 10 m and source range of 25 km.

2 -->

4.4.声速剖面对WMSSD处理增益的影响分析

上文讨论了负梯度声速波导中WMSSD处理增益的变化规律, 结果表明, 模态函数存在反转点使得WMSSD不可避免地出现弱探测区域, 并产生了临界深度. 模态函数的反转点深度由波导环境中的声速剖面决定, 在等声速波导中模态函数不存在反转点, 在正梯度声速波导中反转点深度将随模态阶数的增大而变大.
考虑等声速和正梯度声速的情况, 这两种声速剖面如图12所示, 其他环境参数同图1, f = 300 Hz. 根据环境参数和(28)式计算可得, 这两种声速剖面下声源在波导中都激发了15阶模态, 各阶模态的反转深度如图13所示. 由图13可知, 等声速波导中各阶模态不存在反转深度, 正梯度声速波导中各阶模态的反转深度随阶数增大而变深. 相应的各阶模态函数如图14所示, 在正梯度声速中, 第1—5阶模态函数存在反转点, 在反转点深度以深, 模态函数呈指数衰减, 幅值接近于零, 在反转点深度以浅及高阶模态, 模态函数以一定周期振荡变化, 这与负梯度声速下的变化规律相反.
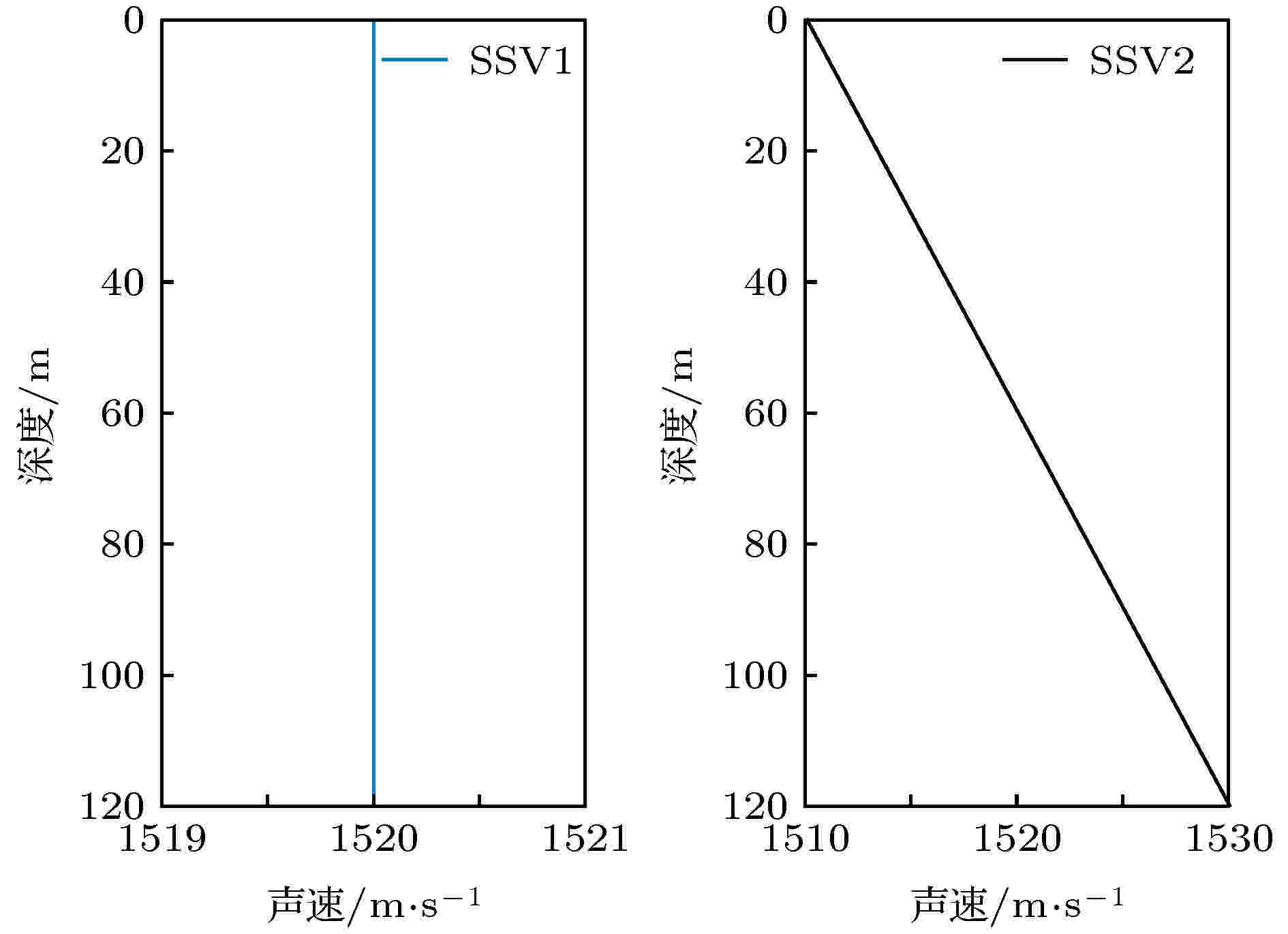图 12 等声速剖面与正梯度声速剖面图
Figure12. Constant sound velocity profile (SVP) and positive gradient SVP.

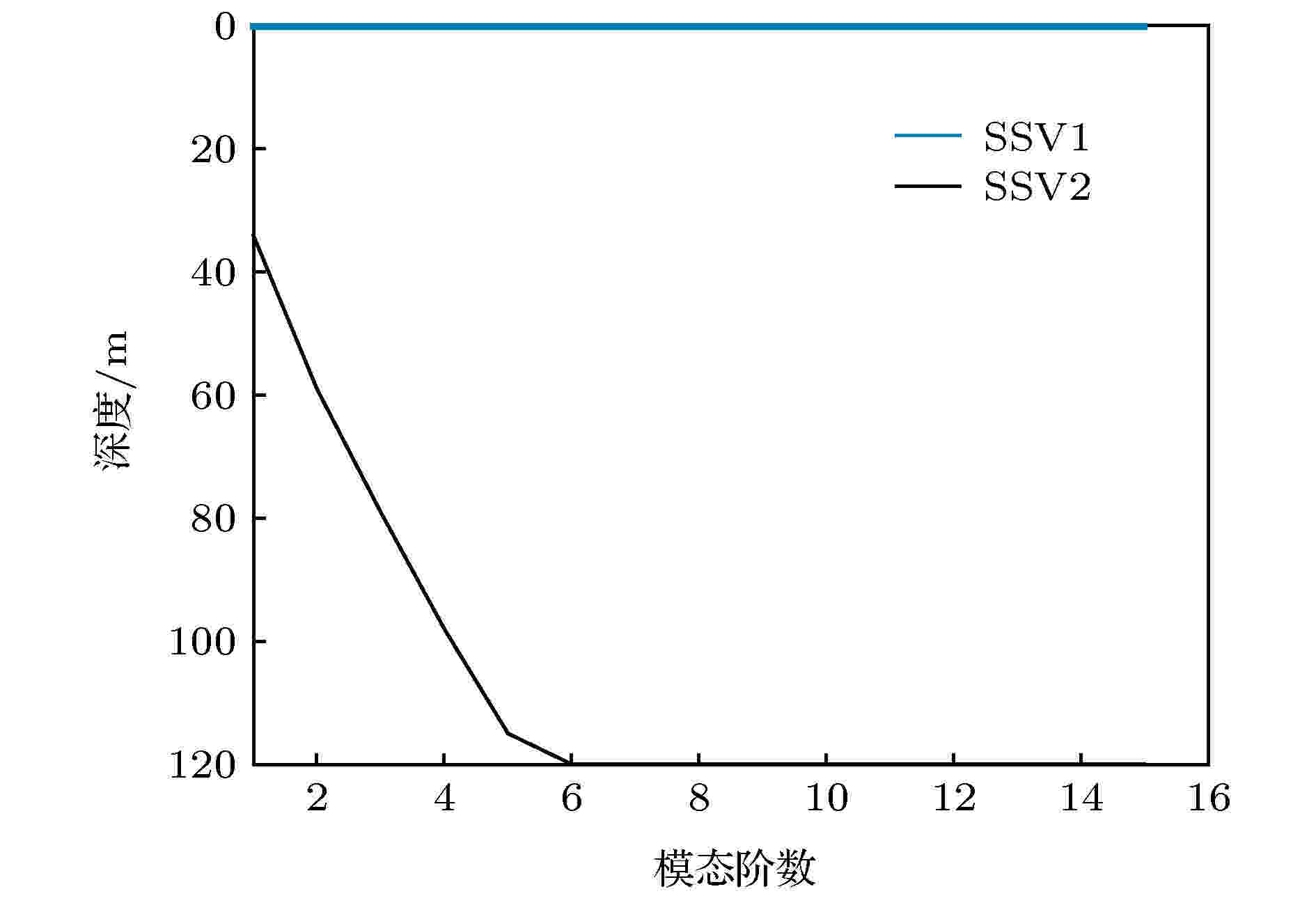图 13 各阶模态函数的反转深度, f = 300 Hz
Figure13. The turning-depth of each modal depth function with f = 300 Hz.

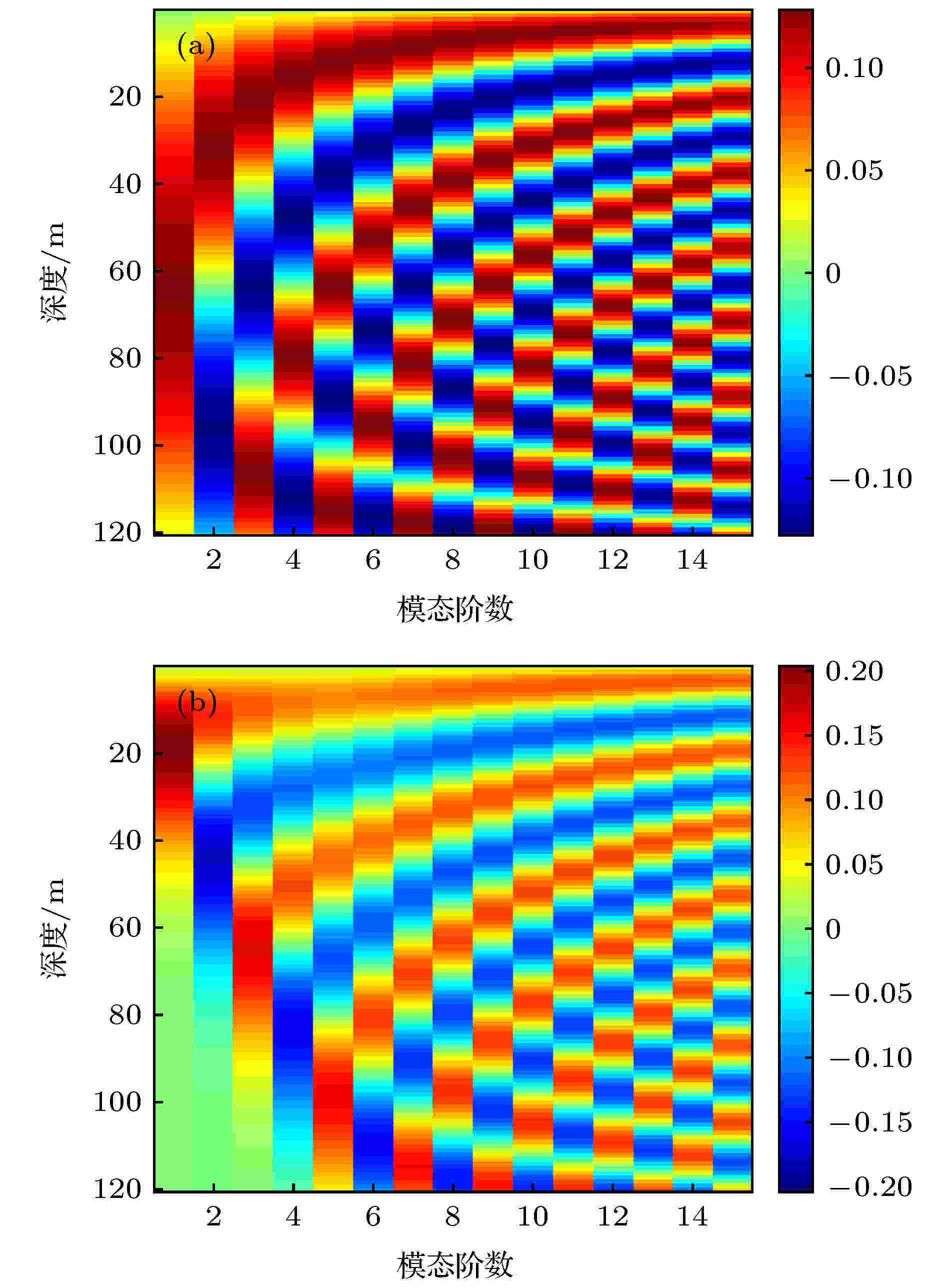图 14 两种声速剖面波导中的各阶模态函数, f = 300 Hz　(a) 等声速剖面; (b) 正梯度声速剖面
Figure14. Each modal depth function in the two kinds of waveguides with f = 300 Hz: (a) Constant SVP; (b) positive gradient SVP.

图15给出了两种声速剖面波导下WMSSD的处理增益(单位为dB), 图中黑线标出了不同距离上的临界深度. 在等声速波导中, 各阶模态函数不存在反转点且呈周期振荡变化, 声源深度上模态函数幅值对各阶MSSD处理增益的影响较小, 因此当声源位于不同深度上时, 各阶MSSD处理增益的变化趋势总是与各阶衰减指数相一致, 使得WMSSD的处理增益在所有深度上都大于MSD, 因此不存在临界深度, 如图15(a)所示. 在正梯度声速波导中, 各阶模态函数的反转深度随阶数增大而增大(与负梯度声速的情况相反), 在反转点以深, 模态函数呈指数衰减, 并很快接近于零. 当声源位于若干阶模态的反转深度以深时, 声源模态幅值对各阶MSSD的非中心参量产生显著影响, 且随着深度增加, 产生的影响也增大. 因此, WMSSD的处理增益下降, 进而出现临界深度, 在临界深度以深WMSSD的处理增益小于MSD, 如图15(b)所示. 而在临界深度以浅的大部分区域, WMSSD的处理增益大于MSD. 临界深度随距离变化的原因与负梯度声速波导相同. 对比图15(a)和图15(b)也可知, 等声速波导中WMSSD的处理增益大于正梯度声速波导.
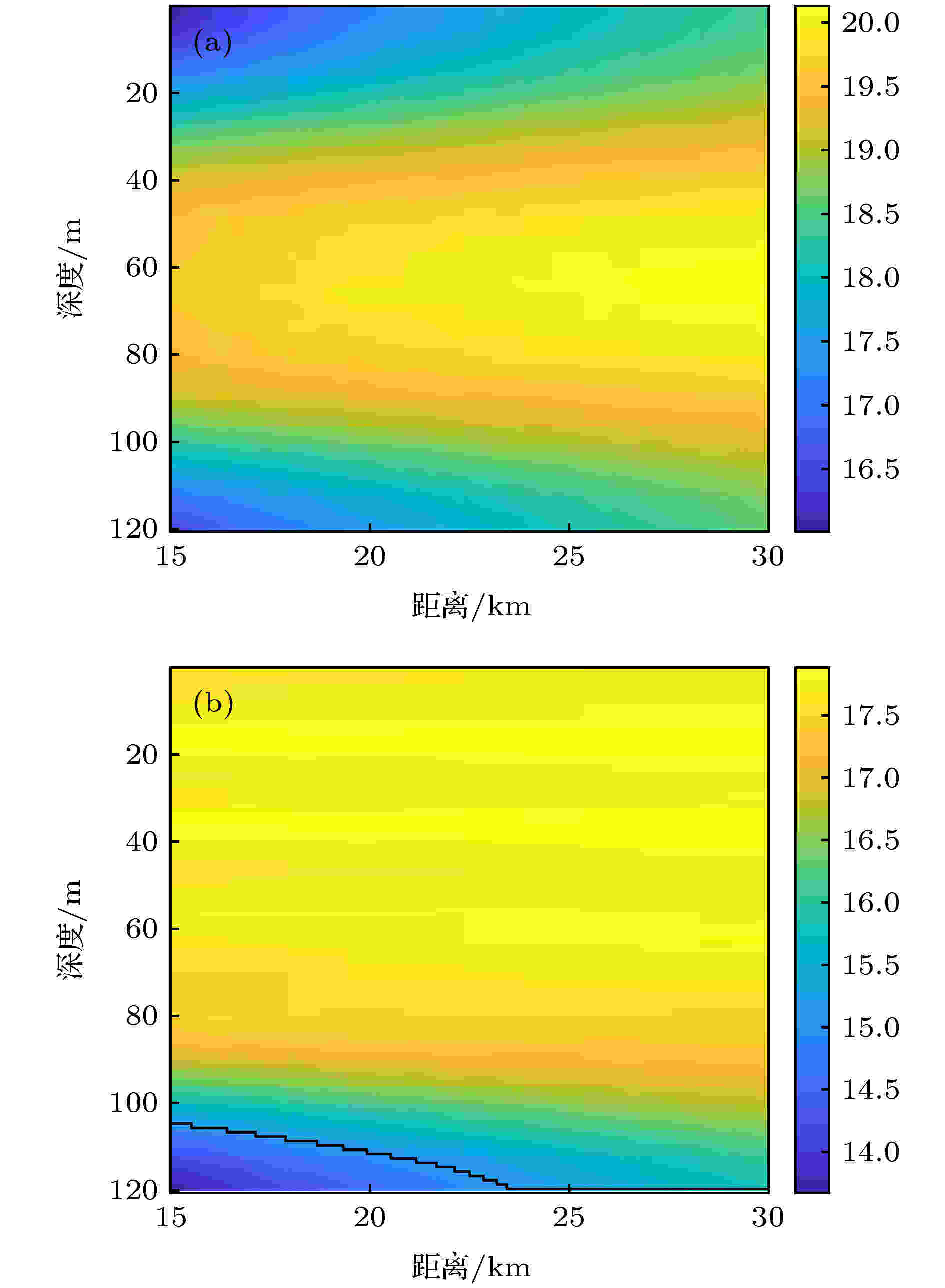图 15 两种声速剖面下, 不同声源位置处的WMSSD处理增益, f = 300 Hz　(a)等声速剖面; (b) 正梯度声速剖面
Figure15. The processing gains of the WMSSD versus acoustic source locations with f = 300 Hz: (a) Constant SVP; (b) positive gradient SVP.

综合上述分析可得, WMSSD在等声速波导中的稳健性最好, 即对位于所有位置区域的声源, 都具有大于MSD的处理增益. 在负梯度声速波导和正梯度声速波导中, 虽然WMSSD的性能稳健性有所下降, 即存在部分的弱探测区域, 但对位于其他大部分区域的声源, WMSSD的处理增益都大于MSD.

本文研究了浅海波导中的子空间检测——模态空间检测方法, 根据各阶简正波模态在传播过程中的衰减规律, 提出了一种基于模态衰减系数加权的子空间检测器——WMSSD. 通过理论分析和仿真实验探究了WMSSD的检测性能及其对声源位置的稳健性, 结果表明: 1) MSD的处理增益与声源在波导环境中激发的模态阶数成负相关, 因此当声源和环境参数变化(如声源频率升高、波导深度增大等)使波导中的模态个数增多时, MSD的处理增益下降导致其检测性能降低, 这对远距离传播的低信噪比目标检测尤为不利; 2) WMSSD的检测性能与声源位置和声速剖面有关, 在等声速波导中WMSSD的性能稳健性最好, 其处理增益总是好于MSD; 3) 对于负梯度声速波导和正梯度声速波导, 由于若干低阶模态函数存在反转点, 造成WMSSD存在部分弱探测区域, 即当声源分别在靠近海面和海底的部分区域, 其处理增益相较于MSD有所下降, 而在其他大部分区域, WMSSD的处理增益相较于MSD都有显著的提升.

由文献[20]可知, 对于二次型检测器,

$ \small T_0\left( {x} \right) = {{x}^{\rm{H}}}{Ax}, \tag{A1} $

式中, x表示待检测数据, A表示加权矩阵, 其输出信噪比可由下式计算:

$\small OSNR = {\rm{tr}}\left( {{A}{{K}_{\rm{s}}}} \right)/{\rm{t}}{{\rm{r}}^{1/2}}\left[ {{{\left( {{A}{{K}_{\rm{n}}}} \right)}^2}} \right],\tag{A2} $

式中, ${{K}_{\rm{s}}}$表示信号协方差矩阵, ${{K}_{\rm{n}}}$表示噪声协方差矩阵, ${\rm{tr}}\left( \cdot \right)$表示求矩阵的迹运算.
对于本文中的MSD,

${A} \!=\! {\varPhi }{\left( {{{\varPhi }^{\rm{T}}}{\varPhi }} \right)^{ - 1}}{{\varPhi }^{\rm{T}}},~~{{K}_{\rm{s}}}\! =\! {s}{{s}^{\rm{H}}} \!=\! {\left| \mu \right|^2}{g}{{g}^{\rm{H}}},~~{{K}_{\rm{n}}} \!= \!\sigma _{\rm{n}}^2{{I}_N},\tag{A3} $

进而可得,

$\small\begin{split} \; & {\rm{tr}}\left( {{A}{{K}_{\rm{s}}}} \right) = {\rm{tr}}\left( {{\varPhi }{{\left( {{{\varPhi }^{\rm{T}}}{\varPhi }} \right)}^{ - 1}}{{\varPhi }^{\rm{T}}}{{\left| \mu \right|}^2}{g}{{g}^{\rm{H}}}} \right) \\= \;&{\left| \mu \right|^2}{\rm{tr}}\left( {{\varPhi }{{\left( {{{\varPhi }^{\rm{T}}}{\varPhi }} \right)}^{ - 1}}{{\varPhi }^{\rm{T}}}{\varPhi a}{{a}^{\rm{H}}}{{\varPhi }^{\rm{T}}}} \right)\\ = \;&{\left| \mu \right|^2}{\rm{tr}}\left( {{{a}^{\rm{H}}}{{\varPhi }^{\rm{T}}}{\varPhi a}} \right) = {\left| \mu \right|^2}{{g}^{\rm{H}}}{g} = {{s}^{\rm{H}}}{s}.\end{split} \tag{A4}$

由正交投影矩阵为幂等矩阵且它的迹等于其秩可得,

$\small\begin{split}&{\rm{t}}{{\rm{r}}^{1/2}}\left[ {{{\left( {{A}{{K}_{\rm{n}}}} \right)}^2}} \right] = \sigma _{\rm{n}}^2{\rm{t}}{{\rm{r}}^{1/2}}\left( {{{A}^2}} \right) \\= \;&\sigma _{\rm{n}}^2{\rm{t}}{{\rm{r}}^{1/2}}\left( {A} \right) = \sigma _{\rm{n}}^2\sqrt M . \end{split}\tag{A5}$

将(32)式和(33)式代入(30)式中可得

$OSNR = {{s}^{\rm{H}}}{s}/\left( {\sigma _{\rm{n}}^2\sqrt M } \right), \tag{A6}$

进而可得MSD的处理增益为

$G = OSNR/SNR = N/\sqrt M .\tag{A7}$

对于第m阶MSSD,

${A} = {{\phi }_m}{\phi }_m^{\rm{H}},~~{{K}_{\rm{s}}} = {s}{{s}^{\rm{H}}} = {\left| \mu \right|^2}{g}{{g}^{\rm{H}}},~~{{K}_{\rm{n}}} = \sigma _{\rm{n}}^2{{I}_N}, \tag{A8}$

进而有

$\begin{split}&{\rm{tr}}\left( {{A}{{K}_{\rm{s}}}} \right) = {\rm{tr}}\left( {{{\phi }_m}{\phi }_m^{\rm{H}}{{\left| \mu \right|}^2}{g}{{g}^{\rm{H}}}} \right)\\= \;&{\left| \mu \right|^2}{\rm{tr}}\left( {{\phi }_m^{\rm{H}}{g}{{g}^{\rm{H}}}{{\phi }_m}} \right)\\ = \;&{\left| \mu \right|^2}{\rm{tr}}\left( {{\phi }_m^{\rm{T}}{\varPhi a}{{a}^{\rm{H}}}{{\varPhi }^{\rm{T}}}{{\phi }_m}} \right),\end{split} \tag{A9}$

由${{\phi }_{ 1}}, \cdots , {{\phi }_m}$之间的近似正交性可得

${\rm{tr}}\left( {{A}{{K}_{\rm{s}}}} \right) = {\left| \mu \right|^2}{a_m} \cdot a_m^*.\tag{A10}$

将(38)式和(33)式代入(30)式中可得MSSD的输出信噪比为

$OSN{R_m} = \frac{{{{\left| \mu \right|}^2}}}{{\sigma _{\rm{n}}^2\sqrt M }}{a_m} \cdot a_m^ * ,\tag{A11} $

进而可得其处理增益为

${G_m} = OSN{R_m}/SNR = l \cdot {a_m} \cdot a_m^ * , \tag{A12}$

式中, $l = \dfrac{N}{{\sqrt M {{g}^{\rm{H}}}{g}}}$为常数.