摘要:仪器的本底是空间天文观测项目实施过程中关注的一个重要内容, 对于聚焦型空间X射线望远镜, 仪器的粒子本底水平直接关系到观测灵敏度及本底重建的系统误差. 因此, 在仪器设计及工程实现迭代过程中, 需要确定仪器粒子本底水平, 保证其在可接受范围内. 本文发展了一种基于面密度插值快速估计聚焦型空间X射线望远镜粒子本底的方法, 该方法同时具有较高的本底估计精度和快的计算速度, 适合于在望远镜方案设计的早期对各种设计方案的本底屏蔽效果进行快速估计并据此提出优化设计的建议, 可以大大提高早期方案设计的有效性, 对于聚焦型空间高能天文仪器的研制及其他类似领域具有一定的参考意义.
关键词: 焦平面探测器/
本底估计/
屏蔽优化

English Abstract

全文HTML

--> --> -->

聚焦型空间X射线望远镜具有收集面积大和粒子本底水平低的优势, 可以实现对天体源的高灵敏度观测. 在仪器物理设计和性能评估中, 仪器粒子本底水平的估计及重建是始终关注的一个重要指标^[1]. 影响仪器粒子本底水平的因素包括运行轨道的空间辐射环境、整体结构屏蔽、聚焦镜响应、焦平面探测器附近区域结构设计、焦平面探测器及电子学设计等^[2]. 在聚焦光学响应和焦平面探测器物理设计及电子学设计确定的前提下, 仪器物理设计工作通常会通过优化整星布局和焦平面探测器附近区域结构来尽量降低粒子本底水平. 目前比较普遍的估计粒子本底水平的方法主要有两种. 一种通过已在轨相似空间辐射环境及焦平面探测器的观测结果作为输入, 同时考虑自身仪器特征引入修正因子加以估计. 这种方法由于没有更多考虑每个载荷的独特性, 结果误差较大^[3]. 另一种是通过蒙特卡罗方法, 使用粒子输运软件, 建立仪器质量模型, 模拟其对空间辐射环境的响应^[4]. 该种方法是目前国内外空间X射线仪器普遍使用的方法, 在很多空间实验中该方法估算的结果与在轨实测结果具有很好的一致性^[5], 在空间X射线仪器的性能评估^[6]、物理设计^[7]、数据处理算法^[8]、在轨本底重建^[9]、观测方案优化^[10]中发挥着重要作用.
受聚焦型空间X射线仪器特点限制, 例如要实现较大的集光面积, 整星结构尺寸需非常大, 通常为几米到十几米量级, 而焦平面探测器敏感探测区域特别小, 通常为厘米量级(考虑到角分辨率和视场), 用蒙特卡罗方法计算粒子本底过程类似于厚屏蔽计算中的深穿透问题^[11], 需要的计算资源巨大. 在解决深穿透问题时, 会使用强迫碰撞、偏倚抽样、几何分裂与轮盘赌、组合减方差等方法尽量提高计算效率^[12], 但对减方差应用技巧要求较高. 同时反向蒙特卡罗方法在模拟全物理过程(主要是强相互作用过程)中又很难实现^[13]. 在仪器设计阶段, 设计方案的优化迭代需要实现快速估算, 同时具有足够的精度, 然后到设计方案基本确定时, 再通过建立实际质量模型精细计算复核. 本文针对仪器设计初级阶段的需要, 提出了一种快速估算聚焦型空间X射线仪器粒子本底的方法. 以增强型X射线时变与偏振(eXTP)^[14]空间天文台上的能谱测量X射线聚焦望远镜阵列(SFA)焦平面探测器核心结构作为研究对象, 通过模拟计算不同尺寸、不同面密度简化球壳对空间辐射环境中不同成份在有效能段内的响应, 发现粒子本底水平主要受面密度影响, 不同成份随面密度变化有各自的特点, 对聚焦型空间X射线望远镜的物理设计具有一定的指导意义.
文章安排如下: 第2节介绍抑制本底设计及面密度分布插值法的假设前提、原理以及主要过程; 第3节简述实现粒子本底计算的主要过程及基本配置; 第4节以SFA为例, 给出面密度对SFA各种成份及总的粒子本底影响; 第5节通过模拟计算eXTP-SFA实际整星结构对应的粒子本底水平, 与快速估算方法对比; 第6节和第7节分别为讨论与总结.

空间X射线仪器粒子本底抑制方法分为主动和被动两种^[7]. 主动方法可以通过符合探测器产生与粒子事例时间一致的符合信号, 实现对粒子事例的识别及筛选, 但受死时间和符合效率限制, 需根据不同轨道、不同载荷自身特点综合评估是否采用; 也可通过对粒子事例的特征(分布特征)加以识别^[15], 降低其对观测的影响. 被动方法通过屏蔽材料屏蔽低能粒子, 或引入磁场偏转低能荷电粒子^[16]. 采用多级屏蔽^[17]能有效抑制本底能谱中的特征X射线结构, 有效地提高天体源特征线观测的信噪比^[18], 同时降低本底重建的工作难度. 被动屏蔽可以抑制视场外宇宙X射线和轨道上低能荷电粒子的影响, 在keV到十几keV能段(典型的聚焦型X射线仪器能段), 相对于没有任何屏蔽, 2 mm等效铝厚度可降低宇宙X射线引起的本底两个量级以上. 但随着屏蔽质量增加, 次级粒子的影响逐渐显著, 包括连续能谱与特征能量的次级粒子. 因此, 在仪器设计中, 整体结构尺寸和质量都是有限制的, 要保证探测器在一个比较合理的质量屏蔽下, 即屏蔽结构既不能因为太少(薄)导致不充分, 也不能因为太多导致次级成份太多. 因此在整体设计中, 首先确保质量屏蔽对应的粒子本底水平在一个合理可接受范围内, 然后对敏感探测区域附近(例如半导体探测器的耗尽层)进行更高级别的设计, 例如内壁增加低Z屏蔽材料, 吸收有效观测能段内的特征X射线, 或在探测器表面增加低次级粒子产额的屏蔽层, 尽量抑制有效观测能段内的次级粒子(焦平面探测器周围材料直接产生的次级粒子及背散射粒子). 因此, 整体质量屏蔽, 是粒子本底水平满足设计要求的第一步.
在keV到十几keV能段, 聚焦型X射线要实现较大的集光面积, 整星结构尺寸非常大, 通常几米到十几米量级, 整星质量也非常重; 同时, 焦平面探测器敏感探测区域特别小, 通常厘米量级(考虑到角分辨率和视场), 周围还会有机壳、安装结构、热控、电子学等结构. 焦平面探测器敏感探测区域相对于整体结构尺寸非常小, 适合使用球壳结构近似代替除焦平面探测器敏感探测区域外的结构, 来研究粒子本底水平随整体结构的演化^[19]. 同时, 在面密度相同的情况下, 不同材料的屏蔽效果差异不大, 因此可以用等效面密度铝来研究不同尺寸、不同面密度下焦平面探测器上的粒子本底, 从而更简单直接地分析整星结构变化对粒子本底的影响.
基于面密度分布插值估算粒子本底方法主要步骤: 首先建立焦平面探测器质量模型, 通过模拟计算得到不同面密度、不同尺寸铝球壳的各种成份粒子本底水平, 得到粒子本底随面密度分布曲线; 其次建立整星质量模型, 计算焦平面探测器敏感区域位置不同方向的面密度分布; 最后依粒子本底随面密度分布曲线, 对敏感区域位置不同方向的面密度分布进行插值, 得到敏感区平均的各种成份粒子本底水平.

为了实现和检验面密度分布插值估计粒子本底方法, 本文基于Geant4^[20]建立了本底计算软件包, 并输入结构质量模型^[21]、空间环境不同成份粒子能谱和流强, 通过模拟计算, 统计敏感能段(0.5—15 keV)的能量沉积事例, 归一之后即可得到粒子本底水平^[22]. 主要过程包括建立简化球壳、SFA焦平面探测器及eXTP整形质量模型, 配置物理过程, 建立空间辐射环境模型, 面密度分布计算(图1).
图 1 模拟计算过程
Figure1. Flowchart of the simulation process.

针对空间应用, Geant4软件有多个建议的预封装物理包^[23]. 参考高能天体物理学先进望远镜(Athena)项目应用经验^[24], 使用QBBC预封装物理包, 包含强相互作用、衰变、输运等过程. 同时为了使低能端响应更准确, 电磁相互作用过程改用精度更高的EmStandardPhysics_option4预封装物理包, 并打开Auger和PIXE过程^[23], 即考虑荷电粒子电离导致的特征X射线以及俄歇电子产生, 实现百eV以上精细物理过程.
对于引起粒子本底的空间辐射环境, 在“慧眼”卫星在轨空间环境模型的研究基础上^[25], 确定eXTP所在轨道(550 km高度, 0°倾角)空间辐射环境, 轨道处各空间粒子成份的入射谱如图2所示. 主要包括宇宙弥散X射线, 大气反照X射线及中子, 宇宙线原初质子、正负电子及氦核, 以及宇宙线与大气作用产生的次级质子和正负电子. 其中原初宇宙线考虑地球遮挡效应, 大气反照射线仅考虑地球所覆盖立体角^[26]. 同时, 观测姿态暂定义为背地指向姿态.
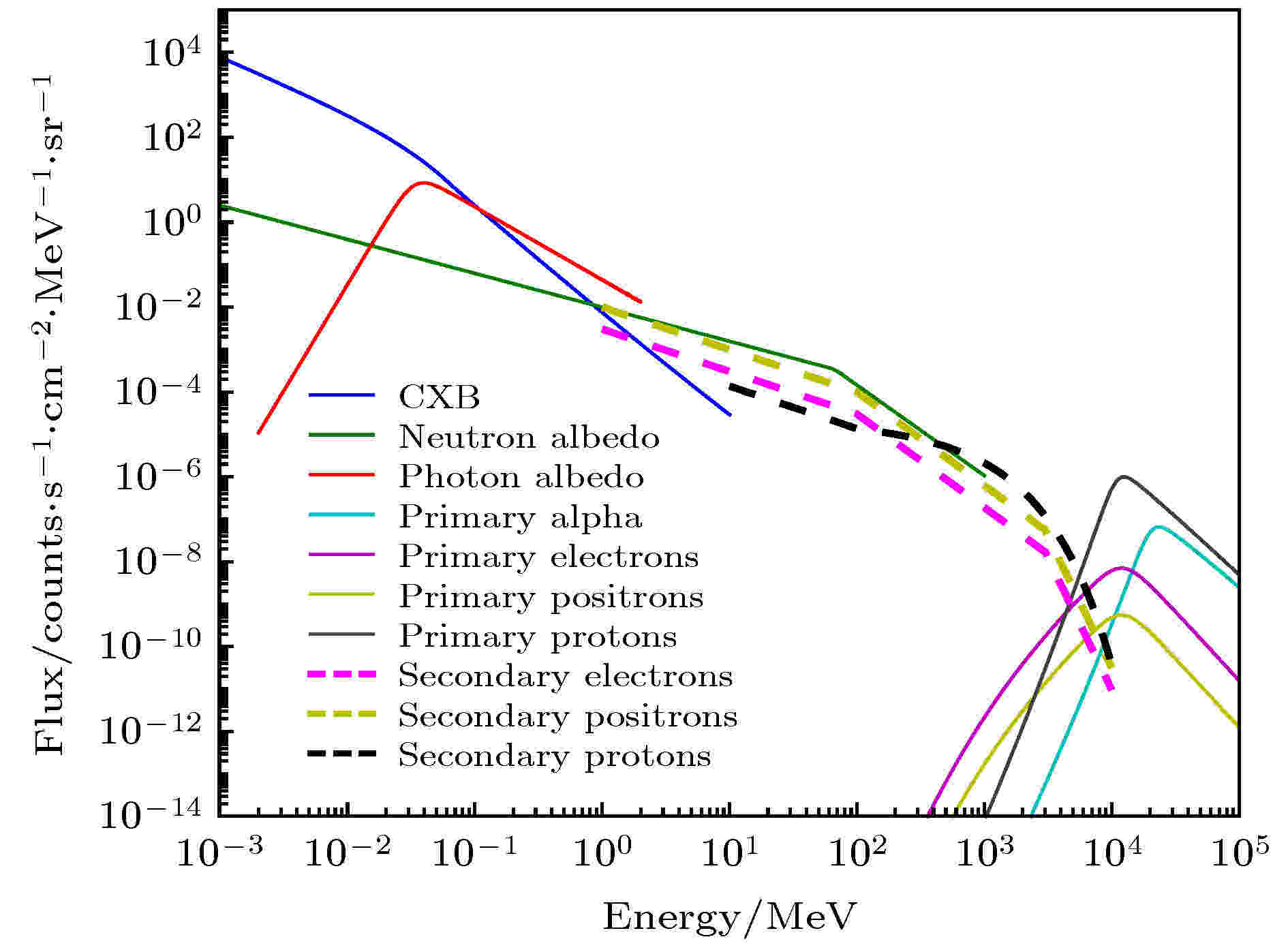图 2 eXTP所在轨道空间辐射环境输入能谱
Figure2. Incident energy spectrum of the space radiation environment in the orbit of eXTP.

eXTP焦平面探测器质量模型如图3所示. SFA焦平面探测器采用19像素的硅漂移探测器(SDD), 其质量模型主要考虑上层铝膜、二氧化硅极层、硅耗尽层及封装陶瓷结构, 并赋予对应材料及密度. 为了研究不同尺寸、不同厚度(面密度)铝球壳对粒子本底的影响, 构建了简化球壳与SDD质量模型, 如图4所示. 铝球壳半径设置为10, 30, 50, 70 cm, 球壳厚度设置为0, 5, 10, 30, 50, 70 mm. SFA探测单元结构如图5所示, 主要包含电子学机箱、探测器机壳、滤光转轮、安装筒、准直筒等结构. 整星模型如图6所示, 主要包括支撑结构、安装板子、外层板、聚焦镜及其他平台仪器简化结构^[14], 基本保持与整星预估质量一致.
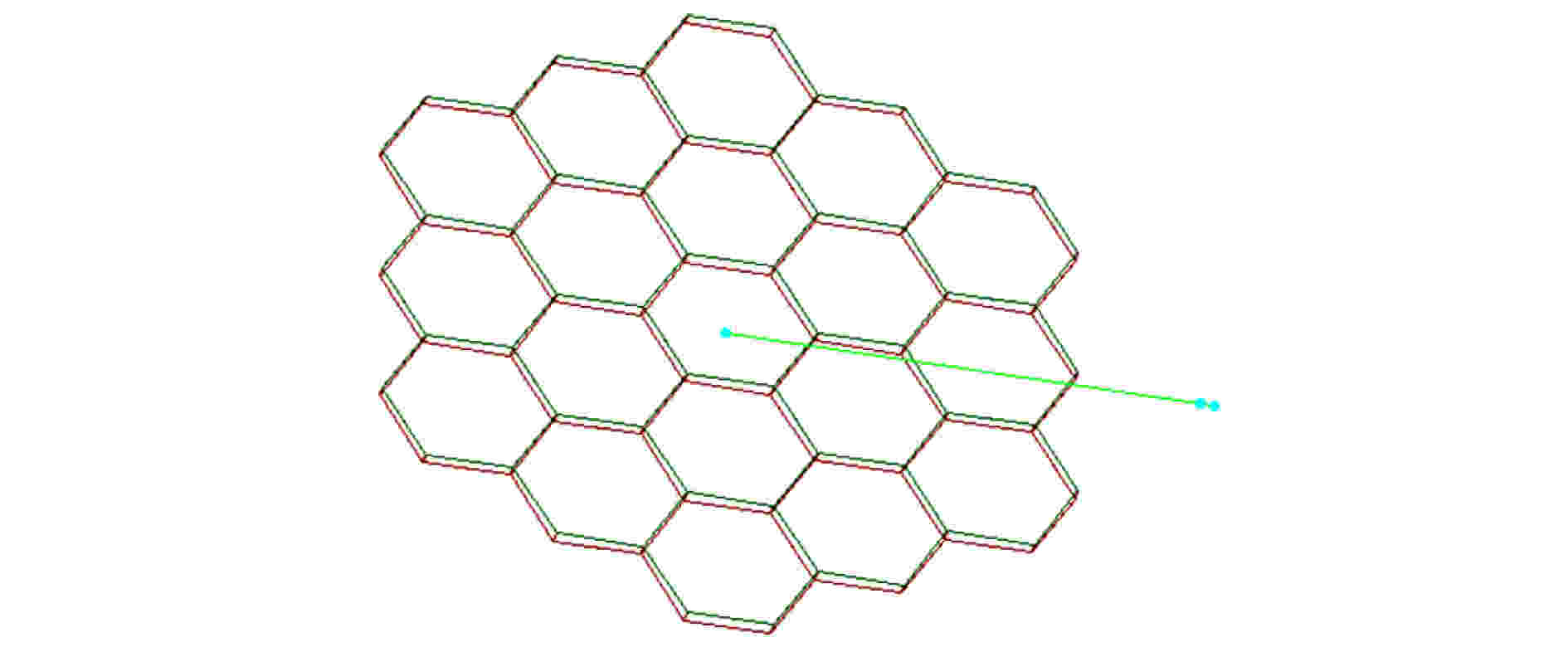图 3 焦平面探测器SDD质量模型
Figure3. Mass model of the focal plane detector SDD.

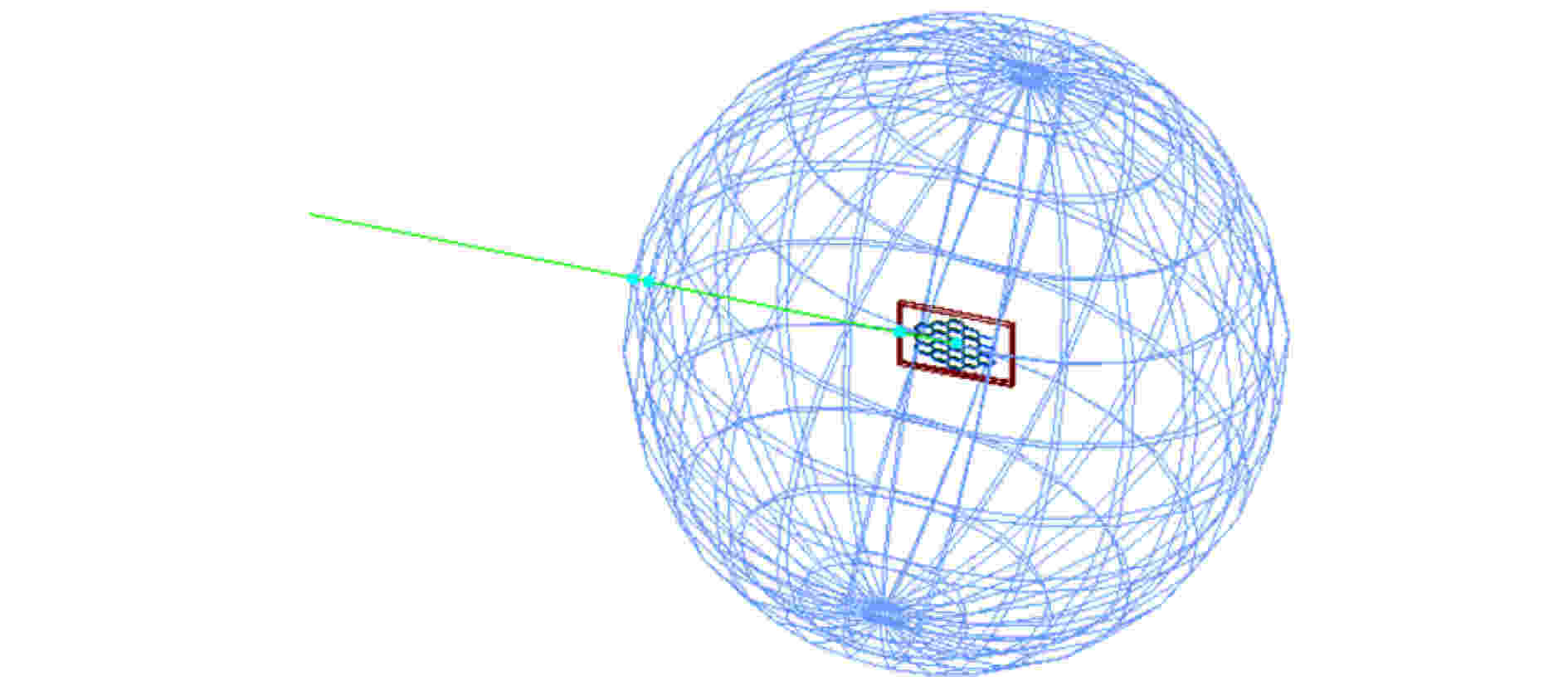图 4 简化球壳和SDD质量模型
Figure4. Mass model of simplified aluminum spherical shell and SDD.

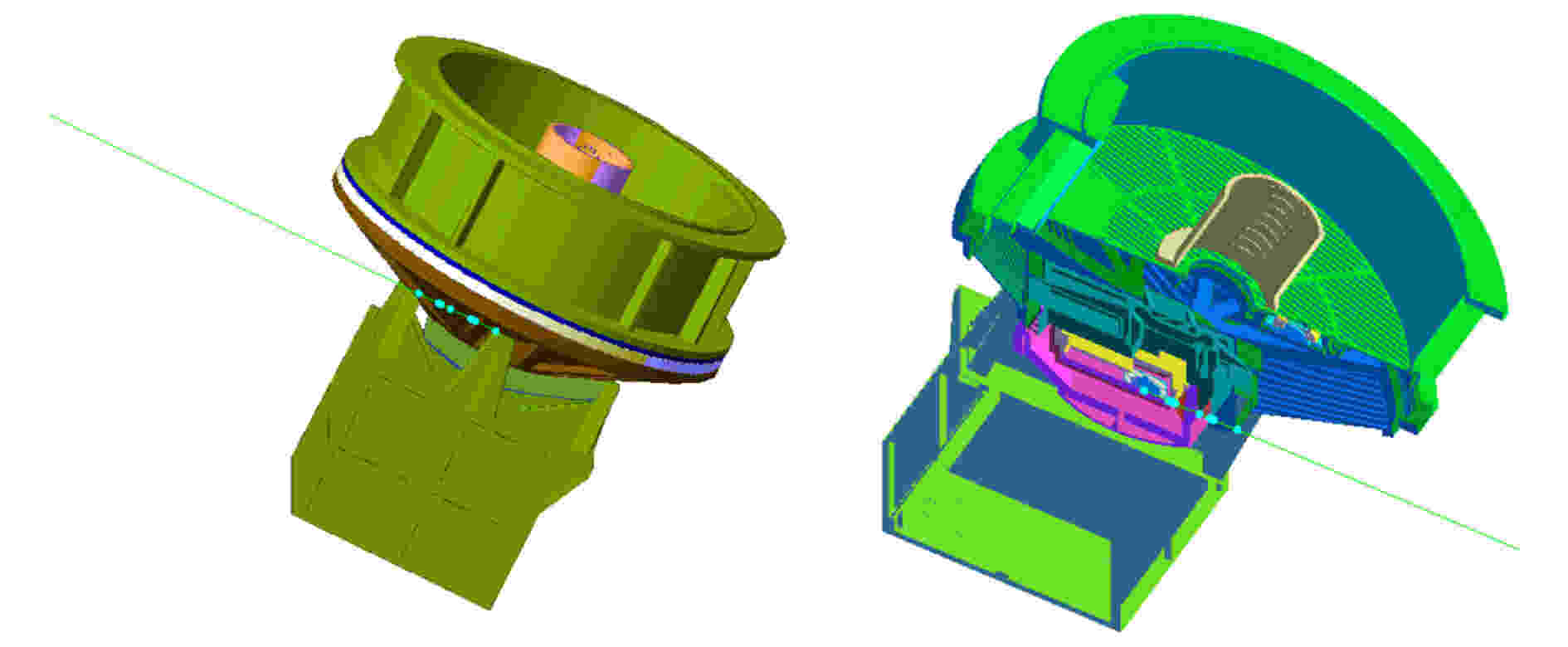图 5 SFA探测单元结构
Figure5. Structure of single SFA module.

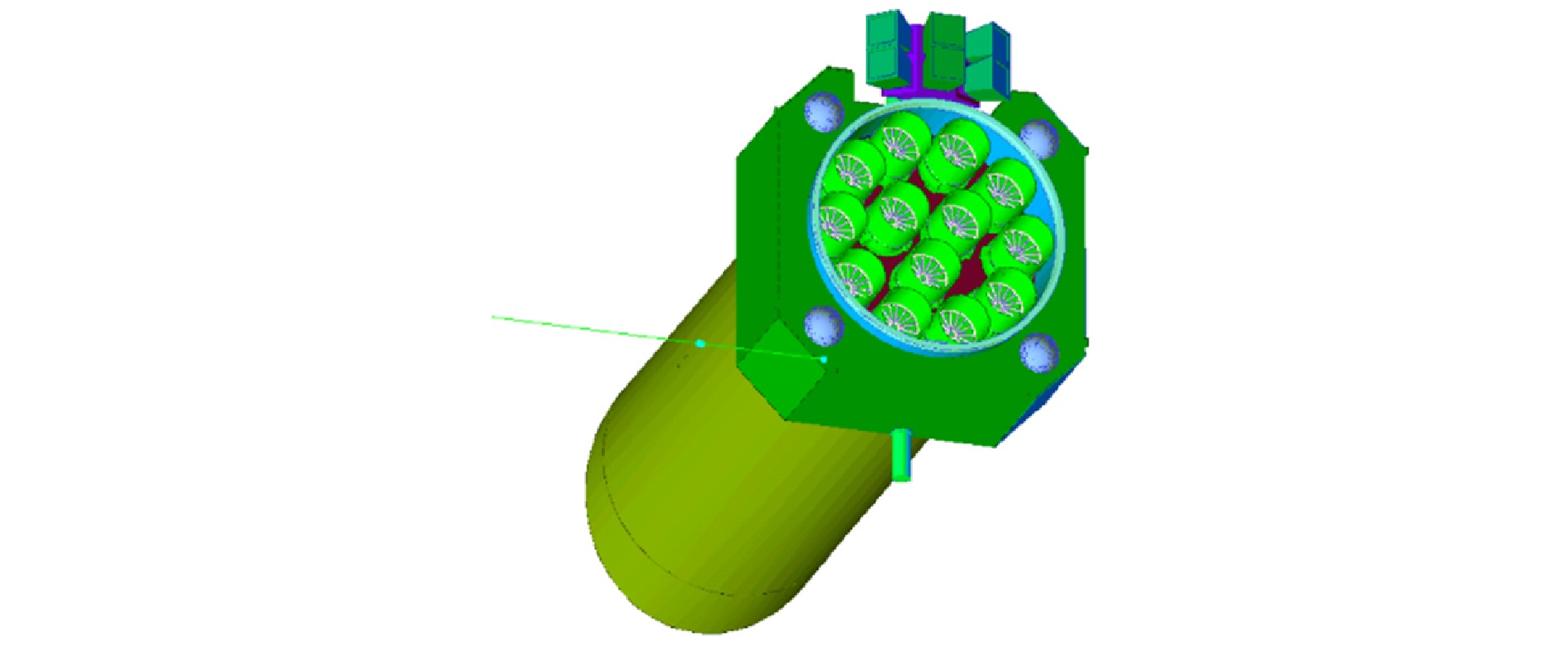图 6 eXTP整星模型
Figure6. Mass model of the eXTP satellite.

面密度分布计算采用径迹追踪方法^[27], 在敏感探测位置(即探测敏感区域, SDD位置)各向同性发射虚粒子, 虚粒子具有直线径迹, 仅实现发射方向直线上经过的各种不同材料结构的位置点统计, 依据在各种结构中的径迹长度与密度, 可计算得到该方向总的面密度值. 图7为SFA中SDD位置的面密度分布图.
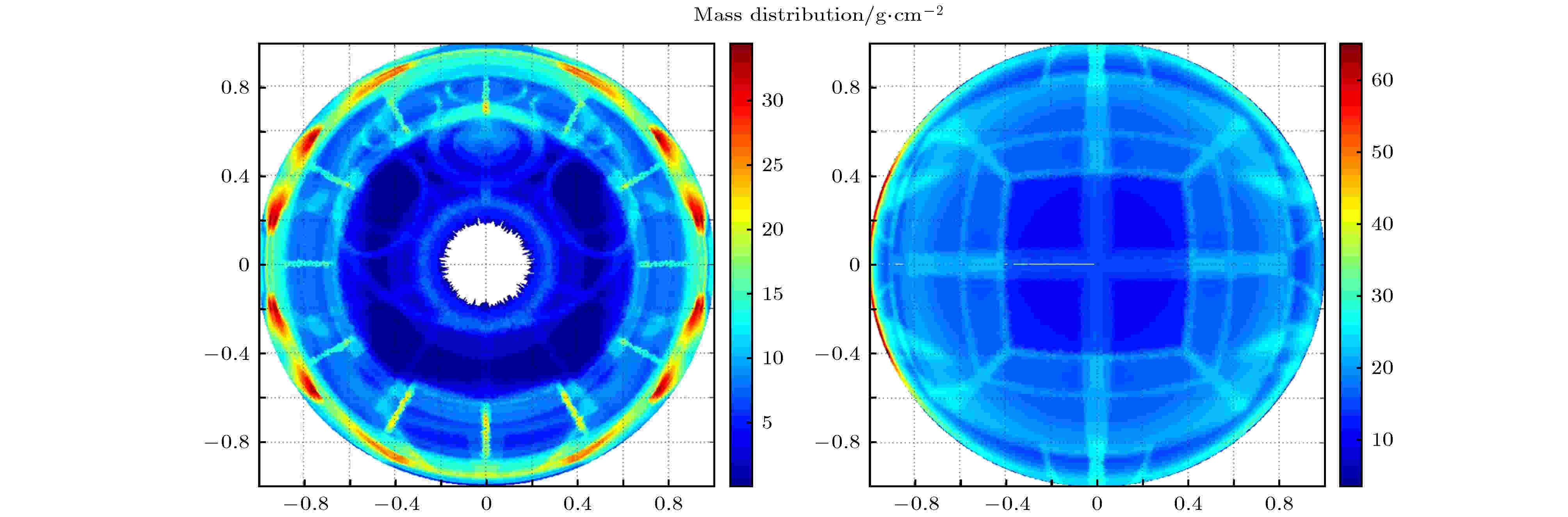图 7 SFA探测单元中SDD位置的面密度分布图(左: 正向; 右: 背向)
Figure7. Planar density distribution at the position of SDD (left: frontview; right: backview).

为了检验球壳尺寸(半径)对粒子本底的影响, 部分成份将球壳半径放大到500 cm, 计算得到的面密度与SFA粒子本底关系见图8.
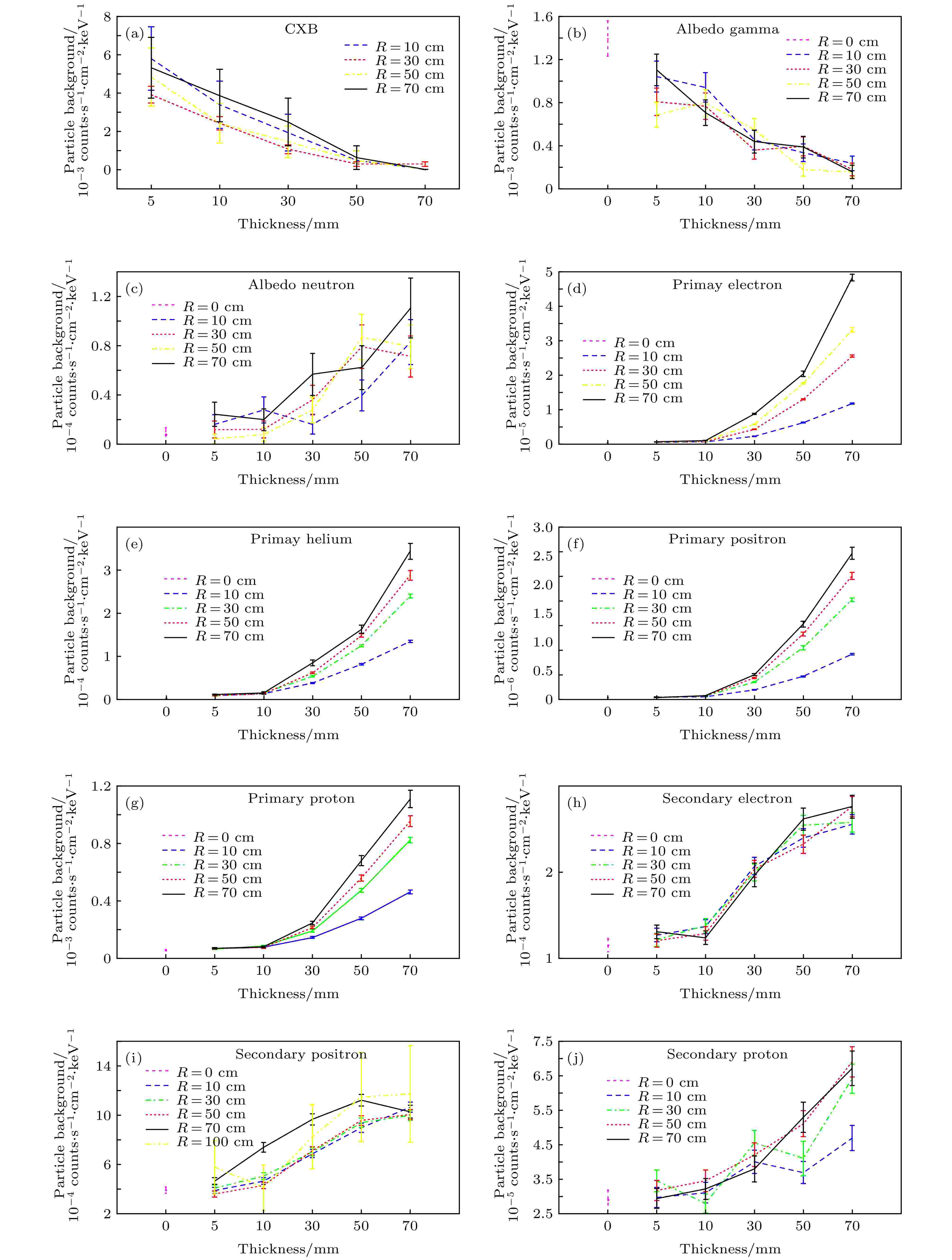图 8 粒子本底水平随球壳尺寸及厚度变化
Figure8. Particle background evolution as a function of the size and the thickness of the aluminum spherical shell.

图8给出了基于简化铝球壳结构得到的不同成份粒子本底水平随球壳半径和厚度的变化, 其中纵坐标为能量沉积在0.5—15 keV范围内的计数率(单位为counts·s^–1·cm^–2·keV^–1). 从图8可以看出, 基于简化铝球壳得到的各种成份粒子本底主要依赖于球壳的厚度变化, 即面密度. 其中, 原初本底成份在铝球壳半径为10 cm时有较大不一致. 由于焦平面探测器尺寸(直径D)为3 cm, 铝球壳半径为10 cm时, 焦平面探测器的几何效应引入较大偏离, 随着球壳半径(R)变大, R/D越来越大, 其影响越来越小. 图9为每种本底成份对应同一厚度不同球壳尺寸粒子本底的平均结果, 显示了各个成份粒子本底水平与铝球厚度(面密度)关系. 可以看出, 面密度大于10 g/cm²后, 粒子本底主要来源于宇宙弥散X射线、宇宙线原初质子及次级正电子. 宇宙弥散X射线造成的本底随屏蔽厚度的增加越来越小, 而原初质子随面密度增加反而有越来越多的趋势. 其中, 宇宙弥散X射线造成的本底对面密度特别敏感. 因此, 在进行屏蔽设计时要首先考虑宇宙弥散X射线的屏蔽, 在其控制在一定水平后, 再综合考虑其他成份的贡献. 图10显示了将图9 中对应各种成份本底相加得到的总的粒子本底水平随铝球厚度(面密度)变化. 可以看出, 总的粒子本底水平在面密度小于13.5 g/cm²时, 呈逐渐减小趋势, 在大于13.5 g/cm²时, 呈增加趋势.
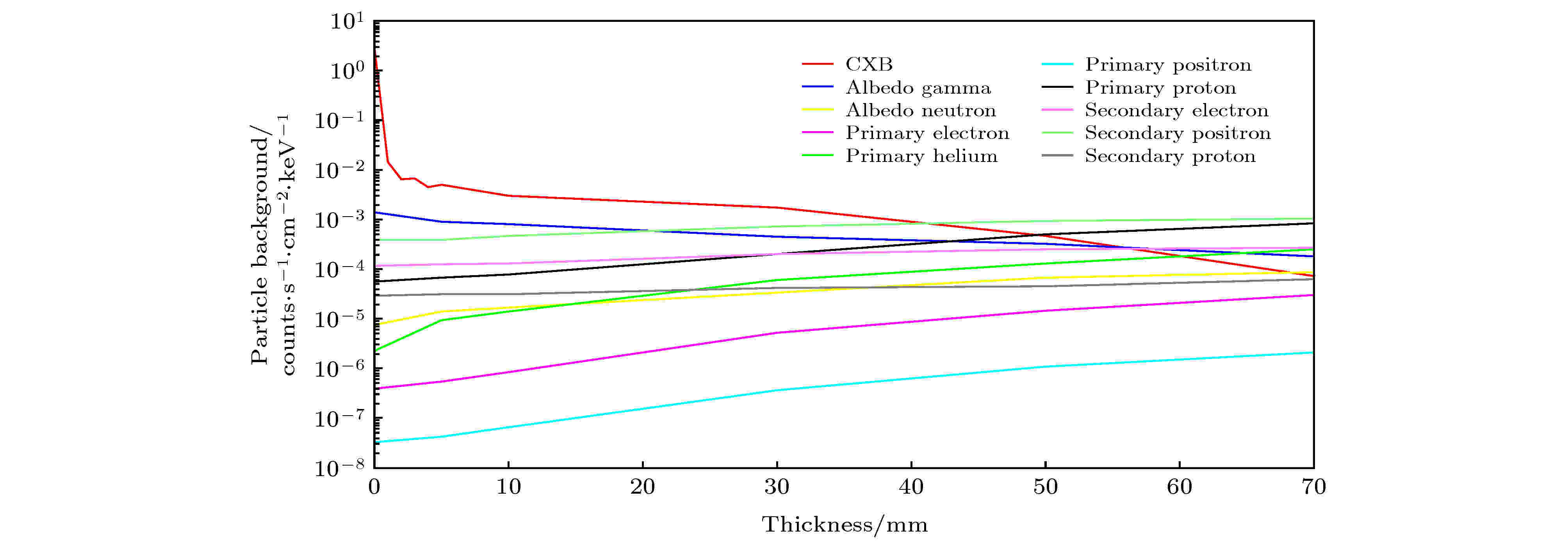图 9 不同成份粒子本底随球壳厚度变化拟合曲线
Figure9. Fitting curves of different particle backgrounds as a function of the thickness of the aluminum spherical shell.

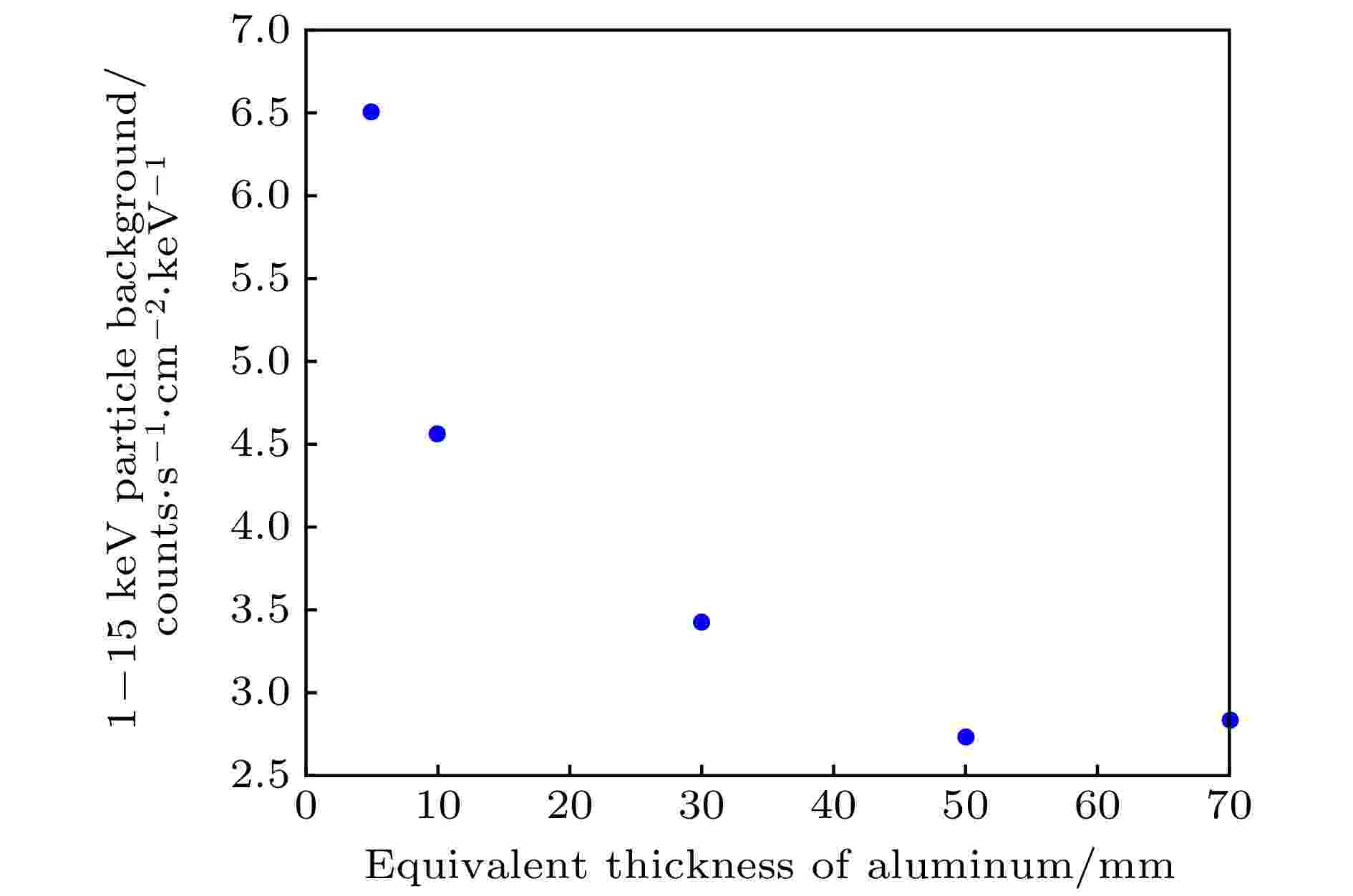图 10 SFA-SDD总的粒子本底水平随简化球壳厚度变化
Figure10. Total particle background evolution as a function of the thickness of the aluminum spherical shell .

为了验证面密度分布插值估计粒子本底方法的可行性, 以实际eXTP整星模型和SFA质量模型作为输入, 计算焦平面探测器SDD粒子本底水平. 计算过程中, 除将简化球壳替换为eXTP实际结构外, 其他输入与简化球壳计算过程一样. 图11给出了eXTP-SFA整星质量模型(见图6)其中一个SFA单元敏感探测区(SDD位置)的不同方向等效铝厚度分布, 图中50 mm代表厚度不小于50 mm. 可以看出, 在焦平面探测器背向和侧面, 等效铝屏蔽厚度通常大于30 mm, 屏蔽厚度小于15 mm的区域主要集中在聚焦镜间隙及SFA准直筒安装板区域(上侧方). 按照第3节给出的计算过程及基本配置, 将简化球结构替换为实际的整星结构和焦平面探测器周围结构, 计算得到整星质量模型对应的粒子本底水平. 图12给出了整星质量模型(对应面密度分布如图11)模拟计算结果与面密度分布插值法结果对比图. 有效探测能段内, 总的粒子本底水平分别为(2.0 ± 0.5) × 10^–3和3.0 × 10^–3 counts·s^–1·cm^–2·keV^–1.
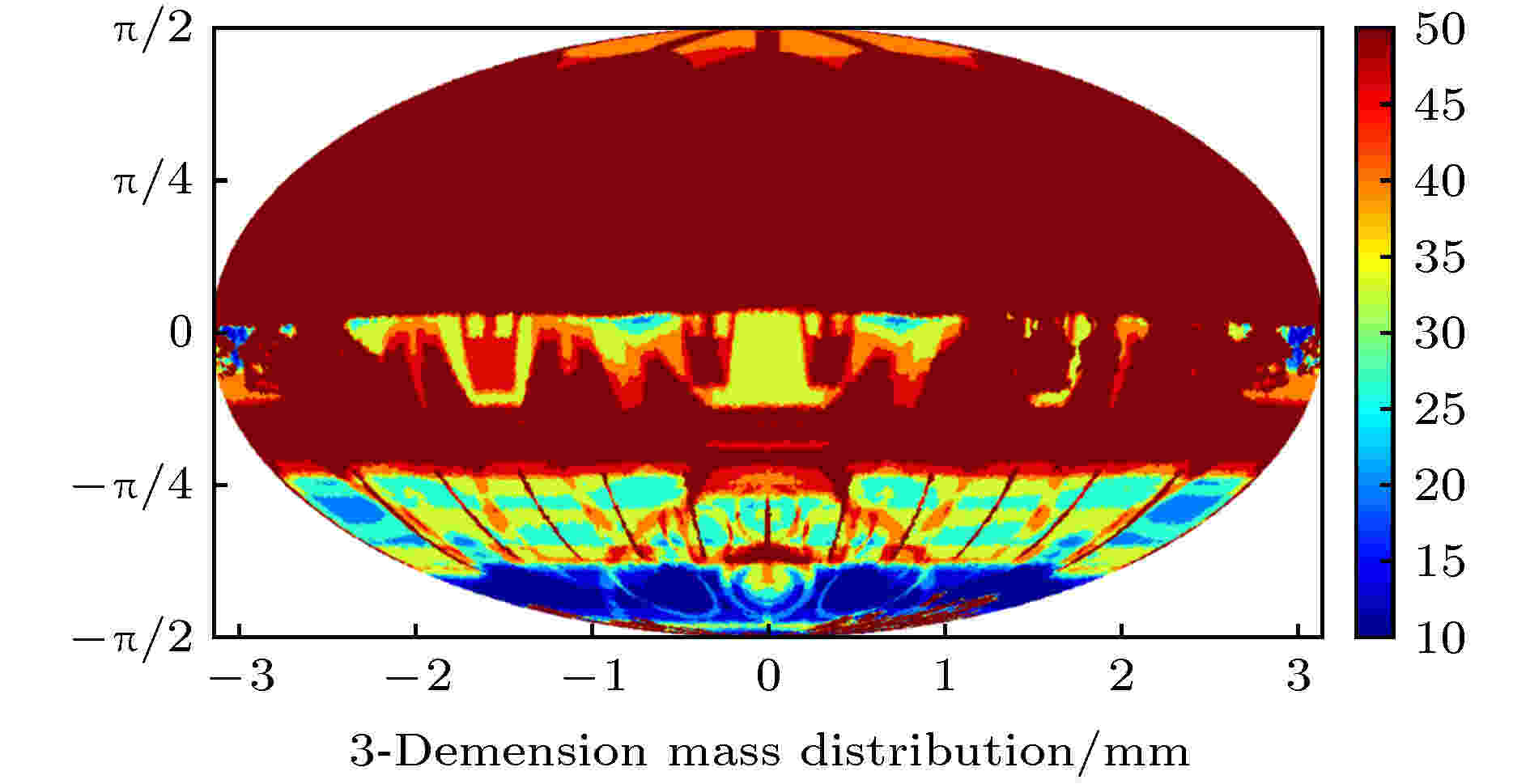图 11 eXTP-SFA整星结构下敏感探测区(SDD位置)的等效铝厚度分布
Figure11. Equivalent aluminum thickness distribution of the whole eXTP at the SDD position.

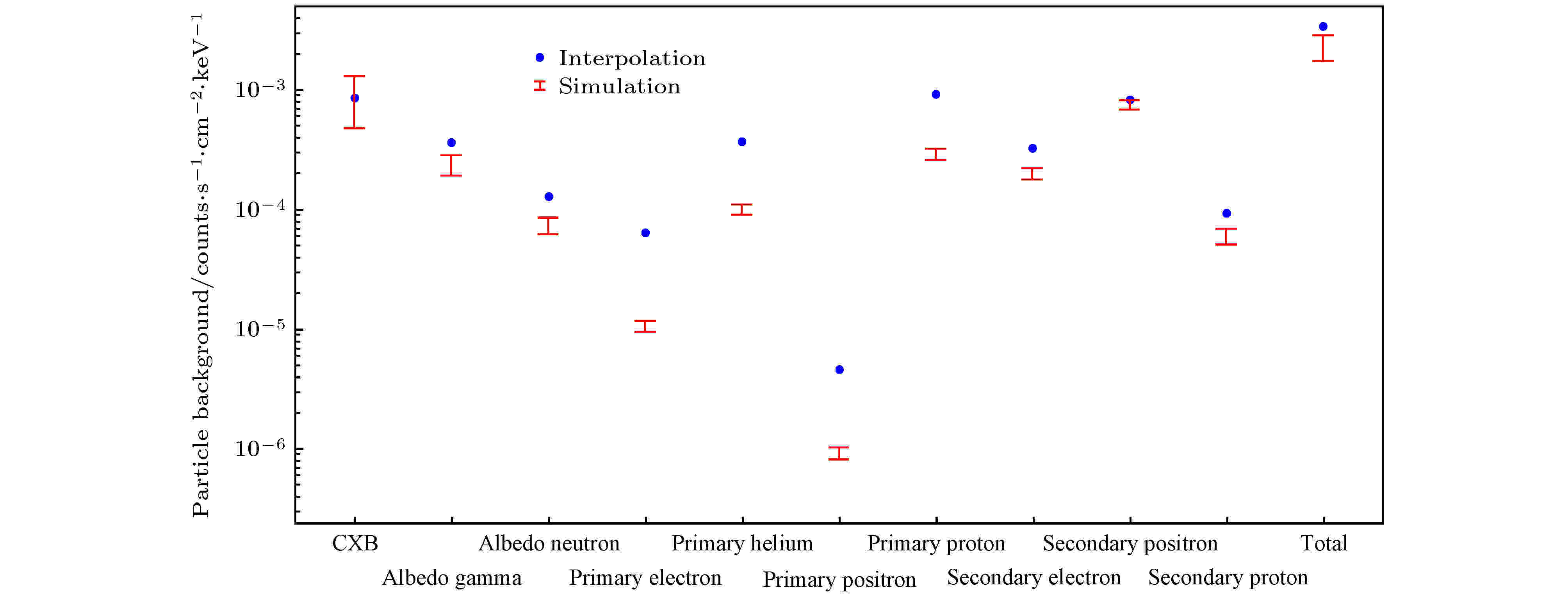图 12 面密度分布插值法得到的粒子本底水平与模拟计算结果对比
Figure12. Comparison of particle background level obtained with interpolation of planar density distribution and with simulation.

为了更进一步检验面密度插值法结果的可靠性, 对这些区域采取加厚屏蔽措施, 即增加准直筒高度使准直筒限制视场与聚焦镜外延衔接, 同时增加准直筒安装板厚度到20 mm, 修改前后结构对比见图13, 其敏感探测区(SDD位置)的不同方向等效铝厚度分布见图14. 图15给出了修改SFA结构后(见图13, 对应面密度分布见图14)模拟计算结果与面密度分布插值法结果的对比图. 有效探测能段内, 总的粒子本底水平分别为(3.0 ± 0.7) × 10^–3 和2.9 × 10^–3 counts·s^–1·cm^–2·keV^–1. 由于整星质量模型的计算效率非常低, 基于质量模型计算结果的差异主要由统计误差引起. 面密度分布插值法估计粒子本底水平与使用实际质量模型通过模拟计算得到的结果有很好的一致性.
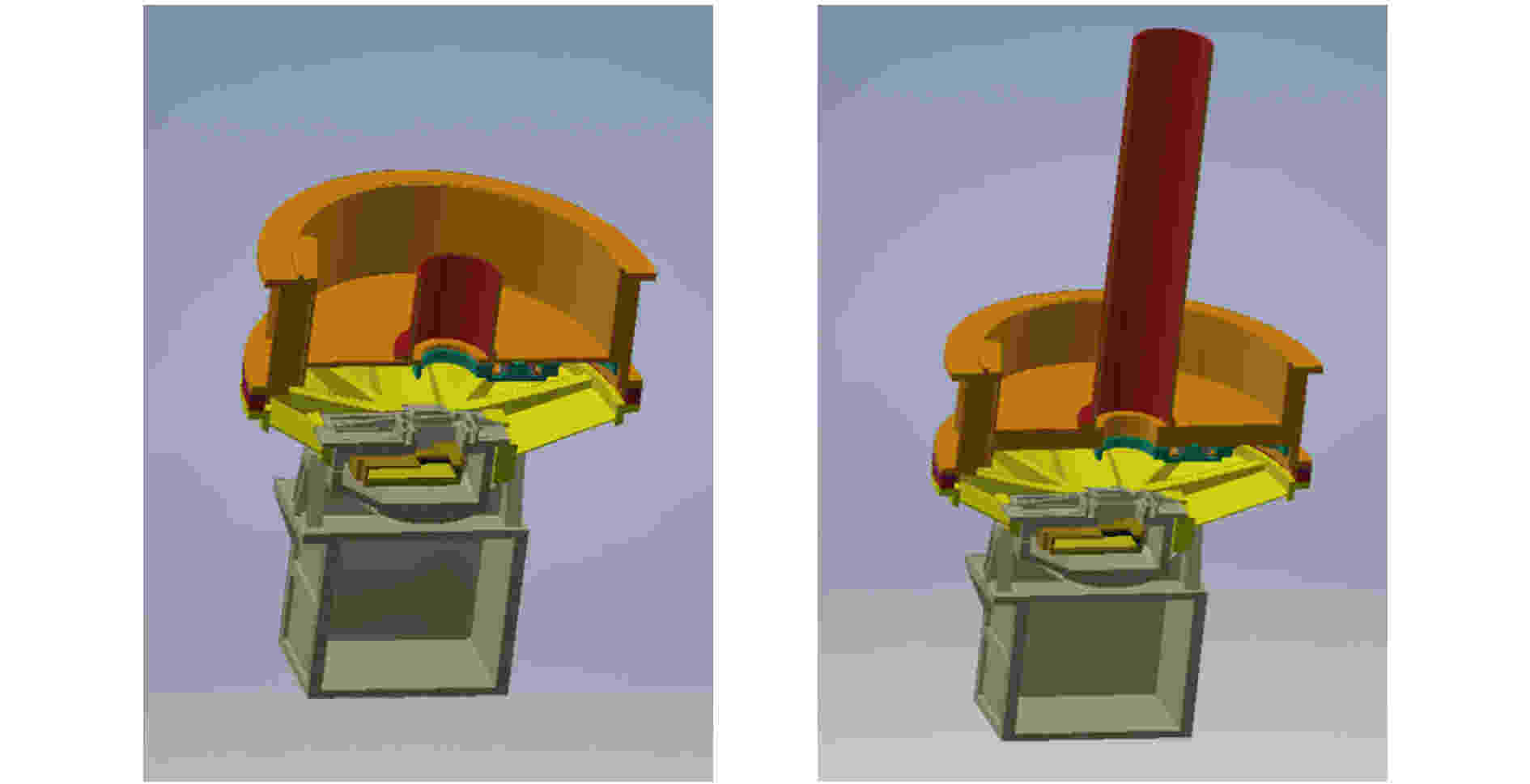图 13 结构更改前后质量模型剖视图(左: 更改前; 右: 更改后)
Figure13. Structure of the mass model before and after structure modifications (left: before modifications; right: after modifications).

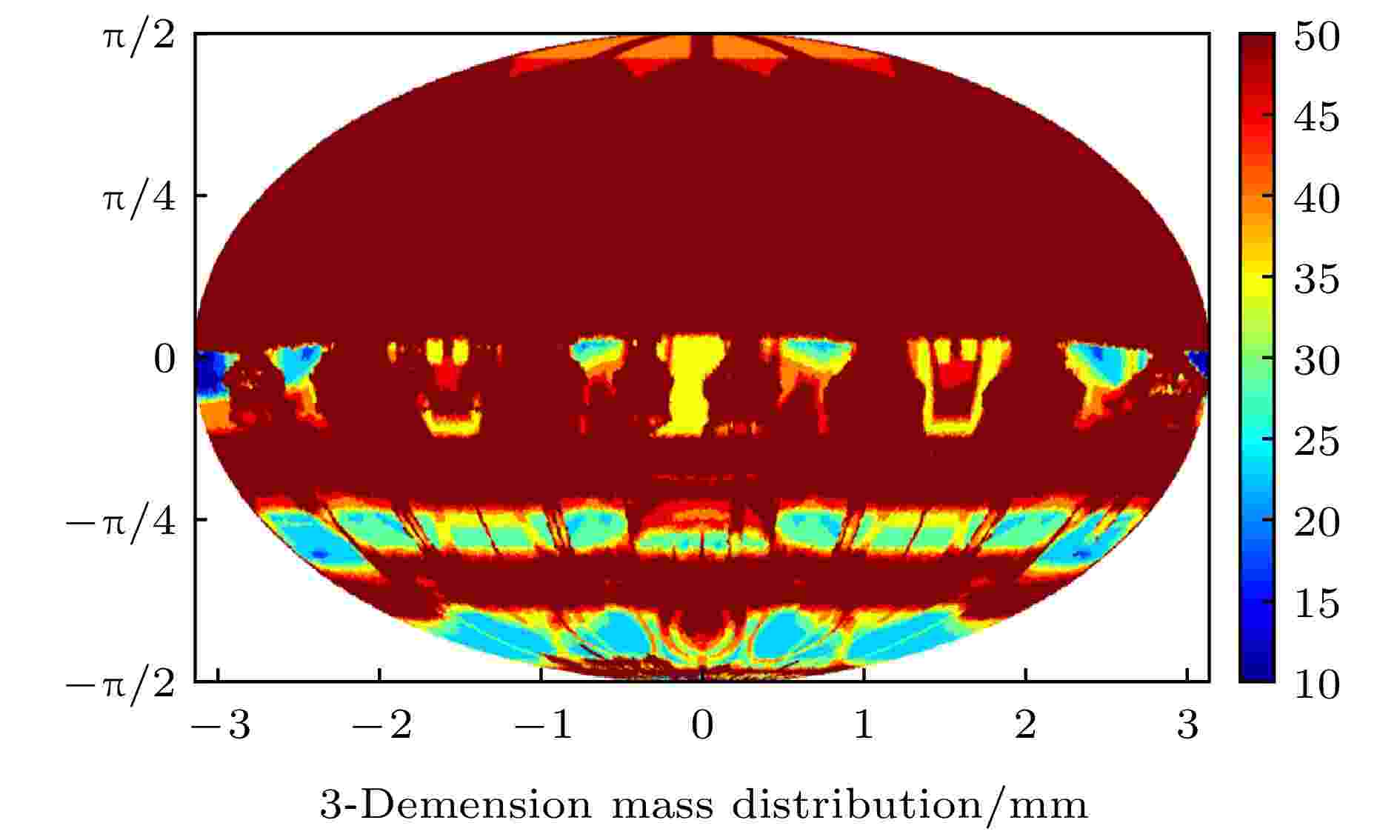图 14 结构更改后等效铝厚度分布
Figure14. Equivalent aluminum thickness distribution after the structure modifications.

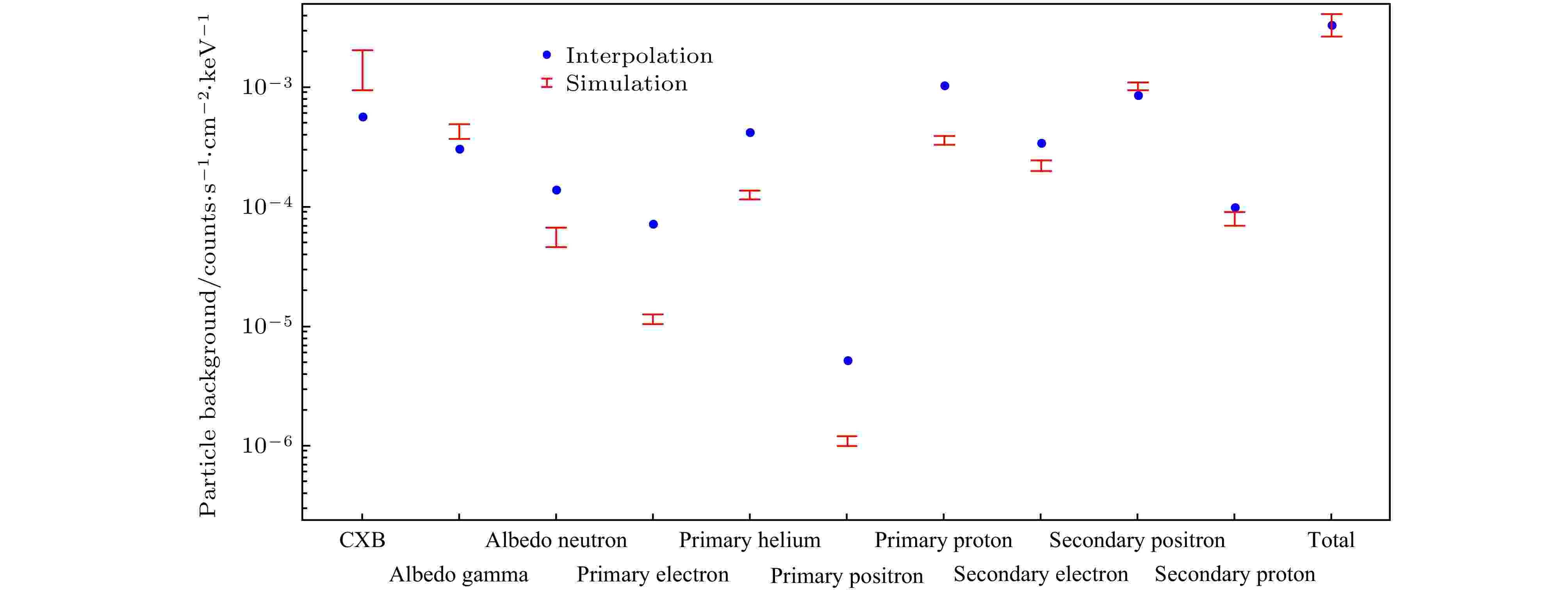图 15 结构更改后面密度分布插值法得到的粒子本底水平与模拟计算结果对比
Figure15. Comparison of the particle background levels after the structure modifications, from the interpolation of planar density distribution and the simulation, respectively.

与eXTP-SFA实际质量模型输入计算得到的结果相比, 面密度分布插值法对聚焦型空间X射线仪器的估计精度在50%左右, 而目前通过质量模型模拟计算得到的粒子本底与在轨实测相比最高精度在20%左右^[9]. 由于本文计算得到的面密度与SFA粒子本底关系基于简化球壳结果, 受统计量限制(厚屏蔽时计算量太大), 未引入空间辐射环境对简化球壳不同方位的影响, 例如地球遮挡导致宇宙线指向天顶方向附近流强更低, 而大气反照成份主要来自地球大气, 这导致插值法结果在较大立体角范围屏蔽较弱时偏离模拟计算结果较大.
屏蔽厚度增加对粒子本底水平的影响, 以占比较高的次级正电子成份为例. 由于次级正电子成份能谱较软, 随厚度再增加, 粒子本底水平开始趋于稳定并逐步减小, 见图16. 随厚度变化趋势主要和空间辐射环境有关. 粒子能谱较软, 则其达到峰值对应的面密度会变大. 影响粒子本底水平的主要为内壁薄层内的次级粒子成份, 屏蔽增厚, 内壁薄层处的粒子流强降低, 粒子本底水平降低.
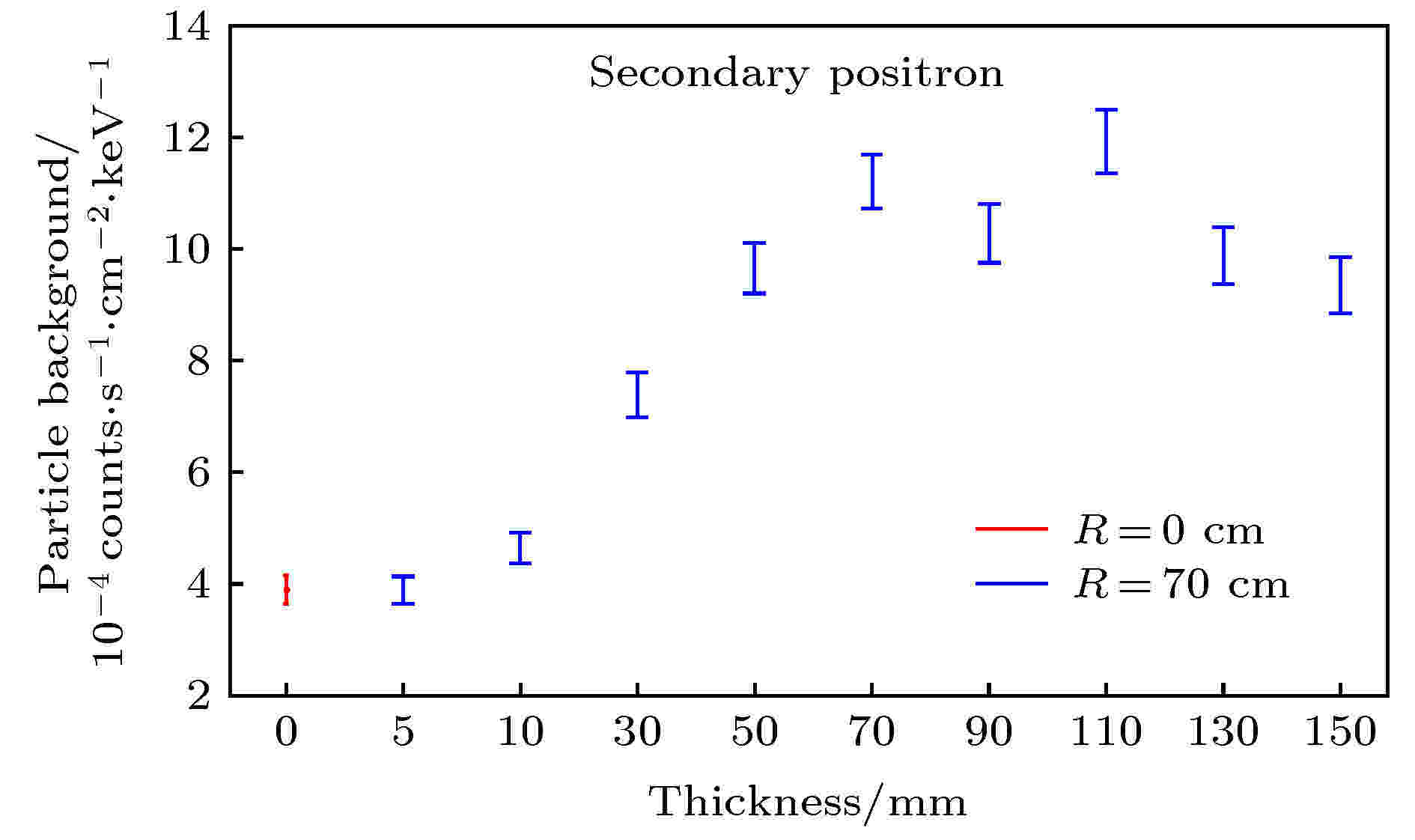图 16 次级正电子成份随屏蔽厚度增加变化趋势
Figure16. Variation of the secondary positron composition as a function of the shielding thickness.

次级粒子对空间聚焦性X-ray粒子本底的贡献. 由于SFA-SDD耗尽层较厚, 宇宙线质子电离能损落在探测能段之外, 对粒子本底贡献更多是次级粒子成份. 次级粒子对仪器本底的贡献, 在神舟二号X 射线探测器上体现得非常明显, 在返回舱与留轨舱分离之后, 安装在留轨舱上的两个XD探头的背景计数率分别减少了50%以上^[28]. 对于聚焦型空间X-ray仪器, 其探测能段更软, 本文没有深入研究能引起粒子本底的次级成份来源、机理及量化, 而只是给出了探测能段内总本底水平量化综合评估的结果.
面密度分布插值法使用的粒子本底随面密度变化曲线是基于eXTP-SFA焦平面探测器SDD设计得到的, 对于不同焦平面探测器类型, 其结果会有差异, 此差异可能来自探测器面积、材料、像素尺寸、耗尽层厚度、封装材料厚度以及视场方向多层结构等^[29]. 因此其描述粒子本底水平随面密度变化更多的是反映整体结构贡献, 而对不同的空间项目可能会有一定差异. 但相对于整星计算, 可以节约大量时间, 初步确定粒子本底水平, 加快方案的尽快确定及后续精细分析进程.

本文提出一种快速估计聚焦型空间X射线望远镜粒子本底的方法, 并通过对eXTP卫星SFA焦平面探测器粒子本底水平的模拟计算加以验证. 该方法基于等效面密度与各种成份粒子本底水平的对应关系, 结合聚焦型空间X射线望远镜自身的结构分布特点, 能够快速估算任意设计配置下总的粒子本底水平, 在空间项目设计论证阶段有一定应用价值. 同时, 文中给出的粒子本底水平随面密度变化的定量描述, 有助于更深入理解粒子本底水平与屏蔽设计的关系, 具有一定指导意义. 对于低粒子本底设计研究, 尤其是焦平面探测器附近观测能段内次级粒子来源、物理机理及本底抑制方案的研究, 将会在后续优化设计阶段继续开展.
感谢中国科学院微小卫星创新研究院提供的eXTP整星结构模型. 感谢中国科学院高能物理研究所卢方军研究员的讨论与建议.