全文HTML
--> --> -->1986年, Mieko和Minoru[4]建立了适用于放电抽运的准分子激光器一维流体模型, 对XeCl准分子激光器的理论研究表明, 激光器放电及动力学特性受电子密度影响较大, 而电子密度主要由Xe和HCl气体的配比决定. 1988年, Shinjin等[5]以及Mieko和Minoru[6]分别从抽运效率、增益系数等方面研究了使用He, Ne作为缓冲气体时系统的输出特性, 并指出使用Ne代替He在能量和效率方面并没有明显优势. 但Ne作为缓冲气体时, 由于Ne与电子的反应更加复杂, 除了直接的电离、激发反应生成电子外, 还包含了大量的步进电离、二次电离, 释放出自由电子, 系统放电稳定性有所提高. 同时,


我国研究者也开展了诸多高压脉冲放电的研究工作. 2006年, 华中科技大学的Jiang和Yang[7]进行了高气压辉光放电的理论与实验研究, 分析了高气压辉光放电的稳定性问题. 2008年, 大连理工大学的石峰[8]进行了高气压超短纳秒脉冲气体放电的数值模拟研究, 给出了不同电极间距、脉冲电压幅值下的大气纳秒脉冲放电结果. 2012年, 华中科技大学的杨晨光等[9]进行了大气压纳秒脉冲放电等离子体数值模拟与实验研究, 分析比较了不同放电条件下的纳秒脉冲放电特性. 但以上研究工作的重点均在大气压、高压脉冲放电形成等离子特性的描述上, 并未将其与准分子激光输出特性以及稳定性相联系. 2015年, 华中科技大学罗时文等[10,11]进行了放电抽运ArF准分子激光器的放电动力学仿真计算, 分析了放电参数对激光输出及系统能量利用效率的影响.
本文以ArF准分子激光系统及其核心系统运转物理机制—气体高压放电等离子体深紫外激光辐射过程为主要研究对象, 参考国际相关领域通用的模型及算法, 系统分析了使用不同缓冲气体时准分子激光系统的放电特性, 深入探讨了光电离过程的重要作用及其对系统稳定性的影响.
 图 1 准分子动力学仿真计算流程
图 1 准分子动力学仿真计算流程Figure1. Simulation process of discharge dynamics of excimer.
图2为ArF准分子激光系统放电电路. 本文使用的等效放电电路与Akashi等[14]的相似, 由电容C1, C2, 电感L1, L2和开关S组成. 该放电电路实际上包括了磁压缩脉冲放电电路的最后一级磁压缩电路和放电腔放电电路. 电感L1约为600 nH, 电感L2约为20 nH, 电容C1约为10 nF, C2约为1.5 nF, R1约为1 Ω. L1为末级磁开关压缩回路的磁开关饱和电感与回路电感和, L2为放电腔内放电电路的回路电感, C1为末级磁开关的储能电容, C2为峰化电容. 开关S1闭合前, 能量由抽运电源转移到电容C1中, 开关S1闭合后(磁开关饱和后), C1中的能量经回路LC振荡转移到峰化电容C2中, C2中的能量经电极放电注入工作气体. 激光谐振腔输出耦合镜反射率约为4%. 不同缓冲气体系统中, 计算过程中考虑的等离子形成过程如表1和表2所示.
| 反应类型 | 反应过程 | 反应系数 | 参考文献 |
| 电子碰撞反应 | Ar + e → Ar+ + 2e | 计算玻尔兹曼方程得到 | |
| Ar + e → Arex + e | 计算玻尔兹曼方程得到 | ||
| Ar + e → Ar* + e | 计算玻尔兹曼方程得到 | ||
| Ar* + e → Ar+ + 2e | 计算玻尔兹曼方程得到 | ||
| F2 + e → F– + F | 计算玻尔兹曼方程得到 | ||
| He + e → He+ + 2e | 计算玻尔兹曼方程得到 | ||
| He + e → Heex + e | 计算玻尔兹曼方程得到 | ||
| He + e → He* + e | 计算玻尔兹曼方程得到 | ||
| 中性粒子反应 | Ar+ + 2 Ar → Ar2+ + Ar | 2.5 × 10–31 cm6·s–1 | [15] |
| Ar+ + F– → ArF* | 1 × 10–6 cm3·s–1 | [15] | |
| Ar2+ + F–→ ArF* + Ar | 1 × 10–6 cm3·s–1 | [15] | |
| Arex → Ar + hγ’ | 1.0 ns | [15] | |
| Ar* + F2 → ArF* + F | 8 × 10–10 cm3·s–1 | [15] | |
| ArF*→Ar + F + hγ | 42 ns | [15] | |
| 受激辐射 | ArF* + hγ → ArF + 2hγ | 4 × 10–16 cm3·s–1 | [15] |
| 光电离 | hγ + F– → F + e | 1 × 10–17 cm3 | [15] |
| Arex + hγ → Ar+ + e | 1 × 10–18 cm3 | [15] |
表1ArF准分子激光器等离子反应过程(He作为缓冲气体)
Table1.Plasma reaction process of ArF excimer laser system (He is the buffer gas).
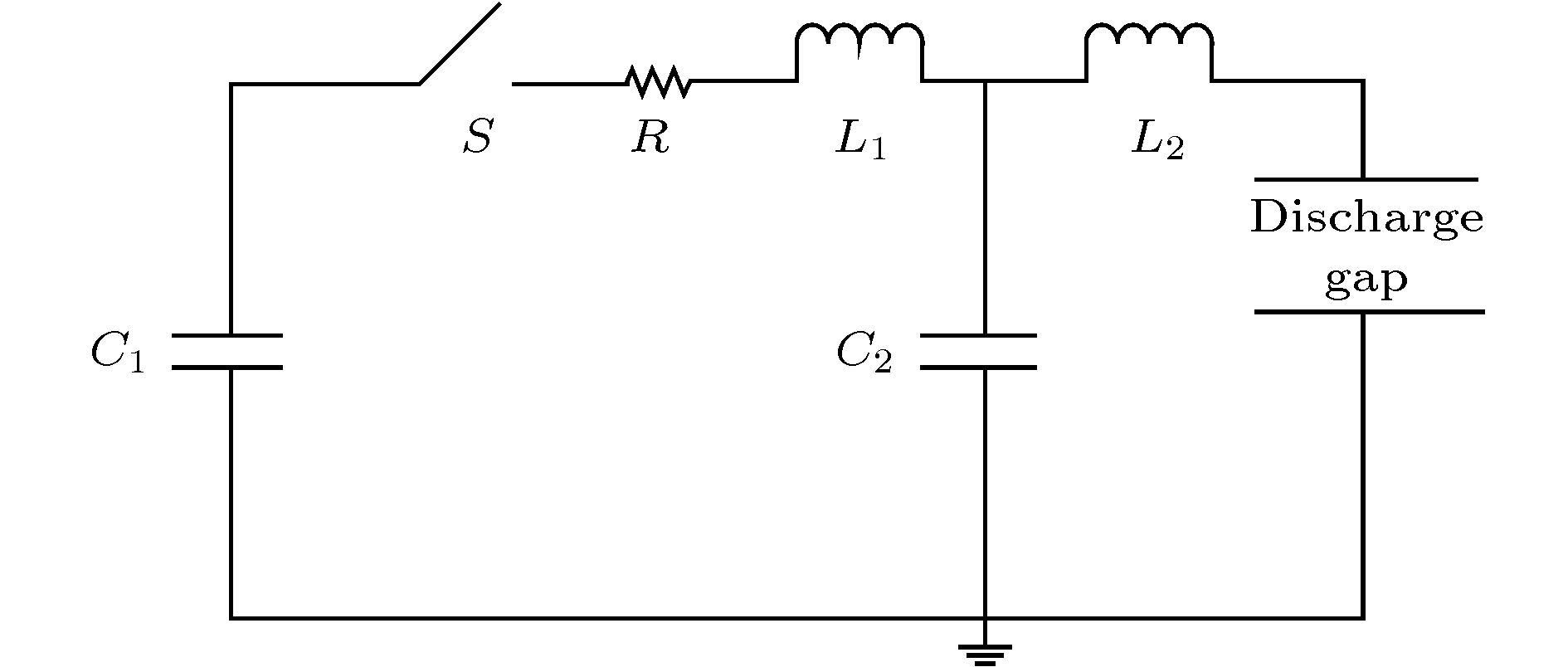 图 2 放电电路
图 2 放电电路Figure2. Discharge circuit.
| 反应类型 | 反应过程 | 反应系数 | 参考文献 |
| 电子碰撞反应 | Ar + e → Ar+ + 2e | 计算玻尔兹曼方程得到 | |
| Ar + e → Arex + e | 计算玻尔兹曼方程得到 | ||
| Ar + e → Ar* + e | 计算玻尔兹曼方程得到 | ||
| Ar* + e → Ar+ + 2e | 计算玻尔兹曼方程得到 | ||
| F2 + e → F – + F | 计算玻尔兹曼方程得到 | ||
| Ne* + e → Ne+ + 2e | 计算玻尔兹曼方程得到 | ||
| Ne + e → Ne+ + 2e | 计算玻尔兹曼方程得到 | ||
| Ne + e → Ne* + e | 计算玻尔兹曼方程得到 | ||
| 中性粒子反应 | Ne2* + e → 2e + Ne2+ | (9.75 × 10–9) × (abs(Te))0.71 × exp(–3.4/abs(Te)) | [16] |
| Ne2+ + e → Ne* + Ne | (3.7 × 10–8) × (abs(Te))–0.43 | [16] | |
| Ar+ + 2Ar → Ar2+ + Ar | 2.5 × 10–31 cm6·s–1 | [15] | |
| Ar+ + F– → ArF* | 1 × 10–6 cm3·s–1 | [15] | |
| Ar2+ + F– → ArF* + Ar | 1 × 10–6 cm3·s–1 | [15] | |
| Arex → Ar + hγ’ | 1.0 ns | [15] | |
| Ar* + F2 → ArF* + F | 8 × 10–10 cm3·s–1 | [15] | |
| 2Ne* → Ne+ + Ne + e | 5 × 10–10 cm3·s–1 | [17] | |
| Ne+ + 2Ne →Ne2+ + Ne | 4.4 × 10–32 cm6·s–1 | [17] | |
| Ne* + Ne + Ne → Ne2* + Ne | 4 × 10–34 cm6·s–1 | [17] | |
| Ar + ArF* → 2Ar + F | 9 e × 10-12 cm3·s–1 | [15] | |
| Ne + ArF* → Ar + Ne + F | 1 × 10–12 cm3·s–1 | [17] | |
| F2 + ArF* → Ar + 3F | 1.9 × 10–9 cm3·s–1 | [15] | |
| 受激辐射 | ArF* + hγ → ArF + 2hγ | 4 × 10–16 cm3·s–1 | [15] |
| 光电离 | hγ + F– → F + e | 1 × 10–17 cm3 | [15] |
| Arex + hγ → Ar+ + e | 1 × 10–18 cm3 | [15] | |
| Xe + hγ’→Xe+ + e | 阈值为 12.1 eV, 截面为1 × 10–16 cm2 | [18] |
表2ArF准分子激光器等离子反应过程(Ne作为缓冲气体)
Table2.Plasma reaction process of ArF excimer laser system (Ne is buffer gas).
ArF*的生成及受激辐射是激光输出的主要过程, 在两种缓冲气体中, ArF*均主要通过三条化学反应通道生成, 即

基于上述理论模型和相关参数设置, 在不同缓冲气体系统, 放电过程中极板间电流、电压及光子数密度随时间演化规律如图3和图4所示. 图3为He作为缓冲气体时极板间电压、电流及光子数密度变化图, 以He为缓冲气体时, F2/Ar/He混合工作气体的比例约为1∶33∶383; 图4为Ne作为缓冲气体时极板间电压、电流及光子数密度变化图, 以Ne作为缓冲气体时, F2/Ar/Ne混合工作气体的比例约为1∶25∶974. 从图4中可以看出, He作为缓冲气体时, 从45 ns左右开始, 工作气体被击穿, 极板间电流开始上升(图3中绿线标示). 极板间电压值达到最大值时(图3中蓝线标示), 电流值开始呈指数上升, 达到最大时, 光子数密度开始呈指数上升(图3中红线标示). 约90 ns时, 光子数回落至初始状态, 一个光脉冲输出结束. Ne作为缓冲气体时, 放电周期约为120 ns, 与He作为缓冲气体时相比(放电周期90 ns), 放电周期延长了30 ns. Ne作为缓冲气体时, 光脉冲长度为25 ns, 与He作为缓冲气体相比(光脉冲长度为15 ns), 光脉冲长度延长了10 ns. 放电周期及光脉冲的延长有利于降低能量密度, 延长光学元件寿命. 另外, Ne作为缓冲气体时, 后期电压、电流振荡现象不明显; 而作为缓冲气体时, 系统放电稳定性较好.
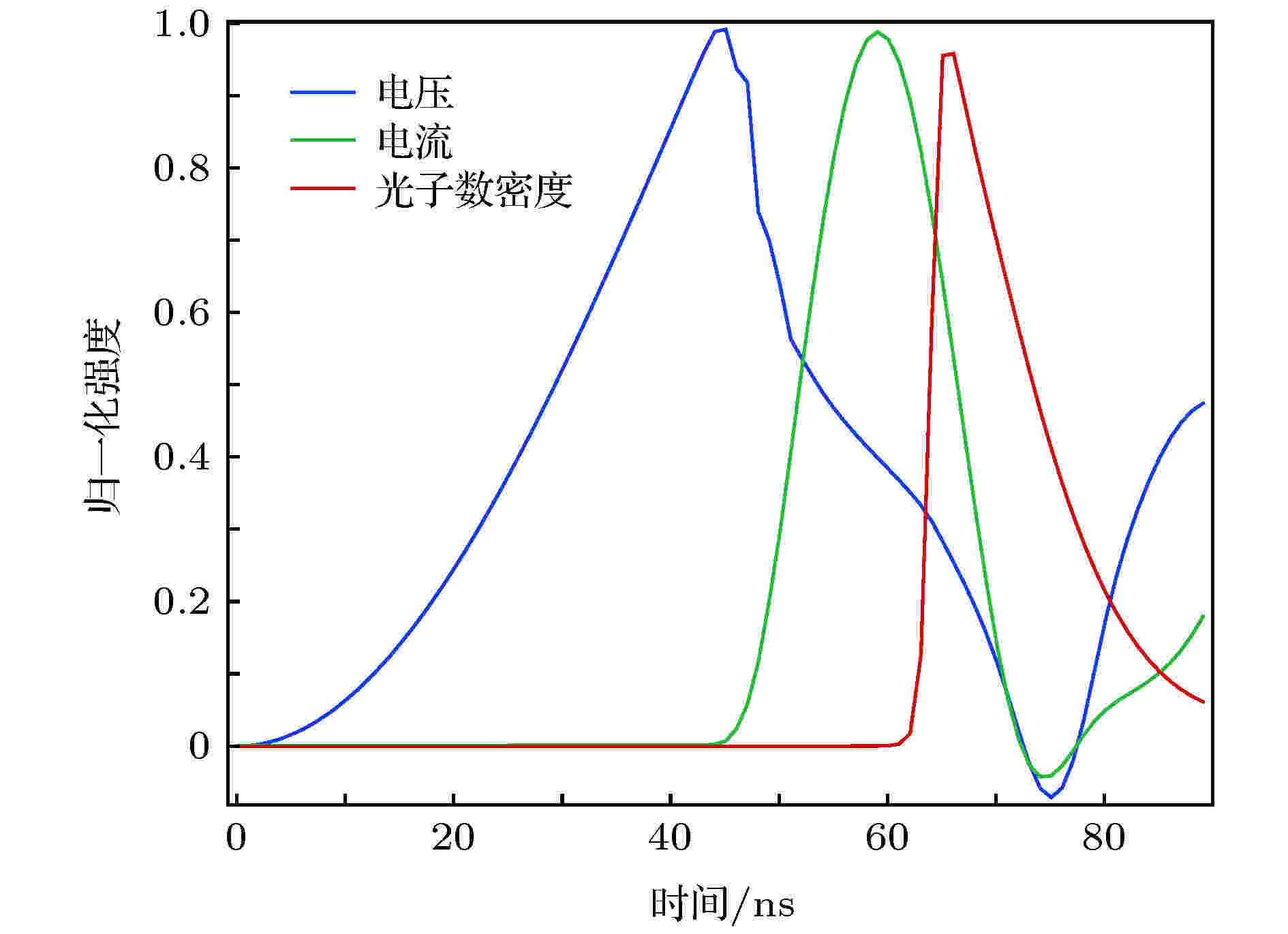 图 3 极板间电压、电流及光子数密度随时间变化图(He为缓冲气体)
图 3 极板间电压、电流及光子数密度随时间变化图(He为缓冲气体)Figure3. Waveforms of discharge voltage, current, and photon number density (He is the buffer gas).
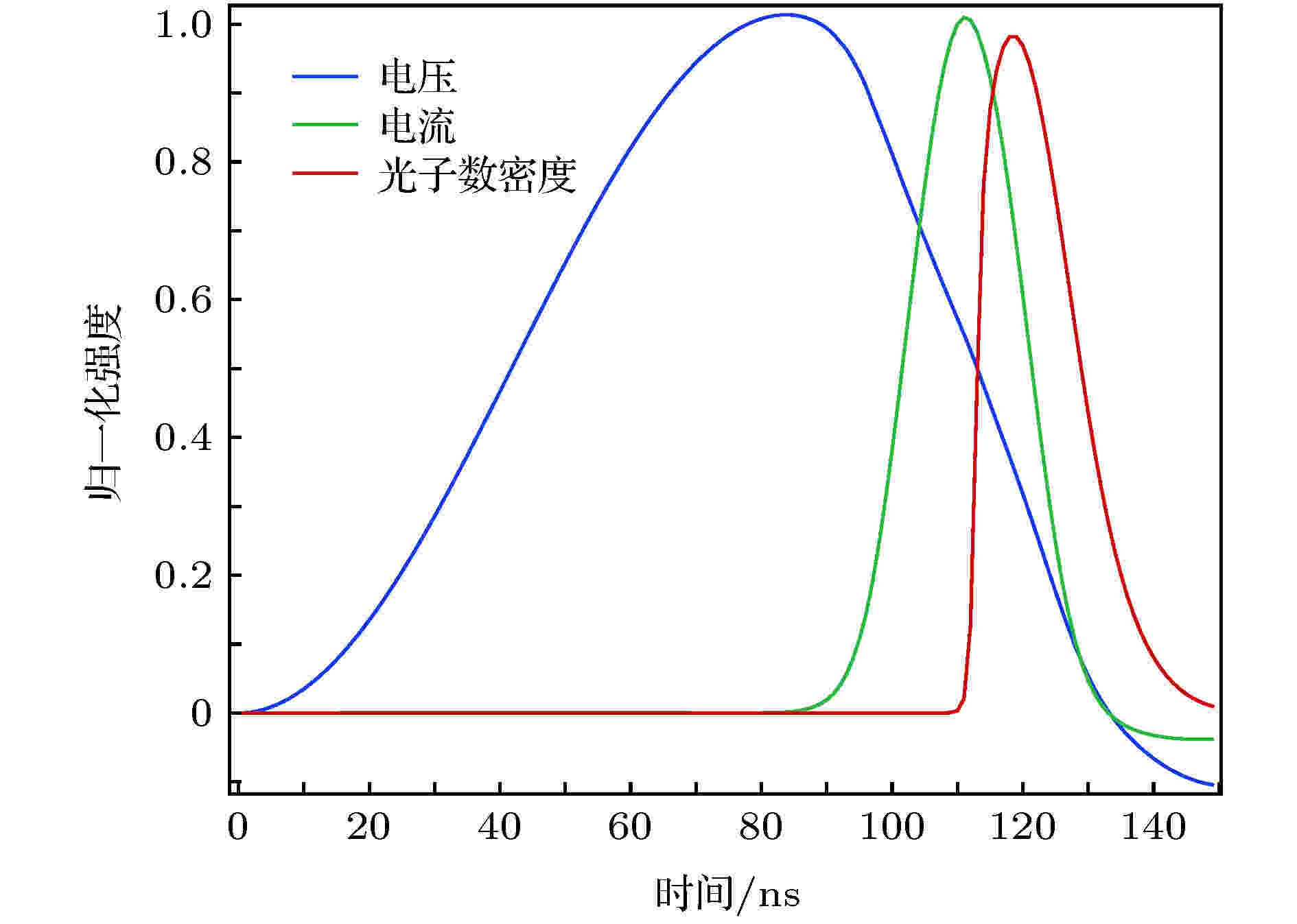 图 4 极板间电压、电流及光子数密度随时间变化图(Ne为缓冲气体)
图 4 极板间电压、电流及光子数密度随时间变化图(Ne为缓冲气体)Figure4. Waveforms of discharge voltage, current, and photon number density (Ne is the buffer gas).
2
3.1.不同缓冲气体中阴极附近电子数密度空间的分布情况
F2与电子反应为附着反应, 无能量损失, 且速度快, 因此, 预电离产生的自由电子会在放电初始时刻被F2快速吸附, 形成F–和F. 电子被吸附, 预电离效果减弱, 阴极表面形成电子耗尽层, 放电不稳定因素增加. 观察电流值达到峰值时, 自由电子分布情况(图5). He作为缓冲气体时, 电子耗尽层宽度约为15 μm, 电子鞘层宽度为20 μm; Ne作为缓冲气体时, 电子耗尽层宽度为7 μm, 阴极鞘层宽度为11 μm. 对比Ne+, Ne*与He+, He*数密度变化曲线图(图6)可知, Ne+, Ne*的数密度比He+, He*高一个数量级. 这是由于Ne激发能量阈值低, 激发生成的Ne*又可以被电离生成Ne+和自由电子, 这在一定程度上补充了阴极附近的自由电子, 使阴极附近的电子耗尽层宽度减小, 鞘层电子数密度梯度减小, 放电稳定性提升.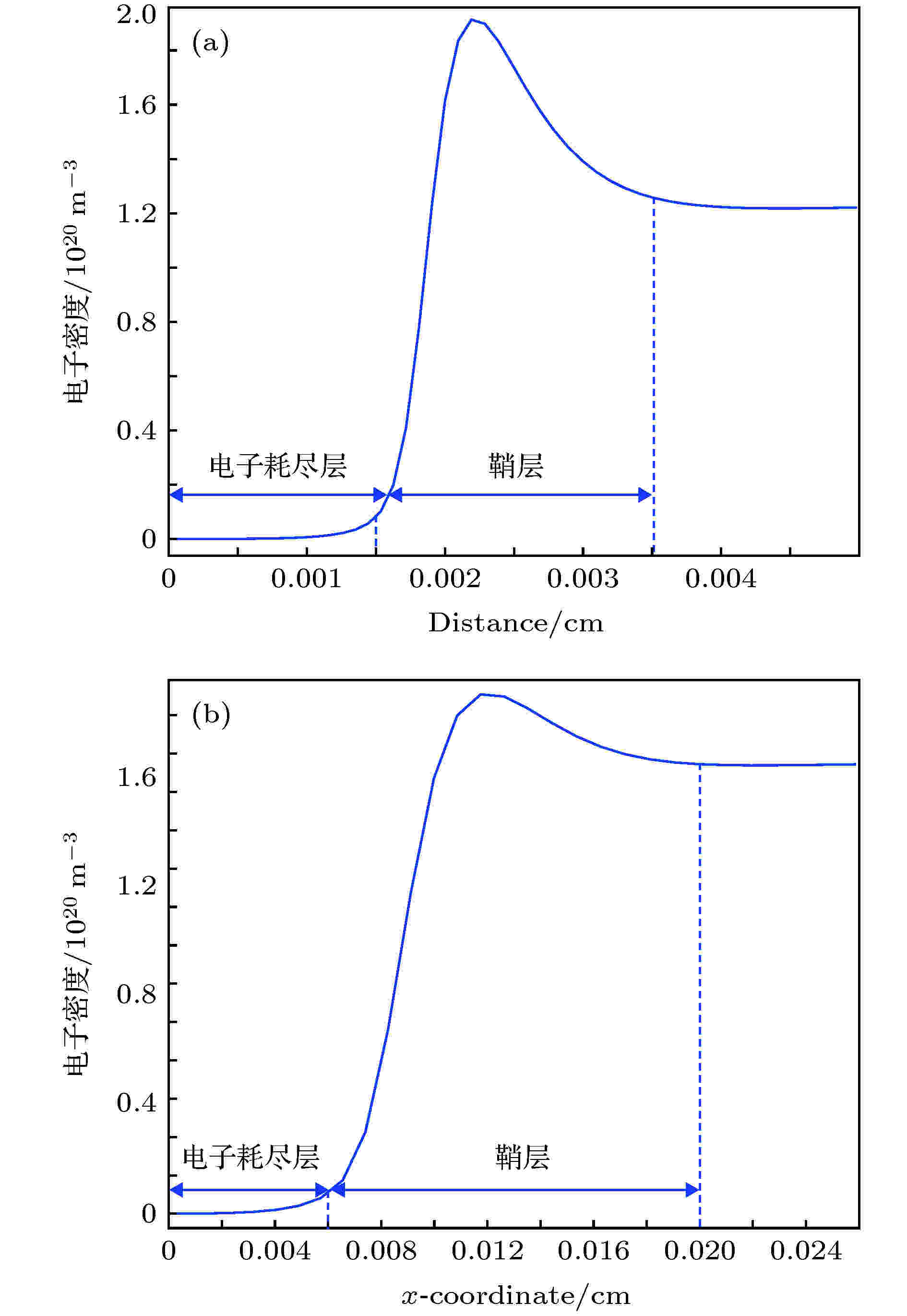 图 5 电子数密度空间分布 (a) He作为缓冲气体; (b) Ne作为缓冲气体
图 5 电子数密度空间分布 (a) He作为缓冲气体; (b) Ne作为缓冲气体Figure5. Electron number density spatial distribution: (a) He as the buffer gas; (b) Ne as the buffer gas.
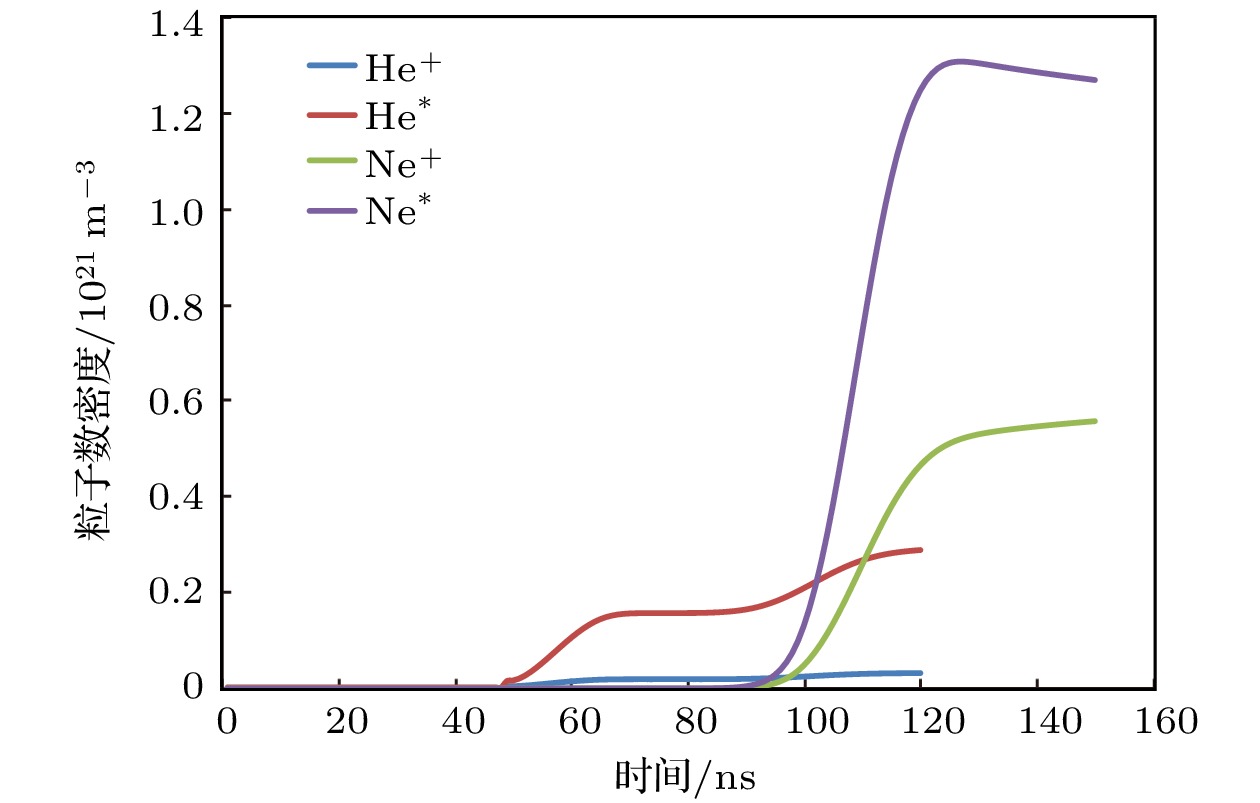 图 6 Ne+, Ne*, He+, He*数密度变化图
图 6 Ne+, Ne*, He+, He*数密度变化图Figure6. Waveforms of Ne+, Ne*, He+, He* number density.
2
3.2.不同缓冲气体中的光电离作用
ArF准分子激光系统输出激光中心波长为193.368 nm, 单光子能量为6.4 eV. Arex, Ar*, F–电离的能量阈值分别为3.57, 4.21, 4.32 eV, 因此, 光子与上述粒子碰撞后可以使其电离, 具体反应如下: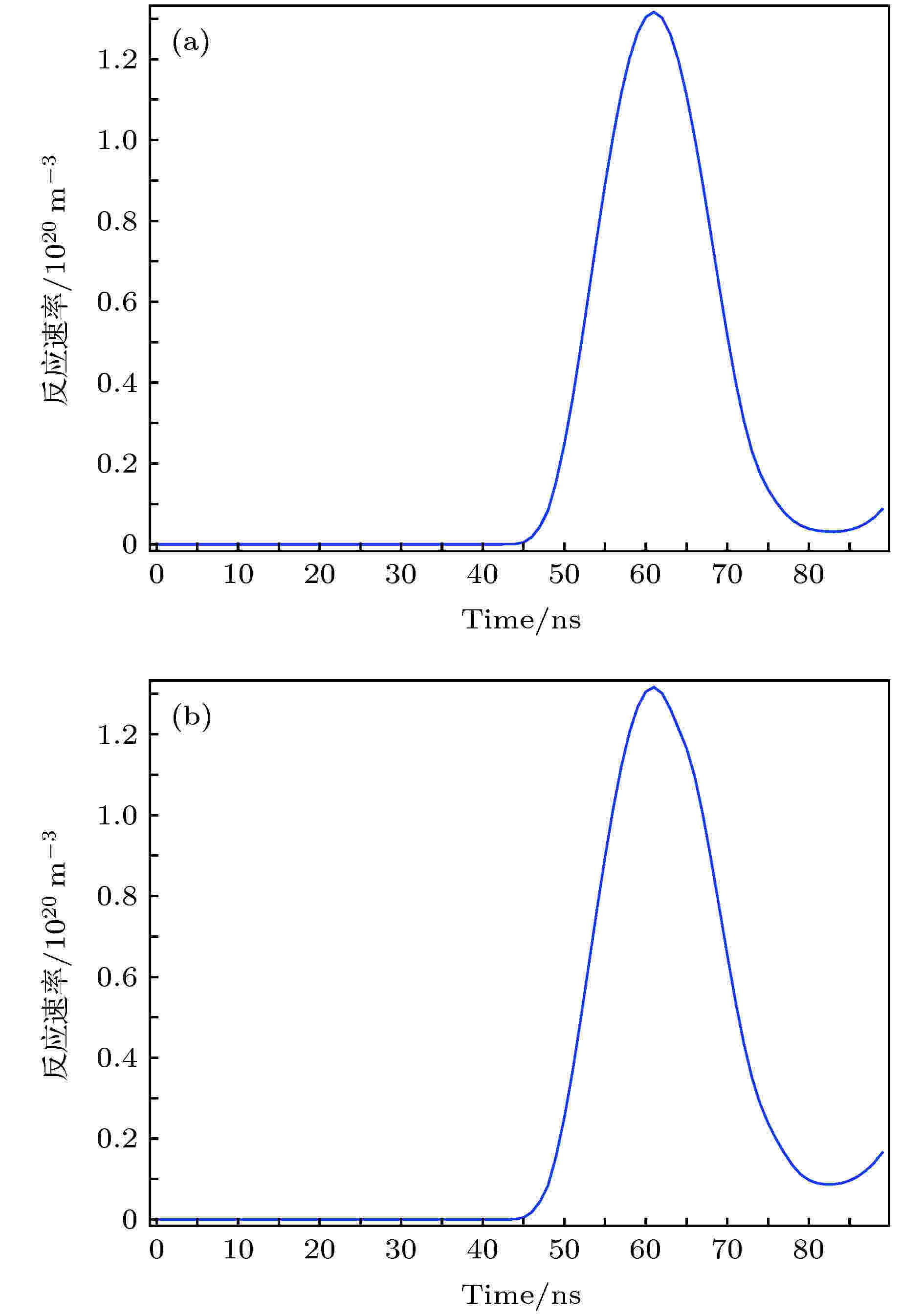 图 7 距离阴极0.2 cm处, 电子数密度随时间分布 (a) 不考虑光电离; (b)考虑光电离
图 7 距离阴极0.2 cm处, 电子数密度随时间分布 (a) 不考虑光电离; (b)考虑光电离Figure7. Waveforms of electron number density at 0.2 cm from cathode: (a) Considering photoionization; (b) without photoionization.
Ne作为缓冲气体时, Ne与电子反应生成的Ne*能够迅速与电子继续反应, 生成Ne2*, Ne2*可辐射出85 nm紫外激光, 单光子能量为14.6 eV. 在工作气体中加入微量的电离能较低的惰性杂质气体, 如Xe (电离能为12.1 eV)会被85 nm光子电离, 生成Xe+和自由电子, 即

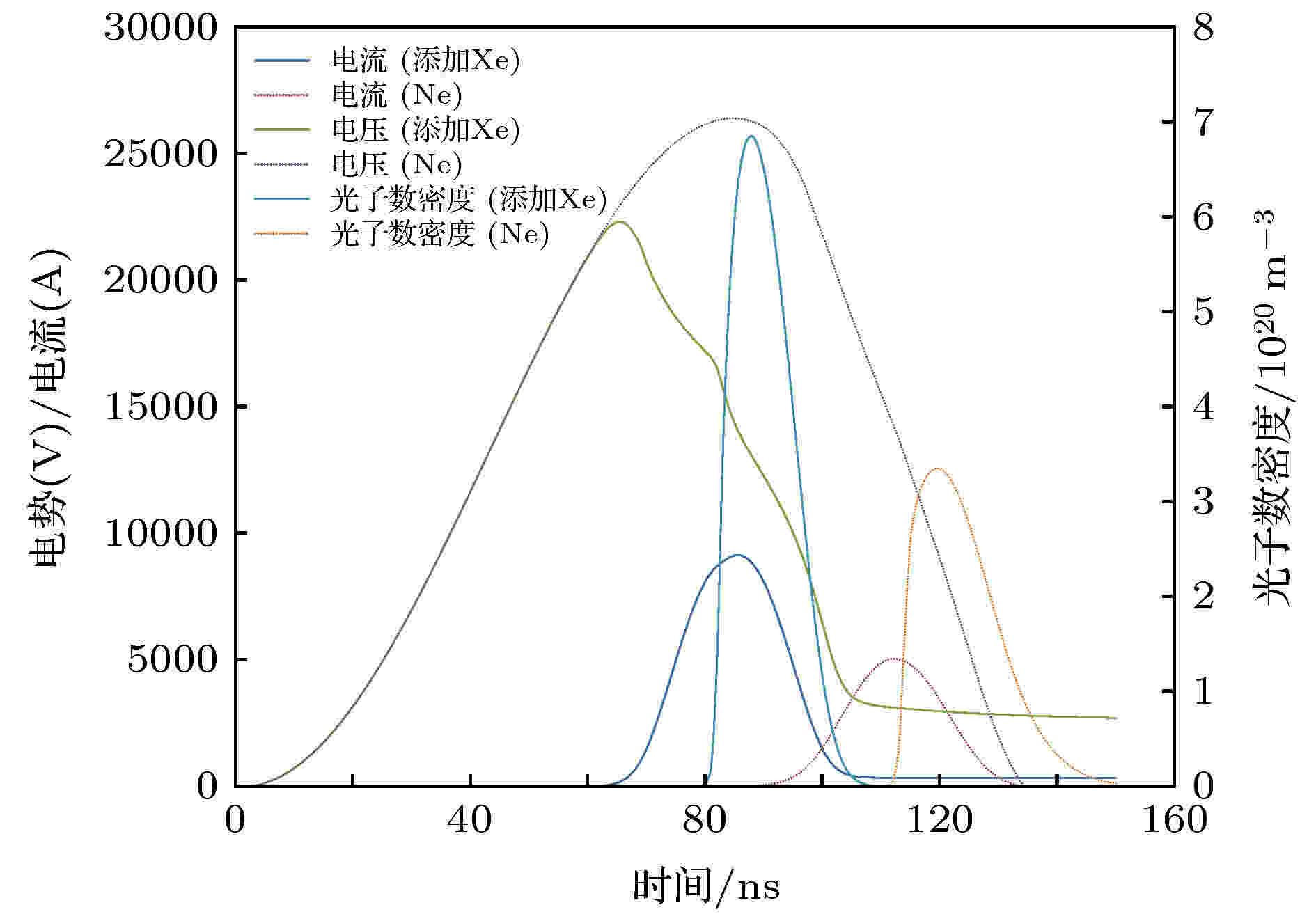 图 8 添加Xe与不添加Xe极板间电流、电压及光子数密度变化图
图 8 添加Xe与不添加Xe极板间电流、电压及光子数密度变化图Figure8. Waveforms of discharge voltage, current, and photon number density with and without Xe.
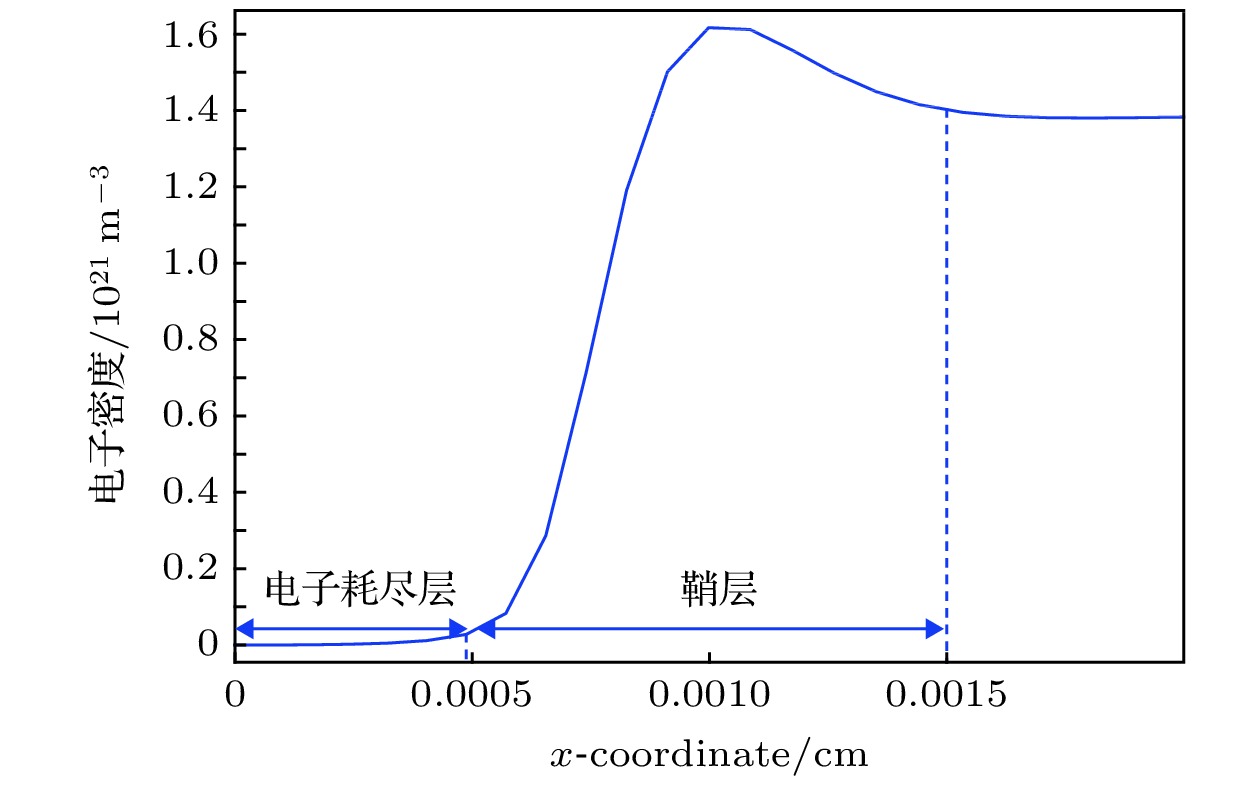 图 9 添加Xe后电子数密度空间分布
图 9 添加Xe后电子数密度空间分布Figure9. Waveforms of electron number density spatial distribution with Xe.
逐步增加杂质气体Xe的含量, 光子数密度变化情况如图10所示. 在一定范围内, 光子数密度随Xe含量的增加而增加, 放电时间逐步提前, 但当Xe含量达到8 × 10–6时, 光子数密度不再增加, 达到饱和状态.
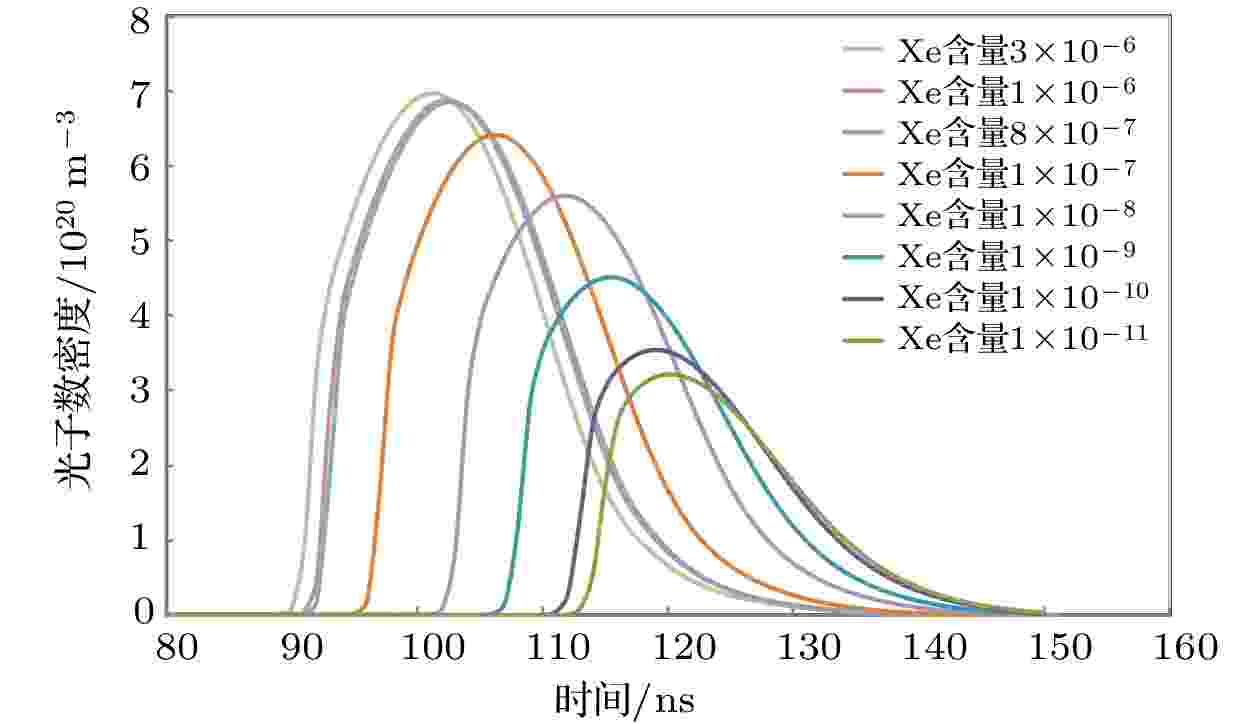 图 10 不同Xe含量光子数密度分布情况
图 10 不同Xe含量光子数密度分布情况Figure10. Waveforms of photon number density with different Xe ratios.
准分子激光器的放电-激光辐射过程非常复杂, 受到多种因素的影响, 本文仅围绕缓冲气体、光电离过程两个方面进行了分析研究. 后续研发工作中将更进一步开展准分子激光系统放电机理的研究, 将仿真模型从一维扩展到二维, 综合多物理因素耦合对准分子放电系统的影响.
