摘要: 本文实验上观察到在
85 Rb原子蒸气D1线系统中, 基于Raman共振的四波混频得到显著地增强; 并且通过模拟看到, 随着耦合光功率的减小或多普勒展宽的增大, 信号线宽呈现被压窄的趋势. 我们利用宏观极化干涉理论对光谱线宽的特点进行了分析, 并诠释了在多普勒增宽Λ-型能级系统中的四波混频与电磁感应透明均来源于受激Raman散射, 区别在于探测方式和对象的不同.
关键词: 受激Raman谱 /
四波混频 /
电磁感应透明 /
极化干涉 English Abstract Enhanced third-order nonlinear processes based on Raman resonance Pei Li-Ya College of Mathematics and Physics, Beijing University of Chemical Technology, Beijing 100029, China Received Date: 20 March 2020Accepted Date: 18 May 2020Available Online: 19 May 2020Published Online: 20 August 2020Abstract: We observe experimentally huge enhanced four-wave mixing based on Raman resonance in an 85 Rb atomic vapor system. With the decrease of coupling field power or the increase of experimental temperature, the signal tends to be narrowed down in linewidth, and be basically the same spectrum as the stimulated Raman spectroscopy. It is found that the macroscopic polarization interference effect plays a crucial role in determining the nonlinear spectra. Further more, in the Doppler-broadened Λ-type energy level system, there is a strong relationship among electromagnetically induced transparency, four-wave mixing and stimulated Raman spectroscopy. The sharp transparent window in electromagnetically induced transparency can be interpreted as the suppression of Raman gain on the linear absorption of the probe field. However, the four-wave mixing signal is a new field generated by the atomic vapor system, and it comes from the Raman gain which is affected and modified by the absorption and dispersion of the nonlinear optical medium. It shows that in a Λ-type Doppler-broadened system, in essence, both the electromagnetically induced transparency and enhanced four-wave mixing stem from stimulated Raman scattering based on the third-order nonlinear processes, just the spectra of which are from different ways and objects of detection.Keywords: stimulated Raman spectroscopy /four-wave mixing /electromagnetically induced transparency /polarization interference 全文HTML --> --> --> 1.引 言 自电磁感应透明(electromagnetically induced transparency, EIT)被提出[1 -3 ] 以来, 由于其在原子共振频率处光的吸收被减小甚至消除的特性, 人们认为利用EIT可以增强四波混频(four-wave mixing, FWM)等多波混频的非线性过程[4 -7 ] . 在均匀增宽系统中, 人们常以量子Fano干涉解释EIT的物理. 而在多普勒增宽系统中, 我们提出[8 -10 ] : EIT是一个线性吸收被共振受激拉曼谱(stimulated Raman spectroscopy, SRS)修正的过程, 其透明窗口的出现来自于Raman增益对线性吸收的补偿. 在此观点的基础上, 本文将进一步全新阐述在多普勒增宽Λ-型能级系统中FWM, EIT与SRS三者之间的本质关系. 实际上, Raman现象与FWM总是存在很强的关联. Jiang等[11 ] 提出了一种研究Raman增强非简并FWM的相敏方法. 在热铷蒸气中, Zibrov等[12 ] 演示了光场对由微波场诱导和维持的原子基态塞曼相干作用从而产生受激Raman散射引起的FWM过程. 而Liu等[13 ] 则在基于Raman驱动相干的高效FWM过程中, 实现和研究了多Raman增益共振. Carrasco-Sanz等[14 ] 报道了通过Raman放大增强的级联FWM产生参考频率梳的研究. 另一方面, Vanholsbeeck等[15 ] 给出了参量FWM影响受激Raman增益的完整实验表征. Michaud等[16 ] 在冷原子中实现了Raman增益与FWM的干涉. 而Silva等[17 ] 则是从理论上分析了高双折射光纤FWM过程中受激Raman散射的影响. 在前人的工作中, 也有与本文相关的研究. Romanov等[18 ] 通过在Rb85 中实现Raman吸收, 从而对Rb87 中产生的基于EIT的FWM信号进行抑制. Parniak等[19 ] 通过基态原子相干得到了Raman散射与FWM信号的强关联. 利用双Λ-型能级系统, Lee等[20 ] 实现了基于EIT的共振FWM的高转换效率. 利用Λ-型EIT系统进行光存储[21 ,22 ] 是近年来的重要研究方向, 而光信息的一次完整写入和读出可以看做是一个FWM过程.[8 ] , 我们来看一下建立Raman增益的过程. 对于Λ-型三能级系统, 当两束入射光场(探测光和耦合光)频率差等于${\omega _{\rm{R}}}$ (原子两基态能级之间的Raman共振频率)时, 在系统中首先形成两基态之间的Raman相干; 当此原子相干进一步与耦合光相互作用时, 就会在${\varDelta _1} = {\varDelta _2}$ 处散射出anti-Stoke光子, 这便是窄线宽Raman增益.[9 ] . 为了将上述Raman增益信号峰与泵浦吸收背底也能进行分离, 本文设计了一个非线性过程: 首先, 介质系统在探测光和耦合光这两束光作用下形成Raman相干, 但与其进一步作用的是线偏振方向偏转90o之后的耦合光, 为了区分称其为控制光. 最终, 得到与探测光偏振分离的Raman增益, 其经过介质之后相应的新光场即为FWM信号. 我们将看到, 在多普勒增宽Λ-型能级系统中的FWM过程被增强, 在本质上是由于Raman共振得到满足而非量子干涉. 同时, 我们提出: FWM与EIT作为两种完全不同的非线性效应, 在本质上均来源于受激Raman散射, 区别在于探测方式和对象的不同, 使其成为了完全不同的两种光谱. 由于在多普勒增宽系统中原子速度呈高斯形式分布, 单个原子的量子特性被淡化; 在一定条件下, 不同速度原子群之间宏观极化干涉成为了影响FWM光谱的主要因素.2.理 论 考虑如图1 所示的原子能级系统. 与之相互作用的耦合光场和控制光场, 分别记为$\mathop {{{{E}}_2}}\limits^{} = {\varepsilon _2}{{\rm{e}}^{ - {\rm{i}}({\omega _2} \cdot t - \mathop {{{{k}}_2}}\limits^{} \cdot \mathop {{r}}\limits^{} )}}$ (作用于态$ | 2\rangle $ 与$ |1 \rangle $ 之间)和$\mathop {{{{E}}_3}}\limits^{} = {\varepsilon _3}{{\rm{e}}^{ - {\rm{i}}({\omega _3} \cdot t - \mathop {{{{k}}_3}}\limits^{} \cdot \mathop {{r}}\limits^{} )}}$ (作用于态$ |2\rangle $ 与$ |1' \rangle $ 之间). 这里, 与不同线偏振方向的耦合光(‖)和控制光(⊥)分别相互作用的, 是两个不同的简并激发态能级, 分别记作$ |1 \rangle $ 和$ |1' \rangle $ 以便区分. 另外, 探测光场(‖)记为$\mathop {{{{E}}_1}}\limits^{} = {\varepsilon _1}{{\rm{e}}^{ - {\rm{i}}({\omega _{\rm{1}}} \cdot t - \mathop {{{{k}}_1}}\limits^{} \cdot \mathop {{r}}\limits^{} )}}$ (作用于态$ |0 \rangle $ 与$ |1 \rangle $ 或$ |1' \rangle $ 之间). 系统的原子跃迁频率记为${\varOmega _1}$ ($i = 1, 2, 3$ ), 与相应激光场频率的失谐可以记为${\varDelta _i} = {\varOmega _i} - {\omega _i}$ ($i = 1, 2, 3$ ). 图1 中, 原子两基态能级之间的Raman共振频率记为${\omega _{\rm{R}}}$ .图 1 85 Rb原子D1线能级系统Figure1. D1 line energy-level diagram of 85 Rb.${\rho _{00}} \approx 1, {\rho _{22}} \approx 0$ 近似条件下, 得到与SRS相关的三阶密度矩阵元, 其相应的极化强度如下:${G_i} = {{{{{\mu}} _i}{{{E}}_i}} / \hbar }$ ($i = 1, 2, 3$ )为光场与原子相互作用的耦合系数, 记${{{\mu}} _i}$ 为相应能级态之间的偶极矩阵元; 取近似${\varGamma _{21}} \approx {\varGamma _{10}}$ , 用${\varGamma _{10}}$ 和${\varGamma _{20}}$ 分别表示激发态与基态、以及两基态之间的横向弛豫率.图1 所示, 我们关注的是三个激光场(${\omega _1}, {\omega _2}, {\omega _3}$ )与原子介质相互作用产生的三阶非线性过程; 若其中两个入射场的频率满足${\omega _{\rm{R}}} = {\omega _1} - {\omega _2}$ 时, 在频率${\omega _{\rm{s}}}$ 处散射的信号就会被Raman共振增强.(1 )式表示, 在两束光(${\omega _2}, {\omega _3}$ )耦合下的弱光(${\omega _1}$ )探测系统, 包含了四个实质上的三阶非线性路径:${\omega _2} = {\omega _3}$ 时, 相应于以上四个路径产生的受激Raman散射光子的频率: A) ${\omega _{\rm{s}}} = {\omega _1} - {\omega _2} + {\omega _3}$ , B) ${\omega _{\rm{s}}} = {\omega _1} - {\omega _3} + {\omega _2}$ , C) ${\omega _{\rm{s}}} = {\omega _1} - {\omega _2} + {\omega _2}$ 和D) ${\omega _{\rm{s}}} = {\omega _1} - {\omega _3} \!+\! {\omega _3}$ , 均为${\omega _{\rm{s}}}\! =\! {\omega _1}$ . 同时, 前两个路径A和B产生的散射光子与探测光的偏振方向相互垂直[23 ] , 从而可以利用偏振分束器进行空间分离, 得到的是无背景的窄线宽FWM信号. 然而, 后两个路径C和D产生的散射光子, 因与探测光的偏振方向相同从而无法分离; 将上面的(1 )式与文献[8 ]中 (10)式[9 ] )进行补偿, 从而在探测光吸收谱的${\varDelta _1} = {\varDelta _2}$ 处(Raman共振增强)看到一个窄线宽的吸收减少, 亦即前人观察到的EIT现象[24 ] .$\rho _{00}^{(0)}\xrightarrow{{{G_1}}} \rho _{10}^{(1)}\xrightarrow{{G_2^*}}\rho _{20, \left| 1 \right\rangle }^{(2)}\xrightarrow{{{G_3}}}\rho _{{1'}0}^{(3)}$ , 其它路径的情况便不难给出. 对于该路径, 探测光(${\omega _1}$ )和耦合光(${\omega _2}$ )与原子介质相互作用会诱导产生基态|0>与|2>之间的原子Raman相干:1 )式可以得到与该路径相应的三阶非线性原子极化(用极点形式表示):3 )式的三个极点, 来看看基于Raman相干的三阶非线性过程. 首先从(2 )式看出, 两光场(探测光和耦合光)与原子介质相互作用会诱导产生基态$|0 \rangle$ 与$ |2 \rangle $ 之间的原子Raman相干${\rho _{20}}$ ; 当形成的原子相干进一步与控制光相互作用时, 就会在单光子共振(${\varDelta _1} = 0$ , 即极点${\varDelta _1} = {\rm{i}}{\varGamma _{10}}$ 的实部)处放出受激Raman散射光子, 也就是(1 )式的第一部分(即路径A)所表达的三阶非线性过程. 而在建立原子相干${\rho _{20}}$ 的过程中形成的缀饰态$\left| \pm \right\rangle $ , 亦会对${\varDelta _1} = {\varDelta _ \pm }$ (即极点${\tilde \varDelta _ \pm }$ 的实部)处的受激Raman散射光子产生吸收. 根据(4 )式, 当耦合光共振(${\varDelta _2} = 0$ )时, 系统的缀饰态位于${\varDelta _1} = \pm \sqrt {{{\left| {{G_2}} \right|}^2} + {{\left| {{G_3}} \right|}^2}}$ 处. 经原子系统产生的FWM信号, 其线宽与系统的吸收系数和色散系数均有关系.3.实 验 如图1 所示, 作用于85 Rb原子D1线$5{{\rm{S}}_{1/2}}, \;{ {F}} = 3 \to 5{{\rm{P}}_{1/2}}, \;{ {F}}' = 2$ 之间的是线偏振相互垂直的耦合光场ω 2 (‖)和控制光场ω 3 (⊥), 需注意的是: 在如图2 所示的实验装置中, 这两个光场来自同一台795 nm半导体激光器DL2, 其频率相等(${\omega _2}= {\omega _3}$ ). 作用于$5{{\rm{S}}_{1/2}}, \;{ {F}} = 2 \to 5{{\rm{P}}_{1/2}}, \;{ {F}}' = 2$ 之间的是水平偏振(‖)的弱探测光场${\omega _1}$ , 该光场来自另一台单独的795 nm半导体激光器DL1. 三束光经过一个偏振分束器合成一路后近似同向传播: 其中耦合光与控制光完全重合, 与探测光在Rb泡(长度75 mm; 室温27 ℃)中心处光斑重合然后以极小的角度分开; 三束光的光斑高斯直径均约为1.5 mm, 其均经过光纤以改良光斑质量. 在这里, 介质的多普勒展宽线宽大约为510 MHz. 我们在与探测光线偏振相互垂直的方向上检测到了窄线宽信号光(${\omega _{\rm{s}}}$ ); 并且若挡住耦合光或控制光时, 信号光均会消失. 实验过程中, 在介质之前利用斩波器对激光器DL2发出的光进行强度调制. 然后, 将经过Rb介质之后的探测光和产生的FWM信号光分别接到锁相放大器进行解调, 得到了高信噪比的探测光(${\omega _1}$ )吸收谱(多普勒展宽背底被滤除)和FWM(${\omega _{\rm{s}}}$ )光谱.图 2 实验装置简图. 其中, DL1和DL2: 半导体激光器; Chopper: 斩波器; PBS: 偏振分束器; PD: 光电探测器; LIA: 锁相放大器Figure2. Experimental setup. DL1 and DL2, diode lasers; PBS, polarizing beam splitter; PD, photodetector; LIA, lock-in amplifier.85 Rb的$5{{\rm{S}}_{1/2}}, {{F}} = 3 \to 5{{\rm{P}}_{1/2}}, {{F}}' = 2$ 原子跃迁线上, 即取${\varDelta _2} = 0$ , 以及正失谐350 MHz的频率处, 即取${\varDelta _2} = 350\;{\rm{MHz}}$ ; 扫描探测光频率, 并始终保持其光强较弱I 1 = 0.10 mW.图3(a) 和图3(b) 给出了两种耦合光失谐大小的情况下, 测得弱探测光吸收谱(I 1 ), 和另一个偏振方向上的FWM信号(I S ). 可以观察到一个共同的特征: 窄线宽FWM信号出现的位置(${\varDelta _1} = {\varDelta _2}$ ), 也是探测光透明窗口出现的位置. 同时, 与在耦合光共振条件下不同的是: 在耦合光失谐时, 探测光有一个从窄线宽的吸收减少(透明窗口)到吸收增强的过渡[10 ] . 根据上面的理论我们知道, 这是测量手段的不同导致的: FWM信号是非线性介质系统产生的新光场, 只有Raman正增益可以被检测到; 因在建立Raman相干过程中产生的缀饰态而引起的Raman损耗, 最多只能消耗相应频率处的散射光子, 而不能让信号强度为负值. 当然, 信号从产生到穿出介质其谱线必然受介质的色散修正.图 3 (a) 耦合光共振(${\varDelta _2} = 0$ )和(b) 耦合光失谐(${\varDelta _2} = 350\;{\rm{MHz}}$ )下的弱探测光吸收谱(黑色实线)和窄线宽FWM信号(红色实线). (注意: 实验中失谐条件下的信号较小, 这里为了看图清楚, 图(b)的光谱强度相应地均增大到实际强度的2.5倍)Figure3. Experimental results for the transmission intensity of the weak probe beam (black solid line) and the FWM signal with narrow linewidth (red solid line) as a function of Δ 1 : (a) Δ 2 = 0; (b) Δ 2 = 350 MHz. (Note that in order to see the details clearly, the spectral intensity in Fig. (b) is the result of magnification to 2.5 times the actual situation.)图3 可以看出, 除了探测光扫描到共振附近的窄线宽凸起峰, 在其它频率失谐处, FWM光谱强度基本是零. 检测到的是优良信噪比的FWM信号. 可以想到, 如果不在探测之前放置偏振分束器, 将得到: 四个路径产生的窄线宽SRS不会空间分离, 其均对探测光泵浦吸收进行补偿, 让探测光吸收谱呈现出窄线宽透明窗口.4.理论模拟与讨论 在前面的理论中, 研究了在均匀增宽系统中的Raman共振增强FWM. 而对于实验, 还要考虑介质的多普勒效应, 需将前面的失谐量分别替换如下:$W\left( v \right)$ 取高斯形式. 与FWM信号对应的系统非线性极化给出如下:I S )正比于${\left| {P_{\rm{T}}^{\rm{FWM}}} \right|^2}$ . 并且, (5 )式中的三阶非线性极化$P_{1({\rm{A}} + {\rm{B}})}^{}\left( v \right)$ 可以被表达如下:${\tilde v_1}$ 反映的是原子从激发态到基态$ | 0 \rangle $ 的跃迁, 极点${\tilde v_2}$ 反映的是原子与缀饰态$| \pm \rangle$ 的共振; 两个极点随着探测光的频率扫描而变化, 其各自的实部${v_1}$ 和${v_2}$ 分别是贡献(5 )式积分的主要部分, 这两个速度的原子群分别诱导产生受激Raman增益与Raman损耗.图4 所示, 任意选取了耦合光共振(${\varDelta _2} = 0$ )的情况进行了理论拟合(黑色-实线). 从图4 可以看出, 除了实验信号(红色-星星)有强度较弱且稳定的杂散光噪声背景之外, 在${\varDelta _1} = {\varDelta _2}$ 处出现的窄线宽FWM信号与理论拟合符合得非常地好.图 4 扫描弱探测光频率时, FWM实验信号(红色-星星)和理论拟合(黑色-实线). 实验采用的耦合光强度I 2 = 1.97 mW, 控制光强度I 3 = 7.4 mW; 理论模拟采用的参数是: ${\varGamma _{10}} = 7.2\;{\rm{MHz}}$ , ${\varGamma _{20}} = 0.72\;{\rm{MHz}}$ , ${G_2} = 10.8\;{\rm{MHz}}$ , ${G_3} = 20.4\;{\rm{MHz}}$ )Figure4. Experimental results (red star) and theoretical fitting (black solid line) for the FWM signal. The coupling field intensity I 2 = 1.97 mW and the control field intensity I 3 = 7.4 mW are used in the experiment. The parameters used in the theoretical simulation are ${\varGamma _{10}} = 7.2\;{\rm{MHz}}$ , ${\varGamma _{20}} = 0.72\;{\rm{MHz}}$ , ${G_2} = 10.8\;{\rm{MHz}}$ , ${G_3} = 20.4\;{\rm{MHz}}$ .图5(a) 和图6(a) 模拟了耦合光共振(${\varDelta _2} = 0$ )条件下的FWM光谱(实线)和SRS光谱(虚线), 在图5(a) 中$ku/\gamma =50.7$ , ${G_2}/\gamma =0.5$ (黑线), 2.5(红线), 4.0(蓝线); 在图6(a) 中${G_2}/\gamma = 4.0$ , $ku/\gamma =50.7$ (黑线), 101.4(红线), 202.8(蓝线). 其中, γ 为激发态与基态之间的纵向弛豫率. 从图5(a) 和图6(a) 可以看出, 随着耦合光强度(I 2 )增大或多普勒展宽线宽(ku) 减小, FWM光谱线宽会相对变宽. 同时, 由于FWM光谱经过了色散的修正, 其相对SRS光谱来说线宽略宽. 但当耦合光强度越小或多普勒展宽线宽越大时, 两种谱线线宽越趋于基本一致, 这是由于此种条件下: 在${\varDelta _1} = {\varDelta _2} = 0$ 处, 色散变化越陡峭[24 ] , 其对受激Raman散射光穿出介质的线宽修正影响越小.图 5 变化耦合光强度(I 2 )条件下的(a)FWM光谱(实线)和SRS光谱(虚线), 和(b)原子共振速度${v_2}/u$ (实线)和${v_1}/u$ (虚线). 所取理论参数为: ${G_2}/\gamma =0.5$ (黑线), 2.5(红线), 4.0(蓝线)Figure5. (a) FWM (solid line) and SRS (dotted line), and (b) corresponding resonant velocities ${v_2}/u$ (solid line) and ${v_1}/u$ (dotted line) as a function of ${\varDelta _1}/\gamma$ when ${G_2}/\gamma = 0.5$ (black), 2.5(red), 4.0(blue).图 6 变化多普勒展宽线宽(ku )条件下的(a) FWM光谱(实线)和SRS光谱(虚线), 和(b) 原子共振速度${v_2}/u$ (实线)和${v_1}/u$ (虚线). 所取理论参数为: $ku/\gamma =50.7$ (黑线), 101.4(红线), 202.8(蓝线)Figure6. (a) FWM (solid line) and SRS (dotted line), and (b) corresponding resonant velocities ${v_2}/u$ (solid line) and ${v_1}/u$ (dotted line) as a function of ${\varDelta _1}/\gamma$ when $ku/\gamma =$ 50.7 (black), 101.4(red), 202.8(blue).${\varDelta _2} = 0$ 时, 共振速度${v_1}$ 和${v_2}$ 对探测光频率的依赖特性, 如图5(b) 和图6(b) 所示. 当${\varDelta _1} = 0$ 时(即在${\omega _1} - {\omega _2} = {\omega _R}$ 处), $\left| {{v_2}/u} \right| \to \infty $ , 即在多普勒展宽线宽内只存在共振速度${v_1}$ , 具有该速度的原子群发射基于Raman共振增强的散射光子, 从而在${\varDelta _1} = {\varDelta _2}$ 处出现信号峰, 如图5(a) 和图6(a) 所示(实线). 当${\varDelta _1}$ 远离${\varDelta _1} = {\varDelta _2}$ , 即探测光远离共振时, 得到${v_1} \simeq {v_2} \simeq 0\;$ , 而这两个速度的原子群分别贡献散射光子和损耗散射光子, 从而相互抵消使得信号趋于零. 而在${\varDelta _1}$ 偏离${\varDelta _1} = {\varDelta _2}$ 的过程中, 当${v_2} \simeq u$ 时, 共振速度${v_2}$ 的原子群便可以有效消耗共振速度${v_1}$ 的原子群贡献的散射光子, 此时探测光频率扫描到${\varDelta _1} = ( {{{|{{G_2}} |}^2} + {{| {{G_3}} |}^2}})/ku$ ; 从图5(b) 和图6(b) (实线)亦可看出, 当耦合光强度(${\left| {{G_2}} \right|^2}$ )减小或多普勒展宽($ku$ )增宽时, 探测光扫描到较小失谐${\varDelta _1}$ 处, 共振速度${v_2}$ 就能有效地消耗受激Raman散射光子让信号迅速衰减, 从而使得最终的信号线宽较窄. 这就解释了图5(a) 和图6(a) 中呈现的FWM信号线宽的特点. 从上述分析可以看出, 与缀饰态共振的速度${v_2}$ , 起到了对共振速度${v_1}$ 贡献的Raman增益线宽进行压窄的作用, 并且FWM光谱线宽${\varGamma _{\rm{FWM}}} \propto ({{{| {{G_2}} |}^2} + {{| {{G_3}} |}^2}} )/ku$ .5.结 论 本文承接前期的工作, 基于对EIT现象提出的新诠释, 进一步阐明了在多普勒增宽Λ-型能级系统中EIT和SRS以及FWM三者之间的关系: 共振EIT吸收光谱的透明窗口, 本质上是基于三阶非线性过程产生的Raman增益对介质线性吸收修正之后的呈现; 而FWM信号之所以被增强, 并不是因为前人提出的EIT的本质---量子干涉, 而是因为相干Raman共振得到了满足. 在本质上, Λ-型能级系统中的FWM信号与EIT透明窗口均是基于受激Raman过程, 区别仅在于探测手段的不同. 通过理论模拟得到, 在耦合光强度相对较小或多普勒展宽较大时, 介质色散对FWM信号线宽的修正可以忽略, 就可以用不同速度原子群之间的宏观极化干涉, 来解释基于非线性过程最终的光谱呈现. 在耦合光共振(${\varDelta _2} = 0$ )条件下, 与缀饰态共振的速度${v_2}$ , 由于在偏离单光子共振的过程中越来越有效的起到消耗光子的作用, 从而对共振速度${v_1}$ 在以${\varDelta _1} = 0$ 为中心的频率处贡献的Raman增益的线宽进行压窄, 使得在双光子共振${\varDelta _1} = {\varDelta _2}$ 处看到窄线宽的凸起峰---FWM信号. 并且, 耦合光强度相对越小或多普勒展宽越大时, FWM信号的线宽越窄. 
































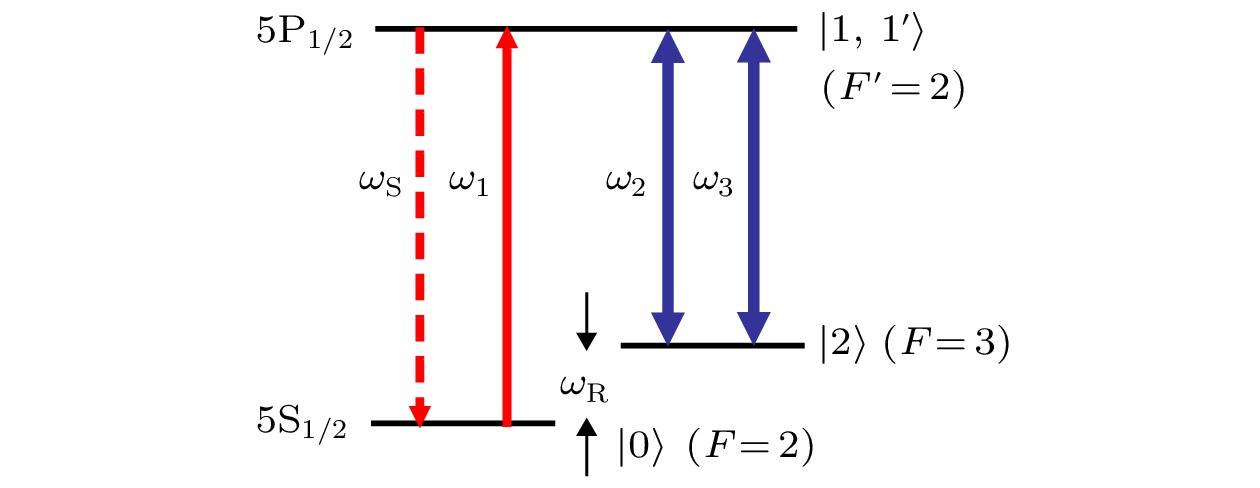 图 1 85Rb原子D1线能级系统
图 1 85Rb原子D1线能级系统













































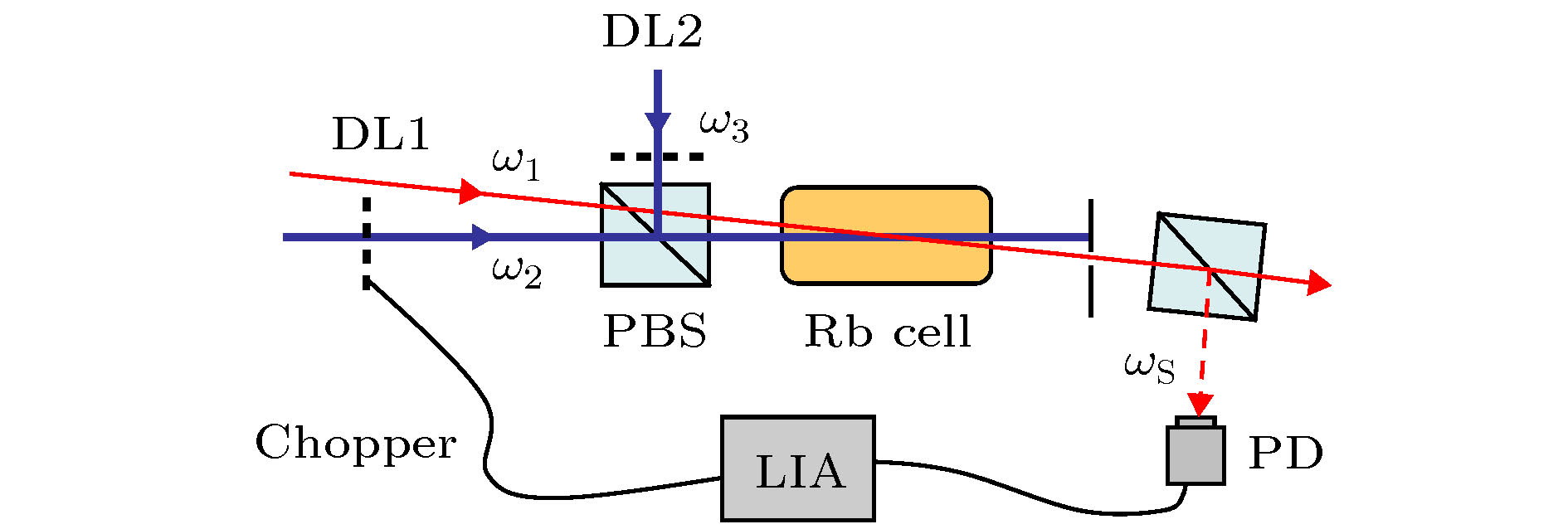 图 2 实验装置简图. 其中, DL1和DL2: 半导体激光器; Chopper: 斩波器; PBS: 偏振分束器; PD: 光电探测器; LIA: 锁相放大器
图 2 实验装置简图. 其中, DL1和DL2: 半导体激光器; Chopper: 斩波器; PBS: 偏振分束器; PD: 光电探测器; LIA: 锁相放大器



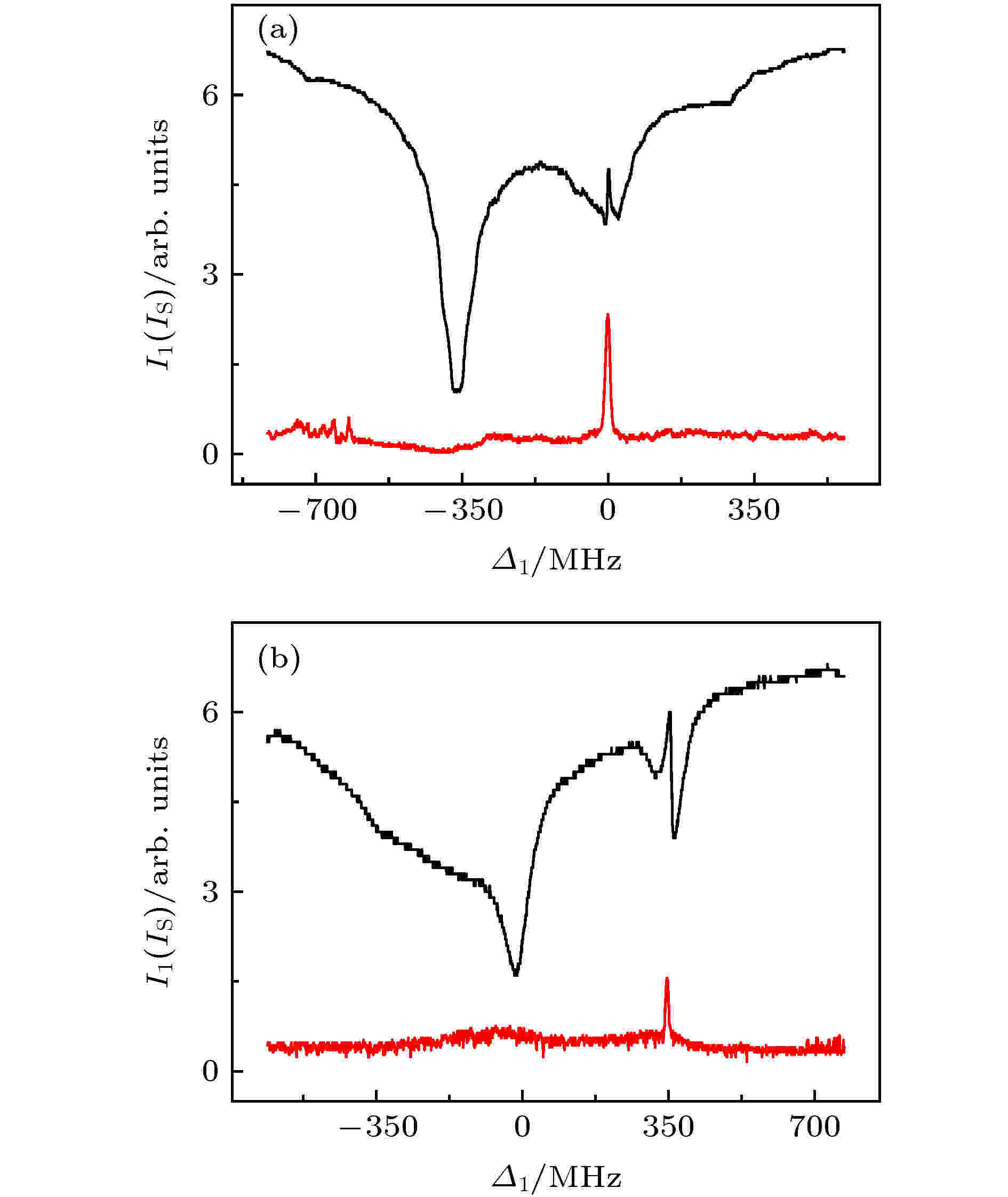 图 3 (a) 耦合光共振(
图 3 (a) 耦合光共振(












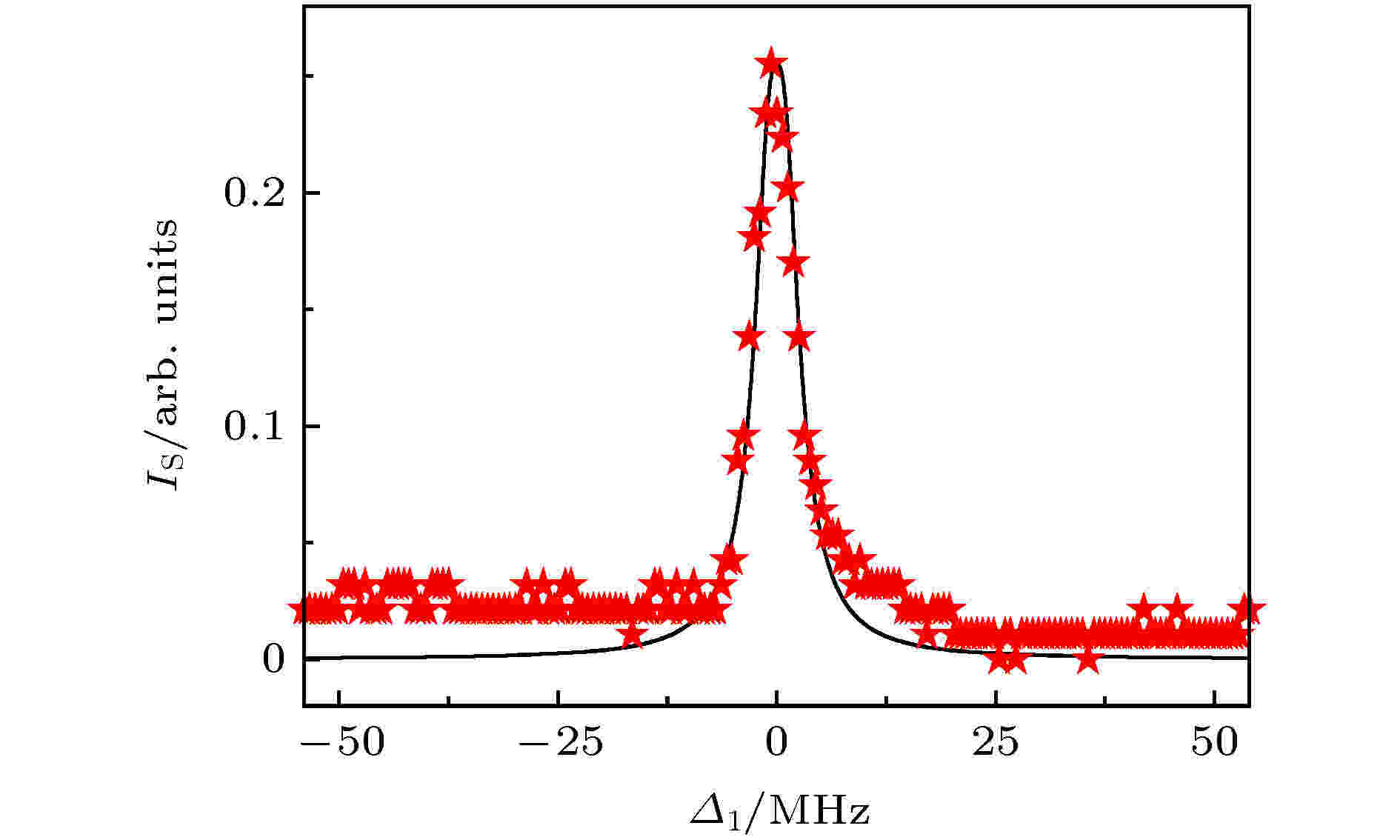 图 4 扫描弱探测光频率时, FWM实验信号(红色-星星)和理论拟合(黑色-实线). 实验采用的耦合光强度I2 = 1.97 mW, 控制光强度I3 = 7.4 mW; 理论模拟采用的参数是:
图 4 扫描弱探测光频率时, FWM实验信号(红色-星星)和理论拟合(黑色-实线). 实验采用的耦合光强度I2 = 1.97 mW, 控制光强度I3 = 7.4 mW; 理论模拟采用的参数是: 















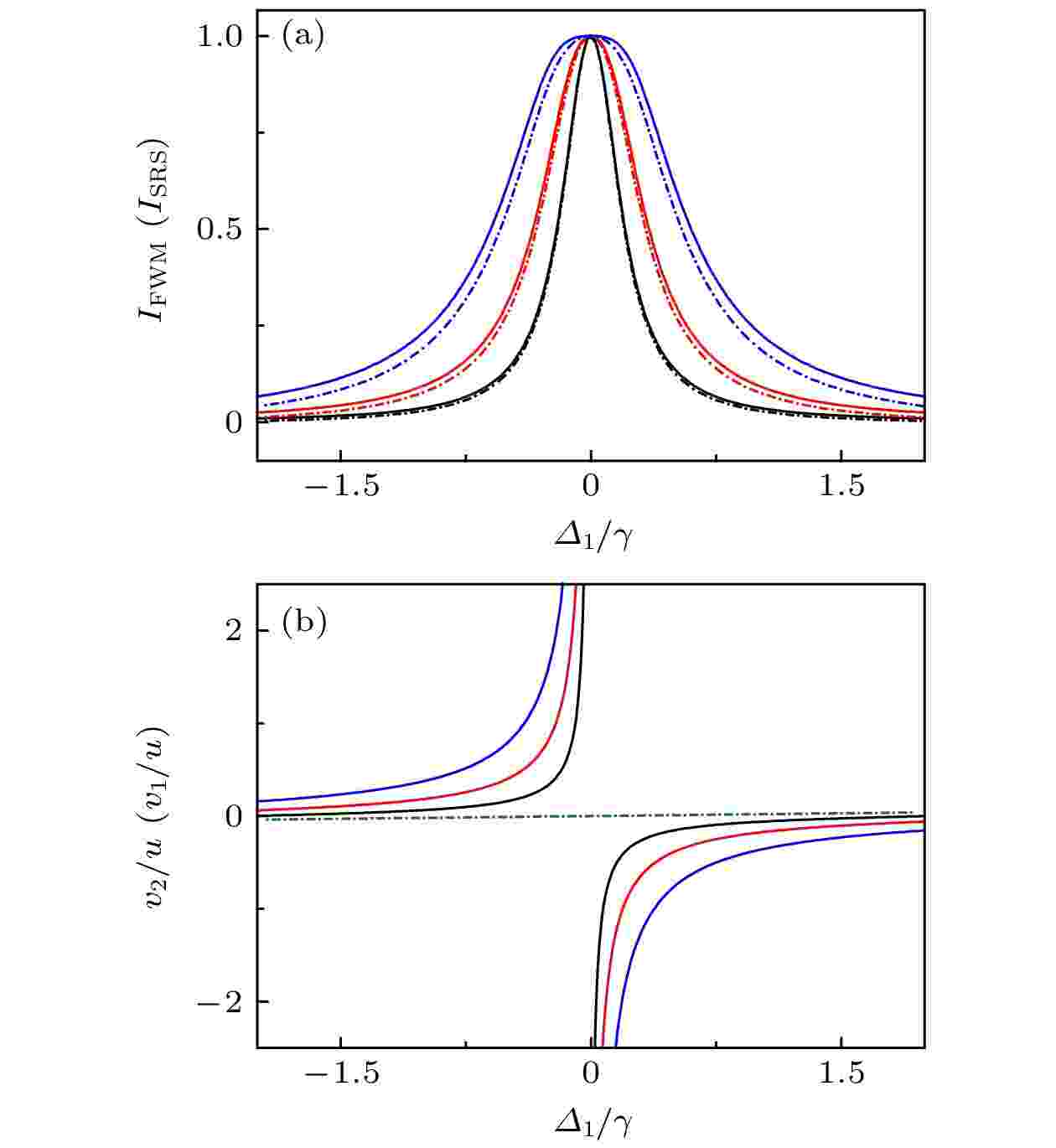 图 5 变化耦合光强度(I2)条件下的(a)FWM光谱(实线)和SRS光谱(虚线), 和(b)原子共振速度
图 5 变化耦合光强度(I2)条件下的(a)FWM光谱(实线)和SRS光谱(虚线), 和(b)原子共振速度






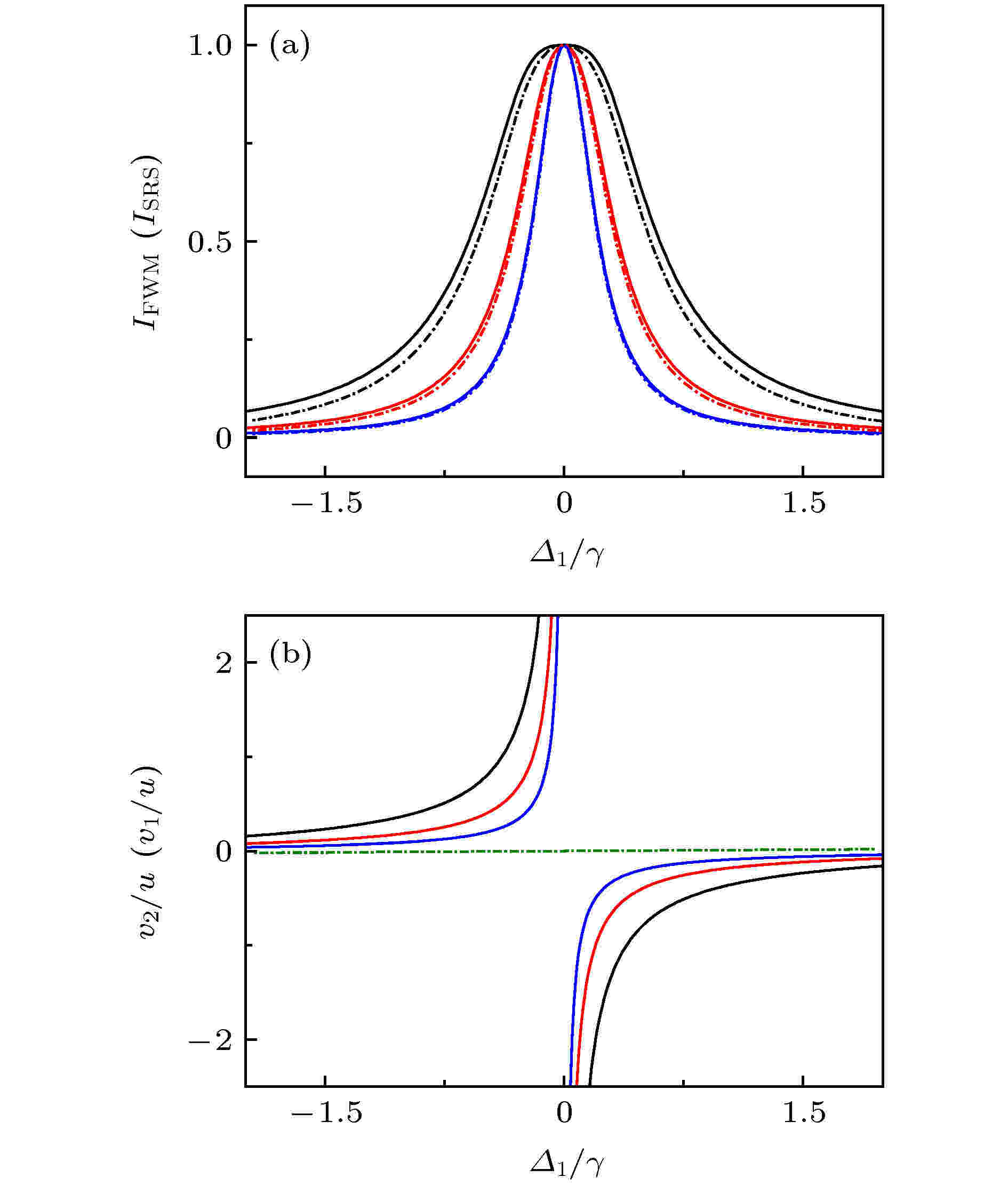 图 6 变化多普勒展宽线宽(ku)条件下的(a) FWM光谱(实线)和SRS光谱(虚线), 和(b) 原子共振速度
图 6 变化多普勒展宽线宽(ku)条件下的(a) FWM光谱(实线)和SRS光谱(虚线), 和(b) 原子共振速度







































































