全文HTML
--> --> -->国内外许多****已经对方腔内纳米流体自然对流现象进行了研究. 例如: 李新芳和朱冬生[2]采用CFD方法对影响纳米流体强化传热的因素进行了分析, 结果表明, 随着纳米颗粒体积分数的增大, 流体的能量传输得到强化. 张晶等[3]采用4种不同的粘度模型计算纳米流体粘度, 并对二维U型腔内Al2O3-H2O纳米流体的自然对流换热进行了数值模拟. Khanafer等[4]数值模拟研究了二维方形腔内的纳米流体自然对流换热, 结果表明, 随着纳米颗粒体积分数的增加, 热效率增强. Hatami[5]采用有限元方法研究了不同纳米流体(TiO2和Al2O3)在加热肋片的矩形腔内的自然对流问题, 结果表明, 随着体积分数的增大, 虽然Al2O3-H2O纳米流体在热肋片处Nuave数缓慢增大, 但是TiO2-H2O纳米流体在热肋片处Nuave数先增大后减小. Chen和Du[6], Selimefendigil 和Oztop[7], Hatami[8]研究了纳米流体在方腔内的自然对流换热, 结果表明, 随着Ra数的增加, 传热速率得到提高. Jahanshahi等[9]采用瞬态热线法和哈密顿模型得到了不同体积分数下的流体导热系数, 分别研究了SiO2-H2O纳米流体在热壁面处不同Ra数下Nuave数随体积分数增加的变化趋势, 结果表明采用哈密顿模型计算得到的Nuave数呈现轻微减小的趋势.
多孔介质中的自然对流与换热问题普遍存在于自然界和工业应用中, 得到了****们的广泛研究. 目前, 对于封闭多孔介质腔体内自然对流的研究大致可以分为两大类: 一类为通过水平多孔介质层的传热问题, 特别是水平多孔层存在高低温壁面, 即经典的Benard流动问题[10], 另一类是具有两个不同温度的垂直壁面以及两个绝热的水平壁面的多孔介质传热问题[11]. Lan和Prakash等[12]采用Darcy-Brinkman-Forchheimer (DBF) 模型探究了不同达西数、Ra数和毕渥数下达西和非达西流体的流动机制. Kaluri和Basak[13]研究了二维多孔介质方腔内纳米流体的自然对流换热问题. Alsabery等[14]研究了倾斜方腔多孔层内纳米流体的自然对流问题, 结果表明施加较小的倾斜角可以显著提高壁面的Nuave数. Toosi和Siavashi[15]对二维多孔介质腔内纳米流体自然对流现象进行了数值模拟, 结果表明同时采用多孔介质和纳米流体可以获得最佳的传热性能. 相比于均匀受热的边界条件, 近年来, ****们对于壁面处于非均匀温度加热的研究不断增多. Wu等[16]采用非达西模型的多孔介质控制方程, 分析了左右壁面均为正弦温度分布的自然对流传热特性. Basak等[17]对比了多孔介质方腔内均匀边界条件和非均匀边界条件影响下自然对流强弱的变化情况, 研究指出, 底部中心加热壁面处为非均匀温度分布时, 换热效率更高. 前面的研究主要分析纯流体的自然对流问题, 由于纳米流体具有强化传热特征, 考虑纳米颗粒影响的多孔介质方腔内自然对流的研究同样受到一些****的关注. 比如: Ghasemi和Siavashi[18]采用LBM方法研究了不同线性温度分布的边界条件对多孔介质内纳米流体换热效率的影响. 此外, Sivasankaran[19]利用交替方向隐式的有限差分方法分析了下壁面为非均匀温度分布的倾斜多孔介质方腔内Cu-H2O纳米流体的自然对流问题, 发现在Ra = 103时Nuave数随纳米颗粒体积分数的增加而减少.
综上所述, 以往研究表明纳米流体在多孔介质方腔内具有强化作用, 但是对于不同边界条件和计算模型, 其流动和换热过程表现出不同结论, 有的结果表现为强化换热效果[20], 有的则表现为削弱换热作用[21]. 值得注意的是, 非均匀温度边界条件对倾斜多孔介质方腔内的纳米流体流动与传热过程产生了重要影响. 与此同时, 由于Al2O3纳米颗粒在分散系中化学性质较为稳定且价格低廉, 故被广泛应用于工业强化传热领域中, 因此, 本文对非均匀温度边界条件下倾斜多孔介质方腔内Al2O3-H2O纳米流体自然对流进行数值模拟, 分析了


2.1.物理模型
本文主要研究多孔介质方腔内纳米流体的自然对流问题. 如图1所示, 方腔内纳米流体受到重力场的作用, 其下壁面与水平方向的夹角为γ, 左壁面温度分布为
 图 1 物理模型示意图
图 1 物理模型示意图Figure1. Schematic diagram of the physical model.
2
2.2.无量纲控制方程
基于上述基本假设, 本文采用DBF模型, 对多孔介质方腔内纳米流体的自然对流问题模型的无因次形式的连续性方程、动量方程和能量方程进行描述[22]:
相应地, 无因次边界条件由以下表达式来确定:
上壁面: Y = 1
2
2.3.纳米流体的物性参数
本文所研究的纳米流体是在基液水中加入一定体积分数的Al2O3纳米颗粒而形成的悬浮液. 假设纳米流体中的水和Al2O3处于热平衡状态, 并且纳米颗粒为球形结构且均匀分布在基液中, 不存在纳米颗粒的团聚和沉淀现象. 表1所示为基液、Al2O3纳米颗粒和多孔介质的物性参数.| 物性参数 | H2O | Al2O3 | Glass fiber[23,24] |
| ρ/kg·m–3 | 997.1 | 397 | 1650 |
| Cp/J·kg–1·K–1 | 4179 | 765 | 750 |
| k/W·m–1·K–1 | 0.613 | 25 | 1.2 |
| β/K–1 | 21 × 10–5 | 1.89 × 10–5 | — |
| ds/nm | — | 47 | — |
表1H2O, Al2O3和玻璃纤维的热物理性质
Table1.Thermophysical properties of water, Al2O3 and glass fibers.
利用这些已知的热物性参数, 可以得到不同体积分数以及不同孔隙率下系统内的热物性参数[25,26], 具体计算公式如表2所示:
| 热物性参数 | 计算表达式 |
| 纳米流体粘度 | $\mu {}_{nf} = \dfrac{{{\mu _f}}}{{{{\left( {1 - \phi } \right)}^{2.5}}}}$ |
| 纳米流体密度 | ${\rho _{nf}} = \left( {1 - \phi } \right){\rho _f} + \phi {\rho _s}$ |
| 纳米流体热容 | ${\left( {\rho {C_p}} \right)_{nf}} = \left( {1 - \phi } \right){\left( {\rho {C_p}} \right)_f} + \phi {\left( {\rho {C_p}} \right)_s}$ |
| 纳米流体热扩散系数 | ${\alpha _{nf}} = \dfrac{{{k_{nf}}}}{{{{\left( {\rho {C_p}} \right)}_{nf}}}}$ |
| 纳米流体热膨胀系数 | ${\left( {\rho \beta } \right)_{nf}} = \left( {1 - \phi } \right){\left( {\rho \beta } \right)_f} + \phi {\left( {\rho \beta } \right)_s}$ |
| 纳米流体导热系数 | ${k_{nf}} = \dfrac{{{k_p} + 2{k_f} - 2\left( {{k_f} - {k_p}} \right)\phi }}{{{k_p} + 2{k_f} + 2\left( {{k_f} - {k_p}} \right)\phi }}{k_f}$ |
| 多孔介质有效 导热系数 | ${k_m} = \left( {1 - \epsilon} \right){k_p} + {\epsilon k_{nf}}$ |
表2纳米流体的热物性参数计算公式
Table2.Calculation formula for thermodynamic properties of nanofluids.
为描述热壁面处自然对流强度, 本研究组分析了壁面处局部Nu数和Nuave数, 其计算公式分别为[26]

| 不同网格数下的Nuave数 | ||||
| 80 × 80 | 100 × 100 | 120 × 120 | 140 × 140 | |
| Nuave数 | 8.528 | 8.670 | 8.744 | 8.785 |
| 误差/% | 3.39% | 1.70% | 0.83% | 0.36% |
表3不同网格数与文献[33]的Nuave数比较
Table3.Comparison of Nuave number with literature[33] in different grids number.
为了进一步验证所采用LBM的可行性, 对二维方腔内的自然对流问题进行数值模拟, 其中, 方腔上下壁面为绝热壁面, 左壁面为高温壁面, 右壁面为低温壁面, 流体在固体壁面处无滑移. 首先验证忽略多孔介质的影响, 即

| Ra数 | 文献[27] | 本文结果 | 误差/% |
| 103 | 1.116 | 1.123 | 0.63 |
| 104 | 2.238 | 2.266 | 1.25 |
| 105 | 4.509 | 4.556 | 1.04 |
| 106 | 8.817 | 8.744 | 0.83 |
表4本文与文献[33]的Nuave数值结果的比较
Table4.Comparison of Nuave number with previous literature[33].
其次, 考虑多孔介质的影响, 采用DBF模型进行数值模拟计算. 在模拟过程中保持

| NO. | Da数 | Ra数 | 文献[34] | 本文结果 | 误差/% |
| 1 | 10–2 | 104 | 1.530 | 1.497 | 2.16 |
| 2 | 10–2 | 105 | 3.555 | 3.441 | 3.09 |
| 3 | 10–2 | 5 × 105 | 5.740 | 5.694 | 0.87 |
表5本文与文献[34]的Nuave数值结果的对比
Table5.Comparison of Nuave number with previous literature[34].
4.1.孔隙率$ \epsilon $
对方腔内流动换热的影响
本文数值模拟了多孔介质方腔内Al2O3-H2O纳米流体的自然对流问题, 分析了不同物理参数对纳米流体换热效率的影响. 在模拟过程中, 无量纲参数的选取为Da = 0.01, ? = 0.01, Ra = 105, Pr = 6.2, 

由于孔隙率与多孔介质渗透率有关, 它的大小会影响多孔介质方腔内纳米流体的流动状态和传热效率. 如图2所示, 当
















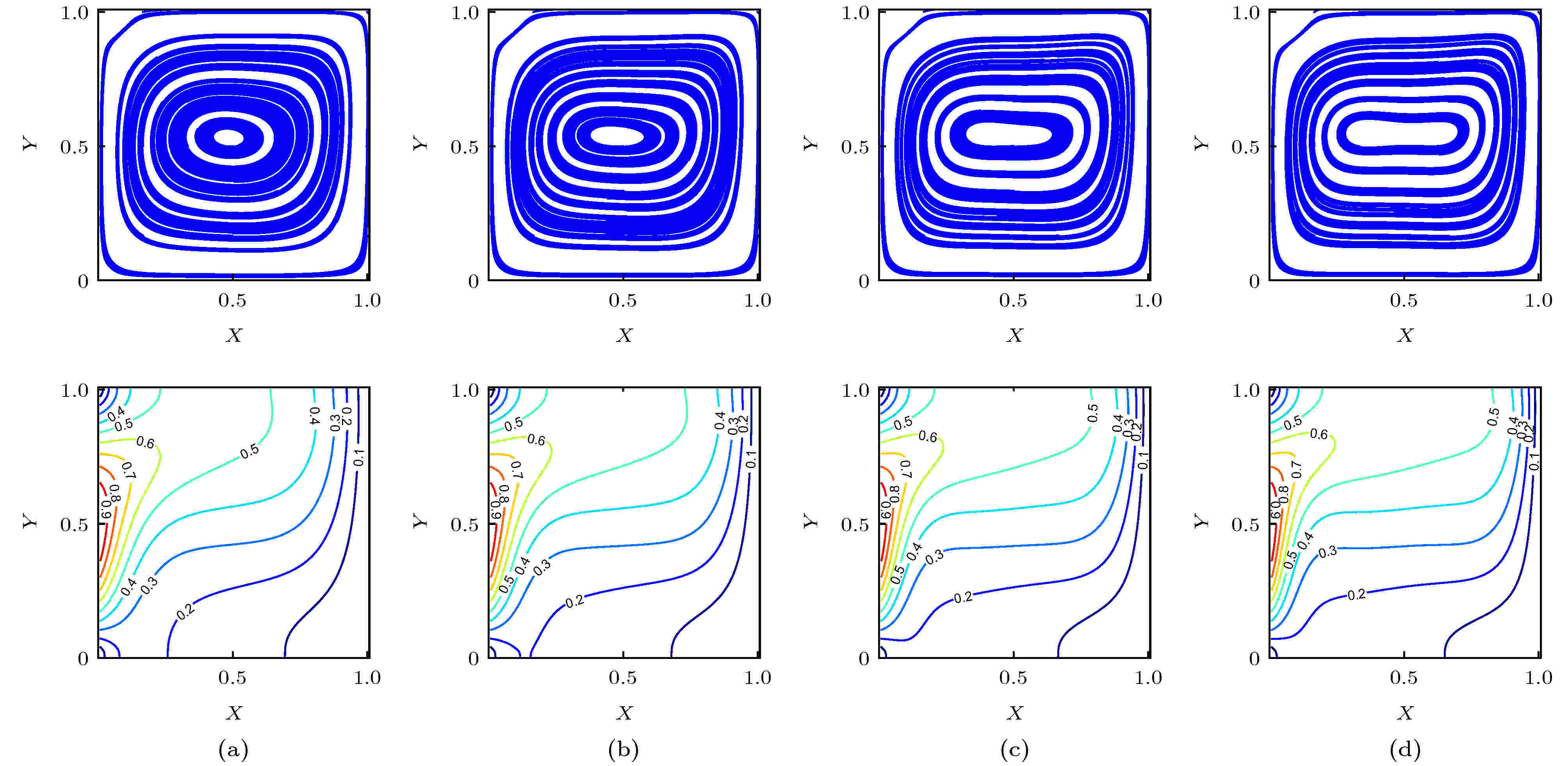 图 2 不同
图 2 不同
















Figure2. Streamlines, isotherms contours for different

























为了分析孔隙率对流体流速的影响, 本研究组还比较了不同

 图 3 (a)不同
图 3 (a)不同
Figure3. (a) Vertical velocity distribution at X = 0; (b) horizontal velocity distribution at Y = 1 for different

如图4(a)所示, 随着孔隙率的增大, Nuave数呈现上升趋势, 然而这种增长幅度逐渐减弱, 这一变化规律与以往均匀温度分布所得的结论相符[35]. 这是由于在较高孔隙率的情况下, 方腔内部多孔介质的阻碍作用较小, 孔隙率对方腔内传热效率的提升不明显. 为了进一步分析孔隙率对热壁面附近局部换热特性的影响, 本研究组还分析了热壁面处的局部Nu数随孔隙率变化的情况, 如图4(b)所示, 热壁面0.2 < Y < 0.6为主换热区域, 不同孔隙率之间的变化差异并不明显. 与此同时, 在热壁面0.6 < Y < 0.8, 随着

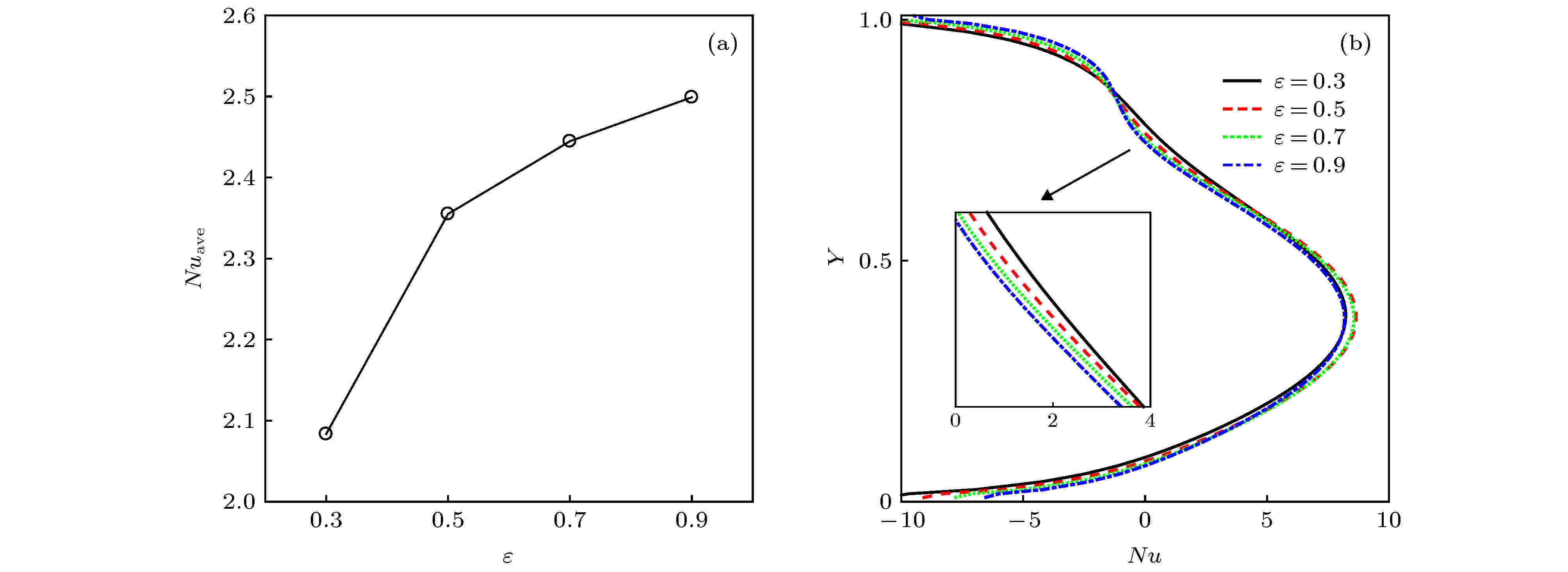 图 4 (a)不同
图 4 (a)不同
Figure4. (a) At the heated wall Nuave number; (b) local Nu number for different

2
4.2.Ra数对方腔内自然对流的影响
在自然对流问题中, Ra数是表征自然对流综合强弱的重要无量纲准则数, 为了研究Ra数对方腔内自然对流的影响, 保持
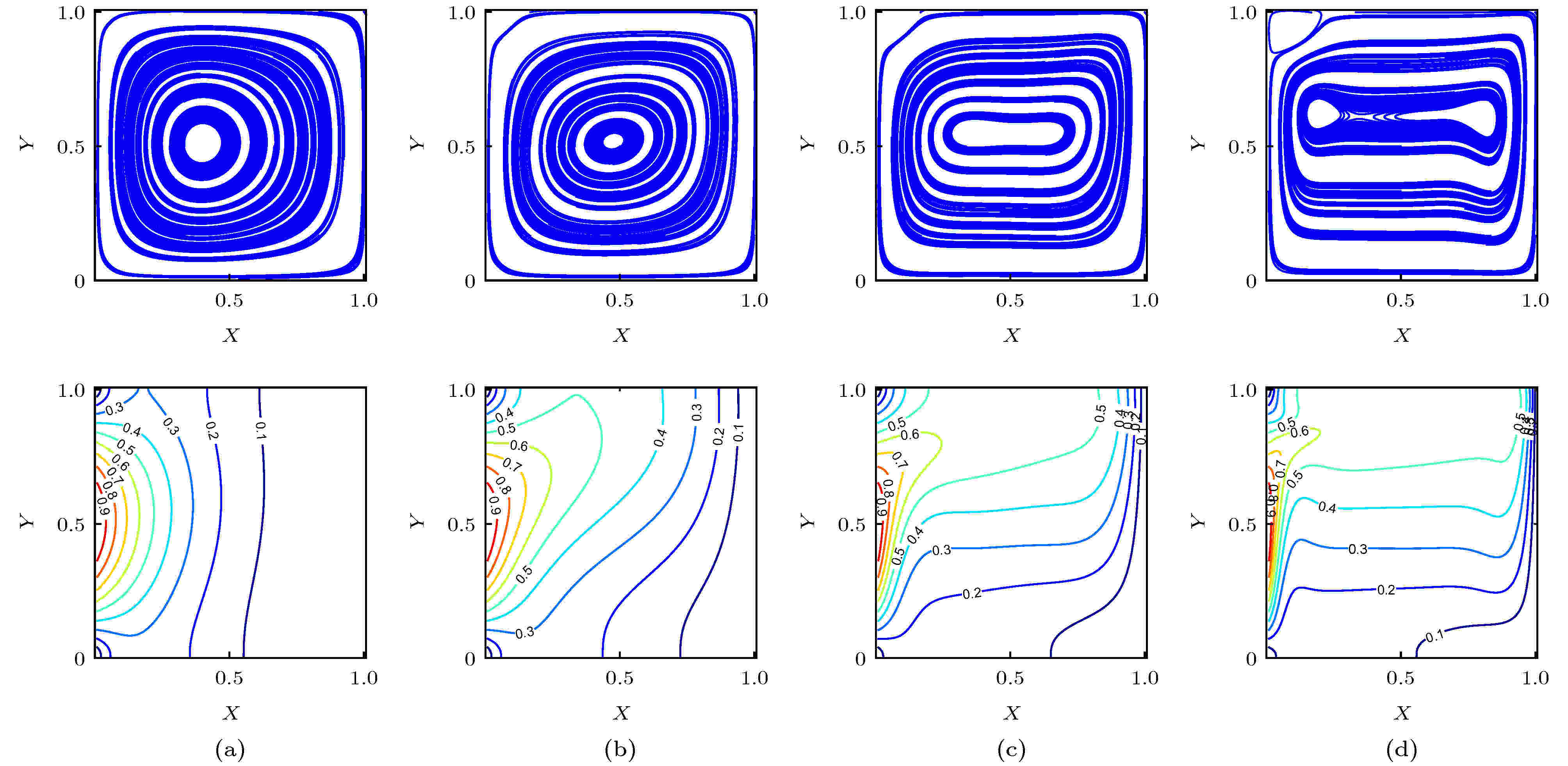 图 5 不同Ra下温度场和流场的分布图像 (a) Ra = 103; (b) Ra = 104; (c) Ra = 105; (d) Ra = 106
图 5 不同Ra下温度场和流场的分布图像 (a) Ra = 103; (b) Ra = 104; (c) Ra = 105; (d) Ra = 106Figure5. Streamlines, isotherms contours for different Ra number: (a) Ra = 103; (b) Ra = 104; (c) Ra = 105; (d) Ra = 106.
本研究组还比较了不同Ra数下热壁面处竖直速度和上壁面处水平速度分布图像. 如图6(a)和图6(b)所示, 在低Ra数时热壁面处的流速十分微弱, 在高Ra数时热壁面处流体流速得到了显著提升, 这意味着Ra数的增加将直接增强方腔内自然对流的强度, 腔体内流胞环流变得越来越剧烈, 流动速率加快, 温度边界层变薄, 强化了壁面处的传热能力, 使得方腔内部温度变得越来越均匀. 随着Ra数的增大, 在主换热区域流速增大的同时, 方腔左上角小漩涡的流动速率也得到增大, 并且速度为负的区域明显扩大.
 图 6 (a) 不同Ra下X = 0处的竖直速度分布; (b) Y = 1处的水平速度分布图
图 6 (a) 不同Ra下X = 0处的竖直速度分布; (b) Y = 1处的水平速度分布图Figure6. (a) Vertical velocity distribution at X = 0; (b) horizontal velocity distribution at Y = 1 for different

如图7(a)所示, 均匀温度分布模型表明热壁面的Nuave数随Ra数增大而增大[20], 但是随着Ra数的增大, 当Ra = 104时, 热壁面Nuave数出现了微弱减小现象. 为了进一步解释这一现象, 本研究组分析了局部Nu数的分布曲线. 如图7(b)所示, 随着瑞利数的增大, 局部Nu数的峰值位置集中在0.2 < Y < 0.5附近, 这是由于热浮升力的增强使得流速加快, 下侧热边界层变薄, 并且在高瑞利数时该换热区域占据主导地位, 因此, 在Ra = 105和106时, 局部Nu数产生了显著的增长趋势. 但是, 在0.6 < Y < 0.8, 当Ra = 103和104时局部会出现Nu数被削弱的现象, 究其原因, 一方面, 是由于流胞逐渐转变为扁平的椭圆形, 对左上侧的热边界层挤压作用减弱; 另一方面, 随着瑞利数的增大, 中心流胞流速增大并转变为椭圆形状, 由于流体流速的增强, 该区间内等温线沿流胞主流区域流动方向扩散, 使得该局部温度边界层变厚. 此外, 由于热壁面为非均匀边界条件, 在上下壁面附近处出现了局部Nu数小于0的情况, 随着瑞利数的增加, 中心区域的换热效率增强, 同时上壁面附近向左的热通量也得到加强, 而下壁面受到主流胞挤压作用向左侧的换热效率微弱下降.
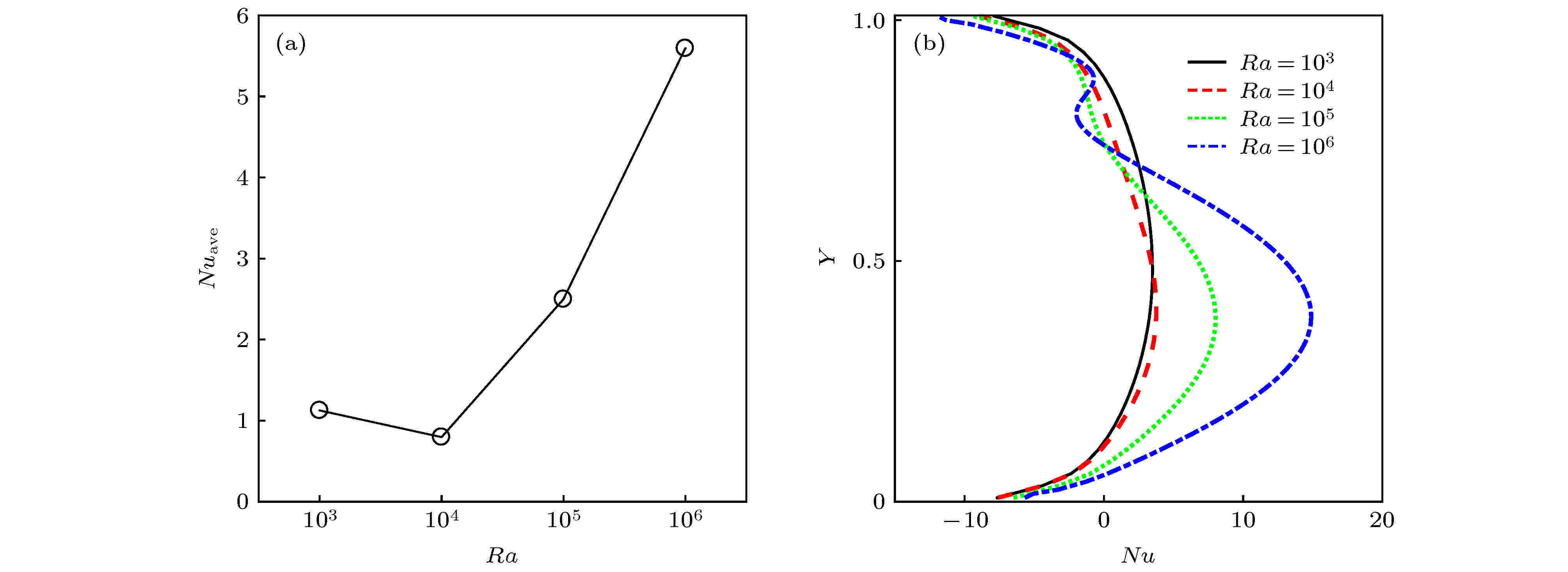 图 7 (a)不同下Ra热壁面处Nuave数; (b)热壁面处局部Nu数分布曲线
图 7 (a)不同下Ra热壁面处Nuave数; (b)热壁面处局部Nu数分布曲线Figure7. (a) At the heated wall Nuave number; (b) local Nu number for different Ra.
通过上述分析发现, 当Ra = 104时, 热壁面上侧局部边界层沿流体流动方向扩散, 局部换热效率下降显著, 并且低温区域吸热现象随Ra数增大而增大, 导致左壁面的Nuave数出现了减小现象. 与此同时, 在高Ra数情况下, 由于方腔内主换热区域换热效率增长更加明显, 其壁面Nuave数增长显著, 受非均匀温度边界层影响较小.
2
4.3.倾斜角γ对流体流动换热的影响
当多孔介质方腔逆时针旋转一定角度时, 流体的流动形态和换热强度将会发生明显变化. 为了分析倾斜角γ的影响, 保持

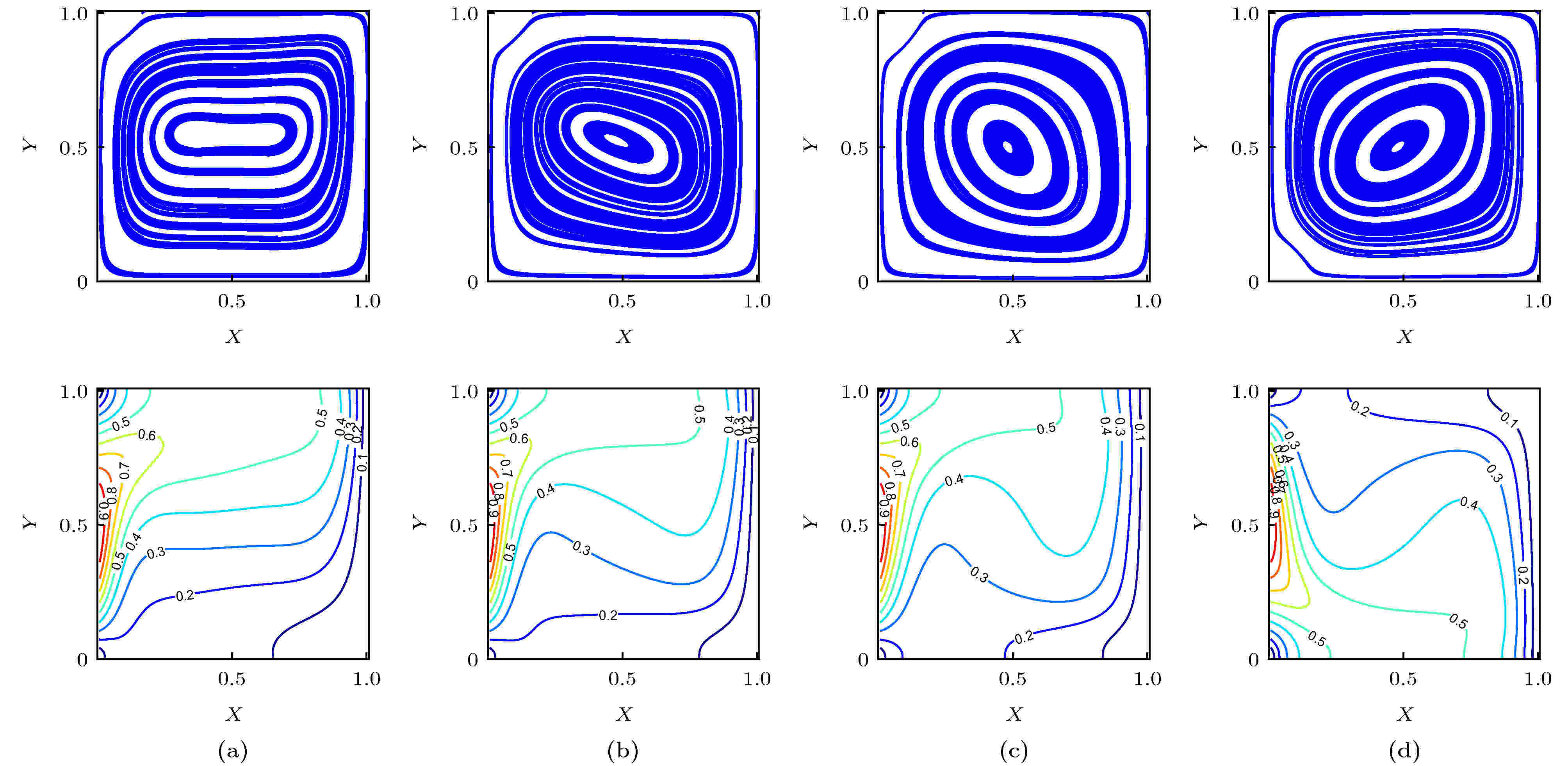 图 8 不同γ下温度场和流场的分布图像 (a) γ = 0°; (b) γ = 40°; (c) γ = 80°; (d) γ = 120°
图 8 不同γ下温度场和流场的分布图像 (a) γ = 0°; (b) γ = 40°; (c) γ = 80°; (d) γ = 120°Figure8. Streamlines, isotherms contours for different γ number: (a) γ = 0°; (b) γ = 40°; (c) γ = 80°; (d) γ = 120°.
因此, 本研究组计算了水平中心线的局部温度分布以及热壁面处Vave/Nuave的对比图, 其中, Vave为沿Y方向的平均速度. 如图9(a)所示, 与γ = 0°相比, 热壁面附近温度下降更为迅速, 这意味着在有倾斜角的情况下热壁面中点附近的温度边界层变薄, 换热效率得到一定加强. 深入分析热壁面整体的换热效率. 如图9(b)所示, 当γ = 40°时, 发现壁面处的换热效率得到了较为显著的提升; 当γ = 80°时, Nuave数存在削弱换热现象; 当γ = 120°时, 其强化传热作用较为微弱, 这一变化规律与以往文献[36]所得结论一致. 由于倾斜角的变化使得热浮升力的方向发生改变, 流体在X方向上存在浮升力的驱动, 影响了热壁面处Vave的大小, 并且壁面处局部V会直接影响温度梯度以及壁面处传热强度, 因此Vave/Nuave的变化趋势基本相同, 并呈现上下波动的趋势.
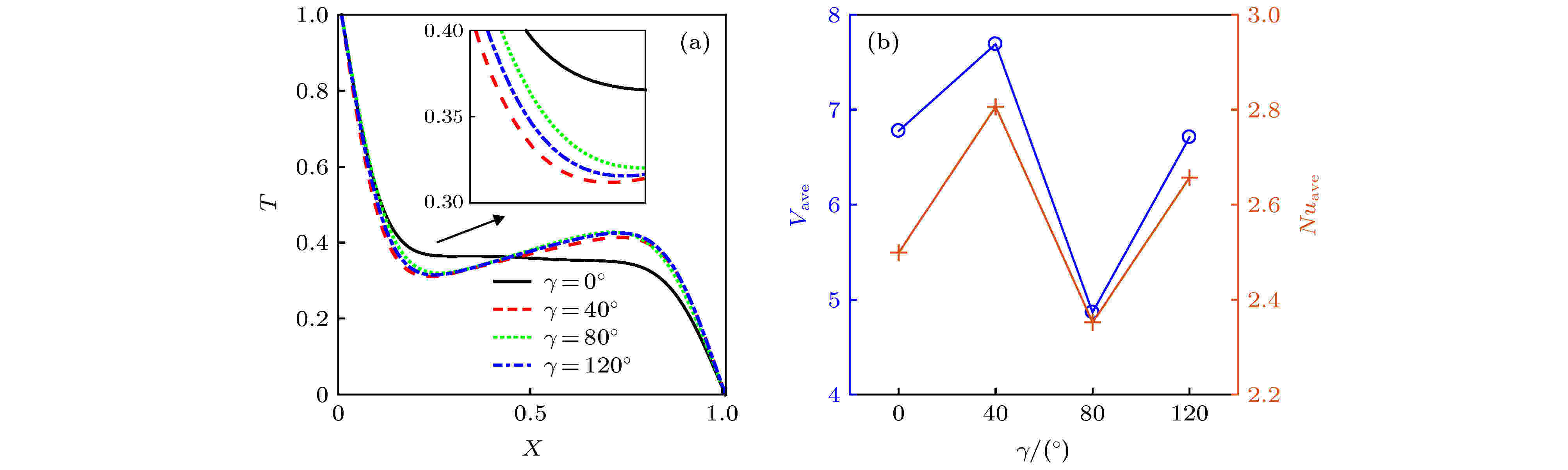 图 9 (a)不同γ时Y = 0.5处局部温度分布曲线; (b)热壁面处Vave/Nuave的分布曲线
图 9 (a)不同γ时Y = 0.5处局部温度分布曲线; (b)热壁面处Vave/Nuave的分布曲线Figure9. (a) Local temperature distribution along the Y = 0.5; (b) average velocity in the y direction & Nuave number at the heated wall in different γ.
为了进一步探究γ对流体传热的影响, 本研究组分析了热壁面处局部V的分布曲线, 由于γ = 120°时旋涡流动方向为逆时针, 本文选取它的相反数作为参考. 从图10(a)可以看出, 当γ = 40°时, 其局部V的峰值存在最大值; 当γ = 80°时, 其局部V的峰值最小, 并且绝大多数区域小于γ = 0°时的数值; 当γ = 120°时, 速度峰值数值与γ = 0°时几乎接近, 因此γ = 40°时强化效果最为明显, 而γ = 80°时则产生削弱现象. 最后, 为了进一步细致分析γ = 120°时局部Nu数的分布规律, 本研究组给出了不同倾角下局部Nu数的分布曲线. 如图10(b)所示, 当γ = 0°, 40°和80°时, 非均匀温度边界条件在中点以上位置出现了与主换热区域相反趋势的分布情况, 而最大局部Nu数存在于热壁面中点以下区域. 这是由于当流体流动方向为顺时针时, 中点以下的流体受到浮升力和主流包挤压作用的影响, 对流换热作用最显著. 由图10(b)可知, 主换热区域内的换热强度由强到弱依次为40°, 0°和80°. 当γ = 120°时, 流胞旋转方向的转变使得热壁面最大局部Nu数出现在壁面中点以上的位置, 而局部Nu数的峰值介于0°和40°之间.
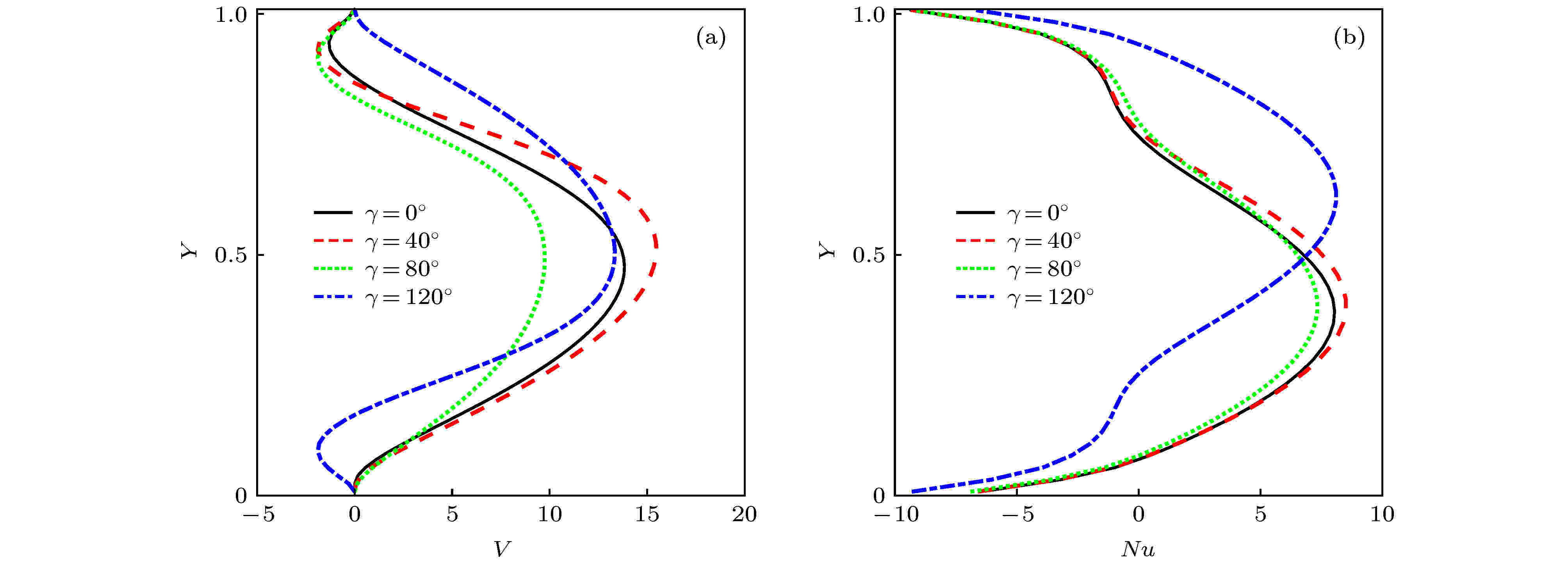 图 10 (a)不同γ下热壁面处局部竖直速度V; (b)热壁面处局部Nu数的分布曲线
图 10 (a)不同γ下热壁面处局部竖直速度V; (b)热壁面处局部Nu数的分布曲线Figure10. (a) Local velocity in the y direction; (b) local Nuave number at the heated wall in different γ.
对方腔施加倾角后, 热浮升力的有效作用发生改变, 使得壁面的竖直速度发生改变, 而壁面Vave与Nuave数关联性增强. 当γ = 40°时, 通过提升主换热区域的竖直速度可以提高该区域内局部Nu数, 使得整体壁面换热效率增强. 类似地, 当γ = 80°时, 壁面竖直速度的削弱对流体传热效率的影响较为明显, 导致壁面换热效率下降显著. 这一规律与文献[36]所得结论相符, 表明主换热区域对壁面Nuave数影响较为明显, 壁面低温区域从方腔内吸热的强度受倾斜角的影响较小, 这是由于主换热区域和主流区域近似重叠, 因此, 随倾斜角的变化, 均匀或非均匀边界条件下主换热区域内Nuave数强化或削弱作用都将起到主导作用.
本研究组还研究了不同倾斜角下孔隙率的增加对方腔内强化传热的影响. 如图11(a)所示, 在施加倾斜角的情况下, 随着孔隙率的增大, 当
















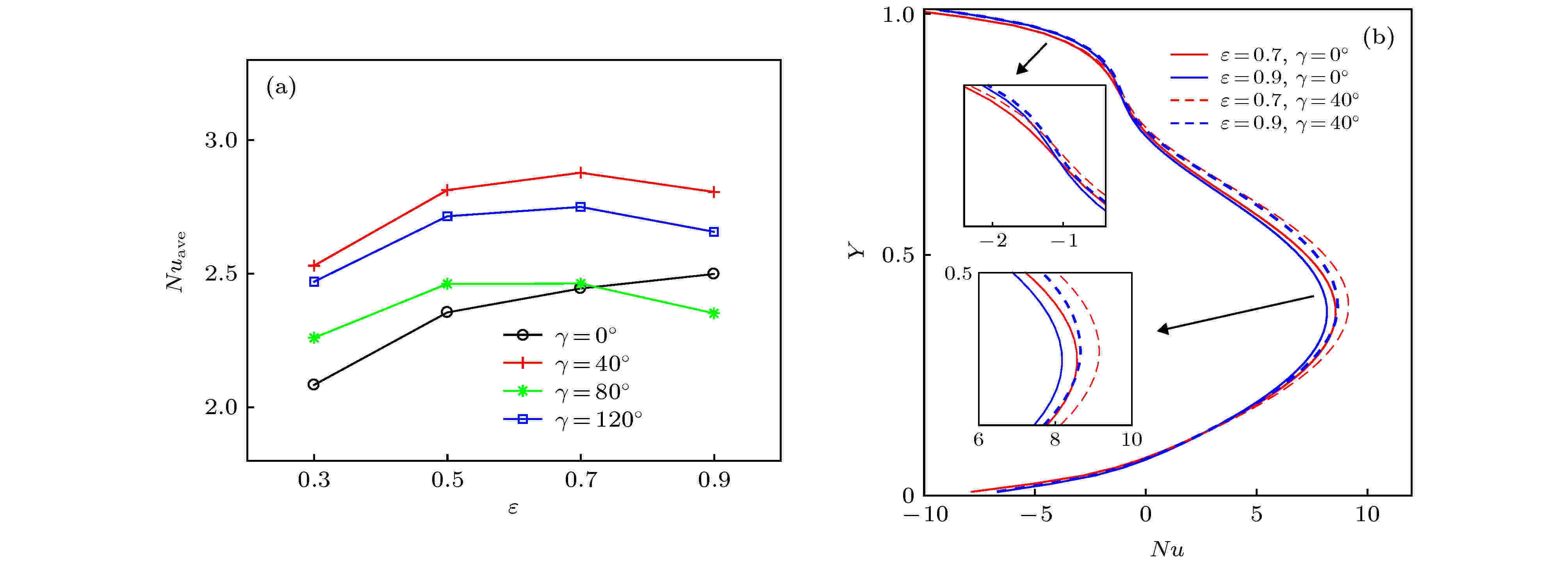 图 11 (a)随着
图 11 (a)随着



Figure11. (a) Variation of Nuave number as a function of




当方腔不施加倾角时, 壁面处的Nuave数随孔隙率增加而增加, 但是在施加倾斜角条件时, 方腔热壁面的Nuave数出现先增加后减小的趋势, 为了解释这一现象, 以γ = 40°和0°时孔隙率为0.7和0.9的情况为例进行分析. 如图11(b)所示, 当γ = 0°时, 在主换热区域内(0.2 < Y < 0.6), 孔隙率增大, 局部Nu数减小的幅度较小, 而位于上壁面附近区域内, 局部Nu数的增长成为主导. 局部Nu数是由导热系数比值km/kf和热壁面温度梯度所组成, 当γ = 0°时, 左壁面温度梯度的增加幅度相对于km/kf减小幅度更加显著, 因此, 随着孔隙率的增加, Nuave数呈现出单调递增的趋势. 当γ = 40°时, 方腔内对换热能力起主导作用的依然位于主换热区域(0.2 < Y < 0.6), 在此区域内, 随着孔隙率的增大, 局部Nu数减小的幅度更为明显, 从而导致了孔隙率为0.9时Nuave数的轻微减小. 这是由于随着孔隙率的进一步增大, 多孔介质导热对方腔传热效率的贡献逐渐变小, 即km随孔隙率增大而减小, 而施加不同倾斜角后, 左壁面处的温度梯度在0.7 <









最后, 本研究组分析了不同γ下随着纳米颗粒体积分数的增加, 方腔内部的换热机理. 如图12(a)所示, 随着纳米颗粒体积分数的增加, 当γ = 40°, 80°和120°时, 热壁面处的Nuave数存在微弱增大的趋势, 且当γ = 40°时, Nuave数最大, 强化换热现象最明显, 而当γ = 0°时, Nuave数反而出现了微弱削弱的趋势, 且




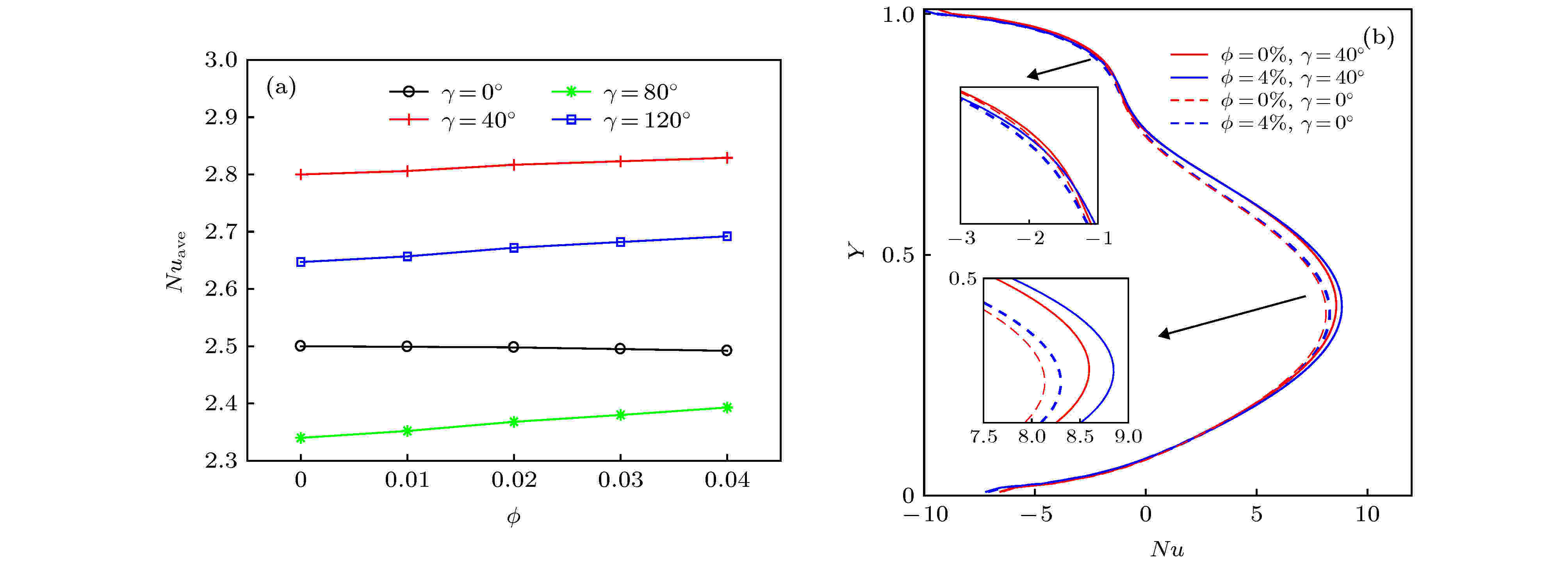 图 12 (a)随着?的增加不同γ下热壁面Nuave数分布曲线; (b)当γ = 0°, 40°时, 不同?下局部Nu数的分布曲线
图 12 (a)随着?的增加不同γ下热壁面Nuave数分布曲线; (b)当γ = 0°, 40°时, 不同?下局部Nu数的分布曲线Figure12. (a) Variation of Nuave number as a function of ? in different γ at the heated wall; (b) when γ = 0°, 40°, variation of local Nu number at the heated wall in different ?.
但是, 当对方腔施加任意倾角时, 热壁面Nuave数缓慢增长, 为了进一步分析这种不同变化趋势的原因, 在图12(b)中, 以γ = 0°和40°, 纳米颗粒体积分数为0%和4%的情况为例进行分析, 一方面, 当γ = 40°时, 在主换热区(0.2 < Y < 0.6)附近, 随着孔隙率的增大, 局部Nu数随之增长; 另一方面, 虽然随体积分数的增大流体, 有效粘度逐渐变大导致流体流速降低, 对流强度缓慢下降, 但是施加不同的倾斜角后, 壁面温度梯度呈现微弱增加趋势, 而km/kf增长幅度固定不变, 使得在γ = 40°时Nuave数单调递增趋势更加明显. 这说明通过对方腔施加一定倾斜角, 改变了壁面温度梯度变化趋势, 进而改变了其Nuave数. 因此, 热壁面的换热效率取决于γ和



主要结论如下:
1)在低Ra数时, 流体受非均匀温度边界层低温区域影响出现吸热现象, 热壁面处的Nuave数出现轻微减小的趋势, 这与以往采用均匀温度分布的文献[20]所得结论存在差异; 在高Ra数时, 由于瑞利数综合表现为热浮升力的强度, 方腔内主换热区域换热效率增长更加明显, 热壁面处Nuave数增大最为显著, 受到非均匀温度边界层影响较小.
2)随着γ的增加, 方腔内热浮升力随之发生改变, 通过对壁面流速的改变, 对其壁面强化换热效果产生不同影响, 当γ = 40°时, 左壁面的Nuave数增长幅度较为明显; 而当γ = 80°时, 左壁面的Nuave数反而产生削弱作用. 这一规律与文献[36]所得结论相符, 这是由于主换热区域和主流区域近似重叠, 而壁面Vave与 Nuave数关联性较强, 因此壁面Nuave数受主换热区域影响较为明显, 而壁面吸热区域受到倾斜角的影响较小.
3)均匀温度边界条件下的研究表明, 壁面处的Nuave数随孔隙率增加而增加[12]; 而非均匀温度边界条件下的结果表明, 在高孔隙率对方腔施加不同倾角时, 增大孔隙率对壁面温度梯度的促进作用减弱, 因此, 孔隙率的增加对热壁面处的传热能力存在抑制作用.
4)对于均匀温度分布边界条件下的研究表明, 热壁面的Nuave数随Al2O3-H2O纳米流体体积分数增加而缓慢增加[20], 而本文非均匀温度边界条件下的研究表明, 当γ = 0°时, 随




通过上述总结归纳发现, 在本文所研究的非均匀温度边界物理模型下, 纳米颗粒体积分数所产生的强化换热作用不再明显. 给定Ra数时, 要有效改善纳米流体流动换热效率, 就需要利用多孔介质对有效导热系数的提升, 以及倾斜角对系统内的扰动作用, 采用合适的孔隙率和方腔倾斜角度对方腔进行干预.


