摘要:用于核反应堆的金属结构材料中氢/氦泡的前躯体——(氢/氦)-空位复合体的形成受到温度、辐照剂量等多方面因素的影响, 研究其在材料中的形成和演化行为对气泡形核的理解及先进核反应堆材料的发展起着至关重要的作用. 然而, 受到分辨率的局限, 这种原子尺度的微结构很难用电镜等常规方法进行表征, 以致于该问题的研究上可利用的数据相对较少. 正电子湮没谱学是一种研究材料中微观缺陷的特色表征方法, 近些年来慢正电子束流和新型核探测谱仪技术的不断发展以及基于慢束发展起来的多种实验测试方法的改进, 使正电子湮没技术应用已拓展到金属材料中氢/氦行为的研究领域, 在金属材料表面氢/氦辐照损伤的研究中发挥了重要作用. 本文结合国内外相关进展以及本课题组的一些研究成果评述了正电子湮没谱学在金属材料氢氦行为研究中的应用, 着重讨论了正电子湮没寿命谱、多普勒展宽谱、符合多普勒展宽三种测量方法在如下金属材料氢/氦行为研究中的优势: 1)氢/氦气泡尺寸和浓度的估算; 2)高能氢/氦离子辐照损伤缺陷及缺陷的退火、时效的演化行为; 3)不同形变程度样品中氢/氦与形变缺陷的相互作用; 4)不同能量或剂量氢/氦离子辐照对材料造成的损伤以及氢氦协同作用.
关键词: 氢氦/
微观缺陷/
正电子湮没/
辐照损伤

English Abstract

全文HTML

--> --> -->

服役于核反应堆、等离子体装置、加速器等辐照环境中的金属/合金材料, 不可避免会受到中子、质子等粒子辐照, 直接或间接地引入氢/氦原子^[1-6]. 氦在金属材料中溶解度较低且不易扩散, 积累的氦将聚集、沉淀在晶格, 可能会与离位损伤产生的缺陷相互作用, 乃至形成气泡, 从而引发材料的表面起泡或内部肿胀^[7]. 在较高温度下, 原子的运动更加激烈, 氦容易在晶界、相界及位错处聚集长大, 导致材料宏观性能下降, 例如反应堆用钢的氦辐照肿胀^[8,9]. 氢及其同位素既是核聚变的反应物又是核嬗变反应的生成物, 它在材料中的扩散、居留等行为是影响核能材料宏观性能的关键因素. 虽然产生的氢在较高温度条件下容易从材料中扩散出去, 但在氢浓度较高的环境中依然会导致工程金属材料的氢脆^[10]. 其次, 间隙原子和空位的移动会促进材料中原子的扩散, 引起材料中元素的偏析和析出相变, 氢在材料中扩散过程中会加剧材料中元素的偏析或析出. 更严重的是, 氦、氢和辐照缺陷同时存在会发生协同效应, 使研究变得更加复杂^[11-13]. 因此, 开发新的研究方法, 弄清材料中氢/氦的存在形态及其演变, 研究其对材料宏观性能的影响, 对于先进核反应堆材料的发展是十分必要的.
正电子湮没谱学(positron annihilation spectroscopy, PAS)是探测金属合金材料微观缺陷的无损测量方法, 并且对于材料中的空位型缺陷(空位、空位团、微孔洞)探测很灵敏. PAS已经成为研究金属合金、半导体材料、聚合物以及一些新型功能材料中微观缺陷、电子密度分布和电子动量分布的特色方法. 如今, 已经发展出了多种PAS测量的方法, 其中包括正电子湮没寿命谱(positron annihilation lifetime spectrum, PALS)、多普勒展宽谱(Doppler broadening spectrum, DBS)、符合多普勒展宽(coincidence Doppler broadening, CDB)等测量方法. 在过去这些测量方法研究合金中微量元素的析出、间隙原子与空位型缺陷的相互作用等方面应用广泛^[14,15]. 例如, Hari Babu等^[16]用寿命谱测量技术研究了Fe9Cr合金在退火过程中位错驱动对Cr析出的影响, 从正电子湮没寿命值变化这一角度, 结合透射电子显微镜 (transmission electron microscope, TEM)等方法辅证了样品中位错的存在及运动对Cr的析出有很大影响这一结论. Cao等^[17]在573 K温度下利用2.5 MeV能量的Fe³⁺对FeCu合金进行多个剂量辐照, 随后用慢正电子多普勒展宽和CDB对辐照样品中缺陷和Cu析出物进行表征, 确定了Cu析出物对辐照剂量的依赖关系, 发现低辐照剂量下Cu原子析出更容易. 氢、氦引入金属合金材料与其中的缺陷相互作用在很大程度上跟间隙原子与缺陷的相互作用类似, PAS在这一方面的检测优势是毋庸置疑的, 但氢、氦是气体元素, 在材料中会迁移、聚集, 最终形成气泡, 正电子对这些气体原子或团簇没有直接的吸引力, 只能通过氢/氦-空位团簇的演化间接研究氢/氦行为. 尽管会有一定局限性, 但无疑也会促进PAS方法自身在研究金属合金氢氦行为上, 开辟新的测量方法. 本文对PALS, DBS和CDB谱三种测量技术研究金属合金氢氦行为的应用进行分类, 分别介绍三种测量技术在研究这一问题时, 各自具有的优势.

目前研究金属材料的氢/氦辐照损伤和氢/氦行为通常采用TEM直接观察或者用热脱附谱仪(thermal desorption spectrometer, TDS)研究氢/氦气体的热力学行为等. 然而, 对于氢/氦辐照产生的点缺陷及氢氦-空位等小尺寸团簇结构的形成与演化过程很难采用TEM或TDS等来表征分析. 此外, TEM通常只能分析局部区域信息, 对于分析氢/氦辐照导致的体效应具有一定局限性, TDS测试则对样品具有破坏性. 正电子湮没技术一系列测试方法的优势使其成为一种研究原子尺度微观缺陷的特色表征手段. 特别是近些年来慢正电子束流技术的进步和基于慢束发展起来的多种实验测试方法, 使正电子湮没技术应用拓展到金属合金中氢氦行为的研究之中, 对金属材料辐照损伤的研究发挥了重要作用. PAS方法对于低浓度小尺寸微观缺陷, 特别是氢氦泡尚未形成之前的氢氦-空位复合体非常灵敏. 相比于其他实验手段, 正电子还具有“自寻找”特性, 即进入材料的正电子易于被微观缺陷捕获并在捕获位置发生湮没. 此外, 正电子测试过程中不会对样品造成损坏.
正电子与电子的质量、电荷量相同, 电负性相反, 热化的正电子与材料中的电子发生湮没并释放γ光子, 实验中可以通过测量γ光子的时间信息、能量信息、动量信息来分析材料内部的微观结构. 随着核技术应用与方法学的发展, 人们发展出多种PAS测量方法, 包括PALS测量、DBS测量和湮没辐射角关联测量(ACAR). 此外, 还发展出CDBS、寿命-动量关联谱(A-MOC)和慢正电子束分析技术. 其中ACAR和A-MOC在研究金属合金氢氦行为的应用极少, 因此不做详细介绍.
材料中, 热化的正电子与电子发生湮没的状态有以下几种: 处于自由状态的正电子与电子发生湮没的过程称为自由态湮没; 当材料中存在缺陷时, 正电子容易被缺陷所捕获, 并在捕获状态下与电子湮没, 称为捕获态湮没; 而当正电子与材料中一个电子形成相对稳定束缚态时, 该结构被称为正电子素(positronium, Ps), 该种湮没类型也被称为Ps湮没. 金属合金中通常不会形成Ps, 因此本文主要考虑的正电子湮没方式为自由态湮没和捕获态湮没.
量子电动力学的结果表明, 正负电子湮没主要有三个途径, 分别为产生一个、两个或三个伽马光子. 其中湮没产生单光子的几率远小于另外两种途径, 而发生三光子湮没与双光子湮没几率比值约为1∶372. 因此, 实验中我们主要讨论双光子湮没过程.
当正负电子相对速度均远小于光速时, 狄拉克计算出发生双光子湮没时的捕获截面为

$\sigma = \dfrac{{{\text{π}}r_0^2c}}{v},$

其中, r₀为电子经典半径, c为光速, v为正电子相对于电子的速度.
正电子湮没率则与湮没截面和湮没区域电子密度直接相关, 即

$\lambda =\sigma {^{*}}{n_{\rm{e}}} ^* v = {\text{π}} r_0^2{n_{\rm{e}}}c,$

式中, n_e为单位体积电子数. 由(2)式可知, 正电子湮没率与电子密度成正比, 电子密度越大, 湮没率越大, 相应正电子湮没寿命τ(τ = 1/λ)越短. 因此, 可通过测量正电子寿命得到湮没位置处的电子密度信息. 在氢/氦辐照的样品中, 由于氢/氦在样品中的迁移, 扩散, 甚至占据空位缺陷而导致空位型缺陷周围电子密度发生很大变化, 这些变化在湮没信息都能很好地反映出来. PALS是最常用的PAS方法之一. 正电子湮没寿命, 即正电子从放射源产生到进入介质发生湮没这段时间. 在金属合金体系中, 空位、空位团及微孔洞等空位型缺陷内电子密度比无缺陷固体内的电子密度低, 正电子在其中湮没概率低, 所以在这些缺陷内的正电子寿命长. 研究表明正电子湮没寿命值与空位型缺陷的尺寸呈正相关.
在实验室坐标系中, 湮没正负电子对有一定的动量, 而湮没辐射是电子-正电子湮没对在运动过程中发射的, 由于多普勒效应, 湮没后放出的γ辐射的能量谱呈现一定的宽度, 即湮没辐射的γ光子能量为${E_0} = {m_0}{c^2} \pm \Delta E$. 当样品中存在缺陷时, 正电子被缺陷捕获, 因缺陷位置电子平均动能降低, 会造成多普勒展宽峰的范围变窄, 进而可以从多普勒能谱的峰宽变化推测缺陷的信息, 这时只需要定义若干参数来描述多普勒展宽能谱峰的形状即可进行物理观察.
DBS测量主要反映材料内部的电子动量分布. 常用的描述多普勒展宽能谱的峰形变化的参数有S参数和W参数. 如图1所示, S参数定义为从多普勒展宽能谱峰的中心511 keV处取一定宽度面积A与峰的总面积Δ之比, 即$S{{ = }}A{{/}}\varDelta $; W参数则是取峰的两侧一定宽度面积B, C之和与峰的总面积Δ之比, 即$W{{ = }}\left( {B{{ + }}C} \right){{/}}\varDelta $. S参数的变化受谱峰中央区光子计数的影响大, 主要反映正电子与低动量电子(金属中为导电电子)湮没的情况. W参数主要反映正电子与高动量电子(金属中为原子的壳层电子)湮没的情况. 而且需要进一步说明的是, S参数与W参数之比, 即$S{{/}}W{{ = }}A{{/}}{\left( {B{{ + }}C} \right)}$, 所得到的曲线可以反映不同位置的缺陷类型, 如空位型位错、空位、空位团. S参数和W参数的变化可以得知材料中缺陷浓度或尺寸的变化, 但是在有些情况下, 这样的分析是不够的, 要同时分析S和W参数以了解缺陷的种类或湮没点周围化学环境的变化. 根据缺陷捕获正电子的两态捕获模型, S和W参数分别可以写成下面的关系式:
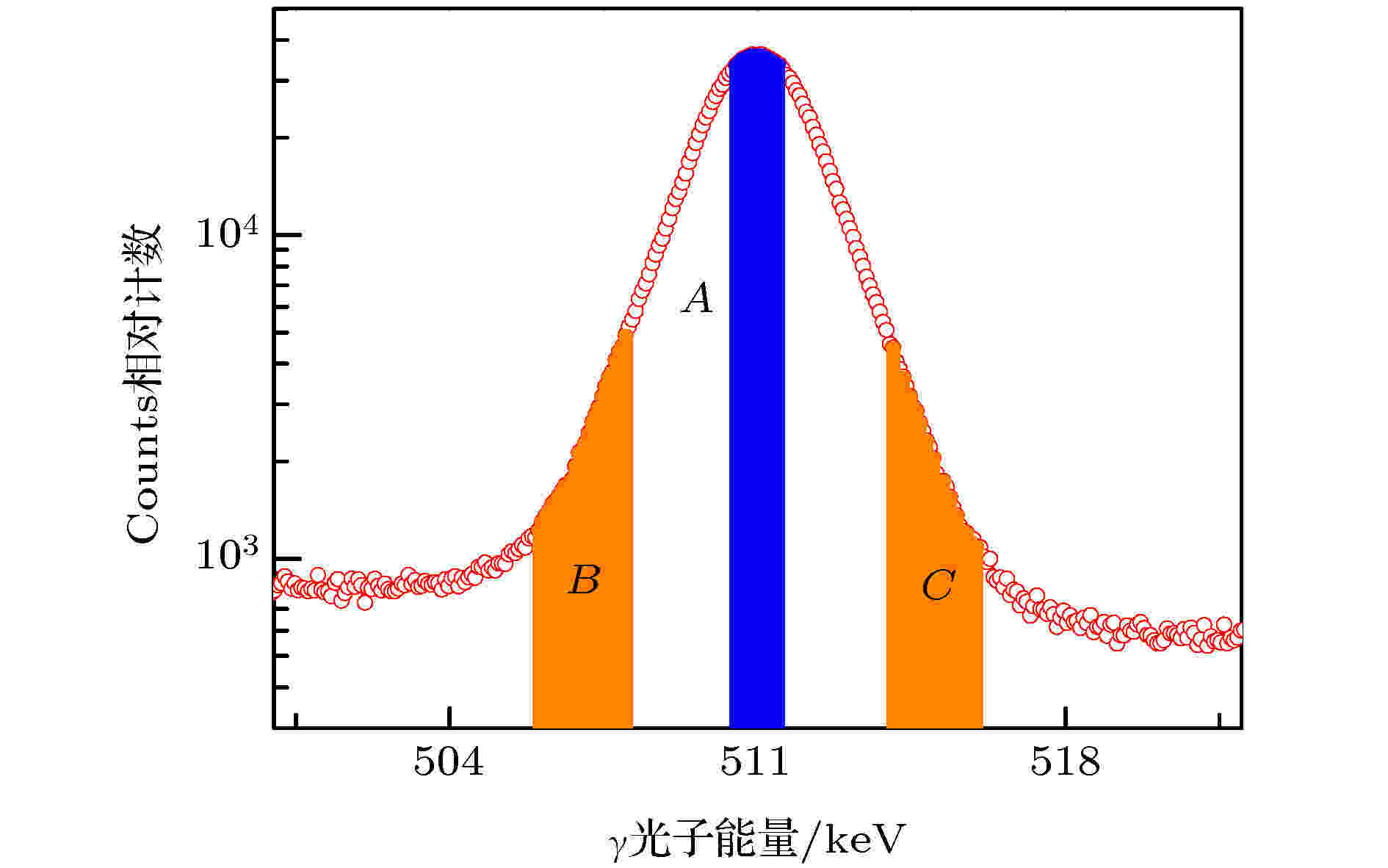图 1 DBS中参数的定义
Figure1. The parameter definition in the Doppler broadening spectrum.

$S{{ = }}\left( {{\rm{1}} - f} \right) \times {S_{\rm{b}}} + f \times {S_{\rm{d}}},$

$W{{ = }}\left( {{\rm{1}} - f} \right) \times {W_{\rm{b}}} + f \times {W_{\rm{d}}}.$

则有${S = R \times \left( {W - {W_{\rm{b}}}} \right) + {S_{\rm{b}}}}$, (3)式和(4)式中, S_d和S_b分别为缺陷态和体态的S参数; W_d和W_b分别为缺陷态和体态的W参数. $R = \left( {{S_{\rm{d}}} - {S_{\rm{b}}}} \right)/{\left( {{W_{\rm{d}}} - {W_{\rm{b}}}} \right)}$, 这个参数只与缺陷的类型有关, 与缺陷的尺寸或浓度没有关系. 因而可以根据该关系做出S-W曲线, 如果所测得的(S, W)数据分布在一条直线上, 则说明缺陷的类型没有变化. 若(S, W)数据分布在不同斜率的几条直线上, 则代表样品中有多种类型的缺陷. 如果缺陷与杂质发生了相互作用, 其S-W曲线将出现转折或聚集在某个区域. 在金属合金材料氢/氦离子辐照研究中, 未辐照的样品S-W曲线基本保持在一条直线上, 说明未辐照样品中在稳定区的缺陷类型基本没有发生变化. 辐照后的样品, S-W曲线发生了明显的变化, 表示缺陷的类型发生转变, 可能是氢氦原子被缺陷捕获并与微观缺陷相互结合, 形成氢/氦-微观缺陷复合体这种新的缺陷类型. 由于氢氦对正电子有一定排斥性, 正电子在氢氦-空位复合体中湮没率比纯空位低, W参数会相应增大, 当氢/氦在复合体中的比例增大时, (S, W)会朝W参数增大的区域聚集.
多普勒展宽的本底来源有很多, 最主要的有1.28 MeV和0.511 MeV伽马光子的康普顿效应峰, 周围环境的辐射本底, 探测器本身的原因等. 常规多普勒展宽测量只用一个探测器进行探测, 测得的湮没光子能谱信噪比较低, 其计数在高动量区的峰背比大约为150∶1, 在低动量区本底更高. 因此, DBS的大量有效信息通常被过高的本底所掩盖. 壳层电子通常带有原子核的特征信息, 根据其动量分布能鉴别元素种类, 有助于研究缺陷的亚点阵, 即湮没点周围的化学环境, 要获得这部分电子有关的信息, 用单探头多普勒展宽测量很难获得.
1976年Lynn等^[18]提出了双探头符合系统的测量思想, 并用一个锗锂探测器和一个NaI(Tl)探头, 两探测器呈180°相对排布, 通过符合测试将峰背比提高为一维多普勒谱仪的30倍. 随后Lynn又利用两个性能相近的Ge(Li)探测器组成双探头CDB系统, 记录二维DBS, 经过处理后得到的一维谱, 其峰背比高达10⁵以上, 且能量分辨率提高了${\sqrt {\rm{2}} }$倍. 如图2所示为纯铁的CDB与常规多普勒展宽能谱的对比, 显然通过双探头符合后有效计数比例大大提高.
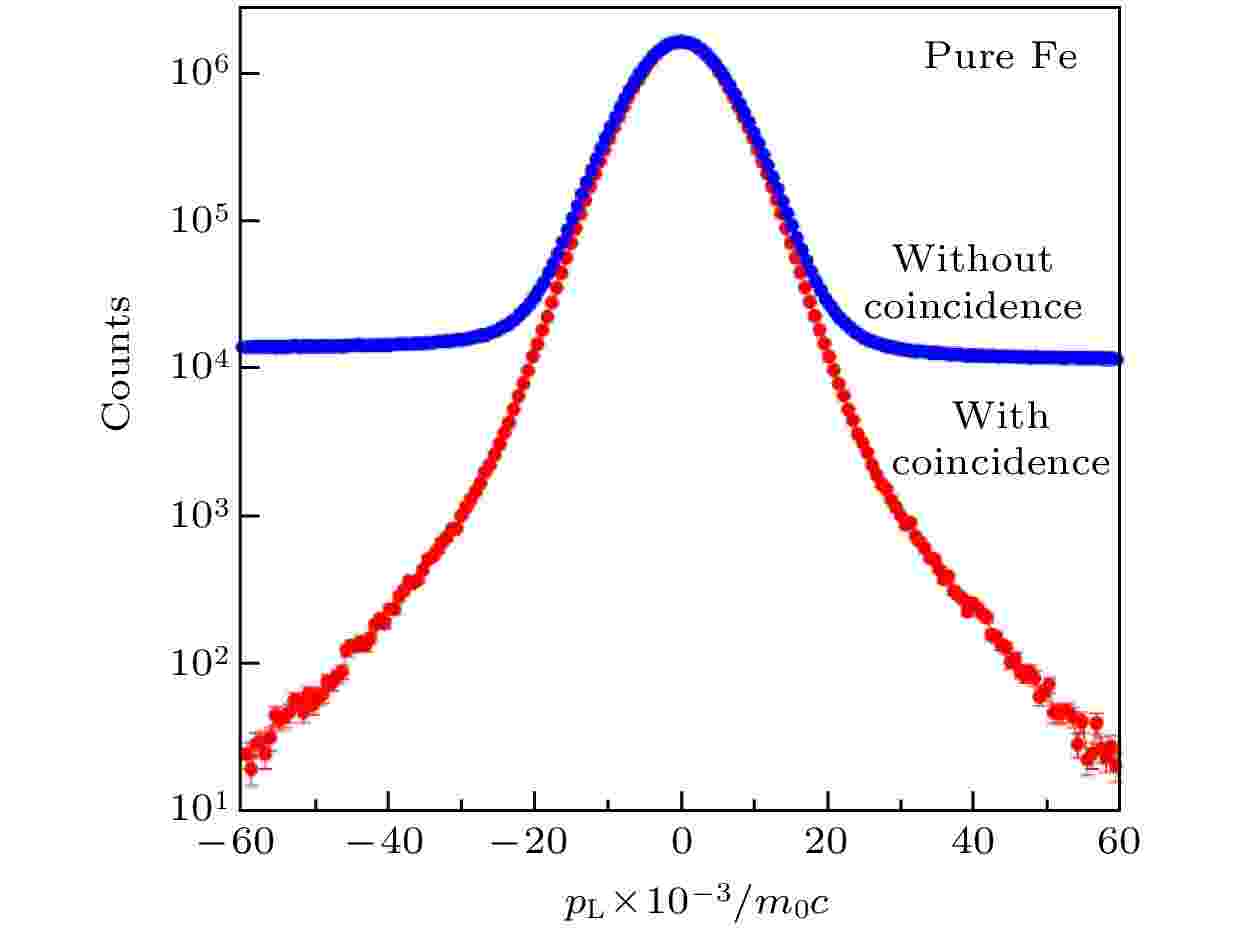图 2 纯铁的CDB与一维多普勒展宽能谱比较
Figure2. Peak-to-valley ratio of CDB system in the pure iron.

两个高纯锗探测器呈180°放置, 其探测到的两个伽马光子能量分别为E₁和E₂, 则有

${E_1} = {m_0}{c^2} + \frac{{c{P_{\rm{L}}}}}{2} - {E_{\rm{b}}}/2,$

${E_1} = {m_0}{c^2} - \frac{{c{P_{\rm{L}}}}}{2} - {E_{\rm{b}}}/2,$

式中, m₀是电子的静止质量, E_b是某壳层电子的结合能, P_L是电子-正电子对沿探头方向的动量分量. 定义两个光子能量之和${{E_{\rm{S}}} = {E_1} + {E_2}}$, 能量之差${{E_{\rm{d}}} = {E_1} - {E_2} = c{P_{\rm{L}}}}$, 即两探测器测得的两个光子能量之差为2倍的多普勒增宽. 因此, 可以通过E₁ – E₂来重建多普勒展宽能谱, 以获得更多有效电子动量分布信息.

2

-->

3.1.寿命谱在金属合金氢/氦行为研究中的应用

正电子寿命谱测量技术在金属合金缺陷研究中主要用于定性和半定量测量缺陷的类型、尺寸和浓度, 可用于研究热时效、辐照参数等实验条件变化下缺陷的演化规律. 由于原子半径小、迁移能低, 氢/氦等气体元素进入金属材料后, 必然会与材料中存在的空位、空位团、位错等缺陷相互作用并与之结合, 形成(He, H)-缺陷复合体. 尽管这些复合体与纯空位型缺陷相比对正电子的吸引力有所下降, 但只要引起明显的电子密度变化, 正电子湮没测试依然相当灵敏. 正是因为这些, 正电子在材料中寿命及强度可以间接反映出材料中气泡尺寸和浓度.
氢/氦离子辐照产生的损伤通常不是整体效应而是在样品的某一层比较集中, 并且辐照深度也比较浅, 因此在用寿命谱测试时一般采用慢正电子束以控制正电子的入射深度实现不同深度有效测量. 对于中子辐照样品或者多种离子能量叠加产生的整体效应, 可以采用常规PALS测量.
3 -->

3.1.1.氢/氦泡浓度和尺寸的估算及氢氦-空位复合体的正电子寿命

20世纪末, Jensen等^[19,20]就建立了正电子湮没寿命数据估算氦泡浓度、尺寸的模型. 对于尺寸较大的气泡(r > 0.5 nm), 他们的理论研究认为正电子在气泡内的湮没寿命主要由气泡中气体原子浓度决定, 并给出了当温度为300 K时, 金属铝中正电子寿命τ(ps)和泡内氦原子浓度n_He (10²⁸ m^–3)之间的计算关系式^[21]:

${\tau = 500 - 23.5{n_{{\rm{He}}}}},$

其中, τ是大空洞饱和正电子寿命, 常数23.5由气体原子及金属决定. 当晶体中存在缺陷(如空位、位错、微空洞等)时, 正电子容易被带负电性的缺陷捕获, 呈现为缺陷捕获态. 缺陷处的电子密度的变化常常导致正电子湮没特性改变, 如空位处的电子密度较低, 因此被空位捕获的正电子湮没寿命将变长. 实验分析中, 一般采用捕获模型对正电子与缺陷的相互作用加以分析. 目前常用的为正电子的“二态捕获模型”, 即假定材料中的正电子除了自由态湮没外, 只有一种缺陷捕获态存在. 根据二态捕获模型, 缺陷中正电子捕获率κ与湮没率λ(寿命值的倒数)之间存在如下关系:

$\kappa = \left( {{\lambda _{\rm{f}}} - {\lambda _{\rm{d}}}} \right) \times {{{I_2}} / {{I_1}}},$

其中, I₁, I₂分别是短寿命和长寿命成分对应的强度, λ_f和λ_d分别是正电子在自由态和缺陷态的湮没率. 通常认为缺陷中正电子捕获率κ正比于缺陷浓度C:

$\kappa = \mu C,$

式中μ为比捕获率, 对于气泡或空洞, 比捕获率取决于温度T和缺陷的半径r^[22,23]. 对于不同的材料, 通常需要依据实验确定r和μ之间的关系. 基于空位、空洞和氦泡的捕获率实验结果, 建立了如下半经验公式^[24]:

$\mu = \left( \dfrac1{Ar} + \dfrac{1}{Br^2}\right)^{-1},$

式中, 常数A = 9.07 × 10¹⁶ nm^–1·s^–1, B = 3.3 × 10¹⁶ nm^–2·s^–1, (10)式适用于r > 0.5 nm的氦泡, 在铝和镍等金属材料都有很好的适用性. 对于小尺寸氦泡、空洞, μ与r³成正比^[22]. 假设样品中总的氦浓度N_He都分布在氦泡中, 且氦泡近似为球体, 则可以得到

${C_B} = \dfrac{3{N_{{\rm{He}}}}}{4{\text{π }}{r^3}{n_{_{{\rm{He}}}}}}.$

结合(7)式—(11)式, 可以得到关于氦泡尺寸的方程:

$B{r^2} + Ar - \frac{{3AB{N_{{\rm{He}}}}}}{{4{\rm{\pi }}{n_{{\rm{He}}}}{I_2}({\lambda _1} - {\lambda _2})}} = 0.$

将测得正电子寿命数据代入(12)式, 就可以得到氦泡的尺寸.
随着计算机模拟技术的迅猛发展, 用正电子寿命研究金属合金中氢/氦行为的理论模拟计算也日渐成熟. Shivachev等^[25]用蒙特卡罗、密度泛函理论和局域密度近似等方法计算了含有氢和氦的镍中缺陷的正电子寿命, 发现有氢/氦占据的空洞中正电子寿命值变小了, 并获得了氢氦-微空洞复合体尺寸与正电子寿命值之间的关系, 认为微空洞中包含超过45个氢原子和30个氦原子时正电子寿命值达到饱和. Troev等^[26]也用模拟方法研究了含氢和氦的钨中缺陷的性质, 理论计算给出了正电子在含有一个氢原子的钨空位缺陷中的波函数如图3所示, 正是由于缺陷中氢/氦原子的存在导致正电子在其中的捕获率减小. 随后, 他们计算了不同空位数和氢/氦原子数的团簇中正电子寿命的变化, 发现空位数相同的团簇中随着氢/氦原子数的增加, 正电子寿命减小, 如图4所示.
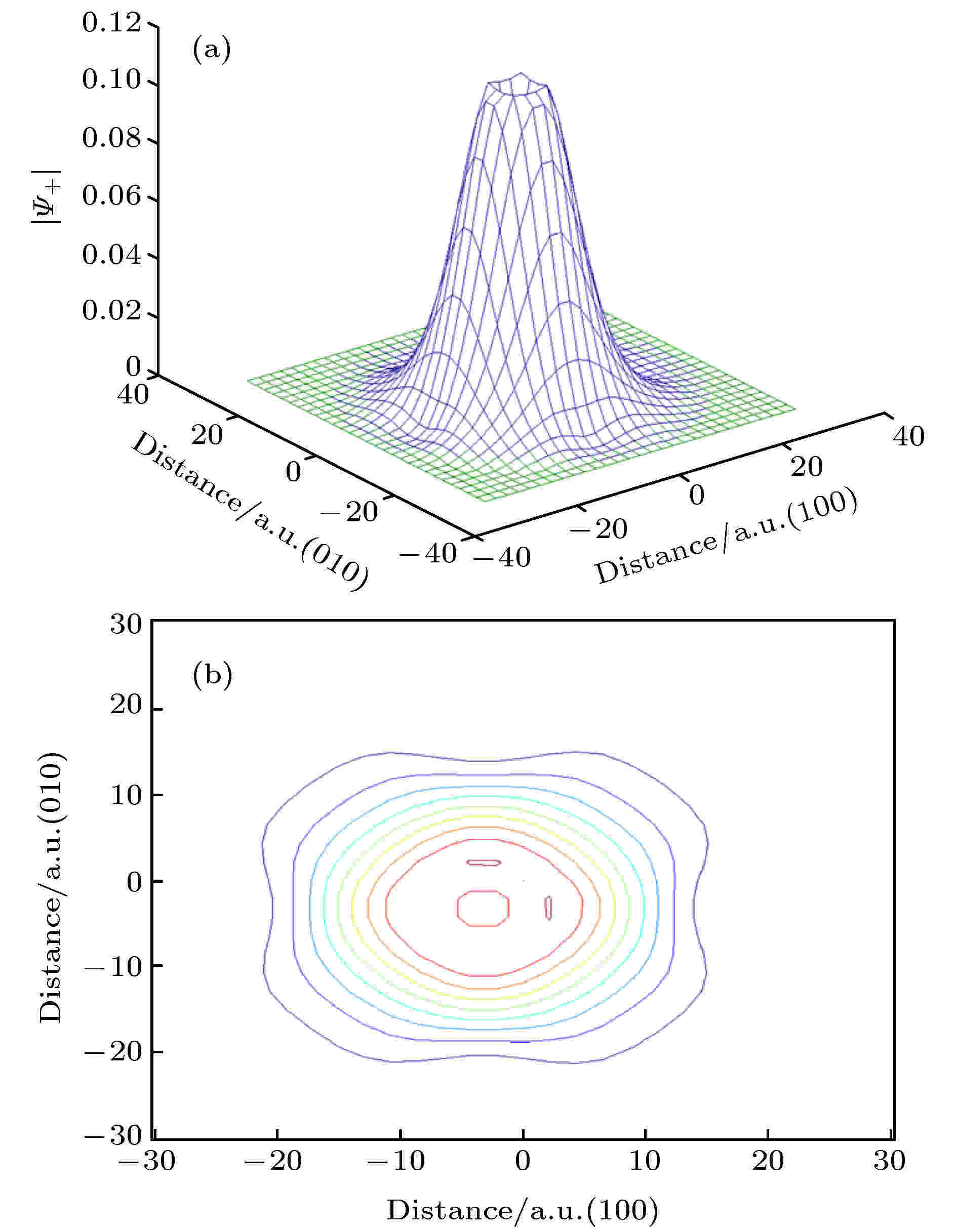图 3 金属钨中单个空位包含单个氢原子时的正电子波函数^[26]　(a) 三维立体图; (b)等高线图
Figure3. Calculated localized wave function of a positron trapped in a mono-vacancy bound with one hydrogen atom in tungsten^[26]: (a) Isometric plot; (b) contour plot.

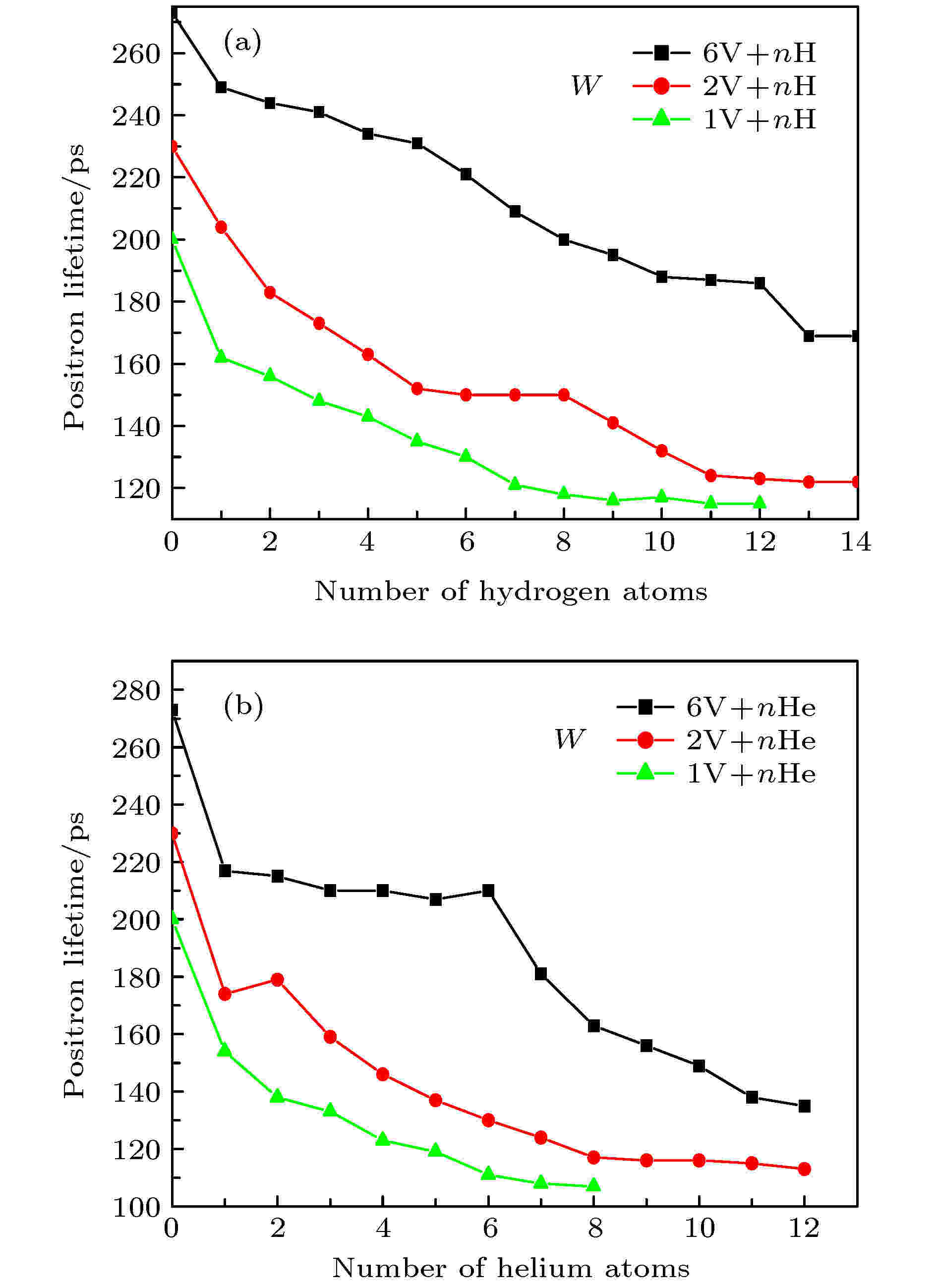图 4 不同尺寸的氢氦-空位复合体中正电子寿命^[26]
Figure4. Calculated positron lifetime in nano-void containing 1 V, 2 V, 6 V, and various H/He atoms^[26].

3 -->

3.1.2.高能氢氦辐照缺陷及氢氦-缺陷复合体表征

正电子寿命谱测量技术在金属合金氢/氦行为研究中, 除了用于直接估算氢/氦气泡尺寸和浓度, 更多是用于研究由高能氢/氦离子辐照产生的离位损伤缺陷及缺陷在退火、时效等热处理过程中的演化行为^[27]. Ishizaki等^[28]用正电子寿命谱研究铁和镍中氢氦对微空洞形成的影响, 正电子寿命结果表明, 镍样品比铁样品中空位团更容易长大, 氦原子比氢原子对微空洞的形成更有效, 但在两种金属中空洞长大对温度的依赖性, 氢辐照样品比氦辐照样品更大. 氢/氦离子辐照条件或模式的不同, 形成的辐照缺陷往往差异很大, 在正电子寿命谱中也能很好地体现出来. Han等^[29]对不同注量的氢离子、氦离子和氢氦离子混合辐照的12Cr-ODS钢进行正电子寿命谱测试, 实验结果表明氢离子辐照样品的正电子寿命随离子注量的增加变化很少, 氦离子辐照对样品产生了更大的损伤, 同时, 他们认为氢氦混合辐照的样品中氢与缺陷的相互作用不同于其他样品, 可能有氦-氢-空位(He-H-V)复合体形成. 寿命谱在形变位错与氢氦的相互作用研究中的应用也具有明显优势. Xu等^[30]用寿命谱研究了形变Ni样品中氦与位错的相互作用对材料机械性能的影响, 发现位错捕获氦的样品极限拉伸强度和总延伸量都有所增加. 他们还用寿命谱研究了氢氦辐照的Fe9Cr样品, 测得了氢氦-空位复合体的正电子寿命, 发现高能低剂量质子辐照后的Fe9Cr合金拉伸应力减小^[31].
2 -->

3.2.DBS在金属合金氢/氦行为研究中的应用

3 -->

3.2.1.高能氢/氦辐照离位损伤缺陷的深度分布

正电子湮没多普勒展宽测试在研究金属合金氢/氦行为中比寿命谱应用更广, 特别是基于慢正电子束流的DBS, 是研究这一问题的利器^[32]. 由于慢正电子束多普勒展宽测量正电子能量可调, 注入的深度可控, 因此可以探测样品表面到内部缺陷的深度分布.
高能氢氦辐照时, 氢氦离子会与样品中的原子发生级联碰撞产生离位损伤, 在表面到样品内部留下不同浓度的缺陷. 通常在注入能量的选择上, 会先根据研究目的使用SRIM程序计算离子的注入深度及离位损伤分布, 选择合适能量进行辐照实验. 正电子注入材料的深度可以用公式$Z(E)= 40000E^{1.6}/\rho$计算得到, 其中Z的单位是nm, ρ为材料的密度, E是正电子注入能量, 单位为keV. 因此可以用慢正电子深度探测敏感, 结合SRIM计算的深度分布讨论样品中缺陷浓度的变化. 如图5和图6所示, 为了更好地讨论不同辐照深度处氢氦与缺陷的相互作用, 采用VEPFIT程序^[33]对正电子数据进行拟合, 可以将氢/氦离子注入深度进行分区, 一般分成表面区(SR)、轨迹区(TR)、级联碰撞区(CR)和未辐照区(NIR).
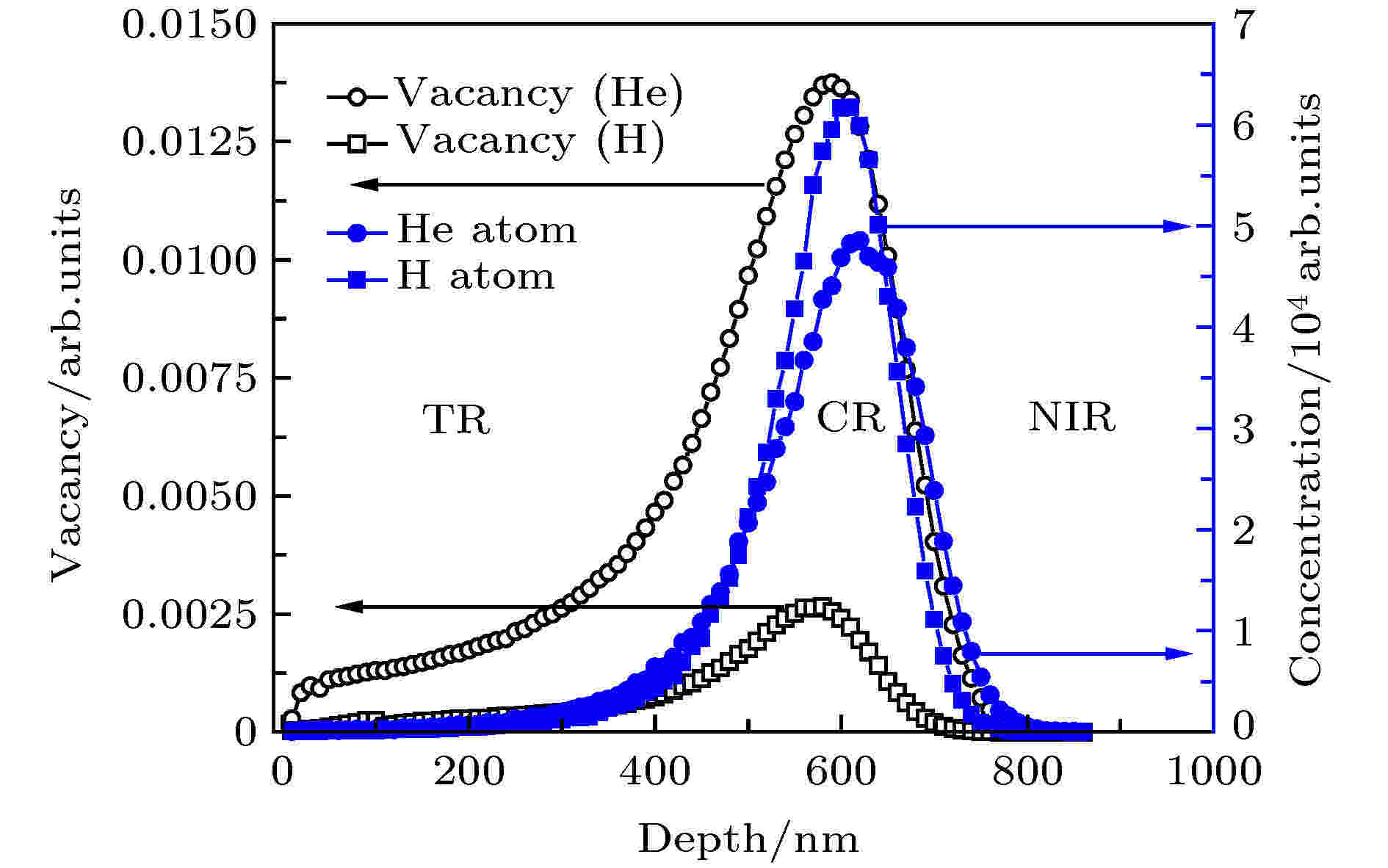图 5 SRIM模拟氢氦离子辐照低活化钢导致的辐照损伤及氢/氦浓度深度分布
Figure5. Profiles of damage and atom concentration in RAFM steel irradiated with 250 keV He²⁺ and 130 keV H⁺ calculated with SRIM.

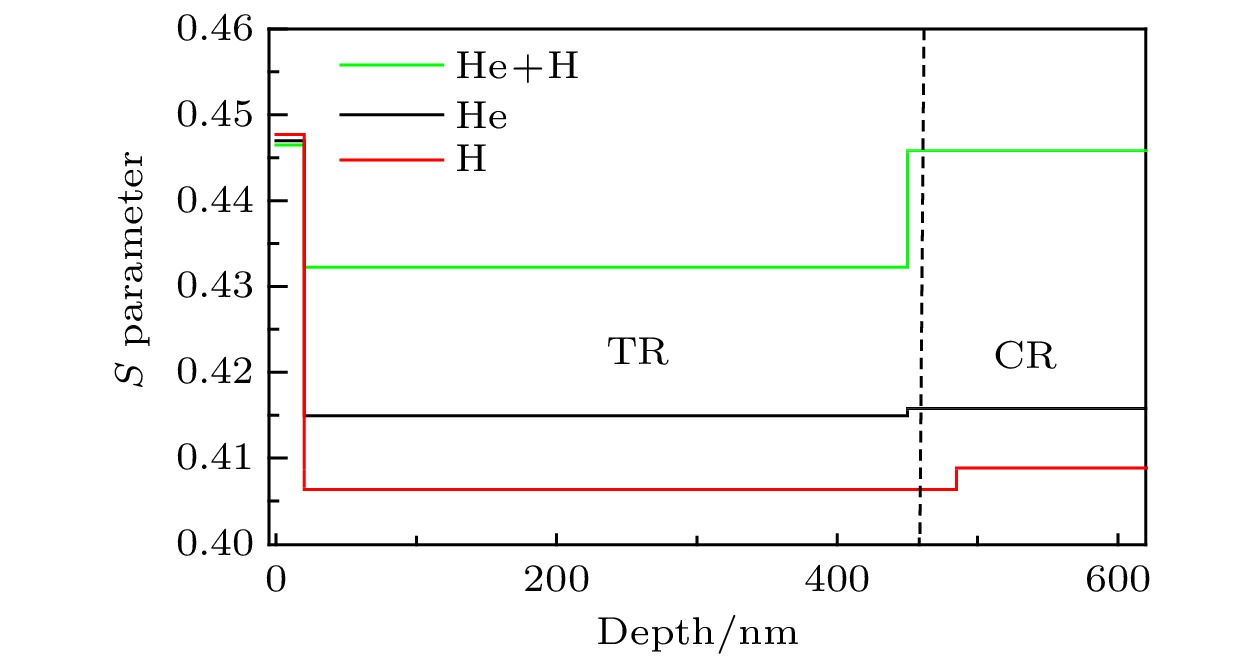图 6 VEPFIT拟合氢氦辐照样品的S参数随注入深度的变化
Figure6. Fitted S parameters versus VEPFIT for irradiated samples.

3 -->

3.2.2.辐照缺陷的演化行为及氢/氦-空位形成对温度的依赖性

正电子湮没DBS测试在研究金属合金中氢氦行为上, 几种典型的研究是氢氦辐照样品等时退火行为过程中的缺陷演化及氢氦的热稳定性、不同形变程度样品中氢氦与形变缺陷的相互作用、不同能量或剂量氢氦离子辐照对材料造成的损伤以及氢氦协同作用等. Lu等^[34]用多普勒展宽技术研究140 keV氦离子辐照的FeCrNi模型钢, 在423—873 K之间每隔50 K等时退火过程中微观缺陷的演化, 如图7所示. 他们研究发现辐照过程形成的不同类型辐照缺陷对氦具有不同的束缚能, 没有氦原子占据的空位在623 K退火后基本回复, He_nV_m复合体结构具有较大的解离能, 需要在温度高于773 K下热处理后才能逐步分解, He-空位复合体分解释放的He原子聚集形成He泡并稳定存在. 对于氢辐照后的金属合金材料, 氢原子会与辐照导致的空位型缺陷结合形成H_nV_m等复合体结构, 这些复合体结构的热力学演化行为也可以用慢正电子DBS来研究. Jin等^[35]用100 keV的氢离子辐照Fe0.6Cu合金, 辐照剂量为0.1 dpa. 在真空下, 辐照的实验样品分别在150, 200, 300, 400 ℃和500 ℃进行0.5 h等时退火处理, 采用多普勒展宽技术研究H_nV_m复合体随退火温度的变化. 研究结果表明: Fe0.6Cu合金经过氢离子辐照后, 相比未辐照样品, ΔS参数增大量不大, 如图8所示. 这初步说明氢离子辐照合金后, 氢占据辐照产生的空位型缺陷形成H_nV_m复合体结构; 在150 ℃退火处理后, 辐照样品的S参数变大, 且在损伤区域出现了峰值, 这说明150 ℃退火处理导致H_nV_m复合体分离; 随着退火温度的升高, S参数的峰向表面方向移动, 这表明氢容易在样品中扩散, 而剩余的空位型缺陷随着退火温度升高逐渐恢复. 同时, 他们利用S-W曲线对缺陷类型及正电子湮没机制进行了讨论. 如图9, S-W实验结果表明不同温度下等时退火, 正电子在缺陷中的湮没机制不同, 尤其是在150, 200和300 ℃退火下出现了a, b和c三个聚集区域, 分析其原因是由氢的逃逸导致剩余的空位团簇增多, 并且随着退火温度的上升, 空位团簇的尺寸逐渐减小; 在退火温度为400和500 ℃时, 空位团簇几乎消失, S-W曲线的斜率几乎与未辐照的样品相同.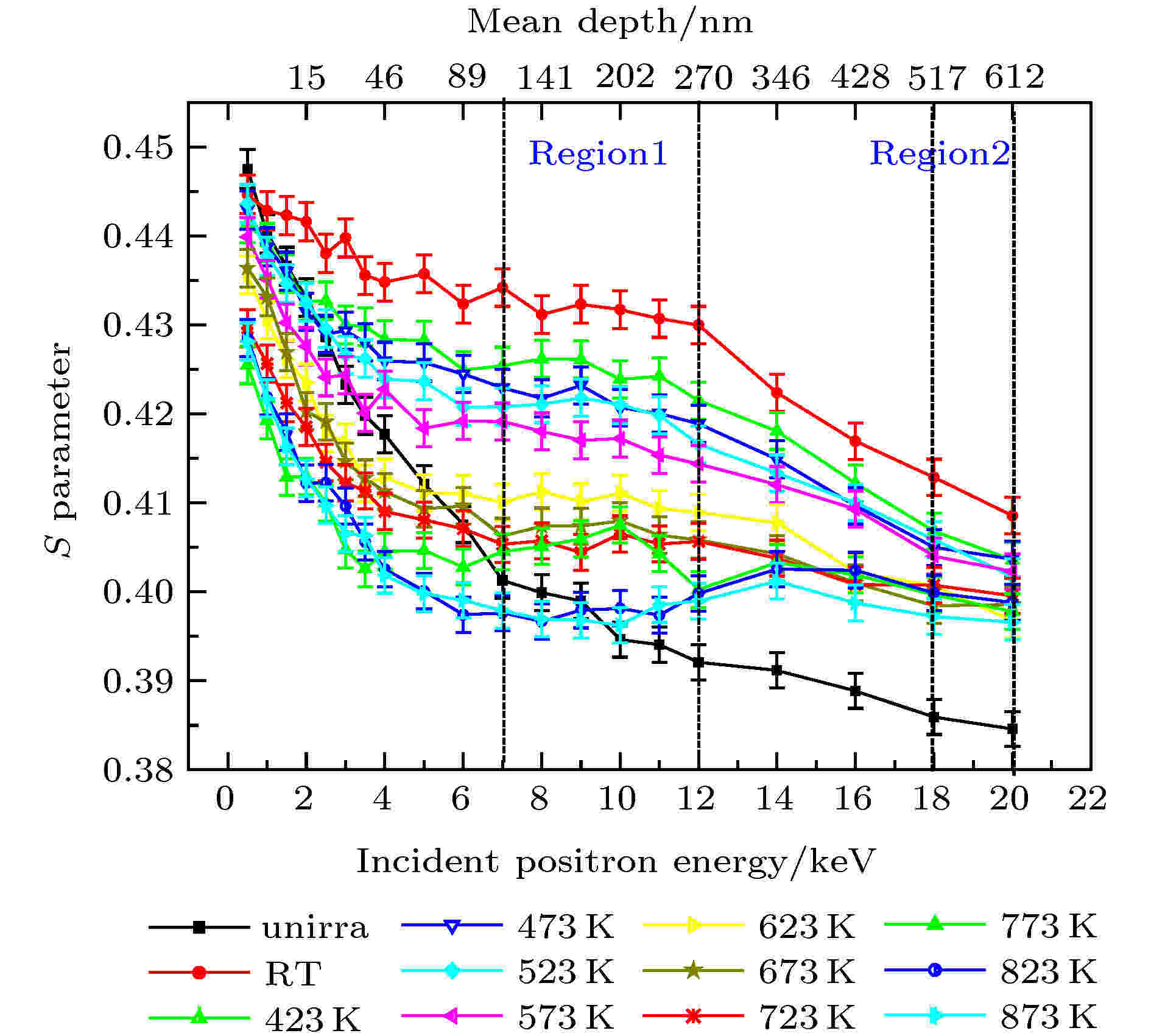
图 7 氦辐照Fe17Cr14.5Ni等时退火过程S-E曲线随温度变化过程^[34]
Figure7. Variation of S parameters versus incident positron energy for He⁺ irradiated Fe17Cr14.5Ni alloy during isochronal annealing^[34].

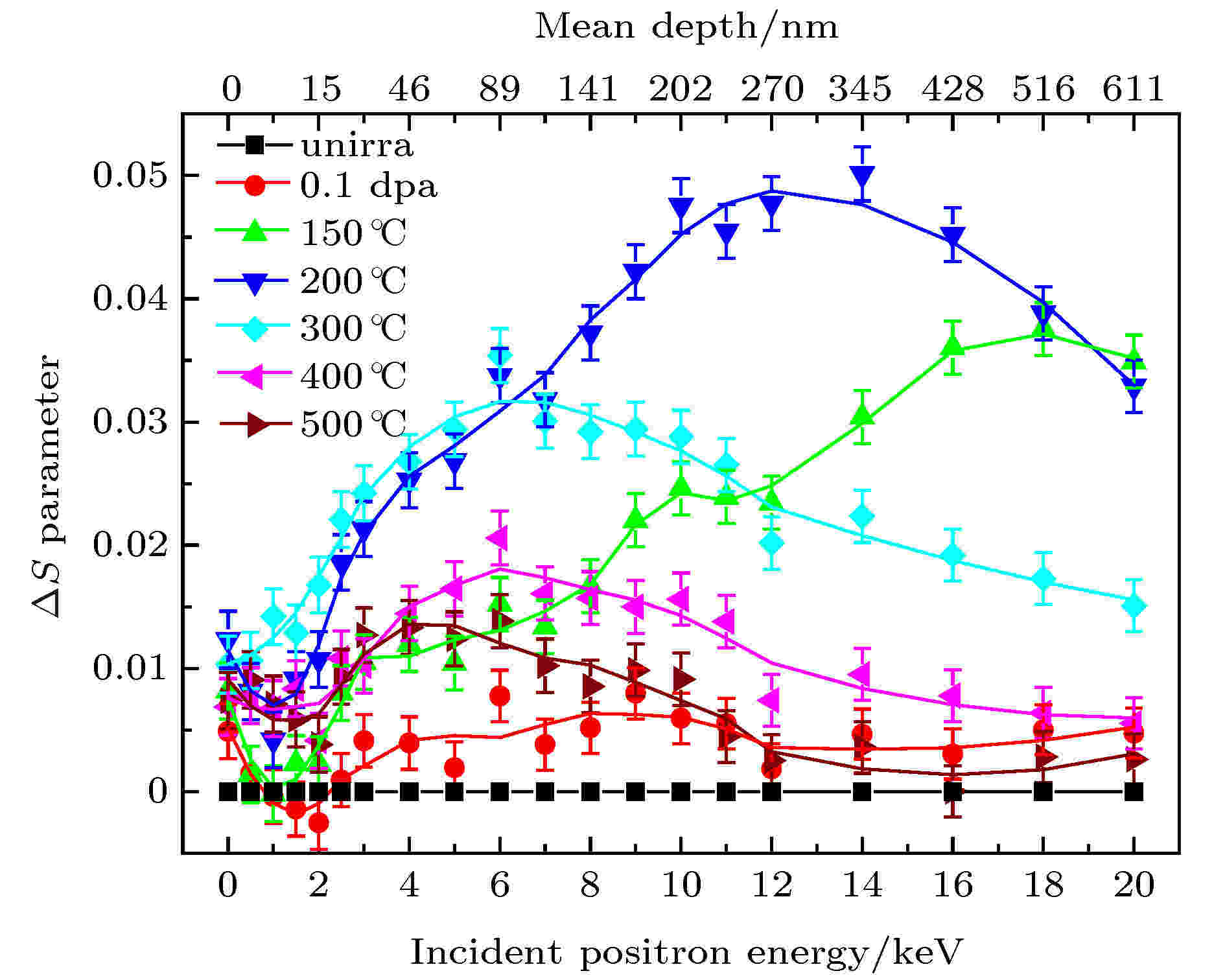图 8 氢辐照FeCu等时退火过程ΔS-E曲线随温度变化过程^[35]
Figure8. Evolution of the S parameters in H-ions irradiated FeCu alloys during isochronal annealing^[35].

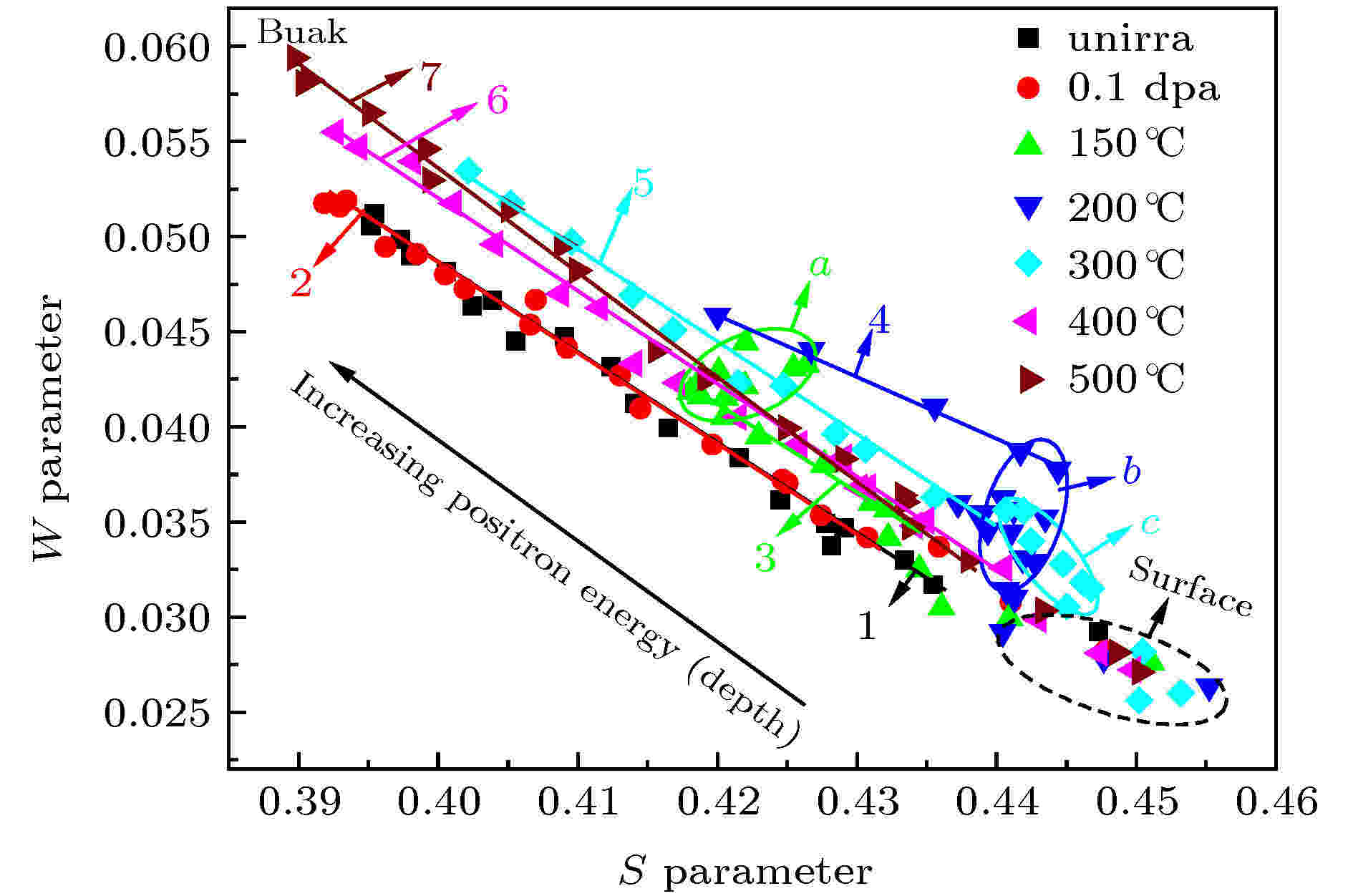图 9 氢离子辐照FeCu等时退火过程S-W参数的变化^[35]
Figure9. S-W plots for the H-ions irradiated samples during isochronal annealing^[35].

在不同温度下材料中缺陷的类型或浓度不同, 因此氢氦辐照后样品中形成的氢氦-缺陷复合体中, 氢氦原子数与缺陷的比例也不同. 图10是本课题组用100 keV的氦离子在不同温度下辐照Fe9Cr合金测得的慢正电子多普勒展宽结果, 图中可以看到不同辐照温度下样品中空位缺陷的分布有很大差异, 这种差异在氦富集区有所减小, 这是因为氦原子占据空位形成了复合体, 使得各个样品中正电子探测的有效开空间体积差异缩小, 但由于复合体中氦原子与空位的比例不一样, 因此需要通过S-W参数进一步分析(如图11所示).
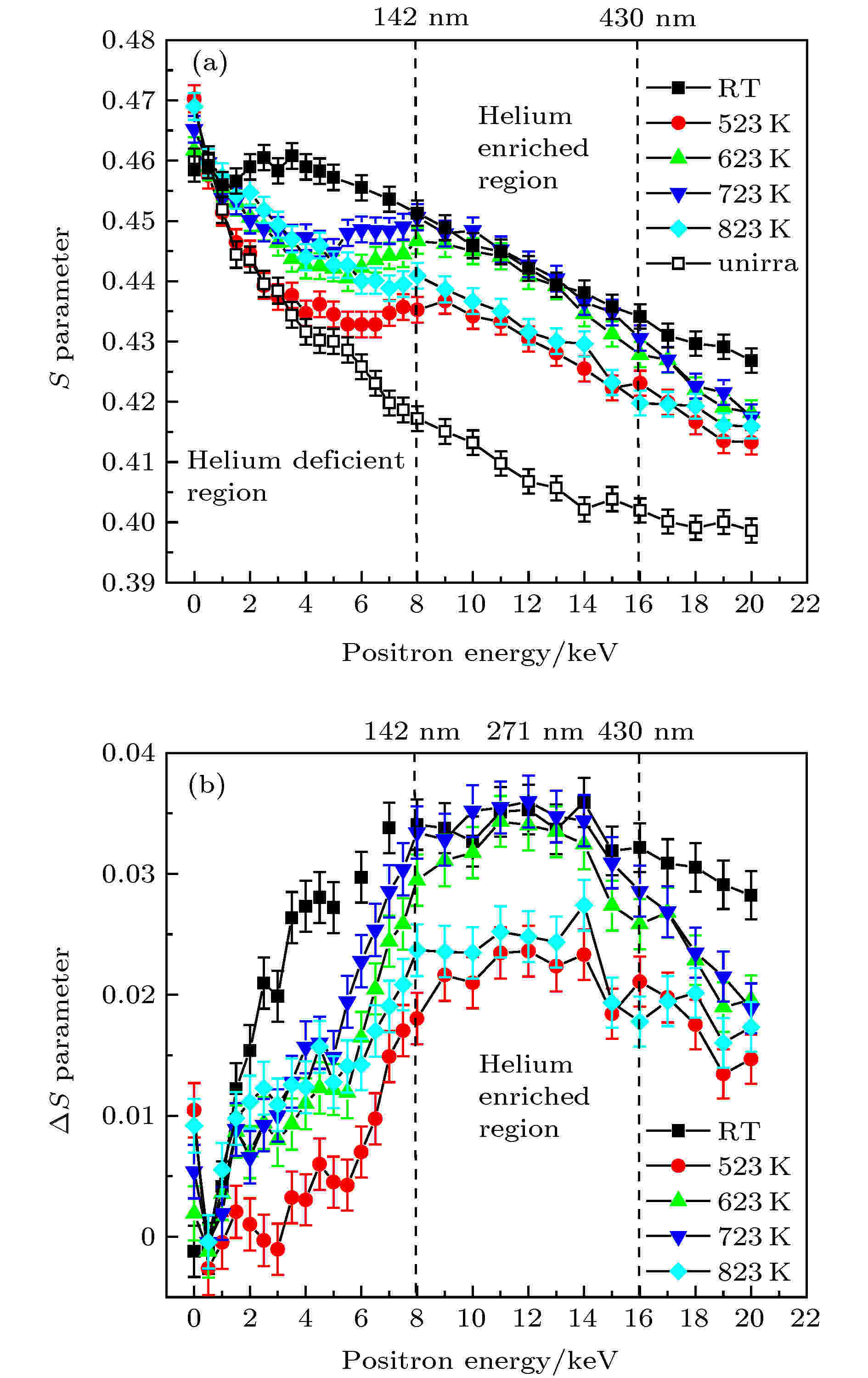图 10 Fe9Cr合金氦离子辐照前后S (?S)参数随正电子注入能量的变化^[36]
Figure10. S-parameter and ?S as a function of positron incident energy (mean implantation depth) in irradiated Fe9Cr alloys and for unirradiated specimen^[36].

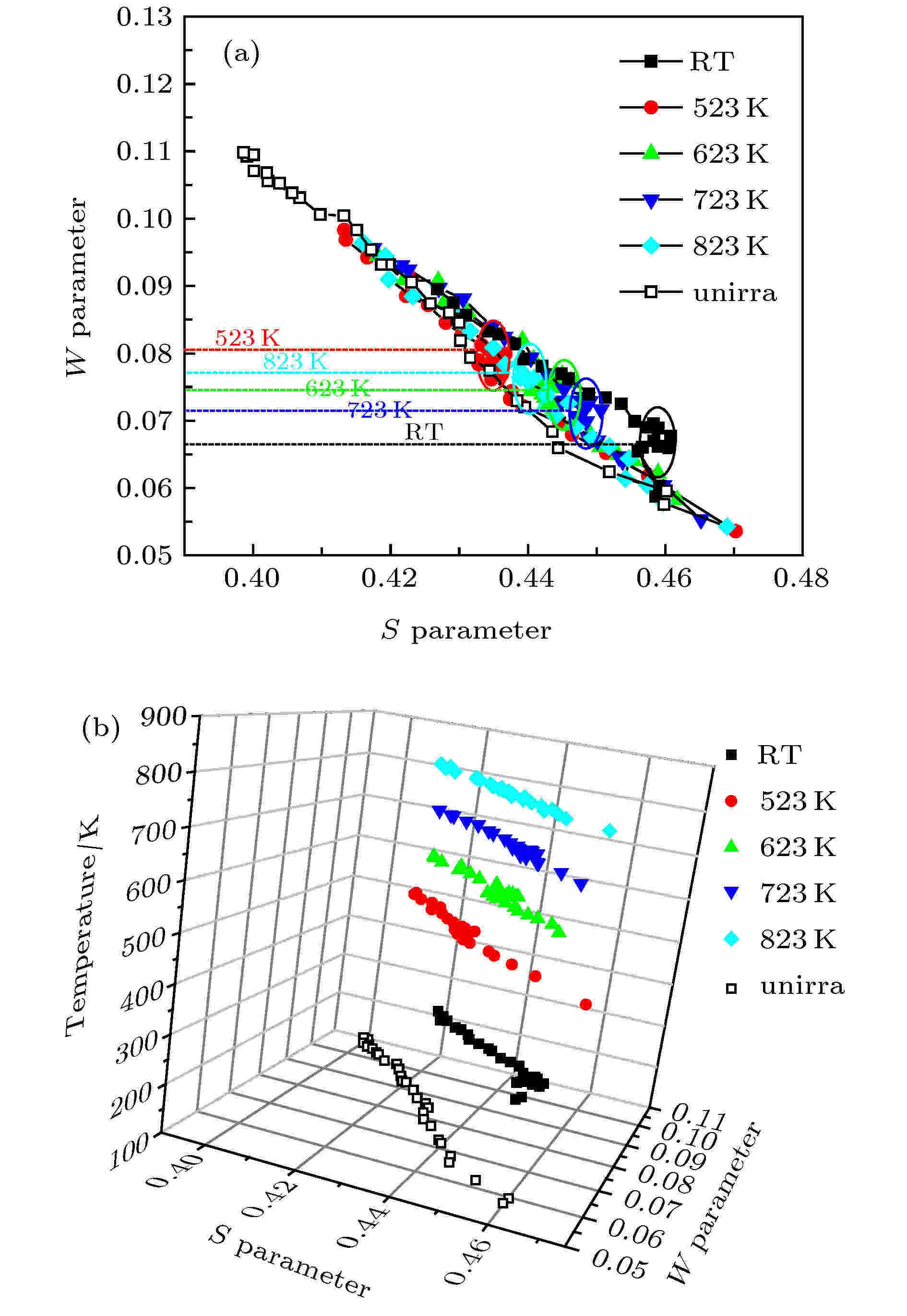图 11 Fe9Cr合金氦离子辐照前后S-W的变化^[36]
Figure11. W-parameter as a function of the S-parameter for irradiated Fe9Cr alloys and for unirradiated one^[36].

由于氦原子占据空位会影响W参数的变化, 在S-W出现(S, W)聚集在某一区域, 可以根据聚集区域的不同来判断复合体中氦原子与空位的比例. 我们对结果进行分析, 发现室温辐照下有大量的He_mV₁和单空位共存, 而氦泡或高压He_mV_n (m > n)团簇容易在523和823 K辐照下通过He_mV_n (m < n)吸收氦原子形成, 在723 K辐照的样品肿胀率最大.
3 -->

3.2.3.氦与位错/界面的相互作用

界面或位错的存在可能吸引氢氦原子在其附近聚集^[37,38], 使得氢氦原子大量被位错捕获, 降低了氢氦原子与材料金属原子的级联碰撞所引起的空位、空洞等点缺陷的数量. 界面或位错与氢氦的相互作用是一个比较热门的课题, 上文介绍了PALS在形变位错与氢氦原子相互作用研究中的应用, 接着简单举几个DBS在这方面的应用实例. Gong等^[39]采用慢正电子束DBS技术研究氦原子在位错的作用下扩散迁移的机制. 图12中可以看出由于表面效应, S参数在注入正电子能量较低处较高, 并随着注入正电子能量增加而降低, 对于形变未注氦的样品, 在正电子能量超过11 keV之后就趋于稳定了, 在稳定区内形变样品注氦之后S参数明显下降, 这是由于氦的迁移能很低(0.08 eV), 在位错线的附近, 氦原子容易迁移, 在很短的时间(2 × 10⁴ s)迁移扩散的深度能到达1 μm, 对于形变样品在稳定区内有大量的氦原子存在, 并且容易被微观缺陷捕获形成氦-微观缺陷复合体, 使得微观缺陷的浓度降低, 从而导致样品中S参数的降低. Hu等^[40]用50 keV氦离子辐照不同形变的304不锈钢, 形变前后均进行慢正电子多普勒展宽测量, 如图13所示, 样品注氦后的S参数均明显升高, 但呈现一定的规律性, 随形变量的增大S参数依次下降. 较高能量的氦离子注入到样品内部, 会与材料内部原子发生非弹性碰撞, 造成空位、间隙原子等辐照缺陷的产生, 从而正电子被这些缺陷大量捕获湮没导致S参数升高. 经过形变后的样品内部本就含有大量的位错型缺陷, 注氦后, 形变量大的样品S参数反而减小, 说明原有的位错型缺陷导致在这一区域处(2—14 keV)正电子与低动量电子的湮没量减少, 也就是说氦离子注入样品后导致的损伤缺陷的密度随形变量的增大而减小.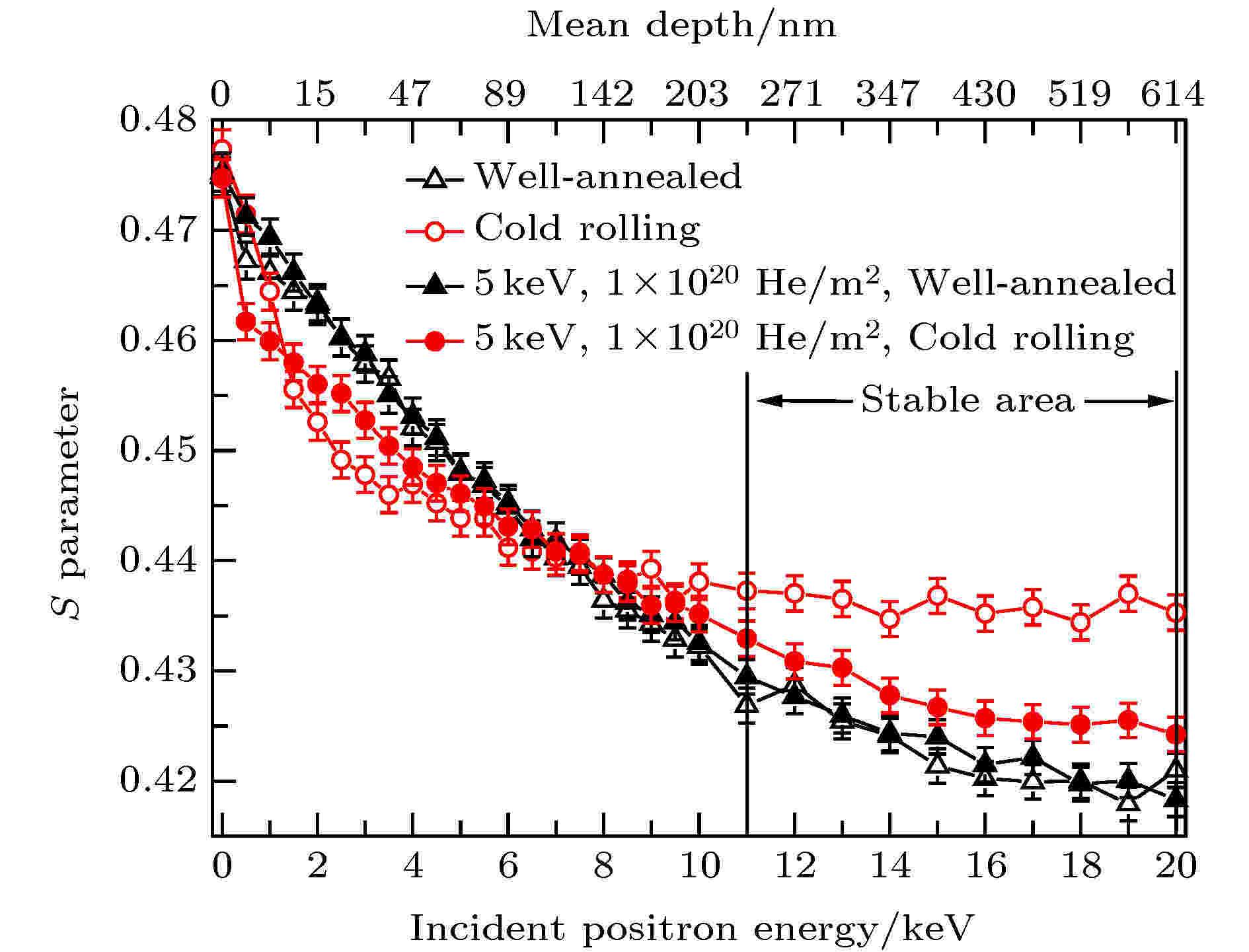
图 12 氦离子注入充分退火和形变的纯铁样品 S-E曲线变化^[39]
Figure12. Evolution of the S parameters in well-annealed Fe and deformed Fe with He-ions irradiation^[39].

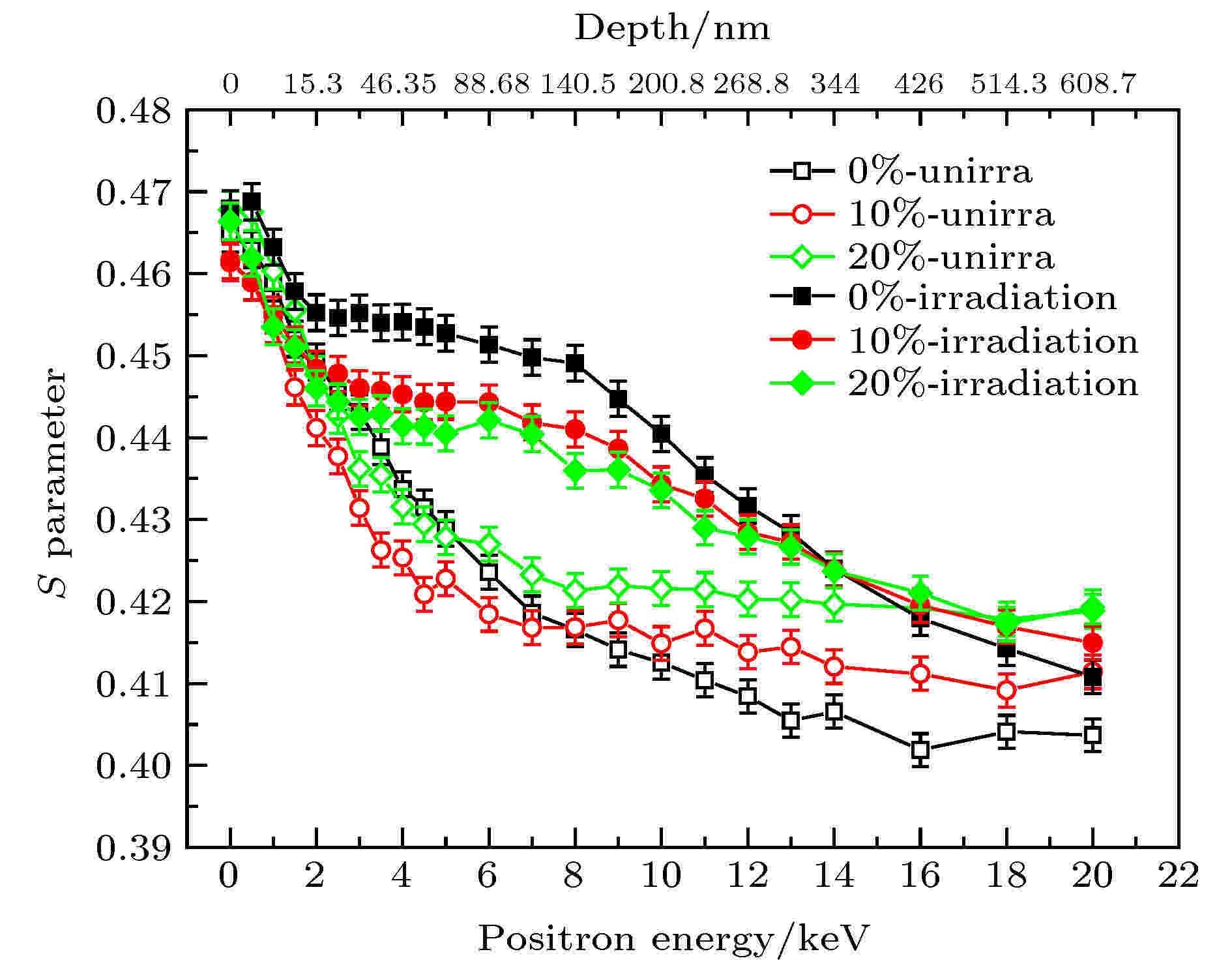图 13 氦离子辐照不同形变量的304不锈钢辐照前后S-E曲线变化^[40]
Figure13. S-E curves for deformed 304 steel irradiated with He-ions^[40].

3 -->

3.2.4.氢氦与离位损伤缺陷的协同效应

在能量、剂量及辐照模式对金属合金辐照损伤的影响方面, Jiang等^[41]对质子和重离子辐照反应堆压力容器钢引入的缺陷进行慢束多普勒展宽测量, 根据S-E曲线的相对变化, 发现空位的迁移、聚集形成空位团的尺寸大小随着质子辐照的剂量增大. Qiu等^[42]采用能量为140 keV的氦和80 keV的氢先后依次辐照RAFM钢, 并改变相应的辐照剂量, 多普勒展宽测量数据表明, 经辐照后的样品内部有空位团、氦-空位复合体、氢-空位复合体缺陷产生, 相比于原始样品只有单一类型的缺陷, 辐照后的样品包含的缺陷类型却有两种; 并且在这一过程中He的注入剂量对产生的辐照损伤起主要作用. Xin等^[43]利用DBS研究由氢和氦先后辐照RAFM钢引入的空位型缺陷, 他们认为在室温下两种离子注入的先后顺序以及辐照剂量大小都会对产生的微观缺陷有一定影响. Yuan等^[44]进行了三种离子(Au, He, H)的辐照损伤实验, 并用多普勒谱测试辐照样品, 比较了离子连续依次辐照和同时辐照之间的差异性.
氢氦在高温下会产生协同效应, 其对材料的影响比单独的氢或氦更大, 是材料中氢氦研究的一个重要课题^[3-6]. 许多应用TEM, 纳米硬度等方法对氢氦协同效应的研究清楚的表明氢氦同时辐照的双束实验比用单一的离子辐照材料造成的辐照损伤更大^[45,46]. Zhu等^[47]采用慢正电子束DBS, 从PAS的角度也观察研究了低活化钢(RAFMs)中氢氦协同效应. H, He离子高温辐照低活化马氏体不锈钢, 分别采用250 keV的氦(5.1 × 10¹⁵ He/cm²)和130 keV的氢(2.1 × 10¹⁶ He/cm²)在450 ℃下注入低活化马氏体不锈钢中, 注入种类和顺序分为三种样品: 仅注氦、仅注氢、先注氦后注氢, 慢正电子多普勒测量结果如图14所示. RAFM钢的S-E曲线中明显可以看到He + H样品的S参数远高于其他样品的S参数, 且?S_{He + H}大于?S_He + ?S_H, 表明高温注入下PAS技术反映了RAFM钢中明显的氢氦协同作用.
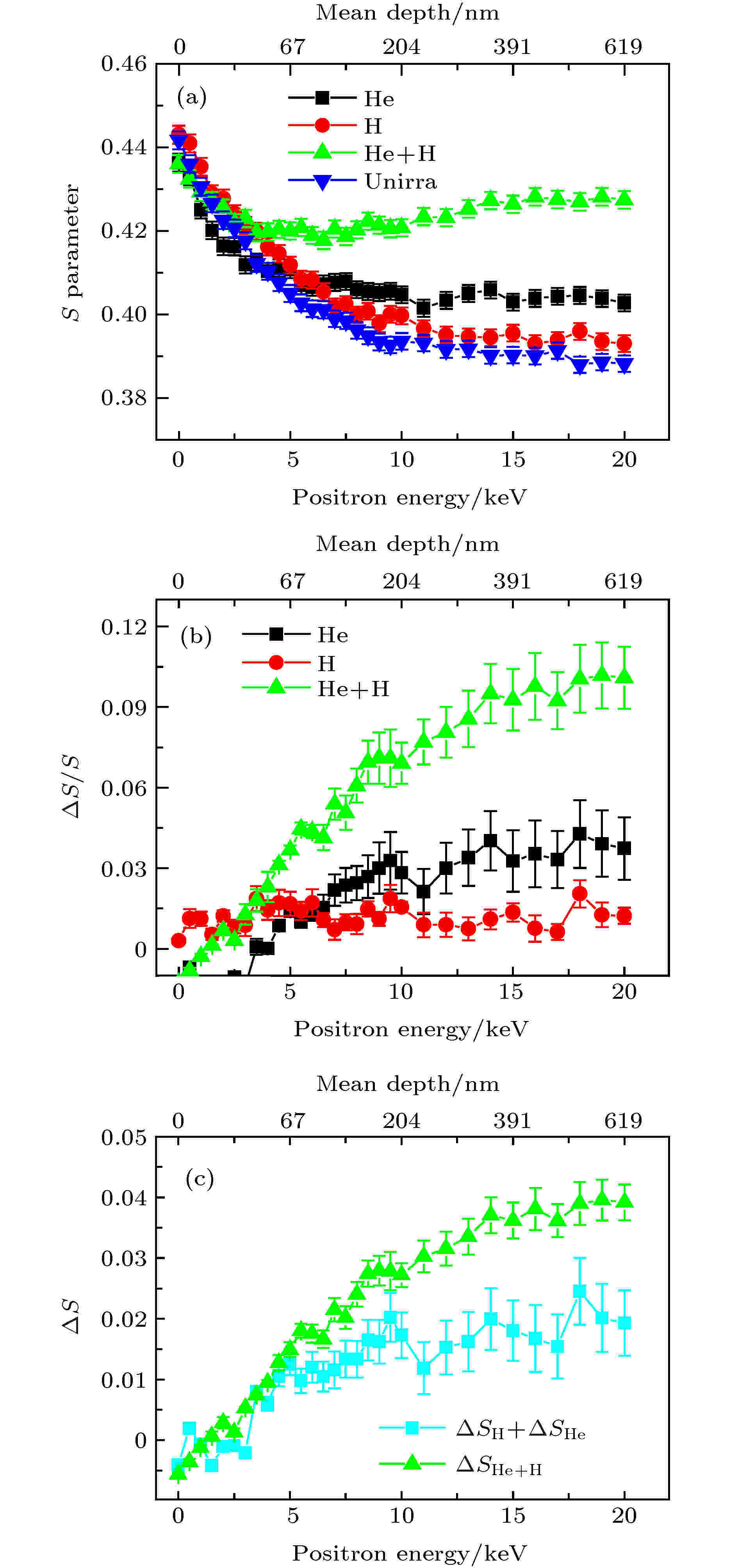图 14 氢氦离子辐照RAFM钢正电子慢束结果^[47]
Figure14. S-parameter (a) and ?S/S (b) as a function of incident positron energy. ?S_He + ?S_H and ?S_{He + H} parameter were also shown in (c)^[47].

3 -->

3.2.5.面向等离子体材料中的氢/氦行为

正电子多普勒展宽测量在面向等离子体材料W合金中(氢、氦)-离位损伤研究的应用也日益广泛. Zhu等^[48]用高能的Ar离子辐照W合金引入离位损伤, 随后将样品暴露在低能高剂量的氘等离子体中, 对注氘前后的样品进行DBS分析, 如图15所示, 结果显示注氘后样品的S参数整体减小, 这说明氘进入样品后会占据高能离子辐照产生的离位损伤.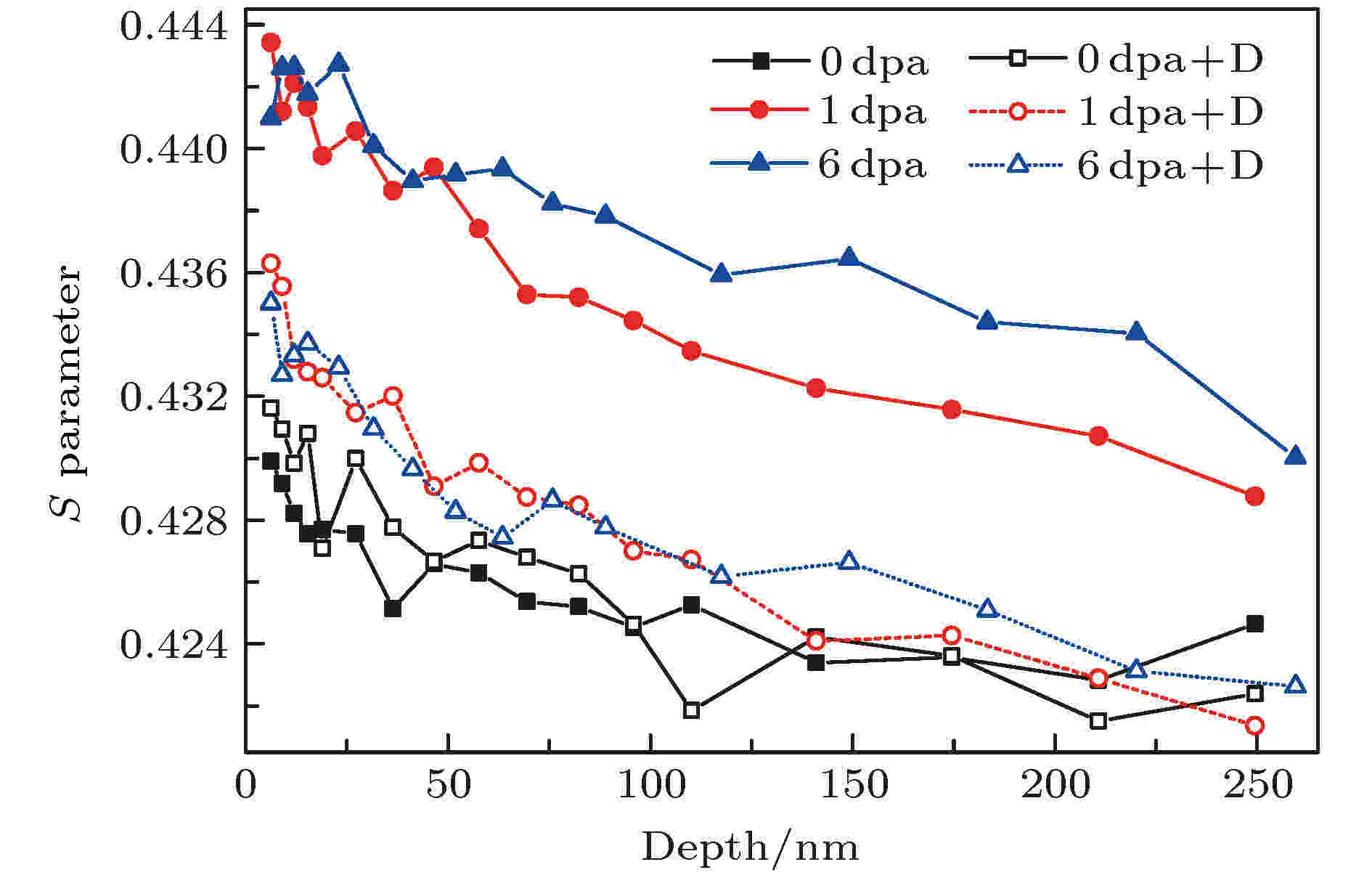
图 15 高能Ar辐照W合金注氘前后的正电子慢束结果^[48]
Figure15. The S parameter versus depth in the argon-damaged tungsten samples (0/1/6 dpa) with and without deuterium plasma exposure^[48].

Kong等^[49]用3 MeV的Au离子对多晶W进行预辐照, 引入辐照损伤, 然后注入不同剂量的氦离子, 用慢束多普勒展宽技术研究了辐照损伤对氦的影响, 结果如图16所示. 他们发现氦的注入剂量在4.8 × 10¹⁵— 4.8 × 10¹⁶ ions/cm²范围内, 空位是氦泡形核初期最重要的氦捕获点.
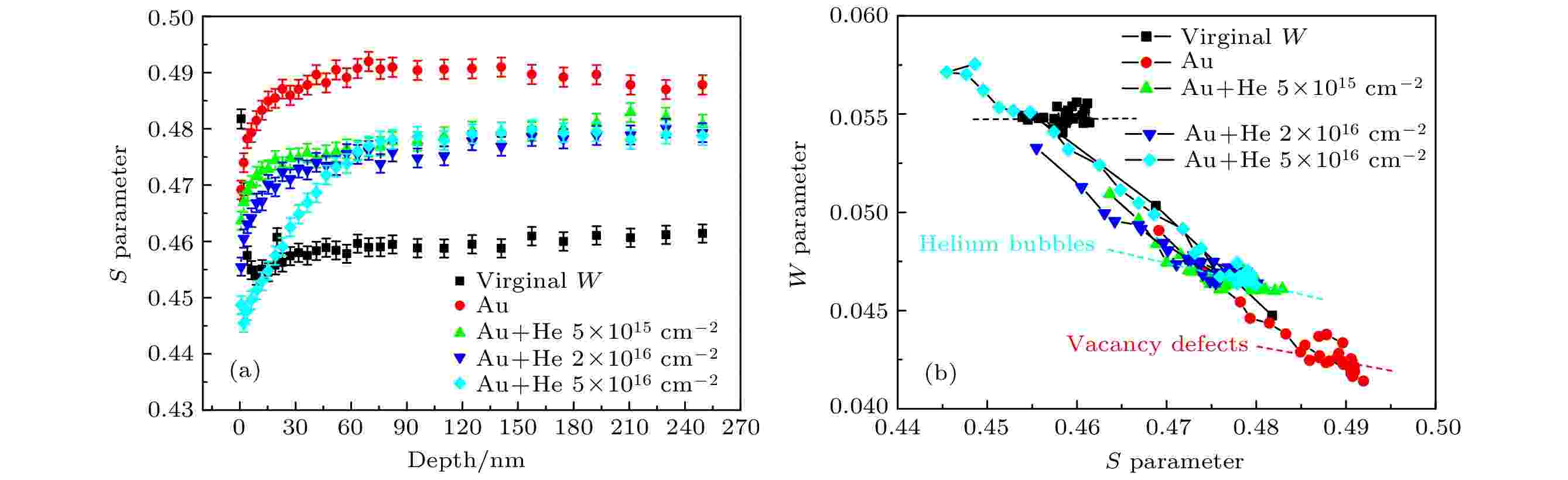图 16 高能Au辐照多晶W样品注氦前后(a) S-D (深度)曲线, (b) S-W 曲线^[49]
Figure16. (a) The S parameter versus depth in the tungsten samples, and the (S, W) plots are shown in (b)^[49].

氦原子的“自捕获”是指多个氦原子聚集在金属中形成团簇后对晶格原子造成挤压导致原子离位形成一个自间隙原子和一个空位, 这些氦团簇最终被该空位“捕获”形成氦-空位复合体. 这一概念是Wilson等^[50,51]1981年提出的, 并且被实验证实. 正电子多普勒展宽测量在研究氦的自捕获现象中也有很大优势, Gong等^[52]对低能高剂量氦等离子注入的形变316L不锈钢进行多普勒展宽测试, 发现辐照样品离表面60—200 nm区域内, 氦的自捕获导致了S参数的增大, 如图17所示, 同时, 他们还证实了位错存在的样品中氦原子的扩散行为.
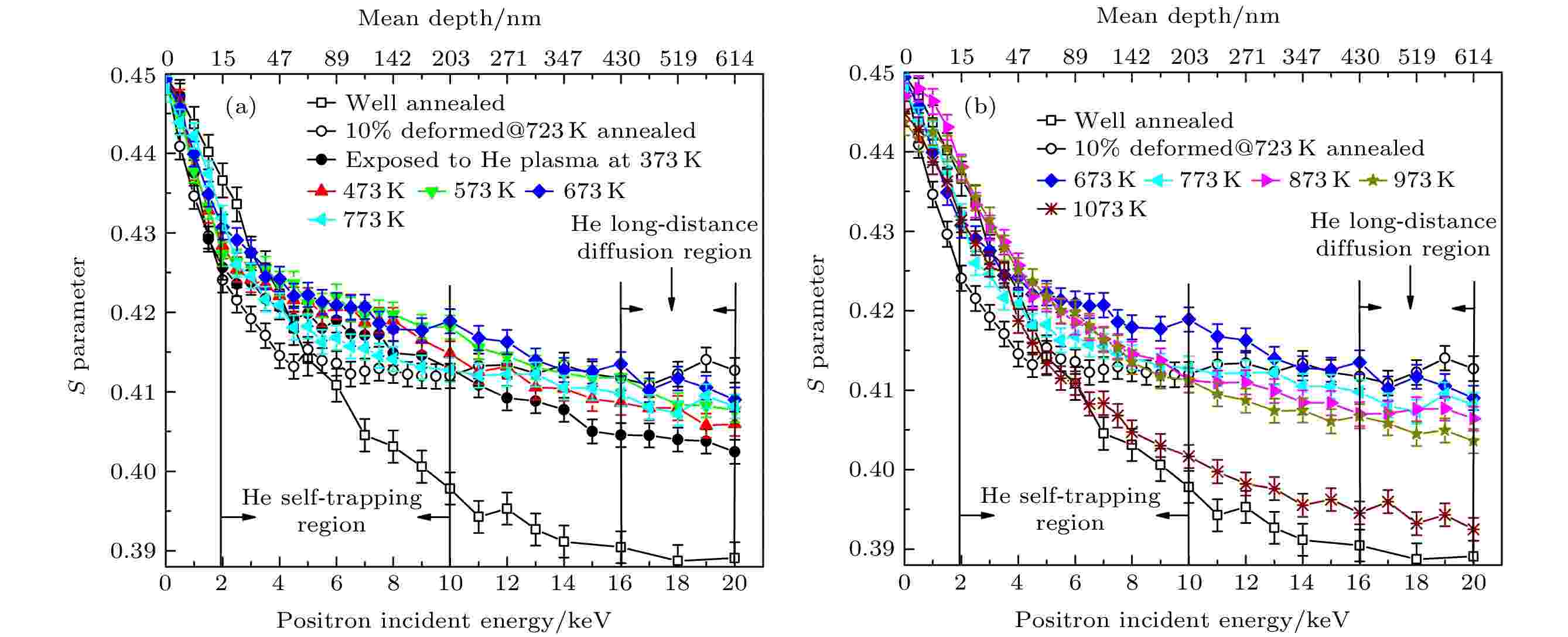图 17 形变316 L钢样品低能高剂量氦等离子体辐照前后的S-E曲线^[52]
Figure17. Evolution of S-E curves in deformed 316 L steel exposed to high flux and low energy helium plasma^[52].

2 -->

3.3.CDB谱在金属合金氢/氦行为研究中的应用

对材料中氢/氦分布的检测方法通常有TEM^[53], TDS^[54-56]和离子束分析(如质子背散射)^[57]等, 但这些方法各有自己的缺点: 1)透射电镜只能观察到氦泡或大孔洞, 氢/氦-缺陷复合体在没有长大前并不能观察到, 而这往往是氢氦在材料中最主要的存在形式; 2) TDS能够研究氢氦在材料中的热力学行为, 但不能给出氢氦在材料的分布信息, 且测量是破坏性的; 3)质子背散射研究还在材料中的分布也有其困难之处, 因为氢氦的原子序数小, 卢瑟福背散射截面随元素原子序数平方的减小而减小. 正电子湮没DBS是无损且对深度灵敏的检测元素在湮没点周围分布的特色核分析方法. 近二十年发展了一种双探头符合系统, 大大提高了峰背比, 从而实现了湮没谱中高动量电子信息分析^[18,58]. 高动量电子是指原子的壳层电子, 正电子与其湮没会在湮没谱的高动量区形成一个峰, 不同元素不同壳层的电子与正电子湮没的几率不同, 因此可以利用这些实现湮没点处元素的鉴别. CDB技术被广泛用于探测合金中元素的析出^[59,60]以及半导体中杂质缺陷复合体元素的鉴定^[61,62], 这些年也逐渐被应用在金属合金中氢氦元素的检测.
3 -->

3.3.1.氢原子对正电子湮没处电子密度的影响

Cao等^[63]将Fe9Cr合金在室温下进行20 keV的氦离子辐照, 随后进行慢正电子测试, 图18是样品的W参数随正电子能量的变化曲线, W参数反映了高动量电子的信息, 与湮没点周围元素的信息有关, 在W-E曲线中正电子能量为4.5 keV附近出现了细微的变化, 这可能是湮没点处高动量电子密度发生了变化. 为进一步分析此处样品中高动量电子的信息, 他们采用慢正电子CDB测试, 将能量为4.5 keV的慢正电子注入辐照后的样品(注入深度约58 nm)进行测试, 实验结果如图19所示, 在电子动量(8—14) × 10^–3m₀c范围内出现由氦引起的峰, 峰值在11.8 × 10^–3m₀c, 这里m₀是电子的静止质量, c是光速, 这个结果与Sabelova等^[64]理论计算的氦原子影响CDB谱的动量范围在(5—12) × 10^–3m₀c比较接近, 可能是氦原子外层电子与金属原子壳层电子发生杂化引起的. Sato等^[65]也研究了F82H钢中氦原子对CDB谱的影响, 结果显示, 氦引起的峰在(3—12) × 10^–3m₀c范围内.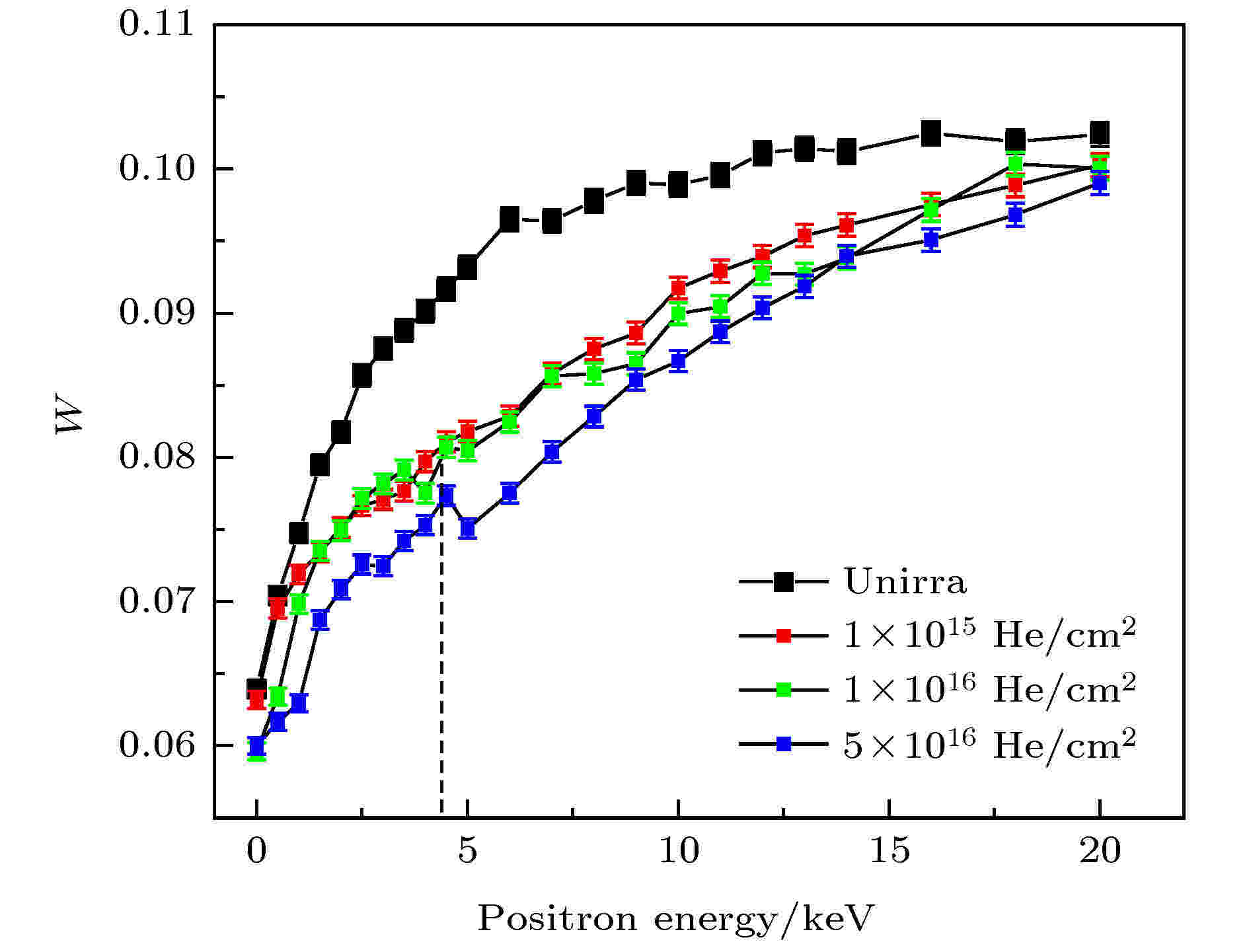
图 18 氦辐照前后Fe9Cr合金中W参数随正电子能量的变化
Figure18. Evolution of the W parameters in Fe9Cr alloy with He-ions irradiation.

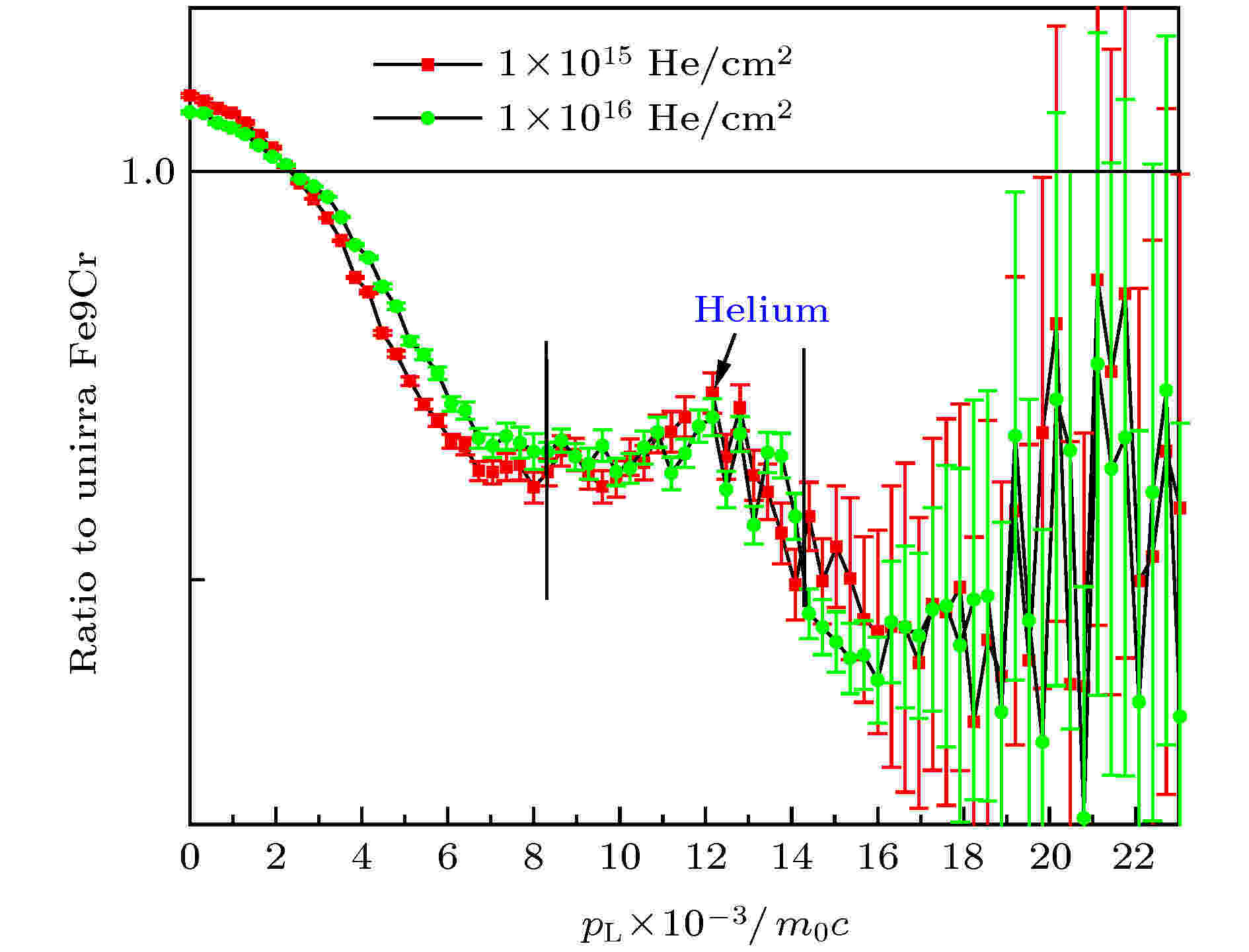图 19 注量为1 × 10¹⁵和1 × 10¹⁶ He⁺/cm²的氦辐照Fe9Cr样品CDB测试曲线^[63]
Figure19. CDB ratio curves for the Fe9Cr alloy irradiated with a dose of 1 × 10¹⁵ and 1 × 10¹⁶ He⁺/cm^2[63].

Xu等^[66]用符合多普勒技术检测了氦辐照的Ni和中子辐照的Cu内部微观空洞中捕获的氦原子, 在13.5×10^–3m₀c处测得氦峰, 如图20所示. 他们认为即便在低氦浓度的金属中也可以用CDB技术检测到氦. 理论上样品中氢原子也会对正电子湮没点处高动量电子密度产生影响, 但由于氢原子相对活跃且不易聚集, 实验上探测到的结果有一定偶然性.
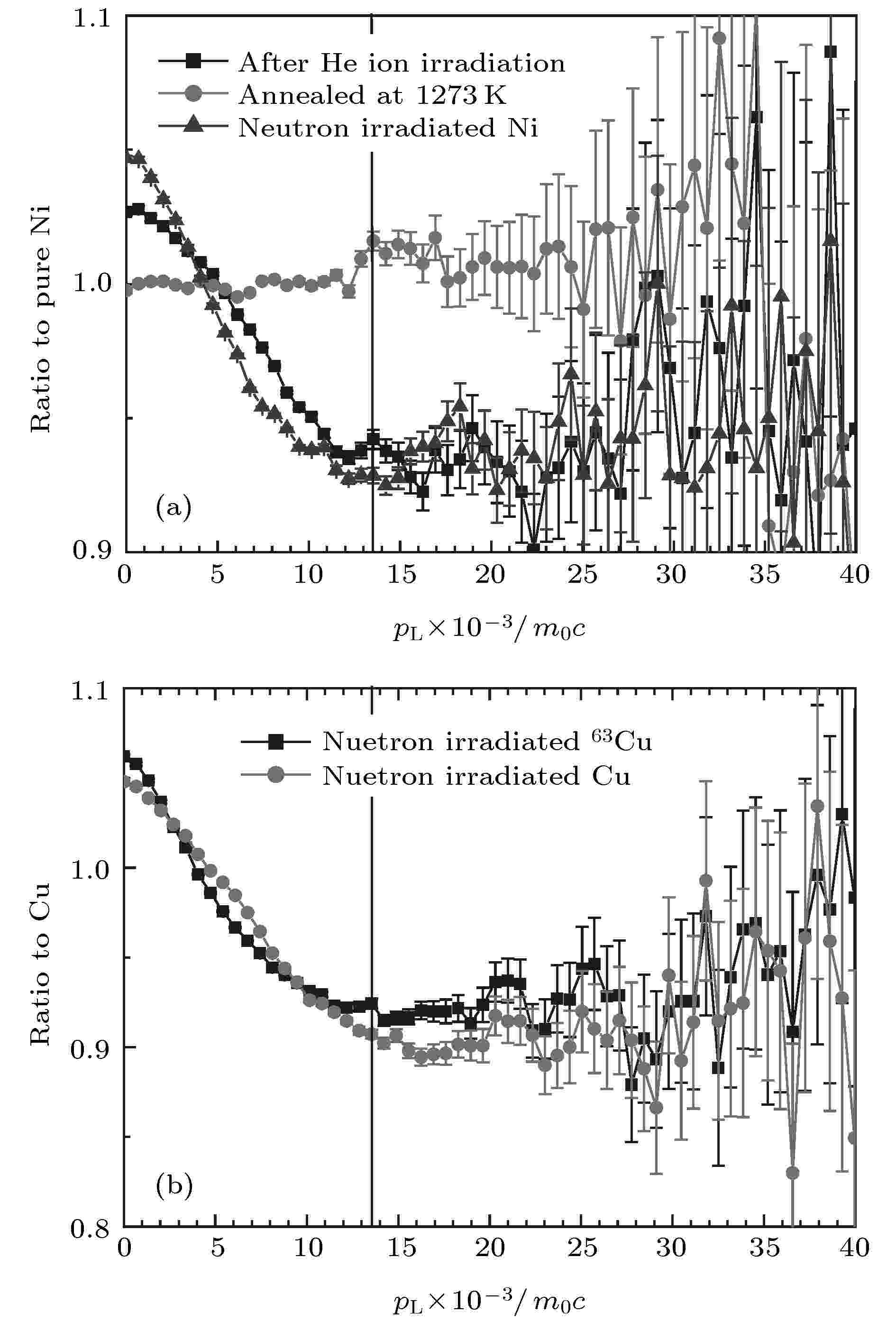图 20 氦或中子辐照的纯Ni(a)和Cu(b)样品的CDB测试曲线^[66]
Figure20. CDB ratio curves for the Ni irradiated with He-ions (a) and for the Cu irradiated with neutron^[66](b).

3 -->

3.3.2.符合多普勒谱表征氦-空位复合体的演化

符合多普勒技术对注氦样品的退火效应也非常灵敏, 图21是本课题组用50 keV氦离子注入316L不锈钢(氦主要沉积在200 nm处, 能量为10 keV的正电子可探测到该深度)后对样品进行退火处理, 退火前后进行CDB测试, 谱线中动量小于2.5 × 10^–3m₀c的部分表示正电子与低动量电子或自由电子湮没部分(S参数), 动量范围在(2.5—22.0) × 10^–3m₀c的部分为正电子与高动量电子湮没部分(W参数). 从图21可以清楚看到这两个动量范围峰值(峰值越高表示该动量的电子与正电子湮没概率或比例越大)随退火温度升高的变化, 退火处理后, 由于空位型缺陷的回复, 正电子与低动量或自由电子湮没比例减小, 因此S参数降低. 由于温度升高促使氦原子运动加剧, 游离的氦原子容易聚集长大形成团簇或氦泡, 当正电子被氦-空位团簇周围的类空位缺陷吸引并湮没时, 在CDB谱的高动量区(3—14) × 10^–3m₀c会有所反映.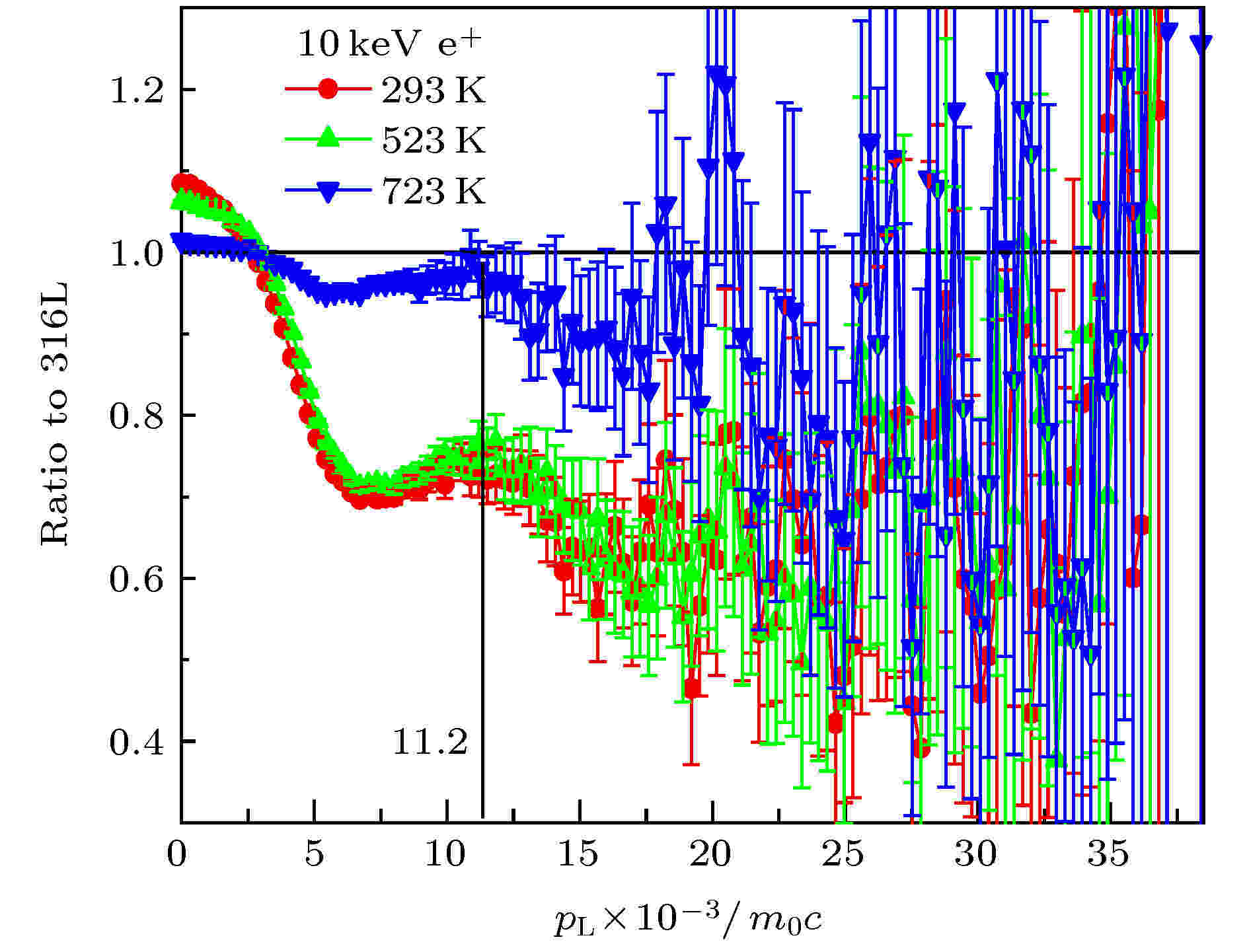
图 21 氦辐照的316L样品退火前后的CDB测试曲线
Figure21. CDB ratio curves for the He-ions irradiated 316L samples during isochronal annealing.

PAS对金属合金中氢氦行为的研究, 一方面是研究高能氢氦对金属合金产生的离位损伤, 另一方面是研究氢氦引入材料后它们在材料中迁移、聚集、被微观缺陷捕获的行为以及氢氦-空位复合体向氢氦泡演化过程. 寿命谱、DBS以及CDB谱在研究这些具体问题上各尽所能, 很好的发挥了它们的优势, 但也存在不足之处, 这些方法多是通过对空位型缺陷的探测来间接推测氢/氦行为, 对氢/氦在金属合金中的直接检测还不够成熟. 为弥补这一不足, 大力发展正电子束团湮没寿命谱测量系统、CDB谱和寿命-动量关联谱(A-MOC)等测量技术是很好的选择. 其次, 要实现正电子研究对金属合金材料中氢氦原子的定量贡献, 一些理论模型需要进一步发展和优化.