摘要:为了在天基远距离条件下估计空间目标的姿态参数, 提出了基于时序光谱信号分级求解目标表面参数及姿态参数的方法. 第一级, 在三轴稳定状态下将空间目标等效为“双面模型”, 引入双向反射分布函数(bidirectional reflectance distribution function, BRDF)的多级融合模型表征复杂材料的光谱反射特性, 基于时谱信号与时谱信号模型对双面光谱BRDF与面积乘积进行重构. 第二级, 为了抑制双面耦合特性对姿态估计的影响, 构建双面特性分离度, 并基于该度量最大化实现光谱波段优选. 第三级, 构建目标姿态运动状态下的时序光谱信号模型, 以模型值与观测值之间的误差为目标函数, 利用Levenberg-Marquardt算法对姿态参数进行估计. 仿真表明, 该方法更适用于方形本体的目标, 且反演误差会随相位角和探测器噪声的增大而增大, 在信噪比SNR ≥ 10条件下反演误差在2%以内.
关键词: 空间目标/
姿态估计/
时谱信号/
可见光/
双向反射分布函数

English Abstract

全文HTML

--> --> -->

在天基光学空间目标态势感知领域, 目前的研究侧重于远距离点目标检测、目标轨迹的预测与确认. 而在远距离成像时, 目标无结构、纹理信息, 此时利用时序点信号对空间目标的工作状态及基本物理属性参量进行反演具有重要的意义, 可有效支撑空间目标探测以及在轨维护的相关决策.
空间目标的可见光波段光度信号由目标反射太阳光得到, 它是目标外形结构、尺寸、姿态、表面材料等属性参量的函数^[1-7]. 在已知的目标表面材料反射特性模型条件下, 国内外开展了一系列对于空间目标姿态、外形的估计研究. Chaudhary等^[8]提出了对空间目标信息求解的匹配方法, 根据实际在轨测量以及仿真得到的目标光度曲线建立数据库, 并且记录其对应的目标大小、种类、位置、周期等信息. 将实测的目标光度曲线通过分级匹配实现目标识别与确认. Cegarra Polo等^[9]结合长时间的观察数据与仿真得到的结果, 针对立方体目标提出了基于匹配的姿态求解方法. Wetterer等^[10]建立旋转火箭体的运动姿态模型, 针对地基探测条件下得到的光度信号, 利用无迹卡尔曼滤波对其旋转轴以及旋转速率进行估计, 误差在10%左右. 在此基础上, Holzinger等^[11]通过建立目标形状不确定性的一阶动力学模型以及角速度的模型, 通过粒子滤波器实现空间目标在姿态变化较快过程中的姿态角估计, 但该方法只能对目标旋转速度做一个大致的估计, 且目标为一个简单的几何体, 没有考虑到目标卫星的帆板结构. Linares等^[12-14]针对已知的六边形模型, 采用Ashikhmin-Shirley和Cook-Torrance两种双向反射分布函数(bidirectional reflectance distribution function, BRDF)模型描述目标表面的反射特性. 利用无迹卡尔曼滤波方法, 在给定目标运动角速度的情况下, 对其表面材料反射率、面积与质量进行了估计. 在此基础上, Linares等^[15]将目标看做一个简单的结合体, 利用Phong模型及辐射压力模型, 建立了一个考虑到位置、速度、姿态、角速率及表面参数的模型, 提出了一种基于光度曲线和角度数据的自适应估计方法, 实现了对空间目标本体的姿态及模型参数的估计, 但该方法需要目标材料表面模型及形状特性的支撑, 并且不适用于含太阳帆板的空间目标的特性参量反演. Furfaro等^[16]采用基于卷积神经网络方案的数据驱动分类方法, 利用实测光度曲线对空间目标进行分类, 卷积神经网络明显优于其他方法, 正确率达到了75%, 而袋装树的正确率为63%, 支持向量机的正确率为53%. Jia等^[17]通过光学重力透镜实验得到不同恒星的光度数据, 研究对比了深度神经网络与其他不同机器学习方法(k-近邻算法、卷积神经网络和递归神经网络)对目标识别的效果, 发现所有方法的准确性均高于94%, 而深度神经网络的准确性最高, 达到了96%以上. Arakawa等^[18]利用卷积神经网络对仿真图像中卫星的姿态角进行了估计, 当无噪声时, 角度估计的平均误差为18.2°; 添加噪声信噪比为5时, 角度估计的平均误差有所上升, 达到了22.4°. Furfaro等^[19]生成了空间目标在预定轨道参数下以不同姿态运动的光度曲线的大型数据集, 采用深度学习来训练光度曲线与空间目标形状之间的逆函数关系, 对四种不同形状进行了识别、训练和验证, 对于包含40000个样本的验证集, 能够达到92.2%的精度.
综上所述, 上述方法对于一定限制条件下的姿态估计具有一定的适用性, 但还存在一定的不足, 分析如下: 第一, 利用机器学习进行反演识别, 往往需要先制作庞大的数据集, 且相对于仿真数据和实测数据的测试结果有一定差异; 第二, 这些方法大都认为目标形状已知, 且只考虑了目标本体的姿态估计问题, 没有考虑到太阳能帆板占比及其对姿态估计的影响, 因此这些方法对存在太阳能帆板的空间目标不适用; 第三, 上述研究在对目标表面材料进行表征时, 用到的均为Phong, Cook-Torrence等单一BRDF模型, 并没有考虑到目标表面材料复杂带来的单一BRDF模型引入的模型表征误差, 会造成姿态滤波估计的结果很难收敛. 因此, 针对含有太阳能帆板的空间目标, 在其形状特性及表面材料光学特性未知的情况下, 需要对其在轨姿态估计方法开展进一步研究. 针对上述问题, 以含太阳帆板的三轴稳定卫星为研究对象, 本文提出了在轨空间目标姿态估计的分级求解方法, 流程如图1所示. 第一级, 在三轴稳定状态下建立了融合帆板在轨动态特性的双面模型, 并引入了BRDF的多级融合模型表征复杂材料表面的光谱反射特性, 以在轨测量的时序光谱信号为输入, 重构每个光谱波段对应的双面模型参数; 第二级, 为了抑制双面耦合特性对姿态反演的影响, 构建双面特性分离度, 基于分离度最大优选最优谱段; 第三级, 在目标姿态运动状态下, 基于最优谱段的双面模型参数构建时序光谱信号模型, 以该模型与实测信号之间的差异为目标函数, 以姿态参数为优化变量, 采用非线性迭代优化算法对姿态参数进行估计, 即求解出了在轨卫星绕Y轴以及Z轴旋转的角速度; 最后, 对算法进行仿真验证.
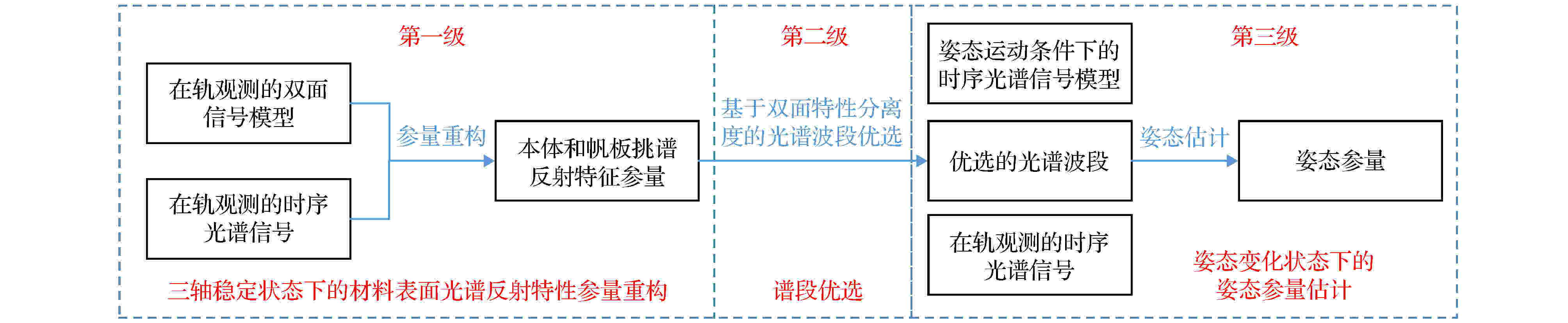图 1 空间目标姿态参数估计方法的流程图
Figure1. Flow chart of attitude parameter estimation of space object.

2

-->

2.1.双面信号模型

3 -->

2.1.1.目标光谱信号模型

对于正常工作状态下的对地定向三轴稳定卫星, 对其进行同轨道面或近轨道面以目标跟踪模式观测时, 如图2所示, 观测卫星的光学系统观测到的目标本体面基本不发生变化, 并且本体和帆板不发生相互遮挡, 因此将卫星模型简化为双面模型, 即本体一个面, 帆板一个面, 探测器入瞳处每个时刻接收到的光谱辐通量为^[20]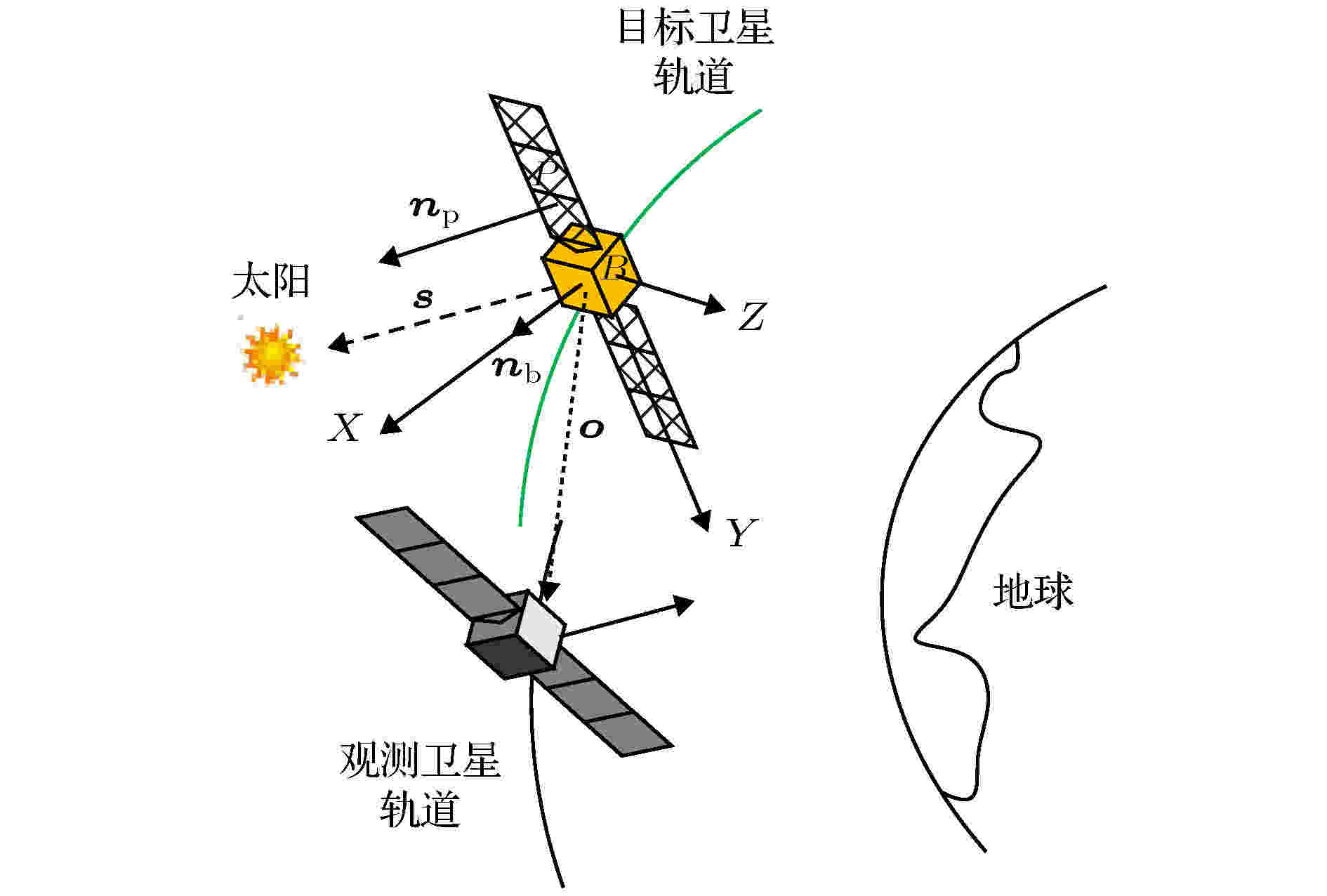
图 2 三轴稳定卫星的在轨观测示意图
Figure2. Observation diagram of the on-orbit three-axis stabilized satellite.

$\varPhi \left( {t,\lambda } \right) = {\varPhi _{\rm{p}}}\left( {t,\lambda } \right) + {\varPhi _{\rm{b}}}\left( {t,\lambda } \right), $

$\begin{split}{\varPhi _{\rm{p}}}\left( {t,\lambda } \right) =\;& \dfrac{{{E_{{\rm{sun}}}}\left( \lambda \right){A_{{\rm{aperture}}}}}}{{{{\left\| {{{{T}}_{\rm{0}}}} \right\|}^2}}}{A_{\rm{p}}}\left\langle {{{{n}}_{\rm{p}}} \cdot {{s}}} \right\rangle \left\langle {{{{n}}_{\rm{p}}} \cdot {{o}}} \right\rangle \\&\times{f_{\rm{p}}}\left( {\lambda,{{{n}}_{\rm{p}}},{{o}},{{s}}} \right), \end{split}$

$\begin{split}{\varPhi _{\rm{b}}}\left( {t,\lambda } \right) =\;& \dfrac{{{E_{{\rm{sun}}}}\left( \lambda \right){A_{{\rm{aperture}}}}}}{{{{\left\| {{{{T}}_{\rm{0}}}} \right\|}^2}}}{A_{\rm{b}}}\left\langle {{{{n}}_{\rm{b}}} \cdot {{s}}} \right\rangle \left\langle {{{{n}}_{\rm{b}}} \cdot {{o}}} \right\rangle \\&\times{f_{\rm{b}}}\left( {\lambda,{{{n}}_{\rm{b}}},{{o}},{{s}}} \right), \end{split}$

式中, ${\varPhi _{\rm{p}}}\left( {t, \lambda } \right)$和${\varPhi _{\rm{b}}}\left( {t, \lambda } \right)$分别为帆板和本体部分反射至入瞳处的光谱辐通量, ${A_{\rm{p}}}$和${A_{\rm{b}}}$分别为帆板和本体被观测表面的面积, ${E_{{\rm{sun}}}}\left( \lambda \right)$为太阳辐照度, ${{{n}}_{\rm{p}}}$和${{{n}}_{\rm{b}}}$分别为本体坐标系(X轴指向卫星运行方向, Z轴指向地球中心, Y轴可由右手惯性系决定)下帆板面和本体面的单位法向量, ${{s}}$和${{o}}$分别为本体坐标系下目标到太阳和到探测器入瞳中心的单位矢量, ${{{T}}_{\rm{0}}}$是相机坐标系原点在本体坐标系下的坐标, ${f_{\rm{p}}}\left( {\lambda, {{{n}}_{\rm{p}}}, {{o}}, {{s}}} \right)$和${f_{\rm{b}}}\left( {\lambda, {{{n}}_{\rm{b}}}, {{o}}, {{s}}} \right)$分别表示帆板面和本体面的BRDF, $\left\langle \cdot \right\rangle $为点积运算, ${\left\| {\cdot} \right\|^2}$为2范数运算.
在轨观测过程中, 光度信号$\varPhi \left( {t, \lambda } \right)$, ${E_{{\rm{sun}}}}\left( \lambda \right)$, ${A_{{\rm{aperture}}}}$由探测系统获得, 为已知量; ${A_{\rm{p}}}{f_{\rm{p}}}\!\left( {\lambda, {{{n}}_{\rm{p}}}, {{o}},\! {{s}}} \right)$和${A_{\rm{b}}}{f_{\rm{b}}}\left( \lambda, {{{n}}_{\rm{b}}}, {{o}}, {{s}} \right)$即本体和帆板的面积与BRDF乘积为未知量. ${{{T}}_{\rm{0}}}$以及${{s}}$, ${{o}}$, ${{{n}}_{\rm{b}}}$与观测的几何位置相关, 可基于空间定轨、定位方法获得, 可认为已知量, ${{{n}}_{\rm{p}}}$可根据帆板对日指向的约束计算得到.
太阳能帆板绕Y轴转动, 为确保太阳能帆板获得最大能量, 帆板在入射光方向的投影面积应达到最大. 根据矢量几何关系可得帆板法向量${{{n}}_{\rm{p}}}$的计算公式为

${{{n}}_{\rm{p}}} = {{Y}} \times {{s}} \times {{Y}}, $

其中× 为叉乘运算, ${{Y}}$为沿着Y轴的单位方向向量.
3 -->

2.1.2.BRDF融合表征模型

对于非合作目标, 其尺寸及表面材料未知, 可能为混合材料表面. 针对这种表面, 选择多级BRDF融合表征模型, 该模型表达式为^[21,22]

$f\left( {{{n}},{{o}},{{s}},\lambda } \right) = \sum\limits_m {{b_m}\beta \left( {{{n}},{{o}},{{s}},{\mu _m}} \right)}, $

式中, ${b_m}$为与$\beta \left( {{{n}}, {{o}}, {{s}}, {\mu _m}} \right)$对应的反射率, ${b_m}$需要满足$0 \leqslant {b_m} \leqslant 1$, $\displaystyle\sum\nolimits_m {{b_m}} \leqslant 1$. $\beta \left( {{{n}}, {{o}}, {{s}}, {\mu _m}} \right)$为Cook-Torrance BRDF参数化模型, 即:

$\beta \left( {{{n}},{{o}},{{s}},{\mu _m}} \right) =\begin{cases}{1 /\pi}, &{m = 0,}\\\left[ {\dfrac{1}{{\pi\left\langle {{{n}} \cdot {{o}}} \right\rangle \left\langle {{{n}} \cdot {{s}}} \right\rangle }}} \right]\left[ {\dfrac{{{{\rm e}^{ - {{\left( {{{\tan \tau } / {{\mu _m}}}} \right)}^2}}}}}{{4\mu _m^2{{\cos }^4}\tau }}} \right], &{m = 1,2, \cdots ,M,}\end{cases}$

其中, $m \!=\! 0$时, 表示漫反射, m逐渐增大, 表示镜面反射的增强; $\tau $为${{n}}$和${{b}}$之间的夹角, ${{b}} = {{\left( {{{s}} + {{o}}} \right)}/2}$; ${\mu _m}$调节BRDF的形状, $0.01 \leqslant {\mu _m} \leqslant 0.5$.
2 -->

2.2.光谱反射特性参量重构

三轴稳定工作状态下, 本体姿态不发生改变, 帆板保持对日指向, 探测器接收到目标信号是太阳相位角及材料表面光谱反射特性的函数. 因此, 可以利用可见光光谱信号对本体及帆板的表面光谱特性参量进行重构.
基于BRDF融合表征模型, (1)式表示为

$\varPhi \left( {t,\lambda } \right) = \frac{{{E_{{\rm{sun}}}}\left( \lambda \right){A_{{\rm{aperture}}}}}}{{{{\left\| {{{{T}}_{\rm{0}}}} \right\|}^2}}}Q\left( {t,\lambda } \right), $

其中,

$\begin{split}Q\left( {t,\lambda } \right) =\;& \left\langle {{{{n}}_{\rm{p}}} \cdot {{s}}} \right\rangle \left\langle {{{{n}}_{\rm{p}}} \cdot {{o}}} \right\rangle {N_{\rm{p}}}\left( \lambda \right) \\&+ \left\langle {{{{n}}_{\rm{b}}} \cdot {{s}}} \right\rangle \left\langle {{{{n}}_{\rm{b}}} \cdot {{o}}} \right\rangle {N_{\rm{b}}}\left( \lambda \right), \end{split}$

${N_{\rm{p}}}\left( \lambda \right) = \sum\limits_i {{A_{\rm{p}}}{b_i}{\beta _i}\left( {{{{n}}_{\rm{p}}},{{o}},{{s}},{\mu _i}} \right)}, $

${N_{\rm{b}}}\left( \lambda \right) = \sum\limits_j {{A_{\rm{b}}}{b_j}{\beta _j}\left( {{{{n}}_{\rm{b}}},{{o}},{{s}},{\mu _j}} \right)} . $

转化成矩阵形式为

${{Q}} = \left[ {\begin{array}{*{20}{c}} {{{{\beta }}^{\rm{p}}}}&{{{{\beta }}^{\rm{b}}}} \end{array}} \right] \cdot {\left[ {\begin{array}{*{20}{c}} {{P}}&{{B}} \end{array}} \right]^{\rm{T}}}$

式中, ${{Q}}$为T × 1维向量, ${{Q}} = [ {Q_1}, {Q_2}, \cdots, {Q_t}, \cdots, {Q_T} ]^{\rm{T}}$; ${{{\beta }}^{\rm{p}}}$为T × M矩阵, 其中向量元素$\beta _{ti}^{\rm{p}} = \left\langle {{{n}}_{{t}}^{\rm{p}} \cdot {{{s}}_{{t}}}} \right\rangle \left\langle {{{n}}_{{t}}^{\rm{p}} \cdot {{{o}}_{{t}}}} \right\rangle {\beta _{ti}}\left( {{{n}}_{{t}}^{\rm{p}}, {{{o}}_{{t}}}, {{{s}}_{{t}}}, {\mu _{ti}}} \right)$; ${{P}} = [ {{P_0}} \;\;{{P_1}}\;\; \cdots \;\;{{P_M}} ]$, ${P_i} = {A_{\rm{p}}}{b_i}$; ${{{\beta }}^{\rm{b}}}$为T × M矩阵, 矩阵元素为$\beta _{tj}^{\rm{b}} = \left\langle {{{n}}_{{t}}^{\rm{b}} \cdot {{{s}}_{{t}}}} \right\rangle \left\langle {{{n}}_{{t}}^{\rm{b}} \cdot {{{o}}_t}} \right\rangle {\beta _{tj}}\left( {{{n}}_{{t}}^{\rm{b}}, {{{o}}_{{t}}}, {{{s}}_{{t}}}, {\mu _{tj}}} \right)$; ${{B}} = \left[ {\begin{array}{*{20}{c}} {{B_0}}&{{B_1}}& \cdots &{{B_M}} \end{array}} \right]$, ${B_j} = {A_{\rm{b}}}{b_j}$.
将(11)式简化为

${{Q}} = {{\beta }}{{{B}}^{\rm{T}}}, $

式中${{\beta }}$为帆板和本体的多级BRDF信息矩阵, 已知; B中元素的物理意义为材料反射率及面积的混合信息, 未知. 以$\left\| {r({{B}})} \right\|_2^2 = \left\| {{{Q}} - {{\beta }}{{{B}}^{\rm{T}}}} \right\|_2^2$最小为目标函数, 根据优化算法即可对B进行求解, 即完成了在选定波长下空间目标复杂材料表面的物性参数反演.

2

-->

3.1.基于双面特性分离度的光谱波段选择

卫星帆板材料为太阳能电池片, 本体材料为聚酰亚胺, 这两种材料在不同光谱波段下BRDF存在差异. 为了减弱本体及帆板信号相耦合对姿态估计精度的影响, 可基于二者信息差异最大化建立评价准则, 优选光谱波段.
由(5)式可以看出, 本体面积反射率乘积${N_{\rm{b}}}\left( \lambda \right)$及帆板面积反射率乘积${N_{\rm{p}}}\left( \lambda \right)$与$\left\langle {{{n}} \cdot {{o}}} \right\rangle $有关, 即与入射角${\theta _{\rm{I}}}$有关. 为了评估本体和帆板反射率乘积分布特性之间的差异, 分别取入射角${\theta _{\rm{I}}}$为30°, 45°, 60°, 基于对应的面积反射率乘积${N_k}\left( {\lambda, {\theta _{\rm{R}}}} \right), k \in \left( {{\rm{p, b}}} \right)$的瓣宽及最大值构建信息差异度量. 某一入射角条件下${N_{\rm{b}}}(\lambda, {\theta _{\rm{R}}})$与${N_{\rm{p}}}(\lambda, {\theta _{\rm{R}}})$的信息差异度量表示为

$\sigma (\lambda,{\theta _{\rm{I}}}) = \frac{{{M_{\rm{b}}} - {M_{\rm{p}}}}}{{{M_{\rm{b}}}}} \cdot \frac{{{W_{\rm{p}}} - {W_{\rm{b}}}}}{{{W_{\rm{p}}}}}$

其中, ${W_{\rm{b}}}$为${N_{\rm{b}}}(\lambda, {\theta _{\rm{R}}})$的瓣宽, ${W_{\rm{p}}}$为${N_{\rm{p}}}(\lambda, {\theta _{\rm{R}}})$的瓣宽; ${M_{\rm{b}}}$为${N_{\rm{b}}}(\lambda, {\theta _{\rm{R}}})$的峰值, ${M_{\rm{p}}}$为${N_{\rm{p}}}(\lambda, {\theta _{\rm{R}}})$的峰值.
某一光谱波长对应的本体及帆板的双面分离度表示为不同入射角下$\sigma (\lambda, {\theta _{\rm{I}}})$(${\theta _{\rm{I}}}$ = 30°, 45°, 60°)的均值:

$\sigma (\lambda ) = \frac{1}{3}\sum {\sigma (\lambda,{\theta _{\rm{I}}})\left| {_{{\theta _{\rm{I}}} = 30^\circ,\;45^\circ,\;60^\circ }} \right.} . $

$\sigma (\lambda )$的输出值在0—1范围, 值越大, 表示本体及帆板信息在该光谱波段的差异更大, 即在该光谱波段更有利于对目标姿态进行估计.
2 -->

3.2.姿态运动状态下的目标时谱信号模型

在实际中, 卫星在轨运行过程中通常保持三轴稳定状态, 此时目标的本体坐标系Z轴指向地心, X轴指向轨道运行方向, 进而根据右手定则可确定沿帆板方向的Y轴方向. 而在其执行任务或出现故障的情况下, 其姿态会发生变化. 为了方便对姿态开展研究, 一般这样约定: 坐标系OXYZ依次绕Z轴、Y轴和X轴旋转, 绕轴转动的角被称为欧拉角, 绕三个轴转动的角度分别为偏航角$\psi $、俯仰角$\varphi $及滚转角$\theta $, 其坐标轴之间的变换关系如图3所示.
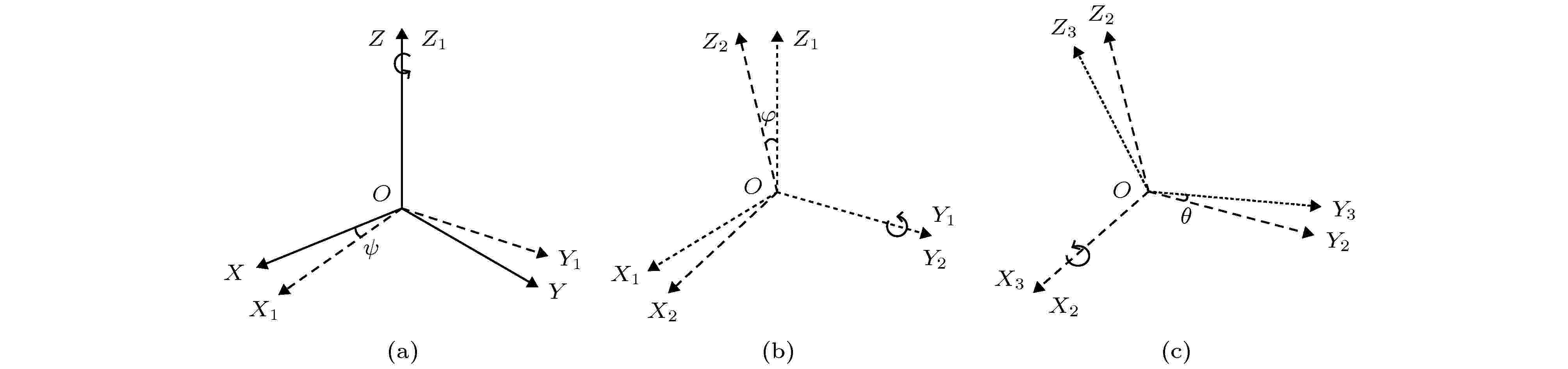图 3 坐标系旋转变换关系示意图　(a)绕Z轴转动; (b)绕Y轴转动; (c)绕X轴转动
Figure3. Diagram of coordinate system rotation transformation: (a) Rotate around Z-axis; (b) rotate around Y-axis; (c) rotate around X-axis.

当卫星姿态发生变化时, 分别绕X, Y, Z轴转动的3个欧拉角$\theta $, $\varphi $, $\psi $均为时间的函数, 假设卫星姿态变化的速度为匀速的, 则在不同时刻的3个欧拉角的值可分别由绕这3个轴转动的角速度${w_x}$, ${w_y}$, ${w_z}$来进行描述:

$ \psi ={\psi }_{0}+{w}_{z}\cdot t,~~\phi ={\phi }_{0}+{w}_{y}\cdot t,~~\theta ={\theta }_{0}+{w}_{x}\cdot t. $

其中, ${\theta _0}$, ${\varphi _0}$, ${\psi _0}$分别为在卫星姿态开始发生变化的前一帧的3个欧拉角, 在本文中, 设卫星均为从三轴稳定状态下开始发生姿态变化, 即初始状态下3个欧拉角均为0, 即${\theta _0} = {\varphi _0} = {\psi _0} = 0$, 代入(15)式可得

$ \psi ={w}_{z}\cdot t\begin{array}{cc}, & \end{array}\phi ={w}_{y}\cdot t\begin{array}{cc}, & \end{array}\theta ={w}_{x}\cdot t. $

当采用绕Z轴、Y轴、X轴的顺序旋转时, 对应的用欧拉角表示的姿态矩阵为

$\begin{split}{{{R}}_{{{ZYX}}}} =\;& \!\left[\! \!{\begin{array}{*{20}{c}} {\cos \psi }&{\sin \psi }&0 \\ { \!-\! \sin \psi }&{\cos \psi }&0 \\ 0&0&1 \end{array}} \!\!\right]\!\!\left[\!\! {\begin{array}{*{20}{c}} {\cos \varphi }&0&{\sin \varphi } \\ 0&1&0 \\ { \!-\! \sin \varphi }&0&{\cos \varphi } \end{array}} \!\!\right]\\&\times\!\left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \theta }&{\sin \theta } \\ 0&{ - \sin \theta }&{\cos \theta } \end{array}} \right].\\[-20pt] \end{split}$

在目标卫星本体坐标系下, 姿态变化仅影响到照明矢量${{s}}$及观测矢量${{o}}$, 相关的转换关系如下:

${{s}}' = {{{R}}_{{{ZYX}}}}{{s}}, $

${{o' = }}{{{R}}_{{{ZYX}}}}{{o}}, $

其中, ${{s}}'$为发生姿态变化后的照明矢量, ${{o'}}$为姿态变化后的观测矢量.
姿态发生变化时探测器入瞳接收到的目标辐通量为

$\begin{split}\varPhi \left( {t,\lambda } \right) =\;& \frac{{{E_{{\rm{sun}}}}\left( \lambda \right){A_{{\rm{aperture}}}}}}{{{{\left\| {{{{T}}_{\rm{0}}}} \right\|}^2}}} \cdot [ \left\langle {{{{n}}_{\rm{p}}} \cdot {{s}}'} \right\rangle \left\langle {{{{n}}_{\rm{p}}} \cdot {{o}}'} \right\rangle {N_{\rm{p}}}\left( \lambda \right)\\&+ \left\langle {{{{n}}_{\rm{b}}} \cdot {{s}}'} \right\rangle \left\langle {{{{n}}_{\rm{b}}} \cdot {{o}}'} \right\rangle {N_{\rm{b}}}\left( \lambda \right) ].\\[-10pt] \end{split}$

将(9)式、(10)式代入(20)式可得

$\begin{split}\varPhi \left( {t,\lambda } \right) =\;& \frac{{{E_{{\rm{sun}}}}\left( \lambda \right){A_{{\rm{aperture}}}}}}{{{\rm{\pi }}{{\left\| {{{{T}}_{\rm{0}}}} \right\|}^2}}} \cdot \Bigg\{ \displaystyle\sum\limits_i {{A_{\rm{p}}}{b_i}\!\!\left[ {\frac{{{{\rm e}^{ - {{\left( {{{\tan {\tau _{\rm{p}}}}/{{\mu _i}}}} \right)}^2}}}}}{{4{\mu _i}^2{{\cos }^4}{\tau _{\rm{p}}}}}} \right]} \\&+ \displaystyle\sum\limits_j {{A_{\rm{b}}}{b_j}\left[ {\frac{{{{\rm{e}}^{ - {{\left( {{{\tan {\tau _b}}/{{\mu _j}}}} \right)}^2}}}}}{{4{\mu _j}^2{{\cos }^4}{\tau _{\rm{b}}}}}} \right]} \Bigg\}. \\[-20pt]\end{split}$

可以看出, 某一时刻下的目标整体光谱信号仅与角度$\tau $有关, 根据其定义可得

$\cos \tau = \left\langle {{{n}},\frac{{{{{R}}_{{{ZYX}}}}{{s}} + {{{R}}_{{{ZYX}}}}{{o}}}}{2}} \right\rangle . $

由(16)式、(17)式、(22)式可见, 目标本体及帆板的时序光谱信号为绕3个轴转动的角速度${w_x}$, ${w_y}$, ${w_z}$的函数, 表示为$f\left( {{p}} \right) = \varPhi \left( {t, {{p}}, \lambda } \right)$, 其中${{p}} = [{w_x}, {w_y}, {w_z}]$.
2 -->

3.3.基于Levenberg-Marquardt算法的姿态参数解算

空间目标反射至探测器光通量的表达式为非线性的, 故采用非线性迭代估计算法对姿态参数${{p}} = [{w_x}, {w_y}, {w_z}]$进行求解, 这里采用Levenberg-Marquardt (LM)非线性迭代估计算法^[23,24]. 该算法的目的是寻找参数向量${{{p}}^ + }$, 使得误差$\varepsilon $最小化, 其中$\varepsilon = {\left\| {\varPhi \left( {t, \lambda } \right) - f\left( {{p}} \right)} \right\|^2}$, $\varPhi \left( {t, \lambda } \right)$为光谱信号测量值, $f\left( {{p}} \right)$为光谱信号模型值.
对于函数$f\left( {{p}} \right) = \varPhi \left( {t, \lambda } \right)$, 在每次迭代过程中, 均可得到一个新的参数向量${{p}}$, 如果更新参数向量${{p}} + {{\delta }}$能够使得误差$\varepsilon $减小, 则这次更新被接受, 即${{p}} = {{p}} + {{\delta }}$. 直到迭代过程收敛至最优的参数向量${{{p}}^ + }$, 使得${\left\| {\varPhi \left( {t, \lambda } \right) - f\left( {{p}} \right)} \right\|^2}$最小化.
算法流程如下:
1)设置参数初始值${{{p}}_{\rm{0}}} = [0, 0, 0]$, 设置迭代步数$k = {\rm{1}}$, 设置最大迭代步数${k_{{\rm{max}}}} = 5000$, 设置迭代终止阈值$\varepsilon = 1.{\rm{0}} \times {10^{ - 22}}$.
2)将初值代入方程计算误差${\varepsilon _{\rm{0}}} = \| \varPhi \left( {t, \lambda } \right) - f\left( {{{{p}}_{{0}}}} \right) \|^2$. 对方程进行泰勒展开, 并对其雅可比矩阵${{J}}$进行计算, ${{J}}$定义为函数$f$对参数向量的偏导, 即${{J}} = {{\partial f\left( {{p}} \right)}}/{{\partial {{p}}}}$.
3)采用最速下降法确定下降方向－${{\delta }}$, 令${{{p}}_{{k}}} = {{{p}}_{{{k - 1}}}} + {{\delta }}$, 计算误差${\varepsilon _k} = {\left\| {\varPhi \left( {t, \lambda } \right) - f\left( {{{{p}}_{{k}}}} \right)} \right\|^2}$. 若${\varepsilon _k}{\rm{ < }}{\varepsilon _{k - 1}}$, 说明当前下降方向为正确的, 此次更新被接受; 若${\varepsilon _k} \geqslant {\varepsilon _{k - 1}}$, 说明下降方向有问题, 需要重新选择. 迭代步数k执行+1操作.
4)重复步骤3), 直到迭代步数达到最大迭代步数${k_{{\rm{max}}}}$或误差小于迭代终止阈值, 迭代终止. 此时的参数向量即为最优解, 即${{{p}}^ + } = {{{p}}_{{k}}}$.

2

-->

4.1.三轴稳定状态下的时序光谱信号仿真

3 -->

4.1.1.仿真输入

本文的研究对象为三轴稳定状态下的在轨卫星, 卫星本体尺寸为1.2 m × 1.2 m × 1.2 m, 帆板尺寸为6.8 m × 1.2 m × 0.1 m, 上圆柱直径为1 m, 高为0.3 m, 下圆柱直径为1 m, 高为0.5 m, 与下圆柱相连接的半球高为0.3 m. 卫星的几何结构以及面元划分结果如图4所示.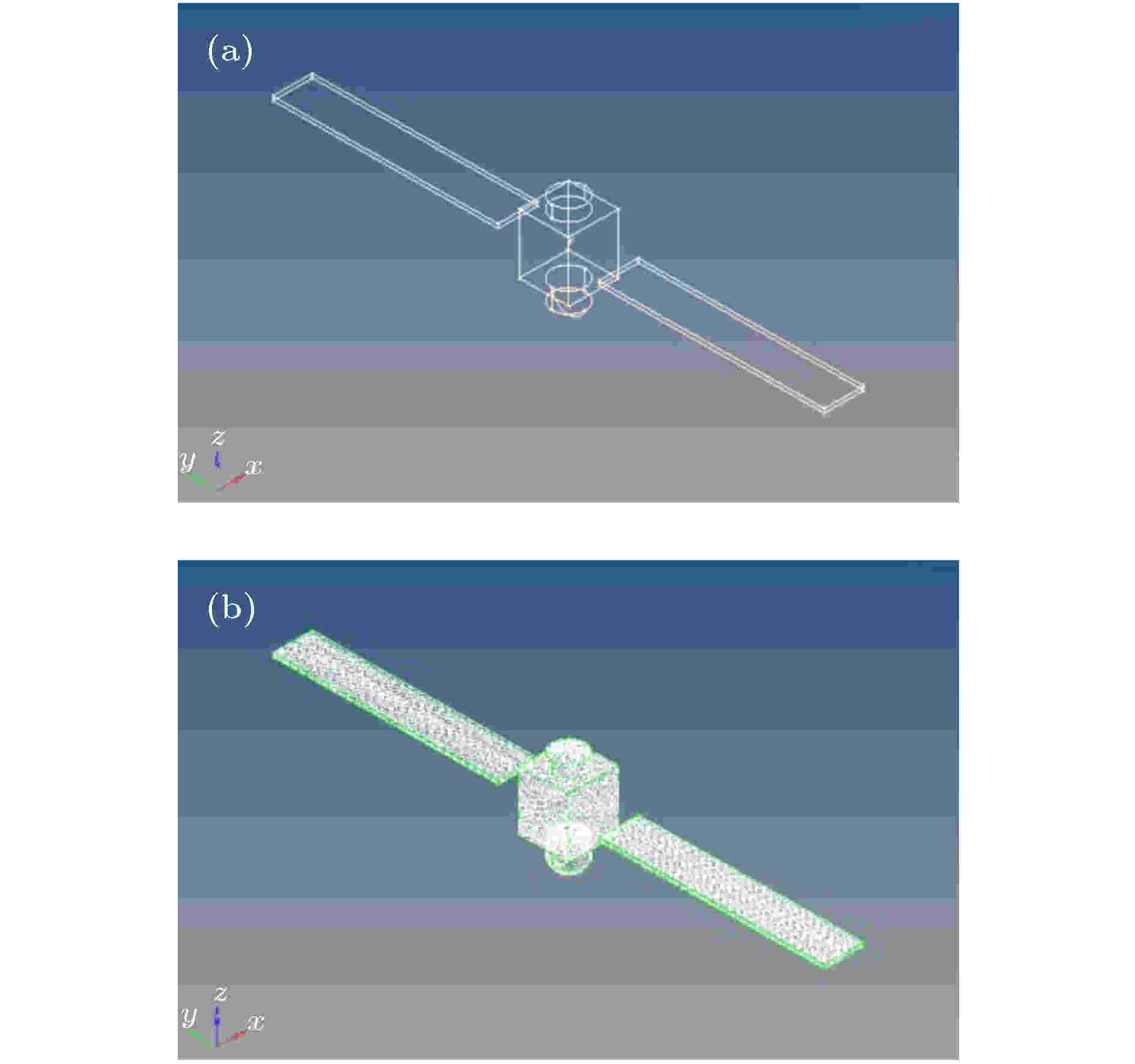
图 4 卫星结构图　(a)面元划分前; (b)面元划分后
Figure4. Diagram of satellite structure: (a) Before surface division; (b) after surface division.

在轨卫星抵近识别过程中, 观测卫星相对于目标卫星, 通常采用三种伴飞模式: 接近、悬停以及绕飞. 不同伴飞模式, 会造成观测距离、观测相位角的差异, 因而会直接影响光度信号的变化规律. 本文的观测模式选择了悬停模式下的同轨观测. 目标卫星与观测卫星的轨道参数如表1所列.

卫星	半长轴/km	偏心 率/(°)	轨道倾 角/(°)	近地点 幅角/(°)	升交点 赤经/(°)	真近点 角/(°)
目标卫星	42378.1	0	0	0	181.803	0
观测卫星	42408.0	0	0	0	184.860	359.93

表1目标卫星与观测卫星的轨道参数
Table1.Orbit parameter of object satellite and observe satellite.

为了体现光谱对于姿态反演的影响, 观测卫星选择的传感器为可见光380—780 nm范围内的光谱探测相机, 其系统参数如表2所列. 在这种轨道和探测系统参数条件下, 输出的为点目标的时序光谱信号, 可用于姿态反演.

参量	光谱宽度/nm	入瞳直径/m	焦距/m	面阵大小	像元尺寸/m	瞬时视场/rad
数值	10	0.1505	0.8	512 × 512	1.5 × 10–5	1.8750 × 10–5

表2观测星探测系统参数
Table2.Detection system parameter of observe satellite.

仿真计算过程中, 卫星本体表面包覆黄色热控材料, 帆板正面贴满太阳能电池片, 背面涂有机黑漆, 本体上下两个组件涂有机白漆. 对于有机黑漆(反射率0.04)和有机白漆(反射率0.9), 其反射特性遵从朗伯漫反射定律^[25]. 黄色热控材料和电池片具有较强的镜反射特性, 利用全谱段探测器可对其在不同光谱波段下的反射特性进行测量, 并利用双向反射分布函数(即BRDF)进行描述. 以入射角为45°为例, 可见光谱段(380—780 nm)黄色热控材料及太阳电池片的BRDF随波长与反射角变化的曲线如图5所示.
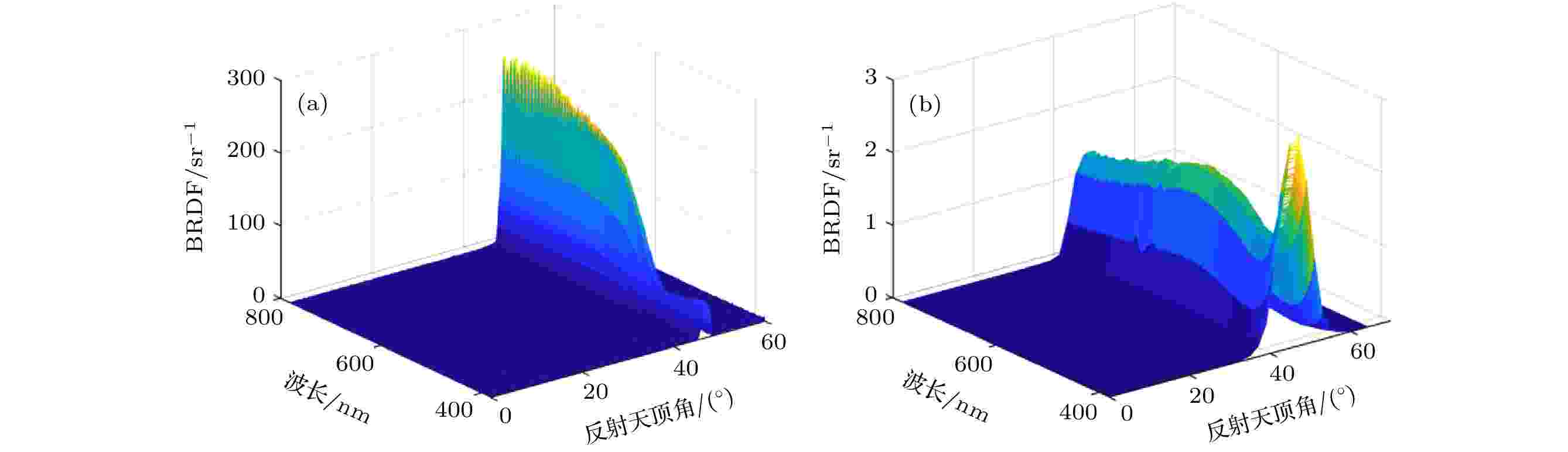图 5 材料BRDF与波长和反射角的关系　(a) 本体包覆材料BRDF; (b)帆板材料BRDF
Figure5. Material BRDF changes with wavelength and reflected angle: (a) BRDF of body coating material; (b) BRDF of solar panel

3 -->

4.1.2.仿真结果

基于上述结构特性、材料特性、轨道特性及探测系统特性, 仿真得到可见光光谱信号, 其中8个波长处的时序光谱信号如图6所示.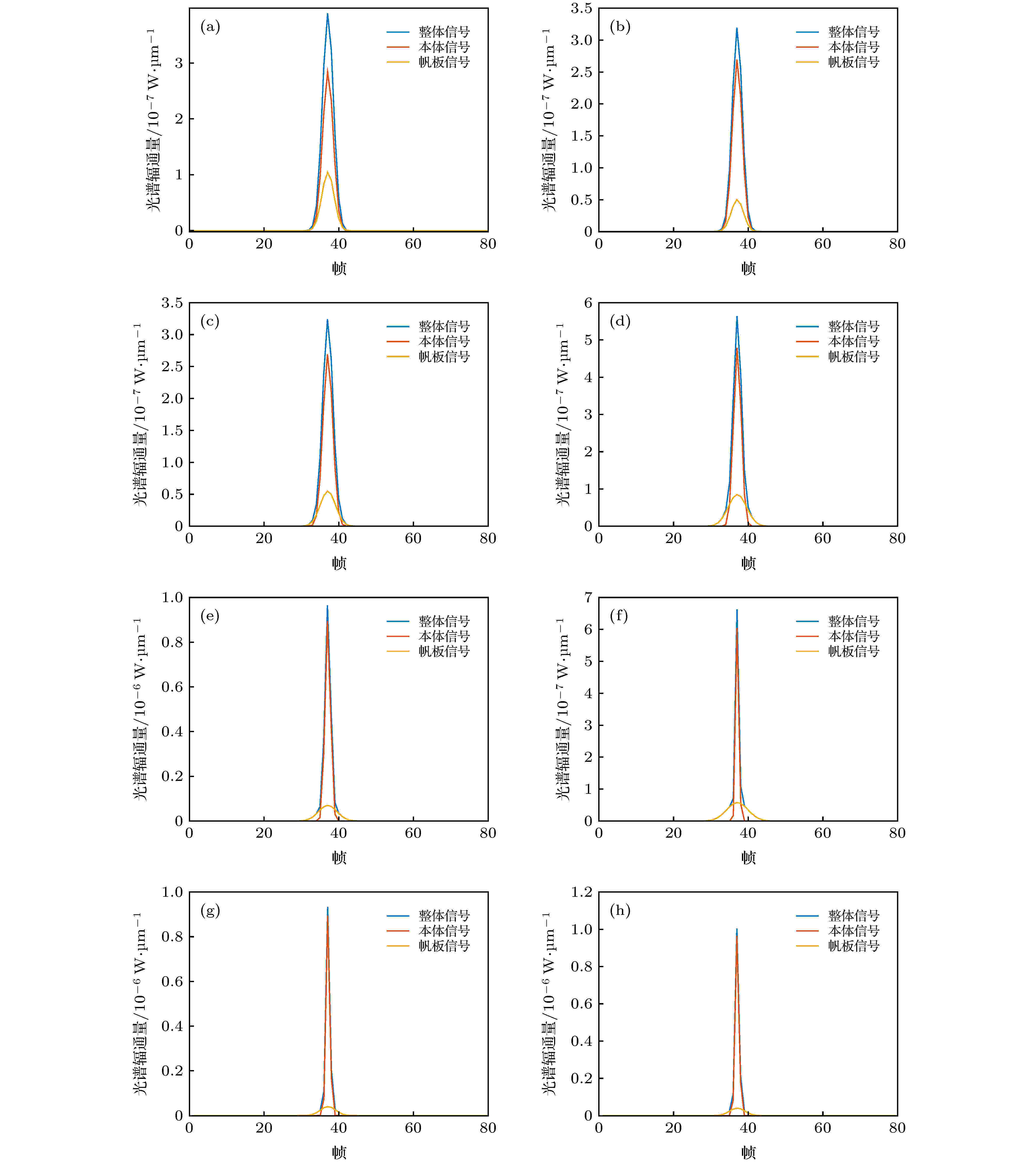
图 6 在不同光谱波段仿真得到的光度信号曲线　(a) 400 nm; (b) 450 nm; (c) 500 nm; (d) 550 nm; (e) 600 nm; (f) 650 nm; (g) 700 nm; (h) 750 nm
Figure6. Simulation curves of photometric signal at different wavelengths: (a) 400 nm; (b) 450 nm; (c) 500 nm; (d) 550 nm; (e) 600 nm; (f) 650 nm; (g) 700 nm; (h) 750 nm

2 -->

4.2.空间目标表面光谱特性参量的在轨重构

3 -->

4.2.1.谱段优选

为了选取出更有利于姿态估计的波段, 对上述8个谱段的信号分别进行重构, 可分别得到不同波长下目标本体及帆板的BRDF及面积反射率乘积. 根据重构所得信息, 计算不同谱段的双面特性分离度, 得到的结果如表3所列.

光谱波长/nm	$\sigma $		光谱波长/nm	$\sigma $
400	0.1593		600	0.6664
450	0.3850		650	0.8574
500	0.4576		700	0.8284
550	0.5862		750	0.8031

表3不同光谱波段的双面特性分离度
Table3.Two-facet characteristics difference at different wavelengths.

可以看出, 在400 nm处该指标值最小, 即本体与帆板信息差异更小, 此时本体及帆板信号耦合程度较高, 对姿态估计精度会造成较大影响. 与之相对的, 在650 nm处该指标值最大, 此时本体与帆板信息差异更大, 利于姿态估计, 故选取650 nm作为姿态估计的最优谱段.
3 -->

4.2.2.重构结果

针对上述卫星模型、卫星轨道参数在可见光谱段中8个光谱波段所得到的目标时序光度曲线, 分别进行基于双面法的光谱特性参量重构. 由于目标本体由多个构件构成, 目标帆板由太阳能电池片以及其连接结构组成, 在对它们的光谱特性参量进行反演时, 本体及帆板两部分的组成参数均在其定义域[0.01 0.5]内取值, 重构结果如表4所列.

序号	本体			帆板
	${A_{\rm{b}}} \cdot {b_j}$	${\mu _j}$		${A_{\rm{p}}} \cdot {b_i}$	${\mu _i}$
1	0.1722	0.01		0.0003	0.01
2	0.0248	0.02		0.0103	0.02
3	0.0102	0.04		0.0837	0.04
4	0.0517	0.05		0.1046	0.05
5	0.0312	0.07		0.8049	0.07
6	0.0083	0.08		0.1153	0.08
7	0.0137	0.10		0.0489	0.10
8	0.0077	0.20		0.0345	0.20
9	0.0002	0.30		0.0003	0.30
10	0	0.50		0.0103	0.50

表4650 nm参数重构结果
Table4.Parameter reconstruction results at 650 nm

650 nm光谱波段对应的本体及帆板的光学特性重构曲线如图7所示. 基于该参量重构得到目标整体、本体、帆板的时序光谱信号, 如图8所示, 可以看出, 重构曲线与原始数据重合度较高, 其误差为$\varepsilon = {\left\| {{\varPhi _{{\rm{sim}}}} - {\varPhi _{{\rm{rec}}}}} \right\|_{\rm{2}}} < {\rm{1}}\% $.
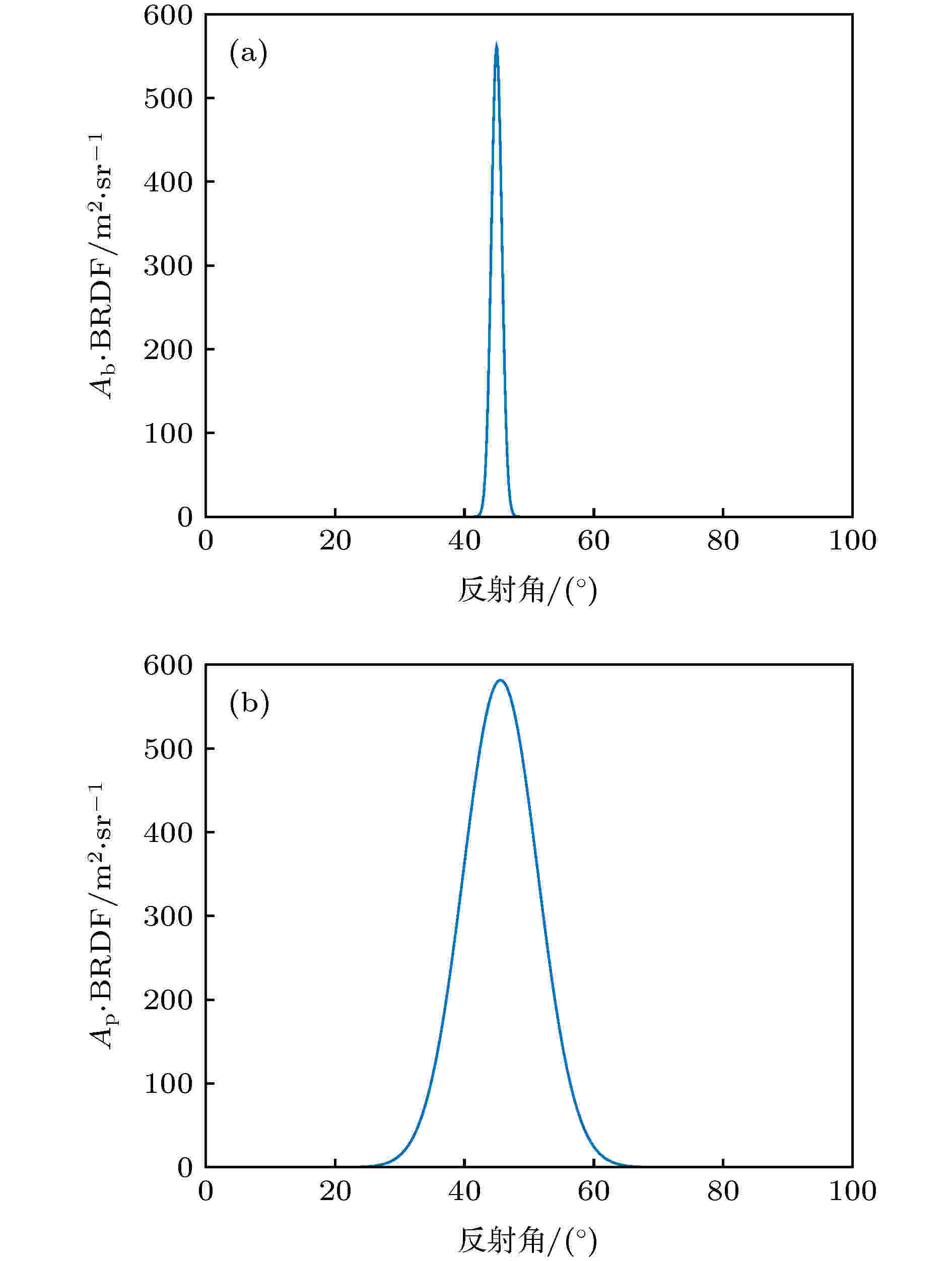图 7 650 nm波段下本体及帆板光学特性重构曲线　(a)本体表面光学特性重构曲线; (b)帆板表面光学特性重构曲线
Figure7. Optical characteristic reconstruction curve of body and solar panel at 650 nm: (a) Reconstruction curve of body; (b) reconstruction curve of solar panel

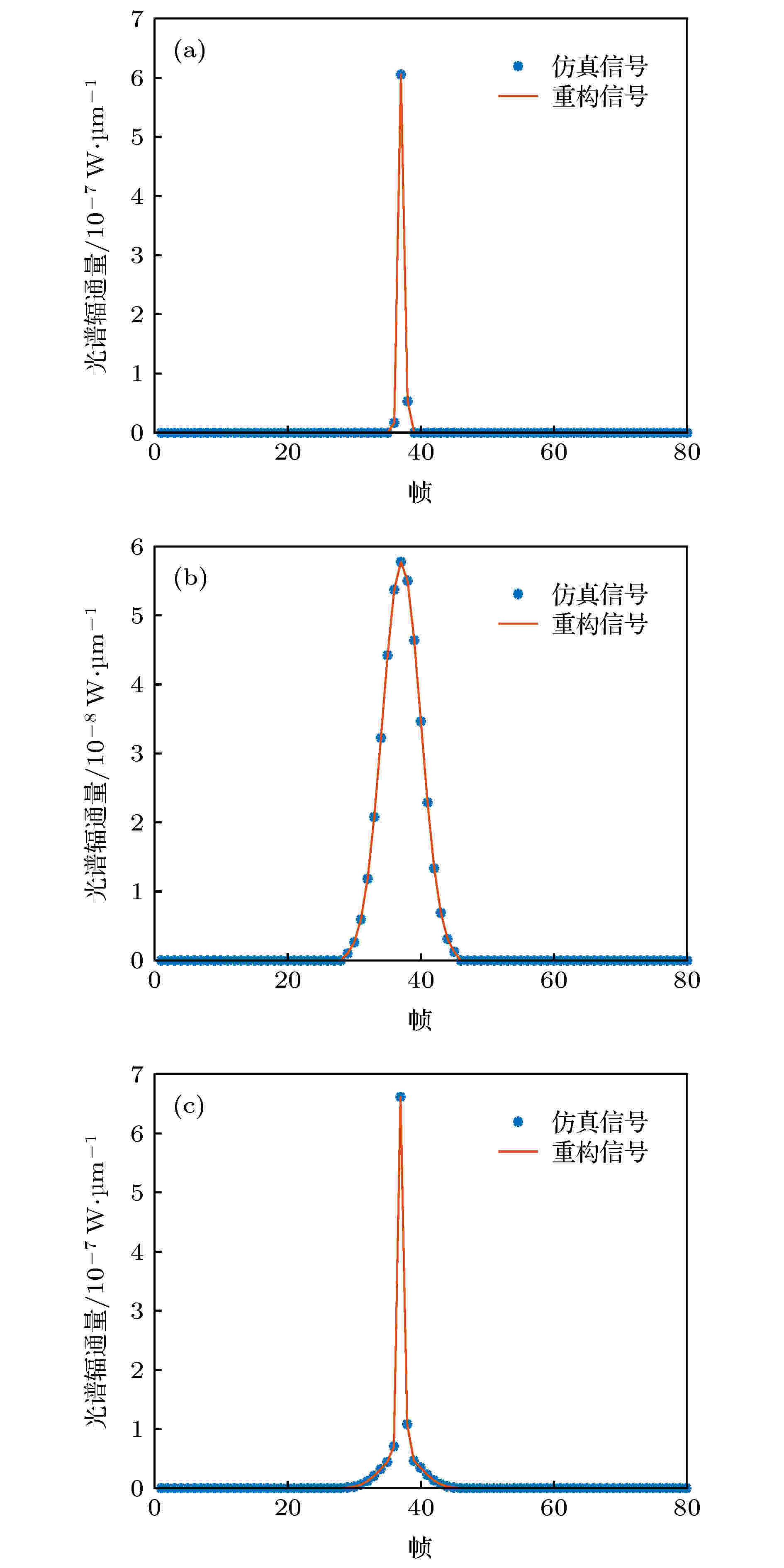图 8 时序光谱信号重构结果　(a)本体重构结果; (b)帆板重构结果; (c)目标整体重构结果
Figure8. Reconstruction result of time-series spectral signals: (a) Reconstruction result of body signal; (b) reconstruction result of solar panel signal; (c) reconstruction result of total signal.

2 -->

4.3.在轨目标姿态参数估计

3 -->

4.3.1.绕Y轴转动时的估计结果

空间目标从2019/3/21 5:30:00开始发生姿态变化, 绕Y轴以0.25°/帧的角速度匀速转动, 即旋转角速度真值为${ p^*} =$[0 0.25 0], 650 nm光谱波段对应的时序光度信号仿真结果如图9所示. 对姿态进行反演, 结果为${{{p}}^ + } = $[0.0237 0.2472 –0.0198], 与真值的误差为
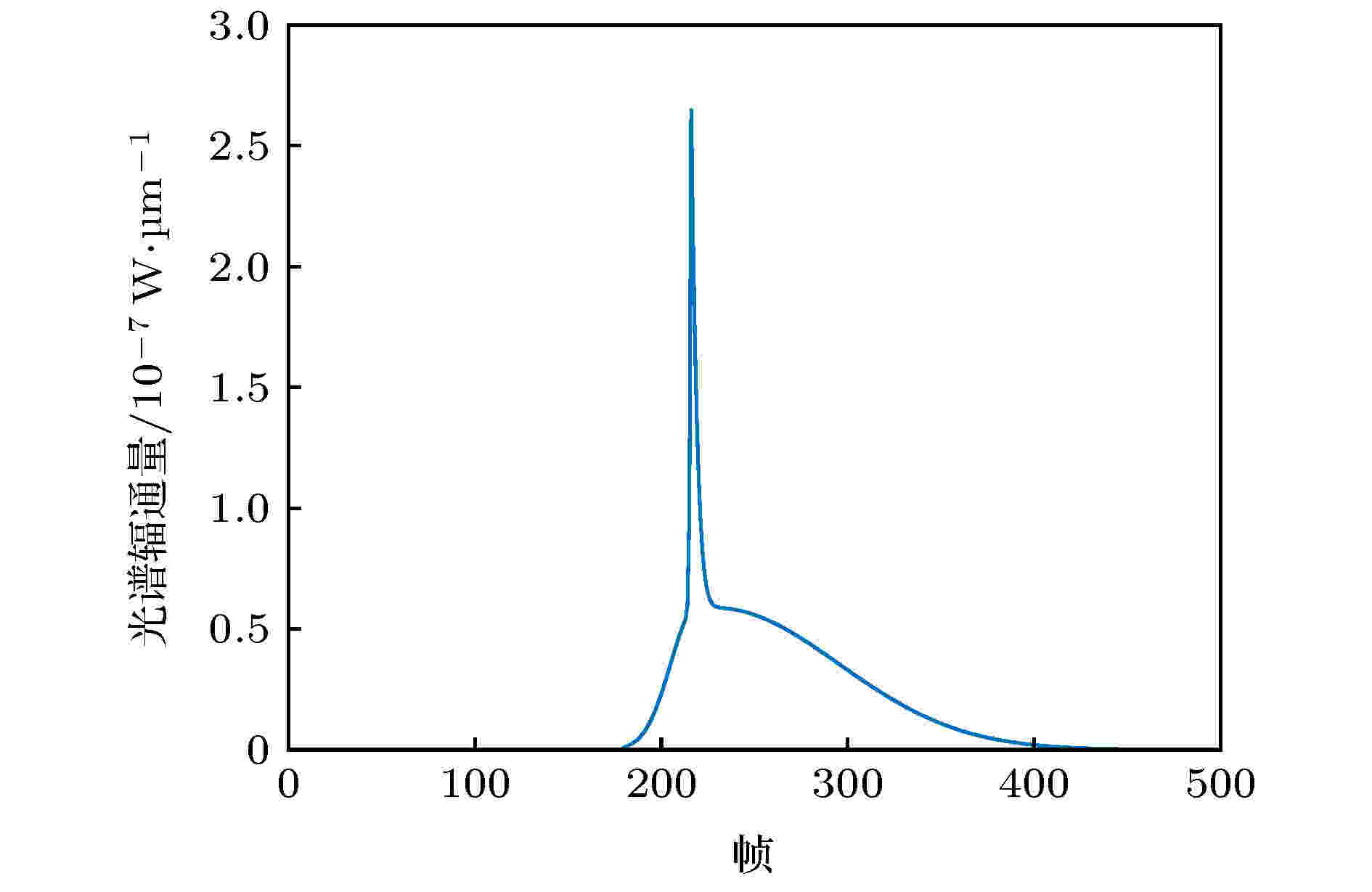图 9 绕Y轴转动得到的时序光谱信号
Figure9. Time-series spectral signals when rotating around Y-axis.

$\varepsilon = {\left\| {{{{p}}^ + }{\rm{ - }}{ p^*}} \right\|_{\rm{2}}}{\rm{ = 2}}{\rm{.41\% }}.$

3 -->

4.3.2.绕Z轴转动时的估计结果

空间目标从2019/3/21 5:30:00开始发生姿态变化, 绕Z轴以0.25°/帧的角速度匀速转动, 即旋转角速度真值为${ p^*} =$[0 0 0.25], 650 nm光谱波段对应的时序光度信号如图10所示. 对姿态进行反演, 结果为${{{p}}^ + } = $[–0.0125 0.0223 0.2458], 与真值的误差为$\varepsilon = {\left\| {{{{p}}^ + }{\rm{ - }}{ p^*}} \right\|_{\rm{2}}}{\rm{ = 2}}{\rm{.59\% }}$.
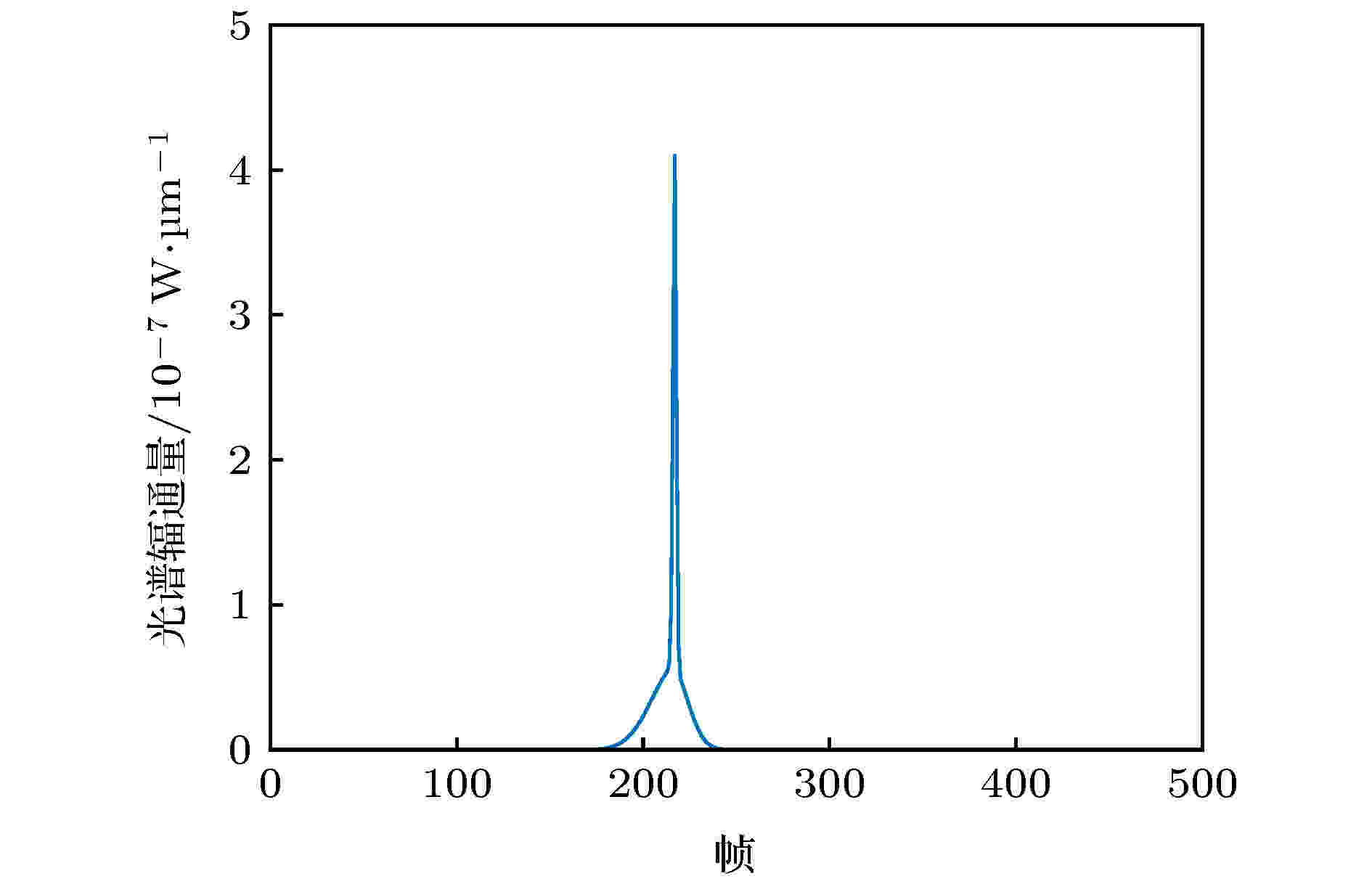图 10 绕Z轴转动得到的时序光谱信号
Figure10. Time-series spectral signals when rotating around Z-axis.

2 -->

4.4.影响因素分析

3 -->

4.4.1.相位角影响

目标在轨运行过程中, 其相位角(入射方向与反射方向的夹角)随时间变化. 在不同相位角处开始绕Z轴以0.25°/帧的角速度匀速转动, 估计得到的姿态角速度与开始相位角之间的关系见表5.

开始 相位角/(°)	估计得到的姿态 参数/rad·帧–1	相对 误差/%
3	[0.0125 –0.00182 0.2567]	1.43
5	[–1.35 × 10–4 0.0176 0.2489]	1.76
10	[–0.0163 –0.0034 0.2567]	1.79
15	[–0.0125 0.0223 0.2458]	2.59
20	[–0.0233 –0.0028 0.2742]	3.37
25	[–0.0132 0.0321 0.2533]	3.49
30	[0.0713 –0.0019 0.3057]	9.05
35	[–0.0679 0.1301 –0.1986]	47.25
40	无解	—

表5在不同相位角开始估计得到的姿态角速度
Table5.Estimate results of attitude angular velocity at different phase angles.

从表5看出, 当初始时刻的相位角在25°以内时, 姿态反演误差在5%以内; 当初始时刻的相位角增大时, 本体信号消失, 仅有帆板信号, 导致反演误差增大; 当初始时刻的相位角大于35°时, 本体与帆板均没有反射信号, 姿态变化不会造成信号变化, 故无法对姿态信息进行求解.
3 -->

4.4.2.本体结构影响

对如图11所示的其他几种本体形状不同目标模型同样进行了仿真与反演, 根据反演结果重构出的曲线与原始曲线的误差如表6所列.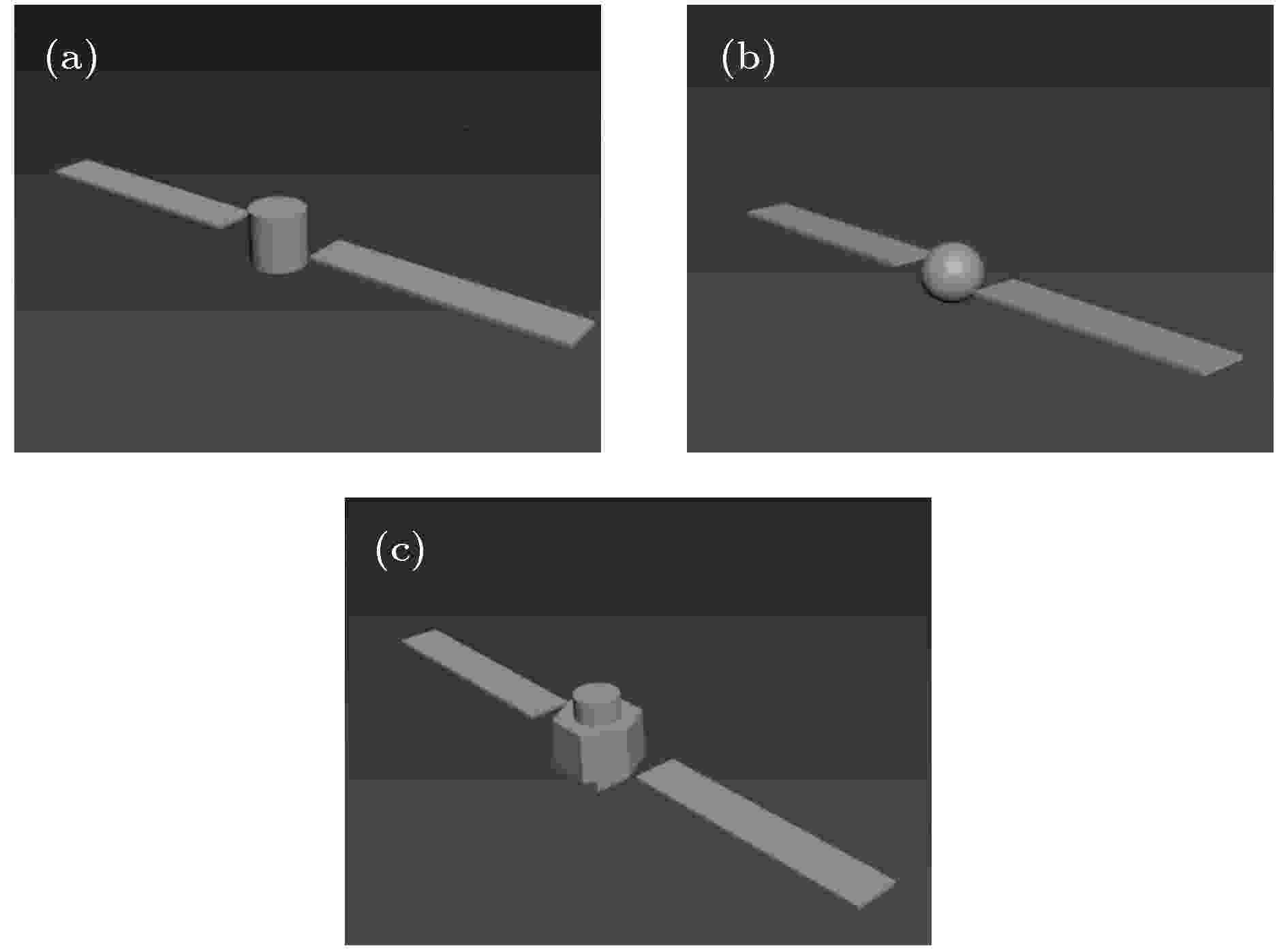
图 11 不同本体形状的目标模型　(a)圆柱体本体; (b)球体本体; (c)六棱柱本体
Figure11. Object model with different body structure: (a) Cylinder body; (b) sphere body; (c) hexagonal prism body.

模型	整体信号	本体信号	帆板信号
球体	41.68%	61.24%	26.77%
圆柱体	29.77%	46.73%	23.82%
六棱柱	3.56%	15.09%	1.21%

表6不同模型重构曲线误差
Table6.Errors of reconstruction curves with different models.

从重构结果可以看出, 当法向量朝向轨道运行方向的面元数量越多的模型, 用该方法能够反演得到的精度更高. 该方法更适用于本体为方形的卫星模型, 对本体为曲面的情况适用程度较低.
3 -->

4.4.3.探测器噪声影响

本文在仿真得到的650 nm下的时序光谱辐通量信号(如图9和图10所示)的基础上, 选取光谱中心10 nm范围进行积分得到645—655 nm谱段的时序辐通量曲线. 由于探测器噪声可等效为时序高斯白噪声, 因此添加不同信噪比(signal noise ratio, SNR)的高斯白噪声, 其中信号利用时序辐通量的均值表示, 不同SNR条件下的姿态反演结果如表7所列, 误差曲线如图12所示. 从图12可以看出, 随着噪声增大, 信噪比减小, 反演结果的误差呈增大趋势, 当SNR ≥ 10时, 反演误差在2%以内.

信噪比	绕Y轴旋转	绕Z轴旋转
SNR = 1	[8.3448 × 10–7 0.2437 0.0081006]	[0.069 0.074087 0.21274]
SNR = 3	[4.5801 × 10–7 0.24959 0.0072132]	[0.0853 0.003516 0.27007]
SNR = 5	[1.9843 × 10–8 0.25191 0.0072818]	[0.073 1.1668 × 10–8 0.26576]
SNR = 10	[1.2073 × 10–10 0.24933 0.0057039]	[0.013255 2.0514 × 10–8 0.25114]
SNR = 20	[7.8452 × 10–7 0.25027 0.0059434]	[0.007916 4.4372 × 10–6 0.25177]
SNR = 50	[8.8736 × 10–8 0.24997 0.0047093]	[0.009675 2.0484 × 10–8 0.25056]

表7不同信噪比下的姿态估计结果
Table7.Attitude estimate results with different SNR.

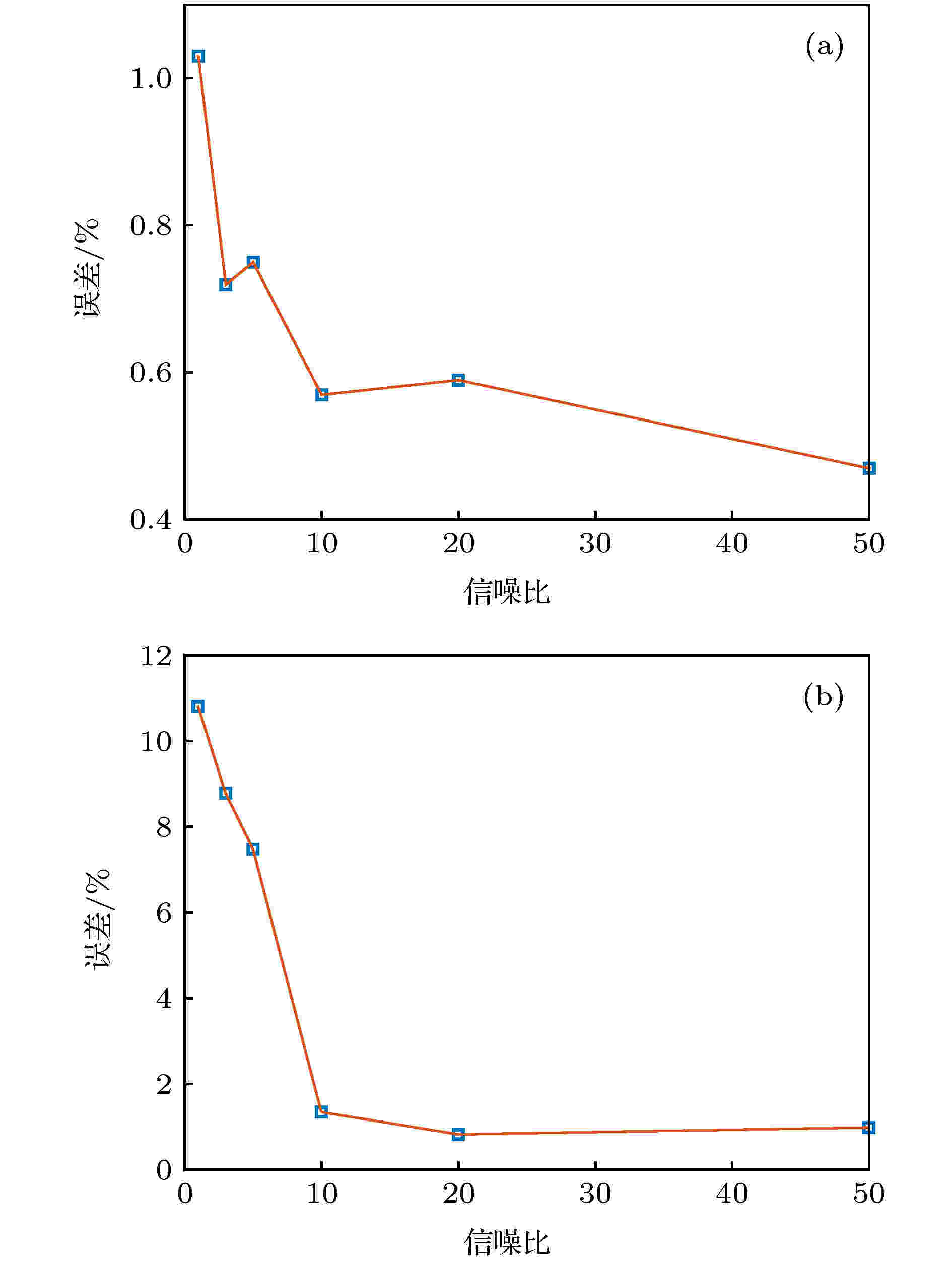图 12 误差随信噪比变化曲线　(a)绕Y轴旋转; (b)绕Z轴旋转
Figure12. Error curve changes with SNR: (a) Rotate around Y-axis; (b) rotate around Z-axis

针对实际在轨应用中的非合作空间目标的姿态感知问题, 提出了基于时序光谱信号分级求解目标表面光谱反射特性参数及姿态运动参数的方法. 首先, 基于目标三轴稳定状态下的时序光谱信号, 完成双面光谱BRDF与面积乘积信息的反演; 其次, 构建双面特性分离度, 基于该度量最大化实现光谱波段优选; 最后, 基于目标姿态运动状态的时序光谱信号, 完成姿态参数的估计. 仿真实验表明: 该方法更适用于方形本体的卫星结构, 而对形状为曲面的本体, 反演误差较大; 对于方形本体的卫星模型, 在有效观测角内, 反演得到的姿态角速度与实际值之间的误差随着相位角增大而增大; 反演结果的误差随噪声的增大呈增大趋势, 信噪比SNR ≥ 10条件下反演误差在2%以内.