全文HTML
--> --> -->近年来的研究结果表明在低维体系中声子扩散是反常的. 一维体系及二维系统中声子的反常热传导已经是一个不需要争辩的事实[6-9]. 有数值计算表明单壁碳纳米管、硅纳米线中的声子输运是反常的, 其热导率(κ)不是常数, 而是一个随长度(L)发散的量: κ-Lα[10]; 同时, 二维材料的热导率也是随着长度发散的: κ-logL[11,12]. 这一关系已经在碳纳米管[13-16]、悬空单层石墨烯[17]和悬空单层/多层过渡金属硫化物[18]的实验中得到证实. 因此, 有大量的工作集中研究这种反常热传导和声子扩散的物理机理[6-9,19]; 同时在研究界面热导的过程中将这一反常行为考虑进去, 尝试去建立一个新的声子界面热输运理论.
二维材料的发现为研究低维系统中声子-声子散射物理过程提供了一个绝佳的平台。本综述文章从微纳尺度热传导实验测量手段出发, 介绍二维材料热传导在实验方面的研究进展及相关物理问题, 阐述二维材料-二维材料界面、二维材料-介电层之间的界面热阻, 并以此为出发点进一步解释二维材料在散热领域的应用前景. 本文的内容安排如下: 第2节介绍二维材料热传导测量技术; 第3节介绍二维材料热传导研究进展及相关物理问题; 第4节和第5节介绍二维材料之间界面热阻、二维材料与介电衬底的界面热阻调控及二维材料在散热方面的研究进展; 第6节为总结部分, 并展望未来的研究方向与前景.
需要特别指出的是, 除了石墨烯、氮化硼和黑磷等以外, 通过元素周期表可以发现二维材料有一个极其庞大的家族[20]. 然而, 目前的热传导研究只是涉及极少部分的二维材料, 其原因可能是二维材料热传导测量存在很大的难度及技术瓶颈. 本文希望通过对近十年来实验工作的综述, 给读者厘清二维材料热传导机理的基本物理图像, 并对其在散热领域的应用起到一定的理论支持.
由于篇幅限制, 本文只集中介绍二维材料热传导及界面热阻调控相关基础问题. 已有很多关于低维材料热学性质的文章可供参考, 比如低维材料反常热传导[7-9]、二维材料热传导研究[6,21-26]、微纳尺度热传导研究[27-29]等等.
2
2.1.悬空热桥法
悬空热桥法的发明得益于微纳加工技术的飞速发展. 由于在测量精度以及实验操作难度上拥有较好的平衡, 该方法已经成为微纳尺度热传导测量的主流方法之一. 2001年悬空热桥法首次被用于微纳尺度热传导测量, 该实验中所测量的样品为单根多壁碳纳米管[35]. 此前采用传统方法只能测量一束纳米线(纳米管)的整体热导率, 而纳米线(或纳米管)之间的声子散射导致无法精确得到单根样品的热导率[36]. 悬空热桥法不仅可以测量微纳尺度样品的热导率, 还能同步测量样品的电导率以及Seebeck系数, 对于低维热电材料的研究是比较适用的[37,38].热桥器件的制备流程是在硅晶片上进行一系列的光刻(或电子束曝光)、金属沉积、腐蚀等操作[21,30]. 该测量器件主要由下列两部分构成: (1) 由厚度为300—500 nm的低应力氮化硅(SiNx)构成的两个悬空平台和连接悬空平台与外部基底的六根悬臂, 如图1(a)中的蓝色背底部分; (2) 由厚度为50—100 nm的铂/金等金属构成的, 位于悬空平台、悬臂以及基底上的一系列电极, 如图1(a)中的黄色部分.
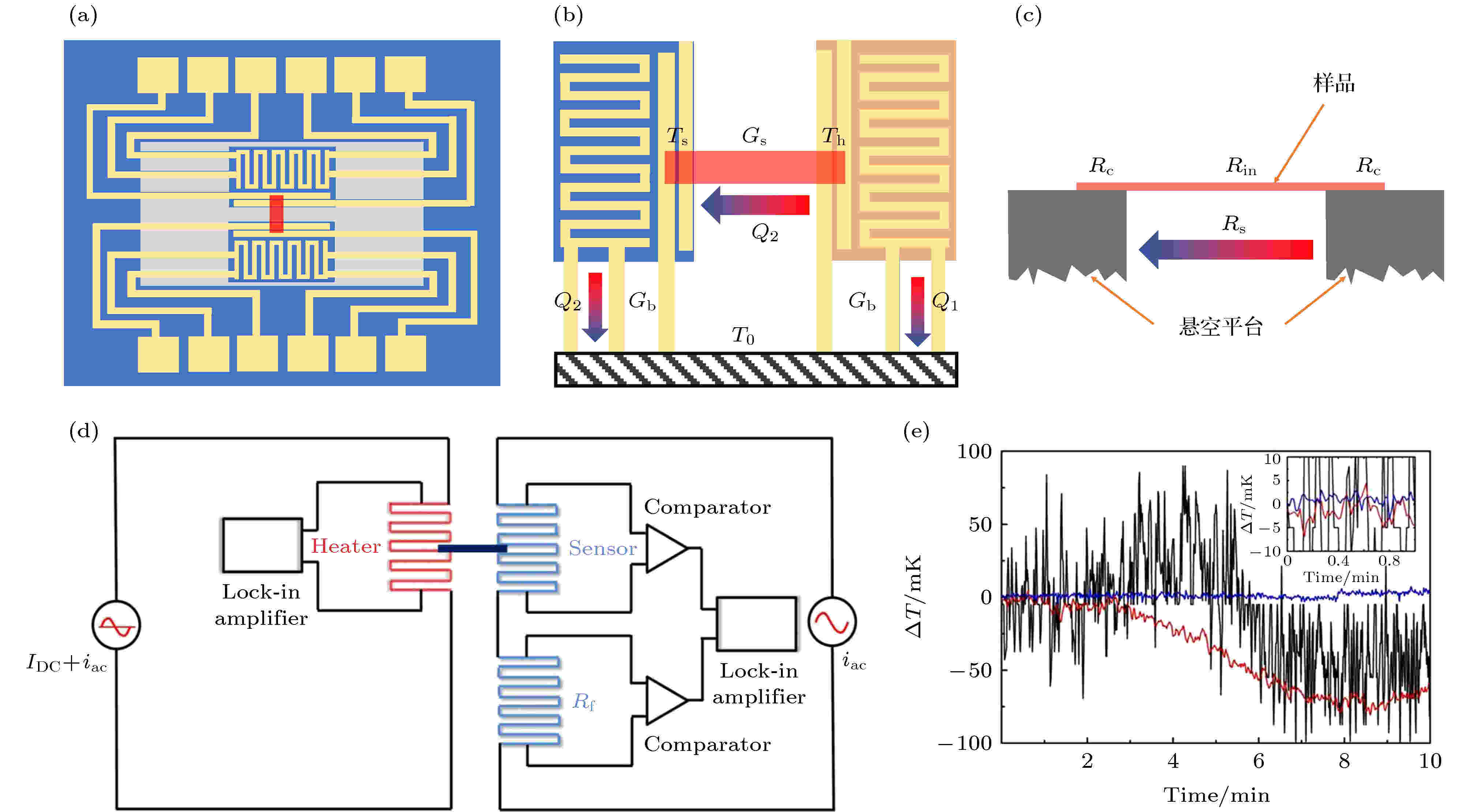图 1 (a)热桥器件示意图; (b)器件热流图; (c)接触热阻对测量的影响; (d)和(e)悬空热桥法改良——比较器法示意图及改良前(黑色实线)和改良后(红色及蓝色)系统温漂随时间变化关系[39]Figure1. (a), (b) Sketch and heat flow of thermal bridge device; (c) influence of thermal contact resistance; (d), (e) diagram of modified comparator method and temperature drift of experimental system[39].
在实验测量过程中, 首先通过纳米机械手转移、湿法转移、干法转移或滴涂等方法将待测样品转移至两个悬空平台之间, 然后在高真空腔体中进行测量(减小热对流的影响). 在进行测量时, 将一个较大的直流电流(微安量级)和较小的交流电流(纳安量级)通入某一侧悬空平台的电极中, 并在另一侧悬空平台的电极中通入较小且大小相同的交流电流. 其中, 直流电流的作用是利用电极的焦耳热效应充当热源, 电极电阻则通过交流电测得. 在很小的温度变化范围内, 金属电极的电阻与温度可近似为线性关系, 因此可以利用电极电阻对悬空平台的温度进行标定.
假设通直流电流的悬空平台上电极所产生的焦耳热为Qh (
根据上述原理, 热桥法用于测量低维材料热导率存在一些问题: (1) (1)式成立的前提条件是假设连接悬空平台与衬底的两组悬臂的热导(Gb)相同. 然而, 由于微纳加工过程工艺的问题, 两组悬臂无法保持绝对一致, Gb之间的差别有时可高达10%, 其结果是热导率测量会出现偏差, 甚至会出现伪热整流效应[40]. (2)悬空平台的内阻问题. 在计算样品热导(Gs)时所需要用到的是样品与悬空平台接触部分的温度, 然而热桥法实际测量的是悬空平台的平均温升(ΔTh和ΔTs). 因此通常将悬空平台的热阻假设为无穷小, 即假设悬空平台内部不存在温差, 但是实际情况是两个悬空平台内部确实存在一定的内阻. 因此, 根据(3)式可知, 对于热导较低的样品, 该假设可近似成立. 然而对于高热导样品(> 5 × 10–8 ), 如多层或者长度小于几百纳米的石墨烯和氮化硼等, 需要用有限元分析对测量结果进行修正[41,42]. (3)两个悬空平台之间存在一定的热辐射, 其值在室温下约为10–10 —10–11 W/K, 因此在测量低热导样品时(如有机纳米线, 无定性纳米线等)需要去除热辐射的影响[39].
近年来悬空热桥法已成功应用于石墨烯[17,43]、氮化硼[41,44]、硫化钼[45-47]、黑磷[48,49]等二维材料的热导率测量. 虽然悬空热桥法的测量精度相较于下述拉曼法(2.3节)有比较明显的优势, 但是仍然有一些问题值得注意. 首先, 样品转移的过程中, 传统的湿法转移方法会在样品表面引入大量有机物残留, 严重影响测量结果[43]. 为了解决这一难题, 科研人员开发了干法转移[41]以及酒精辅助机械手转移[46]等多种转移方法. 其次, 待测样品的热阻(Rs = 1/Gs)不仅包含了样品的本征热阻(Rin), 还包括样品与悬空平台之间的接触热阻(Rc): Rs = Rin+2Rc, 如图1(c)所示. 在某些实验中, 上述接触热阻占实验所得到的总热阻的比例可达到30% — 40%, 甚至更高[41,50], 因此仅仅根据上述数据处理方法所得到的结果存在严重的误差. 在接触点沉积金属(金、铂等), 可以在一定程度上改善接触状态, 降低接触热阻的影响[17,51]. 此外, 截距法[45]与接触热阻计算[43]是目前解决该问题最常见的两种方法. 除了上述两个问题以外, 普通的悬空热桥法测量系统对测量低热导的样品(非晶材料、有机物等)是非常棘手的. 由于测量过程中悬空平台的温度变化会非常小, 信噪比太低, 样品信号容易淹没在环境温漂中. 但是近年来对微纳尺度低热导材料的热传导性质测量的需求非常强烈, 因此针对测量系统进行改良所开发的惠斯通电桥法[52]以及比较器法[39]便应运而出, 如图1(d)所示. 同济大学徐象繁课题组[39]利用比较器法测量了单根聚酰亚胺纳米纤维的热导率, 该实验中样品热导约为1.0 × 10–10 W/K, 比普通热桥法所能测量的下限低一个数量级, 由此可见该方法的使用极大的拓宽了热桥法的使用范围. Zheng等[53]采用交流加热法消除白噪声, 可进一步将测量精度提升至约0.25 pW/K.
2
2.2.电子束自加热法
在上述悬空热桥法中, 样品与悬空平台之间的接触热阻是该方法的主要缺陷之一. 虽然已经有一些方法可以对其进行改善, 但是终究无法从实验原理上消除该缺陷的影响. 2010年新加坡国立大学John Thong课题组和李保文课题组共同开发了一种基于悬空热桥法的新型测量方法——电子束自加热法[42,54]. 该方法不仅可以从原理上消除样品与悬空平台之间的接触热阻对实验结果的影响, 而且还能够测量微纳尺度异质结材料热阻的空间分布(悬空热桥法只能对样品整体的热阻进行测量). 电子束自加热法的测量过程是在扫描电子显微镜(SEM)中完成的. 利用SEM中的高能电子束与样品之间的相互作用充当热源, 并且电子束(热源)可以在样品上连续扫描(移动), 如图2(a)所示.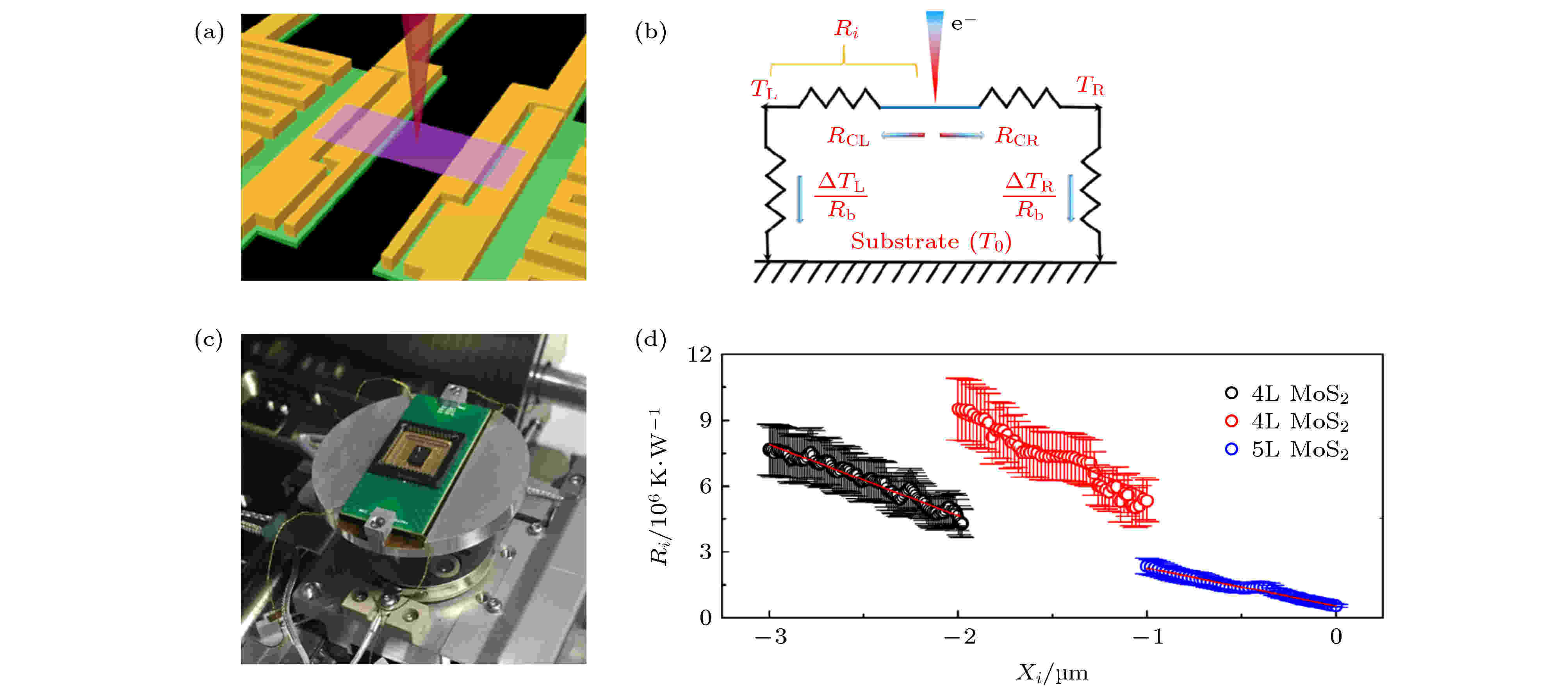
图 2 电子束自加热法[54] (a)示意图; (b)热流图; (c)同济大学测量装置图; (d)利用电子束自加热法测量多层硫化钼的热导率Figure2. The electron-beam self-heating method [54]: (a) Sketch; (b) heat flow of device; (c) experimental setup in Tongji University; (d) measuring thermal conductivity of few-layer MoS2.
假设电子束扫描的位置坐标为x, 该处样品的温度变化为ΔTi(x), 同时热量将从扫描处往两侧传导, 引起两端悬空平台的温度变化分别为ΔTL(左侧), ΔTR(右侧). 热量会通过六根悬臂传导至基底上, 基底温度为T0, 热流如图2(b)所示. 建立热传导平衡方程为[55]
在同一个样品中, 利用悬空热桥法测量, 左侧悬空平台为加热端, 可测得左侧与右侧悬空平台温度变化分别为ΔTL0和ΔTR0. 结合上式以及悬空热桥法测量原理, 可得
2
2.3.拉曼法
2008年首次实验测量二维材料——单层石墨烯的悬空面内热导率所使用的方法便是拉曼法[31]. 自此, 拉曼法逐渐成为二维材料热传导领域中重要的实验测量方法, 并已成功应用于氮化硼[56,57]、黑磷[58]、硫化钼[18,59,60]等多种二维材料的热导率测量. 拉曼法测量二维材料热导率的原理主要基于以下两点: (1) 二维材料对拉曼激光具有一定的吸收作用, 因此拉曼激光可以作为热源; (2) 二维材料的拉曼光谱吸收峰位置与温度存在一定的线性关系[58,61,62], 因此可以利用材料的拉曼光谱确定其表面温度. 结合以上两点原理, 并通过热传导模型计算, 即可得到二维材料的热导率.拉曼法测量二维材料热导率的原理图如图3(a)所示. 假设热传导模型为圆形, 该二维材料的热导率可表示为[31]
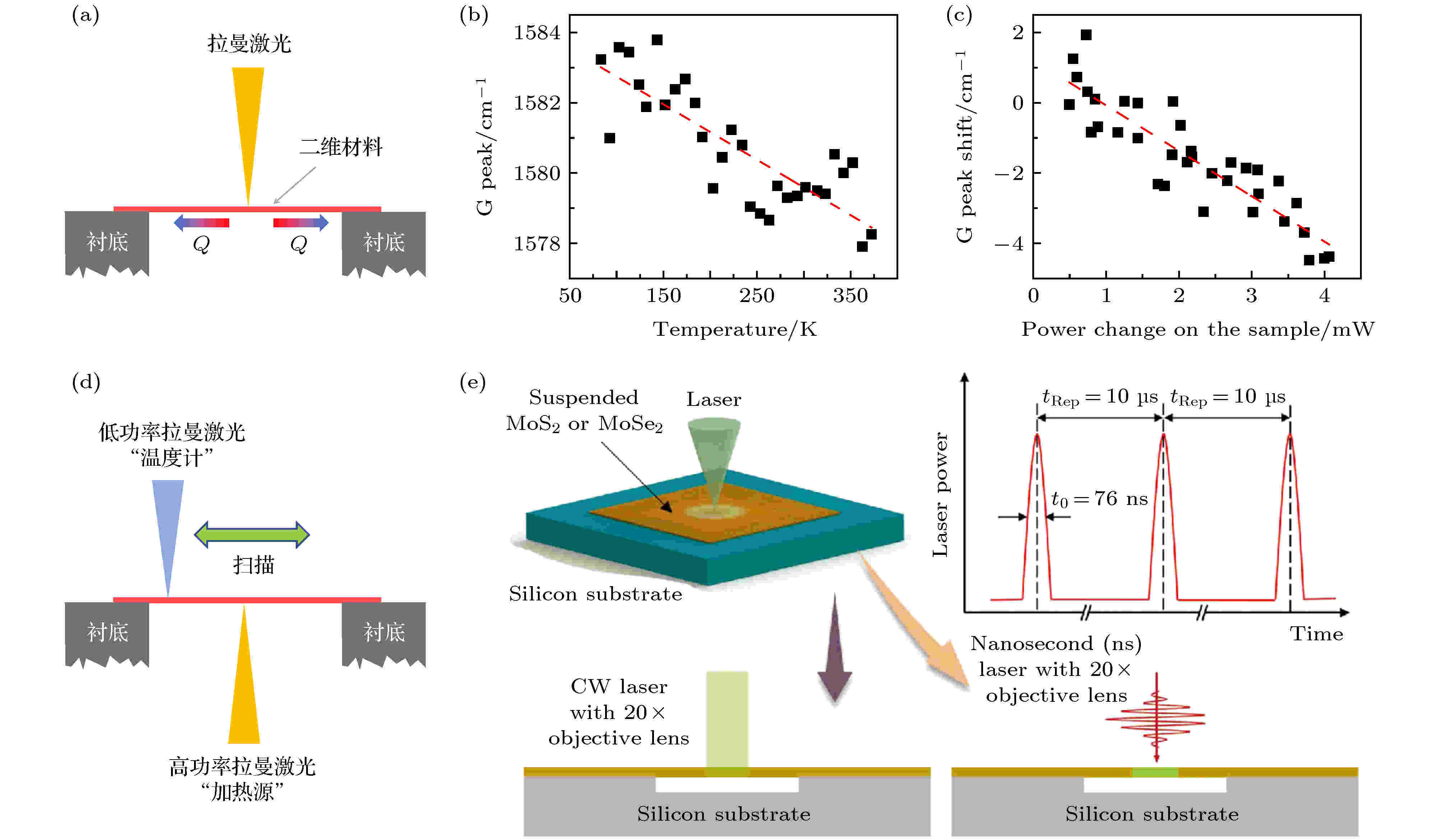图 3 (a) 拉曼法测量原理图; (b) (c) 单层悬空石墨烯拉曼G峰频率与温度以及激光能量的关系[31,61]; (d) 双拉曼法示意图[67]; (e) ET-Raman法示意图[70]Figure3. (a) Sketch of the Raman method; (b), (c) experimental data for the Raman G peak shift with respect to temperature and laser power[31,61]; (d), (e) sketch of the Two-Raman method[67] and ET-Raman method[70].
实验中可测得该材料拉曼吸收峰与表面温度的关系, 通过线性拟合可得到:
以上模型只针对圆形(corbino)样品. 矩形、一维样品测量原理一样, 但其热导模型略有不同, 可查阅相关文献.
通过上述分析, 可以看出使用拉曼法测量二维材料热导率是可行且有效的, 但是在实际测量中却存在一些不可忽视的问题. 首先, 在早期的几个实验中准确测量材料对拉曼激光的吸收功率存在一定难度, 其所影响的实验结果不确定度能达到30% — 50%[24]. 例如, 在不同文献中所使用的悬空单层石墨烯对拉曼激光的吸收率数值差别非常大(2.3%—13%), 导致所得到的悬空单层石墨烯面内热导率存在较大差异(5300—630 W/(m·K), T = 300 K)[31,63]. 其次, 利用拉曼光谱吸收峰位置变化确定材料表面的温度, 其精度较低(8— 40 K), 严重影响测量结果的精确性[31,64]. 另外, 因为其较低的温度测量精度, 使得拉曼法测量通常会将样品的温度加热几十度甚至一两百度, 导致测量结果有严重偏差. 如Geim等[63]测量悬空单层石墨烯热导率约为630 W/(m·K), 实验中他们发现虽然衬底温度保持T = 295 K, 但是在功率为6.2 mW的激光加热情况下悬空石墨烯中间位置温度达到了约660 K. 除了上述技术难点以外, 衬底对激光的反射、非悬空二维材料的热导率(材料与衬底接触部分)、拉曼激光光斑尺寸、二维材料与衬底之间的接触热阻等未知因素同样会对测量结果产生一定影响[65].
为了针对部分上述问题进行改良, 科研人员通过改进实验设备或计算模型, 在提高拉曼法的测量精确度上有了一定的突破. 例如, 2010年蔡伟伟等[66]利用激光功率计同步测量单层石墨烯对拉曼激光的吸收率, 并且在计算模型中加入了衬底的影响, 一定程度上提高了测量结果的精确性. 2014年Reparaz 等[67]开发出一种双拉曼激光的测量方法, 其中一束高功率激光作为固定加热源, 另一束低功率激光扫描二维材料悬空部分, 并通过拉曼吸收谱得到悬空部分的温度场分布. 该方法的优点在于可以排除衬底对测量结果的影响, 如图3(d)所示. 2016年清华大学张兴课题组[68,69]结合连续激光与脉冲方波激光, 通过改变光斑半径以及脉冲激光周期, 能够在无需知道二维材料对拉曼激光的吸收率的情况下得到材料的热导率. 同年, 爱荷华州立大学王信伟课题组[70]引入一种新型拉曼技术(ET-Raman), 该方法不仅不需要获得二维材料对拉曼激光的吸收率同时无需利用拉曼吸收峰对材料表面进行温度标定, 如图3(e)所示. 随着拉曼法的不断发展与完善, 其已逐渐成为一种微纳尺度热传导测量的成熟方法[71].
2
2.4.时域热反射法
1983年Eesley将皮秒级脉冲激光应用于探测金属铜中的非平衡热输运过程[72], 自此时域热反射法(time-domain thermoreflectance, TDTR)正式被应用于材料热物性的测量. 经过30多年的发展, TDTR已经成为一种被广泛使用的材料热物性非稳态测量方法, 通常应用于测量块材或薄膜的热导率以及界面热阻[73-75]. 其基本原理为: 将一束飞秒级脉冲激光通过分光镜分为泵浦光及探测光, 其中泵浦光充当热源对材料表面进行加热, 而探测光用于测量材料表面温度的变化(材料表面对激光的反射率与温度有关). 通过位移平台可以精准控制两束光之间的光程差, 进而控制它们到达材料表面的时间间隔, 产生一定的时间延迟(td), 由此可以测量从加热到恢复环境温度过程中, 材料表面温度随延迟时间的变化, 该温度的变化过程与材料热物性有关.TDTR的测量系统包括飞秒激光发生器、分光器、位移平台、电光(声光)调制器、光电二极管探测器、锁相放大器等[33], 如图4(a)所示. 在测量之前, 一般需要在待测样品表面镀一层金属薄膜作为传感层, 因为在很小温升情况下金属表面对激光的反射率与温度之间近似呈线性关系, 能够更加精确地标定其表面温度. 通过上述测量过程, 锁相放大器将输出基于调制频率的同相信号(Vin)和反相信号(Vout), 该信号中包含了样品表面温度变化的信息, 随之可以得到同相信号与反相信号之比(Vin/Vout)与延迟时间之间的关系, 如图4(b)和图4(c)所示, 最终通过建立热传导模型并拟合实验数据即可得到样品热物性的相关数据. TDTR已被适用于测量石墨烯[76]、黑磷[77]、硫化钼[74,75]、硒化钨[78]等二维材料的热物性.
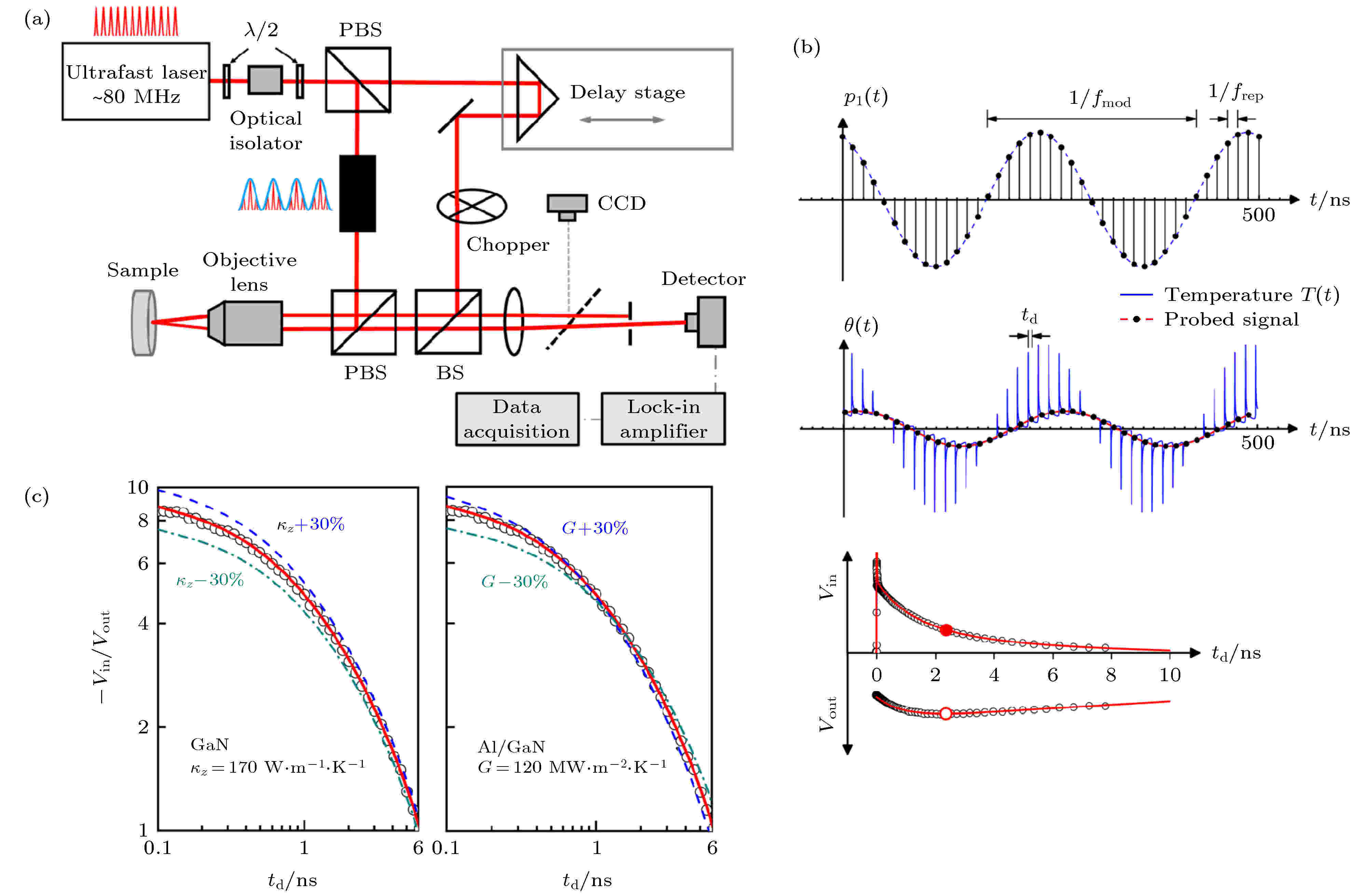图 4 (a)时域热反射法测量系统; (b)经正弦调制的飞秒脉冲激光、材料表面温度响应、锁相放大器所输出的同相信号和反相信号与延迟时间之间的关系; (c)采用时域热反射法测量GaN热导率及Al/GaN界面热导[33]Figure4. (a) Experimental setup of the TDTR method; (b) femtosecond pulse laser with sinusoidal modulation, temperature response of sample surface, the in-phase signal and out-of-phase signal of Lock-in Amplifier versus delay-time; (c) using TDTR method to measure thermal conductivity of GaN and interface thermal conductance of Al/GaN[33].
与稳态热测量方法相比, TDTR无需在真空腔体中进行测量, 其次它可以用于超快热输运机理研究(电声相互作用等). 但是其缺点也是比较明显的, 例如该方法对样品表面的光滑程度要求比较高, 一般需要表面粗糙度小于15 nm. 其次, 测量之前需要在样品表面沉积几十个纳米的金属薄膜用作传感层. 然而很多二维材料, 特别是单层或者多层二维材料, 其表面吸附杂质或者沉积物会抑制面外声学声子, 导致该方法无法准确测量单层/多层二维材料的本征热导率[79]. 这点我们会在本文后续进行详细讨论. 近年来, 经过不断的改进与发展, 在TDTR的基础之上已衍生出频域热反射法(frequency-domain thermoreflectance, FTDR)[80]以及结合time-resolved magneto-optic Kerr effect (TR-MOKE)[81]、asynchronous optical sampling (ASOPS)[82]等技术提高TDTR的测量精度或扩大其适用范围.
2
2.5.其他微纳尺度热传导测量方法
除了上述三种方法以外, 微纳尺度热传导的测量方法还包括: (1) 瞬态测量3ω法[32,83,84]. 该方法对样品的厚度有一定的要求, 因此通常用于测量块材或薄膜的面间热导率或接触热阻; (2) 基于原子力显微镜(atomic force microscope, AFM)改装的热探针扫描法(scanning thermal microscopy, SThM)[85-87], 该方法可提供材料纳米尺度的热阻分布图像; (3) T-bridge 法[88]、悬空Four-Point热测量法[89]、激光脉冲热测量法[34]、薄膜自加热法[90]等.上述方法均有各自的优缺点, 在实际测量中需根据材料特性以及实验设备酌情选择. 欲进一步了解各测量方法的细节情况, 可查阅相关文献 [6,21,23,91-93].
3.1.各种二维材料的热传导性质
33.1.1.石墨烯
石墨烯作为第一种被成功制备的二维材料, 一经发现便成为科研界的“宠儿”. 其拥有一系列优异的物理性质—狄拉克锥能带、超高电导率、超高载流子迁移率等[94-96]. 在热传导方面, 石墨烯同样表现出色, 其室温本征热导率能达到2000—3000 W/(m·K), 是迄今为止发现的热导率最高的材料. 2008年, Balandin等[31]通过拉曼法首次测量了室温环境中悬空单层石墨烯的热导率, 测量结果显示其热导率远高于金刚石(当时已知热导率最高的材料)和石墨块材, 达到4840—5300 W/(m·K); 然而随着科研人员进一步的研究, 发现该实验对石墨烯的拉曼激光吸收功率可能存在过大的估计, 导致结果偏大4—6倍[31,97]. 2010年, 蔡伟伟等[66]采用同样的方法测量了悬空单层石墨烯的热导率, 并同步使用激光功率计测量了石墨烯的拉曼激光吸收率, 结果显示化学气相沉积法(CVD)所生长的单层石墨烯的热导率约为2500—3100 W/(m·K) (T = 350 K)和1200—1400 W/(m·K) (T = 500 K), 并发现石墨烯悬空部分的形状、尺寸和测量环境(空气、真空等)对最终的结果会产生一定的影响. 除了激光吸收率存在争议以外, 造成不同实验结果之间存在较大差异的另一主要原因是石墨烯的制备方式不同(机械剥离或化学气相沉积法), 导致其品质(杂质、晶界、有机物残留等)存在一定的差别, 这些因素会对声子产生额外的散射. 表1中列举了包括拉曼法在内的不同实验方法所测量的悬空单层/多层石墨烯的热导率.| 制备方式 | 石墨烯层数 | 热导率 κ /W·(m·K)–1 | 备注 |
| 拉曼法 | |||
| 机械剥离[31] | 1层 | ~4840—5300 (室温) | 数值高估, 见本节文字部分 |
| 机械剥离[97] | 1层 | ~3080—5150 (室温) | |
| 化学气相沉积[66] | 1层 | ~2500 +1100/–1050 (T = 350 K) | / |
| 化学气相沉积[66] | 1层 | ~1400 +500/–480 (T = 500 K) | / |
| 化学气相沉积[98] | 1层 | ~2600 — 3100 (T = 350 K) | / |
| 机械剥离[63] | 1层 | ~630 (T = 660 K) | / |
| 机械剥离[99] | 1层 | ~1800 (T = 325 K) | / |
| 机械剥离[99] | 1层 | ~710 (T = 500 K) | / |
| 化学气相沉积[69] | 1层 | ~850—1100 (T = 303—644 K) | / |
| 机械剥离[69] | 1层 | ~1500 (T = 330—445 K) | / |
| 机械剥离[69] | 2层 | ~970 (T = 303—630 K) | / |
| 悬空热桥法 | |||
| 化学气相沉积[100] | 1层 | ~190(T = 280 K, L = 0.5 μm) | / |
| 化学气相沉积[43] | 2层 | ~560—620(室温, L = 5 μm) | / |
| 化学气相沉积[17] | 1层 | ~1689—1831(T = 300 K, L = 9 μm) | / |
| SThM | |||
| 化学气相沉积[85] | 1层 | ~2100—2430(T = 335 K) | / |
表1不同文献中测量悬空石墨烯热导率实验细节
Table1.Experimental detail of thermal conductivity in suspended single/few-layer graphene from different literature.
为了进一步理解石墨烯中超高热导率的物理机制, 了解不同声子模式对热导率的贡献是至关重要的. 在石墨烯中, 热量主要通过声学声子传输, 其声学声子模式包括面内声学纵波(LA)、面内声学横波(TA)—与波矢q之间呈线性关系, 以及面外声学横波(ZA)—与波矢q之间呈平方关系. Nika等[101]认为单层石墨烯中热输运过程几乎全部由LA/TA声子模承担, 而ZA声子模对热导率的贡献可以忽略不计, 这主要是因为当波矢q较小时ZA声子的群速度将趋近于零, 而且面外方向的Grüneisen常数比较大. 但是, Lindsay等[102,103]认为ZA声子模具有比较大的低频声子态密度, 因而其对热导率的贡献会比较大, 并预测室温下ZA声子模对单层石墨烯热导率的贡献能达到约70%, 如图5(a)所示. 同时提出在低温下, LA/TA声子模与ZA声子模所引起的热导率与温度之间分别呈κ-T 2和
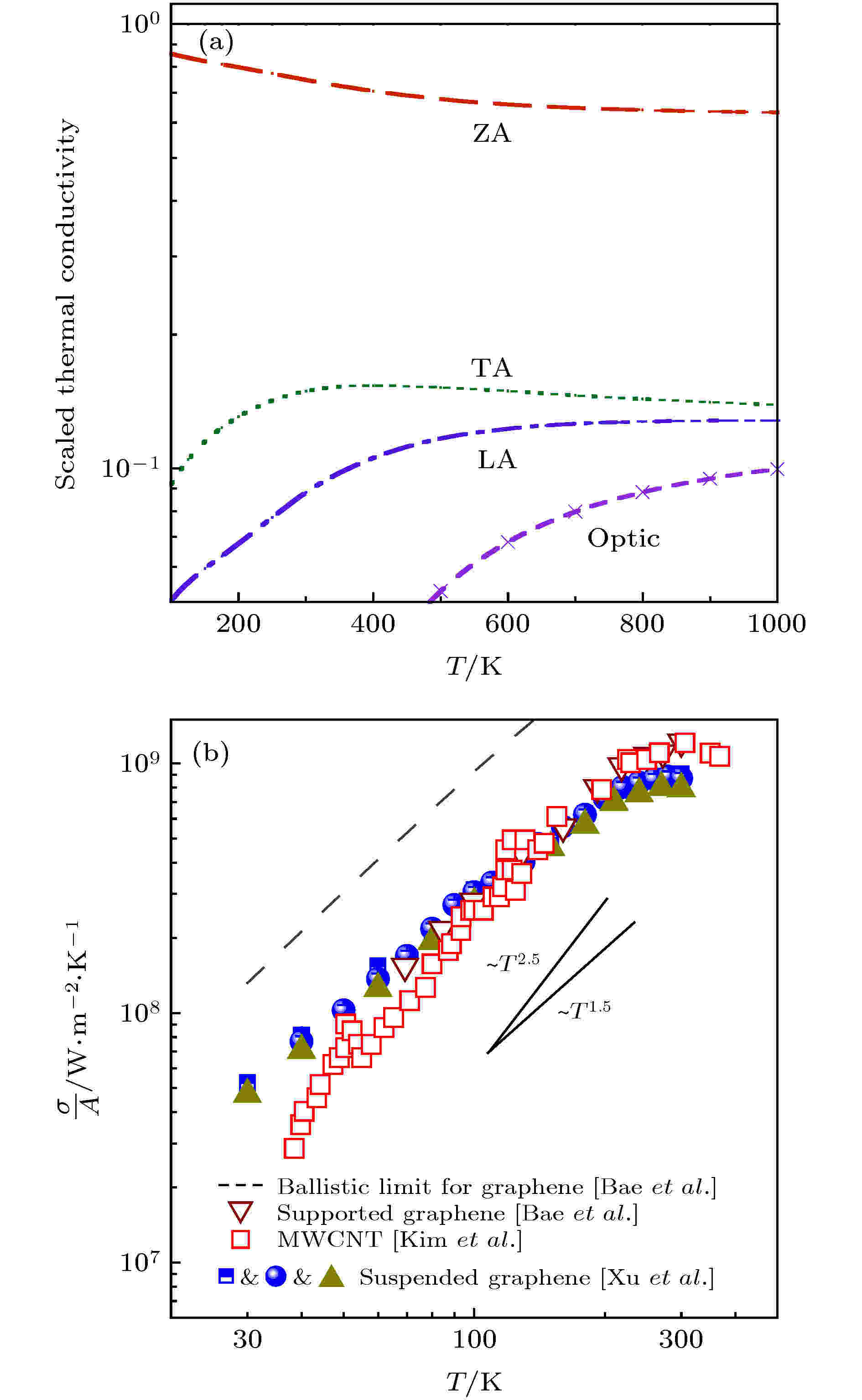图 5 (a) 悬空单层石墨烯中各声子模式贡献热导率比例[102]; (b)实验观测单层悬空石墨烯中声子的(准)弹道输运[17,35,111]Figure5. (a) Phonon modes contribution to thermal conductivity in suspended single-layer graphene[102]; (b) experimental observation of (quasi-) ballistic phonon transport in suspended single-layer graphene[17,35,111].
以上讨论的热导率理论是基于三声子散射模型计算. 四声子散射往往被直接忽略, 因为其是只有在高温区才会逐渐出现的一类声子散射行为[106]. 但是近年理论研究发现即使是在室温环境下, 单层石墨烯中大量的低能ZA模声子导致其四声子散射过程是不容忽视的, 因此此前只使用三声子散射模型计算的单层石墨烯热导率可能是偏高的[107,108]. 通过求解玻尔兹曼方程并引入四声子散射, Feng等[107]发现室温下单层石墨烯的热导率仅为810 W/(m·K), 该数值远低于仅包含三声子散射的计算结果(约3383 W/(m·K)), 同时结果显示在四声子散射的影响下ZA声子模对热导率的贡献也仅为31%. 该工作在计算室温下单层石墨烯热导率的过程中所使用的原子力常数为0 K值. 随后上海交通大学顾骁坤等[108]对上述结果进行修正, 所得到的结果数值相较上述文献稍大, 进一步证实了室温下四声子散射对单层石墨烯热导率的严重影响.
由此可见, 单层悬空石墨烯的热导率值到底是多少仍未有定论. 这个问题不管是在理论还是实验上都存在一定的争议.
在实际应用中, 石墨烯更可能是附于某一衬底上. 因此除了悬空石墨烯以外, 研究衬底上石墨烯的面内热传导性能也是必要的. Seol等[103]测量了氧化硅衬底上单层石墨烯的面内热导率(约600 W/(m·K), 300 K). 当石墨烯附于衬底上时, ZA声子模将会被抑制, 因而其面内热导率比悬空石墨烯低. 如上述理论计算结果所示室温下ZA声子对热导率的贡献能达到约70%, 但是当存在衬底时ZA声子模的贡献将被严重抑制甚至消失, 热导率数值将从~3000 W/(m·K)降至~600 W/(m·K). 该实验有效验证了石墨烯中ZA声子对其热导率起主要贡献. 除了氧化硅以外, 氮化硅也是一种常见的衬底材料, Thong等[42]测量了氮化硅衬底上多层石墨烯的面内热导率, 其数值为~150—1250 W/(m·K) (室温). 为进一步验证ZA声子对热导率的贡献. Wang等[109]将金原子沉积到悬空三层石墨烯表面, 发现其热导率从约1500 W/(m·K)降至约270 W/(m·K), 降幅达82%, 得到了与Seol等一样的结论. Jang等[110]研究了SiO2-石墨烯-SiO2三明治结构热输运性质, 发现热导率会进一步降低; 特别是单层三明治结构石墨烯, 其室温热导率远低于160 W/(m·K)(该文中具体数值过低无法测出, 只给了一个上限), 表明衬底对石墨烯的热导率有着非常显著的抑制作用.
相较面内热导率而言, 石墨烯面间热导率的研究是较少的. 石墨烯的层间作用力属于较弱的范德瓦尔斯力, 因此最初普遍认为石墨烯的面间声子平均自由程非常短(几个纳米). 但是2012年Harb等[112]测量了厚度为35 nm的石墨烯的面间热导率(约0.7 W/(m·K), T = 300 K), 比块材石墨的面间热导率(约7 W/(m·K), T = 300 K)低一个数量级, 因此他们认为该现象的出现可能是由于之前对石墨烯的面间声子平均自由程的估计偏小. 随后东南大学陈云飞课题组[113]通过分子动力学模拟发现石墨烯的面间声子自由程能达到数微米, 远超出之前的理解. 2015年Fu等[114]测量了不同厚度的石墨烯(24 nm—714 nm)的室温面间热导率, 发现随着厚度增加石墨烯的面间热导率逐渐变大, 同时热导率的数值未观测到一个饱和阈值, 他们认为石墨烯的面间声子自由程能够达到200 nm. 此后, Minnich等[115]进一步测量了厚度为(24 nm—21.9 μm)的石墨烯/石墨薄片的面间热导率, 结果显示在低温区(高温区)面间热导率直到厚度约为2 μm(800 nm)才达到饱和阈值, 并接近石墨块材的面间热导率. 因此他们认为石墨烯的面间声子自由程至少为40—250 nm(室温)和100—600 nm(低温), 如图6所示.
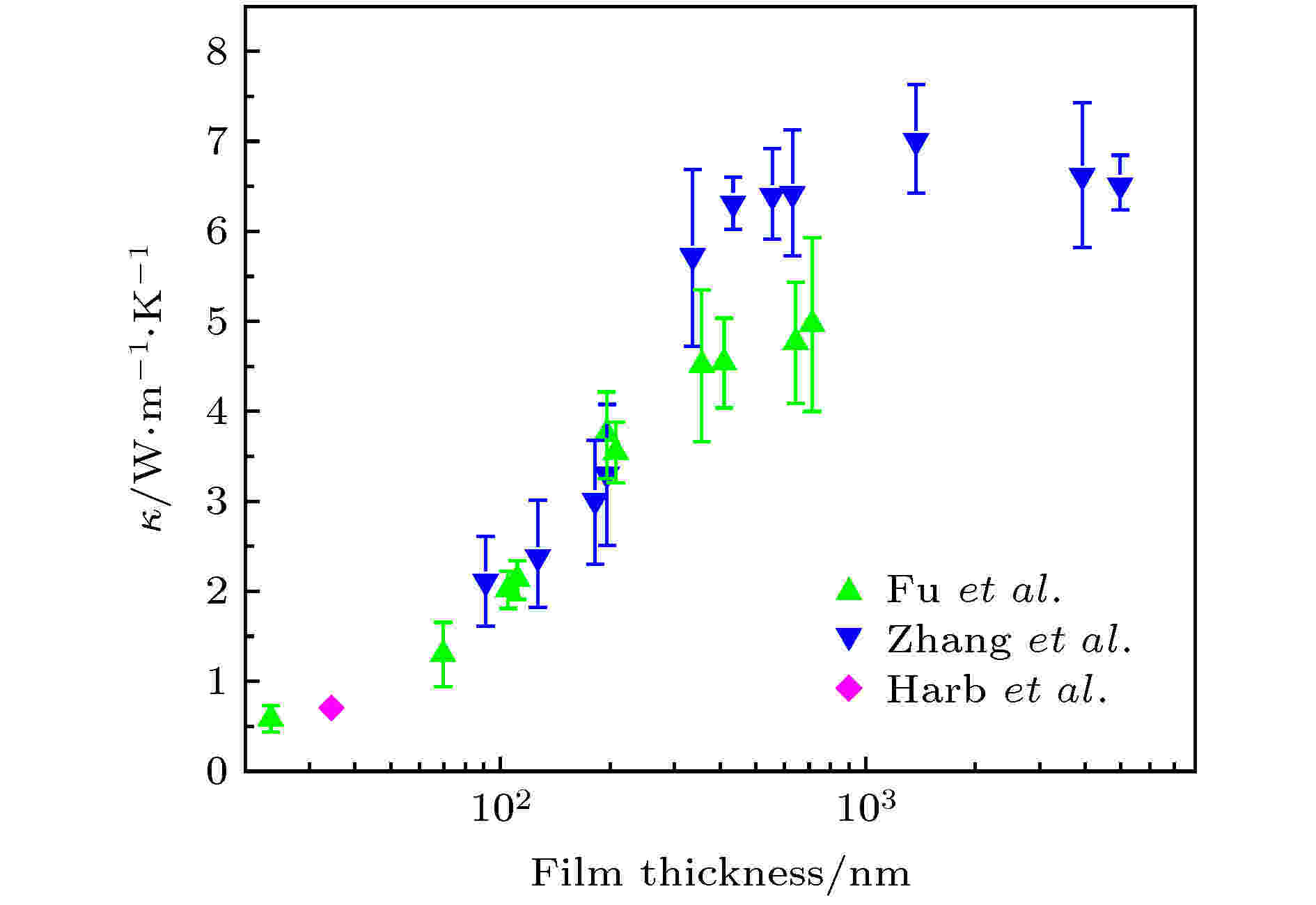图 6 实验测量石墨面间热导率与厚度的关系[112,114,115]Figure6. out-of-plane thermal conductivity of graphite versus thickness in experiment[112,114,115].
3
3.1.2.氮化硼
因带隙较大(5.5—6.0 eV)且表面非常光滑, 氮化硼(h-BN)是非常理想的一类介电材料. 同时氮化硼块材的热导率(约400 W/(m·K), 室温)与铜很接近, 且相同体积下其质量比铜低很多, 因此在电子器件散热的方面拥有广阔的应用前景[116,117].氮化硼被称为白色石墨烯, 其晶体结构与石墨烯类似. 其面内氮原子与硼原子相互交错形成蜂窝状结构, 层间依靠范德瓦尔斯力相互结合, 属于较早被发现的二维材料之一[118]. 由于拥有相似的晶体结构, 氮化硼与石墨烯的物理性质也就具有一定的相似之处. Lindsay等[119]通过求解玻尔兹曼方程的理论研究, 预测单层氮化硼的室温面内热导率为600 W/(m·K), 高于氮化硼块材, 同时还发现其面外ZA声子模对热导率贡献能达到~60%.
2013年Jo等[120]采用微桥电阻温度计法测量了多层氮化硼的悬空面内热导率(250 W/(m·K), 5层; 360 W/(m·K), 11层; T = 300 K). 他们认为之所以测量数据较理论预测偏低, 甚至比氮化硼块材热导率低, 主要是因为在实验过程中氮化硼表面存在大量有机物残留导致声子散射严重. 在后续的多层氮化硼悬空面内热导率的实验中均未观察到热导率超过其块材, 其中样品的质量是关键因素[57,62,121]. 直到2016年同济大学徐象繁课题组[41]通过改善样品转移方法——PDMS辅助干法转移使得氮化硼薄膜表面有机残留大大减少. 同时他们使用质量较高的块材机械剥离制备多层氮化硼, 首次测得悬空双层氮化硼的热导率较块材高, 室温下达到460—625 W/(m·K). 随后, 迪肯大学李璐华等[56]使用拉曼法测量了室温附近单层/双层以及三层悬空氮化硼的热导率, 随着厚度增加热导率数值会有所降低, 但是均高于块材氮化硼热导率, 其中单层氮化硼的热导率达到~751 W/(m·K), 是迄今为止实验上得到的单层/多层氮化硼热导率的最高值. 表2中列举了不同文献中测得的悬空氮化硼面内热导率. 从表中数据可以看出, 采用机械剥离方法制备的多层氮化硼热导率普遍高于采用CVD方法制备的多层氮化硼, 其中原因是由于化学气相沉积法往往会在样品中引入较多的缺陷, 而机械剥离法在控制样品质量方面则表现得更好一些.
| 制备方式 | 氮化硼薄膜层数 | 测量方法 | 热导率(室温/300 K) |
| κ /(W(m·K)–1) | |||
| 机械剥离[120] | 5层 | 微桥电阻温度计法 | ~250 |
| 机械剥离[120] | 11层 | 微桥电阻温度计法 | ~360 |
| 化学气相沉积[62] | 9层 | 拉曼法 | ~227—280 |
| 化学气相沉积[57] | 2.1 nm | 拉曼法 | ~223 |
| 化学气相沉积[121] | 10 nm/20 nm | 稳态/瞬态 | ~100 |
| 机械剥离[41] | 2层 | 热桥法 | ~484 +141/–24 |
| 机械剥离[44] | 4层 | 热桥法 | ~286 |
| 机械剥离[56] | 1层 | 拉曼法 | 751 ± 340 |
| 机械剥离[56] | 2层 | 拉曼法 | 646 ± 242 |
| 机械剥离[56] | 3层 | 拉曼法 | 602 ± 247 |
表2不同实验中悬空单层/多层h-BN热导率实验测量细节表
Table2.Experimental detail of thermal conductivity of suspended single/few-layer h-BN in different literature.
3
3.1.3.硫化钼及其他过渡金属硫化物
过渡金属硫化物(MX2, 其中M代表Mo, W, Ti等过渡金属元素, X代表硫族元素, 包括S, Se, Te)是非常重要的一族二维材料, 它们的晶体结构属于“三明治”型层状结构[122]. 与单层石墨烯、单层氮化硼等只包含一个原子层的二维材料不同, 单层过渡金属硫化物包含三个原子层——过渡金属原子层被硫族元素原子层“夹”在中间[123], 如图7(a)所示.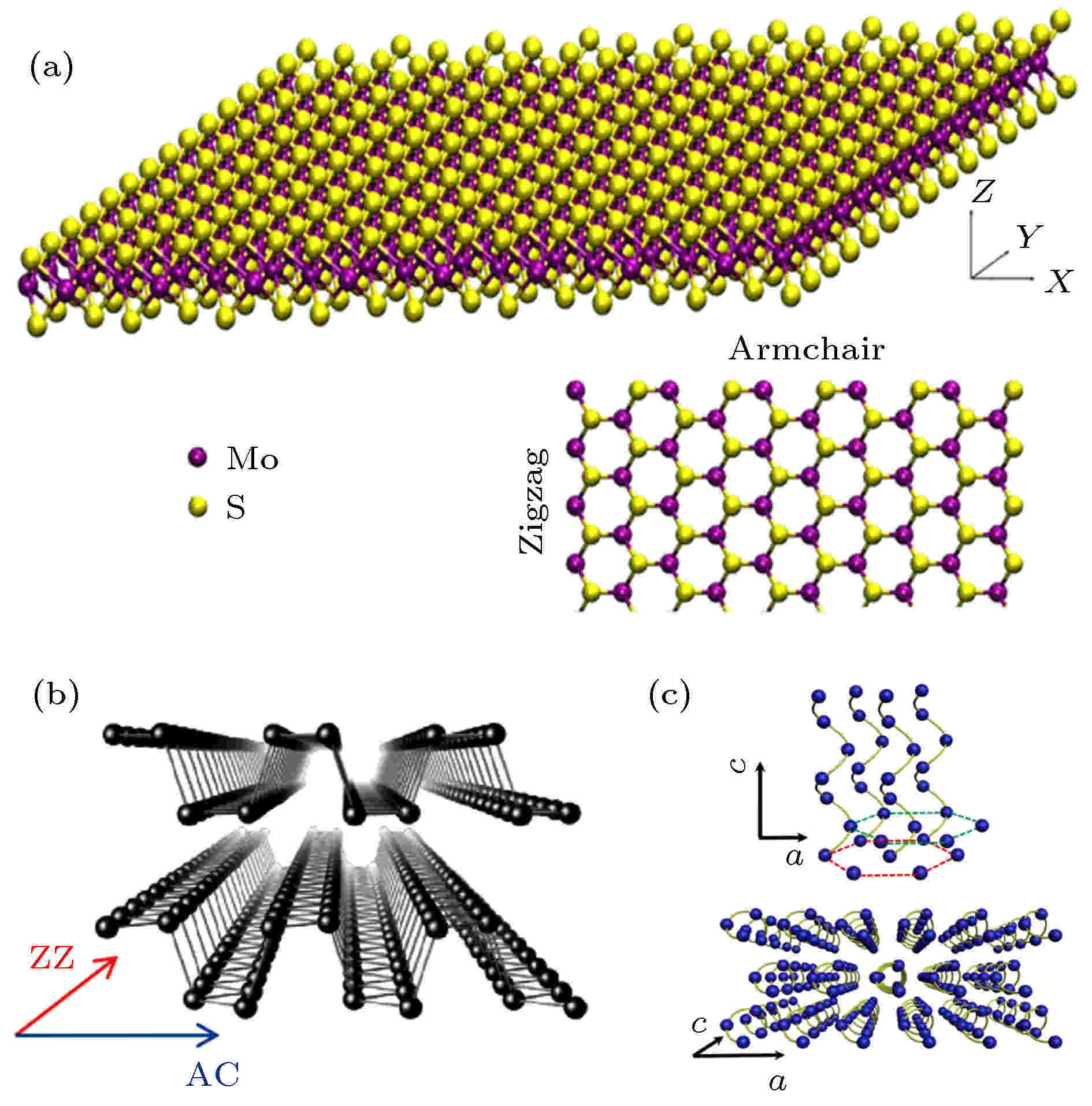
图 7 晶体结构 (a)硫化钼[123]; (b)黑磷[48]; (c)块体碲[150]Figure7. crystal structure of (a) MoS2[123], (b) BP[48], (c) bulk Te [150].
硫化钼是被研究的最为广泛的一种过渡金属硫化物, 因带隙可控且电学性质优良, 同时能够在空气中稳定存在, 被认为是极具潜力的下一代微电子器件材料, 并且在光学、热电等领域同样存在一定的应用前景[122,124,125]. 2013年Sahoo等[59]使用拉曼法测量了11层硫化钼的悬空面内热导率(约52 W/(m·K), 室温). 随后, Yan等[60]和Jo等[126]分别测量了室温下单层以及多层硫化钼的悬空面内热导率, 其数值为35—52 W/(m·K). 但是2015年Hone等[127]同样采用拉曼法测量单层/双层硫化钼的悬空面内热导率, 其结果(77—84 W/(m·K))远大于之前实验的数据, 他们认为主要是由于实验中所得到的硫化钼的拉曼峰频率变化与温度关系、拉曼激光吸收功率以及接触热阻等关键数据均与之前的文献存在较大差异. 2018年同济大学徐象繁课题组[54]使用电子束自加热法测量了多层硫化钼的悬空面内热导率, 这是首次将该方法应用于实验测量二维材料的热导率, 实验结果也证实了该方法的可行性. 表3中列举了不同文献中硫化钼面内热导率的实验测量结果.
| 制备方式 | 硫化钼薄膜层数 | 测量方法 | 热导率 (300 K/室温) |
| κ /(W·(m·K)–1) | |||
| 悬空 | |||
| 化学气相沉积[59] | 11层 | 拉曼法 | ~52 |
| 机械剥离[60] | 1层 | 拉曼法 | 34.5 ± 4 |
| 机械剥离[126] | 4层 | 热桥法 | ~44—45 |
| 机械剥离[126] | 7层 | 热桥法 | ~48—52 |
| 机械剥离[127] | 1层 | 拉曼法 | 84 ± 17 |
| 机械剥离[127] | 2层 | 拉曼法 | 77 ± 25 |
| 机械剥离[54] | 4层 | 电子束自加热 | 34 ± 6 |
| 机械剥离[54] | 5层 | 电子束自加热 | 30 ± 3 |
| 化学气相沉积[128] | 1层 | 拉曼法 | 13.3 ± 1.4 |
| 化学气相沉积[128] | 2层 | 拉曼法 | 15.6 ± 1.5 |
| 化学气相沉积[47] | 1层 | 热桥法 | ~21—24 |
| 化学气相沉积[18] | 1层 | 拉曼法 | 60.3 ± 5.2 |
| 化学气相沉积[18] | 2层 | 拉曼法 | 38.4 ± 3.1 |
| 化学气相沉积[18] | 3层 | 拉曼法 | 44.8 ± 5.9 |
| 化学气相沉积[18] | 4层 | 拉曼法 | 36.9 ± 4.9 |
| 衬底 | |||
| 机械剥离[129] | 1层 | 拉曼法 | ~62.2 |
| 机械剥离[65] | 4层 | 拉曼法 | 60.3 ± 5 |
表3不同文献中硫化钼单层/多层热导率实验测量细节表
Table3.Experimental detail of thermal conductivity of single/few-layer MoS2 in different literature.
硫化钼的晶体结构相较石墨烯以及氮化硼存在一定的差异, 因此其热传导性质也会有所不同, 主要体现如下: 首先单层硫化钼的热导率较单层石墨烯和单层氮化硼低1—2数量级. 新加坡高性能计算研究所张刚课题组[130]通过理论计算发现单层硫化钼低热导率的原因在于较低的声子群速度以及较大的Grüneisen常数, 进而导致其声子平均自由程仅为14.6 nm. 其次, 在单层石墨烯以及单层氮化硼中, 面外ZA声子模对热导率贡献占比均超过50%, 但是在单层硫化钼中面内声子模式对热导率的贡献超过了面外的声子模式[130]. 最后, 与石墨烯以及氮化硼所不同, 迄今为止实验上测得单层/多层硫化钼的面内热导率均比硫化钼块材面内热导率(85—110 W/(m·K), 室温)要低. 该现象与理论上的预测不一致. 顾骁坤等[131]预测单层硫化钼的室温面内热导率能达到138 W/(m·K), 其中原因可能是这些实验中硫化钼的质量均未达到较好的情况, 或者背后隐藏着更深层次的原因有待进一步研究.
除了面内热导率以外, 硫化钼的面间热导率也是值得研究的问题之一, 但是该方向的研究相对较少. 最初Muratore等[138]和Cahill等[139]测量了块材硫化钼的室温面间热导率, 仅为2—3 W/(m·K). 但是, 随后科罗拉多博尔德分校杨荣贵课题组[75]在实验上得到了一个数值更高的结果(约 4.75 W/(m·K)), 并且该结果与理论预测更加接近. 上述实验结果之间的差异在后续Sood等[74]的实验中得到解释. 他们通过TDTR方法测量了不同厚度硫化钼的室温面间热导率, 结果显示厚度为240 nm和20 nm的样品室温面间热导率分别为2.0 ± 0.3 W/(m·K), 0.9 ± 0.2 W/(m·K). 通过与上述实验数据的对比, 发现随着厚度增大, 硫化钼的面间热导率呈增大的趋势, 当厚度达到1 μm左右面间热导率数值逐渐趋近于饱和阈值(约5 W/(m·K)). 理论计算结果显示硫化钼面间声子的平均自由程远超之前的估计数值(1.5—4 nm), 超过80%的热量输运是平均自由程为10—500 nm的声子所贡献的.
随着二维材料的制备技术不断发展, 越来越多的多层过渡金属硫化物被发现, 因此它们的热传导性也在逐渐被研究. 表4中列举了不同文献中除硫化钼外其他过渡金属硫化物的悬空面内热导率实验测量值. 从表中数据看出, 虽然这些材料的晶体结构很类似, 但是其热传导性质却存在明显差异.
| 制备方式 | 薄膜层数 | 测量方法 | 热导率 (300 K/室温) |
| κ/(W·(m·K)–1) | |||
| 硒化钼 | |||
| 机械剥离[127] | 1层 | 拉曼法 | 59 ± 18 |
| 机械剥离[127] | 2层 | 拉曼法 | 42 ± 13 |
| 机械剥离[70] | 45 nm | 拉曼法 | 11.1 ± 0.4 |
| 机械剥离[70] | 140 nm | 拉曼法 | 20.3 ± 0.9 |
| 机械剥离[132] | 5 nm | 拉曼法 | 6.2 ± 0.9 |
| 机械剥离[132] | 36 nm | 拉曼法 | 10.8 ± 1.7 |
| 硒化钽 | |||
| 机械剥离[133] | 45 nm | 拉曼法 | ~9 |
| 机械剥离[133] | 55 nm | 拉曼法 | ~11 |
| 硫化钨 | |||
| 化学气相沉积[134] | 1层 | 拉曼法 | ~32 |
| 化学气相沉积[134] | 2层 | 拉曼法 | ~53 |
| 化学气相沉积[18] | 1层 | 拉曼法 | 74.8 ± 17.2 |
| 硒化钨 | |||
| 化学气相沉积[18] | 1层 | 拉曼法 | 66 ± 20.9 |
| 碲化钨 | |||
| 机械剥离[135] | 220 nm | TDTR | ~2 |
| 机械剥离[136] | 11.2 nm | 拉曼 | ~0.639—0.743 |
| 硫化铼 | |||
| 机械剥离[137] | 150 nm | TDTR | ~50—70 |
表4除硫化钼外, 其他单层/多层过渡金属硫化物的悬空热导率实验测量细节表
Table4.Experimental detail of thermal conductivity of single/few-layer transition metal sulfide (expect MoS2) in different literature.
3
3.1.4.黑磷、黑砷
同样因带隙可控、开关比较高等优点, 黑磷(BP)是最早被研究的下一代微电子器件材料之一[140-142]. 但是最初研究人员对黑磷的热传导性质产生浓厚兴趣, 主要是因为其面内各向异性的“长城”状结构[48], 可能会导致热导率的各向异性[143], 如图7(b)所示. 值得注意的是, 黑磷极易氧化, 因此在有关黑磷的实验中对于样品在空气中的暴露时间需要严格控制.2015年中国科学院闫清波课题组[144]通过理论研究预测单层黑磷沿ZZ方向与AC方向的室温面内热导率比值能达到2.2(30.15 W/(m·K), ZZ方向; 13.65 W/(m·K), AC方向), 并且由于其“长城”状结构导致面外声子模式对热导率的贡献极低(约5%). 很快, 普渡大学Xianfan Xu课题组[58]在实验上测量了室温下不同厚度多层黑磷的悬空面内热导率, 在厚度最小(~10 nm)的样品中ZZ方向热导率为20 W/(m·K), 而AC方向的热导率仅为~10 W/(m·K), 从而证实了上述理论预测. 作为磷元素的同主族元素——砷, 黑砷(BAs)的晶体结构与黑磷类似, 因此其同样具有明显的面内热导率各向异性效应. 2018年伯克利大学吴军桥课题组[145]首次在实验上测量了厚度为124 nm的黑砷沿ZZ方向与AC方向的悬空面内热导率(5 W/(m·K), ZZ方向; 3 W/(m·K), AC方向, 350 K).
后续实验中, 科研人员通过拉曼法、热桥法等方法测量了不同厚度的多层黑磷的面内热导率, 均发现了面内热导率的各向异性[48,49,73,77,146,147], 具体内容见3.2.2及3.2.3节. 在这些实验中多层黑磷的厚度均在10 nm以上, 这正是由于黑磷的化学性质过于活泼, 在热传导实验中单层黑磷的制备极其困难, 因此关于单层或少层黑磷的热传导性质还有待进一步深入研究.
3
3.1.5.碲 烯
块体碲(Te)是一种新型优质的热电材料[148]. 同时其二维结构碲烯可以作为一种进一步提高其热电性能的有效手段[149]. 在块材中, 碲原子通过共价键与一个邻近原子相结合, 并呈螺旋状延伸, 相邻的螺旋链之间则通过范德瓦尔斯力结合[150], 如图7(c)所示, 因此块材碲属于准一维的链状结构. 但是理论预测单层碲烯的结构与块体碲不同, 共有三种可能的晶体结构(α-Te、β-Te、γ-Te)[151]. Gao等[152,153]通过第一性原理计算研究了不同结构的单层碲烯的热传导及热电性能, 发现它们的热导率均较低, 并且热电性质优异. 但是迄今为止在实验上只合成出β型碲烯, 并且合成条件比较苛刻, 因此暂未有关单层碲烯物理性质的实验研究[154,155].随后2017年普渡大学Peide D. Ye课题组开发出一种液相合成方法[156], 可以大量制备与块材结构相同的多层碲烯. 在进一步研究中, 该课题组及其合作者通过拉曼法测量了厚度为35 nm碲烯的链内方向的室温悬空热导率(约1.5 W/(m·K)), 与块材(约3 W/(m·K), 300 K)相比而言有一定程度的降低, 他们认为其主要原因是多层碲烯的表面对声子会产生一定的散射[157]. 由于该类碲烯的结构与块材相同, 因此其面内热导率沿链内方向和链间方向会存在一定的差异, 关于该类碲烯面内热导率各向异性介绍, 具体内容见3.2.3节.
3
3.1.6.硅 烯
石墨烯被发现以后, 作为碳的同族元素, 硅烯自然而然被关注到. 但是直到2012年硅烯才被合成出来, 且生长条件极其苛刻[158,159]. 因此对于硅烯的热传导性质迄今为止均是围绕理论研究而进行的, 实验研究暂无进展.从结构而言, 硅烯与石墨烯很相似, 均为蜂窝状结构. 但是又有所不同, 石墨烯的原子层平面比较平整, 但是硅烯的原子层平面存在一定程度的褶皱, 因此理论预测硅烯的热导率较石墨烯至少低两个数量级, 并且面外ZA声子模对热导率的贡献会比较低(约10%)[160,161]. 除了本征热导率外, 理论上还研究了利用应力[162]、电场[163]、缺陷[164]、同位素[165]等方法调控硅烯的热导率, 为未来硅烯的实验研究提供指导.
3
3.1.7.其他二维材料
随着纳米材料制备技术和计算模拟技术的不断发展, 二维材料家族越来越庞大, 不仅可以在实验上合成某种新型二维材料, 还可以通过理论模拟预测一些未知的二维材料. 因此除了上述几种材料以外, 还有许多其他二维材料的热传导性质同样已被研究. 实验方面, 科研人员利用不同方法测量了多层碲化铋[166]、多层硒化铟[167]、多层硫化锡[168]、碲化锆纳米带[38]、多层氧化硒铋[169]等二维材料的面内热导率. 理论方面也已经对硼烯[170]、单层氮化镓[171]、单层氮化碳[172]、单层氮碳化硼[173]等二维材料的热导率及相关性质进行了一定的预测研究.2
3.2.尺寸效应及各向异性
由傅里叶定律可知, 在块体材料中热导率与材料的尺寸无关. 这主要是因为块体材料的几何尺寸远大于声子的平均自由程, 此时声子的输运过程属于扩散运动. 但是在二维材料中, 材料的几何尺寸可以接近甚至小于声子的平均自由程, 使得声子会从扩散输运变为(准)弹道输运, 并且材料的表面或者边界对声子的散射效果会越发明显, 因而材料的热导率会随材料的几何尺寸的改变而变化, 出现长度效应、宽度效应以及厚度效应.与尺寸效应不同, 结构各向异性导致材料热导率的各向异性是比较常见一种现象. 例如在石墨、氮化硼、硫化钼等块体材料中, 面内与面间的结合力性质不同, 致使面内热导率与面间热导率的差别非常大, 能达到两个数量级左右. 与此同时, 某些二维材料(黑磷、碲烯等)不仅面内与面间的结构不同, 其面内沿不同方向的结构同样存在较大差异, 因此这类二维材料为热导率各向异性的研究提供了新的平台.
3
3.2.1.长度效应和宽度效应
有关二维材料热导率长度效应的理论研究, 最早的研究对象是二维晶格Fermi-Pasta-Ulam lattice (FPU) 体系. 在该体系中发现材料热导率与长度呈现对数发散的关系(κ-log L)[11]. 石墨烯超高热导率的发现提供了一个研究二维材料热导率长度效应的理想对象. Nika等[101]认为随着石墨烯的长度增大越来越多的低频声子被激发并参与热传导, 因此当长度小于10 μm时, 石墨烯室温热导率随长度变大而增加的趋势将会非常明显. 通过进一步的研究, 他们发现石墨烯热导率的长度效应不仅仅取决于纳米带的长度, 还与宽度以及边界的粗糙度有关[174]. 在有限宽度以及边界粗糙度较小的情况下, 石墨烯纳米带热导率与长度之间呈现一种非单调——先增大后减小的关系(取决于边界粗糙度), 并且室温下长度效应范围扩大至100 μm. 但是, Munoz等[105]通过弹道输运研究提出石墨烯室温热导率的长度效应只有长度小于3 μm才足够明显, 这主要是基于他们认为室温下石墨烯中声子的平均自由程仅为0.6—1 μm. 可以看出声子平均自由程大小是决定石墨烯长度效应范围的关键因素. Knezevic等[104]通过蒙特卡罗模拟发现室温下石墨烯中声子的平均自由程远超上述估计, 其中约20%声子的平均自由程大于100 μm, 约10%声子的平均自由程超过200 μm, 如图8(a)所示.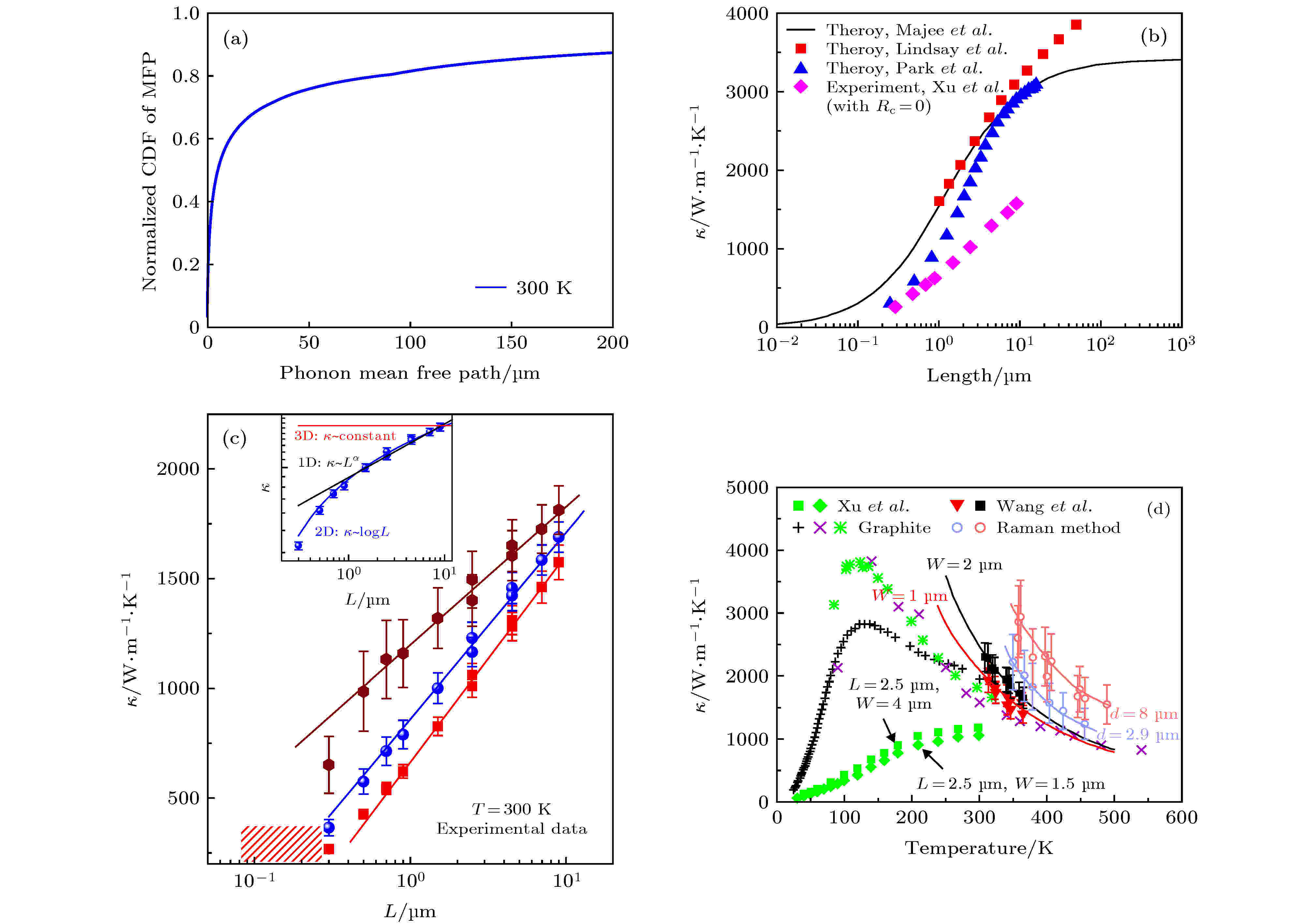
图 8 (a) 室温下单层悬空石墨烯中声子平均自由程[104]; (b), (c)理论及实验上单层悬空石墨烯室温热导率随长度变化[17,102,175,176]; (d)实验上不同宽度的单层石墨烯悬空热导率随温度变化[17,98,177-180]Figure8. Single-layer suspended graphene (a) the mean free path at room temperature[104]; (b), (c) length-dependent thermal conductivity in theory and experiment respectively[17,102,175,176]; (d) width-dependent thermal conductivity in experiment[17,98,177-180].
关于石墨烯热导率与长度之间具体的数值关系, 理论研究结果显示室温下长度为10—60 nm的石墨烯热导率与长度呈指数关系(κ-L0.4)[181], 与单壁碳纳米管热导率的长度效应类似. 但是随着长度进一步增大(1—100 μm), 其热导率随长度变长呈对数增长(κ-log L), 并当长度超过100 μm热导率将逐渐趋近于某一饱和阈值[175], 如图8(b)所示.
在石墨烯热导率宽度效应方面, 声子的边界散射是核心因素. 在块材石墨中边界散射对声子整体的输运影响可以忽略, 但是在石墨烯中其宽度能够与声子波长相近, 因此边界散射的影响会非常明显. 理论研究的结果比较统一, 随着宽度变大, 声子的边界散射逐渐减弱, 其热导率随之增大, 但是宽度效应的范围问题还未有具体的研究结果.
实验方面, 2014年徐象繁等[17]使用悬空热桥法测量了不同长度(300 nm—9 μm)的悬空单层CVD石墨烯的面内热导率, 在接触热阻占比不同的情况下均发现石墨烯室温本征面内热导率与长度之间呈对数发散的关系, 且未观测到饱和阈值, 如图8(c)所示. 同时, 对宽度效应也进行了实验证实. 在相同的长度(2.5 μm)情况下, 石墨烯宽度变小(4 μm→1.5 μm)时其室温热导率数值也会有所降低(约1186 W/(m·K)→约1054 W/(m·K)). 同年, Bae等[111]对石墨烯在衬底上的室温热导率的长度效应也进行了研究, 相较悬空石墨烯而言其达到饱和阈值的长度(约5 μm)要低很多, 他们认为这主要是因为石墨烯在衬底上导致声子的平均自由程降低(90 nm, 300 K), 并且也观测到了热导率随宽度减小而降低的现象. 此后, Takamatsu等[177]通过实验研究在单层悬空石墨烯中观察到了热导率的宽度效应与温度的关系, 室温下热导率的宽度效应很明显, 宽度为2 μm和1 μm的样品热导率分别为2295 W/(m·K)、1739 W/(m·K). 但是随着温度进一步升高宽度效应将逐渐消失, 他们认为这主要是因为温度越高, 声子的U型散射越严重, 导致声子的平均自由程降低, 边界散射的影响逐渐减弱, 如图8(d)所示.
此外, 最近北卡罗莱纳州立大学Cao linyou课题组[18]在单层、双层以及三层硫化钼、单层硒化钨和单层硫化钨中同样观察到了悬空样品室温热导率的尺寸效应. 该实验所采用的测量方法为拉曼法, 样品悬空部分形状为圆形. 通过改变悬空部分的半径尺寸(1.8—6.0 μm), 发现样品的室温热导率与半径(D)之间同样呈现对数发散关系(κ-logD), 与理论预测一致[182,183]. 他们认为热导率随半径增大是由于更多的低频声子被激发并参与热输运过程. 通过与相关实验文献对比, 发现使用拉曼法测量单层/多层硫化钼时热导率与悬空部分尺寸之间的确存在一定的关系, 如图9所示.
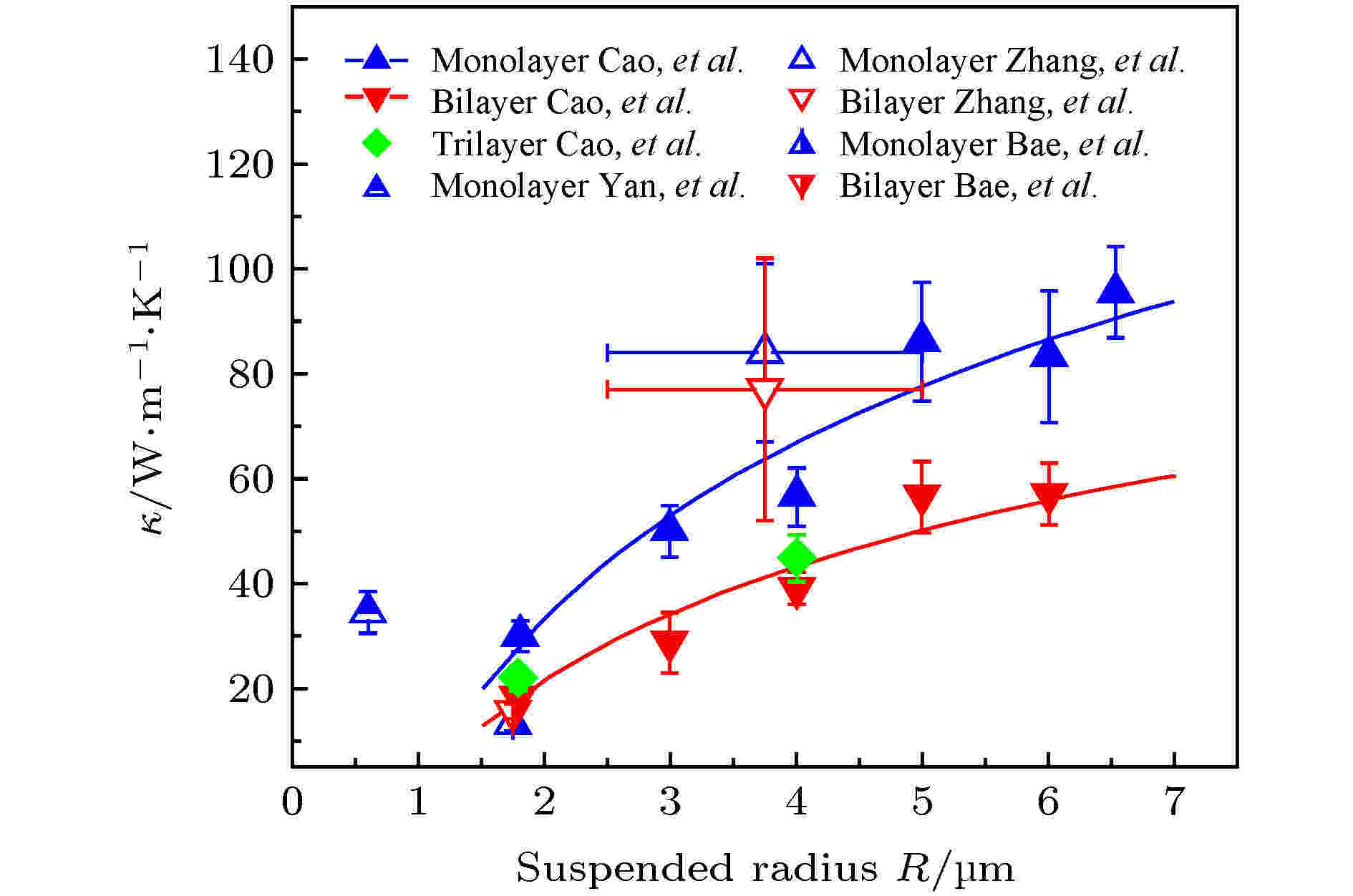图 9 使用拉曼法测量单层/多层硫化钼时热导率与悬空部分半径之间的关系[18,60,127,128]Figure9. Thermal conductivity of single/multi-layer MoS2 versus suspended radius using the Raman method. [18,60,127,128]
关于氮化硼、黑磷等二维材料热导率的长度效应或宽度效应均未有实验报道, 但是在理论方面拥有一些研究. 例如, Mukherjee等[184]利用第一性原理计算发现在单层氮化硼中面内热导率的长度效应与石墨烯很相似, 当长度处于1—100 μm范围内时室温热导率与长度之间呈对数关系. 李保文课题组[185]采用求解玻尔兹曼方程的方法预测在单层黑磷中ZZ方向室温热导率的长度效应能达到100 μm, 但是AC方向室温热导率的长度效应仅在1 μm以下才足够明显.
最新研究结果显示, 二维材料特别是石墨烯和氮化硼中的高热导率及反常热导率可能与声子流体动力学及由此产生的第二声有一定的关联. 传统的声波(或叫做第一声)是指压力在空间的周期变化. 第二声的概念源于氦Ⅱ, 在低温下声子可传播几毫米甚至厘米的距离而不受散射(弹道输运); 在高温下由于三声子的U型散射而进行扩散输运. 声子流体动力学行为通常出现在弹道输运和扩散输运之间狭小的温度窗口[186,187]. 强烈的U型散射会抑制声子流体动力学行为的发生, 使得初期观测到的第二声行为都是在极低温环境下, 如3He (T = 0.42 K–0.58 K)[188], Bi (T = 1.2—4 K)[189], NaF (T = 11—14.5 K)[190,191]. 有理论预测, 二维材料存在的面外声子模式可引起增强的正常散射(N-scattering), 同时随着厚度降低导致U型散射的减弱, 这使得石墨烯等二维材料中的声子流体动力学行为温度窗口会大大增加[192-194]. 虽然未有实验可以验证理论的合理性, 但是最近的两个石墨热导率的工作显示石墨块体/薄片中的第二声可在高达T = 100 K的温度下存在[194,195]. 同时由于第二声的贡献, 石墨薄片的热导率最高可达4300 W/(m·K). Wang等[90]最近的实验也显示石墨薄片的热导率随着厚度的降低而增加, 并在800 nm厚的石墨薄片中观测到3200 W/(m·K)的热导率; 虽然该文作者将其归纳为样品质量的变化, 但是其高热导率及厚度效应也可能与第二声有关.
3
3.2.2.厚度效应
从三维块体到(准)二维平面, 材料的热导率会发生非常大的变化, 因此研究二维材料热导率的厚度效应对解释上述变化是至关重要的. 同时, 该项课题涉及到一个非常有意思的科学问题: 几层二维材料可视为三维块体?实验上所观察到的二维材料悬空热导率的厚度效应可以分为两类: (1)以石墨烯、氮化硼为代表的二维材料, 随着厚度的增大, 其热导率逐渐下降, 直至与块材相近; (2)以黑磷为代表的其他二维材料, 由于边界散射, 其热导率随厚度增加而增大.
2010年Ghosh等[64]测量了不同层数(1—10层)的悬空石墨烯室温热导率, 发现随着层数增加热导率数值逐渐下降, 当层数达到4层时其数值已基本接近块材热导率, 如图10(a)所示. 他们认为上述现象的出现是由于层间耦合导致低频声子散射变强, 引起热导率降低. 除了悬空热导率的厚度效应外, 衬底上的石墨烯热导率同样具有厚度效应, 但是变化趋势与悬空石墨烯有所不同——随层数增加, 热导率呈现变大或不变的趋势[103,110,196,197]. 主要原因是非悬空样品中ZA声子得到了极大抑制, 这点我们在前文中已做过相应讨论.
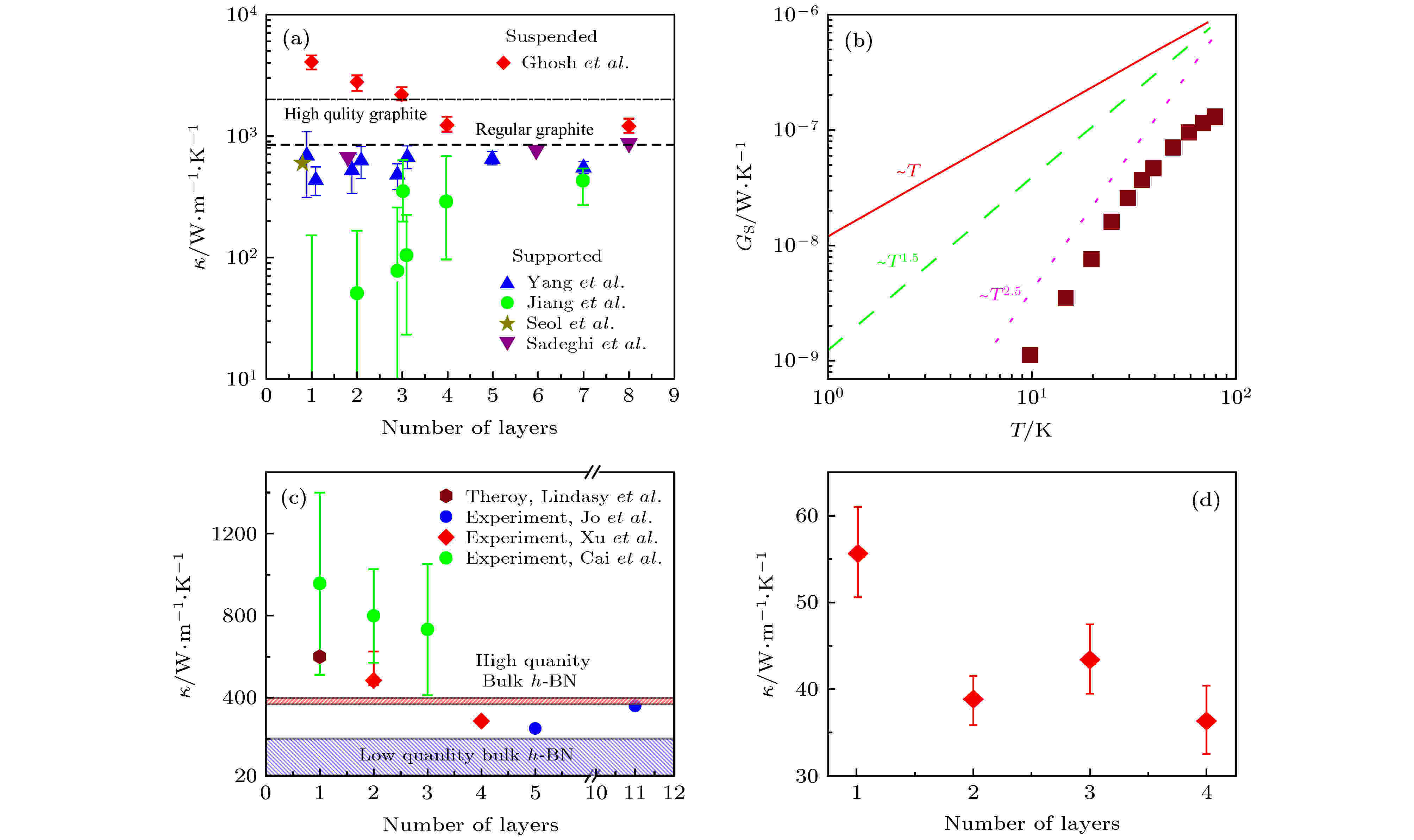图 10 (a) 石墨烯(悬空/衬底)面内热导率的厚度效应[64,103,110,196,197]; (b) 四层氮化硼悬空热导率与温度之间的关系[44]; (c) 氮化硼(悬空)面内热导率的厚度效应[41,44,56,120,198]; (d) 硫化钼(悬空)面内热导率的厚度效应[18]Figure10. (a) Thickness-dependent in-plane thermal conductivity of graphene (suspended and supported) [64,103,110,196,197]; (b) thermal conductivity of four-layers h-BN (suspended) versus temperature[44]; (c) thickness-dependent in-plane thermal conductivity of h-BN (suspended) [41,44,56,120,198]; (d) thickness-dependent in-plane thermal conductivity of MoS2 (suspended)[18].
Lindsay等[119]通过模拟计算预测单层氮化硼的热导率厚度效应与石墨烯很类似. 随后同济大学徐象繁课题组[41,44]测量了两层和四层氮化硼的悬空热导率, 通过比较可以看出热导率随厚度增大有逐渐减小的趋势. 当厚度增加到四层时, 热导率值已经接近文献报道块体热导率, 同时四层样品低温热导率随着温度呈现T2.5行为, 表明四层氮化硼热导行为可能已经接近块体, 如图10(b)所示. 最近李璐华等[56]测量了不同厚度(1—3层)的氮化硼的悬空热导率, 同样观察到随着厚度增大, 热导率逐渐下降, 但是与石墨烯相比氮化硼厚度效应不是特别明显, 如图10(c)所示. 通过分子动力学模拟, 他们发现随着层数增大, 氮化硼的Grüneisen常数以及ZA声子模(对热导率贡献很大)的频率会变大, 从而导致了声子的散射会加强, 热导率降低.
然而, 单层石墨烯和单层氮化硼热导率的极限值是多少仍未有定论, 这个问题不管是实验还是理论方面都存在争议. 同时, 块体石墨和块体氮化硼热导率值也未有定论. 因此, 四层石墨烯和四层氮化硼的热导率是否和块体本征热导率一致仍有所质疑, 需大量实验工作验证.
黑磷热导率的厚度效应在实验上的结果相对比较统一, 其热导率随厚度增大而增大, 如图11所示. 但是在这些实验中黑磷的厚度基本都是10 nm以上(层数至少在10层以上), 因此厚度为10 nm以下的黑磷热导率随厚度变化的趋势有待进一步研究, 可能存在与现有结果不一样的情况. 除了黑磷以外, 在碲烯[199]、多层硒化铟[167]、多层硫化锡[168]、多层碲化钨[136]、多层碲化铋[43]、多层氧化硒铋[169]、碲化锆纳米带[38]等二维材料中均观察到了类似的热导率随厚度变化的关系.
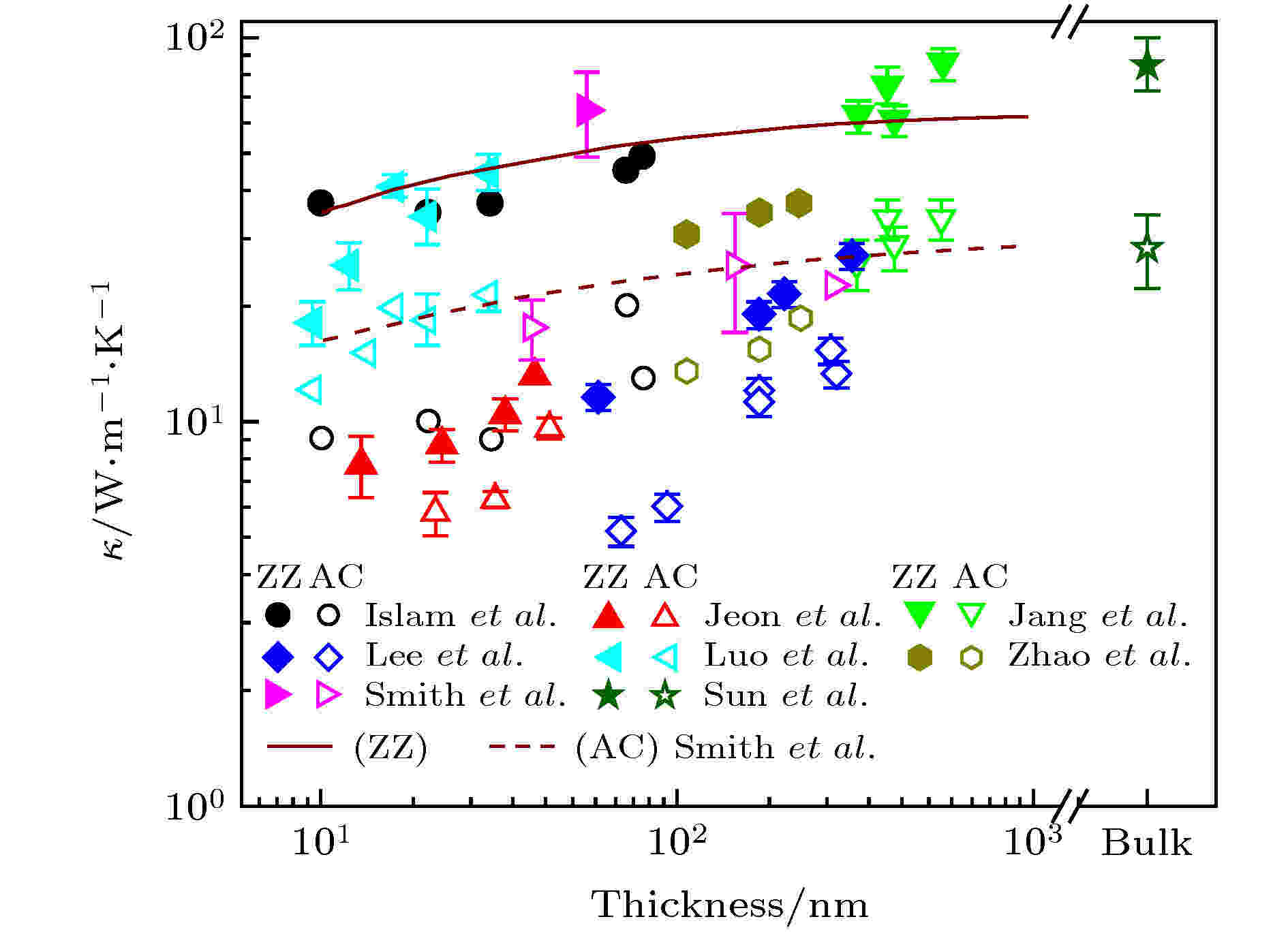图 11 室温下黑磷面内热导率的厚度效应及各向异性[48,49,73,77,146,147,168,200]Figure11. Thickness-dependent and anisotropic in-plane thermal conductivity of the BP[48,49,73,77,146,147,168,200].
理论上预测硫化钼的热导率与其厚度(层数)之间的关系为随厚度增大室温热导率会呈现降低的趋势, 并在四层左右接近于块材的室温热导率[131]. 但是实验上观测悬空硫化钼热导率的厚度效应存在一定的争议: 有些实验没有观测到明显的厚度效应[54], 还有一些观测到的厚度效应与悬空石墨烯相反—随厚度增大热导率也逐渐增大[128]. 稍显诧异的是在某些实验中发现悬空硫化钼热导率与层数之间呈现一种非单调的变化关系(先减小后增大)[70]. 上述结论均是在不同文献的实验数据之间进行比较而得出的, 因此可靠性还有待进一步确认. 但是2018年王信伟课题组[65]在实验上观测到了衬底上的硫化钼热导率与厚度(2.4 nm—37.8 nm)之间的非单调变化, 随着厚度增大, 热导率先减小后变大. 他们认为在较薄的硫化钼中声速随着厚度增大而减小, 并且材料的对称性被破坏, 因此会出现热导率降低的趋势. 但是在较厚的硫化钼中, 声子的表面散射的影响会随厚度增大而减弱, 进而出现热导率增大的现象. 最近, Yu等[18]在实验中观测到悬空硫化钼的室温热导率随层数增加(一层至四层)而减小, 如图10(d)所示. 但是其热导率数值是从约60.3 W/(m·K)减小至约36.9 W/(m·K), 最终并未与硫化钼块材室温热导率相接近, 因此关于悬空硫化钼的热导率随层数的变化关系还有待实验上进一步的验证.
3
3.2.3.各向异性
在石墨烯、氮化硼、硫化钼等二维材料中面内不同方向的结构差别较小. 虽然在理论计算中热导率能够体现出微小差别, 但是在实验上还未观测到热导率各向异性的存在. 比较特殊的是黑磷、黑砷以及碲烯, 它们的面内结构各向异性非常明显, 因而其热导率各向异性的现象会比较突出, 能够在实验上观察到.利用拉曼法, Xu Xianfan课题组[58]首次测量了不同厚度以及不同方向的黑磷室温面内热导率, 结果显示其热导率数值具有明显的各向异性, 同时随着厚度变化, ZZ方向的热导率与AC方向热导率的比值也会有所变化——当厚度大于15 nm时, 上述比值能达到2左右; 但是在最薄(厚度9.5 nm)的样品中, 上述比值变成了3左右. 他们认为黑磷面内热导率的各向异性是由结构的各向异性导致声子色散关系各向异性而引起的. 同年, Lee等[48]发现黑磷面内热导率的各向异性除了与厚度有关外, 还与温度有关. 当温度低于100 K时, ZZ方向与AC方向热导率数值差别很小, 但是随着温度升高, 其各向异性愈发明显. 图11中列举了不同文献中关于黑磷面内热导率各向异性的实验结果. 在多层黑砷中, 同样存在热导率的各向异性现象. 吴军桥等[145]发现室温下黑砷ZZ方向的热导率与AC方向的热导率的比值接近1.8, 与黑磷的情况类似, 如图12(a)所示.
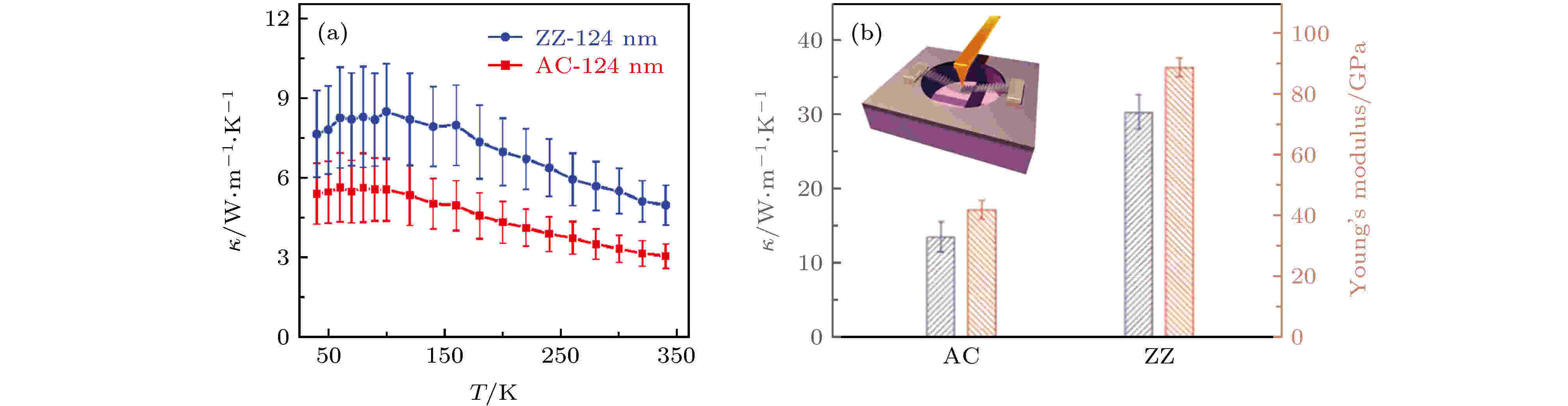图 12 (a) 多层黑砷悬空面内热导率的各向异性[145]; (b)黑磷沿ZZ方向、AC方向悬空面内热导率以及杨氏模量数值(300 K)[49]Figure12. (a) Anisotropic in-plane thermal conductivity of suspended few-layer BAs[145]; (b) the Young modulus and in-plane thermal conductivity of suspended BP along AC and ZZ direction respectively at 300 K[49].
近期, 关于碲烯的面内热导率各向异性在实验上也被证实, Xu Xianfan课题组[199]使用拉曼法测量了碲烯面内不同方向的热导率, 结果显示室温下链内热导率与链间热导率的比值能够达到1.3以上, 呈现出明显的各向异性特性. 同时通过第一性原理计算, 他们认为链内声速大于链间声速是导致碲烯热导率各向异性的根本原因.
关于黑磷面内热导率各向异性的起源, 文献中的观点主要集中在两个方面[48,73,77,146,147]: (1) 声子色散关系的各向异性; (2)声子弛豫时间的各向异性. 2018年赵云山等[49]在实验中不仅测量了黑磷面内热导率, 还使用AFM测量了同一样品的杨氏模量, 如图12(b)所示, 结果显示黑磷的面内热导率的各向异性比值与杨氏模量各向异性比值非常接近, 因此他们认为黑磷面内热导率各向异性的真正起源应该是声速的各向异性.
2
3.3.二维材料热导率调控
33.3.1.同位素效应
厦门大学蔡伟伟课题组通过13C掺杂调控单层石墨烯的悬空热导率, 结果显示随着13C掺杂比例的提高, 石墨烯热导率呈现先下降后上升的趋势[201]. 开始阶段随着同位素掺杂比例提高, 声子受到的散射会愈发严重, 因此热导率存在降低的情况. 例如与掺杂比例为0.01%的样品相比, 掺杂比例为50%的样品室温热导率降低了50%. 当掺杂比例达到一定程度后, 掺杂原子13C反而主导了热输运过程, 此后提高13C掺杂比例, 其实是降低了“杂质”(12C)比例, 因此高掺杂样品热导率反而有所上升. 该实验现象的发现引起了一定的关注, 相关理论研究相继发表[202-204]. Fugallo等[202]通过求解玻尔兹曼输运方程的方法, 改变石墨烯中13C的掺杂比例所得到的热导率变化趋势与实验测量相同, 如图13(a)所示.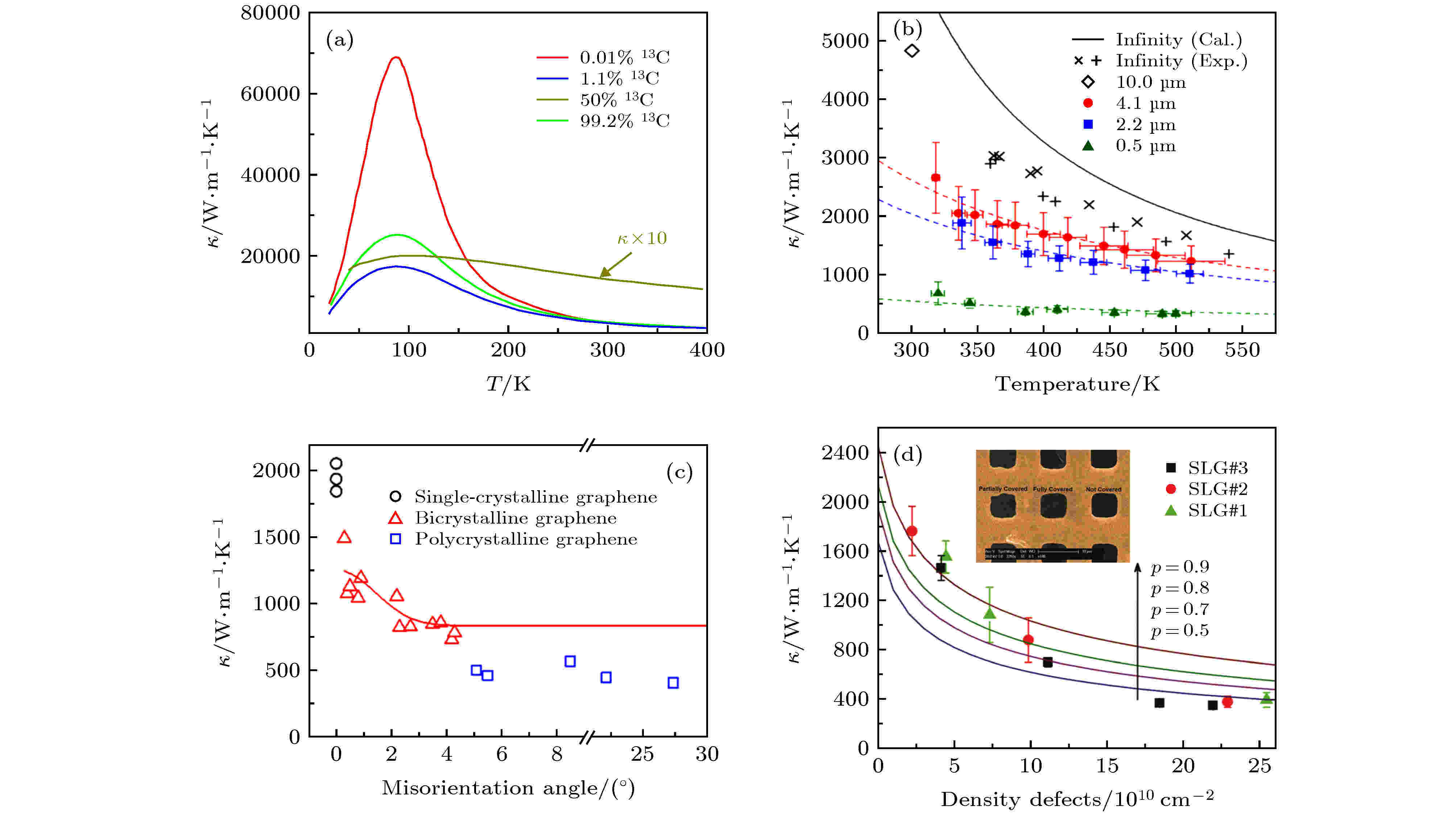
图 13 悬空石墨烯面内热导率 (a) 同位素效应[202]; (b) 晶粒尺寸的影响[205]; (c) 晶界夹角的影响[207]; (d) 空位率的影响[208]Figure13. In-plane thermal conductivity of suspended graphene: (a) Isotope effect[202]; (b) influence of grain size[205]; (c) influence of misorientation angle between grains[207]; (d) influence of vacancy ratio[208].
3
3.3.2.晶粒/晶界效应
材料内部晶粒的大小以及晶界的夹角等均会影响声子的弛豫时间, 导致材料的热导率降低. Lee等[205]通过控制合成条件进而控制石墨烯中晶粒的尺寸, 并发现石墨烯的悬空热导率随晶粒尺寸的减小而降低, 如图13(b)所示. 他们认为石墨烯中热导率主要由低频长波声子贡献, 晶粒尺寸愈小, 声子的散射愈严重. 此外Malekpour等[206]在石墨烯压层材料中观察到材料热导率随石墨烯片尺寸变大而呈增大的趋势. 由于石墨烯片的尺寸较小(微米级别, 与声子平均自由程相似), 可以将其理解成晶粒, 因此同样可以利用上述理论解释该现象.此外, 可以用镜面反射系数P描述在晶界处的声子散射行为. 镜面反射系数与界面夹角(θ)之间的关系可以表述为P-exp(–C1 × sin2 θ), 其中C1为经验常数. 可以看出小角度情况下随着晶界夹角增大, 镜面反射系数会降低, 从而导致声子散射加强. Lee等[207]在单晶/双晶/多晶石墨烯中证实了上述现象, 双晶石墨烯的悬空热导率随着晶界夹角增大呈现下降趋势, 尤其是小角度(< 4°)时, 随着晶界夹角的增大, 热导率下降的非常迅速, 如图13(c)所示. 同时当夹角较大时, 热导率数值将出现饱和, 不再继续减小, 用上述理论可以很贴切的解释该实验现象.
3
3.3.3.杂质/缺陷效应
与同位素效应相似, 在二维材料中引入杂质或缺陷, 同样能够起到调控热导率的作用. 通过在石墨烯上沉积金原子并改变金原子在石墨烯上的覆盖率, 李保文课题组[109]发现随着金原子覆盖率的增大, 石墨烯热导率呈先减小后增大的趋势. 他们认为金原子较重, 能够抑制石墨烯中的ZA声子模, 因此出现热导率降低的现象. 但是当金原子覆盖率达到一定程度后, 金原子本身就能形成一个传热网络, 导致后续热导率呈增大趋势.其次理论上预测石墨烯的热导率会随其晶格结构中的空位率的增大而降低, 但是在石墨烯制备过程很难控制空位形成的比例及其均匀性[209]. Malekpour等[208]以及Lee等[210]利用电子束轰击石墨烯表面形成规则且均匀的孔洞代替晶格中的空位, 结果显示随着孔洞面积占比增大, 其热导率呈下降趋势, 与理论预测一致, 如图13(d)所示. 随后Oh等[211]通过进一步研究发现除了孔洞面积占比外, 相邻孔洞之间的距离也是影响石墨烯热导率的一个关键因素. 声子散射会随孔洞间距的减小而增强, 石墨烯热导率随之减小. 此外, Yarali等[212]在制备单层硒化钼的过程中进行钨原子替代硒原子并产生一定的空位, 测量结果显示经过处理的样品热导率比未经处理的样品热导率偏低.
与此同时, 通过掺杂引入杂质原子进而调控热导率也是一种行之有效的方法[213,214]. 利用氧等离子体对石墨烯[215]及多层硫化钼[45,216]进行掺杂在实验上已经得以实现. 同济大学徐象繁课题组[45]采用上述方法并结合电子束自加热法研究了多层硫化钼室温悬空热导率与氧离子的掺杂浓度之间的关系, 实现了从多晶到非晶的热导率连续调控(约30 W/(m·K)→约2 W/(m·K)). 结合分子动力学模拟, 他们发现当掺杂浓度比较低的时候, 声子-缺陷散射导致声子透射系数下降并引起热导率的快速且大幅度的减小; 随着掺杂浓度继续提高, 热导率的下降趋势则相对平缓, 最终能够接近非晶材料热导率的极限值, 如图14所示. 通过高分辨率透射电子显微镜也证实晶体结构从多晶到非晶的转变.
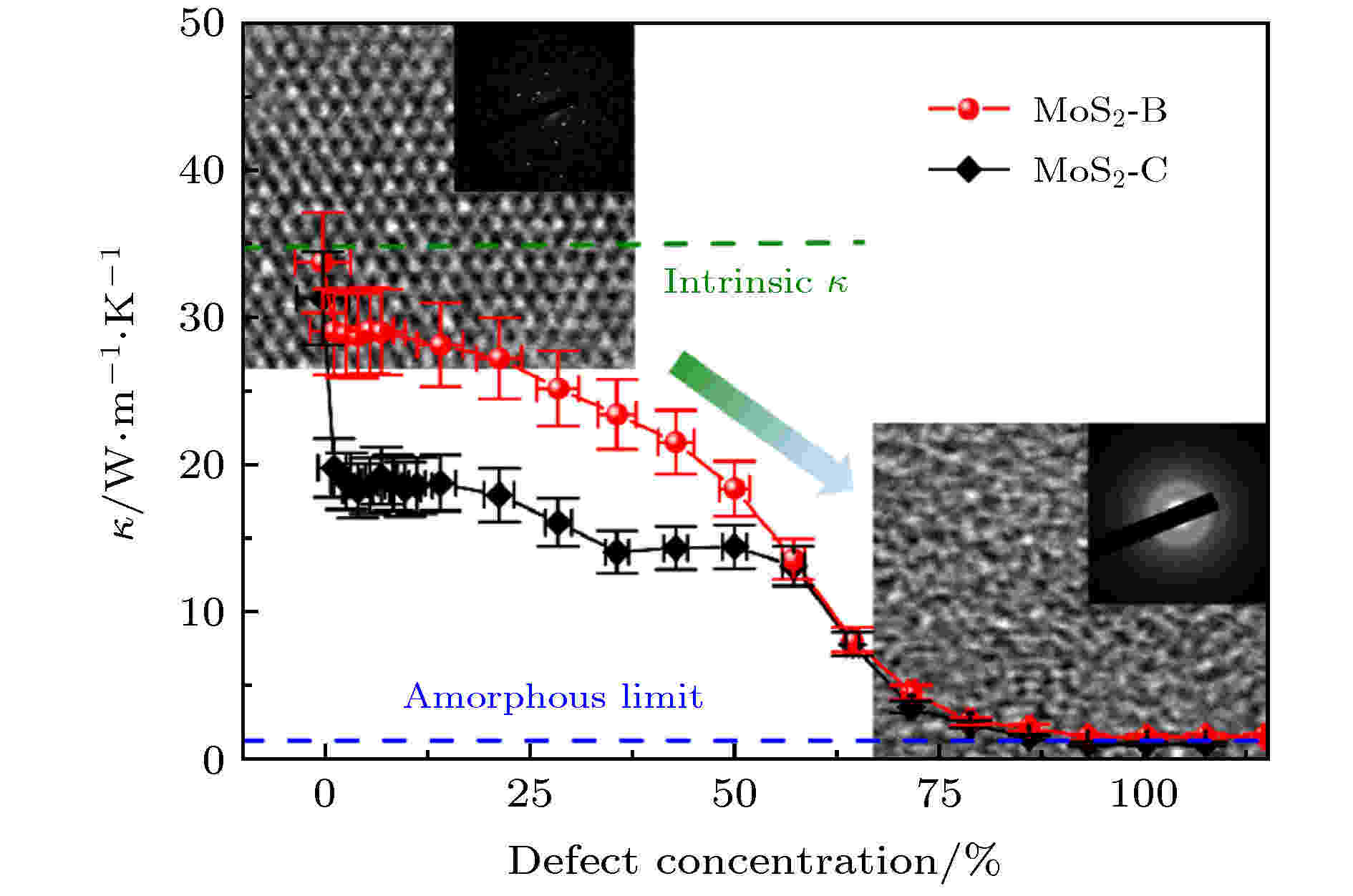图 14 悬空硫化钼面内热导率[45]: 缺陷浓度的影响Figure14. In-plane thermal conductivity of suspended MoS2 [45]: influence of defect concentration.
3
3.3.4.热整流效应
与电流二极管类似, 热整流效应是指热流沿某一方向较相反方向更容易通过的现象. 热整流效应是实现热二极管、热三极管、热逻辑门以及声子计算机的基础. 1936年Starr等[217]首次在铜以及氧化亚铜界面处发现热二极管现象[217]. 随之一系列热二极管的理论与实验相继出现[218]. 在块体材料中热二极管的设计理论主要包括: (1)利用界面处电流二极管现象产生热二极管效应; (2)利用界面处两种材料的接触应力或接触面粗糙度随温度改变产生热二极管效应; (3) 利用界面处的热势垒产生热二极管效应; (4)利用界面两侧材料的热导率与温度依赖关系不同产生热二极管现象.随着集成电路的微型化, 微纳尺度的热二极管在散热方面的应用越发受到重视. 微纳尺度热二极管的设计理论与块材有相似之处, 也存在一定区别. 非对称结构(形貌、应力、缺陷等)是实现微纳尺度热二极管的主要方法, 其物理机制存在以下两种解释: (1) 两种结构的热导率随温度变化的趋势不同. 例如A结构的热导率随温度升高而增大, 但是B结构的热导率随温度升高而降低, 改变热流方向它们整体的平均热导率会发生变化, 即能够实现热二极管效应, 如图15(a)所示; (2) 两种结构的声子谱不一致, 热流方向不同时声子谱之间的重叠情况会发生变化, 声子谱重叠程度越高, 热流能够更顺利的通过[219], 如图15(b)所示. 实验上低维材料的热整流效应最开始是通过在碳纳米管以及氮化硼纳米管上非均匀沉积重金属原子实现的[220]. 随后在形貌非对称的氧化钒纳米线[221]、Y-型碳纳米管[40,222]中以及聚酰亚胺纳米线/硅纳米线异质结构[223]中均观测到了热整流效应.
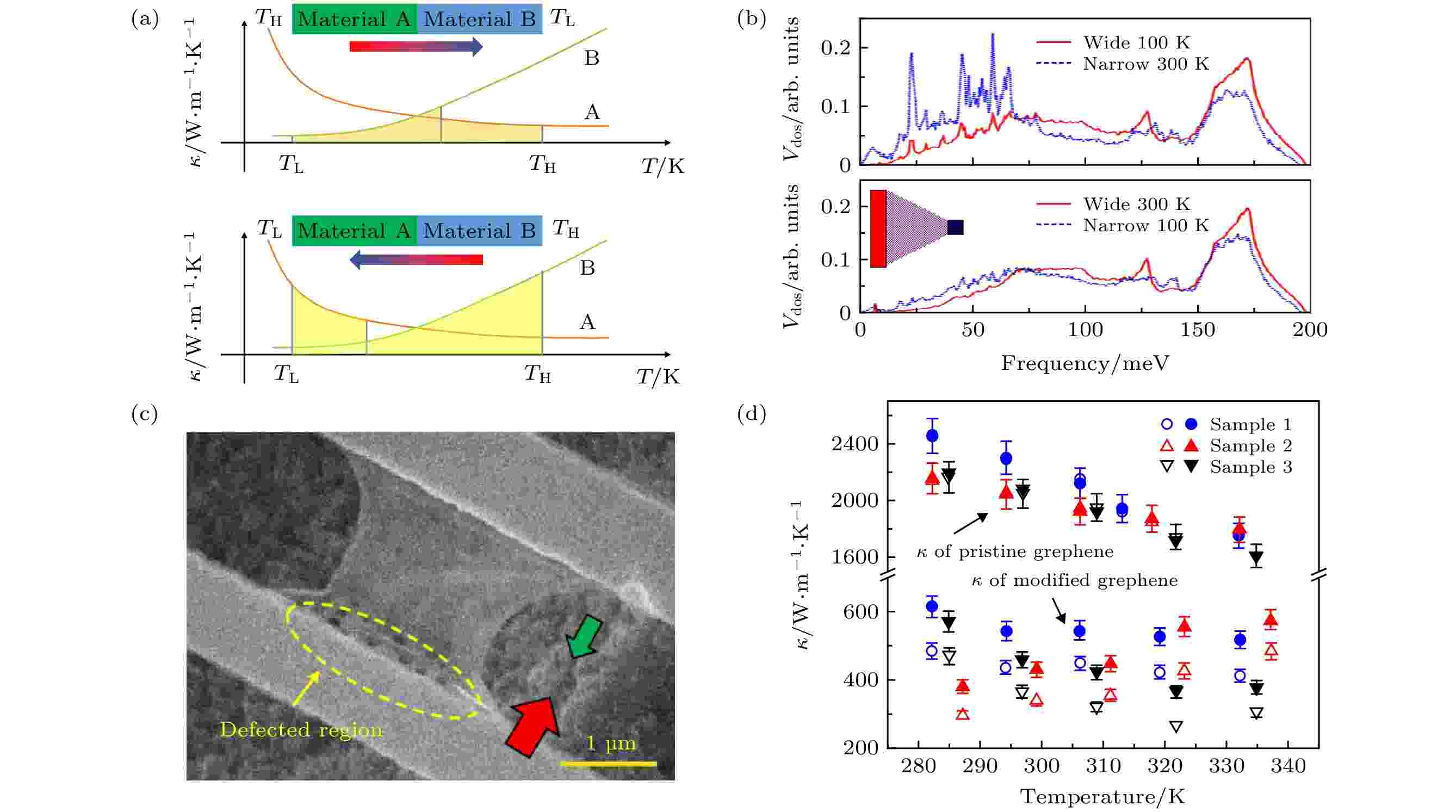图 15 微纳尺度热二极管设计原理 (a) 热导率随温度变化趋势不同; (b) 声子透射率不对称[219]; 非对称结构悬空石墨烯[224] (c)SEM图; (d) 热二极管实验结果Figure15. Design principle of thermal diode in micro/nano-scale: (a) Different tendency between thermal conductivity and temperature; (b) asymmetric phonon transmission ratio[219]; asymmetric structure of suspended graphene[224] (c) SEM image; (b) the experiment result of thermal diode.
由于二维材料非对称结构的制备技术存在一定难度, 因此最初关于二维材料的热整流效应研究主要集中在理论方面. 2009年杨诺等[225]利用分子动力学模拟在非对称单层石墨烯结构(梯形以及双矩形)中发现了热整流现象. 随后大量关于非对称二维材料结构(三角形、Y-型、缺陷等)的热整流效应的理论工作接踵而出, 为后续实验观测提供一定指导[219,226-230].
直到2017年Takamatsu课题组[224]才在实验上实现了悬空单层石墨烯中的热整流现象. 在该实验中, 石墨烯一侧保持完整结构, 但是在另一侧被掏孔、沉积重原子或剪裁, 如图15(c)所示. 在一侧被掏孔的石墨烯样品中, 当热流从结构完整一侧往结构被破坏一侧传导时所受阻碍较大, 因而观测到了约27%的平均整流率, 如图15(d)所示. 他们认为完整结构部分和被掏孔部分石墨烯热导率的不一致是导致热整流效应出现的主要原因.
1941年Kapitza在铜与液氦的界面上观察到温度场的突变, 从而提出了界面热阻(Kapitza热阻)的概念. 界面热阻Rint = ΔT/J, 其中ΔT为界面处温度场的突变值, J为单位时间内通过单位面积的热流大小. 关于界面热阻的大小, 主要有两种理论进行估算——声子失配理论(acoustic mismatch model, AMM)[251]与扩散失配理论(diffusive mismatch model, DMM)[252]. AMM模型假设界面是理想光滑的, 在界面处声子发生完全镜面反射或透射, 因此只有在低温环境中或对于低频声子, 即当声子波长远大于界面粗糙尺寸, 该模型是成立的. DMM模型则假设声子在界面处发生散射时失去了除频率外的所有信息, 因而声子透射率与界面两侧材料的声子态密度的匹配程度密切相关. 很显然, 上述两种模型对于界面处声子行为的假设过于简单. 大量实验结果也证实, 上述两种理论的计算值与实验值普遍存在巨大差别, 因此对于界面热阻的机理还有待进一步研究[253].
作为衬底, 介电材料和金属材料是被研究较多的[254]. 2009年Dames等[237]利用3ω法测量了机械剥离石墨烯与氧化硅衬底之间的界面热阻. 他们发现随温度升高界面热阻数值逐渐降低, 室温下界面热阻Rint = 5.6—12 × 10–9 m2·K/W, 同时发现界面热阻与石墨烯厚度(1.2—3 nm)之间不存在明显的联系. 随后Villaroman等[239]研究了CVD石墨烯与不同金属(Au, Ti, Al)之间的界面热阻, 其数值为(2—5) × 10–8 m2·K/W. 随着二维材料家族的不断发展, 同济大学徐象繁课题组[234]测量了多层氮化硼与氧化硅衬底之间的界面热阻((1.3—3.5) × 10–8 m2·K/W), 并发现界面热阻数值与氮化硼厚度之间呈一定正相关, 如图16(a)所示. 他们认为这是由于使用机械剥离的方法制备较厚的氮化硼会在界面处引入比较多的空位以及空隙所造成的. 在硫化钼与晶体硅衬底的界面热阻实验中, 王信伟课题组[244]观察到界面热阻数值随硫化钼厚度增大而减小的现象, 同样与硫化钼与衬底的接触情况有关.
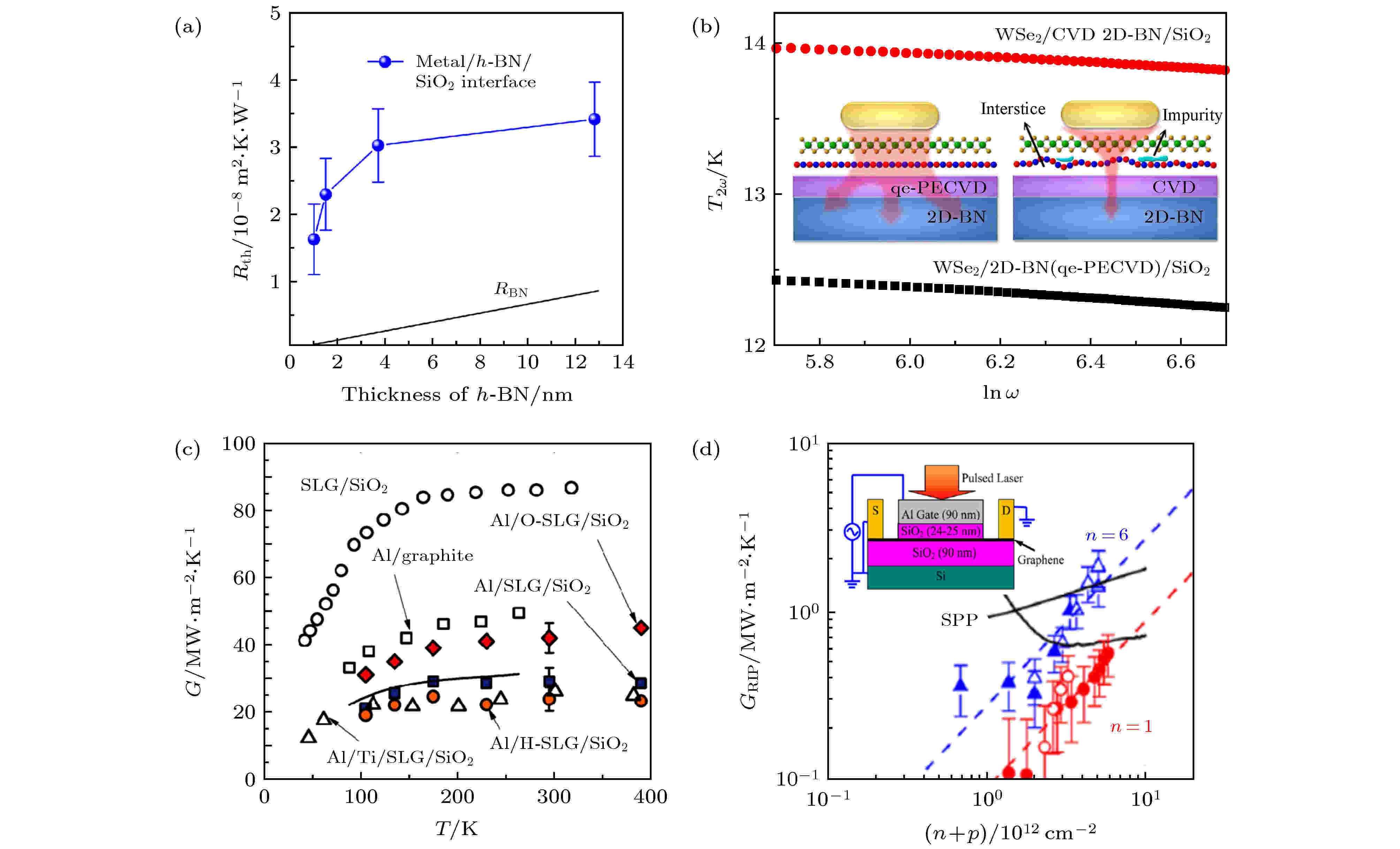图 16 (a) 氮化硼厚度对金属/氮化硼/氧化硅界面热阻的影响[234]; (b)利用3ω法测量不同方法制备的氮化硼对硒化钨器件的界面热阻的影响[250]; (c)在界面处引入化学键对金属/单层石墨烯/氧化硅界面热导的影响[256]; (d) 在界面处加电压对氧化硅/多层石墨烯/氧化硅界面热阻的影响[257]Figure16. (a) Thickness-depend interfacial thermal resistance of metal/h-BN/SiO2[234]; (b) interfacial thermal resistance of WSe2 device with h-BN prepared by different method[250]; (c) improving interfacial thermal resistance of Al/single-layer graphene/SiO2 by introducing chemical bond[256]; (d) the influence of voltage at interface to interfacial thermal resistance of SiO2/graphene/ SiO2[257].
表5中列举了部分常见二维材料与衬底之间界面热导Gint = 1/Rint的实验测量值. 从表5中数据可以看出, 衬底材料对界面热传导的影响非常大. 对于同种二维材料与不同衬底之间的界面热导数值变化能达到1—2个数量级的变化, 因此选择合适的衬底材料对于提高二维材料的界面热导是至关重要的. 在分析界面热导时, 声子透射率是一个关键的因素. 界面处声子透射率越大, 往往界面热导越高. 石墨烯/碳化硅之间的界面热导(约28 MW/(m2·K), 室温)相较石墨烯与氮化硼之间的界面热导(约186 MW/(m2·K), 室温)要低很多, 其核心原因就是石墨烯与氮化硅之间的声子透射率非常低[255]. 其次, 两种材料的德拜温度的匹配程度也可以作为分析依据. 界面热导会随着两种材料德拜温度的差值增大而减小. 金刚石的德拜温度较石墨烯德拜温度高出很多, 导致石墨烯与金刚石之间的界面热导相较其他介电衬底偏低[245].
| 界面结构 | 室温界面热导 | 界面结构 | 室温界面热导 |
| Gint/MW·(m2·K)–1 | Gint/MW·(m2·K)–1 | ||
| 石墨烯 (G) | G/h-BN[235] | ~17 | |
| MoS2/h-BN[236] | ~52.2 | ||
| SiO2/G/SiO2[237] | ~83—179 | 硫化钼 (MoS2)、硒化钼 (MoSe2) | |
| G/SiO2[238] | ~50 | ||
| G/Al2O3[239] | ~17 | MoS2/SiO2 or AlN[240] | ~15 |
| Au/Ti/G/SiO2[241] | ~25 | MoS2/Au[127] | ~0.44—0.74 |
| Au/Ti/G/SiO2[196] | ~20 | MoS2/SiO2[129] | ~1.94 |
| Al/G/Si[242] | ~62—65 | MoS2/SiO2[243] | ~14 |
| Al/G/SiO2[242] | ~21—24 | MoS2/SiO2[244] | ~21 |
| Au/Ti/G/sapphire[245] | ~33.5 | MoSe2/SiO2[127] | ~0.09—0.13 |
| Au/Ti/G/diamond[245] | ~6.2 | MoSe2/SiO2[243] | ~2 |
| G/Au[76] | ~23 | 黑磷 (BP) | |
| G/Al[76] | ~27 | ||
| G/Ti[76] | ~31 | BP/SiOX[246] | ~21.7—114 |
| G/Au[66] | ~18.8—44 | BP/SiOX[247] | ~202—60 |
| 氮化硼 (h-BN) | 硒化钨 (WSe2) | ||
| h-BN/SiO2/Si[248] | ~8.3 | WSe2/Si/SiO2[249] | ~10—32 |
| Metal/h-BN/SiO2[234] | ~29—63 | WSe2/SiO2[250] | ~22 |
表5常见二维材料的界面热导实验测量值
Table5.Experimental results of interfacial thermal conductance of two-dimensional materials.
除了声子透射率以及德拜温度匹配程度以外, 即使是相同的界面材料, 其界面热阻可能依旧存在较大差别, 这主要与界面处材料之间的结合情况有关. 例如采用机械剥离方法制备的二维材料与衬底之间往往会存在一定空隙、缺陷、水蒸气、有机物残留等, 从而使用CVD方法直接在衬底上生长二维材料将大大改善上述问题. 例如同济大学徐象繁课题组测量了硫化钼/氧化硅之间的界面热阻, 在该实验中多层硫化钼是直接利用CVD方法生长在氧化硅衬底上的, 其实验结果(约4.76 × 10–8 m2·K/W)较其他通过转移所制备的样品要低至少一个数量级[243]. 此外, 他们在硒化钨器件的界面热导实验中发现通过等离子增强CVD法所制备的单层氮化硼比普通CVD法所制备的单层氮化硼能够使器件的界面热导降低的更多一些(图16(b)), 其中原因就在于前者与衬底之间结合更加紧密[250].
在普通界面处两种材料是通过范德瓦尔斯力结合在一起的, 如果能够在界面处引入相互作用更强的结合键(共价键等)将能够在一定程度上提高界面热导[256,258]. Hopkins等[256]通过氧等离子轰击在金属/石墨烯界面引入C-O共价键, 测量结果显示相较未经处理的样品, 经过等离子处理的样品的界面热导提高了一倍, 如图16(c)所示. 除此之外, 实验还发现经过退火处理能够在金属钛/石墨烯的界面处引入Ti—C健, 从而也可以提高其界面热导[239]. 更进一步, Koh等[257]通过在石墨烯/氧化硅界面处加上一定电压, 增强界面耦合的强度, 同样可以起到提高界面热输运的作用, 如图16(d)所示.
一般而言, 声子是非金属中热能输运的主要载流子, 而电子则是金属中的主要热载流子. 当热流通过金属和非金属的界面处时, 两者界面处存在热能的传递, 如图17插图所示. 其中Q表示要通过界面的热流总量, 蓝色和紫色的圆球分别代表两种材料中的声子和电子, 绿色(左)和黄绿色方块(右)分别表示金属和非金属材料. 考虑到所有可能存在的热输运通道, 可以将其大致分为三类, 即Q = Q1 + Q2 + Q3, 其中, Q1表示界面处金属中的电子和非金属中的声子直接耦合以实现热能的传递, 用蓝色的箭头表示[260]; Q2表示金属内部的电子和声子首先耦合将能量传给声子, 随后在界面处实现声子-声子耦合来传递热能, 用红色的箭头表示; Q3表示金属中的声子和非金属中的声子耦合来传递热能, 用黑色的箭头表示. 通过这三种方式(主要是Q3), 共同传递了界面处总量为Q的热能. 因此, 如果在非金属表面引入一薄导电层, 则可以重新增加一个导热通道Q4: 即金属中的电子首先传导至非金属表面导电层, 然后再通过电-声耦合将热量传导至非金属. 在此基础之上利用氧离子轰击非金属表面, 同济大学徐象繁课题组[259]发现金-氧化铝的界面热阻会大幅度降低, 如图17所示. 在排除接触面粗糙度变化、产生化学键等因素的情况下, 他们提出经氧离子处理的非金属表面载流子浓度会随处理时间增大而增大, 进而会出现一种新的热量传递机制—金属一侧的电子与非金属表面的载流子产生耦合随之载流子会与非金属的声子进行耦合并传递热量. 如果将该方法用于改善石墨烯与介电衬底之间的界面热阻同样是适用的.
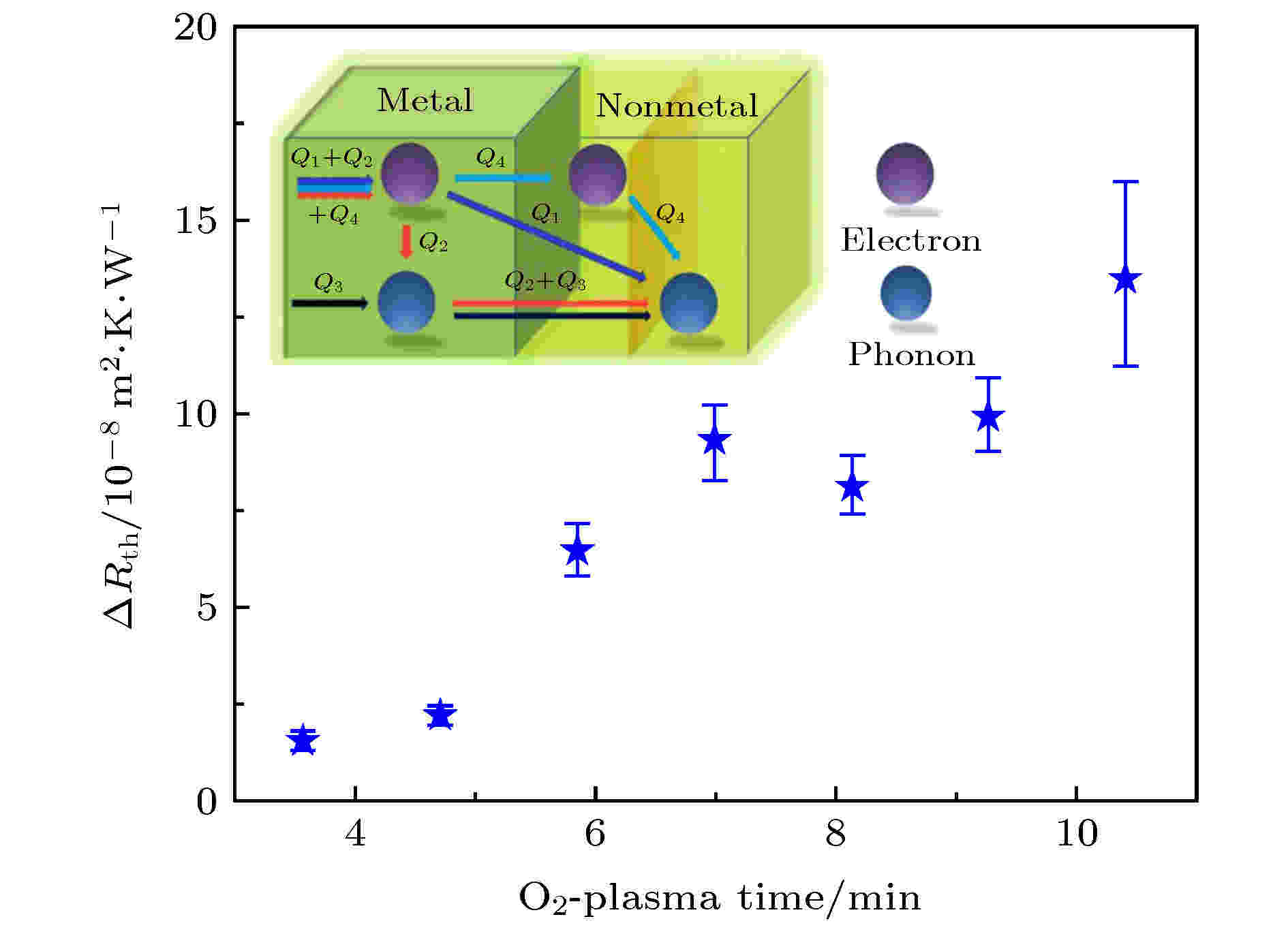图 17 通过氧离子束轰击改善金属与非金属的界面热阻[259]Figure17. Improving interfacial thermal resistance of metal/nonmetal by O2-plasma[259].
通过上述分析可以看出, 影响界面热阻的因素比较多, 通过某种单一措施想获得超低的界面热阻是比较困难的, 因此在未来的研究中需要更多的考虑多重因素共同作用的效果.
在散热方面的应用, 石墨烯在众多二维材料中最具代表性[23]. 其具有超高热导率并可以将单层/多层石墨烯直接作为散热材料[261]. Balandin等[262]利用高度取向的热解石墨(HOPG)进行机械剥离获得多层石墨烯并将其转移至氮化硅衬底上. 当衬底上的AlGaN/GaN晶体管以约13 W/mm2的高功率运行时器件“热点”温度较无石墨烯的情况降低了20 ℃, 说明石墨烯能够快速的将“热点”处的热量扩散出去, 预测器件的使用寿命至少能够延长十倍. 上海大学刘建影课题组[263]进一步将CVD单层及多层石墨烯转移到硅衬底上, 当衬底上的器件运行时同样观察到“热点”的温度有明显的降低. 同时单层石墨烯较多层石墨烯散热效果更加理想一些. 通过对比, Bae等[264]发现以石墨烯为基础的散热元件与以金材质为基础的散热元件相比, 衬底上的温度分布更加均匀.
虽然机械剥离石墨烯较CVD石墨烯质量普遍要好一些且热导率更高, 但是机械剥离方法不适用于大规模的工业制备和生产, 因此提高CVD石墨烯的质量是非常有必要的. 随着近几年CVD制备技术的不断进步, CVD石墨烯的质量已经有了一定的提高. 例如Lee等[265]成功在锗衬底上生长出晶圆尺度且光滑无褶皱的单层单晶石墨烯. 中国科学院谢晓明课题组[266]在CuNi合金衬底上实现快速生长英寸尺度的单晶石墨烯.
尽管单层/多层石墨烯已经证实可以直接作为电学器件的散热材料, 但是其散热能力有限, 面对高密度热流其散热效果会大打折扣, 因而将大量石墨烯制成薄膜可以作为一种新的方案. 在实际操作中制备石墨烯薄膜一般需要经过两个步骤——原材料解离和制膜. 解离步骤常见方法包括超声解离、球磨等, 制膜流程的常见方法包括真空过滤、静电纺丝、喷涂印刷、自组装、旋涂等. 实验上石墨烯薄膜的热导率基本维持在1000—1400 W/(m·K)[267-269], 虽然该数值较商业热解石墨片偏低, 但是石墨烯薄膜在柔韧型以及尺寸控制方面的优势很突出. 石墨烯薄膜低热导率主要原因是薄膜中晶粒小而多, 还存在大量褶皱、错位排列等导致声子散射严重. 为了解决这一问题, 上海大学刘建影课题组[90]通过严格控制制膜过程中的温度以及压强大幅度提高了石墨烯薄膜的热导率, 厚度为0.8 μm的薄膜热导率能够达到3200 W/(m·K), 如图18(a)所示.
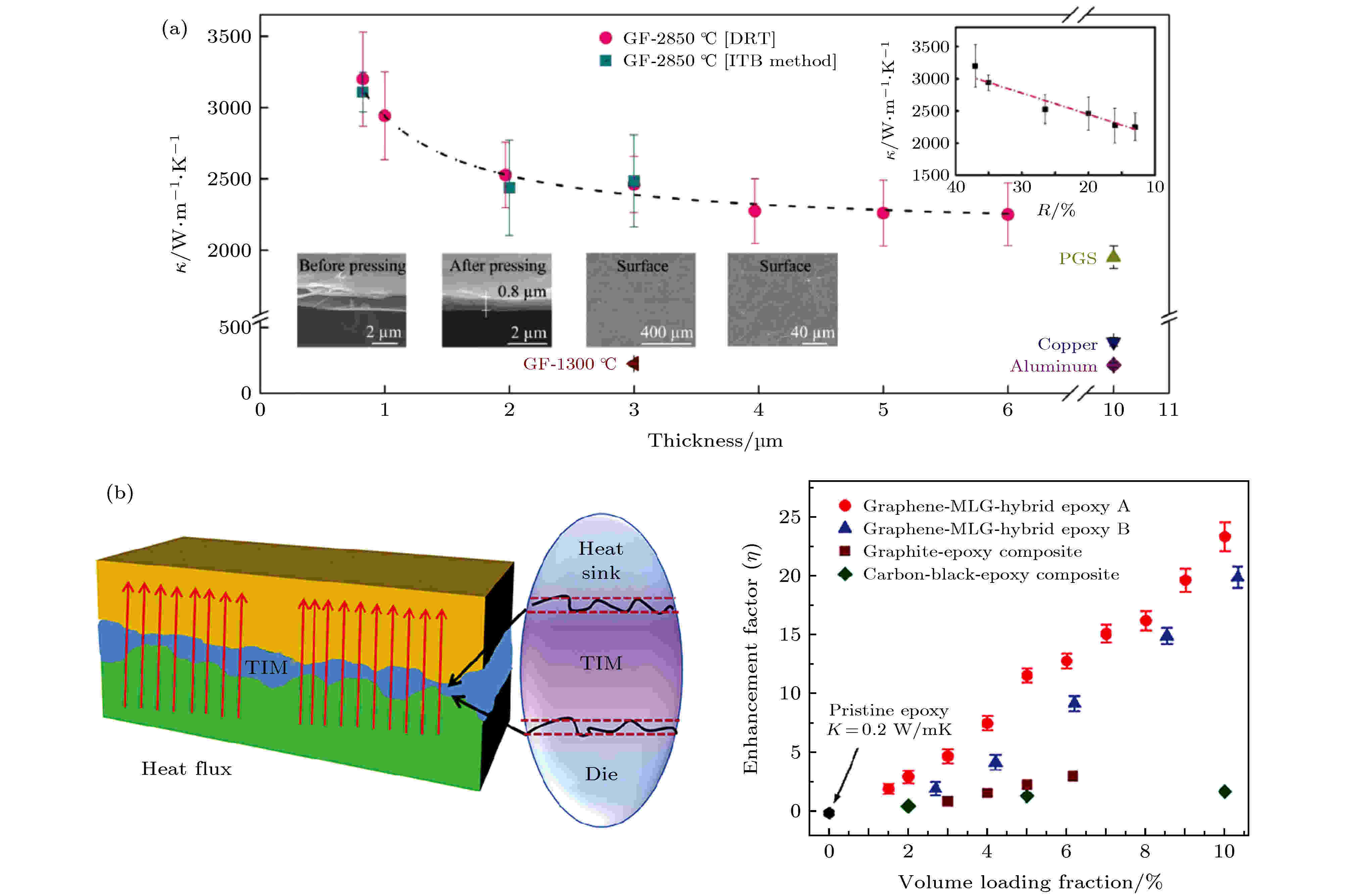图 18 (a)经高温退火的石墨烯薄膜的热导率与厚度之间的关系[90]; (b) 石墨烯与环氧树脂混合作为TIMs材料[270]Figure18. (a) Thickness-depend thermal conductivity of graphene film with high-temperature annealing[90]; (b) mixture of graphene and epoxy as TIMs [270].
石墨烯不仅可以直接作为散热材料, 将其与其他材料混合制成的复合材料能够在一定程度上提高原有材料的散热性能, 例如将其与有机物混合可以作为热界面材料(thermal interface materials, TIMs). 将单层/多层石墨烯与环氧树脂混合, Shahil等[270]发现随着掺杂比例提高混合物的热导率逐渐变大, 掺杂体积比为10%的样品热导率较环氧树脂增加了2300%, 达到约5.2 W/(m·K), 如图18(b)所示. 同时他们在商业导热油脂中做了同样的掺杂实验, 发现掺杂比例仅为2%就能将室温热导率由原来的约5.8 W/(m·K)提高到约14 W/(m·K), 并且力学性质在掺杂前后并未发生明显变化.
石墨烯面内热导率远远高于其面间热导率, 如果能够使石墨烯在界面处纵向排列, 利用其面内的高热导率充当热界面材料将会有比较好的效果. 北京大学白树林课题组[271]将大量石墨烯带进行卷曲随之纵向切割, 便成功的实现了上述想法. 通过该实验可获得比传统热界面材料热导率高出了两个数量级的高热导率界面材料(614.85 W/(m·K)). 此外, 石墨烯泡沫也是理想的界面材料之一, 其具有质轻、高热导率、高压缩比等优点. Loeblein等[272]利用金属镍泡沫为模板并通过CVD方法在镍骨架上生长多层石墨烯, 最后将镍骨架腐蚀清除即得到石墨烯泡沫, 经压缩其热导率能够达到86 W/(m·K).
除了上述材料外, 石墨烯纤维[273]、石墨烯压层材料[206]、石墨烯纳米流体[274]等均是较好的基于石墨烯的散热材料, 这些材料可以满足各种环境下的不同需求.
在二维材料中, 氮化硼因高热导率且表面非常光滑等特点同样是非常具有潜能的散热材料. 氮化硼还具有一个比较明显的优点—绝缘, 因此它可以与电学器件直接接触而不必担心出现电路短路的问题. Choi等[248]通过热扫描探针SThM扫描石墨烯器件表面温度, 发现当热流密度为1600 W/cm2时器件表面温度变化最大值为42 K. 相同功率情况下在器件与衬底之间加上多层氮化硼, 器件表面温度变化最大值则降低了2.2倍, 仅为18 K. 在硒化钨器件和硒化钼器件中, 复旦大学魏大程课题组和同济大学徐象繁课题组[250]也观察到了类似的现象, 如图19(a)—图19(f)所示, 同时发现在单层氮化硼的辅助下器件的饱和功率得到了一定提高. 可以看出单层/多层氮化硼能够将器件运行所产生的热量快速且有效的输送出去, 避免“热点”的出现对器件造成损坏.
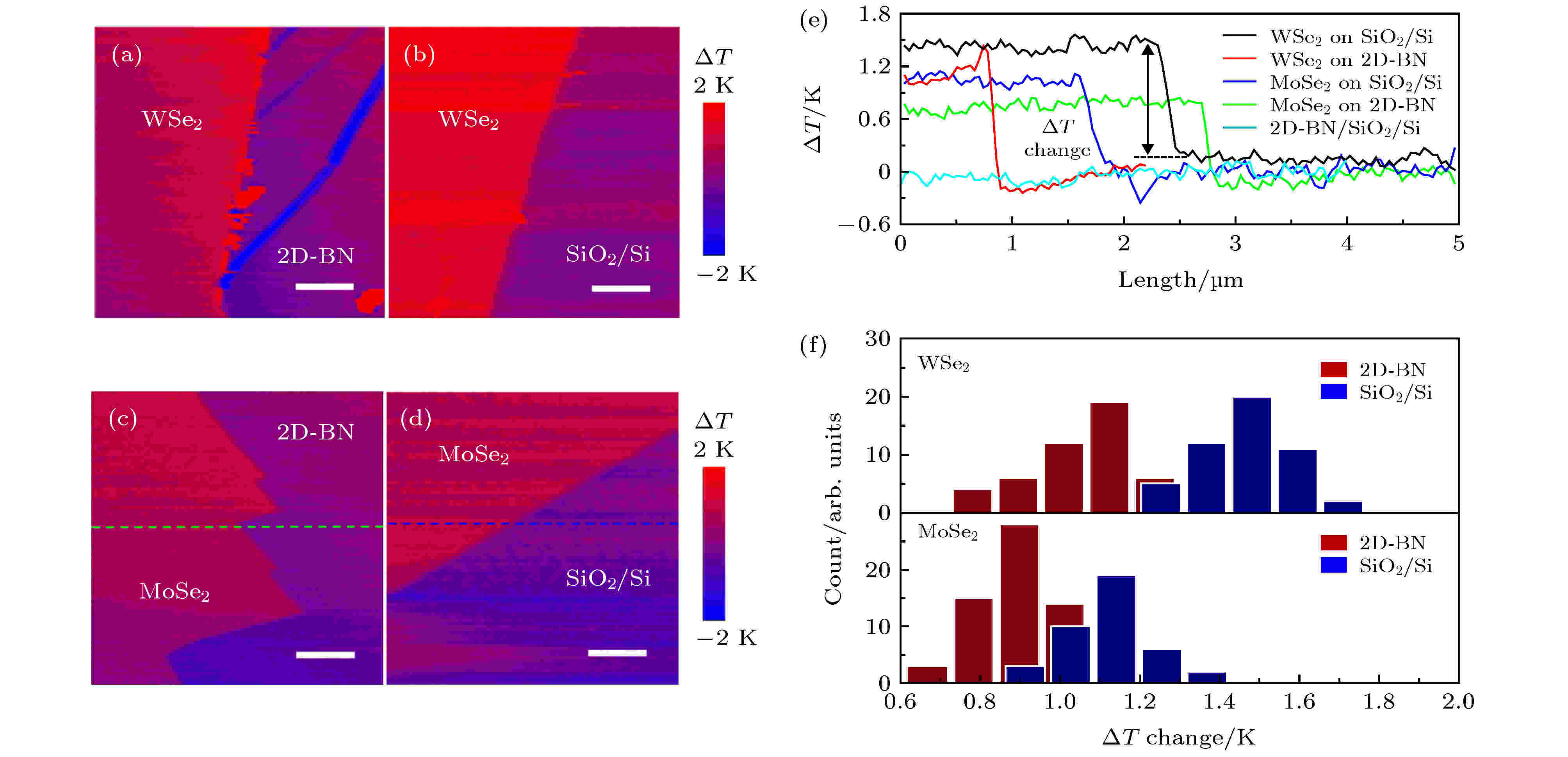图 19 氮化硼对硒化钨以及硫化钼器件中温度分布的影响[250]: (a)?(d) SThM温度扫描图; (e)器件边界处温度变化图; (f)器件中温度分布柱状统计图Figure19. Effect of h-BN on temperature distribution in WSe2 and MoSe2 devices [250]: (a)?(d) Temperature scanned by SThM; (e) temperature variation at device boundary; (f) histogram of temperature distribution in devices.
本文只提纲挈领介绍二维材料界面热阻研究进展及其在散热领域的应用. 更多内容可参考相关文献[23,275].
通过以上介绍, 可以看出二维材料在散热方面的应用主要集中于两个方向: 作为热扩散材料避免器件中热量的积聚及充当热界面材料提高界面热输运能力. 如在消费电子领域, 芯片功耗增大和机身结构变化及小巧化是其发热的主要原因. 在手机芯片方面, 4G芯片的功耗为1—2 W, 而5G芯片的功耗可高达5—7 W. 华为M20X手机以及小米10手机已将石墨烯散热膜用于热管理系统中, 石墨烯助力的锂电池也将在手机中推广, 其目的在于快速将CPU或电池工作时产生的热量导出提高零件的使用寿命和改善用户使用体验. 与此同时, 充当热界面材料, 二维材料的前景还是比较光明的, 但是在实际应用之前还需要解决一些技术问题, 例如进一步提高其性能、使用寿命、与现有技术之间的融合度等.
1)到目前为止, 没有关于二维材料反常热传导的严格解析解. 现存的反常热传导模型只局限在二维晶格[11,12,276]. 二维晶格系统里是没有面外声子模式的(即ZA声子), 然而在真实二维材料如石墨烯和氮化硼, 面外声学声子对热导率起着决定性的作用[102].
2)石墨烯热导率是多少? 不同的实验之间存在很大的差异, 而三声子散射和四声子散射计算结果也不能自洽. 公认的是悬空单层石墨烯热导率比石墨块体更高, 然而最近的实验显示石墨块体/薄片的室温热导率达3200—4300 W/(m·K)[90,194]. 目前采用的热桥法和拉曼法在测量热导率时, 其样品表面往往会吸附少量小分子, 进而抑制声子振动. 研究人员一般采用退火(约200—300 ℃)的办法去除表面杂质, 但是由于存在负热膨胀系数, 高温退火会使得ZA声子受到抑制从而影响最终实验结果. 同时, 悬空大尺寸(如大于50 μm)石墨烯用于热导测量也存在很大的技术瓶颈. 以目前掌握的实验测量技术, 测量单层悬空石墨烯本征热导率似乎是“不可能的任务”.
3)在当前的理论框架里, 四声子散射往往被直接忽略, 因为其是只有在高温区才会逐渐出现的一类声子散射行为[106]. 但是有部分理论研究发现即使是在室温下, 单层石墨烯中大量的低能ZA模声子导致其四声子散过程是不容忽视的[107,108]. 因此有必要用四声子散射理论重新审视二维材料热传导行为.
4)二维到三维的维度效应也是一个非常有意义的研究方向. 二维材料为热导率的维度效应研究提供了一个绝佳的平台. 有部分结果显示, 石墨烯和氮化硼的热导率随着厚度的增加而降低, 并在四层的时候达到和块体类似的热导率[44,56,64]. 但是多厚的二维材料才可以变为三维材料? 解决这个问题仍需要大量的实验工作.
5)虽然有理论工作表明即使当样品的尺度到了毫米甚至厘米量级仍存在热导率的尺度效应[174,202], 然而目前的实验中样品长度最多只有9 μm [17]. 还需要大量的实验来对理论进行验证.
6)近期的研究表明石墨块材中存在声子流体动力学行为及第二声, 并可解释石墨块体/薄片中的高热导率及热导率尺度效应[194,195]. 虽然早期的理论显示二维材料中也存在声子流和第二声[192,193], 但是到目前为止没有任何发表的实验数据可支持这个论点.
7)目前普遍采用的界面热阻理论, 如AMM模型[251]和DMM模型[252], 都是简单地假设声子以弹道传输或者扩散传输的形式通过界面, 因此这两个模型与实验结果都有一定的差别. 而最新理论和实验显示, 在低维系统中, 声子不是以简单的弹道或扩散传输, 而是以超扩散的形式传输. 由此需要一种新的模型, 在考虑界面热阻时引入超扩散的概念.
8)热导率测量, 如拉曼法及热桥法, 都不可避免地存在接触热阻问题, 这将大大影响实验结果. 虽然有部分课题组采用双拉曼激光法[67]和电子束自加热法[54]以消除接触热阻的影响, 但是苛刻地实验条件及昂贵的实验设备使得大多数课题组无法进行相关实验.
9)通常采用的界面热导测量, 如TDTR和3ω法可以提供微米尺度的空间分辨率, 但是它只能用于薄膜材料界面热阻测量, 同时其在面内的空间分辨率也局限于其加热激光的光斑大小(通常为微米左右). 由此, 有必要开发一种全新的测量手段, 要求其空间分辨率能达到纳米尺度, 并且可探测二维材料的界面热阻信息[54,55]. 虽然电子束自加热法可用于测量部分材料界面热阻, 但是目前该测量方法局限于扫描电子显微镜腔体内, 不能进行变温测量, 也无法进行多物理场调控, 如光场, 磁场等[54,55]. 因此, 有必要开发一种新的测量手段, 可对结构复杂界面进行热阻测量, 同时兼容商业仪器如变温强磁系统, 进行光、热、电和磁场等多物理场耦合测量, 以获得更多界面热阻信息.
