删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

二维过渡金属硫化物二次谐波: 材料表征、信号调控及增强

本站小编 Free考研考试/2021-12-29
摘要:二维过渡金属硫化物(transition metal dichalcogenides, TMDCs)由于可实现从间接带隙到直接带隙半导体的转变, 能带宽度涵盖可见光到红外波段, 及二维限域所带来的优异光电特性, 在集成光子以及光电器件领域受到了广泛的关注. 最近随着二维材料基础非线性光学研究的深入, 二维TMDCs也展现出了在非线性光学器件应用上的巨大潜能. 本综述聚焦于二维层状TMDCs中关于二次谐波的研究工作. 首先简述一些基本的非线性光学定则, 然后讨论二维TMDCs中原子层数、偏振、激子共振、能谷等相关的二次谐波特性. 之后将回顾这些材料二次谐波信号的调制及增强工作, 讨论外加电场、应变、表面等离激元结构、纳米微腔等方法和手段的影响机理. 最后进行总结和对未来本领域工作的展望. 理解二维TMDCs二次谐波的产生机制及材料自身结构与外场调控机理, 将对未来超薄的二维非线性光学器件的发展产生深远的意义.
关键词: 过渡金属硫化物/
二维材料/
非线性光学/
二次谐波

English Abstract


全文HTML

--> --> -->
1.引　言
自从2004年单层石墨烯被成功剥离以来, 二维层状材料(two dimensional layered materials, 2DLMs)作为一种单原子层的纳米材料受到了极大的关注. 石墨烯展现出了较大的载流子迁移率与良好的韧性等一系列优异性质, 许多基于石墨烯的应用如光电探测器、锂离子电池、超级电容等被设计出来[1,2]. 然而, 石墨烯表现出零带隙和半金属特性, 限制了其在光电领域的应用[3]. 因此寻找一种天然的类石墨烯的二维半导体材料成为了新的研究热点. 此时, 以过渡金属硫化物(transition metal dichalcogenides, TMDCs)为代表的二维层状半导体材料进入了研究者的视野[4,5]. 这些二维半导体材料层间通过范德瓦耳斯力相结合, 除了拥有良好的电学性质以外[6,7], 它们还展现出了独特的光学特性, 比如从可见光到太赫兹波段的宽带光响应[8-10], 室温下较大的激子结合能[11], 以及存在光学的各向异性 [12]. 此外, TMDCs还展现出许多层数依赖的光学现象. 当它们的厚度从块体逐渐降低到单层时, 由于减小的介电屏蔽效应, 它们通常由间接带隙半导体转变为直接带隙半导体[13]并且拥有打破的反演对称性[14]. 由于自旋-轨道耦合, TMDCs产生新的能谷自由度并且展现出能谷相关的圆偏振光选择吸收效应[15]. 在非线性光学方面, 层数的变化使得它们展现出更多层数依赖的非线性光学效应, 比如随奇偶层数振荡的二次谐波强度[16]. 相对于传统的半导体纳米材料, 二维材料也展现出更大的非线性极化率, 因此它们在非线性光学领域有着天然的优势.
非线性光学是研究材料在强相干光相互作用下产生的非线性效应及应用, 在激光技术、光通信和集成光学等多个领域得到广泛应用. 比如饱和性吸收效应, 它来源于材料在高功率激发光作用下产生的对于激发光完全透过的现象, 对于具有这一特性的材料, 称之为可饱和吸收体(saturable absorber, SA)[17,18]. 利用饱和吸收体, 一系列的超短脉冲激光器被研究制成[19,20], 为光通信领域奠定了重要基础. 另外一类重要的非线性光学效应称为谐波效应, 比如二次谐波(second harmonic generation, SHG)、三次谐波(third harmonic generation, THG)以及高次谐波(high harmonic generation, HHG), 它们来自于材料对基频光场的不同阶次的非线性极化. 其中在二(三)次谐波的过程中, 两(三)个频率为ω的光子与非线性光学材料相互作用, 辐射出一个频率为2ω (3ω)的光子. 二次谐波是最基本的二阶非线性光学过程之一, 它涵盖从高分辨生物成像[21]、探测晶体结构[22]、倍频晶体[23]到非线性光学器件[24]等一系列应用. 二次谐波用于表征晶体结构时, 作为一种全光学的表征手段, 对材料的形貌没有要求, 在测试过程中也不会破坏材料结构, 对于难以进行透射电子显微镜表征的样品是一种优秀的备用手段. 传统用于产生二次谐波的倍频晶体材料如β相偏硼酸钡晶体(β-BaB2O4, BBO)、铌酸锂(LiNbO3)、钛酸钡(BaTiO3)或石英等通常是块体材料, 不易用于小型化和可集成化器件. 近年来二维半导体展现出了较大的非线性光学强度以及独特的非线性光学特点, 在非线性光学领域引起了广泛的关注并取得了一系列重要的研究成果[25]. 二维材料非线性光学的进一步研究与发展有望满足目前新型超薄非线性器件小型化、多功能、低损耗等的需求.
本文将回顾近年来二维材料在二次谐波领域相关的一些工作. 第2节首先简述一些非线性光学定则, 讨论二次谐波产生的基本条件. 第3节将讨论二维TMDCs中二次谐波相关的一些特性, 包括层数依赖效应、偏振效应、激子共振以及能谷选择效应. 其中部分化学气相沉积方法生长的材料拥有独特的打破反演对称性的结构使得它们产生增强的二次谐波效应, 展现了巨大的应用潜力. 第4节和第5节将回顾二次谐波信号在二维材料中的调制及增强工作. 其中外加电场、应变、表面等离激元结构、纳米微腔等方法将会被讨论. 最后对二维材料二次谐波的工作进行总结并展望未来可能的研究方向.
2.二次谐波相关的非线性光学定则
光与物质相互作用, 产生电极化强度P(t). 当施加光场为强激光时, P(t)可展开为光场强度E(t)的幂函数:
$\begin{split}{{P}}\left( t \right) =\; &{\varepsilon _0}\Big[ {\chi ^{\left( 1 \right)}}{{E}}\left( t \right) + {\chi ^{\left( 2 \right)}}{{{E}}^2}\left( t \right) + {\chi ^{\left( 3 \right)}}{{{E}}^3}\left( t \right)\\&+ \cdots + {\chi ^{\left( n \right)}}{{{E}}^n}\left( t \right) + {\rm{ }}\cdots \Big],\end{split}$
式中, ε0为真空介电系数; χ为极化率; χ(1)为线性极化率, 用来描述传统的线性光学效应; χ(2)为二阶非线性极化率, 描述二阶的非线性过程. 在非线性光学的研究中, 当材料的非线性光学极化率足够大时, 高阶的非线性光学作用则变得重要. 前面已经提到过, 二次谐波是最简单的二阶非线性过程, 接下来通过耦合波动方程, 将讨论二次谐波过程中满足的一些最基本的非线性光学定则.
首先写出在非磁非导电无自由电荷的色散介质中传播光场的波动方程(此时假定光波是平面波且为横电波):
$\begin{split}&{\nabla ^2}{{{E}}_n} - \dfrac{{{\varepsilon ^{\rm{L}}}{\rm{(}}{\omega _{\rm{n}}}{\rm{)}}}}{{{c^{\rm{2}}}}}\dfrac{{{\partial ^2}}}{{\partial {t^2}}}{{{E}}_n} = \dfrac{1}{{{\varepsilon _0}{c^2}}}\dfrac{{{\partial ^2}}}{{\partial {t^2}}}{{P}}_n^{{\rm{NL}}} \\& \qquad \qquad \left( {n = 1,2,3, \cdots } \right),\end{split}$
其中, En代表不同频率ωn光场的电场强度, $ {\varepsilon }^{\rm{L}}\left({\omega }_{n}\right) $是不同频率ωn下线性极化的复介电常数, $ {{P}}_n^{{\rm{NL}}} $是不同频率ωn下的非线性极化强度, 它们都是位移r和时间t的函数, $c = {1}/{{\sqrt {{\varepsilon _0}{\mu _0}} }}$是真空中的光速, μ0为真空磁导率. 为了定量分析二次谐波过程中基频光与倍频光的相互作用与结果, 假设入射光场E1的频率为ω1, 经过长为L的非线性介质后, 出射倍频光场E2的频率为ω2, 且为了简化此时认为入射光场与出射光场延z方向共线传播, 并令ω1 = ω, ω2 = 2ω, 那么此时出射(入射)光场可以写为
${{{E}}_{2\left( 1 \right)}}\left( {{{z}},t} \right) = {{{A}}_{2\left( 1 \right)}}{{\rm{e}}^{{\rm{i}}\left( {{k_{2\left( 1 \right)}}{{z}} - {\omega _{2\left( 1 \right)}}t} \right)}} + {\rm{c}}.{\rm{c}}.,$
其中, k2(1)是出射(入射)光场波矢的绝对值, A2(1)是出射(入射)光场复振幅, 它是位移z的函数. 将(3)式代入波动方程(2), 只考虑z方向的作用, 在缓变振幅近似下, 二次谐波的耦合波方程为
$\dfrac{{{\rm{d}}{{{A}}_2}}}{{{\rm{d}}{{z}}}} = \dfrac{{2{\rm{i}}{ d}_{\rm eff}\omega _2}}{{{n_2}c}}{{A}}_1^2{{\rm{e}}^{{\rm{i}}\Delta k{{z}}}},$
其中, ni是介质的折射率, Δk = 2k1 – k2, deff = 1/2χ(2)为有效二阶非线性系数. (4)式是入射光场与出射光场延z轴共线传播的二次谐波耦合波方程, 假如此时认为二次谐波的转化效率较低, 入射光场只有少部分能量转化给出射的倍频光场, 亦即认为入射光场的振幅不变为常数, 那么可以得到出射光场振幅随传播距离的变化情况:
$\begin{split}{{{A}}_2}({{z}}) &= \dfrac{{2{\rm{i}}{{{d}}_{{\rm{eff}}}}{\omega _2}}}{{{n_2}c}}\int_0^L {{{\rm{e}}^{{\rm{i}}\Delta k{{z}}}}} {\rm{d}}{{z}}\\& = \dfrac{{2{\rm{i}}{{ d}_{{\rm{eff}}}}{\omega _2}}}{{{n_2}c}}\dfrac{{{{\rm{e}}^{{\rm{i}}\Delta kL}} - 1}}{{{\rm{i}}\Delta k}},\end{split}$
以及倍频效率:
$\begin{split}\eta = & \dfrac{P_2}{P_1} = \left( {\dfrac{2}{{n_1^2{n_2}{c^3}{\varepsilon _0}}}{{d}}_{{\rm{eff}}}^2\omega _2^2} \right)\\& \times \left( \dfrac{P_1}{S} \right){L^2}\dfrac{{{{\sin }^2}\Delta kL/2}}{{{{\left( {\Delta kL/2} \right)}^2}}}.\end{split}$
其中, Pn为光功率, P = IS (S为光束截面), I为光强, I = 1/2ε0cn|A|2.
根据(6)式二次谐波的倍频效率来讨论二次谐波的产生情况. 首先讨论二次谐波产生的相位匹配条件. 当Δk = 0时, (6)式倍频效率中的最后一项$\dfrac{{{{\sin }^2}\Delta kL/2}}{{{{\left( {\Delta kL/2} \right)}^2}}}$有极大值:
${\eta _{\max }} = \dfrac{P_2}{P_1} = \left( {\dfrac{2}{{n_1^2{n_2}{c^3}{\varepsilon _0}}}{{d}}_{{\rm{eff}}}^2\omega _2^2} \right)\left( {\dfrac{P_1}S} \right){L^2},$
此时要求2k1 = k2, 而根据波矢k公式ki = ni ωi/c和相速度公式νi = c/ni, 因此要求n1(ω1) = n2(ω2), 也就是相位匹配的条件为材料在倍频的折射率等于入射基频的折射率. 而对于其他的波矢条件, 二次谐波的转化效率会迅速衰减.
在相位匹配的条件下, (6)式二次谐波的转化效率与入射光场和非线性介质的作用长度L的平方成正比. 而当Δk ≠ 0时, 称为相位失配, 此时当ΔkL/2 = nπ (其中n为 ± 1, ± 2, ···)时, 转化效率η有最小值为0, 而当ΔkL/2 = nπ/2 (其中n为± 1, ± 3, ± 5, ···)时, η极大值正比于4/(Δk)2. 因此相位失配时, 二次谐波的转化效率随非线性介质的作用长度L呈振荡趋势.
另外, 二次谐波的产生对非线性介质的晶体结构非常敏感, 它要求晶体存在中心反演对称性的打破. 对于中心对称的晶体, 假如反转晶体(此时考虑为反转实验室坐标轴):
$ - {{{P}}^{(2)}}({{E}}) = {\varepsilon _0}{\chi ^{(2)}}( - {{E}})( - {{E}}) = {{{P}}^{(2)}}({{E}}),$
此时产生的极化强度P与电场E应该都与反转前相反, 而计算出的电极化强度P不变, 因此中心对称晶体的二阶非线性系数χ(2) = 0.
根据不同的材料体系, 二次谐波还展现出偏振的特性. 为了获得偏振的二次谐波, 将二次谐波的电场方向表示为材料二阶非线性系数以及入射电场的函数[16]:
${{E}}(2\omega ) \cdot {{{\hat e}}_{{{2\omega }}}} = C{{{\hat e}}_{{{2}}{{\omega }}}} \cdot {\chi ^{(2)}}:{{{\hat e}}_{{\omega }}}{{{\hat e}}_{{\omega }}},$
其中, ${{{\hat e}}_{{\omega }}}$和${{{\hat e}}_{{{2}}{{\omega }}}}$分别是入射和出射的电场方向, C是包含局部电场因子的比例因子, 它由局部介电环境确定. 定义有效二阶非线性系数deff = 1/2χ(2), 那么有效二阶非线性系数可以写为
${{{d}}_{{\rm{eff}}}} = \left[ {\begin{array}{*{20}{c}}{{d_{11}}}&{{d_{12}}}&{{d_{13}}}&{{d_{14}}}&{{d_{15}}}&{{d_{16}}}\\{{d_{21}}}&{{d_{22}}}&{{d_{23}}}&{{d_{24}}}&{{d_{25}}}&{{d_{26}}}\\{{d_{31}}}&{{d_{32}}}&{{d_{33}}}&{{d_{34}}}&{{d_{35}}}&{{d_{36}}}\end{array}} \right],$
同时考虑到二次谐波的强度ISHG是电场强度的平方, 那么(9)式将演变为[26]
${I_{{\rm{SHG}}}} = {\left| {{{{{\hat e}}}_{{{2 }}{{\omega}}}} \cdot {{{d}}_{{\rm{eff}}}}\cdot {{\hat e}}_{{\omega }}^2} \right|^2},$
(11)式描述了入射电场为${{{\hat e}}_{{\omega }}}$取向时, 产生的二次谐波在${{{{\hat e}}}_{{\bf{2 }}{{\omega}}}}$出射方向上的强度.
以上简单讨论了二次谐波产生的相位匹配条件, 随非线性介质长度的变化情况以及偏振情况等, 下面将在二维材料中具体讨论二次谐波产生的情况, 并且将看到在特殊的二维TMDCs体系中, 二次谐波的产生条件及特性将会强烈地受到材料性质的影响.
3.二维TMDCs中的二次谐波现象
层状的TMDCs主要可以通过机械剥离和化学气相沉积(chemical vapor deposition, CVD)生长获得. 它们通常可以用结构式MX2表示, 其中M代表过渡金属原子(如Mo, W), X代表硫族原子(如S, Se, Te). 单层TMDCs结构上两个硫族原子像三明治一样上下夹住一个过渡金属原子构成, 层间由范德瓦耳斯力相结合(图1(a)). 典型的TMDCs如二硫化钼(MoS2)、二硫化钨(WS2)单层约0.7 nm, 当厚度从块体降低到单层时, 它们由间接带隙转变为直接带隙, 并且逐渐产生较强二次谐波信号[14]. 在传统机械剥离的二维TMDCs中, 二次谐波展现出奇偶层数依赖效应、偏振效应、激子共振效应以及能谷选择效应等.
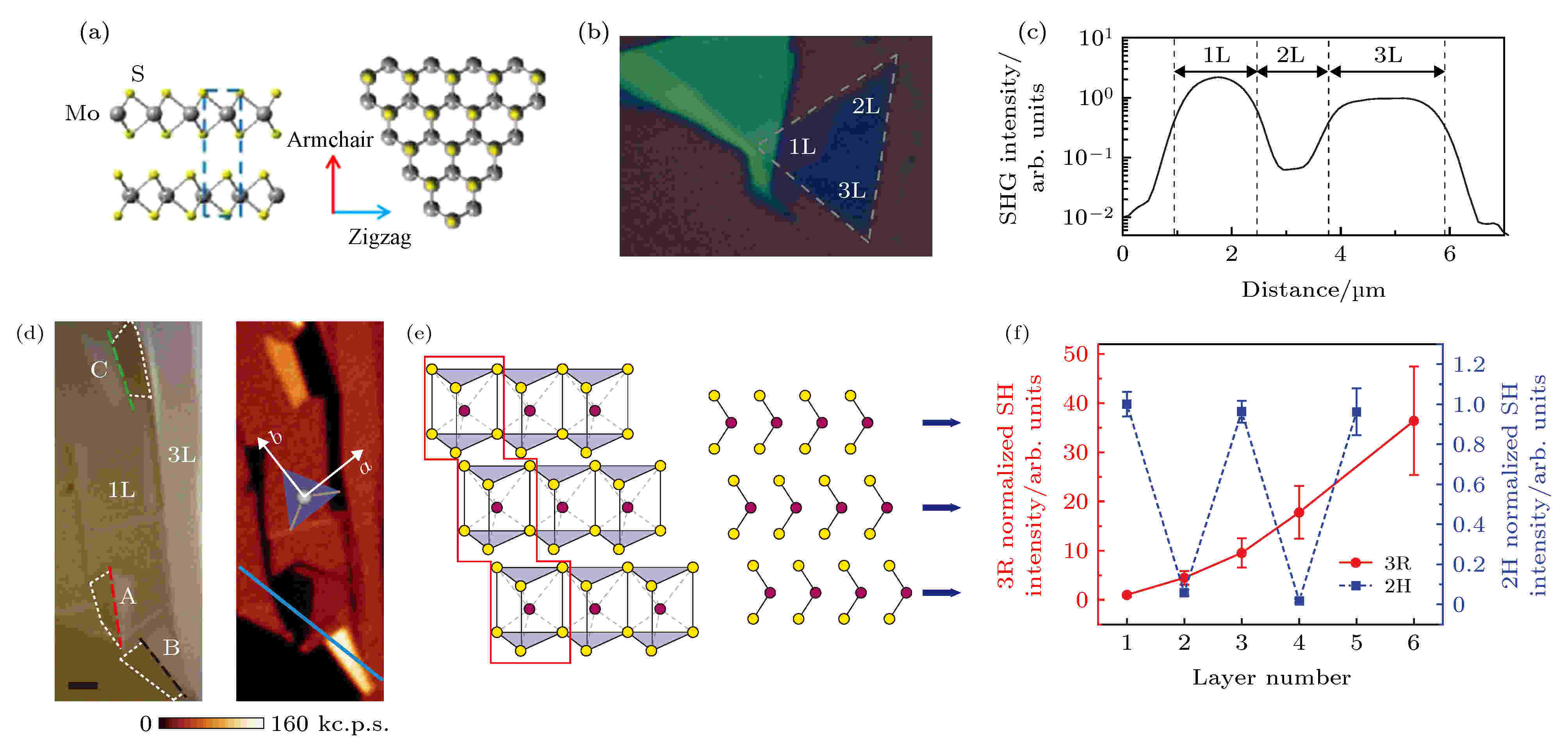图 1 (a) MoS2原子排列的侧视图(左)和俯视图(右), 其中俯视图中对应扶手椅和Z字形两个晶体取向; (b) 机械剥离方法得到的不同层数MoS2的光学照片[16]; (c) 2H相MoS2二次谐波信号随层数增加呈振荡减小的趋势[16]; (d)人工折叠的两层MoS2 (左)以及对应的二次谐波成像(右)[31]; (e) 3R相MoS2晶体结构及倍频偶极排列[32]; (f) 3R相MoS2二次谐波呈平方递增的趋势[32]
Figure1. (a) Side view (left) and top view (right) of MoS2 atomic structure. The highlighted armchair direction and zigzag direction correspond to the top view. (b) Mechanical exfoliated MoS2 with different layers[16]. (c) 2H phase MoS2 layers show diminishing the oscillation in SHG signal[16]. (d) Optical image of artificial folded MoS2 (left) and its corresponding SHG image(right)[31]. (e) Crystal structure of 3R phase MoS2 and corresponding SH dipole[32]. (f) 3R phase MoS2 layers show quadratic enhanced SHG with the increase of layers[32].

2
3.1.层数依赖
-->

3.1.层数依赖

2013年, Malard等[16], Kumar等[27]以及Zeng等[28]3个研究组报道, 不同于块体材料, 当MoS2(WS2)的层数减小到单层时, 他们观察到了非常强的二次谐波效应(单层MoS2中二阶非线性系数χ(2)约0.6 nm/V[16], 单层WS2中约0.5 nm/V[29]), 这种现象来自于单层时反演对称性的打破. 通常来说机械剥离的二维TMDCs是2H (2-hexagonal)相, 这使得它们在奇数层时存在反演对称性的打破而偶数层反演对称性的恢复, 因此最终出现奇数层存在二次谐波而偶数层二次谐波的信号消失的现象(图1(b)和图1(c)). 当层数缓慢增加至5—7层时, 奇数层MoS2也会出现二次谐波信号迅速递减的趋势. 这种现象可以理解为每一个奇数层是底部单层与上部分偶数层二次谐波信号的叠加, 当层数增加时, 上面的偶数层不贡献信号反对底部单层产生的二次谐波信号吸收增加, 使得总的信号减小. 所以最终随着层数的增加, MoS2的二次谐波信号呈现出振荡减小的趋势, 最终形成块体时非线性极化率χ(2)只有10–14 m/V[30].
尽管在以MoS2为代表的少层二维TMDCs材料中能够探测到较强的二次谐波信号, 单层的TMDCs因为其单原子层薄的特点, 与激发光的作用截面十分有限, 导致其二阶非线性极化率χ(2)较小, 产生二次谐波信号在应用上依然面临挑战. 因此想要二维材料在非线性光学器件中得到应用, 还需要能够高效产生二次谐波的二维层状材料.
不同于直接剥离得到两层的MoS2, 复旦大学的Jiang等[31]将单层的MoS2折叠, 得到了多种不同堆垛结构的两层MoS2. 在图1(d)中, 左侧的a, b, c三个区域都是由单层MoS2通过人工折叠形成的两层MoS2区域. 在右侧对应的二次谐波成像中可看到, a区域表现出二次谐波信号的消失, 这与直接机械剥离获得的两层MoS2情况相同, 因为偶数层存在反演对称性的恢复. 但是b区域与c区域相对于单层, 呈现出增强的二次谐波信号, 这表明它们依然存在打破的反演对称性, 并且层数的增加使对称性破缺更加明显. 单层的MoS2中存在两个晶体取向, 分别为扶手椅(armchair)晶向和Z字形(zigzag)晶向, 见图1(a). 如果单层的MoS2沿着Z字形晶向折叠, 那么形成的双层MoS2类似于天然的2H相两层MoS2, 不存在反演对称性的打破, 称之为2H-like结构, 图1(d)中a区域就是这样. 如果单层的MoS2沿着扶手椅晶向折叠, 那么第二层的Mo原子将处于第一层Mo原子的正上方, 第二层的MoS2的原子排列相对于第一层完全重复, 因此将打破反演对称性从而产生增强的二次谐波信号. 这种结构称之为3R-like结构, 图1(d)中b区域就属于这种情况. 如果折叠的晶向既不平行于Z字形晶向又不平行于扶手椅晶向, 那么得到的两层MoS2结构也不存在反演对称性, 因此图1(d)中c区域也会出现二次谐波信号. 对于b区域这种特殊的情况, 加州大学伯利克分校的Zhao等[32]进行了进一步的研究. 通过化学气相运输(chemical vapor transport, CVT)的方法, 他们直接生长出了3R (3-rhombohedral)相的MoS2晶体, 并通过机械剥离的方式得到了少层的MoS2纳米片. 图1(e)是3R相MoS2的原子排列以及其产生二次谐波偶极矩的叠加情况. 可以看出与Jiang等[31]折叠形成的结构稍有不同, 自然的3R相结构可以看作每一层为单层MoS2在垂直方向上的复制并在面内产生一定的平移(而不是处于每一层的正上方), 这符合能量最低的原理. 同时这种原子结构每一层产生倍频偶极取向都相同, 因此保证了层与层间存在增强的叠加效应. 通过表征不同层数的3R相MoS2, 最终发现随着层数的增加二次谐波信号与层数呈平方递增的关系, 并且这种关系直到十层也仅仅因为吸收的原因而减弱20%.
这种不同原子堆垛导致反演对称性破缺从而产生二次谐波差异性的情况常常被用来分辨不同晶相的二维材料. 湖南大学的Zeng等[33]以及华中科技大学的Yang等[34]分别合成了2H, 3R相的WS2、二硒化钨(WSe2)以及二碲化钼原子晶体, 并且借助二次谐波的表征区分了不同相的沉积温区, 实现了大面积3R相的可控合成. 西北工业大学的Song等[35]对比了半导体2H相和半金属1T'(monoclinic)相二碲化钼, 发现1T' 相二碲化钼二次谐波转化效率极大降低, 且转变为$ {C}_{2 h}^{2} $点群, 展现出不同的偏振特性. 加州大学伯克利分校的Wang等[36]通过静电掺杂实现了单层二碲化钼2H相到1T' 相的转变, 偏振的二次谐波测试表明相变后的1T' 相二碲化钼依然保持原2H相的晶体取向. 深圳大学的Hao等[37]可控合成了ε相的硒化铟(InSe)、碲硒化铟(InSe1–xTex)以及硫硒化铟(InSe1–xSx)原子晶体, 并且展现出相比于普通2H相TMDCs高一到两个量级的二阶非线性系数.
利用化学气相沉积的方法, 还能可控合成具有特殊结构的二维材料. 化学气相沉积法利用含过渡金属原子以及硫族原子的化合物作为目标材料的前驱体在高温进行反应并沉积生长在硅片上, 这个过程中通常受到温度、流速、过饱和度等因素的影响[38], 因此合成出的二维材料可以拥有特殊打破反演对称性的结构. 利用这种方法设计生长新型的二维材料, 能够产生高效的二次谐波.
湖南大学的潘安练课题组[39,40]可控合成了在形貌结构上产生对称性破缺的螺旋结构WS2, 展现出增强二次谐波的同时解释了其生长的机理. 图2(a)是螺旋WS2的光学图片, 螺旋WS2通过高温的化学气相沉积方法直接生长在镀有二氧化硅的硅片上. 图2(a)中右图是左图光学照片样品中心处的原子力显微镜(atomic force microscopy, AFM)表征, AFM扫描成像清晰地显示出WS2中心的螺旋结构. 这种螺旋结构由独立的单层通过螺位错螺旋生长而来, 螺位错的引入是因为沉积温区存在不同的过饱和度. 它不仅使得生长的WS2具有独特的形貌, 同时螺位错的引入打破了层与层之间的对称中心, 因此使得螺旋WS2的二次谐波强度随层数递增, 中心区域可达单层强度的上百倍(图2(b)).
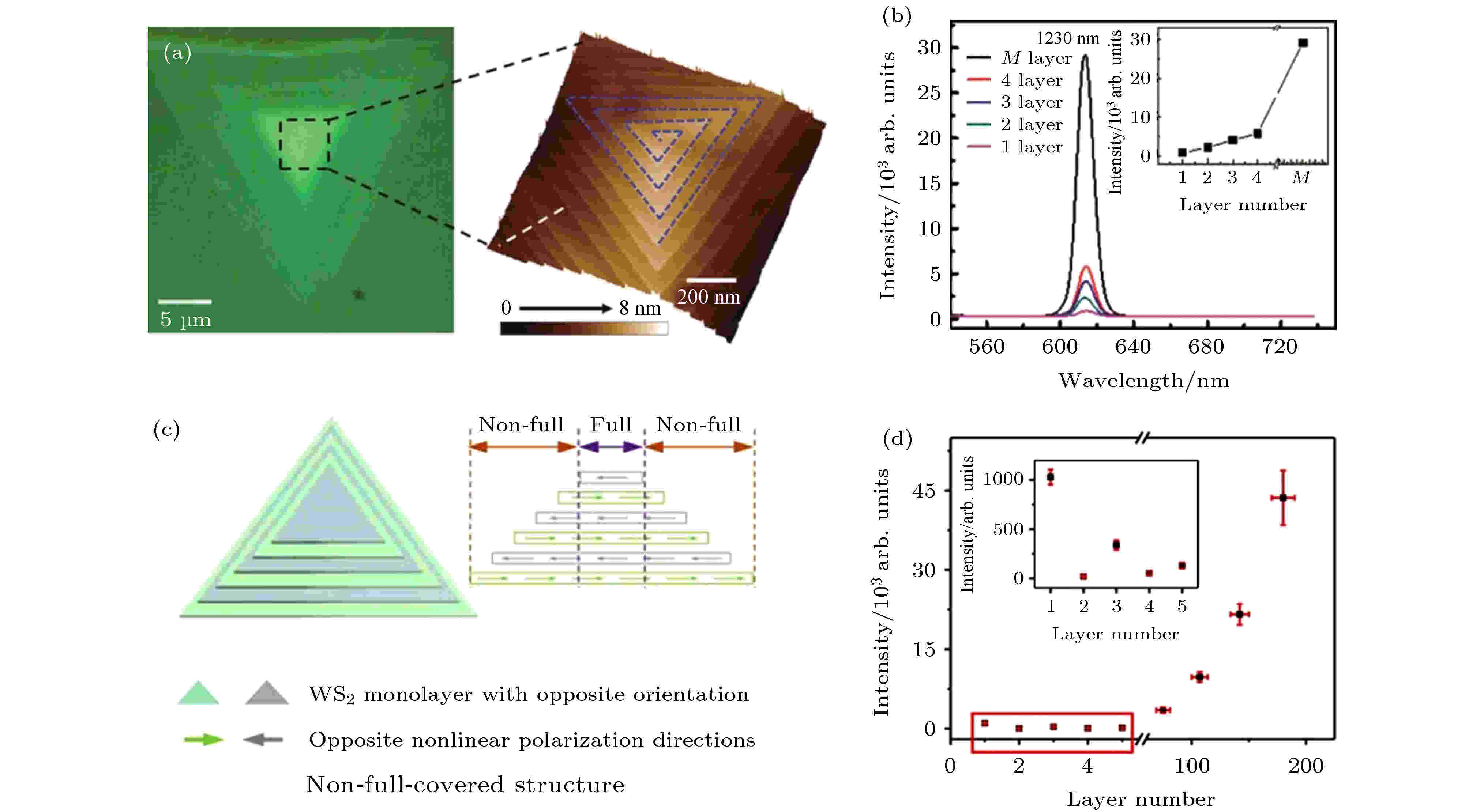图 2 产生高效二次谐波的二维材料　(a)螺旋WS2的光学照片及图中虚线正方形区域内放大的螺旋WS2样品中心AFM图片[39]; (b)螺旋WS2的二次谐波强度随层数递增[39]; (c) 金字塔结构的WS2纳米片结构示意图[41]; (d)金字塔形的WS2纳米片边缘形成高效二次谐波[41]
Figure2. CVD grown TMDCs with highly efficient SHG: (a) Optical image (left) and zoom in AFM image (right) of spiral WS2 flake[39]; (b) layer dependent SHG of spiral WS2 flake[39]; (c) schematic illustration of pyramid-like WS2 structure[41]; (d) pyramid-like WS2 displays high intensity of residual edge SHG signal[41].

中国科学院化学研究所的Lin等[41]报道合成了金字塔形的WS2 (图2(c)). 金字塔形的WS2每一层由不完全覆盖的三角形单层WS2组成, 厚度可达一百多纳米(200多层), 这种独特的结构通过在生长过程中逐渐减小载气的流速获得. 金字塔形的WS2层间是2H相的堆垛结构, 因此它的二次谐波强度随着厚度的增大最初表现为与2H相类似的振荡减小趋势. 然而当层数增加到约70层时, 金字塔形的WS2表现出急剧的二次谐波信号强度增大. 这些二次谐波信号来自于材料残存不完全覆盖的边缘. 金字塔形的WS2自身形成一个类似于回音壁模式的纳米腔, 它将限域并放大边缘产生的二次谐波信号, 最终相比单层可达40倍的信号增强. 同时这种纳米腔的特性还反映在波长依赖的二次谐波信号上, 通过改变腔长(即金字塔形WS2的大小), 二次谐波的强度能够周期性的随激发光的波长产生变化, 并且它的模式间隔满足: Δλ = λ2/(nL) = 2λ2/(3nD), 其中n是WS2反射系数, λ是激发光的波长, D是金字塔形WS2的边长.
利用化学气相沉积生长的这些具有高对称性破缺的二维TMDCs在一定程度上弥补了2H相机械剥离二维材料光物质相互作用截面小, 二次谐波效率低的劣势, 根据计算它们的二次谐波转化效率已能够匹敌现今商业化的BBO倍频晶体[39], 这也为将来超薄非线性倍频器件的应用打下了基础.
2
3.2.偏振特性
-->

3.2.偏振特性

二次谐波作为表征手段其中最重要的一种作用是可以通过偏振的测试反映材料的晶体取向, 二次谐波的偏振检测手段也作为一种全光学无损的手段广泛地应用于各种材料体系[22,42,43]. 前面提到过, 二次谐波的偏振方向由入射电场的方向以及材料的有效二阶非线性系数deff决定. 在2H相二维材料中, 奇数层结构属于D3h点群, 通过晶体对称性的简化, 它的有效二阶非线性系数矩阵为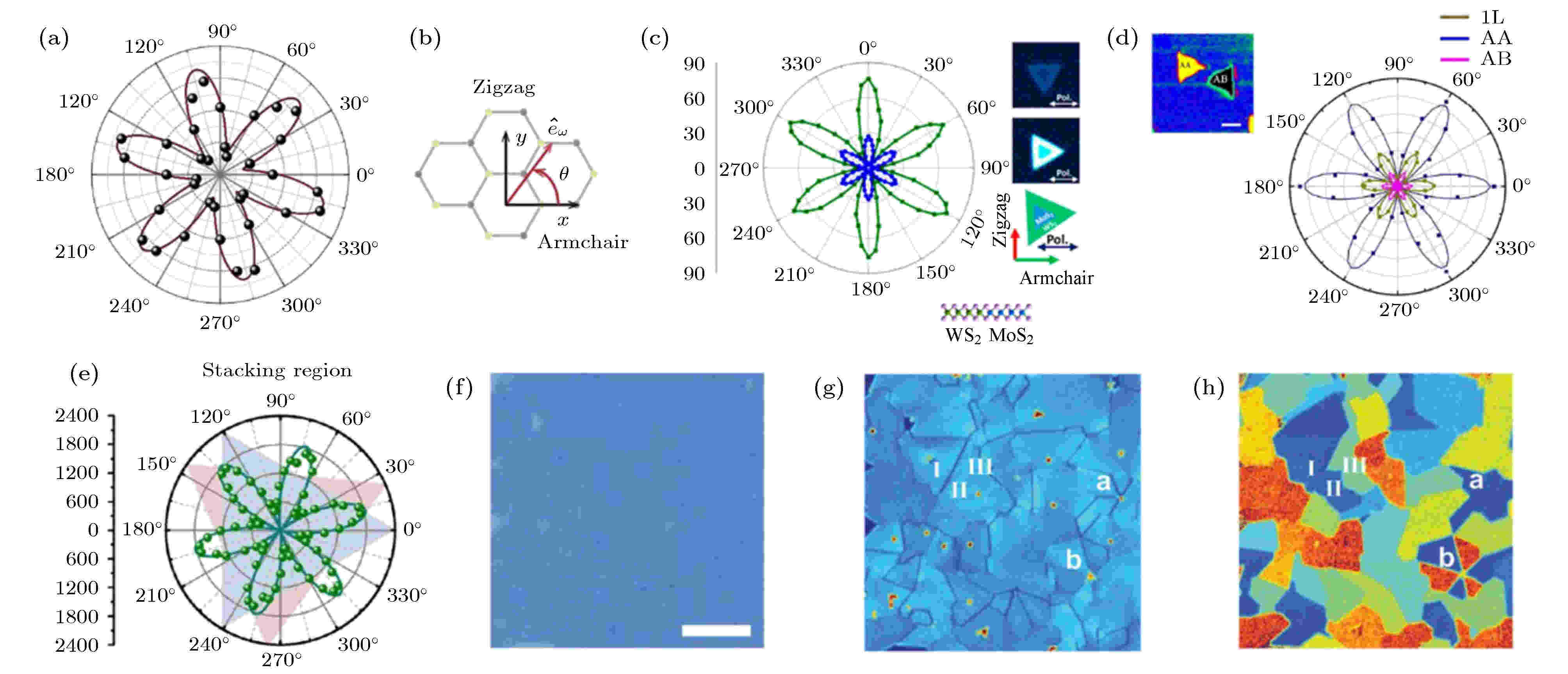
${{{d}}_{{\rm{eff}}}} = \left[ {\begin{array}{*{20}{c}}0&0&0&0&0&{{d_{16}}}\\{{d_{21}}}&{{d_{22}}}&0&0&0&0\\0&0&0&0&0&0\end{array}} \right],$
其中, d21 = d16 = –d22. 根据(11)式, 若入射光垂直入射到样品上并将入射电场投影到样品的扶手椅方向上, 2H相TMDCs中平行和垂直的二次谐波可以写为[16,26]
${I_{{\rm{SHG}}/\!/}} = {\left| {{d_{22}}\cos 3\theta } \right|^2},$
${I_{{\rm{SHG}} \bot }} = {\left| {{d_{22}}\sin 3\theta } \right|^2},$
其中, θ角定义为入射光电场方向与样品扶手椅方向的夹角(图3(b)). 因此2H相TMDCs中偏振的二次谐波极化图展现出六瓣花瓣的形状(图3(a)), 每个花瓣(即二次谐波的最大值)对应于样品的扶手椅晶向, 这种六倍的旋转对称性也符合D3h点群结构. 对于未知晶体取向的样品, 也可以通过偏振的二次谐波测定样品的晶体取向.
图 3 二次谐波的偏振特性　(a) 单层MoS2的二次谐波偏振极化图[16]; (b)单层MoS2晶体取向俯视图, 其中x方向代表扶手椅方向, y方向代表Z字形方向, θ角是激发光入射方向与扶手椅方向的夹角[16]; (c) WS2/MoS2横向外延异质结[44]以及(d) WSe2/WS2 AA和AB堆垛结构纵向外延异质结[45]的二次谐波偏振极化图, 其中插图是异质结的二次谐波成像; (e) 人工堆垛两种二维材料使二次谐波极化方向产生叠加[46]; (f)—(h)利用二次谐波偏振区分单层MoS2中不同晶界与畴界[47]
Figure3. Polarization properties of SHG in TMDCs: (a) SHG polarization in monolayer MoS2 shows six fold rotation symmetry[16]; (b) top view of MoS2 crystallographic orientation, where x represents armchair direction, y represents zigzag direction and θ is the angle between input laser and armchair direction [16]; SHG polarization in (c) WS2/MoS2 laterally epitaxial heterostructure[44] and (d) WSe2/WS2 AA, AB vertical heterostructure[45], where the insets shows correspongding SHG mapping; (e) superposition of SHG polarization by artificial stacks of two different 2D materials[46]; (f)?(h) demonstration of distinguishing of different grain boundary in monolayer MoS2 thin film be SHG polarization[47].

清华大学的Zhang等[44], 以及湖南大学的Wu等[45]通过化学气相沉积的方法分别可控生长了横向外延的WS2/MoS2, WSe2/ MoSe2, 以及纵向外延的WSe2/WS2异质结. 在Zhang等[44]的实验中, 中间的钨原子结构TMDCs与外延的钼原子TMDCs展现出相同的六倍旋转对称极化图像, 且极化图的最大值取向相同(图3(c)), 这证明生长的异质结结构没有受晶格失配的影响, 横向外延异质结的异质界面是两种材料的Z字形晶向; 而在Wu等[45]的实验中, 同样的极化现象出现在底层的WS2以及顶层的WSe2上(图3(d)), 证明垂直结构的异质结呈完美的AA和AB堆垛.
2014年, Hsu等[46]通过湿法化学转移了两种不同二维材料得到了不同堆垛角度的双层结构, 并且在偏振的二次谐波表征中发现一个明显的叠加规律. 通常来说, 化学气相沉积生长的三角形形状的二维材料扶手椅方向对应于三角形高的方向, 而Z字形方向对应于三角形边的方向. Hsu等[46]首先通过偏振确定了两种单层的MoS2晶体取向与极化方向, 然后将它们堆叠成任意角度的两层. 在能够获得二次谐波的两层样品中(即堆垛角不等于60°), 发现两层MoS2的二次谐波偏振依然表现为六瓣的旋转对称, 但是花瓣的位置(即极化最强的方向)出现在两层MoS2三角形叠加角的平分线上. 通过大量的不同二维材料叠加二次谐波偏振测试, 总结出了两层二维材料任意角度堆垛时二次谐波极化的叠加方向:
${I_{\rm{s}}}(\theta ) = {I_1} + {I_2} + 2\sqrt {{I_1}{I_2}} \cos 3\theta ,$
其中, I1, I2和Is分别为第一层、第二层以及堆垛区域总的二维材料二次谐波强度; θ是堆垛角, 它代表两个三角形二维材料最临近的两个角(属于不同的两层)的垂直平分线所夹的角度(图3(e)的极化图中即为红色与蓝色三角形垂直平分线所夹的最小的角度). 对于θ = 60°的情况, 此时可以看作一个完全的2H相堆垛导致了两层叠加后二次谐波完全抵消, 而对于θ = 0°的情况可以看作3R相堆垛导致叠加区域的二次谐波强度翻倍. 因此二次谐波极化的偏振可以看成两层材料二次谐波极化方向的矢量叠加. 理解基本的二维材料二次谐波叠加规律对后续研究者的调制工作有着非常重要的意义.
利用偏振的二次谐波检测手段还可有效地分辨出单层多晶二维材料的晶界取向. 图3(f)—(h)是Yin等[47]报道的在单层MoS2上通过二次谐波偏振的成像将看似均匀的薄膜区分出不同的畴界区域. 图3(f)是一个大面积的单层MoS2薄膜, 其尺寸可达上百微米, 在光学显微镜的观察下, 薄膜展现出良好的均匀性, 只能看出上面存在许多成核的位点. 二次谐波的成像(图3(g))则展现出了更加丰富的信息, 整个单层的MoS2薄膜虽然拥有相对均匀的二次谐波信号, 但是它却是由许多20—40 μm单晶畴界组合形成的多晶. 在畴界交界的区域, 由于相邻边界取向不同, 它们或叠加增强或相干相消, 因此展现出明显的晶界. 在早期透射电镜的表征中, 晶界被观察到是只有几个原子尺度宽的狭窄区域[48], 但是在二次谐波的成像中却清晰地呈现为一条条黑线把相邻的畴界隔开. 由于MoS2三倍旋转对称的晶体结构, 单纯的二次谐波成像并不包含相位信息, 因此不能区分出相反的晶体取向, 此时二次谐波的偏振则能够进一步挖掘内部存在的信息. 根据上面的推导结论: ${I_{{\rm{SHG}}/\!/}} = {\left| {{d_{22}}\cos 3\theta } \right|^2}$, ${I_{{\rm{SHG}} \bot }} = {\left| {{d_{22}}\sin 3\theta } \right|^2}$, 如果将同一个单层薄膜区域分别进行平行和垂直的二次谐波偏振表征, 那么就能反过来计算出不同畴界之间的晶体取向:
$\theta = \dfrac{1}{3}{\rm{ arctan }}\sqrt {\dfrac{{{I_{{\rm{SHG}} \bot }}}}{{{I_{{\rm{SHG/\!/}}}}}}} .$
结合二次谐波成像以及偏振的信息就能得到完整的晶体取向. 例如, 在图3(h)色彩取向图中Ⅰ与Ⅱ区域, 虽然呈现出相同的颜色, 但是通过图3(g)二次谐波成像可以看出Ⅰ与Ⅱ区域间存在明显的晶界, 因此这两个畴界存在完全相反的晶体取向; 而图3(f)中Ⅱ与Ⅲ区域在二次谐波的成像中表现出近乎相同的颜色衬度, 但是经过偏振的二次谐波计算后, 它们在色彩取向图3(h)中展现出晶体取向差异约12°.
2
3.3.激子共振特性
-->

3.3.激子共振特性

二维TMDCs的二次谐波还展现出激发波长依赖的激子共振特性. 由于二维材料在垂直方向上只有一个或几个原子层的厚度, 因此在这个方向上它们表现出非常强的量子限域的效应以及减小的静电屏蔽作用, 且因为库仑相互作用产生激子. 激子是一种电子空穴对, 通常由于结合能较小在室温下会被解离. 而单层MoS2的厚度约0.7 nm小于激子的玻尔半径(约0.93 nm), 这使得它拥有非常大的激子结合能并形成稳定的万尼尔激子(Wannier exciton)[11]. 另外在MoS2和WS2中, 由于价带的劈裂还会形成A和B两种不同类型的激子, 它们的存在早先也都通过理论与实验得到验证[49]. 为了确定二次谐波与激子直接的关系, 法国图卢兹大学的Wang等[50]在4 K的低温下进行了激发光波长依赖的二次谐波测试. 他们发现当倍频信号的能量与WSe2的1s态A激子以及1s态的B激子共振时, 最大将会产生三个量级增强的二次谐波信号. 而双光子荧光激发的实验中, 这种增强的现象并没有出现. 因此他们认为除了电偶极矩耦合光物质相互作用外, 还存在一些其他的因素影响二维材料中的二次谐波信号产生, 并且他们将这种因素解释为激子效应. 上面提到过, 二次谐波的产生是通过基态吸收两个相同频率为ω的光子到虚拟态, 辐射出一个频率为2ω的光子. 其中, 在这个过程中没有电子转移的出现, 称为参量过程. 在激子共振的情况下, 二次谐波的产生可以利用能量相近激子态作为中间态. 激子态是一个实态, 相比于二次谐波过程的中间虚拟态, 它拥有更长的寿命, 这将极大地增强二次谐波产生的效率, 因此在二次谐波能量与激子能量发生共振时, 会产生数量级程度的增强. 这种激子共振的效应也被纽约哥伦比亚大学的Malard等[16]所观测到. 在图4(c)中, 单层(深蓝)与三层(绿)的MoS2展现出的吸收峰(实线)中可以明显看到在布里渊区K点形成的A和B激子以及Γ形成的C激子, 并且由于能带排列的原因它们的峰位稍有偏移. 在波长依赖的二次谐波(散点)信号中, C激子共振的波长出现了明显的增强并且同样的偏移也反映在了其中.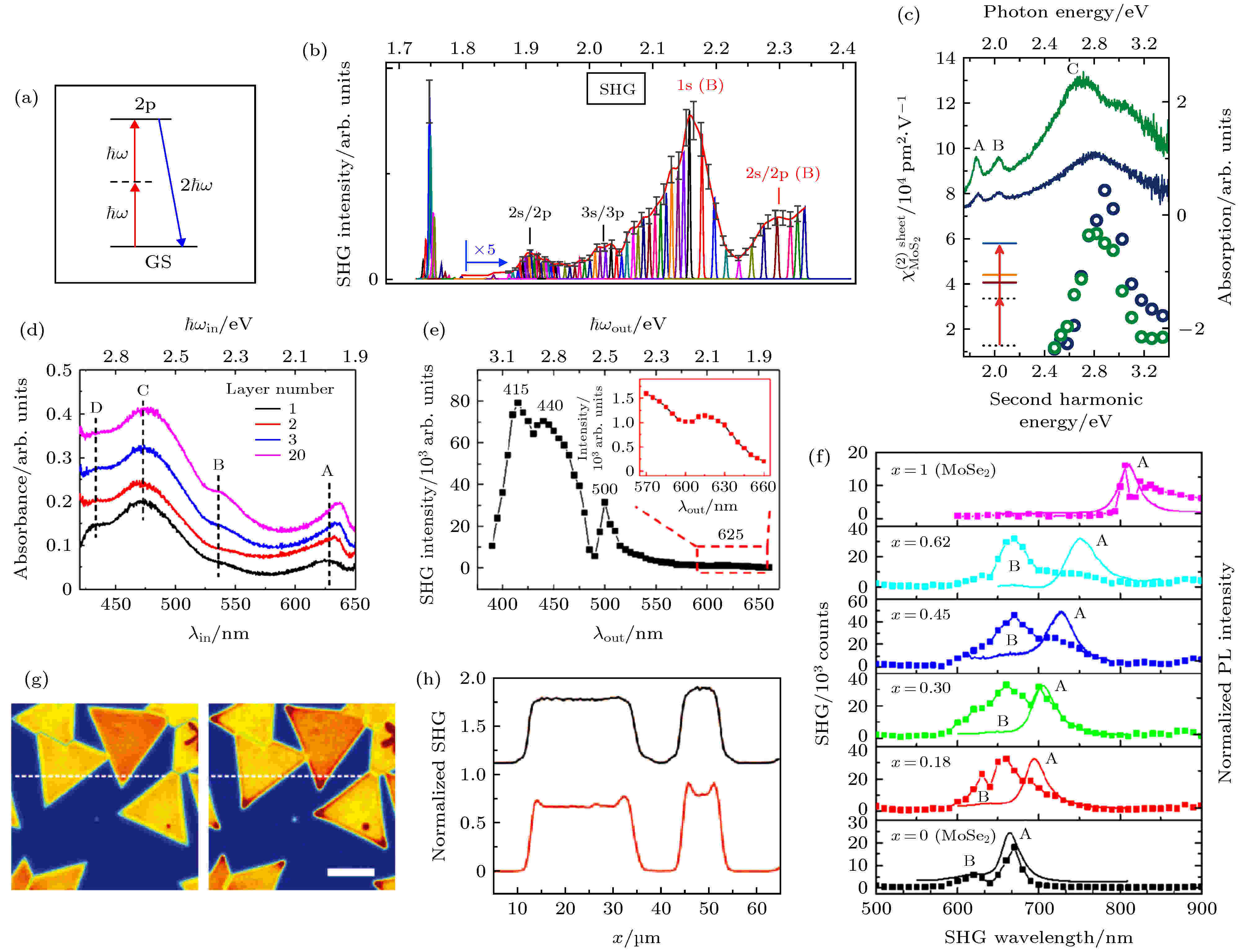
图 4 二次谐波的激子共振特性　(a) 原理图解释两个入射光子共振A激子的2p态产生二次谐波[50]; (b) 4 K下单层WSe2波长依赖的二次谐波信号[50]; (c) 单层(深蓝)与三层(绿) MoS2二阶非线性极化率与吸收光谱作为激发光波长的函数[16]; (d), (e) 对比螺旋WS2二次谐波激子共振与吸收光谱说明二次谐波增强在稍高于带隙能量处[51]; (f) 对比单层硒硫化钼合金二次谐波(散点)与荧光光谱(实线)[52]; (g), (h) 气象生长单层MoS2边缘增强效应[47]
Figure4. Exciton resonance properties of SHG in TMDCs: (a) Schematic illustration of SHG when two incident photons are resonant with 2p state of A exciton[50]; (b) excitation wavelength dependent SHG of monolayer WSe2 at T = 4 K[50]; (c) second order nonlinear susceptibility and absorption served as the function of pump laser energy in monolayer (blue) and trilayer (green) MoS2[16]; (d), (e) illustration of SHG enhancement in spiral WS2 flake when the excitation energy slightly above bandgap by comparison of reflective spectrum with SHG spectrum[51]; (f) SHG spectra (dotted traces) of monolayer alloys and corresponding room-temperature PL spectra (solid traces)[52]; (g), (h) CVD grown monolayer MoS2 flakes show edge enhanced SHG[47].

在化学气相生长的样品中, 由于材料结构的不均匀, 掺杂元素的不同或边缘效应, 激子共振的特性还会受到能带或能态的影响. 2020年湖南大学Fan等[51]报道, 在化学气相生长的螺旋结构WS2中, 他们观察到了除激子共振外, 还存在激发光能量稍高于电学带隙时的二次谐波增强(图4(e)). 2016 年, 韩国蔚山大学的Le等[52]合成了单层不同组分的硒硫化钼三元合金, 并且研究了硒掺杂对二次谐波的影响. 如图4(f)所示, 从下到上是增加硒原子含量后从纯的MoS2调控为硒硫化钼合金再变成纯的MoSe2时不同组分的二次谐波光谱(散点)与荧光(曲线)光谱. 可以看出, 随着硒原子含量的增加, 共振的二次谐波光谱呈红移趋势, 并且表现出相对A激子更加明显的B激子共振. 当硒硫化钼MoS2(1–x)Se2x中x的组分为 0.18和 0.3时, B激子附近的二次谐波强度慢慢接近A激子的强度, 而当x = 0.62时, B激子共振的二次谐波强度已经是A激子的两倍. 实际上这种B激子共振在纯的二硫(硒)化钼中是被抑制的. 对于这种二次谐波共振扩宽的现象, Le等[52]通过合金样品的能态改变进行了解释. 在硒硫化钼合金样品的合成过程中, 随机的硒原子替换会导致局部的电子结构发生改变, 这种现象已经通过扫描隧道显微镜被观察到[53]. 同时这种能态的拓宽也反映在随样品红移逐渐拓宽的荧光光谱半高宽上. 因此激子共振和缺陷态的拓宽共同造成了B激子共振的增强, 且随着硒元素的掺杂, 合金样品的二阶非线性系数逐渐增大, 这对于调控高效的非线性光学材料同样提供了新的思路.
2014年加州大学伯利克分校的Yin等[47]报道了一种边缘效应导致的独特二次谐波共振现象. 在大面积生长的单层MoS2中, Yin等用稍高于两倍A激子共振的波长(0.93—0.97 eV)对其进行二次谐波成像, 可以看出在一些特定的波长下, 单层材料边缘由于边缘态共振, 实现了二次谐波信号增强(图4(g)—(h)). 这一现象被台湾成功大学的Lin等[54]做了进一步的研究. 通过球差透射电子显微镜的表征可以发现, 生长的单层MoS2存在两种不同的截止边(即三角形纳米片的边缘), 其中三角形边缘稍微内凹的是硫截止边, 而三角形边缘更直的是硫-钼Klein截止边(类似于石墨烯中的Klein边). 对于这两种不同的截止边, 通过计算发现它们存在不同的边缘态对应不同的共振能量, 因此可以观察到不同激发波长下不同的边缘二次谐波增强效应[54].
2
3.4.能谷选择特性
-->

3.4.能谷选择特性

二维TMDCs的另一个独特的特点是其具有新的能谷自由度. 基于能谷自由度, 许多不同于其他纳米材料新的物理现象被发现. 能谷是指布洛赫电子能带的最高处或最低处, 二维材料的能谷极化特性简单来说源于其布里渊区+K与–K点对于右圆(σ+)光子与左圆(σ–)光子的选择性吸收[55]. 如果基于这种选择特性对二维材料中非简并的能谷进行调控, 那么就能形成分立的能谷自由度. 单光子的过程中, 二维的TMDCs在低温下展现出极大的谷极化率[56,57], 特别的WS2由于硫钨键的原因在室温下展现出超过20%的谷极化率[58], 这些现象对二维的谷逻辑器件铺下了坚实的基础. 同时, 能谷的效应在双光子过程中也有着重要的发现. 2015年Seyler等[59]报道了A激子共振时WSe2的二次谐波能够产生近乎100%的圆偏振极化度. 如图5(a)所示, 当圆偏振的激发光与WSe2的A激子共振时, 两个基频(ω)的左圆(σ–)光子将产生一个几乎偏振一致的右圆(σ+)倍频(2ω)光子, 而右圆(σ+)激发时情况正好相反. Seyler等将这种现象解释为单层WSe2由于D3h晶体结构存在反演对称性的打破以及三倍的旋转对称, 使得晶格产生了角动量吸收与发射光子的不匹配. 通常来说, 在单光子的过程中, 二维材料的布里渊区的+K (–K)点只吸收σ+ (σ–)的光子. 而对于双光子的带间转移过程, 展现出了翻转的选择定则: 两个σ+ (σ–)光子可以被–K (+K)点同时吸收, 并辐射出相反的σ– (σ+)光子(图5(b)). 这种二维材料中独特的高偏振度的双光子选择定则在2015年被Xiao等[60]做了进一步的总结. 在二维材料光物质相互作用的过程中, 三倍的旋转对称要求材料保证总角动量守恒. 因此材料的能谷角动量$\Delta \tau \hbar $, 激子角动量$\Delta l\hbar $, 晶格角动量$3 N\hbar $和光子自旋角动量$\Delta m\hbar $将满足以下关系:
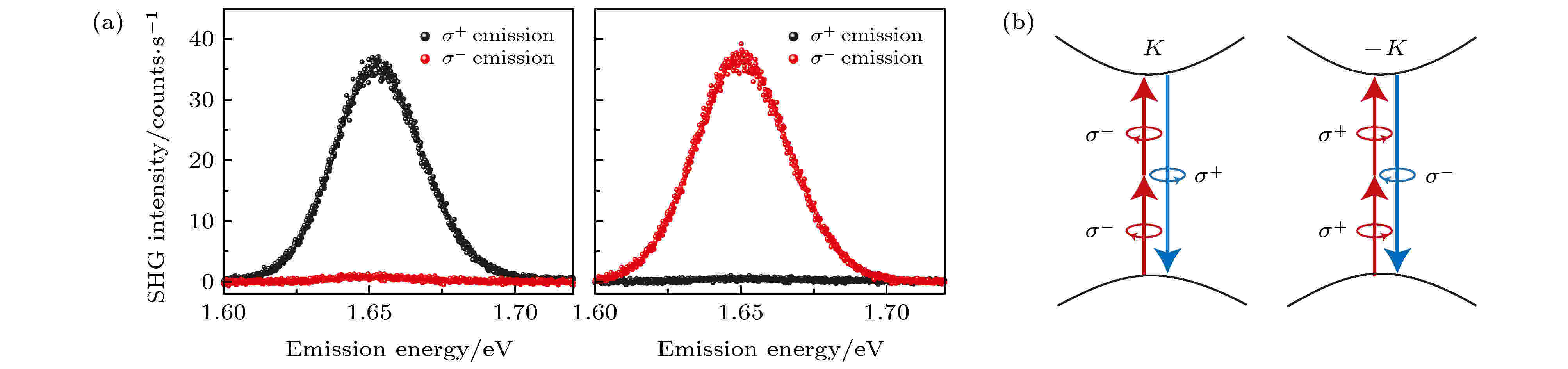图 5 二次谐波的能谷选择特性　(a)单层的WSe2展现出与激发光相反的圆偏振二次谐波[59]; (b)二维材料二次谐波能谷光学选择定则[59]
Figure5. SHG valley selection rules: (a) Circular polarization-resolved SHG spectra showing the generation of counter-circular SHG in monolayer WSe2[59]; (b) interband valley optical selection rules for SHG in 2D TMDCs[59].

$\Delta m\hbar = \Delta \tau \hbar + \Delta l\hbar + 3N\hbar ,$
即双光子吸收过程中, 自旋角动量的变化将引起能谷、激子以及晶格角动量的变化. 基于这个选择定则, 双光子过程如双光子荧光与二次谐波都将展现出能谷-激子锁定的效应, 也就是说在激子共振的情况下, 纯的σ–或σ+激发都将只在确定的能谷中发生[60]. 例如, 在1s态共振激发的WS2二次谐波中, +K谷基态到1s态的转移要求$ - 1\hbar $的能谷角动量变化以及$0\hbar $的激子角动量变化, 因此这个过程只有通过吸收两个纯的带有$2\hbar $动量的σ+光子, 并辐射出剩余的$3\hbar $角动量进入晶格. +K点的1s态将辐射出σ–的倍频光子. 这个选择定则将总结并归纳了共振的双光子过程中, 圆偏振光激发允许以及禁止的跃迁态, 它对控制能谷光电器件的应用如光开关逻辑器件有着重要意义.
4.二次谐波信号调制
二维材料中二次谐波信号的可调制性源于二维材料自身受热力光电产生的二阶非线性系数的变化, 同时这也使得二维材料产生的二次谐波有了更为广泛的应用. 基于各种调制下的二次谐波, 许多非线性光电器件被设计出来, 有望成为将来高效超薄低阈值非线性器件的基础.
2
4.1.电调控二次谐波
-->

4.1.电调控二次谐波

电调控二次谐波(electric field-induced 2nd-harmonic generation, EFISHG), 作为一种最为广泛的调制手段之前在各种纳米材料与结构中有着许多先例[61-63]. 电调控二次谐波最早在1962年由方解石上施加一个很强的电场来打破其反演对称性被观测到[64]. 电调控二次谐波的基本原理可以认为是电场与三阶非线性系数的相互作用, 即产生的有效的二阶非线性系数为[65]
$\begin{split}&\chi _{ijk}^{(2)}(2\omega ;\omega ,\omega ,0) \\=&\; \chi _{ijk}^{(2)}(2\omega ;\omega ,\omega ) + \chi _{ijkl}^{(3)}(2\omega ;\omega ,\omega ,0){F_1},\end{split}$
(18)式右侧第一项$\chi _{ijk}^{(2)}(2\omega ;\omega , \omega )$是材料本征的二阶非线性系数, 它对应于传统的二次谐波过程, 第二项$\chi _{ijkl}^{(3)} (2\omega ; \omega , \omega , 0){F_1}$对应于电场产生的二阶非线性系数. 有效二阶非线性系数$\chi _{ijk}^{(2)}(2\omega ;\omega , \omega , 0)$中的0代表直流电场ω = 0. 因此想要通过电场调制材料的二次谐波, 需要材料本身拥有足够大的三阶非线性系数且能够承受足够大的电压.
在二维材料中一个有趣的想法是能否通过施加电场打破2H相两层材料的反演对称性产生二次谐波. 这个想法随后便由Yu等[66]以及Klein等[67]实现. 在2015年和2017年Yu等以及Klein等分别通过施加垂直电场在二层WSe2以及MoS2中成功调制出了二次谐波信号. Klein等的器件结构如图6(a)所示, 双层的二硫化钼被夹在290 nm的二氧化硅以及20 nm三氧化二铝的介电层之间, 然后在顶部的钛/金电极与底部的n掺杂硅上施加垂直电场, 整个器件没有电流产生避免烧坏样品. 首先在较低–20 V的电压下, Klein等在MoS2 C激子共振的能量附近E = 2.75 eV, 将天然存在反演对称性的双层MoS2调制出了二次谐波信号, 并且产生的二次谐波在偏离C激子的共振位置后有一个量级的衰弱, 这个现象可以由激子的共振效应解释. 接下来他们将调制的二次谐波同时表征为电压(–120 V ≤ Vg ≤ 120 V)与激发波长(Eω～1.25—1.47 eV)的函数(图6(b)), 此时他们发现调制出的最大二次谐波出现在电压为120 V, 能量为E2ω – Ec = –0.26 eV偏离C激子共振的位置, 且最大调制出二次谐波信号为–20 V偏压下的60倍. 对于这种共振的偏移, Klein等计算了外加电场对MoS2波函数的影响. 当正好与C激子发生共振时, 外加电场对于MoS2布里渊区的Γ以及M点只有非常微弱的影响, 而当激发偏移C激子能量一定值时, 布里渊区的Σ点发生了明显的变化, 这是由于相对于C激子共振的情况, 外加电场使得其原子轨道耦合布洛赫态, 因此布里渊区展现出了更强的对称性打破[67]. 类似的器件结构以及结果由Yu等在双层2H相的WSe2中获得. 它们在正负40 V的垂直外加电场下将双层的WSe2成功调制出了二次谐波信号, 但调制出的信号相比单层低了2个数量级. 对于调制的机理, 与Klein等不同, Yu等认为是电荷导致的二次谐波(charge induced second harmonic generation, CHISHG), 并且他们用键电荷模型加以解释[66]. 在这个模型中, 双层WSe2中的硒离子与钨离子由各自的键bn相连接, 它们的键电荷qn相对于键中心的移动导致了二阶键超极化率βn(2), 而所有二阶超极化率的叠加导致了整体的二阶非线性极化率χ(2). 如果考虑在单层的WSe2是由顶部和底部的硒原子连接中间三个相同的钨原子, 施加向下的垂直电场后, 对于总的六个键都会导致键电荷q1—3向上移动. 但是对于单层中下半层的超极化率$ \beta_{1—3}^{(2)} $将会被削弱, 因为键电荷q1—3会向中间的钨离子移动, 而上半层的键电荷q4—6会向硒离子移动, 因此使上半层的超极化率$ \beta_{4—6}^{(2)} $增强. 所以, 总的二阶非线性极化率χ(2)不变, 而直流电场下EFISHG理论对单层WSe2不存在调控, 因此不是EFISHG理论使得双层WSe2产生了二次谐波信号. 在Yu等的CHISHG理论中, 当垂直电场Vg的强度超过阈值时, 钨的$5{{\rm{d}}_{{x^2} - {y^2}, xy}}$道上将形成空穴收集层, 并且它将作为屏蔽电荷层阻止电场进一步对穿透. 微观上, 屏蔽的电场Vg与键电荷qn相互作用, 使得单层中底部半层的键电荷q1—3朝着中间的钨原子移动, 而对于上半层的键电荷由于空穴收集层的屏蔽效应将不受到影响, 上下半层的超极化率βn(2)不再相互抵消, 因此整个单层的二阶非线性极化率χ(2)将受到电场调控. 对于两层的WSe2而言, 理论上还是会由于对称的屏蔽效应而抵消补偿. 但是实际上由于带边态的密度太大, 整个空间的静电荷会局域在底部的钨原子面上. 简单来说顶层钨原子面的带电量仅为底部的4%, 因此双层WSe2的底部单层依然有很大一部分不受抵消, 因此二阶非线性系数χ(2)不为0, 它正比于垂直电场与阈值电压差的绝对值$\left| {{V_{\rm g}}} \right. - \left. {{V_{\rm t}}} \right|$.
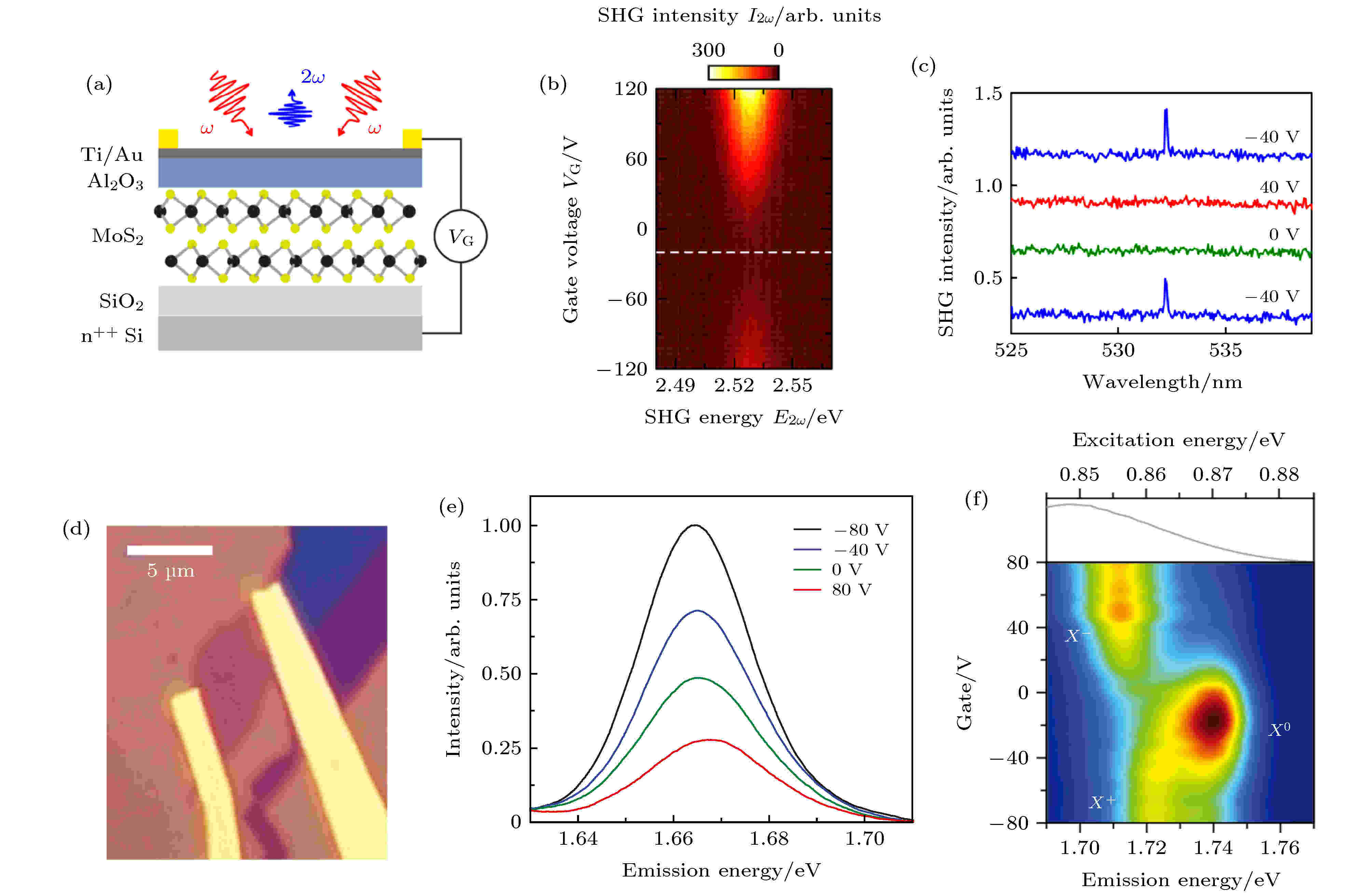图 6 电调控二次谐波　(a) 双层MoS2微电容器件原理图[67]; (b) 双层MoS2的二次谐波作为施加电压以及发射波长的函数[67]; (c) 双层WSe2中背栅调控可逆的二次谐波[66]; (d) 单层WSe2晶体管的光学图片[59]; (e) 单层WSe2二次谐波在共振激发下随选定栅压的变化[59]; (f) 单层WSe2二次谐波作为栅压和激发能量函数的强度图[59]
Figure6. Electric field modulated SHG: (a) Schematic illustration of bilayer MoS2 microcapacitor device[67]; (b) bilayer MoS2 SHG intensity as the function of applied voltage and SHG emission energy[67]; (c) reversible SHG induced by back gate in bilayer WSe2[66]; (d) optical image of monolayer WSe2 transistor[59]; (e) exciton resonant monolayer WSe2 SHG spectra at selected gate voltage[59]; (f) monolayer WSe2 SHG intensity as the function of applied gate voltage and SHG emission energy[59].

除了将天然反演对称的双层TMDCs调制出二次谐波信号外, 另一类重要的工作是电调控单层的材料. 单层的TMDCs受限于较小的光物质相互作用截面, 只能产生有限的二阶非线性极化率. 电调控二维材料的二次谐波将对集成的二维非线性器件产生巨大的影响. 华盛顿大学的Seyler等[59]在2015年报道了单层WSe2室温下四倍, 低温下接近一个量级的二次谐波电调制增强, 并且他们将这种二次谐波极大的可调性解释为在激子共振附近带电载流子掺杂的结果. 图6(d)为其器件结构图, 机械剥离在300 nm二氧化硅/硅上的单层WSe2上通过电子束曝光与热蒸发做了钒/金电极, 同样为了避免烧坏器件, 此处通过顶部的金电极与背栅的n掺杂硅形成垂直电场. 室温下, Seyler等首先在WSe2的A激子(Eg = 1.66 eV)共振能量附近发现, 最大的二次谐波调制出现在激发能量正好与A激子产生共振的情况下, 并且正向与反向的偏压会分别抑制与增强WSe2的二次谐波信号. 此时最大的调制范围约为不加偏压时的4倍 (图6(e)), 而激发波长偏离A激子共振仅30 meV后将不会出现任何调制作用. 这种极大依赖激发波长且与激子共振密切相关的现象使Seyler等进一步进行了低温的实验. 在低温下他们将激发光的能量从0.85 eV到0.875 eV进行了扫描, 在偏压为–40 V时1.74 eV处出现一个二次谐波信号峰, 而当正向增加偏压信号峰消失直到更高的正向偏压时1.71 eV低能量处出现另一个二次谐波信号峰. 这种二次谐波调制信号随激发能量以及偏压的变化本质上其实是因为垂直电场造成了WSe2中的中性激子X0的掺杂, 使其在高的正向偏压下吸收负电荷形成带负电的三激子X–, 而在高的负向偏压下吸引正电荷形成带正电的三激子X+[15]. 单层的WSe2被夹在n掺杂硅与金电极之间像被至于一个平行板电容器之间, 垂直电场虽然不会产生电流但是会额外引入正负电荷, 正负电荷在电场的作用下被拉开吸附于平行板电容器的上下两侧也就造成了材料的掺杂. 又因为不同带电激子和中性激子的发射波长不同(一般来说中性激子的发射波长更蓝), 因此激子共振导致的WSe2二次谐波出射呈现出对于电场以及激发波长特别敏感的特性. 不同激子种类对于二维材料二次谐波强的可调性有着非常重要的意义.
2
4.2.应变调控二次谐波
-->

4.2.应变调控二次谐波

应变调控在纳米材料的研究中也是广泛存在的, 它通常能够改善纳米材料的光电性能. 比如现代的硅基场效应晶体管中, 应变被用来减小载流子的有效质量并提高载流子迁移率[68]; 同时应变还能使某些间接带隙的半导体材料变为直接带隙, 极大地提高了它们的辐射符合效率[69]. 在二维TMDCs中, 较好的韧性使它们成为了应变场调控天然的备选材料, 二维材料能够承受最大约10%的应变[70,71], 相比硅的应变阈值约1.5%高了6倍以上. 扭曲或折叠二维TMDCs已经取得了很多光电效应上的调制, 比如使层状二维半导体中激子形成激子凝聚态[72], 或产生单光子出射[72,73]. 在非线性光学的领域中, 应变调制二次谐波的历史已经有数十年之久, 在块体中心对称的硅中, 应变曾被用来打破其中心反演对称产生二次谐波[74]. 在层状的二维材料中, 由于二次谐波对于应变非常敏感, 因此应变调制二维材料二次谐波是非常有前景的.
2017年Liang等[26]报道通过单轴的微弱拉伸应变, 实现了对二硒化钼二次谐波偏振的调控. 在Liang等的实验中, 化学气相沉积生长的三角形单层二硒化钼首先通过湿法转移到了可弯曲的丙烯酸(云母)衬底上, 在施加微弱单轴应变的情况下, 二硒化钼的二次谐波强度发生迅速衰减, 这表明二次谐波对于应变的影响非常敏感. 随后, Liang等在单层二硒化钼的扶手椅以及Z字形方向分别施加单轴应变, 并通过同时旋转激发光与检偏器记录不同应变大小与二次谐波的偏振情况. 理论上, 在没有应变作用的情况下, 总的二次谐波强度等于平行与垂直的二次谐波偏振的叠加, 即ISHG = ISHG//+ ISHG⊥, 与激发光和样品的扶手椅方向无关, 是一个定值, 并且它没有极化方向, 因此极化图是一个圆(图7(a)下图, 橙色). 但是当在二硒化钼的扶手椅方向上施加单轴应变后, 偏振的二次谐波极化图出现了扭曲的现象, 平行偏振时施加应变方向的花瓣明显极化强度减小并随着应变增加而越发减弱, 总的二次谐波也不再是个定值而在施加应变的方向极化图内陷(图7(a)下图, 紫色). 施加应变后的这种变化可以由二硒化钼各向异性的打破来解释. 在扶手椅方向施加单轴应变后, 因为C3对称轴的消失, 二硒化钼的晶体对称性由三倍旋转对称的D3h变成了C2v, 且它的二阶非线性矩阵也发生了变化, 这使得偏振的二次谐波强度不再遵循公式${I_{{\rm{SHG}}/\!/}} = {\left| {{d_{22}}\cos 3\theta } \right|^2}$, 而是[26]由
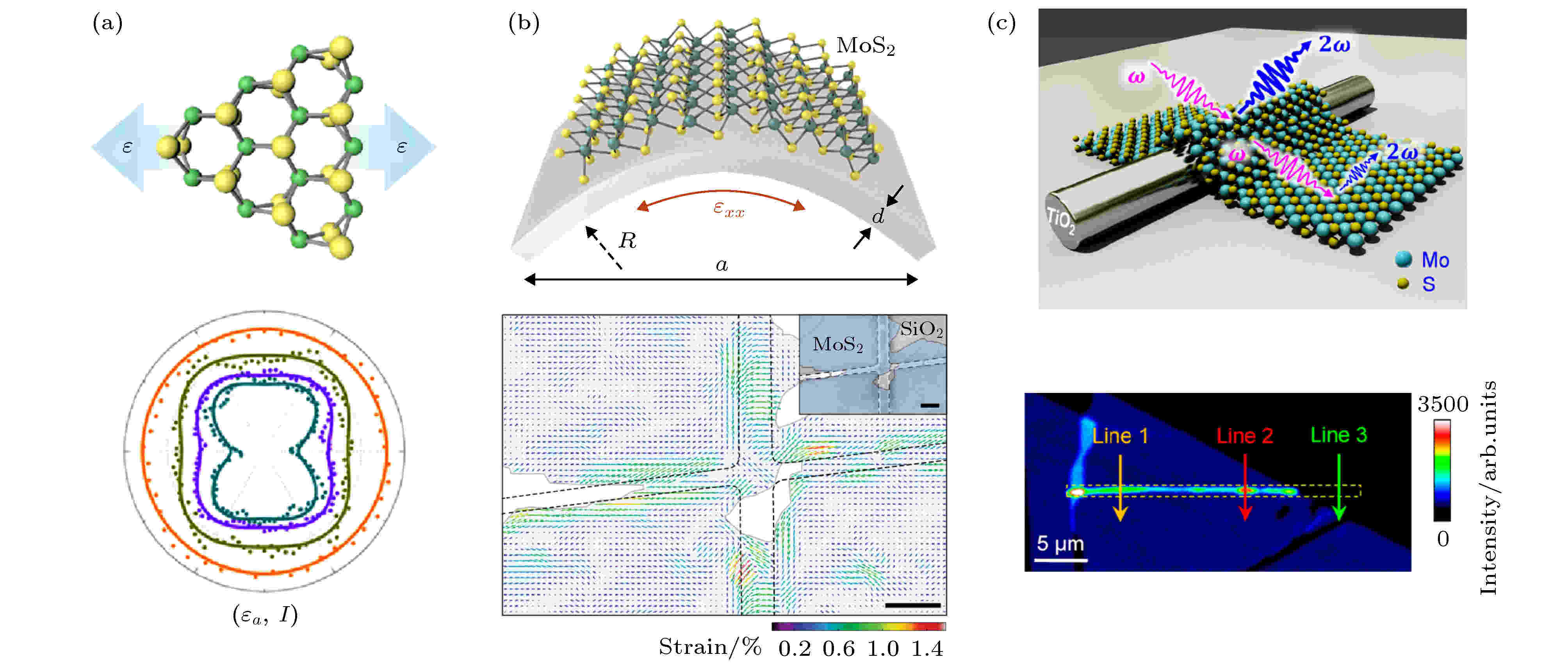图 7 应变调控二次谐波　(a)轴向拉升应变导致MoSe2二次谐波偏振变化[26]; (b)通过二次谐波表征MoS2的全应变场[75]; (c) TiO2/MoS2异质结结区处应变提高MoS2二次谐波[77]
Figure7. Strain modulated SHG: (a) MoSe2 SHG polarization changed by uniaxial tensile strain[26]; (b) uniaxial strain map of MoS2 monolayer flake[75]; (c) schematic illustration (up) and SHG mapping (down) of TiO2/MoS2 structure[77].

$\begin{split}{I_{/\!/}}\left( {{C_{2v}}} \right) =\;& \Big| {d_{22}}^{(D_{3h})}\big[ \cos 3\theta + \varepsilon_a\big( {{a_1}{\cos }^3}\theta \\&- {b_1}{{\sin }^3}\theta \cos \theta - 2{c_1}{{\sin }^3}\theta \cos \theta \big) \big] \Big|^2\end{split}$
确定, 其中a1, b1, c1是由应变引入的二硒化钼二阶非线性矩阵的变化, εa是指施加在扶手椅方向上的应变. 因此, 基于二次谐波偏振对应变的敏感变化, 使得通过二次谐波监控微弱应变成为可能.
2018年, Mennel等[75]在此基础之上, 借用了Lyubchanskii等[76]提出的光弹性效应张量理论, 将机械剥离二维材料的应变场张量成像精确到了衍射极限. 在Mennel等的理论中, 应变与二阶非线性极化率可以由光弹张量联系起来[75]:
$\chi _{ijk}^{(2)} = \chi _{ijk}^{(2,0)} + {{{P}}_{ijklm}}{{{u}}_{lm}},$
其中, $\chi _{ijk}^{(2, 0)}$是材料自身用于产生二次谐波的二阶非线性极化率; ${{{P}}_{ijklm}}$光弹张量, 它将应变张量${{{u}}_{lm}}$转变成了非线性极化率的贡献. 在入射电场与收集二次谐波平行的情况下, 平行偏振的二次谐波可以表达为
${I_{//}}(2\omega ) \propto \dfrac{1}{4}{[(A\cos 3\phi ) + B\cos (2\theta + \phi )]^2},$
式中, A = (1－ν)(p1 + p2)(εxx + εyy) + 2χ0, 而B = (1 + ν)(p1－p2)(εxx－εyy), 其中p1和p2是光弹参数, εxx εyy是基本的应变, θ是基本应变取向, ?是偏振角(即入射电场方向与二维材料扶手椅方向的夹角), χ0是不加任何应变下的二阶非线性极化率. 根据(20)式, 计算出了光弹张量就能通过二次谐波的测试反过来计算施加在材料上的应变场. 因此, 在通过单层MoS2上施加不同方向的单轴应变场并检测二次谐波偏振, Mennel等得到了光弹张量的大小并最终通过计算多个角度的二次谐波偏振成像出单层MoS2的应变场分部, 其分辨率达入射光的衍射极限为280 nm (图7(b)).
2019年, Li等[77]报道了将机械剥离的MoS2与二氧化钛(TiO2)纳米线相结合, 在二维/一维的体系中通过不同取向的自发应变实现了对MoS2二次谐波偏振的调控. 在二次谐波强度成像的表征中, MoS2/TiO2异质结的区域比单层MoS2不均匀的增强了十倍, 而纯TiO2区域却不会产生任何信号. 因此这种异质结区域二次谐波信号的增强并不是来源于二氧化钛的直接贡献. 通过时域有限差分模拟计算, Li等确定顶层的MoS2与纳米线之间贴合的区域对入射电场产生极大的限域作用, 这是由于TiO2在可见波段是一种高反射系数低损耗的材料, 因此异质结区域的二次谐波强度将被大大提高. 随后纳米线长轴与MoS2扶手椅方向呈不同夹角θ的异质结被制备出来, 并且偏振的二次谐波表征发现异质结区域的极化图不在表现出6倍的旋转对称性图样, 而是与夹角θ相关, 证明异质结的二次谐波可以被方向性的调制. Li等通过二维材料应变场来解释这一现象[77]:
$\begin{split}I_{{\rm{Mo}}{{\rm{S}}_2}/{\rm{NW}}}^{{\rm{SHG}}} =& \left[ {A\cos 3( {\varphi + {\varphi _0}}) + B{{\cos }^3}({\varphi + {\varphi _0}}) } \right.\\&{{-\left. {C{{\sin }^3} (\varphi \!+\! {\varphi _0})\cos (\varphi \!+\! \varphi _0)} \right]}^2} \!+\! {I_0},\end{split}$
其中, φ0是初始MoS2扶手椅方向与入射光方向的夹角; φ是测试时样品旋转的角度; A, B和C是根据异质结结构决定的三个张量元, 它们都是常数. (22)式中, 第一项代表MoS2晶体结构导致的二次谐波, 而后两项是由纳米线产生的应变场造成的二次谐波, 它将影响整体异质结的二次谐波偏振. 通过对比异质结区域与纯的单层MoS2二次谐波偏振, 不同取向的应变场对于MoS2二次谐波的提高也被计算出来.
2
4.3.其他调制方式
-->

4.3.其他调制方式

除了上述介绍的在二维材料中常见的调制方式, 近年来诸如周期性阵列结构以及超表面[78]等特殊结构可以调控入射光的相位[79,80]从而控制二维材料二次谐波的出射. 这些新型的调制方式与调制结果开拓了集成非线性光电器件新的领域.
2019年, Busschaert等[81]报道通过结合MoS2与周期性含有相位的表面等离激元阵列, 实现了方向可控的二次谐波出射. 在Busschaert等的实验中, 周期性的阵列由电子束曝光制作的金纳米天线组成, 通过调整金纳米棒的长度, 可以控制局域表面等离子体共振与激发光相匹配, 因此提高MoS2/阵列二次谐波的发射效率. 特别地, 通过控制纳米天线的长度及距离, 带有相位的阵列结构得以实现, 它由阵列因子决定[81]:
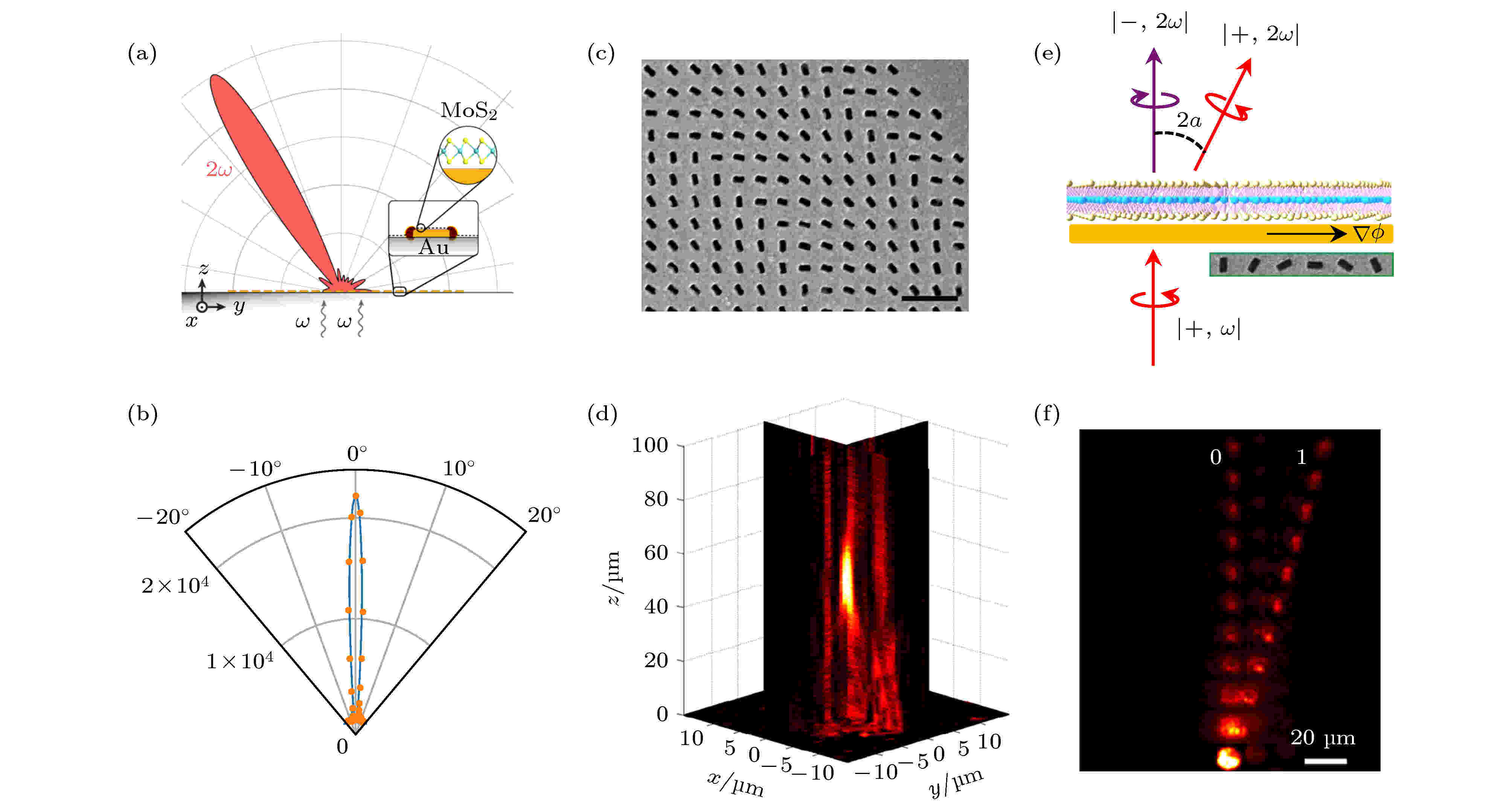$\begin{split}AF\left( {{\phi _x},{\phi _y}} \right) =\;&\dfrac{1}{{{M^2}}}\Bigg| \dfrac{{\sin 0.5M\left( {kd\sin {\phi _x} + {\delta _x}} \right)}}{{\sin 0.5\left( {kd\sin {\phi _x} + {\delta _x}} \right)}}\\& \times\dfrac{{\sin 0.5M\left( {kd\sin {\phi _y} + {\delta _y}} \right)}}{{\sin 0.5\left( {kd\sin {\phi _y} + {\delta _y}} \right)}} \Bigg|^2,\end{split}$
式中, M是每一行(列)的天线数目; d是天线间的距离; k是玻璃衬底上二次谐波出射的波矢, k = 2πnglass/λSH, 其中nglass = 1.55; ?x和?y是出射角度; δx和δy是纳米天线x和y方向上的相位梯度. 总的来说, 大面积的纳米天线阵列可以产生一个带有梯度的二次谐波辐射场, 而相位梯度的控制可以通过设计δx以及δy完成. 图8(b)是Busschaert等在相位δx = δy = 0时的实验(散点)和模拟(连线)的结果, 可以看出它们非常符合.
图 8 超表面调控二次谐波　(a)控制纳米天线相位梯度导向二次谐波出射方向[81]; (b) 相位δx = δy = 0时MoS2二次谐波出射在0°[81]; (c) 周期性的矩形金小孔构成的超表面结构[82]; (d)超表面/WS2构成的超透镜对二次谐波在传播方向上形成聚焦效果[82]; (e)金超表面导向二阶谷光子的原理图[79]; (f)实际的二阶光场变化, 0和1代表强度等级[79]
Figure8. Metasurfaces modulated SHG: (a) Schematic illustration of a MoS2-gold phased array antenna steering SHG emission[81]; (b) polar plot of the calculated (line) and measured (points) SH pattern along the intensity maximum when phase delay δx = δy = 0[81]; (c) the SEM image of the fabricated gold metasurface with rectangular nanoholes of different orientation[82]; (d) the experimental results of SHG focusing by using the hybrid metasurfaces[82]; (e) schematic representations of steering second-harmonic waves on RCP pumping with monolayer WS2[79]; (f) evolution of the light field for the case shown in (c), “0” and “1” label the intensity order[79].

2018年, 华中科技大学的Chen等[82]结合表面等离激元超表面和WS2构成了超透镜, 实现了对二次谐波在出射方向上的聚焦. 超表面上存在不同方向的矩形小孔, 它们的长轴与实验室坐标x轴的夹角定义为θ. 根据理论, 左圆(右圆)偏振的基频光通过超表面上的矩形小孔时, 带有右圆(左圆)偏振的基频光将会被延迟2θ个相位同时保持原有的振幅. 当基频光继续激发超表面上的WS2后, 因为产生的二次谐波是二阶非线性光学过程, 相位延迟将会变成4θ. 基于上述超表面调控入射光相位的理论, Chen等制备了含特殊变化角度θ的超表面, 并将其设计成了超透镜. 同普通的光学透镜类似, 在满足了相位φ(x, y)条件[82]:
$\varphi (x,y) = 2\pi \left( {f - \sqrt {{x^2} + {y^2} + {f^2}} } \right)/\lambda + 2n\pi $
的情况下, 超透镜能够实现对入射光的聚焦. 其中λ是激发光波长, 实验中设定为405 nm对应于产生的二次谐波波长, f是透镜的焦距, 实验中设为50 μm. 相位条件2θ(x, y) (2θ(x, y) = φ(x, y)/2)则通过模拟获得. 最终在实验上入射光通过超表面激发WS2后, 在传播方向z上50 μm处聚焦的的二次谐波被观测到(图8(d)). 这种在可见光波段通过超表面调控二维材料非线性的方法在超表面的研究中开创了先例并且为全光学产生漩涡光束提供了可能.
超表面调控入射光的相位能力结合二维TMDCs双光子能谷选择效应赋予了研究者操纵能谷出射光电子的可能. 2019年新加坡国立大学的Hu等[79]报道了通过金属超表面可以控制和导向WS2的二阶非线性谷光子. 图8(e)是他们实验的简化示意图, 由聚焦离子束刻蚀形成的金超表面上有几百纳米的矩形小孔呈一定规则周期性排列, 激发光通过超表面后不但能形成表面等离激元效应限域基频电场, 同时还能被周期性排列的小孔导向形成Pancharantnam-Berry相位梯度, 因此可以将非线性谷光子导向自由空间. 理论上, 对于右圆偏振(right circularly polarized, RCP)的入射光($\left| { + , \omega } \right\rangle $)经过金的超表面将会被分成两部分: 没有任何几何相位残余的右圆偏振光以及带有几何相位ei2θ的左圆偏振(left circularly polarized, LCP)光($\left| { - , \omega } \right\rangle $). 在二次谐波的过程中, 这两个分量将会根据第3节提到的双光子选择定则变化: 来自+K谷的二阶右圆偏振光子将会拥有两倍的几何相位ei4θ, 而来自－K谷的二阶左圆偏振光子将不会拥有任何几何相位. 因此通过设计超表面上矩形小孔的周期性及角度, 可以形成动量匹配并导向二阶谷光子的相位梯度. 图8(f)是Hu等的实验结果图, 带有相位梯度的激发光激发WS2后形成二次谐波并在不同的传播长度形成不同的传播方向. 其中有两阶能够清晰的辨认: 第0阶来自－K谷的垂直偏振光($\left| { - , 2\omega } \right\rangle $)以及第1阶来自K谷的平行偏振光($\left| { + , 2\omega } \right\rangle $).
5.二次谐波信号增强
原位生长相位匹配的二维材料以及外部施加电场、应变场的调制方法在二次谐波的信号增强方面已经展现出了许多成果, 但二维材料一个或几个原子层的厚度、与光相互作用截面小依然在一定程度上限制了它的二次谐波转化效率. 除了通过二维材料结构设计, 也可以利用增强相互作用的局域光场, 得到增强的二次谐波信号. 表面等离激元结构、光子晶体及纳米微腔, 能够限域入射电场产生局域高效的电场增强从而改变二维材料光物质相互作用弱这一劣势. 同时它们还能结合新型材料或者调制工艺, 最终甚至能达到相比单层好几个量级增强的二次谐波效应.
2
5.1.表面等离激元增强二次谐波
-->

5.1.表面等离激元增强二次谐波

表面等离激元效应源于金属的自由电子在入射光场的作用下产生的集体振荡行为, 它分为局域表面等离激元和表面等离极化激元两种[83]. 在近数十年的发展中, 表面等离激元结构已经由纳米颗粒[84]逐渐转变成通过电子束曝光制作的特殊金属纳米周期性结构, 后者将能更好的限域入射光场, 并且已经在提高材料量子效率[85-87]、产生法诺共振[88]和激子-表面等离极化基元强耦合 [89-91]等研究上产生了非常大的突破.
2020年, Han等[92]通过将NPoM (nanoparticle on the mirror)模型构成的表面等离激元纳米腔, 实现了超过300倍的二次谐波增强. 在实验中, 单层的WS2置于银纳米颗粒与银膜之间, 中间通过三氧化二铝作为介电层防止电子转移. 因为银纳米颗粒与银膜可以形成强的电磁场耦合, 因此可以调控其表面等离激元共振(即调整介电层的厚度)与WS2二次谐波发射波长相匹配. 这种经典的NPoM纳米腔模型利用了局域表面等离激元共振产生的电场限域, 使得波长匹配下的纳米腔能极大地提高入射电场强度, 因此提高WS2的二次谐波效率.
除了局域表面等离激元共振, 利用表面等离极化激元也能打破反演对称性, 实现对目标信号的增强. 2018年, Wen等[93]报道通过表面等离激元热电子的注入使机械剥离2H相两层的WSe2产生了二次谐波. 如图9(b)所示, 由电子束曝光与热蒸发制作的金纳米棒周期性阵列选择性的修饰在了部分机械剥离的两层的WSe2上, 构成了表面等离激元/半导体的结构. 同时为了进行对照, 另一组实验中表面等离激元阵列与两层WSe2之间插入了四层的氮化硼作为介电层. 随后, 与表面等离激元共振的800 nm飞秒激光用来激发混合结构的二次谐波. 如图9(b)下图光谱, 两层的二硒化钨几乎测不到二次谐波的信号, 这是由于其存在的反演对称性所致. 最强的二次谐波信号出现在表面等离激元结构与两层WSe2直接接触的结构中, 而插入了四层氮化硼的结构与纯的表面等离激元结构信号差不多比直接接触的结构信号低了一个量级. 造成这种现象的原因在于表面等离激元结构与WSe2直接接触的情况下, 由于热电子转移到半导体中打破了反演对称性, 从而大大提升了两层WSe2的二次谐波; 四层的氮化硼阻碍了热电子的转移, 进而只能测到和表面等离极化基元金属结构相同的信号. 因此相对于局域表面等离激元对入射电场的增强, 此时表面等离极化激元产生注入的热电子是二次谐波增强的主要贡献. 通过表面等离激元激发热电子打破反演对称性能够实现瞬态的二次谐波增强(转移时间约为2 ps), 也为将来瞬态的全光学逻辑电路打下基础.
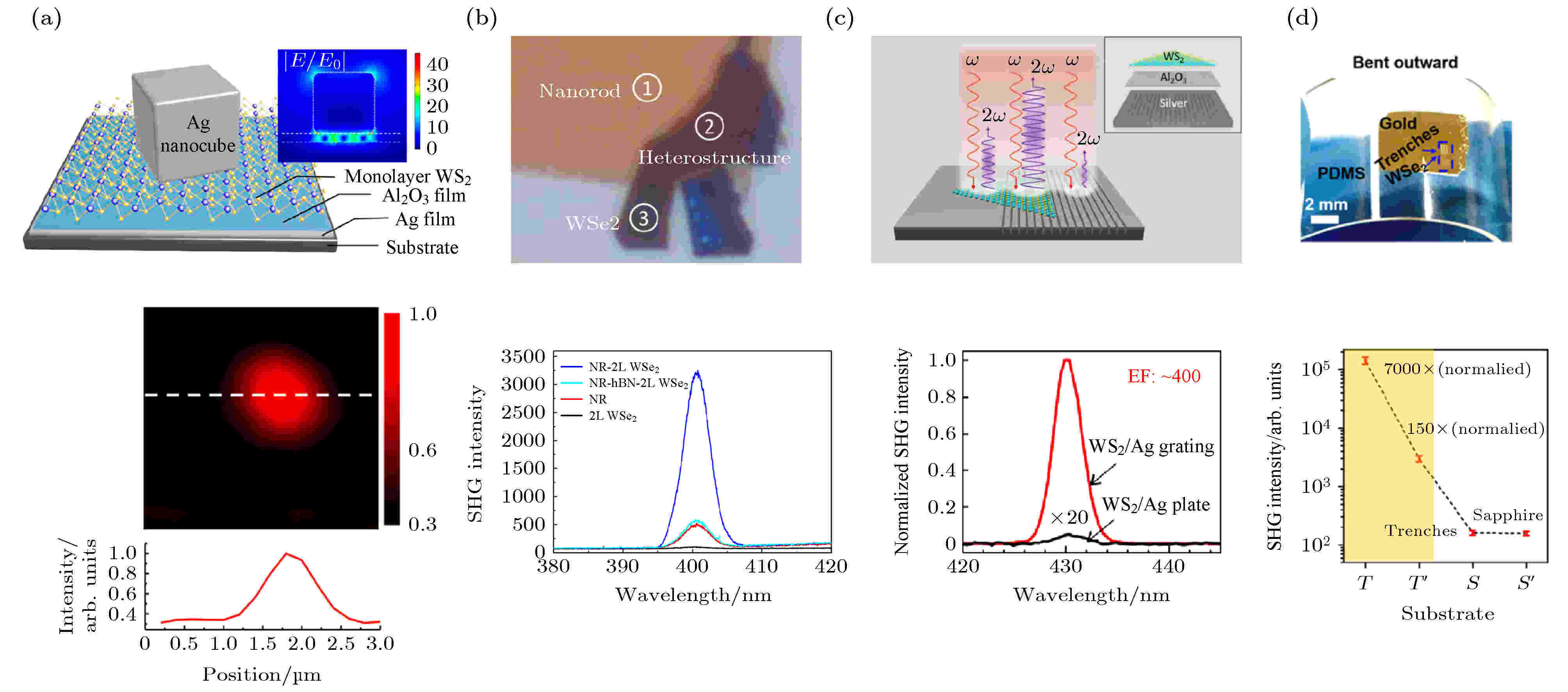图 9 表面等离激元提高二维材料二次谐波　(a) NPoM模型中, 纳米腔对入射电场产生限域作用(上), 单个纳米银颗粒对WS2二次谐波成像的增强(下)[92]; (b)对比不同结构的表面等离激元阵列/半导体二次谐波, 其中123区域分别代表阵列, 两层WSe2/阵列, 与两层WSe2区域[93]; (c) 银纳米栅表面等离激元结构增强WS2二次谐波达400倍[94]; (d) PDMS上表面等离激元阵列对WSe2二次谐波增强三个量级[95]
Figure9. SHG enhancement by plasmonics: (a) Nano cavity strongly confines incident light field (up), and SHG enhancement by Ag nanoparticle in monolayer WS2 (down)[92]; (b) compare of SHG signal in different plasmonic array/semiconductor, where points 1, 2, 3 represent the area of nanorod, nanorod/bilayer WSe2, and bilayer WSe2, respectively[93]; (c) SHG enhancement factor over 400 in monolayer WS2 reached by Ag nanogroove grating[94]; (d) SHG enhancement over 3 orders in monolayer WSe2 by plasmonic structure on PDMS[95].

随着表面等离激元工艺的成熟和对局域表面等离激元共振理解的深入, 更加精细能够更好限域入射电场的结构也被设计出来. 2018年Shi等[94]报道通过结合银纳米栅表面等离激元阵列与化学气相沉积生长的单层WS2, 在C激子共振下得到了最大约400倍的二次谐波增强(图9(c)). 同年Wang等[95]结合单层的WS2与柔性衬底上表面等离激元结构, 实现了超过3个量级的二次谐波增强. 柔性衬底上样品工艺通过模板剥离法 [96]制作而来, 其上具有最小达15 nm沟道的条状表面等离激元结构. 当入射电场的偏振方向与沟道方向垂直时, 入射电场将被极大的限域在沟道处, 而当入射电场的偏振方向与沟道方向平行时, 则不会出现限域效果. Wang等对比在沟道处限域电场时与平整的纯金衬底上二次谐波的变化, 通过调控条状结构的大小使局域表面等离激元与800 nm的激发光共振, 最终获得了沟道处7000倍的二次谐波增强(图9(d)), 并且这种增强效果在向外弯曲柔性衬底达40°、弯曲次数达50次时依然能保持70%.
2
5.2.光学微腔、光子晶体增强二次谐波
-->

5.2.光学微腔、光子晶体增强二次谐波

提高二次谐波转化效率的另一个方法是耦合光学微腔. 光学谐振腔可以限制激光在腔体中来回振荡, 从而增强激光与材料的相互作用光程, 极大地提高器件的光转换效率, 实现器件在低功率下的工作能力[97]. 但是, 一般的光学谐振腔, 如光共振器, 通常被用于实现二维材料器件的线性光学功能, 如荧光增强等[98,99], 其并不适用于二次谐波激发. 原因是这种光学谐振腔只能实现基频激光共振, 并不能实现二次谐波的同步共振. 基于这个思路, Yi等[100]设计了双共振微腔倍频器件. 这种器件基于一个电压控制的腔长可调型法布里帕罗微腔. 微腔主要由分布式布拉格反射镜、MoS2和生长在氮化硅薄膜上的电压驱动的银镜构成(图10(a)). 当调控法布里帕罗微腔的腔长至共振时, 入射电场与二次谐波发射的电场能同时被增强. 通过电磁场计算, Yi等设计了特定的氮化硅和氧化物层数的布拉格反射镜和腔体结构, 以获得最大的电磁场增强效应. 实验结果表明, 腔体共振增强后, 器件的二次谐波输出光强提高了3000倍.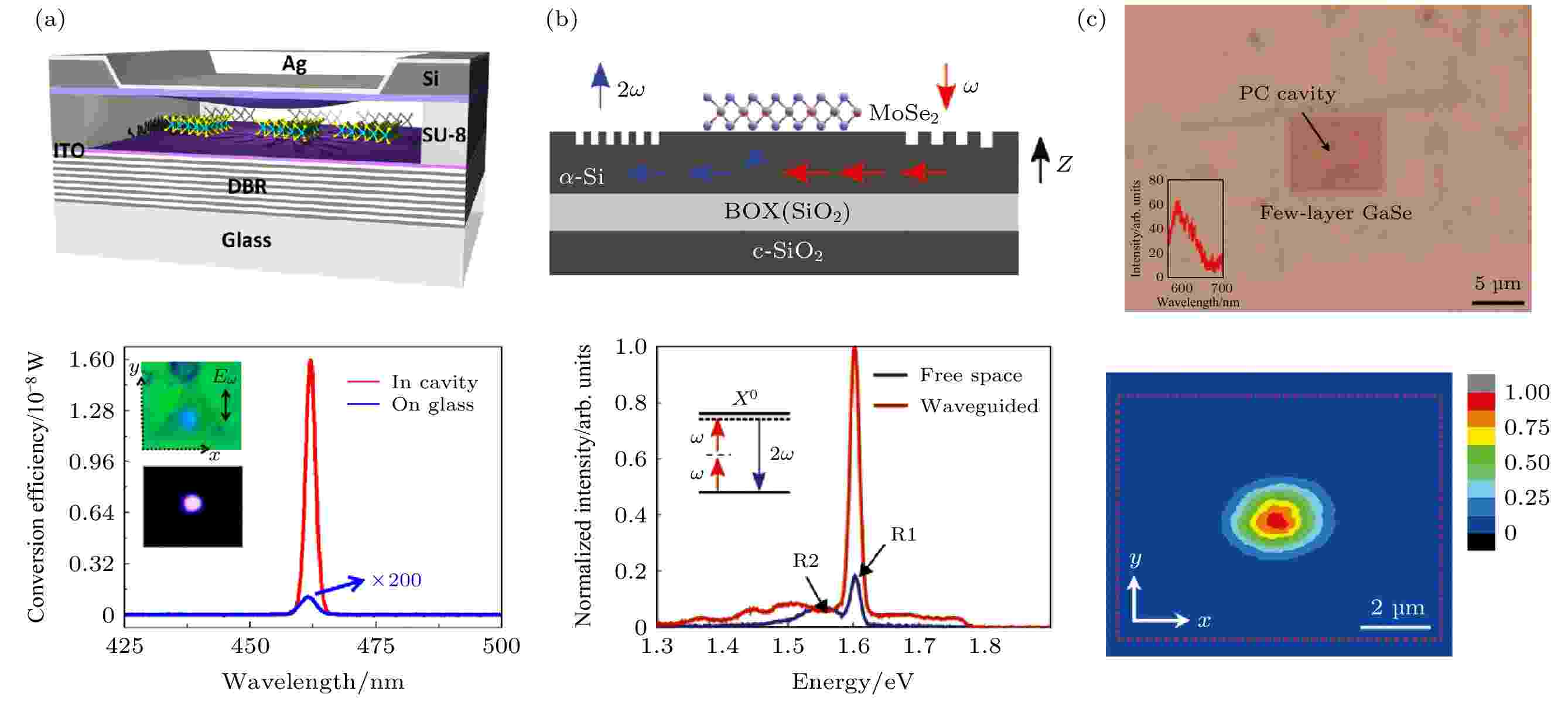
图 10 微腔、光子晶体增强二维材料二次谐波　(a)双共振法帕纳米微腔增强二次谐波[100]; (b)硅波导增强二硒化钼二次谐波[105]; (c)连续激光激发硒化镓/硅光子晶体结构二次谐波[106]
Figure10. SHG enhancement by micro cavity and photonic crystal: (a) Enhancement of SHG from monolayer MoS2 in a doubly resonant on-chip optical cavity[100]; (b) enhancement of SHG by silicon waveguide[105]; (c) CW excitation of SHG from GaSe/photonic crystal[106].

光子晶体是由不同折射率的介质周期性排列而成的人工微结构, 它能够调制入射光(电磁波)的传播行为. 光子晶体的概念最早在1987 年由Yablonovitch[101]在一篇研究自发辐射的论文中提出, 它也可以看成是一种特殊结构的纳米微腔. 当电磁波入射到光子晶体表面后, 由于光子晶体的周期性结构与入射波长近似, 所以会使入射光在光子晶体内部反复反射形成类似“能带”的光学结构, 最终能够限域特定波长的光而使其他波长的光通过. 光子晶体在调制电子-光子相互作用[102]、低阈值激光器[103]、量子信息处理[104]等许多物理和工程领域取得了广泛的应用. 二维TMDCs与接触表面存在很强的范德瓦耳斯相互作用, 因此结合光子晶体有着天然的优势, 同时由于其超薄的特点, 二维TMDCs不会干扰光子晶体中波导的传播或其他功能的实现.
2017 年, Chen等[105]报道了集成单层的二硒化钼与硅波导, 实现了二次谐波出射的增强. 实验的结构原理图(侧视图)如图10(b)所示, 在圆形氮化非晶硅/二氧化硅的表面有被刻成光栅状的结构, 不同大小及周期性的光栅分居表面两侧并分别被用来耦合自由空间的入射电场以及波导产生的倍频场进入自由空间. 在圆形光栅结构中间的波导区域是机械剥离的单层二硒化钼, 波导形成的隐失场(evanescent field)将激发二硒化钼产生二次谐波. 在这个结构中, 为了能够更好地耦合自由空间的入射电场, 氮化非晶硅的反射系数、入射光的射束轮廓、入射角度、光栅的刻蚀深度及周期性首先通过理论计算得到了优化. 在非线性光学测试中, 1550 nm的飞秒激光用来激发二次谐波, 它的双光子能量与二硒化钼的激子产生共振, 这将极大地提高二次谐波过程的效率. 当激发光聚焦在光栅区域时, 对比直接聚焦在单层二硒化钼, 产生了约5倍的二次谐波增强. 硅波导增强二次谐波的原理是因为相比于单层的二维材料与激发光有限的作用面积, 这种特殊结构使得整个二硒化钼都与硅波导相互作用, 极大地拓宽了产生二次谐波的范围, 同时它也为将来二维半导体材料与硅基结构相结合打下了基础.
2018年, Gan等[106]报道通过低能量的连续激光激发了二维硒化镓/硅光子晶体结构的二次谐波. 由于纳米材料非线性系数较小, 非线性过程效率低, 因此通常需要脉冲激光的峰值能量才能激发产生有效的二次谐波. 二维硒化镓自身有着超过单层MoS2一到两个量级的二阶非线性系数[107], 这使得它成为非常优秀的非线性材料, 同时确保与纳米腔隐失场有效的相互作用. 在硒化镓/硅光子晶体结构中, 光子晶体纳米腔被设计成非对称小孔的基础上又人为引入了适量缺陷, 这将极大地耦合入射光进入纳米腔并且在垂直方向上提高辐射效率[108]. 这样设计的纳米腔品质因数Q接近2000, 共振激发时二阶非线性过程的增强正比于$ Q^2 $, 因此即使当0.1 mW的低能量连续激光垂直入射光子晶体时, 纳米腔模共振的隐失场也能有效地激发硒化镓的二次谐波. 图10(c)下图是硒化镓/硅光子晶体产生二次谐波的成像, 其中有信号的区域在2.5 μm × 2 μm引入缺陷至非对称小孔的腔体区域, 也证明了光子晶体纳米腔耦合对二次谐波的贡献. 低能量连续激光激发二次谐波的实现极大地拓宽了二维材料非线性光学的应用领域, 为连续激光频率转换器, 上转换探测器的应用提供了可能.
6.总结与展望
非线性光学是光学领域中一个非常重要的研究方向, 非线性光学的发展对于现代社会的技术进步有着至关重要的作用. 以二维TMDCs为代表的二维半导体材料的兴起带来了对二维层状材料非线性光学特别是二次谐波的研究热潮. 本文从材料到应用的角度总结了二维材料二次谐波的一些相关工作, 首先从材料自身的特点介绍了与二次谐波相关的特性, 然后通过电、应变场以及最新的超表面等手段介绍了不同的调制工作, 最后对如何实现二次谐波信号的提高进行了总结.
最近二维TMDCs二次谐波的研究也朝着一些新的方向发展. 比如, Jang等[109]报道, 结合泵浦探测, 他们实现了对机械剥离MoS2瞬态的二次谐波成像, 并且观察到了强的激子-声子耦合现象. 激子的能量会通过非辐射复合传递给声子, 这种激子-声子耦合的现象将通过晶格振荡表现在二次谐波的寿命上: MoS2二次谐波此时存在两个寿命组分, 其中最初的一两个皮秒对应于直接带隙转移的激子动力学过程, 而之后受晶格的影响则会表现出振荡的行为[109]. Lin等[110]报道, 在A激子附近共振激发WSe2时, 他们发现二次谐波光谱的劈裂, 并解释为量子干涉效应. 量子干涉效应是波粒二象性的标志, 当电子转移存在不同路径并且相互作用时, 量子干涉在光谱上常表现为类似法诺共振的非对称曲线. 这些新的研究方向让我们看到了二维材料不同于传统半导体新的特性, 也为发展基于二维材料二次谐波新的应用(如探测系统, 光参量放大系统)提供了可能. 在庞大的二维半导体家族, 找出拥有良好的稳定性、可大面积制备层数可控且拥有非常大的二阶非线性系数的最适合用于非线性光学的材料, 基于此实现面向实际应用的高性能非线性光电器件及集成器件, 可能是今后发展的重要方向.
相关话题/材料 结构 光学 光子 信号
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于二维材料的全光器件
    摘要:近年通信技术的飞跃,对光学设备的紧凑性、响应速度、工作带宽和控制效率提出新的挑战.石墨烯的发现,使得二维材料飞速发展,不断涌现出一系列新材料,如MXene、黑磷、过渡金属硫化物等.这些新型二维材料有着出色的非线性光学效应、强光-物质交互作用、超宽的工作带宽.利用其热光效应、非线性效应并结合光学 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 低维半导体材料在非线性光学领域的研究进展
    摘要:自从第一台红宝石激光器发明以来,研究人员将目光集中到激光这种普通光源达不到的强光上,由此发现了非线性光学材料以及一系列丰富多彩的相关特性—饱和吸收、反饱和吸收和非线性折射等,并将其运用到光电子器件、光开关器件和光通信当中.同时,随着工业生产对于器件集成度需求的提升,以普通三维材料为基础的器件已 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于二维纳米材料可饱和吸收体的中红外超快光纤激光器
    摘要:以石墨烯为代表的二维纳米材料可饱和吸收体以其独特的非线性光学特性被广泛应用于超快光纤激光器.本文总结了近年来二维纳米材料作为可饱和吸收体在中红外超快光纤激光器中的研究发展,介绍了二维纳米材料原子结构、非线性光学特性、可饱和吸收体器件集成方式,及其在中红外超快光纤激光器中的应用,重点阐述了基于黑 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于等离激元纳米结构非线性响应的超快光开关及脉冲激光器
    摘要:非线性光学作为现代光学的一门重要分支,在各个领域都有着重要的研究意义和应用价值.然而,受限于材料固有的非线性极化率和与外来光场的有限作用长度,其非线性光学响应很弱.等离激元纳米结构可以将外来光场束缚在纳米结构周围,在光谱共振局域空间内形成一个巨大的电磁场增强,从而极大地促进光与物质的相互作用, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于二维材料异质结可饱和吸收体的超快激光器
    摘要:可饱和吸收体作为非线性光学行为的物质载体,是获得超快激光的关键材料.基于石墨烯、过渡金属硫化物、拓扑绝缘体、黑磷等二维材料为代表的可饱和吸收体具有不同的光学优点,但仅依赖某一方面光学优势的单一材料,很难避免其应用的局限性.通过异质结结构结合不同二维材料的优势,达到光学互补效应,为制备高性能的新 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • GeSe<sub>2</sub>中强各向异性偏振相关的非线性光学响应
    摘要:二硒化锗(GeSe2)作为一种层状IV-VI族半导体,具有面内各向异性结构及宽能带间隙,表现出了独特的光、电及热学性能.本文利用偏振拉曼光谱和线性吸收谱分别对GeSe2纳米片的晶轴取向和能带特性进行表征,并以此为依据采用微区I扫描系统研究了GeSe2在共振能带附近的光学非线性吸收机制.结果表明 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Ag@SiO<sub>2</sub>耦合结构设计及其对薄膜太阳电池的响应调控
    摘要:Ag@SiO2纳米耦合结构同时具有等离激发和衍射散射特性,可有效调控光波的行进路径和能量分布,在薄膜太阳电池陷光领域极具潜力.本文基于时域有限差分方法和严格耦合波分析,建立三维电磁仿真模型,研究Ag@SiO2耦合结构对非晶硅电池光谱响应的调控机理,通过优化设计,得到高陷光电池器件.结果表明:当 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于结构反转二维光子晶体的拓扑相变及拓扑边界态的构建
    摘要:构建了二维六角蜂窝晶格的两种结构,让散射体和基体材料反转.由于特有的点群对称,该晶格在布里渊区中心具有类比电子体系的p轨道和d轨道.在散射体和基体反转的两种结构中,p轨道和d轨道也直接实现了反转.定量分析了产生轨道反转的原因来自于低频局域共振产生空气带和介质带的反转.通过p轨道和d轨道的宇称特 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 金薄膜衬底上介质-金属核壳结构的光学力调控
    摘要:采用时域有限差分法和麦克斯韦应力张量法,系统研究了金薄膜衬底上介质-金属核壳结构所受的光学力.研究结果表明:由于核壳结构与衬底之间强的等离激元模式杂化效应,其所受的光学力相较于单个核壳结构实现了一个数量级的增强;同时,通过改变激发波长,实现了局域电场分布的调控,以此观察到了核壳结构光学力方向的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 用于光学薛定谔猫态制备的滤波设计与滤波腔腔长测量
    摘要:光学薛定谔猫态不仅是量子力学基本问题的主要研究对象之一,也是连续变量量子信息的重要资源.在其实验制备中,对触发光路进行滤波操作是决定猫态的纯度、产率等重要参数的关键环节.本文介绍实验中的滤波设计以及滤波腔腔长的测量方法.依据设计要求,腔长${l_{{m{FC}}}}$应满足条件$189\; ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.