摘要:二硒化锗(GeSe₂)作为一种层状IV-VI族半导体, 具有面内各向异性结构及宽能带间隙, 表现出了独特的光、电及热学性能. 本文利用偏振拉曼光谱和线性吸收谱分别对GeSe₂纳米片的晶轴取向和能带特性进行表征, 并以此为依据采用微区I扫描系统研究了GeSe₂在共振能带附近的光学非线性吸收机制. 结果表明, GeSe₂中非线性吸收机制为饱和吸收与激发态吸收的叠加, 且对入射光偏振与波长均有强烈的依赖. 近共振激发(450 nm)条件下, 激发态吸收对偏振的依赖程度比较大, 随着入射光偏振的不同, 非线性调制深度可由4.6%变化至9.9%; 而非共振激发(400 nm)时, 该调制深度仅由7.0%变化至9.7%. 同时, 相比于饱和吸收, 激发态吸收的偏振依赖程度受远离共振激发波长的影响而变化更大.
关键词: 各向异性/
激发态吸收/
微区I扫描

English Abstract

全文HTML

--> --> -->

自2004年石墨烯成功问世以来^[1], 以石墨烯为代表的众多二维材料, 例如过渡金属硫族化合物^[2-7]、拓扑绝缘体^[8-12]、黑磷^[13-15]等, 获得了研究者们的大量关注^[16-18]. 其中, 黑磷因其超高的电子迁移率及层厚相关的能带特性, 成为近年来研究的热点材料之一. 具体而言, 10 nm厚的黑磷迁移率可达10³ cm²·V^–1·s^–1, 其带隙可由体材料的0.3 eV增加至单层的2.0 eV^[19]. 除此之外, 黑磷独特的面内各向异性结构也使得它有着与众不同的各向异性的光学、电学响应^[13,20,21]. 然而, 黑磷在空气中的不稳定性及易挥发性, 使其难以进一步被广泛利用. 因此, 亟需找到与黑磷性质相似且稳定的二维材料.
目前, 研究者们主要将目光聚焦于以下两类材料. 第一类为黑磷的等电子体, IV-VI族MX (其中M = Ge, Sn; X = S, Se)型化合物, 如GeS^[22,23]和SnSe^[24]等. 第二类是极少部分特殊的过渡金属硫族化合物, 如ReS₂和ReSe₂等. 它们的光学^[22,25]、振动^[26]、热学^[27,28]和电子传输^[29,30]特性均具有强各向异性的特点, 使其在传感器和电子设备中都具有广阔的应用前景. 但是这两类材料的禁带较窄(<2 eV), 导致工作波段受限. 因此, 非常有必要探索宽禁带的各向异性二维材料.
近年来兴起的各向异性半导体GeSe₂, 由于其具有宽禁带的优势, 获得了众多****的广泛关注^[31]. 华中科技大学翟天佑团队^[32]通过化学气相沉积法成功制备了7 nm (约10层)的GeSe₂纳米片, 并基于该材料的大吸收系数实现了具有高响应度和快速响应的GeSe₂的光电探测器. 中国科学院化学研究所的胡劲松团队^[33]通过机械剥离法得到了3.5 nm (6层)的β相GeSe₂, 其在短波区域表现出高度偏振相关的光电响应, 并且在空气环境中有较好的稳定性. 作为一种典型的IV-VI族化合物, 相比于α相和γ相, β相的GeSe₂是最稳定的. 该相的GeSe₂体态带隙为2.7 eV, 而单层带隙可以达到3 eV. 在光学特性方面, GeSe₂的吸收系数可达10⁴ cm^–1, 光电探测器的开关比可超过10^2[34]; 在电学特性方面, 掺杂后的GeSe₂空穴迁移率可以达到690 cm²·V^–1·s^–1[35], 光电响应度可达2.5 A·W^–1, 且上升沿与下降沿响应时间为0.2 s^[32]. 上述表明了GeSe₂有着优良的线性光学和电学特性, 但截至目前, 该材料的光学非线性特性暂未发现有团队报道过. 而宽带隙各向异性半导体材料一般有着较优良的非线性光学响应^[24]. 基于此, 本文的工作主要围绕GeSe₂的非线性光学效应展开.
本文对GeSe₂纳米片在近共振吸收峰附近的非线性光学吸收特性进行了研究. 首先通过偏振选择的拉曼光谱表征GeSe₂纳米片晶轴取向, 并利用偏振选择的线性吸收谱对其各向异性能带进行表征, 得到其共振波长在450 nm (2.72 eV)附近. 进一步, 为了研究GeSe₂纳米片在共振能带附近的非线性吸收模式, 本文使用偏振可调的微区I扫描系统对其进行测试. 结果表明, GeSe₂中非线性吸收模式为饱和吸收与激发态吸收的叠加吸收状态, 且对入射光偏振与波长均有强烈的依赖, 尤其是激发态吸收. 在450 nm近共振激发时, 随着入射光偏振的不同, 非线性吸收调制深度可由4.6%变化至9.9%, 其动态调制深度(不同偏振激发下的调制深度差)为5.3%; 而在400 nm非共振激发时, 调制深度由7.0%变化至9.7%, 动态调制深度仅2.7%. 其中, 相比于饱和吸收, 激发态吸收模式的偏振依赖程度对波长更为敏感, 这是动态调制深度对波长有较大依赖的主要原因. 本文为GeSe₂纳米片各向异性非线性光学特性的应用打下了理论基础, 为全光开关的实现提供了一种偏振调控的方案.

采用机械剥离的方法制备GeSe₂纳米片样品, 并使用原子力显微镜(atomic force microscope, AFM)对其厚度和粗糙度进行表征. 为确定GeSe₂薄片的晶轴取向, 使用532 nm的低功率连续激光测量其偏振相关拉曼光谱. 使用商用微型光谱仪(Micro, ideaoptics, China)对不同入射偏振下样品的反射谱(R )和透射谱(T )进行测试, 其中控制灯箱在低峰值功率工作, 避免非线性光学效应, 并通过$ A = 1-R-T $计算得到样品的偏振相关线性吸收谱. 两光谱测试过程中, 偏振均以15°为步长旋转, 共旋转180°.
光学非线性吸收实验采用的是偏振可调节的微区I扫描系统. 其中, 由钛宝石激光器(Spectra-Physics, 35 fs, 800 nm, 1 kHz)输出的飞秒激光经过光学参量放大器(TOPAS)转换到实验所需波长(400 nm & 450 nm, 1 kHz), 并通过中性密度滤光片(Thorlabs, NDL-10C-4)连续改变光强, 实现I扫描. 入射激光的偏振方向由半波片和格兰棱镜组合进行调节, 以15°为步长旋转180°. 激光由共焦显微镜(徕卡DM 2700M)以及宽范围波长物镜(Mitutoyo 50×, NA = 0.65, 400—1700 nm)在样品表面聚焦为直径2 μm的光斑. 在信号检测方面, 使用斩波器(Thorlabs, MC2000 B-EC)将光的重复频率调制到500 Hz, 与双通道锁相放大器(Sine Scientific Instrument, OE1022D)组合, 降低测试噪声.

2

-->

3.1.GeSe₂的制备和表征

图1(b)为GeSe₂薄片的AFM图. 可以看出, 样品厚度为88 nm, 表面平整, 符合实验要求. 样品偏振相关的拉曼光谱如图1(c)所示, 在波数为118, 212, 251和307 cm^–1处分别有4个拉曼峰, 对应着β-GeSe₂的典型A_g振动模式^[19,32]. 为了定量研究拉曼强度的偏振相关性, 将四种典型拉曼模式的强度绘成极坐标图, 并且引入经典Placzek模型对结果进行拟合和解释. 拉曼强度可以表示为$I\propto \left|{{e}}_{\mathrm{i}}\cdot \tilde{ R}\cdot {{e}}_{\mathrm{s}}^{\mathrm{T}}\right|$, 其中$ {{e}}_{\mathrm{i}} $和$ {{e}}_{\mathrm{s}}^{\mathrm{T}} $分别表示入射光和散射光的单位电极化矢量, $ \tilde{ R} $是拉曼张量. 在本实验条件中, $ {{e}}_{\mathrm{i}} $和$ {{e}}_{\mathrm{s}} $位于a-b平面, 对于与a方向夹角为θ的入射光, 矢量$ {{e}}_{\mathrm{i}} $可表示为$ (0, \mathrm{c}\mathrm{o}\mathrm{s}\theta , \mathrm{s}\mathrm{i}\mathrm{n}\theta ) $. 在平行收集条件下, 散射光方向$ {{e}}_{\mathrm{s}} $同样表示为$ (0, \mathrm{c}\mathrm{o}\mathrm{s}\theta , \mathrm{s}\mathrm{i}\mathrm{n}\theta ) $. A_g模式的拉曼张量由下式给出:
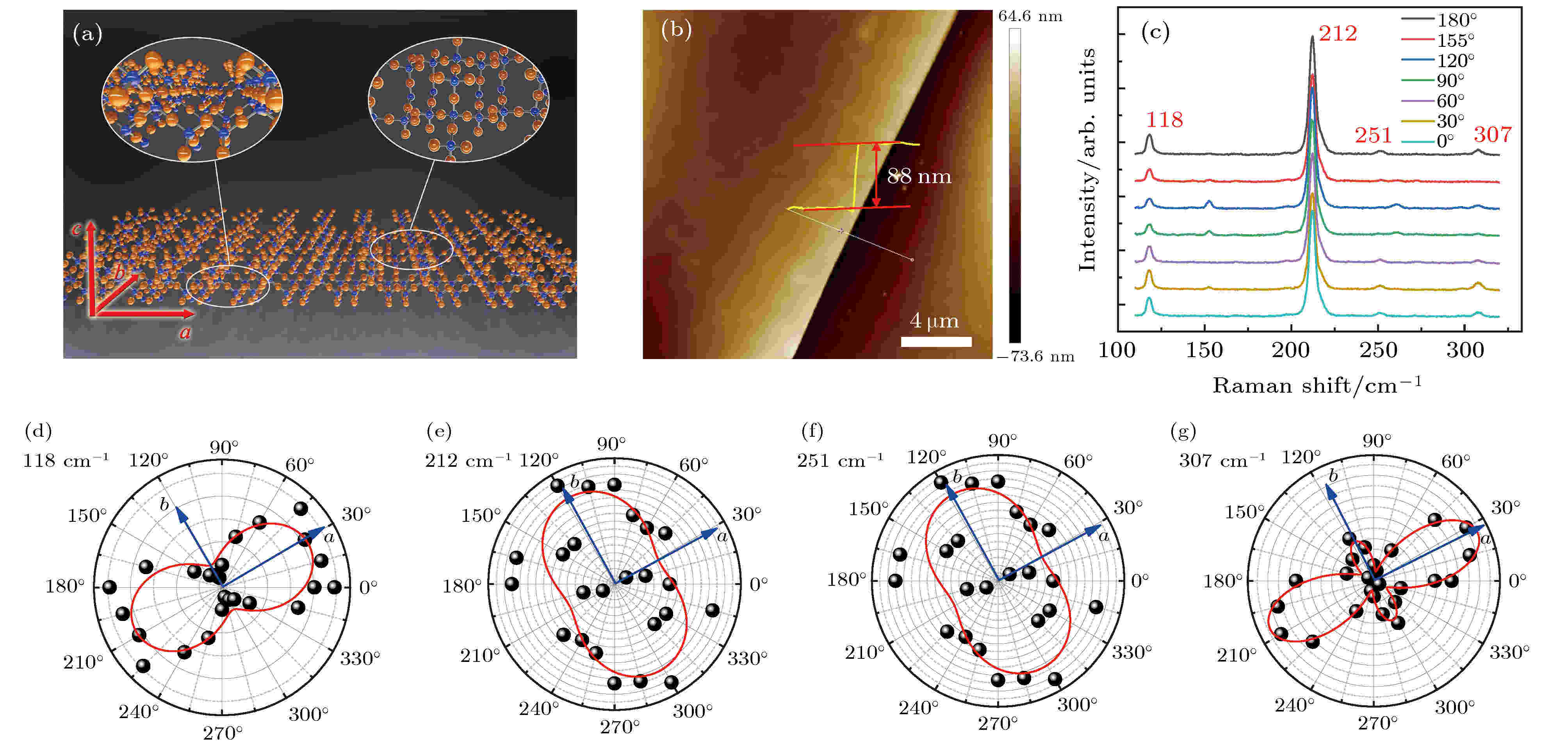图 1 (a) GeSe₂原子结构示意图; (b) 机械剥离GeSe₂纳米片的AFM图, 样品的厚度为88 nm; (c) 偏振选择的拉曼光谱, 其中4个拉曼峰位置分别在118, 212, 251, 307 cm^–1; (d)—(g) 4个拉曼峰强度分别对应的极坐标示意图
Figure1. (a) Schematic diagram of the atomic structure of GeSe₂; (b) AFM image of GeSe₂ flake by mechanical exfoliation. The thickness of the sample is 88 nm; (c) polarization-dependent Raman spectrum. Four Raman peak positions are at 118, 212, 251, 307 cm^–1, respectively; (d)–(g) polar diagrams of the intensity of the four Raman peaks.

${\tilde { R}_{{{\rm{A}}_{\rm{g}}}}} = \left( {\begin{array}{*{20}{c}}a&0&0\\0&b&0\\0&0&c\end{array}} \right).$

因此, A_g模式强度随θ的变化可表示为^[24]

$I_{{{\rm{A}}_{\rm{g}}}}^{//} \propto {\left( {\left| b \right|{{\cos }^2}\theta + \left| c \right|\cos {\varphi _{bc}}{{\sin }^2}\theta } \right)^2} + {\left| c \right|^2}{\sin ^2}{\varphi _{bc}}{\sin ^4}\theta ,$

其中, 吸收样品的拉曼张量元a, b, c均为复数; φ_bc为b和c之间的相位差φ_b－φ_c. 利用(2)式对A_g模式的偏振相关拉曼峰值强度进行拟合, 结果如图1(d)—(g)中红色曲线所示, 并确定了GeSe₂样品的a轴和b轴方向, 用蓝色箭头进行了标记.
2 -->

3.2.偏振相关线性吸收谱表征GeSe₂的能带

线性吸收谱可用于表征二维材料在不同光谱区域吸收光子的能力分布, 从而间接推断出材料的能级位置, 为光学非线性吸收测试的波长选择提供参考依据. GeSe₂纳米片的线性吸收谱如图2(a)所示. 总体而言, 样品对各偏振方向的激光, 线性吸收率均由360 nm波长位置处的40%—50%先下降至420 nm处的约5%, 而后呈现上升趋势; 对于不同偏振方向的激光, 线性吸收率在波长小于380 nm和波长大于410 nm的区域相差较大, 而在400 nm处差异最小.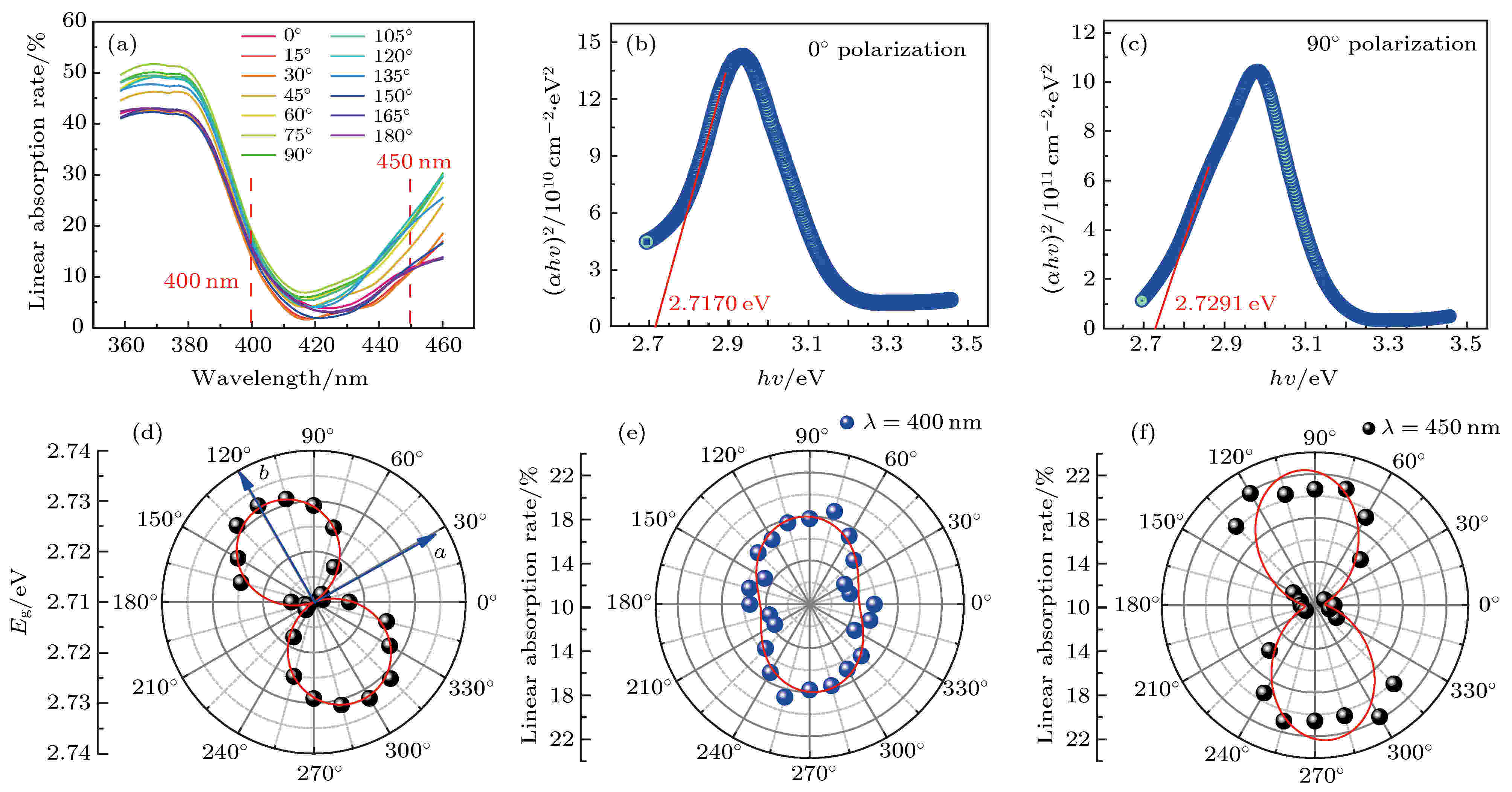
图 2 线性吸收谱对层状GeSe₂的各向异性能带表征　(a) 0°—180°偏振方向的线性吸收谱, 其中间隔15°; (b) 0°偏振方向的能带确定; 由陶克定理间接得到的能带位置, 其中切线与横坐标交点位置为2.717 eV; (c) 90°偏振方向的能带确定; 由陶克定理间接得到的能带位置, 其中切线与横坐标交点位置为2.7291 eV; (d) 层状GeSe₂的各向异性能带; b轴方向上的带隙最大, 而a轴方向的带隙最小; (e) 层状GeSe₂在400 nm处的各向异性线性吸收率极坐标图; (f) 层状GeSe₂在450 nm处的各向异性线性吸收率极坐标图
Figure2. Characterization of anisotropic bands of layered GeSe₂ by linear absorption spectrum: (a) Linear absorption spectrum with polarization directions from 0° to 180° with intervals of 15°; (b) the energy band of the 0° polarization direction is determined. The band position obtained indirectly from Tauc’s theorem, where the position of the intersection of the tangent and the abscissa is 2.717 eV; (c) determination of the energy band of the 90° polarization direction. The band position obtained indirectly from Tauc’s theorem, where the position of the intersection of the tangent and the abscissa is 2.7291 eV; (d) anisotropic energy bands of layered GeSe₂. The band gap in the b-axis direction is the largest, and the band gap in the a-axis direction is the smallest; (e) polar graph of anisotropic linear absorptivity of layered GeSe₂ at 400 nm; (f) polar graph of anisotropic linear absorption of layered GeSe₂ at 450 nm.

为了对能隙进行定量表征, 接下来使用陶克模型(Tauc model)对不同偏振激发下样品的线性吸收谱进行拟合,

$ \alpha h\nu =A\cdot {(h\nu -{E}_{\mathrm{g}})}^{1/2}, $

式中, $ \alpha $为线性吸收系数, A为矩阵元相关常数, E_g为材料的带隙. 0°与90°偏振的拟合结果如图2(b)和图2(c)所示, 能隙分别为2.717 eV与2.729 eV. 将所有偏振方向的能隙结果E_g(θ)绘制在极坐标中, 可以更直观地看到纺锤形的偏振相关带隙分布, 如图2(d)所示, 其中光学带隙最大的位置出现在120°偏振方向(样品的b轴方向), 其数值为2.732 eV (453 nm); 光学带隙最小的位置是在30°偏振方向(样品的a轴方向), 其值为2.711 eV (457 nm), 与文献报道相近^[32,34].
如前所述, 波长400 nm (非共振区域)附近, 样品对不同偏振激光的线性吸收率差异最小(约4%), 而在450 nm (近共振区域)处差别较大(约10%), 如图2(e)和图2(f)所示. 一般来说, 非线性吸收的偏振依赖性与线性吸收谱的各向异性密切相关^[24], 故选用400和450 nm波长的激光, 研究GeSe₂纳米片的偏振相关光学非线性吸收特性.
下面进一步分析层状GeSe₂的线性吸收依赖于入射光偏振的原因. 基于费米黄金定则, 跃迁速率为单位时间内由初态i跃迁到终态f的概率^[24]:

$ {\varGamma }_{i\to f}=\frac{2\mathrm{\pi }}{\hbar }{\left|\left\langle f\left|{H}_{\mathrm{o}\mathrm{p}}\right|i \right\rangle \right|}^{2}{\rho }_{{f}}, $

其中, ${\rho }_{{f}}$为终态的态密度; $ {H}_{\mathrm{o}\mathrm{p}} $是光-电微扰项; $ \left\langle f\left|{H}_{\mathrm{o}\mathrm{p}}\right|i \right\rangle $是由微扰导致的终态与初态间的跃迁矩阵元, 其正比关系如下:

$ \left\langle f\left|{H}_{\mathrm{o}\mathrm{p}}\right|i \right\rangle \propto {P}\cdot {{D}}_{{f}{i}}. $

这里, P是入射光的偏振矢量; D_fi是偶极子矢量, $ {{D}}_{{f}{i}}=\left\langle f\left|\nabla \right|i \right\rangle $. 则线性吸收强度可以用吸收系数α来表征^[36]:

$\alpha \left( {{E_{\rm{L}}}} \right) \propto \sum\nolimits_{f,i} {{{\left| {\left\langle {f\left| {{H_{{\rm{op}}}}} \right|i} \right\rangle } \right|}^2}} \delta \left( {{E_{{f}}} - {E_{{i}}} - {E_{\rm{L}}}} \right),$

其中, E_L是入射光子的能量, E_i (E_f)是电子态i (f )的能量. 根据跃迁选择定则可知, 不同偏振方向的激光会激发不同能带间的跃迁, 即不同的初态i与终态f ^[37]. 而从(5)式和(6)式可以看出, 随着入射光的偏振方向改变, 偏振矢量P和偶极矢量D_fi的内积也发生变化, 进而影响跃迁矩阵元, 从而得到不同的偏振相关的吸收系数α, 进一步推出光学带隙也具有偏振依赖性.
2 -->

3.3.GeSe₂中的各向异性非线性光学响应

接下来利用I扫描技术对GeSe₂的偏振相关的非线性光学吸收特性进行详细研究. 非线性光学特性的常用研究手段包括Z扫描技术和I扫描技术^[3,38,39], 前者通过样品在光轴方向的位移Z改变光斑半径大小, 从而获得连续变化的光功率密度^[40], 而后者则是通过1/2波片加格兰棱镜或者衰减片, 直接改变入射激光的光功率达到相同效果^[10]. 由于Z扫描技术中光斑大小随样品移动而不断变化, 对于大多数机械剥离的样品而言, 光斑极可能超出样品区域, 无法保证测试的准确性. 本文将传统的I扫描系统改进为微区I扫描系统, 提高了信噪比的同时将光斑大小控制在5 μm以内, 适用于机械剥离样品的测试.
首先用400 nm飞秒激光入射GeSe₂样品, 激光偏振以15°为步长旋转180°, 实验结果见图3(a), 为显示清晰, 仅给出间隔30°的数据外加90°附近两个数据. 400 nm激光的光子能量(3.1 eV)大于GeSe₂的带隙(约2.73 eV), 通常呈现饱和吸收特征, 即当高峰值功率激光入射材料时, 由于价带电子不断吸收光子跃迁进入导带, 可供激发的电子减少, 导带能态逐渐被占满, 材料吸收系数$ \alpha $随光强的增大而减小, 使得材料的透过率T先增大而后达到饱和值. 但是图3(a)呈现的反饱和趋势表明, 传统的饱和吸收模型不能很好描述此时的非线性吸收过程, 其中很可能伴有激发态吸收, 它是在光强更强的情况下, 由于价带中的电子吸收光子跃迁至导带后, 导带内部的激发态电子进一步吸收光子继续向上能级跃迁导致的, 故会使得材料吸收增加, 透过率下降, 呈现与饱和吸收相反的趋势.
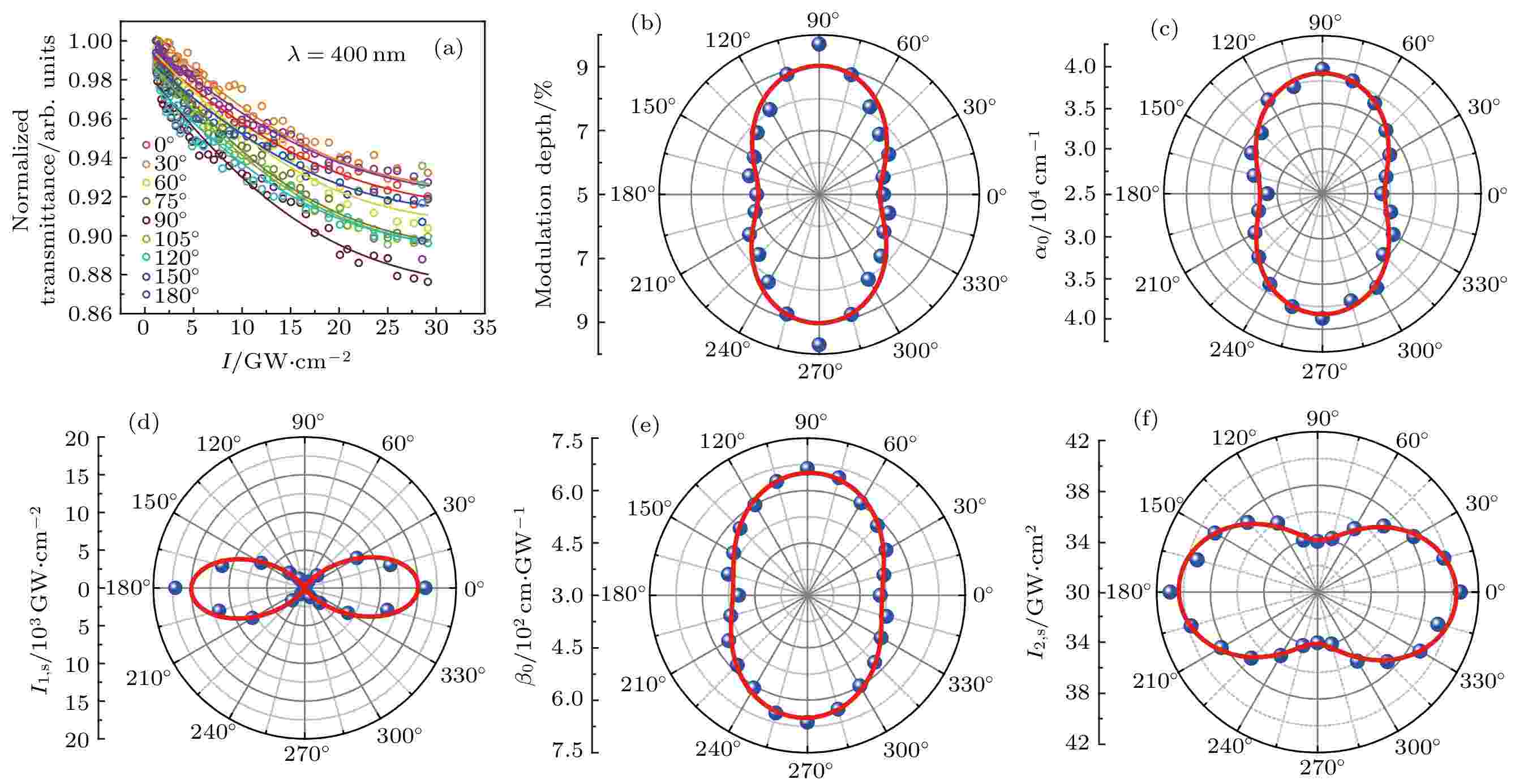图 3 400 nm非共振激发下不同偏振方向的叠加态吸收实验结果　(a) I扫描实验结果, 圆圈表示实验数据, 实线表示激发态吸收拟合曲线; (b) 偏振相关的非线性调制深度极坐标图; (c) 偏振相关的线性吸收系数α₀变化趋势极坐标图; (d) 偏振相关饱和吸收光强I_1,s极坐标图; (e) 偏振相关的激发态吸收系数β₀变化趋势极坐标图; (f) 激发态吸收的偏振相关饱和光强I_2,s极坐标图
Figure3. Experimental results of superposition state absorption of different polarization directions under 400 nm non-resonant excitation: (a) Results of the I-scan experiment. The circles indicate the experimental data, and the solid lines indicate the excited state absorption curve; (b) polarization-dependent non-linear modulation depth polar plot; (c) polar plot of the change in polarization-dependent linear absorption coefficient α₀; (d) polarization diagram of polarization-dependent saturated absorption intensity I_1,s; (e) polarization diagram of the polarization-dependent excited state absorption coefficient β₀; (f) polarized graph of polarization-dependent saturation light intensity I_2,s absorbed by the excited state.

基于比尔-朗伯定律, 光经过一个厚度为z的光学介质后, 光强I的变化为

$ \frac{\mathrm{d}I}{\mathrm{d}z}=-\alpha \left(I\right)I,$

式中, $ \alpha \left(I\right) $为与光强相关的吸收系数, 传统饱和吸收情况下

$ \alpha \left(I\right)=\frac{{\alpha }_{0}}{1+I/{I}_{\mathrm{s}}},$

其中, $ {\alpha }_{0} $为线性吸收系数, $ {I}_{\mathrm{s}} $为饱和吸收光强. 但是该模型不适用于当前情况, 需额外考虑激发态吸收项, 则吸收系数表示为^[41]

$ \alpha \left(I\right)=\frac{{\alpha }_{0}}{1+I/{I}_{1,\mathrm{s}}}+\frac{{\beta }_{0}I}{1+({I/{I}_{2,\mathrm{s}})}^{2}},$

式中, $ {I}_{1, \mathrm{s}} $表示线性吸收系数$ {\alpha }_{0} $的饱和光强, $ {\beta }_{0} $表示激发态吸收系数, $ {I}_{2, \mathrm{s}} $表示激发态吸收的饱和光强. 利用模型(7)式和(9)式对I扫描的实验结果进行拟合, 可以得到调制深度δT = T_max－T_min (表征非线性吸收的整体特性)、线性吸收系数$ {\alpha }_{0} $、饱和吸收光强$ {I}_{1, \mathrm{s}} $、激发态吸收系数$ {\beta }_{0} $及激发态吸收的饱和项$ {I}_{2, \mathrm{s}} $. 拟合结果的极坐标分别如图3(b)—(f)所示, 部分拟合数据由表1列出.

Polarization/(°)	α0/cm–1	β0/cm·GW–1	I1,s/GW·cm–2	I2,s/GW·cm–2	δT/%
0	31559	508	15947	41	7.0
30	33593	559	7962	38	7.5
60	36579	606	972	35	8.2
90	38790	663	349	34	9.7
120	36972	599	1394	36	8.1
150	34029	543	6629	39	7.3
180	31062	496	17082	41	7.0

表1400 nm非共振激发偏振相关的I扫描非线性叠加态吸收参数的拟合结果
Table1.Fitting results of I-scan nonlinear superposition state absorption parameters related to 400 nm non-resonant excitation polarization

通过对比图3(b)与图2(e)发现, 调制深度的极坐标图轴向与线性吸收率的基本符合, 即非线性吸收整体的偏振依赖特性与线性吸收相似. 入射激光偏振90°时, 调制深度最大, 为9.7%, 0°时最小, 为7.0%. 通过改变偏振方向, 调制深度的动态可调范围为2.7%. 由于GeSe₂的非线性吸收为饱和吸收与激发态吸收的叠加, 下面进行具体讨论.
饱和吸收对应于(9)式中的前项. 线性吸收系数$ {\alpha }_{0} $的拟合结果如图3(c)所示, 该参数反映出电子由下能级至上能级跃迁的概率, 0°偏振方向激发GeSe₂中的电子由价带跃迁至导带内部的概率最低, 90°偏振方向概率最高. 饱和吸收光强$ {I}_{1, \mathrm{s}} $取决于两个因素: 从下能级到上能级的跃迁概率以及上、下能级的态密度^[41], 前者由线性吸收系数$ {\alpha }_{0} $反映, 后者为单位能量间隔的可占据状态数, 决定了下能级可被激发的电子以及上能级可供电子填充的能态数, 与电子能带结构有关. 跃迁概率越小, 态密度越大, 材料吸收越难饱和, 饱和光强越大. 因此, 饱和吸收光强$ {I}_{1, \mathrm{s}} $的偏振依赖特性不仅与线性吸收系数$ {\alpha }_{0} $相关, 而且上、下能级受态密度的影响, 故其极坐标图的纺锤形长轴与$ {\alpha }_{0} $的短轴恰好相合, 但偏振依赖程度比之更高.
激发态吸收对应于(9)式中的后一项, 激发态吸收系数$ {\beta }_{0} $可以反映电子由激发态跃迁至上能级的概率, 激发态吸收的饱和项$ {I}_{2, \mathrm{s}} $类似于饱和吸收光强, 由激发态向上能级的跃迁概率以及态密度共同决定. 如图3(e)所示, 激发态吸收系数$ {\beta }_{0} $最小的偏振方向与$ {\alpha }_{0} $是一致的, 即在400 nm非共振激发的情况下, 激发态电子向更高能态跃迁与价带电子向导带跃迁的概率具有相同的偏振依赖特性. 对激发态吸收而言, 价带电子跃迁到导带的概率越大将会导致激发态电子填充的密度越大, 使得激发态吸收更难饱和, 而较高的激发态电子跃迁概率会使得激发态吸收更易于饱和, 二者相反的作用减小了激发态吸收的偏振依赖程度, 导致在400 nm非共振激发波段, 材料对不同偏振激光的非线性吸收程度差异较小.
450 nm近共振激发条件下的非线性响应实验结果如图4(a)所示, 可明显看出样品对此波段不同偏振激光的非线性吸收区别更大. 当峰值功率达到50 GW/cm²时, 0°偏振光的归一化透过率趋于定值, 非线性吸收出现较为明显的反饱和趋势, 与之不同的是, 90°偏振光的归一化透过率继续呈明显下降的趋势. 同样采用拟合公式(7)和(9)对不同偏振下的实验结果进行拟合, 可得调制深度由0°偏振方向的4.6%增长至90°偏振方向的9.9%, 动态调制深度可达5.3%, 远高于400 nm非共振激发条件下的2.7%.
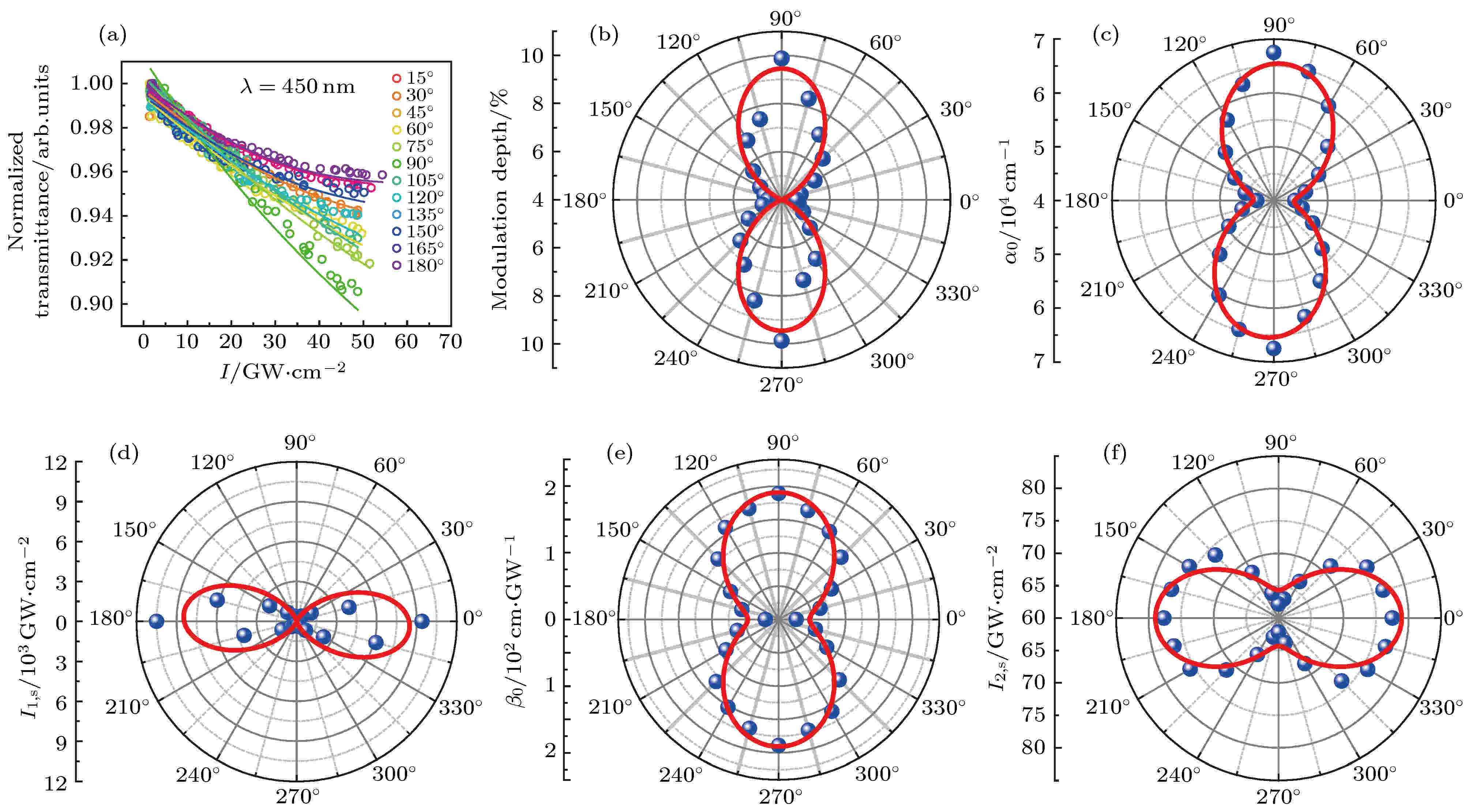图 4 450 nm近共振激发下不同偏振方向的叠加态吸收实验结果　(a) I扫描实验结果, 圆圈表示实验数据, 实线表示激发态吸收拟合曲线; (b) 偏振相关的非线性调制深度极坐标图; (c) 偏振相关的线性吸收系数α₀变化趋势极坐标图; (d) 饱和吸收的偏振相关饱和光强I_1,s极坐标图; (e) 偏振相关的激发态吸收系数β₀变化趋势极坐标图; (f) 激发态吸收的偏振相关饱和光强I_2,s极坐标图
Figure4. Experimental results of superposition state absorption of different polarization directions under 450 nm non-resonant excitation: (a) Results of the I-scan experiment. The circles indicate the experimental data, and the solid lines indicate the excited state absorption curve: (b) polarization-dependent non-linear modulation depth polar plot: (c) polar plot of the change in polarization-dependent linear absorption coefficient α₀; (d) polarization diagram of polarization-dependent saturated absorption intensity I_1,s; (e) polarization diagram of the polarization-dependent excited state absorption coefficient β₀; (f) polarized graph of polarization-dependent saturation light intensity I_2,s absorbed by the excited state.

值得注意的是, 在450 nm近共振激发状态下, 线性吸收系数$ {\alpha }_{0} $与激发态吸收系数$ {\beta }_{0} $对偏振的依赖特性恰好相反, 如图4(c)和图4(e)所示. 以0°偏振方向非线性吸收为例, 该偏振方向的线性吸收系数$ {\alpha }_{0} $极小, 表明此时电子由价带跃迁至导带底的概率最低, 则相应激发态电子密度低, 同时该偏振激光的激发态吸收系数$ {\beta }_{0} $为极大值, 即此时激发态吸收发生的概率最大, 二者均使得该偏振下激发态吸收更快饱和, 它们的共同作用加强了激发态吸收的偏振依赖程度, 导致在450 nm近共振激发波段, 材料对不同偏振激光的非线性吸收程度差异很大. 450 nm近共振激发偏振相关的I扫描部分相关参数的拟合结果见表2, 表中所列拟合参数与图4对应.

Polarization/(°)	α0/cm–1	β0/cm·GW–1	I1,s/GW·cm–2	I2,s/GW·cm–2	δT/%
0	43909	175	9390	63	4.6
30	49631	157	1258	69	5.6
60	60289	65	409	75	7.1
90	67501	22	188	79	9.9
120	57266	81	469	76	6.8
150	48345	158	2333	68	5.0
180	43173	176	10483	62	4.6

表2450 nm近共振激发偏振相关的I扫描非线性叠加态吸收参数的拟合结果
Table2.Fitting results of I-scan nonlinear superposition state absorption parameters related to 450 nm non-resonant excitation polarization

对比400与450 nm的波长处的偏振选择非线性光学响应, 它们的饱和吸收模式对偏振的依赖特性是类似的, 最大的区别在于线性吸收系数$ {\alpha }_{0} $与激发态吸收系数$ {\beta }_{0} $对偏振的依赖特性是否相同, 二者相反的偏振依赖特性可以放大偏振对激发态吸收模式的影响, 从而导致了不同波段非线性吸收曲线偏振依赖程度的明显差异. 进一步对非线性吸收中的饱和吸收与激发态吸收的占比进行讨论. 由于微区I-扫描在不同波长处GeSe₂实验结果呈现的都是反饱和趋势, 说明了在共振与非共振波长处激发态吸收都是占据主导地位. 但是, 激发态吸收所占的比例随波长与偏振的不同而略微有所区别. 首先, 在共振激发与非共振波长的情况下, 沿90°偏振方向的激发态吸收的占比高于沿0°偏振方向激发态吸收的占比, 且该占比随着偏振角度的减小而减小. 另外一方面, 同样对于90°偏振方向, 在近共振时由价带向导带跃迁的概率较低, 此时激发态更易于发生, 故此时激发态吸收的占比将高于非共振时的占比; 同样的趋势也出现在0°偏振方向. 值得注意的是, 由于激发吸收在共振条件下与偏振的相关性更强, 因此在90°方向上随波长远离共振区激发态吸收的占比减小量大于0°方向的占比减小量.
由于GeSe₂材料的光学非线性吸收在不同偏振下动态调制深度很大, 它将有潜力应用于偏振选择的非线性吸收型全光开关^[42]. 目前, 研究者对全光开关的研究主要集中于两类: 一类是线性全光开关, 另一类则是非线性全光开关. 线性全光开关是利用光学干涉效应实现的. 而非线性全光开关则是利用了材料的非线性光学特性实现一束调制光对另一束被调制光的控制, 使得被调制光的状态可被识别为“开”或“关”. 近年来, 随着光计算和光学神经网络的兴起, 全光开关需要以更快地发展速度跟上时代的步伐. 二维材料在全光开关的应用中, 有两类主流的非线性光学解决方案, 一类是利用光克尔效应实现的全光开关^[43,44], 另一类则是偏振选择的非线性吸收型的全光开关^[24]. 其中, 光克尔效应型的全光开关一个较为明显的优势是可实现在高达18 GHz的频率下调制高速信号的波长转换. 对于各向异性材料GeSe₂而言, 则适用于偏振选择的非线性吸收型的全光开关(后文简称偏振型全光开关)应用. 偏振选择型全光开关则以高达44%的调制深度差而凸显其优势^[24]. 偏振型全光开关是利用一束不同偏振的调制光激发二维材料, 使之处于不同的非线性吸收状态, 进而改变信号光的透过率. 由于GeSe₂是一类各向异性强的二维半导体, 且在非线性光学中表现出较好的性能. 在应用于全光开关时, 可以分别利用偏振方向沿着a轴和b轴的高脉冲功率的调制光对二维材料的非线性吸收状态进行调制, 进而改变信号光的透过率. 具体而言, 根据GeSe₂的非线性吸收结果, 可以预测一种偏振全光开关的实现方案, 如图5所示: 利用格兰棱镜将调制光的偏振方向设置为沿x轴(a-轴)入射GeSe₂, 此时将使得二维材料对信号光的透过率为“开”的状态; 另外, 偏振方向设置为沿y轴(b-轴)入射GeSe₂时, 此时二维材料对信号光的透过率调制为“关”的状态. 通过该手段, 最后可利用GeSe₂的各向异性特性来实现偏振型全光开关.
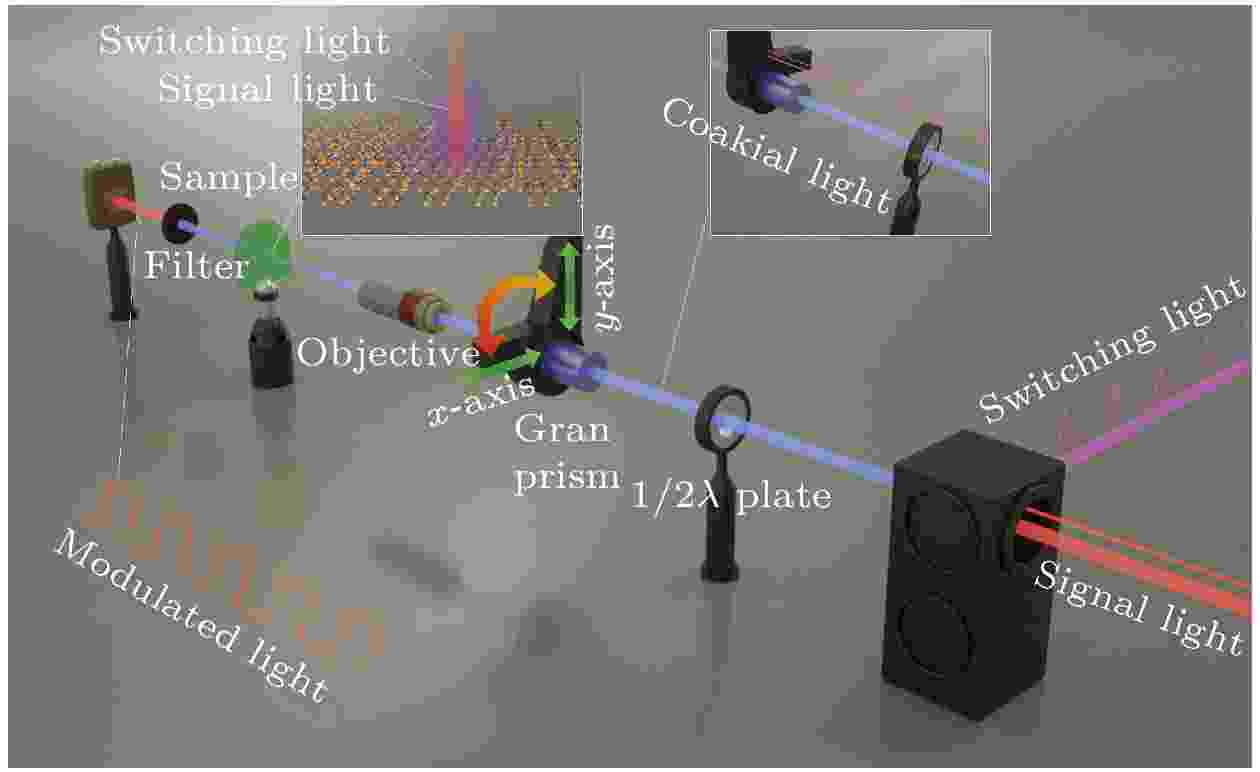图 5 GeSe₂偏振型全光开关的原理示意图
Figure5. Schematic diagram of GeSe₂ based polarized-dependent all-optical switching

利用机械剥离的方式得到了88 nm厚的各向异性GeSe₂纳米片, 通过AFM和偏振相关的拉曼光谱分别对GeSe₂纳米片的层厚、晶格取向进行了表征. 为摸索非线性测试波长条件, 本文使用偏振选择的线性吸收谱研究了GeSe₂的各向异性吸收能带, 其中a轴方向的能带$ {E}_{\mathrm{g}, a} $最小, 为2.711 eV, 而b轴方向的能带$ {E}_{\mathrm{g}, b} $最大, 为2.732 eV. 最后利用偏振选择的微区I扫描实验系统, 分别在400和450 nm波段对该样品的各向异性非线性吸收响应进行测试. 结果表明, 样品的非线性吸收模式为饱和吸收和激发态吸收的叠加态, 动态调制深度在450 nm近共振能带位置处值最大, 达到5.3%, 400 nm处仅为2.7%. 而且, 激发态吸收模式的偏振选择特性在近共振波长处对偏振较为敏感, 因此可以通过控制不同位置处的激发波长主动调整动态调制深度. 本工作为GeSe₂在全光开关的应用上打下了理论基础.