摘要:不同的频率失谐会在耦合光学微腔激发出不同的工作模式. 以两个耦合光场的非线性薛定谔方程为理论模型, 分别研究了失谐参量正调谐和负调谐过程中微腔内光场的变化. 理论分析结果表明, 在正失谐区域中, 腔内光场可由多脉冲形式演变为亮孤子, 但亮孤子存在范围较小, 当失谐参量过大时, 腔内光场会演化为直流分布. 在负失谐区域, 腔内可以形成较高功率“图灵环”形式的光场. 当耦合微腔没有发生频率失谐, 或者失谐参量接近0时, 腔内只能形成混沌形式的光场分布. 当耦合微腔内激发出光孤子后, 通过选取合适的失谐参量和抽运功率, 可在腔内维持稳定的亮孤子. 此外还可通过继续调谐第一个微腔的失谐参量, 将亮孤子转变为低功率的“图灵环”. 理论分析结果对耦合微腔的实验研究具有重要意义.
关键词: 光学微腔/
频率失谐/
亮孤子

English Abstract

全文HTML

--> --> -->

目前, 基于光学微腔的光频梳技术凭借体积小、集成度高、低损耗, 尤其是梳齿间频率间隔大等优点, 广泛应用于频率测量、绝对距离测量、任意波形产生、精密光钟等领域^[1-4]. 光学微腔内, 由于其结构对光场的束缚, 使得腔内的光场因具有极高的功率密度而产生级联的四波混频效应, 从而将抽运光模式转移到邻近的模式上, 在腔内产生一系列宽带的梳状光谱^[5]. 目前, 国内外很多单位已经开展了关于光学微腔的研究, 已经在理论和实验上得到了各种形式的光场, 比如亮孤子、暗孤子、图灵环、混沌等^[6-9]. 其中, 模式锁定的孤子光频梳对于光学微腔的实际应用具有重大意义, 也为光频信号和微波电信号之间的转换提供了重要的技术支持^[10]. 此外, 将以Si为基底的Si₃N₄光学微腔和具有光放大功能的光纤环结合起来, 能够获得更加稳定的光频梳, 并且能够有效避免热效应和环境振动对系统产生的干扰^[11], 这样一种结构也被应用于测量锁模激光器的光谱^[12]. 光学微腔也因其优异的光学性能, 成为当前的研究热点.
近些年, 由于精密光刻技术的不断发展, 以Si为基底的Si₃N₄光学微腔的加工水平和加工精度都不断提升^[13]. 在此基础上, 研究者提出了一种新型的耦合双微腔结构. 通过采用双微腔耦合的方式, 可以极大地增大抽运模式到其他模式的转换效率, 抽运光的利用率被提高了一个数量级^[14]. 且相比于单个微腔, 双微腔耦合的光学系统能够在实验中提供更多的可调节参数, 以产生各种形式的稳定光场, 但由于参数较多, 使得对其工作状态和内部光场的控制变得更加复杂. 此外, 在普通微腔色散、非线性、损耗等作用的基础上, 双微腔结构中两个微腔内的光场会相互作用, 因此还需要考虑两个微腔之间的耦合效应. 所以, 需要更有效的方式对腔内光场进行调控. 研究中发现, 通过调谐双微腔的失谐参量, 可以激发出耦合微腔的多种工作状态, 因此对耦合微腔的调谐过程进行研究具有重要意义. 目前, 关于耦合光学微腔的研究范围还比较局限. 基于离散的非线性薛定谔方程, 有****研究了耦合光学微腔中的自脉冲和混沌现象, 然而他们研究的耦合微腔采用的是波导阻隔微腔的结构, 即波导和微腔之间是串联的结构^[15,16], 这完全区别于我们讨论的波导和微腔耦合的光学结构. 此外, 在由若干个光学微腔耦合形成的微腔链结构中, 也可产生光学脉冲, 但是缺少对微腔内光场调谐和演化过程的研究^[17,18]. 因此, 关于耦合光学微腔调谐过程对工作状态的激发和影响, 还没有相关报道. 本文以双微腔耦合的非线性薛定谔方程为理论模型, 分别研究了失谐参量正调谐和负调谐过程中各阶段微腔内光场和光功率的变化, 并且通过选择合适失谐参数维持调谐过程中激发出的光孤子.

以Si为基底的Si₃N₄双微腔耦合的结构如图1所示, 抽运光通过腔2一侧的波导结构耦合进入微腔, 当两个微腔的间距满足适当条件时, 光场在两个微腔之间发生耦合, 最终的光场由D端口输出. 分别由E₁和E₂表示两个微腔中的光场, 两个微腔内的光场满足以下耦合的非线性薛定谔方程^[14]:
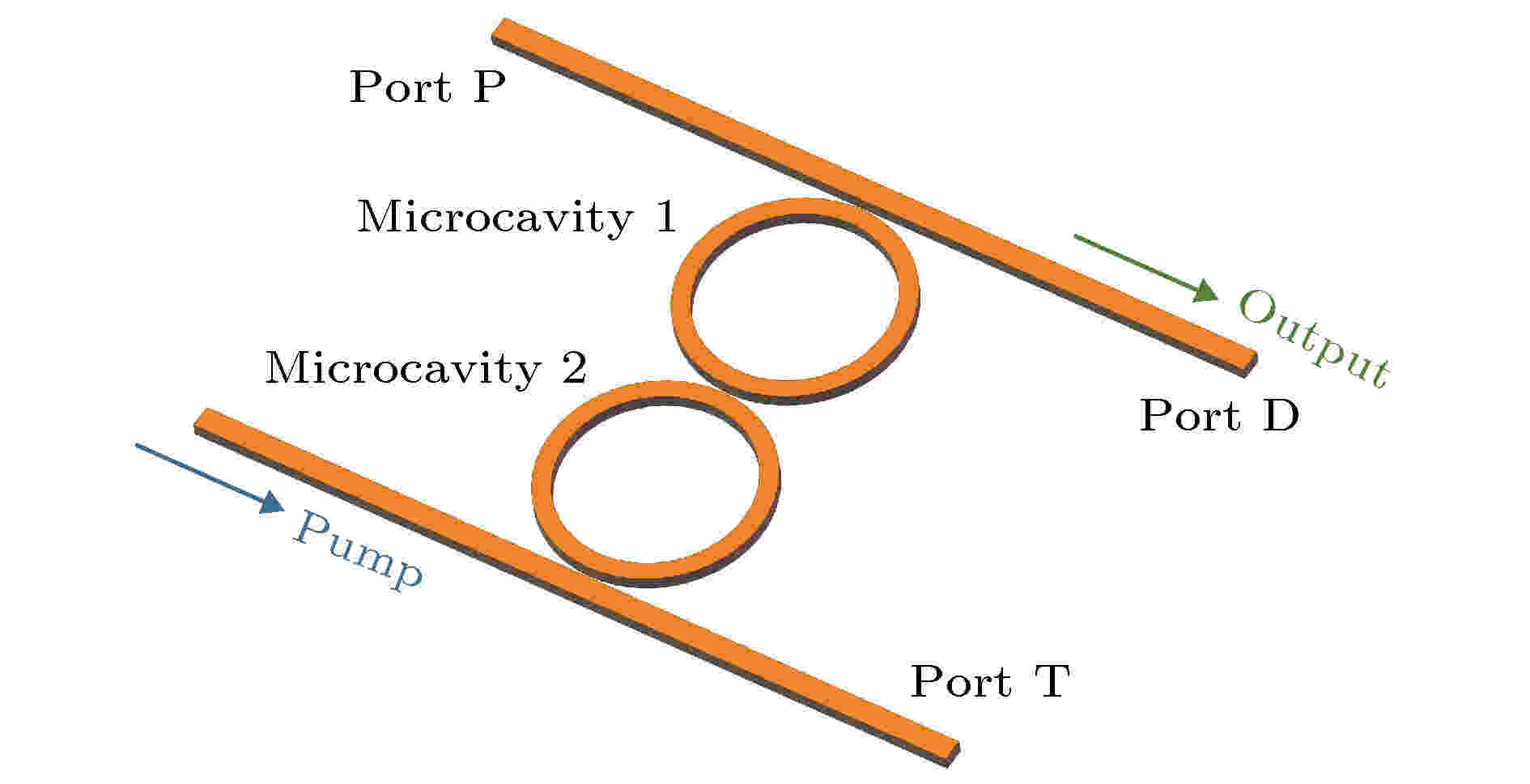图 1 双微腔耦合结构示意图
Figure1. Structure of the dual coupled optical microcavities.

$\begin{split} \frac{{\partial {E_1}}}{{\partial z}} = \; & \bigg[ - \left( {{\alpha _{{\rm{i1}}}} + {\alpha _{{\rm{c1}}}}} \right) - {\rm{i}}{\delta _1} - {\rm{i}}\frac{{k_1''}}{2}\frac{{{\partial ^2}}}{{\partial {\tau ^2}}} \\ &+ {\rm{i}}{\gamma _1}{{\left| {{E_1}} \right|}^2} \bigg]{E_1} + {\rm{i}}{\kappa _{12}}{E_2},\end{split}$

$\begin{split}\frac{{\partial {E_2}}}{{\partial z}} =\; & \bigg[ - \left( {{\alpha _{{\rm{i2}}}} + {\alpha _{{\rm{c2}}}}} \right) - {\rm{i}}{\delta _2} - \Delta k'\frac{\partial }{{\partial \tau }} \\ & -{\rm{i}}\frac{{k_2''}}{2}\frac{{{\partial ^2}}}{{\partial {\tau ^2}}} + {\rm{i}}{\gamma _2}{{\left| {{E_2}} \right|}^2} \bigg] {E_2}\\ & +{\rm{i}}{\kappa _{21}}{E_1} + {\rm{i}}{\kappa _{\rm{p}}}{E_{{\rm{in}}}}. \end{split}$

T端口和D端口的输出光场E_T和E_D分别为

${E_{\rm{T}}} = {\rm{i}}{\kappa _{\rm{p}}}L{E_2} + {E_{{\rm{in}}}}, $

${E_{\rm{D}}} = {\rm{i}}{\kappa _{\rm{d}}}L{E_1}.$

这里, z表示光场在微腔中的传播距离; τ是光的传播时间, 即快时间, 可以用来表征圆形微腔的方位角; α_i1和α_i2分别为光场在两个腔内传播时的损耗, 损耗的大小主要取决于材料对光的吸收, 对Si₃N₄材料的光学微腔, 一般采用波长为1550 nm的连续光抽运, Si₃N₄材料对这一波长的光吸收效率非常低, 因此为了简化模型, 本文中不考虑光在微腔传播中的损耗, 即α_i1 = α_i2 = 0; δ₁和δ₂是两个微腔抽运光频率和微腔谐振频率间的失谐参数, 它们是由微腔自身的结构和抽运波长决定的, 在实验中通过调节抽运光的波长可达到对失谐参数进行调节的目的; γ₁和γ₂是非线性系数, Δk' 是群速度失配, $k_1''$和$k_2''$为光场的二阶色散系数, 这些参数都和光学微腔的材料相关; L是微腔的长度, 在实验中可根据对输出光场的需求设计这一参数; α_c1 = θ₁/(2L), α_c2 = θ₂/(2L), θ₁和θ₂分别表示两个微腔和抽运光场之间的耦合效率, 它由抽运光的输入波导和第二个光学微腔之间的距离决定; ${\kappa _{\rm{p}}} =$$ \sqrt {{\theta _2}} /L$, ${\kappa _{\rm{d}}} \!=\! \sqrt {{\theta _1}} /L$, ${\kappa _{12}} \!= {\kappa _{21}} \! = \sqrt {{\theta _{12}}} /L =$ $ \sqrt {{\theta _{21}}} /L$, θ₁₂ = θ₂₁是两个微腔之间的耦合效率, 当两个光学微腔之间的距离过大或者过小, 都会导致耦合效率的降低, 因此在设计双微腔耦合系统时, 需要找到两个微腔间的最佳间距, 以达到最大的耦合效率; P_in为抽运光的功率, ${E_{{\rm{in}}}} = \sqrt {{P_{{\rm{in}}}}} $. 此外, 光场在腔内循环一周的时间用t_R表示, 自由光谱范围FSR = 1/t_R. 采用分布傅里叶法求解方程(1)和(2), 可以分别得到两个微腔中光场分布随时间的变化情况, 结合方程(3)和(4)可以得到耦合微腔的D端口的输出光场和T端口输出的残余光场.

2

-->

3.1.失谐参量调谐过程中耦合光场的变化

以Si为基底的Si₃N₄耦合微腔的各项参数如下: γ₁ = γ₂ = 1 m ^–1·W ^–1, Δk' = 1.282 × 10 ^–10 s·m ^–1, θ₁ = 9.114 × 10 ^–3, θ₂ = 1.063 × 10 ^–2, θ₁₂ = 3.038 × 10^–3, $k_1'' \!=\! - 100$ ps²/km, $k_2'' \!=\! - 100$ ps²/km. 此外, 假设耦合的两个微腔尺寸相同, FSR₁ = FSR₂ = 200 GHz. 失谐参量δ_{1, 2} = 2π·Δf_{1, 2}/(FSR_{1, 2}·L), 其中, Δf_{1, 2}是抽运和微腔谐振之间的失谐频率, 改变Δf_{1, 2}可通过调节抽运光频率或给光学微腔施加外力产生微小形变来实现. 假设耦合的光学微腔初始的失谐参量δ_{1, 2} = 0, 使用连续光对两个微腔进行抽运, 抽运光功率P_in = 10 W. 腔内初始的光场是由调制不稳定性(modulation instability, MI)产生的, 因此可以假设两个微腔内的初始光场符合高斯分布: E₁₀ = E₂₀ = E₀ exp [ –(τ/τ₀)²]^[19]. 在抽运过程中, 失谐频率Δf_{1, 2}均以12.73 GHz/μs的速度变化, 即失谐参量δ_{1, 2}的值不断增加, 这一调谐过程称为正失谐区域. 根据(4)式可知, 双耦合微腔结构中, 输出的光场是由第一个光学微腔中的光场决定的, 因此重点讨论第一个光学微腔中的光场分布.
在耦合效应、非线性效应和色散的作用下, 第一个光学微腔中光场随时间的演化如图2(a)所示, 可以看到, 光场的演化过程可分为四个阶段, 各阶段区分明显, 四个阶段的划分和相应阶段中第一个微腔内的光场总功率随时间的变化曲线如图2(b)所示, 图2(c)是各阶段光场的分布情况和对应的光谱. 在第一阶段中, 虽然两个微腔的失谐参量较小, 但第一个微腔内处于混沌状态^[20], 光场由一系列不规则的、功率较大的尖峰组成, 且分布随时间随机变化, 此时的光谱由杂乱的梳齿组成, 每个梳齿的功率也随时间时刻变化(图2(c)中的(1-1), (1-2)). 混沌光场是由抽运在腔内激发出很多不稳定的谐振模式产生的, 这些不稳定的模式在抽运的作用下继续产生二阶或者更高阶的梳齿, 最终导致腔内模式混乱, 光场分布无规则. 这种混沌光场也造成了图2(b)中功率曲线的剧烈振荡, 但两个微腔内的功率总体呈增长趋势, D端口输出的光功率和T端口残余的光功率相对较弱. 从第一阶段到第二阶段, 在图2(b)的功率曲线中, 可以看到腔内功率出现了突变, 因此在实际中, 可以通过监测D端口输出的光功率, 来判断此时光场的状态. 光场的演化也出现了明显的分界线, 第一个微腔内随机地出现了若干脉冲, 对应的腔内光谱仍是无规则的梳齿, 但各梳齿的功率相对稳定(图2(c)中的(2-1), (2-2)), 由于微腔对光场模式具有选择性, 产生的脉冲在维持一段时间后逐渐消失, 最终只剩下单脉冲形式的光场, 此时的光场归纳为光场演变过程中的第三阶段. 在这一阶段中, 腔内始终保持单脉冲的形式, 即在腔内形成了亮孤子, 此时的光谱是一个平整的宽带梳状光谱(图2(c)中的(3-1), (3-2)), 腔内功率也相对稳定. 由于失谐参量继续不断增大, 导致抽运光无法在腔内激发产生谐振模式, 亮孤子在腔内维持一段时间后消失, 此时为第四阶段的光场. 在这一阶段, 腔内光功率处于较低水平, 且腔内各位置的光功率差值仅为10^–15 W数量级, 因此可以认为腔内为直流光场, 对应的光谱仅存在一个抽运光模式, 无梳状光谱产生(图2(c)中的(4-1), (4-2)). 此时两个腔内的光功率都处于较弱的水平, 大部分的能量作为残余的光场由D端口输出.
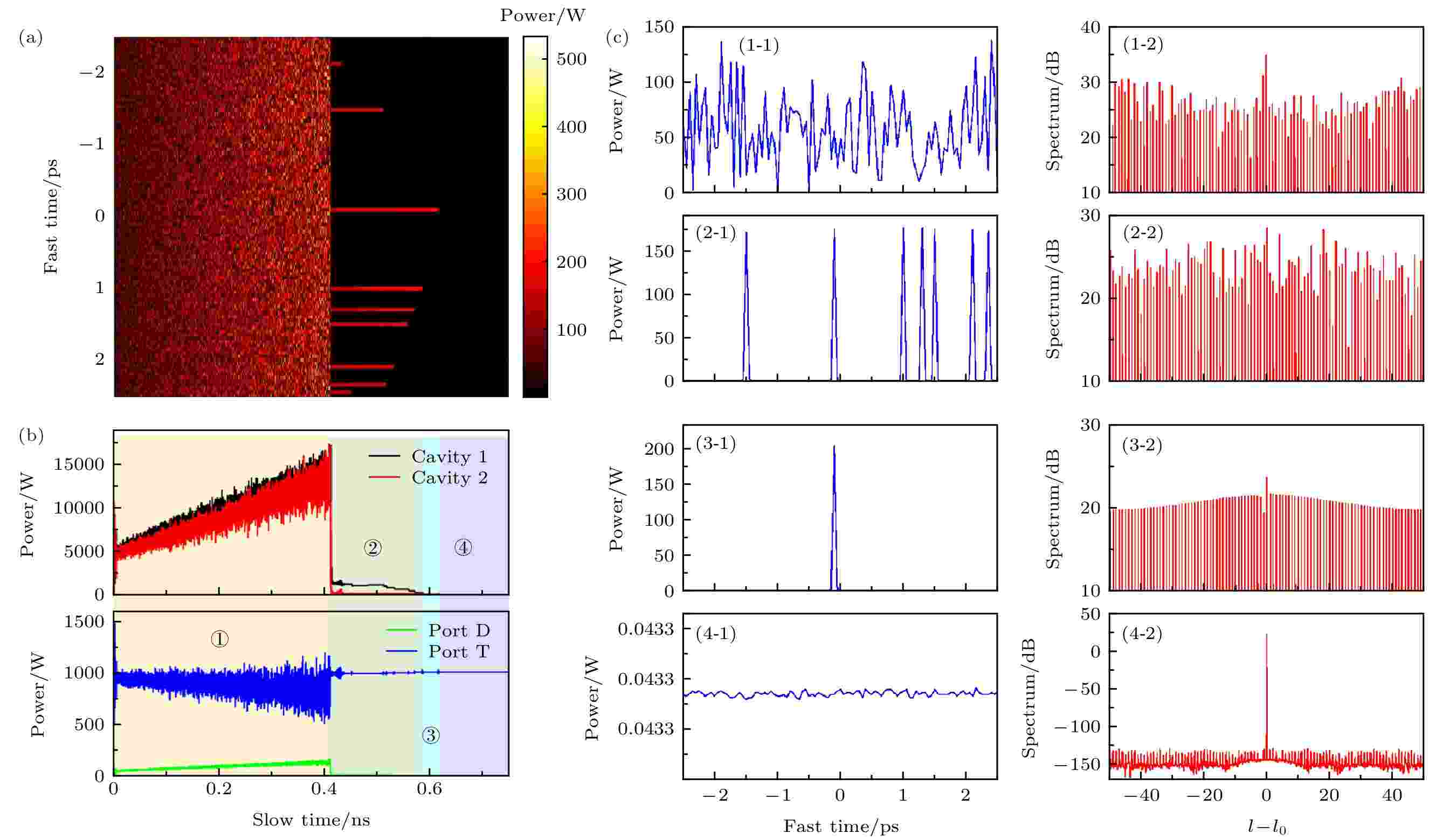图 2 (a)失谐参量在正方向调谐过程中, 第一个光学微腔内光场分布随时间的演化; (b) 失谐参量调谐过程中, 光功率随时间的变化曲线; (c)与图(b)中各个阶段对应的光场分布和光谱图
Figure2. (a) Evolution of the optical field inside the first microcavity in the region of positive frequency tuning; (b) curves of the optical power variation in the process of frequency tuning; (c) field distribution and spectra corresponding to each stage in Fig. (b).

在以上讨论的基础上, 图2中各参数取值不变, 仅改变失谐频率Δf_{1, 2}的变化方向, Δf_{1, 2}均以–12.73 GHz/μs的速度发生改变, 即失谐参量δ_{1, 2}的值往负方向不断增加, 这一过程称为负调谐区域, 光场分布的演化和腔内光功率的变化曲线如图3所示. 根据光场分布的变化, 将调谐的过程也分为四个阶段. 在第一阶段中, 抽运和微腔谐振频率间轻微地失谐, 微腔内产生混沌光场(图3(c)中的(1-1), (1-2)), 腔内的光功率同样出现大幅的振荡, 但总的功率呈现衰减的趋势, 说明随着频率失谐参量在负方向上增加, 腔内由频率失谐引起的损耗逐渐增大, 导致腔内的功率下降. 随着失谐的进一步加剧, 腔内的MI导致微腔工作于“图灵环”状态^[21], 腔内光场演化出36个近似的脉冲结构, 光谱每隔36FSR, 就会有一个功率较大的梳齿 (图3(c)中的(2-1), (2-2)), 此时的脉冲峰值功率大约25 W. 失谐增加使得微腔光场的演化进入第三阶段, 腔内仍然存在等间距的脉冲光场, 但由于MI作用的增强, 光场强度明显减弱, 脉冲数目增加为41个, 相应的光谱图中两个相邻的峰值间隔了41FSR. 到第四阶段, 微腔内的光场由于失谐过大, 腔内仅存在直流光场分布, 无法产生梳状光谱.
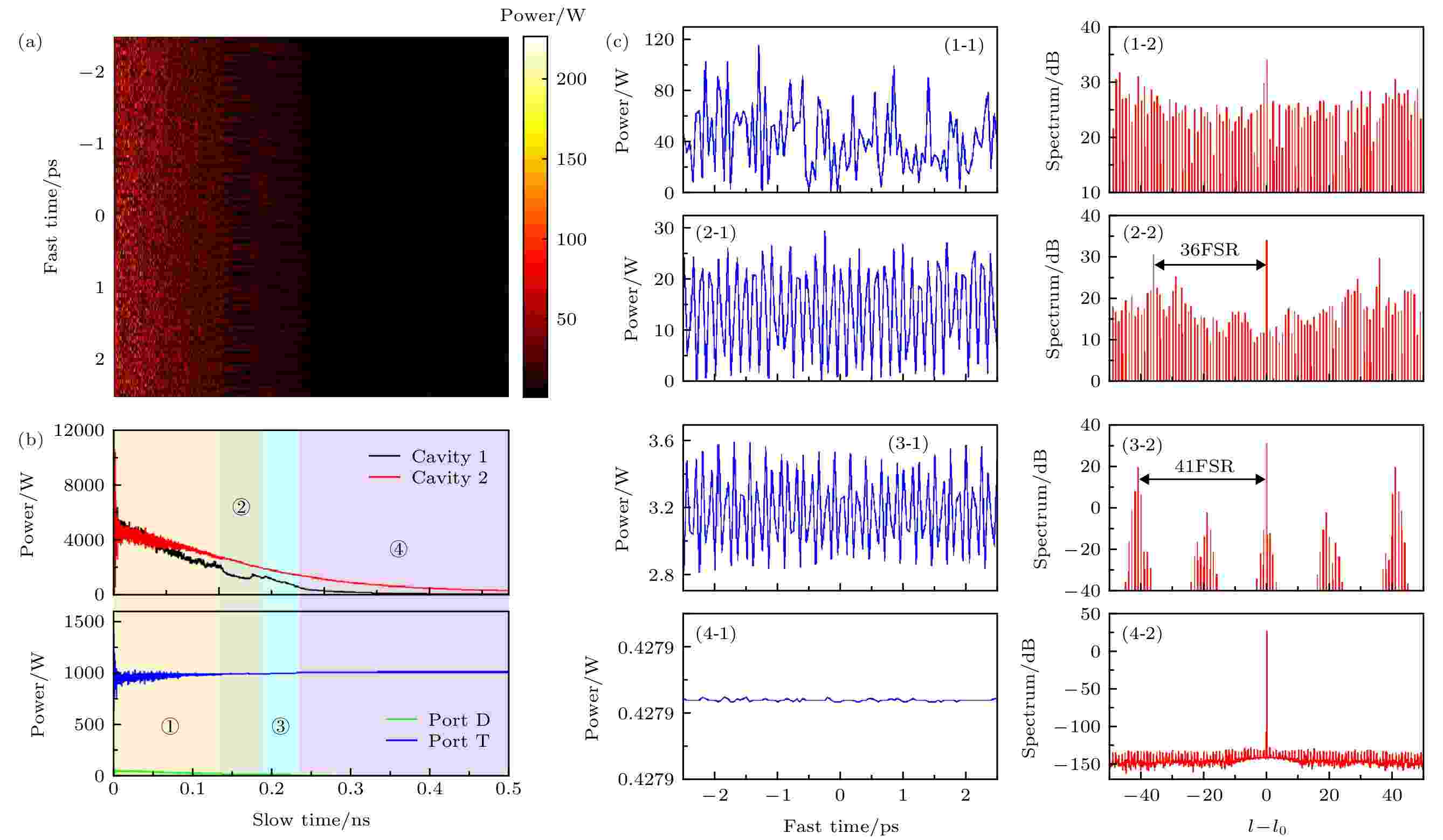图 3 (a)失谐参量在负方向调谐过程中, 第一个光学微腔内光场分布随时间的演化; (b) 失谐参量调谐过程中, 光功率随时间的变化曲线; (c)与图(b)中各个阶段对应的光场分布和光谱图
Figure3. (a) Evolution of the optical field inside the first microcavity in the process of negative frequency tuning; (b) curves of the optical power variation in the process of frequency tuning; (c) field distribution and spectra corresponding to each stage in Fig. (b).

结合图2和图3可以看到, 耦合双微腔结构中, 在正失谐区域腔内由于微腔对光场模式的选择性, 在腔内可形成亮孤子形式的光场, 但亮孤子存在区域较小, 因此失谐参量需要选取合适的范围来激发亮孤子光场. 在负失谐区域中, 耦合微腔内会因MI形成“图灵环”形式的多脉冲光场, 同样地, 该区域范围也较小. 而当耦合微腔没有发生频率失谐, 或者失谐参量接近0时, 腔内只能形成混沌形式的光场分布, 因此低失谐并不利于腔内亮孤子或者多脉冲形式的光场产生.
在耦合光学微腔中, 两个微腔之间的耦合距离会对耦合强度κ₁₂和κ₂₁以及微腔的谐振频率产生重要影响, 进而影响耦合微腔的频率调谐过程. 当双微腔的间距小于某一特定值时, 两微腔之间的模式耦合强度较大, 同时会产生模式劈裂效应, 引起腔内失谐加重, 模式分布混乱, 进而导致微腔的品质因子降低、散射损耗增加; 而双微腔间距较大时, 虽然耦合作用减弱, 模式劈裂效应也会消失, 但也会无法在腔内激发出有效光场^[22,23]. 为研究双微腔强耦合过程中的模式劈裂效应对频率调谐过程产生的影响, 在图2和图3耦合强度取值(κ₁₂ = κ₂₁ = 37)的基础上, 增加耦合强度进行了研究. 当κ₁₂ = κ₂₁ = 80时, 在正调谐过程中, 光场经历了混沌模式, 从混沌光场中演化出了稳定的双脉冲形式的光场分布, 且双脉冲在腔内同时出现和消失, 腔内最终仍然为直流光场, 结果如图4(a)所示. 图4(b)是强耦合光学微腔的失谐频率负调谐过程中光场的演化, 光场从混沌状态直接演变为直流光场, 与图3(a)相比, 缺少了“图灵环”的过程. 研究中发现, 进一步增加耦合强度(κ₁₂ = κ₂₁ = 100), 腔内的模式劈裂和散射损耗过强, 腔内的光场直接衰减为直流光场. 因此, 当双微腔耦合距离太小, 耦合强度过大的情况下, 强耦合作用和模式劈裂共同作用, 会导致腔内失谐加重, 光场分布更加混乱, 损耗更加严重, 因而在调谐过程中无法激发出有效的稳定光场. 因此, 在对双微腔结构设计时, 需要选取合适的耦合距离, 在保证耦合效率的同时, 减小由强耦合产生的模式劈裂效应, 避免腔内光场的混乱.
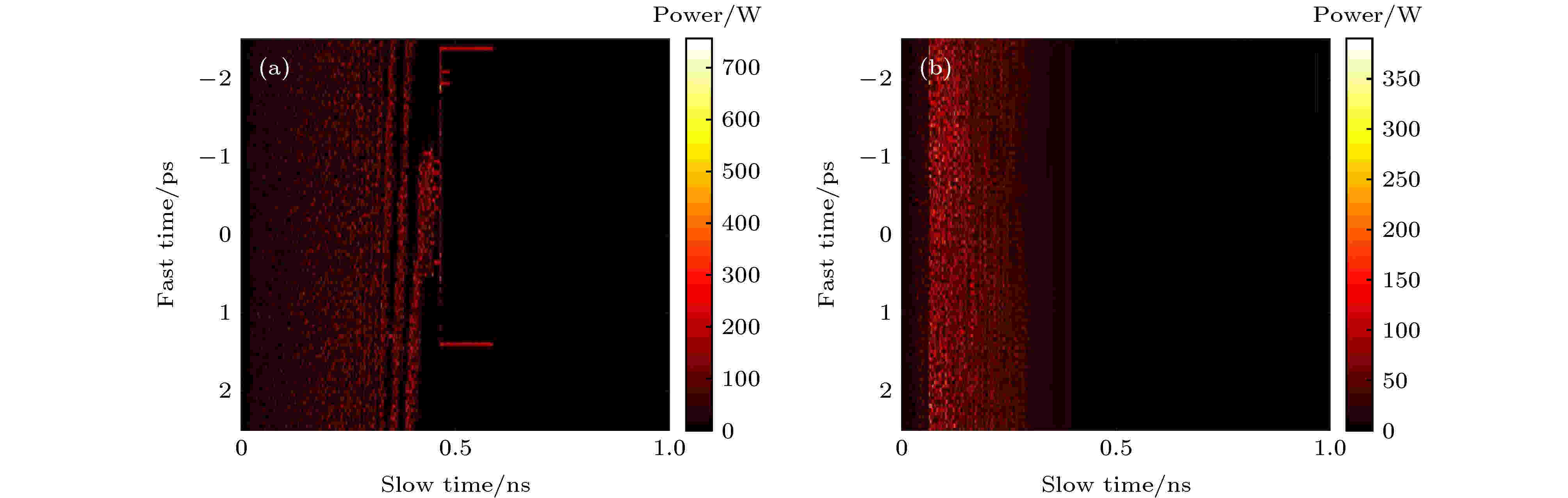图 4 (a)强耦合光学微腔在失谐频率正调谐过程中光场的演化; (b) 强耦合光学微腔在失谐频率负调谐过程中光场的演化
Figure4. (a) Evolution of the optical field inside the first microcavity with strong coupling in the region of positive frequency tuning; (b) evolution of the optical field inside the first microcavity with strong coupling in the region of negative frequency tuning.

2 -->

3.2.孤子产生后的调谐过程

亮孤子是光学微腔中重要的一种光场形式, 它对应的光谱是宽带的梳状光谱, 梳齿间的频率间隔可以从十几吉赫兹至几百吉赫兹, 弥补了传统基于锁模激光器的光频梳重复频率受到腔长限制的缺点^[24]. 因此, 需要研究在失谐参量调谐过程中产生的光孤子状态. 研究发现, 当腔内产生孤子后, 选取合适的失谐参量可维持腔内稳定的孤子状态. 对图2(a)中产生的亮孤子光场进行调谐, 设置失谐参量δ₁ = 1.201 × 10² m^–1, δ₂ = 8.809 m^–1, 亮孤子可在微腔内稳定存在, 光场演化的过程如图5(a)所示, 在初始阶段光场发生振荡, 对应到图5(d)和图5(e)中两个微腔内的光功率以及D端口和T端口输出光功率曲线也出现振荡. 经过一段时间振荡后, 光场分布变得稳定, 此时腔内的非线性、色散、损耗等作用处于平衡状态. 需要特别说明的是, 此阶段抽运功率降低为1 W, 因为过高的抽运功率会使得非线性效应对腔内光场的分布起到主要作用, 导致腔内模数混乱, 出现混沌光场. 图5(b)对比了调谐过程中的初始光场和最终稳定的光场分布, 由于抽运功率降低, 稳定后的光场峰值功率略有下降, 光谱如图5(c)所示, 腔内也仍然保持宽带的梳状光谱.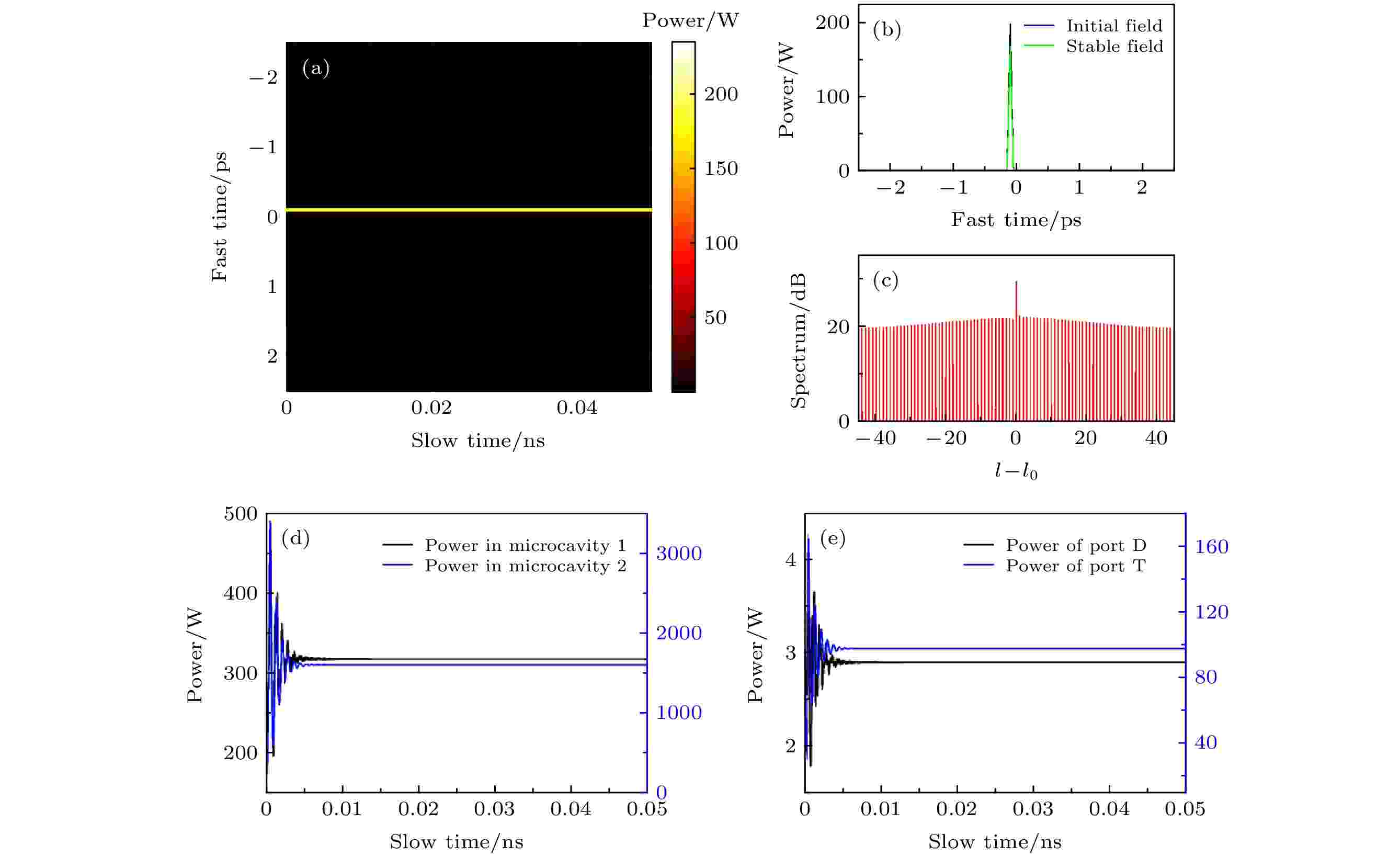
图 5 (a) 亮孤子在腔内稳定存在的演化过程(δ₁ = 1.201 × 10² m^–1, δ₂ = 8.809 m^–1, P_in = 1 W); (b) 亮孤子的光场分布; (c) 亮孤子的光谱图; (d) 两个微腔内的光功率随时间的变化曲线; (e) D端口和T端口输出功率随时间的变化曲线
Figure5. (a) Evolution of the stable existence of bright soliton in the microcavity (δ₁ = 1.201 × 10² m^–1, δ₂ = 8.809 m^–1, P_in = 1 W); (b) field distribution of the bright soliton; (c) spectrum of the bright soliton; (d) curves of the dual power inside the dual coupled microcavities vary with the slow time; (e) curves of the dual power of Port D and T vary with the slow time.

通过对亮孤子光场进行不同的调谐, 可以得到其他形式的光场. 仍然对图2(a)中的亮孤子进行调谐, 当按照图2(a)中的调谐方式产生亮孤子后, 保持第二个微腔的失谐频率Δf₂ = 770 GHz不变, 对应的失谐参数δ₂ = 16.1411 m^–1, 第一个微腔的失谐频率Δf₁仍然以12.73 GHz/μs的速度变化. 此外, 为避免抽运功率过高引起的非线性效应, 抽运功率同样减小为P_in = 1 W. 这一过程的光场演化情况如图6(a)所示. 图6(a)给出了不同时刻的光场分布, 由于失谐参量δ₁增加, 导致腔内的MI作用加强, 孤子脉冲逐渐分裂成多脉冲形式的光场. 在初始阶段, 中间脉冲的功率较强, 两侧的脉冲功率较弱, 在频率失谐引起的MI作用下, 中间脉冲的功率逐渐降低, 光场演化成等振幅的9个脉冲(图6(a)中的红色曲线), 即多脉冲形式的光场. 对应的光谱如图6(b)所示, 在梳状光谱的基础上, 梳齿强度增加了明显的慢调制, 相邻两个峰值的之间相差了9FSR. 随着Δf₁的不断增加, 腔内失谐也越来越严重, 光场也会逐渐演化为直流光场, 除抽运模式外腔内无其他的模式产生.
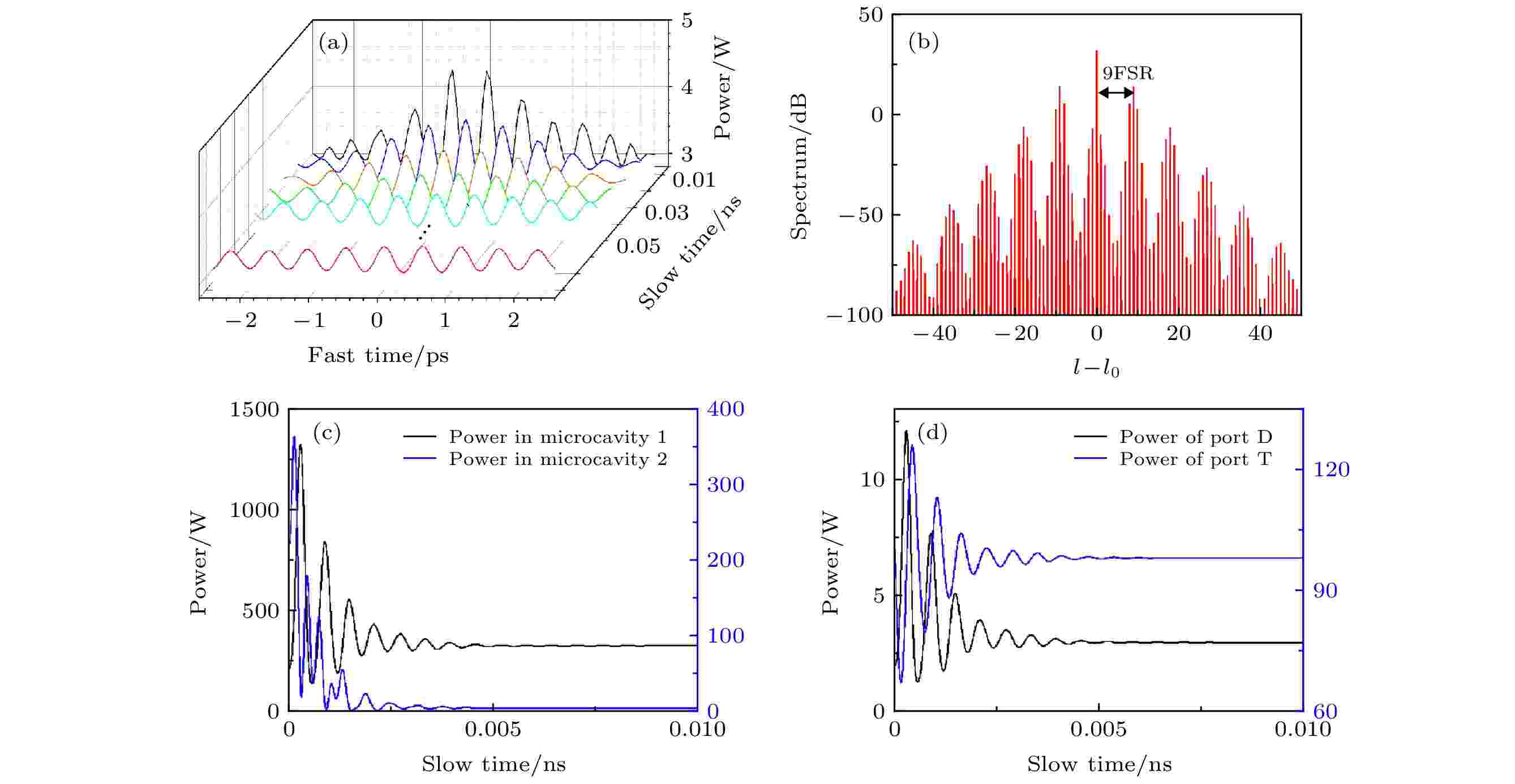图 6 (a) 亮孤子向多脉冲光场演化的过程(δ₂ = 16.1411 m^–1, Δf₁初始值为770 GHz, 以2.73 GHz/μs的速度变化, P_in = 1 W); (b) 多脉冲光场的光谱图; (c) 两个微腔内的光功率随时间的变化曲线; (d) D端口和T端口输出功率随时间的变化曲线
Figure6. (a) Evolution of a bright soliton to a multi-pulse optical field (δ₂ = 16.1411 m^–1, the initial value of Δf₁ is 770 GHz, and the change speed of Δf₁ is 2.73 GHz/μs, P_in = 1 W); (b) spectrum of the multi-pulse; (c) curves of the dual power inside the dual coupled microcavities vary with the slow time; (d) curves of the dual power of Port D and T vary with the slow time.

本文在耦合微腔的非线性薛定谔方程的基础上, 讨论了双微腔频率调谐过程中腔内光场的演化. 研究结果表明, 在正调谐区域中, 光场的演化可明显地分为四个阶段. 当失谐频率较小, 失谐参量接近零点的区域, 微腔内产生无规则的混沌光场, 两个微腔内的功率出现剧烈的振荡, 但总体呈增长的趋势. 随着失谐频率的增加, 第一个光学微腔内的光场发生突变, 在随机的位置产生若干脉冲, 这些脉冲在演化过程中逐渐消失, 最终剩下微腔中心处的单脉冲, 即腔内产生亮孤子. 这一过程中, 腔内的光功率骤降. 由频率调谐过程激发出的亮孤子在腔内稳定存在一段时间后消失, 光场变为近似直流的分布, 腔内功率也处于较弱的水平.
在负调谐区域中, 也可将光场的演化划分为四个阶段. 初始时, 由于失谐作用不明显, 在抽运的作用下腔内只存在混沌形式的光场分布. 在频率调谐过程中, 由于MI的作用, 混沌光场逐渐演化为高功率的 “图灵环”, 腔内可存在36个形状近似的脉冲. 进一步频率调谐后, 光场发生变化, 原先的36个脉冲演化为41个脉冲, 功率也相应减小. 最后在腔内失谐严重的情况下, 腔内演变为直流光场.
根据以上频率调谐过程, 耦合微腔没有发生频率失谐, 或者失谐参量接近0时, 腔内只能形成混沌形式的光场分布, 因此低失谐并不利于腔内亮孤子或者多脉冲形式的光场产生. 亮孤子只有在正失谐区域中能够被激发, 并且存在区域较小. 而当双微腔耦合强度过大时, 强耦合和模式劈裂效应会造成腔内光场分布混乱, 散射损耗增大, 在频率调谐过程中无法激发出稳定的亮孤子, 因此在实际中要尽量避免这种情况的发生. 对调谐过程激发出的亮孤子, 通过选取合适的失谐参量, 可使亮孤子在腔内稳定存在. 此外, 通过对第一个光学微腔继续进行失谐频率的调节, 也可将亮孤子转化为“图灵环”光场. 该理论分析结果对耦合微腔的实验研究具有重要意义.