全文HTML
--> --> -->目前大多数有关HD QKD协议的工作都集中于通过提升光子的某一种自由度的希尔伯特空间维度来提升QKD协议的信息容量[25], 例如基于空间模式、基于时间能量纠缠光子对以及基于轨道角动量的HD QKD协议等[26-31], 其中, Ali-Khan等[26]在2007年完成第一个基于时间能量纠缠光子对的HD QKD协议, 而在2017年, Sit等[29]在渥太华进行了基于轨道角动量的HD QKD协议的实地测试实验, 这些工作有力地证明了HD QKD协议的可行性. HD QKD协议不仅可以在一个自由度(degree of freedom, DOF)上进行编码, 还可以同时在多个DOF上进行编码, 即混合编码协议[32]. 例如2010年wang等[33]提出的基于DPS编码和偏振编码的HD QKD协议, 2019年Mao等[34]提出的基于RRDPS和偏振编码的HD QKD协议. 最近, 有人提出利用HD编码来提升MDI-QKD协议的安全码率, 例如Dellantonio等[31]在2018年提出的两种分别基于空间和时间模式的HD MDI-QKD协议和Cui等[35]于2019年提出的基于空间模式和偏振模式的混合编码HD MDI-QKD协议, 但是这两种协议在实际应用上都面临一些困难, 前者提出的基于空间模式编码的方案中其解码装置需要更多的单光子探测器, 基于时间模式编码的方案中对其编码装置的带宽要求更高, 而后者提出的混合编码方案需要分辨高维贝尔态, 所以目前该协议在实验上仍然是一个挑战[25].
本文提出了一种另外一种基于相位和偏振的混合编码HD MDI-QKD协议. 该协议利用了光子的相位和偏振两种自由度进行编码[4,8-9], 但是解码装置还是和原MDI-QKD协议一样, 只利用了4个单光子探测器(single-photon detector, SPD)进行部分贝尔态检测(bell-state measurement, BSM)[4], 因此该协议完全可以利用现有实验条件实现. 而且该协议不需要用户端增加其设备的重复频率就可以增加系统的安全码率, 所以该协议可能在未来具有潜在的应用前景.
本文的安排如下. 第2节详细介绍了本协议的编解码规则. 第3节在考虑某些实际情况的影响下, 得出该协议的安全码率, 并且进行数值仿真, 证明该协议对于安全码率的提升. 第4节讨论该协议的实验实现需要满足的条件并且在第5节给出本文的结论.
图 1 基于混和编码的MDI-QKD协议原理图. 其中, LD为光源, Pol-M, PM和IM分别为偏振调制器、相位调制器和强度调制器, DL为光延时线, BS为50:50的光分束耦合器, PBS为偏振分束器, DH和DV为单光子探测器. 首先, Alice和Bob分别通过Pol-M将偏振信息加载到光脉冲上, 然后又通过PM和IM加载时间-相位信息. Charlie将接收两者发出的光子并进行部分BSM, 然后公开其测量结果. Alice和Bob通过基比对然后利用Charlie所公开的BSM结果就能在他们原始密钥之间建立关联Figure1. Schematic diagram of MDI-QKD protocol based on hyper-encoding. LD is the light source. Pol-M, PM and IM are polarization modulator, phase modulator and intensity modulator, respectively. DL is the optical delay line, BS is the 50:50 optical beam splitter, PBS is the polarization beam splitter, DH and DV are single-photon detector. First, Alice and Bob load the polarization information to the light pulse through Pol-M, respectively, and then load the phase information through PM and IM. Charlie or Eve will receive the photons emitted by both and perform part of the BSM, and then disclose their measurements. Alice and Bob can correlate their original keys by comparing the basis information and using Charlie's published BSM results.
本协议的编码过程与BB84协议类似, 不同之处在于要同时利用偏振和相位这两个自由度对光脉冲进行调制. 首先Alice和Bob分别从两组共轭的偏振基Z基和X基中随机选取一个偏振态, 然后通过Pol-M将偏振比特(Po-bits)信息加载到光脉冲上. 接着光脉冲通过50∶50的分束器(BS)和光延时线(DL)后被分为参考和信号两种模式, 在Alice端的两个模式分别标记为ar, as, 在Bob端的两个模式分别标记为
2
2.1.相位比特在X基中选择
首先考虑相位比特在X基中选取的情况, 在不考虑编码误差的情况下, Alice和Bob制备的量子态可以表示为
接下来, 将详细介绍该协议的解码过程. 从(1)式可以看出, 到达Charlie端进行干涉的光子模式分为两大类, 一类是双光子干涉, 包括第一项和第四项, 另一类是单光子干涉, 包括中间两项. 因此, 后文会继续分为两种情况讨论BSM的结果以及对应的解码规则.
3
2.1.1.双光子干涉
对于双光子干涉的一类, 加载的相位
将BB84协议的四种偏振态代入(4)式中就可以得到BSM的结果. 显然, 该协议的解码过程与偏振编码MDI-QKD协议类似, 唯一的区别是前者可能在r和s两个时刻发生符合计数事件. 根据Charlie公布的符合计数事件和Alice与Bob所使用的基, 他们就可以知道其数据比特之间的关联性. 这里以一个简单的例子进行说明, 当
a)事件D1: a端的两个探测器在r时刻或者s时刻同时响应;
b)事件D2: a端的DV探测器和b端的DH探测器在r时刻或者s时刻同时响应;
c)事件D3: a端的DH探测器和b端的DV探测器在r时刻或者s时刻同时响应;
d)事件D4: b端的两个探测器在r时刻或者s时刻同时响应;
其他的情况也可以做类似的分析, 下面分析单光子干涉的情况.
3
2.1.2.单光子干涉
对于单光子干涉的情况, 入射态的剩余两项经过50∶50分束器的作用后的结果可以由式得到:1)j = k且
2)
3)
4)
| Alice & Bob | $ {\theta }_{\mathrm{a}}-{\theta }_{\mathrm{b}} $ | |
| $0$ | $ \pm {\text{π}}$ | |
| $j = k$且$j, k \in X$ | A0, B0 | A1, B1 |
| $j \ne k$且$j, k \in X$ | A0, B1 | A1, B0 |
表1当相位比特在X基中选择时, 本协议单光子干涉的第3类和第4类情况的BSM结果比较
Table1.BSM results for class 3 and class 4 cases of single-photon interference in this protocol are compared when phase bits are selected in the X basis.
由表1可知, 在第三类和第四类情况下, 只要事件A0(A1)发生, 那么就可以断定发送方的Ph-bits相同(相反). 对于B0和B1事件, 发送方可以通过公布其Po-bits的信息, 来获取Ph-bits的信息.
5)j与k所代表的Po-bits相同, 且
由于对称性, 容易得出关于偏振基不匹配的其他三种情况的干涉结果也是类似的, 这里就不再赘述. 上文对所有相位比特在X基中选择的情况进行了讨论, 下文将分别讨论相位比特在Z基中选择和相位比特在不同基中选择的情况.
2
2.2.相位比特在Z基中选择时
接下来讨论相位比特在Z基中选择的情况. 假设用l和m和分别表示Alice和Bob选取的Ph-bits, 即l (m) = 0 (1)时表示Alice (Bob)选择的Ph-bits为0 (1). 下面分情况讨论解码过程.1)
2)
2
2.3.相位比特在不同的基中选择时
接下来讨论当相位比特的基不匹配的情况. 根据l, m是否相等以及属于两种不同的基, 可以分成四种不同的情况讨论, 但是又根据Alice和Bob的对称性以及比特0, 1之间的对称性, 发现只需要讨论其中一种情况就够了. 下面以
| 偏振基 | 相位基 | |||||||
| $l, m \in Z$ | $l, m \in X$ | 相位基不匹配 | ||||||
| Flip | No flip | Flip | No flip | Flip | No flip | |||
| $j, k \in Z$ | C0, D1, D2, D3, D4 | 0 | A0, B0, B1, D1, D2, D3, D4 | A1 | D1, D2, D3, D4 | 0 | ||
| $j, k \in X$ | C0, D2, D3 | D1, D4 | A0, D2, D3, B0 $(j = k)$ B1$(j \ne k)$ | A1, D1, D4, B0 $(j \ne k)$ B1$(j = k)$ | D2, D3 | D1, D4 | ||
| 偏振基不匹配 | C0 | 0 | A0 | A1 | 0 | 0 | ||
表2本协议的解码规则, 其中flip表示比特翻转, No flip表示比特相同, C0表示事件{在r时刻和s时刻分别有且只有一个探测器响应}, 0表示没有成功事件
Table2.The decoding rules of this protocol, where flip represents the bit flip, No flip represents the same bit, C0 represents the event {there is only one detector response at time r and time s respectively}, and 0 indicates that no success event occurred.
2
2.4.高信息容量
本节将分析在理想单光子源的情况下, 本文提出的协议与原始协议相比的优势. 在后文中将比较在诱骗态协议下的优势.将本协议所有情况下的信息容量总结在表3中. 假设选择两种基的概率相等, 那么由表中的数据可以计算出本协议每个光子传送的信息容量, 即光子利用效率为11/32, 而原始MDI-QKD协议, 无论是基于相位编码还是偏振编码, 其光子利用效率都只有1/4, 那么容易得出本协议相比于原始MDI-QKD协议提升的效率为
| 偏振基 | 相位基 | ||||||
| $l, m \in Z$ | $l, m \in X$ | 相位基不匹配 | |||||
| $l = m$ | $l \ne m$ | 单光子干涉 | 双光子干涉 | ||||
| $j, k \in Z$ | $j = k$ | 0 | 1 Ph-z | 1 Ph-x | 0 | 0 | |
| $j \ne k$ | 1 Po-z | 1 Ph-z | 1 Po-z | 1 Po-z | 1/2 Po-z | ||
| $j, k \in X$ | $j = k$ | 1/2 Po-x | 1 Ph-z | 1 Ph-x | 1/2 Po-x | 1/4 Po-x | |
| $j \ne k$ | 1/2 Po-x | 1 Ph-z | 1 Ph-x | 1/2 Po-x | 1/4 Po-x | ||
| 偏振基不匹配 | 0 | 1 Ph-z | 1/2 Ph-x | 0 | 0 | ||
表3本协议不同情况下可能获得的比特信息及其相应的概率. 其中Ph (Po)-z (x)表示获取以Z(X)基编码的Ph-bits(Po-bits)信息
Table3.The bitwise information that may be obtained under different circumstances in this agreement and its corresponding probability. Where Ph(Po)-z(x) represents the Ph-bits (Po-bits) information encoded by z (x) basis.
2
3.1.诱骗态方法
众所周知, 诱骗态方法的目的是为了更加紧凑地估计单光子响应率的下界
用下标A或B来定义光源是属于Alice或者Bob. 在光子数空间中, 四种不同强度光源发出的量子态可以分别表示为
| Bob | Alice | ||||||
| Po-Z | Po-X | ||||||
| Ph-Z | Ph-X | Ph-Z | Ph-X | ||||
| ${p_z}$ | $1/2{p_y}$ | $1/2{p_y}$ | ${p_x}$ | ||||
| Po-Z | Ph-Z | ${p_z}$ | 1/4 z-po 1/2 z-ph | 1/4 z-po | 1/2 z-ph | 0 | |
| Ph-X | $1/2{p_y}$ | 1/4 z-po | 1/4 x-ph 1/2 z-po | 0 | 1/4 x-ph | ||
| Po-X | Ph-Z | $1/2{p_y}$ | 1/2 z-ph | 0 | 1/4 x-po 1/2 z-ph | 1/4 x-po | |
| Ph-X | ${p_x}$ | 0 | 1/4 x-ph | 1/4 x-po | 1/4 x-po 1/2 x-ph | ||
表4本协议的诱骗态方案以及不同强度光源所获得的比特信息. 其中Po-X(Z)和Ph-Z(X)分别表示加载信息时偏振基选择Z(X)基和相位基选择Z(X)基,
Table4.The scheme of decoy state and the bit information obtained by different intensity light sources. Where, Po-X (Z) and Ph-Z (X) respectively represent the polarization basis selection Z(X) basis and phase basis selection Z(X) basis when loading information,
显然, 本协议的诱骗态方法所获取的安全密钥由Ph-bits和Po-bits两部分组成. 但是, 与原MDI-QKD协议不同的是, 本协议不同源lr所获得的不同基的比特信息是不一样的(如表5所示), 那么这就导致不同源的X基和Z基的单光子对的响应率不相等, 即
| Bob | Alice | |||||||
| z | y | x | ||||||
| Ph | Po | Ph | Po | Ph | Po | |||
| z | 1/2 z | 1/4 z | 1/4 z | 1/8 z | 0 | 0 | ||
| y | 1/4 z | 1/8 z | 1/8 z 1/16 x | 1/8 z 1/16 x | 1/8 x | 1/8 x | ||
| x | 0 | 0 | 1/8 x | 1/8 x | 1/2 x | 1/4 x | ||
表5本协议的诱骗态方法获得的比特信息. 其中x, y, z分别表示三种强度的光源, Ph和Po分别表示相位比特和偏振比特, 数字表示获得比特信息的概率, z和x表示获得信息所属的基
Table5.The bit information obtained by the decoy state method of this protocol. Where x, y and z represent the light source of three kinds of intensity, Ph and Po respectively represent phase bit and polarization bit, fraction represents the probability of obtaining bit information, and z and x represent the basis to which the obtained information belongs.
下面以本协议获取的Ph-bits信息去估计单光子对响应率的下界
得到
2
3.2.数值仿真
本节将展现本协议的数值仿真结果, 并与文献[36]的结果进行比较. 为了简化计算, 只关注对称的情形, 即Alice端的实验装置与Bob端完全一样, 两者信道也完全相同. 并且假设Charlie端的4个探测器是相同的, 即它们有相同的暗计数和探测效率, 而且探测效率不依赖于入射的信号. 除此之外, 还假设两发送端都是随机弱相干态光源, 那么以强度为
| L / km | ${\mu _x}$ | ${\mu _y}$ | ${\mu _z}$ | ${p_x}$ | ${p_y}$ | ${p_z}$ | |
| a | 40 | 0.0601 | 0.2907 | 0.2992 | 0.4636 | 0.0310 | 0.4009 |
| b | 50 | 0.0659 | 0.3200 | 0.2744 | 0.5212 | 0.0351 | 0.3283 |
表7本协议两种条件下的参数优化结果.
Table7.Parameter optimization results under the two conditions of this agreement.
首先利用文献[38]中的MDI的线性模型模拟出原始MDI协议中不同源和不同基的响应率和误码率, 当然, 与文献[38]中的模型不同的是, 在这一过程中考虑了本协议每个比特解码过程都会使用8个SPD的门, 也就是说通过时分复用的方法每台SPD都使用了两个门, 而不是1个门. 此时如果令
为了便于和文献[36]中的结果进行比较, 在仿真中也使用了两组不同的参数, 具体参数见表6. 安全码率随距离变化的数值仿真结果见图2和图3, 图中红色实线为本协议的结果, 黑色虚线为文献[36]的结果. 从图中可以看出, 本协议对于安全密钥确实有一定的提升作用. 具体来说, 本协议在两种条件下分别使最优安全码率提升了52.83%和50.55%, 相关结果总结在表8中.
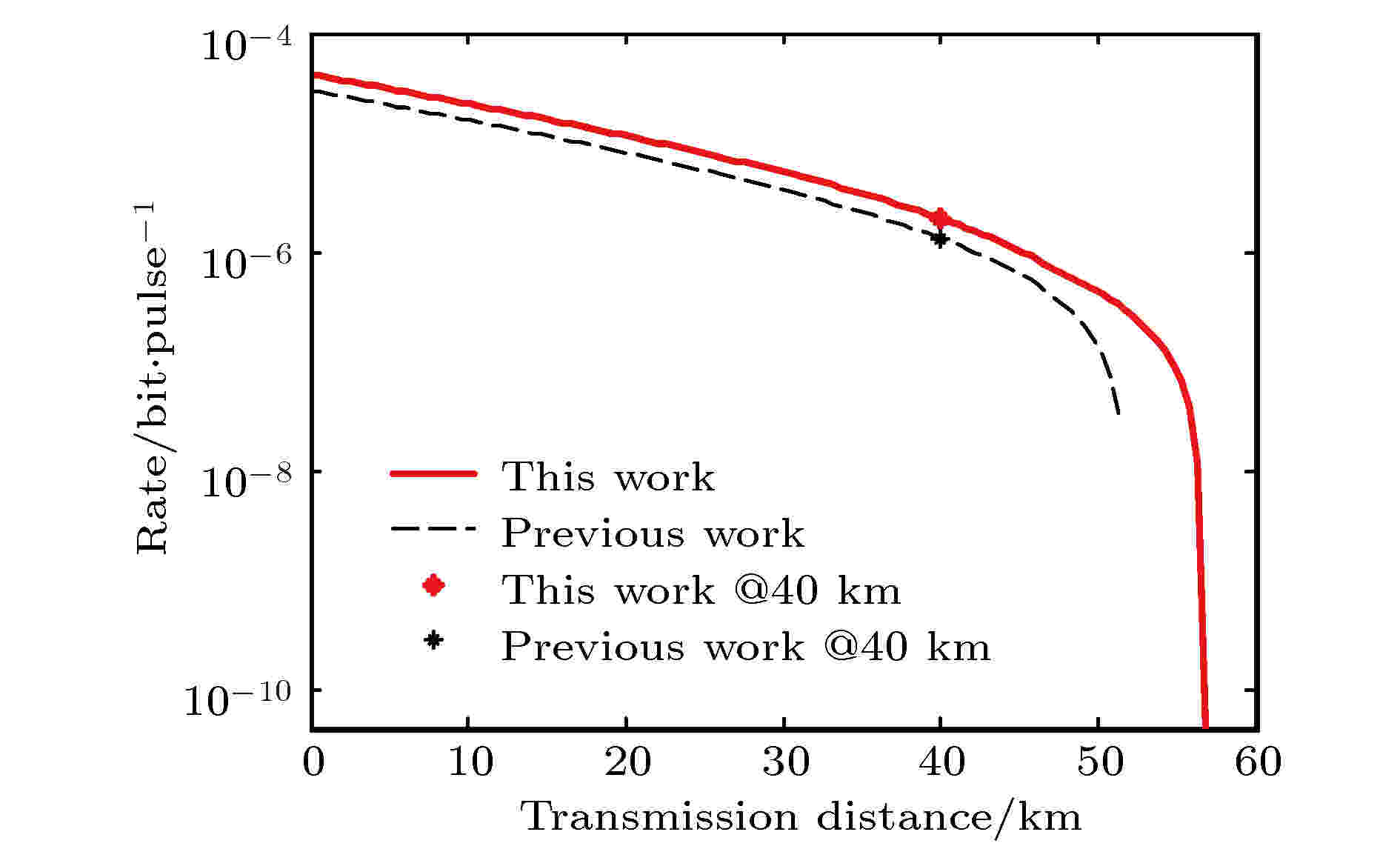图 2 不同协议的最优安全码率比较. 这里我们利用了表6第a列的条件, 并且是以40 km处的安全码率为优化目标, 本协议的参数优化结果见表7第a列. 图中红色实线表示本协议的结果, 黑色虚线表示文献 [36]的结果Figure2. Comparison of optimal security key rates for different protocols. Here, we take advantageof the conditions in column a of Table 6, and take the security key rate at 40 km as the optimizationobjective. The parameter optimization results of this protocol are shown in column a of Table 7.The solid red line in the figure represents the result of this agreement, and the dotted black linerepresents the result of Ref. [33].
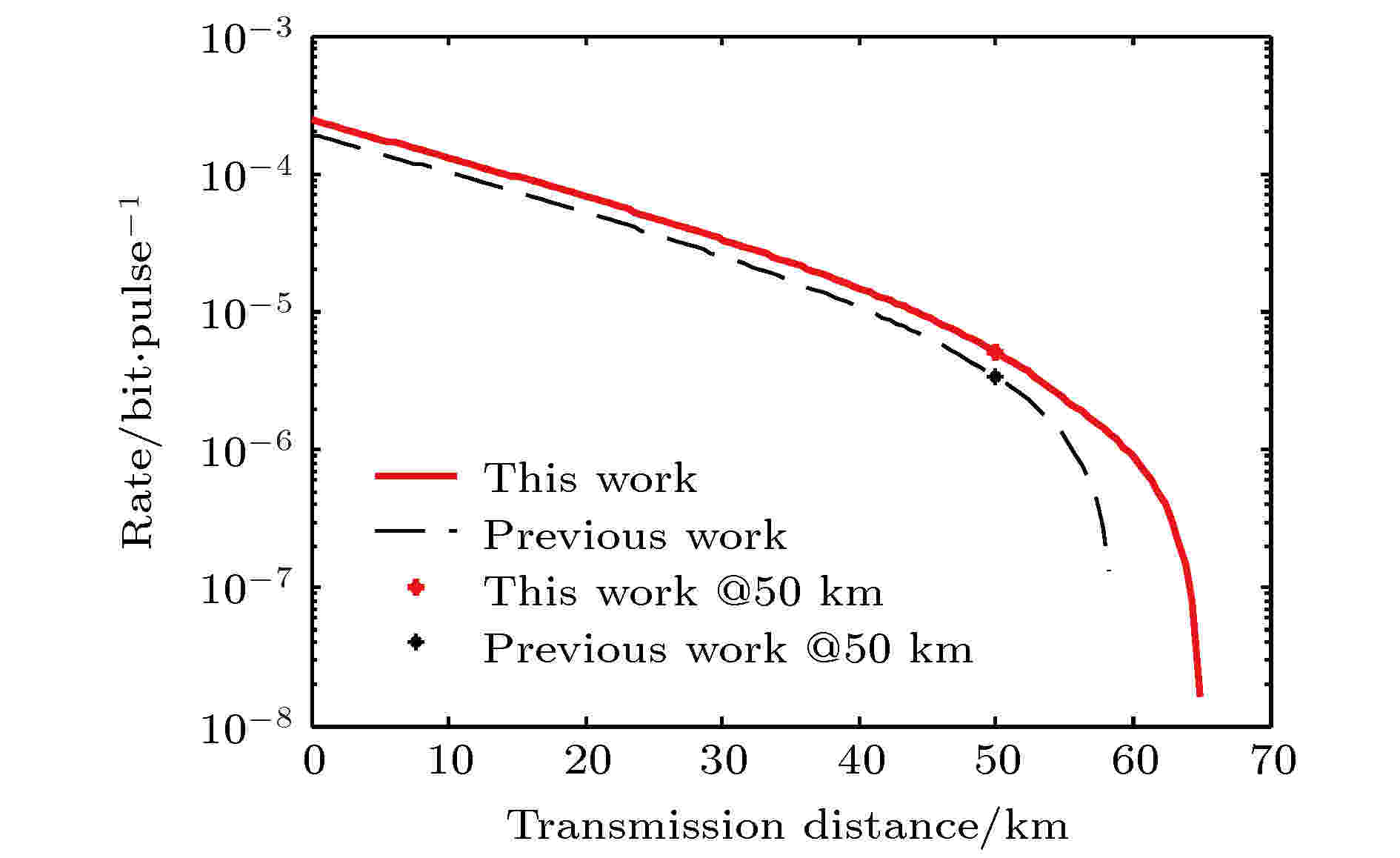图 3 不同协议的最优安全码率比较. 这里利用了表6中第b列的条件, 并且是以50 km处的安全码率为优化目标, 本协议的参数优化结果见表7中第b列. 图中红色实线表示本协议的结果, 黑色虚线表示文献[36]的结果Figure3. Comparison of optimal security key rates for different protocols. Here, we take advantage of the conditions in column b of Table 6, and take the security key rate at 50 km as the optimization objective. The parameter optimization results of this protocol are shown in column b of Table 7. The red solid line in the figure represents the result of this agreement, and the black dotted line represents the result of Ref. [36].
| ${e_0}$ | ${e_{\rm{d}}}$/% | ${p_{\rm{d}}}$ | ${\eta _{\rm{d}}}$/% | ${f_{\rm{e}}}$ | N | $\epsilon $ | |
| a | 0.5 | 1.5 | $6.02 \times {10^{ - 6}}$ | 14.5 | 1.16 | ${10^{10}}$ | ${10^{{\rm{ - }}7}}$ |
| b | 0.5 | 1.5 | ${10^{ - 7}}$ | 40 | 1.16 | ${10^9}$ | ${10^{{\rm{ - }}7}}$ |
表6数值模拟相关参数.
Table6.Relevant parameters of numerical simulation.
| L / km | ${R_{\rm{p}}}$ | ${R_{\rm{t}}}$ | Improvement/% | |
| a | 40 | $1.3394 \times {10^{ - 6}}$ | $2.047 \times {10^{ - 6}}$ | 52.83 |
| b | 50 | $3.3983 \times {10^{ - 6}}$ | $5.116 \times {10^{ - 6}}$ | 50.55 |
表8最优安全码率的比较.
Table8.Comparison of optimal security key rates.
接下来将从两方面来说明为什么数值模拟部分只对文献[36]的结果进行比较. 一方面, 相比对于其他的基于高维编码的MDI-QKD协议来说, 本协议主要的优势在于实验实现更加简单, 而在安全码率上不一定有提升, 所以与其他的基于高维编码的MDI-QKD协议的数值模拟结果的比较并不能完全体现本协议的优势; 另一方面, 对于原MDI-QKD协议来说, 四诱骗态协议[36]是目前在实验中性能最好的诱骗态MDI-QKD协议. 因此, 基于上述理由, 证明本协议相比于原四诱骗态MDI-QKD协议在性能上的提升已经足够说明本协议的意义.
一方面, 对于原始的时间编码MDI-QKD协议来说[8], 要改进为本协议需要满足三个条件: 首先需要在发送方增加偏振编码装置, 其次信道中需要增加偏振补偿模块[40-43], 最后接收方需要增加两台单光子探测器. 目前, 第一个条件很容易满足. 对于第二个条件, 最近的文献中已经报道了最远达到68 km的偏振补偿实地测试实验[43], 说明基于偏振编码的协议已经可以满足在较短距离的应用. 对于第三个条件, 在星型量子网络结构中[44-45], 接收方增加两台单光子探测器就可以使多个用户的密钥效率提高, 可认为这种成本增加是值得的.
另一方面, 对于原始的偏振编码MDI-QKD协议来说[4], 与本协议不同的地方在于三点: 其一需要在发送方增加相位编码装置; 其二需要增加相位补偿装置; 其三为需要使接收方单光子探测器的饱和计数率增加一倍. 前两个条件都可以利用现有的实验设备实现[23], 针对最后一个条件同样以星型量子网络为例来进行说明, 此时仅仅只需要一个接收方的成本增加, 而且所有的本地用户的设备重复频率不用变化, 就可以使全部本地用户的密钥率得到提高, 所以同样认为这种成本增加是可以接受的.
另外, 需要指出的是, 上述有关利用4强度诱骗态方法[36]来估计本协议单光子对的相关参数的分析还比较粗糙, 更加细致的讨论可能会进一步提升安全码率. 比如在估计参数
感谢清华大学物理系于宗文博士的讨论.
