摘要:准二维范德瓦耳斯磁性材料CrSiTe₃同时具有本征磁性与半导体能带结构, 在光电子学和纳米自旋电子学领域中具有广泛的应用, 近年来吸引了广大科研工作者的兴趣. 利用超快太赫兹光谱技术, 本文对准二维范德瓦耳斯铁磁半导体CrSiTe₃进行了系统的研究, 包括太赫兹时域光谱, 光抽运-太赫兹探测光谱及太赫兹发射光谱. 实验结果表明, 样品的太赫兹电导率随温度的变化表现得十分稳定, 且样品ab面对太赫兹波的响应呈现为各向同性; 800 nm光抽运后的光生载流子表现为一种双指数形式的弛豫变化, 复光电导率可以用Drude-Smith模型很好地拟合, 光载流子的弛豫过程由电子-空穴对的复合所主导; 飞秒脉冲入射到样品表面后可以产生太赫兹辐射, 且具有0—2 THz的带宽. 本文给出了CrSiTe₃在光学及太赫兹波段的光谱, 为其在电子及光电子器件方面的设计和优化提供了借鉴与参考.
关键词: 范德瓦耳斯铁磁半导体/
太赫兹光谱/
时间分辨光谱

English Abstract

全文HTML

--> --> -->

自石墨烯发现以来, 二维材料由于其在材料科学及光电子学等领域的巨大应用价值一直是学术界的研究热点^[1-3]. 根据各向同性海森伯模型, 在二维材料体系中由于热涨落抑制了自发对称性破缺, 因此不能实现长程磁有序^[4,5]. 然而, 近年来, 科研人员发现具有二维层状结构的磁性材料(如CrSiTe₃, Fe₃GeTe₂, CrI₃等)低温下其剥离到单层或少数层情况下依然保持着长程磁有序, 从而引发了人们极大的关注^[6-9]. 2017年, Huang等^[7]利用磁光克尔效应显微镜证明了单层的CrI₃是一种具有面外自旋取向的伊辛铁磁体, 表明铁磁性能够持续到单层极限. 2018年, Zhang等^[10]在原子层厚度的Fe₃GeTe₂中发现了二维巡游铁磁性, 更重要的是, 他们通过锂离子插层调控, 在Fe₃GeTe₂薄层中获得了室温以上的铁磁有序温度, 为未来研发室温可用的磁电子学器件提供了可能. 2019年, Gao等^[11]运用自旋极化扫描隧道显微镜技术, 探索并阐明了双层二维磁性CrBr₃的层间堆叠和磁耦合间的关联, 为二维自旋器件的研制提供了思路. 二维磁性半导体为理解二维磁体的基态、激发态和磁动力学提供了理想的研究模型^[6], 也为对二维磁性的控制及对单原子层的磁阻、磁光和磁电器件的设计提供了机遇, 展现了巨大的应用前景.
作为一种准二维范德瓦耳斯磁性半导体材料, CrSiTe₃(CST)可以被剥离至少数层甚至单层, 且同时保留着本征磁性与半导体带结构^[12-15], 是光电子学和纳米自旋技术应用的理想材料, 近年来引发了人们极大的兴趣. CST由$ R\bar{3} $ 空间群和C_3i点群所描述, 在常温下为顺磁, 而在居里温度约33 K时发生铁磁相变^[14,16]. 2014年, Li等^[12]通过第一性原理计算发现, 当块体CST厚度降低至单层时, 其铁磁性和半导体性可以共存, 更有意思的是, 单层的居里温度比块体更高. 2015年, Casto等^[14]结合光学测量和第一性原理电子结构计算表明, CST是一种间接带隙半导体, 其间接带隙和直接带隙分别为0.4 eV和1.2 eV; 热导率测量显示了很强的磁子-声子散射效应. 2016年, Lin等^[13]实现了在Si/SiO₂衬底上将块体CST剥离至单层和少数层, 为二维CST磁体的存在提供了直接证据. 而最近, Zhang等^[17]结合多体相互作用的理论计算及角分辨的光电发射光谱(ARPES), 探究了CST中的强电子关联以及铁磁超交换机理. 目前, 研究人员把大量的兴趣和注意力放在了CST的磁性方面, 而在光学甚至是THz波段的研究却鲜有报道.
THz波是频率位于0.1—10.0 THz的电磁波, 由于其在成像、通信及医学等领域的巨大应用价值已成为近年来科研领域的研究热点. THz光子能量覆盖了激子结合能、半导体量子点带内跃迁和声子共振等能量范围, 及对载流子极其敏感的特性, 结合THz脉冲具有亚皮秒的时间分辨特征, THz光谱技术, 如THz时域光谱, 光抽运-THz探测光谱和THz发射光谱, 在表征材料基本参数, 提取频率分辨的复电导率和介电响应, 以及探究材料的载流子动力学、反铁磁共振及瞬态光电流等方面已成为一种强有力的工具^[18-21]. 用THz光谱对二维半导体材料的研究已经屡见不鲜, 如少层WS₂中电子-空穴对的复合^[22], 单层MoS₂中带电激子的形成^[23]等, 但对二维磁性半导体的研究未见报道.
本文以时间分辨的THz光谱为手段, 系统研究了准二维磁性半导体材料CST的THz时域光谱及光载流子动力学特性. 结果表明, 透射的THz波对温度几乎没有依赖性; 光激发后的载流子动力学表现为双指数弛豫过程, 几个皮秒的快过程和十几皮秒的慢过程, 当温度高于100 K时, 载流子弛豫寿命均随温度的增加而显著增加; 光激发CST后可以产生THz辐射, 提供了一种新型THz发射器候选者. 对CST的超快THz光谱研究将为超快、超紧凑的光电子器件的设计与调控提供重要的实验依据和参考.

实验中用到的c切的CST单晶样品是通过自助熔剂法制备的. 首先将高纯度的Cr, Si及Te粉末原料按1∶2∶6的摩尔比完全混合, 放入氧化铝坩埚中. 然后将坩埚密封在真空的石英管中, 在15 h内加热至1150 ℃. 在这个温度下保持20 h, 然后以1.5 ℃/h的速度冷却到800 ℃. 在此温度下维持5 h, 期间将多余的Si和Te用离心机中去除, 最终生长出尺寸约8 mm的表面有光泽的黑色CST晶体.
实验中采用如图1(c)所示的系统对样品进行THz波段的光谱研究. 所用的光源是钛蓝宝石激光放大系统, 其输出激光中心波长为800 nm, 脉冲宽度为120 fs, 重复频率为1 kHz. 激光被分成三束: 一束是超快抽运光, 用来激发样品; 一束是THz产生光, 入射到1 mm厚、(110)取向的ZnTe产生THz脉冲; 最后一束为取样光, 通过电光取样的方法获得THz波前信号. 实验中, 入射到样品上的THz波光斑直径约为2 mm, 而样品表面用于超快抽运的激发光光斑直径约为6.5 mm, 较大的激发光光斑以确保THz探测到的是均匀的光激发区域. 为了避免水蒸汽的影响, 所有的测量均是在干燥的氮气氛围中进行的. 进行变温实验时, 样品被放置在低温恒温器中, 可实现温度从5—300 K的连续调节. 在进行THz-TDS实验时, 将抽运光路挡住; 当进行THz发射实验时, 挡住抽运光束, 将CST样品替代发射ZnTe.
图 1 CST原子结构的　(a) 俯视图和 (b) 侧视图; (c) 时间分辨的超快光抽运-THz探测实验光路示意图; (d) 基于第一性原理计算的CST的能带图及 (e) 对应的态密度
Figure1. Schematic illustration of the crystal structure of CST seen from (a) the top view and (b) the side view; (c) experimental setup for time-resolved ultrafast optical pump-THz probe spectroscopy; (d) the calculated band structure and (e) density of states of CST single crystal by means of the first-principle with the Vienna ab Initio Simulation Package.

为了解CST电子结构性质, 我们采用基于密度泛函理论(DFT)第一性原理的Vienna ab initio simulation package(VASP)^[24]计算CST能带结构. 采用投影缀加平面波(projector-augmented-wave, PAW) 赝势来描述电子-离子之间的相互作用, 并使用基于Perdew-Burke-Ernzerhof (PBE)参数的广义梯度近似方法(generalized-gradient-approxi-mation, GGA)^[25]来处理交换关联相互作用. 同时用4 × 4 × 1的Monkhorst-Pack网格对布里渊区进行k点抽样. 在计算过程中截断能设为 450 eV, 所有的晶格常数和原子位置都被弛豫, 能量和力收敛精度分别为10^–6 eV和 0.01 eV/?.

如图1(a),(b)所示分别为CST原子结构的俯视图和侧视图. 每个单胞由3层以ABC顺序堆叠的CST原子层构成, 层间距为3.3 ?. 每个Cr原子位于由6个Te原子组成的稍微扭曲的八面体的中心^[13,14], 计算得到的晶格参数分别为a = b = 6.837 ?, c = 20.599 ?. 如图1(c)与1(d)所示分别为通过第一性原理计算得到的能带图和态密度图, 计算结果显示, 价带顶位于Γ点, 导带底位于Γ点和K点之间, 其直接带隙1.2 eV, 间接带隙0.43 eV, 这与Casto等^[14]实验和计算的结果十分接近.
THz-TDS可以对材料频率分辨的性质进行表征. 由于THz波与材料的相互作用, 透射后的THz波的振幅和相位会发生变化, 再结合参考信号便可以获得样品的光学参数如复折射率、复电导率和复介电常数等.
图2(a)所示为测得的透过样品后的THz时域信号与没有放置样品时的参考信号, 根据这两个信号结合样品厚度便可得到样品在THz波段的折射率. 先将这两条时域谱分别做傅里叶变换, 得到它们的振幅与相位, 然后便可得到在频域上的复透射率:
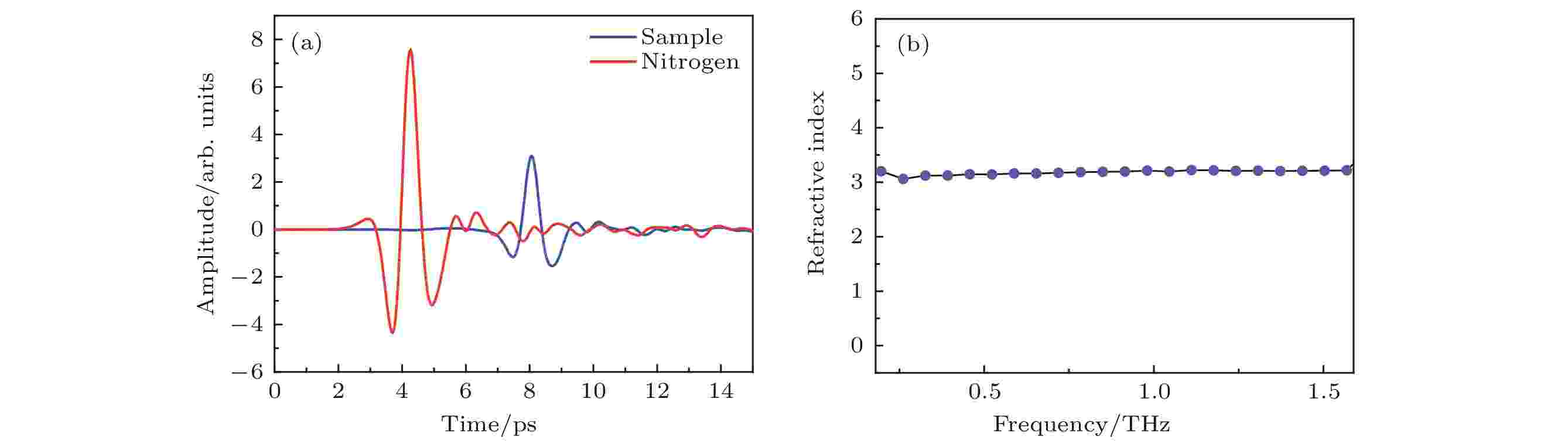图 2 (a) 透过CST样品后的THz时域信号 (蓝色) 与没有样品时的参考信号 (红色); (b) 计算的CST在THz波段的折射率
Figure2. (a) The THz-TDS signal through the sample (blue) and the reference signal (red) without placing sample; (b) the calculated refractive index of CST in THz frequency range.

$\tilde T\left( \omega \right) = \dfrac{{{{\rm{E}}_{{\rm{sample}}}}\left( \omega \right)}}{{{{\rm{E}}_{{\rm{ref}}}}\left( \omega \right)}} = A{{\rm{e}}^{{\rm{i}}\phi }},$

式中, A为样品的透射信号与参考信号在频谱上的振幅之比, ?为相位之差. 实验中样品的厚度d为0.43 mm, 再根据提取光学参数的物理模型^[26,27]便可得到样品在THz波段的折射率:

$n\left( \omega \right) = \phi \left( \omega \right) \cdot \dfrac{c}{{\omega d}} + 1,$

其中, c为真空中的光速. 如图2(b)所示为求得的CST在THz波段的折射率, 可看到0.2—1.6 THz内其平均折射率约为3.17.
由于THz电场对自由载流子有着敏感的响应, 透射THz波振幅的衰减主要与自由载流子的吸收有关, 因此透射的THz信号可以直观地反映样品的电导率信息. 如果对提取的复电导率进行如Drude或Drude-Smith模型等的拟合和分析还可以获取样品自由载流子浓度、迁移率以及载流子的局域程度等信息. 为了观测温度对THz透射信号的影响, 进而探究温度对样品电导率的影响, 我们进行了变温的THz-TDS实验.
图3(a)是CST温度依赖的THz时域谱, 图3(b)则是与之对应的经过傅里叶变换的频谱, 不同的颜色表示振幅的强度. 在实验仪器的灵敏度范围内, 从图3(a)可以看到, 透射THz信号的振幅几乎不随温度变化, 图3(b)中频谱随温度也没有显著的变化, 稍微有随温度的升高而变窄的趋势, 这可能是由于随着温度的升高, 热激发导致导带中的电子增多, 从而对THz波吸收略有增强所致, 但总体上反映出电导率随温度变化的稳定性.
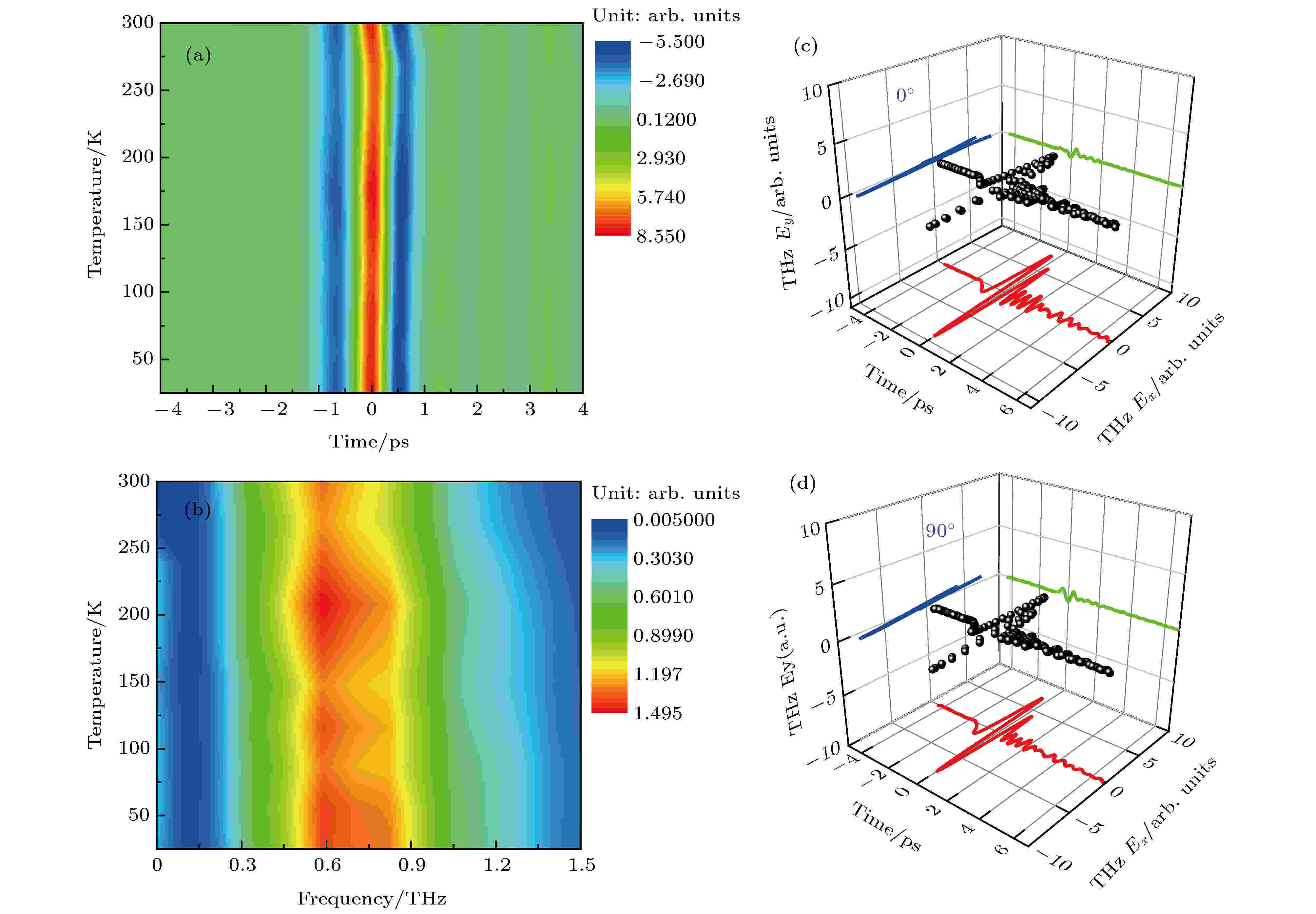图 3 (a) CST温度依赖的THz-TDS及 (b) 经过傅里叶变换后的频谱; 室温下CST晶体方位角0° (c) 和 90° (d)下的3D透射光谱
Figure3. (a) Temperature dependent THz transmission in time domain and (b) in frequency domain via Fourier transformation; 3D plot of THz transmission of CST crystal at the azimuthal angle 0° (c) and 90° (d) at room temperature.

为研究CST的(001)晶面上不同取向对THz波的调制, 室温下我们进行了转样品方位角的THz-TDS实验. 以样品的c轴为旋转轴、以30°为测量间隔将样品转动了180°, 实验结果显示, 不同方位角下透射的THz信号的偏振与振幅几乎没有变化, 这表明样品的ab面对透射THz波是各向同性的. 图3(c), (d)分别展示了样品方位角处于0°和90°时测得的THz空间时域信号.
时间分辨的超快OPTP系统可以探测非平衡态下费米面以上的载流子超快动力学以及材料的光电导响应, 利用图1(e)中的OPTP系统我们对CST光激发后的载流子动力学进行了研究. 图4为CST样品时间分辨的光激发载流子的超快动力学演化.
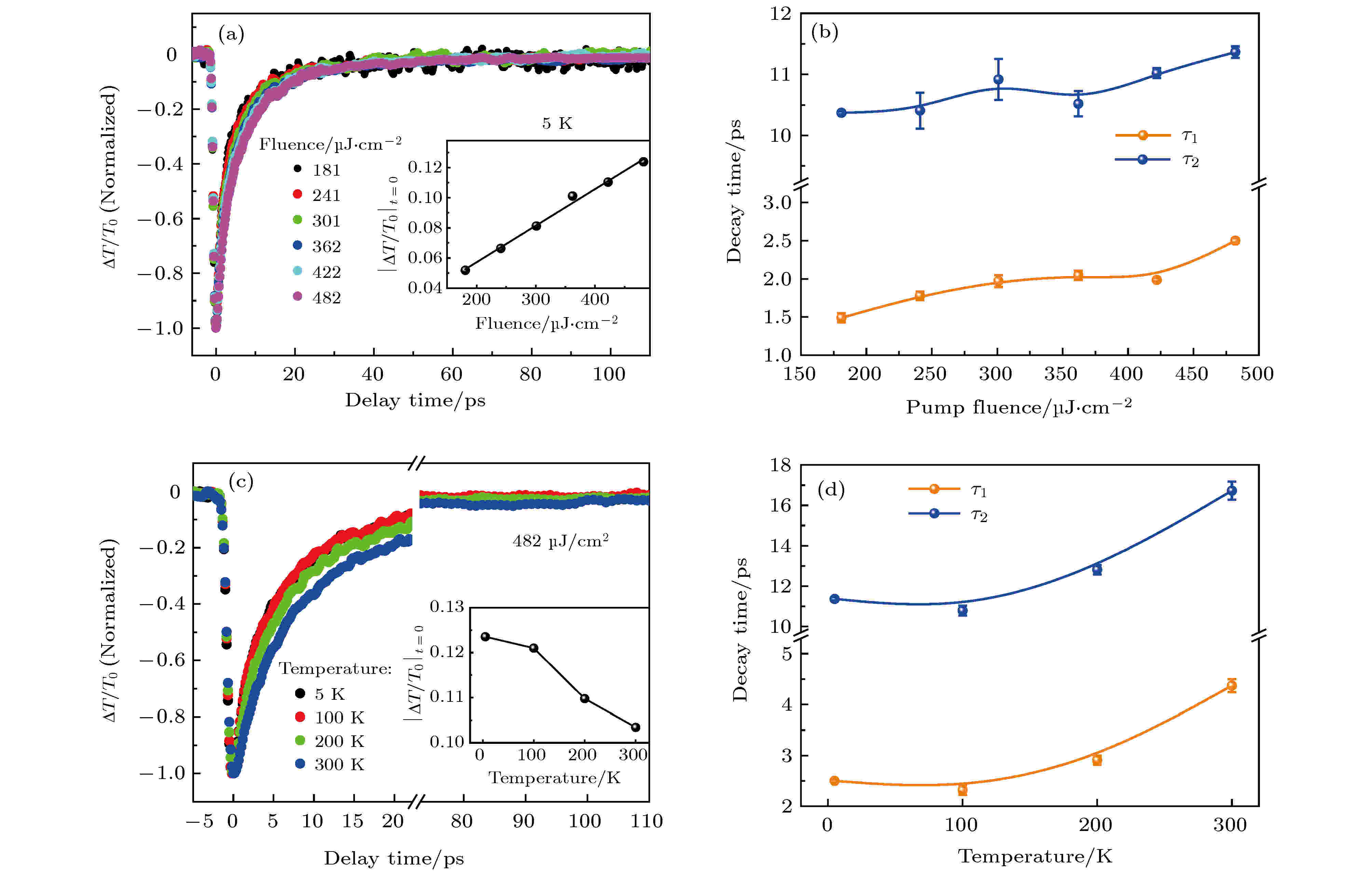图 4 (a) 温度5 K、不同抽运功率下的瞬态动力学演化ΔT/T₀, 插图为抽运-探测零时间延迟时抽运功率依赖的调制深度, 实线是线性拟合的结果; (b) 通过双指数函数拟合得到的不同抽运功率下的弛豫时间常数; (c) 抽运功率482 μJ/cm²、不同温度下的THz透射响应, 插图为抽运-探测零时间延迟时温度依赖的调制深度; (d) 通过双指数函数拟合得到的不同温度下的弛豫时间常数
Figure4. (a) The transient dynamics evolution ΔT/T₀ under various pump fluence at 5 K, inset gives the fluence dependent modulation depth at the delay time of zero, and the solid line is linear fitting; (b) the decay time constants obtained from biexponential function fitting with respect to pump fluence; (c) the THz transmission response at different temperature under pump fluence of 482 μJ/cm², inset gives the temperature dependent modulation depth at the delay time of zero; (d) the decay time constants obtained from biexponential function fitting at different temperature, the solid lines are guide to the eyes.

图4(a)为温度5 K时、不同抽运功率下归一化了的THz透射响应ΔT/T₀ = (T–T₀)/T₀, 这里的T表示光激发后透射的THz峰值信号, 而T₀表示没有激发时的THz参考信号. 可以看到光激发后样品先是表现出对THz吸收的突然增强, 然后逐渐弛豫回到平衡态. 插图所示为抽运-探测延迟时间为0时刻的调制深度, 可看出, 随着抽运功率的增大调制深度线性增大. 根据文献[14]的吸收光谱可以计算样品在800 nm处的趋肤深度约为67 nm. 应该指出的是THz透射变化与光电导响应成反比关系^[28]: $\Delta T/{T_0} \propto - \Delta \sigma $, 这里Δσ指的是THz光电导率. 根据公式σ = Neμ, 其中e为电子电荷, N与μ分别为载流子的浓度和迁移率, 可以得知材料的电导率由载流子的浓度和迁移率决定. 忽略光激发产生的热效应, 抽运光激发后, 光电导率的突然增加来源于载流子浓度的增加, 光激发使电子从价带跃迁到导带, 而空穴留在价带. 抽运功率越大, 光生载流子数量越多, 电导率的变化越大, 调制深度越大, 这与图4(a)插图中的实验结果是一致的.
为了对光载流子的弛豫时间进行定量分析, 我们用双指数衰减函数对其动力学过程进行了拟合, 表达式为

$\Delta T/{T_0} = A\cdot{{\rm{e}}^{ - t/{\tau _1}}} + B\cdot{{\rm{e}}^{ - t/{\tau _2}}} + C,$

式中, t是抽运-探测延迟时间, τ₁与τ₂是弛豫过程的寿命, A, B和C是振幅. 图4(b)为拟合得到的弛豫寿命, 可以看到, 快的寿命τ₁约为2 ps, 慢的寿命τ₂约为11 ps, 它们都随着抽运功率的增加轻微增大. 将快的过程归因于电子-声子耦合, 即激发态电子被晶格散射回导带底; 考虑到CST是间接带隙半导体, 将慢过程归因于声子或表面缺陷辅助的电子-空穴对的复合. 抽运功率越大, 产生的载流子数目越多, 由非平衡态弛豫回平衡态所需的时间则越长, 这与图4(b)中的实验结果是一致的.
为了进一步证实我们的推断, 进行了变温的OPTP测量. 图4(c)为同一抽运功率(482 μJ/cm²)、不同温度下的载流子动力学响应. 可以看到温度处于5 K和100 K时载流子弛豫快慢相当; 有趣的是, 当温度处于200 K和300 K时, 弛豫过程明显变缓. 插图为温度依赖的调制深度, 可以看出温度越高, 调制深度越小. 图4(d)为不同温度下用双指数函数拟合得到的载流子弛豫寿命, 可以看出从10 K到100 K弛豫时间轻微减少, 而当温度大于100 K时, 随着温度的升高时间常数τ₁与τ₂都明显增大, 弛豫寿命显著变长. Casto等^[14]在CST中观测到三个很强的红外声子模A_u, ¹E_u和²E_u, 当温度从10 K升高到300 K, A_u与¹E_u声子表现出了软化, 而²E_u声子随温度升高则先硬化, 当温度高于100 K再出现软化. 这与我们的实验结果是一致的, 随着温度的升高声子频率减小, 声子能量减小, 导致电子通过电子-声子相互作用弛豫回导带底所需的时间变长. τ₁从10 K到100 K弛豫时间的轻微减少可能与²E_u有关; 而τ₂也随温度升高而增加, 这可以排除表面缺陷辅助的自由电子-空穴复合这种可能性, 因为缺陷与温度没有依赖关系. 因此变温的OPTP实验证实了我们的推断, 即τ₁由电子-声子耦合主导, τ₂来源于声子辅助的电子-空穴复合.
为进一步分析光激发后的载流子弛豫及电导率动态响应, 通过公式^[29]:

$\varDelta {\sigma _{\rm{r}}} = \left( {\frac{{\cos \phi }}{A} - 1} \right)\frac{{1 + {n_{{\rm{sub}}}}}}{{{Z_0}}},$

$\Delta {{\rm{\sigma }}_{\rm{i}}} = - \frac{{\left( {1 + {n_{{\rm{sub}}}}} \right)\sin \phi }}{{A{Z_0}}},$

对室温下的光诱导复面电导率进行了计算. 式中n_sub为样品在THz波段的折射率, Z₀ = 377 Ω为自由空间阻抗. 图5(a)所示为同一抽运功率(603 μJ/cm²)、不同延迟时间下的频率分辨的复光电导率, 图5(b)所示为同一抽运-探测延迟时间(Δt = 2 ps)、不同功率下的复光电导率. 可以看出, 电导率的实部总体上随着频率的增加而减小, 虚部随着频率的增加而增加, 且复电导率的实部和虚部都是正的. 根据复电导率的特点, 我们采用Drude-Smith模型对复光电导率进行了拟合, 其表达式为
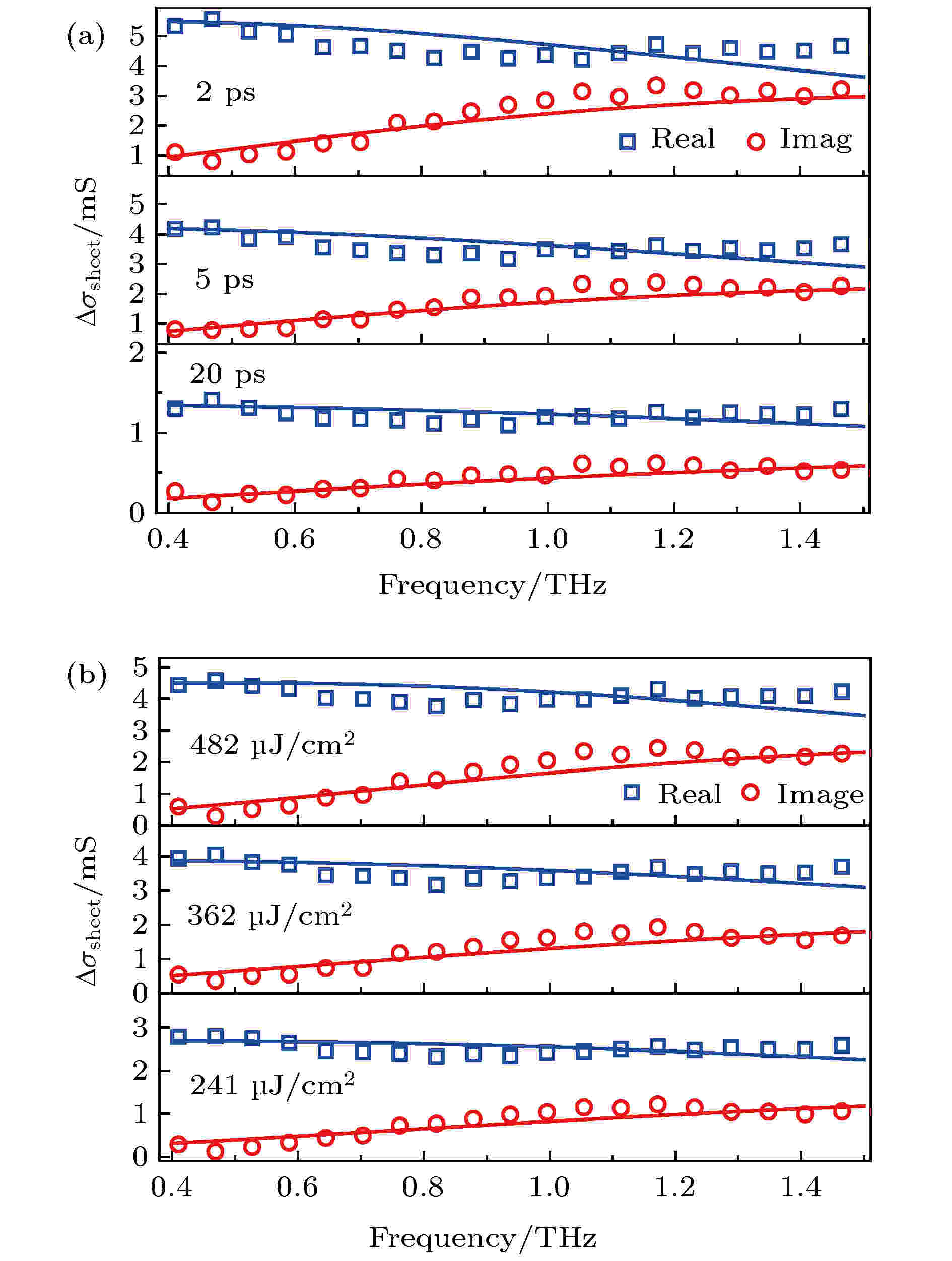图 5 (a) 抽运功率603 μJ/cm²、不同抽运-探测延迟时间下的频率分辨的复面电导率 (蓝色和红色的空心点), 实线为Drude-Smith模型拟合的结果; (b) 抽运-探测延迟时间2 ps、不同抽运功率下的复面电导率
Figure5. (a) The complex frequency-resolved sheet photoconductivity (blue and red circle spots) with a fixed pump fluence of 603 μJ/cm² measured at various pump-probe time delays. The solid lines are the Drude-Smith model fitting; (b) the complex frequency-resolved sheet photoconductivity with a fixed pump-probe time delay of Δt = 2 ps measured at various pump fluence.

$\Delta \tilde \sigma \left( \omega \right) = \frac{{\omega _{\rm{p}}^2{\varepsilon _0}\tau }}{{1 - {\rm{i}}\tau \omega }} \cdot \left( {1 + \frac{c}{{1 - {\rm{i}}\tau \omega }}} \right),$

式中, ε₀为真空介电常数, ${\omega _p} \propto \sqrt N $是与载流子浓度N有关的等离子体频率, τ为载流子动量散射时间, c为背散射常数, 它的取值为–1到0, 当c为0时, 则为标准的Drude模型, 表示载流子的散射事件完全随机; 而当c为–1时, 则表示载流子完全的背散射或完全局域. 图5(a), (b)中的实线则是拟合的结果, 可以看出与实验数据有着很好的拟合, 拟合参数则如表1和表2所示.

Delay time/ps	ωp/1010 Hz	τ/fs	c
2	8.62	127	–0.3338
5	7.82	109	–0.2768
20	5.12	76	–0.2294

表1抽运功率603 μJ/cm²、不同抽运-探测延迟时间下, 基于Drude-Smith模型拟合的参数
Table1.The fitting parameters based on the Drude-Smith model at different pump-probe delay time with a excitation fluence of 603 μJ/cm².

Fluence/μJ·cm–2	ωp/1010 Hz	τ/fs	c
241	7.30	85	–0.3212
362	8.36	91	–0.3076
482	8.50	114	–0.3929

表2抽运-探测延迟时间Δt = 2 ps、不同抽运功率下, 基于Drude-Smith模型拟合的参数
Table2.The fitting parameters based on the Drude-Smith model under different pump fluence at delay time Δt = 2 ps.

从表中可以看出c 约为–0.3, 这表明, 载流子局域程度较小, 接近自由. 等离子体频率随着抽运-探测延迟时间的延长而减小, 表明随着时间的演化, 载流子数目在减少. 等离子体频率随着抽运功率的增大在增加, 说明载流子浓度的增加在光激发后占了主导. 以上分析表明, 光激发后载流子浓度的增加导致了光电导率的迅速增加, 而随后的弛豫过程由电子-空穴对的复合所主导.
当超快飞秒脉冲辐照到材料上时, 产生的THz时域发射光谱可以反映材料的线性和非线性光学性质, 提供样品的表面耗散场^[30]、光致丹倍场^[31]、光整流^[32]及光伏效应^[33]等信息. 这里, 室温下将800 nm线偏振光脉冲入射到c切的CST表面上, 探测到了强的THz辐射信号. 图5(a)为透射式THz发射示意图, 入射面为ab面. 图5(b)为THz发射信号的峰-峰值与激发功率的依赖关系, 可以看到发射信号的大小随激发功率的增大而线性增大. 为了观测发射的THz信号的空间偏振, 与水平方向成 ±45°的线栅偏振片放置于实验光路中. 图5(c)是典型的时域波形, 可以看出发射的THz信号是线偏振的. 而图5(d)则是与之对应的水平和垂直方向的经过傅里叶变换后的频谱, 可以看到THz辐射具有0—2 THz较宽的带宽, 中心频率在0.6 THz左右. 由于CST具有中心对称结构, 800 nm的激发光的光子能量远高于其直接和间接带隙, THz发射机制来源于表面数个原子层的瞬态光电流效应. 由于我们采用的是正入射透射式THz发射光谱, 可以容易排除光致丹倍效应(photo-Dember effect)诱导的扩散光电流(diffusion current)和表面耗尽场(surface depletion field)产生的漂移电流(drift current)对THz辐射的贡献. 从图4还可以看到, 光激发后其表面载流子的最快弛豫时间为数ps, 不可能辐射中心频率为0.6 THz的THz波, 可以排除激发态载流子弛豫对THz辐射的贡献. 基于所产生的THz辐射峰值强度与激光光强间的线性关系(图6(b)), THz辐射应与二阶非线性光电导相关, 具体的模型分析表明该宽带强THz辐射来自表面位移光电流(shift current)的贡献^[34].
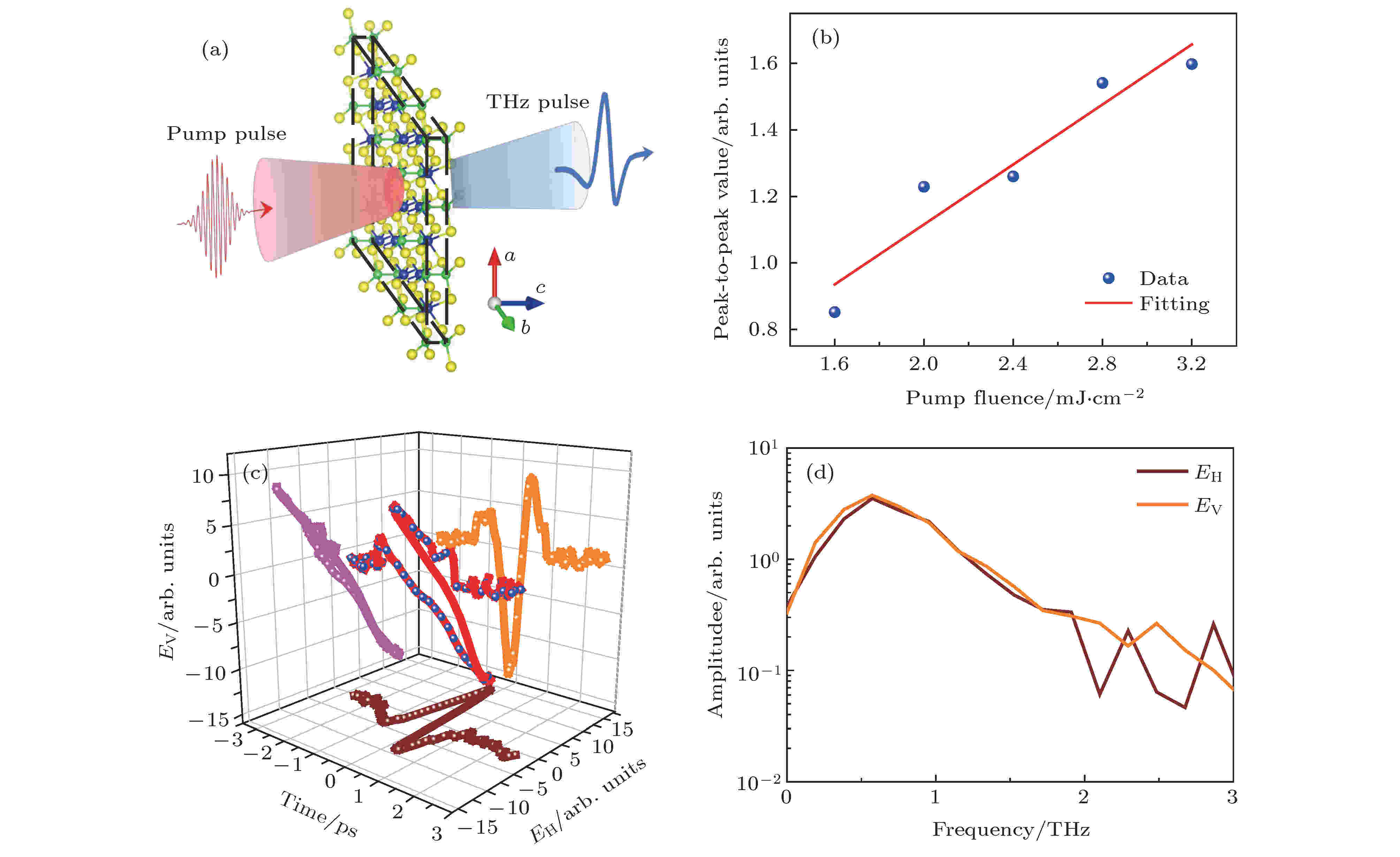图 6 (a) 透射式THz发射光谱示意图, 入射面为样品的ab面; (b) 功率依赖的THz辐射的峰峰值, 实线为线性拟合的结果; (c) 典型的THz辐射的3D图像, 紫色的线为THz波在时间上的投影, 表明发射的THz波为线偏振的; (d) 图 (c) 中水平和竖直面上的THz波经傅里叶变换后的频谱
Figure6. (a) Illustration for THz emission spectroscopy with transmission configuration, and the fs pulse is incident on ab-plane of the sample; (b) the peak-to-peak value of THz radiation with respect to the pump fluence, and the solid line represents linear fitting; (c) a typical 3D plot of THz radiation. The purple line shows the projection of the THz wave on time, which indicates the radiant THz wave is linearly polarized; (d) the Fourier transformation spectrum of THz waves corresponding to the horizontal and vertical directions in figure (c).

本文利用THz光谱, 包括THz时域光谱、激发态载流子超快动力学光谱及THz发射光谱, 对准二维铁磁半导体CST进行了系统研究. 实验结果表明, CST在THz波段的折射率约为3.17, 透射的THz波几乎对样品温度和ab面内的方位角没有依赖性; 光抽运后的载流子具有两个特征寿命, 复光电导率色散关系可以很好地用Drude-Smith模型描述; 光激发后基于非线性光电流效应产生宽频强THz辐射. 本文所展示的CST的超快THz光谱信息, 为该材料在未来电子、光子及自旋等器件的应用提供了重要参考信息.