摘要:基线校正是拉曼光谱数据预处理的关键步骤之一, 是消除荧光干扰的有效方法. 传统的多项式拟合和均匀B样条拟合算法原理简单、易于实现, 但拟合阶数和内节点的不确定性限制了其灵活性. 因此, 本文提出了一种基于中值滤波和非均匀B样条的拉曼光谱基线校正算法. 该算法首先通过平滑预处理、差分计算和设置阈值筛选波谷点, 并根据光谱数据的波谷位置自适应地选择非均匀B样条的内节点; 接着利用中值滤波算法对光谱数据进行处理, 使非均匀B样条算法能够更好地拟合基线. 该算法克服了传统B样条算法需要根据不同的拉曼光谱手动选择内节点的缺点, 同时避免了光谱数据中的随机噪声对基线拟合的影响, 且进一步提高了光谱基线校正效果. 实验结果表明, 该算法能较好地消除拉曼信号基线漂移, 且不存在过拟合和欠拟合现象. 因此, 该算法可以为光谱数据的进一步分析提供更准确、可靠的信息.
关键词: 基线校正/
拉曼光谱/
非均匀B样条/
中值滤波/
自适应节点

English Abstract

全文HTML

--> --> -->

拉曼光谱由印度物理学家Raman于1919年从水分子的散射现象中首次发现, 并将其发表于杂志《Nature》上^[1]. 拉曼光谱作为一种用于分析分子化学成分、结构等信息的检测技术, 具有无侵入、特异性高、无标记、无电离辐射、不受水的干扰等优点, 被广泛应用于生物医学、材料生产、化学化工等领域^[2,3]. 然而由于荧光干扰等因素的存在, 基线漂移现象通常存在于光谱信号中, 而基线校正算法是解决该现象的必要手段^[4-7].
目前, 常用的基线校正算法有多项式拟合算法(polynomial fitting)、B样条拟合算法(B-spline fitting)、小波变换(wavelet transform)和自适应迭代重加权惩罚最小二乘(adaptive iterative reweighted penalty least square, airPLS)等算法^[8-13]. 多项式拟合算法简单易实现, 但是在处理不同的光谱信号时难以确定拟合阶数. 小波变换则是通过用一系列的正弦波进行叠加来代替每条拉曼光谱, 能够有效地将拉曼光谱的低频和高频进行区分. 但是, 由于不同的光谱具有不同的频率和噪声, 很难找出一个适用于所有拉曼光谱的分解办法, 且其计算量相比其他算法也相对较高. 均匀B样条拟合算法在面对基线漂移较为平缓的拉曼光谱信号时, 其基线校正效果良好. 然而由于均匀B样条内节点的选择缺乏目的性, 随着基线漂移程度越来越剧烈, 通常导致最终基线校正效果一般. 而若非均匀选择内节点, 则需要针对每条光谱信号进行手动选择, 工作量也会随之增加, 且普适性和灵活性较差. 范贤光等^[14]通过小波变换找到光谱数据的峰值并作为内结点, 该方法可以解决内结点选择的问题, 但其计算复杂度和计算量较高, 且过拟合和欠拟合仍不能完全消除.
因此, 本文提出一种基于中值滤波和非均匀B样条(median filtering and un-uniform B-spline, MF-UUB)的拉曼光谱基线校正算法. 该算法不仅可以根据不同的拉曼光谱信号自适应地选择内结点, 且通过使用中值滤波和非均匀B样条算法能获得更好的基线校正效果.

2

-->

2.1.非均匀B样条理论

B样条算法因其具有低阶平滑性而广泛应用于曲线和曲面拟合中^[15]. 在本文中, 将该算法用于拉曼光谱的基线拟合.
假设输入拉曼光谱数据r, 用节点符号t将数据点列在x轴上进行区间划分, 点序列如下所示:

$\begin{split}&{t_{ - k + 1}} \leqslant \cdots \leqslant {t_{ - 1}} \leqslant {t_0} < {t_1} < \cdots < {t_N} \\& < {t_{N + 1}} \leqslant {t_{N + 2}} \leqslant \cdots \leqslant {t_{N + k}},\end{split}$

其中${t_1}$到${t_N}$为内节点, 其余的为外节点. 如果内节点在区间内均匀划分则为均匀B样条, 反之, 则为非均匀B样条^[16]; 而外节点对算法的影响较小, 其区间大小一般取内节点区间的平均值. N为区域内内节点数, k为B样条的阶数, 且一般取4. x的k阶B样条曲线如(2)式所示:

$y{{ = }}\sum\limits_{i = - k + 1}^N {{c_i}} B_i^k\left( x \right),$

式中${c_i}$为控制系数列向量, B样条曲线的控制多边形就是由这些控制点依次连接而成; $B_i^k\left( x \right)$为B样条基函数, 定义为^[17]:

$B_i^1\left( x \right)= \begin{cases} 1,& {t_i} \leqslant x \leqslant {t_{i + 1}}, \\ 0,& x < {t_i}, \; x > {t_{i + 1}}, \end{cases} $

$B_i^k\left( x \right) = \dfrac{{x \!-\! {t_i}}}{{{t_{i + k - 1}} \!-\! {t_i}}}B_i^{k - 1}\left( x \right) + \dfrac{{{t_{i + k}} \!-\! x}}{{{t_{i + k}} \!-\! {t_{i + 1}}}}B_{i + 1}^{k - 1}\left( x \right).$

2 -->

2.2.局部加权线性回归理论

局部加权线性回归(locally weighted linear regression, LWLR)^[18]是线性回归方法的一个改进, 可有效应用于光谱信号的平滑. 因此, 本文通过使用局部加权线性回归对原始光谱数据进行平滑预处理, 以便后续有效地进行内节点的选取. 它通过预测数据与输入数据的距离赋予不同权重, 距离越近则权重越大, 然后再通过最小二乘法进行计算求解. 该方法的本质是基于加权的均方误差最小化进行求解:

$\sum\limits_{i = 1}^n {{w_i}\left( {{r_i} - \theta {y_i}} \right)} \to \min ,$

式中r为输入的光谱数据; y为预测数据; $\theta $为回归系数; ${w_i}$为权重, 该值可通过权重函数计算得到, 一般选用高斯函数作为权重函数, 权重函数如下所示:

${w_i} = \exp \bigg( {{{ - }}\frac{{{{\left\| {{y_i} - {r_i}} \right\|}^2}}}{{2{\delta ^2}}}} \bigg),$

式中$\delta $为带宽参数.
2 -->

2.3.自适应选取内节点方法

通过非均匀B样条算法进行基线拟合, 其拟合效果的好坏主要取决于原始拉曼光谱的基线能否尽可能地被内节点划分为几个平缓的波段. 因此, 如何根据不同的拉曼光谱自适应地选取内节点, 则为非均匀B样条的核心问题. 为保证扣除基线后仍能最大程度的保留原始光谱的特征峰, 且尽可能地在基线变化较为剧烈的位置处选择内节点, 同时有效地将基线划分为几个平缓的波段. 在本文中, 内节点的选取则根据原始光谱信号的波谷点进行确定, 因此, 内节点的选取步骤如下.
1)使用局部加权线性回归对原始光谱数据进行平滑预处理. 由于光谱数据中伴随着随机噪声, 若直接对光谱数据进行筛选波谷点, 则会导致筛选后的数据点中存在无效数据点. 局部加权线性回归的窗口长度可通过设置窗口数量计算得到, 窗口数量一般取10²个. 原始光谱数据与平滑后的数据如图1所示.
图 1 波谷点选择策略
Figure1. Strategy of selection of trough points.

2)筛选光谱数据的波谷点. 对平滑后的光谱信号的每个数据点逐个进行差分计算, 并设置两波谷点间的最小距离阈值${\xi _{\rm{L}}}$, 从而初步筛选出波谷点(图1中红色数据点)并设为${{K}} = \left[ {{k_{\rm{0}}}, {k_{\rm{1}}}, \cdots, {k_n}} \right]$. 最小距离阈值${\xi _{\rm{L}}}$通过内节点预设值计算得到, 如(7)式:

${\xi _{\rm{L}}} = {\rm{Round}}\left( {\frac{P}{{{s_{{\rm{ik}}}}}}} \right),$

式中s_ik为内节点数量预设值, 一般设为30; P为原始光谱数据点数; ${\rm{Round}}\left[ \cdot \right]$为四舍五入取整. 将从平滑后的光谱数据中筛选的波谷点K对应至原始光谱数据上. 由于对应点并非都准确地位于原始数据的波谷上, 因此对每个数据点进行加窗, 一般窗口距离取0.2倍的最小距离阈值${\xi _{\rm{L}}}$, 并求得每个窗口内的最小值. 求得的数据点则为原始光谱数据的波谷点(图1中蓝色数据点), 并设为${{P}} = \left[ {{p_{\rm{0}}}, {p_{\rm{1}}}, \cdots, {p_n}} \right]$.
3)扣除无效的数据点. 计算两波谷点区间内最大值与最小值之差, 设为${h_i}$, 并设置最小高度阈值${\xi _{\rm{H}}}$, 其值一般取0.05倍的原始光谱数据中最大值与最小值之差:

${\xi _{\rm{H}}} = \alpha \left( {{\rm{max}}\left( {{r}} \right) - {\rm{min}}\left( {{r}} \right)} \right),$

式中$\alpha $值一般取0.05, r为原始拉曼光谱数据. 若波谷点${p_i}$和${p_{i + 1}}$之间的高度差${h_i}$小于阈值${\xi _{\rm{H}}}$, 则扣除数据点${p_{i + 1}}$. 无效的数据点(图2中绿色数据点)如图2所示, 剩余的有效数据点设为${{d}} = \left[ {{d_{\rm{0}}}, {d_{\rm{1}}}, \cdots, {d_n}} \right]$.
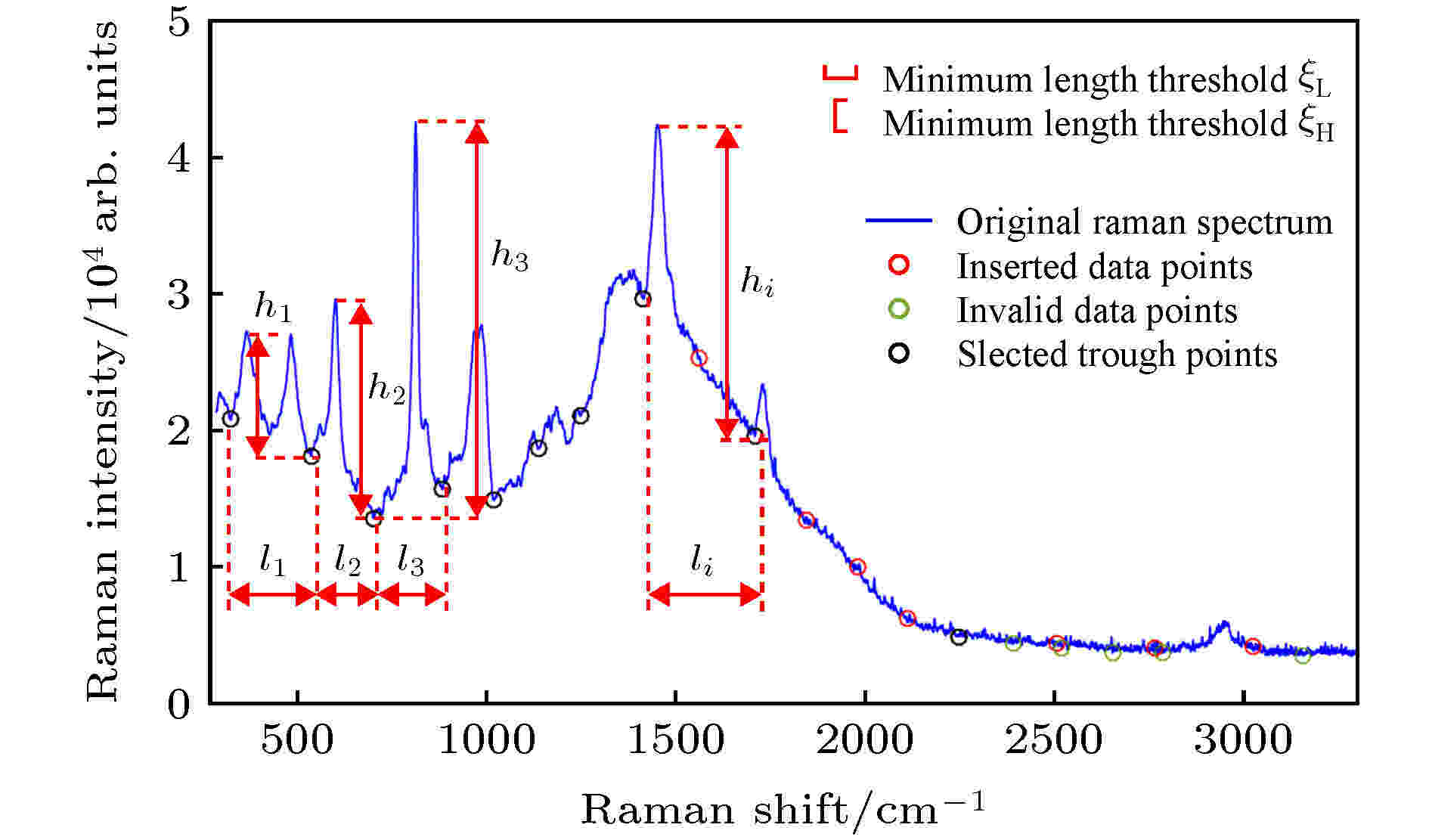图 2 内节点选择策略
Figure2. Strategy of selection of internal knots

4)插入额外数据点. 计算两数据点${d_i}$和${d_{i + 1}}$间的距离, 并设为${l_i}$; 若${l_i}$大于内节点距离阈值(3倍的最小距离阈值${\xi _{\rm{L}}}$), 则在数据点${d_i}$和${d_{i + 1}}$间插入另一数据点${q_i}$. 循环执行该步骤, 直至两数据点间的距离均小于内节点距离阈值. 插入的数据点(图2中红色数据点)设为${{q}} = \left[ {{q_{\rm{0}}}, {q_{\rm{1}}}, \cdots, {q_n}} \right]$, 如图2所示.
5)使用确定的数据点作为非均匀B样条的内节点. 数据点d和q之和得到的数据点${{T}} = [ {t_{\rm{0}}}, {t_{\rm{1}}}, \cdots, {t_n} ]$则作为内节点(图2中黑色与红色数据点之和).
2 -->

2.4.中值滤波

中值滤波(median filtering)^[19]是一种非线性的平滑滤波技术, 它通过把一串数字序列或者数字图像中的某一个点的值用其相邻区域内所有值的中值进行代替. 在本文中, 利用中值滤波算法对原始拉曼光谱数据进行处理, 使光谱数据中的波峰趋于平缓, 从而优化B样条曲线的控制系数列向量${c_i}$, 以便后续的非均匀B样条能在波峰过渡到平滑波段的位置处更好地进行基线拟合. 使其拟合的基线在该位置处变化更加平缓, 能有效地减少欠拟合现象的发生. 中值滤波的公式为:

${y_j} = {\rm{Med}}\left[ {{x_{j{{ - }}N}}, \cdots,{x_j}, \cdots,{x_{j + N}}} \right],$

式中${\rm{Med}}\left[ \cdot \right]$为取输入数据点列的中值. 此外, 中值滤波的窗口数量越少则拟合的基线越趋于平缓, 但窗口数量过少则会影响拟合基线的准确性. 因此, 窗口数量一般取与内节点数量一致.
2 -->

2.5.基于中值滤波和非均匀B样条的基线校正算法

将内节点选取方法、中值滤波算法和非均匀B样条拟合等算法应用于拉曼光谱的荧光背景扣除, 该算法步骤如下:
1)使用局部加权线性回归对原始光谱数据r进行平滑预处理, 得到数据z;
2)对数据z进行逐点差分计算和设置最小距离阈值${\xi _{\rm{L}}}$得到数据z的波谷点, 并通过加窗处理得到数据r的波谷点${{P}} = \left[ {{p_{\rm{0}}}, {p_{\rm{1}}}, \cdots, {p_n}} \right]$;
3)利用最小高度阈值${\xi _{\rm{H}}}$扣除无效波谷点, 并设置内节点距离阈值进行插值, 得到内节点${{T}} = \left[ {{t_{\rm{0}}}, {t_{\rm{1}}}, \cdots, {t_n}} \right]$;
4)将内节点数量作为中值滤波窗口数量, 对数据r进行中值滤波处理, 得到数据u;
5)对数据u进行非均匀B样条拟合, 得到拟合基线v;
6)计算u和v的误差绝对值, 若误差值大于所设定的阈值$\xi $(阈值$\xi $一般取0.05), 则将v赋值给u并回到步骤4); 误差绝对值公式为

$\xi {{ = }}\sum\limits_{i = 1}^n {\frac{{{u_i} - {v_i}}}{{{u_i}}}} ;$

7)从原始拉曼光谱r中扣除基线v.
由上述流程可知, 该算法需要调节的参数仅包含最小距离阈值${\xi _{\rm{L}}}$和局部加权线性回归窗口数量. 其中最小距离阈值${\xi _{\rm{L}}}$通过设置内节点数量预设值s_ik计算得到. 且内节点数量预设值s_ik一般取30个, 局部加权线性回归窗口数量一般取10²个即可获得良好的基线校正效果.

2

-->

3.1.实验材料

本文选用聚甲基丙烯酸甲酯(polymethyl methacrylate, PMMA)和正辛烷(N-OCTANE)作为待测样品. N-OCTANE拉曼光谱在光谱仪积分时间为1 s下获得, PMMA拉曼光谱在光谱仪积分时间为10 s下获得.
2 -->

3.2.实验结果

图3(a),(b)分别是N-OCTANE和PMMA的原始拉曼光谱, 其中N-OCTANE拉曼光谱的基线漂移程度较小, 而PMMA拉曼光谱的基线漂移程度则较为剧烈, 尤其在拉曼位移为1500 cm^–1处, 基线的存在会淹没原本就微弱的谱峰, 这些现象使得光谱信号难以被直观地辨识. 通过本文所提的MF-UUB基线校正算法对两种样品的拉曼光谱分别进行基线拟合, 得到的拟合基线同样如图3所示, 基线校正后的拉曼光谱如图4所示. 其中, 局部加权线性回归的窗口数量设为10²个, 内节点数量预设值设为30个, 因此对于两条拉曼光谱分别得到的内节点数量为14个和17个; 中值滤波的窗口数量分别与各自光谱数据的内节点数量一致. 由图3可知, 该算法能有效地随波峰的变化进行基线拟合, 且在线性波段和曲线波段的拟合中均有较好的拟合效果, 这证明了MF-UUB算法的灵活性. 由图4可知, 基线校正后的拉曼光谱能有效地保留所有特征峰信息, 且没有因为荧光背景的扣除而出现多余的无效特征峰或凸包. 对于大部分的拉曼光谱, 使用固定的参数设置, 便能获得较好的基线拟合效果. 在后续对拉曼信号的进一步分析中, 如拉曼组分识别的应用, 识别的过程主要根据谱峰的位置等特点进行识别, 而若无法有效且完整地扣除荧光背景, 将使得某些谱峰的位置发生偏移, 或在一定程度上改变特征峰形状及大小, 这将影响对物质的有效识别. 而本文所提算法则能有效地避免上述问题, 能为后续的进一步分析提供更可靠有效的信息.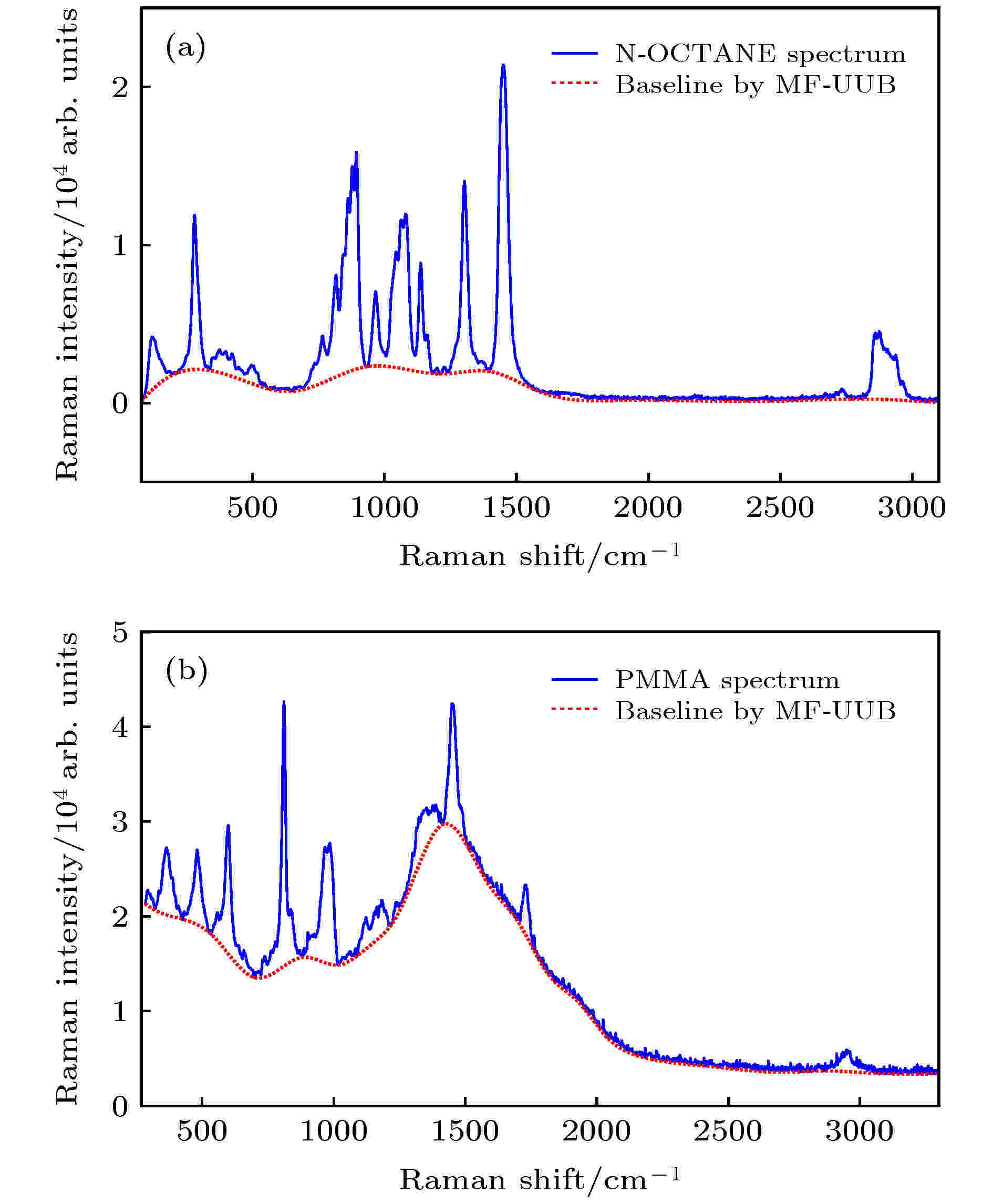
图 3 原始拉曼光谱和基于MF-UUB算法拟合的基线　(a) N-OCTANE拉曼光谱; (b) PMMA拉曼光谱
Figure3. Original Raman spectra and fitted baseline by MF-UUB: (a) N-OCTANE Raman spectrum; (b) PMMA Raman spectrum.

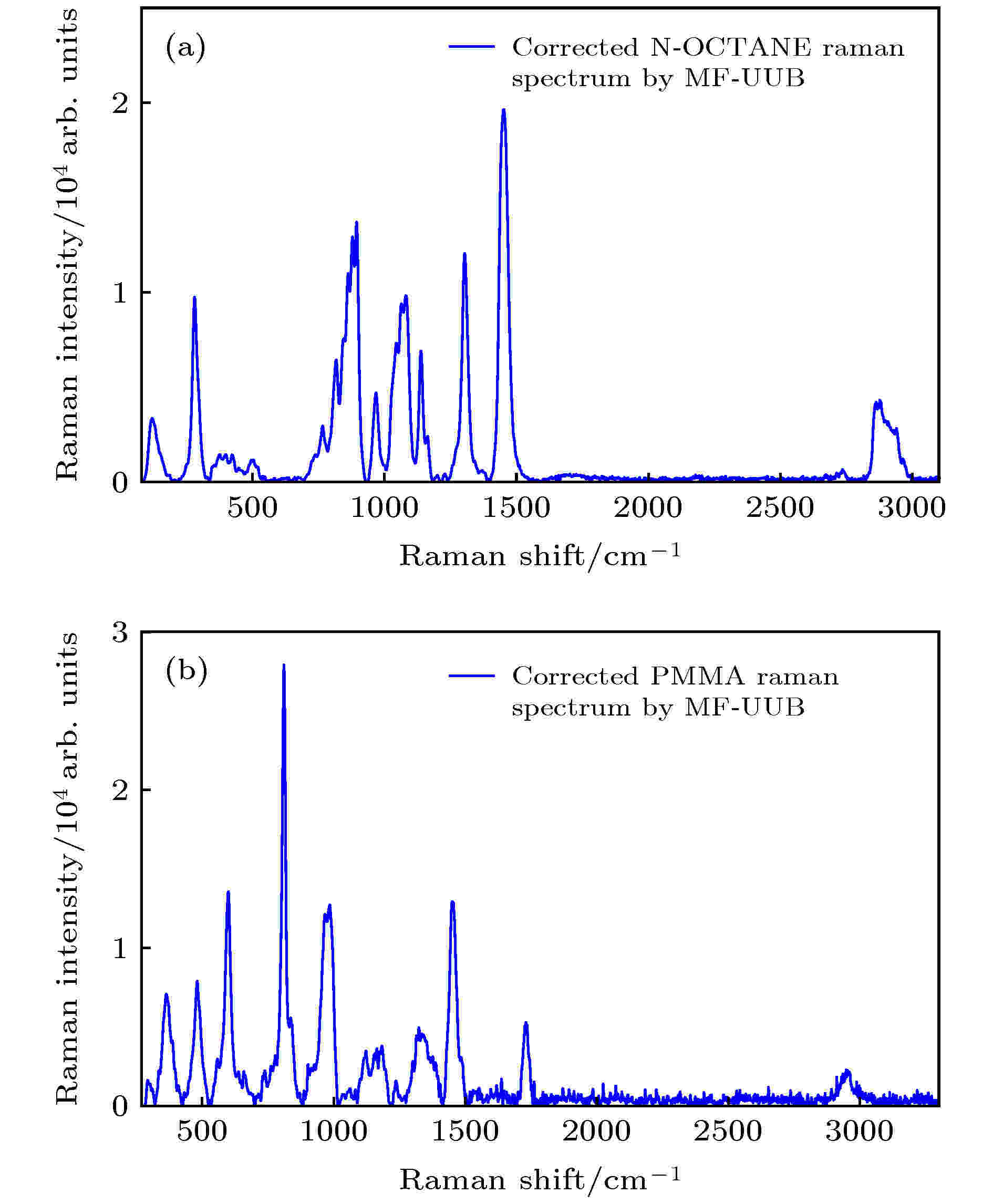图 4 基于MF-UUB算法基线校正后的光谱　(a) N-OCTANE拉曼光谱; (b)PMMA拉曼光谱
Figure4. Corrected Raman spectra by MF-UUB: (a) N-OCTANE Raman spectrum; (b) PMMA Raman spectrum.

2 -->

3.3.中值滤波算法有效性验证

为验证中值滤波算法是否能有效地提升拟合基线的准确性, 通过使用不加中值滤波处理的非均匀B样条拟合算法进行基线拟合, 拟合的基线如图5所示. 由图5(a)可知, 拟合的基线与本文所提算法拟合的基线在整体上基本一致. 但是在波峰过渡到平滑波段的位置, 如拉曼位移为1400—2000 cm^–1等处, 拟合的基线存在一定的欠拟合现象. 而通过使用中值滤波算法处理后, 则可以有效地改善这一缺陷. 这是因为通过中值滤波处理后的拉曼光谱的波峰会趋于平缓, 使得拟合的基线变化幅度变小, 从而能更好地在波峰过渡到平滑波段的位置处进行拟合.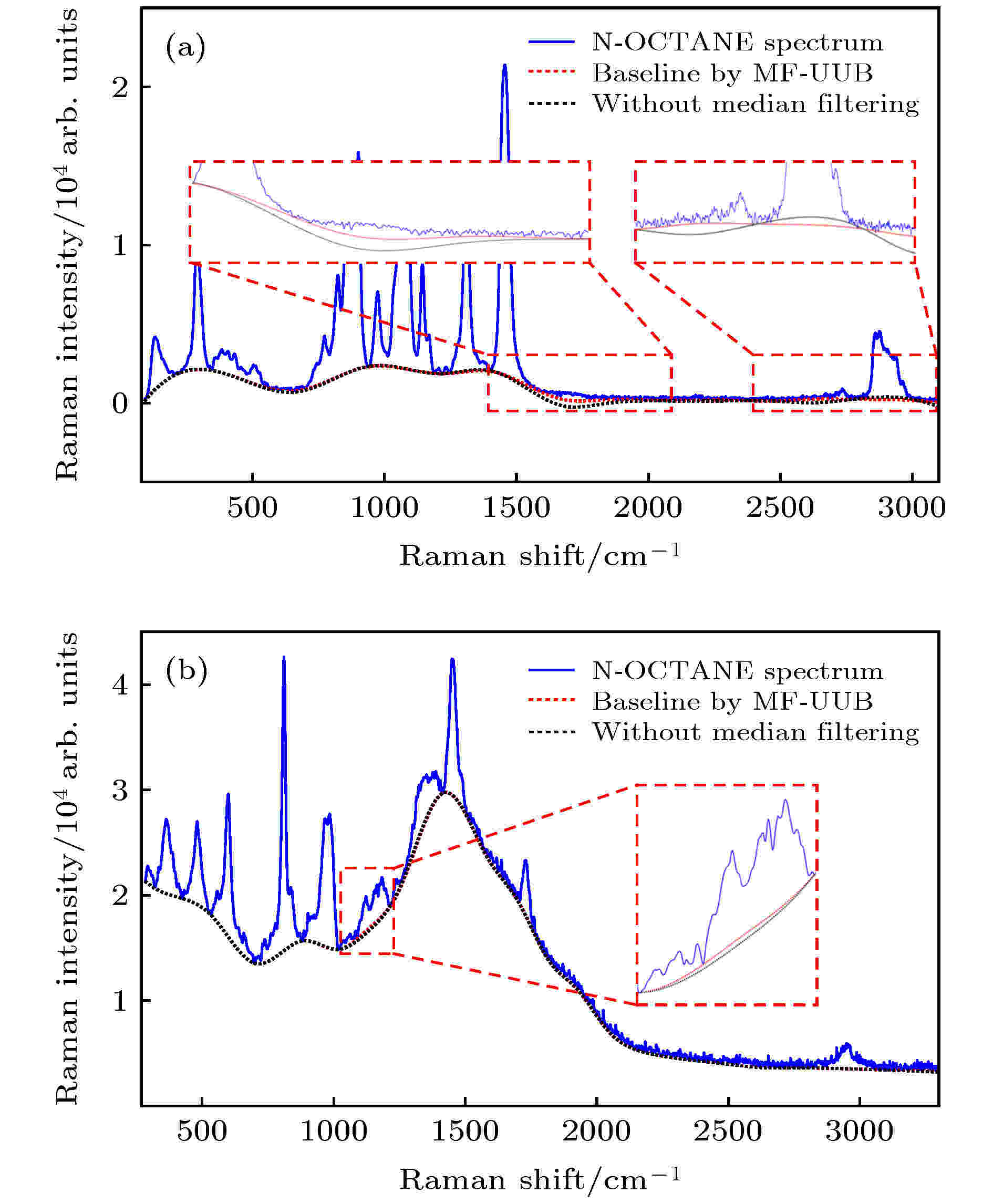
图 5 原始拉曼光谱和基于非均匀B样条算法拟合的基线　(a) N-OCTANE拉曼光谱; (b)PMMA拉曼光谱
Figure5. Original Raman spectra and fitted baseline by un-uniform B-spline algorithm: (a) N-OCTANE Raman spectrum; (b) PMMA Raman spectrum.

此外, 如果通过非均匀B样条拟合算法便能获得较好的拟合基线, 则中值滤波算法不会对拟合的基线有太大的改变. 由图5(b)可知, 该光谱的基线拟合效果好于图5(a), 且不存在欠拟合现象. 因此, 通过中值滤波进行处理后再进行基线拟合的效果则提升相对有限, 仅在拉曼位移为1000—1300 cm^–1处存在一定程度的改善.
2 -->

3.4.均匀B样条算法、多项式拟合算法和airPLS的基线校正情况

为进一步验证该算法能有效地进行基线拟合且优于传统算法, 分别使用多项式拟合算法和均匀B样条拟合算法对N-OCTANE和PMMA原始拉曼光谱进行基线拟合. 此外, 由于多项式拟合算法的拟合阶数难以确定, 因此同时选用5阶、7阶和9阶多项式拟合算法对原始光谱进行基线拟合. 而均匀B样条拟合算法则采用4阶3次B样条, 且为保证验证的有效性, 均匀B样条的内节点数与本文所提算法保持一致, 分别设为14个和17个. 基于均匀B样条算法和多项式拟合算法拟合的基线分别如图6和图7所示.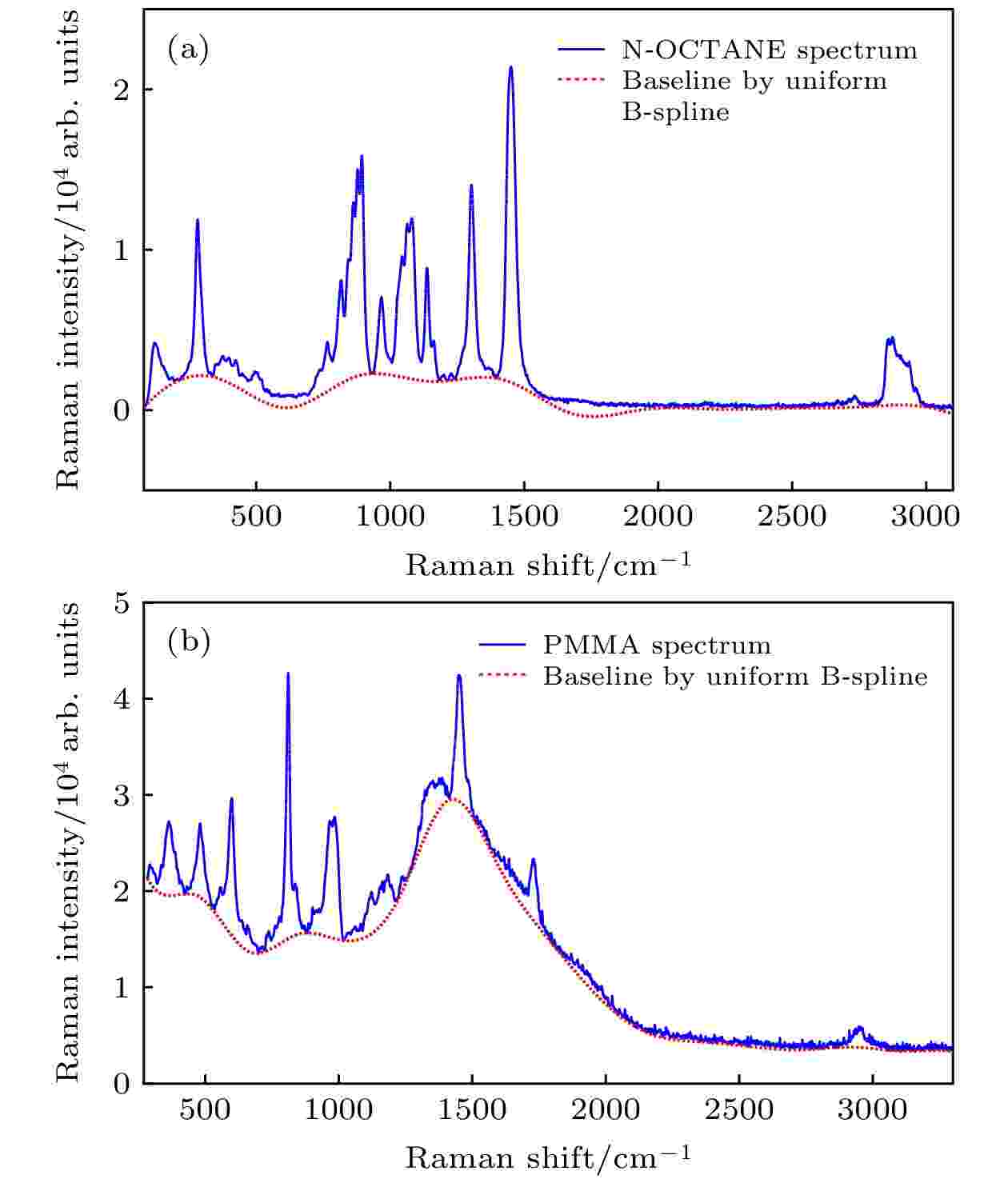
图 6 原始拉曼光谱和基于均匀B样条算法拟合的基线　(a) N-OCTANE原始拉曼光谱; (b) PMMA原始拉曼光谱
Figure6. Original Raman spectra and fitted baseline by uniform B-spline algorithm: (a) N-OCTANE Raman spectrum; (b) PMMA Raman spectrum.

图 7 原始拉曼光谱和基于多项式拟合算法拟合的基线　(a) N-OCTANE拉曼光谱; (b)PMMA拉曼光谱
Figure7. Original Raman spectra and fitted baseline by polynomial fitting algorithm: (a) N-OCTANE Raman spectrum; (b) PMMA Raman spectrum.

由图6可知, 均匀B样条拟合算法在整体上能有效地进行基线拟合. 但由于内节点的选择缺乏目的性, 无法有效地在正确位置处将光谱数据的基线划分为几个平滑波段, 这导致拟合的基线存在欠拟合现象, 如图6(a)中拉曼位移为300—700 cm^–1以及图6(b)中拉曼位移为1000—1200 cm^–1等多处波段中. 由于无法有效且完整地扣除荧光背景, 将导致扣除荧光背景后的拉曼光谱在某些波段处出现无效的凸包, 且在一定程度上改变特征峰的形状.
由图7可知, 多项式拟合算法在N-OCTANE原始拉曼光谱的基线拟合中表现效果好于PMMA原始拉曼光谱, 能相对有效地进行基线拟合, 但整体上仍存在着一定的拟合缺陷. 随着多项式拟合阶数的增加, 拟合的基线在某些波段处会得到改善, 如图7(a)中拉曼位移为700—1200 cm^–1以及图7(b)中拉曼位移为1100—1800 cm^–1处. 但同时随着拟合阶数的增加, 拟合的基线在某些波段处的拟合效果也会变差, 如图7(a)中拉曼位移为1200—1600 cm^–1以及图7(b)中拉曼位移为800—1100 cm^–1处. 因此可以得出, 多项式拟合算法的阶数难以确定, 且欠拟合和过拟合现象难以控制和预料. 针对基线漂移较为剧烈的原始拉曼光谱, 通过多项式拟合算法拟合的基线效果较为一般, 无法有效且完整地扣除荧光背景.
此外, airPLS是一种应用广泛且效果良好的基线校正算法^[20], 因此, 通过该算法拟合的基线如图8所示. 由图8可知, 该算法整体基线拟合效果良好, 在大部分波段处均能准确有效地进行基线拟合, 且拟合的基线与通过本文所提算法拟合的基线基本一致. 但是, 仍然有一些拟合缺陷产生, 如拟合的基线通过波谷点时存在着一定的过拟合现象.
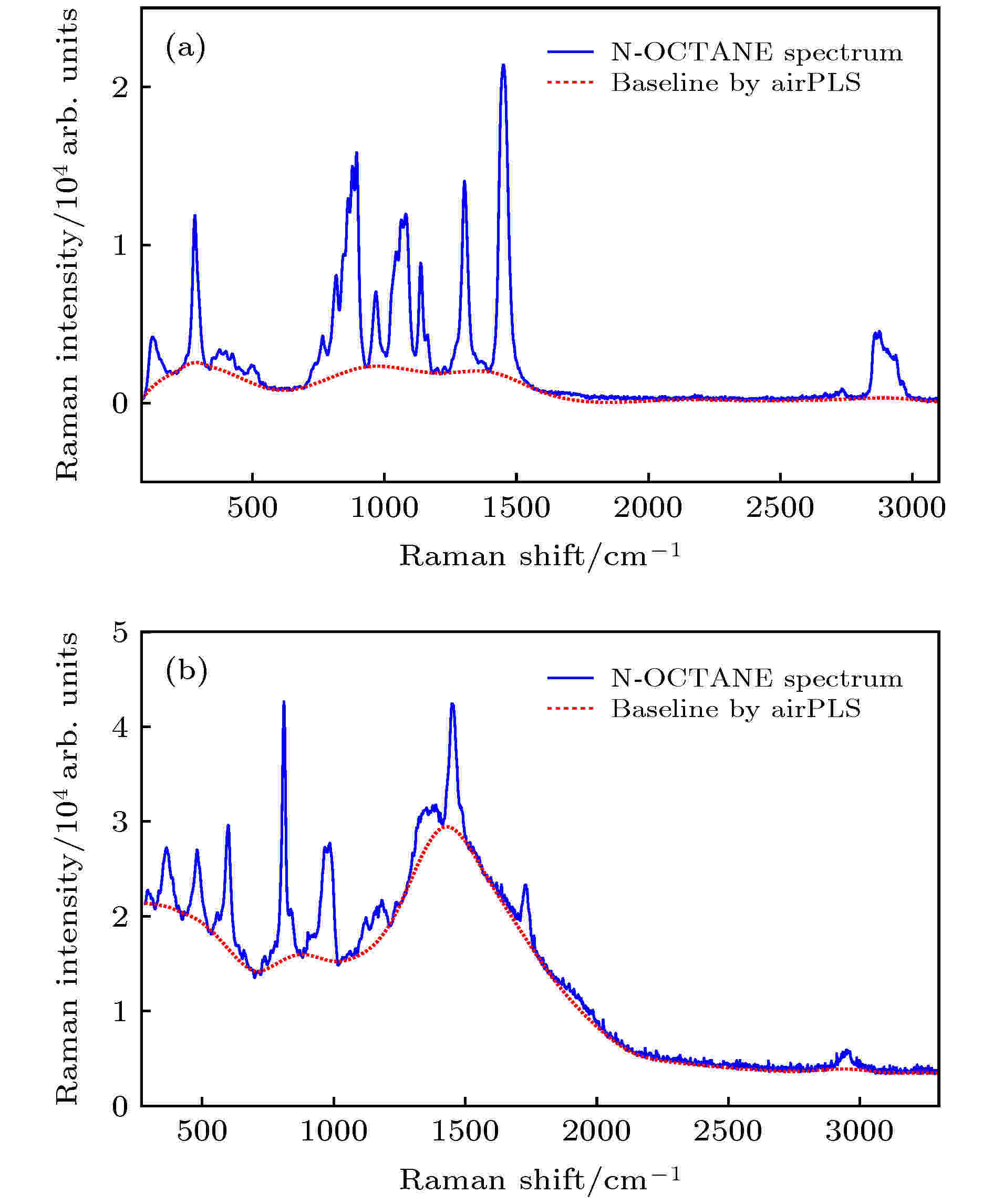图 8 原始拉曼光谱和基于airPLS拟合的基线　(a) N-OCTANE拉曼光谱; (b)PMMA拉曼光谱
Figure8. Original Raman spectra and fitted baseline by airPLS algorithm: (a) N-OCTANE Raman spectrum; (b) PMMA Raman spectrum.

综上所述, 本文提出MF-UUB算法能有效地进行基线校正. 与多项式拟合算法相比, 本文所提算法能以固定的阶数进行拟合; 与均匀B样条算法相比, 本文所提算法能根据不同的拉曼光谱自适应选择内节点; 与非均匀B样条算法和airPLS相比, 本文所提算法具有更好的基线拟合效果.

本文提出了一种简单灵活且有效的拉曼光谱基线校正算法. 该方法能自适应地根据不同光谱数据选取内节点, 且通过中值滤波算法优化B样条曲线控制系数, 使非均匀B样条算法对拉曼光谱数据进行拟合时能获得更好的基线拟合效果. 与多项式拟合, 均匀B样条和airPLS算法相比, 该算法具有更好的基线校正效果, 且不存在欠拟合和过拟合等缺陷. 此外, 该算法具有广泛的适用性和灵活性, 针对不同的基线漂移情况, 可以有效地进行基线拟合. 因此, 本文所提算法能为拉曼光谱信号的进一步分析提供更准确可靠的信息.