摘要: 随着社会经济的快速发展, 社会成员及群体之间的关系呈现出了更复杂、更多元化的特点. 超网络作为一种描述复杂多元关系的网络, 已在不同领域中得到了广泛的应用. 服从泊松度分布的随机网络是研究复杂网络的开创性模型之一, 而在现有的超网络研究中, 基于ER随机图的超网络模型尚属空白. 本文首先在基于超图的超网络结构中引入ER随机图理论, 提出了一种ER随机超网络模型, 对超网络中的节点超度分布进行了理论分析, 并通过计算机仿真了在不同超边连接概率条件下的节点超度分布情况, 结果表明节点超度分布服从泊松分布, 符合随机网络特征并且与理论推导相一致. 进一步, 为更准确有效地描述现实生活中的多层、异质关系, 本文构建了节点超度分布具有双峰特性, 层间采用随机方式连接, 层内分别为ER-ER, BA-BA和BA-ER三种不同类型的双层超网络模型, 理论分析得到了三种双层超网络节点超度分布的解析表达式, 三种双层超网络在仿真实验中的节点超度分布均具有双峰特性.
关键词: 超图 /
ER随机超网络 /
双峰特性 /
双层超网络 English Abstract Double-layer hypernetwork model with bimodal peak characteristics Lu Wen 1,2,3,4 ,Zhao Hai-Xing 3,4 ,Meng Lei 2,3,4 ,Hu Feng 2,3,4 1.School of Computer Science, Shaanxi Normal University, Xi’an 710119, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos.11661069, 61663041), the Science and Technology Plan of Qinghai Province, China (Grant No. 2018-ZJ-777), and the Chun Hui Project from the Ministry of Education of China (Grant No. Z2016101)Received Date: 04 July 2020Accepted Date: 31 August 2020Available Online: 22 December 2020Published Online: 05 January 2021Abstract: With the rapid development of social economy, the relationship between social members and groups has shown more complex and diverse characteristics. As a network depicting complex relation and multi-layer, hyper network has been widely used in different fields. Random network that obeys Poisson distribution is one of the pioneering models studying complex networks. In the existing hyper network researches, the hyper network based on ER random graph is still a blank. In this paper, we first propose an ER random hyper network model which is based on the hypergraph structure and it adopts the ER random graph theory. Furthermore, using this model, the node hyper degree distribution of this hyper network model is analyzed theoretically, and the node hyper degree distribution is simulated under different hyper edge probabilities: $ p=0.004$ , $ p=0.006$ , $ p=0.008$ and $ p=0.01$ . The results show that the node hyper degree distribution of this hyper network model complies to the Poisson distribution $p(k)\approx \dfrac{{{\left\langle \lambda \right\rangle }^{k}}}{k!}{{e}^{-\left\langle \lambda \right\rangle }}$ , which conforms with the characteristics of random networks and is consistent with the theoretical derivation. Further, in order to more accurately and effectively describe the multiple heterogeneous relationship in real life, in this paper we construct three different kinds of double-layer hyper network models with node hyper degree distribution with bimodal peak characteristics. The three kinds respectively are ER-ER, BA-BA and BA-ER, where ER represents the ER random hyper network, and BA denotes the scale-free hyper network, and the layers are connected by a random manner. The analytical expressions of node hyper degree distribution of the three kinds of double-layer hyper network models are obtained by theoretical analysis, and the average node hyper degrees of the three double-layer hyper networks are closely related to the inter-layer hyper edge probability. As the inter-layer hyper edge probability increases, the average node hyper degree increases. The results of simulation experiments show that the node hyper degree distributions of three kinds of double-layer hyper network models proposed in this paper possess the characteristics of bimodal peaks. The ER random hyper network model and the double-layer hyper network model proposed in this paper provide the theories for further studying the hyper network entropy, hyper network dynamics, hyper network representation learning, hyper network link prediction, and traffic hyper network optimization of such hyper networks in the future, and also it has certain reference significance for studying the evolution of multilayer hyper networks.Keywords: hypergraph /ER random hyper network /bimodal peaks characteristic /double-layer hyper network 全文HTML --> --> --> 1.引 言 复杂网络作为描述和分析现实生活中真实网络的网络系统, 在不同领域中得到了广泛的应用并取得了丰硕的成果[1 -8 ] . 随着社会经济的快速发展, 现实生活中的网络呈现出了关系更复杂、节点属性更多元化的特点, 而一般的复杂网络难以全面、准确地刻画现实网络的特征. 鉴于超网络具有大数据、复杂性、多维性和多层次等特点, 使得描述和分析关系更复杂、节点属性更多元化的网络具有一定的实际应用价值[9 -12 ] . 例如, 在航空超网络和铁路超网络之间根据乘客换乘行为依次连接机场和铁路站点, 形成“航空-铁路”双层超网络模型并在此网络模型的结构基础之上, 利用超图理论优化交通规划和乘客换乘行为. 如图1 所示, 第一层超网络为航空超网络, 其中超边${A_1}$ 表示航班, 包含的节点${a_1}$ , ${a_2}$ 和${a_3}$ 表示该航班经过的三个机场; 第二层超网络为铁路超网络, 其中超边${R_1}$ 为铁路运营线路, 包含的节点${b_1}$ , ${b_2}$ , ${b_3}$ , ${b_4}$ , ${b_5}$ , ${b_6}$ 和${b_7}$ 表示该趟列车途经的站点. 两层超网络之间的超边${C_1}$ 表示乘客乘坐动车在${b_4}$ 站下车后可以选择${a_2}$ 或${a_3}$ 机场换乘飞机, 超边${C_2}$ 表示若乘客乘坐动车在${b_{20}}$ 或${b_{21}}$ 站下车, 如果打算继续换乘飞机那么就只能选择${a_6}$ 机场.图 1 “航空-铁路”双层超网络模型Figure1. Airline-Railway double-layer hyper network.[13 ] 对超网络的子图中心度和聚集系数进行了系统研究, 并采用超网络描述了马来西亚热带雨林中的食物网络, 通过分析得到了食物竞争关系. Ghoshal等[14 ] 提出并利用随机三部超图对社会化标签网络中的资源、用户和标签三类节点的度分布进行了理论分析, 得到了一些重要的结果. Zlati?等[15 ] 在三部随机超图的基础之上, 扩展了超度分布、节点相似性和节点间最短路径等拓扑指标的定义, 为进一步研究社会化标签网络提供了一个标准工具. Zhang和Liu[16 ] 提出了一种社会化标签网络的三部超图演化模型, 研究了该模型的超度、聚集系数和平均路径长度等拓扑特性, 并与实证数据做了对比. Wang等[17 ] 和胡枫等[18 ] 构建了基于超图理论的无标度超网络演化模型, 理论分析了该超网络模型的节点超度分布服从幂律分布, 并通过仿真实验验证了理论分析结果. 郭进利等[19 ,20 ] 将文献[17 ]和文献[18 ]提出的超网络模型进行了统一, 分析了该统一超网络的无标度特性演化机理和拓扑特性. Zhou等[21 ] 构建了一种同时考虑新超边增加和已存在超边消失的超网络模型. 李甍娜等[22 ] 以唐诗为节点, 以韵母为超边构建了唐诗超网络, 发现该超网络服从无标度分布且具有较高的聚集性和异配性. 胡枫等[23 ] 构建了蛋白复合物超网络模型, 并分析得出了识别关键蛋白的方法. 与此同时, 多层超网络的发展也极为迅速. 方锦清等[24 ,25 ] 从多角度出发思考和探索了多层超网络, 提出了三层超网络演化模型, 定义了两种层次交叉度, 并用其描述了层间节点的合作竞争关系和超网络的鲁棒性. Boccaletti等[26 ] 详细描述了多层网络, 并从基本结构入手分析了多层网络的动态变化过程. 蒋文君等[27 ] 就多层网络级联失效的预防和级联失效后的恢复做了整体性讨论. 杨喜艳等[28 ] 基于马尔科夫链方法建立了双层谣言传播网络模型, 并提出了一种能够有效阻止多层社交网络谣言传播的动态控制策略.[29 ] 20世纪50年代末提出的, 是复杂网络和现实生活中最为常用的一种随机网络模型. 近年来, ER随机网络在不同领域得到了广泛的研究与应用, Xu[30 ] 在ER随机网络模型中研究了经典的量子游走问题, 结果表明, 量子在游走过程中的返回概率, 即在初始节点找到量子的概率正比于ER随机网络的边连接概率, 且当ER随机网络趋于全连通时, 其返回概率会出现激增的现象. Xue[31 ] 在ER随机网络中利用大数定律改进了SIR传播模型. Lima等[32 ] 在有向ER随机网络上研究了多数投票模型, 通过蒙特卡罗模拟得到了“有序-无序”相变的关键参数. Zehmakan[33 ] 将社会网络抽象为ER随机网络, 发现了社会成员的观念在网络连通性达到某个阈值时会发生改变. 李炎等[34 ] 研究了ER随机网络中的Achlioptas爆炸渗流模型的相变性质, 结果表明, ER随机网络中的爆炸渗流相变是一种奇异相变, 它既不是标准的不连续相变, 又与常规随机渗流表现出的连续相变处于不同的普适类. 在经济快速发展和“大数据”时代的社会背景下, 超网络已经成为了网络科学的重要研究方向之一, 为更好地应用超网络, 超网络模型的构建是不能忽略的. 目前, 超网络模型的研究成果主要集中在无标度超网络模型的构建中, 对基于ER随机图理论的ER随机超网络模型研究尚属空白. 本文针对此问题, 首先提出了一种ER随机超网络模型的构建方法, 并分析得出了节点超度分布的解析表达式, 仿真实验结果表明, 本文提出的ER随机超网络的节点超度分布服从泊松分布, 符合随机网络特征并与理论推导一致. 为描述更为复杂的多层、异质关系的网络, 进一步构建了节点超度分布具有双峰特性, 层间采用随机方式连接, 层内分别为ER-ER, BA-BA和BA-ER三种不同类型的双层超网络模型, 理论分析得到了三种双层超网络节点超度分布的解析表达式, 并通过仿真实验对其进行了验证.2.ER随机超网络 22.1.ER随机超网络模型的构建方法 2.1.ER随机超网络模型的构建方法 在超图结构中引入ER随机图理论, 提出了一种ER随机超网络模型, 记为$H(N, p)$ , 构建过程如下:N 和超边连接概率p , $p \in \left[ {0, 1} \right]$ ;N 个节点中任意选择r 个不相同的节点, $r \leqslant N$ ;s , $s \in \left( {0, 1} \right)$ ;$s < p$ , 将第2步中选择的r 个节点组成一条超边;r 个不相同的节点都被选择一次.r 个节点形成一条超边, 因此本模型构建的超网络为r 均匀超网络. 最终生成的超边数量$m \approx p\left(\!\!\! {\begin{array}{*{20}{c}} N \\ r \end{array}}\!\!\! \right)$ .2.2.ER随机超网络节点超度分布理论分析 -->2.2.ER随机超网络节点超度分布理论分析 在本文提出的ER随机超网络中, 一个节点与其他$r - 1$ 个节点组成一条超边的概率为${p^k}{(1 - p)^{{{F}} - k}}$ , 其中${{F}} = \left(\!\!\! {\begin{array}{*{20}{c}} {N - 1} \\ {r - 1} \end{array}}\!\!\! \right)$ , 则网络中一个给定节点超度为k 的概率分布为:N 较大并且超边连接概率p 较小时, 节点超度为k 的二项分布近似为泊松分布:$ \left\langle \lambda \right\rangle = p \times {{F}}.$ 2.3.仿真实验 -->2.3.仿真实验 图2 为$N = 500$ , $r = 3$ 时, 在超边连接概率$p = 0.004$ , $p = 0.006$ , $p = 0.008$ 和$p = 0.01$ 四种不同条件下取100次平均值的节点超度分布情况.图 2 500个节点的随机3均匀超网络在不同连接概率p 值时的节点超度分布 (a) $p = 0.004$ ; (b) $p = 0.006$ ; (c) $p = 0.008$ ; (d) $p = 0.01$ Figure2. The hyper degree distribution of 3-uniform random hyper networks under different p : (a) $p = 0.004$ ; (b) $p = 0.006$ ; (c) $p = 0.008$ ; (d) $p = 0.01$ .图2(a) —图2(d) 可以看出, 本文提出的ER随机超网络模型的节点超度分布在四种不同超边连接概率条件下均服从泊松分布并与理论分析结果一致, 符合随机网络特征.3.双层超网络模型 超网络在描述复杂多元关系的系统时有着较强的优势, 而随着一些实际研究工作的展开, 我们发现单层超网络在描述多层异质关系时会略显不足. 例如在交通网络中, 如何准确地描述航空超网络和铁路超网络之间的关系等. 针对此类问题, 本文构建了节点超度分布具有双峰特性的双层超网络模型, 层间采用随机方式连接, 层内分别为ER-ER, BA-BA和BA-ER三种不同类型的双层超网络模型(简记为EE, BB和BE, 其中E代表本文提出的ER随机超网络; B代表BA 无标度超网络). 本文以双层3均匀超网络为例, 分析三种不同类型的双层超网络模型.3.1.EE双层3均匀超网络 3.1.EE双层3均匀超网络 EE双层3均匀超网络包含两层ER随机3均匀超网络, 层与层之间采用随机连接方式.3.1.1.构建方法 -->3.1.1.构建方法 EE双层3均匀超网络模型的构建过程如下:$H(N, p)$ 构建第一层和第二层超网络${H_1}({N_1}, {p_1})$ 和${H_2}({N_2}, {p_2})$ ;${p_{12}}$ 组合生成一条超边, 直至层间形成${N_1}\left(\!\!\! {\begin{array}{*{20}{c}} {{N_2}} \\ 2 \end{array}}\!\!\! \right){p_{12}}$ 条超边为止.3.1.2.理论分析 -->3.1.2.理论分析 根据以上构建方法中的第2步可知, EE双层超网络的节点平均超度$\left\langle k \right\rangle $ 由第一层超网络的节点平均超度$\left\langle {{k_1}} \right\rangle $ 和第二层超网络的节点平均超度$\left\langle {{k_2}} \right\rangle $ 决定. 其中, EE双层超网络中第一层网络中的任意一个节点与层内其他任意两个节点形成超边的数量为$\left(\!\!\! {\begin{array}{*{20}{c}} {{N_1} - 1} \\ 2 \end{array}}\!\!\! \right){p_1}$ , 与第二层超网络中的任意两个节点形成超边的数量为$\left(\!\!\! {\begin{array}{*{20}{c}} {{N_2}} \\ 2 \end{array}} \!\!\! \right){p_{12}}$ ; 同理, 第二层超网络中任意一个节点在层内形成的超边数量为$\left(\!\!\! {\begin{array}{*{20}{c}} {{N_2} - 1} \\ 2 \end{array}}\!\!\! \right){p_2}$ , 第二层超网络中任意两个节点与第一层超网络中任意一个节点形成超边的数量为${N_2}\left( {{N_2} - 1} \right){p_{12}}$ , 故第一层和第二层超网络节点平均超度的计算表达式为:${N_1}$ 和${N_2}$ 分别为第一层和第二层超网络的节点数, ${p_1}$ 和${p_2}$ 分别为第一层和第二层超网络的层内超边连接概率, ${p_{12}}$ 为层间超边连接概率. 由(4 )式和(5 )式可得$\left\langle k \right\rangle = \dfrac{\left( {\left\langle {{k_1}} \right\rangle \times {N_1} + \left\langle {{k_2}} \right\rangle \times {N_2}} \right)} {\left( {{N_1} + {N_2}} \right)}$ .${p^{{\rm{1 st}}}}(k)$ 和第二层超网络的节点超度分布${p^{{\rm{2 nd}}}}(k)$ 组成. 第一层超网络中任意一个节点与其他两个节点组成一条超边的概率为${p_1}^i(1 - {{p_1})^{{{{F}}_1} - i}}$ , 其中${{{F}}_1} = \left(\!\!\! {\begin{array}{*{20}{c}} {{N_1} - 1} \\ 2 \end{array}}\!\!\! \right)$ , 与第二层超网络中的任意两个节点组成一条超边的概率为$p_{12}^{k - i} \times {(1 - {p_{12}})^{{{{Q}}_1} - (k - i)}}$ , 其中${{{Q}}_1} = \left(\!\!\! {\begin{array}{*{20}{c}} {{N_2}} \\ 2 \end{array}}\!\!\! \right)$ . 由此可以得出第一层超网络中节点超度为k 的概率分布为k 的概率分布为${{{F}}_2} = \left(\!\!\! {\begin{array}{*{20}{c}} {{N_2} - 1} \\ 2 \end{array}}\!\!\! \right)$ , ${{{Q}}_2} = {N_2}\left( {{N_2} - 1} \right)$ , ${{{Q}}_2} = 2{{{Q}}_1}$ , 则:3.1.3.仿真实验 -->3.1.3.仿真实验 在EE双层超网络节点超度分布仿真实验中, ${N_1}$ 和${N_2}$ 取值为500, 层内连接概率${p_1}$ 和${p_2}$ 为0.006, 层间连接概率${p_{12}}$ 分别为0.001和0.01, 为了结果的合理有效, 实验结果取了100次的平均值.表1 为EE双层超网络节点超度分布实验的统计信息, 其中N 代表双层网络的总节点数, M 为层间的超边数量. 实验结果表明, EE双层超网络的节点超度分布在不同层间超边连接概率条件下均具有双峰特性, 如图3(a) 和图3(b) 所示.${N_1}$ ${N_2}$ N ${p_1} = {p_2}$ ${p_{12}}$ M $\left\langle {{k_1}} \right\rangle $ $\left\langle {{k_2}} \right\rangle $ $\left\langle k \right\rangle $ 500 500 1000 0.006 0.001 62375 870 994 932 0.01 623750 1992 3240 2616
表1 EE双层3 均匀超网络实验统计Table1. Experimental statistics of EE hyper network.图 3 双层3均匀EE超网络在不同层间超边连接概率时的节点超度分布 (a)${p_{12}} = 0.001$ ; (b)${p_{12}} = 0.01$ Figure3. The EE hyper degree distribution of double-layer 3-uniform hyper network under different ${p_{12}}$ : (a)${p_{12}} = 0.001$ ; (b)${p_{12}} = 0.01$ .3.2.BB双层3均匀超网络 -->3.2.BB双层3均匀超网络 BB双层3均匀超网络包含两层3均匀无标度超网络, 层与层之间采用随机连接方式. 在构建3均匀无标度超网络时, 采用文献[17 ]提出的均匀无标度超网络模型构建方法, 记为$H({m_0}, m)$ . 该超网络模型的节点超度分布服从幂律分布, 符合无标度网络特征. $H({m_0}, m)$ 模型的构建过程如下:${m_0}$ 个节点$\{ {v_1}, {v_2}, {v_3}, \cdots , {v_{m0}} \}$ 与一条包含这些节点的超边${E_0} = \{ {v_1}, {v_2}, {v_{3, }} \cdots , {v_{m0}} \}$ ;t 添加m 个节点$\left\{{v}_{t1}, {v}_{t2}, {v}_{t3}, \cdots , {v}_{tm}\right\}$ 与一个已存在的节点${v_i}$ 组合成一条新的超边${E}_{t}=\left\{{v}_{t1}, {v}_{t2}, {v}_{t3}, \cdots , {v}_{tm}, {v}_{i}\right\}$ . 这个已存在节点的选取方式为“超度优先连接”, 即节点vi 被选中的概率正比于这个节点的超度, 定义为:${d_H}\left( {{v_i}} \right)$ 为节点${v_i}$ 的超度, 分母表示当前网络中所有节点超度之和. 在该均匀无标度超网络中, 一个给定节点超度为k 的概率分布为[18 ] m 为每次添加新节点的个数, 当$m = 2$ 时, 该超网络为3均匀无标度超网络.3.2.1.构建方法 -->3.2.1.构建方法 BB双层3均匀超网络模型的构建过程如下:$H\left( {{m_0}, \;m} \right)$ 模型构建第一层和第二层3均匀无标度超网络${H_1}\left( {{m_{10}}, \;{m_1}} \right)$ 和${H_2}\left( {{m_{20}}, \;{m_2}} \right)$ ;${p_{12}}$ 组合生成一条超边, 直至形成$({m_{10}} + {m_1})\left(\!\!\! {\begin{array}{*{20}{c}} {({m_{20}} + {m_2})} \\ 2 \end{array}} \!\!\! \right){p_{12}}$ 条超边为止.3.2.2.理论分析 -->3.2.2.理论分析 由于第一层与第二层超网络均为3均匀无标度超网络, 每次增加2个新节点与1个已存在节点组合生成一条超边, 所以在层间连接之前, 各层超网络的节点平均超度约为${3 / 2}$ . 由此可得, 第一层超网络的节点平均超度$\left\langle {{k_1}} \right\rangle $ 和第二层超网络的节点平均超度$\left\langle {{k_2}} \right\rangle $ 分别为:${N_2}$ 为第二层超网络的节点数, 则BB超网络的节点平均超度$\left\langle k \right\rangle = \dfrac{ {\left\langle {{k_1}} \right\rangle \times {N_1} + \left\langle {{k_2}} \right\rangle \times {N_2}} } {\left( {{N_1} + {N_2}} \right)}$ .N 个节点的3均匀无标度超网络中, 超度为1的节点数$M(1)$ 的上下界为$ {N}/{2} + 1 \leqslant M(1) \leqslant N - 1$ , 超度为2的节点数$M(2)$ 的上界为$M(2) \leqslant {N}/{2}$ . 所以, BB双层超网络的第一层超网络中节点超度为k 的概率分布为${W}_{1}(1)={M}_{1}(1)\!\times\! \left(\!\!\! \begin{array}{c}{{Q}}_{1}\\ k-1\end{array}\!\!\! \right){p}_{12}^{k-1}\!\times\! {(1-{p}_{12})}^{{{Q}}_{1}-(k-1)}, \;{W}_{1}(2)={M}_{1}(2)\!\times\! \left(\!\!\! \begin{array}{c}{{Q}}\\ k-2\end{array}\!\!\! \right){p}_{12}^{k-2}\!\times\! {(1-{p}_{12})}^{{{Q}}_{1}-(k-2)}.$ k 的概率分布为${W}_{2}(1)={M}_{2}(1)\!\times\! \left(\!\!\! \begin{array}{c}2{{Q}}_{1}\\ k-1\end{array}\!\!\! \right){p}_{12}^{k-1}\!\times\! {(1\!-\!{p}_{12})}^{2{{Q}}_{1}-(k-1)},\; {W}_{2}(2)={M}_{2}(2)\!\times\! \left(\!\!\! \begin{array}{c}2{{Q}}_{1}\\ k-2\end{array}\!\!\! \right){p}_{12}^{k-2}\!\times\! {(1\!-\!{p}_{12})}^{2{{Q}}_{1}-(k-2)}.$ 3.2.3.仿真实验 -->3.2.3.仿真实验 在BB双层超网络节点超度分布的仿真实验中, 第一层与第二层超网络的节点数${N_1} = {m_{10}} + {m_1}$ 和${N_2} = {m_{20}} + {m_2}$ 取值为500, 其中各层初始节点${m_{10}}$ 和${m_{20}}$ 均为3, 层间连接概率${p_{12}}$ 分别为0.001和0.01, 为了结果的合理有效, 实验结果取了100次的平均值.表2 为BB超网络节点超度分布实验的统计信息. 与EE双层超网络的结果相同, BB双层超网络的节点超度分布在不同层间超边连接概率条件下均具有双峰特性, 如图4(a) 和图4(b) 所示.${N_1}$ ${N_2}$ N ${m_{10}} = {m_{20}}$ ${p_{12}}$ M $\left\langle {{k_1}} \right\rangle $ $\left\langle {{k_2}} \right\rangle $ $\left\langle k \right\rangle $ 500 500 1000 3 0.001 62375 126 251 188 0.01 623750 1992 3240 2616
表2 BB双层3均匀超网络实验统计Table2. Experimental statistics of BB hyper network.图 4 双层3均匀BB超网络节点超度分布 (a)${p_{12}} = 0.001$ ; (b)${p_{12}} = 0.01$ Figure4. The BB hyper degree distribution of double-layer 3-uniform hyper network under different ${p_{12}}$ : (a)${p_{12}} = 0.001$ ; (b)${p_{12}} = 0.01$ .3.3.BE双层3均匀超网络 -->3.3.BE双层3均匀超网络 BE双层3均匀超网络由第一层3均匀无标度超网络和第二层ER随机3均匀超网络组成, 层与层之间采用随机连接方式.3.3.1.构建方法 -->3.3.1.构建方法 BE双层3均匀超网络模型的构建过程如下:$H\left( {{m_0}, \;m} \right)$ 模型构建第一层超网络${H_1}\left( {{m_{10}}, \;{m_1}} \right)$ ;$H\left( {N, \;p} \right)$ 模型构建第二层超网络${H_2}\left( {{N_2}, \;{p_2}} \right)$ ;${p_{12}}$ 组合生成一条超边, 直至形成$({m_{10}} + {m_1})\left(\!\!\! {\begin{array}{*{20}{c}} {{N_2}} \\ 2 \end{array}} \!\!\! \right){p_{12}}$ 条超边为止.3.3.2.理论分析 -->3.3.2.理论分析 BE双层超网络的节点平均超度$\left\langle k \right\rangle $ 由第一层无标度超网络的节点平均超度$\left\langle {{k_1}} \right\rangle $ 和第二层ER随机超网络的节点平均超度$\left\langle {{k_2}} \right\rangle $ 决定, 分别为:${N_2}$ 为第二层超网络的节点数, ${p_2}$ 为第二层超网络的层内超边连接概率, ${p_{12}}$ 为层间超边连接概率, 则$\left\langle k \right\rangle = {{\left( {\left\langle {{k_1}} \right\rangle \times {N_1} + \left\langle {{k_2}} \right\rangle \times {N_2}} \right)} / {\left( {{N_1} + {N_2}} \right)}}$ .k 的概率分布为${W}_{1}(1)={M}_{1}(1)\!\times\! \left(\!\!\! \begin{array}{c}{{Q}}_{1}\\ k-1\end{array}\!\!\! \right){p}_{12}^{k-1}\times {(1\!-\!{p}_{12})}^{{{Q}}_{1}-(k-1)}, {W}_{1}(2)={M}_{1}(2)\!\times\! \left(\!\!\! \begin{array}{c}{{Q}}_{1}\\ k-2\end{array}\!\!\! \right){p}_{12}^{k-2}\!\times\! {(1\!-\!{p}_{12})}^{{{Q}}_{1}-(k-2)}.$ k 的概率分布为${{{F}}_2} = \left(\!\!\! {\begin{array}{*{20}{c}} {{N_2} - 1} \\ 2 \end{array}} \!\!\! \right), {{{Q}}_1} = \left(\!\!\! {\begin{array}{*{20}{c}} {{N_2}} \\ 2 \end{array}} \!\!\! \right)$ , ${p_2}$ 为第二层随机超网络的超边连接概率.3.3.3.仿真实验 -->3.3.3.仿真实验 在BE双层超网络的节点超度分布实验中, 第一层与第二层超网络的节点数${N_1} = {m_{10}} + {m_1}$ 和${N_2}$ 取值为500, 其中第一层超网络的初始节点${m_{10}}$ 为3, 第二层超网络的超边连接概率${p_2}$ 为0.006, 层间连接概率${p_{12}}$ 分别为0.001和0.01, 为了结果的合理有效, 实验结果取了100次的平均值.表3 为BE超网络节点超度分布实验的统计信息. BE双层超网络的节点超度分布与以上两种类型的双层超网络情况相同, 在不同的层间超边连接概率的条件下, 节点超度分布均具有双峰特性, 如图5(a) 和图5(b) 所示.${N_1}$ ${N_2}$ N ${m_{10}}$ ${p_2}$ ${p_{12}}$ M $\left\langle {{k_1}} \right\rangle $ $\left\langle {{k_2}} \right\rangle $ $\left\langle k \right\rangle $ 500 500 1000 3 0.006 0.001 62375 126 994 560 0.01 623750 1249 3240 2244
表3 BE双层3均匀超网络实验统计Table3. Experimental statistics of BE hyper network.图 5 双层3均匀BE超网络模型节点超度分布 (a)${p_{12}} = 0.001$ ; (b)${p_{12}} = 0.01$ Figure5. The BE hyper degree distribution of double-layer 3 -uniform hyper network under different ${p_{12}}$ : (a)${p_{12}} = 0.001$ ; (b)${p_{12}} = 0.01$ .4.结 论 本文基于经典的ER随机模型构建了基于超图的ER随机超网络模型, 通过理论分析得到了该模型的节点超度分布$p(k) \approx \dfrac{{{{\left\langle \lambda \right\rangle }^k}}}{{k!}}{{\rm{e}}^{ - \left\langle \lambda \right\rangle }}$ , 其中泊松分布的期望值$\lambda $ 与超边连接概率p 有关, 计算机仿真实验结果与理论分析一致. 与普通的ER随机网络相比, 本文提出的ER随机超网络模型对于描述和分析关系更复杂、节点属性更多元化的随机社会网络具有一定的实际应用价值. 同时, 在ER随机超网络模型的基础之上, 构建了ER-ER, BA-BA和BA-ER三种不同类型的双层超网络模型. 理论分析发现, 三种双层超网络的节点平均超度与层间超边连接概率密切相关, 随着层间超边连接概率的增大网络节点的平均超度也随之增大; 仿真实验结果表明, 三种模型的节点超度分布在不同的层间超边连接概率条件下均具有双峰特性. 

























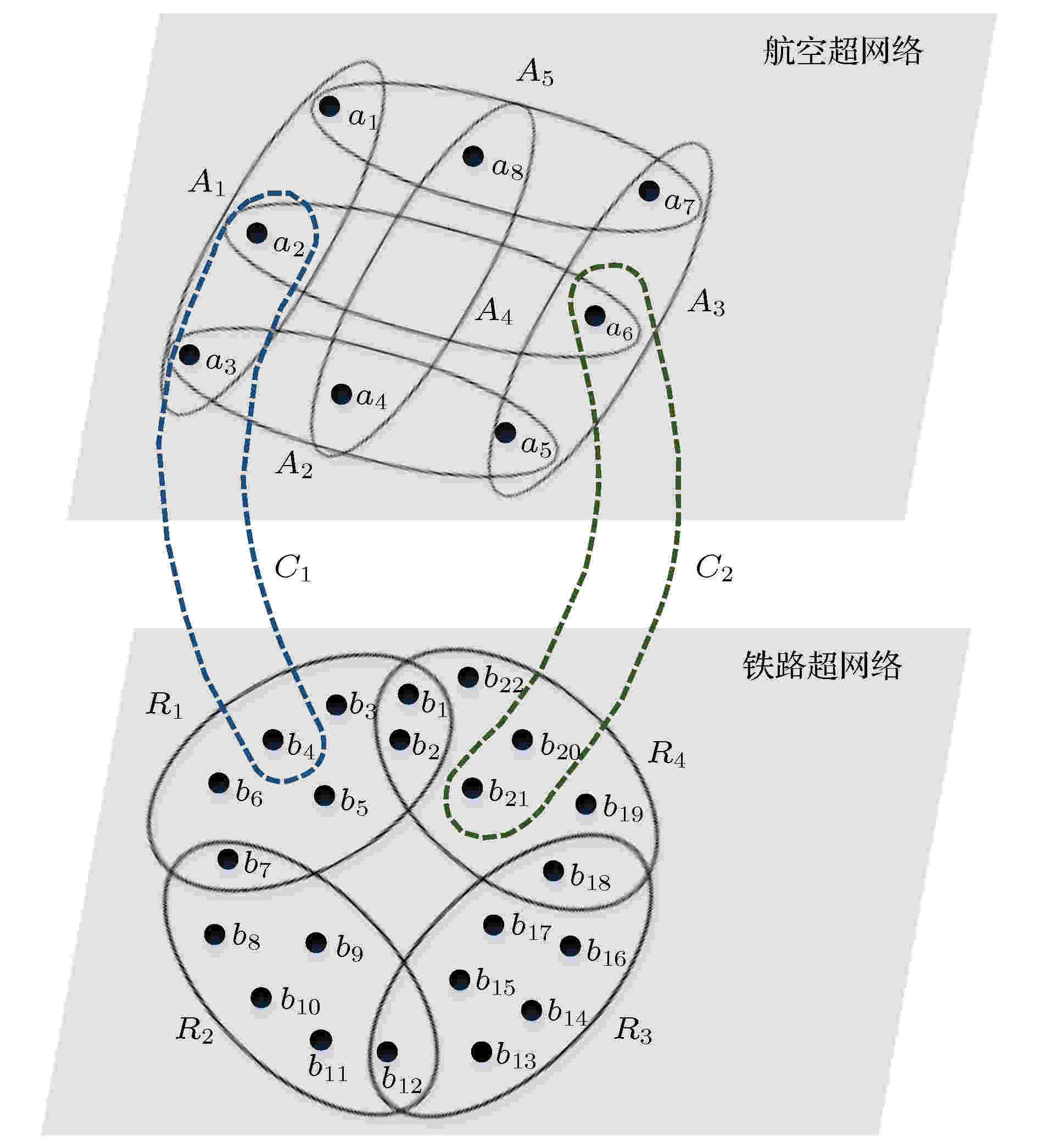 图 1 “航空-铁路”双层超网络模型
图 1 “航空-铁路”双层超网络模型















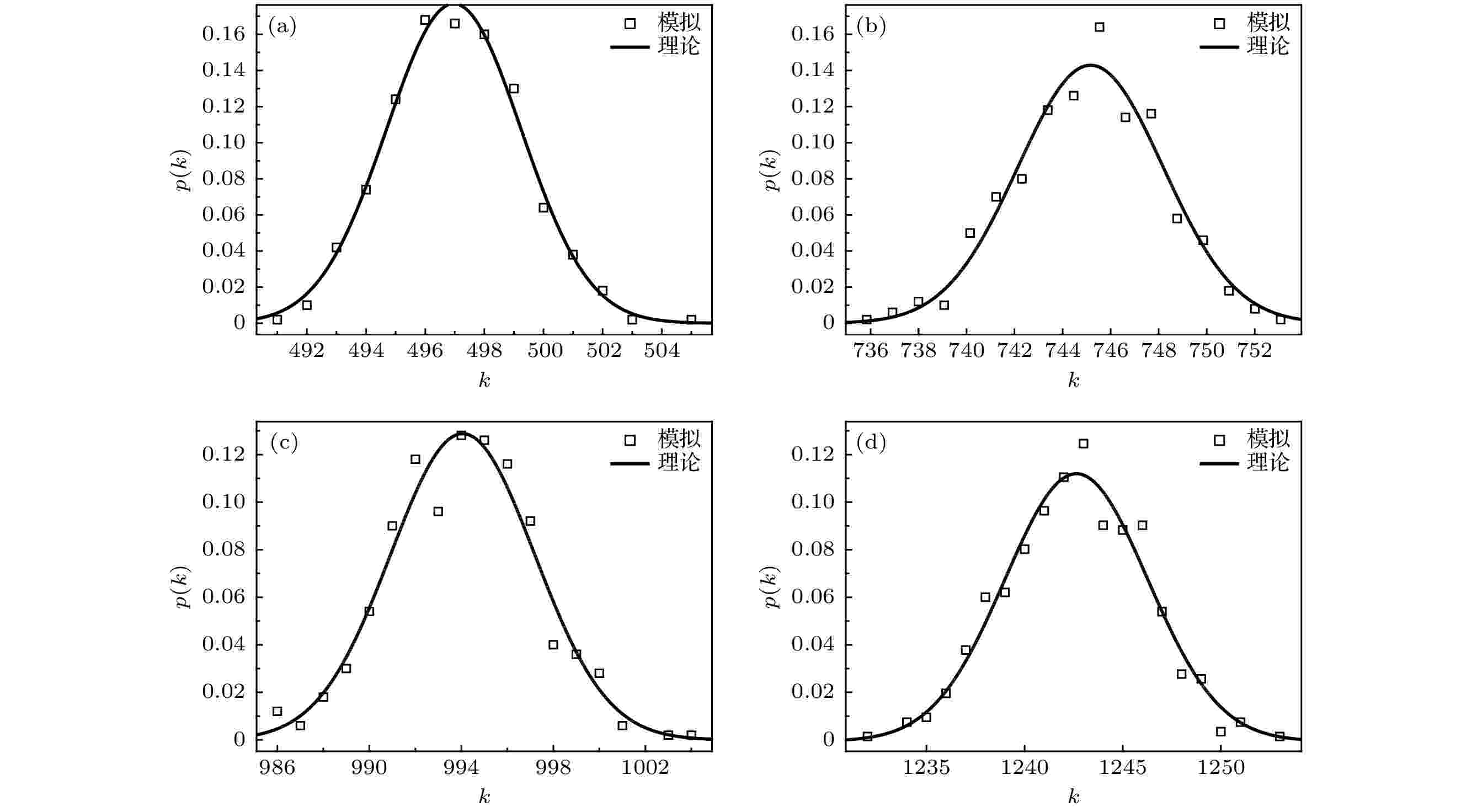 图 2 500个节点的随机3均匀超网络在不同连接概率p值时的节点超度分布 (a)
图 2 500个节点的随机3均匀超网络在不同连接概率p值时的节点超度分布 (a) 







































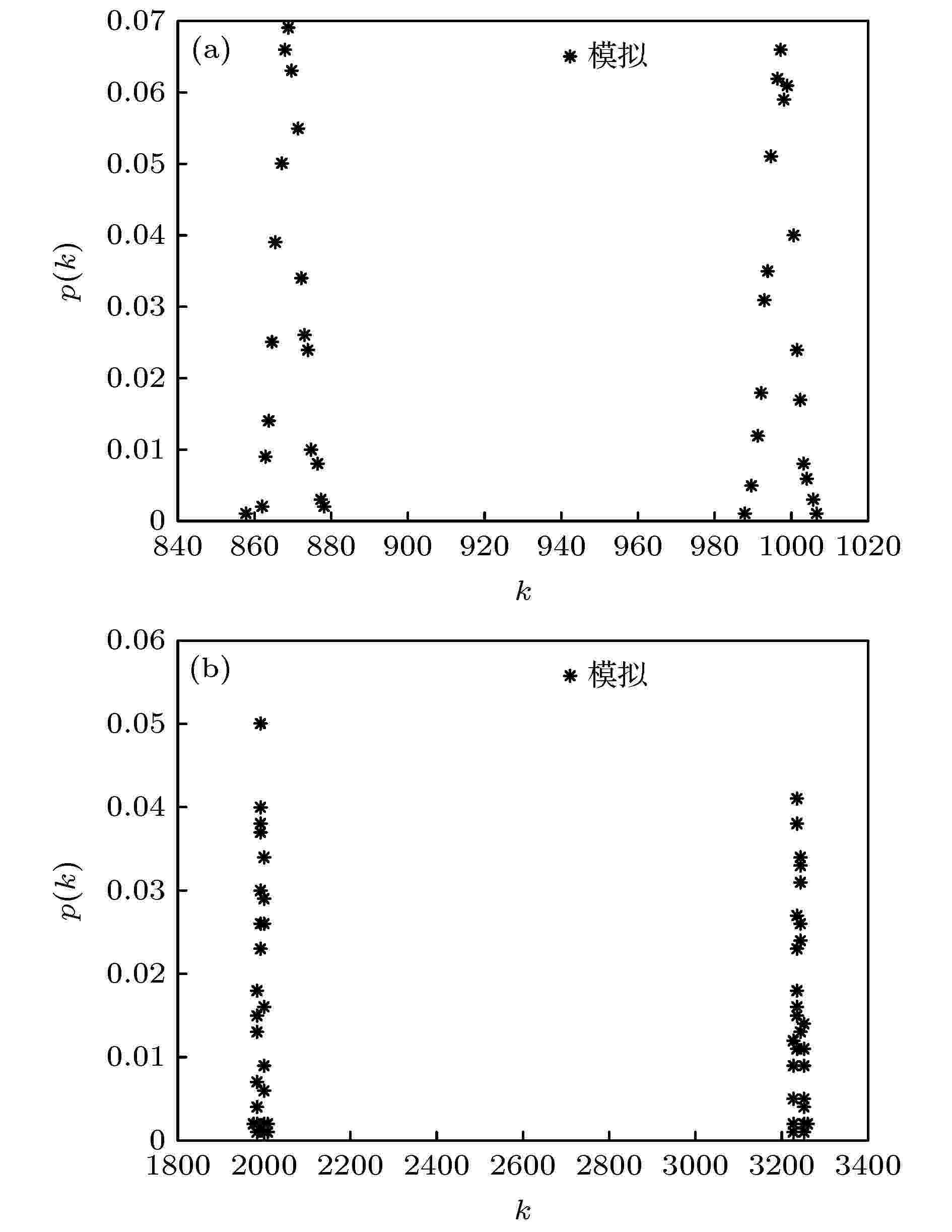 图 3 双层3均匀EE超网络在不同层间超边连接概率时的节点超度分布 (a)
图 3 双层3均匀EE超网络在不同层间超边连接概率时的节点超度分布 (a)






































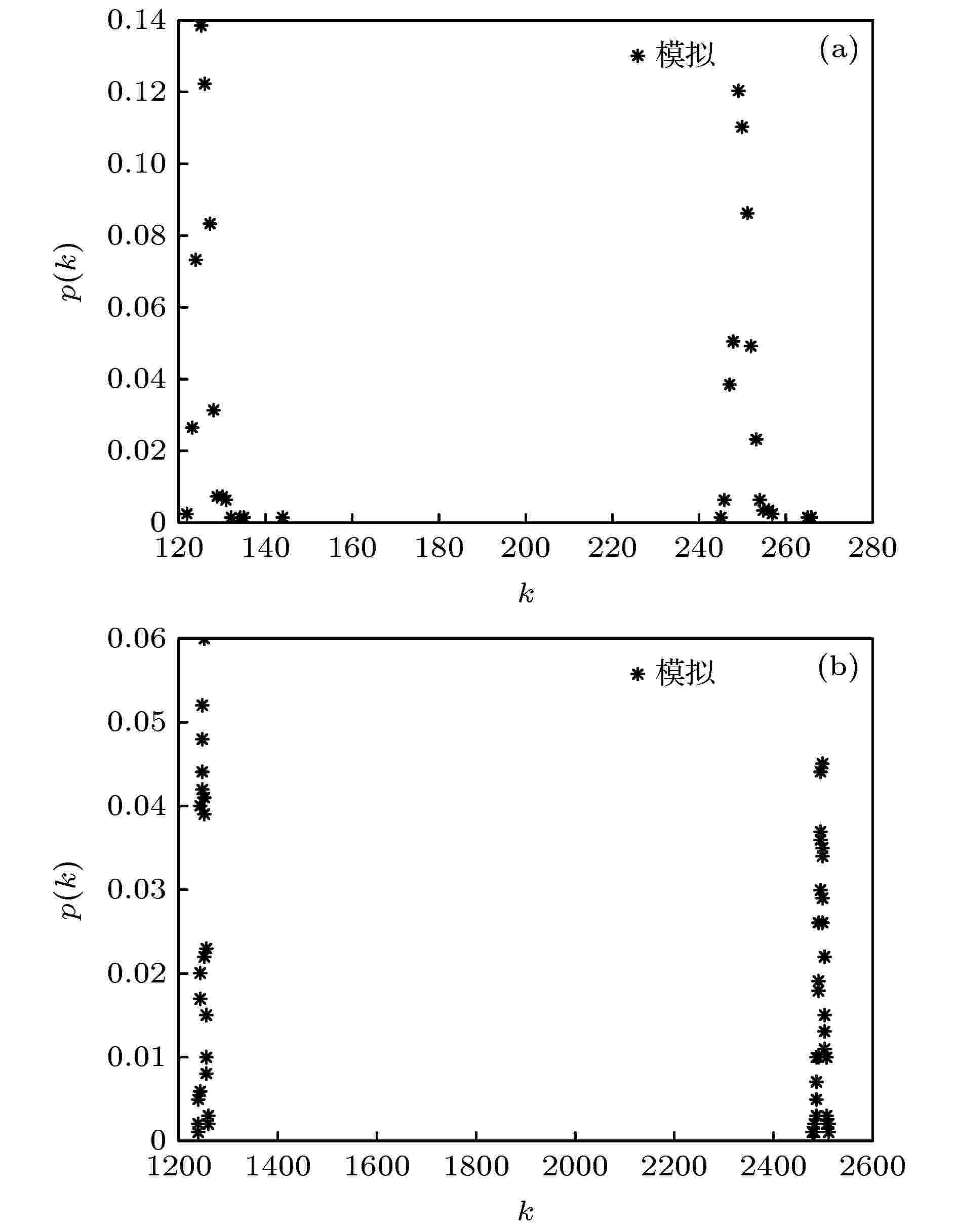 图 4 双层3均匀BB超网络节点超度分布 (a)
图 4 双层3均匀BB超网络节点超度分布 (a)

























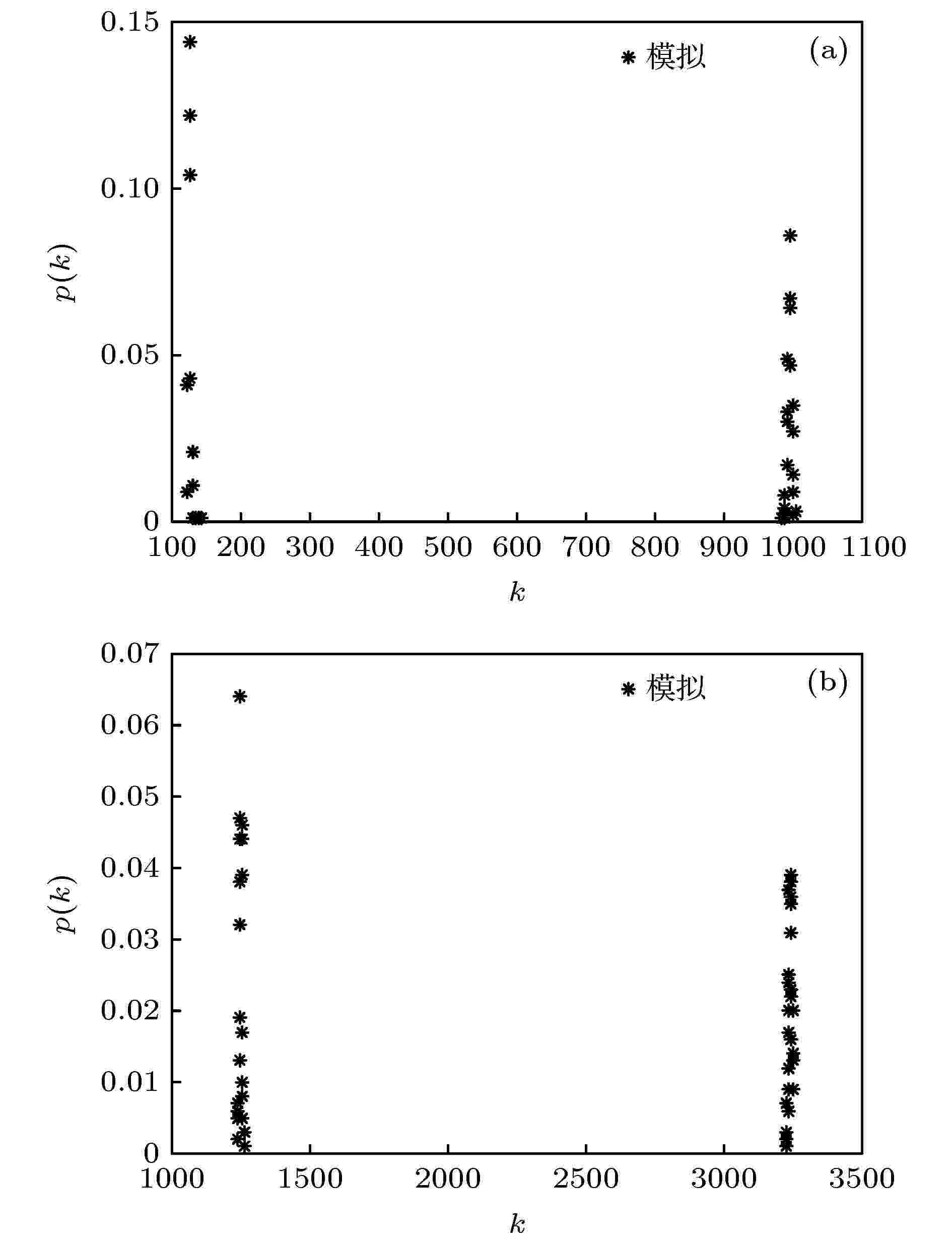 图 5 双层3均匀BE超网络模型节点超度分布 (a)
图 5 双层3均匀BE超网络模型节点超度分布 (a)











