摘要:多孔介质在工程领域中的应用非常广泛, 其中有效导热率和孔隙率为多孔介质材料非常重要的性质, 得到一个符合需要的有效导热率和孔隙率的多孔介质材料具有重要意义. 本文使用四参数随机生成方法制作了训练数据集, 搭建了一个条件生成对抗网络(CGAN), 使用预定的有效导热率和孔隙率作为输入, 生成一个满足输入条件的多孔介质结构. 特别地, 由于多孔介质的孔隙结构分布对材料的有效导热率影响巨大, 提出局部结构损失函数参与网络训练, 使得网络更好地学习到孔隙分布与导热率之前的关系. 通过使用格子Boltzmann方法验证神经网络生成的多孔介质结构的有效导热率, 结果表明该方法能够快速且准确地生成预定参数的多孔介质结构.
关键词: 多孔介质/
结构生成/
条件生成对抗网络/
有效导热率

English Abstract

全文HTML

--> --> -->

多孔介质在工程领域的应用非常广泛, 其有效导热率是衡量多孔介质传热能力的重要物理参数. 一般而言, 导热率高的多孔介质可以用于制作散热器件^[1,2], 而导热率低的多孔介质可用于制作热阻器件^[3,4]. 据此, 研究多孔介质微观结构与其宏观表征参数(例如有效导热率)的关系对探究多孔介质内流体输运过程具有重要的科学意义和现实价值^[5].
目前, 国内外已有许多研究人员从表征体元尺度和孔隙尺度对多孔介质内流体输运问题开展了研究^[6,7], 结果表明多孔介质内流体流动和传热问题与传统流体输运问题有较大不同. 不同于前人研究工作, 本文聚焦于多孔介质微观孔隙结构与和宏观有效导热率之间的映射关系. 关于此问题, 已有不少****通过采用计算流体力学中的各类数值方法, 数值模拟多孔介质内传热过程, 进而预测出多孔介质的有效导热率^[8,9]. 例如Fang等^[8]考虑传导和辐射的综合作用, 采用离散纵坐标法求解辐射传递方程, 采用格子Boltzmann方法(LBM)预测了多孔介质的有效导热系数. Wang和Pan^[9]采用LBM对开孔泡沫材料的有效热导率进行了预测, 并将预测结果与实验结果进行了对比, 结果显示吻合较好. 需要指出, 这种直接数值模拟方式尽管为预测多孔介质有效导热率提供了一种行之有效的计算方法, 但该方法往往需要较高的计算成本和计算时间. 近年来, 机器学习方法迅速发展, 其在多个工程应用邻域都展示了独特的优势, 其作为一种数据驱动的模型, 在完成模型训练后具有快速预测的特点^[10,11]. 鉴于此, 最近Han等^[12]通过使用二维多孔介质作为模型的输入, 训练了一个序列式的卷积网络模型进而对多孔介质的有效导热率进行预测, 结果表明基于卷积网络模型的预测结果与数值模拟方法得到的有效导热率数据吻合较好；他们还发现: 与传统数值模拟方法相比, 机器学习方法能够很大程度节省预测时间, 通过实验测得训练好的机器学习模型在单核2.4 GHz CPU工况下预测128 × 128尺寸多孔介质有效导热率只需0.06 s, LBM方法在相同的硬件下计算128 × 128的多孔介质导热率需106 s. 实际工程应用中, 除上述基于多孔介质结构进行有效导热率的直接预测外, 人们往往也关注其逆过程, 即基于人为给定的预定导热率设计出一类合理的多孔介质结构^[13-16]. 针对该问题, 较为常用的方法是通过使用三维成像技术, 对有限个多孔介质的二维切片数据进行重构^[17,18], 重构的方法包括多点统计(MPS)^[19-21]、直接采样(DS)^[22]和互相关的仿真算法(CCSIM) ^[23-27]等. 显然, 对于上述重构方法, 所获得的二维切片信息越多, 算法表现就越好. 但由于实验过程中只能获取局部的结构信息, 所以直接从不完善的二维图像信息重建三维图像往往十分困难. 为此, 已有科研人员提出另外一种重构思路, 即先对具有有限信息的二维图像进行重构, 然后再将所得的二维重构图像应用于三维图像的重建^[28]. 基于这种思路, 研究人员将许多机器学习技术应用于多孔介质的重构过程中, 包括决策树方法^[29,30]、二维生成对抗网络(GAN)和二维条件生成对抗网络(CGAN)^[31-33], 三维GAN和三维CGAN ^[34-38], 以及基于卷积神经网络(CNN) ^[39]的方法等. 例如, Feng等^[28]使用CGAN把多孔介质的二维多孔介质的局部结构作为输入用于恢复整体二维多孔介质结构. Denis等^[40]使用二维多孔介质切片作为输入用于恢复完整的三维多孔介质结构. 这些工作的目的都是通过已知的局部多孔介质结构来重建整体结构, 评判的标准为重建结构与标签结构的相似性, 取得了较好的效果.
上述的机器学习方法在重建多孔介质孔隙结构方面表现良好, 但其关注的是多孔介质结构的宏观结构, 没有关注多孔介质结构与有效导热率之间的关系. 一般而言, 孔隙率大的多孔介质对应的有效导热率往往越小, 但应该注意相同孔隙率条件下, 不同的孔隙分布的多孔介质对应的有效导热率也会存在一定差异^[41,42]. 如图1所示, 图1中各多孔介质的孔隙率皆为0.45, 黑色部分为孔隙, ${K}_{1}, \;{K}_{2}$和${K}_{3} $表示多孔介质导热率, 但是不同的结构分布导致它们拥有不同的导热率. 此外, 多孔介质的结构对导热率也有巨大影响, 细微结构的变化会改变其导热率^[41,42], 如图2所示, ${K}_{1}$和${K}_{2} $表示多孔介质导热率, 图中使用5个颜色不同的框标出了局部结构的细微差异, 表明多孔介质的微观结构对其有效导热率有一定的影响, 其中存在着某种映射关系. 鉴于此, 本文使用条件生成对抗网络来学习这种映射关系, 其中训练网络所需要数据集主要是通过使用四参数随机生成方法(quartet structure generation set, QSGS)^[42]来生成, 网络模型训练完毕后通过输入人为预定的导热率和孔隙率来生成多孔介质结构, LBM计算的多孔介质导热率已被验证具有合理性, 如表1所列^[42], 然后使用LBM来验证生成多孔介质导热率的合理性^[43,44], 并考察神经网络模型生成多孔介质结构的效率.
图 1 不同孔隙分布多孔介质示意图　(a) K₁ = 5.52; (b) K₂ = 6.37; (c) K₂ = 7.32
Figure1. Schematic diagram of porous media with different pore distributions: (a) K₁ = 5.52; (b) K₂ = 6.37; (c) K₂ = 7.32

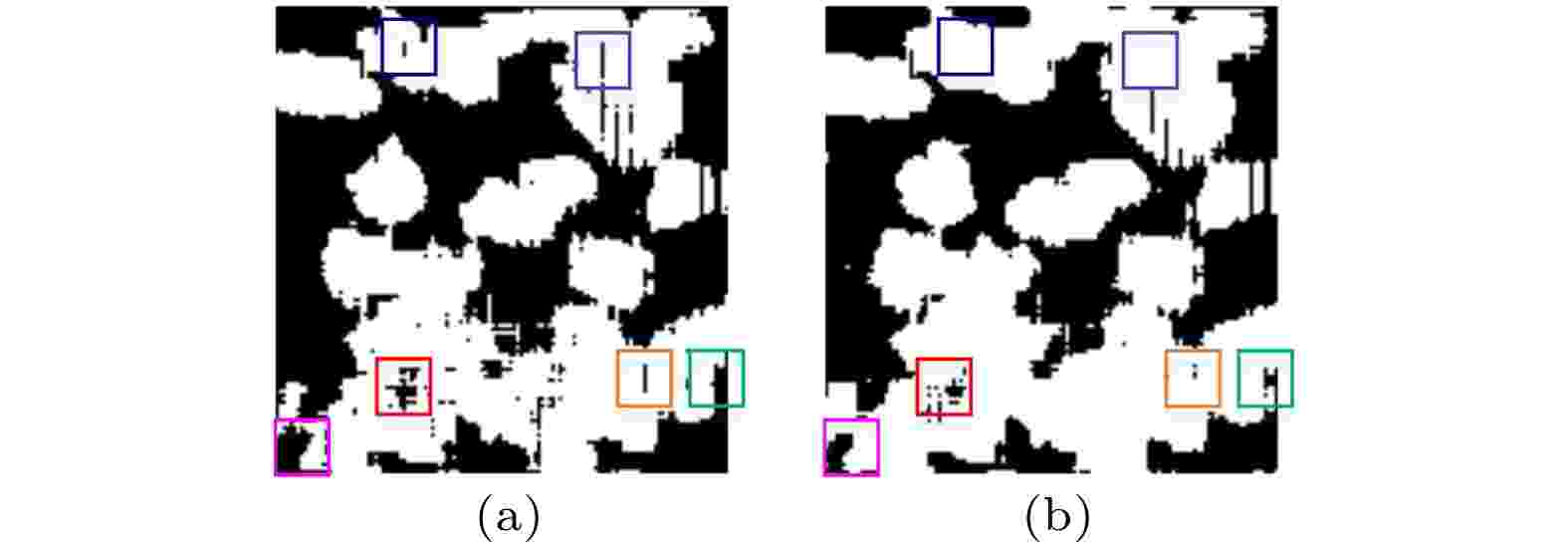图 2 局部结构差异　(a) K₁ = 6.0; (b) K₂ = 6.4
Figure2. Local structural differences: (a) K₁ = 6.0; (b) K₂ = 6.4

Along the foam growing direction				Across the foam growing direction
Prediction/(W·mK–1)	Experiment/(W·mK–1)	Deviation/%		Prediction/ (W·mK–1)	Experiment/(W·mK–1)	Deviation/%
0.0253	0.0220	15.0		0.0265	0.0245	8.16

表1LBM计算多孔介质导热率与实验值比较
Table1.Comparison between LBM calculation of thermal conductivity of porous media and experimental values.

2

-->

2.1.使用QSGS算法和LBM制作训练数据

QSGS算法是一种十分简单快捷的多孔介质生成法, 它主要由生成多孔介质尺寸、孔隙率、初始成核概率以及各方向生成概率参数等控制多孔介质的生成. 主要的工作原理是, 先设置生成的多孔介质尺寸为$d \times d$, 再设初始设置的孔隙率为x且$x < 1$, 初始成核概率为${p_1}$且${p_1} < 1$, 各方向生成概率${p_2}$且${p_2} < 1$. 首先以此开始遍历预生成多孔介质上的每一个点, 在每一个点上生成一个0—1之间的随机数, 若随机数小于${p_1}$, 则把这一点作为初始核, 指导遍历完全部的点. 然后以生成的初始核为基础, 在每个初始核的各个生成方向分别(二维多孔介质具有8个生成方向, 如图3所示)生成0—1之间的随机数；若生成的随机数小于${p_2}$, 则把该方向对应的点转换为实体点, 同时统计所有实体点的数量, 当实体点的数量大于或等于设定的实体点总数$\left( {d \times d \times d} \right)$时, 结束生成, 并输出生成好的多孔介质结构. 调整孔隙率以及各方向生长概率等参数可以生成不同形态的多孔介质结构, 图4为四参数随机生成法生成的多孔介质示例, 再使用LBM计算QSGS算法所生成多孔介质的有效导热率作为训练集的标签导热率.
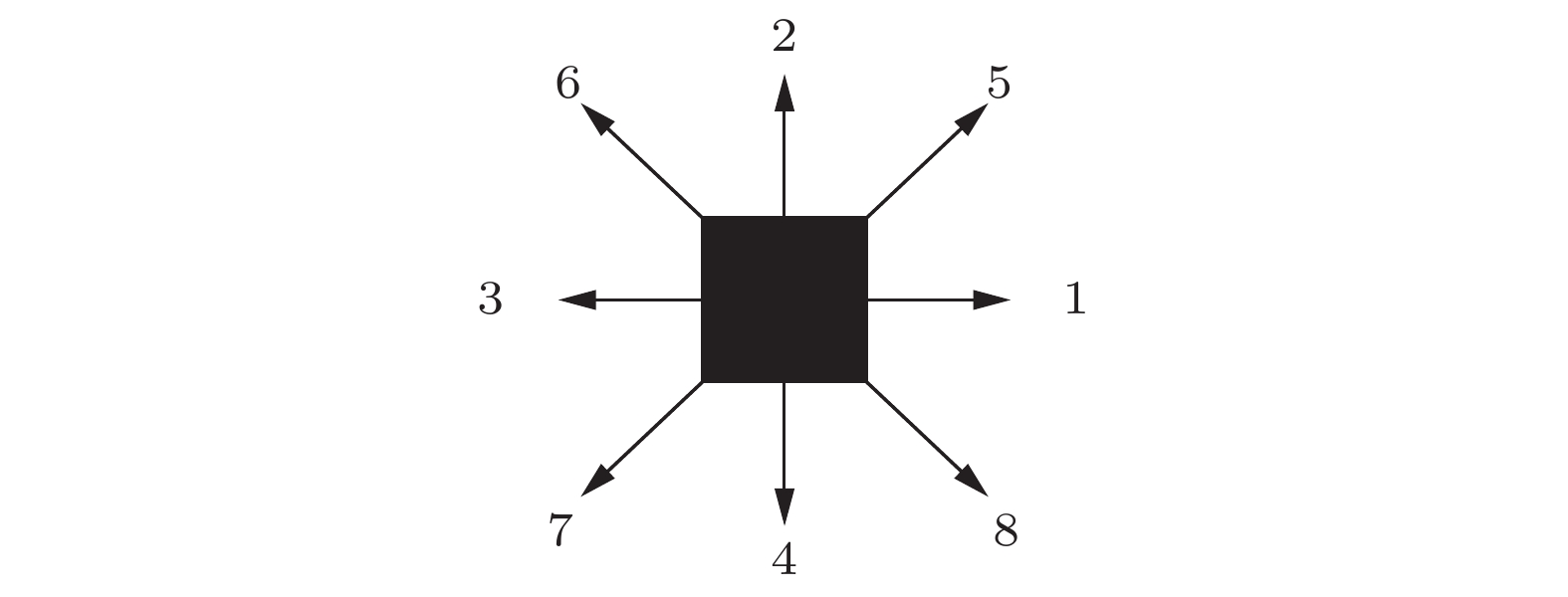图 3 二维多孔介质各方向生成示意图
Figure3. Schematic diagram of the generation of two-dimensional porous media in all directions.

图 4 四参数随机生成法生成二维多孔介质示例图
Figure4. An example of two-dimensional porous media generated by the four-parameter random production method.

2 -->

2.2.条件生成对抗网络

3 -->

2.2.1.原　理

CGAN是GAN的拓展, 下面先介绍生成对抗网络的原理. 生成对抗网络由两个对抗模块组成: 生成模型G和判别模型D. 生成模型G用于学习数据的分布, 判别模型D用于估计样本是来自训练数据而不是生成模型G的概率大小, 生成模型G和判别模型D都与多层感知机类似为一个非线性的映射函数.
为了在训练数据x上学习到生成分布${p_{\rm{g}}}$, 生成器建立了一个从先验噪声分布${p_z}(z)$到数据空间$G(z;{\theta _{\rm{g}}})$的映射函数. 而判别器$D(x;{\theta _{\rm{d}}})$输出一个表示x来自训练数据而不是生成分布${p_{\rm{g}}}$的概率. G和D同时训练, 调整G的参数使得最小化$\log (1\!-\! D(G(z))$, 调整D的参数使得最小化$\log D(X)$, 且需服从two-player min-max game 公式$V(G, D)$, 如下所示:

$ \begin{split}&\mathop {\min }\limits_G \mathop {\max }\limits_D V(G,D) = {{ E}_{x\sim {P_{{\rm{data}}}}(x)}}[\log D(x)] \\& \qquad + {{E}_{z\sim {P_z}(z)}}[\log (1 - D(G(z)))]. \end{split}$

生成器G暗示概率分布${p_{\rm{g}}}$定义为当$z\sim {p_z}$时获得的样本$G(z)$的分布. 因此, 如果给定足够的模型容量和训练时间, 算法可以使${p_{{\rm{data}}}}$收敛到最优的情况. 此部分的结果是在非参数设置中完成的, 例如通过研究概率密度函数空间中的收敛来表示具有无限容量的模型. 下面证明minimax game可以使${p_{\rm{g}}} = {p_{{\rm{data}}}}$得到全局最优解. 首先考虑对于任意给定的生成器G对应的最佳判别器D.
命题　对于给定的生成器G, 最优判别器D为

$D_G^*(x) = \frac{{{p_{{\rm{data}}}}(x)}}{{{p_{{\rm{data}}}}(x) + {p_{\rm{g}}}(x)}}{\rm{.}}$

对于任何生成器G, 判别器D的训练标准是最大化$V(G, D)$:

$\begin{split} V(G,D) =\;& \int_x {{p_{{\rm{data}}}}(x)\log (D(x))} {\rm{d}}x \\ &+ \int_z {{p_z}(z)\log (1 - D(g(z)))} {\rm{d}}z \\ =\;& \int_x{p_{{\rm{data}}}}(x)\log (D(x)) \\ &+ {p_{\rm{g}}}(x)\log (1 - D(x)){\rm{d}}x{\rm{ }}{\rm{.}} \end{split}$

在(3)式中, 对于任意的$(a, b) \in {\mathbb{R}^2}\backslash \{ 0, 0\} $, 函数$y \to a\log (y) + b\log (1 - y)$在区间$[0, 1]$中的$\dfrac{a}{{a + b}}$上取得其最大值. 注意到, 判别器D的训练目标可以描述为最大化用于估计条件概率$P(Y = y|x)$的对数似然, 其中Y表示x是来自${p_{{\rm{data}}}}(y = 1)$还是来自${p_{{\rm{data}}}}(y = 0)$.
如果生成器和判别器包含了一个额外的输入数据y, 则生成对抗网络可以拓展为条件生成对抗网络, y可以是任意类型的辅助输入信息, 如输入数据的类别标签或用其他方法表示的输入数据. 可以把条件生成对抗网络中的条件表现为一个使用y来填充的额外输入层添加到生成器和判别器中. 在生成器中, 由先验高斯噪声${p_z}(z)$和y共同组成输入, 加入先验高斯噪声${p_z}(z)$的目的是使生成器具有一定的随机性, 否则生成器将训练为一个自回归模型, 无法具备泛化性能. 而在判别器中, 由x和y共同组成输入. 所以条件生成对抗网络中two-player minimax game的目标函数为

$\begin{split}&\mathop {\min }\limits_G \mathop {\max }\limits_D V(G,D) = {{ E}_{x\sim {P_{{\rm{data}}}}(x)}}[\log D(x|y)] \\& \qquad + {E_{z\sim {P_z}(z)}}[\log (1 - D(G(z|y)))]. \end{split}$

3 -->

2.2.2.生成器网络结构

首先使用三个全连接层把三个输入扩展为包含16384个元素的向量, 把这个向量转换为128$ \times $128的二维矩阵使得后续能使用卷积进行数据处理. 引入一个先验高斯噪声${p_z}(z)$组成的方阵与数据矩阵在深度上融合, 这使得输入数据具有一定的随机性, 避免生成模型被训练为一个自回归模型. 再使用尺寸为(6, 6)且步长为(2, 2)的卷积核对融合数据进行下采样使其维度逐渐降低, 对卷积中的权重采用L2正则化防止模型过拟合, 这是提高模型泛化能力的有效方法. 利用下采样操作使特征图下降到一定程度后, 使用尺寸为(2, 2)的反池化操作对特征图进行上采样再使用不变卷积(卷积后特征图尺寸不会变化)核进行卷积操作, 使其还原到二维多孔介质原本的尺寸, 在每次反卷积操作后同样进行批量归一化和激活操作, 具体的框架图如图5所示.
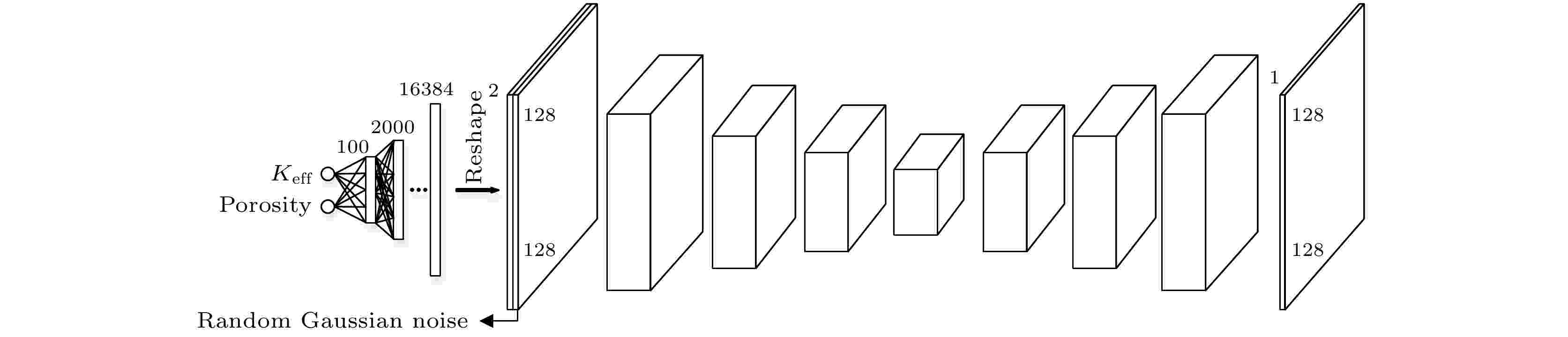图 5 生成器网络结构图
Figure5. Generator network structure diagram.

3 -->

2.2.3.判别器网络结构

判别器的输入为生成器输出的多孔介质数据或训练数据中的多孔介质数据, 对输入的数据进行卷积核尺寸为(7, 7), 步长为(2, 2)卷积等多层次下采样操作提取其深层次的特征, 在每次卷积后进行批量归一化和激活操作, 在引入Dropout随机失活防止模型过拟合, 通过一系列的上采样卷积等操作得到一个深层次的特征矩阵, 然后把矩阵形式的数据拉平为一个长向量的形式, 再把长向量通过全连接层计算输出一个值, 这个值最后经过sigmoid激活函数变为一个0—1的输出, 表示输入的多孔介质数据来自训练数据的概率大小. 具体的判别器网络结构如图6所示.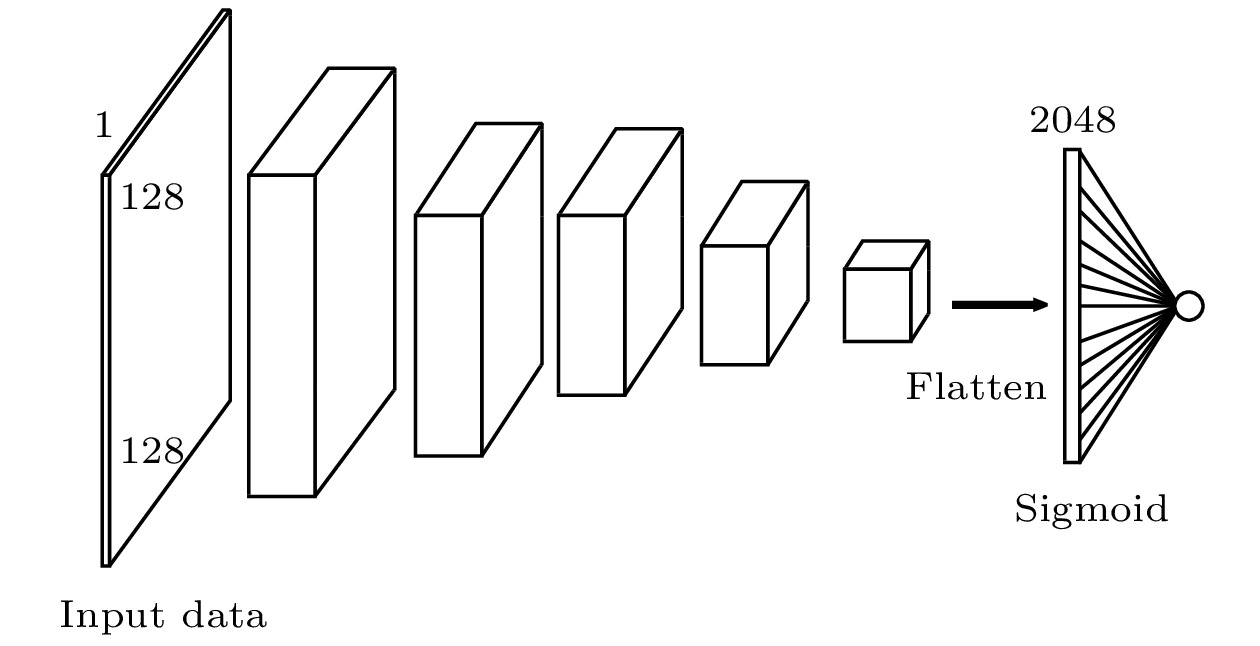
图 6 判别器网络结构图
Figure6. Discriminator network structure diagram.

3 -->

2.2.4.局部结构损失函数

传统的条件生成对抗网络还不足以满足多孔介质数据生成, 因为其无法关注多孔介质中局部细微的结构, 生成的多孔介质如图7所示, 无法生成精确的局部细节, 而局部结构对于多孔介质的有效导热率有重大的影响, 所以在条件生成对抗网络原有的损失函数基础上, 设计加入了一个额外的局部结构损失函数, 它主要关注生成器输出的多孔介质局部结构与训练数据中多孔介质局部结构隐含的相似性, 确保生成器学习到正确有效的隐含映射. 局部结构损失函数如图8所示.
图 7 传统条件生成对抗网络生成的多孔介质
Figure7. Porous media generated by traditional conditional generation adversarial network.

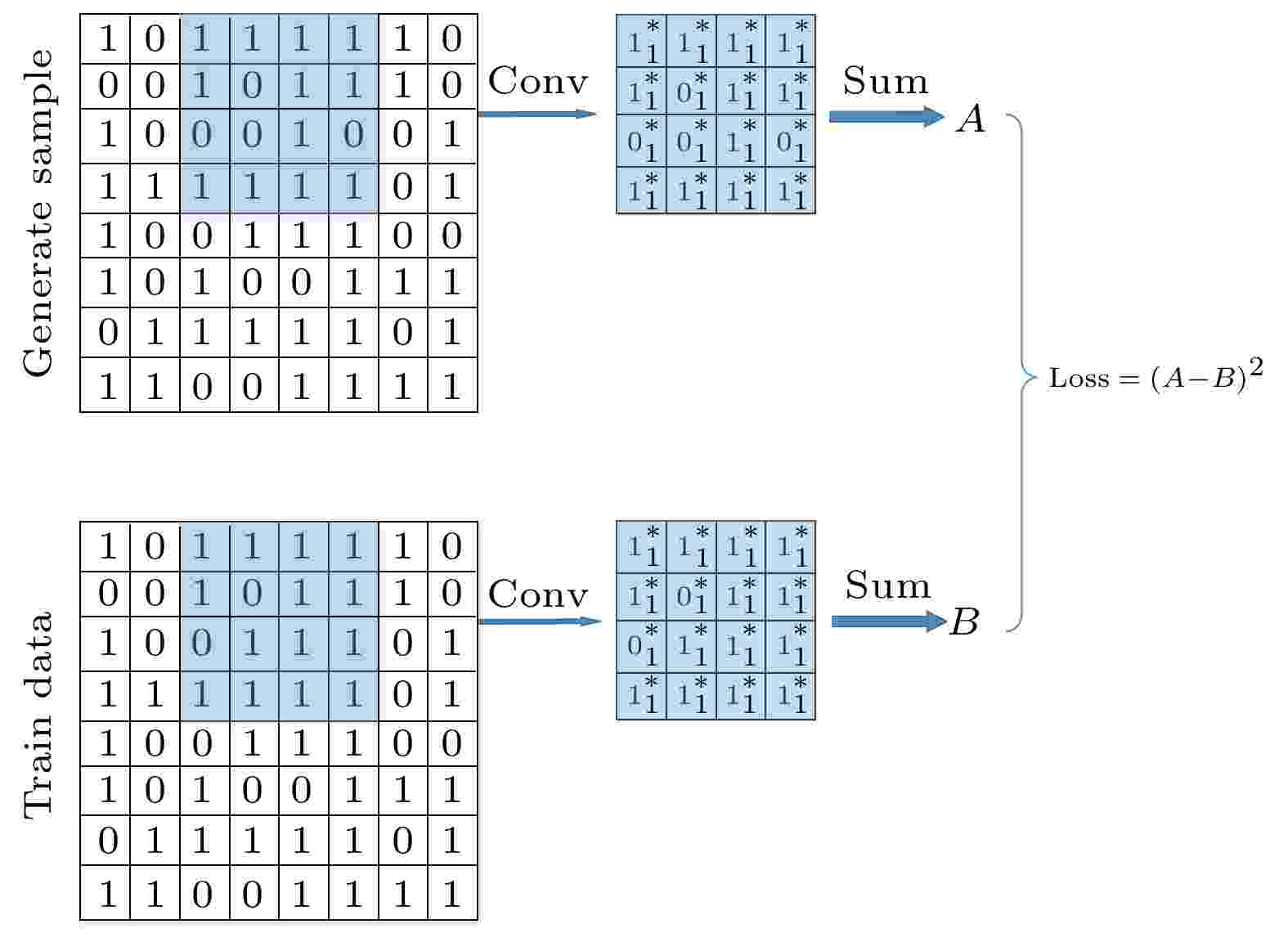图 8 局部结构损失结构图
Figure8. Structure diagram of local structure loss.

如图8所示, 局部结构损失函数的实现原理与卷积操作类似, 但是其滑动窗口中的权值都固定为1, 在生成器生成的多孔介质数据上使用这种特殊的损失核进行计算, 在对应的训练数据中的多孔介质上也进行同样的操作, 然后对分别其求和, 最后计算两者的平方误差. 如此设计的局部结构损失函数可以使得生成器从训练数据中学习到多孔介质局部结构对导热率影响的隐性映射.

所提出的模型在搭载单张1080 Ti GPU及32核CPU服务器上使用tensorflow框架训练和推理, 生成128 × 128尺寸多孔介质需0.08 s. 训练好的生成模型可以有效学习到多孔介质结构和有效导热率之前的隐藏映射, 模型会根据从训练数据中学习到的规律对已有的多孔介质结构进行调整, 从而生成一个数据集中没有的导热率对应的多孔介质结构. 为了测试训练好的生成模型的泛化性能, 可以输入一个训练集中不存在的导热率让生成模型生成一个多孔介质结构, 并使用LBM验证生成的多孔介质结构的有效导热率, 相关模型的具体介绍, 可参考文献[40,41]. 如图9所示. 图9(a)—(d)左侧为训练数据中的多孔介质结构, 右侧为生成模型生成的特定导热率对应的多孔介质结构.
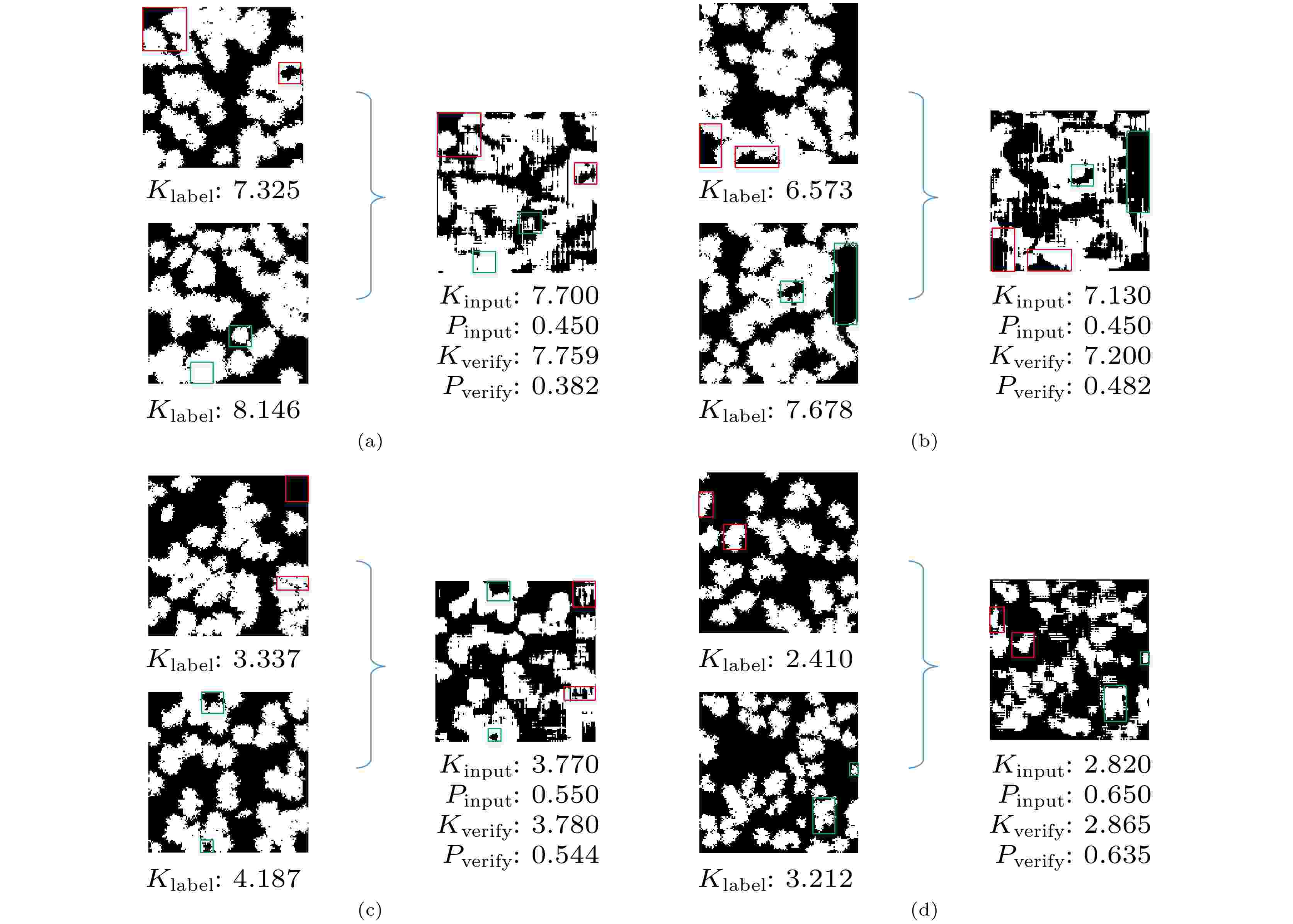图 9 生成多孔介质结构示意图
Figure9. Schematic diagram of generating porous media.

图9中K_input和P_input分别为输入生成模型的人为预定导热率和人为预定孔隙率; K_verify和P_verify分别为生成模型生成多孔介质的有效导热率和孔隙率; K_label为训练集中多孔介质对应的导热率标签.

由模型生成的多孔介质结构, 可在训练集中找到比其有效导热率高和低得多孔介质结构, 从图9中可明显看出生成的多孔介质在结构上与训练中的已有多孔介质结构有一定的相似, 这说明生成模型是在训练集中已有的多孔介质结构的基础上对其进行细节调整, 从而得到新的多孔介质结构, 表明生成模型有效地学习了训练集中导热率和多孔介质结构之间的隐藏映射, 通过输入训练集中不存在的导热率进行验证, 证明生成模型具有了良好的泛化性能. 为了证明模型的有效性与泛化性, 使用LBM方法对生成的多孔介质进行导热率验证, 同时也验证其孔隙率, 并给出生成的导热率和孔隙率的误差.
生成的多孔介质导热率验证结果如图10所示, 图10包含5个子图, 每个子图表示输入不同孔隙率和导热率比生成多孔介质验证结果, 各子图右下角给出一个生成示例并标明生成导热率, 红色点数据点表示输入人为预定导热率与LBM验证生成多孔介质导热率的对比, 若生成的多孔介质导热率没有误差, 则数据点应表现为45o线, 可以明显看出数据点基本与45o的标签线重合, 说明生成多孔介质符合要求. 下面给出生成多孔介质导热率验证误差.
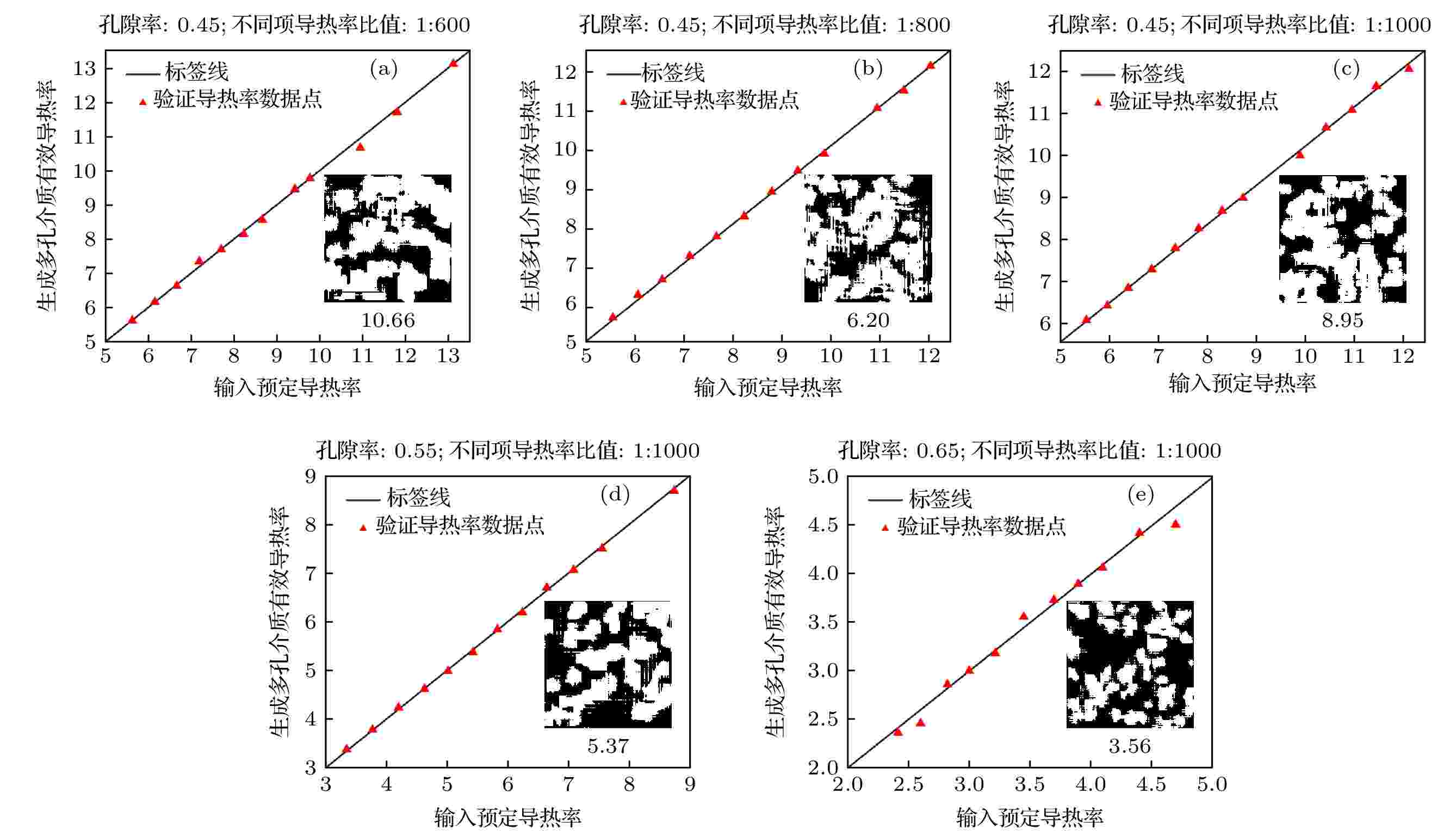图 10 生成多孔介质有效导热率验证图
Figure10. Generate verification chart of effective thermal conductivity of porous media.

图11中包含5个子图, 分别对应图10中各子图生成导热率的误差, 其误差计算公式为
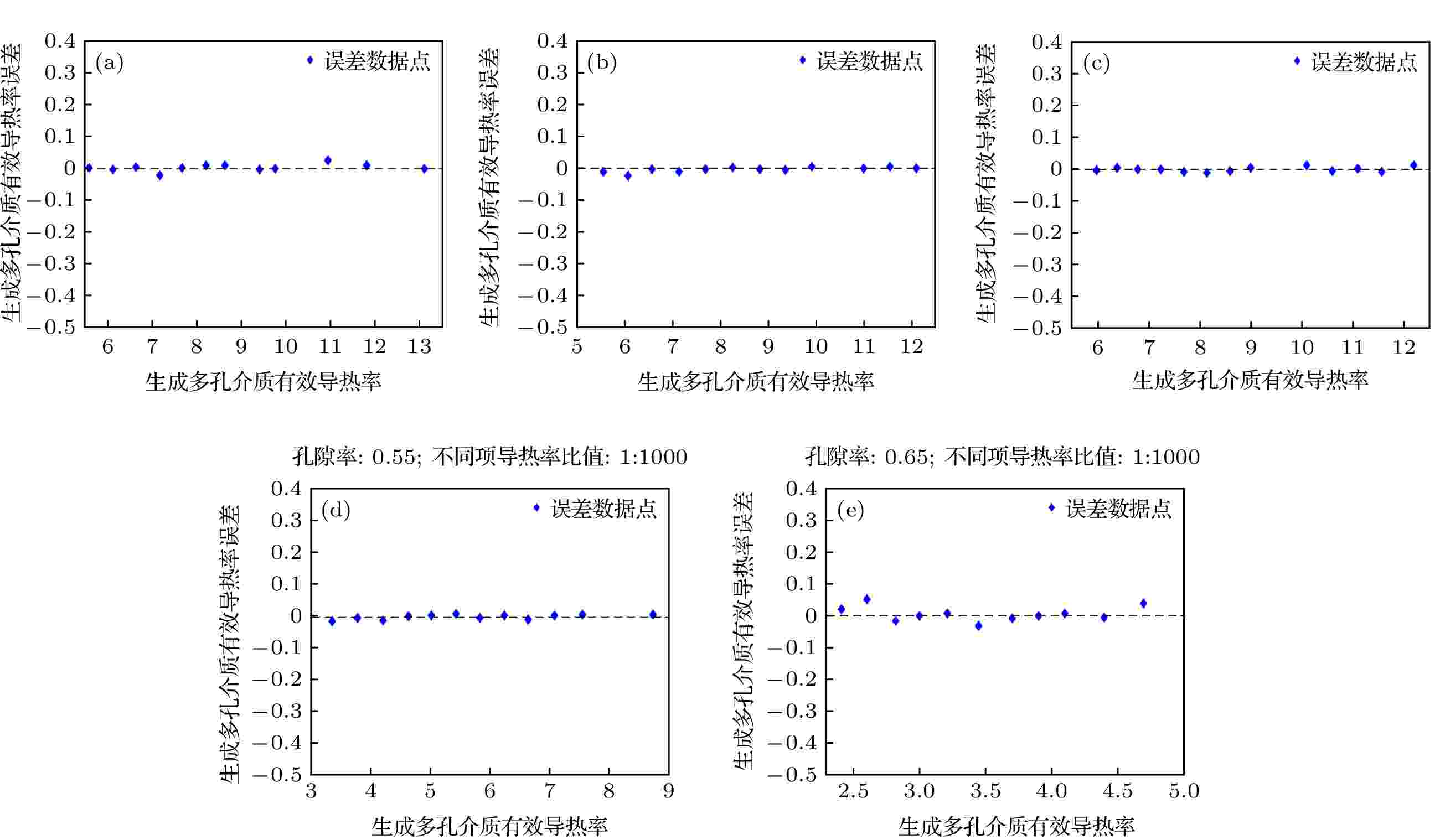图 11 生成多孔介质有效导热率误差图
Figure11. Error chart of effective thermal conductivity of porous media.

${\rm{Error}} = \left| ({{{{k_{{\rm{LBM}}}}{\rm{ - }}{k_{{\rm{generate}}}}}})/{{{k_{{\rm{LBM}}}}}}} \right|,$

式中, ${k}_{\rm{LBM}}$和${k}_{\rm{generate}} $分别为LBM验证生成的多孔介质有效导热率标签和输入生成模型的人为预定导热率. 把所有验证数据和误差汇总如图12所示.
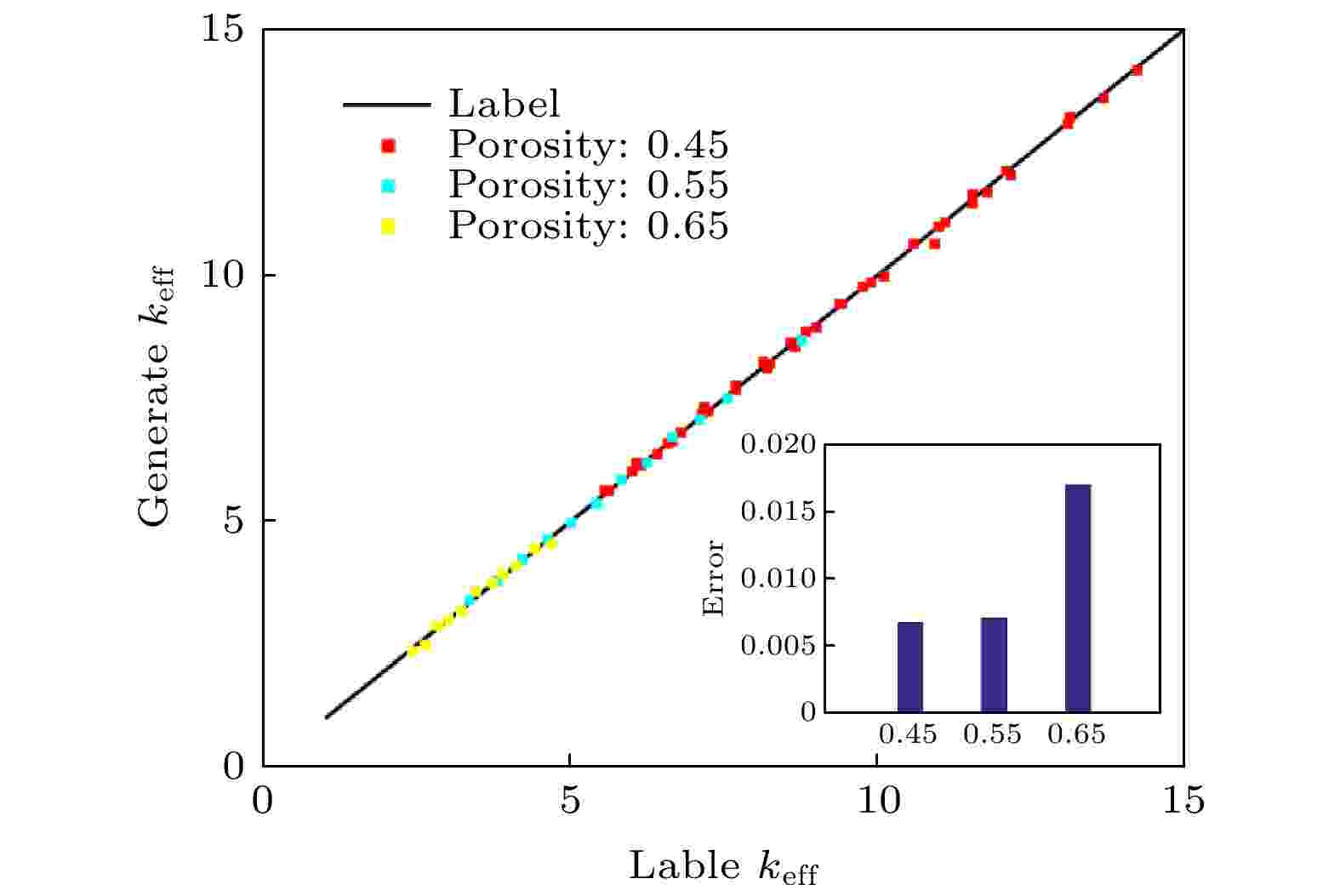图 12 生成多孔介质有效导热率验证数据集误差汇总图
Figure12. The error summary of the validation data set for the effective thermal conductivity of porous media.

从图12中可看出, 生成多孔介质导热率验证误差随着孔隙率增大呈现单调递增, 这是因为多孔介质的导热率与其孔隙率基本呈反比关系, 孔隙率越大其导热率越小, 导致在大孔隙率条件下, 不同孔隙率分布对有效导热率的影响也变小, 出现较大差异的孔隙分布但导热率相差却很小的情况, 使得生成模型更难以学习多孔介质结构与导热率的隐藏映射, 所以误差会上升. 但即便如此, 生成多孔介质的导热率验证误差最大也没有超过2%, 说明生成模型取得了比较好的泛化性能.
下面给出生成多孔介质孔隙率的综合验证结构集误差, 如图13所示.
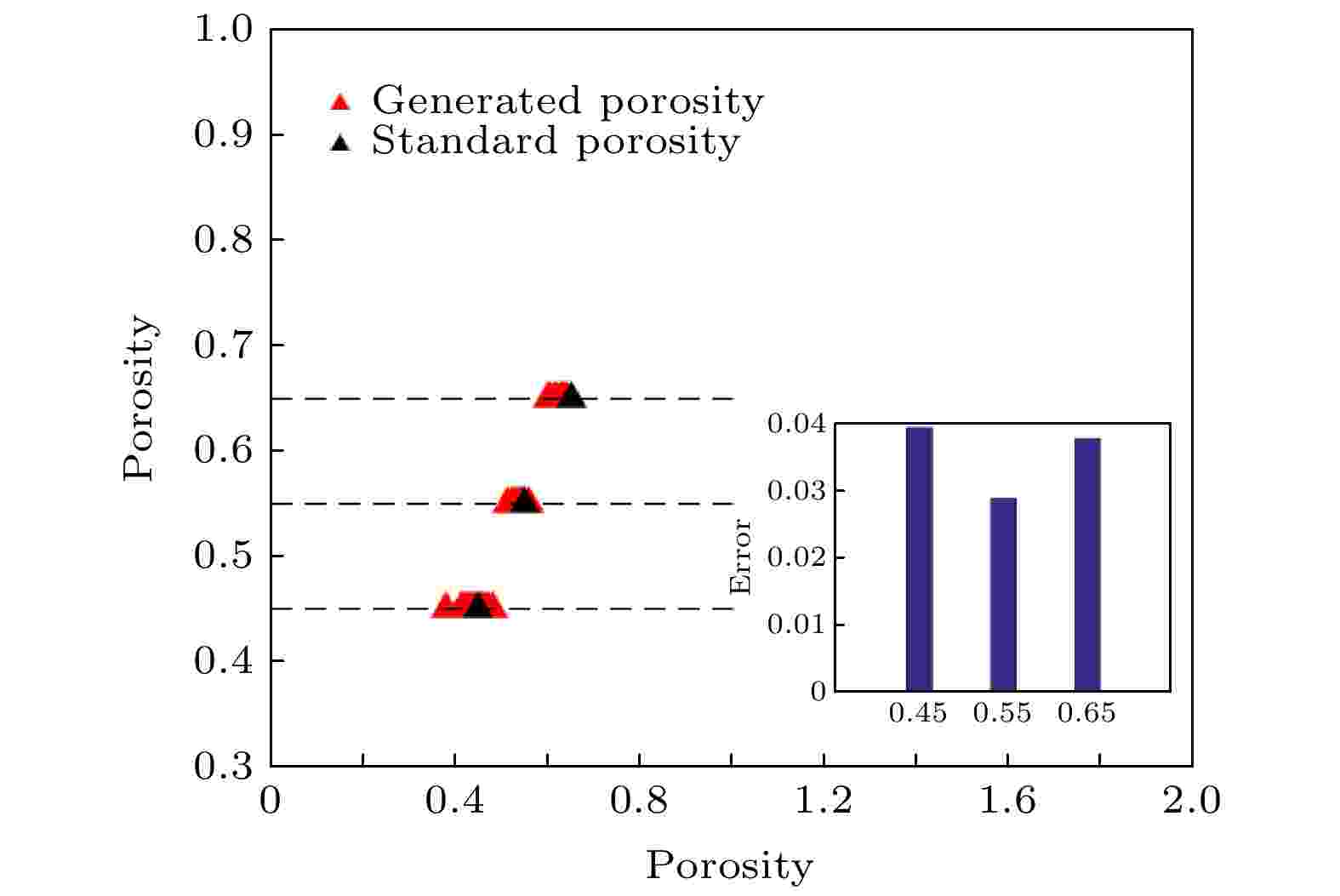图 13 生成多孔介质孔隙对比图及误差
Figure13. The effect diagram and error of generating pores in porous media.

图13中黑色的点代表输入模型的孔隙率, 红色的点代表模型生成的多孔介质的孔隙率, 红色点与黑色点的距离越近表示模型效果越好, 从图13中可明显看出, 红色点与黑色点距离都很小, 并给出孔隙率误差. 下面给出量化误差, 如表2所列. 从表2中也可看出整体的误差均值不超过4%.

Porosity	0.45	0.45	0.45	0.55	0.65	Mean error
Keff ratio	1∶1000	1∶800	1∶600	1∶1000	1∶1000
Keff error	0.006	0.006	0.008	0.007	0.017	0.009
Porosity error	0.049	0.031	0.039	0.029	0.038	0.037

表2生成多孔介质导热率及孔隙率误差表
Table2.Generated thermal conductivity and porosity error table of porous media

本文使用了条件生成对抗网络来生成特定导热率和孔隙率的多孔介质结构, 对传统的条件生成对抗网络进行了改进, 引入了一个额外的局部结构损失函数, 这种额外的注意机制使得生成模型可以学习到多孔介质局部机构与有效导热率之间的隐藏关系, 使得生成的多孔介质局部结构更为合理. 生成模型是从数据集中已存在的多孔介质结构学习到了结构与有效导热率之间的隐藏映射, 在其生成的新的多孔介质结构中可以发现与训练集中已有的多孔介质结构有相似的地方, 表明模型确实从训练数据集中学习到了规律并具有了良好的泛化性能. 从实验的效果图和误差图可以看出, 本文提出的改进后的条件生成对抗网络在生成特定导热率和孔隙率的多孔介质上平均误差均小于0.05, 取得了良好的效果.