摘要:基于一维声栅中的Rayleigh-Bloch (RB)模式基本特点, 设计了一种单层结构弯曲声波导. 利用有限元方法从时域和频域两方面验证了弯曲声波导的有效性, RB模式波可以沿着波导的弯曲界面传播. 研究发现, 由于采用了环形结构基本单元, 在该波导中存在两种传播模式, 分别对应能量局域在单元间(模式-1)和单元内部(模式-2)两种情况. 其中, 模式-2声传输效果更佳, 几乎可实现无损传输. 时域研究中分别采用了调制脉冲和高斯脉冲两种信号形式, 分析了它们在弯曲声波导中的传输过程. 由于波导中只允许RB模式波传播, 因此对于宽频信号来说, 可起到滤波的效果. 并且, 不同模式(频率)的信号会出现在声波导的不同位置, 所得结果对于声波定向传输、声探测与识别等研究具有理论与应用价值.
关键词: Rayleigh-Bloch模式/
弯曲声波导/
无损传输/
声探测

English Abstract

全文HTML

--> --> -->

声波导是一种重要的声学基础结构, 既存在于自然环境中(如海洋波导), 也存在于人工结构中. 近年来, 基于人工结构单元实现声波导效应的研究得到人们的广泛关注^[1]. 利用变换声学理论和超材料技术设计的各向异性声波导^[2], 由零参数超材料构造的无损声传输波导结构^[3], 以及利用拓扑边界态在周期拓扑结构的边界处产生的波导效应等^[4], 均成为近来的研究热点.
在由单层散射体单元构成的衍射声栅中存在一种特殊的声场分布模式, 即Rayleigh-Bloch (RB)模式^[5,6]. 该模式下, 在垂直于声栅的方向上, 声场能量呈Rayleigh波模式衰减, 而在沿着声栅排列的方向上, 却按照Bloch模式周期分布^[7]. 当声场中出现RB模式时, 能量被集中在声栅附近不能向外传播, 便形成了一种声波导. 研究表明, RB模式只存在于具有Neumen边界条件(硬声场边界)的声栅中, 而Dirichrit边界条件(软声场边界)下是不存在的^[8,9].
对于RB模式的研究由来已久, 且广泛存在于各领域当中. 从周期散射体对水波的能量局域特性^[10,11], 到电磁波、弹性波中的周期分布模式等现象均展开了丰富的理论研究^[12-14]. Li等^[15]基于理论与实验方法研究了一维声栅中能量局域的模式, 并从表面波(边界态)相互作用机理解释了这种RB模式分布产生的原因, 进而分析了其中拍的特性^[16]. 对于实际研究中产生的有限长结构, 除了会产生周期分布的局域模式外, 在出射端还会产生定向辐射的现象, 对于提高结构声场指向性有一定意义. 近期, Chaplain等^[17]报告了一种基于环形单元的梯度结构, 在RB模式下, 结构中会产生分叉和闭合等现象, 大大拓展了RB模式的应用范畴.
关于RB模式研究的模型多为基于简单单元的直线型声栅结构^[18,19]. 根据弯曲波导理论, 当界面曲率半径较大时, 可以将单位距离内近似为直线. 一定条件下, 入射波可以沿着弯曲界面传播, 产生波导效应^[20]. 本文以环形排列的散射体作为基本单元, 设计了一种弯曲声波导. 基于有限元方法模拟了声栅波导结构中频域和时域声场的基本特性. 研究结果表明, 具有较大曲率半径的声栅结构中支持多种RB模式声波传播, 形成一种单层结构的弯曲声波导. 此外, 由于环形单元的能量局域特性, 提高了弯曲波导能量传输效率. 该研究对于声波定向传输、声探测与识别等研究具有理论与应用意义, 丰富了RB模式的应用案例与研究范围^[13,21-23]. 此外, 对于波导耦合的Floquet型声学拓扑绝缘体^[24,25]和基于波导阵列的声学超透镜^[26]等方面的研究也有潜在的促进作用.

设散射体簇单元沿x轴周期排列, 形成一维衍射声栅, 周期间隔为d, 置于流体介质(密度和声速分别为$ {\rho }_{\mathrm{b}} $和$ {c}_{\mathrm{b}} $)中, 结构如图1(a)所示.
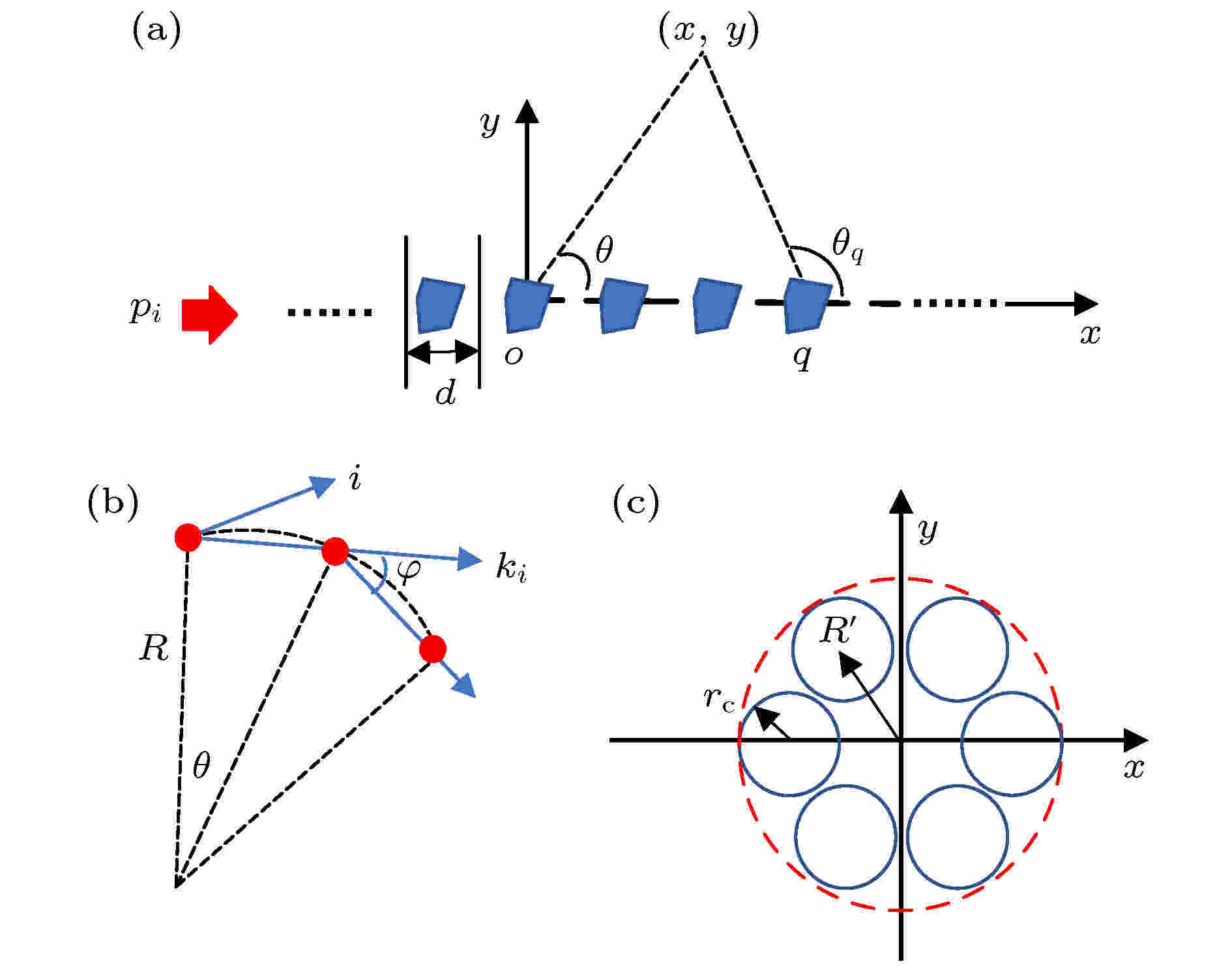图 1 一维衍射声栅示意图
Figure1. Schematic of one-dimensional diffraction grating.

对于流体声场来说, Helmholtz方程可以表示为

$ \left({\nabla }^{2}+{k}^{2}\right)p\left({{r}}\right)=0, $

其中${\nabla }^{2}=\dfrac{{\partial }^{2}}{\partial {x}^{2}}+\dfrac{{\partial }^{2}}{\partial {y}^{2}}, k= \dfrac \omega c$, k表示入射波数, $ \omega $为角速度, c为背景介质声速.
假设一列简谐声波沿x轴正方向传播, 在x方向形成周期分布, 可表示为

$ p\left(x+nd,y\right)={\mathrm{e}}^{\mathrm{i}nd\beta }p\left(x,y\right),~~ n\in \mathbb{Z}, $

其中$ {{\beta }} $为Bloch波矢.
此外, 周期分布声场还可以写为

$ p\left(x,y\right)={\mathrm{e}}^{\mathrm{i}\beta x}\varnothing \left(y\right). $

由于(2)式对任意整数n存在, 所以(3)式还可以写为

$ p\left(x,y\right)=\sum\limits_{j=-\infty }^{\infty }{\mathrm{e}}^{\mathrm{i}\left(\beta +2{j}\pi /d\right)x}{\varnothing }_{j}\left(y\right). $

由(4)式可见, $ \beta $以$ 2\mathrm{\pi }/d $为周期, 所以可不失一般性地假设

$ -\frac{\mathrm{\pi }}{d}\leqslant \beta \leqslant \frac{\mathrm{\pi }}{d}. $

对于Bloch波矢来说, 这里只需关注其向x正方向传播的波, 所以进一步地

$ 0<\beta \leqslant \frac{\mathrm{\pi }}{d} .$

将(4)式代入Helmholtz方程(1)可得到

$\begin{split} &\sum\limits_{j=-\infty }^{\infty }\Big\{{\varnothing }_{j}''\left(y\right)-\Big[{\left(\beta +2j\mathrm{\pi }/d\right)}^{2} -{k}^{2}\Big]{\varnothing }_{j}\left(y\right)\Big\}\\& \times{\mathrm{e}}^{\mathrm{i}\left(\beta +2j\mathrm{\pi }/d\right)x}=0, \end{split}$

要使(7)式成立, 只能有

$ {\varnothing }_{j}''\left(y\right)-\left[{\left(\beta +2j\mathrm{\pi }/d\right)}^{2}-{k}^{2}\right]{\varnothing }_{j}\left(y\right)=0. $

令${\varOmega }^{2}({\beta }_{j}) \!=\! {(\beta +2 j\mathrm{\pi }/d)}^{2}-{k}^{2}$, 其中${\beta }_{j} \!=\! \beta + 2 j\mathrm{\pi }/d$. 不难得到(8)式的解为

$ {\varnothing }_{j}\left(y\right)={A}_{j}^{+}{\mathrm{e}}^{-\varOmega \left({\beta }_{j}\right)y}+{A}_{j}^{-}{\mathrm{e}}^{\varOmega \left({\beta }_{j}\right)y}. $

由(9)式可见, 在y方向是否存在传播波, 取决于$ \varOmega \left({\beta }_{j}\right) $的结果, 这里有

$ \varOmega \left({\beta }_{j}\right)=\left\{\begin{aligned}&\sqrt{{\beta }_{j}^{2}-{k}^{2}}, & \left|{\beta }_{j}\right|>k \\ &-\mathrm{i}\sqrt{{k}^{2}-{\beta }_{j}^{2}}, & \left|{\beta }_{j}\right|\leqslant k \end{aligned}.\right. $

因此, 当$\left|{\beta }_{j}\right|\leqslant k$时, $ \varOmega \left({\beta }_{j}\right) $为纯虚数, 声场在y方向传播; 相反地, 当$ \left|{\beta }_{j}\right|>k $, 声场在y方向为倏逝波.
只有当波动在x方向传播, 而在y方向上不能传播时, 才能形成RB模式. 因此结合(6)式进一步确定Bloch波矢的范围为

$ k<\beta \leqslant \mathrm{\pi }/d, $

此时, 声场在y方向没有传播波, 即能量都局域在声栅单元周围.
将(9)式代入(4)式得到RB模式下声场的分布, 即

$ p\left(x,y\right)=\sum\limits_{j=-\infty }^{\infty }{A}_{j}^{+}{\mathrm{e}}^{\mathrm{i}{\beta }_{j}x-\varOmega \left({\beta }_{j}\right)y}+{A}_{j}^{-}{\mathrm{e}}^{\mathrm{i}{\beta }_{j}x+\varOmega \left({\beta }_{j}\right)y}, $

式中第一部分代表y > 0半空间声场, 第二部分代表y < 0半空间声场.
至此, 已经得到一维衍射声栅中RB模式声场分布的表达式, 但是(12)式中仍然存在两个系数未定, 它们与单元具体特性相关.
假设声栅以一定的曲率半径R呈弯曲排列, 并且满足$ R\gg \lambda $, 也就是说声栅以非常平缓的程度弯曲, 局部范围内可认为是平坦的, 如图1(b)所示. 两个相邻单元间夹角为θ, 则$ \varphi =\theta $. 对于一个单元来说, 入射波只有$ k\mathrm{cos}\theta $方向的分量能够沿着声栅排列方向传播, 而另一部分则向声栅外部传播, 属于泄漏波^[20]. 为了确定RB模式的波矢范围, (11)式可改写为

$ \begin{split} &{k}_{i}\mathrm{cos}\theta <{\beta }_{i}'\leqslant \mathrm{\pi }/\left[2R\mathrm{sin}\left(\theta /2\right)\right] ,\;\\&i = 0,{\rm{ }}1,{\rm{ }}2, \cdots ,N - 1. \end{split}$

可见, 随着传播距离的增加, Bloch波矢的范围越来越大. 不过由于$ \theta $非常小, 也可以近似认为$ {k}_{i}\mathrm{cos}\theta \approx k_{i}, 2 R\sin(\theta /2)\approx R\theta, {k}_{i}=k $. 由于Bloch波矢最大时, 声场的能量局域效果最佳, 所以一般计算过程中, 只要选取Bloch波矢的上限对应的频率作为RB模式的频率就可以了, 即(13)式中$ \mathrm{\pi }/(R\theta) $对应的特征频率.
上述过程确定了弯曲声波导中RB模式的求解思路, 但对单元特性并没有特殊要求. 本文为了增强能量的局域传输效果, 设计了一种由6个圆柱形散射体单元组成的环形结构作为衍射声栅的基本单元, 基本结构如图1(c)所示, 具体几何参数见表1. 此时, 在计算RB模式声场的过程中, 必须考虑两次多重散射过程. 首先, 散射体簇单元内部是一次多重散射, 可以得到其局部声场的散射波系数与入射波系数之间的关系, 将其代入一维声栅的多重散射声场中, 就可以得到整体声场的入射波系数与散射波系数间的关系.

rc	R'	R	θ	单元个数N
10	22.5	2700/π	π/90	46

表1散射体簇几何参数(单位: mm)
Table1.Geometrical parameters of the scattering cluster (Unit: mm).

基于有限元方法, 根据表1给出的几何参数, 计算了由6个散射体组成的直线型声栅的频散曲线(蓝色点画线), 如图2所示, 其中红色实线代表对应的背景介质(空气)的频散关系.
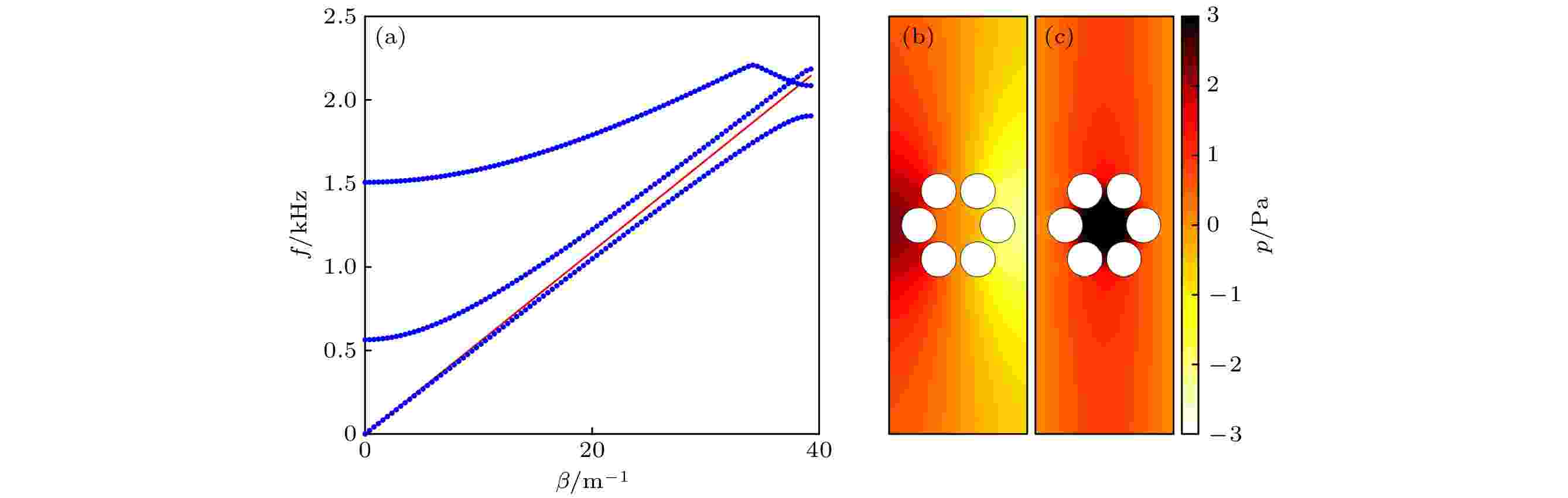图 2 RB模式波矢图(a)及声压分布(b), (c)
Figure2. Band structure of the scattering cluster (a) and acoustic pressure distributions (b), (c) of RB mode waves.

由图2(a)可见, 在Bloch波矢范围内((13)式), 存在两种RB模式, 分别为1904 Hz (模式-1)和2086 Hz (模式-2). 图2(b)和图2(c)分别给出了对应的两种模式下的特征声场分布情况. 在模式-1中, 声场能量主要集中在散射单元之间, 在垂直于声栅的方向上声压向两侧呈指数衰减, 声场分布形式符合典型RB模式声场情况. 在模式-2中, 由于能量被局域在了环形单元的内部, 而且受到多散射体的限制, 无法向两侧衰减, 使得能量局域效果更佳. 在单元之间, 声场几乎是均匀的, 也不存在周期变化.

为了清晰地认识弯曲波导中RB模式的基本特性, 根据表1所列几何参数构建了仿真模型, 基于有限元方法计算了弯曲波导的频域特性, 计算范围为1500—2500 Hz. 提取了弯曲波导各单元间(图3(a))和各单元内部(图3(b))的声压值, 如图3所示. 图中色度条表示提取位置声压与入射波声压幅值的比$ p/\left|{p}_{i}\right| $.
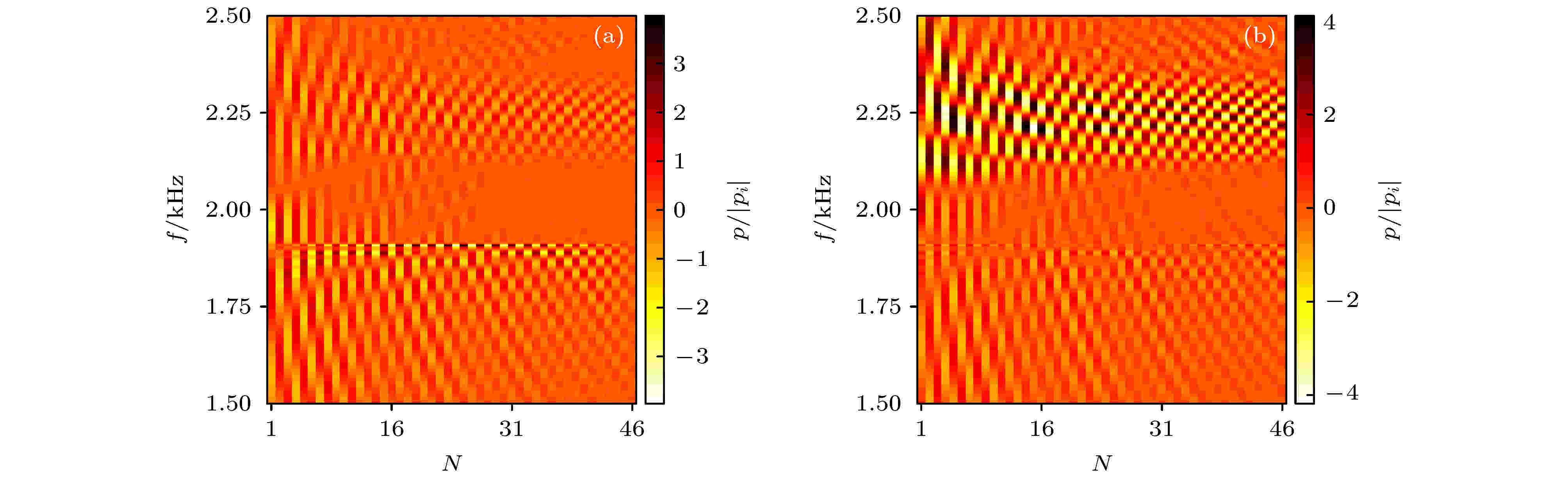图 3 散射体簇单元间(a)和单元内部(b)不同位置频谱分布
Figure3. Frequency spectra of the points between (a) and in (b) the scattering clusters.

由图3可见, 在单元内外分别出现了两种不同的RB模式, 两种情况下均出现了声压周期波动分布的情况. 在图3(a)中, RB模式出现在1900 Hz处, 对应于模式-1; 而在图3(b)中, RB模式出现在2100—2350 Hz范围内, 对应于模式-2. 从频率上来看, 有限元仿真结果得到的模式频率与图2中频散曲线得到的结果基本相同. 不过, 从图3可以发现, 模式-1只对应了1900 Hz附近非常窄的频率段. 而模式-2对应了一个较宽的频率段, 在该频率段内, 声场表现出了良好的周期分布特点. 产生这一现象的原因主要是因为在模式-2中, 能量主要局域在单元内部, 受到上下两侧单元的限制, 局域声场更容易形成, 且局域效果更好, 在很宽的频段内都不易衰减. 而在模式-1中, 能量虽产生了局域效应, 但是在声栅两侧衰减方向上为自由空间, 频率的变动会导致衰减效果差异很大, 局域现象也就不明显了.
图3结果表明, 在弯曲声栅中存在两种典型的RB模式, 且由于采用了环形单元结构, 模式-2具有明显的宽频带效果, 能量局域效果更好.
选取图3中模式-1和模式-2对应的频率, 给出了不同RB模式下弯曲波导中的声场分布情况, 如图4所示, 插图所示为各声场结果中局部声场的分布情况. 模型计算区域内, 位于左侧边界上的正对波导左端的有限长线声源辐射声波, 同时在其他3个边界上添加了完美匹配层, 以减小边界处的反射. 图4清晰地表明了一定条件下, 弯曲波导中同样存在RB模式, 并且由于引入了环形结构单元, 可以同时存在多种RB模式. 在声压级分布结果中, 图4(a)中高声压级区域主要集中在单元与单元之间, 而由图4(b)可见, 高声压级区域主要集中在单元内部, 单元间的声压级相对要低15 dB左右, 体现了优异的能量局域效果. 插图中截取的局部声场分布情况更清晰地体现了两种不同的RB模式实际声场特点, 完全符合图2(b)和图2(c)所示结果.
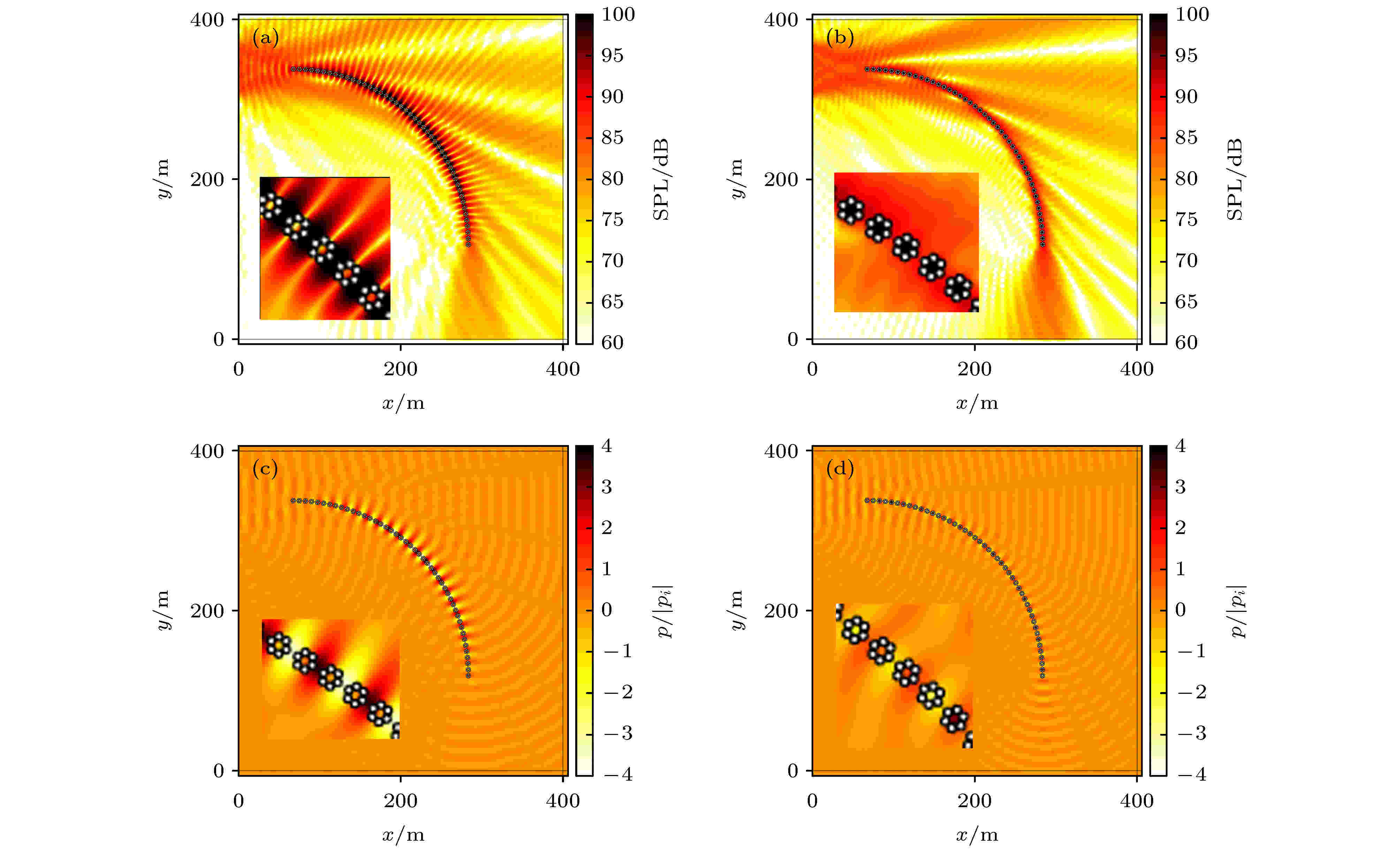图 4 弯曲波导中的RB模式声场(插图为相应波导局部声场分布结果)　(a), (b)声压级分布; (c), (d)声压分布
Figure4. RB mode acoustic wave fields in the bend waveguide: (a), (b) Sound pressure level (SPL) distributions; (c), (d) acoustic pressure distributions. The sub-pictures are local acoustic field distributions of corresponding gratings.

值得注意的是, 由于波导是弯曲的, 一部分声波沿着波导传播, 同时另一部分则沿着相邻单元的连线方向向波导外部传播, 即产生了泄漏波. 在模式-1(图4(a))中, 泄漏波声场明显出现了较强的干涉现象, 这也说明相对于模式-2, 模式-1中由于能量局域在单元之间, 同时也是向波导外部衰减的, 与泄漏波二者叠加, 遂产生了干涉现象. 此外, 在弯曲波导的出射端, 出现了明显的定向辐射现象, 该现象是由有限长波导的截断效应导致的^[19].
为了更清晰地认识弯曲波导中RB模式的声场特性, 图5给出了两种模式(1904和2242 Hz)单元间和单元内部声压分布结果, 发现不同模式下弯曲波导中声压分布周期性差异较大. 模式-1对应的声场中, 只存在一个Bloch周期, 从入射端到出射端声压幅值分布先增大后减小. 而在模式-2对应的声场中, 却存在多个周期, 如图5(b)所示(红色虚线为包络线), 图中存在7个完整的Bloch周期. 不过, 从周期分布情况来看, 图5中的结果并不完美. 一方面, 本文研究的是一种具有一定曲率的声栅结构, 声散射特性相对直线型声栅更为复杂, 周期性声场分布受到一定影响. 另一方面, 图5(b)中在最右侧单元中存在半个Bloch周期, 这是由有限长声栅截断效应决定的, 根据截断位置的不同, 出现周期的数量也不同.
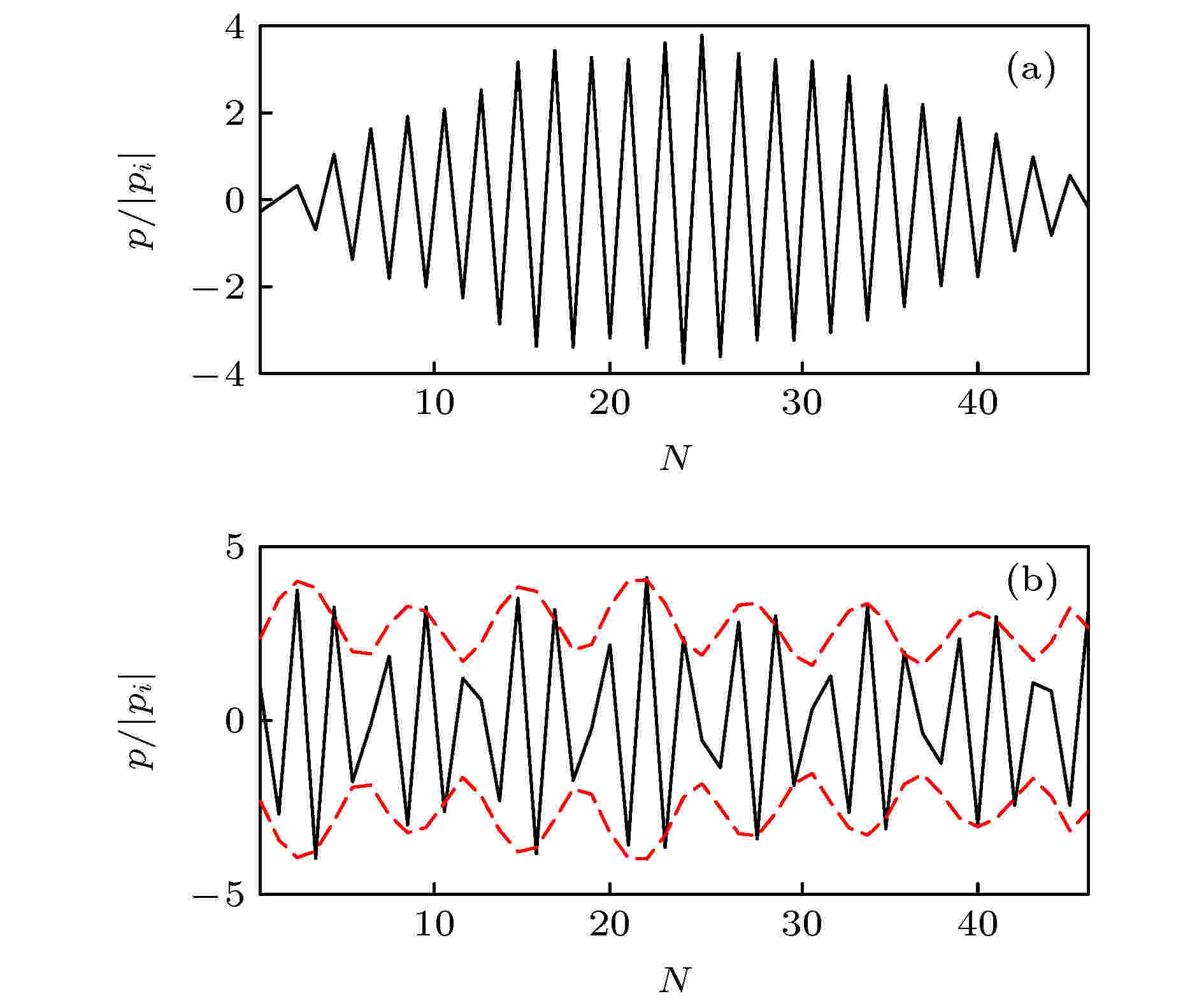图 5 不同模式下单元间(a)和单元内部(b)声压分布曲线
Figure5. Acoustic pressure curves for the points between (a) and in (b) the cluster under different modes.

对比图5(a)和图5(b)可以发现, 模式-2的声场强度要比模式-1更大. 最主要的, 在模式-1中, 由于只有一个Bloch周期, 最大幅值只局限在中间少数几个单元附近; 而在模式-2中, 周期增多, 且幅值衰减较小, 表明环形单元中模式-2具有较好的声波能量传递能力.

上述频域研究是一种近似的长时间作用后的均匀声场结果, 与实际应用情况还存在一定的差异, 有必要进一步开展时域研究来理解弯曲波导结构中的声传播行为.
对于图4结构模型, 设入射波是随时间变化的正弦调制信号, 表达式为

$ p=\left({A}_{0}/2\right)\left[1-\mathrm{cos}\left(2\mathrm{\pi }ft/N\right)\right]\mathrm{sin}\left(2\mathrm{\pi }ft\right) ,\;t <N/f,$

其中A₀ = 1为入射波幅值, N = 10为调制信号的周期, f为入射波频率.
基于有限元方法, 模拟了声波的时域传播过程. 考虑到具有能量局域效果的模式-2有更好的无损传输效果, 模拟时将入射波中心频率设为f = 2242 Hz.
在0—0.04 s范围内模拟了调制正弦信号的传播过程, 根据模式-2的特点, 采集了各单元内部点的声压时域信号, 如图6(a)所示. 图中用两条带箭头的虚线标示了两条声波路径. 其中, 方向B的信号到达时间更短, 传播速度更快, 但是能量显然更小. 而方向A的信号, 虽然到达时间长, 传播速度慢, 但是声场的能量主要沿着这一通道传递. 通过对具体结构的分析不难发现, 具有更快传播速度的传播路径是从声源到达各个单元的直达波(方向B), 而另一条(方向A)则是沿着弯曲界面传播的波.
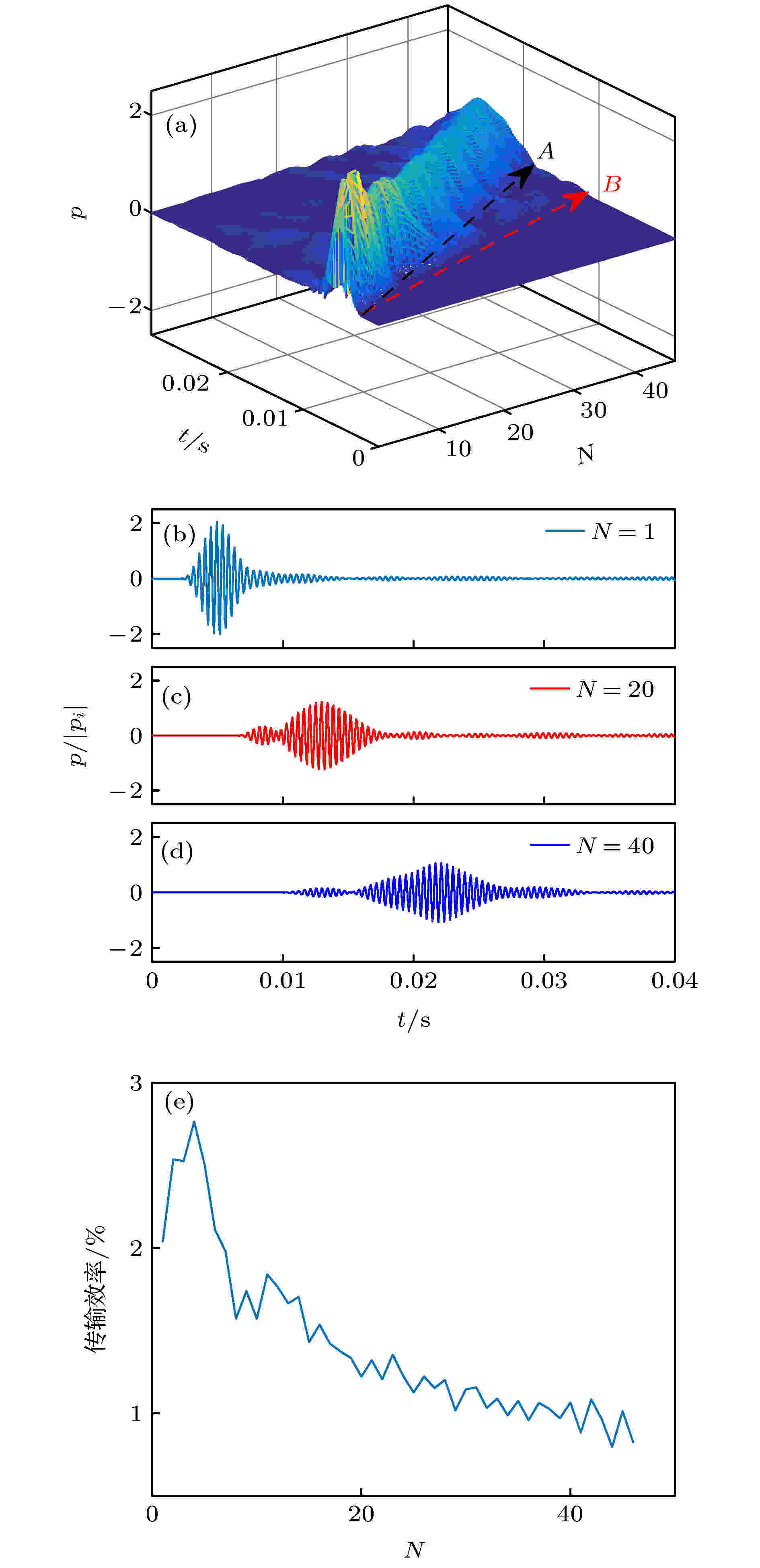图 6 (a)?(d)各单元内部点声压时域信号((a)所有时域信号结果; (b)?(d)第1, 20和40号单元时域信号结果)及(e)传输效率
Figure6. (a)?(d) Time-domain signals ((a) all of the signals; (b)?(d) three signals at unit 1, 20 and 40, respectively) and (e) transmission efficiency for the points in the cluster.

对照图6(b)—(d)中分别选取的第1, 20和40号单元时域信号也可以发现, 当声波信号入射到弯曲波导前端的单元时, 由于单元内散射波的相互叠加, 声场幅值快速增大, 并形成一个高能量的波包. 该波包继续在散射体簇各单元中传播, 不过由于弯曲波导的传播路径更长, 随着传播距离的增大, 初始入射波与导波界面慢慢分开, 如图6(c)和图6(d)的结果所示. 不过, 由于泄漏波的存在, 声栅中导波波包的最大幅值随着传播距离的增大也在减小. 由于相互作用次数增多, 波包在时域上越来越长.
图6(a)—(d)中的结果表明, 时域信号同样可以沿着本文设计的弯曲声波导传播, 并且随着直达波与波导波包的进一步分离, 也证明了波导中传播的能量主要还是初始入射到声栅中的能量, 而非其他方向的入射波.
为了定量描述所设计弯曲声波导的传输效率, 定义各点时域波形中最大值与入射波幅值的比为该点的传输效率, 即$ {E}_{N}=\mathrm{M}\mathrm{A}\mathrm{X}\left({p}_{N}\right)/{A}_{0} $ (%), 结果如图6(e)所示. 可以看出, 随着传播距离的增大, 传输效率先短暂增大之后不断减小. 增大过程发生在声波导入口处, 是由于入射波与反射波相互作用产生的增强. 而对于后续单元来说, 由于泄漏波的存在, 能量不断地溢出, 存在于声波导中的声波能量进一步减小. 从数值来看, 绝大多数单元(> 40 个)中传输效率都大于1, 也就是说此处声波信号的幅值比入射波幅值还要大, 证明了所设计声波导优异的信号传输能力.
对各点时域信号进行傅里叶变换, 提取其频谱特征, 绘于图7. 由图7可见, 各点信号的能量主要还是分布于2200 Hz附近, 证明了基于RB模式的弯曲声波导中信号传输的有效性.
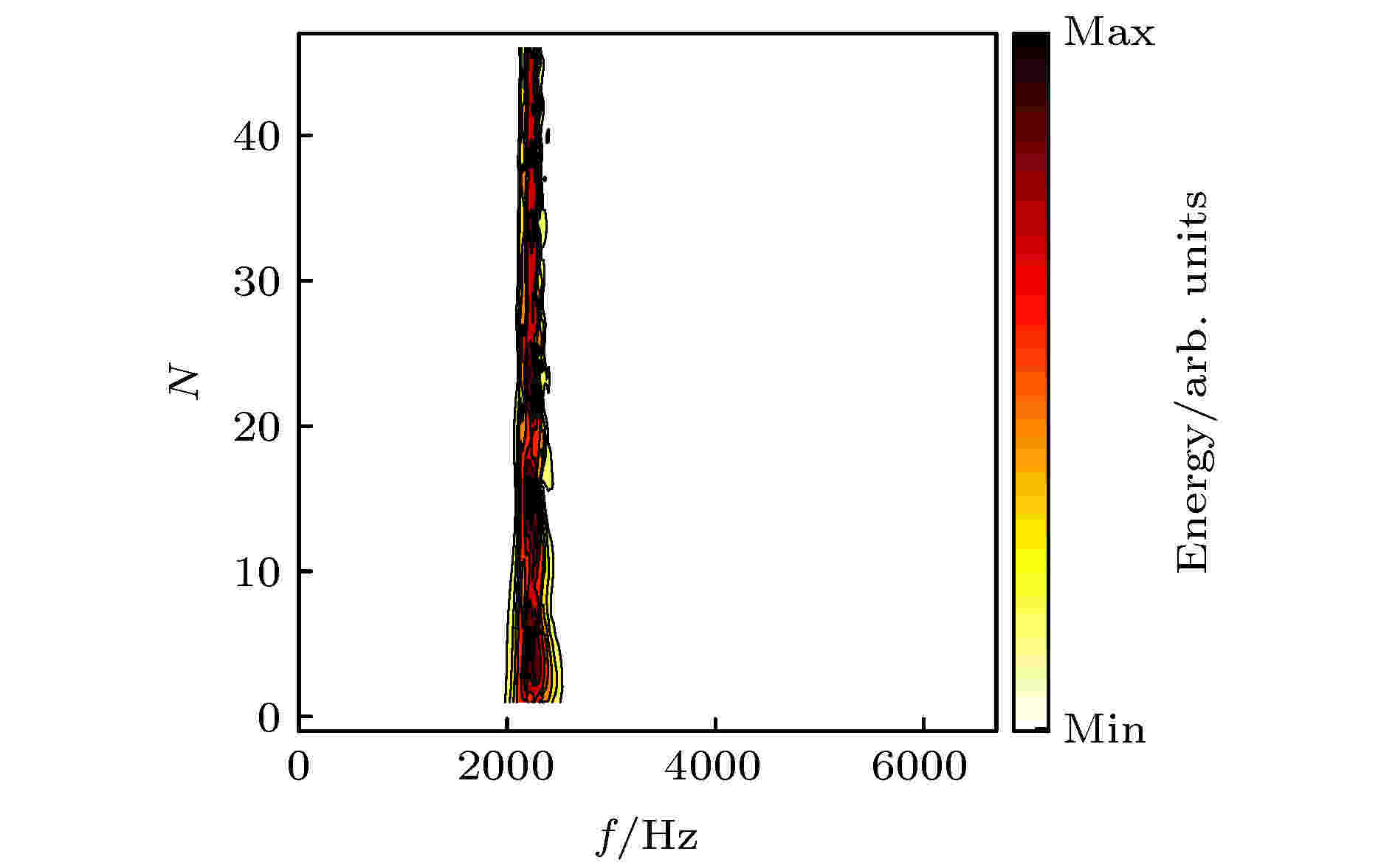图 7 各单元点的频谱图
Figure7. Frequency spectra for the points in the cluster.

为了验证本文所设计声栅波导的特性, 选取宽频高斯脉冲信号作为入射波, 模拟了声波传播过程. 信号表达式为$ p={A}_{0}{\mathrm{e}}^{-{\left(t/\tau \right)}^{2}} $, 其中A₀ = 1为入射波的幅值, $ \tau =0.01 $.
同样地, 提取第1, 20和40号单元的内部时域信号, 如图8(a)—(c)所示. 正如图中所见, 由于干涉作用的存在, 脉冲声波的下降沿出现了声压波动. 并且随着传播距离的增大, 波动起伏越来越大, 持续时间越来越长. 虽然单元间存在的模式与单元内部不同, 但是从信号的形式上来讲区别不大, 这里不再给出.
图 8 脉冲波入射时单元内部时域波形
Figure8. Time-domain signals using Gaussian pulse incidence.

图9给出了单元内部和单元间信号的频谱分布情况, 由于低频能量过大, 从显示角度考虑, 图中未给出1000 Hz以下能量分布. 如图9所示, 对于单元内部各点来说(图9(a)), 2200 Hz附近有显著的能量分布, 证明此频率下的声波能够沿着声栅波导传播, 并在单元内部形成局域声场. 类似地, 在图9(b)中, 1900 Hz附近的高能量带显而易见, 也正对应了频域结果中的模式-1的情况. 此时, 2200 Hz附近也有一个传播态, 这是由于模式-2过强导致的. 从能量的角度来看, 模式-2的能量相对模式-1要小得多, 因此可以认为此时波导中主要传播的是模式-1波. 图9中, 两种模式的基本特点与频域结果基本相似, 这里不再赘述.
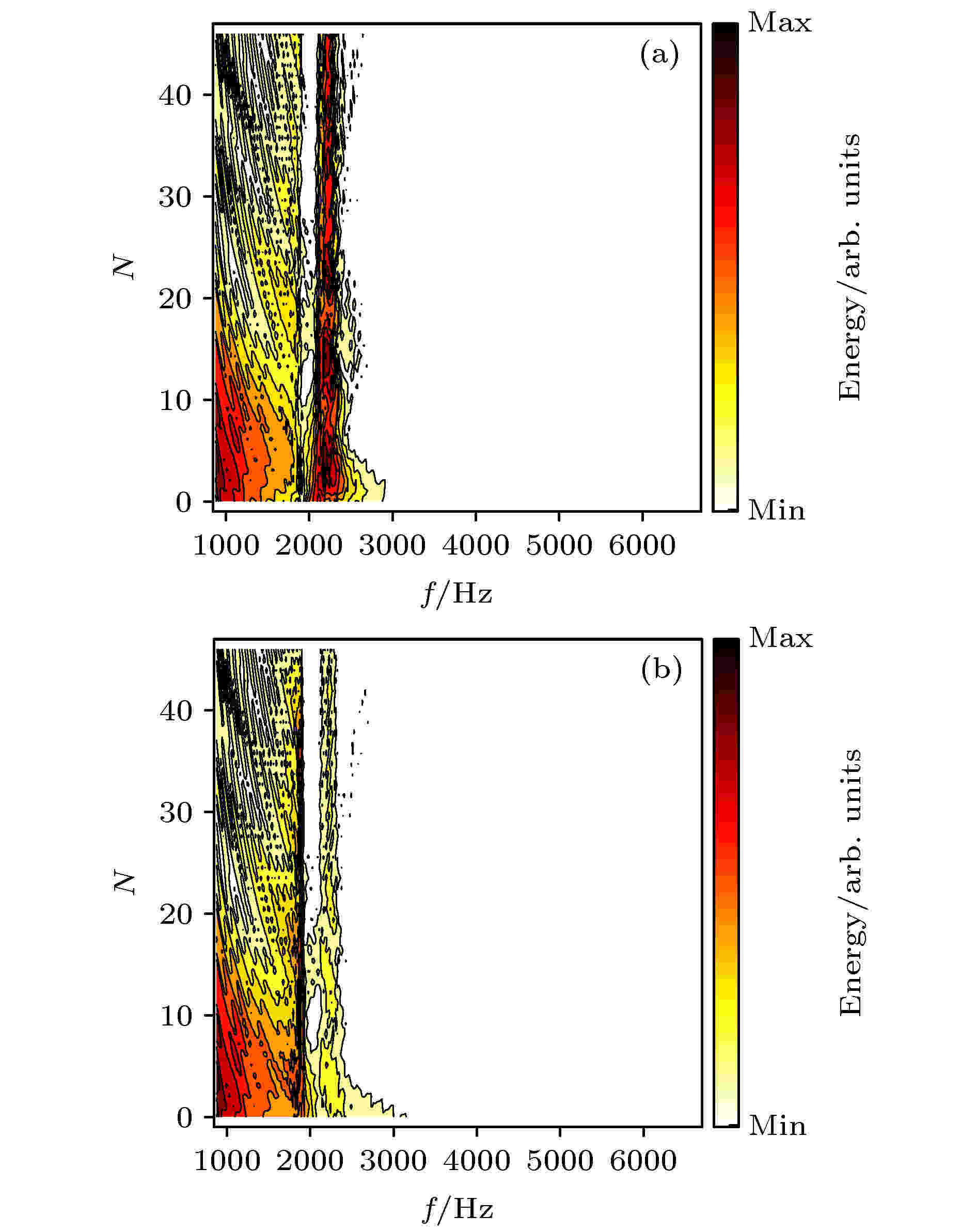图 9 高斯脉冲入射时单元内部(a)与单元间(b)信号频谱
Figure9. Frequency spectra in (a) and between (b) the clusters using Gaussian pulse incidence

图8与图9中的结果证明了脉冲信号在所设计弯曲波导中的传播特性, 由于RB模式的频率选择性, 只能允许特定的频率在波导中传播, 并且单元内部与单元间传播的频率是不同的. 也就是说, 同时可以有两种频率的波在声波导中传播.

本文基于RB模式基本原理, 设计了一种弯曲声波导, 特定频率的声波以特定模式在声栅中传播. 研究过程中, 从频域和时域两个方面考察了弯曲波导的特性. 波导中存在两种不同的RB能量局域模式, 一种分布在单元与单元之间, 另一种模式中能量被更好地局域在环形单元内部. 由于作用位置不同, 两种模式具有不同的频带宽度以及Bloch周期分布特性. 时域结果更好地检测了弯曲声波导在实际使用中的基本特性. 对于特定频率的调制脉冲信号来说, 能够以接近无损的状态沿着波导设计的路径传播. 而对于高斯脉冲信号来说, 只有符合RB模式频率的那部分能量在波导中传播, 可以提高信号滤波和检测的能力. RB模式不但可以在直线型声栅中传播, 同样可以沿着弯曲声栅传播, 拓展了RB模式的应用范围, 进而还可以通过优化单元设计、改变声栅结构、设计不同功能组合等方面的工作, 实现更丰富的声传播控制能力.