全文HTML
--> --> -->铜氧化物高温超导体的发现[6-8]和铁基高温超导电性的发现[9-15]代表着超导研究中的两个重大突破, 不仅提供了超导应用的广阔前景, 而且其奇异正常态和非常规超导电性突破了传统的朗道费米液体理论和BCS超导理论, 促进了强关联电子体系的发展, 为建立新的凝聚态量子理论提供了契机.
铜氧化物高温超导体和铁基超导体作为典型的强关联电子体系, 存在着许多共同特性. 首先, 它们的晶体结构中都包含基本的组成单元, 表现出显著的二维特性. 例如铜氧化物超导体中的CuO2面和铁基超导体中的FeAs层或者FeSe层, 是超导发生的必要结构单元. 其次, 它们的母体一般都具有反铁磁序, 通过掺杂引入载流子可以有效地压制磁有序而诱发超导, 铜氧化物超导体和铁基超导体分享类似的相图. 第三, 这两类高温超导体中由于电荷、自旋、轨道和晶格之间的相互作用, 存在着多种物态及其与超导电性的协同或竞争, 如电荷密度波、自旋密度波、轨道有序和向列相等. 然而, 铜氧化物超导体和铁基超导体也存在一些显著的区别. 在能带结构方面, 铜氧化物超导体主要是单带结构, 而铁基超导体中Fe 3d的五个轨道均对电子结构和超导电性有贡献, 属于典型的多轨道多能带体系. 此外, 两者的母体尽管都是磁有序态, 但是铜氧化物超导体的母体普遍认为是莫特绝缘体, 而铁基超导体的母体则是坏金属. 对铜氧化物超导体和铁基超导体电子结构的研究及相互比较, 对于甄别决定高温超导机理的本征电子结构特征, 发掘高温超导的共性机理, 具有重要的意义.
角分辨光电子能谱由于具备直接测量材料电子结构的独特优势, 已成为研究高温超导体的重要实验手段. 在不断深入的科学问题推动下, 角分辨光电子能谱的水平一直不断地得到创新和提高, 在超导领域发挥着越来越重要的作用. 本文主要介绍了角分辨光电子能谱(ARPES)技术在铜氧化物和铁基高温超导体研究中的一些最新进展. 首先, 简要介绍了ARPES技术的原理, 并着重介绍了自主研制的真空紫外激光ARPES的进展和优势; 然后分别介绍了利用光电子能谱技术, 在铜氧化物和铁基高温超导体的电子结构和超导机理研究方面取得的一些进展. 在铜氧化物高温超导体方面, 主要针对Bi系单层和双层材料以及绝缘母体等材料, 在以下方面开展研究: 母体的掺杂莫特绝缘体行为、奇异正常态电子结构、超导态的电子结构和超导能隙特征等; 特别是针对真空紫外激光ARPES具有高分辨率的优势, 对铜氧化物高温超导体在正常态和超导态下的多体相互作用的研究做了详细介绍, 这些结果为理解与超导机理最相关的电子配对机制提供了重要信息. 在铁基超导体方面, 本文将在之前综述文章[16]的基础上, 对最新的进展进行介绍. 主要包括FeSe单层薄膜的母体电子结构以及可能高达80 K以上超导配对证据, FeSe块材中双费米面电子结构的发现, (Ba, K)Fe2As2超导体的正常态非费米液体行为以及新发现的铁基超导KCa2Fe4As4F2的双层劈裂和超导能隙.
2
2.1.原 理
角分辨光电子能谱的工作原理是基于光电效应. 当入射光子的能量大于材料的功函数时(一般金属的功函数大约为4—5 eV), 就会有一定的几率从材料中激发出光电子. 激发出的光电子沿不同出射方向的信息被电子能量分析器接收和分析, 根据能量守恒和动量守恒等关系, 可以得到固体材料内部的电子结构信息(如图1(a)). ARPES独特的直接获取电子能量、动量甚至自旋的能力, 使其可以直接得到许多微观参量, 如通过色散关系、谱线线型以及费米面等(如图1(b))可获得电子速度、有效质量、散射率以及费米面结构及能隙大小和对称性等. 这些参量是材料微观电子结构的基础和关键因素, 对于理解材料的宏观物理性质起着决定性的作用.
图 1 (a) ARPES的原理示意图; (b) 微观电子参量的直接获取Figure1. (a) Schematic diagram for the angle-resolved photoemission spectroscopy (ARPES); (b) Direct detection of various fundamental physical quantities using ARPES.
2
2.2.ARPES技术的发展和应用
ARPES系统主要由三个部分组成: 1) 光源. 常用的有同步辐射光源、气体放电灯以及固态激光源等; 2)样品传样与测量系统. 主要用于被测样品的进样, 以及维持样品的超高真空和低温无磁测量环境; 3) 数据采集分析系统, 主要由电子能量分析器以及控制软件组成. 其中光源和电子能量分析器在提升系统整体性能方面发挥着决定性的作用. 利用我国自主知识产权的核心技术KBBF晶体以及棱镜耦合技术发展起来的真空紫外固态激光作为光源, 显著提升了ARPES的性能, 把ARPES技术提高到一个新的水平[20,22]. 相应地, 电子能量分析器也得到了迅速的发展, 在能量和动量分辨率不断提高的同时, 新型功能不断出现, 例如自旋分辨和飞行时间探测等.ARPES技术的最新发展, 是实现对电子动量的同时二维探测. 最新一代飞行时间电子能量分析器的出现, 使得实现这一功能成为可能. 由于该分析器采用电子飞行的时间来测量电子的能量, 从而让探测器可以同时测量二维动量空间一个面中的电子信息(如图2所示). 和绝大多数目前使用的一维动量探测的能谱仪相比, 该能谱仪在动量探测效率上提高了两个量级以上. 结合真空紫外激光光源的使用, 该系统仍然保持着超高能量分辨率. 该谱仪在非常规超导体和拓扑材料的精细电子结构研究方面已经显示出明显的优势, 发挥着重要的作用[20,23].
图 2 飞行时间电子能量分析器的结构示意图以及原位观测到的Sb(111)费米面(左下角)和探测器的结构图(右下角)[20]Figure2. Schematic three dimensional drawing of ARToF electron energy analyzer. The analyzer consists of an electrostatic lens system and an MCP/DLD detector. The bottom-left inset shows a Fermi surface of Sb(111) that is in situ observed. The bottom-right inset shows a zoom-in view of the MCP/DLD unit[20].
3.1.高温超导体的晶体结构
铜氧化物高温超导体和铁基超导体的晶体结构都表现出很强的二维特性, 晶体的堆垛方式也很类似. 图3和图4分别显示了铜氧化物高温超导体和铁基超导体具有代表性的晶体结构, 二者在结构上的共同特征是具有导电层和载流子库层. 例如铜氧化物中的CuO2面和铁基超导体中的FeSe或FeAs面都是导电层, 对应着超导产生的地方, 而导电层之间的结构则承担着支撑和载流子库的作用. 不同的地方在于, 铜氧化物超导体中铜氧面中的Cu和O基本处于一个平面, 而铁基超导体的FeAs/FeSe层则是由As-Fe-As/Se-Fe-Se的三层类三明治的结构组成. 另外一个不同在于载流子库层, 铜氧化物超导体中的载流子库层绝缘性比较强, 隔绝了相邻CuO2面之间的耦合作用, 因此可以根据两个绝缘层之间的CuO2面的层数大体分为1层、2层、3层乃至无限层铜氧化物超导体(图3). 相对而言, 大多数铁基超导体中的载流子库层绝缘性差, 相邻的FeSe或者FeAs层之间的耦合仍然存在, 所以长期以来, 一直不存在类似于铜基高温超导体意义上的多层铁基超导体. 最近发现的KCa2Fe4As4F2铁基超导体, 由于Ca2F2层出现较强的绝缘性, 成为第一个真正意义上的双层铁基超导体[26,27].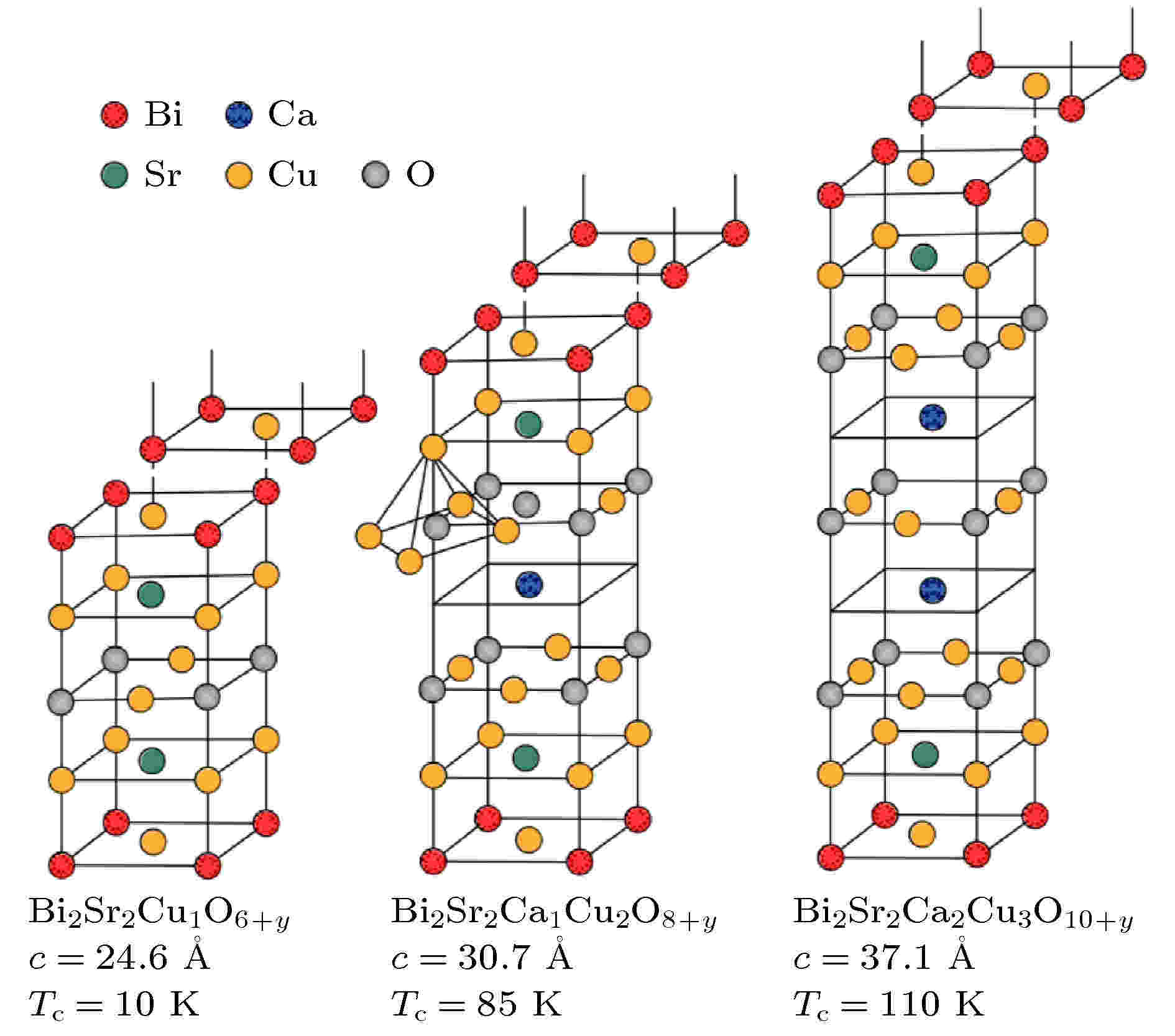
图 3 不同层数铜基高温超导体的晶体结构(从左到右依次为单层、双层和三层铜基超导体)[24]Figure3. Crystal structure of cuprates with different layer numbers from 1 to 3[24].
图 4 不同体系铁基超导体的晶体结构以及导电层的投影图[25]Figure4. Crystal structures for several major classes of iron-based superconductors and their conducting layer projection[25].
2
3.2.高温超导体的能带结构
铜氧化物高温超导体和铁基超导体的低能电子结构都是由Cu或者Fe的3d轨道组成, 但它们之间具有显著的差别. 铜氧化物中Cu的5个d轨道中, 由于晶体场的作用,
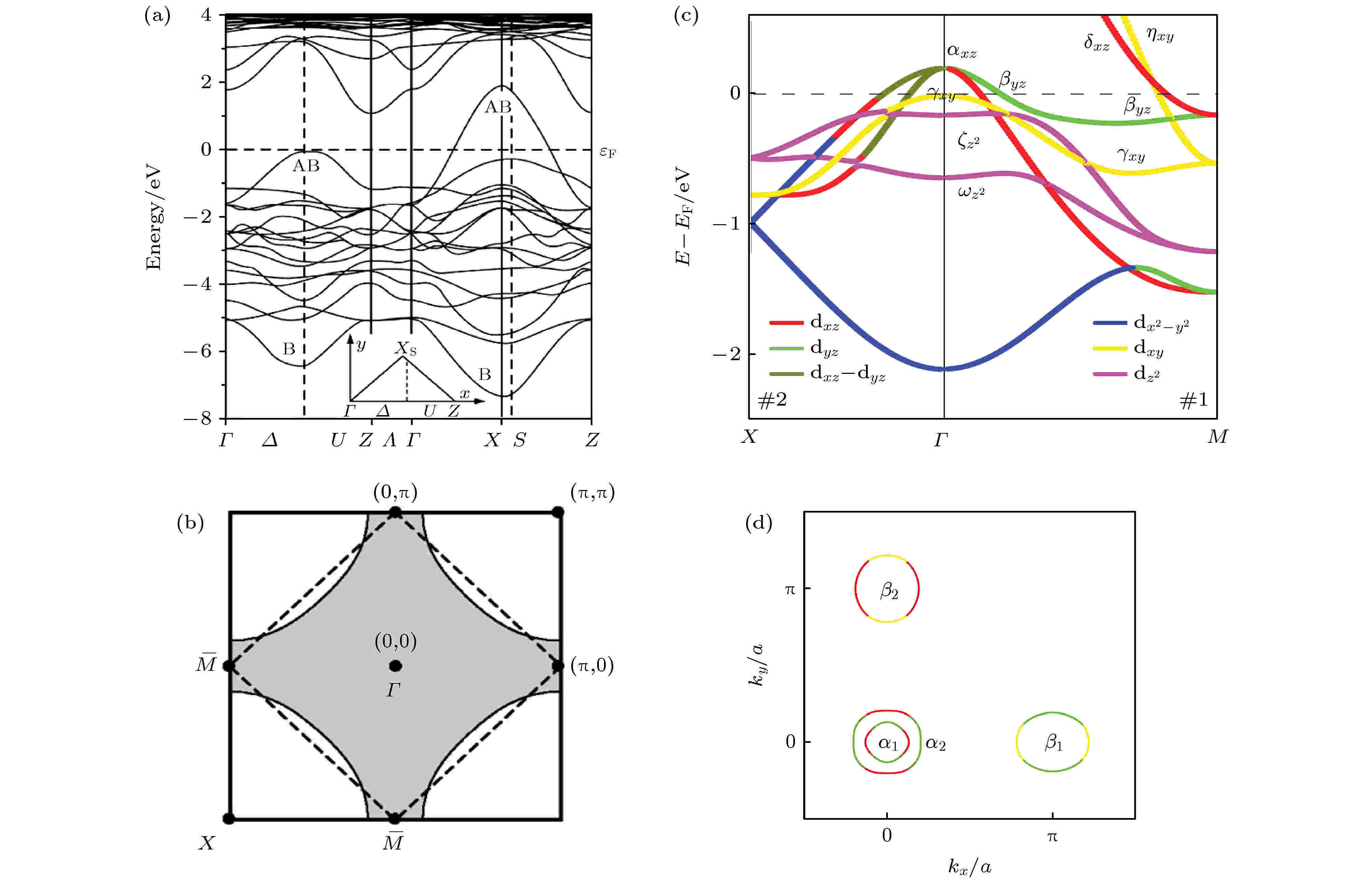图 5 铜氧化物高温超导体和铁基超导体中的能带结构和费米面 (a) La2CuO4的能带结构; (b) La2CuO4的费米面; (c) 典型铁基超导体系的计算能带结构; (d) 典型铁基超导体系的费米面[29,30]Figure5. Band structures and Fermi surfaces of high temperature cuprate superconductors and iron-based superconductors: (a) Band structures of La2CuO4; (b) Fermi surfaces of La2CuO4; (c) band structures of iron-based superconductors; (d) Fermi surfaces of iron-based superconductors [29,30]
4.1.电子相图
铜氧化物高温超导体属于典型的强关联电子体系, 具有复杂的电学特性, 在相图上体现出各种各样的有序态. 因为后文中介绍的铜氧化物均为母体或者空穴掺杂超导体, 因此图6给出了铜氧化物高温超导体的物态在空穴掺杂端随着载流子掺杂浓度和温度变化而体现出来的各种有序态. 在零掺杂, 铜氧化物的母体为绝缘体, 而且处于三维反铁磁的磁有序态. 随着载流子浓度的增加, 磁有序态逐渐被压制, 绝缘性消失, 超导开始出现. 接着超导转变温度逐渐提高, 在最佳掺杂浓度时达到最高, 然后随着掺杂进一步增加, 超导临界温度反而开始降低, 直至在掺杂浓度pmax时消失, 从而在一个大的掺杂范围内超导临界温度表现为圆屋顶形的掺杂浓度关系. 除了超导相外, 整个相图上还出现了许多其他有序态. 在欠掺杂区域最显著的就是赝能隙态, 其定义为超导临界温度之上, 赝能隙温度T*之下的一定温度范围内, 尽管材料还没有超导, 但已经有能隙打开. 赝能隙的起源主要有两种理解: 一种认为赝能隙是超导能隙的前驱, 进入超导态后, 赝能隙自然过渡到超导能隙[31-34]; 另一种认为, 赝能隙与超导无关, 赝能隙是由于其他有序态的存在, 如自旋/电荷密度波或者电子向列相序等[35,36], 它们与超导竞争或者共存. 进入最佳掺杂区域, 正常态进入到奇异金属态, 主要体现为电阻随着温度呈现出线性变化关系, 而不是费米液体理论所预测的二次方的关系. 对于这种奇异金属态的起源目前仍处于争论当中[37]. 最后在过掺杂区域, 直至重过掺不超导区域, 这里的正常态表现为类似费米液体的性质.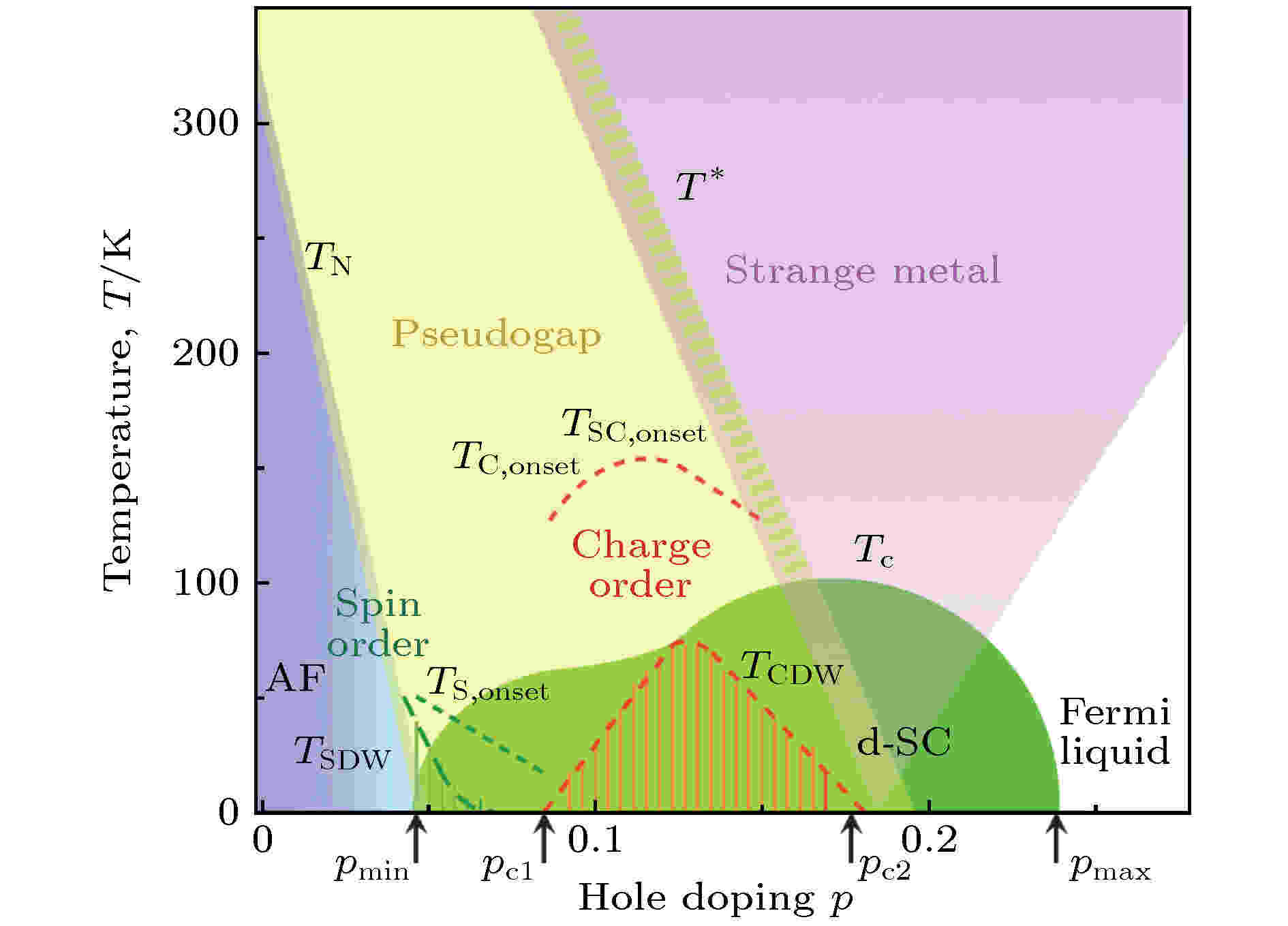
图 6 铜氧化物高温超导体的电子结构相图[8]Figure6. Electronic phase diagram of high temperature cuprate superconductors[8].
2
4.2.铜氧化物母体的电子结构
根据Cu 3d轨道上电子的占据情况, 铜氧化物母体最高的Cu
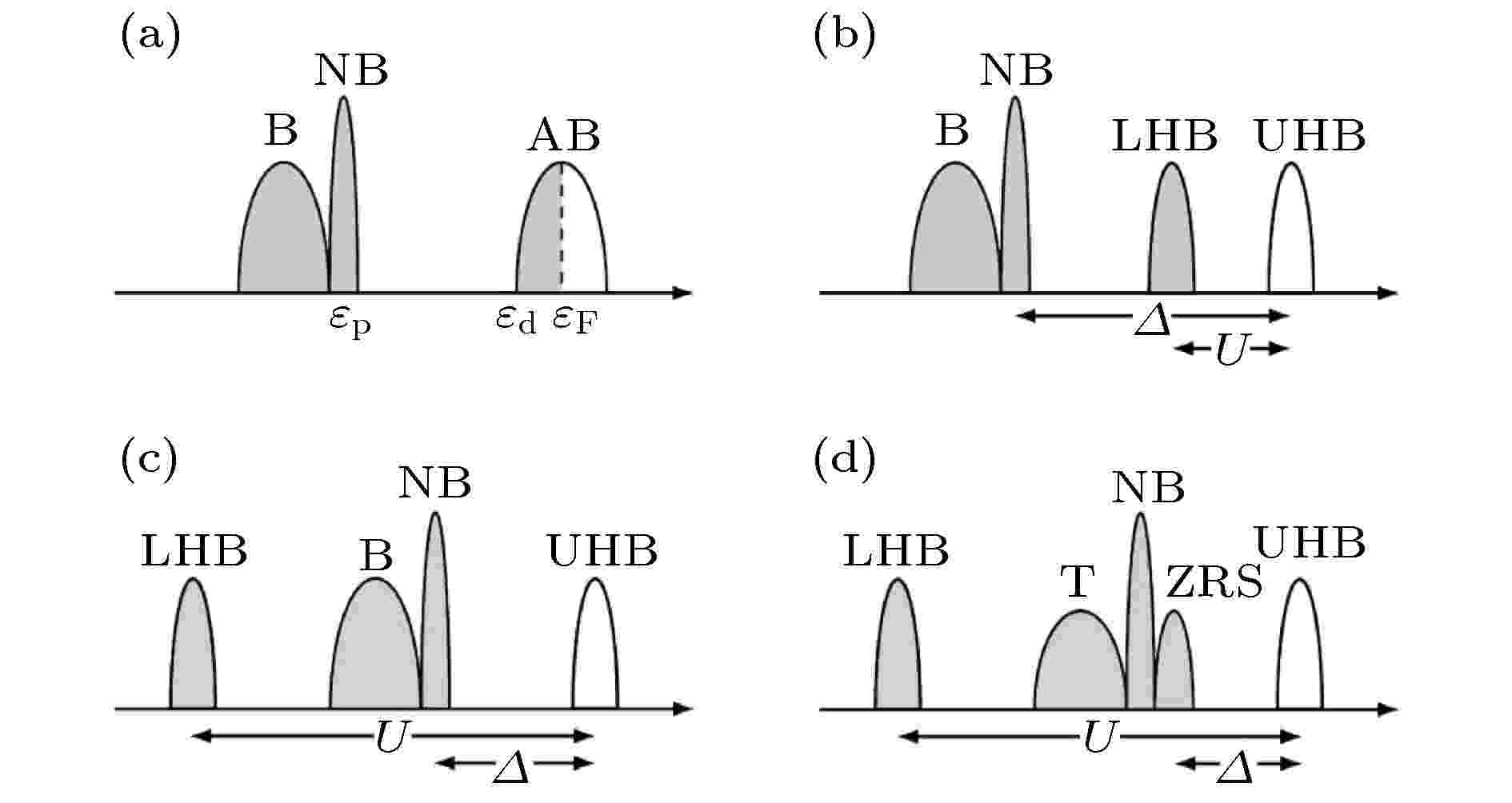图 7 半填充关联电子系统能隙打开的情况[17] (a)无关联金属态; (b)莫特绝缘体态; (c)电荷转移绝缘体; (d) Zhang-Rice单态Figure7. Opening of a correlation gap in the half-filled correlated materials[17]: (a) The system is metallic in the absence of electronic correlations; (b) a Mott insulator; (c) a charge-transfer insulator; (d) Zhang-Rice singlet (ZRS) states.
铜氧化物高温超导体的超导电性, 是通过电子或者空穴掺杂为莫特绝缘体的母体, 压制反铁磁序而实现的, 因此, 母体的电子结构是理解铜氧化物高温超导体的奇异正常态和非常规超导电性的基础. 然而, 真正处于零掺杂的铜氧化物超导体母体材料很少, Ca2CuO2Cl2是公认的具有La2CuO4结构的半填充的莫特绝缘体[44]. 早期对Ca2CuO2Cl2有一些ARPES研究[45-48], 但随着ARPES技术的发展, 在对该体系电子结构的研究中取得了一些新的进展[49].
图8给出了Ca2CuO2Cl2的等能面以及能带结构, 图8(a)和图8(b)分别为束缚能0.25 eV和0.6 eV的两个等能面. 图8(a)的等能面几乎没有任何谱重, 表明所有能带在费米能级以下很大能隙范围内都不存在谱重, 这与其是绝缘体相符. 图8(b)在0.6 eV的束缚能处显示出了比较清楚的等能面. 通过这些能带能获得潜在的费米动量, 从而发现Ca2CuO2Cl2具有两个潜在费米面(图8(c)): 一个是以(π, π)点为中心的空穴型潜在费米面, 另一个是以(0, 0)为中心的电子型潜在费米面. 这是首次揭示出Ca2CuO2Cl2中存在多重潜在费米面的结构. 在对沿着这两个潜在费米面上的光电子能谱分析中, 发现两个能量尺度表现出显著不同的动量依赖关系. 光电子能谱的低能峰表现出各向异性、类似于d-波的动量变化形式, 而有效下哈伯带(effective LHB)能隙则呈现出近各向同性的变化关系(图8(d)). 该实验结果提供的母体莫特绝缘体的电子结构, 为检验描述母体的相关理论, 提供了关键的信息.
图 8 Ca2CuO2Cl2的等能面 (a)在0.25 eV束缚能; (b)在0.6 eV束缚能. (c)观测到的两个潜在费米面. (d)沿着两个潜在费米面上的能带顶部能量分布[49]Figure8. Constant energy contour of Ca2CuO2Cl2 at a binding energy of 0.25 eV (a) and 0.60 eV (b). (c) Two remnant Fermi surface sheets observed. (d) The energy distribution along the two remnant Fermi surface sheets[49].
2
4.3.莫特绝缘体的掺杂和绝缘体-超导转变
铜氧化物高温超导体是通过对莫特绝缘体母体引入载流子后诱发出超导的. 一个关键的问题是其电子结构是如何从莫特绝缘母体到超导体演变的. 前面介绍了母体Ca2CuO2Cl2的电子结构, 那么接着将关注母体掺入少量的载流子时, 电子结构是如何演化的. 对于Ca2CuO2Cl2的空穴掺杂, 有一些ARPES对电子结构进行了研究[50,51], 但还缺乏在微小掺杂区域, 通过精细调控载流子浓度来研究母体电子结构演变的报道. 碱金属表面沉积方法可以有效地引入电子型载流子, 而且由于沉积连续, 沉积速率和时间可控, 因此可以实现精确的载流子浓度掺杂. 在双层铜氧化物超导体Bi2Sr2CaCu2O8(Bi2212)中, 通过原位K元素在样品表面沉积, 可以成功地将过掺的Bi2212连续掺杂到欠掺杂区域, 并且观测到了电子结构随着掺杂的演化[52]. 类似的方法被应用到导电性比Ca2CuO2Cl2稍高的双层Ca3Cu2O4Cl2母体, 并选择提供载流子能力更强的Rb进行表面沉积, 第一次实现对母体的连续电子掺杂, 并同时在原位测量了母体电子结构随电子掺杂的演变[53].图9给出了对Ca3Cu2O4Cl2母体通过表面Rb沉积进行电子掺杂后的能带演化. 实验发现, 母体一旦进行微量的电子掺杂, 化学势瞬间表现出很大的跳跃(达~1 eV), 对应掺杂的电子进入了上哈伯带. 在此之后, 化学势随掺杂逐渐增加. 这种化学势跳跃第一次使得整个莫特能隙区域都可以被ARPES观察到, 从而为观察价带、能隙区域和导带随掺杂的演变成为可能.
图 9 Ca3Cu2O4Cl2母体随电子掺杂的电子结构演化[53] (a)沿(0, 0)–(π, π)节点方向能带结构随掺杂的演变; (b)在(π, 0)反节点区域能带结构随掺杂的演变; (c), (d)分别对应于图(a)和图(b)的角积分光电子能谱; (e), (f)从实验结果获得的节点和反节点电子结构随掺杂演变的示意图[53]Figure9. Electronic structure evolution with electron doping for the parent compound Ca3Cu2O4Cl2: (a) Doping evolution of bands along (0, 0)–(π, π) nodal direction; (b) Doping evolution of bands near (π, 0) antinodal region; (c), (d) Integrated energy distribution curves (EDCs) corresponding to Fig.(a) and Fig.(b), respectively; (e), (f) Schematic representations of electronic structure evolution with doping for the nodal region and antinodal region, respectively[53].
随着电子掺杂的进一步增加, 母体的电子结构演变表现在如下几个方面. 首先, 一些新的能带在原先的1.2 eV能隙中出现, 而且其谱重随着掺杂的增加而变强; 其次, 原来母体的能带随着电子掺杂浓度的增加而变弱, 在掺杂浓度约为0.04 e/Cu时基本消失, 表现为谱重从原来能带向能隙区间的转移; 第三, 在能隙中新产生的能带, 表现出显著的动量依赖关系. 在(π, 0)反节点附近, 少量的电子掺杂, 形成的能带已经抵达费米能级, 而且随着掺杂的增加逐渐发展成为电子型抛物线能带(图9(b)). 与此不同的是, 沿着(0, 0)–(π, π)节点方向的能带, 在能隙中刚开始出现时, 其能带顶部仍远离费米能级. 随着电子掺杂的增加, 能带的顶部逐渐靠近费米能级, 并最终穿过费米能级(图9(a)). 以上这些结果, 为电子掺杂铜氧化物母体提供了最为系统和详细的信息, 由此可以获得母体中原先的价带、莫特能隙和上哈伯带、以及新产生的隙间态随着掺杂的演变图像(图9(e)和图9(f)). 这是首次通过ARPES观察到的具有动量分辨的电子结构的演变, 这些信息为理解掺杂莫特绝缘体的图像提供了重要的实验依据, 为铜氧化物高温超导的相关理论提供了实验基础.
同样重要的是, 如何用ARPES来探测铜氧化物母体在微量空穴掺杂时电子结构的演变. 目前对于铜氧化物母体, 缺乏表面沉积导致连续空穴掺杂的有效手段, 所以无法开展类似于微量电子掺杂(图9)的空穴掺杂的ARPES研究. 为了克服这个问题, 我们设计了先选择重欠掺杂的Bi2212样品(对应空穴掺杂浓度约0.066), 然后在样品表面连续沉积Rb进行电子掺杂, 从而把表面的空穴掺杂浓度逐渐减低到零. 通过这种方式, 成功地研究了铜氧化物母体在微量空穴掺杂时其电子结构随空穴掺杂的演变[54].
图10左给出了欠掺杂Bi2212沿着节点方向的能带随着空穴浓度在0—0.066之间变化时的演变过程, 和前面电子掺杂有显著的不同. 首先, 空穴掺杂时, 靠近费米能级的能态最先出现在节点方向(图10). 而电子掺杂时, 靠近费米能级的能态最先出现在反节点区域(图9(b)). 其次, 空穴掺杂母体时, 化学势没有表现出一个类似电子掺杂那样的跳跃, 而是逐渐随着空穴掺杂浓度的增加而逐渐降低(图10左). 但从母体到掺杂浓度0.066时, 化学势表现出很明显的变化, 达到约1.2 eV (图10左). 第三, 在母体状态时, 价带的最高点约在费米能级以下近1 eV. 随着空穴浓度的增加, 价带的顶部越来越靠近费米能级, 在0.066时穿过费米能级, 并且在费米能级形成准粒子峰. 值得注意的是, Bi2212体系中的绝缘体-超导体转变, 也发生在0.066附近. 根据这些结果, 可以建立一个空穴掺杂铜氧化物母体的图像, 如图10右所示. 这为理解绝缘体-超导体转变, 建立空穴掺杂莫特绝缘体的理论提供了重要信息.
图 10 Bi2212沿(0, 0)–(π, π)节点方向的能带结构, 在空穴掺杂浓度0?0.066之间随掺杂浓度的演变[54]Figure10. Band structure evolution with hole doping in the doping range of 0?0.066 in Bi2212 measured along the (0, 0)–(π, π) nodal direction[54].
类似的空穴掺杂引起的电子结构演变, 在单层铋系超导体Bi2Sr2CuO6(Bi2201)中也观察到过[55]. Bi2201体系通过La掺杂可以涵盖大范围空穴掺杂, 并且空穴浓度可以靠近母体(约0.03), 进入非超导的反铁磁绝缘体相. 因此, Bi2201体系是研究从莫特绝缘体到超导演变的另一个理想体系. 图11给出了Bi2201沿节点方向的能带结构、光电子谱图随着空穴载流子浓度的演变[55].
图 11 Bi2201中沿节点方向能带结构随空穴掺杂浓度的演变. (a)?(g) 能带结构的演变; (h), (i) 光电子能谱谱线随空穴掺杂的变化; (j) Bi2201的电子相图[55]Figure11. Band structure evolution with hole doping in Bi2201: (a)?(g) Band structure along (0, 0)–(π, π) nodal direction; (h) Photoemission spectra (EDCs) at Fermi momentum for different doping levels; (i)The corresponding symmetrized EDCs; (j) Electronic phase diagram of Bi2201[55].
图11(a)—图11(g)给出了Bi2201从靠近母体的极度欠掺杂(p = 0.03)到开始进入超导相(p = 0.105)之间的沿着节点方向能带随空穴掺杂的演变. 可以看出, 在最低掺杂时, 费米能级附近的谱重存在着明显压制(图11(a)). 随着掺杂增加, 谱重压制在逐渐减弱, 在p ≈ 0.1之后, 谱重压制消失, 能带穿越费米能级. 从图11(h)和图11(i)也清晰地看出, 在低掺杂时, 光电子谱线缺少相干峰, 存在着大的能隙. 随着掺杂增加, 能隙逐渐减少, 到最后尖锐的相干峰出现, 能隙彻底消失. 这种演化行为总结在图11(j)的电子相图中. 可以看出, 该演变规律和前面Bi2212中(图10)观察到的结果基本一致. 在Bi2201中, p ≈ 0.1是一个关键的掺杂浓度. 在这个浓度, 节点能隙为零, 三维反铁磁序消失, 超导出现, 表明在这个掺杂浓度发生了绝缘体-超导转变. 这个结果表明, 节点能隙、反铁磁序以及超导之间存在着密切的关系[55].
2
4.4.正常态电子结构
铜氧化物高温超导体的超导区域可以分成三个部分: 具有最高超导温度的最佳掺杂区域, 比最佳掺杂浓度低的欠掺杂区域, 和比最佳掺杂浓度高的过掺杂区域(图6). 超导温度之上正常态表现出许多奇异的物理性质, 对正常态电子结构的研究和了解被认为是理解高温超导机理的前提和基础.首先来看欠掺杂区域. 如图6相图所示, 高温超导体在欠掺杂区域表现出一系列奇异的正常态性质, 明显偏离经典的金属理论—朗道费米液体理论. 一个尤为奇异的现象是“赝能隙”的存在. 理解奇异正常态的本质及其与超导电性的关系, 对理解高温超导机理具有关键的作用. 费米面的拓扑结构是材料微观电子结构最直观的体现, 是材料物性最相关的电子结构. 欠掺杂区域, 费米面应具有什么样的拓扑形状? 在理论上, 不同的理论框架对费米面的拓扑形状给出截然不同的预言. 如有的认为可能形成大的费米面, 有的认为应该形成费米弧(Fermi arc)[56-62], 有的则认为应该形成费米口袋(Fermi pocket)[63-66]. 在实验上, 不同的实验方法得到的结果也不一致.
图12给出了Bi2201体系中欠掺杂样品随着掺杂演化的费米面[67]. 从图12(b)和图12(c)中可以直接观察到费米口袋的存在, 仔细的数据分析还可以观察到费米弧的存在, 表现为费米口袋与费米弧共存的一种特别的费米面拓扑结构(如图12(i)所示). 在Bi2201中观察到的费米口袋表现出几个特性. 首先, 发现的费米口袋都不是以(π/2, π/2)为中心, 因此可以排除阴影能带[68,69]和d密度波[70,71]的起源. 其次, 费米口袋表现出明显的掺杂依赖关系, 其只在欠掺杂区域适当的掺杂范围内存在, 在最佳掺杂以及过掺杂区域都没有观测到[67]. 费米口袋为空穴型, 它的面积大小与样品的掺杂浓度相对应. 仔细的研究表明, 观察到的费米口袋及其随掺杂的演变, 不能用Bi2201中存在阴影能带和超结构能带来解释[67]. 考虑额外存在的超结构波矢, 可能解释费米口袋的形成[72], 但这也导致许多其他的实验现象难以解释[73]. 在欠掺杂区域, 理论预计会出现费米口袋[74], 而且存在各种有序相, 需要进一步的理论和实验工作, 来确定观察到的费米口袋的起源.
图 12 欠掺杂Bi2Sr2CuO6样品的费米面随掺杂的演化[67]: (a)?(d) 不同掺杂浓度(0.10, 0.11, 0.12, 0.16)的Bi2201观察到的费米面; (e)?(h)沿节点方向能带在费米能级处对应的动量分布曲线; (i)Bi2201观察到的费米面的总结Figure12. Fermi surface evolution with hole doping for the underdoped Bi2Sr2CuO6[67]: (a)?(d) Fermi surface mappings for Bi2201 with different hole-doping levels(0.10, 0.11, 0.12 and 0.16); (e)?(h)Momentum distribution curves (MDCs) at the Fermi level for the bands measured along the nodal direction; (i) Summary of measured Fermi surface for Bi2201 with different doping levels.
Bi2212作为被ARPES研究最广泛的铜氧化物超导体, 我们通过高分辨激光ARPES测量, 在Bi2212中发现了异常的能带杂化现象[75]. 在Bi2201和Bi2212中, 存在沿着b*方向[(0, 0)–(π, π)方向]的超结构, 导致产生新的超结构费米面和能带, 如图13(a)所示. 在布里渊区第一象限, 主费米面和超结构费米面平行移动, 在动量空间可以明显分开. 但在第二象限, 主能带与超结构能带之间则相互交错, 可能会出现能带杂化. 对Bi2212第二象限的测量发现奇特的费米面杂化现象(图13(b)), 不能简单地用预计的图13(a)中的结果来解释. 实验结果表明, 并不是所有的交叉位置都会产生能带杂化, 只有主能带的反成键带(成键带)和超结构能带的成键带(反成键带)之间存在着杂化, 如图13(c)所示. 这种能带选择性杂化的现象直接证明了超结构能带是直接来自于CuO2层, 是本征的能带. 这个结果为Bi2212提供了一个全新的完整的费米面结构, 在研究其物理性质时应该考虑所有的主能带、超结构能带以及它们之间的杂化[75].
图 13 Bi2212中观察到的费米面和能带的选择性杂化[75] (a)Bi2212的主能带和超结构能带; (b) 实验测得的在第二象限的费米面结构; (c)费米面结构的选择性杂化能解释实验现象Figure13. Selective band hybridization in Bi2212[75] (a) Schematic main Fermi surface and superstructure Fermi surface in Bi2212; (b) Measured Fermi surface in the second quadrant; (c) Selective band structure hybridization that can explain the observed result
高分辨激光ARPES对Bi2212的测量, 也对双层劈裂提供了新的信息[76]. 图14给出了过掺杂Bi2212(Tc = 75 K)的费米面和能带结构[76]. 该结果由于采用了11 eV光子能量的飞行时间ARPES技术, 费米面是一次同时测量获得的. 如图14(a)和图14(b)所示, 不仅主能带和其超结构能带被探测到, 而且Bi2212中由于双层铜氧面相互作用引起的双层劈裂在主能带和超结构带中都清晰可见. 特别是如图14(c)和图14(d)所示, 更精细的能带以及费米能级上的动量分部曲线结果显示, 沿着节点方向((0, 0)–(π, π))双层劈裂依然存在[76].
图 14 过掺杂Bi2212(Tc = 75 K)的费米面和能带结构[76]; (a), (b) 在20和90 K测量的费米面; (c), (d)沿两个动量方向测得的能带及在费米能级处的动量分布曲线Figure14. Fermi surface and band structure for the overdoped Bi2212(Tc = 75 K)[76]: (a), (b) Fermi surface measured at 20 K and 90 K; (c), (d) Band structures measured along two momentum cuts, and the corresponding MDCs at the Fermi level.
当铜氧化物超导体进入重过掺杂区域时, 其正常态通常被认为符合费米液体理论. 超过一个临界的掺杂浓度, 赝能隙等奇异正常态也不存在, 超导电性也会逐渐消失. 在费米液体理论框架下, 研究高温超导的机理相对要简单一些. 如果超导机理对于欠掺、最佳掺杂和过掺的材料是相同的话, 对过掺区域的研究, 为研究高温超导机理提供了另一种思路和途径. 因此, 研究重过掺杂区域的样品, 如何从超导到不超导的电子结构演化也非常重要. Bi2212体系通过化学掺杂很难在过掺杂区域进入不超导相. Bi2201体系则可以通过化学掺杂, 尤其Pb元素替代后, 不仅可以有效地去除超结构, 而且能够让样品进入重过掺杂区域甚至不超导. 进一步配合真空退火去除氧减少空穴以及高压氧退火增加空穴的方式, 可以实现无超结构的Pb-Bi2201在重过掺杂区域从超导20 K到不超导的连续掺杂样品[77].
图15给出了Pb掺杂的Bi2201样品的费米面结构, 掺杂浓度涵盖从过掺杂的超导温度17 K直到极度过掺杂不超导的样品. 首先可以看到非常清晰的费米面结构, 除了主能带费米面外, 也可以看到较弱的影子带(其与主能带关于(0, π)–(π, 0)连线对称). 在Bi系超导体中常见的超结构带在这些样品中并不存在, 表明其中的超结构得到了有效的压制. 图15(f)总结了所有掺杂对应的费米面, 结果表明随着Tc的降低, 空穴浓度增加, 费米面拓扑结构由空穴型转变为电子型, 发生了Lifshitz相变. 这个相变刚好发生在Tc = 3 K与不超导样品之间, 表明了超导与Lifshitz相变之间存在着密切的关系[77].
图 15 Bi2201过掺杂区域费米面随着掺杂浓度的演化[77]Figure15. Fermi surface evolution with the hole doping level for Bi2201 in heavily overdoped region[77].
2
4.5.超导态电子结构和超导能隙
随着温度降低, 铜氧化物超导体进入到超导态, 超导能隙打开. 超导能隙对称性与超导体的超导机制密切相关. 不同于常规超导体各向同性的s波超导能隙对称性, 铜氧化物超导体的超导能隙普遍认为是各向异性的, 主要体现为d波对称性. 但是超导能隙对称性的具体形式, 以及与赝能隙的关系等, 目前仍存在着争论. 采用高质量的样品, 开展高精度的能隙测量是解决超导能隙的具体形式、厘清超导能隙与赝能隙关系的重要途径.真空紫外激光光电子能谱系统具有超高的能量和动量分辨率(典型能量分辨率好于1 meV)[22], 对开展能隙测量具有独特的优势. 图16给出了对最佳掺杂Bi2Sr1.6La0.4CuO6超导能隙测量的结果, 表明超导能隙遵循简单的d波形式
图 16 最佳掺杂Bi2Sr1.6La0.4CuO6的超导能隙以及能隙的温度演化行为[78] (a) 测量的费米面; (b) 超导能隙随着动量的变化; (c) 超导能隙随温度的变化Figure16. Momentum dependence and temperature dependence of the superconducting gap in the optimally-doped Bi2Sr1.6La0.4CuO6[78].
利用高分辨激光ARPES, 也对Bi2212的超导能隙进行了高精度测量. 图17左图给出了最佳掺杂Bi2212超导能隙的动量依赖关系. 最佳掺杂的Bi2212样品, 在使用真空紫外激光光源时, 由于矩阵元效应只观察到了反成键费米面. 与Bi2201不同, 它的能隙结构不再是简单的d波形式, 而是需要引入d波高次项才能很好地描述[79]. 另外, 图17右图还给出了近反节点区域的费米动量随温度的变化情况. 可以看到, 随着温度升高, 经历超导态进入正常态并超过赝能隙温度时, 费米动量并没有发生变化. 这个结果不同于Bi2201中报道的在赝能隙温度T*发生能带重组的结果[80-82], 表明这个能带重组可能不是一个普遍的行为.
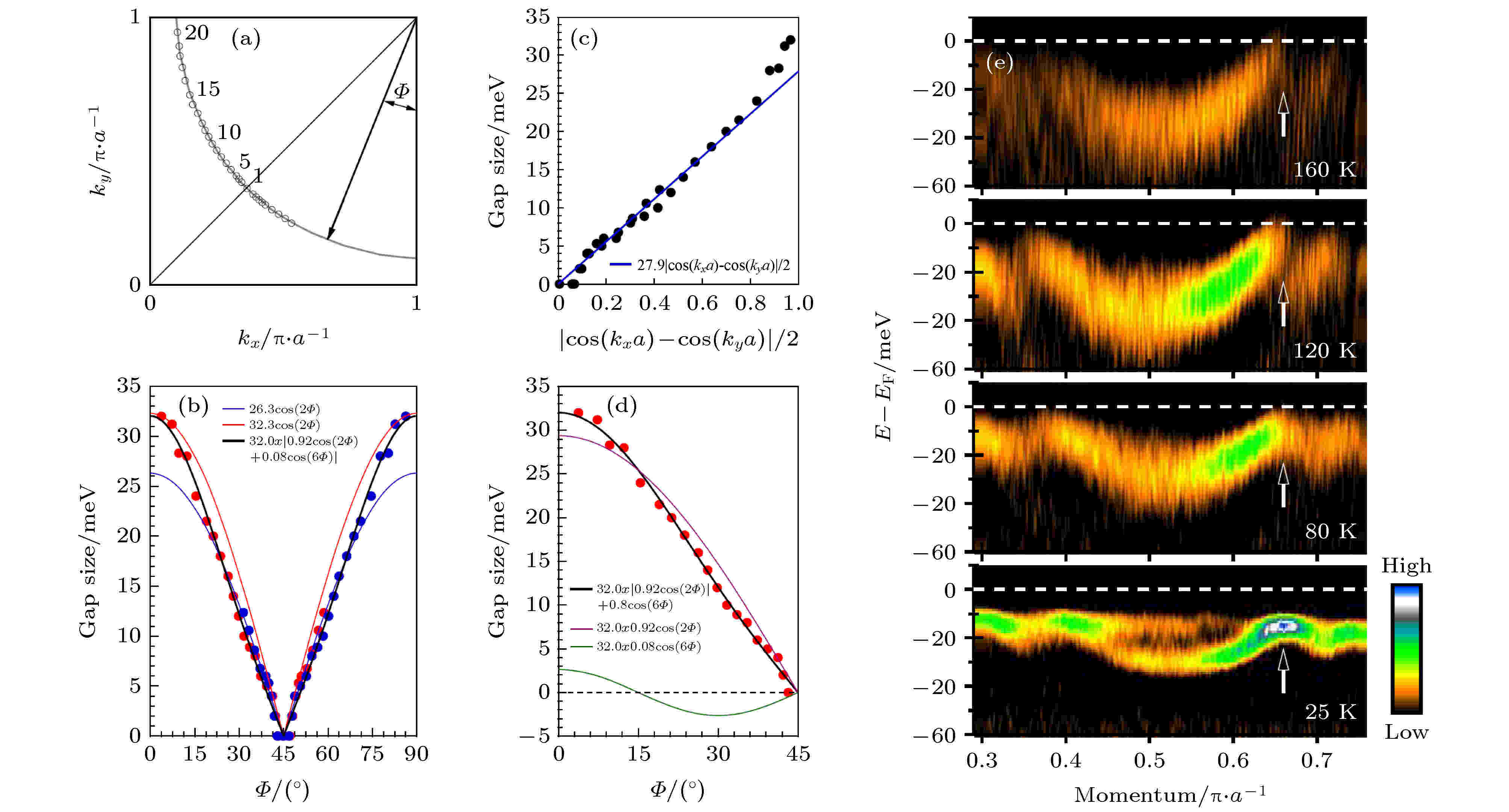图 17 最佳掺杂Bi2212 (Tc = 91 K)超导能隙的动量分布, 和反节点区域的费米动量随温度的演化[79]Figure17. Momentum dependence of superconducting gap for the optimally-doped Bi2212 with Tc = 91 K and temperature dependence of the Fermi momentum near the antinodal region[79].
长期以来, 实验上和理论上都认为, Bi2212中双层劈裂产生的两个费米面可能具有相同的超导能隙. 我们通过高分辨激光光电子能谱的测量, 发现这两个费米面具有不同的超导能隙结构[76]. 图18给出了过掺杂Bi2212样品中两个费米面上超导能隙的测量结果. 通过采用11 eV激光和飞行时间能量分析器的光电子能谱测量, 可以清晰地看到双层劈裂产生的成键费米面和反键费米面(图18(a)). 图18(b)和图18(c)给出了这两个费米面上超导能隙的动量依赖关系[76]. 首先, 与之前报导的结果不同, 这些结果清晰地表明, 这两个费米面具有不同的超导能隙大小. 而且, 这两个费米面的超导能隙具有不同的动量依赖关系: 反成键费米面的能隙可用简单的d波描述, 而成键费米面的能隙则偏离简单的d波形式, 需要引入高次项来描述, 造成这个结果的原因可能在于两个费米面对应的掺杂浓度不同.
图 18 过掺杂Bi2212(Tc = 75 K)中两个费米面上的超导能隙[76]Figure18. Different superconducting gap observed on the two Fermi surface sheets in Bi2212 (Overdoped, Tc = 75 K)[76].
2
4.6.多体相互作用和配对相互作用谱函数
电子的微观动力学特征对决定材料宏观物理性质起着重要的作用. 电子与其他激发模式(例如声子、磁子等)的相互作用, 一般归为多体效应, 它决定了材料的一些重要的宏观物理性质. 在常规超导体中, 电子与声子的相互作用是电子配对的起源. 在高温超导体中, 对于多体相互作用的探测和研究, 对理解其奇异正常态性质和高温超导机理具有关键的作用.多体效应在电子结构上的体现, 主要表现在电子的自能. 一个直观的体现就是电子色散关系上的扭折结构, 如铜氧化物高温超导体中最著名的70 meV扭折结构以及40 meV的扭折[83-88]. 利用真空紫外激光光电子能谱系统的高能量和动量分辨率的优势, 我们在对铜氧化物高温超导体中多体效应研究中取得了进展. 首先, 如图19所示, 在最佳掺杂Bi2212沿节点方向的色散中, 除了可以清楚看到70 meV的扭折外, 在有效电子自能中还观察到两个新的结构, 分别处于115和150 meV. 由于这两个模式的能量明显大于Bi2212中已知声子或者磁共振模式能量, 因此不可能来源于电子与它们的耦合, 表明存在一种新的耦合模式. 另外, 通过进一步研究更高能处的色散关系(费米能级以下0.3—1 eV), 对高能扭折的起源提出了新的认识, 指出这种近乎垂直的色散关系不是本征的, 既不能代表裸带, 也不代表电子与某种高能模式的耦合[90].
图 19 最佳掺杂Bi2212沿着节点高对称方向的色散和有效电子自能[89]Figure19. Band structure and effective self-energy along nodal direction for optimally-doped Bi2212[89].
进一步地, 对铜氧化物超导体Bi2212中70 meV的节点扭折和40 meV的反节点扭折在动量空间的演变开展了详细的研究. 图20给出了过掺杂Bi2212沿着节点方向的色散. 从偏离节点方向上的二次微分谱图以及有效自能上, 可以清楚地看到在反节点区域40和70 meV两个耦合模式的同时存在. 随着往节点方向靠近, 70 meV扭折保持不变而40 meV扭折则逐渐增大, 到节点时已经接近于70 meV, 并且这种演化行为在欠掺杂、最佳掺杂和过掺杂样品中都存在[91]. 在Bi2201体系中, 也发现了两个扭折结构的存在, 一个是常见的50—80 meV扭折, 随着掺杂浓度的增加从欠掺杂到过掺杂扭折能量单调稍有增加. 另外一个是低于10 meV的低能扭折, 不随掺杂变化而变化[92]. 这些扭折能量都在80 meV以下, 而Bi系中CuO2面对应的声子能量也基本在这个能量范围内, 因此上述扭折很多都归因于电声子耦合的结果.
图 20 Bi2212的两个耦合模式的动量依赖关系[91]Figure20. Momentum dependence of two coupling modes in Bi2212[91].
要理解电子与其他模式的耦合情况, 单单获得几个模式的耦合能量是不够的, 还必须知道耦合的强度和分布, 即需要获得定量的电子耦合函数(Eliashberg函数
ARPES测量的实验数据可用单粒子谱函数
而电子自能实部表示为
因为裸带代表不包含多体相互作用的原始电子色散, 因此一般来说它不依赖于温度变化, 当两个温度下测量的电子自能相减时, 裸带会被消除. 根据(2)式和(3)式可以得到:
图21给出了基于(4)式, 获得的Pb-Bi2201中Eliashberg函数的数据反演过程. 在实际的运算过程中采取了迭代的方法. 该方法利用真空紫外激光ARPES的高分辨率高统计的能带色散温度依赖关系, 不依赖裸带选取成功地解析出了Eliashberg函数. 从解析得到的Eliashberg函数上看, 在过掺杂Pb-Bi2201中, 不仅仅是扭折上看到的40 meV和70 meV, 还显示了多个其他玻色子耦合能量[96].
图 21 Pb-Bi2201正常态的能带色散以及Eliashberg函数数据反演过程[96]Figure21. Normal state dispersion of Pb-Bi2201 and inversion process of extracting the Eliashberg function[96].
进入超导态后, 除了正常态电子自能外, 还需要引入超导态配对自能. 基于格林函数方法, 超导态的单粒子谱函数可表示为
如图22所示, 利用(6)式, 通过对Bi2212样品高精度的光电子能谱测量, 可以获得超导态的正常自能和配对自能的实虚部[97]. 一个采用类似方法扩展到其他动量区域的获取正常自能和配对自能的结果, 可以参见文献[98].
图 22 轻度欠掺杂Bi2212(Tc = 89 K)样品节点方向反演获得的正常自能和配对自能[97]Figure22. Normal self energy and pairing self energy subtracted from lightly underdoped Bi2212 (Tc = 89 K)along nodal direction[97].
从光电子能谱中正常态与超导态的电子态密度比值可以获得能隙函数的信息:
图 23 通过角分辨光电子能谱测量获得的高温超导体Bi2212的正常自能和配对自能[99]Figure23. Normal self-energy and pairing self-energy for Bi2212 from ARPES measurements[99].
图 24 高温超导体Bi2212通过Eliashberg方程反演获得的正常关联谱函数以及配对关联谱函数[99]Figure24. Normal Eliashberg function and pairing Eliashberg function for Bi2212[99].
图23给出了对两种不同掺杂Bi2212样品成功提取的在不同动量方向和不同温度下的正常自能和配对自能. 图24给出的是结合Eliashberg理论和运用最大熵方法, 通过反演获得的正常Eliashberg函数和配对Eliashberg函数及其随动量和温度的演变关系. 这些结果表明: 1) 不论是正常关联谱函数(normal Eliashberg function), 还是配对关联谱函数(pairing Eliashberg function), 除了低能(约50 meV)结构之外, 都包含类似的不随能量演变的高能部分, 体现出与传统超导体关联谱函数显著不同的电子配对来源; 2) 正常关联谱函数基本不随动量演变; 3) 在低温超导态时, 正常关联谱函数和配对关联谱函数趋于一致. 这些结果首次直接揭示出了铜氧化物高温超导体中超导驱动激发谱的能量和动量特征, 为甄别和确立高温超导配对机理和进一步的理论研究提供了决定性的关键信息. 同时围绕这项工作所发展的实验技术、理论研究和数值方法等, 为研究其他超导体的超导机理开辟了一种统一而有效的途径.
2
5.1.铁基超导体中的奇异正常态
(Ba0.6K0.4)Fe2As2是铁基超导体中得到最早最广泛研究的超导体系, 但是围绕该超导体的研究仍然存在着许多重要问题和争议. 一个显著的问题是关于超导能隙. 早期的结果基本认同了(Ba0.6K0.4)Fe2As2围绕布里渊区中心的两个空穴型费米面展现了大小不同的近各向同性的超导能隙[101-104]. 但是后来日本小组采用真空紫外激光的高分辨率光电子能谱测量, 却发现各个费米面的超导能隙大小一致, 而且能隙很小, 对应的
图 25 Ba0.6K0.4Fe2As2的两个费米面的超导态能隙对称性以及能隙和准粒子寿命的温度演化[100]Figure25. Momentum dependent superconducting gap and temperature dependent gap and lifetime of single quasiparticle[100].
2
5.2.铁基超导体中的双层劈裂和层间配对
在铜氧化物高温超导体中, CuO2面的层间耦合对超导电性有重要的影响, 比如超导转变温度随着一个结构单位内的CuO2面数目变化而有规律地演变. KCa2Fe4As4F2是一个新的铁基超导体系, 晶体结构中每两层FeAs层被绝缘的Ca2F2层分开(如图26(a)所示), 是目前发现的铁基超导体中惟一一种真正的双层材料, 可以研究双层劈裂及层间耦合作用[26,27].
图 26 KCa2Fe4As4F2的晶体结构, 能带结构和超导能隙[106]Figure26. Crystal structure, band structure and superconducting gap symmetry for KCa2Fe4As4F2[106].
图26给出了KCa2Fe4As4F2的晶体结构、能带结构和超导能隙, 结果显示了非常清楚的双层劈裂现象(图26(c)中). 这样围绕布里渊区中心总共发现了5个空穴型费米面, 比任何其他的铁基超导体系都多, 围绕M点是一个电子型的费米面. 观测到的所有费米面上都显示了清晰的超导能隙打开的特征. 所有的超导能隙表现出费米面依赖、无能隙节点的行为(图26(d)). 尤其是非常靠近的双层劈裂费米面, 尽管费米面大小很接近, 但是能隙大小差别很大, 显示出了层间耦合对超导能隙的影响. 这种超导能隙的分布可以用考虑层间配对的、基于反铁磁涨落的能隙方程进行拟合. 该结果对于理解层间耦合对超导的影响提供了新的信息.
2
5.3.FeSe/SrTiO3单层薄膜的绝缘母体和高达83 K超导配对证据
单层铁硒(FeSe/STO)薄膜因具有非常简单的晶体结构、奇特的电子结构和铁基超导体中可能的最高超导转变温度而吸引了广泛的关注. 研究表明, 通过电子掺杂可以在单层铁硒中实现高温超导. 然而, 单层铁硒的高温超导起源问题, 特别是单层铁硒的母体的性质仍然存在广泛争议. 之前的报道认为, 单层FeSe/STO的母体是向列相的结果[107]或者是存在着狄拉克锥的结构[108].通过进一步优化单层FeSe/STO薄膜的生长条件, 成功生长出具有非常低掺杂浓度的完美单层FeSe/STO薄膜, 并通过真空退火原位引入电子, 测量电子结构随电子掺杂增加的演变. 另一方面, 先制备超导的完美单层FeSe/STO薄膜, 在表面逐渐沉积Se原子, 有效减少电子载流子浓度, 并测量其电子结构随电子浓度减少的演变[109]. 结果表明, 具有非常低电子浓度的靠近母体的单层FeSe/STO薄膜为绝缘体, 在费米能级附近没有任何谱重(图27(a)). 随着电子浓度的增加, 低能电子结构逐渐显现, 发生绝缘体-超导转变并进入超导. 低电子浓度电子结构的演化行为, 也得到了扫描隧道谱实验的证实(图27(b)). 这样建立起来的单层FeSe/STO的完整相图(图27(c))[109]主要分为三个区域: 当载流子浓度很低时, 没有观测到费米面和能带结构, 为绝缘态; 当载流子浓度增加时, 开始出现电子结构, 绝缘能隙逐渐减小; 当载流子浓度继续增加, 出现超导. 这种演化行为与铜氧化物超导体中掺杂Mott绝缘体的演化行为很相似, 这样在铜氧化物高温超导体和铁基高温超导体间建立了联系.
图 27 单层FeSe/STO薄膜母体的ARPES和STM结果以及电子结构相图[109]Figure27. ARPES, STS results Phase diagram for the single layer FeSe/STO film[109].
单层FeSe/STO在STM/STS中观测到了20 meV的超导能隙, 其对应的超导转变温度可能达到80 K[110], 但是在其他的输运以及抗磁信号的测量中, 绝大多数结果都认为Tc为40 K左右[111-115], 明显低于ARPES报道的结果, 即Tc约65 K左右[107,116-118]. FeSe/STO是否存在更高的超导临界温度或者是否存在赝能隙成为大家关注的焦点. 超导单层FeSe/STO薄膜在优化生长条件后, 超导特性的测量让我们有了新的认识[119].
图28给出了超导单层FeSe/STO薄膜的费米面和电子结构[119]. 沿着高对称方向Cut 1的能带结构(图28(b))显示了非常清晰的能带劈裂结构, 这在之前的光电子能谱测量中是很难能分辨出来的[107,116-118], 表明了该薄膜的质量非常高. 除此之外, 图28(c)中的两个能带都显示了非常清楚的能带回弯现象, 并且回弯延伸到了非常高束缚能(费米能级下近100 meV), 在扣除了更高温度的能带结构后, 回弯结构更加清楚了(图28(d)). 这个回弯结构在整个费米面都存在(图28(b)), 表明其是由于超导电子配对引起的波格留波夫准粒子的行为. 通过追踪费米动量处的能量分布曲线, 发现这种回弯行为以及其引起的费米能级处的谱重减弱一直持续到了83 K左右(图28(e)). 这样整个过程可以分为三个阶段: 83 K之上正常态; 64—83 K, 超导涨落; 64 K以下电子配对并相干实现超导. 上述结果表明在单层FeSe/STO可能实现80 K以上超导, 或者单层FeSe/STO薄膜也存在赝能隙. 加上之前介绍的单层FeSe/STO的绝缘性母体显著区别于其他铁基超导体的坏金属母体, 以及可能存在的赝能隙的行为显示了单层FeSe/STO薄膜与铜氧化物超导体存在着更多的相似性, 这为理解单层FeSe/STO中高温超导电性的起源, 以及铁基超导体的超导机理提供了新的思路.
图 28 (a)单层FeSe/STO薄膜的费米面以及(b)二次微分费米面; (c), (d)高对称方向的能带结构和对应的扣除高温能带后的结果; (e) 费米动量处能量分布曲线的尖峰与低谷之间差值的温度演化[119]Figure28. (a), (b) Fermi surface and second derived Fermi surface for the single layer FeSe/STO film; (c), (d) Band structures along two cuts marked in Fig. (a) and band structures divided by their corresponding band structure at high temperature; (e) Temperature evolution of the difference between the peak and dip for the EDCs at kF[119].
2
5.4.FeSe中双空穴费米面的发现及存在额外的对称性破缺
FeSe块材具有铁基超导体中最简单的晶体结构, 只由基本的FeSe层堆积而成, FeSe的电子结构研究对理解其物理性质和超导机理至关重要. 早期的所有ARPES对其向列序下的电子结构测量表明, 在布里渊区中心只存在一个空穴型费米面[120-125]. 扫描隧道显微镜和量子震荡测量结果, 也都是基于在FeSe向列序下布里渊区中心只有一个费米面的假设下去理解的[126-128]. 通过考虑向列序或自旋轨道耦合, 在理论上也是给出FeSe在布里渊区中心只有单个空穴型费米面图像[125,127,129,130]. 而且理论上对FeSe的物理性质和超导机理也是基于在FeSe向列序下只存在一个费米面的图像去理解的.借助于真空紫外激光飞行时间ARPES的高分辨率和同时二维动量空间探测的优势, 在一定的偏振下, 看到了单个费米面, 与之前结果一致[125]. 但是选择合适的偏振光, 在块材FeSe中, 清晰地发现围绕布里渊区中心的双费米面结构, 如图29所示. 这个结果推翻了之前普遍认为的单费米面结构, 表明FeSe块材中, 除了向列相之外还存在着隐藏序, 破坏了时间反演对称性或者空间反演对称性.
图 29 块材单畴FeSe在不同极化光条件下的费米面和能带[131]Figure29. Fermi surface and band structure for single domain bulk FeSe measured under different polarization geometries[131].
不同于铜基超导体的单带结构, 铁基超导体表现为多轨道多能带结构特性. 这对于铁基超导体中磁有序基态的形成、费米面依赖的超导能隙对称性, 以及电子向列相的形成都有重要的影响, 产生了许多不同于铜氧化物超导体的特性. 随着新的铁基超导体的出现和对其电子结构的深入研究, 将为与铜氧化物高温超导体的比对提供越来越多的信息, 从而发现决定高温超导电性的共同特征. 例如本文介绍的单层FeSe/STO薄膜的母体就与铜基的母体很类似, 预示着二者的高临界温度可能来自于共同的起源.
